旧版博士数论坛
标题: 旧版博士论坛帖子合集.htm ( http://old.math.org.cn)
作者:xiaohuhu 时间:2013年2月 博士数学论坛建立九周年
标题:旧版博士论坛帖子合集,按照帖子发布的顺序。如有bug,请及时反馈。www.boss@163.com
目录:旧博士数学论坛帖子题目2004年-2009年.pdf
正文:
17311向斑竹致敬!感谢斑竹的辛勤劳动!
17311引用 (hfg
1964 @ 2005年08月29日
14时15分) |
|
哈哈,最后告诉大家一个好消息,全部解答我打包在此,不收一分钱.够大方的吧!
|
寒
老大不厚道,竟然放最后
哈哈
不过收个5-10个pt是应该的
辛苦辛苦了
17311实在太感谢了,好人呀!
17311有没有相应的教材呀?没有的话,看得有些头晕呀
17311向斑竹致敬!感谢斑竹的辛勤劳动!
太感谢了!!
17311感谢hfg
1964~~解燃眉之急哈!!
17311大
17311太感谢了,好人呀
17311感谢斑竹的辛勤劳动,致敬!!
17311我是先看完回复,然后再决定下载与否,不想这次占了便宜了,不好意思啊,谢谢!!
17311太感谢了哦!
17311很好的楼主,继续努力
17311好东西!谢谢!!!!!!!!!!!!!11
17311再接再厉!
17311感谢hfg
1964~~解燃眉之急哈!!
17311不知道有没有丘维声96年高教出版的<<高等代数>>第一版(是32开的,不是现在的小16开第二版)下册的习题解答.当时大一用的是这套书.比第二版的内容要多不少(尤其是下册).而且那个版本的习题配得很好.做到是有些辛苦.特别是最后几章小字和选学内容的.比如酉空间,群那几章.有答案就可以对一下啦.
17311版主辛苦了!最近看到陕西师范大学出版社的<高等代数辅导及习题精解>(2005年3月版),竟然也是丘维声书的解答,真是感叹现在的学生找资料真的方便.
17311感谢楼主!!
17311谢谢了,
支持
17311谢了!
17311谢谢了,太好了``````````````````````
17311谢谢!我已经有纸版的了!陕师大出的
17311谢谢了
17311斑竹真是个好人,佩服佩服
17311xie le hehe
17311如何付费!!!
17311太感谢!!
17311大家觉得哪个版本的《高等代数》教材比较好??
17311恩人啊!
17311积分不足啊
:(
17311县谢谢了
17311非常感谢楼主!!!!
17311
引用 (hfg
1964 @ 2005年08月29日
14时15分) |
|
哈哈,最后告诉大家一个好消息,全部解答我打包在此,不收一分钱.够大方的吧!
|
助人乃做人之根本!
还是支持你一下!!
17311真得很不错,我找了好久。
辛苦了。
17311辛苦
感谢
17311楼猪要是弄个WORD版本多好啊
17311好人
好贴
17311真是雪中送炭!太感谢了。
17311好人
17311基本上还可以!谢谢老兄!
17311这是雪中送炭,谢谢
17311谢谢
17311谢谢
17311谢谢
17311呵呵,看到后面居然捡便宜啦
17311不错
17311谢谢了,我的积分不够啊
17311非常感谢
17311谢谢
17311我要下载 帮帮 给点积分
17311给点积分吧
17311
引用 (hfg
1964 @ 2005年08月28日
23时25分) |
| 第4章
|
谢谢!
17311我的qq是280428000,希望能和各位同任交朋友.
有资源大家共享.
17311太感谢了.......
17311感谢hfg
1964,谢谢
17311谢谢
17311有这本书吗
17311xiexiei
17311谢谢你
17311给点积分 谢谢 帮助 太感谢了
17311无论如何,还是要感谢楼主的慷慨,让我们受益不浅
17311
引用 (hfg
1964 @ 2005年08月29日
14时15分) |
|
哈哈,最后告诉大家一个好消息,全部解答我打包在此,不收一分钱.够大方的吧!
|
xiexie
我刚好看过一遍了
17311谢谢!!!



17311谢谢
17311谢谢了,楼主
17311thank you!
17311好东西,谢谢楼主!!! 就是太贵
17311怎么这本书没有第一章吗?
谢谢!
17311好像没有题目啊。
17311非常感谢
17311楼主真好!多谢了!
17311太好了
17311感谢斑竹!
17311谢谢
17311不错,谢谢
17311谢谢大虾门提供这么好的资料
17311hao xiexie
17311怎么打开有很多误漆抹黑的东西盖住了?怎么除掉呀?谢了
17311怎么都是感谢就我有问题呀?打开有好多脏东西,怎么除呀?
17311大赞!
17311谢谢拉
17311竟然到最后还有免费的,不早说。。。。。。
17311穷死了
17311好东西 感激啊
17311好人啊
17311我渴望啊 谢谢
17311太好了,非常感谢!
17311多谢楼主
17311向斑竹致敬!感谢斑竹的辛勤劳动!
17311这位老哥真是厚道。
17311谢谢
17311看看,谢谢楼主!
17311谢谢
17311丘维声<<高等代数>>解答,好书呀!!!
17311xiexie!
17311真是好人。
17311谢谢!
17311吼吼!!!!
17311谢谢啦!楼主真好
17311丘维生的高等代数确是一本好书,可是答案太简洁了,几乎没有过程!
17311谁还有给我传一下谢谢
wangxuanyemokey@yahoo.com.cn
17311为什么现在不能下载呢???555555
17311斑竹能不能把李炯生,查建国<<线形代数>>的答案发上来呀,我特别需要呀,谢谢了
17311楼主辛苦了
17311不错,很好,真的感谢了
17311
为什么不免费啊》》》》》
17311哎呀,我怎么一个也不能打开呢》
17311为什么会这样呀》
17313学方程的帮忙看一下,谢谢了post-21-1125273506.ibf
17313这是应求作答的,我找不到原帖子来回复,希望发问的朋友可以看到。
原题是:
设u 是
R
3 (Ω)
中的光滑区域,
u ∈H
1(Ω)
是如下问题的解
u
=|u|
2u,x∈Ω;u=0,x∈∂Ω
试证存在
α
∈(0,1)
使得
u
∈C 2
,α(Ω)
简单说明一下思路吧。由边界条件可知
u
∈H 0
1(Ω)
,因为空间维数等于3,所以这时的Sobolev嵌入临界指数n/(n-2)=3,可知这时从Sobolev空间
H
0 1
(Ω)
到
L
3 (Ω)
空间是连续嵌入但不紧的。所以可知 u属于holder空间[MATH]
C
2
,α
(Ω) 顺便说一句,目前对于一般的非线性椭圆型方程来说,都有
α
∈(0,1)
,很少有
α 不属于(0,1)的情况。
17313我上次贴的附件里 Delta
前面有个负号,可能忘记了。
还有嵌入的临界指数应该是2n/n-2=6,这样能说明u属于Holder空间么?
17313抱歉,犯低级错误了,2n/(n-2)=6,这时嵌入不但是连续的而且是紧的,那就更没有问题了。
173
17设A

Mn(K),rand(A)=r<n.证明:存在n-r个矩阵Bi

Mn(K),i=1,2,...n-r,使得A=B1*B2*

Bn-r.
173
17
| 引用 (qiangzhaang @ 2005年08月29日
09时20分) |
设A
 Mn(K),rand(A)=r<n.证明:存在n-r个矩阵Bi
Mn(K),rand(A)=r<n.证明:存在n-r个矩阵Bi  Mn(K),i=1,2,...n-r,使得A=B1*B2*
Mn(K),i=1,2,...n-r,使得A=B1*B2*  Bn-r. Bn-r.
|
题目有问题啊
要是没有别的限制不是显然了
取若干个单位阵就是了
173
17各位仁兄真是识货!
原来我草草抄来的考题有敝:
可能是如此:
设A

Mn(K),rand(A)=r<n.证明:存在n-r个秩等于n-1的矩阵Bi

Mn(K),i=1,2,...n-r,使得A=B1*B2*Bn-r.
173
17很容易的,分解不唯一,我给出一种:post-38-1125632316.ibf
173
17致谢!
173
18谁知道艾森思坦因判别法的推广?书上没有呀?!
173
18Eisenstein判别法的推广:将Eisenstein判别法中的条件“p|a_{n-1}”换为“f(x)无有理根”的条件。
173
18可以将使用范围推广啊,比如从整数推广到唯一分解整环啊
17320
请问基础数学专业的研究生课程都开那些课,先后次序如何安排的?偶这学期要去华师大学习,想提前有个准备
17320多谢斑竹!
17320
偶要去华师大进修学习,想请教各位师兄弟:基础数学专业的研究生课程都开那些课,先后次序如何安排的.我好有个准备(偶是几何方向)凡事预则立
17320走过的,路过的,只要您是知道的,恳求支持一下的
17321确界原理不是公理吗?怎么华东师大数分第3板却给出了证明?
17321
引用 (whgg_
1999 @ 2005年08月29日
09时53分) |
|
确界原理不是公理吗?怎么华东师大数分第3板却给出了证明? |
这是几个等价的实属连续性命题之一
从任何一个出发都可以推出其他的命题
不同的教材出发点不同
这应该就是你要的答复了
17321同意
17322谁知道zermelo不动点定理在距离空间中应用需要完备性不???
望高手给回答一下
还有Kuratowski轨道概念是怎么描述的?
谢谢
17322当然需要:原因很简单,几乎所有的不动点定理都需要收敛性,而此需要完备性.
Kuratowski orbit:
设f:X\mapsto X是紧距离空间X到自身的连续映射,则所谓Kuratowski轨道是下列集合:对任意x\in
X,
Kur_{x}={y\in X:f^m(y)=f^n(x),for some m,n\geq 0}.
173223X 十分感谢 嘿嘿
17322不过我觉得第一个完备性不一定需要
Schauder不动点定理
就是说实线性赋范空间中的有界闭凸子集D,T:D->D全连续,那么T在D上必有不动点
所以我觉得完备性不是必要的
17322(Zermelo不动点定理)
设 X是一个半序集,且X 中任意一条链都有上确界,T:X->X ,使得算子
T是累进的(progressive),即满足 x<=Tx 对 x in X
则算子T 有不动点。
17322好像没有完备要求啊
17322gg 我觉得你的回答和我要问的一点关系都没有 呵呵 我只想知道完备性是不是必须的
17322哦,我已经删了
17323那位师兄给指点一下 计量预测模型......急急急!!!!!!
17324如下post-38-1125283071.jpg
17324注意知识的综合运用:这个要用到多项式的知识;特征多项式的知识等。
设A的特征多项式为
φ (x)
, 则 φ
(A)=0
, 而 f (A)
可逆,
从而有 (
φ(x),f(x))=1
由裴蜀定理存在多项式h(x),g(x)使得
h
(x)φ(x)+g(x)f(x))=1
将A代入有
h
(A)φ(A)+g(A)f(A))=I
从而 (
f(A))
-
1=g(A)
17324Easy. Let B be the inverse of f(A). Then B=f(A)^{-1}. However, the
inverse X^{-1} of X is a polynomial matrix of X, so B=g[f(A)} for some
polynomial g(x). Thus B=gf(A)=h(A), ok.
17326第一印象
复旦大学新闻中心的老师告诉记者:一大片草坪后面,那幢尖顶的小洋房3楼,汤教授在数学金融研究所的办公室等你们。
这是间红顶的小洋楼,外表并不出众,然而,踏上楼内暗红色的楼梯,我们恍如回到上世纪30年代的大上海。
带着一身清凉之气,汤善健从一间暗红的木门后探出头来,脑袋圆圆的,眼镜圆圆的,略带憨厚地微笑着,全然不见专与数字打交道的那种“精明”。
人物引擎
汤善健,
1966年4月生于山东省五莲县。分别于
1987年和
1990年在山东大学数学系获得学士和硕士学位。
1993年1月,在复旦大学数学研究所获得博士学位。
1993年3月至5月,在复旦大学数学系任助教。
1993年6月被聘为讲师,
1996年5月被聘为副教授,2001年11月被聘为教授。2003年2月被聘为复旦大学运筹学与控制论专业博士生指导老师。
2003年获国家杰出青年科学基金。
现任复旦大学数学金融研究所副所长、复旦大学数学科学学院金融数学与控制科学系主任。
科学新思维
做研究,搞清问题的背景是很重要的。有时,背景清楚了,问题的求解线索甚至答案也就浮现出来了。搞清背景的另一意义在于,指引你去探讨有价值和价值更大的问题。人的生命总是有限的,如何在有限的时间里作出更多的贡献,自然是值得人们去认真思考的。
这种观点,并不是我的发现,放在本栏目里是不妥当的。这只是我的一点体会而已。但我很看重这一点,认为这是科学研究的要义。在具体的数学研究过程中,我在搞清问题背景上花费的时间远比解决问题花的时间多(实际上这两者很难分清)。这样做了,就不会人云亦云、盲目跟潮流,自己的研究就有特色,有创意,经得起时间的考验。
如此“老调”,放在“科学新思维”栏目里重“谈”,虽有“名不副其实”之嫌,却也不妨看作是“自认重要、以期与青年读者共勉”之意。
土博士的留洋史
问:很多杰青都有过国外留学的背景,你似乎很特殊,从你的经历上看,没有这段经历?
答(笑):我是个土博士,拿到博士学位之前,我没有出国。后来出国,也都是访问性质的。
1995年10月在法国Provence大学一个实验室访问了6个月;
1998年9月,访问意大利Trieste的国际理论物理中心;
1999年10月至2001年11月,在德国Alexander
von Humboldt基金会的资助下,作为“洪堡学者”在德国Schwaebish
Hall歌德语言学院学习德语4个月,然后在Konstanz大学访问近两年。
这些,几乎就是我全部的“留学”故事了。
问:听说你自己申请参加过国际数学家大会,并获得了资助?
答:那是
1998年,我自由申请获得国际数学联盟(IMU)和德国组织委员会的资助,参加了8月份在德国柏林召开的国际数学家大会,并作了一个很小的发言(只有15分钟)。
纸上谈兵做研究
问:你为什么能够获得杰青基金?
答:我想大概是因为我在解决两个比较有背景的数学理论问题上有点成绩吧。一个问题是:由布朗运动驱动的一般的随机系数的倒向随机Riccati微分方程的解存在惟一性,这是法国科学院院士J.
M.
Bismut在他的博士论文中遗留下来、在
1978年公开提出的,它是关于线性二次随机最优控制理论的一个很基本的问题,长期悬而未决,直到2003年。
另一个问题是Brockett在
1982年国际数学家大会上的45分钟报告中提出来的、有关非线性滤波理论的有限维估计代数的分类问题。
问:你获得杰青资助的项目是什么?
答:随机系统的控制理论。这个专业,我大学里就选了,硕士研究生也是这个专业,博士研究生实际上还是这个专业。
控制理论,本身是探讨一个动态过程中,如何调整控制变量,使得过程按照人们的合理愿望进行。
控制理论本身是一种方法,它不局限于某个特殊的系统,作为自动控制的基础理论,具有普适性,好比微积分、线性代数,在很多领域都有应用。
现代控制理论的诞生是由于工程上的需要,是在解决航天、自动化等领域中的一些理论问题上发展起来的。钱学森的学术背景,实际上就是工程控制论。l954年钱学森先生在其出版的《工程控制论》中,就深刻揭示了控制论这一新兴学科对航空、航天、工业制造和电子通讯等技术和产业发展的重大影响和重要意义,迅速得到全世界工程技术界的关注。
问:那为什么你现在是在金融数学研究所?两者有关吗?
答:我大学的专业是控制理论,而金融数学中的很多模型,就是控制问题。所以很自然地,我就开始做这个问题。
控制理论的相关领域很多。控制理论介入经济和金融,有力地推动了经济数学和金融数学的发展。
金融问题中,就有很多最优控制的例子。比如,投资者的财富过程,可以看作一个受控过程;投资,实际上,就是一个控制问题。
实际上,是我的老师、同事们推动了金融数学在中国的发展。
问:我刚才偷偷观察了你的办公室,没发现很特别的研究仪器,你们平时怎么做科研?
答:我们的工作,就是翻阅大量的材料,提出好的问题并加以解决。这是个综合归纳的问题。盯住好的方向,提出合适的数学模型,建立相应的解决方法和理论,这是目前我的工作的非常基本和重要的一部分。
“笨鸟”学途起伏记
问:可以说说你的求学故事吗?
答:我家是农村的,我受的教育并不全面。
小时候,我其实没有表现出超人的聪明。我记得,小学三年级之前,我们都不考试。我只觉得,自己打算盘反应很慢,也不明白打算盘的规则,感觉自己悟性很差。
那时候,教育没有指标,都从基本上着手。在我小学阶段的前两年里,在村小学里,我们的班主任是位女的公派老师。她教学非常认真、规矩,经常手把手地教我们写字,这对我后来的影响很大。
记得是在小学三年级前后,我们的老师被换成了另一位公派老师,他为人随和,再加上那个年代对教育也不重视,学生经常被组织去参加生产队的集体劳动,有一年的时间我们的学习几乎停止。
幸亏不久高考恢复了,主管部门又开始重视教育了,公派老师也要参加考试评比,学生也有会考比赛。我们的班主任也被换成了一位有较高文化水平、对学生也认真要求的村办教师。
此后的统一会考,我突然考到了前几名,从那时起开始引起周围人的注意。
问:你就一路这么顺利地过来了?
答:不是的。我的人生,可以说是大起大落。中考那年,我因为成绩好,等着保送,没有好好准备。那时候,我们住校,因为我不需要考试,我就被指派为同学们做后勤服务——给厨房师父打下手。没想到后来又通知我要参加考试,真有点儿措手不及。幸运的是,我还是考上了县重点高中。
后来高考,我的第一志愿是南开大学,但因为数学没发挥好,进了山东大学数学系。那年,总分120分的数学,我只考了99分,而平时,数学是我的强项,我有70%~80%的时间都在学数学。可以说,损失很大。
失意高考快意大学
问:这样看来,你从小就喜欢数学?
答:学数学,开始,只是因为周围的老师经常出一些好的应用题,很有挑战性,我觉得有兴趣,心里又好强,就慢慢去思考、找答案。这样慢慢就喜欢上数学了。
那时候,真要说我对数学有感情,其实谈不上。在别人看来,我能把复杂的题目做出来,很聪明;而我觉得,把基础做好了,有些问题就不难了。
实际上,我是喜欢纯粹数学的。高考考砸的一个很重要原因,就是我高中后期时,觉得自己的数学概念模糊,一些基础薄弱,但那时候,可供参考的资料很少,我只能反复看教材,忽视了看一些参考书、多做题。结果,反而影响了高考复习。
问:这种读书方法,到了大学里有没有改变?
答:到了大学,我的学习思路还没改,还是注重基础,没想到,这反而适合大学的学习要求。
山东大学地域偏僻,而且我是农村出来,不善于交际,整天就是埋头读书。刚进大学的半年里,大家都不怎么关注我。第一学期考完后,我的主干课程的成绩在最前面,班里的同学都很惊讶,因为我的入学成绩是很低的。
不强求儿子学数学
问:听说你有个儿子,能说说他吗?
答:我的儿子很小,今年才4周岁。很遗憾,我花在儿子身上的精力、时间很少。孩子的很多教育,都是他外公外婆做的。
对于孩子,我对他没有特别的要求,以后怎么样,要让他自己发展,我会提一些建设性的意见。我很注重的一点,是在他成长的基础阶段,要全面发展,打好基础素质,培养兴趣和能力。我们大人不应过分干预孩子的成长,过早地灌输专业知识,这实际上是拔苗助长、扼杀孩童的天性,不是科学的做法。
问:想让儿子学数学吗?
答:他如果喜欢数学,我会鼓励他,但我不会强迫他走我走过的路。
17326牛人啊!顶!
17326文中说山大位置偏僻,怎么会?
17328高等代数题目求解答post-38-1125291457.gif
17328这个只需用其若当阵形式考虑即可
17328如果这个题目是在Jordan标准型前面出现的话可以就题目给的概念来做:
⇐
这个应该是不言而喻的。
⇒
如果f的幂零指数为n,那么存在向量v使得
f n
-1
v≠0
然后证明:
{
v,f(v),f
2
(v),⋅
⋅ ⋅f n
-1(v)}
线性无关并且这就是所要的基。
17329等待中post-38-1125291661.gif
17329见附件:post-38-1125293758.ibf
17330
| 引用 (FARSEER @ 2005年08月30日
10时25分) |
| 谢谢两位,明白了,但是第一道题是求N阶导数,不是N次方,所以作案可能不对,还请继续指教。谢谢。
|
我那里求的就是n阶导数
只是编辑公式的时候出了问题
一阶导数就是函数本身乘以一个常数
这么n阶导数就是我所说的样子的
17330第三个:
由于这个函数在x=0处不连续。
17330有三道题,请教大家:
如下,非常感谢你们的回复。
post-8-112529
1727.gif
17330第一个不算什么问题吧!
f'=lna a x
那么 f (
n) = (
lna) n
a x
所以
f (
n)
(0) = (
lna) n
第二个:
∫ xf(x)dx=
∫ xdtan
2 x = xtan 2
x-∫tan
2 xdx
=
xtan 2
x-∫sin
2
xcos
2
xdx =
xtan 2
x-∫(1
cos 2
x-1)dx
= xtan 2
x+x-tanx
第三个:
由于这个函数在x=0处不可导。
17330谢谢两位,明白了,但是第一道题是求N阶导数,不是N次方,所以作案可能不对,还请继续指教。谢谢。
17332设f(x,y)=(x ^{3} + y^{3} )/(x ^{2}
+y),
证明:当(x,y)--〉(0,0)时,f(x,y)极限不存在
17332令x=r*cos(t),y=r*sin(t),分别求t=0和t=pi的极限即可知道结论
17332当(x,y)于y=-x ^{2}趋向于(0,0)的时候极限部存在!
17332不能吧,都是零呀
应该确定别的点集
17332
引用 (janssen @ 2005年08月29日
17时11分) |
| 当(x,y)于y=-x
^{2}趋向于(0,0)的时候极限部存在! |
不能呀,那不在定义域范围内
我试过分别讨论,x是y的低阶,同阶和高阶无穷小的情形,都不能证明极限不存在
可能要选比较特殊的点集,研究沿他们的极限情况
17332就是,就是
17332这个你取 y
=x 4
-x
2 就OK了
17332谢谢
看来我以前的讨论是有问题的
17333有点意思
17333应该学会欣赏数学
去寻找她的美
虽然现在功力还差得远
但不会放弃
那是我的梦
17333看你学数学的目的是什么,如果你确实对数学感兴趣,你就做数学研究吧;如果你对数学不感兴趣,只是误打误撞学数学,我建议你学到本科已足够了,转行做应用吧,例如经济,生物等。
17333半年前无意间注册家园
直到今日才完完整整观赏了一圈
看兄弟姐妹如此之努力
心中好喜
曾出于个人爱好报研两次
成绩极不理想
现在终于想通了
学数学比考数学更迷人
超越不了自己的极限
那就经常在此把心收敛
数学是中华民族擅长的学问
一点没错
我们都需要刻苦付出
做个真正自我
永远爱着数学
17333你的诗还可以
17333赞!
17333
引用 (xq103 @ 2005年08月29日
17时39分) |
| 你的诗还可以
|
再押点韵就好了。
17333数学是独立于考试而存在的。
考数学是为得到别人的承认,学数学是承认自己
17333寻找真我,就是快乐啊
17333痛,并快乐着
17333为是数学人高兴
17333那确实
17333有同感啊
17333学问是相通的,他的诗多么棒
17333我顶
17333我也爱数学,并且要考数学!!
17333学数学很好玩!
17333偶也觉得学数学很入迷。但是考数学也有它的意义。偶本身就不是数学类的学生,而且以后可能也不会考数学系的研究生。但偶会坚持的学数学,数学是多么引人入胜的东西啊!
17333是这样
17333同上
17333想起一个大牛,赫米特(Hermite)。这位大牛年轻的时候数学很强,就是不会考试,每次考试,就连最容易的文科试题,都是痛苦万分地勉强通过。与大家共勉。
17333我太欣赏那句:学数学比考数学更迷人
我也要好好加油了
不要再为考试而苦战!
对把
17333看不懂
不过题目说得有点道理
17333我本科读的是一个工科,之所以要考数学,是因为考上数学的研究生可以有更多的机会学更多的东西,认识更多的良师益友.考数学是为了有一个更好的环境学数学.如果没有考上,我还没想过怎么做.找个工作应该不难吧.那个时候我想还会继续学数学
17333话虽这么说,但还是要不断的考数学啊
17333我也觉得这样
17333数学好玩,学数学比考数学更好玩
17333晕死对数学的爱不是说出来的
如果真的爱数学的话就应该能感觉到她在指引自己在她的国度里遨游
还有不得不指出一点的中国人学数学好似东施效颦
只知其美(作题)不知其所以美(题目中到底蕴涵着什么)
只会做模式识别似的工作
这个计算机会处理的很好的
而且所谓的那些教授和博导对数学的理解是很那个的
17333呵呵,诗和思想都不错!
17334我做了个程序,可是我的lingo运不出来,是软件的局限,哪位大虾可以帮忙啊。谢谢!!!!!!!
model:
sets:
dui/1..7/:o,a;
cuo/1..7/:b,d;
link(dui,cuo):t,c,c0;
endsets
data:
t=0
128
1937.5 71
1797.5 326833.5 213057 504516.5 370
198
128
1937.5 0
606
196.5 16
1811 253322 302781.5 99207
71
1797.5 606
196.5 0
170277.5
172659 337256 160537.5
326833.5 16
1811
170277.5 0 40753.5 133412.5
91367.5
213057 253322
172659 40753.5 0 72158 30008.5
504516.5
302781.5 337256 133412.5 72158 0 247382.5
370
198 99207 160537.5
91367.5 30008.5 247382.5 0;
c0=0 110 165 100 120 150 220
110 0 115
110 70 135 160
165 115 0 135 100 115 135
100 110 135 0 70 80
105
120 70 100 70 0 100 120
150 135 115 80 100 0 60
220 160
135 105 120 60 0;
d=3408340 2705255.5 2158724 924455.5 78
1958 1597507
998701;
o=3408340 2705255.5 2158724 924455.5 78
1958 1597507
998701;
enddata
min=@sum(link(i,j):((t(i,j)-o(i)*a(i)*b(j)*@exp(-(beta)*c(i,j)))/t(i,j))^2);
@for(dui(i):a(i)=(@sum(cuo(j):b(j)*@exp(-(beta)*c(i,j))))^(-1));
@for(cuo(j):b(j)=d(j)*(@sum(dui(i):a(i)*o(i)*@exp(-(beta)*c(i,j))))^(-1));
@for(link(i,j):c0=@sum(link(i,j):c(i,j)*o(i)*a(i)*b(j)*@exp(-(beta)*c(i,j))));
beta>0.0075;
@for(link(i,j):c(i,j)>=0);
end
同时如果想让beta的步长设定为0.0001,怎么办啊?也就是让beta以0.0001递增,有没有什么好方法啊?谢谢ing!!!!!!!!!!!
17334我的Lingo算得结果是没有可行解!
17335讨论微分方程稳定性里面有鞍点的概念,好像最优化条件里面也有鞍点的概念,两者有联系吗?谢谢
17336
引用 (Buffalo_Hua @ 2005年08月29日
17时35分) |
| 试一下这个连接,或许可以的
|
点了几个,都是空链接啊
17336大家好:
我最近在网上找到了一个免费的数学书籍下载网页,请尝试一下看能用么?
(不记得是否有人发过了,但我还是愿意拿出与大家共享.
ftp://202.103.207.135/mathbook/谢谢
Buffalo_Hua
17336不行啊
遗憾
17336请尝试一下先输入ftp://202.103.207.135/看看可以么?
另,我也把原件附上,可以打开了吗?post-33-1125307906.ibf
17336试一下这个连接,或许可以的post-33-1125308115.ibf
17336我看了一下,
用这个绝对可以:
ftp://math:math@202.103.207.135/mathbook/
17336好东东啊!顶一下
17336好
谢谢!
17336可以进的,内容还可以
17336还好的的
17336好!顶一下!!!
17336为何打不开?
17337谢谢呼呼斑竹
不过怎么没人肯帮我啊?是不是问题太幼稚啦?呜~~
17337首先要指出,你这里的
f
(a) 并不能认为是
g
(a)
的原函数,因为你的积分变量为
x
,而不是
a .
这几天有些忙,请谅解
17337哎呀呀,不好意思啦,一时疏忽,已经改正了。
17337
g
(a)=x
a
在定义域中连续
f
(a)=∫x
a dx 在
a
=-1 处不连续。
能解释吗?
初学数学分析不多久,对其本质了解甚浅,望高手们不要嫌弃我那些也许幼稚的问题呵。
17337晕啊!!!!公式改了N回还不成。
版主提示:注意将LATEX命令中的“杠”字代换为“\”
17337问题不是已经解答了吗!!
17339请问那位大哥有gPROMS软件可以分享?
gPROMS&#
174;, for general PROcess Modelling
System, is the most advanced general purpose process modelling, simulation
and optimisation software available to the process industries today.
gPROMS is used for model-based decision support in process and product
design and process operations.
17340高等代数求解!请写详细一点!谢谢了!post-38-1125305601.ibf
17340由已知得A=1/2*E+B,其中B'=-B,不难知道B的特征值是0或虚数,则A必可逆
17340这个题目有人问过了啊
而且就在最近几天
:)
17341小弟非数学专业,现在遇到一个难题,是一个三元偏微分方程组,详见附件,请各位高手不吝赐教,谢谢啦!
静候佳音!
E-mail: fwater@126.com
QQ:370895
170post-27-1125306590.ibf
17341怎么没人会贴阿,5555555555555555。
17343为什么要利用统计量?
如何理解统计量的信息提取功能??
17343样本是一堆原始的没经过处理的数据,不易直接用于统计推断
,统计量精简了数据,(如果是充分统计量,这样的精简是不损失信息的),因此可以方便推断
17345题目没有问题!
1. 不妨设
x 1
≤x 2
那么
x 2
=
f
(x 1
)≤f(x
2 ) =
x 3
以此类推即得到
x n
单调递增。
2. 不妨设
x
1
≤x 3
那么
x
2
≥x 4
从而有
x
3
≤x 5
如此下去就得到结论了。
17345设I是某个取间,数列X(n)由X(n+1)=f(X(n))产生,如果对任意X(n)属于I,求证:
1,当f在区间I上严格单调增加时,{X(n)}为严格单调数列
2,当f在区间I上严格单调减少时,
{X(2n)}和{X(2n+1)}为严格单调数列,且具有相反的单调性
17345没有问题
可以证明
这里只证明第二个问题
f(x)严格单调递减,很容易得到那么f(f(x))是严格单调递增的
x(n+1)=f(xn)=f(f(x(n-1)))
这样就可以得到命题的结论了,第一题的结论包含在第二题当中
17345
引用 (zhubin846152 @ 2005年08月29日
18时47分) |
没有问题
可以证明
这里只证明第二个问题
f(x)严格单调递减,很容易得到那么f(f(x))是严格单调递增的
x(n+1)=f(xn)=f(f(x(n-1)))
这样就可以得到命题的结论了,第一题的结论包含在第二题当中
|
呵呵,这么就更直接起到一举两得的效果了。
good
17345但是如果取f(x)=x,严格单调增加,得到的数列显然不严格单调啊
17345
| 引用 (zys @ 2005年08月30日
00时28分) |
|
但是如果取f(x)=x,严格单调增加,得到的数列显然不严格单调啊 |
哈哈
原来你说这里啊
那没有必要发上来问了
这个是取决于初试几项的
17345但是我说的那个不能算是一个反例吗,它完全满足题目的条件啊,但是没有最后的结论,
17345我的意思是
题目是不严格
但是这个问题是算显然的啊
而且我个人认为就是减弱结论还是一个不错的题目
17345f(x)=x不能作为反例,因为题目要求严格单调
17345难道它不严格增加吗
17345不好意思,没看前面
题目逻辑上没问题
17346题目如下:post-38-1125311613.gif
17346不是太难,只是麻烦一点而已
17346作代换x=aX,y=bY,z=cZ
则积分区域变成:X^2+Y^2+Z^2<=R^2
被积分式变成pa^2m*X^2m+……
只算第一个的积分:
由X,Y,Z的对称性
知第一个的积分=1/3*
pa^2m*(X^2+Y^2+Z^2)的积分,后者用球坐标好算。
17346看来似乎都被迷惑了
其实就是把其中的y=0,z=0的情况求出来就有方法了啊!没有必要当作整体来积分,那样就十分郁闷了,被积分的函数没有什么大的规律!
17347没有错的
自己没有证明出来
17347第二个用代数基本定理(我要得是多项式分解)
然后应用1的结论进行归纳
也就是每个因子都是两个的平方和
对乘积的个数归纳即可啊
17347可以证明:这样的f(x)一定是最高次幂为偶数的多项式
17347不明白,麻烦详细些
17347我们知道任何一个实多项式可以分成一次和二次不可约多项式的乘积(不妨设最高项系数为1)
如果f(x)含有一次x-a这样的因子,那么它的重数一定是偶数
否则在a附近有小于的零的部分!
那么这些一次的就可以表示成
g
(x) 2
而对于那些二次的因式应该是
x 2
+2ax+b
而且
a 2
-b<0
这样
x 2
+2ax+b
=
(
x+a)
2+(b
-a
2)
2 然后对他们应用第一问的结论进行归纳!
17347好哇
第二题对吗,好象应该是最高次幂为偶数的多项式
17347多项式试题求解post-38-1125313737.gif
17347第一个展开配方就好了:
( a
2
+b
2
)(c
2
+d
2 ) =
a 2
c 2
+b
2 c
2
+b
2 d
2
+a
2 d
2 =
a 2
c 2
+2abcd+b
2 d
2
+b
2 c
2
-2abcd+a
2 d
2 =
(
ac+bd)
2
+(bc-ad)
2
17347高,tobyqin解决了这个问题
对最简因式的个数归纳,好哇
17348题目表述应该更清楚一些吧
∂
(p(x))≥0
中的x是怎么取值的啊?!
17348题目就是这样的
感觉限制没有?
17348这个应该是限制在F上的,限制在复数域是不成立的
不过又感觉怪怪的
17348一道线形空间的试题post-38-1125314033.gif
17348没有问题吧
限制在F上是自然的也是应该的
F是数域,则F(X)是局部函数域。
17348也不是说有问题,就是我现在证明充分性的时候根本就用不到那个条件
而反过来我还不知道怎么去构造那么一个多项式
呵呵
17348我也搞错了,还想当然的认为F[X]为有理函数全体了
17349某一特定数字在一次中出现的概率为1/49,不出现的概率为48/49;
这个数字在N次中均不出现的概率为(48/49)^N
这个数字在N次中至少出现一次的概率便为1-(48/49)^N
17349有那位高手擅长计算概率:
1,2,3..........48,49.
49个数字,出现N次,求N次时每个数字出现的概率?
恳求给解。送你一张
手机冲值卡 表示感谢!
17349楼主题目没说清楚,再解释下
17350X

N(a1,b1);Y

N(a2,b2)
X与Y与相互独立
X平方属于什么分布,概率密度是多少?
Y平方属于什么分布,
X平方+Y平方属于什么分布,概率密度是多少?
17350找本初等的概率书 自己学着按定义算算就是了
17351若序列<
x
n
>存在极限则有
lim
/x n
-x
n
-1/=0(n→∞)
但其反命题为假
请大家举举例子呵^_^
17351先举一个:
x
n =∑
1 n
k -
1
17351这类序列有其他共同特征吗?有判别方法吗?………………(有研究价值吗?~)
17352设F(x,y)=
∫ 0
+ ∞
(sint
y
)/t
x 关于t在(0
,
+
∞ )上的积分。
试求:F(x,y)的定义域?
17352没有人会吗
17352楼主能不能用图片贴出来?
上面写的看不懂啊
17352用mathplayer 就可以看清楚了
17352我用贴图弄一下好了,应该会更清楚一些:post-38-1126791691.gif
17352还是做一下了,看看我的解答,
我不知道是不是漏了什么,有点困了
如下:post-38-1126795024.gif
17353
20世纪我国自然科学基础研究的艰辛历程
郝柏林
中国传统文化中没有现代意义的自然科学基础研究。起步甚晚的的研究工作又受到急功近利、科技混谈政策的影响,多年在似曾相识的压力下挣扎。时至今日,我国自然科学基础研究在某些方面还没有摆脱半殖民地的心理状态,严重影响着我国工业早日立足于自己坚实的创新成果。作为曾以一般科学生涯从事应用研究、并且始终坚持在第一线的自然科学基础研究工作者,笔者以亲身所历,列举事实分析共和国成立半个多世纪以来基础研究政策的得失,以及目前仍然存在的弊病,为今后的科学史研究存照。将特别着重回顾近二十年来,第一线科学工作者和科技政策制定者、执行者之间的认识差距,以及这些差距的历史文化根源。
中国几百年的闭关自锁早被帝国主义打碎。沉重的内忧外患由多少代仁人志士抛头颅、洒热血排解。中华民族终于要在政治单极化阴影笼罩下的经济全球化环境中崛起。经历15年谈判加入基本上已由先人者制定了游戏规则的世界贸易组织,带着背水而战、志在必得的豪情,我国民族工业多么需要建立在自主知识产权基础上的支柱产业!我国自然科学多么需要对人类历史发展作出真正的创新贡献!然而,为何多年来我国自然科学基础研究在种种“重视”、“稳定”的提法下举步维艰,许多深层次的问题令人担忧?
首先,本文论及的自然科学基础研究,是指那些以认识世界、发现自然规律和解释自然现象为首要任务的科学研究。这包括了数学、物理学、天文学、基础化学、基础生物学、基础地球和空间科学等。这是包含实验在内的“理论科学”。
1883年,恩格斯在马克思墓前演说中,有如下一段话:“在马克思看来,科学是一种在历史上起推动作用的、革命的力量。任何一门理论科学中的每一个新发现,即使它的实际应用甚至还无法预见,都使马克思感到衷心喜悦,但是当有了立即会对工业、对一般历史发展产生革命影响的发现的时候他的喜悦就完全不同了。例如,他曾经密切地注意电学方面各种发现的发展情况。”①
可见马克思对理论科学的态度是两个喜悦。我们有一些科学事业的负责人士对理论科学的态度却是“一个喜悦”,或“一个喜悦,一个不喜悦”。就此一点而言,他们不是马克思主义者。抛开“顺风保官”等不必涉及的因素,这里有文化和历史的根源。中国传统文化中没有现代意义的自然科学基础研究。指出这一根源,是希望科学技术政策的制定者和执行者们对人民负责、对未来负责,比一般政府工作人员更自觉地跳出文化历史的局限。
古代忽视自然现象研究和现代的科技混谈
中国有长期不重视对自然现象的研究,以及把科学与技术混为一谈、以技术涵盖科学、以技术代替科学的历史传统。两千多年前,太史公抱怨“文史星历,近乎卜祝之王间,固主上所戏弄,倡优所畜,流俗之所轻也”(《报任安书》)。其实,司马迁所说文史星历,几乎概括了当时全部自然科学和社会科学。国人一向引以为荣的四大发明,指南针、火药、造纸和活字印刷,都是技术。世界各民族的早期发明均属技术。但我们后来也没有提出可能由四大发明引发的科学问题。地磁、磁场,乃至燃烧的解释,都与中国无缘。对磁石吸铁的解释,限于“磁者慈也”的泛论。磁偏角的发现,其实是记录事实。沈括有科学态度提出过问题:“磁石之指南,犹柏之指西,莫可原其理”(《梦溪笔谈》)。
说起记录,中国确实与众不同。自鲁文公14年(公元前613年)到
1910年,34次哈雷彗星回归,中国有31次记录夹杂在360多次彗星记录中。然而,中国人从未提出彗星运行轨道问题,更没有发现这原来是同一颗彗星。
与此相应,中国也没有自然哲学的历史。孔孟学说基本上是统治者处理相互关系和如何对付人民的准则,即现在所谓“人际关系学”。他们,特别是他们的追随鼓吹者,从来不研究大自然,以及人同自然的关系。墨子想过一点自然规律的问题(杠杆原理、凸镜和凹镜的成像等等),他更关心的仍是手工技术,也想为统治者出些主意。老子“天地不仁,以万物为鱼狗”的思想,并未在后世导致物竞天择的进化理论。虽然他也为统治者出过“无为而治”的馒主意③,可也讲过“圣人不仁,以百姓为鱼狗”的怪话,结果还是骑青牛西去,不知所终。庄子虽更富哲学韵味,但科学性更少,他留下一个疯疯癫癫的形象和一些更重思辨而缺乏具体分析的故事。
中国使用图像化的文字而没有采用基于有限个字母的符号系统。它不利于简捷、定量地表达客观规律,可能是限制了自然科学发展的一种技术性的原因。古代中国数学体系以解决具体问题为中心,而不强调证明。一千多年的科举考试中,没有涉及自然科学的内容,教育界的高层领导根本不懂科学③,“是故废而不理”。这更是比今日“高考”强大得多的指挥棒,长期决定性地影响了整个教育体系及其内容。“文章千古事,得失寸心知”,多少代优秀知识分子把毕生精力消耗在遣词造句的文字游戏中,使我们这个民族浪费了多少大脑资源!
19世纪末20世纪初,到国外深造的知识分子在列强欺辱的背景下,必然以掌握技术、振兴实业、富国强兵为主流。部分研习自然科学者,归国后对于我国第一批现代大学和研究机构的建立,起了不可磨灭的作用。
李约瑟的巨著,英文原名(Science and Civilization in
China)直译是《中国的科学与文明》。中文书名却成了《中国科学技术史》。去掉了“文明”,加上了“技术”,恰好反映出科学与技术混为一谈、以技术涵盖科学的传统。
19世纪“中学为体,西学为用”的主张,前些年知识分子政策中的“用其一技之长”,强调的也都是技术。邹承鲁曾在美国《科学》周刊撰文④,说中国有一个词叫“科技”(SciTech),主要甚至全部指技术,很少指科学,其意想亦在此。
总之,现代自然科学研究在我国起步甚晚。
1915年一批年轻学者倡议成立中国科学社和发行《科学》杂志,是在这片土地上自主从事现代自然科学研究的开端。
1920年代,中华医学会的一些学术刊物问世。
1928和
1929年,先后成立了国家级的中央研究院和北平研究院。
1935年,国民党政府决定建立博士学位制度,但从未实行。
中国起步甚晚的自然科学研究工作,又受到急功近利、科技混谈的思想和政策影响,多次在似曾相识的压力下挣扎。其实,不同时期政策要求的相似性,跨越了意识形态和政权更迭的差异反映了历史文化传统的沉重束缚。
1943年,中央和北平两研究院的副院长李书华应商务印书馆王云五之邀,组织编写了《科学概论》一书。其中钱临照撰写的《物理学篇》结尾处云:“物理学之研究,初非以谋实用为唯一鹄的也。然其研究之结果,在今日应用之广,实无其匹,富国利民之例,岂胜枚举。若日务汲汲于事功之较量,何者宜加以奖励,何者宜加以限制,则实为舍本求末,吾人期期以为不可也。”⑤这段文字,翻译成白话,难道不会在今天引起共鸣?
基础研究中实践与理论关系的扭曲
1953年朝鲜停战之后,中国第一次有可能在较为稳定的环境中全力从事经济建设。当时工业部门的研究力量几乎等于零,中国科学院的许多研究所都为工业部门解决过大量实际问题。以物理研究所(
1950年代初曾经称为应用物理研究所)为例,它承担过的任务包括:为黑龙江阿城仪表厂解决铝镍钴永磁合金浇铸余料的再利用问题,为鞍山钢铁公司解决延长耐火材料寿命问题,为建筑部门研究加速水泥凝固的方法,为飞机制造工业研究铝合金相图,为电机工业研制单取向和双取向硅钢片,等等。
这些工作多数没有总结成学术论文,留下来的完整记录很少。前辈理论物理学家彭桓武为冶金部提出的连续轧钢中的钢绽冷却速度研究,专门解决了一个热传导问题,成文三十多年以后才发表在庆祝周培源先生80寿辰的文集中,可算是一个特例。总之,当时科学工作者们投身思想改造和经济建设,并没有十分强调自然科学基础研究的意义。
1956年制定的12年科学技术发展规划,也没有把基础研究置于特别地位。这是符合当时的国情、国力的。
1956年1月14日,周恩来在中共中央召开的关于知识分子问题会议上的报告中说:“在过去几年中间,我国的各种工作都在开始,我们在目前需要和技术工作方面多投一些力量,而对于长远需要和理论工作方面注意得比较少,这是难免的,也是可以理解的。但是到了现在,如果我们还不及时地加强对于长远需要和理论工作的注意,那么,我们就要犯很大的错误。没有一定的理论科学的研究作基础,技术上就不可能有根本性质的进步和革新。但是理论力量的生长,总是要比技术力量的生长慢一些,而理论工作的效果一般也是间接的,不容易一下子就看出来。正因为这样,有许多同志现在还有一种近视的倾向,他们不肯在科学研究方面拿出必要的力量,并且经常要求科学家给他们解决比较简单的技术应用和生产操作方面的问题。当然,理论决不可以脱离实际,任何脱离实际的“理论研究”都是我们所必须反对的,但是目前的主要倾向,却是对于理论研究的忽视。”⑥周恩来曾是何等清醒啊!
然而,此后46年间,近视的倾向、简单的要求,何曾稍减。从积极的方面回顾,三年大跃进(
1958-
1960年)中发生的许多事情,在外国人和后人看来,近乎荒唐,却也反映着我们对于工业化、现代化的强烈愿望。毕竟中国科学院的规模是在那些年代奠定的,电子学、半导体、自动化、计算机的发展是从那时开始的。
1960年代初,苏联撕毁协议、撤退专家。中国人民发“愤”图强,自力更生。三年困难时期(
1966-
1962年),国防科研战线的无名英雄们饿着肚子坚持工作,创造出使中华民族扬眉吐气的丰功伟绩。那不是我国科学事业的黄金时代,却永远作为一个英雄时代记入史册。中国科学院的许多研究所,直接、间接地参与国防研究,为国防科研机构的建立输送人才和技术。张劲夫的长文“请历史记住他们——关于中国科学院与‘两弹一星'的回忆”,是那一时期的生动写照。
到
1960年代中期,经历了支持经济建设和国防建设的我国自然科学,确实到了应当作加大纵深的战略调整的时刻。然而,十年“文化革命”(
1966-
1976年)不仅耽误了时机,还对本来就很薄弱的自然科学基础研究进行了全面冲击。看一看这后面的“社会舆论”,是颇富教益的。我国理论物理研究在“文革”期间的经历,正好用以典型地说明传统的理论实践观的作用。
理论物理研究可以粗略地划分为四个领域:粒子和场、原子核理论、凝聚态和统计物理、天体和引力。
粒子物理研究由于毛泽东主席
1964年同坂田昌一谈话中所表现的重视,以及与“一分为二”哲学命题的关系,得以保存队伍,并以
1970年代初杨振宁、李政道相继访华和
1973年高能物理代表团访美为契机,有所复苏。
核物理因为有国防背景和“核参数”任务的要求,基本维持原状,还得以在“工农兵大学生”中要求一定的培养数目。
凝聚态和统计物理是四个领域中最接近实际的,却从哈尔滨到广州,全部解散改行。正是因为接近实际,自认为有发言权的批评家也多。中国科学院军代表向越南科委主任介绍中科院物理所情况时说,“从前有一个理论研究室,理论脱离实际的典型,解散了!”
与此成鲜明对照,最为“好高骛远”、“不食人间烟火”的天体和引力理论,在此期间有所壮大。原因却也是“理论联系实际”。我国一些优秀的数学家转入这一领域,在“军宣队”眼里,这是联系物理实际,他们仍然可以作一点现代微分几何,同时训练了一些年轻人。
工厂技术员到车间当工人,实验物理工作者下厂作技术员,理论物理人员去作实验,数学家来搞理论物理。这发生在“弯曲时空”中的“平移”,使许多人联系了“实际”。
1985年3月全国科技工作会议上,当时的一位领导的报告中说:“……改革科技体制,就是要动员千军万马上山摘桃子。千军万马,是指整个科技界,知识界”。“摘什么桃子?大桃子小桃子都要。”⑧就拿桃子作比喻,从选种育苗、灌溉施肥讲起,恰好说明科学的作用。不过在那位演讲人看来,科学技术成果已是漫山遍野的桃子,科学技术界却视而不见或不愿采摘,要加以动员。
这里涉及到对中国科学工作者的基本估计。
1976年初,中国科学院“革委会”某负责人向上级汇报时,就说过“最难办的是那一批红帽子”,指的是那些时而被誉为“又红又专”、时而被批成“修正主义苗子”的中青年业务骨干。
1985年科技界某领
17354求救啊!!!
17354建议你读读数理统计方面的教材
我在这里可以给你一个表达式
post-28-1125407370.ibf
17355
[原创]写给自己,也写给所有可以为未来割舍,放弃,和选择的人
一直以为,自己不会在有关学习的版块,写下篇幅大于100字的东西.但是现在,在我面对电脑屏幕的时候,在我心里浅浅地充盈着兴奋的未知的时候,如此地想写.
大3下了,大家开始莫名地躁动.空气也变得微热和不安分.以前老感觉有大把大把的时间和青春可以肆意挥霍,现在,吝啬了犹豫了.我们这个年纪的人,可能已经没有多少资格去寻找刺激和新鲜.考研,托业,公务员,考证就业...种种选择摆在面前.不是不痛苦的.
我是一个任性的孩子,很小的时候,和小伙伴们玩捉迷藏.当我被别人抓住的时候,我总是蒙住自己的眼睛,说你看不见我你看不见我.我是一个如此害怕面对和承受的人.喜欢把头埋进沙里的鸵鸟.可是我没有办法,在现在这个时候.除了抬起头来正视和面对,我没有选择.
一直是一个讨厌复杂和动荡的环境的人.15岁的时候曾天真地想,如果我可以天天窝在家里,有东西吃有小说看,我可以安然地一直呆下去,与世无争,到老到死.但是,我不可以.
喜欢原谅自己,大一的时候,红灯一片,我告诉自己是我不适应.大2的时候,不过不失,我告诉自己只是奋斗的时候还没有到.现在,一片兵荒马乱,我只能对自己说:
是时候了.
不想工作,因为还不到时候.我是一个从小被宠坏的孩子,身边好多爱我关心我的人,在享受的同时我忘记了控制和谦逊.不敢想象自己现在进入社会穿上中规中矩的职业套裙是什么样子.还有我的专业,和冰冷的统计表格打交道,我们的盈利就建立在别人的病痛和死亡上.我害怕看见残缺.
于是,考研吧,风风火火,哄哄烈烈.劈头盖脸地看我痛苦至极的数学.然后,意料中的,厌了烦了,看见那本绿皮书就忍不住想吐.郁闷不已.仿佛是自然中的改专业.痛苦的抉择后,我选了一个别人看来疯狂至极的专业.跨校考现当代文学.
大学里面,我学的是计算数学
别人问我,怎么选的专业跨度那么大,就业也不比现在容易.我说:因为我的心灵太自由.
我还没有说的是,我马上23岁了.我想在23岁前,真正做一件自己喜欢的事情.
没别的了,因为我喜欢.所以我考研.
17355
我也是计算数学!有同样的感受!我们都加油吧!
17355放着那么好的数学不学
真是无言了
17355唉,不喜欢数学,却又学的是数学系,唉,还要千山万水去考文学,不能不说是中国大学生的悲哀,中国教育界的悲哀,是我们这一代人的悲哀啊!!
但是数学果真有那么痛苦吗??我是很不理解的
17355安稀饭这么有个性的妹妹!不管你还爱不爱数学!
加油!
没钱了的时候到这里告诉你的帐号,我们给你汇!:)
17355牛呀!!! 干自己相干的事情!!
17355相信自己
17355thank you!
17355
| 引用 (Dionisus @ 2005年09月10日
14时30分) |
安稀饭这么有个性的妹妹!不管你还爱不爱数学!
加油!
没钱了的时候到这里告诉你的帐号,我们给你汇!:)
|
大款
17355也许我也该好好想一想了
17355有时候是该回复赚点钱下东西了.
17355为什么老的回复再下载啊?
我想下载无限制啊!
17355想下啊1
17355没有什么大不了的
17355女孩子就是奇怪
17355只要自己不后悔!!
17355不要应世俗潮流改变自己的信念
17355
| 引用 (mathpanda @ 2005年09月20日
22时29分) |
| 也许我也该好好想一想了
|
祝福你们
17355走自己的路,让别人说去!
17355
| 引用 (footprint @ 2005年09月01日
01时12分) |
放着那么好的数学不学
真是无言了
|
就是阿,看来你学数学的那几年时间是白白的浪费了哦
17355楼上的那些说放着好好的数学不学的人,请你们自己在自己的角度上考虑下,让你学你根本不爱学的学科,你是什么心情。让你去学机械,学生物,学化学,而你最钟情于数学,你会有什么心情学!!
楼主!我非常理解你的心情,而且我认为你做了个非常正确的决定。目前我能帮你做到的只是在这里祝你成功。
还有希望你能对自己也公平些!多给自己些时间!用三年的时间完成自己的心愿!还有即使不学数学了也可以常回这个论坛看看!:)
要做到象你的个性签名那样!!!
17355
| 引用 (Dionisus @ 2005年09月10日
14时30分) |
安稀饭这么有个性的妹妹!不管你还爱不爱数学!
加油!
没钱了的时候到这里告诉你的帐号,我们给你汇!:)
|
!!!!!!!!!!!!!!
17355“学你根本不爱学的学科,你是什么心情。让你去学机械,学生物,学化学,而你最钟情于数学,你会有什么心情学!!”说到我的痛处了。我和师姐相反,是在学别的学科而想转学数学的。觉得现实太残酷,我担心学数学的时间不够用。然而我认为我和师姐都是幸运的人,毕竟我们知道自己真正想做的是什么。还有我建议师姐尝试写科幻小说,因为国内没有这方面太欠缺了。
17355
| 引用 (陈凌云 @ 2006年04月22日
16时10分) |
|
“学你根本不爱学的学科,你是什么心情。让你去学机械,学生物,学化学,而你最钟情于数学,你会有什么心情学!!”说到我的痛处了。我和师姐相反,是在学别的学科而想转学数学的。觉得现实太残酷,我担心学数学的时间不够用。然而我认为我和师姐都是幸运的人,毕竟我们知道自己真正想做的是什么。还有我建议师姐尝试写科幻小说,因为国内没有这方面太欠缺了。
|
陈凌云,哈哈
,我找到你论坛的名字了!
不过要不是你那天把QQ名字改了我还不知道呢!呵呵!
加油吧!!
对了!你对科幻奇幻有见解?看过很多?我看过些奇幻,最近没关注,比较大的就是江南他们的九州,燕大叔的天行健等吧!呵呵!
17355追随自己内心的呼唤 支持你
17355心无束,路自远,现在改行还来得及。
17355自己走自己的路!
17355只要是你已经决定了,不要管别人怎么说,因为只要是选择,都是有道理的,只要相信自己,不要管别人怎么说了。。。
17355 能选择自己喜欢的事去做,这可是大多数人羡慕的啊。中国少的不是研究数学的人,而是缺少有明确目标的人,少了能把自己的兴趣当工作并成为自己奋斗一生事业的人。
祝中国少一位心累的数学教师,而多一位开心的文学大师!
17355不知道楼主现在如何了?
17356判断你的数学天赋在几何还是代数很简单——物理与几何是孪生兄弟,物理好一定有几何天赋。
学分析最辛苦,但这是其他学科的基础,就像体育中的田径一样。现代的代数和几何是不分家的,几何是目标,代数是交通工具。分析嘛,就是你每天必吃的饭了!
17356分析 代数 几何 ? 怎么知道自己适合做哪个方向呢
17356要看自己的兴趣,
几何是现代数学的大方向,可在中国没有太多的人做,但是几何代数分析的区别不大,他们是相互联系的
17356其实还是看兴趣。
其实无论读做那个方向,都不可能只了解一个方向的,对其他的东西多少有些了解!
17356我对潜意识里就对分析比代数、几何更感兴趣 也不知道为什么 ?
另外对量子力学弦论也很感兴趣,想做这方面的数学
但是这些理论跟群论和微分几何联系最紧密,我现在很矛盾阿 。
哪位大牛能给指点一二
17357RT
谢谢
17357这个似乎是属于 运筹学与控制论 中的系统控制方面的东西
17357听名字感觉应该是随机行为或是模糊系统方面的,不太清楚,望高人指点
17357这个貌似好象川大有几个牛人在搞.貌似不是用仅用概率和随机控制来搞,因为那几个牛人是搞拓扑\泛函方向的.
据说好象是根据具体情况构造新的测度函数,然后研究这个空间的性质来搞的.
17358不理解你的逻辑
能更详细些吗
17358讨论一致收敛性:

x^n*ln(x)定义域为[0,1]
我顺便补充一点:
若函数项级数点点收敛于一点集E,且通项函数列在E上一致收敛,
是否有函数项级数一致收敛?
另外:证明

x^n*lnx/(1+|lnln1/x| )在[0,1]上一致收敛但不能用控制判别法?
17358这个似乎不是级数也不是数列吧。
17358求导考虑max|x^n*ln(x)|,可知是一致收敛的
17358昨晚看的时候似乎没看到求和符号..........@_@
这个也不难,在[0,1)上的n~inf的求和为x^n*lnx/(1-x),而该式子当x->1时极限为-1,从而易导出不一致收敛的结论
至于另外一个问题用上面类似的方法即可解决
17358
| 引用 (reijin @ 2005年08月30日
00时33分) |
|
求导考虑max|x^n*ln(x)|,可知是一致收敛的 |
用到求导,此逻辑不通吧

x^n*ln(x)上[0,1]是不一致收敛的
17358晕倒
说一致收敛的时候应该指明是级数还是函数列吧
我想renjin以为你问函数列的一致收敛性呢
呵呵
17358在[0,1)上的n~inf的求和为x^n*lnx/(1-x),对每一个固定的n,该式子当x->1时极限为-1,那么则在[0,1)上存在x0(n),使得|x0(n)^n*ln[x0(n)]/(1-x0(n))|>1/2,也就是说对任意的n,总有x0(n)使得该级数在n~inf求和的那部分的绝对值大于一个常数,从而该级数不一致收敛
17358呵呵明白了
研究尾级数,证明其不一致收敛于零。
我一直想着应该
构造那样的数列
所以没领会到
17359线形空间与变换的试题,我自己感觉两者等价的条件不是很清楚
等价的证明详细格式的解答
谢谢post-38-1125325479.gif
173591 kerf=ranf
可考虑f在某一组基下的表示
17359
| 引用 (流形 @ 2005年08月30日
07时10分) |
1
kerf=ranf
可考虑f在某一组基下的表示 |
呵呵,详细就是:
必要性:
有题设f(V)=
f - 1
(0) =Kerf
由于dim Kerf=rankf 而n=dimf(V)+dim Kerf=rankf+dim Kerf=2
rankf
所以n为偶数,而且rankf=n/2
充分性:
反之,如果 f 2
=0,rankf= 1
2 n
则首先有Kerf ⊃
f(V) ,另外dimKerf=n-rankf= 1
2 n
=rankf=dimf(V)
所以f(V)=Kerf=
f - 1
(0)
17359没有哇
就是f(v)=f-1(v)
哪一个是2呀,我以为是L
哈哈,还是你厉害,看来我想的复杂了
17360这是一道高等几何教材中帕斯卡定理部分的习题!求助大家解一下post-8-1125325987.jpg
17360将六边形ABCC1B1A1看成六边形ABCA1B1C1即可
17360
| 引用 (奔跑者 @ 2005年08月30日
16时25分) |
|
将六边形ABCC1B1A1看成六边形ABCA1B1C1即可 |
呵呵,明白了!谢谢你!
17360其实,这道题目你可以用完全的初等方法解决啊!要用到著名的梅勒劳斯定理和塞瓦定理!
17360
引用 (lwd
1981 @ 2005年09月01日
21时55分) |
|
其实,这道题目你可以用完全的初等方法解决啊!要用到著名的梅勒劳斯定理和塞瓦定理!
|
很想听听你的想法!
17360单墫的初中版数学奥林匹克里面有阿
17361本人一直在考虑是考武大还是考华科(概率论与数理统计),不知道它们两个哪个好考些,一直都在找它们的历年的录取比例,但是一直都没找到,不知道大家有没有??
17361武大和华科的研究生院的网页上都有具体的报考和录取的数据。
17361概率的话,建议考华科!~
17361谢谢了!!
17361考华中科技大学
17361我还是比较赞同武汉大学
17362这教案和课本内容一模一样吗?
17362
引用 (hfg
1964 @ 2005年08月29日
23时46分) |
| 供上课教师参考
|
事实
17362Thanks very much!
17362thank you
17362keyi
17362下载了,谢谢啦
17362供上课教师参考post-67-1125330385.ibf
17362verygood,thanks!!!!!!!!!
17362Thank you
17362我想download没有积分 真是郁闷
17362不错不错,就是贵了点!
17362thinks!!
17362xiexie
17362many thanks
17362确实很期待,但是没分可用啊.遗憾...
17362Thank you
17362xiexie
17362天哪,这是教材啊?!是我们的课本啊!我晕!
17362原来就是课本的内容呀,不然就要浪费我三个积分了
17362确实有点贵了
17362谢谢啊啊啊
17362谢谢。。就是好贵哦。。一下子就没分了。。无奈啊
17362好人阿,但就是贵了点
17362谢(一字千金)
17362还是看看课本好些
只讲课本不如不看的
17362多谢了啊啊
17362多谢了,呵呵!!
17362是怀化学院的么?
17362这是教材啊?!是我们的课本啊!
17362谢谢了
17362谢谢
17362很好
17362verygood,thanks!!!!!!!!!
17362xieixe !!!
17362谢谢!!!
17362thank you very much!
17362感谢!
17362感谢楼主辛勤劳动!!!!
17362感谢楼主辛勤劳动!!!!
17362感谢楼主!!!不过好像是课本阿!
17362好贵啊老天
17362very good,thanks
17362感谢
17362谢谢
17362.0
.
0.
173621221
17362谢谢
17362再次感谢楼主辛勤劳动!!!!这本书很好!
17362非常感谢!
17362大力支持!!!
17362谢谢!
17362很好,谢谢!
17362谢谢
17362谢谢了!!!
17362谢谢
17362楼主辛苦了。谢谢
17362谢谢了,只是自己的积分太少!
17362好像与北大前代数小组编的那本经典教材一样啊
17362非常感谢!
17362钱不够了,没办法买:(
17362积分不够啊
17362好人一个,多谢了 呵呵[COLOR=red]
17362多谢hfg
1964!好东西啊!
17362谢谢!
17362谢谢了,只是自己的积分太少!!!
17362不错,很想看这本书.很多大学都是用这本书的
17362thx!!!
17362已经下载,谢谢!
顺便问一句,这是那个学校的教案?
17362好!
17362thanks
17362very good
17362真棒,顶一个
17362怎么样才可以下载啊?怎么样可以得到高分啊?
17362本人积分9分啊,怎么买不了下载啊???
17362请教啊,我急需这个版的教案,如何下载啊,为什么我下载了的是0字节啊??请指正!
17362很好,谢
17362做数学课件需要花大量的时间,是否有简单省时的新办法,特别是用公式编辑方面的,谢谢!!
17362不错.
17362xiexie
17362收藏了,谢谢班主
17362楼主简直富可敌国啊!
17362好想下啊,但不知如何挣分啊
17362我有分了,但是如何购买呢?
17362终于会了,发现我好笨笨啊。
17362有点贵啊,看来要努力赚分啦
17362感谢楼主了
17362谢谢楼主
17362谢谢
17362非常感谢!
17362找了好久了,谢谢楼主啊
17362谢谢
17362降价阿
17362你好 ,能优惠吗?
17362狂谢了
17362感谢
17362

Thank you
17362thanks
17362take a look.
17362十分及时啊,谢谢你了啊!
17362xiexie!!!!!!!!!!!1
17362和教材真的差不多!!!!!!
17362是不是下了就要扣三分的积分啊。太惨了吧。我才7分
17362非常感谢!
17362太谢谢了
17362多谢!
17362thanks
17362这是你上课用的教案吗>连重点,难点都没说,就是课本啊
17362谢谢,thanks very much
17362555555555,原来是课本,害我失掉3分,我可是穷人啊,楼主一博士后还欺负我们小学生,555555555555
17362好用!!


173623X a lot
17362谢谢哈
呵呵
17362不错不错,贵了点也无所谓!
17362很不错的东西啊,对学习高代很有帮助。多谢了
17362xiexie
17362不错不错,贵了点也无所谓!
17362不错不错,就是贵了点!
17362就是贵了点!谢了!
17362没有钱那
17362敬爱的朋友:
下次请写好哪个学校的教案
再次感谢
17362好,不错
17362谢谢!
17362这就是书上的内容呀 各位仁兄有没有PPT的高代教案呢
17362我虽然不教这门课
不过还是很有用的
谢谢!
17362谢谢,下来看看!!
17362谢谢!!!!!!!!!!!!!
17362支持哦,都是好人!
17362不太好,还比较贵
17362确实有点贵了
17362确实不错啊
17362希望有ppt的,哪个上课好用
173623分啊,吐血了!不过还是要说声:谢谢!
17362great!
17362期待
17362就是课本吗?太贵了
17362回复表示谢谢!
17362谢谢楼主的救急
17362
引用 (hfg
1964 @ 2005年08月29日
23时46分) |
| 供上课教师参考
|
你好,我的积分不够用,但我现在很需要这个教案,能否将发一份给我,多谢了!
17362谢谢楼主!
17362呵呵,,,,谢谢分享啊
17362thanks
17362
刚刚下载了,看了看。小学校的教案就是这样,
很详细,但是跟教材上完全一样,没有突出的地方,
也没有教师个人的想法和认识,很遗憾。
17362thanks
17362very very good ,mang thanks
17362好贵啊,是好东西么?
17362ddddddddddddddd
17362Thanks!
17362Thank you !!!
17362good,thanks
17362还行!
17362Thank you !!!
17362谢谢!
17362谢谢,我下了
17362thanks
17362谢谢分享啊
17362多谢
17362非常感谢
17362谢谢了!!
17362谢谢
17362谢谢啊啊啊
17362好人阿,但就是贵了点
17362好是好啊,可惜就是买不起啊。
17362没的钱钱
17362原来是高代的,还以为是高数的呢:(
不过还是很感谢楼主,我留到以后再看
17362我考博士的高等代数的教材就是北大数学系编的教材,很想看看此教案怎么样?
17362无限感激!!
17362many thanks
17362好东西,但没钱买
17362好东西!感谢!
17362hao好贵啊
17362是什么就是什么
17362谢谢啊
17362好像有点贵,不过正需要,下载了,谢谢楼主
17362十分感谢!早了很久
17362Thank you
17362谢谢,很好看。
17362感谢搂住!!
17362谢谢楼主了,找了好久了!!
17362下了,感谢
17362还可以
17362谢谢!

17362下了,感谢
17362谢谢~正是我要找的
17362谢谢楼主
17362我可是上当了,我下了,但是还是打不开的,我的机器版本不能打开这个压缩包,真是被气死了!
17362thank you
17362真是极品哦啊!!
17362谢谢,真的不错。
17362
就是课本呀,还要钱!!
17362我看看
173623Q`~~~~~~~~~~~~~~~~```
17362多谢了呵呵
17362太感谢了!!
17362谢谢啦
17362谢谢
17362有些遗憾,该教案没有新意,还是谢谢了
17362真是好东西啊?
17362顶一下!
17362谢谢了先!
17362

xiexiela
17362谢谢!
17362谢谢!
17362ddddddddddd
173623x
17362thanks!
17362太谢谢了!
17362路过!!看看!!
17362谢谢, 就是有点贵啊!
17362支持
17362谢谢啦
17362谢谢,论坛不能下载的问题解决了。
17362手头的积分不足,能不能把那些急用的东西降下价啊?
17362太好了,多谢!
17362
引用 (hfg
1964 @ 2005年08月29日
23时46分) |
| 供上课教师参考
|
谢谢,我要看看!
17362谢谢
17362课本而已阿!!
17362不错不错,就是贵了点!
17362谢谢啦
17362北大版高代课本是我们上大学时的教科书。内容全面,选材精当,是一本在中国高校比较被普遍采用的教科书,至少在八十年代至九十年代如此。当年授课老师严谨、认真的丰采还历历在目呢。但勿用违言,近年来随着国外那套数学名著系列的陆续出版,国际水平的数学大师的著作也陆续进入人们视眼;北大版高代课本与国际同类书籍水平还是存在较大差距。
17362谢谢楼主分享真是太感謝你了
17362谢谢 了
17362没分怎么办
17362谢谢
17362谢谢了哈,不过分太高了!
17362非常感谢!
17362非常感谢。
17362感谢,不过做的一般
17362very good ,Thanks!
17362挺好的,谢谢了
17362呵呵,我可是博士生啊,竟然在论坛里变成了小学生,哈哈
17362谢谢阿
17362谢谢你的提供!
17362好贵啊!不过还是谢谢!
17362谢谢了
17362谢谢楼主提供!
17362顶
17362不错不错,就是贵了点!
17362要了吧,就是贵啊
17362不错不错,就是贵了点!
17362还没打开看,真的跟教材一样吗?
不过还是要谢谢楼主!
17362Thank you
17362贵了些
17362好好好
17362谢谢楼主,感谢楼主分享
17362好的,看过了
17362very good
17362还要花钱,心疼啊
17362
谢谢啊,可惜就是分太多了
17362不错,就是贵了点!
17362谢谢,再次下载了
17362实在是有点贵
17362要是能够免费共享就好了,不过还是谢谢
17362原来就是课本的翻版啊!
17364Thang you!
17364如题post-68-1120626571.ibf
17364thanks
17364哦,原来这么先进呀!我是现在才打算学习数学的,所以我现在在不基础,谢谢你们的资料了!
17364下载来看看,谢谢
17364似乎很基础,是期末试题吗?
17364谢了,是那个学校的题
17364呵呵,看看先
17364参考一下,谢谢了
17364谢谢
17364谢谢楼主了.
17364真的很好,谢谢楼主了
17364谢谢
17364说明学校,所用教材啊
17364LZ,请问是哪个学校的题?
17365如果S是一个点集,

》0,我能不能构造这样一个集合,
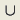
O(x,

),任意x

S
17365其实问题是这样的post-38-1125334399.gif
17365这是所谓的点集的分离性质,与点集和空间的拓扑有关。
原问题是没有答案的
加上一定的条件后就可以,
在欧式空间中,按自然拓扑若A,B均为闭集,则是肯定的
17365这是拓扑学中的分离性问题
在熊金城的点集拓扑中有讲的
满足可以用开集把闭集分开是某一类拓扑空间的性质
而且有的时候它们也被作为同一类空间来考虑问题
建议你看一看拓扑学的相关知识
17365好象原题是有A,B是闭集
不好意思,打漏了
但是就是不明白流形的那几句话
什么是点集的分离性质啊
17365建议你找一本数学百科全书,或数学辞海,找一找与拓扑有关的条目看一看
比较直接些
17365是啊
不知道拓扑的内容似乎对于
R n
中的问题很难做出来
不过如果是
R 上的还有点希望
17365这在n维空间上还是比较好证的,分别考虑A中每个点x到B的距离rx=d(x,B)和B中每个点y到A的距离ry=d(y,A),由于其均为闭集,则可证rx>0,ry>0,此时只要对A、B各作一个半径为rx/3和ry/3的开覆盖即可得到结论。
17365在欧空间中该结论不真.需加强条件,在江泽坚<实变函数论>中有一个所谓分隔性定理.在拓扑学中是一个定义中的一个条件(公理体系)
173661,如何判断一个二重极限是否存在啊
2,有没有求二重极限的一般的方法啊
17366想问的是二次极限吧
1按定义判断
2 若有一致收敛性,可考虑极限交换顺序或求二重极限
17368问

取何值时,fn(x)=n^

*x*e^-nx
1 在[0,1]收敛?
2 在[0,1]一致收敛?
3 使lim

[0,1]fn(x)dx可在积分号下取极限?
173681


R
2 至少档

满足小于0时,可以,还有没有可能有更大的范围?
3 至少档

满足小于0时,可以,还有没有可能有更大的范围?
17369这个问题毫无意义,很多人都很爱数学,那有什么好比较的呢???
17369一个古老的话题 谁是最牛的数学狂徒?1
17369克罗内克,为数学而生,为数学而死!
17369阿基米德,牛顿,高斯数学三强
17369欧拉
17369无聊之极
17369很多人喜欢数学,但是不能够作出什么,不是一码子事
中国近代被老美称道的只有陈省身/华罗庚/丘成桐,北大数学中国牛比,又被丘成桐贬得够可以的了.有种学人家丘夫子也拿一块菲尔兹奖牌.
陈省身---中国是数学大国,但不是数学强国
大!=强
17369伽罗瓦
17369高斯
17369高斯
17369爱因斯坦
17369相对于物理而言,爱因斯坦数学并不算很出色。
爱因斯坦晚年的时候,自己也承认由于自身数学基础的薄弱,很多研究、计算无法向更深入的方向发展。
把爱因斯坦列为数学家,多少有些不合适。
17369我还是觉得高斯
伽罗瓦
Abel
最牛了
17369个人感觉埃萨克·牛顿是在是大牛中的大牛,再由就是冯·诺伊曼,然后是欧拉、高斯、费尔马……,不过前两位不仅仅在数学中做出了超出历史的成就,在其他领域的任何一项成就都足以彻底的改变人类的生活方式。
17369高斯
永远的数学王子!
17369欧拉,伽罗瓦,高斯
17369无法比较.
若要推荐,我推荐
ZFC公理系统的建立者们.数学与我们同在!
17369咱们都有机会
17369阿基米德
17369Grothendieck
17369欧拉
17369我觉得柯西很好,我很喜欢柯西不等式。他的证明简直惊艳!
17369牛顿,欧拉
还有华罗庚,受他影响的人最多
17369不知道,没有研究
17369发此帖的目的:我们要争做21世界牛比的数学人
难道我们中没有人比古人、前辈强吗?
哈哈 真是不幸啊
!!!!!!!!!!!!
17369呵呵,快没钱了。看文章顺便打点水呵呵,不好意思没钱了呵呵
17369伽罗瓦
高斯
哈密顿
17369数学之神:阿基米德
流星:Abel.galois
数学王子:Gauss
Newton,Euler
17369牛顿
17369我是不是牛人呢?呵呵,大家评价一下!
我感觉我也挺牛的,呵呵,不过只是自己认为罢了,关着门我可以这么说,碰到高手了就不敢了!
17369冯·诺伊曼
17369都比我牛
17369
欧拉,我也投票欧拉,一般说,数学家的排名欧拉被排在阿基米德,牛顿,高斯
之后,从对数学的贡献来说,也许是,但如果以纯数学天才来说,所谓比牛的话
我觉得更应该是欧拉,可惜欧拉的数学风采,我们大部分人没有机会领略,我希望
中国像出版托尔斯泰全集那样,出版欧拉全集。
17369
| 引用 (中子星05 @ 2005年08月30日
09时28分) |
| 一个古老的话题 谁是最牛的数学狂徒?1
|
Galois
17369迦罗华
17369不同意牛顿
17369数学家有各种类型
最早欧几里得:是古希腊几何学集大成者,但更多实事无法考证,其写作,传授的才能可能更好于数学才能,更难得的是把以前视为神秘的数学,向更多人传播。他应该是最早最伟大的数学教育家
欧拉:至今为此,最多产的数学家,学术论文约千篇。 然而,遗憾地是极少有原创的思想,尽管其名字在数学文献中随处可见,但绝大多数是把他人已有的东西,简洁公式化,复数的指数形式是他数学一生的写照。 他应该是最伟大的数学工作者。
牛顿: 其对科学的贡献远不止城数学。很多人认为他是古今最伟大的科学家
所谓数学天才应首推 H。Poincare。 他是拓扑学,动力系统,大范围分析等许多数学分支的创始人,对数学敏税的洞察力让现代人叹为观止。
数学家有几种, 分别会
(1)解决问题
(2)提出问题
(3)告诉别人想(提出,解决)问题的方向
一个比一个更重要。 欧拉是第一类, HIlbert 第二类, 而Poincare是第三类。其著名的Poincare猜想的百年解决过程 带动了更多数学分支发展, 将这个猜想与Fermat猜比较一下就会明了了
17369Erdos
17369牛顿,高斯。
我崇拜他们都想把他们的大幅彩照挂在墙上:)
因为我是学统计的,所以更推崇高斯。
17369Gerraewa,Abell!!!!!!!!!!!
17369阿贝尔
17369高斯没有人品!牛的是欧拉,巴斯加,费马,伽罗瓦!另外加个毕达哥拉斯学派
17369江山代有才人出,各领风骚数百年。
17369中国数学史上有个陆家羲,埋没的数学家,成就很高。
17369拉马努金
思维无迹可循,这就是天才
17369最伟大的数学天才当然首推H.Poincare.
其次是我,接下来就是格罗腾迪克.呵呵.
17369GAUSS
17369高斯
17369柯尔莫哥洛夫
17369的确无聊!
17369每个数学家在自己的领域里都有贡献.
就算把所有数学家放到一起,也比不出到底谁最牛.,
17369個人觀點:
必定是下四人之一
Simon Donaldson, Shing Tung Yau, Edward
Witten, Maxim Kontsevich,
17370用线性方程组或线性空间的思想也容易得证
17370设N阶阵A的秩为r.是否存在秩为n-r的N阶阵B和C,使得AB=0以及CA=0?
我证明用的阵的具体,但感觉比较麻烦...
17370相抵标准型
很容易写出答案的啊,附件:post-38-1125367264.ibf
17370我证明用的是分块与初等变换,奇怪了,我们的教材上居然没有提相抵标准型,清华的教材上有...看来还是多掌握些做题容易啊
谢谢了
17370好久以前的题目了 原来前辈们给的答案都看不了了 有人能给出详尽答案么?
17370111111post-38-1242610462.jpg
17370设N阶阵A的秩为r.是否存在秩为n-r的N阶阵B和C,使得AB=0以及CA=0
AB=0那么A的行和B的列垂直,所以让A的行向量生成行空间,求他的垂直正交补,写成列,其余列补0。
CA=0那么C的行和A的列垂直,所以让A的列向量生成列空间,求他的垂直正交补,写成行,其余行补0。
矩阵运算和欧式空间联系起来,对这道题目的解答就很清楚了。
当然矩阵的相抵,相似,相合几个最基本的概念产生了矩阵的不同分类,对每类找出形式最优美的表达,也就是标准型,是他的根本思想。
17371Xn Yn是随机向量吧?
Xn的那个二次型似乎一般都是收敛到卡方的,怎么收殓到正态了
17371现有独立随机变量列{X_n},非独立随机变量列{Y_n} (其均值为零),{X_n}与{Y_n}独立;
A_n 是
对称但未必是非负定的矩阵,
已经知道:X_n'*A_n* X_n/\sqrt(n) 依分布收敛于
标准正态分布N(0,1);
Y_n'*A_n*Y_n/\sqrt(n) 依概率收敛于某常数 a .
现请问:
X_n'A_nY_n/\sqrt(n)
分布的极限行为?(也可添加适当条件)
我猜测,可能收敛到某个分布,但又不知如何处理?请教大家,谢谢!
17371是的,Xn Yn都是随机向量,并且可以假设Xn是零均值的多元正态分布(可以假设其协方差阵为单位阵)。
的确,Xn的二次型Xn'AnXn通常情况下(即An对称幂等时)是卡方的(小样本分布)
但Xn'AnXn/\sqrt(n)的极限分布可以在适当条件下收敛到正态分布。这是对的。
只是X_n'A_nY_n/\sqrt(n) 这种情况,我没见过,不知怎样处理?
谢谢。
17371能不能做Y_n到X_n的变换,然后通过Jacbo来做?
17371谢谢了。
17372请问怎么附图啊
17372
请教几道题,对大家来说比较简单,对我来说很重要。希望能得到您详细的解答,真心感谢谢!!post-8-1125370490.gif
17372第一个就是复合求导的问题了,
再说你可以这样做啊:
f(x)=
∫ 1
x
ln(xt)dt
=
∫ 1
x
lnxdt+∫
1 xlntdt
= (x-1)
lnx
+∫ 1
xlntdt 这样子导数就出来了。
第二个:
cos2x=
cos 2
x-sin
2x 那么原来的积分化成:
∫ 0
a
(cosx-sinx)dx
就可以求出a了
第三个:
前两个定义域都是不同的,所以不是同一个函数
但是最后一个定义域等等都是相同的
第四个:
泰勒展开,结果2x
第五个:
在0点不可导
这些题目最好先仔细看看课本,争取自己解决!
17372第二题:sina+cosa=0,所以a=k

+ 杠frac{3}/{4}

17372
引用 (FARSEER @ 2005年08月31日
18时32分) |
先谢谢两位,tobyqin朋友,我确实笨,这是个事实,所以你的答案我还有点不明白的地方:
(1)题中,你的积分号我这里看到全是“Integral;”
这种符号,所以看不太懂,你说是复合求导,这个我明白,那第一步是对ln(xt)对t求导得1/xt*x吗?然后把t=x代入?然后减去把1代入?还是对ln(xt)不用求导了,直接对里面的(xt)求导得X?
(3)题中我知道同一函数的条件是定义域相同,函数对应关系相同。但是对第一个函数来说这两个指数函数根本就是同一个函数么,怎么会出现定义域不同的情况呢?把2放到指数符号里面成为2方,这两个是一样的呀。第二个,两个乘起来是同一函数呀。
(4)题因为我做的是选择题,只有答案没有过程,但是答案是sinX。与你说的不同,不知道是否是答案错了。
谢谢还请给解答解答。
|
首先你要装一个软件来阅读公式,名字叫:MathPlayerSetup
具体可在一些置顶的文章中提到
否则你看到的就不会是清楚的公式了。
(1)你这么说不对吧!
如果被积函数为f(x,t),积分上限为a(x),下限为b(x)
那么对x求导是这个样子的三部分:
(1)
a'(x)f(x,a(x))
(2) -b'(x)f(x,b(x))
(3)
f(x,t)对x的导数从b(x)到a(x)对t的积分
(3)题:第一个中,第一个函数定义域是不能等于-2,但是第二个函数定义域是x>-2,后面两个是类似的原因。
(4)题:答案是对的啊,只要看
x
→0
的时候两个商的极限是不是非零的有限数。
17372先谢谢两位,tobyqin朋友,我确实笨,这是个事实,所以你的答案我还有点不明白的地方:
(1)题中,你的积分号我这里看到全是“Integral;”
这种符号,所以看不太懂,你说是复合求导,这个我明白,那第一步是对ln(xt)对t求导得1/xt*x吗?然后把t=x代入?然后减去把1代入?还是对ln(xt)不用求导了,直接对里面的(xt)求导得X?
(3)题中我知道同一函数的条件是定义域相同,函数对应关系相同。但是对第一个函数来说这两个指数函数根本就是同一个函数么,怎么会出现定义域不同的情况呢?把2放到指数符号里面成为2方,这两个是一样的呀。第二个,两个乘起来是同一函数呀。
(4)题因为我做的是选择题,只有答案没有过程,但是答案是sinX。与你说的不同,不知道是否是答案错了。
谢谢还请给解答解答。
17372是不是 叶奕盛编的 高等数学选择题集, 那本书我也看过,挺有意思
17372谢谢tobyqin,这次能看到公式了。
第(1)题你看这样对不:先去掉积分号,把X代入T,得lnx2(2是平方)乘以对上限X的导数1,(但我还是不明白,X在这里算是常数还是变量?)。然后再把1代入得lnx,乘以1的导数0,得2lnx?但答案得1+2lnx所以我想我还是错的。你给的那种方法是不是把积分全求出来后然后整体求导?我得出是2lnx+1+1/x,还有点不一样。还请你给具体解一下。谢谢。
第(4)题你的意思到底得SINX还是2X?必须用泰勒公式吗?用e的X方减1等价于x能不能求呀?
还得麻烦你解答一下。谢谢。
17372
| 引用 (FARSEER @ 2005年09月01日
11时46分) |
谢谢tobyqin,这次能看到公式了。
第(1)题你看这样对不:先去掉积分号,把X代入T,得lnx2(2是平方)乘以对上限X的导数1,(但我还是不明白,X在这里算是常数还是变量?)。然后再把1代入得lnx,乘以1的导数0,得2lnx?但答案得1+2lnx所以我想我还是错的。你给的那种方法是不是把积分全求出来后然后整体求导?我得出是2lnx+1+1/x,还有点不一样。还请你给具体解一下。谢谢。
第(4)题你的意思到底得SINX还是2X?必须用泰勒公式吗?用e的X方减1等价于x能不能求呀?
还得麻烦你解答一下。谢谢。
|
咣噹
(1)我那里明明说了是三个部分,你怎么就给出了两个部分啊:先去掉积分号,把X代入T,得lnx2(2是平方)乘以对上限X的导数1,然后再把1代入得lnx,乘以1的导数0,得2lnx,然后再对被积函数求导再积分就是
∫ 1
x 1
x dt
=1,从而所求的为2lnx+1
(4)等价无穷小不止有一个,这种选择题不要以问答题的形势给出,这样大家根本不知道你的目的!自己看看定义就知道两个是等价的无穷小了。
17374设二元函数f(x,y)在区域D内分别对每个变量x,y是连续的,并且对y是单调的,证明
f在D内是连续的
老是觉得跟单调没有什么关系
17374
| 引用 (zys @ 2005年08月30日
11时23分) |
设二元函数f(x,y)在区域D内分别对每个变量x,y是连续的,并且对y是单调的,证明 f在D内是连续的
老是觉得跟单调没有什么关系
|
如果你有这样的感觉,而且你要是能做出答案就把答案一起写出来
这样让大家看看也就知道你哪里弄错了(或者题目的问题)
大家帮你指出来对你的帮助比知道这个题的标准答案要更有用
17374我是这样想的,
|f(x,y)-f(x0,y0)|<=|f(x,y)-f(x,y0)|+|f(x,y0)-f(x0,y0)|--0
17374
| 引用 (zys @ 2005年08月30日
14时23分) |
我是这样想的,
|f(x,y)-f(x0,y0)|<=|f(x,y)-f(x,y0)|+|f(x,y0)-f(x0,y0)|--0
|
你给出的两项中
第一项是怎么得到趋于0的啊?!
对于不等的x要分别讨论(如果不用单调)
没有那种一致性质啊
17374
| 引用 (zys @ 2005年08月30日
14时23分) |
我是这样想的,
|f(x,y)-f(x0,y0)|<=|f(x,y)-f(x,y0)|+|f(x,y0)-f(x0,y0)|--0
|
这样分析好象行不通,单调性用不上。
该问题中的单调性是不可少的,否则有反例。哪一本教材上有。论坛上有人提过。
17374多谢指点
17374这是Dini定理呀
17374
引用 (pere10
1782 @ 2005年09月05日
13时26分) |
| 这是Dini定理呀
|
要证明在(x,y)点的连续性,首先使用"Dini定理"就说明函数关于y一致收敛,再加上关于x收敛,就可以证明连续性在不包含(x,y)点所处的行列之外的区域连续.((x,y)点所处的行列的连续性显然)
17374
引用 (流形 @ 2005年08月30日
18时42分) |
| 引用 (zys @ 2005年08月30日
14时23分) |
我是这样想的,
|f(x,y)-f(x0,y0)|<=|f(x,y)-f(x,y0)|+|f(x,y0)-f(x0,y0)|--0
|
这样分析好象行不通,单调性用不上。
该问题中的单调性是不可少的,否则有反例。哪一本教材上有。论坛上有人提过。
|
to流形:这样分析不行.那怎样分析?哪有链接?
17374还有Cauchy行列式是怎样的行列式?怎么从没听说过?
17374谁能据个例子说明下?万分感谢.因为我现在逃学在家所以手上没有什么资料可以查.
17374该问题的详细证明请见裴礼文《数学分析中的典型问题与方法》p.529,例6.1.21
17374单调是必不可少的。
17375S 是凸集又是闭集,a不属于S ,证明S中存在唯一的点X0最靠近a
17375在泛函分析中,这叫严格凸性。
若是在
R n
中考虑,
首先X0的存在性是没问题的,唯一性可用反证法
17375
| 引用 (zys @ 2005年08月30日
11时29分) |
| S 是凸集又是闭集,a不属于S
,证明S中存在唯一的点X0最靠近a |
这个问题关键是存在性吧?!
我建议你考虑应用有界闭集的点列有收敛子列来做一做,其实并不是太难的。
17375
对,利用最小距离构造所谓的极小化序列,又因为有限维欧式空间为局部紧的。
从而极小化序列有收敛子列。
17375唯一性怎么证啊
17375唯一性用反证法
其实就要你说明等腰三角形的底边中线小于高
17375这个问题应该在希尔伯特空间(内积空间)上讨论更有意义,通过三角不等式和平行四边形等式可证明
17377因为教学需要,希望有word版电子教案的大哥帮个忙,告诉
下载网址,或者发到论坛,谢谢啊。post-67-1125376468.gif
17378你失望过吗?
再坚持一下
也许电石火光之间
一个新的想法
解决了问题
改变了你
你失望过吗?
再坚持一下
也许嘘寒问暖之间
一据不经意的话
解决了问题
改变了你
数学就是这样
即使庞加莱发现了混沌
他对数学的信仰并没有影响他对数学的信念
十几年的艰辛劳动
开创了动力系统
你失望过吗?
再坚持一下
17378坚持就是胜利
17378好啊
17378顶!
17378我坚持我奋斗
17378大家一齐来加油
17378我坚持了一下,但就是坚持不了第二下!
17378我肯定坚持到底
17378本来想写长点,结果有事就结尾了。
最近正在搜集资料,文章写好了一定告诉大家。
17378对
坚持到底
17378真不错,定
17378坚持
17378我坚持,我成功
17378我要努力!坚持
17378我觉得沮丧的时候总是喜欢从数学家们的生平介绍中涉取力量。
读一读欧拉,高斯,庞嘉莱,阿贝尔等人所遇到的挫折和苦难,再看看自己面前的那些问题,根本就不值得一提。
17378坚持就是胜利
17378胜利源于坚持
17378丘吉尔的三个成功信条
1, never give up
2, never never give up
3,
never never never give up
17378坚持到底
努力
17378我顶!
17378坚持到底,永不放弃!
——送给忧郁中的自己
17378也许,坚持总是太难。
17378但为了真理,还需坚持.
-----------------
数学与我们同在!
17378你是不是像我在太阳下低头
流着汗水默默辛苦的工作
你是不是像我就算受了冷漠
也不放弃自己想要的生活
你是不是像我整天忙着追求
追求一种意想不到的温柔
你是不是像我曾经茫然失措
一次一次徘徊在十字街头
因为我不在乎别人怎么说
我从来没有忘记我
对自己的承诺对爱的执著
我知道我的未来不是梦
我认真的过每一分钟
我的未来不是梦
我的心跟着希望在动
17378如果失望了,休息是必不可少的。
学过概率的就知道,
这样的奇迹出现的机率少得可怜。有很多关于这样的奇迹的故事都有后人杜撰之嫌。
与其再苦苦地坚持一下,还不如休息一段时间,以精神饱满的状态迎接挑战。
17378呵呵,这水太大,我就在学术杂谈室发了一篇小文。
各位有时间看看。
谢谢了:)
17378
http://www.math.org.cn/forums/index.php?act=...ST&f=51&t=23031
17378我有一句格言是:只因为选择了跋涉,我更加快了脚步
也许这就是坚持吧
17378不到最后,决不认输!!!
17378人生的哲学
17378坚持就是

符号能使自己越来越提高。
为了自己的数学梦想,绝对要坚持......
17378有人说:“成功就是当你感觉到你再也坚持不下去的时候再坚持下去...”
17378顶
17378好诗
17378男人嘛,就要坚持
17381如题:
如何用较少的测量次数计算出一不规则土堆的方数?
先谢谢了
17381有很多学科的方法可以近似,听说数论方法次数较少.
具体哦我也不知道.
17381没学过~
17382我们知道,极限是针对变量的变化趋势而言的,考察的是变量的最终趋势.那么我问下面一个问题:
一个集列的极限也是一个集合,那么这个集合的元素与集列中集合的元素有什么关系??
譬如说:A1
A2 A3 .....An......这个集列的极限是A,那么A中的元素与:A1 A2 A3
.....An......这些集合的元素之间有什么关系?
17382集列有各种各样的极限。
凡是从概念的定义出发,从概念的功用上来考虑,认识和理解概念的重要性和必要性。
17383对于一个函数序列来说,作为它的极限的那个函数指的究竟是什么?
17383在对应的点上,函数值为函数序列在那一点上所确定的数列的极限,这样的函数就是
17383这个俺明白,可是俺的意思不是这样,等过几天俺想好该怎么把俺的问题说清楚了再来问你,谢谢
17384设A、B为n级矩阵,AB=BA,且A的k次方为0矩阵,k为某一整数k>=1
求证: |A+B|=|B|
17384比较欣赏springboshi的第2种解法,我给你加点技术分,虽然此方法常用,但不容易注意到.多数代数专业人员容易从AB=BA联想到A,B可同时上三角化.
17384对我的第一个答案的更正
很抱歉post-38-1125420752.ibf
17384这个方法倒是不错
就是用到公共特征向量还是要证明的吧
不难,但是还是要写几行
17384该题是浙江大学的一道考研题,它的前一道题是:若AB=BA,证明存在可逆阵,使
P^(-1)AP与,P^(-1)BP都是上三角阵.
利用此结果,本题结论不证自明.
17384我的两种解法。post-38-1125450605.ibf
17384第2种解法较好,她不借助于其它结论.至于第一种解法,要用到同时复上三角化.实际上Laffey及Chio于
1978-
1980年期间还推广到:若rank(AB-BA)<=1,则A与B可以同时复上三角化.
17384楼上的看法正确,可在有关参考资料上找到。
17385
引用 (978301 @ 2005年08月30日
17时01分) |
有没有人能用最简单易懂的最好是形象的比喻什么的方式告诉我:什么是完备性?
当然,是对于一个集合序列而言!!
|
通俗地说,完备性就是指连续性。
17385楼上说的好像不是很准确.应该是极限点属于这个区域.
17385有没有人能用最简单易懂的最好是形象的比喻什么的方式告诉我:什么是完备性?
当然,是对于一个集合序列而言!!
17385分析中的完备性可以在度量空间或类度量空间,一致拓扑空间中定义。
既有度量完备性,和拓扑完备性之分
度量空间中,完备性就是空间中收敛序列和柯西列的等价性。
但它又不是拓扑性质,因为度量没有拓扑等价性,有别于紧的概念。
17385简言之,Cauchy列有极限
17385
| 引用 (流形 @ 2005年08月30日
21时04分) |
分析中的完备性可以在度量空间或类度量空间,一致拓扑空间中定义。
既有度量完备性,和拓扑完备性之分
度量空间中,完备性就是空间中收敛序列和柯西列的等价性。
但它又不是拓扑性质,因为度量没有拓扑等价性,有别于紧的概念。
|
老大,你的测度论学的很好吧!!
俺什么都不懂,刚开始学习这个东西.很多东西都不懂.以后请多帮帮小弟!!!
还有,不知道怎么和你联系?能不能告诉我怎么和你联系?
17385简单来说吧,我举例子来说明一下完备和不完备的区别你就明白了。
有理数集合是不完备的,因为它不存在属于有理数的连续收敛子列,也就是说,虽然有
x
n →x
0 ,但是
x n
,x 0
不可能同时属于有理数。 而实数集合是完备的,因为
x n 虽然几乎都是无理数,但是还是实数。
17385完备性是与度量有关的
17385为什么完备要和度量有关呢,只规定拓扑不行么。
17385使柯西列有极限
17385
引用 (Georgexue_
1999 @ 2005年09月08日
10时27分) |
|
为什么完备要和度量有关呢,只规定拓扑不行么。 |
可以.但要求其拓扑要类似与度量空间的拓扑,称之为一致拓扑,
(不一定是可度量化的)
17385可以.但要求其拓扑要类似与度量空间的拓扑,称之为一致拓扑
17385我看了大家的补充,不知道我用这样一句话概括起来对不对:所谓完备性,就是一个集类对
以下运算封闭:若集列An是集合类的一个基本列,那么它的极限也是属于这个集类的.
大家以为如何??????
17385完备性应该是度量空间里的事,它要求柯西序列必须有极限,而定义柯西序列本身是基于度量(距离)的定义的。另一方面,序列在拓扑空间中不一定收敛到唯一一点,拓扑空间中定义的序列收敛自然只能依赖于开集,而自度量空间后,序列收敛都是以度量来衡量的。所以,完备性是描述度量空间序列的属性(从而也反映了该度量空间的特性),完备的度量空间就是给度量空间加上了完备性约束(限制),从而区分了非完备的度量空间,或者说完备度量空间排除了度量空间中非完备的度量空间。
我的理解是否正确,请多指点。
17386我也发点上来:
大连市第三届高等数学竞赛试题post-62-1125396211.ibf
17386就这么两个:
大连市第七届高等数学竞赛试题post-62-11253963
17.ibf
17386有解析吗
17386
引用 (tobyqin @ 2005年08月30日
18时03分) |
我也发点上来:
大连市第三届高等数学竞赛试题 |
楼主大好人啊:)
17386大连市第七届高等数学竞赛试题post-60-1145004846.ibf
17386大连市第三届高等数学竞赛试题post-60-1145004938.ibf
17386感谢搂主!顶顶顶。。。。。。。。!
17386hehe
好人啊
17386好人,不要分的。我都不知道那分怎么得。
17386好东西啊
谢谢楼主
17386
http://www.21maths.com/sxjm/gdsx/gsjs/Index.html这里也有,大家去看看
17386很渴望结识各位,多多教导post-62-1152883333.ibf
17386题目估计有错。
做到第三届的第3题,可以举出个反例:
f(x)=-8x^2+8x,
大家试试就知道
17386大连市第4届高等数学竞赛试题
post-62-1
184554
175.ibf
17386大连市第5届高等数学竞赛试题-理工专科
post-62-1
184554399.ibf
17386大连市第6届高等数学竞赛题-理工本科post-62-1
184554641.ibf
17386大连市第8届大学生数学竞赛(理工本科)post-62-1
184554768.ibf
17386大连市第9届大学生数学竞赛-理工本科post-62-1
184554855.ibf
17386大连市第5届高等数学竞赛-理工本科post-62-1
184554945.ibf
17386
大连市第3~9届高等数学竞赛试题大连市第三届大学生高等数学竞赛试题post-62-1203398411.ibf
17386大连市第四届大学生高等数学竞赛试题post-62-1203398587.ibf
17386大连市第五届大学生高等数学竞赛试题(理工本科)post-62-1203398743.ibf
17386大连市第五届大学生高等数学竞赛试题(理工专科)post-62-1203398798.ibf
17386大连市第六届大学生高等数学竞赛试题(本)post-62-1203398874.ibf
17386大连市第七届大学生高等数学竞赛试题(理工本科)post-62-1203398932.ibf
17386大连市第八届大学生高等数学竞赛试题(理工本科)post-62-1203398975.ibf
17386大连市第九届大学生高等数学竞赛试题(理工本科)post-62-1203399023.ibf
17386万分感谢!
17386非常感谢楼主!
17386同志们,大连市高等数学竞赛的试题也太难了,哪个高手能把答案做出来共同分享啊!
17387好,我这里有陕西省的大学生的竞赛试题,可是没有电子版的

17387
1999年陕西省大学生高等数学竞赛试题:post-62-1125396441.ibf
17387陕西省第四次大学生高等数学竞赛试题及简答:
2001年post-62-1125396584.ibf
17387早知道就好拉!!!
17387不知道陕西省的高等数学竞赛几年一次呢??
17387一年一次 吧
17387我参加过这个竞赛啊
17387我也参加过
应该是两年一次
17387
引用 (tobyqin @ 2005年08月30日
18时07分) |
1999年陕西省大学生高等数学竞赛试题: |
谢谢
17387
引用 (tobyqin @ 2005年08月30日
18时07分) |
1999年陕西省大学生高等数学竞赛试题: |
谢谢
17387有没2005的阿
173872003年的题目没有啊??
17387
1999年陕西省大学生高等数学竞赛试题post-60-1145004659.ibf
17387陕西省第四次大学生高等数学竞赛试题及答案post-60-1145005773.ibf
17387谢谢你啊!
17387为什么我下载不下啊?!!!!!!!!!
17387谢谢+——
17387好的啊
17387陕西省第六次高等数学竞赛初赛试题(2006年)post-62-1
173578456.ibf
17387好啊!友人重复.
17387
非常感谢,不过有些是一样的!
17387应该没问题下载
17387有没有第五次的?
17388呵呵,昨天在上传的时候传错了,先传第二届了.
17388首届高等数学竞赛post-8-1087089296.ibf
17388原来把首届放这里了..谢谢楼主.
这次是免费的...楼主好伟大!
17388楼主,我爱死尼洛!!!
不知楼主是男是女?
17388
| 引用 (jhqyh @ 2004年06月13日
09时14分) |
| 首届高等数学竞赛
|
和考研题挺接近的,陕西省的初赛题目我也看了,难度差不多,题量比这个大写
17388先下再看,谢谢啦
17388thanks!!


17388

还不错,不过只有微积分

17388Thanks very much!
17388真是爱死楼主了啊!!!!!!!!!!!!!!!!!!!!!
17388thanks
17388

供大家参考post-8-1106153060.ibf
17388谢谢!!很不错呀!!
17388不能搞成WORD吗。
17388真不错,谢谢了!
17388正需要這樣的內容,謝謝
17388thanks a lot
17388真好,用到!谢谢
17388xiexie
17388谢谢
17388还有!post-62-1122625
193.ibf
17388一
1.2/5.
2.略
3.4X-16/5*2SQRT
4.0,0,1.
5.-1.
二.O
三.略
四.可用泰勒展开.
五.条件收敛.
六.存在,存在,不存在
17388浙江省首届高等数学竞赛试题:post-62-1125397006.ibf
17388浙江省第二届高等数学竞赛试题:post-62-1125397153.ibf
17388浙江省第三届高等数学竞赛试题:post-62-1125397242.ibf
173882004年浙江省大学生高等数学竞赛参考答案:
即为浙江省第三届高等数学竞赛参考答案
希望大家能先独立的做一做post-62-1125397563.ibf
17388浙江省首届数学分析竞赛试题:post-62-1125397760.ibf
17388浙江省第二届数学分析竞赛试题:post-62-1125397881.ibf
17388浙江省第三届数学分析竞赛试题:post-62-1125398009.ibf
173882004年浙江省大学生数学分析竞赛参考答案:
即浙江省第三届数学分析竞赛答案.post-62-1125398295.ibf
17388我要。。。。。。。
17388很好,谢谢
17388
引用 (tobyqin @ 2005年08月30日
18时26分) |
2004年浙江省大学生高等数学竞赛参考答案:
希望大家能先独立的做一做
|
第3题我的解答:
f(x,y)=x^2+4*y^2+15*y
≤x^2+4*y^2+15/2*(y^2+1)
=-45*x^2+23/2*(4*x^2+y^2)+15/2
≤-0+23/2+15/2
=
19=f(0,1);
f(x,y)=x^2+4*y^2+15*y
≥x^2+4*y^2-15/2*(y^2+1)
=15*x^2-7/2*(4*x^2+y^2)-15/2
=-11=f(0,-1).
17388
引用 (tobyqin @ 2005年08月30日
18时38分) |
|
2004年浙江省大学生数学分析竞赛参考答案 |
2004年浙江省大学生数学分析竞赛第六题的解答提示:
(1/n)^n<1/n!<(e/n)^n.
17388
引用 (tobyqin @ 2005年08月30日
18时
19分) |
| 浙江省第二届高等数学竞赛试题
|
2003年浙江省高等数学竞赛第4题的解答:
f(n,k)=(n+k)/(n^2+k)+(2*n+1-k)/(n^2+n+1-k)
=(3*n^3+2*n^2+2*n*k-2*k^2+n+2*k)/(n^2+k)/(n^2+n+1-k),
limit(n*f(n,k),n=infinity)=3,
2*sum((n+k)/(n^2+k),k=1..n)=sum(f(n,k),k=1..n),
limit(sum((n+k)/(n^2+k),n=infinity)=3/2.
17388有没有其他试卷的答案啊?
17388有05年的吗 兄弟。。。。。
17388不错
17388怎么没有答案啊???
17388这里;
的试题 还是不错的吗??
不知道今年的难度是怎样??
17388
引用 (断肠人在工大 @ 2005年11月
18日
20时37分) |
| 有05年的吗
|
等朱晓睿先生上传电子版~
工科类第四题我先给个证明:
设f=x-arctan(x+x^3/3+2/15*x^5+x^7/63),则
f'=1-(1+x^2+2/3*x^4+1/9*x^6)/(1+(x+1/3*x^3+2/15*x^5+1/63*x^7)^2)
=(4/15*x^6+38/315*x^8+134/4725*x^10+4/945*x^12+1/3969*x^14)/(1+(x+1/3*x^3+2/15*x^5+1/63*x^7)^2)>0,
故当0<x<Pi/2时有tan(x)>x+x^3/3+2/15*x^5+x^7/63.
17388陈老师的证法好 明年继续努力
173882005年浙江省第四届高等数学竞赛(文、专科类)试题3post-62-1134067591.jpg
173882005年浙江省第四届高等数学竞赛(文、专科类)试题2post-62-1134067511.jpg
173882005年浙江省第四届高等数学竞赛(文、专科类)试题1post-62-1134067378.jpg
173882005年浙江省第四届高等数学竞赛(文、专科类)试题4post-62-1134067650.jpg
173882005年浙江省第四届高等数学竞赛(数学类)试题1post-62-1134067951.jpg
173882005年浙江省第四届高等数学竞赛(数学类)试题2post-62-1134068026.jpg
173882005年浙江省第四届高等数学竞赛(数学类)试题3post-62-1134068
177.jpg
173882005年浙江省第四届高等数学竞赛(数学类)试题4post-62-1134068244.jpg
17388很好,谢谢了!
17388支持
17388谢谢!!!!!!!!!
17388太好了,正需要这个东西呢
17388谢谢
17388谢谢分享
17388干吗要银子啊55555~~~~
17388谢谢了
向你学习!
17388
| 引用 (mikehz @ 2005年01月20日
00时44分) |
| :haha: 供大家参考
|
thank you very much
17388
引用 (花间候 @ 2005年04月12日
19时13分) |
| 不能搞成WORD吗。
|
顶,赞
为什么要银子?
17388xiexie
17388谢谢大家了!
17388哈哈,说声谢谢就得两分.
17388谢谢啦:)
17388谢谢,试试
17388那经济类的呢
还有解题方法
17388xiexieli
17388太感谢了!
就是以后可不可以多用文挡格式 而不要pdf格式呀
因为它比较难打开
173882004年浙江省大学生高等数学竞赛参考答案post-60-1145004755.ibf
17388浙江省第二届高等数学竞赛试题post-60-1145005999.ibf
17388谢谢...
17388非常感谢!
17388谢谢
17388怎么没人顶一下呀?上传的试题最好是专门给数学专业的学生做的。
17388先看一下先~~~~~~
17388谢了
17388有没有数学专业的竞赛试题呀?
17388真是好东西啊,谢谢了
17388hao
17388谢谢各位给我的帮助
17388谢个!
17388thank you
17388谢谢,很是有用!
17388谢谢
17388不错耶, thanks
17388十分感谢哈
17388还可以
17388谢谢
17388谢谢.太好了
17388有谁把2005的答案发发post-62-1158113
181.ibf
17388
有没有浙江省高等数学竞赛和浙江省数学分析竞赛的历年试题?有的话提供一下,谢谢了.还有我是数学专业的应该参加浙江省高等数学竞赛还是浙江省数学分析竞赛?
17388豪强啊
17388谢谢啊,好人啊~ 找了好多地方,试题有的,但就是没有答案啊
17388谢谢!!!
17388非常感谢
17388楼主辛苦了,感激不尽。
17388谢谢
17388是啊!这么好的东西,我下了。谢谢版主。
17388正在找这个,十分感谢
17388一般吧。
17388有历届高等数学竞赛试题及答案吗
173882005年浙江省第四届高等数学竞赛(工科类)试题post-62-1163234523.ibf
17388好人,十分感谢提供!
17388
各位,谁有历届的高等数学竞赛试题的答案啊,拜托帮帮忙。
QQ:95524011
happyshanqing@163.com
这里先谢过了
1738806年的成绩大概什么时候能知道啊
17388thank a lot.
17388谢谢了
173882006年浙江省高等数学竞赛试题及答案(数学专业)post-62-1165740862.ibf
17388谢谢了!!
17388这里有没有浙江省工商大学的
17388谢谢版主了!!
17388下载完了请各位顶一下哦post-62-1
195372748.ibf
17388好资源与人共享post-62-1
195372922.ibf
17388看来这里浙江的学生还真不少啊!!!
17388请大家分享答案!post-8-1
196654667.ibf
17388哪一类别的?完全吗?
17388里面是部分有价值的题目.
17388第一题我是这么做的
我考的是工科的其他题目不是工科的post-8-1
197598670.ibf
17388万分感谢!
17388无比感谢楼主和后面继续提供试题的同志的无私贡献!
173882007年浙江省高等数学(微积分)竞赛(经管类)试题post-62-1227480871.jpg
173882007年浙江省高等数学(微积分)竞赛(数学类)试题post-62-1227511639.jpg
17388第一页的两个文件我都下载不了
17388我这也不能下载,是不是过时了
17390
如何证明 :

1/n^x
在x>1上的光滑性
17390对
x 0 >1的任何一点有任意阶导数。
这是由于它在 [
x 0
-δ,+∞)
上一致收敛,导函数也一致收敛,等等。
17391题目如下:
设函数f(X),X为变量矢量,其分量可为连续和离散。
又设min f(X)或max
f(X)存在整体最优解或者多个局部最优解。
现将X作为随机变量矢量,进行足够多的抽样,因而得到足够多的相应f值,再将f值关于X的每一个分量xi的上下界fs(xi)/fx(xi)确定下来。
请证明:
在变量分量xi的可行域中,使得fs(xi)/fx(xi)取整体/局部最大/最小值的xi值就是使min
f(X)/max f(X)最优解的对应分量值
17392不好意思,我又 弄错了,北师大数分第三题在钱吉林数分习题精粹上,不过解答错误!再一次谢谢你帮我解决那道积分不等式。
17392请高手解决几道数分题,谢谢!post-21-11254047
18.ibf
17392第一题:我的做答见附件,没太细检查:
二、三我在《数学分析中的典型问题与方法》中看到了,还没怎么做。post-21-1125466228.ibf
17392不利用连续性,
怎么证明:f((x+y)/2)〉=(f(x)+f(y))/2<==>f(lx+(1-l)y)〉=l*f(x)+(1-l)f(y),
x,y为任意,0<
l〈1
不好意思,改一下
17392
| 引用 (流形 @ 2005年08月31日
13时56分) |
不利用连续性,
怎么证明:f((x+y)/2)〉=(f(x)+f(y))/2<==>f(lx+(1-l)y)<=l*f(x)+(1-l)f(y),
x,y为任意,0<
l〈1 |
后面一个写错了吧?
不等号方向怎么是相反的
:)
17392
| 引用 (tobyqin @ 2005年08月31日
13时30分) |
第一题:我的做答见附件,没太细检查:
二、三我在《数学分析中的典型问题与方法》中看到了,还没怎么做。
|
谢谢!解答很巧妙。你还记得前几天被抵达三道数分题,你告诉我第一体大概思路在解答库,我怎么没找着,还有不知道你第二题做得怎么样?期待你的回复,非常谢谢!
17392后面的题目没再做了
我回头再做做吧
北师大的那个我在解答库里你问问题后面跟上了很详细的解答
链接在这里:其中我贴的一个附件里是解答。
http://www.math.org.cn/forums/index.php?show...topic=
17053&hl=
17392
你的数分很强,思维很敏捷而且深邃,不得不令人佩服!顺便一句,你应是研究生吧!北师大第三题我用你告诉的方法试了一下结果也是无穷大,你说有问题,我回去再看一下。北师大第二道题不知道你做出来没有?不过第二道题是一个大题,上面还有两道题,我想会对你解题有帮助,我把这道题完整发给你.在附件中。 post-21-1125572300.ibf
17392这个你贴错了吧?!
17392不好意思 ,我弄错了。在请看附件!post-21-1125666627.ibf
17392楼主怎么不打出来啊
17392
引用 (rocktree @ 2005年09月01日
18时58分) |
|
北师大第三题我用你告诉的方法试了一下结果也是无穷大,你说有问题,我回去再看一下。北师大第二道题不知道你做出来没有?不过第二道题是一个大题,上面还有两道题,我想会对你解题有帮助,我把这道题完整发给你.在附件中。
|
注意,你对第三个下的结论是错误的,可能和我第一次做的时候犯了一样的错误,如果这个极限存在,那么绝对值一定是不大于2+sin1,当然很容易估到更小一些数,但是离答案还是很远(刚刚算了个近似的数值解:
-1.6689560053123258)。第二个题目我在整理思路,希望能早点给出。
17392现在把第二题的解答贴上来,见附件:
另注:尽管第一问的一致连续也很容易得到,不过我个人认为应该是证明一致收敛,这样三个问题才显得更连贯一些,请rocktree再看看原题。呵呵,要不然还要自己另外证明一下。
顺便问一句rocktree,最后一个题目还有其他问吗?就是这么一个孤立的题目?!post-21-1125722821.ibf
17392非常感谢!你的分析 实在太牛太牛!我非常非常想认识你!不知道怎磨合你联系,你邮箱是多少?以后不懂的题要多向你请教。北师大第三题就只有一题
,钱吉林编的高代习题村精粹有原题,不过解答错误!
17393今天机器挂拉,要用lingo,但是破解文件找不到啦,那位好心的兄弟如果再用请传一个上来,
记得是破解的
dll文件!!!
17394fn(x)在[a,b]上连续,且一致收敛于f(x),f(x)在[a,b]上无零点
证明:1/fn(x)一致收敛于1/f(x)
17394好像注意f(x)在[a,b]于的值于0有距离就可以了。
也就是连续函数的性质
17394是的,有一致收敛性,f(x)连续,由于[a,b]为紧集,可证
当n足够大时,fn(x)也无零点
好象还应该考虑fn(x)的值域吧
能否把1/fn(x)换成g(fn(x)),g为任意连续函数?
17394fn(x)在[a,b]上连续,且一致收敛于f(x),f(x)在[a,b]上无零点
证明:1/fn(x)一致收敛于1/f(x)
|f(x)|在[a,b]上的最小值m>0,对任意的e>0,存在N,当n>N,|fn(x)-f(x)|<e,特别,取e=m/2,则存在N,n>N,|f(x)|-|fn(x)|<m/2,|fn(x)|>m/2,当n>N,|fn(x)|*|f(x)|>m^2/2
17396没有最高,只有更高
17396高手一般都对痴迷的东西有异乎寻常的兴趣,不会随大流,有自己的见地,深刻地。因而有持续的动力去思考,去探索。但很多高手都有一颗孤独的心,高处不胜寒。别人无法理解。
17396什么样的就算是高手 或者说大家所说的牛人
畅所欲言
17396我想是那些把多个命题变成一个,又把一个命题拓展成多个的人
17396有深刻的洞察力,能看出本质
和很强的牵移能力
17396大凡一个数学高手,他的第一印象往往有一种 很平实的感觉,伟大的人物常有很强的内敛性,有着常人难以想象的专注力和一种痴劲,他们有着非凡的创造力,他们的成果往往具有划时代的意义,可以揭示物质的本质,而本身又不失其简洁性,他们的论文真正蕴涵了数学的美.
17396高手是个形容词,是你我所给予他人的肯定.不论他有多聪明和本事.如果没有他人的肯定,也只不过是个傻子.所谓天才和白痴只有一线只差
17396这个太复杂
呵呵
17396能够以全局的眼光来看待问题,不拘泥于细节
17396“有深刻的洞察力,能看出本质
和很强的牵移能力 ”
同意
17396本人认为是能把复杂问题弄简单,把简单问题弄复杂的人.
此外,我认为数学高手都具备:
1\自信
2\坚韧不拔
3\创新意识
4\良好的心理调节能力
5\很强的逻辑思维能力
6\适合自己的学习方法
……
以后继续总结吧!
17396为积分
17396还是为积分来的,嘿嘿
17396不为积分,对不住老天啊
17396用完了,就再来,嘿嘿
17396不够不够,还要
17396男人就要狠点
17396嘿嘿
17396哈哈
17396再来
17396黑
17396原谅我
17396来了
17396不是故意的
17396来了了了了
17396????????
17396???
17396哈哈哈哈哈
17396哦哦哦哦哦哦哦哦
17396我也来灌灌水啊。
17396
| 引用 (奔跑者 @ 2005年08月31日
20时22分) |
|
我想是那些把多个命题变成一个,又把一个命题拓展成多个的人 |
我也是这样想!
17396不错啊
17396hao!!!!!!!!1
17396痴迷,对数学的投入到了无可复加的地步
17396难说
17397设fn(x)在[a,b]上满足李普希兹条件,fn(x)点点收敛于f(x)
则fn(x)一致收敛于f(x)?
17397若fn(x)在区间上一致满足李普希兹条件,即对任意n,都有|fn(x)-fn(y)|<L|x-y|,则命题成立,否则不成立
具体用定义证明时,把区间分成足够小的多个区间讨论即可
17397谢谢
明白了
不过你的否则不成立
有反例吗
17397fn(x)=x^n [0,1],显然对每个fn,其李普希兹系数为n,但fn(x)在并不一致满足李普希兹条件,也不一致收敛
17397把区间分成足够小的多个区间,是个很常用的方法。
要是能够多找几个用此方法的题就好了
17397哦。原来如此
17399我原来是用matlab的,现在想学这个新的不知道难不难,希望有经验的能给我点建议!谢谢!~
17399很简单的,但学好还是要花一点时间的。
17399lingo 语言要掌握的东西不是很多,主要是要理解集函数的概念。
还有,lingo做规划方面比matlab强,还是建议学一下。
17399对阿,多学学有好处
17399如果对运筹基本了解,最好看软件自带的help,按照章节顺序看下来,连同案例。大概花上个20个小时就差不多搞定了。我也是刚刚看完,感觉收获不小。
17400见题,还有什么positive spanning set,positive linear dependence都是什么含义?
17400紧集的最简单定义:具有有限开覆盖(即从任意覆盖该集合的开集组中总能选出有限个就已经覆盖了此集合);
positive
spanning set:所有正系数的线性组合构成的集合
positive linear
independence:即在正线性组合的意义下线性无关
17400
| 引用 (zhangyuehui @ 2005年09月01日
09时32分) |
紧集的最简单定义:具有有限开覆盖(即从任意覆盖该集合的开集组中总能选出有限个就已经覆盖了此集合);
positive spanning
set:所有正系数的线性组合构成的集合
positive linear independence:即在正线性组合的意义下线性无关
|
能不能告诉俺,具有这样(从任意覆盖该集合的开集组中总能选出有限个就已经覆盖了此集合)特点的集合有什么作用???
17400首先:在中我认为R1中闭集是很重要的。它可又有很都很好的性质
其次:在抽象空间中。例如Hilbert,Banach
space,就用闭集这个概念,来代替。我们可以在无限有界序列中找到收敛子列这个不是很好么?
17400看看拓扑学就清楚了
17400
引用 (978301 @ 2005年09月02日
17时51分) |
| 引用 (zhangyuehui @ 2005年09月01日
09时32分) |
紧集的最简单定义:具有有限开覆盖(即从任意覆盖该集合的开集组中总能选出有限个就已经覆盖了此集合);
positive spanning
set:所有正系数的线性组合构成的集合
positive linear independence:即在正线性组合的意义下线性无关
|
能不能告诉俺,具有这样(从任意覆盖该集合的开集组中总能选出有限个就已经覆盖了此集合)特点的集合有什么作用???
|
在其中任意序列都有收敛子列
17400在代数拓扑和李群里,紧集是必要的因素
17400紧致集有很多很好的性质
比如说Euclid空间中从紧致集到紧致集的连续映射可以取到最值
17400我也一头雾水,请给出几个紧集和非紧集的例子,在任意度量空间都行。
有一组有限个开集所无法覆盖的集合吗?不解!
(-
无穷大,+无穷大)难道不能覆盖R上的任意集合么?难道R上的任何集合都是紧的?
17400注意是任意开覆盖都有有限子覆盖啊.
17400
| 引用 (birds @ 2006年12月29日
21时57分) |
| 注意是任意开覆盖都有有限子覆盖啊.
|
懂了些,“任意开覆盖都有有限子覆盖(就够了)”,反例就是要满足“至少存在一个开覆盖的开子集个数需要是无限的”?
所以R上,[0,
1]是紧的,[0,1)不紧。
真费劲!做题去!
17400
引用 (Jevuxe @ 2007年07月
17日
19时02分) |
引用 (mazl @ 2007年07月
17日
18时41分) |
引用 (Jevuxe @ 2007年07月
17日
08时03分) |
可数紧集:任何开覆盖都有可数覆盖的紧集.
聚点紧集:有限或是任何一个无穷子集都有聚点的集合.
|
可数紧好像是“每个可数开覆盖均有有限子覆盖“.
聚点紧好像是“每个无穷子集都有聚点“.
|
聚点紧集你我的定义等价的,我的定义累赘一点.因为有限集它不能有无穷子集,前提为假,必然紧.
可数紧你说得没错.我记成林德洛夫性质了.
|
有限或是任何一个无穷子集都有聚点的集合
叙述有歧义:
一种是
(有限或是任何一个无穷)子集都有聚点的集合
一种是
有限(集)或是(任何一个无穷子集都有聚点的集合)
我明白了,你用的是第二种含义,
而我看成了第一种含义.
17400对紧集这个概念感觉不是很好把握。它有不少相关的概念:
1 紧集:存在有限覆盖。2 列紧集:任意有向序存在收敛子序
3
可数紧集:任意有向序存在极限点
他们又可以导出相对*紧的概念。但问题在于这些个概念之间相互递推关系。如在一般的拓扑空间紧集不能推出列紧,而列紧也不能推出紧。
但我感觉这个地方过于繁琐。只要知道再度量空间中它们相互等价就差不多了。
17400compact set 紧集,从名字上看,一个紧字。
1。如果你把集合想象成教授在黑板上画的圆圈的话,那么‘紧’就表现在集合
边界上。你可以想象集合的边界‘严丝合缝’,不会‘模糊不清’,有限的
集合就能盖住它。如果边儿上‘模糊不清’的话
保证不了明确的几个集合
能盖住
2。如果你把集合象想成一群离散的点,那么‘紧’就是说 它们(元素)不会
太‘散’,有限的集合就能盖住。
这是我想出的最简单的image了,从数学角度已经很不严密了,全当帮助理解
17400我在一本书上看到有界闭集就叫紧集
17400
| 引用 (foxwyp @ 2007年05月25日
09时49分) |
| 我在一本书上看到有界闭集就叫紧集
|
这种说法是错的,在度量空间中一个集合是否有界是由它的度量决定的,是一个度量性质,而紧性是拓扑性质;一个可度量化的拓扑空间中可以有不同的度量,它们诱导的拓扑都为原来的拓扑。如欧式空间可以看成是度量为普通距离d(x,y)的度量空间,也可以看成是度量为D(x,y)=min{d(x,y),1}的度量空间,在后一种情况下有界闭集就不一定是紧集。
17400在有限维空间中成立
17400
引用 (chaoyueyuechao @ 2007年07月12日
15时
17分) |
| 在有限维空间中成立
|
在拓扑矢量空间的情况下,集合的有界性有另外一种定义,在此定义下任何一个紧集都是有界的,不需要空间为有限维,具体可以参考Rudin的Functional
Analysis。
17400紧集有N个相关概念
紧集:任何开覆盖都有有限覆盖的集合.
可数紧集:任何可数开覆盖都有有限覆盖的集合.
有界闭集:有界的和闭的点集.
列紧集:任何列点都有极限的点集.
聚点紧集:有限或是任何一个无穷子集都有聚点的集合.
......未必完备,欢迎补充
又有N个相关空间
R^n:使用Euclid度量的RxR....空间
完备空间:柯西列收敛的度量空间
一般度量空间:定义了距离函数的向量空间
一般拓扑空间
还有豪斯道夫空间,巴拿贺空间,希尔伯特空间,索伯列夫空间,这些我都不懂了.
其中的充分条件必要条件,欢迎补充
17400
引用 (Jevuxe @ 2007年07月
17日
08时03分) |
可数紧集:任何开覆盖都有可数覆盖的紧集.
聚点紧集:有限或是任何一个无穷子集都有聚点的集合.
|
可数紧好像是“每个可数开覆盖均有有限子覆盖“.
聚点紧好像是“每个无穷子集都有聚点“.
17400
引用 (mazl @ 2007年07月
17日
18时41分) |
引用 (Jevuxe @ 2007年07月
17日
08时03分) |
可数紧集:任何开覆盖都有可数覆盖的紧集.
聚点紧集:有限或是任何一个无穷子集都有聚点的集合.
|
可数紧好像是“每个可数开覆盖均有有限子覆盖“.
聚点紧好像是“每个无穷子集都有聚点“.
|
聚点紧集你我的定义等价的,我的定义累赘一点.因为有限集它不能有无穷子集,前提为假,必然紧.
可数紧你说得没错.我记成林德洛夫性质了.
17400紧集作为拓扑概念是从分析上而来。在R^n空间 闭区间上我们用极值定理等一些漂亮的性质,人们就开
17402我不是搞数学的,遇到一方程不知怎么解?请各位数学高手帮忙,十分感谢和景仰!!post-27-1125412325.ibf
17402哪位高手如果擅长解决这类问题,可以回一下,以便具体讨论,如果我发文章给您挂名。谢谢!
17402我打不开你的文件啊
17402
[ a
b c
c d
c ]
17402
∫ 0
∞
f(x)dx
怎么k是到无穷吗?
17402i know how to solve this equations , please contact me , my e-mail is
lightisgood2005@yahoo.com.hk
17404我发表新贴的时后,想把图片作为附图,可时发表完是发现,附图看不到,请各位告知我为什么,THANKS
17404什么格式的图片?请控制在上传大小范围之内。
174068月28日
19时许,“费马大定理”的终结者第一次来到中国,两所世界著名学府的数学系掌门人在北京国际机场聚首。
北京大学数学科学院院长张继平(中)前来迎接美国普林斯顿大学数学系主任安德鲁·怀尔斯(右),北大数学系02级本科生陈璐(左)向这位数学界的超级偶像献上了鲜花。
安德鲁·怀尔斯因成功破解“费马大定理”而闻名于世。这个最著名的数学难题困惑了世界数学界长达3个多世纪,最终由安德鲁·怀尔斯完成了全部证明,他因此成为数学界的“诺贝尔奖”———“菲尔茨奖”惟一的特别奖获得者,并荣获“沃尔夫奖”。
安德鲁·怀尔斯在京期间将和北京大学数学院的教授进行学术交流,并作两场重要演讲,一场为8月30日下午4时在北大英杰交流中心的公众报告;另一场为8月31日在北大数学院的专题学术报告。
9月1日,安德鲁·怀尔斯将取道香港,领取2005年度“邵逸夫数学科学奖”,该奖为表彰他对最终破解“费马大定理”所作出的巨大贡献而颁。
昨日下午,数学家安德鲁·怀尔斯在北京大学的公众演讲似乎让听众有些遗憾,不但现场没有翻译,而且怀尔斯并没有特别提及自己证明费马大定理的过程。
“费马大定理终结者”第一次到访亚洲
美国普林斯顿大学教授、被誉为“费马大定理终结者”的安德鲁·怀尔斯于2005年8月28日至9月1日到北京大学数学科学院访问,并于昨日在北京大学英杰交流中心阳光大厅举行了一场公众报告。这也是这位世界惟一菲尔茨奖特别奖获得者、沃尔夫奖和邵逸夫奖获得者第一次到访亚洲。除了昨天的公众报告,他还将于今天在北大数学科学院进行一场专题学术报告。
昨日不少学生慕名而来聆听安德鲁·怀尔斯的公众报告,整个阳光大厅座无虚席,而且两旁的走道和大厅后排也都站满了学生。北大数学科学院的文兰院士说,很少有这么多人来听一场数学报告,当然其中也不排除有人是冲着安德鲁·怀尔斯的名字过来的,“因为他算是目前世界上名气最大的数学家了。”
怀尔斯的谦和留下遗憾
学术报告上,安德鲁·怀尔斯讲述了费马大定理的历史过程,他从古希腊讲述费马、再讲述到高斯,其中也讲述到他自己,“虽然他证明出了费马大定律,但他还是把这一过程讲述了很少,可以看出他的谦和之处。”文兰院士认为,其实安德鲁·怀尔斯自己七年的证明过程是他最困难的时期,但他却没有过多地强调这一点。他认为这是安德鲁·怀尔斯的谦和的精神所致。他讲述了前人的历史主要是想说明自己的研究是站在前人的肩上的,然后他又讲述了以后还面对的一些问题。
不过前来听讲的学生和专家还是觉得比较遗憾,因为他们没有亲耳听到安德鲁·怀尔斯教授讲述自己证明费马大定理的过程。虽然其中很多人也了解一些费马大定律的证明过程是把数字问题转化为几何图形问题,但有专家认为这可能是安德鲁·怀尔斯考虑到听众的接受能力,因为这个问题讲起来也比较复杂。报告中确实有人退现场,一位退出现场的女生说,她听不懂这些问题。文兰院士估计,其中除了专业问题外,还有语言上的问题才会让有些人不太感兴趣。
文兰院士还是中国数学会第九届理事长。他说,现在我国的数学研究进步很快,但其中因为整个社会比较浮躁,这在数学研究界的反映就是有些人急功近利。同时有些评估太多,“他们需要花时间去包装,大大超过了数学界应该有的评估,占去了数学研究者太多的时间,”文兰院士说,如果安德鲁·怀尔斯也要面临这么多数学评估的话,他也许不可能在七年内证明出费马大定理的。
■访谈
怀尔斯:坚强的信念一直支持我
记者:你多年前偶然在公共图书馆接触了费马大定理,然后就被吸引。此前你一直喜爱数学吗?
怀尔斯:我从八岁开始就很喜爱数学,这种喜爱是自发的,也没有受到谁的影响。
记者:从青少年时代起,你就研究其他人对费马大定理的证明,当时就想自己做这个研究吗?
怀尔斯:在我上研究生以前,我确实一直在尝试证明费马大定理,但都是不成功的。
然后,研究就中止了。因为以前有很多人耗费了大量精力却没有成功,所以我这个时候也不能持续做下去。
记者:后来又是什么原因使你丢下别的工作,全力去证明费马大定理?
怀尔斯:
1986年,格哈德·弗赖提出,费马大定理的真实性将使谷山-志村猜想一经证明之后的直接结果并演算出一个椭圆方程,于是,我决定重新研究原来搁置的问题,并可以运用一些新的方法。
记者:你在重新开始研究的时候想到过自己会成功吗?
怀尔斯:那时很难说,主要是有坚强的信念一直支持我。
记者:你
1986年在家里做秘密研究,为什么不想让其他人知道?你害怕自己失败吗?
怀尔斯:我开始的时候也对一些人说过我对这个新的方法很感兴趣,他们就问了我很多问题。这样我就不能静心研究,所以才这样。
记者:在证明费马大定理之前,数学对你来说意味着什么?证明费马大定理之后,数学对你又意味着什么?
怀尔斯:在证明之前,我觉得数学对我好像不太友好,之后我觉得数学还是很自然的,什么东西都是可及的。

17406安德鲁·怀尔斯和费马大定理
2005年度邵逸夫奖授予了美国普林斯顿大学数学系教授安德鲁·怀尔斯,以表彰他为
最终解决费马大定理所做出的巨大贡献。此前,著名美籍华人数学家陈省身曾于2003年获
此殊荣。
大家熟知的勾股定理常有整数解,如勾三股四弦五。然而三百多年前,法国数学家费
马(1601-1665)在他读过的《算术》一书的空白处写到:不可能将一个立方数写成两个
立方数之和;或者将一个四次幂写成两个四次幂之和;或者,所总的来说,不可能将一个
高于二次的幂写成两个同样次幂的和。他还称自己已有一个对此命题的十分美妙的证明,
但这里空白太小,写不下。
这是一个中学生都能理解的数学命题,称为费马大定理。许多数学家为此耗尽了毕生
心血。然而200年过去了,人们仅仅对3次幂,4次幂,5次幂和7次幂这四种情形证明费马
的断言是成立的。第二次世界大战之后,借助于计算机,数学家对500以内,然后在1000
以内,再是10000以内的幂次证明了费马大定理。到上个世纪八十年代,这个范围提高到
了25000,然后是400万以内。但这样永远到不了无穷,数学家希望寻求的是统一的、完整
的严密证明。
这样统一、完整的严密证明最终是由安德鲁·怀尔斯经过七、八年时间的努力得以完
成。
1986年夏,安德鲁·怀尔斯听说肯·里贝特证明了谷山-志村猜测蕴涵费马大定理,
便开始专心致志来证明谷山-志村猜测。
怀尔斯于
1953年出生在英国,
1974年毕业于牛津大学,之后在剑桥大学取得博士学位
,研究的题目为椭圆曲线的Iwasawa理论。
1980年他来到普林斯顿大学任教。从
1986年开
始,怀尔斯为专心研究,放弃了所有与证明费马大定理无直接关系的工作,只要有可能就
回到家里工作,完全独立和保密地在自己书房里思考问题。期间只有他的妻子知道他在证
明费马大定理。他说:
我意识到与费马大定理有关的任何事情都会引起太多人的兴趣。你
确实不可能很多年都使自己精力集中,除非你的专心不被他人分散,而这一点会因旁观者
太多而做不到。
1993年6月,怀尔斯在英国剑桥大学新成立的牛顿研究所做了一系列学术报告。在最
后一次演讲结束时,他完成了谷山-志村猜测的证明。听众报以热烈掌声并以最快速度把
这一消息传递给世界各地的同事。《纽约时报》也在头版报道了费马大定理被证明的消息
。
随后怀尔斯长达200页的手稿交由六位同行审阅,许多毛病被发现并迅速得以修正,
然而其中一个缺陷却不容易修补,通过与泰勒8个多月的合作,
1994年9月怀尔斯终于完成
了全部证明。
费马大定理最终得以证明,是人类智力活动的一曲凯歌。怀尔斯因此获得菲尔茨奖特
别奖和沃尔夫奖。
17406今天特地到北大去听他讲座
真爽post-52-1125505626.jpg
17406得奖无数的大师!希望尽快看到他的讲座的电子板!!
17406费马大定理终结者
――数学大师安德鲁•怀尔斯北京纪行
2005年08月31日
张立宪/撰文
2005年8月29日,我吃了平生最智慧的一顿晚餐。
在座12人中,有北京大学数学院院长张继平、副院长刘化荣,中科院院士田刚、张恭庆、姜伯驹、丁伟岳、文兰等。他们为之接风洗尘的是费马大定理的终结者———美国科学院外籍院士安德鲁·怀尔斯。此前一天,他第一次踏上中国的土地,这甚至是他第一次来到亚洲。
我坚信,这是全北京有史以来平均智商最高的一次饭局。
29日,我和北大数学院的宗传明教授陪同怀尔斯走过了天坛、天安门、故宫和北海,虽说已经入秋,这天的北京还是闷热异常,每到一块荫凉的地方,我就看到胳膊上起了一层盐粒。怀尔斯一路上气定神闲,或温和地笑或专注地思考,望着熙熙攘攘与他擦肩而过的人流,双眼在镜片后射出和善而腼腆的目光。人多的场合,他多是安安静静地倾听,即使说话,声音也恒定在某个分贝数之下。一如所有接触过他的人对他的评价:温文尔雅。这位颇具风度的英国绅士,在张继平院长眼中是数学家中的“Superstar”(巨星)。
这一天,在浏览了北京的名胜,品尝了北京的烤鸭和清蒸桂鱼,乘坐过北京的出租车和公共汽车后,我们坐在昔日的皇家公园北海的湖边。
安德鲁·怀尔斯
1953年出生在英国,
1974年毕业于牛津大学,之后在剑桥大学取得博士学位,
1980年到美国普林斯顿大学任教。他金发稀疏,脸色略显苍白,身材单薄高大,有一米八○左右。他那充满了智慧的脑袋,看起来好像没有什么特别之处,甚至比例上比常人还要稍小些。此前的热身采访中,任普林斯顿大学教授的田刚院士描述这位同行:低调,不常露面,只出现在全系大会上,说话很少,对工作认真负责,录取学生时,会很仔细地看每一份学生的材料,受到同事们的尊敬。
这次采访之后,张继平院长笑着问我:“领略到一个真正的数学家的谈吐了吧?”
是的,最像数学家的回答出现在这里。我问:“介意说说你和太太是如何相爱并结婚的吗?”
“我们在普林斯顿相识,我们在普林斯顿结婚。”
“您在费马大定理的研究过程中,靠的是纸、笔和头脑,没有用电脑,现在您开始用电脑了吗?电脑今后在数学家的工作中是否会扮演越来越重要的角色?”我问。“我如今仅仅是用计算机去找一些例子,并予以验证,以及搜集一些特殊情况下的信息,我从来不用电脑做直接的证明。不同的数学家对电脑有不同的态度。我自己很少用计算机,但我的一个学生却用计算机解决了一个很重要的问题。当然他用计算机解决的这个问题的特征与我的很不一样。数学领域中只有很少的问题是能够通过计算机来解决的。”他的回答简直像在叙说一个定理。
“通过对费马大定理的证明,全世界都在关注您。那么,公众的关注对您的生活有影响和改变吗?”
“当然有所改变。对我个人来说,最大的改变是我不用再做费马大定理这道题了。”
“美国电影《美丽心灵》中,主人公约翰·纳什获得诺贝尔奖之后,一群数学家在会议厅里纷纷向他献上钢笔,作为一种致敬的方式,这是普林斯顿大学的传统吗?您收到过钢笔吗?”
“当然是虚构的。”他笑出声来,“不过这倒是个好主意,应该从现在开始就这么做。”
一问一答中,怀尔斯的眼神常常越过对面的我,投向更远的去处,他的谈话,充满停顿、沉吟,说出来的,就像数学公式一样简约而周密。
“我已经解决了费马大定理”
17世纪的法国数学家费马死后,他在一本数学书里留下的边注被人们发现,由此诞生了一个让后人难以解答的问题:“不可能将一个立方数写成两个立方数之和;或者将一个4次幂写成两个4次幂之和;或者,总的来说,不可能将一个高于2次的幂写成两个同样次幂的和。”
这是一个用每个中学生都熟悉的话来表达的谜,却难住了世界上最聪明的头脑。更折磨人的是,费马还留下一个注记,暗示他已经有了一个解答,不过他没有写出这个证明。
于是,一代又一代的数学天才前赴后继,向这一猜想发起挑战。300多年过去了,这个定理依然缺少一个完整严密的证明。还没有什么问题表达起来如此简单清晰,破解的旅途却如此漫长和艰难。
安德鲁·怀尔斯10岁时,就被费马大定理吸引住了,并从此选择了数学作为终身职业。上大学之后,“我一直在想,历史上许多人把可想到的办法都想到了,最终也没有解决费马大定理,所以,我必须要学习更高深的数学。从研究生阶段,我把更多的精力放在了拓宽自己的视野方面。”采访中回忆起当时的情景,他认为,那段时间“看起来我似乎暂时离开了大定理。”
1986年,安德鲁·怀尔斯决定向费马大定理发动冲击。他先用
18个月的时间,收集了这次战斗所必要的数学工具,而他全面的估计是:接下来要做的,是可能长达10年的专心致志的努力。
我问:“当时有许多数学家觉得这个问题很难,或者觉得解决这个问题的希望很渺茫,放弃了,而你坚持了7年。当时着手研究的时候,你把握大吗?是否明知道把握不大也要做?”
“从历史上来看,真正的严肃的数学家中,决定研究费马大定理的人并不是很多,因为他们首先要考虑在他们所处的历史条件下,数学的发展是否给他们提供了工具,足够达到解决这个问题的水平。到
1986年我决定研究大定理,那个时候绝大多数的人认为手中的工具也不够,而我认为是有希望的。”他否认自己具有那种明知不可为而为之的鲁莽,“所以我并不是浪漫,而是有很现实的把握。”
有一种普遍的说法,怀尔斯在完全保密的状态下进行专心研究,不让任何人知道他所做的事情,也不与任何人进行交流。在那7年时间里,只有他的妻子知道他在做什么。
采访中,怀尔斯澄清了这种说法:“其实一开始的时候,我还是告诉了一些同事,但他们知道后,一见到我就不断地问我进展情况,使我感到很大的压力和干扰。所以我觉得还是不要讲出来更好一些。我意识到,要解决这个问题,需要很长很长的时间。在这个过程中不断被人问及,要承受的压力是很大的。就像一个孩子,成长的过程中,如果老是被人问多大了,几岁了,成长中有什么问题?那是很难堪的。”
就这样,他逐渐转入一种秘密状态下的战斗。终于有一天,他对妻子说:“我已经解决了费马大定理。”
1993年6月,安德鲁·怀尔斯在英国剑桥大学牛顿研究所做了三次学术报告,在最后一次演讲结束时,他完成了对费马大定理的证明。这个消息迅速登上世界各大报纸头版的位置,在数学界更是奔走相告。消息在第一时间传到巴黎,几位数学家举杯相庆,其中有当年的沃尔夫奖得主蒂茨,法国数学家布鲁埃、普伊赫、鲁基耶和当时正在巴黎高等师范学校任访问教授的张继平。
当世界各地的数学家为他举杯庆祝时,安德鲁·怀尔斯向《数学发明》杂志递交的论文正在进行严格的审稿。审查人在论文的第三章中碰到了一个问题,使得怀尔斯无法像原来设想的那样保证某个方法行得通。他必须加强他的证明。
在距离生日还有两周的时候,安德鲁·怀尔斯的妻子对他说,她惟一想要的生日礼物是一个正确的证明。
遗憾的是,两周后,安德鲁·怀尔斯没能献出这份生日礼物。
随着时间的推移,刚刚欢呼的人们又把心悬了起来。300多年来,在众多尝试过的对费马大定理的证明中,还没有一个人能补救出现过的漏洞。时间最近的一次失败是
1988年3月8日,《华盛顿邮报》和《纽约时报》宣称东京大学的宫冈洋一发现了费马大定理的解法,一个月后又不得不宣布收回。难道怀尔斯也不能逃脱这种宿命?BBC电视台的科学编辑约翰·林奇说:“我很难想像安德鲁不会是那片数学墓园中的另一块墓碑。”
这次证明工作几乎是在全世界的关注下进行的,据说当时普林斯顿大学的同事们在一起谈论的只有两件事:辛普森案件和怀尔斯的证明。
安德鲁·怀尔斯如今回忆起这段时光,仍然历历在目:“第一个阶段我非常幸福,是在享受那个过程。第二个阶段,我就像置身于大庭广众之下了,在数学界的会议上,许多人不断地问我,我不喜欢这种状态。”
在最绝望的时候,他甚至已经准备好公开承认自己的证明有缺陷。他的同事田刚教授在接受我的采访时,评价安德鲁·怀尔斯是一个“勇敢的人”,因为那段时间他承受的是超乎寻常的巨大压力。我问怀尔斯:“你认为自己是个‘勇敢的人’吗?”
他回答:“我只知道这个问题能够解决,并且也希望能够解决。即便我承认我的证明有缺陷,也会有成百上千的人看到希望,看到我们已经有了足够的好的工具,他们会进一步把这个问题解决掉。也许他们会用一些时间,8年,10年,但工具已经有了,方向已经有了。”
安德鲁·怀尔斯的判断没有错,14个月之后,他向《数学年刊》递交了第二份论文,由《模椭圆曲线和费马大定理》和《某些赫克代数的环论性质》两篇组成,这一次对证明不再有怀疑了。
怀尔斯夫人最终得到了她想要的生日礼物。“你妻子对这个迟到了一年的生日礼物有什么反应?”我问。
他笑道:“她比一年前得到这个礼物还高兴。”
“不,费马不可能解决这个问题”
中科院院士、北大数学院教授姜伯驹,评价安德鲁·怀尔斯对费马大定理的证明是“20世纪最辉煌的数学成就”。
荣誉接踵而至,
1996年,怀尔斯和罗伯特·朗兰兹分享了10万美元的沃尔夫奖。朗兰兹提出的朗兰兹纲领,是一个使数学各领域之间证明统一化的猜想,而怀尔斯通过对谷山-志村猜想的证明,将椭圆曲线和模形式统一了起来,这个成功为朗兰兹纲领注入了生命力———一个领域中的问题可以通过并行领域中的对应问题来解决,这是一个可能使数学进入又一个解决难题的黄金时期的突破性工作。
1998年,国际数学家大会在柏林召开,数学界的“诺贝尔奖”菲尔兹奖授予安德鲁·怀尔斯特别奖。
菲尔兹奖以加拿大数学家约翰·菲尔兹的名字命名,用于奖励那些年龄在40岁以下的青年才俊作出的杰出成就。安德鲁成功证明费马大定理时,刚刚过了40岁。目睹怀尔斯获奖并当场听取了他报告的中科院院士张恭庆教授对此评价道:这个300多年的问题得以解决,在数学界具有里程碑意义,这也是菲尔兹奖历史上惟一的一个特别奖。
环绕在普通公众心中的疑问是,提出这个问题的费马曾经写过“我有一个对这个命题的十分美妙的证明,这里空白太小,写不下”,而在300多年前费马所处的时代,他并没有安德鲁·怀尔斯所用的证明大定理的工具:椭圆曲线、模形式、谷山-志村猜想、伽罗瓦群论、岩泽理论和科利瓦金-弗莱切方法。那么,费马本人是用什么方法证明他所提出的猜想的呢?
安德鲁·怀尔斯第一次递交《数学发明》杂志的论文有200页,第二次递交《数学年刊》的论文有130页。张继平院长说,这是对费马大定理惟一无懈可击的,最严密也最经济的证明了。那么有没有更简单的证明呢?
北大数学院的老师们说,数学界关于费马大定理有种种传言,但是到目前为止,经过严格审查的其他证明,都是错的。“你有没有想过费马的证明方法是什么?如果他写论文的话,会有多少页?”我问安德鲁·怀尔斯。
“费马并没有写出过论文。”他简洁地答道。
“许多普通读者都会有这个疑问,费马本人真的能证明费马大定理吗?”我继续问道。
担任翻译的宗传明教授直接回答了我:数学界普遍认为,费马所说的他的解法是不会有的。
安德鲁·怀尔斯听完宗的翻译,肯定道:“不,费马不可能解决这个问题。”
“您认为会有别的解法吗?”
“尽管任何事情都有可能发生,但我还是认为不会有比我更简单的证明了。也许我的证明还可能再简化一些,但关于费马大定理的证明的基本思想和复杂程度是不会变的。”
费马大定理被证明后,又有10年过去了,作为一个数学家,安德鲁·怀尔斯的生活并没有改变。他还是像以前一样,早晨起来,去办公室,研究新的数学问题。“您认为当今数学界最有趣的题目是什么?”我问。
“当然是黎曼假设。”
黎曼假设是数学界人士所共知的7个“世纪问题”之一,由
19世纪德国数学家黎曼提出。我在网上查到的对该假设的简要叙述是:素数的分布频率紧密相关于一个精心构造的所谓黎曼蔡塔函数z(s)的性态。著名的黎曼假设断言,方程z(s)=0的所有有意义的解都在一条直线上。
“你是否现在在研究黎曼假设?”
“我有时候也考虑这个问题,但是用的时间很少。
1986年我开始证明费马大定理的时候,别人发现的方法正好是我擅长的领域,并且是我能够解决的。但迄今为止世界上没有任何人对黎曼假设可以提出什么方向,或属于什么领域,没有人知道,黎曼假设是该由一个数论学家,还是函数论学家来证明。如果破解的工具在数论领域,我当然会用更多的时间来研究。”
他描述自己闻名天下后的情形说:“费马大定理让我跟数学界之外的人有了很多接触,体会到别人对数学的感受。我收到世界各地的邀请———包括这一次来北京大学。其间遇到世界各地非常友好的人,我非常高兴,但这样的机会我用的不多。”
据说,普林斯顿大学的老师们之间流传一个笑话:建议安德鲁·怀尔斯去接拍广告,包括男式内衣。于是我向他求证:“你真的接到过拍摄广告的邀请吗?”
他的回答出乎我的意料:“确实有过,但那家服装公司的名字叫‘G.A.P’(gap意即‘缺陷’),所以我拒绝了。”
今年7月1日,安德鲁·怀尔斯就任普林斯顿大学数学系系主任。作为国际顶尖的研究与教学机构,普林斯顿的数学系被称为“定义什么是好数学的地方”,当我问他是否喜欢这个职务时,他用一种淡定的口吻答道:“只有到结束了这个职务时,我才能断定自己喜不喜欢。”
“是这个问题选择了我”
北大数学院陈大岳教授早早就将安德鲁·怀尔斯即将访问北大的消息发布到校园网上了。两天之内,5000多人次浏览了这条信息。
8月30日下午1时30分,北京理工大学数学系02级本科生秦晋赶到北京大学英杰交流中心阳光大厅占座,北京大学以及附近人大、理工大学的同学也陆续赶来,下午3时30分,300余人的座位已经座无虚席。
下午4时整,安德鲁·怀尔斯在掌声中开始了他的公众演讲。在讲台上,他不再像接受采访时那样时常沉吟,而是如同回到自己的王国一样从容自在,流利的英语具有音乐的韵律。在一个小时的时间里,他回顾了费马大定理的历史,和300多年来数学界攻克费马大定理的灿烂历程。然后提出了一些数学领域有待解决的问题,结束于abc猜想。幻灯最后定格在一组巨大的数字上,阳光大厅里发出一阵会心的微笑。
在其后的交流中,北大数学院03级直博生刘琦问怀尔斯教授为什么要选择这个耗时达七八年之久的研究课题?怀尔斯回答:“不是我选择了这个问题,是这个问题选择了我。”前一天,他对北大数学院的同行简单谈起对北京的印象:皇帝居住的故宫比他此前所想像的还要宏伟得多,不过,“我不愿意当皇帝,我宁肯做个数学家”。
1995年毕业于北大数学系的袁喜利今天偶然来到母校,碰到了这次演讲。他站在座位旁边听完安德鲁·怀尔斯的演讲,深有感触地说:“这种不求实用,全身心投入理论研究的数学家,目前在我们国内太少了。”
安德鲁·怀尔斯的治学经历令北大的同行感叹不已。北京大学数学研究所所长丁伟岳院士说:“怀尔斯教授用7年时间专门攻克一个世界难题,如今已很少有人耐得住这种寂寞了。许多人急功近利,急于求成,大家应该向安德鲁·怀尔斯学习。”北大数学院副院长刘化荣说得更直白:“他为科学献身的精神值得我们学习。”
一些数学家则对我们的科研体制提出质疑。姜伯驹说:“在中国,即使有人有破解费马大定理的智慧,恐怕也不一定能成功。如今大家都忙于应付评估,必须出一些短平快的成果,许多精力、智慧都被浪费了。”
“300年的难题,7年的投入,对我们来说,光是评估就把时间占没了。”北京大学数学院文兰院士说。
“像安德鲁·怀尔斯这样,7年潜心研究一个问题,不出成果,不发表论文,要在中国,早就没津贴,没经费了。”张恭庆补充道。
“归根到底,还是科技体制需要改革的问题。”张继平一言以蔽之。
8月31日上午,安德鲁·怀尔斯将在北大数学院做一次专题学术报告,然后将取道香港,领取2005年度的邵逸夫数学科学奖,以及100万美元奖金。
张继平评价安德鲁·怀尔斯的中国之行“是中国数学发展史上的一件大事”。
当安德鲁·怀尔斯即将完成此次的北京之行时,他应邀为中国青年报的读者赠言—————我认为中国的年轻人工作非常努力,希望他们勇于追求自己所挚爱的东西,因为对事业的投入和热爱将使他们在前进的途中所向披靡。
17406向数学界的超级偶像致敬!
17406没有去听真是遗憾。偶27号就离开北京了。哎。
17406在中国如果你七年默默无闻,什么也不发表,很难想象你是否早就被赶走了.
17406费马大定理最后的证明
(转自《科学时报》)
自费马大定理提出后的350年以来,许多优秀的数学家采用种种方法试图补证这个定理,
但始终都未获得成功。英国的数学家怀尔斯十年磨一剑,终于于
1995年彻底解决了这一问
题。
怀尔斯:谨慎的屠龙者
十七世纪法国数学家费尔马(Fermat)在刁番都(Diophantine)著作的一页边上写了一
个猜测“Xn+Yn=Zn当n>2时没有正整数解。”后人称此猜想为费尔马大定理。费尔马接着
写道:“对此,我已发现了一个巧妙的证明,可惜这里页边的空白太小,写不下。”
费尔马去世之后,他的儿子把费尔马的著述、书信以及费尔马校订刁番都的著作都一
起发表了,但没有发现费尔马大定理的证明,费尔马是否真正能够证明这个猜想,至今仍
然是个谜。
三百多年以来,许多优秀的数学家采用种种方法试图补证这个定理,但始终都未获得
成功,直至最近才有英国的怀尔斯(Andrew
Wiles)解决。历史性的转变发生在
1993年6
月21日至23日这三天,当时在普林斯顿数学系任教的40岁的怀尔斯正在英国剑桥大学举行
一次约有40至60人出席的数学会议上,每天做一段演讲,题目是“模形式,椭圆曲线和伽
罗华表示”。从题目上看不出他要讲的是费尔马大定理,但是他演讲的最后一句话是:“
这表明费尔马大定理成立,证毕。”
怀尔斯的证明引起了数学界的很大关注,他的初稿虽然有少许瑕疵,但是稍后被怀尔
斯自己修正过来。纽约时报曾在
1993年6月29日以“安德鲁·怀尔斯放出数学卫星,350年
的古老问题已被攻克”为题发表有关报道。
费马大定理最后的证明
为了寻求费马大定理的解答,三个多世纪以来,一代又一代的数学家们前赴后继,却壮志
未酬。
1995年,美国普林斯顿大学的安德鲁·怀尔斯教授经过8年的孤军奋战,用130页长
的篇幅证明了费马大定理。怀尔斯成为整个数学界的英雄。
大问题
在物理学、化学或生物学中,还没有任何问题可以叙述得如此简单和清晰,却长久不
解。E·T·贝尔(Eric Temple
Bell)在他的《大问题》(The Last
Problem)一书中写
到,文明世界也许在费马大定理得以解决之前就已走到了尽头。证明费马大定理成为数论
中最值得为之奋斗的事。
安德鲁·怀尔斯
1953年出生在英国剑桥,父亲是一位工程学教授。少年时代的怀尔斯
已着迷于数学了。他在后来的回忆中写到:“在学校里我喜欢做题目,我把它们带回家,
编写成我自己的新题目。不过我以前找到的最好的题目是在我们社区的图书馆里发现的。
”一天,小怀尔斯在弥尔顿街上的图书馆看见了一本书,这本书只有一个问题而没有解答
,怀尔斯被吸引住了。
这就是E·T·贝尔写的《大问题》。它叙述了费马大定理的历史,这个定理让一个又
一个的数学家望而生畏,在长达300多年的时间里没有人能解决它。怀尔斯30多年后回忆
起被引向费马大定理时的感觉:“它看上去如此简单,但历史上所有的大数学家都未能解
决它。这里正摆着我——一个10岁的孩子——能理解的问题,从那个时刻起,我知道我永
远不会放弃它。我必须解决它。”
怀尔斯
1974年从牛津大学的Merton学院获得数学学士学位,之后进入剑桥大学Clare
学院做博士。在研究生阶段,怀尔斯并没有从事费马大定理研究。他说:“研究费马可能
带来的问题是:你花费了多年的时间而最终一事无成。我的导师约翰·科茨(John
Coates)正在研究椭圆曲线的Iwasawa理论,我开始跟随他工作。”
科茨说:“我记得一
位同事告诉我,他有一个非常好的、刚完成数学学士荣誉学位第三部考试的学生,他催促
我收其为学生。我非常荣幸有安德鲁这样的学生。即使从对研究生的要求来看,他也有很
深刻的思想,非常清楚他将是一个做大事情的数学家。当然,任何研究生在那个阶段直接
开始研究费马大定理是不可能的,即使对资历很深的数学家来说,它也太困难了。”科茨
的责任是为怀尔斯找到某种至少能使他在今后三年里有兴趣去研究的问题。他说:“我认
为研究生导师能为学生做的一切就是设法把他推向一个富有成果的方向。当然,不能保证
它一定是一个富有成果的研究方向,但是也许年长的数学家在这个过程中能做的一件事是
使用他的常识、他对好领域的直觉。然后,学生能在这个方向上有多大成绩就是他自己的
事了。”
科茨决定怀尔斯应该研究数学中称为椭圆曲线的领域。这个决定成为怀尔斯职业生涯
中的一个转折点,椭圆方程的研究是他实现梦想的工具。
孤独的战士
1980年怀尔斯在剑桥大学取得博士学位后来到了美国普林斯顿大学,并成为这所大学
的教授。在科茨的指导下,怀尔斯或许比世界上其他人都更懂得椭圆方程,他已经成为一
个著名的数论学家,但他清楚地意识到,即使以他广博的基础知识和数学修养,证明费马
大定理的任务也是极为艰巨的。
在怀尔斯的费马大定理的证明中,核心是证明“谷山-志村猜想”,该猜想在两个非
常不同的数学领域间建立了一座新的桥梁。“那是
1986年夏末的一个傍晚,我正在一个朋
友家中啜饮冰茶。谈话间他随意告诉我,肯·里贝特已经证明了谷山-志村猜想与费马大
定理间的联系。我感到极大的震动。我记得那个时刻,那个改变我生命历程的时刻,因为
这意味着为了证明费马大定理,我必须做的一切就是证明谷山-志村猜想……我十分清楚
我应该回家去研究谷山-志村猜想。”怀尔斯望见了一条实现他童年梦想的道路。
20世纪初,有人问伟大的数学家大卫·希尔伯特为什么不去尝试证明费马大定理,他
回答说:“在开始着手之前,我必须用3年的时间作深入的研究,而我没有那么多的时间
浪费在一件可能会失败的事情上。”怀尔斯知道,为了找到证明,他必须全身心地投入到
这个问题中,但是与希尔伯特不一样,他愿意冒这个风险。
怀尔斯作了一个重大的决定:要完全独立和保密地进行研究。他说:“我意识到与费
马大定理有关的任何事情都会引起太多人的兴趣。你确实不可能很多年都使自己精力集中
,除非你的专心不被他人分散,而这一点会因旁观者太多而做不到。”怀尔斯放弃了所有
与证明费马大定理无直接关系的工作,任何时候只要可能他就回到家里工作,在家里的顶
楼书房里他开始了通过谷山-志村猜想来证明费马大定理的战斗。
这是一场长达7年的持久战,这期间只有他的妻子知道他在证明费马大定理。
欢呼与等待
经过7年的努力,怀尔斯完成了谷山-志村猜想的证明。作为一个结果,他也证明了费
马大定理。现在是向世界公布的时候了。
1993年6月底,有一个重要的会议要在剑桥大学
的牛顿研究所举行。怀尔斯决定利用这个机会向一群杰出的听众宣
17406我们崇拜明星,但我们更需要在乎那些默默无闻执着自己所钟爱的东西的数学家们!
17406值得尊敬,值得学习。但愿中国在科研上不要再急功近利了。
17406
引用 (njustlmathslst @ 2005年09月01日
17时
19分) |
|
在中国如果你七年默默无闻,什么也不发表,很难想象你是否早就被赶走了. |
中国有很多象他这样的人在默默工作,只是成功者太少罢了!象他那样的人在中国更容易生存,他其实是普林斯顿有史以来唯一的一个,撞大运了!
17409那位大虾给指点一下!多谢!
17410n points (vertices) on a plane form a unique polygon if and only if
it is convex.
17411Prove that a concave polygon will be concave when you add new
vertices. (the equivalent statement is that a convex n-gon will be convex
when you remove a vertex, n>3)
17413希望子青兄帮助解答一下以前残留的问题,谢谢!
以前的解答见pdf文件,我的问题见word文件!post-
17-1125446
176.ibf
17413请见附件!post-
17-1125446551.ibf
17413哦,我再看了一下,好象∑的下标有点问题.
里面那个∑的下标应该是x_j /in
B_i,表示对所有同一个区间B_i内的x_j求和
外面一个∑的下标是i,表示对所有的区间求和
思想就是原来求和是按x_i的下标计算的,现在把顺序整理一下,按区间B_i的下标来计算,先计算所有同一区间内的x_j,再按区间B_i的下标求和.
17413还不是很明白,问题见附件!post-
17-1125506208.ibf
17413对,就是这么改,第三项不用改
17413明白了,谢谢子青兄:)
174141 是否存在这样一个函数,f(x)在[0,1}上处处有有限值,但是在每一点的任何邻域内无界
2 设 {
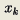
}是一个正无穷大数列,即对任意正数M,存在一个相当大的N,当k〉N时,
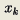
〉M,设E是{
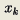
}的所有元素所组成的数集,求证存在某个k,使
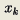
=infE
17414
| 引用 (矛与盾 @ 2005年08月31日
08时02分) |
1
是否存在这样一个函数,f(x)在[0,1}上处处有有限值,但是在每一点的任何邻域内无界
2 设 { 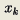 }是一个正无穷大数列,即对任意正数M,存在一个相当大的N,当k〉N时,
}是一个正无穷大数列,即对任意正数M,存在一个相当大的N,当k〉N时, 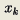 〉M,设E是{ 〉M,设E是{
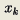 }的所有元素所组成的数集,求证存在某个k,使
}的所有元素所组成的数集,求证存在某个k,使 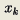 =infE =infE
|
第一个不难构造吧:
定义一个函数,把无理数映到0;有理数映到相应的既约分数的分子。
这个肯定是满足题目要求的吧
第二个不知道是不是我理解错了:
好像这个问题去个M,把
x k 分成两部分就好了。
17414
| 引用 (矛与盾 @ 2005年08月31日
09时58分) |
| 能帮证明一下函数是如何无界的吗
|
你不能说明它有界就是无界啊!
假设在a(不妨设大于0)的一个开邻域是有界M的
那么说明邻域内有理数的分子都是小于M的
能取的分母(使这个分数在这个邻域内的)也是有限的
这样邻域内的有理数就是有限个
矛盾
附件可以添加,下面有浏览选出来就是了
17414第一个,是这样做的。但是,我不明白,对任意一点x,取有理点列趋近于x时,为什么有理点列的分母可以趋近于无穷大呀
17414
| 引用 (矛与盾 @ 2005年08月31日
09时36分) |
|
第一个,是这样做的。但是,我不明白,对任意一点x,取有理点列趋近于x时,为什么有理点列的分母可以趋近于无穷大呀
|
没说要趋进于啊
这个肯定是没有极限的啊
你题目的要求也不是和极限有关啊
只是如何的数都不能限制
这就是无界吧
对于无界的一般要反正的思想去考虑
找极限一般反而不好
17414能帮证明一下函数是如何无界的吗
17414如何添加附件呀
17414谢谢,我明白了
17414另外,还想问个问题,矩阵是正定的一定是半正定的吗
17414
引用 (矛与盾 @ 2005年08月31日
10时
19分) |
|
另外,还想问个问题,矩阵是正定的一定是半正定的吗 |
肯定是啊
仔细看看定义就是了
17414有意思
17414那男生该怎样说呀
17414北大高代参考书中有一道题中提到,“若矩阵是半正定的,则矩阵的秩等于正惯性指数,小于矩阵的阶数”
17414
| 引用 (矛与盾 @ 2005年08月31日
15时29分) |
|
北大高代参考书中有一道题中提到,“若矩阵是半正定的,则矩阵的秩等于正惯性指数,小于矩阵的阶数”
|
那只能说定义的问题
这个只是在玩玩什么文字游戏
你仔细看看定义就自明了
17414第2问证明思路,也可用反证法post-38-1125579500.ibf
17414
第一题是一个处处局部无界函数的好例子
第二题,首先必有有下确界l,这是显然的,对l+1,存在N
任意的n<N,a^n<=l+1,由l的性质,l也是前面有限项的的最小值。
17414谢谢大家
第二题,下确界不一定非底是1吧
17414
| 引用 (矛与盾 @ 2005年09月01日
20时35分) |
谢谢大家
第二题,下确界不一定非底是1吧 |
呵呵,对,是字母 l 不是 1
17414第二题解答!post-38-1125624851.ibf
17415在大学课堂 尤其是数学课堂发展探究性学习 可行性分析
大伙 畅所欲言
17415这阵风还没刮到我们学校,拭目以待
17415我们大学比较小,估计5年内还没这意向
17415不知道要多少年才刮到我们这里,我也曾试着给学生这样上过,可是,学生自己没有看书,就等着灌,再努力控究也没用。
17415我已经在自己的教学中适当的采用了探索性的教学,学生普遍反映感觉不错,学习兴趣提高了,学习热情被调动起来了。
17415大学的考试成绩是用来给谁看的,学生?老师?.....不,他们都知道考试成绩是什么东西(缺乏自主思考的产物),是给上级行政部门看的,我们再看中国的大部分大学生的论文是怎样写的,估计是摘抄的多巴,要知道国外的好的大学论文比考试成绩更重要,那是要有自己的见解的,不过新的教育方式要学生的素质要高一些,中国现在的大学的扩招象是普及大学教育,大学应该学识要比技术学校和中专等的广和更理论,是为了能学了之后进一步学习再去创新,结果大学生的质量跟不上(和招生质量与学风有关),理论理论没学好,技术技术又不专,还不如技术学校的(这从大片的大学生找不到工作可见一斑)。强烈呼吁不要将大学生看成一种“产业”,大学生要“宁缺毋滥”,要用有限的资源培养出高质量的人才,不要用有限的资源养一群庸才,在学术上三个臭皮匠顶不了一个诸葛亮!!!!!!!!!!
教育和医疗的进步才是一个国家和社会进步的真正标志,不要“只”看钱。
原祖国真正的强大起来。
17415成绩是要考核的,考试成绩不好是要挨批的,学生探说是不可能的
174
18复旦和清华的怎么样?麻烦给点建议
174
18北大
中山
174
18还有北师
174
18北师好,而且近几年发展很快
174
18国家统计学院
174
18恩.好象北师两个院士都是搞概率的
174
18北师大最强,有两名中科院院士。
如果是
174
19博士家园自实行技术积分以来,涌现出很多热心成员,默默无闻,不辞辛苦的解答问题,热心参与讨论等等,我们将不定期给这些精英进行加分奖励!希望更多的成员参与进来,学习讨论共同进步!
当然,我们也有很多不足,例如没有及时对个别用户进行技术加分等,希望各版斑竹切实行动起来,按照标准给出技术加分。
也希望您能给出您要求加分的帖子的链接,方便为您加技术分。
排名
用户名 技术积分
1-hhhh31415926 13
2-zhubin846152 12
3-zhangdaming 11
4-reijin 11
5-tobyqin 9
6-xor 8
7-子青 8
8-蓝戈 8
9-jcc0107 7
10-smog 7
以上用户奖励300分,同时聘为家园顾问(已是版主顾问的除外)
gauss2004 5
dreams 5
wangjian881 5
武锐 5
yqli 5
Newton 4
bigprime 4
ji23 4
tshixing 4
windvalley 4
linli101 4
paulgilbert 4
toshine 4
reeyarn 4
beaver 4
提西教长 4
hfg
1964 3
ytht 3
天涯明月刀 3
quantum_le 3
baimnt 3
mazl 3
jshixu 3
acmwwy 3
luting5 3
luowan2000 3
leitingok 3
jimclever
3
xtuyyy 3
以上奖励200分
希望大家继续支持我们的家园!
174
19很高兴再一次,得到奖励。
17421"adventures in stochastic processes" Sidney I.
Resnick。该书的答案,有的大虾能否共享一下。谢谢!
17421路过
17422今天机器挂拉,要用lingo,但是破解文件找不到啦,那位好心的兄弟如果再用请传一个上来,
记得是破解的
dll文件!!!
17422安一个正式的demo版,然后输入一个序列号即可.
17422问题多多啊,必须要破解文件
17425简单的可以不说post-38-1125465533.ibf
17425我给个pdf的文件吧:post-38-1125466465.ibf
17425第一题按定义好证
先说说第二题吧
17425先泰勒展开再把级数分成两部分讨论即可
17425看样子要用泰勒公式吧
17425
| 引用 (reijin @ 2005年08月31日
13时48分) |
| 先泰勒展开再把级数分成两部分讨论即可
|
还要用到各阶导数的有界性
谢谢
第三题有思路吗?
17425反证法,若结论不成立,则f'最多存在一个0解(设为x0),可知在[a,x0),(x0,b]上的f'均为负数,则必有f(a)<f(b),矛盾
17425
引用 (reijin @ 2005年08月31日
17时44分) |
|
反证法,若结论不成立,则f'最多存在一个0解(设为x0),可知在[a,x0),(x0,b]上的f'均为负数,则必有f(a)<f(b),矛盾
|
那样的话还要讨论不存在零点的情况
我有一个思路:就是证明函数在区间内部取到极大和极小值。
这样似乎就太简单了,呵呵不知对不对
17425
| 引用 (流形 @ 2005年08月31日
20时31分) |
引用 (reijin @ 2005年08月31日
17时44分) | |
反证法,若结论不成立,则f'最多存在一个0解(设为x0),可知在[a,x0),(x0,b]上的f'均为负数,则必有f(a)<f(b),矛盾
|
那样的话还要讨论不存在零点的情况
我有一个思路:就是证明函数在区间内部取到极大和极小值。
这样似乎就太简单了,呵呵不知对不对
|
第七九题,也不是容易的,
它们有思路吗?
17425第三题你的想法是对的
七八九我给你说了
呵呵
17425第四道题目怎么做?
17426???你的单点集怎么定义?
17426子青老师,
向您请教。post-
17-1125470938.ibf
17426sigma 代数还有取补。
17426哦,这个问题我认为大概思路是这个样子的
1.证明不属于,那基本就是用反证思路了:
首先花体A是一个sigma-algbra,也就是说花体A是一个簇,它里面的元素是一个不可数集合里的单点集的并交这些,那么为了证明A不属于花体A的叉乘空间,只需要证明A的某分量的集合不属于花体A就可以了.注意到花体A是由不可数集里的单点集簇生成的sigma-algbra,也就是说花体A里的每个元素都是可数集(这么就是sigma-algbra的定义了,生成子的有限交可列并),但你A的随便哪个分量的集合都是不可数集本身,是不可数的,所以矛盾。反证结束.
2.么就简单了,随便哪个分量确定以后,另外一个分量也就确定了(因为是对角线集合),也就是说某个分量确定以后,你定义的那两个集合都是单点集,当然属于sigma-algbra了。
这个题目是要告诉你,单点集合生成的sigma-algbra的元素肯定是可数的,但是sigma-algbra本身可以是不可数的,sigma-algbra是集合的集合,是一个簇.
17426
引用 (子青 @ 2005年08月31日
19时35分) |
| ???你的单点集怎么定义?
|
定义见附件post-
17-1125964978.ibf
17426
引用 (youya @ 2005年09月07日
22时
19分) |
| sigma 代数还有取补。
|
哦,对,那这样的话,我觉得第一问有问题,A的每个分量的集合都是那个不可数集合自己,不可数集合自己自然是包含在sigma-algbra里的,因为空集必然属于sigma-algbra.那两个簇的叉乘空间是怎么定义的?
17426请问 这个题 出自哪儿?
可以 的话 请 将页 共享一下
谢谢
17427可微函数为凸的<==〉导函数单增?
17427
| 引用 (流形 @ 2005年08月31日
15时12分) |
|
可微函数为凸的<==〉导函数单增? |
nod
书中定理
17427充要性中有一个好证,另一个不太容易
17428十月就要报考研志愿了,本想考北理的运筹学与控制论,但发现有好多人都要考那,有点惧,于是就想报北科的应用数学,但又有点没底,不甘心。不知能否指教一下,这两个学校的区别大吗?考研报哪一个比较好,比较稳?
17430由于本帖附件为该校之“最优”保证书,除相关名日期字用XX代替外,其余均未变,故无法免费提供,售价2分,希望大家捧场。需要写类似保证书的同志可参考。
“鄙生保證不可提前畢業”中的“可”字是“可能”还是“可以”的意思?本人没搞清楚,这个“可”字到底要不要?欢迎大家讨论。post-1-1125477142.ibf
17430晕,怎么这老体字啊
香港的吗,
17430没意思
17430非常感谢捧场!
将附件下载后可以将它转换成简体字。
我想香港的学校应该不会有这种事情吧。你要你有本事,就算你只读一年能毕业,学校也会支持你呀。
我估计是原作者不想写又不得不写(确实无聊),所以干脆转换成繁体字,并写成古文形式。让收“保证书”的人看得云里雾里,看到最关键一句的时候已经分不清东西南北了。
17430看 不到
17430这是啥??
17430乙酉年应该是
1945年吧。
突然想起,前几天我也签了一份类似的卖身契。直到博士毕业前不准退学、工作、出国……
17430呵呵,哪位高人的
17430哈哈
17431我想得到复旦数学系的学长学姐的e-mail地址.我相信从你们身上一定可以学到很多.thanks a lot.
17432附件post-38-1125480139.ibf
17432是不是用行列市的乘法做啊
17432这个题目是中科大线性代数P1
17(16)
题目还是不错的,综合了:
(1)三角函数倍角公式;
(2)行列式基本性质;
(3)Vandermonde行列式等。
具体解答见附件:post-38-1125485738.ibf
17432
引用 (tobyqin @ 2005年08月31日
18时55分) |
这个题目是中科大线性代数P1
17(16)
题目还是不错的,综合了:
(1)三角函数倍角公式;
(2)行列式基本性质;
(3)Vandermonde行列式等。
具体解答见附件:
|
楼上的牛了,是不是科大的研究生啊?
给个提示post-38-1125491007.ibf
17432呵呵,牛人!
17433试题集里浙大05年数学分析好象是假的吧
看起来和
1998年的怎么一样啊
斑竹回复:确实如此,已经撤销,谢谢您的举报!
17435请大家务必用公式编辑器把答案写清楚,谢谢post-38-1125488680.ibf
17435这个题目我已经把详细过程给了出来了吧?!
那时候zhubin给了思路我就没贴,下面贴出来:
就用Word了。post-38-1125491564.ibf
17435wunan001你是不是台湾人,怎么帖了这么多Nation tinghua的试题?
17436本人的方向是学小波分析,专业是应用数学,以前我听别人说小波分析是十分实用的,但
一年的宝贵时光已经过去了,我每天面对的是大量的小波理论和理论性十分强的论文,根本看不到它实用的一面,所以每天在郁闷中渡过,而新的一天迎接我的同样是郁闷,我怎么办啊,各位大侠给我指点迷津好吗?不胜感激!
17436我没搞过小波啦,但在看文献的时候看到一点,现在电力系统的谐波分析,PMU的应用中小波都是相对新的东西,在这些方面,我感觉小波还是会有很大市场的.
17436小波在实践中很有用,但要注意它在理论上完全是傅立叶分析的附庸,没有意义。学小波一定要用!
17436我也要修小波,应该有用的
17436我也使应数小波分析方向的,刚研一啊。
现在也是一头雾水,不知向何方发展,望高人指点一条明路。
17436我知道小波能用在图象方面,不知还有什么应用?
17436楼主和其他专业人士,如果您们想应用一下小波理论,那我来麻烦您们,愿意否?主要做序列分析。
17436恭喜楼主了,能选到这样一个很有应用价值的方向。我是学机械设计的,目前正在进行机械方面的试验,为了处理和分析试验中得到的许多的数据、结果,现在正在苦学小波分析呢,头都大了。其实在很多的领域内,都用到了小波分析,象通信、电力及我们的机械行业等等,可以得到很多其它方法无法得到的本质的特征。所以,楼主完全没有必要着急,现在你目前只是处于打基础阶段,当然接触的都是理论方面的东西了,慢慢就知道他的用处了。努力!
17436楼主:你好啊,我也是应用数学专业的研究生,今年研2,我的方向也是小波分析,现在还没有什么头绪,马上论文就要开题拉,我的QQ:315
192360,加我QQ,我们可以共同探讨一下如何学习小波啊!加我注明“小波”二字!谢谢!
17436
| 引用 (dadaliuhua @ 2005年09月06日
13时14分) |
|
小波在实践中很有用,但要注意它在理论上完全是傅立叶分析的附庸,没有意义。学小波一定要用!
|
愚昧啊,小波和傅立叶分析虽然有联系,但是怎么也说不上附庸吧~
小波的应用的广泛,我认为就是他的理论基础的极其扎实,比其他的那些新的东西扎实,这才是小波越来越发达的原因.
ps:小波理论很难,但是也说不上没有用吧,比方在偏微分方程上,在流体力学上,都有很大的用处.
学习小波前,请了解泛函分析
17436我赞成上面大虾说的话,泛函分析对小波理论来说是最重要的基础!
17436我已完成小波变换图像处理程序,想要着请与我联系,小波贵在应用,理论多说无益
Email:michaelth@163.com
QQ:626034667
17436请各位不要郁闷。请阅读曾让我开窍的一本书
《实用小波方法》,徐长发,华中科技大学出版社
在这本书里,有基本的方法原理,也有基本的应用原理和应用举例
很好读的。
17436首先把理论掌握扎实,以后还怕派不上用场。
17436拿偶自己做个比方吧:
高中时已经有昔日玩伴社会工作了,跟他比较,觉得自己的数学已经不错了,没必要继续学下去好像。但是学好了数学才进入大学,而进入大学后的我好像走进一个崭新的天地,跟以前的生活是好大的飞跃。
这个比喻可能不太恰当。但希望楼主坚信:道路是曲折的,前途是光明的!
17436我也是正在学习小波变换,
但是看到很多方面的应用
17436我业是学习小波的,还行,有可以交流的加我71130248
17436请问<<实用小波方法>>徐长发著在什麽地方可买到
17436呵呵 师兄 说的心里有点凉凉的。。。。。。。。。
17436q确实不知道从哪里开始,最好有些直接应用的书籍能够介绍介绍,特别的编程的实现!
17436我的方向才确定为小波分析的图象处理,
看了两本简单的书,
然后boss就说我看的书太简单了.
让我换个多点数学分析的.
现在在忙着看书看书....
还没有接触程序...
17436小波分解的最高频率怎么总是5000?为什么不能自己设置呢?求各位大侠帮帮忙
17436
| 引用 (lovebeyond @ 2005年08月31日
20时03分) |
本人的方向是学小波分析,专业是应用数学,以前我听别人说小波分析是十分实用的,但
一年的宝贵时光已经过去了,我每天面对的是大量的小波理论和理论性十分强的论文,根本看不到它实用的一面,所以每天在郁闷中渡过,而新的一天迎接我的同样是郁闷,我怎么办啊,各位大侠给我指点迷津好吗?不胜感激!
|
你陷入了误区,一开始不要看那些理论书籍和理论性十分强的论文,我以前和你有类似经历,
其实小波理论很简单,和傅立叶变换类似,傅立叶变换是小波变换的特殊形式,只是采用了特殊基,然后了解小波的分解方法(这要大量看前人做的示例),回过头再看那些理论书籍和理论性十分强的论文,你会发现,那些作者只把小波变型或复杂化.
只一点经验,相互切磋.
17436小波的应用的确很广.比如我现在的专业,地球物理学,小波在地震资料分析上就是一个发展方向.找石油就很挣钱,不用为以后担忧
17436说多了没有用
理论深
不过入门倒不难
最好看英文文献
国内小波应用,比如图像分析的文献,我看,大多难以相信呵呵
17439新人报到,请多多
17440哪位大侠可以提供数学软件的下载地址啊!?
斑竹回复:看看家园的主页。
17440
http://mcm.ustc.edu.cn/download.htm上去看看
17441呵呵,没看答案就会了,谢谢
17441若正项级数

a ^n
发散,Sn表示部分和,如何证明:

a^n/Sn
也发散?
17441
| 引用 (流形 @ 2005年08月31日
21时38分) |
若正项级数
 a ^n
发散,Sn表示部分和,如何证明: a ^n
发散,Sn表示部分和,如何证明:  a^n/Sn
a^n/Sn
也发散? |
Cauchy判别法的逆命题
这个仔细考虑一下了
我把解答放在附件里
先想再看post-38-1125499084.ibf
17442同意jshixu的观点,当x=0时原函数为0,且x在R上连续
17442F(x)= ∫ 0
∞
x/
x
2 +y 2
dx
x ∈
R.
讨论F(x)的连续性?
先确定F(x)的定义域为何?
F(x)=x
∫ 0
∞ 1/
x
2 +y 2
dx
的定义域和连续性如何?
17442是这样吗?post-38-1125645925.jpg
17442是含变量积分的一致连续性把
17442有知道答案的吗
17442可以证明在任何闭区间上 Y是关于X一致收敛的 所以连续
17442还要求一直连续吧
17442x大于0时,$F(x)= \Pi /2,$ x小于0时,
$F(x)=-\Pi/2.$
17443A,B,C,D四个物体的位置具有不确定性,因此给他们的位置设置一个不确定性区间,在此区间内物体的位置以一种概率密度函数分布。假设A(1,4),B(2,6),C(5,7),D(3,4.5),位置都是Y轴坐标,而原点是查询点O,假设已经查出距离O点的最近物体,结果返回都带有其概率值,(A,0.4),(B,0.5),(C,0.1),即以此概率值作为O点的最近物体。能不能在这基础上计算出第二近,第三近物体的概率值啊?要是查询的物体很多的话。
17443没看懂,A(1,4),B(2,6),C(5,7),D(3,4.5)这些不是二维坐标么?
返回的时候D到哪儿去了?A,B,C,D的概率密度函数都一样?如果是概率密度函数的话,在某一点出现的概率都是0,因为是连续分布
17443to:子青
我没讲清楚。
1.A(1,4),B(2,6),C(5,7),D(3,4.5)代表的是一个在Y轴上的区间,可以这么看,A(1,4)是从坐标(0,1)到(0,4)的这一段,A
在这一段上必然存在。
2.而且我写错了,返回的是(A,0.4),(B,0.5),(D,0.1),C由于是位于(5,7)之间上的一点,所以必然不是最近的。
3.A,B,C,D概率密度可以一样,也可以不一样,A(1,4),如果是均匀分布的话,代表A的精确位置在(1,2)、(2,3)、(3,4)上的概率分别是1/3。
不知道我有没有讲清楚。
17444大家来讨论数学期望有那些运用
17444....这个问题太大了吧
17444我想在给学生上课的时候尽量讲些运用,我也才是个研究生,水平很差,所以请各位高手举些例子,讨论么
17444你可以讲讲Monte
Carlo,用期望来求积分,EM算法什么的,MCMC,重要性抽样,都可以具体的用法。我的QQ,99800969,有什么问题,可以探讨一下。
17444随机变量的取值总是以最大概率靠近其期望吗?
17444显然不是
17445这个题目用Jordan标准型来考虑!
见附件:post-38-112550
1869.ibf
17445请大家帮忙做一下第3题,请用公式编辑器写出详细过程,谢谢!post-38-1125499430.jpg
17445为什么 rankA=2003-k?
17445每个Jordan块的秩是比它的阶数小1
另外刚才解的时候遗漏了
还要讨论一下r,当r<2004,r是幂零指数的时候才可能去大一些的秩
如果r>2003,那么幂零指数为2003的时候秩最大,为2002
这里就不详细写了
17445一般是:( n - 1 ) - [ (n-1)/k ] 吗?
17445怎么删除自己的帖子啊?
17445作了一点修改,看看是否好理解一些。(附件)post-38-1125754712.ibf
17446现在有这样一道题:平面中由全体有理数组成的集合E,请问他的内点,外点,边界点是什么?我的回答是无内点,外点,边界点是其本身,请问是否正确?
另外我在学习常微分方程里遇到很多问题,在哪个版面能够找到帮助?这里的东西实在是太多了,论坛我泡的时间很少,上手很慢,请斑竹和大哥大姐帮助,谢谢!
17446correct. Since it's dense and so is its complement.
17446无内点,无外点,
边界点为全平面
到分析版块
17446谢谢
17447如题
17447是的
17447没这个条件呀
17447不一定的,可以建立在任何区间上,当然可积性要和被积函数有关,对被积区间,任意分割,极限都相同,由于它对于被积函数的要求没有一种一般的限制,所以积分的难点转移到了积分区域的分析上,并且显得理论比较杂乱,因为不可能给出一般的通用的理论。勒呗各限制了被积函数的局部的性状,这样的话各种定理就很简洁了
17447积分的定义与面积(测度)的定义是一致的,Riemann可积的话,它的积分区域要满足Jordan可测,这是必须的,但不一定就是有界闭区间了,而对于Riemann可积中的无穷积分和瑕积分情况也作特殊考虑,而Lebesgue测度满足可列的诸多性质,所以其适用范围相对较广
17447何谓Jordan可测
17447这应该是数分的一个预设.
17447黎曼积分里面有叫广义积分的吧
那样函数还是区间都不一定要有界啊
17447个人认为,广义积分是黎曼积分的推广,不能属于黎曼积分
17447
| 引用 (andychen @ 2005年09月25日
13时27分) |
引用 (primeshu @ 2005年09月21日
18时02分) | |
个人认为,广义积分是黎曼积分的推广,不能属于黎曼积分 |
寒一下,不是“个人认为”而是“本来就是”……
|
如此:黎曼积分一定是定义在有界闭区间上的
17447
引用 (primeshu @ 2005年09月21日
18时02分) |
|
个人认为,广义积分是黎曼积分的推广,不能属于黎曼积分 |
寒一下,不是“个人认为”而是“本来就是”……
17447闭区间到不必要,但一定得有界,这是可积函数的一个定理,其实黎曼可积是要其分割中幅度不能无限小的部分区间的总和不能太大。
参见《数学分析》陈传璋
等编 复旦的书 高教出版 上册 276页 定理6
17448请高手说说思路
点出要点即可
特别4,5,6三题post-38-1125505202.ibf
174484。留数
5。sum(sin(nx))的变换
6。用定义分两个积分证明
17448这是98年的,不是05的.
17448浙大每年考试划范围吗?他们指定的分析书上连实变的内容都有啊,考不?
17448哪为兄弟知道,告诉我啊
17448这个问题只有浙大的学生可以回答。
在大学里,范围一般还是要划的吧,不可能全考
17448第五题第三问怎么做啊????
17448阿贝尔判别法
17448华东师范课本上有这种方法的!
17448第四题;用复变当然简单,但是数学分析内容也能解的!构造e的-yx乘sinx/x这个含参变量积分,证明一致收敛,积分换续,得
派/2-arctany 再令y为零即得!
17449请高手说说思路,点到即可post-38-1125505599.ibf
17449第2题,其余等下次再发post-38-1125535513.ibf
174493,4,5已证,第6题post-38-1125535912.ibf
17449第二题最近在论坛上有人问过了:
http://www.math.org.cn/forums/index.php?show...topic=
17324&hl=
174497题post-38-1125537025.ibf
17449第8题是常规题,第9题post-38-1125622151.ibf
17449太感谢谢了
17449
| 引用 (iii @ 2005年09月15日
21时37分) |
| 不懂哦,和零化多项式有什么关系啊?
|
最小多项式无重根则可相似于对角型
这个是一些线代课本里的结论
有的时候特别好用
而最小多项式是化零多项式的因子
故hfg
1964那么说吧
17449不懂哦,和零化多项式有什么关系啊?
17449tobyqin说的没错,最小多项式无重根是A可对角化的充分必要条件,故零化多项式无重根是A可对角化的充分条件就是很自然的了.
17449如果一个

矩阵是对角阵且为一次的

-

i,为什么说它的不变因子就是它们?
17449
| 引用 (iii @ 2005年09月16日
22时15分) |
如果一个
 矩阵是对角阵且为一次的 矩阵是对角阵且为一次的
 - -
 i,为什么说它的不变因子就是它们?
i,为什么说它的不变因子就是它们? |
你可以把它化成标准的样子来看
这个因式不会变,不会出现高阶的啊
17449谢谢了
17449谢谢了
17451问题:若A为n阶方阵,f,g,h两两互素,证明:秩[f(A)g(A)h(A)]+秩[g(A)]
=秩[f(A)g(A)]+秩[g(A)h(A)].
本问题采用结论:秩[f(A)g(A)]=秩[f(A)]+秩[g(A)]-n可以直接获证,是否还有其它方法?
17451我给你一个方法不知道是不是够好,题目中两两互素的条件太强了,见附件:post-38-1125536800.ibf
17451to tobyqin:厉害,敢问你是考哪个学校的研究生?实在佩服你1
17451是个高材生,呵呵
17451tobyqin的证法确实很好,佩服!基本思路大楷是(广义)初等变换得到的.有一点笔误.post-38-1125563876.ibf
17451顺便请教诸位同仁:已知sylvester不等式r(AB)>=r(A)+r(B)-n取等号的充要条件是存在X,Y使得XA+BY=I(参见张贤科<高等代数学>),
那么Frobenius不等式r(ABC)>=r(AB)+r(BC)-r(B)取等号的充要条件是什么?
注:本人无答案!
17451
引用 (hfg
1964 @ 2005年09月01日
16时37分) |
|
tobyqin的证法确实很好,佩服!基本思路大楷是(广义)初等变换得到的.有一点笔误.
|
谢谢,当时是我打第二遍了,第一遍都弄完了保存的时候软件出现bug,极其郁闷,后来估计没注意,呵呵。
另外你问的问题我在书里找到答案了!
充要条件是:ABX+YBC=B
17451Frobenius不等式r(ABC)>=r(AB)+r(BC)-r(B)取等号的充要条件是存在X,Y使得XA+CY=B
请问在什么文献中有?
17451
引用 (hfg
1964 @ 2005年09月02日
09时22分) |
Frobenius不等式r(ABC)>=r(AB)+r(BC)-r(B)取等号的充要条件是存在X,Y使得XA+CY=B
请问在什么文献中有?
|
昨天晚上写的时候迷迷糊糊的,照葫芦画瓢还是画错了
现在在上面更改了
结论是通过一个矩阵的结果(Roth
1952年的结果)得到的
矩阵的结论在中科大线性代数P
181中以例题的形势出现
17451A为n阶方阵,f(x),g(x)互素,证明:r[f(A)]+r[g(A)]=n+r[f(A)g(A)]
这个应该怎么证呀?我没有学过你说的矩阵打洞的方法,那本书中介绍的详细一点呀?
请你帮忙!谢谢!
17451附件我怎么下不了啊?哪位仁兄能下了发给我吗?谢谢了!
邮箱: fuzhongqing666@163.com
17453看不出你问t分布的分布函数和你要想做的问题之间有什么关系,
你要产生服从t分布的样本,直接产生正态样本然后变换过去就行了
17453student分布的概率密度函数 p.d.f
我们都知道:
其分布函数是什么?(自己积分积不出来)
查到mathworld上面有这个:
http://mathworld.wolfram.com/images/equati...on/inline30.gif
网页地址:Eric W. Weisstein.
"Student's t-Distribution." From MathWorld--A Wolfram Web
Resource.
http://mathworld.wolfram.com/Studentst-Dis...stribution.html
但是不明白其中的

2是什么意思?还有F1...
或者谁能告诉我分布函数?
我的目的是想抽样出一组数据来生成符合Student分布的高维数据来,有没有更好的方法?
my QQ: 3600974
17453就没有人懂这个的吗? 还是我没说明白阿
17453
引用 (Fisher @ 2005年09月02日
17时34分) |
看不出你问t分布的分布函数和你要想做的问题之间有什么关系,
你要产生服从t分布的样本,直接产生正态样本然后变换过去就行了
|
正态样本要怎么变化为T分布? 而且若是高维的呢?还请指点
17453
| 引用 (dingzj @ 2005年09月04日
20时24分) |
引用 (Fisher @ 2005年09月02日
17时34分) |
看不出你问t分布的分布函数和你要想做的问题之间有什么关系,
你要产生服从t分布的样本,直接产生正态样本然后变换过去就行了
|
正态样本要怎么变化为T分布? 而且若是高维的呢?还请指点
|
搞定了,多谢
17454常微分方程:
d\phi/dx = \sqrt{(e^{-\phi}-1+\phi) +
(e^{\phi}-1-\phi)e^{fn}}
请教各位高手,如何给出一个比较好的近似解?最粗略的近似解是:
phi(x) =
(-x/2+\sqrt{phi0})^2
17457“连续n个负整数”如何译成英语?
17457n sequence negative integers??
17457谢谢小红帽,
能否用series代替sequence?
17457或者用seial?
17457
| 引用 (sunmo @ 2005年09月13日
14时05分) |
谢谢小红帽,
能否用series代替sequence? |
连续不一定刚好是次序,故sequence更好一些
17457多谢了!
17459随机分布场是指什么?能否用随机场表达一个动态过程,如交通流的变化?
17459小弟懂得不多,说说看看,看能不能对你有用.
你应该懂得随机变量吧,随机场就是随机变量的推广.简单点说吧,如果我们把随机变量的取值规定为全体实数,而每个取值所对于的概率比喻成为该点的质量,那么一个随机变量的分布恰好就是一个质量为1的数轴,并且不是每点处的质量都相等.
不知道这样解释对你有没有用.我开始学概率的时候用了三个多月的时间才明白什么叫做概率.很多学数学出身的人,谈到数学上的概念的时候,就只是简单的根据书上的定义作出解释,但是实际上很多概念都可以从日常生活中的简单道理中得到更清楚的理解.
譬如说概率这个概念吧,就可以这么理解.从数学上看,所谓概率,就是一种测度.但是如果我们连测度都不明白,那什么是概率我们还是不明白.实际上如果我们从另外的方面加以理解,概率这个概念还是非常容易懂的.一个物体,总会有很多性质的,当我们谈物体的性质的时候,实际上涉及到两点,第一是,是指该物体,第二是指该物体的性质,而且是该物体的某个具体的性质.如果我们抽象一下,把该性质抽象成为可以表示任何具体性质的一种抽象性质,那么我们就可以称该性质为测度,因为测度实际上就是对某中性质的一种测量啊.
如果这样理解,那我们可以很容易的接受概率这个概念.也许有人对这种理解方式不能接受,认为是不正确的.实际上,从随机变量的特征数字上,我们也可以知道,这种解释是正确的.随机变量的特征数字一般都冠以矩的称谓,在物理学上,所谓矩,相信大家都很清楚,这是个简单饿初中物理概念.后来我查看了相关资料,发现当初一些数学家在命名这些特征数字的时候也的确是借用了物理里面的这个概念.
懂得了这些,那么就更容易明白什么叫做随机场了.场的概念相信你应该明白.所谓场实际上你就可以从空间的角度去理解,只不过这个空间是个充满某种有方向的性质的东西.那么随机场就可以理解成为一个分布于空间的随机变量.当然了,如果你说,它可不可以变化,以表示现实中的实际现象,当然可以!
刚才我们说的都是静态的随机变量,而你说的实际上就是一个动态的随机变量.一个动态的随机变量在随机数学中就是随机过程.也就是说,时间不同,同一个空间中的质量分布(概率)是变化的.这个就是随机过程.虽然从理论上说,任何一个变动的现象都可以考虑用一个随机过程来表达,但是介于数学处理和数学认识的局限,我们现在只能对有限的过程加以认识和分析.
我所知道的就这么多,希望能对你有帮助,谢谢!!
17460我发现 中山大学的 常微分方程
证明题好难啊,不知道大家是不是同感??
如果考试要考证明题,肯定完蛋...
我的QQ 406983033
与你交个朋友啊
17460我查到了2004年9月论坛上发过一次 中山大学编的 常微分方程 答案;但是已经无法下载了,可否再发一次,谢谢啦
17460书上有答案,一般的题目都可以自己做出来,其实这样效果还好些
17460没着落了
17460我也正学这本书呢。都那些学校用这本书啊?咱们每人做几个,再汇总一下吧:-)
17461谁能告诉我质量分布原理吗
17461是几何还是物理?
17461分型中有关维数的计算中要用到质量分布原理,应该是物理当中的,
17462我最近所研究的最大流问题也是多点对多点的传输,不知道有否相似之处,liulf@seu.edu.cn
17462我找了很多书,但是讲多点对多点传输问题的特别少,如果有高人能帮忙推荐良书一册也将感激不尽!
17462我想你所说的问题和我做的有向超图很类似,也许我们可以讨论一下,
chengji306@163.com
17463有一个地方有误。即
0
=d(A)B-Bd(A)
应该等于
∑
i =0
k ia
iA
i
,
而不是
∑ k
=0 n
ka
kA
k ,
所以推不出
d
(x)=x
k.
请再看看。
应该说,方法是很好的。
17463tobyqin的证法,我仔细检查过,应该没错,而且方法非常之好.我想考研题中加强条件,无非是简化其证明,降低难度.或者出题人不知道可对角化条件可去掉.
17463再发一个证明,最开始我就希望得到这么一个证明,还好现在给出来了,不过我有个疑问:怎么这个题目的条件又多了?!
最近论坛好像相对冷清了一些,希望大家能积极的上来讨论问题,这么好的论坛应该有很好的人气啊!
我认为题目可以修改成这样:
V是有理数域Q上的线性空间,V的维数是n,A与B是V的线性变换,并且AB-BA=A 。证明:存在正整数k,使得
A k
是零变换。post-38-1125835782.ibf
17463请用公式编辑器写清楚,谢谢!post-38-1125559530.ibf
17463第一题是显然的detA*detA^-1=1
17463两个题目的解答都在附件里:post-38-1125622138.ibf
17463还有一种方法:先证A的任意特征值为0(不容易或用tobyqin
的方法)
,由哈密耳顿定理即得.
不过对AB-BA类型,两边左乘P^(-1),右乘P,化为[P^(-1)AP]P^(-1)BP]-P^(-1)BP]P^(-1)AP],是一种常用方法
17463证明完全正确。应该建议加分才是。
17463
引用 (hfg
1964 @ 2005年09月05日
16时52分) |
|
tobyqin的证明中有点小笔误,从前文中看出,求和范围应该是1到k.(用n表示不好,可能把最小多项式误导为特征多项式),仅仅是笔误而已,哈哈
|
现在我在原附件里应该都是做了改正的
每次都会这样的
毕竟不像自己写,每次粘贴总是忘了修改一些地方
见笑见笑
17463
引用 (springboshi @ 2005年09月04日
19时47分) |
有一个地方有误。即
0
=d(A)B-Bd(A)
应该等于
∑
i =0
k ia
iA
i
,
而不是
∑ k
=0 n
ka
kA
k ,
所以推不出
d
(x)=x
k.
请再看看。
应该说,方法是很好的。
|
证明是没有问题
就是我在草纸上写最小多项式的时候设的正好和后面写的混乱了
现在我已经修改过了
谢谢指出笔误
17463
| 引用 (springboshi @ 2005年09月04日
20时57分) |
再讨论一下:
d
(x)|∑
i =0
kia
ix
i ,
也推不出
ka i
=ia
i,0≤i≤k-1
.
合理的推论是:
存在多项式
f (x),
使得
d
(x)f(x)=∑
i =0
kia
ix
i
.
欢迎再讨论。 |
最小多项式整除任何化零多项式!
而且现在这两个多项式的次数是一样的啊
那么就相差一个常数倍
比较一下系数应该就是我给出的吧?!
17463tobyqin的证明中有点小笔误,从前文中看出,求和范围应该是1到k.(用n表示不好,可能把最小多项式误导为特征多项式),仅仅是笔误而已,哈哈
17463厉害啊.我还联系不到苏大近几年高代数分的试题,你有吗?有的话帮忙发一下,谢谢
17463这附件怎么不能下啊
17464e如何表示?像里面有pi,那么e如何表示?难道就的用exp(1),没有简短的?
17464是这样的啊
EXP(1)
17466俺准备考2006年的浙大计算机博士,但是浙大对自己的考博英语试题太保密了,google了一把还是没有找到实实在在的东西,有的只是一鳞半爪的回忆试题。我到现在还没搞清楚试题的形式什么样子的,尤其是那英语听力,据说比较难,俺就更加心虚了。这里的达人请帮小弟啊!有志同道合的朋友更好了,我的邮箱:avlong915@163.com
斑竹回复:请到试题集找找“博士英语试题专贴”
17466我也向考 但资料 没有 我QQ12349262
17466版主: 下不下来 它说连接失败
17468数学建模究竟需要几门知识准备,可有同志有过这方面的经验,望赐教
17468不多的
要会编程,运筹学,概率论等,及创新能力,要有一定的数学基础,基本没什么问题了
呵呵
另外三个人的团队意识和好的老师也很重要
17468以前参加过两次,不过效果不太好,就得一个省一等奖!
17468请问:自然科学的知识需要的多不多?
17469完备化啥意思
17469对于任意一个距离空间,如何把它完备化?
17469
引用 (Fisher @ 2005年09月02日
17时31分) |
| 完备化啥意思
|
所谓距离空间的完备,是指该距离空间具有这样的特征:它里面的基本列都收敛于该空间.
有定理指出,任何一个距离空间都可以唯一完备化.可惜的是我所看到的书上并没有告诉我们怎么样对一个任给的距离空间做完备化.
不知道哪位大哥大姐能帮个忙,告诉一下该怎么做.告诉一个思路都可以.谢谢!!@
17469和有理数完备化成实数的过程与方法一样!
17469《泛函分析》第2版高教版 江泽坚p
17 定理5.1
17469类似于数学分析,用距离函数构造柯西列。
17469加上所有的极限点就可以了.
17469这个距离空间内全部cauchy列的集合就是这个空间的完备化
然后定义距离为cauchy列极限的在原来那个距离空间中的距离
17470有没有研究泛函分析基础理论的?能不能给推荐几本这方面的书?
17470俞鑫泰《Banach空间几何理论》,华东师范大学出版社.以及该书的后继篇.
17470定光桂《Banach空间引论》,高等教育出版社
17472先富裕起来的人遗忘了他们!
17472新手上路,还望各位好好帮助哦。post-1-1125568811.jpg
17472就这样被震撼!!!post-1-11255690
19.jpg
17472真的很让人落泪啊
我对中国的贫富差感到当心啊
17472寒心啊
中国的基础教育条件太差了啊
17472被人遗忘的孩子们
祝你们走好
174772005年阿贝尔奖得主拉克斯简介
(转自《广州日报》)
彼得·拉克斯
彼得·拉克斯是匈牙利裔美国数学家。作为一名数学神童,他
19岁时就参与了研制原子弹的“曼哈顿计划”。终于在79岁时,他获得了世界数学界的最高荣誉———阿贝尔奖。
获奖后,拉克斯坦言说,他不会把它们乱花掉,因为他并不是很富。不过这些钱中的大部分将会花在科学研究上面。
二战结束后,拉克斯重新返回大学深造,
1949年,拉克斯在纽约大学获博士学位,此后他又到洛斯阿拉莫斯国家实验室工作了一年。
1951年,拉克斯在纽约大学获得教授职务,
1963年任库兰特数学科学研究所计算及应用数学中心主任,
1972年到
1980年任库兰特研究所所长,其后任库兰特数学和计算实验室主任。
在此期间,拉克斯在纯数学及应用数学方面均做出巨大贡献,获得了极高的荣誉,堪称世界数学界泰斗级的人物。拉克斯曾先后担任过美国数学学会主席、美国原子能委员会计算和应用数学中心主任,他还身兼美国国家科学院院士、巴黎科学院及苏联科学院等外籍院士等荣誉称号。
1975年,拉克斯获得了美国数学会维纳应用数学奖,
1983年获得美国国家科学院应用数学奖,
1986年获得美国国家科学奖章,
1987年因“在分析许多领域和应用数学中做出突出贡献”而获沃尔夫奖,
1993年获得斯蒂里奖的终身成就奖。
今年,在拉克斯的荣誉室里又添加了耀眼的阿贝尔奖。
5月24日,挪威首都奥斯陆,挪威王储哈肯亲王把2005年度的阿贝尔奖授予了匈牙利裔美国数学家彼得·拉克斯。众所周知,诺贝尔奖并没有在数学领域设立奖项,而挪威的阿贝尔奖是世界数学界公认的最高荣誉。这一奖项的奖金高达600万克郎(约78万欧元、98万美元)。
(转自《广州日报》)
17478呵呵
17478《易经》的核心思想是还原论与决定论。
还原论认为万物虽有万象之别,但在一定的微小层次上是统一的,如几个基本的笔画构成了所有的汉字,26个英文字母构成了任何一篇英语文章,7个音符构成了每一首乐曲,中子
质子
电子则构成了整个宇宙------(《易经》认为天,地,风,火,雷,泽组合出了整个世界。)
若人间万事亦由一些基本元素构成的话,那么通过对这些基本元素的演义便可预测事态的发展。这就是决定论。
当然朴素的还原论和决定论都有局限性。
数学与我们同在!
17478吴文俊:曲解背后的美丽故事
<<科学时报>> 杨虚杰
(2005-06-03 15:24:47)
吴文俊先生一不小心“卷”入到一场争论之中。这场争论的规模说大也不大,争论的关键问题说新也不新……
今年4月,《环球》杂志第八期策划了一组特别报道:“东方思维能否拯救东方科技”,其中一篇《东方思维拯救现代科学的悖论》采访了吴文俊先生,吴先生的话赫然与何祚庥先生的话并列在一起,“虽然我从来没看过《易经》,但我间接从各方面了解到《易经》的一些内容,例如提倡阴阳五行,我就非常反感,我觉得《易经》对中国科学的发展起到了阻碍作用”。
因为此文一开始就提到朱清时院士与新华社记者姜岩合写的《东方科学文化的复兴》一书。(本刊作过报道,吴文俊院士为此书写了一万多字的序言),那么,吴文俊先生的观点到底是怎样的,他怎样看待中国传统文化中的科学思想?
很快,《环球》杂志与新浪网合作开设了专题:中科院三院士激辩东方思维能否拯救中国科技?话题的展开多少有些类似于前一段时间因杨振宁而起的对《易经》的争论。
但是,因为杂志刚刚出来的那一天,正赶上在北京召开一个由科技部牵头的“中医药大发展”的会,国内许多中医参会,有人看到这期杂志赶快复印下来,有中医正巧写了《阴阳五行在中医上的应用》的论文。
浑然不知与一笑了之
很快,吴文俊先生接受了记者采访。他对已经发生的事情还浑然不知。但是他很快就知道了问题所在。一位86岁的数学家,反应之快,性格之豁达令人难忘。
吴文俊并不太知道,此前关于杨振宁先生于《易经》的争论,他问记者,杨振宁是什么观点?他说:“《环球》杂志的文章再加上后来有些报刊转载,将有些问题曲解,有些问题混为一谈了,给读者的感觉似乎我既批判中国传统文化,又批判朱、姜的这本书。”当然会受到“批评”了。
同时,吴老说,阴阳五行与《易经》与中国传统科学思想之间有严格的界线,三者之间不是等同的关系。阴阳五行与《易经》并不就是中国传统思想的全部,而中国传统科学思想中有很荒谬、很糟糕的地方,应该抛弃,吴先生以科学家的精神特别反对算命和迷信的内容,他说:阴阳五行在中医上的应用我不懂,但过去就知道,它用来占卜算卦,这些肯定不是科学的,吴老说,他没看过《易经》,记者得知,后来吴老亲自去图书大厦买到原法原味而不是后人注释的《周易》,他认为,如果要研读,就不能在后人解读的基础上进行。
坐在吴老并不豁亮的办公室,却有一种阳光灿烂的感觉。这是眼前这位鹤发童颜,有着孩子一般坦率、真诚笑声的老人赋予的。老人已经全白了的头发向后梳得一丝不苟,还能看出梳子梳过的痕迹,可是,那件已经有些发白和过时的中山装上,却有斑斑驳驳的印渍,两相比较,非常鲜明的对照,让人禁不住哑然失笑!
采访中笑得最多的是吴文俊先生,随着话题的展开,才知道,他对中国传统科学思想有着深入的研究,并且这一研究,已经在30年前就开始了,他不仅总结了中国传统思想精髓所在,而且在他后来取得非常重要成果的“吴方法”的研究上,也得益于中国传统科学思想的启发。
吴文俊院士在一次科普讲座中与听众现场交流 摄影/侯艺兵
三十年前开始的中国数学史研究
吴文俊先生接受采访时,带来一些资料,其中有一些已经发黄的报纸,记者打开一看,是吴老保存的
1974年6月10日、
1974年7月
17日和
1974年8月8日的《参考消息》,上面有近乎整版的几大篇文章,如:香港《大公报》转载美国科学家李约瑟的一篇讲演——《古代中国科学对世界的影响》,还有香港《七十年代》月刊文章——《李约瑟教授及其演讲》、《李约瑟博士对中国儒家思想评价很低》等等。
三十年以前,吴文俊先生就开始对中国传统科学的研究发生兴趣,就开始研究中国古代数学史了,这在中国搞基础研究的科学家中并不多见,回忆起历史,吴文俊说,这要感谢当初创建了系统所的关肇直先生。
1974年,文革尚没有结束,当时在数学界开展学习马克思数学手稿的活动,同时也允许学习数学史。关肇直先生号召大家读一些中国数学历史方面的书,作为接受过西方教育,在法国获得博士学位的吴文俊来说,对古代数学是了解不多的,于是他就跟着所里的人一起读,他说,当时这方面的书籍不多,于是,他从关肇直那里借来一些数学史的资料,包括我国李俨、钱宝琮的《中算史》以及中国的经典书籍,如《算经十书》等,开始了他的数学史的学习。在那两三年中,他博览中外的数学史著作,花费大量精力直接钻研中国古代数学的文献,围绕中国数学的特点,展开深入系统的研究,他广泛阅读的数学史书籍包括:钱宝琮、李俨、严敦杰等的数学史著作;李约瑟的《中国科学技术史》;有关古希腊时代的著作;《九章算术》与《海岛算经》;《周髀算经》与《缉古算经》等;沈康身的《我国古代测量技术的成就》;徐光启、利玛窦等人关于测量方面的著作。
就像吴老的许多次研究转型一样,他进入了这个新的领域,一发不可收拾,并且做出了许多成绩。
1975年,吴文俊就发表了关于数学史研究的论文《中国古代数学对世界文化的伟大贡献》(发表在《数学学报》上),有意思的是,用的笔名是“顾今用”,取“古为今用”之谐音。
从此展现了吴文俊对古代数学思想的深刻理解与认识,他认为,中国古代建立了世界上最先进的中国古代数学,并且直至16世纪,我国数学在最主要的领域都一直居于世界领先的地位。
除此之外,还写了《对中国传统数学的再认识》的文章,对十进位位值制、古代几何学、古代代数学都进行了深入的研究,关于李约瑟演讲的文章就是那个时候收集的。
运用计算机进行数学研究,工作中的吴文俊(
1988年)
得益于古代数学精髓的“吴方法”
吴文俊先生认为,我国传统数学有着它自己的体系与形式,有着它自己的发展途径与独创的思想体系,不能以西方的数学模式生搬硬套,吴老认为,西方数学从古希腊欧几里得系统发展下来的,是公理化的体系,它的思想是因果关系的追求,从原因证明结果,如此一步步推导出来。中国数学的思想体系是从实用主义出发,是从解决形形色色的问题出发,对这一点,吴先生反复强调:“我很赞成。”他认为,对一些原始的数据,要找出答案,要在原始数据与要求得的数据之间找到关联,就通过某种方程的形式联系起来以解决多种问题。这是中国古算发展的一条主线。吴老说,从地下挖掘的“算术书”,证明在战国时期就有简单的解线性方程的例子。
吴老对数学史的研究使他对数学科学的认识发生了一次大的转变,使后来从事的“脑力劳动的机械化”直接来源于对中国古代数学的研习,他认识到,中国古代数学所蕴涵的数学机械化思想,对当代数学的发展发挥了重大作用,也必将为信息时代的数学现代化做出巨大贡献,
吴先生认为,人类要从体力劳动中解放出来,于是发明了机器,实现了体力劳动的机械化,而数学这样的脑力劳动,是否也能机械化?电子计算机的发展,为人类实现脑力劳动的机械化创造了条件。
恰巧,在
1971年时,数学所落实“三面向”,吴文俊被分配到“北京无线电一厂”劳动,当时该厂正在生产电子计算机,计算机的性能,即刻引起吴文俊的深厚兴趣,他敏锐地察觉到,计算机必将在不远的将来成为数学研究的有力工具。吴先生也由此开始学习计算机,从最简单处学起,他要尝试着用计算机来证明定理。
1976年年底,他开始着手进行研究。到
1977年春节的时候,取得初步成果,他证明了初等几何主要一类定理的证明可以机械化。他在记者的采访本上写下了他的第一个证明的定理。
1977年,吴文俊的论文《初等几何判定问题与机械化问题》在《中国科学》发表,后来,以此为起点,他建立了多项式组特征列的概念,以此概念为核心,提出了多项式组的整序原理,创立了机证定理的“吴方法”,首次实现了高效的几何定理的机器证明,由此,吴文俊先生万千感慨,他非常赞成某些同志提出的“脑力劳动机械化是永恒的主题”,计算机的出现使脑力劳动机械化成为可能,但最要紧的是数学本身,怎样使得数学工作者的典型的脑力劳动机械化成为可能。
天下谁人不识君
套用一句过去常说的话,“没有研究就没有发言权。”吴文俊先生毕30年之功,潜心揣摩古代数学思想的精华,并用研究实践取得蜚声国内外的成果,这再一次印证了他做人做事的准则,也是一贯告诫大家的,要少说一些,要多做一些,“不要光磨嘴皮子”。
也许,朱清时院士和姜岩所著书中的“东方思维”的外延要比吴文俊先生研究的古代数学的思想范筹要大得多,现在,新浪网上还正在做调查:一个问题是:“你认为东方思维能否拯救中国科技?”认为“不能”的占41.68%,认为“能”的占39.9%,认为“不好说”的占
18.39%;还有一个问题是:“你认为近代科学没有在中国萌芽有哪些原因?”
48.99%的人认为是思维方法,48.76%的人认为是科举制度,48.2%的人认为是“不重视技术”等等……
也许,还是吴文俊先生的做法更为可敬,剔除传统文化中的糟粕,而将真正有价值的东西与现代化的工具相联接,创造出新的辉煌。
陈省身先生有一段评价吴文俊先生的话是这样说的:“他的机器证明理论,保持了中国数学的传统:数学上一个普通的问题,是解方程组,代数的或微分的。数学的许多基本结果是所谓‘存在定理’:在某种条件下断定方程组有解。中算则注意求解的方法,寻求最有效的手段。文俊最近的工作,符合中算的精神。”
17478易经这东西真是科学吗?我没看出来,见龙在田,飞龙在天,亢龙有悔,呵呵,这和科学精神有什么关系??或许是我太愚钝了吧!
17478易经的模糊、似是而非从本质上来说与数学的严格和精确是完全相反的。
所以,易经 = - 数学
17478来源:科学网
一位大科学家的人生态度——记著名数学家吴文俊
本刊记者
王莉萍
用“人在家中坐,奖从天上来”形容数学家吴文俊的屡次获奖是比较恰当的。由于“对数学机械化这一新兴交叉学科的贡献”,吴文俊于9月11日又荣获了2006年度邵逸夫数学奖。
9月25日,中国数学会与中国科学院数学与系统科学研究院在北京友谊宾馆举行了“吴文俊先生荣获邵逸夫数学科学奖庆祝会”。
吴文俊的学术生涯起步于纯数学,随后将主要精力转向与计算机科学密切相关的应用数学——几何领域的计算机证明,在拓扑学方面做出了先驱性的工作。邵逸夫数学奖委员对其学术评价为:“在学术研究和学科发展上做出了先驱性的突出贡献。这些领域中许多主要科学家都曾接受他们的指导,或是跟随他们的足迹进行研究。”
伟大的数学让数学家们去求索,记者则离开数学的范畴,试图追随着吴先生和他周围的人们的回忆轨迹,勾画一位杰出科学家的人生态度。
歪打正着走上数学路
“在上学时我最喜欢物理,因为离现实的事物更接近。但是现在想来,如果我沿着物理的方向走下去,我不会取得什么大的成果。因为和我个人训练习惯有关,我不喜欢动手,有点中国古代传统思想观念,君子是不动手的,而做物理、化学有试验要求,动手能力应该强一些,以前和同学两个人搭档做实验,我总是闯祸的那一个。数学用不着动手的。”吴文俊说这话时,笑得非常开心。
将时间回拨。
1933年,吴文俊在上海正始中学读高中。一次物理考试,题目特别难,但吴文俊的成绩极为出色,引起物理老师和校方的重视。但是这位物理老师认为,吴文俊物理好主要是因为数学特别强。
以优异成绩结束3年的中学路程,吴文俊获得了学校特设的奖学金,每年100块银元的资助,在当年这笔钱相当可观,几乎是一家人一年的花销,如果没有这笔奖学金,家里支撑他读大学将会很艰难,但这笔奖学金有个条件,要报考校方指定的学校和系科。
1936年秋,吴文俊走进了学校指定的上海交通大学数学系。期间,那笔可贵的支撑他的学业的奖学金由于战乱中断了。在《吴文俊之路》这本书中则记录了:在日本占领期间,原正始中学校长当了汉奸,他派人找到吴文俊,表示要继续支持他的学业时,这位热血青年严辞拒绝了。
“因为这笔奖学金,我歪打正着走上数学这条路,可以说一半主动,一半被动。”吴文俊说。
但无论如何,这第一笔奖学金拉开了吴文俊其后几十年获得各种荣誉的数学生涯。记者获得的一份资料显示:吴文俊曾获得首届国家自然科学一等奖(
1956年),中国科学院自然科学一等奖(
1979年),第三世界科学院数学奖(
1990年),陈嘉庚数理科学奖(
1993年),首届香港求是科技基金会杰出科学家奖(
1994年),Herbrand自动推理杰出成就奖(
1997年)及首届国家最高科技奖(2000年)等等,除了文革期间,基本上每隔几年吴文俊就会获一次奖,而这些奖项中的任一个拿出来,就已经可以让获奖人受益终身了。
吴先生从边门溜走了
“你看照片上的吴先生像个孩子似的,但我很尊敬吴先生,甚至不太敢接近,因为吴先生经常是远远看见人就溜走了,为了尊敬吴先生的习惯,我也只好见了吴先生不太打招呼,有一次我俩坐同一辆车从天津回北京,这一路我俩一句话也没有说。吴先生这个习惯很久了。以前每逢春节我们都成群结队去华罗庚先生家拜访,我记得唯一从来没有去拜访过的就是吴文俊。有一次大概是数学成立理事会,会后大家都排队去和华先生握手,也是吴文俊一个人悄悄从边门溜走了,他从不搞关系,串门子。”著名数学家、中国科学院院士林群对吴先生有这样一番描述,他希望有更多的媒体去报道他,以便让他这种不搞关系、专注于研究的精神成为年轻一代的楷模。
2002年之前,除了数学界,知道吴文俊的人还非常少,吴先生不但不和媒体打交道,甚至连周边的人他也不会凑得很近。但是老校友的悼念会,八十多岁的他会一个人悄悄坐地铁去八宝山参加,并不惊动任何人。他也曾在一次获奖答谢发言中,历数了曾给予他帮助的很多人的名字以示感谢,他说:“奖不是我一个人的,不管一个人做出什么工作,都是在社会、国家的支持下完成的,是在许多前辈所做的工作的基础上更进一步而已。”
吴文俊对一些所谓的“俗务”也是很关注,并且直言不讳。全国人大常委会副委员长丁石孙说:“可能现在的年轻人不知道,其实,早年在吴文俊的倡议下,中国数学会定了很多好规矩,比如,就是在他自己当数学会理事长时,他定下了理事长只任一届的规矩。”
早已卸任的理事长吴文俊更愿意在家里工作,有事、讨论专业问题或者有相关的会议才到所里,“所以,所里好多人我都不大认识。”他说,“有时我喜欢一个人到处走走,没有很具体的目的地,就是转悠。”
1947年,在陈省身先生推荐下,吴文俊去法国研读深造。他后来在接受中央电视台10频道《大家》栏目采访时,沉浸在感念中回忆:“陈省身先生没有让我去当时欧洲的数学中心巴黎,而是把我安排在法国的一个边界小城里,陈先生说,‘你是去学习,做研究,应该离那些繁华喧嚣的城市远些’。”
在法国寂静的边城,吴文俊一如当地的学者,在咖啡馆的一角独自日复一日地进行缜密的思考和运算,埋头沉入到拓扑学中。在这一时期,他证明了4K维球无近复结构,在拓扑学界引起不小的震动,当年的拓扑学界大师霍普夫质疑这个结果,“他带了助手来‘兴师问罪’了,在校园中坐下我们就开始讨论,最后他还是服气了。”时隔多年后,吴文俊依然能清晰地回忆起当年这段“官司”,并且为此而发笑。
“你要认真去做,不要去考虑是否得奖这类的问题。如果只想着我要做一个得奖的工作,那么你什么工作恐怕也做不出来。”吴文俊对记者讲了自己屡次获奖的心得。
教授动动手,开拓一个领域
“在文革期间,吴文俊被下放到北京海淀区学院路附近的北京无线电一厂劳动,引起厂里工人的好奇心,大家纷纷跑去看一位教授是怎么工作的。在车间里,吴文俊戴着眼睛,正在认真地焊接线路,脸凑得很近,围观的工人看着都笑了,有人就说:‘教授干活要把自己的鼻子焊上去。’”原南开大学副校长胡国定回忆起吴文俊的一段小插曲。
即便是谈到文革时期的遭遇,吴文俊认为自己也受益颇多。首先,不得不劳动改变了他的一些思想观念。“我的习惯是不动手的,家务事我到现在也不做。但在文革期间思想受到冲击,认识到人不能不动手。那时候买了一套工具,我也这儿钻钻,那儿捅捅地瞎碰,总是出问题,但文革期间我还是有收获,知道人还要动手。数学机械化研究就是得益于这一时期的动手工作。”
而当时北京无线电一厂正在生产电子计算机。计算机的性能引起吴文俊浓厚的兴趣。上世纪七十年代吴文俊把注意力转向了计算问题,特别是寻找几何中自动机器证明的有效方法。基于Ritt特征集概念,
1977年吴引入了一种强大的机械方法,将初等几何问题转化为多项式表示的代数问题,由此导致了有效的计算方法。
1978年,吴文俊这样描述电子计算机对数学的发展将产生的影响:“对于数学未来发展具有决定性影响的一个不可估量的方面是,计算机对数学带来的冲击。”
吴文俊倡导数学机械化研究,是从数学科学发展的大局出发的,反映他本人对数学科学的认识和理解。于是,在近耳顺之年,吴文俊居然开始学习计算机,并且在若干年内,他的上机时间都遥居全所之冠。经常早上不到8点,他已在机房外等候开门,甚至24小时连轴转的情况也时有发生。正是这番努力,使吴文俊开拓了数学机械化领域,也因此荣获了2006年度邵逸夫数学奖,吴文俊自己认为这个成就高于他早年的被引用多次的“吴方法”。他认为,开拓新的领域对今天的中国数学尤为重要。
吴的这一方法使该领域发生了一次彻底的革命性变化,并导致了该领域研究方法的变革。在吴文俊之前,占统治地位的方法是AI搜索法,此方法被证明在计算上是行不通的。通过引入深邃的数学想法,吴开辟了一种全新的方法,该方法被证明在解决一大类问题上都是极为有效的,而不仅仅是局限在初等几何领域。
吴文俊认为另一大受益之处是对中国古代数学史的“挖掘”。文革期间,不能读专业书刊,但能读史书,吴文俊转而研究数学史,对中国古代数学有了深刻的认识,使之在后来的数学研究中获益匪浅。他说,“我在香港做报告时就特别强调了解中国古代数学史对我后来工作帮助良多。搞清了数学的历史发展,不但对数学现状知道得更清楚、深刻,还可以对未来的数学起一种指导作用,知道数学应该按怎样的方向发展可以收到最大的效益。”
英雄是落后的标志
“在老百姓眼里,获奖就和中彩票一样,值得羡慕的就是运气,但是对大科学家来讲,获奖其实是早已做足了功课。记得我
1983年去法国,一位著名的数学家问我,‘吴先生现在在做什么?’在听了我的简单介绍后,他说了一句我至今难忘的话,‘吴先生做的,那一定是有道理的。’
1986年,我推荐一名学生去法国深造,法国的教授在看了他要研修的方向后拿出了一些资料说,‘我讲课的这些资料很重要的一部分就是来自吴先生的研究,你在中国学习会更好。’”清华大学数学系主任文志英教授的这番介绍进一步证明了吴文俊早年就享誉国外。
如今,早已诸多奖项加身的吴文俊,被誉为我国数学界的杰出代表与楷模。对此,吴文俊说:“对我个人而言,每次获奖都是高兴的事儿。”但,对一个国家的科学发展而言,“稍做出成绩,就被大家捧成英雄,像朝圣一样,这个现象不是好事情,甚至可以说是坏事情。这说明我们的科研还在一个相对落后的阶段。有个吴文俊,那能说明什么?要是在这一个领域,发现有十个、八个研究人员的工作都非常好,无法判定谁是英雄,那才说明我们发展了,进步了。”吴文俊说,“这可能是我的怪论。但确实曾有人说过‘英雄是落后国家的产物’,在科学界,至少在数学领域,我很认同这句话。”
1961年,美国著名数学家、国际数学联盟第一届主席斯通(M.stone)说:“整体上中国人的贡献在数学界影响不是很大,但少数被公认为富有成就的数学家,他们新近的贡献被高度评价。”这从一个侧面为吴文俊的论断提供了耐人寻味的论据。
科学界需要一个没有英雄的时代,吴文俊进一步诠释这个理念:以前法国是欧洲数学中心,数学家都去巴黎朝圣。那时德国数学相对落后,因此,高斯、希尔伯特成为一代英雄式的人物。其后,没有再听到德国又出了这样的英雄人物。但是,现在德国数学被认为是“后起之秀”,水平很高。“再比如拓扑学,美国有一批高水平的研究拓扑学的人员,你要说谁是英雄,比不出来,大家都很杰出,都在某个方向作出了重要贡献,这就说明在这个领域美国是拔尖的。”吴文俊说,“评价一个国家的科学发展,不会只针对某一个人的成绩,而是群体的高度。这才是真正的进步。”
做数学大国的功课
“吴先生总是念念不忘,多次在各种场合呼吁:做数学研究,要开创自己的领域。
1989年在胡国定、吴文俊等数学家的倡议下,国家为增强对数学研究支持设立了‘数学天元基金’,吴先生对它寄予了非常大的希望。他对基金的使用和管理提出许多重要主张,强调从整个数学事业的发展全局出发。”国际数学联盟执委会副主席马志明院士没有谈有关吴先生的趣事,而是谈了吴先生对如何使中国成为数学大国所做的努力。
1999年,数学天元基金成立10周年时,吴文俊曾谈到中国成为数学大国的步骤:第一步是规划,规划当时已经有了;第二步是赶超日本;第三步,赶欧美。时隔7年,吴文俊在接受本刊记者采访时再次谈到中国数学与日本的距离。“在一些领域日本做得还是比较有水平,但在某些点上,比如拓扑学,我觉得他们并不高明。但是,总的来说,日本能举出很多人做出了杰出工作,可以说他们已经到了一个没有英雄的境界。”
由于近几年,国内一大批青年科学家的研究成果纷纷涌现,吴文俊非常乐观地表示,“数学界的学术风气还是比较正、洁净,我看到的年轻人都在埋头苦干,中国离没有英雄的境界很近了,已经能看到这个苗头。”
早些年,与吴文俊同辈的老一代科学家都曾在不同的场合表达过类似的观点,“现在我们做的工作很出色。但是,领域是人家开创的,问题也是人家提出的,我们做出了非常好的工作,有些把人家未解决的问题解决了,而且在人家的领域做出了使人家佩服的工作,但我觉得这还不够。这就好像别人已经开辟出了一片天地,你在这片天地中,即便翻江倒海、苦心经营,也很难超过人家,这片天地终究是人家的。”
那么今后做什么?吴文俊认为,最重要的是如何开拓属于我们自己的领域,创造自己的方法,提出自己的问题。讲求效率的他也在不断地思考以何种方法、方式来完成这个目标。数学家多是单兵作战,吴文俊笑指自己说:“我以前也是这样,但现在我看到有一个多学科组合模式,我很欣赏。‘文革’期间,关肇直同志在思想上给了我非常大的启发。他说的‘不要扎根外国、追随外国,立足国内’的这种思想是行得通的。起码在我这儿得到了很好的验证。”
“外国人做的我不做,外国人没想到做的我才要去做。”吴先生说这句话时不由地提高了声音。
数学从娃娃抓起?
“前几年,吴先生去香港参加一个学术会议,会议休息期间,吴先生和谁也没有打招呼就自己出去转悠了。很久没回来,随行的年轻同事都很着急,好不容易把老先生等回来了一问,大家又都吓得直冒冷汗,老先生居然一个人跑去坐过山车了,游乐园的工作人员一看他满头白发,就不让他上,但他假装弄不明白人家说什么,最终上去玩了一把悬的。”数学与系统研究院的一位工作人员在带领记者前往吴先生的办公室途中,讲了这段逸事。记者一见吴先生就求证,吴先生笑说:“上去就害怕了,可是下不来了,回来以后所里的老同事
17478愿中国早日成为世界数学强国!
17478吴文俊是伟大的数学家,而易经并不是数学书。
17484我不是搞数学的,但遇到一方程,可能要编程解决,请各位高手帮忙解一下,十分感谢和景仰!!
post-37-1125574279.ibf
17489请各位高手推荐一下二层规划方面的书,如果有案例,更加感激不尽啊1
17489滕春贤, 李智慧. 二层规划的理论与应用. 北京:科学出版社, 2002
17489谁能买到(滕春贤, 李智慧. 二层规划的理论与应用. 北京:科学出版社, 2002 )这本书啊?网上买都缺货啊!
17493问题:建立满足下面性质的微分方程
曲线上任一点的切线介于两坐标轴之间的部分等于定长L;
我是这样想的:他的横截距和纵截距分别为x-y/y'和y-xy',这样可以列出以下式子:
L*L=(x-y/y')的平方*(y-xy')的平方
但是怎么解?
对倒数的平方求积分怎么求?不会,我数分学得不好。请大哥大姐帮忙!
17493对,但是怎么解呢?斑竹请指导
17493L*L=(x-y/y')的平方*(y-xy')的平方
应该是L*L=(x-y/y')的平方+(y-xy')的平方吧
17493初步思路:整理一下得y*l^2/(1+y)=(xy'-y)^2
在开方讨论就好解了
17493不对吧,您解错了吧?我演算了推不出来
17493象流形这样解是正确的!!!
你慢慢检查一下看看那里出错啊!!!
17493象流形这样解是正确的!!!
你慢慢检查一下看看那里出错啊!!!
17493真佩服!
17497
引用 (gzchenyin @ 2005年09月05日
18时39分) |
| 引用 (zhaoming @ 2005年09月02日
20时08分) |
我在计算机系呆了N(N>10)年,刚开始我和你一样,也很奇怪,计算机和数学还有关系?
但后来我明白了,计算机科学就是从数学的一个分支发展过来的.象你说的社会上的培训班,学的是"计算机操作"!那不是"计算机科学"!你刚上大学,大概给你解释不清"计算机科学"这个词的含义,但它的确是很数学的.
不学数学你肯定做不了计算机专家,只能做用户,充其量是熟练的代码工人.
写程序也不是计算机科学,就象望远镜不是天文学一样,对了,这话不是我说的,是一位图灵奖(计算机科学领域的诺贝尔奖)得主说的.
|
写程序也不是计算机科学,就象望远镜不是天文学一样,对了,这话不是我说的,是一位图灵奖(计算机科学领域的诺贝尔奖)得主说的.
=======
Edsger
W. Dijkstra
|
=======
Edsger W. Dijkstra
没错,正是这位算法大师的原话.
17497对啊,这一点我们信息与计算科学最具说服力,我们现在完全和传统数学专业学的一样的东西,虽然刚开始的时候觉得很不理解,但学到层次深点的时候,你就会看到数学对计算机有多大的作用,没有数学基础你根本不可能学好计算机!
17497你只要知道一件事就行,计算机界的最高奖Turing Prize(图灵奖) 的得主均是数学家出身的计算机学家。可见数学对学计算机的重要性.
17497我已经度过了两年大学生活,所学专业是计算机,但是从大一开始学的仅仅是数学分析(复旦大学出版),线性代数(清华出版),实变函数,空间解析几何,常微分方程,关于计算机方面的我们只学了c语言,还学的是皮毛,我问了我们老师,他说这是给计算机打基础,我现在计算机水平还不如在大街上交几百块钱上的补习班学得好,老师说我们学的是计算机科学,我也不太明白,我们都有电脑,说明白了是高级游戏机,我很担心这样下去我怎么办,数学把我不如数学专业,计算机把我又什么都不会,请问你们这些过来人的建议?
17497现在才问这句话,说明数学对你已经没有太大意义了!计算机的使用者不等于计算机专家不需要太多数学。
17497
引用 (dadaliuhua @ 2005年09月05日
19时28分) |
|
现在才问这句话,说明数学对你已经没有太大意义了!计算机的使用者不等于计算机专家不需要太多数学。
|
你说的对
现在计算机本科生也就是做个计算机使用者,顶多做程序员,既然不做专家,学数学也没用.
17497你的数学可以很差,但绝对不要比用户更差,否则有你受罪的,根本听不懂对方说啥
至于编程,那是毫不重要的,任何一个编程语言都可以两星期学会
多学点计算机原理,算法和应用数学才是正经
编程什么的,自己喜欢哪个就去买本书学,用得着别人教你么???
17497我在计算机系呆了N(N>10)年,刚开始我和你一样,也很奇怪,计算机和数学还有关系?
但后来我明白了,计算机科学就是从数学的一个分支发展过来的.象你说的社会上的培训班,学的是"计算机操作"!那不是"计算机科学"!你刚上大学,大概给你解释不清"计算机科学"这个词的含义,但它的确是很数学的.
不学数学你肯定做不了计算机专家,只能做用户,充其量是熟练的代码工人.
写程序也不是计算机科学,就象望远镜不是天文学一样,对了,这话不是我说的,是一位图灵奖(计算机科学领域的诺贝尔奖)得主说的.
17497
| 引用 (zhaoming @ 2005年09月02日
20时08分) |
我在计算机系呆了N(N>10)年,刚开始我和你一样,也很奇怪,计算机和数学还有关系?
但后来我明白了,计算机科学就是从数学的一个分支发展过来的.象你说的社会上的培训班,学的是"计算机操作"!那不是"计算机科学"!你刚上大学,大概给你解释不清"计算机科学"这个词的含义,但它的确是很数学的.
不学数学你肯定做不了计算机专家,只能做用户,充其量是熟练的代码工人.
写程序也不是计算机科学,就象望远镜不是天文学一样,对了,这话不是我说的,是一位图灵奖(计算机科学领域的诺贝尔奖)得主说的.
=======
Edsger
W. Dijkstra |
写程序也不是计算机科学,就象望远镜不是天文学一样,对了,这话不是我说的,是一位图灵奖(计算机科学领域的诺贝尔奖)得主说的.
=======
Edsger
W. Dijkstra
17497不知楼主chefcui可否告知你是哪所大学的吗
计算机系才大二就学实变函数
难道是北大
17497而且听你说你学的课程名来看
只有线性代数不是数学系所学(一般数学系叫做高等代数)
其余都是数学系的专业课
这样学四年应该获得理学学士了
17497没有,我对数学还是很感兴趣的,不过我们寝室的每人又对她感兴趣,平时连一个讨论的人都没有,我平时就是写一些作业他们拿去抄,这样也没什么意思,大家不要对我没信心,我只不过提出疑问,数学我还是回复出自己最大的努力的,特别是听了这么多大虾的话,谢谢!
17497算法就像灵魂,程序就像躯壳,人都拥有相同的躯壳,但却有着不同的灵魂
17497如果楼主将计算机当作高级游戏机的话,那是不用很多数学的
17497我觉得你的思考,有道理,我也这样思考过,我也引一位图灵奖的话,高德纳说
过现代的数学,有很多计算机科学都用不上,上面有一位引用了,
Dijkstra
但是计算机科学绝对属于数学,它本身是一种比较奇怪的数学,一般的说
计算机的数学和数理逻辑有关,数理逻辑又是由分析,和数论发展而来。从
数学分析,线性代数来学确实比较绕,如果你学的非常好的话,对你的计算机
研究也有用,它是间接的有用,因为它能提高你的数学素质,这种数学素质的
东西,只有当你学的很通的时候才能体会出来。
一般讲,数学中的数论和数理逻辑可能和计算机科学有直接的关系,但全世界
的计算机教育,没有人敢这样教,这或者因为数学分析是整个数学的基础,也
可能因为数论太难了,一般大学没有那么多老师能教这个。
这是我的看法。
17497是的,谈到CS和数学的关系,我认为可以更祥细的说,
软件,应用和硬件几个学科中有科学成份,但更有技术成份,这些学科中,大致上数学是应用和工具.包括形式化方法,统计学等在内的数学方法经常用来实现更先进的计算机技术.(比如数据挖掘,比如多媒体).
在Theoretical
Computer
Science学科,情况不大一样,计算理论,自动机理论,形式语言,形式语义等等形式系统在数学中有极高的抽象度,TCS的重要研究内容之一是形式逻辑.模型论,抽象代数都为TCS提供了基础.计算机科学的核心是算法,组合学算法是计算机的灵魂.
我的理解,构造性数学和离散数学为计算机运行提供了抽象描述,因此,只要是计算机系统和运行直接相关的数学抽象,都是CS的研究内容.当然了,数学范围太广,CS直接关注的只是其中很小的一部分.
17497说到数学分析,它和CS的关系比较间接.学它更多的为了有助于CS专家的思维能力.
说到计算机教育.很少有人深入地学离散数学,学数学分析的更少.我个人认为原因是这样:
计算机有科学的一面(数学理论),也有技术的一面(电子学实现),还有产业的一面.
所以计算机教育差别太大.有的是教广大用户怎样使用计算机,还有的教IT专业人员怎样开发软件,当然,极少数是培养计算机科学研究人员的.最后一种是真正的专家,IT领域每一种重要的新技术和重大的发明创造得以出现和产生,都是这些专家的成果.当然,前两种人不用学数学,最后一种人则必须是数学高手.
17497我晕,怎么有乱码来者,我说我们学校一般,反正课就是这么开的,天天学数学,弄得我大二才过四级,嘿嘿
17497不过计算机系必竟不是数学系,象楼主那样的开数学课,连我这样的学术激进派都觉得有点过份.---计算机科学系怎能照搬数学系课程呢?计算机工程系就更不该照搬了.
真要是重视数学,我看数学分析,线性代数,矩阵论,统计学,随机过程就够了,接下来应该深入学离散数学,比如应该开4门课:数理逻辑,组合数学,图论,抽象代数,顶多加上模型论,有这10门数学课就行了,再接下来应该重点放到计算机科学上,应该学这几门课:数据结构,计算机组成原理,操作系统原理,编译原理,可计算性理论,计算复杂性理论,形式语言与自动机理论,算法设计与分析,形式语义学,程序理论,形式化方法......
这才是我认为理想的CS系.
17497谢谢提醒,好像马上就要开了
17497
| 引用 |
不过计算机系必竟不是数学系,象楼主那样的开数学课,连我这样的学术激进派都觉得有点过份.---计算机科学系怎能照搬数学系课程呢?计算机工程系就更不该照搬了.
真要是重视数学,我看数学分析,线性代数,矩阵论,统计学,随机过程就够了,接下来应该深入学离散数学,比如应该开4门课:数理逻辑,组合数学,图论,抽象代数,顶多加上模型论,有这10门数学课就行了,再接下来应该重点放到计算机科学上,应该学这几门课:数据结构,计算机组成原理,操作系统原理,编译原理,可计算性理论,计算复杂性理论,形式语言与自动机理论,算法设计与分析,形式语义学,程序理论,形式化方法......
这才是我认为理想的CS系.
|
说得有理 跟我想的差不多 很想跟你交个朋友 呵呵
17497不过,本科阶段,很少有如此强调数学的CS系
17497
引用 (yuto @ 2005年09月12日
18时02分) |
| 引用 | 不过计算机系必竟不是数学系,象楼主那样的开数学课,连我这样的学术激进派都觉得有点过份.---计算机科学系怎能照搬数学系课程呢?计算机工程系就更不该照搬了.
真要是重视数学,我看数学分析,线性代数,矩阵论,统计学,随机过程就够了,接下来应该深入学离散数学,比如应该开4门课:数理逻辑,组合数学,图论,抽象代数,顶多加上模型论,有这10门数学课就行了,再接下来应该重点放到计算机科学上,应该学这几门课:数据结构,计算机组成原理,操作系统原理,编译原理,可计算性理论,计算复杂性理论,形式语言与自动机理论,算法设计与分析,形式语义学,程序理论,形式化方法......
这才是我认为理想的CS系.
|
说得有理 跟我想的差不多 很想跟你交个朋友 呵呵
|
我也愿意交你这个朋友.哈哈
看来你也很有一些想法.
17497
引用 (yuto @ 2005年09月07日
18时36分) |
而且听你说你学的课程名来看
只有线性代数不是数学系所学(一般数学系叫做高等代数)
其余都是数学系的专业课
这样学四年应该获得理学学士了
|
有一些CS系是理学的学位,但更多的是工学的.
17497数学是科学之母。记住
17497楼主,你好,我本科学的是数学专业,学的就是你说的那几门课,现在上了计算机的研究生,目前还没发现实质的作用,但是我确定,对我的潜意识,内在的素质有很大的帮助,因为我发现我会比那些没有数学基础的同门学得好象会有点成绩,所以学校开这些课是有道理的
17497
| 引用 (静165455 @ 2005年09月13日
16时11分) |
|
楼主,你好,我本科学的是数学专业,学的就是你说的那几门课,现在上了计算机的研究生,目前还没发现实质的作用,但是我确定,对我的潜意识,内在的素质有很大的帮助,因为我发现我会比那些没有数学基础的同门学得好象会有点成绩,所以学校开这些课是有道理的
|
我读研的时候,班上有不少数学系跨专业过来的,可惜他们转过来是对数学没兴趣,也不知道计算机和数学的结合点在哪里,所以天天只知道学编程语言,结果在班上很不起眼,一点优势也没有.
所以,我觉得还是要找准计算机和数学的结合点.比如你说做网络安全,我看就很不错,本身就是热门方向,前景很好,如果你的数学不错的话,也容易在这个方向上出成果.
17497
| 引用 (zhaoming @ 2005年09月08日
22时12分) |
不过计算机系必竟不是数学系,象楼主那样的开数学课,连我这样的
真要是重视数学,我看数学分析,线性代数,矩阵论,统计学,随机过程就够了,接下来应该深入学离散数学,比如应该开4门课:数理逻辑,组合数学,图论,抽象代数,顶多加上模型论,有这10门数学课就行了,再接下来应该重点放到计算机科学上,应该学这几门课:数据结构,计算机组成原理,操作系统原理,编译原理,可计算性理论,计算复杂性理论,形式语言与自动机理论,算法设计与分析,形式语义学,程序理论,形式化方法......
|
这位老兄说的这些,我也很同意,但好像大部分学校本科阶段都不开可计算性理论,计算复杂性理论,形式语言与自动机理论,形式语义学,程序理论,形式化方法......这些课程,不过我们应该培养自学能力,自已看吧
17497
| 引用 (pgs @ 2005年09月14日
08时48分) |
| 引用 (zhaoming @ 2005年09月08日
22时12分) |
不过计算机系必竟不是数学系,象楼主那样的开数学课,连我这样的
真要是重视数学,我看数学分析,线性代数,矩阵论,统计学,随机过程就够了,接下来应该深入学离散数学,比如应该开4门课:数理逻辑,组合数学,图论,抽象代数,顶多加上模型论,有这10门数学课就行了,再接下来应该重点放到计算机科学上,应该学这几门课:数据结构,计算机组成原理,操作系统原理,编译原理,可计算性理论,计算复杂性理论,形式语言与自动机理论,算法设计与分析,形式语义学,程序理论,形式化方法......
|
这位老兄说的这些,我也很同意,但好像大部分学校本科阶段都不开可计算性理论,计算复杂性理论,形式语言与自动机理论,形式语义学,程序理论,形式化方法......这些课程,不过我们应该培养自学能力,自已看吧
|
是的,本科一般不会学这些,如果真能自己看下来,做为本科生,他的自学能力,抽象思维能力,逻辑思维能力就很强了!将来决不是普通程序员的料,而是有当领军人物的潜力了.
也正因为此,多数学校把这些课开到研究生以上的阶段.
17497不可能是北大,北大不会用别的学校教研组的教材
17497要用计算机来谋生,也不需要那么多数学知识;系统管理或网管,做得很好,也不需要;开发了许多软件的工程师也不需要了解实变函数,泛函分析
17497我看了很生气,不同意有些人的观点,cs系的学生怎么就不动动脑子呢?说的话都是从导师那里学来的。等你们毕业工作了五六年,而不是还在上学。你们回头看看吧。你关心的是网络的安全,linux,操作系统,编程语言。是的,根本用不到,回想一下大一学的矩阵乘法,没有用到过一次。更不要说群论什么了。
你会去研究加密算法?你会去研究压缩算法吗?
如果用计算机模拟,比如做一个网络游戏,如果你是虚拟世界的创造者,你会用简单的数学的,而不是复杂的。
我不知道你们和别人所谓的cs是什么。看看社会上360行,哪一行用到了?
即使用到了,用在什么地方了?有多少人在这一行。醒醒吧!
或者你能给我一些高等数学用在计算机软件里的例子吗?
17497你怎么知道用不上?你的经验很有局限性.有不少工作5年以上的不赞成你的看法.
我举个例子,如果李开复不研究语音的统计学算法,他不会做到今天的高度,如果百度老总不手握美国专利,他不会有风险投资,更不会有中国富豪榜的前几位!什么叫新经济富豪?就是这些手握IT核心技术的精英!装个WINDOWS,写几段.NET,你永远给人打工去吧.30以后做不到中层,出体力都没人要.
这些离我们太远,说点近的.
怎样做到中高层,不同的地方要求不一样.但有一点,做管理,做科研都行!例子还用举吗?看看公司里哪些人混得牛?是管理人员和研究人员,还是开发人员?在学校里,又是哪些人混得牛?
有些CS的学生的确该长长脑子了.当大家都在说当代码编写工人很累的时候,是不是了解一下,搞CS比当代码编写工要爽得多.
至于什么是CS,很多教材有解释.我要说的是,计算机科学怎样联系计算机产业?核心技术怎样变成经济效益?做为个人,怎样利用学术价值来追求经济政治的利益最大化?这些都很有意思,比闷着头写代码强.
现在电脑爱好者论坛太多了,CS论坛很难找到.既然这里是数学论坛,我当然要大谈计算机的高深数学基础---这也是事实!是不容否认的.
要说用不上,我看关键是你个人想怎样发展,想做专家,还是想做工人.没错,前者数量少,但收入高!
17497
引用 (neoedmund @ 2005年09月
18日
18时01分) |
|
或者你能给我一些高等数学用在计算机软件里的例子吗? |
嗯,虽然我没有挑起争端的意思,但是我恰好就是一个在大量使用高等数学,线性代数,微分几何,组合数学,少量拓扑、概率论等数学工具的计算机行业从业者。
我从事的是计算机图形学方面的工作,需要不少数学学科的知识。
17497
引用 (justlikethewind @ 2005年09月22日
17时13分) |
引用 (neoedmund @ 2005年09月
18日
18时01分) | |
或者你能给我一些高等数学用在计算机软件里的例子吗? |
嗯,虽然我没有挑起争端的意思,但是我恰好就是一个在大量使用高等数学,线性代数,微分几何,组合数学,少量拓扑、概率论等数学工具的计算机行业从业者。
我从事的是计算机图形学方面的工作,需要不少数学学科的知识。
|
我估计你肯定不是普通程序员,不是系统分析员,就是高级工程人员,要不就是科研人员.计算机图形学用到大量的微积分和其它更高阶的数学工具.如果您不懂这个,我猜您只能用别人的算法.别人的游戏界面是怎样的,你不可能做的更好,现在有了数学基础,自己可以提出新算法,情况就不一样了.
那位朋友说对了,网络安全也是很数学的.我们讨论网络入侵检测,它的几个模型都是数学的,你提出改进模型和算法,你就能做到更有效的检测.
我想说的是,工作人员从事不同的工作,看法不在一个层次.所以,学生们不要盲目听"有工作经验的人"建议,要自己动脑子思考才对.
人才的金字塔结构,学CS的也不例外.
17497我比较气愤的是,现在总有人不承认计算机是科学---外行的理由是计算机只是工具,(这种看法不值一驳,数学还是工具呢,不照样是科学之王);业内人士的理由是科学挣不到钱,这种看法也不对,生命科学是科学吧?生物产业照样有很多大企业.计算机和生物一样------一方面有高深的计算机科学,另一方面有发达的IT产业------计算机专家兼高层管理的人大有人在,还能说学数学没用?你看看IT高层经理是懂数学懂理论的博士硕士多,还是只会闷头当代码工人的本科多?
有些在校生没有工作经验,对导师劝他学理论不以为然,工作以后当了一段程序员感觉累,就开始抱怨---可是,你不长脑子,听不懂好话,又能埋怨谁呢?
看看人家生命科学的学术论坛满天飞,再看看计算机科学的学术论坛只有小百合一家,电脑爱好者论坛倒是满天飞.真是差距太大了.
17497我看你所学的好象我们信息专业所学的课程啊!
17497数学重要!!
17497等你读到博士就知道为什么需要那么多数学了!
17497
引用 (neoedmund @ 2005年09月
18日
18时01分) |
我看了很生气,不同意有些人的观点,cs系的学生怎么就不动动脑子呢?说的话都是从导师那里学来的。等你们毕业工作了五六年,而不是还在上学。你们回头看看吧。你关心的是网络的安全,linux,操作系统,编程语言。是的,根本用不到,回想一下大一学的矩阵乘法,没有用到过一次。更不要说群论什么了。
你会去研究加密算法?你会去研究压缩算法吗?
如果用计算机模拟,比如做一个网络游戏,如果你是虚拟世界的创造者,你会用简单的数学的,而不是复杂的。
我不知道你们和别人所谓的cs是什么。看看社会上360行,哪一行用到了?
即使用到了,用在什么地方了?有多少人在这一行。醒醒吧!
或者你能给我一些高等数学用在计算机软件里的例子吗?
|
黎叔很生气,后果很严重!!
呵呵
17497顺便提一个问题,计算机课学系学生学常微分方程似乎没有必要吧,计算机科学是离散科学,而常微分方程考虑的是连续的事件,还不如开数论来的爽呢。
17497说的太有道理了,我大学四年学过来,才知道,中国大部分人都不知道什么叫CS,大部分人都以为是搞搞程序(这还算是好的学生咯),呵呵.,我最近才认识到数学的重要.呵呵.
17497楼上说的对,的确很多人不知道CS
以前去书店和图书馆,现在基本不去,因为那里号称计算机专业书籍最多,现在发现不少都是低水平重复的书目,一点价值都没有.不过一些从国外引进的还是很不错的.
国内出版的计算机书目大多数是科普读物,无非是把老外做的成熟工具做一介绍,我们真正关心的是工具背后的理论,技术,原理,算法!!特别关心的是正在研究与发展的理论,技术,原理,算法......因为这才是决定了明天的流行工具趋势,是明天的流行趋势得以实现的关键!!换句话说,不做今天流行工具的使用者,而做未来流行技术的创造者!!!
要做到这一点,才称得上计算机学科的高端人才.从网上下载的英文书写的研究论文和英文原版书籍的确很有价值,从它们中可以亲眼看到计算机科学与技术是怎样走向明天的,它是发展方向和趋势是怎样,它是怎样实现这个发展的,一切都一目了然.
17497理论与实验都是计算机学科的研究方法.
理论就是用数学方法证明,分析,验证;
做试验不用望远镜,也不用显微镜,而是用程序,来观查你的结论是否正确,所以,对计算机学科的多数研究人员来说,写段程序上机运行仅仅是一个实验工具,程序本身并不是你的研究对象.
既使是研究软件的人,也是如此.这一点外行很难理解,但却是事实.
17497看这篇文章《什么叫“我是搞计算机的”? 》,说得很好:
My Webpage
17497楼上的,看过了,说的不错.
现在"计算机应用"一词相当混乱,有不少计算机专业的本科生甚至教师都没搞情,别说外行了.
"计算机应用"和"使用操作计算机"根本就不是一回事,不少人把后者当成了前者.就象"应用数学"和"数学工具的使用"一样,意思差别太大了.
"计算机理论"一词更是混乱,不少人把操作电脑用到的名词当成了"理论",其实,"理论计算机科学"是一个和离散数学很接近的学科.
在那些外行改行"搞计算机的"人眼里,计算机是什么,最容易犯的错误就是把他们专业需要使用计算机和计算机应用专业混为一谈.
17497我当初上本科时,那时老师讲过两个不断线,即数学不断线,英语不断线。
17497我要的书,谁能帮帮忙?
递归论
1 Anil Nerode, Richard A. Shore合著的《Logic
for applications》,Springer出版社
1997出版
2 Nigel
Cutland在
1980年写的《Computability: an introduction to recursive function
theory》,Cambridge University Press
3 Robert I. Soare
1987年写的《Recursively enumerable sets and degrees :a study of computable
functions and computably generated sets》,Springer出版社
1987出版
4
Piergiorgio Ddifreddi写的《Classical recursion theory :the theory of
functions and sets of natural numbers》(North-Holland
1989年)
5 Rogers,
H.写的《Theory of recursive functions and effective
computability》
模型论
6 C.C.Chang和H.J.Keisler合著的《Model
theory》,North-Holland
1973年出版
7 David Marker在2002年刚出版的《Model theory :an
introduction》
该书是Springer出版社的GTM丛书中的一本
集合论
8 Kenneth
Kunen的《Set theory :an introduction to independence
proofs》,这本书是North-Holland出版社在
1980年出版的书
9 Thomas Jech的《Set
theory》(Springer,
1997出版)
10 On Formally Undecidable
Propositions of Principia Mathematica and Related Systems (Basic Books,
1962)
我的Email:chenshi23@tom.com
手机:013509932656
17497有些老书很经典.
17497
引用 (justlikethewind @ 2005年09月22日
17时13分) |
引用 (neoedmund @
2005年09月
18日
18时01分) | |
或者你能给我一些高等数学用在计算机软件里的例子吗? |
嗯,虽然我没有挑起争端的意思,但是我恰好就是一个在大量使用高等数学,线性代数,微分几何,组合数学,少量拓扑、概率论等数学工具的计算机行业从业者。
我从事的是计算机图形学方面的工作,需要不少数学学科的知识。
|
图形学要用到几何,几何就要关联到很多数学。
除了图形学还有什么?
对了,最近发现判定垃圾邮件的概率算法也算是一个应用。不过也不是100%解决垃圾邮件问题的。
当然有一些数学偶尔的这里那里的应用到计算机。但是和计算机打交道的人,95%+平时都不怎么用高深的数学吧。
to:
zhaoming
你没有工作超过5年吧,而且我猜你还是学生。 希望你工作了3年以后还能来反驳我。
17497最近下载到一个数学百科全书,瞎看瞎搜索中,无意发现了这个帖。
啊,这正是我以前思考过的问题。而我的结论是,这取决于你想做一个计算机科学家,还是一个计算机专家。
比如Dijkstra,他就是计算机科学家,人们记住他,因为他的算法。
我觉得现在的计算机教育,大致有两个方向,一个就是培养代码工人,一个就是培养理论研究者。
但实际上这两个方向都是没有错误,错就错在这两个方向目前都没有搞好。代码工人搞成了个人英雄。搞过计算机程序设计的人都应该知道,国内的代码编写依然还处于个人英雄时代。其中弊病在CSDN上有很多讨论的。
理论方面就更气人了。纯粹算法就不提了,中国落后太多了。中国每年投入那么多人民币,那么多博士教授,结果一个操作系统都没有搞出来(我知道那个麒麟系统,还说要在2010年占领5%以上的国内服务器市场,可那个只是修改老外的BSD系统,还死不承认,非说完全自己搞的,在国外都让人骂死了。),一个C语言编译器都没有搞出来。
反正没有看到国内有那个“优秀”博士教授搞出点叫得响的软件来。感觉飘得很。不过论文没少发,科研经费没少拿。大家如果也在高校,应该能够查到那些论文的,反正空谈家太多,可能大家都学《老子》出身的,正是“玄之又玄”啊。
17497
| 引用 (neoedmund @ 2006年03月16日
15时40分) |
引用 (justlikethewind @ 2005年09月22日
17时13分) | 引用 (neoedmund @
2005年09月
18日
18时01分) | |
或者你能给我一些高等数学用在计算机软件里的例子吗? |
嗯,虽然我没有挑起争端的意思,但是我恰好就是一个在大量使用高等数学,线性代数,微分几何,组合数学,少量拓扑、概率论等数学工具的计算机行业从业者。
我从事的是计算机图形学方面的工作,需要不少数学学科的知识。
|
图形学要用到几何,几何就要关联到很多数学。
除了图形学还有什么?
对了,最近发现判定垃圾邮件的概率算法也算是一个应用。不过也不是100%解决垃圾邮件问题的。
当然有一些数学偶尔的这里那里的应用到计算机。但是和计算机打交道的人,95%+平时都不怎么用高深的数学吧。
to:
zhaoming
你没有工作超过5年吧,而且我猜你还是学生。 希望你工作了3年以后还能来反驳我。
|
那还是现在说把,工作了快10年了,和产业界和学术界都要接触.坦白说,大多数工程师的确没有用到高深的数学,但我还是接触到一些人在做很数学的东西.产业界和学校都有,只是学校更多一些,而且有一些也是直接面向市场的.
如果你想创新的话,数学的重要性就不用说了,不想创新的话,不学也行.
17497如果想做一背子程序民工,别说3年,就是30年,也反驳不了neoedmund
搞计算机的高端人士,有一些是商人科学家.
也许我们还没有做到这个高度,但这个发展方向不错,写程序的人永远是被人指挥的人,管理者根本不写程序,neoedmund工作多年,经验丰富,相信应该明白.
17497
引用 (火焰c @ 2006年03月
17日
14时59分) |
最近下载到一个数学百科全书,瞎看瞎搜索中,无意发现了这个帖。
啊,这正是我以前思考过的问题。而我的结论是,这取决于你想做一个计算机科学家,还是一个计算机专家。
比如Dijkstra,他就是计算机科学家,人们记住他,因为他的算法。
我觉得现在的计算机教育,大致有两个方向,一个就是培养代码工人,一个就是培养理论研究者。
但实际上这两个方向都是没有错误,错就错在这两个方向目前都没有搞好。代码工人搞成了个人英雄。搞过计算机程序设计的人都应该知道,国内的代码编写依然还处于个人英雄时代。其中弊病在CSDN上有很多讨论的。
理论方面就更气人了。纯粹算法就不提了,中国落后太多了。中国每年投入那么多人民币,那么多博士教授,结果一个操作系统都没有搞出来(我知道那个麒麟系统,还说要在2010年占领5%以上的国内服务器市场,可那个只是修改老外的BSD系统,还死不承认,非说完全自己搞的,在国外都让人骂死了。),一个C语言编译器都没有搞出来。
反正没有看到国内有那个“优秀”博士教授搞出点叫得响的软件来。感觉飘得很。不过论文没少发,科研经费没少拿。大家如果也在高校,应该能够查到那些论文的,反正空谈家太多,可能大家都学《老子》出身的,正是“玄之又玄”啊。
|
说的是
17497不专门去学数学了,因为没时间了,我已经没有雄心壮志,做个代码工养家糊口算.
17497
| 引用 (neoedmund @ 2006年03月16日
15时40分) |
引用 (justlikethewind @ 2005年09月22日
17时13分) | 引用 (neoedmund @
2005年09月
18日
18时01分) | |
或者你能给我一些高等数学用在计算机软件里的例子吗? |
嗯,虽然我没有挑起争端的意思,但是我恰好就是一个在大量使用高等数学,线性代数,微分几何,组合数学,少量拓扑、概率论等数学工具的计算机行业从业者。
我从事的是计算机图形学方面的工作,需要不少数学学科的知识。
|
图形学要用到几何,几何就要关联到很多数学。
除了图形学还有什么?
对了,最近发现判定垃圾邮件的概率算法也算是一个应用。不过也不是100%解决垃圾邮件问题的。
当然有一些数学偶尔的这里那里的应用到计算机。但是和计算机打交道的人,95%+平时都不怎么用高深的数学吧。
to:
zhaoming
你没有工作超过5年吧,而且我猜你还是学生。 希望你工作了3年以后还能来反驳我。
|
不知道你这个“和计算机打交道的人”指的是哪些人,不过他们肯定不能代表全部,但要讨论“计算机是否能用到高深的数学”应该从全局来考虑。国内的大部分和计算机打交道的人可能都用不上,那是因为我们做得不好(包括科研工作者),我们现在还在跟着国外跑,看看图灵奖和计算机先驱奖得主,有多少都是学数学的?图灵、克努特、麦卡锡、冯诺依曼、艾肯、赫柏、霍尔、科德、古德、霍尔勃顿、米尔斯等等。另外,理论计算机科学本身就是数学的一个分支!
17497这是当然需要的了
现在有几个牛的计算机不是数学学得相当好么?
17497大量的事实
17497
| 引用 (pgs @ 2006年03月31日
15时14分) |
| 引用 (neoedmund @ 2006年03月16日
15时40分) |
引用 (justlikethewind @ 2005年09月22日
17时13分) | 引用 (neoedmund @
2005年09月
18日
18时01分) | |
或者你能给我一些高等数学用在计算机软件里的例子吗? |
嗯,虽然我没有挑起争端的意思,但是我恰好就是一个在大量使用高等数学,线性代数,微分几何,组合数学,少量拓扑、概率论等数学工具的计算机行业从业者。
我从事的是计算机图形学方面的工作,需要不少数学学科的知识。
|
图形学要用到几何,几何就要关联到很多数学。
除了图形学还有什么?
对了,最近发现判定垃圾邮件的概率算法也算是一个应用。不过也不是100%解决垃圾邮件问题的。
当然有一些数学偶尔的这里那里的应用到计算机。但是和计算机打交道的人,95%+平时都不怎么用高深的数学吧。
to:
zhaoming
你没有工作超过5年吧,而且我猜你还是学生。 希望你工作了3年以后还能来反驳我。
|
不知道你这个“和计算机打交道的人”指的是哪些人,不过他们肯定不能代表全部,但要讨论“计算机是否能用到高深的数学”应该从全局来考虑。国内的大部分和计算机打交道的人可能都用不上,那是因为我们做得不好(包括科研工作者),我们现在还在跟着国外跑,看看图灵奖和计算机先驱奖得主,有多少都是学数学的?图灵、克努特、麦卡锡、冯诺依曼、艾肯、赫柏、霍尔、科德、古德、霍尔勃顿、米尔斯等等。另外,理论计算机科学本身就是数学的一个分支!
|
赞,我觉得应该有分工,不是所有人都去写程序
17497如果楼主只是想学习计算机操作,那就不用学习数学,只要到某某培训班去培训几个月,你就是一个熟练的操作员了。如果楼主想学习计算机科学,那就先把数学学好吧,没有学好数学,你是学不懂计算机科学的。个人看法,不妥请见谅!
17497呵呵,至少我没有小看程序的作用,只是觉得一个"程序员"的作用远不能和一个计算机科学家比美.
克努特是个不错的例子,我们看看他的贡献---
计算机科学技术中两个最基本的概念:“算法”(Algorithm)和“数据结构”(Data
Structure)就是克努特于29岁时提出来的。
1973年他首创双向链表。在编译器设计方面,著名的LR(k)文法也是克努特在对自左至右、自底向上的移进一归约分析进行了深刻剖析的基础上,经过高度概括和集中以后发明的,它表示具有从左(L)到右®的分析而向前看k个符号,以确定所要进行的归约和应用何种语法解释。LR(k)文法的识别效率高,在从左至右扫描输入串时,就能发现其中的语法错误,并能准确地指出出错位置,因此被广泛应用。此外,利用LR(众)文法还能正确区分像Flying
planes is fun和Flying planes can
crash这类句子(前一个句子“开飞机很有趣”中flying是动名词,而后一个句子“飞行中的飞机可能出事”中Flying是现在分词当形容词)。以著名的巴克斯—诺尔范式为基础的“属性文法”(attribute
grammar)也是克努特首先提出来的。属性文法在普通的上下文无关文法(context-free
grammar)的基础上,对每一个终结点或非终结点加上一些属性,和对这些属性进行估值的语义规则集,从而形成一种新的、有更强表达与描述能力的文法。其中属性是由<属性名、属性值>的有序偶对组成的。属性的内容则可包括模式标识符表等。
在算法方面,有他和他的学生共同设计的诸如Knuth-Bendix算法和Knuth-Morris-Pratt算法,前者是为了考察数学公理及其推论是否“完全”而构造标准重写规则集(rewriting
rule
set)的算法,曾成功地用它解决了群论中的等式的证明问题,是定理机器证明的一个范例。后者是在文本中查找字符串的简单而高效的算法。此外,克努特还设计与实现过最早的随机数发生器(random
number
generator)。
虽然程序设计语言在不断地发展与完善之中,但“理想语言”并未出现,可能永远也不会出现。但新一代人会不断进取。克努特在20世纪80年代所倡导的“作文式程序设计”(literate
programming,国内有人将它译为“文化程序设计”)就是这一努力的又一体现和成果.
1983年,克努特推出了第一个这样的程序设计系统WEB
17497好象有几位老兄对编写程序很不屑啊。其实这也没必要吧,我个人觉得编写程序和计算机科学来说就象做习题和数学的关系,还是很必要的。(可能不太恰当,一时想不出别的比方)很多计算机科学家都沉浸其中而乐此不彼,如克努特,还有开发C语言的里奇、汤普森等。毕竟计算机应用到实际中还要以程序为载体!
17497
引用 (zhaoming @ 2006年04月05日
19时48分) |
呵呵,至少我没有小看程序的作用,只是觉得一个"程序员"的作用远不能和一个计算机科学家比美.
克努特是个不错的例子,我们看看他的贡献---
计算机科学技术中两个最基本的概念:“算法”(Algorithm)和“数据结构”(Data
Structure)就是克努特于29岁时提出来的。
1973年他首创双向链表。在编译器设计方面,著名的LR(k)文法也是克努特在对自左至右、自底向上的移进一归约分析进行了深刻剖析的基础上,经过高度概括和集中以后发明的,它表示具有从左(L)到右®的分析而向前看k个符号,以确定所要进行的归约和应用何种语法解释。LR(k)文法的识别效率高,在从左至右扫描输入串时,就能发现其中的语法错误,并能准确地指出出错位置,因此被广泛应用。此外,利用LR(众)文法还能正确区分像Flying
planes is fun和Flying planes can
crash这类句子(前一个句子“开飞机很有趣”中flying是动名词,而后一个句子“飞行中的飞机可能出事”中Flying是现在分词当形容词)。以著名的巴克斯—诺尔范式为基础的“属性文法”(attribute
grammar)也是克努特首先提出来的。属性文法在普通的上下文无关文法(context-free
grammar)的基础上,对每一个终结点或非终结点加上一些属性,和对这些属性进行估值的语义规则集,从而形成一种新的、有更强表达与描述能力的文法。其中属性是由<属性名、属性值>的有序偶对组成的。属性的内容则可包括模式标识符表等。
在算法方面,有他和他的学生共同设计的诸如Knuth-Bendix算法和Knuth-Morris-Pratt算法,前者是为了考察数学公理及其推论是否“完全”而构造标准重写规则集(rewriting
rule
set)的算法,曾成功地用它解决了群论中的等式的证明问题,是定理机器证明的一个范例。后者是在文本中查找字符串的简单而高效的算法。此外,克努特还设计与实现过最早的随机数发生器(random
number
generator)。
虽然程序设计语言在不断地发展与完善之中,但“理想语言”并未出现,可能永远也不会出现。但新一代人会不断进取。克努特在20世纪80年代所倡导的“作文式程序设计”(literate
programming,国内有人将它译为“文化程序设计”)就是这一努力的又一体现和成果.
1983年,克努特推出了第一个这样的程序设计系统WEB
|
咱俩握握手!
17497克努特,一个伟大的科学家,他自己谦虚自称为"一个程序员",但我们可以想想,今天我们经常见到的"程序员"在干嘛?---多数在微软的VISUAL环境下按几个鼠标,画几个控件出来,然后写上几行代码-----再看克努特这个"程序员"在干嘛?---亲自去发展上下文无关文法的数学理论,然后用到编绎器设计中去,去发明新的语言,---看看这位"程序员",再看看我们理解的多数"程序员",真是天壤之别啊.
人家的"程序员"为计算机科学的大厦打下了坚实的地基,然后盖好了摩天大楼-------我们的"程序员"躺在人家盖好的摩天大楼里扫扫地抹抹桌,有的人一背子都在第
18层扫地,根本看不到底下
17层是什么样,甚至压根都不知道下边还有17层,更别说地下的地基了----------正因为如此,"程序员"克努特是一位伟大的计算机科学家,而相比之下,我们日常见到的"程序员"就只好叫"代码工人"了.---这就是差别,不服不行.
17497克努特、里奇、汤普森发明的编程语言被我们千千万万的程序员来用,难道我们这千千万万的人还好意思和人家一块叫"程序员"?
诺一曼发明计算机,让我们今天上亿的人来使用,难道我们这上亿的人还好意思和人家诺一曼教授一起号称"精通电脑"?
牛顿发明微积分,他的一些基本公式被我们全球几百万的大一新生做数学题时代入公式来计算,来使用,难道我们这几百万的大一新生好意思和人牛顿一起号称"伟大的科学家"?
让我们记住:
同样一件东西,我们觉得越好用越简单,发明它的人一定研究的越高深越复杂,电脑如此好用,是因为计算机科学家们把深奥复杂的都做了,留给我们用户的就只有简单易用了,
本来电脑是一堆废铁,没有任何价值,让人办好一件事不难,因为人有智商,让狗办好一件事才是真难,因为狗的智商比人低.现在我们让一堆废铁来办事,那可是比让狗办难多了,因为废铁根本没有生命!更何况是办很多事,不是一件事!可见让电脑为我们广返服务有多难?想想自然界除了人是万能的,还有哪些事物能应用如此之广,恐怕除了电脑没别的了.把一堆废铁变的无所不能,想想有多难?但为何我们用户和程序员不觉得难?那是因为计算机科学家们把难得做了,给咱整个最简单的来做,咱当然不觉得难了.
17497我搞了半年多的计算机,还没有发现数学有什么用,这个东西见效咋这么慢呢???
17497当然,我并不是说只有算法重要,程序不重要.
再好的算法,最后也要变成程序,程序的效率提高了,算法的优越性就算是体现出来了.
所以,那些研究算法的科学家,当然不是"没用",你提出的新算法提高了实际的计算机工程的效率,这些算法才有意义
17497我觉得比较好的一个情况是:
有的人做理论研究,研究计算模型与算法
有的人做工程设计,比如做工程需求与系统分析
有的人做代码实现,比如编写代码
有的人做项目管理,...
总之,都应该有人做,写程序的蓝领应该人数最多,但绝对不应该是全部!绝对不应该所有人都做这个.
17497同样一个事物,人家发明人是科学家,你拿来当工具用你就只能叫用户,
不要以为---你们都接触到了这件事物,你就和人家一样伟大了,
创造新事物的人和熟练操作工具的人不在一个层次
17497
引用 (pgs @ 2006年04月05日
19时56分) |
引用 (zhaoming @ 2006年04月05日
19时48分) |
呵呵,至少我没有小看程序的作用,只是觉得一个"程序员"的作用远不能和一个计算机科学家比美.
克努特是个不错的例子,我们看看他的贡献---
计算机科学技术中两个最基本的概念:“算法”(Algorithm)和“数据结构”(Data
Structure)就是克努特于29岁时提出来的。
1973年他首创双向链表。在编译器设计方面,著名的LR(k)文法也是克努特在对自左至右、自底向上的移进一归约分析进行了深刻剖析的基础上,经过高度概括和集中以后发明的,它表示具有从左(L)到右®的分析而向前看k个符号,以确定所要进行的归约和应用何种语法解释。LR(k)文法的识别效率高,在从左至右扫描输入串时,就能发现其中的语法错误,并能准确地指出出错位置,因此被广泛应用。此外,利用LR(众)文法还能正确区分像Flying
planes is fun和Flying planes can
crash这类句子(前一个句子“开飞机很有趣”中flying是动名词,而后一个句子“飞行中的飞机可能出事”中Flying是现在分词当形容词)。以著名的巴克斯—诺尔范式为基础的“属性文法”(attribute
grammar)也是克努特首先提出来的。属性文法在普通的上下文无关文法(context-free
grammar)的基础上,对每一个终结点或非终结点加上一些属性,和对这些属性进行估值的语义规则集,从而形成一种新的、有更强表达与描述能力的文法。其中属性是由<属性名、属性值>的有序偶对组成的。属性的内容则可包括模式标识符表等。
在算法方面,有他和他的学生共同设计的诸如Knuth-Bendix算法和Knuth-Morris-Pratt算法,前者是为了考察数学公理及其推论是否“完全”而构造标准重写规则集(rewriting
rule
set)的算法,曾成功地用它解决了群论中的等式的证明问题,是定理机器证明的一个范例。后者是在文本中查找字符串的简单而高效的算法。此外,克努特还设计与实现过最早的随机数发生器(random
number
generator)。
虽然程序设计语言在不断地发展与完善之中,但“理想语言”并未出现,可能永远也不会出现。但新一代人会不断进取。克努特在20世纪80年代所倡导的“作文式程序设计”(literate
programming,国内有人将它译为“文化程序设计”)就是这一努力的又一体现和成果.
1983年,克努特推出了第一个这样的程序设计系统WEB
|
咱俩握握手!
|
好!
17497说到数学和计算机,其实初学计算机的人接触的是"机"而不是"计算",专家眼中的"计算机"则是最主要是"计算",次要的才是"机"------这样的话,我们可以想一下--难道"计算"和"数学"关系不大?---这样说可就搞笑了吧---所以,专家眼中的"计算机"绝对和"数学"关系密切的.
有的人搞了7,8年,才知道计算机是具体怎样和数学联系,也有些人一直做熟练重复劳动,也就一直不知道计算机是具体怎样和数学联系(当然他们也不用知道)
17497当然了,计算机科学家关心的"计算"和数学家关心的"计算"还是不大一样.
计算机科学家关心的"计算"要考滤能在机器上实际运行,更关心机器在各个领域应用时的"计算"的共性抽象归类,(只有这样才能使计算机的应用面广)
所以,计算机科学家嘴里的"计算"多数都是构造的离散的组合的形式化的数学模型与算法,只是计算的一个分支,对更广义的计算甚至更广阔的数学,就不大关心了,那都是数学家的事了
17497
| 引用 (zhaoming @ 2006年04月05日
20时46分) |
当然,我并不是说只有算法重要,程序不重要.
再好的算法,最后也要变成程序,程序的效率提高了,算法的优越性就算是体现出来了.
所以,那些研究算法的科学家,当然不是"没用",你提出的新算法提高了实际的计算机工程的效率,这些算法才有意义
|
我不了解,不知道是不是有一些纯数学的理论能够几十年上百年找不到应用价值?有数学界的朋友给介绍一下就好了
不过在计算机界,的确很难出现这种情况---一种形式化的理论,一种算法或模型,能长期找不到应用---这样的理论当初就不会有人去搞.但长期找不到应用不代表更长期就没有重要价值,所以,计算机科学的发展还是需要更基础更长期的数学研究,这恐怕就靠数学界了.
17497恩,想不到国内还有认认真真讨论计算机科学的论坛,,太不容易了。支持!!
我很同意一些朋友的看法,中国计算机科学的水平比较低。不管是理论还是应用上。我们还需要努力啊。
对于这个议题,我想关键是楼主自己以后想选择什么样的职业。如果不想做科学研究,基本就不用去学高深的数学。
但是如果要做科研一定要学好数学,,毕竟现在计算机科学和其他科学的交叉应用很多。你做了研究以后就会嫌以前的数学学得太少了。当然,编程也很重要,但是做科研的编程大多数情况下不是在什么高级开发环境下去做一个应用程序。
计算机科学有很多方向,不同方向对数学和编程的要求也不一样。但不管怎么说,所有这些都是基于科学方法来做的,和做产品高软件工程很不一样的,那是属于CE而不是CS。
举个例子,,去比较一下微软研究院和微软产品开发部门的各个组做的东西,,应该就能
看到区别了。
17497
| 引用 (zhaoming @ 2005年09月02日
20时08分) |
我在计算机系呆了N(N>10)年,刚开始我和你一样,也很奇怪,计算机和数学还有关系?
但后来我明白了,计算机科学就是从数学的一个分支发展过来的.象你说的社会上的培训班,学的是"计算机操作"!那不是"计算机科学"!你刚上大学,大概给你解释不清"计算机科学"这个词的含义,但它的确是很数学的.
不学数学你肯定做不了计算机专家,只能做用户,充其量是熟练的代码工人.
写程序也不是计算机科学,就象望远镜不是天文学一样,对了,这话不是我说的,是一位图灵奖(计算机科学领域的诺贝尔奖)得主说的.
|
同感!
17497看了大家的讨论,
收获非浅.
这个问题似乎是理论与实际运用的问题
关键要搞清楚理论在实际中的需求量
17497其实就算是有些人说是自己在工作上真正用不了多少数学知识,但是回头你想一想,数学是科学的王后啊,数学对培养人分析问题的逻辑思维能力可是无虚致疑的,计算机的好多东西就是靠用数学模型去实现的,没有数学知识,请问你怎么来分析这个问题,难道现在计算机可以智能高到自己知道去解决任何问题吗?
17497楼上说的是
就算有一天,计算机真的知道怎样自行解决任何问题了,那也是人类找到了更高阶的数学,使计算机有了更高的智能
17497似乎又有观点说,算法不是数学而是计算机,这个我觉得算法既是计算机又是构造性数学
17497当我们说西方计算机科学界的数学学派占主流地位时,当我们说西方的计算机技术水平领先于我们时,----难道看到这样两个事实还不够吗?难道这两个事实没有关系吗?数学学派在西方的计算机科学界占主流是因为他们特别学霸?而不是因为他们的研究推动了计算机技术的进步?西方的计算机技术水平的领先是因为什么?不是因为和数学有千丝万缕联系的计算机科学?
我个人更倾向认为算法更多属于计算机科学本身,但它是由数学语言书写的,学过计算理论的人都知道.
想完全抛开数学,想法不错,但怎样落实?太难了.现在不是谈论我们想不想不要数学发展计算机,而是能不能的问题?
分析网络协议,不用数学,你能证明它的安全性?
提高图形质量,不找更优的数学模型与算法,能提高质量?
寻找更优的数据挖倔与搜锁算法,能不考滤数学模型?
发明一种新语言,要写编绎器把?不懂它的数学原理行吗?
更不要说人工智能,软件形式化....
要说可以离开数学发展计算机,不要说图灵奖得主那些科学家笑了,就连大公司大企业里边的李开复们都会笑了,因为就连这些精英都是靠在计算机某个领域研究数学模型起家的,你敢说数学和计算机没关系?
离开数学发展计算机,是赶超西方的捷径?喊喊口号不错,但怎样落实呢?就象研发飞机可以不必考滤空气动力学一样,我实在想不出该怎样做,不过还是盼着有大牛能做到这一点.
我倒是同意一点:计算机科学不是数学的真子集,要想发展计算机,只有数学是远远不够的,更多要靠计算机科学本身.事实上,我们也根本没必要区分的很清楚说,计算机科学中那些是数学,哪些不是,已经高度溶合发展了.
17497{数学}交{计算机科学}不等于空!
17497算法说白了,就是把一种解决问题的办法写成计算机所能识别的语言的形式交给计算机去做事情,这个东西不用数学谁要是给我能交给计算机,我真服他,呵呵。
就再说说看,当你学其他学科的时候感觉心情挺烦躁,又看不进去的时候,放下心来去好好学学数数,你再回头去看那些原来没看懂的东西,好像一下变简单似的,这是我个人的一点体验,不拘于泥,只能做参考。
17497这个帖子的讨论非常有意思。
很有代表性。
可以说,没有数学的计算机应该叫做“计算机技术“。
有了数学的计算机才可以叫做“计算机科学“ (cs)
17497
| 引用 (lalgebral @ 2006年07月15日
16时52分) |
| {数学}交{计算机科学}不等于空!
|
呵呵,这个贴子形像啊。
如果有 集合A:计算机科学
集合B:数学
那么A - B = ? 请各位坛友看看这个集应该是什么啊?
17497估计楼主是学计算数学的,现在计算数学在本科阶段叫做“信息与计算科学”,现在这个社会都流行包装,哈哈。
17497to:zhaoming
我想请教一下这个问题,
现在针对大学生就业难的现象(偏计算机),出现了好多的IT软件培训机构,他们都在说学软件重注的是学员的逻辑思维能力,真正的数学功底有高中的就够了,只要学员具有高中数学底子就可以了,而且他们说他们说学员只要在他们那学出来之后就可以在任何软件领域内胜任。我想请问一下软件这个行业里面有那么普通性吗?比如说现在热门的网络安全和网络游戏产业,学了网络安全编程的就可以胜任网络游戏开发吗?相反的学了网络游戏的开发就可以在网络安全软件领域开发软件吗?(此提问关系到我一亲戚的的切身利益)
谢谢!
17497有空可以研究《算法设计得艺术》
呵呵
17497
引用 (newtoncas @ 2006年11月27日
18时28分) |
有空可以研究《算法设计得艺术》
呵呵 |
请问一下:这本书是哪个出版社,哪个作家写的,我在china-pub上搜索怎么找不到啊?
谢帮忙告诉我。谢谢
17497
| 引用 (zhaoming @ 2005年09月08日
22时12分) |
不过计算机系必竟不是数学系,象楼主那样的开数学课,连我这样的学术激进派都觉得有点过份.---计算机科学系怎能照搬数学系课程呢?计算机工程系就更不该照搬了.
真要是重视数学,我看数学分析,线性代数,矩阵论,统计学,随机过程就够了,接下来应该深入学离散数学,比如应该开4门课:数理逻辑,组合数学,图论,抽象代数,顶多加上模型论,有这10门数学课就行了,再接下来应该重点放到计算机科学上,应该学这几门课:数据结构,计算机组成原理,操作系统原理,编译原理,可计算性理论,计算复杂性理论,形式语言与自动机理论,算法设计与分析,形式语义学,程序理论,形式化方法......
这才是我认为理想的CS系.
|
zhaoming,您在这个话题中给了大家许多极富建设性的学习建议和独特的见解,相信让到本坛看过本贴的人都是大受裨益的。但是,进入这个坛的人有搞科研做学术的,还有在读的在校本、专科及职高等学生和部分计算机爱好者。您给大家列出的这个学习大纲上的一些课目的确是精典,有些科目在校虽然在读,但是是模棱两可,也不知道该去做什么,往哪用,怎么用得最好。但是我建议你能分门别类地介绍一下各课程的起源及在计算机的应用范围及重要性,如果能根据您在行业的经验能举点例子就更好了。
希望广大坛友都勇跃参与到这个话题中讨论中来,相互学习,受益。
17497学好数学,学数据结构竟然变得轻松了!
17497
| 引用 (xznuzzt @ 2006年12月05日
12时33分) |
......还记得
1988年贝尔实验室副总裁亲自来访问我的学校,目的就是为了想了解为什么他们的语音识别系统比我开发的慢几十倍,而且,在扩大至大词汇系统后,速度差异更有几百倍之多。他们虽然买了几台超级计算机,勉强让系统跑了起来,但这么贵的计算资源让他们的产品部门很反感,因为“昂贵”的技术是没有应用前景的。在与他们探讨的过程中,我惊讶地发现一个O(n*m)的动态规划(dynamic
programming)居然被他们做成了O(n*n*m)。更惊讶的是,他们还为此发表了不少文章,甚至为自己的算法起了一个很特别的名字,并将算法提名到一个科学会议里,希望能得到大奖。当时,贝尔实验室的研究员当然绝顶聪明,但他们全都是学数学、物理或电机出身,从未学过计算机科学或算法,才犯了这么基本的错误。我想那些人以后再也不会嘲笑学计算机科学的人了吧!
|
这是李开复在“算法的力量”中的一段话,由此看来,算法需要数学基础,但毕竟还有着与数学不同的一面。
现在的高校开设的专业都称作“计算机科学与技术”,可见计算机是科学与技术的结合体,它既有着以逻辑思维为基础的“科学”的一面,也有着以实践以主的“技术”的一面,因此“计算机”这三个字包含了太多的东西,故而它的发展所依靠的基础也不一样,看一看计算机先驱奖的得主中,有数学出身的,他们大多在理论计算机科学中大显身手;也有学物理的,他们大多在硬件设计中一展才华;还有一些可归为杂类的,这些人中有学机械的(威登海姆);有学教育学的(约翰逊);甚至还有学文学的(弗洛伊德)。
计算机经过70年的发展,已经形成了以多种学科为基础,而又自成一派的新学科,这里面必然有其它学科所接触不到的东西。但有一点可以确信:理论计算机科学是离不开数学的!
因此,数学基础好的可以为计算机的发展做出贡献,数学基础差的同样可以为计算机的发展做出贡献(在工程方面)。
17497
| 引用 (lanlishi @ 2006年11月28日
13时23分) |
引用 (newtoncas @ 2006年11月27日
18时28分) |
有空可以研究《算法设计得艺术》
呵呵 |
请问一下:这本书是哪个出版社,哪个作家写的,我在china-pub上搜索怎么找不到啊?
谢帮忙告诉我。谢谢
|
是这套书吧《计算机程序设计艺术》(The Art of Computer
Programming),(美)Donald E.Knuth(高德纳)著。现在出到第四卷了。读这套书对数学要求很高。
17497
| 引用 (xznuzzt @ 2006年12月05日
12时33分) |
| 学好数学,学数据结构竟然变得轻松了!
|
离散数学的大功劳
学好了数学,不但学数据结构,计算机,对以后其他学科都是极有帮助的,祝你好运!
17497我觉得哈,一般的小编程是小打小闹,楼主chefcui你说大街上交几百块钱上的补习班就能学好,他们仅是表面功夫,是土八路!你先学好数学,打好基础,出来后再大的项目也是不怕的,是正规军!所以不要气馁,基础还是要抓的!
17497
| 引用 (matcray @ 2006年12月08日
09时34分) |
|
我觉得哈,一般的小编程是小打小闹,楼主chefcui你说大街上交几百块钱上的补习班就能学好,他们仅是表面功夫,是土八路!你先学好数学,打好基础,出来后再大的项目也是不怕的,是正规军!所以不要气馁,基础还是要抓的!
|
支持!俗话说“万太高楼平地起!”,只在扎实打好了你的数学基础在计算机科学的一些核心课程,以后无论是继续学习深造还是参加工作向计算机的某个方向发展都是很有利的。人的一生很长,千万不要被眼前的某些小道消息(像“计算机现在是冷门,没前途”)给一叶遮目,不见泰山了,对自己要有信心,但也不能光有口号,行动起来,坚持到底一定会成功的,记住在校期间一定要学好最基本的东西,同时还要培养自己思考问题和解析问题的能力。基本打扎实了,以后要根据自己的爱好及天天赋去找准一个结合点,不要做“万事通”,精一个面就可以了。
17497
| 引用 (lanlishi @ 2006年11月28日
14时25分) |
| 引用 (zhaoming @ 2005年09月08日
22时12分) |
不过计算机系必竟不是数学系,象楼主那样的开数学课,连我这样的学术激进派都觉得有点过份.---计算机科学系怎能照搬数学系课程呢?计算机工程系就更不该照搬了.
真要是重视数学,我看数学分析,线性代数,矩阵论,统计学,随机过程就够了,接下来应该深入学离散数学,比如应该开4门课:数理逻辑,组合数学,图论,抽象代数,顶多加上模型论,有这10门数学课就行了,再接下来应该重点放到计算机科学上,应该学这几门课:数据结构,计算机组成原理,操作系统原理,编译原理,可计算性理论,计算复杂性理论,形式语言与自动机理论,算法设计与分析,形式语义学,程序理论,形式化方法......
这才是我认为理想的CS系.
|
zhaoming,您在这个话题中给了大家许多极富建设性的学习建议和独特的见解,相信让到本坛看过本贴的人都是大受裨益的。但是,进入这个坛的人有搞科研做学术的,还有在读的在校本、专科及职高等学生和部分计算机爱好者。您给大家列出的这个学习大纲上的一些课目的确是精典,有些科目在校虽然在读,但是是模棱两可,也不知道该去做什么,往哪用,怎么用得最好。但是我建议你能分门别类地介绍一下各课程的起源及在计算机的应用范围及重要性,如果能根据您在行业的经验能举点例子就更好了。
希望广大坛友都勇跃参与到这个话题中讨论中来,相互学习,受益。
|
同感啊~最可怜的就是像我这样想努力,却又瞎摸乱转的人,记得在概率那个板块有个概率的科学树,感觉颇深,要是每一们学科都能像那样总结下来,扫清了迷茫的大雾,会使初学者重新拾回方向感,至少有力有处使吧
敬佩一个~
17497个人感觉,数学对计算机科学还是很重要的!
17497太精彩了
支持这样的讨论
我认为观念的更新才是最重要的,任何一门学科都是一个支撑系统,一般认为是金字塔形的
从下往上,底层的建筑最为结实,如前面所说的
我门用起来简单是因为人家已经做好其他很难的工作了,我还认为我门用的简单是因为我门懂的少,我门的知识系统就象一个圆圈,随着圆圈的变大
所未知的就越多(与未知世界的接触更多),计算机科学由数学而来,是一个反馈的过程,也会使数学得到新的发展,历史上数学的每一个分支都使得数学更数学,她们的紧密联系是无疑的,虽然看上去计算机领域所用的数学比较的离散可执行可操作,然而我很模糊的认为那是因为现在的计算机科学相对于未来的计算机科学就象早期的初等数学和现在庞大精密的数学之间的关系,那是一个系统吧,只有系统扩大之后,才能看清楚她的具体位置。
我门可以各取所需,如果觉的自己只要这样或那样就够了,那可以。
恩,肯定要有某些人不能只停留在应用层面,相信有很多很多人还是怀有那样一个梦想,梦想自己可以跟那些大牛一样做事情,这是肯定可以的。
晕死,很没逻辑,不说了,数学和计算机都学的很好的话,或者说素养很好也可以,也许是个不错的选择,少数人去实现吧。
17497
| 引用 (前沿 @ 2006年12月06日
12时38分) |
| 引用 (lanlishi @ 2006年11月28日
13时23分) |
引用 (newtoncas @ 2006年11月27日
18时28分) |
有空可以研究《算法设计得艺术》
呵呵 |
请问一下:这本书是哪个出版社,哪个作家写的,我在china-pub上搜索怎么找不到啊?
谢帮忙告诉我。谢谢
|
是这套书吧《计算机程序设计艺术》(The Art of Computer
Programming),(美)Donald E.Knuth(高德纳)著。现在出到第四卷了。读这套书对数学要求很高。
|
找到了这本书的电子版看了很少一部分,作者写的的确是强,可是我数学底子太弱了,读不下去,呵呵建议大家先不要急着去看《算法导论》这本书,这是地址
http://www.china-pub.com/computers/common/...fo.asp?id=3
1701
17497对于理解数学和计算机科学关系的人, 不说也没有问题.
对于不理解的人,
也懒得去做传教士.
计算机科学不是一门可以科普式的学科.
17497看了各位前辈的讨论,获益非浅啊,现在偶也准备趁还在学校准备重修基础课程了,向各位学习啊
17497这个贴说啥也的恢复一个——竟然从2005讨论到2007年。
我认为搞计算机需要数学基础和计算机的专业基础,一个不能少。
数学基础重要,编程语言的把握程度也很重要。
举几个简单例子:
1、一个数的8次访:可以是8个8相乘,可以使用pow函数,也可以x<<3,不同的编程方法决定了不同的速度。(你得熟悉语言)
2、矩阵相乘:可以直接相乘,可以采用其他算法如:strassen来降低运算两,据说还有更好的算法。(你得熟悉算法)
3、C语言中有两种循环方式:While模式和For模式,但是在不同的硬件平台上,汇编代码是不一样的,自然所使用的指令数量(时间)也是不一样的,——你要熟悉语言,一直到指令层。
4、如果你手头上有一套算法库,对同一个问题的不同算法实现,那么在解决一个具体事例的时候,有多种算法组合——速度和效果成为相互制约的因素,如何构造出最好的算法组合?这可能是一个线性规划或者图论的问题。如何恰当的估算每个算法的时间复杂度呢,不同硬件、操作系统上的时间复杂度一样么?代码如何优化呢?——这有可能是计算机硬件、程序语言、编译器等问题了。
如此说,数学和计算机基础那个都少不——当然你要是搞理论那就另一回事了。
另外,说一句题外话,不要小瞧了计算机语言,会用的人很多,可是真正搞明白的没有多少。也许你可以写一个软件,可是代码不一定是最优的。
低质量的代码会糟践了一个好的算法。
一个愚蠢的算法也会使高明的程序员显得低能。
如果你想搞好C语言,一定要好好看看specification.
17497感谢这里几位朋友的厚爱,最近太忙了,数学与CS,以后有空接着聊,感谢你们,希望你们都成大牛
17497
| 引用 (zhaoming @ 2007年05月25日
00时14分) |
|
感谢这里几位朋友的厚爱,最近太忙了,数学与CS,以后有空接着聊,感谢你们,希望你们都成大牛
|
zhaoming老大:
最近还好吧?!呵呵,N久不见你光临本坛,也好长时间没听到你独到的见解了。如果您很忙的话,祝你身体健康,有空了来我们这给大家讲讲经啊。
也祝广大坛友,身体健康,学习/事业有成!
17497做研究和做算法的话,数学太重要了。
做应用,就无所谓了。
17497
| 引用 (chefcui @ 2005年09月01日
20时24分) |
|
我已经度过了两年大学生活,所学专业是计算机,但是从大一开始学的仅仅是数学分析(复旦大学出版),线性代数(清华出版),实变函数,空间解析几何,常微分方程,关于计算机方面的我们只学了c语言,还学的是皮毛,我问了我们老师,他说这是给计算机打基础,我现在计算机水平还不如在大街上交几百块钱上的补习班学得好,老师说我们学的是计算机科学,我也不太明白,我们都有电脑,说明白了是高级游戏机,我很担心这样下去我怎么办,数学把我不如数学专业,计算机把我又什么都不会,请问你们这些过来人的建议?
|
用不着。实话一句。太多的数学让你在做项目的时候也会有约束。现在的东西,只要你做出来了,能用就可以了,除非你想进MS,IBM...
17497我是新手,听了各位高手讨论数学对计算机程序的影响,我觉得我要好好学数学!
17497计算机系大二也要学实变函数?夸张了吧。
17497离开了数学的计算机科学,就好比从一座大厦抽去了基底。很快它就会倒塌。
17497我也是学计算机的,与楼主不同,我的数学很差,计算机技术还可以。在编程序的时候只能做一些简单的事情,其原因就在数学有阻碍。所以我才来到这里想提高我自己的数学。
有人说,学习编程不需要数学,他们一定不真正懂得编程。无论是编程还是这个世界,都是由数字组成的。数学才是真理,编程是将真理体现
17497感觉数学能够提供点计算机的思想,但提供思想的又不仅仅是数学!
17497用建筑来比喻计算机吧
计算机领域还是比较混沌的,计算机领域的“土木工程师”,“结构设计师”,“建筑师”,“工程力学家”,“建筑工人”
,“测量专家”还没有分清楚。。。。
建筑学需要美术,而土木就需要大量的力学,数学了
前者“画”死人,后者“算”死人
而我们国家可爱的程序员们,大多是建筑工人这个级别的,而不是软件大师,硬件大师,设计大师,系统分析大师。。。。更没有多少是计算机科学家,自然用不到多少密码学,组合数学。。。。。
17497我刚刚注册,看完了这个帖子,说说我的感受。作为计算机专业出身的,我同样认为数学很重要,对于伟大如Dj和knuth的人无比崇拜。但是,现在缺少的是大批有经验的计算机工程师,而不是理论基础雄厚的计算机科学家。
我学习数学的功利性是很强的,就是为了取得之前的研究者的成果和经验,进行应用。所以对我这样的人来说,学习了高等数学,初等概率论,同时进行数据结构算法的学习也就可以了。一句话,就是用斧子,不用懂怎样做斧子。知道主定理,用主定理可以基本判别算法复杂度,不用了解主定理的证明。
17497我学数学的,学了四年了,还不知道做什么,
计算机很好啊!
以后想去那个方向
17497数学不是有用,而是非常非常有用!可惜我那时没有什么经验可以借鉴,数学基础不是很好。
以我为例吧,我在telecom也干了差不多10年了,telecom
现在也可算是CS的一个分支吧, 从开始比较简单的coding,到后面各种复杂的traffic engineering,image
processing,数学发挥的做用越来越大,很简单,很多数学模型很难看懂,看不懂就没法实现,各种线路编码,加密算法也是如此。仅仅从CS专家(不是科学家)的角度来看,数学不仅是锦上添花,而是雪中送炭。至少能帮你在公司中地位上升吧。
17497准备读计算机的博,导师就跟我说考虑一句话:要想做学问、出高质量的成果,就必须深挖数学!
其实我倒是希望计算机用不上那么高深的数学啊!
17497关于这篇横跨了05、06、07、08四个赛季的强力贴的一点看法。
造物弄人。
本科在一重点大学SS大学数学、信息与计算科学专业。
现在在另一所重点大学B大读软件研究生,快一年了,也真正的做了几个项目。
说说cs
& math的关系吧:
1
本科的时候,还算刻苦,数分啊,高代啊,这些课的基础还算扎实,当时也没有感觉到数学和计算机有什么暧昧的关系,当时最大的感受是,数学学多了,心静如水+思维缜密
2
开始读研,选了一门课叫做算法分析与设计,通俗点就是算法高级,是算法界德尔一个大N教的,没人不说好的,虽然大部分人听不大懂。我拜数学所赐,觉得听得还蛮爽,作业也能高效的完成,考试也觉得可以。可能这就是数学的内功加了把力吧。
3
我的专业是嵌入式,移动通信方向,要学硬件的好多东西,那个头疼啊,幸亏我还旁听了一门课——数字图像处理,虽是旁听,如沐春风啊。
4
其实我现在也在寻找数学专业、计算机专业最佳的契合点是哪些?
图像处理——很多的编码算法
网络、通信——大热门啊,3G、WiFi、Wimax、LTE这些的诞生
数据挖掘、数据库——理论实验室的一个博士,数据挖掘的,去了Google,40W/Y,小G啊,我最想去的地方啊。
信息安全——我宿舍有个信息安全的,他们上学期的应用密码学是国内数一数二的人教的,由于很多人没有数论的基础,云里雾里雨里的......
算法——这是从另外一个角度的分类了。
我门这边也就这些方向了,其他的我不是很熟悉,请大家讨论、补充。
后记:明天考系统设计,发个祝福帖吧。
17497凑个热闹。
友好的问大家个问题,什么是“计算机”,或者"computer" ?
17497也来说几句,献给这个生命力超强的帖子。虽然想必LZ已经顺利毕业了
……
17497也来说几句,献给这个生命力超强的帖子。虽然想必LZ已经顺利毕业了
首先LZ学校的一些课程开设值得商榷。我们可以预见,一门课程的开设是否达到预期值,或者暂且笼统说是否达到好的效果,取决于教材,师资,学生的能力。所以在清华这样top10的大学开设的课程未必适合在任何别的大学开设。如果这些事实我们都可以抛开,直接研究最理想的状况,那么显然数学在CS中的地位不可撼动(基础阶段实变,空间解析几何,常微分方程实在不必)。除去在一些领域的固定运用(这些建模已经完成),最重要的,数学培养你的抽象能力。这个能力在CS中直接决定了能不能抓住事物的本质,仅此而已。不论是学术研究还是终身学习(包括编程语言),快速发现本质无疑是事半功倍的。所以说数学对于CS,不仅是技术上的,更是素质上的。
我的看法,好的大学CS应该开设一下数学或相关课程,线性代数,代数,集合论,逻辑学,数学分析,概率,统计,数值分析,复杂性可算性分析,自动机理论。其中不少有交叉的,压缩下可能开7,8门就行了。
另外OO也是必须开设的。C倒是可以选修。
17497
| 引用 (pgs @ 2006年12月06日
10时14分) |
| 引用 (xznuzzt @ 2006年12月05日
12时33分) |
......还记得
1988年贝尔实验室副总裁亲自来访问我的学校,目的就是为了想了解为什么他们的语音识别系统比我开发的慢几十倍,而且,在扩大至大词汇系统后,速度差异更有几百倍之多。他们虽然买了几台超级计算机,勉强让系统跑了起来,但这么贵的计算资源让他们的产品部门很反感,因为“昂贵”的技术是没有应用前景的。在与他们探讨的过程中,我惊讶地发现一个O(n*m)的动态规划(dynamic
programming)居然被他们做成了O(n*n*m)。更惊讶的是,他们还为此发表了不少文章,甚至为自己的算法起了一个很特别的名字,并将算法提名到一个科学会议里,希望能得到大奖。当时,贝尔实验室的研究员当然绝顶聪明,但他们全都是学数学、物理或电机出身,从未学过计算机科学或算法,才犯了这么基本的错误。我想那些人以后再也不会嘲笑学计算机科学的人了吧!
|
这是李开复在“算法的力量”中的一段话,由此看来,算法需要数学基础,但毕竟还有着与数学不同的一面。
现在的高校开设的专业都称作“计算机科学与技术”,可见计算机是科学与技术的结合体,它既有着以逻辑思维为基础的“科学”的一面,也有着以实践以主的“技术”的一面,因此“计算机”这三个字包含了太多的东西,故而它的发展所依靠的基础也不一样,看一看计算机先驱奖的得主中,有数学出身的,他们大多在理论计算机科学中大显身手;也有学物理的,他们大多在硬件设计中一展才华;还有一些可归为杂类的,这些人中有学机械的(威登海姆);有学教育学的(约翰逊);甚至还有学文学的(弗洛伊德)。
计算机经过70年的发展,已经形成了以多种学科为基础,而又自成一派的新学科,这里面必然有其它学科所接触不到的东西。但有一点可以确信:理论计算机科学是离不开数学的!
因此,数学基础好的可以为计算机的发展做出贡献,数学基础差的同样可以为计算机的发展做出贡献(在工程方面)。
|
实际上,是numeric的东西,所以我说这课也是必须开的。
17497图形学应该要会线性代数和解析几何,三维图形还要知道微分几何;傅立叶分析,复分析,实分析,泛函分析是信号处理和图像处理的基础;搞网络需要知道图论,拓扑;通信方面,不知道概率和随机过程好像不行吧?计算机理论基础方面,抽象代数,数理逻辑,组合什么的,更是十分的重要!算法编程用到了大量的数学模型和数学思想,学密码学要知道数论。
综上,本科阶段最好尽早找准自己的方向,采取专修数学辅修计算机的办法最为有效!
17497身在福中不知福
17497身在福中不知福
17497
关于这个帖子,我再补充一些:
程序员,大方向分,一般分为两种:
一种是理论计算机,就像高德纳,也有译为克努特
的。这样的人,算法要好,算法是灵魂,数学素养很重要,但很和一般大学
的,以数学分析,和线性代数的数学,在内容不太相同。应该需要离散数学
的直觉要好一些,数论,组合,图论,比较重要,但很多学校开不出这样的课来。
另一种是黑客,计算机技术。典型的如苹果的创始人,沃兹尼克,或比尔盖茨
他们并没有做原创性的,新算法发现的工作,但是他们知道利用一些计算机科学
家的结果,计算机技术,在这里主要具有工具性意义。工具掌握的熟练不容易,用
它做出,可以使你成为亿万富翁的产品更不容易。
我如果开计算机课的话,会适当减少数学的课程,尤其传统的非离散数学的课。
CS,与数学的不同的是,应该有操作系统,编译原理及程序设计,计算机构成
这样同样非常理论的课,这些课,对于做理论计算机也很重要,有些像计算机物理
的意思,其中也有深刻的意味,不易理解。
17497
关于这个帖子,我再补充一些:
程序员,大方向分,一般分为两种:
一种是理论计算机,就像高德纳,也有译为克努特
的。这样的人,算法要好,算法是灵魂,数学素养很重要,但很和一般大学
的,以数学分析,和线性代数的数学,在内容不太相同。应该需要离散数学
的直觉要好一些,数论,组合,图论,比较重要,但很多学校开不出这样的课来。
另一种是黑客,计算机技术。典型的如苹果的创始人,沃兹尼克,或比尔盖茨
他们并没有做原创性的,新算法发现的工作,但是他们知道利用一些计算机科学
家的结果,计算机技术,在这里主要具有工具性意义。工具掌握的熟练不容易,用
它做出,可以使你成为亿万富翁的产品更不容易。
我如果开计算机课的话,会适当减少数学的课程,尤其传统的非离散数学的课。
CS,与数学的不同的是,应该有操作系统,编译原理及程序设计,计算机构成
这样同样非常理论的课,这些课,对于做理论计算机也很重要,有些像计算机物理
的意思,其中也有深刻的意味,不易理解。
17497
| 引用 (weishenm @ 2009年02月05日
12时49分) |
关于这个帖子,我再补充一些:
程序员,大方向分,一般分为两种:
一种是理论计算机,就像高德纳,也有译为克努特
的。这样的人,算法要好,算法是灵魂,数学素养很重要,但很和一般大学
的,以数学分析,和线性代数的数学,在内容不太相同。应该需要离散数学
的直觉要好一些,数论,组合,图论,比较重要,但很多学校开不出这样的课来。
另一种是黑客,计算机技术。典型的如苹果的创始人,沃兹尼克,或比尔盖茨
他们并没有做原创性的,新算法发现的工作,但是他们知道利用一些计算机科学
家的结果,计算机技术,在这里主要具有工具性意义。工具掌握的熟练不容易,用
它做出,可以使你成为亿万富翁的产品更不容易。
我如果开计算机课的话,会适当减少数学的课程,尤其传统的非离散数学的课。
CS,与数学的不同的是,应该有操作系统,编译原理及程序设计,计算机构成
这样同样非常理论的课,这些课,对于做理论计算机也很重要,有些像计算机物理
的意思,其中也有深刻的意味,不易理解。
|
高德纳是他的中文名
17497
引用 (pgs @ 2006年04月05日
18时33分) |
|
好象有几位老兄对编写程序很不屑啊。其实这也没必要吧,我个人觉得编写程序和计算机科学来说就象做习题和数学的关系,还是很必要的。(可能不太恰当,一时想不出别的比方)很多计算机科学家都沉浸其中而乐此不彼,如克努特,还有开发C语言的里奇、汤普森等。毕竟计算机应用到实际中还要以程序为载体!
|
编程VS.CS 和 做题VS.math 进行类比 ,确实有点不妥
改进一下:
编程-写算法/想架构-CS 与 进行具体的计算(算数)-思考解题思路-math
可能更合适点。
17497数学在乎代数,算法更在乎解决。
17504oh my god, it runs wrongly, sorry
17510高代post-38-1125580374.ibf
17510A的标准型为
[ 0,0,0,0;
1,0,0,0;
0,1,0,0;
0,0,1,0 ]
17510这很容易想到并判断出约当标准型的形式,但是如何应用一个很有逻辑的方法说明呢,这一点我也不太明白,还请高手指教
17510
| 引用 (流形 @ 2005年09月01日
21时23分) |
A的标准型为
[
0,0,0,0;
1,0,0,0;
0,1,0,0;
0,0,1,0 ]
|
这个我知道啊
可下边呢?
17510相当于我们知道:
PAP - 1 =
[
0
0 0
0 1
0 0
0 0
1 0
0 0
0 1
0 ]
,那么
PA 2
P - 1 =
[
0
0 0
0 0
0 0
0 1
0 0
0 0
1 0
0 ]
所以
A 2
是这样的阵:秩为2,并且是2阶幂零的。
那么我们立即得到它的Jordan标准型为:
[
0
0 0
0 1
0 0
0 0
0 0
0 0
0 1
0 ]
。
17513syms a1 real;
syms a2 real;
syms a3 real;
syms b1
real;
syms b2 real;
syms b3 real;
syms c1 real;
syms c2
real;
syms c3 real;
syms theta real
X=[1;1];
A=[1 0;0
0];
B=[cos(a1) sin(a1);-sin(a1) cos(a1)];
C1=[1 0;0
exp(i*(c1))];
C=[1 0;0 exp(i*(b1))];
D=[cos((a2)-(a1))
sin((a2)-(a1));-sin((a2)-(a1)) cos((a2)-(a1))];
C1=[1 0;0
exp(i*(c2))];
E=[1 0;0 exp(i*(b2))];
F=[cos((a3)-(a2))
sin((a3)-(a2));-sin((a3)-(a2)) cos((a3)-(a2))];
C1=[1 0;0
exp(i*(c3))];
G=[1 0;0 exp(i*(b3))];
H=[cos(-(a3))
sin(-(a3));-sin(-(a3)) cos(-(a3))];
I=[cos(theta)*cos(theta)
sin(theta)*cos(theta);sin(theta)*cos(theta)
sin(theta)*sin(theta)];
K=I*H*G*C1*F*E*C1*D*C*C1*B*A*X
n=K'*K
simple(n)
请问:最后得到的结果如何整理成以(。。)cos(b1)+(...)cos(b2)+(...)cos(b3)+(...)cos(b1+b2)+(...)cos(b2+b3)+......+cos(b1-b2)+cos(b2-b3)+......+cos(b1+b2+3)的形式?其中(。。。)等为系数?
困扰了我好久的问题,希望高手解答,谢谢!
17513看不懂啊~~~~~~~~~~~```````````````
17529
http://www.yanxun.com/
17529非常及时,非常有用,非常感谢!
17529十分感谢
17529thank you!!
17529Thanks!!
17529为什么打不开网页?
17530再一次谢谢tobyqin
17530请高手帮忙解决裴礼文书上的二道题**post-21-1125583408.ibf
17530其中第二题的解答在附件里:post-21-1125799004.ibf
17531前半部分很好证啦,后半部分若是R可积的话,可以举出反例的f(x)=xsin(1/x),f(0)=0
17531假设f(x)在[0,1]上连续,在(0,1)内可微,且f(0)=0,求证:
\int_{0}^{1}{f^2(x)dx}\leq\int_{0}^{1}{[f'x)]^2dx}
17531怎么我的公式打不出来啊
17531公式编辑如下:
假设f(x)在[0,1]上连续,在(0,1)内可微,且f(0)=0,求证:
∫ 0
1
f 2
(x)dx≤∫
0 1
( f
`
(x))
2dx
17531
| 引用 (tobyqin @ 2005年09月02日
10时22分) |
公式编辑如下:
假设f(x)在[0,1]上连续,在(0,1)内可微,且f(0)=0,求证:
∫ 0
1
f 2
(x)dx≤∫
0 1
( f
`
(x))
2dx
|
由题设f'(x)^2不一定黎曼可积
17531我也知道不一定可积,如果不可积的话那就更加成立了。
17533影院座位设计优化模型 (详细大家见附件啊)
摘 要:本文针对影院座位设计问题,利用三角形正切,建立了视角 与仰角 关于地板线倾角
的数学模型。并通过 、 、 等软件,利用求极值的方法解答了问题一,得当倾角 为 时,最佳座位在 处。对于问题二,我们通过泛函分析等方法,将座位分成
排,得出排与排之间的距离是 ,对每排观众的视角 和仰角 进行求和,得出视角 和仰角 的平均值,从而取得平均满意度,再通过求极值的方法算出当 为
时,观众的平均满意度最大。此外,在 角不超过
的前提下我们还对地板线的设计进行改进(将第一排座位抬高),通过方程组(7)的解答,可得到最佳的地板线设计,进一步提高观众的满意度。我们还对模型进行了误差分析,若
越大,模型的精确度就越高。
关键词: 座位设计 仰角 视角
平均满意度
一、问题的重述
下图为影院的剖面示意图,座位的满意程度主要取决于视角 和仰角 。视角
是观众眼睛到屏幕上、下边缘视线的夹角, 越大越好;仰角 是观众眼睛到屏幕上边缘视线与水平线的夹角,
如果太大会使人的头部过分上仰,引起不舒适感,一般要求 不超过 。
(1) 地板线倾角 = ,问最佳座位在什么地方。
(2) 求地板线倾角
(一般不超过 ),使所有观众的平均满意程度最大。
(3) 地板线设计成什么形状可以进一步提高观众的满意程度。
二、模型假设
1、 假设观众的座高是一致的;
2、 影院排与排之间的距离相等;
3、 观众的平均满意度只取决于视角 和仰角
,其他因素忽略不计;
4、 假设屏幕的长度与座位的排长相等;
5、
把观众的眼睛看作一个点。
post-37-11256
17403.ibf
17533哈哈,
大家给带意见啊
17533看不了哈
17533谢谢了!
17538【Phil Gibbs 著 杉原广 补充柯南 译】奥卡姆剃刀(Occam's Razor, Ockham's
Razor)是由14世纪逻辑学家、圣方济各会修士奥卡姆的威廉(William of
Occam)提出的一个原理。奥卡姆(Ockham)在英格兰的萨里郡,那是他出生的地方。
这个原理称为“如无必要,勿增实体”(Entities should not be multiplied
unnecessarily)。有时为了显示其权威性,人们也使用它原始的拉丁文形式:
Pluralitas non est
ponenda sine necessitate.
Frustra fit per plura quod potest fieri per
pauciora.
Entia non sunt multiplicanda praeter necessitatem.
事实上,只有前两种形式见于他现存的著作中,而第三种形式则由后来的一位学者撰写。威廉使用这个原理证明了许多结论,包括“通过思辨不能得出上帝存在的结论”。这使他不受罗马教皇的欢迎。
许多科学家接受或者(独立的)提出了奥卡姆剃刀原理,例如莱布尼兹的“不可观测事物的同一性原理”和牛顿提出的一个原则:如果某一原因既真又足以解释自然事物的特性,则我们不应当接受比这更多的原因。“奥卡姆剃刀”是消除欧洲中世纪经院哲学对人们思想禁锢的最好武器。
对于科学家,这一原理最常见的形式是:
当你有两个处于竞争地位的理论能得出同样的结论,那么简单的那个更好。
在物理学中我们使用奥卡姆剃刀切掉形而上学的概念。爱因斯坦的狭义相对论与洛仑兹的理论就是一个范例。洛仑兹的理论认为在以太中运动的尺收缩、钟变慢。爱因斯坦关于空—时变换的方程与洛仑兹方程在钟慢尺短效应上一致,但是爱因斯坦和庞加莱(法国数学家——译注)认为以太不能根据洛仑兹和麦克斯韦方程组检测到。根据奥卡姆剃刀,以太就被排除了。
这一原理也被用来证明量子力学的不确定性。海森堡从光的量子本性和测量效应中推出了不确定原理。
史蒂芬·霍金在他的《时间简史》中解释说:我们仍然可以想像,对于一些超自然的生物,存在一组完全地决定事件的定律,它们能够观测宇宙现在的状态而不必干扰它。然而,我们人类对于这样的宇宙模型并没有太大的兴趣。看来,最好是采用称为奥卡姆剃刀的原理,将理论中不能被观测到的所有特征都割除掉。
但是“不能确定以太的存在”和“以太的不存在”都不能仅仅根据奥卡姆剃刀推出。它可以区分两个能做出同样结论的理论,但是不能区分其他可能做出不同结论的理论。实验的证据仍然是必需的,并且奥卡姆本人支持经验主义,而不是反对。
厄恩斯特·马赫提倡奥卡姆剃刀的一个版本,他称作“经济原理”,表述为:“科学家应该使用最简单的手段达到他们的结论,并排除一切不能被认识到的事物”。把它引入哲学就形成了实证主义哲学,即认为某物存在但无法观测与根本不存在是一码事。马赫影响了爱因斯坦关于时空不是绝对的论述,但是他(马赫)也把实证主义应用到分子的概念。马赫和他的追随者认为分子是形而上学的概念,因为它们太小而不能被直接探测到。这种主张不顾分子论在解释化学反应和热力学上的成功。具有讽刺意味的是,当使用经济原理抛弃了以太和绝对参照系的时候,爱因斯坦几乎同时发表了一篇关于布朗运动的论文,它证实了分子的实在性,这就打击了实证主义的使用。这个故事意味着,我们不能盲目使用奥卡姆剃刀。正如爱因斯坦在他的《自传笔记》中写道:
即使是大胆而天才的学者也会因为哲学上的偏见而妨碍他认清事实,这是一个很有趣的例子。
人们常常引用奥卡姆剃刀的一个强形式,叙述如下:
如果你有两个原理,它们都能解释观测到的事实,那么你应该使用简单的那个,直到发现更多的证据。
对于现象最简单的解释往往比较复杂的解释更正确。
如果你有两个类似的解决方案,选择最简单的。
需要最少假设的解释最有可能是正确的。
……或者以这种自我肯定的形式出现:
让事情保持简单!
注意到这个原理是如何在上述形式中被加强的。严格的说,它们应该被称为吝啬定律,或者称为朴素原则。最开始的时候我们使用奥卡姆剃刀区分能够做出相似结论的理论。现在我们试图选择做出不同结论的理论。这不是奥卡姆剃刀的本意。我们不用检验这些结论吗?显然最终不是这样,除非我们处于理论的早期阶段,并且还没有为实验做好准备。我们只是为理论的发展寻求一种指导。
这个原理最早至少能追溯到亚里士多德的“自然界选择最短的道路”。亚里士多德在相信实验和观测并无必要上走得太远。朴素原理是一个启发式的经验规则,但是有些人引用它,仿佛它是一条物理学公理。它不是。它在哲学和粒子物理中使用的很好,但是在宇宙学和心理学中就不是特别好,这些领域中的事务往往比你想象的还要复杂。或许引用莎士比亚的一句话要胜过引用奥卡姆剃刀:“天地之大,
赫瑞修, 比你所能梦想到的多出更多”(出自《哈姆雷特》,第一幕,第五景——译注)
朴素是主观的,宇宙并不总是像我们认为的那样简单。成功的理论往往涉及到对称、美与简单。
1939年保罗·狄拉克写道:
研究者在把自然法则转变为数学形式的时候,应该为数学的美而努力。对于简单和美的需求往往是等价的,然而当它们发生冲突的时候,后者应该优先。
吝啬原理不能取代洞察力、逻辑和科学方法。永远也不能依靠它创造或者维护一个理论。作为正确性的判别方法,只有逻辑上的连贯性和实验的证据才是绝对的。狄拉克的理论很成功,他构造了电子的相对论场方程,并用它预言了正电子。但是他并没有主张物理学仅仅应该基于数学的美。他完全赞同实验检验的必要性。
最后的结论来自爱因斯坦,他本身也是一位格言大师。他警告说:
“万事万物应该尽量简单,而不是更简单。”
相关网址:
http://www.public.iastate.edu/~physics/sci.../faq/occam.html
17539康德(Immanuel Kant)出生于柯尼斯堡,是近代西方哲学史上划时代的哲学家,同时也是一位自然科学家。
康德深居简出,终身未娶,一辈子过着单调刻板的学者生活,直到
1804年去世为止,从未踏出过出生地半步,因此诗人海涅说,康德是没有什么生平可说的。
康德生活中的每一项活动,如起床、喝咖啡、写作、讲学、进餐、散步,时间几乎从未有过变化,就像机器那么准确。每天下午3点半,工作了一天的康德先生便会踱出家门。
和许多伟大的德国学者一样,康德家境也很贫寒,以至在金钱观念方面给后人留下笑料。据说这位大学者经常声称,他最大的优点是不欠任何人的一文钱。他曾说:“当任何人敲我的门时,我可以永远怀着平静愉快的心情说:‘请进。’因为我肯定,门外站着的不是我的债主。”
康德思想的发展,以
1770年他提出教授就职论文为界,分为“前批判时期”和“批判时期”。在“前批判时期”,他埋头于自然科学研究,提出了“关于潮汐延缓地球自转的假说”和“关于天体起源的星云假说”。这两大假说从物质自身的运动和发展来解释自然现象,摒弃了神学创世说和自然界永恒不变的观点。
在“批判时期”,康德对他以前的以莱布尼茨为代表的唯理论及以休漠为代表的怀疑主义进行了批判。
1781年,康德发表了《纯粹理性批判》这部哲学名著。恰如康德枯燥乏味的生活一样,这本洋洋数十万言的大作非常晦涩难懂。一个读者对康德抱怨说:“读你的书十个指头都不够用,因为你写的句子太长了,我用一个手指按住一个从句,十个指头用完了,一句话还没有读完!”但是艰深的语句掩不住思想的光辉,康德哲学真的像他自己所说的那样成了哲学领域内“哥白尼式的革命”。此后他又陆续发表了《实践理性批判》(
1788)和《判断力批判》(
1790)这两部著作。三部著作的相继间世,成为康德批判哲学体系诞生的真正标志。
由于推翻了当时流行于欧洲的形而上学体系,由于开拓了从主客体关系去探讨哲学根本问题的新方向,由于提出了以“二律背反”为核心的消极辩证法,康德的哲学具有划时代的意义。有人把它比作蓄水池,前人的思想汇集于此,后人的思想则从中流出来;也有人将他的哲学比作一座桥,想入哲学之门就得通过康德之桥。
17541奥地利物理学家及数学家多普勒 ,克里斯琴·约翰(Doppler, Christian
Johann)
1803年11月29日出生于奥地利的萨尔茨堡 (Salzburg)。
1842年,他在文章 "On the Colored
Light of Double Stars" 提出“多普勒效应”(Doppler Effect),因而闻名于世。
从
1674年开始,克里斯琴·多普勒家族在奥地利的萨尔茨堡从事的石匠生意日渐兴隆。他们在 Hannibal Platz“现名 Makart
Platz”靠近河畔的地方建造了很好的房子,多普勒就在这所房子里出生。当然,按照家庭的传统会让他接管石匠的生意。然而他的健康状况一直不好而且相当虚弱,因此他没有从事传统的家族生意。
多普勒在萨尔茨堡上完小学然后进入了林茨中学。
1822 年他开始在维也纳工学院学习,他在数学方面显示出超常的水平,
1825
年他以各科优异的成绩毕业。在这之后他回到萨尔茨堡,在Salzburg Lyceum教授哲学, 然后去维也纳大学学习高等数学,力学和天文学。
当多普勒在
1829
年在维也纳大学学习结束的时候,他被任命为高等数学和力学教授助理,他在四年期间发表了四篇数学论文。之后又当过工厂的会计员,然后到了布拉格一所技术中学任教,同时任布拉格理工学院的兼职讲师。到了
1841年,他才正式成为理工学院的数学教授。多普勒是一位严谨的老师。他曾经被学生投诉考试过于严厉而被学校调查。繁重的教务和沉重的压力使多普勒的健康每况愈下,但他的科学成就使他闻名于世。
1850年,他获委任为维也纳大学物理学院的第一任院长,可是他在三年后
1853
年3月
17日在意大利的威尼斯去世,年仅四十九岁。
著名的多普勒效应首次出现在
1842年发表的一篇论文上。多普勒推导出当波源和观察者有相对运动时,观察者接收到的波频会改变。他试图用这个原理来解释双星的颜色变化。虽然多普勒误将光波当作纵波,但多普勒效应这个结论却是正确的。多普勒效应对双星的颜色只有些微的影响,在那个时代,根本没有仪器能够量度出那些变化。不过,从
1845年开始,便有人利用声波来进行实验。他们让一些乐手在火车上奏出乐音,请另一些乐手在月台上写下火车逐渐接近和离开时听到的音高。实验结果支持多普勒效应的存在。多普勒效应有很多应用,例如天文学家观察到遥远星体光谱的红移现象,可以计算出星体与地球的相对速度;警方可用雷达侦测车速等。
多普勒的研究范围还包括光学、电磁学和天文学,他设计和改良了很多实验仪器,例如光学仪器。多普勒天才横溢,创意无限,脑里充满各种新奇的点子。虽然不是每一个构想都行得通,但往往为未来的新发现提供线索。
相关网址:
http://www.qiji.cn/eprint/abs/831.html
17543看着版上的帖子题目,分不清是考研的还是考博的。
比如"xx高校的数学怎么样啊"之类,不清楚是讨论考研还是考博。
能不能做的更醒目一些,把2者分成2个版呢
斑竹回复:谢谢建议,机会成熟自然分版!
17545总分394学长授考研真经自卑自考生的考研路
我是一名学计算机信息管理的自考生,以前我很自卑,因为高考失败,求学路上的坎坷给了我太多的伤痛,看着统招生们背着书包走在美丽的花园大学,我是又羡慕又痛恨……
只因为自己的一次失败,就这样永远的放弃人生的理想了吗?我没有,为了证明我自己的真正实力,为了不让那些自以为了不起的统招生们再用异样的目光看我,为了给我们自考生挣一口气,我选择了考研。
2005年3月
18号晚上11点多,同学突然打来电话说考研成绩可以查了,我兴奋极了,也很害怕,马上输入姓名,准考证号开始查询,然后闭着眼睛点击了确定按钮。当我睁开眼睛的时候,我笑了,然后又哭了(数学:116
政治:82 英语62 专业课134 总分:394),谁也无法理解我当时的心情。然后我含着眼泪拨通老家的电话,我要让家人同时感受这一快乐的时刻。
我是一名自考生,还是以同等学历的身份报考,选择了考研,经历了考研,我无怨无悔。现在回想起来去年考研的情景,心里有一种说不出的滋味,所以想给自考生们,还有同等学历的考研族们打打气。
首先我想对自考生同等学历的考生说一句话:一定要相信自己,自已一定能行。在心理上一定要学会心静,找到平衡点,不要以为别人都比自己强。有许多自考生都很自卑,也包括我(已经找回了自信^_^),认为自考生就是比统招生差,然而事实并非如此,只是自己心理的作用。如果你自己都认为你自己不行,那么谁还会相信你行呢?心理问题解决了什么是都好解决。对于同等学历考研可能第一关就是报考,因为有好多学校都对同等学历考生有这样那样的限制,有的是要专科毕业两年,有四六级证书,本科要通过多少门课程,还有的要什么发表的论文等,所以如果你达不到这些条件就不能报考该校,但是也有好多学校就没有什么特别的要求,在这一点上我就很赞赏复旦大学的做法,不管你是否是同等学历都可以报考,只要你有能力,都欢迎报考。所以说选一个你能报考的学校,一个好专业就是同等学历考生的第一件大事。
说实在的,考研真的很容易。只要你能坚持,你就会胜利。复习过程中一定要学会调节自己的心情,这一点很重要。英语学习要赶早,而且一定要特别重视英语,因为有好多考生都是因英语单科拉住了而名落孙山。我想对于一些英语差的同学一定要抓基础,看课本(新概念,大学英语精读都行),通过课本不仅可以提高词汇量,阅读能力,更重要的是打好了基础。然后再通过专题训练,再一次提高词汇量,阅读能力,完型填空,作文等。数学必须也得抓基础,课本一定要吃透,公式,定理必须得理解,然后才能灵活运用,课本吃透后,再去做一些大师的习题。只要不是特别讨厌政治的人,应该都能考个不错的成绩,所以就不再多说了,只建议上个冲刺班就行了,不必花太多的时间。专业科最好打听一下你所报考的学校,看有没有辅导班,如果有的话,一定要上一个,上专业科辅导班一定会受益匪浅的。在时间安排上,英语,数学要占大段的时间,一般应该在2,3月份就开始复习了,政治到8,9月份开始着手都不晚,专业课就看自己的了,因为各个专业不一样专业课也不一样。
至于参考书数学有陈文灯,英语有朱泰祺,石春祯,政治有任汝芬,这些大师的书都是不错的,辅导班可以根据自己的情况上或是不是,我个人认为辅导班没有多大作用。不过政治,专业课还是要上冲刺班的。另外还要多注意搜集你所报考学校,专业课,导师的信息,我在这方面就做的很好,要注意我可是情报学专业的。
本人的一点经验,仅供参考。自己还是要有自己的一套学习方法的。
17545该向你学习啊
我现在也是在努力考研啊
希望可以给一点经验
17545一定要相信自己,自已一定能行。在心理上一定要学会心静,找到平衡点,不要以为别人都比自己强。有许多自考生都很自卑,也包括我(已经找回了自信^_^),
有同感
一路上有你这句话就行了
我会走得很稳的
17545成功靠一个公式,即 求和所有的小成功。
17545成功属于自己的泪水和汗水!!
17545呵呵,各位考研的朋友加油啊,一定行的!
17545顶
敬佩
17545这么厉害!佩服!
17545佩服啊!~希望我也通过努力考个好成绩顺利进入数学研究生!
17545考研不是无间道
而是开往春天的地铁!
祝福每一位考研的朋友,一路走好!
17545自信、坚持
我一定要考上中科院!!!
17545这个世界总是强人出没的地方
17545大哥,以后跟你混了
17545你不错啊 我要向你学习哦 我也要努力
17545强的。我也高考失败过,后来也就挺过来了。相信自己,永远不要自卑,走出一条不平凡的成功之路。风雨过后总会见到彩虹。
17545佩服啊 祝你以后都好运
17545该向你学习啊
17548还有Stolz公式,对分式形式的数列极限很有用的!
17548谢谢归纳呀。不错。不过我觉得还是第10个比较用
17548补充一下,虽然不常用,不过也挺好用的,利用无穷级数的收敛性判别法则来判断极限收敛,极限的判定个人认为所用工具很多,看你的知识面而言了,把知识融合的话,会有n多可以利用的工具,小红帽的应该是数学分析中比较常用的几种了
175481、利用定义求极限:
例如:很多就不必写了!
2、利用柯西准则来求!
柯西准则:要使{xn}有极限的充要条件使任给ε>0,存在自然数N,使得当n>N时,对于
任意的自然数m有|xn-xm|<ε.
3、利用极限的运算性质及已知的极限来求!
如:lim(x+x^0.5)^0.5/(x+1)^0.5
=lim(x^0.5)(1+1/x^0.5)^0.5/(x^0.5)(1+1/x)^0.5
=1.
4、利用不等式即:夹挤定理!
例子就不举了!
5、利用变量替换求极限!
例如lim
(x^1/m-1)/(x^1/n-1)
可令x=y^mn
得:=n/m.
6、利用两个重要极限来求极限。
(1)lim sinx/x=1
??x->0
(2)lim
(1+1/n)^n=e
??n->∞?
7、利用单调有界必有极限来求!
8、利用函数连续得性质求极限
9、用洛必达法则求,这是用得最多得。
10、用泰勒公式来求,这用得也十很经常得。
17548那位师兄能帮忙归纳一下求极限的方法
我感觉极限很难求
方法越多越好
17548受益无穷,虽然有些不常用,但毕竟是多归纳出了些解题的方法,希望楼主以后多发点类似的解题技巧的帖子,必顶~
17548关于解题方法,在本版的置顶主题中的大学数学的解题方法中有,可参考
17548不错!!! 很好!! 继续!!!
17548对于一些有迭代关系的数列的极限,可以用矩阵解决.主要运用矩阵的相似标准型容易求高次幂.
17548还有两种方法:
(1)利用数列的递推公式可求极限
(2)利用数列极限的某些重要定理(如已知几何均值的极限,可以求出一般项的极限)
17548这里就十种解法,刚才在那边看到,有一个发了十三种解法,不过跟这里的情况差不多,都是给出这些解法名称,没有实际的例题供大家参考一下,希望提供者可以再给出一些实例。谢谢!!!1
17548用等价无穷小代换也是比较常用的!而且可以减少很多运算!
17548还有许多极限问题可以用Stoze公式解决,例如:
x(n)=1,x(n+1)=sin(x(n)),则limn*x(n)*x(n)=3
17549我一直有一个梦想,想自己站在讲台上,将自己的所有都交给所有需要帮助的人,或许这样的帮助也是我们互相的一种鼓励,搀扶,我们在这样的搀扶中共同的实现了我们的梦想!
大家觉得数学的复习,解题,思路有什么疑惑,尽管提出来,我还给大家满意的答复,大家需要什么样的帮助,都可以说啊,也希望刚考过的同学一起参与讨论,大家一起提高:)
http://bbs.kaoyan.com/ibbs.dll?bbsdisp?t_i...89794&bp=1&bt=0
先谈谈自己的数学复习历程:
我考的是理工类,数学一:
从2003年的三月份开始翻开第一页考研辅导书:陈文灯的《复习指南》,因为学校的课程和离考研还早没有什么心里压力,断断续续,将近一个月的时间看完高数部分。
“非典”从天而降,一个多月的时间自己忙着防控“非典”去了:)(其实是给自己放了假:))非典过后,又忙学校的期末考试,前前后后几个月都没有看考研。直到七月中旬,才再次将考研提上日程。暑假在家里呆了没几天便赶回北京,安心看了几天书,将高数部分复习完。恰好一位同学报的陈文灯的暑假班,只听完高数,不想再听了,就把听课证转让于我,于是听了黄开先老师讲的线数和概率,也借此草草完成数学第一轮基础知识的复习。这期间主要以陈的《复习指南》为指导。八月中旬到九月初,参考陈文灯的《题型集粹与练习题集》,完成第一次题型熟悉,知识点与具体题目结合起来,这一边完成的比较草。随后按照李永乐的《数学复习全书》为指南,查漏补缺,着重线数于概率的小知识点,完成知识梳理工作。整个九月就是全面系统的回顾,保证没有知识点的纰漏,为随后的综合模拟打下基础,也算完成了第二阶段的复习。接着就在十月份开始李永乐的《经典400题》,每天一套,十二天完成数学一,拿出两天回顾做过的题目,然后在十月底结束数学二。经典四百题完成后,再进行一遍基础知识结合基本题型,基本分析方法的回顾,大约用一个星期左右的时间吧,以保证之前的学习成果得到巩固。接着做胡金德《二十套模拟题》,也是每天一套,整个十一月份连做带复习回顾,将二十套题完成。十二月初先结合前一阶段做的题目,将知识结合题目重新认识一遍,然后做往年真题(只做了95年之后的),到十二月中旬基本将往年题做完,穿插和同学一起精选作了市面上如恩波,考试虫,陈文灯临考演练,黑博士,北清人的几套题目,然后十二月中下旬,再结合自己的实际情况,精选几套题目作为保持状态只用,进入一月份,将《经典四百题》,《胡金德二十题》等题目拿出来再回顾一遍,又做了两套题练手,最后回归课本和李永乐的《复习全书》,升华对知识,对命题,对考试,的认识,最后顺理成章的数学拿下:)
自己在回顾自己的这段历程时,一幕幕如昨日重现......最后由衷的祝福每一位考完研究生的朋友,考研不易,我们从考研中走过!我们走出来了,我们便没有什么不能战胜!也祝愿每一位正在准备考研的朋友,考研不易,我们接受的是励炼,是锤磨,是挑战!我们要做的和正在做的,是成就自己的勇敢,不屈和坚强,“凤凰涅槃,洛火而生,十刀不死,遂成图腾”!于是,便的走了下去......
关于数学,关于复习,关于做题,关于考试,有几点是必须从思想上认识的:
第一,
基础知识的理解:我们需要把握知识点,需要从一定的深度去把握和理解知识点,同时又能够从不同的角度去理解知识点,去掌握知识点之间的联系,熟悉常见的变通形式,能够透过现象抓住本质。认识是不断丰富和发展(是不是政治背太多了,呵呵,可是不得不承认背背政治还是有好处的),这就要求我们与时俱进,随着复习的深入,随着知识点与题目的结合,对知识点的认识和理解,都是要不断加深的,这就是为什么我们要不断的重复着回归课本,回归最基本的概念,方法。数学题实际上就是基础知识的具体运用,就是知识的实践!那么我们就需要解决题目的过程中,在实践的基础上,来反复加深对题目所用知识的理解,从而加深对整个数学知识体系的理解!
第二,
做题的作用:对具体题目的解决,这就是我们考试的形式!也是检验我们知识水平和认识水平的一种方式!因此,一道题目的正确解决,首先需要你对这道题目所涉及的知识点的正确的,深刻的理解;同时,需要你能够采用正确高效的方法,将知识合理运用,进行正确的推理,计算,到最后正确的给出题目的解答。我们平时的做题和考试时又有着不同的侧重点,平时我们的题目演练,目的是为了我们自身的提高。而一道题目能给我们的提高又是有两方面的:一方面是加深了我们对基础知识的认识的提高,另一方面加强我们分析问题解决问题的能力。而真正考试的时候,那是作为一种检验,我们需要做的不惜一切代价的去展示自己,去在乎每一道题的正确与否,去对分数斤斤计较。因此,作为平时的做题练习,包括模拟考试,我们不去在乎会做与否,不必去为了一次模考不如意而对自己产生怀疑产生懊恼的情绪,我们需要做的,是从这一点一滴中来发掘自己的不足,来丰富自己的知识,来弥补自己的不足,来进步自己的思维,来升华自己的认识。因此,每一次做题,都需要一个比做题时间更多的回顾过程,从这中间挖掘出里面优美的东西。
第三,
解题的实质:我们可以这样来看,每一道具体的题目都是由“已知条件”和“待求”来构成的。我们需要做的就是运用已知的条件,加以推导,计算,以得到“待求”或“待证”的结论。说白了就是建立“已知”和“待求”之间的联系,如何建立呢?就是以“已知”为原材料,以具体的理论方法和原理为手段和工具,来“建造”出“待求”来!举一个简单的例子:已知一个三角形的两条边和两边夹角,问你这个三角形的面积是多少?这是这道题目实质上就是运用正弦定理,建立了两边,夹角和面积的关系,只经过一步推理即可完成。而较为复杂的题目,也不外乎是这个道理。当已知和待求的关系不是那么直接时,就要发散的考虑,应该采用什么方法来建立其两者之间的关系。从已知中挖掘出更深层的条件,一步一步推进到待求,题目就得到了解决。因此我们可以看出,一道题目的解决,第一离不开对题目所涉及的知识点的熟练,这是基础知识层次上的要求;第二离不开你正确的方法的选择,即用什么手段来建立“已知”与“待求”的关系,这是思维方式即思路层次上的要求。基础知识与思维方式是我们正确建立已知与待求关系,正确完整解决具体题目的两个必要的条件,因此,在具体的复习过程中,我们要注意这两方面的提高。第一轮复习,侧重于基础知识,覆盖所有的知识点,没有知识上的纰漏;第二轮复习,是题目与知识相融合的的阶段,一方面结合题目深刻对基础知识的理解,另一方面提升自己的思维水平,拓展思路。两方面齐头并进,那么不管多么复杂,多么难的题目都能够迎刃而解!
第四,
考试的构成:在我们面对一份试卷的时候,实际上是三个人在发生关系:命题者,我,将来的判卷老师。我们在解题答卷的时候,一定要在头脑中装着这三个人:命题者,就是他设置了一个个陷阱,一堆堆暗礁,一道题目的设置,特别是考研这样经过命题者深思熟虑命制而成的,一定有它的道理,我们不一定去分析他是怎么命题的,但是我们在做题时头脑中装着这样一位狡猾,多谋的命题者,肯定可以加深对题目的理解!也就是,有必要对命题者的心理进行揣摩;我,无疑是最聪明最有可能击败命题者,赢得判卷老师欣赏的主角,一方面,我绕过了如“纸老虎”一般的命题者处心积虑设下的陷阱,另一方面,我尽情的挥洒着自己的才能与智慧,让自己在这样的一个舞台上,淋漓尽致,征服了命题者和判卷老师,那就“不只是吸引”:);判卷老师我们要认为他是最最善良的,我们不要写的太乱,只要老师觉得你小子还有两下子,就会给你高高的分数的:)记住,不要认为判卷老师是严厉苛刻的,只要你愿意展示,你就一定能够征服他!那么,所有的人都是伴舞者,那么,只有你才是舞台的主角!
我们可以看到,复习的过程是一个多么美妙和浪漫的:You work hard,you just keep on doing
it,and gradually you make it difference,and finally you make
it!记住,复习中两方面的提高:基础知识和思维方法!
下面分阶段来总结一下应该怎样开展完整的复习:
第一轮:从头开始,进行基础知识的复习。第一要保证所有知识点都覆盖到,第二要保证对所有的知识点都形成自己的认识和理解,熟悉各个知识点最基本的运用。这是整个复习的基础环节,因此一定要稳,不着急,但是同时不能拖的时间太长,一般应该保证在两个月内完成,时间用的太长了会看了后面忘了前面。同时一定要注意进行阶段性的回顾和总结,比如复习完了积分,就要回过头将所有积分的内容,包括定积分,不定积分,二重,三重积分,曲面,曲线积分进行全面的总结,比较出异同点,深刻对整个积分体系的理解。这样边回顾总结,边赶进度,在巩固的基础上提高。至于说用什么参考书,首先要明确参考书的作用:课本知识是最基础的,也是最有用最体系的,第一轮重在理解,任何参考书,包括陈的《复习指南》和李的《数学复习全书》,都不能帮助你理解知识,参考书只是将知识点进行总结和归类,并配合上强化知识点的题型。因此不能脱离课本单看参考书,也不能只看课本上的理论而脱离参考书上的归纳和总结。应该说任何参考书上所作的归纳和概括,肯定比你自己总结要更好一点,至于陈,李哪个更好一点,不能一言而论,只能根据个人情况。陈的《复习指南》从纯数学意义上而言,明显比李的《数学复习全书》差一个档次,也就是说,陈的书对你数学能力的提高,可以说没有什么帮助,而是纯靠老陈总结的一套做题经验,而真正考研试题肯定不是靠套用陈旧的套路方法就能够解决的,所以看陈的书一定要跳出他的思路,从自己的角度来读,把他的东西转化为你自己的东西。李的《数学复习全书》充分显示了编著者在数学上的深刻理解,应该说是令人茅塞顿开的经典之作,对你数学水平的提高有很大的帮助,如果时间紧或者不想两本都买,还是推荐李的《数学复习全书》,大师之笔,启迪智慧,善哉善哉J这样第一轮复习的目标和具体措施就比较明确了:两个月左右的时间内,掌握基础知识,课本与参考书结合。
完成第一轮复习,胸中基本可以呈现出整个高数,线数和概率的知识结构和体系,如果各个知识点都能够做到了然于胸,历历在目,那么无疑你的基础知识是过关了,完成第一个阶段,就给自己一个小小的奖励,呵呵,然后再拿出三到五天,系统回顾一下,抓住纲领,又不漏过细节,这样基础更加牢固!就开始第二轮的题目演练。
第二轮:做题。与前一阶段的做题不一样的是,这个时候的题目应该跳出孤立的章节,以综合题目演练为主,同时,又要将各个部分典型的题目都熟悉熟练!在最初开始复习的时候,因为基础知识不全面,对题目的解决方法肯定也不一定很全面,而在这个阶段,你所有的知识都有了掌握,做题的思路肯定就更广。也是有两方面的练习:一方面,典型题目的多角度处理:比如这时候无穷小的阶数的确定,就要不仅会用洛必达法则进行运算,也要会用泰勒公式来做,实现知识纵向的融合,达到融会贯通的效果;另一方面,对于涉及到多个知识点,甚至有的高数,线数,概率结合的综合题目,更要具备能够纵向结合知识点的能力,这样横向的基础知识加上纵向的融合贯通,从而形成完整的知识网络。结合题目加深对知识的理解和知识运用的理解,编织知识网络,是这个阶段的一个目的。另一个目的,如前面所言,就是对思维方法的练习与提高,跳出具体的知识之后,再仔细的回过头看看一道题目从分析到解决的过程,就是一个美妙的思维的过程,我们在这个过程中,用优美的数学语言,进行的是最富有激情和想象力的创造,“生如夏花之绚烂,死若秋叶之静美”,如诗一般......
至于这个阶段所选用的参考书,我当时用的陈的《题型集粹与练习题集》,该书的写作方向特别适合与这个阶段使用,可是老陈总是沉醉于他的那套滲透着古板迂腐,缺乏创造性和诗意的“套路说”,因此感觉读后效果一般。而李的《经典四百题》侧重与上述第二方面综合性题目的演练,而缺乏第一方面典型题目的演练,不利于思路体系的形成,但是李永乐老师在其《数学复习全书》中的典型题目选择和讲解都特别到位,不失为第一方面的比较好的练习素材,所以在整个第二轮复习中,建议以《经典四百题》+《数学复习全书》,大概用一个月左右的时间。《经典四百题》以套题的形势编排,但是本身并不适合模考,所以还是作为综合题目演练之用,早早动手,站在高起点上,居高临下。这个阶段的做题一定以从题目中收获知识,提高思维为目的,所以,对于题目本身涉及的知识,以及相关的知识,都要有意的去回顾,去查《数学复习全书》中的相应章节。题目完整解答完之后,一定要有一个整体回顾的过程,仔细研究一下,到底是如何完成从已知到待求的推论的,在这个过程中,我的思路和答案的思路有什么相同和不同,从审题到动笔做题,是怎样的一个思维过程,题目的入手点是如何找到了......自己的提高还是要靠自己,靠自己在这个过程中融入自己的思考。这样第二轮复习的目标和具体措施也明确了:用一个多月的时间,将各种题型都熟悉一遍,通过题目达到深化知识理解,提升思维水平的目的,题目练习和题目回顾总结并重。
系统的第二轮复习的完成,无疑极大地增强了自己的自信心和战胜数学的把握,我积累了丰富的经验值,我自己的等级也飞速的提升,我还有什么害怕的呢?稍事休整,再回回头看看走过的路,再抬起头看准方向,再出发:)用两三天进行查漏补缺,就开始第三轮的综合演练了!
第三轮:模拟演练:做成套的模拟题除了对知识的补充,对思维的训练,还有两个重要的作用:做题节奏和考试心理!首先,要通过不断的模拟练习,把握做题的节奏,清楚自己各部分应该分配多少时间,练习多了,就自然形成了自己的节奏,遇到难题或者做了半天也没作出了的题目,根据自己的节奏进行调整,所以这个阶段的模考应该严格的按照三个小时来完成;其次,要刻意给自己制造一个紧张的气氛,比如可以叫上几个一起准备考研的,同样的时间,同样的题目。因为在考场上,往往不是别人将你击败了,而是自己将自己击败了。所以一定提前给自己一些荷枪实弹的演习,提前去体会那种怦怦的心跳,提前去适应一切需要你去适应的环境和气氛。这个阶段便不要给自己太大的压力了,提前完成相应的数量的题目,迅速提升自己的应试水平,早早让自己去适应考研,胸有成竹,以避免最后阶段的浮躁心理。每套题做完后的回顾总结同样是特别的重要,某种意义上其重要性甚至超过做题的过程,因为你本身的提高是在对整个卷子再次分析的基础上的自我认识,了解了自己的不足(包括基础知识,解题思路,及运算等多个方面的不足),才能有针对性的进行自我的补救和提升。模拟题目的套数应该在二十套左右,推荐用胡金德的《二十套模拟题》,每天一套,连回顾一起,大概一个月完成。第三轮复习的目标和具体措施也明确了:用一个月左右的时间,将自己前阶段的成绩反映到试卷上,再次实现知识水平,思维水平的提高,同时提升实战应试水平,模拟+回顾总结=全方位提升!
三个阶段如同三大战役,一个又一个战略目标的实现,已经使你会当凌绝顶,不胜耳边的阵阵寒风.
17552问题一:为什么要考?必须有一个能够说服你自己的考研动机,才会有排除万难的勇
气。是为了学位和文凭以便将来找个好工作还是真的对某一学科很感兴趣觉得大有继续研究下去的必要。如果仅仅只是前者,量力而行地选一个好找工作又竞争不是很激烈的专业(如机械)去准备,不必考虑太多的其他因素,或者干脆选择读第二学士学位(较之研究生考试,双学位考试要容易得多,一般是读完两年成绩合格者可以拿到所属学校院系的第二学士学位的毕业证书和学位证书,而且此类招考有很强的院系自主性,本科双学位毕业生进京指标不受限制,就业时起点工资与研究生相同)。否则最好评估一下自己的兴趣和潜力,广泛听取你周围的人(父母、老师和朋友)的意见,最后自己作决定学什么专业。
问题二:到哪里去读?沿海开放城市经济相对发达并有更好的就业机会,但是考研时的竞争相对会更加激烈,读研时的花费可能也要高一些。如果你对自己的智力充满信心经济上也没有后顾之忧,考沿海地区的重点院校或者研究所可以使你在学习期间得到更多的锻炼机会和就业时的地理优势。但是你很可能被调剂,上海有一个研究所去年的招生计划大约是80人,但是其中却有50人是保送的,最后一大半上线的都只能被动地等待命运的安排,虽然还有选择的机会,但是好机会肯定不会多了。所以,如果你没有绝对的把握,选择一个你喜欢的西部城市的招生单位是比较明智的。
选择好拟报考单位所在的城市后,就要调查该城市符合自己胃口的报考单位,对于立志报考重点院校和研究所的考生来说,这一点没有太多好说的。但是对报考一般院校的考生来说,这里面有很多的问题需要调查清楚。对专业的选择必须理性。不能一窝蜂奔向热门专业,必须考虑自己专业本身的情况,有明确想法和通盘的计划,要了解所选专业的培养方案如何设置、课程特色、毕业生就业情况、导师阵容和专业发展方向等。
问题三:跟谁读?换句话说就是导师的选择问题。我认为在选择导师时,道德水平比学术水平更重要。如果某个导师多数学生都不认为他是个好导师的话,千万不要拿自己的青春开玩笑。
最后说一下搜索有价值信息的几条途径。如果有师兄师姐在拟报考的单位读研或者读博,直接和他们联系就行了。以下的方法可以适当参考。1.到该单位的论坛上去找,一般每个学校都有聊天室,问题不要太直露;2.利用学校图书馆的期刊数据库(如维普中文期刊数据库等)查找想要报考的导师情况,如果某导师在同级刊物上有一稿多投现象,建议不要报;3.利用上面搜索的结果,看与该导师共同发表文章的其他作者对他的评价。这些作者有很多都是这位导师的学生,如果能够取得这些作者的信任,他的意见将是十分有用的。至于这些人的联系方法可以到编辑部找,也可以到网上的同学录里查找。
来源:中国青年报
17552谢谢!!
17552及其正确
17556诚挚的感谢 To You !!
17556级数一章看似简单,但实际需要注意的地方也比较的多,特别如∑的下标是从0开始还是从1开始?X∑Un中的X在求和函数时是放在积分符号之内呢还是放在其之外?等等,象这种细微的差别就有可能使您的求解结果相差十万八千里。以下是一些关于本人在求解级数试题时所作的技巧和注意点总结,看一下您是否曾经也犯过类似的错误。
1)∑(0,∞)sin(aπ)=∑(0,∞)(-1)^nsin(aπ-nπ)
2)在运用莱布尼兹判敛法则时的第二个条件可以运用单调性判断;即f’(x)是否大于0?
3)在解展开幂级数或求幂级数的和函数时,收敛域的求解勿忘。
4)在某点处展开幂级数除了写出收敛域外还要去除该点。
5)在解幂级数展开时应注意,∑的下标是从0开始还是从1开始,在具有积分时还需看f(0)是否为0。即∫f‘(x)dx+f(0)=f(x).这一点作了新的修订
6)在求幂级数和函数时,积分,导数既可对∑内的X起作用,也可以对∑外的X起作用,但需要一一对应,即对被处理项用一次积分同时必须对其用一次导数;反之也然。
7)求得和函数表达式时,还要看属于收敛域,但并不属于定义域的点,这些点需要单独列出来,求得和函数的值。
8)当∑(0,∞)Un中的U0=0时,∑(0,∞)Un=∑(1,∞)Un,而且在套用积分时必须写成后者形式,以免出现∫(0,x)0dx=1的错误情况。注意:有的下表甚至从2开始。如陈《复习指南》02版例8,31,(2)
9)数项级数求和的四类方法:简单转换法,拆项相消法,递推法,阿尔贝法。其中阿尔贝法最重要。
10)求解傅立叶级数时的四点总结
a、对于一个级数既可以奇开拓,又可以偶开拓,按题目的要求确定求正弦级数还是余弦级数
b、开拓后的级数按平常级数展开,并注意写上定义域
c、定义域的端点的傅立叶级数是没有意义的,如要求值,则需用狄莱克利定理求解
d、在求an或bn时出现[1-(-1)^n]这样的项时,一般情况下使n=2k,n=2k+1分开讨论,使结果更简洁
因nanxingstar网友的要求,以下是如何求级数敛散性的总结
如何求级数的敛散性(拿到一个敛散性判断问题时怎样入手)
首先判断级数的类型
1,如果级数为正项级数:则先看当n趋于无穷时Un是否等于0,不为0则级数发散,等于0则用以下三种方法判断
1)比较法
2)比值法
3)根值法
技巧:
1)如果级数项中含有阶乘的形式一般用比值法
2)如果级数项中含有指数项P^n则一般用根值法
3)既有阶乘项又有指数项则一般用比值法
4)其它的一般用比较法
a、两个定理
差形式和极限形式
b、两个推论
数乘差形式和P-级数形式
2,如果级数是交错级数
则运用莱布尼兹定理
技巧:
在判断第二个条件时一般用单调性判断
3,如果是任意项级数
则转化成正项级数,运用任意项级数和正项级数的关系试判断(定理七)
注意点:
1)比值法,根值法是充分但不必要条件
2)涉及证明一般只能用比较法
3)但在判断级数发散时,比值法,根值法同样适用
来源:考研论坛
加入时间:2004-9-1
17556太感谢了!!!
17560以前写的一个paper,数模比赛在即,拿出来分享了,希望有所帮助。
post-37-1125638876.ibf
17560建议要参赛队员阅读一下。
17560看了,很好,谢谢!
17560谢谢!!!
祝愿大家在本次竞赛中取得优异的成绩!
17560hao
17561A题:小球定位问题
注:这篇文章两个部分一起下载再解压方可打开。post-37-1125639753.ibf
17561part2post-37-11256405
17.ibf
17561实用下料问题post-37-1125658327.ibf
17561研究生选取1post-37-1125658551.ibf
17561研究生选取2post-37-1125661080.ibf
17561谢谢!
17561谢谢!
17561谢谢了
17561谢谢了
17561唉,我大学生的都不会,希望几年后我也能做研究生的............
17561谢谢阿
175613Q
17561谢谢,收下了
17561不错,谢谢了!
17561谢谢
17561谢谢,非常不错
17561不说谢谢是不对的,哈哈,多谢了。
17561好啊
17561
请问有没有“实用下料”论文的附录程序啊 ?斑竹,偶看不懂,有急用。能不能也把它上传呢?
17561谢谢
17561

谢谢啊
17561谢谢提供这么多的资料!
17561好也!
17561感谢感谢!
17561谢谢
17561谢谢
17561谢谢
17561欢迎大家访问www.shumo.com
17561太感谢搂住了
17562你问的就是一个拟合优度检验问题,你说的分组的方法是
指的是pearson卡方检验,这个方法本质上是离散数据的拟合优度,
用于连续分布
就必须分组,这就带来了你说的这种由分组引起的问题。其实做拟合优度检验
还有很多方法,常用的比如kolmogrov-simirov检验(可能没拼对
呵呵)
中文的书可以看杨振海的拟合优度检验一书
17562如果需要检验一组样本点是否符合一个特定的概率分布,那么就首先需要对样本点进行分
组。这种分组有没有特定的规律可循?工作中发现:对同一种数据采用某种分组方式就可
以满足假设检验,采用另一种分组方式就不能满足假设检验,为什么?怎么解决?
有没有这方面解释的比较好的书?谢谢
17562谢谢了。有没有相关的英文资料,最好有网上能下载的。好像《拟合优度检验 》杨振海著. 只有国图有阿。
17562英文的有本书Smooth tests of goodness of fit / J.C.W. Rayner, D.J. Best.
其实很多数理统计的基础教材都有这方面的一点内容 如陈希孺的数理统计引论
我不知道哪里有网上下载的
17562
| 引用 (jasoncooler @ 2005年09月03日
10时03分) |
|
谢谢了。有没有相关的英文资料,最好有网上能下载的。好像《拟合优度检验 》杨振海著. 只有国图有阿。
|
my text is
really good. chi-squared goodness-of-fit is introduced in chapter 2 of
attached pdf.post-
17-1125787268.ibf
17562part 2post-
17-1125787433.ibf
17563怎么一个人都没有啊
17563matlab怎么表示一个集合
如何判断一个元素是否属于这个集合?
17563matlab 中通常用矩阵的概念而不是集合!!
17563ismember
Detect members of a specific set
Syntax
tf = ismember(A,S)
tf =
ismember(A,S,'rows')
>> A=[ 1: 4,
0:-1:-4]
A =
1 2 3 4 0 -1 -2 -3 -4
>>
ismember(A,5)
ans =
0 0 0 0 0 0 0 0 0
>>
ismember(A,4)
ans =
0 0 0 1 0 0 0 0 0
17566你这个是分析里的东西,可以看rudin的经典书
17566什么是稠密集?
书上说,如果A

B,并且若A与B的任何一个子开集的交都是非空的,那么就说A在B中稠.另外我又查看了一个结论:因为任意两个有理数之间总存在无穷个有理数,所以有理数集是稠密集.
两个结论让我糊涂了.有没有人能够帮我解释解释清楚.究竟什么是稠密集.上面两个结论之间是什么关系?
什么是疏朗集?
有一种说法是:若A的闭包不包含任何非空开集,则说A是疏朗集.
还有一种说法是:若A中的任何一点的任何一个邻域都包含有一个不包含A中元素的开集,则A是疏朗集.
两种说法是等价的吗?有没有人能够用最简单易懂的语言帮我解释解释??
17567一致收敛性post-38-1125650547.ibf
17567不对,对函数怎么提一致收敛性
17567就是这样的
东北大学
2002年
17567不太可能吧!!
17567一致连续性吧
17568统计就是从数据做未知事物的推断
17568
| 引用 (invariant @ 2005年09月06日
07时45分) |
| 引用 (978301 @ 2005年09月05日
07时52分) |
| 引用 (invariant @ 2005年09月03日
15时08分) | | 别人回答的很对,
我感觉你提的这个问题和独立随机变量分布的问题倒是只有傻瓜才问得出来的问题.
|
那就请教你这个聪明人:独立是什么意思?
你要是能说明白俺就佩服你
不过你最好不要用书上的那些什么定义来敷衍俺们
最要能用你自己的话语给大家说个明白
|
那你就错了, 任何一个数学概念都是从定义开始的,
所以独立当然是从定义而且也只能从定义解释, 其它的任何解释都是辅助的.
|
这点同意.
数学的推导只能按照严格的定义,哪怕定义是错的,也只能在发现矛盾以后把原来的定义重新严格定义或者把原来的定义推广.
如果加入直观的理解,会导致逻辑混乱,一个比较明显的例子就是复数被人们接受的过程.
17568
| 引用 (978301 @ 2005年09月05日
07时52分) |
| 引用 (invariant @ 2005年09月03日
15时08分) | | 别人回答的很对,
我感觉你提的这个问题和独立随机变量分布的问题倒是只有傻瓜才问得出来的问题.
|
那就请教你这个聪明人:独立是什么意思?
你要是能说明白俺就佩服你
不过你最好不要用书上的那些什么定义来敷衍俺们
最要能用你自己的话语给大家说个明白
|
那你就错了, 任何一个数学概念都是从定义开始的, 所以独立当然是从定义而且也只能从定义解释,
其它的任何解释都是辅助的.
17568在参数的点估计中,我们都是用一个统计量来估计一个参数.虽然我接触这个已经很久了,但是直到今天我才发现:为什么要用一个统计量来估计一个参数这个问题我并不太清楚.出于一种什么考虑才提出用统计量来估计一个参数的?
17568
引用 (Fisher @ 2005年09月02日
17时47分) |
| 统计就是从数据做未知事物的推断
|
说了等于白说.傻瓜都知道统计是从数据做对未知的推断,可是这个并不能说明为什么要用统计量去估计一个参数.
统计量的确是可以把得到的纵多样本值转化成为一个个精简的统计值,**********************不说了,这个问题俺突然明白了.谢谢你.不过以后还请多帮助.
17568别人回答的很对, 我感觉你提的这个问题和独立随机变量分布的问题倒是只有傻瓜才问得出来的问题.
17568老大虚心一点好不好!人家说的很概括,很好啊!你到厉害!一句说了等于没说!能把人噎死!
17568
| 引用 (科尔沁之子 @ 2005年09月03日
15时45分) |
|
老大虚心一点好不好!人家说的很概括,很好啊!你到厉害!一句说了等于没说!能把人噎死!
|
如果一个回答对于我来说没有任何可取信息,那真的是白说.
是什么就是什么
不要对我说态度好不好之类的话
我最讨厌这类政工人员的话语
你要是不乐意
可以不回答
17568
| 引用 (invariant @ 2005年09月03日
15时08分) |
| 别人回答的很对,
我感觉你提的这个问题和独立随机变量分布的问题倒是只有傻瓜才问得出来的问题.
|
那就请教你这个聪明人:独立是什么意思?
你要是能说明白俺就佩服你
不过你最好不要用书上的那些什么定义来敷衍俺们
最要能用你自己的话语给大家说个明白
17568请各位注意语言
17570按照独立的定义直接就得到
17570大家都知道,若总体X

F(X),那么独立同分布样本(X1,X2,X3...Xn)的分布就是F(X1)*F(X2)*....*F(Xn)
我想问的是,为什么会是这样?有没有人能从测度论的角度给我解释解释.谢谢!!
17570
引用 (Fisher @ 2005年09月02日
17时49分) |
| 按照独立的定义直接就得到
|
老大,如果这样回答俺,俺还要你来说?
也不知道你有没有看清楚俺的问题!1
17570就是按照定义 由X_i生成的杠sigma代数独立的定义直接得到
随便找本由测度论为基础写的概率论书就有 可参看严世健等的概率论基础
17571我们学习数理统计都是从讨论统计量开始的.俺觉得很奇怪.为什么要从统计量开始呢?俺学了几年了,今天才开始考虑这个问题.请大家发发高论!!
17572论学数学的作用。
一、使人沉静。
若论修身养性,诸理工学科莫过于数学者。夫习数学者,读无静则惘,写无静则乱,思无静则怠,居无静
则烦。古人谓“静以修身”。心静则气敛,气敛则神聚,神聚则思敏,思敏则情悦。实乃致理。静方可明
理,静方可怡情,静方可自省。静观万事,万事皆明。
二、使人深刻。
习数学者,遇事善思。透表及里,直达本质,不为假相所迷。夫世间万象,虽常理亦须推敲。于平常之处
见真理者多胜繁星。牛顿见苹果落地而探万有引力,爱因斯坦思时空之象终得相对论。皆于人所见惯之处
而发。则学之愈久,思之愈深;思之愈深,则理之愈明。深至极处,究天地之神奥,探古今之玄变。
三、使人精明。
既万物皆透,则各种关节,重重联系,尽收眼底。虽浓雾层层亦不为所迷,虽盘根错节亦可条分缕析。于
九霄云外鸟瞰弹丸之地,焉有不清之处?则既知己,又知彼,虽百战不殆,况他事乎。
四、使人理性。
理性者,不以感情用事,不以感觉行事,不以感受论事。亲见亦不定为实。客观为先,逻辑为上。推理而
得之事实,虽距预期千里,亦信之不疑。虽盛怒之下,亦不不以情役体。
五、使人远见卓识。
习数学者,须具大观。统筹全局,规划部署,差之一步,满盘皆输。未行半步已运筹千里之外,层层推进
,步步为营。其中亦有奇思巧构,殊途同归。奇正相生,存于一心。正如数学,推理与技巧共存,相得益
彰,技巧非是凭空而得,乃更深层次之理解。故具大观者,运奇正如手足,不以奇为奇,不以正为正。水
乳交融,到手皆利器也。
17572为什么只道好处,不讲坏处呢
17578用方差
17578我们公司现在想对业务员的工作考核,其中一项是针对他对下月的业务量预估的考核。
举个例子,张丽预估下月她会有500万的订单,但实际到下月她的订单量只有200万或700万,那么计算一下她对订单预估的准确率?开始我认为知是简单的:预估与实际的差值去
除以实际或预估值。但是在实际与预估值差异较大时就不成立了。请高手能否告诉我个准确的公式,然后再附带一点简单说明。先谢谢了!
17583那些精品课程的教学录象只有一 小部分啊
怎么能进行系统的学习啊?!!!
17583
http://www.hebtu.edu.cn/col90/col157/index.htm1?id=157
17584裴立文和吉米里都有讲 但教材里都没有 我看了钱吉林德也没有这方面的题 那还需要看吗
17584一般考研上下极限靠的很少!
17585

[1]$
$[/

]
sinx^2是条件收敛 求证 可能写的不规范,大家将就把
17585求助呀
17585积分算式是 sinx^2,在(1,+

)的范围内的广义积分是
条件收敛的
17585高手回答呀,小弟感激不尽
17588发现这里有生物数学,有经济数学,可惜没有计算机数学.
大概是因为计算机科学本身已经太数学了,所以没有这个版?
从来没有一个学科象CS这样和数学联系如此紧密.
数学在生物学中应用,在经济学中应用,但理论计算机科学本身都成了数学了.比如那些计算理论,比如形式语言与自动机理论.
17588信息与计算科学?!
17588计算机科学---信息与计算科学
不大一样.我理解,前者是非数值计算,而后者是数值计算
17589qing jiaopost-33-1125670744.ibf
17589见附件post-33-1132480697.ibf
17590见附件post-8-1125670931.ibf
17590如附件:post-8-1125672220.ibf
17592谢谢post-38-1125677503.gif
17592极限为a
a=0显然为0,
a ≠ 0,就有:post-38-1125707669.gif
17592直接用等价无穷小就可以了!arctanx等价于x(x趋于0时)
17592那个tan^(-1)是arctan吗,我还以为是正切的倒数呢
谢谢
17593什么是稠密集?
书上说,如果A
B,并且若A与B的任何一个子开集的交都是非空的,那么就说A在B中稠.另外我又查看了一个结论:因为任意两个有理数之间总存在无穷个有理数,所以有理数集是稠密集.
两个结论让我糊涂了.有没有人能够帮我解释解释清楚.究竟什么是稠密集.上面两个结论之间是什么关系?
什么是疏朗集?
有一种说法是:若A的闭包不包含任何非空开集,则说A是疏朗集.
还有一种说法是:若A中的任何一点的任何一个邻域都包含有一个不包含A中元素的开集,则A是疏朗集.
两种说法是等价的吗?
有没有人能够用最简单易懂的语言帮我解释解释什么叫做稠密集什么叫做疏朗集??
17593有理数的测度等于0。
17593简单来说就是这样的,若
A ‾
=B ,则称A在B中稠密。
若集合A=B,则稠密不用说了,下面说的是不相等的情况。
用任意——存在语言来说就是:若满足
1、对任意x属于A,都存在x的一个邻域使得这个邻域里都有点属于B;
2、对任意x属于B,都存在x的一个邻域使得这个邻域里都有点属于A;
3、存在x属于B但不属于A。
则称A在B中稠密。
17593有理数当然是稠密的
17593稠密性和疏朗集是和拓扑有关的。
17593很好理解,就是有理数集在实数集中稠密。
17593这么说吧,若B中的任意一点的任意邻域内都含A的点,B就在A中稠密。或者说,B的闭包包含A,B在A中稠密。
若B在A的任何开子集中不稠密,就是疏朗集。
注意:稠密和疏朗不是两个互补的概念。不稠密不一定就是疏朗集。疏朗是处处不稠密。
17593A在B中稠密意思是说,B中任何一点都可用A中的点逼近,就像所有多项式组成之集在连续函数空间稠密一样。
而疏朗集,他的闭包不含任何内点。就像康托集。
这两个概念确实和所定义的拓扑有关。
17593拿有理数集来说,“有理数集在实数集中稠密”也可以这样想:对于实数集中的任何一个点a,都可以在有理数集中找到一个序列以a为极限。
17594我想找一些有详细讨论或证明一个函数能否满足Lipschitz条件的书或文献
我要证明的方程比较复杂(放在附件里),有些书提到只要证明方程的偏导连续,但我找不到相关的证明例子.希望高手帮帮忙post-33-1125711463.ibf
17595不简单.
更佩服的是还考上了一所著名学校概率专业的研究生.
17595非数学专业的兄弟们,我们可算是同路人了
我也是学经济的,学着学着就对那玩意烦了.于是开始动脑筋学数学.呵呵
兄弟我的运气比较好,也比较不好.大学时候逃课时间达到整个上课时间的2/3,却没有被老
师抓住,这些逃出来的时间都被我用在了自学数学上面.第一次俺考概率专业,一们专业可是
概率论得了13分,另外一门是数里统计得了37分.两门一起得了50分.俺心理那个滋味真不好
受.不过俺就是不服气,俺不信俺学不好这个东西,所以俺在接下来的一年里,把自己关在一
个小教室里努力学习.因为基础比较差,所以学的特别慢,就概率论的第一节基础概念部分俺
就扎扎实实花了三个月的时候去啃.
后来漫漫地进入了状态就好了很多,所以第二次俺顺利
地考上了一所著名学校概率专业的研究生.
虽然如此考试结果非常棒总成绩达到410,概率论得了89分,数理统计得了96分,可是俺知道
俺的基础还是非常差的,所以在学校里读概率的时候一直在努力用功.现在,俺都毕业了,越
是觉得对于数学,俺懂得太少了,所以俺一直在这里流串,想向这里隐藏着的高手多学习学
习.
俺的经历应该是比较特殊的了.俺把俺的经历写出来,就是为了勉励各位非数学专业的数学
爱好者门,不要泄气,一定要坚持努力,最终还是会让你有收获的.数学这个东西太重要了,就
算是经济,现在哪个地方不用到数学??只要你沉下心来慢慢学,你一定会成功的.不要跟我说
你的智商啊天赋啊不适合学数学,难道你比俺更白痴?告诉你,俺一直到大学毕业还不清楚什
叫做因式分解!!
17595非数学专业的兄弟们,我们可算是同路人了
我也是学经济的,学着学着就对那玩意烦了.于是开始动脑筋学数学.呵呵
兄弟我的运气比较好,也比较不好.大学时候逃课时间达到整个上课时间的2/3,却没有被老
师抓住,这些逃出来的时间都被我用在了自学数学上面.第一次俺考概率专业,一们专业可是
概率论得了13分,另外一门是数里统计得了37分.两门一起得了50分.俺心理那个滋味真不好
受.不过俺就是不服气,俺不信俺学不好这个东西,所以俺在接下来的一年里,把自己关在一
个小教室里努力学习.因为基础比较差,所以学的特别慢,就概率论的第一节基础概念部分俺
就扎扎实实花了三个月的时候去啃.
后来漫漫地进入了状态就好了很多,所以第二次俺顺利
地考上了一所著名学校概率专业的研究生.
虽然如此考试结果非常棒总成绩达到410,概率论得了89分,数理统计得了96分,可是俺知道
俺的基础还是非常差的,所以在学校里读概率的时候一直在努力用功.现在,俺都毕业了,越
是觉得对于数学,俺懂得太少了,所以俺一直在这里流串,想向这里隐藏着的高手多学习学
习.
俺的经历应该是比较特殊的了.俺把俺的经历写出来,就是为了勉励各位非数学专业的数学
爱好者门,不要泄气,一定要坚持努力,最终还是会让你有收获的.数学这个东西太重要了,就
算是经济,现在哪个地方不用到数学??只要你沉下心来慢慢学,你一定会成功的.不要跟我说
你的智商啊天赋啊不适合学数学,难道你比俺更白痴?告诉你,俺一直到大学毕业还不清楚什
叫做因式分解!!
17595I服了YOU!
你这样热情,不如考个其它专业算了,要不你研究生毕业就只能在高校教书了,数学这东西是到是基础,可是你知道吗,煤是电的基础,可是挖煤的人很贫困,卖电的人确富的流油!老兄,你太倔了些,读书期间要注意全面发展呀!!!!!一言难尽!
17595佩服!
17595非常佩服
17595佩服!!没得说的
17596原创声明,转载请联系
复变函数诞生的曲折历程
熊
辉
中国科大数学系
从十六世纪开始,数学家们就在使用向量的概念。一个向量,通常画为一条有向线段,既有大小也有方向。它用来代表力、速度或其他方向和大小都有意义的量。同一平面内的向量可在几何上通过加减乘除的运算而得到一个新的向量。十六世纪还引入了形如a+bi
的复数,其中 ,而a,b 是实数。即使对数学家来说,这些数也是深奥莫测。因此当
1800年左右,魏塞尔(C.Wessel),阿尔冈(J-R
Argand),
高斯(K.F.Gauss)等几个数学家意识到可用平面上的有向线段来表示复数时,它的表示才变得方便起来。这些人马上看出复数不仅可以用来表示平面上的向量,还可以用来表示向量的加减乘除等运算。即,复数被用作为向量的代数,正如整数和小数用来表示商业事务。因此,不需要用几何进行运算而只要代数运算就可以了。举例来说,就是我们现在知道的,
(3+2i)+(1+4i)=4+6i了。顺便说一句,这种用复数来表示平面上的向量及其运算的方法到
1830年时已经差不多是众所周知的了。
就在十六世纪,欧洲人还在为无理数和负数寻找理论支持,然而他们还没有从这个困境中摆脱出来,就又糊里糊涂地陷入了我们现在称之为复数的泥淖之中。他们把平方根的算术运算推广到所有已出现的数上时,例如在求解二次方程的过程中,得到这种所谓的新数。像卡丹(J.Cardan)则在《重要的艺术》(1545年)的第37章中提出并解决了把10分为两部分,使其乘积为40的问题。这一看似荒谬的问题确实有解。因为正如达朗贝尔(J.L.R.D’
Alembert)所说的那样,“代数是慷慨的,它的给予常常超过你的要求。”卡丹求得上面问题的解为
5
+- 15 和
5
-- 15 。接着他指出它们是一些“尽管本身具有独创性,却没有什么用的诡辩的量”。“不管会受到多大的良心遣责”,将
5
+- 15 和
5
-- 15 相乘,得到40后,他又说:“算术是如此微妙地发展着,而它的尽头,却正如常言所说,虽然精致,却无用处。”
卡丹在求解三次方程的代数方法中进一步与复数打交道,这种代数方法在他的著作中得以体现,尽管他寻求的只是实根,但在有复根存在的情况下,他也会给出。这样看来,他应将复数的地位提高些,但是,因为他不知道如何求复数的立方根以获得实根,所以他就把这个难点搁置起来,用另一种方法来代替。
庞贝利(R.Bombelli)也考虑了三次方程的复数解,并且实际上采用了和现代形式一样的公式,来表述复数的四则运算。但他仍认为复数是无用而诡辩的。吉德拉(Albert
Girard)则承认复数至少可以作为方程的形式解,在《代数的新发明》中,他说:“有人会说,这些不可能的解(复根)是什么?我的回答是:有三方面的解释,一是一般法则的必然性,二是没有其他的解,三是因为它们有用。”但是卡丹的先进观点并没有对他们产生什么影响。
尽管16、
17世纪人们对复数缺乏任何清晰的认识,但实数和复数的运算步骤却得到改进和推广。在《代数》(1685)一书中,瓦里斯(John
Wallis)说明了如何在几何上表示实系数二次方程的复数根。瓦里斯说,实际上复数并不比负数荒诞,由于负数可以在一条直线上表示出来,那么复数也就可能在一个平面上表示。他确实给出了不很完善的表示法,当方程
ax
2
+bx+c=0
有实根或复根时,他还给出了其根的几何作图。尽管瓦里斯的工作是正确的,但却被人们所忽略了,因为数学家们不肯接受复数。
笛卡尔(R.Descartes)也摒弃复数,并造出“虚数”这个名称。他在《几何》一书中说:“真根和假根(负根)并不总是实在的,有时它们是虚的。”他认为负根至少可以在将出现它们的方程转化为由正根的方程后变成“实的”,但对复根却不能这么做。因此,复根不是实的,而是虚的。甚至牛顿(I.Newton)也不认为复根是有意义的,极有可能是因为在他那个时代复根缺乏物理意义,实际上,在《普遍的算术》(第二版
1728年)中他说:“正是那些方程的根应该经常出现不可能的情况(复根),才不会使那些本应不可能的问题看起来是可能的。”也就是说,在物理和几何上没有解的问题应该具有复根。
常被人引述的莱布尼茨(G.W.Leibniz)的一段话反映了对复数缺乏清晰认识的情况:“在那个分析的奇观里,上帝的精神找到了一个超凡的宣泄口,这就是我们称之为-1的虚根的东西。”尽管莱布尼茨已在形式上运用复数,但他还是不理解复数本质。为了证实他和约翰.贝努里(John
Bernoulli)在计算中对复数的应用,莱布尼茨指出这样做并无伤害。
十八世纪的数学家们在致力于理解和证实他们有关无理数、负数和复数以及代数的工作中遇到重重困难,甚至直到这时,仍有许多人反对负数,而关于复数的意义和用途的争论也越来越尖锐。一些数学家引入了负数的对数(以及复数的对数)作为复数,这一举措,使复数处境更加尴尬。
从
1712年开始,莱布尼茨、欧拉(Leonhard
Euler)和约翰.贝努里通过信件与论文在复数的意义上,特别是负数和复数的对数问题上争论不休。莱布尼茨与贝努里利用笛卡尔的“虚的”一词来描述复数,“虚的”就是说这种数(以及负数)是不存在的,尽管他们两个人都在计算中不可思议地成功运用了这种不存在的数。
正如我们所提到的那样,莱布尼茨给出了各种证明来说明负数的对数是不存在的。约翰.贝努里认为
log (-a)=loga
,他还用了好几个证明作为依据,其中一个用了正数的对数定理:
log (-a)=1
2
log(-a)
2=1
2
loga
2=loga
。另外一个证明采用了微积分,也得到同样的结论。莱布尼茨和约翰.贝努里在这几年中有许多通信往来,但其中大多都是些废话。
欧拉找到了真正的答案,其结论在
1751年的一篇论文《方程中虚根的研究》中发表,虽然他的最终结论是正确的,但其证明却是错误的。这一结论适用于所有的复数,也包括实数(因为x+iy中y=0的话,该数就变成了实数)。这一结论是:
log
(x+iy)=log(re
i
θ)=logr+i(θ+2kπ)
其中r 和
θ
分别就是我们今天所称为的复数x+iy的模和主辐角。然而,欧拉的这一论文却不为他的同时代的人所理解。今天,可以说每一个学过复变函数这门课的人都应该很熟悉这个公式。
欧拉在
1747年4月15日给达朗贝尔的一封信中阐述了其结论,他甚至指出一个正实数有无穷多个对数值,但只有一个值是实数,这个实数值就是我们在计算实数的对数是常用的那一个。欧拉的信和论文并没有说服达朗贝尔。在《负数的对数》一文中,达朗贝尔举出各种玄奥莫测的分析学和几何学的论证来否定这种对数的存在,他使这一问题变得更加神秘。他还说这仅仅是一个措辞的问题,并以此来掩盖他与大师欧拉之间的分歧。
所有卷入这场轮战的人都坚持自己的想法是正确的。在十八世纪前半叶,人们还认为一些复数的运算,如复数的复数幂,将产生一种全新的数。但正是达朗贝尔本人,在《关于风的一般成因的考虑》一文中,证明了复数的所有运算的结果只能是复数。尽管在这一问题上,达朗贝尔迈出了举足轻重的一步,但他的证明确实是由欧拉和拉格朗日(Joseph-Louis
Lagrange)所完善的。也许达朗贝尔已意思到了他的关于复数的思想处于一种很混乱的状态,因为在他为《百科全书》写数学条目的时候,并没有提及复数。
不过欧拉也没能弄明白复数,在十八世纪最优秀的代数课本,它的《代数》(
1770年)一书中,他说:
负数的平方根既不是零,也不是比零小或比零大的数。显然负数的平方根不能被划归为任何可能的数(实数),因此我们必须说它们是不可能的数。而由这种情况,我们将导出这样一种数的概念,它们在本质上是不可能的,并且通常被称为虚数或幻想中的数,因为他们仅存在于想象之中。
对于复数他还犯了一些错误,在他的《代数》中他认为
-
1 -
4=4
=2 ,因为
a
b
=ab
。
尽管欧拉将复数称为不可能的数,但他又说复数是有用的。他认为复数的作用在于能够告诉我们那个问题是有解的,哪个问题是无解的。这样,当我们要求把10分成两部分,并使两部分乘积为40(卡丹的幽灵)时,我们得到这两部分为
和 。因此,欧拉指出,我们可以得知这个问题是没有解的。
尽管对于复数有如此众多的反对意见,在十八世纪,人们还是像使用实数一样有效地使用复数,数学家们也因此对它产生一些信心。在数学证明时,运用复数,最后的结果总是正确的,并且复数在其中发挥着显著的作用。关于这些证明的有效性,甚至往往是结果的正确性的疑虑依然困扰着数学家们。
达朗贝尔在《百科全书》一书中关于负数的表述,反映了人们对待接受几种有些麻烦的数的普遍态度,这些数包括无理数、负数和复数。达朗贝尔的这一条目,写锝一点也不清楚,他得到这样一个结论:“不管我们如何看待这些量,复数的代数运算法则已普遍地为人们所接受并被认为是正确的。”达朗贝尔对于无理数、负数更加是复数的既爱又恨的心态,由此可见一斑。
十八世纪关于负数和复数取对数的争论使许多数学家非常困惑,以致到了十九世纪,他们仍对此喋喋不休。
1801年,剑桥大学的伍德豪斯(Robert
Woodhouse)发表了一篇题为《关于一个借助虚构的数得到的结论的正确性》的论文。他在文中说道:“在关于负数和复数取对数的争论中,许多数学家互相攻击对方的理论时所指出的矛盾和谬误,都可以作为说明那些数不可用的证据。”
柯西(Augustin-Louis Cauchy),最伟大的数学家之一,在十九世纪初创立了复变函数理论,也不同意把表达式
a
+b- 1 当作数。在他的名著《分析教程》(
1821年)中,柯西认为将这些表达式作为一个整体是毫无意义的。然而,他还是说明了实数a,b
的一些情况。例如,由方程
a +b-
1=c+d-
1 ,可推出
a=c,b=d,“每一个虚数方程仅仅是两个实数方程的符号表达式。”
1847年,晚年的柯西又提出了一个相当复杂的理论,可以用来判断用复数进行运算是否正确。但没有使用虚数单位-i
,对此,他说:“我们可以毫无遗憾地完全否定和抛弃一个我们不知道它表示什么,也不知道应该让它表示什么的数。”
1831年,著名的数理逻辑学家,并在代数领域有所贡献的笛.摩根(D.Morgan)在他的著作《论数学的研究和困难》中表示了对负数和复数的反对。他写道:
虚数式
-
a
和负数-b式有一种相似之处,即只要它们中的任一个作为问题的解出现,就说明一定有某种矛盾和谬误。只要一涉及到实际的含义,二者都是同样的虚构,因为0-a和
-
a
同样是不可思议的。
然后他举了个有关负数的例子来说明不可思议,恕不赘述。谈到复数,他说:
我们已经证明了记号
-
a
是没有意义的,甚至可以说是自相矛盾的,荒谬绝伦的。然而,通过这些记号,代数中极其有用的一部分便建立起来了。它依赖于一个必须用经验来检验的事实,即代数的一般规则都可以应用于这些式子(复数),而不会导致任何错误的结果。要把这个性质求助于经验,那是与本书开头所写的基本原理相违背的。我们不能否认实际情况却是如此,但必须想到这只不过是一门很大的学科中的一个小小的孤立部分,对于这门学科的其余一切分支,这些原理将完整地得到应用。
这里的原理,他指的是数学真理应该由公理经过演绎推理得出来。
接着,他对负根和复根加以比较:
在负的结果和虚的结果之间有截然不同的区别。当一个问题的答案是负的时候,在产生这个结果的方程里变换一下x的符号,我们就可以发现形成那个方程的方法有错误,或可证明问题的提法太受局限,因而可以扩展,使之容许一个令人满意的答案。但当一个问题的答案是虚的时候,得到的就不是这样了。
哈密顿(William
R.Hamilton),这位在其他领域也颇有建树的伟大数学家,也不愿意接受负数和复数。
1837年他在一篇文章中表明了他的反对意见:
毋庸置疑,当它从以下的原理出发(正如通常已是如此)时,负数和复数学说,很值得怀疑,甚至是不可信的:小数可以减大数,其结果小于零;两个负数,或者说两个代表的量小于零的数相乘,其结果将是一个正数,即一个代表的量大于零的数;尽管一个数,不管其正负,他的平方(也就是自身相乘)总是正数,但我们却可以找到或者说想象这样一类被称之为虚数的数,虽然其具有负的平方值,并因此而被假定为一类非正非负也非零的数,而它们所被认为代表的量既非大于零,又非小于零,更不等于零,尽管在此基础上逻辑形式可以建立成一个表示式的对称系统,而且通过正确应用有用的以此基础建立的规则,可以学会一种应用的技巧,但在这样一种基础上,哪里有什么科学可言。
布尔(George
Boole),这位和笛.摩根同负盛名的逻辑学大师,在《思维规律研究》(
1854年)中说:
-
1
是一个令人费解的符号,但是如果在三角学中运用它,我们就可以从可解释的表达式经过不可解释的表达式,而得到可解释的表达式。
使数学家们相信复数的不是逻辑,而是魏塞尔(C.Wessel),阿尔冈(J-R
Argand),
高斯等人的几何表示。但是,在高斯的著作中,仍然能发现他并不愿意承认复数。高斯给出了代数基本定理(每个n次多项式的方程有n个解)的四个证明。在前三个证明中(
1799、
1815、
1816年),他处理的是实系数的多项式,他又预先假定与笛卡尔平面中的点是一一对应的,尽管没有明确地定义对应。实际上,在实数平面内并不能标出
的值,另外,高斯的证明并没有真正用到复变函数的理论,因为他将涉及到的函数实部虚部分开了。
1811年,他在给F.W.Bessel的一封信中更明确地指出,a+bi
可以用点(a,b)表示,在复平面上从一点到另一点有多条路径可走。如果从这三个证明和其他未出版的著作中显示的思想来判断,高斯无疑仍在关注复数和复函数的地位问题。
最初高斯似乎得出数学中没有真理的结论,在
1811年11月21日写给贝塞尔的信中他说:“我们不该忘记,(复变)函数与其它所有的数学构造一样,只是我们自己的创造物,因此当我们由之开始的定义不再有意义的时候,我们就不应当再问它是什么,而应该问,如何作出合适的假设,使它继续有意义。”但没有人乐意放弃囊中宝物,高斯显然重新考虑了数学的真理问题。
1825年12月11日,他在一封信中说自己“不能从负数和复数的玄奥中摆脱出来。
-
1 的真正意义始终在我的脑海中显现,但是很难用言辞把它表达出来。”
然而,如果说高斯还对自己和其他数学家是否承认复数心存顾忌的话,到
1831年,他已经无所牵挂了。他公开陈述了复数的几何表示,在同年发表的一篇论文中,高斯非常清楚地将
表示为复数平面中一点,而且用几何方法实现了复数的加法和乘法。他又指出:虽然现在已充分理解了分数、复数和实数,但对于复数只是抱了一种容忍的态度,而不顾它们的巨大价值。对许多人来说,它们不过是一种符号游戏,但是,
-
1
的直观意思完全可以从复数的几何表示中得到,不需要增加其它什么就能将这些数归入算数的范畴。因此,高斯满足于这种直观理解,他认为,如果1,-1,
-
1 不被称为正、负、虚单位,而是被称为直、反和侧单位的话,人们就不会觉得这些数非常晦涩难懂。他说几何表述将原本深奥的虚数变得清晰明白了。他引入术语“复数”与笛卡尔的术语“虚数”相对应,并用之代替
-
1
。对当时同样重要的另一事实,即高斯自己和他的同时代人随意地使用没有事实基础的实数,高斯未置一词。
在
1849年的一篇论文中,高斯更加随心所欲地使用复数,因为他认为人们已经对复数很熟悉了,对此我们以后还将提到。但事实上情况并不完全如此,复变量的复函数理论主要是由柯西与十九世纪的头三十年发展起来并应用于流体力学的,在这之后很长一段时间剑桥大学的教授们仍顽固反对有争议的
-
1 ,而且不惜采取各种麻烦蠢笨的方法避免它的出现和任何可能的使用。
十九世纪上半期,人们又注意到代数也缺乏逻辑基础,主要问题是字母被用来表示各类数并参与运算,好像它们具有正整数的所有被人熟知且易于理解的性质,而且任何数——无理数、负数和复数被字母代替时——运算结果都是正确的。然而,因为此类数还未被真正理解,它们的性质也缺乏逻辑基础,所以使用字母代替更不合理。因此在
18世纪30年代数学家们着手处理用文字或符号表达式进行运算的正确性问题。首先考虑这个问题的是剑桥大学的数学教授皮科克(George
Peacock),他区分了算术代数和符号代数,前者是处理表示正整数的符号,所以基础牢固,它只允许运算结果为正整数;而后者,皮科克以为他采取了算数的代数规则,但是除去了只适用正整数的限制,在算术代数中推出的全部结果与符号代数中的结果一样,但算术代数中的表达式在形式上是普遍的,在数值上是特殊的;而符号代数中的表达式,从数值到形式上都是普遍的。皮科克的论证被称为等价型的永恒性原理,是他在
1833年给皇家科学促进会题为《关于分析的某些分支的新近成就和理性的报告》中提出的,他武断地肯定:
无论什么代数的型,当符号在形式上是普遍的,而在数值(正整数)上是特殊的时候是等价的,则当符号在数值上和形式上都是普遍的时候同样是等价的。
皮科克特地用此原理去证明复数运算是合理的,他试图依靠“当符号在形式上是普遍的”来维护自己的观点。在十九世纪的大部分期间里,由皮科克肯定的代数观点被接受了。格雷戈里(David
Gregory),笛.摩根和汉克尔(Hermann
Hankel)在支持它的同时,在小的方面有所改进。这条原理基本上是主观臆测的,它借助于未必成立的假定来论证为什么不同类型的数与整数具有相同的性质。虽然它的成立缺乏严密的逻辑性,但在实际运用上是正确的,所以被人们接受了。
显然,皮科克、格雷戈里、笛.摩根和汉克尔认为他们创立了一门源于代数学却独立于实数和复数性质的科学。然而,将一些单凭经验的方法称为原理无助于改善其逻辑状况,正如红衣主教贝克莱(B.G.
Berkeley)所说的:“根深蒂固的偏见也会常常演变为原理,这些性质一旦获得了原理所具有的力量和声望,不仅它自身,而且由它推出的任何结论,都会无需验证地被人们接受。”
————未完,待续。
17596还以为这么长不能发出去呢,早知道就多写点。
17596期待下文!
17596不错,但复变函数的兴起的最重要的原因是围道积分的运用!
17596是各好帖,楼主怎么不写了。遗憾,哪天我再续一个·····
17599具体怎么评价我还没想清楚,有没有这方面的研究成果?
17599这方面的模型应该有
但是没见过
17600向大家请教:
我有一个问题想问各位大拿不侠。如何证明,若F(x)是随机变量X的分布函数,则F(X) 服从均匀分布。
谢谢。
17600需要条件, F 必须是连续的.
17600
| 引用 (invariant @ 2005年09月03日
15时12分) |
| 需要条件, F 必须是连续的.
|
这是<高等数理统计>里的题,没有连续这个条件。
17600应该需要F处处连续这个条件,可以看陈希孺高等数理统计
183页
17600
| 引用 (huhuabi @ 2005年09月03日
10时10分) |
向大家请教:
我有一个问题想问各位大拿不侠。如何证明,若F(x)是随机变量X的分布函数,则F(X) 服从均匀分布。
谢谢。
|
please refer to
http://www.math.org.cn/forums/index.php?show...topic=15622&hl=
.exactly same question. sorted.
17601圆明园:该怎样保护你
已经进行了两年的圆明园公园铺设防渗膜工程最近引起了社会各界的极大关注。一方认为,防渗处理隔断了水的自然循环,破坏圆明园的整体生态系统和园林风格;另一方认为这样做是为了更好地保护圆明园的生态环境。
请你在了解双方观点依据的基础上,提出你自己的见解,建立数学模型支持你的观点。
注意:所用资料一定写明出处。
背景资料(仅供参考):
1.圆明园历史 从
1709年开始营建,至
1809年
基本建成,历时一个世纪。此后的嘉庆、道光、咸丰三代屡有修缮扩建,历时150 多年。圆明园总面积近352万平方米,水面面积约123万平方米。
2.圆明园湖底防渗漏问题
可以确定清河在圆明园的分布范围,在地下10.3米深度范围内,渗漏系数较大,渗水性较强。圆明园极为缺水,2000多亩的水面,每年枯水期约有七八个月,由于降水量少,很多植被旱死。经初步测算,如果圆明园要想保持水深是0.8米,总需水量合计为98.4万立方米;若常年保持1.5米深的水面,每年蓄水量为900万方。现在水务局能提供的水量是150万立方米。
3.水费问题
2004年8月1日前,北京市公园湖泊生态环境用水的收费标准是每立方米0.3元,现在环境用水涨到了每立方米1.3元。生态环境用水在城市用水量中占的比例很低。以2002年北京市的数据来看,生态用水只占全年用水量的2.3%。
4.防渗膜的相关问题
防渗工程的一些相关技术,采用复合土工膜材料;在做法上,允许了一个侧防渗,防渗方式在技术处理上,能留有0.5到1.5米的覆土,可以栽植水生植物,以保持良好的水生生态环境。另外,保留了部分的侧防渗。
这种白色的防渗层由一层稍厚的塑料膜和一层软膜组合而成。据工人介绍,塑料膜是起到防渗漏的作用,而附在上面的白色软膜,是为了在施工时防止塑料膜被石块等硬物破坏。施工时,先用挖掘机将湖底的淤泥挖出,铺好塑料膜后再用大约有1米厚的土层掩埋。
17604Q为n阶正定方阵,x为n维实向量,证明
0<=x'(Q+xx')-1
x<1,,其中,(Q+xx')-1为(Q+xx')的逆矩阵。x'为x的转置post-38-1125725337.jpg
17604这是第二步post-38-1125725375.jpg
17604对吧
17604第二步开头就不正确。
因为Q正定,只能有可逆矩阵P,使
Q =P T
P
过几天,给你上传一个很漂亮的解答。
17604很久以前就有人问过=_=
http://www.math.org.cn/forums/index.php?showtopic=13049
17608公式实在编辑不出来。
在此欲求
(z-1)lnz 的倒数的不定积分。
请各位高手,试试
17608
引用 (hhldf @ 2005年09月06日
18时47分) |
| 原问题无初等原函数
|
你是如何判断的?
17608原问题无初等原函数
17608感谢二位的留言!但是同问:你是如何判断的?
17608勿需判断,而需记住一些常见的,不可积的不定积分
17608
| 引用 (sunenfa @ 2005年09月09日
02时12分) |
|
勿需判断,而需记住一些常见的,不可积的不定积分 |
请教仁兄,从何处看到的这样的积分不可积的?能告知我具体的书?期刊?或论文么?谢谢
17609天大的近两年的题
也找不到
郁闷啊
同病相怜
呵呵
17609因为没人上传呀!呵呵
17609请问:
为什么,中国科技大学 2000年以后的 硕士试题 找不到呢?
17609到别的地方买也买不到呀 要是能买到我就上传了
17609我也是,郁闷
17609找的到的同学一定说一声,我急啊!
17610
求哪位好心人帮我编个程序,很简单的,只要用用C++/C语言
说明 :由于我最近忙于数学建模,所以没有时间 去编这个程序,请那位好心人帮我写下,这是我一个老乡求我的,可我又没有时间,她们又快要交作业了,急啊。在此先谢过了,最好用C++/C语言。
题目:设计一酒店管理系统
其中包括:
预定管理(预订人的姓名,姓别,订房日期,抵达日期,退房日期,房间号,是单人房还是双人房,该客房包括的服务项目),
前台收银管理(姓名,日期,收金额),
客房状态(可用户查询,在住房客报表),
财务核查(对当日入住的客房数,开房数进行统计)
17611 我们正活在一个高速发展、急剧变化的时期,我们的身边随时会发生许多未知的事情,我们对未来的前途很迷惘。
当你确信:通过你自己的努力,可以在十年后达到现在大你十岁的某个人的某种状态时,你可以无怨无悔地默默奉献,你的心情会很放松。当你有一个同龄朋友和你受过类似教育,从事类似行业,彼此间收入不悬殊时,你会发现:天还是蓝蓝的天,地还是塌实的地。
当你活到四十岁时,你突然发现几个二十来岁的小伙子,发表了若干篇SCI的文章,可能比你多,影响因子也比你的大,从而,小伙子的职称和收入都接近了你的水平,你觉得你还能保持内心平静吗?你能不浮躁吗?
现在的学术研究,在一定程度上符合经济规律(容易发文章的领域出来后,能转过去的都尽量转过去,当这个领域充分发展到无文章可发的时候,能退出来的自然都会退出来),但不会自动形成一个健康的体系。哪个方向好发文章,哪个方向发表的文章级别高、影响因子高,就往哪个方向钻。道理很简单,科学研究者有衣食住行的需要,更需要尊严。
许多人不愿意转自己的研究方向,他们很执着,或许是无奈;别的方向年轻许多的人都已经评上了“XX”职称了,收入也比自己高,项目也更多更大。如果是我,我一定不服气,自己不比他们笨,在科研上花的时间不比他们少,研究方法和手段也不见得比他们差。于是,沉不住气了!先把手头上的东西整理整理投出去,能分成几篇就分成几篇,没做出来的问题先放着,小错误能蒙就蒙,能混就混,发文章要紧。
项目申报下来后,需要经常性地汇报、总结,还要时时刻刻想着如何申请后续项目及其他项目,真正用于研究项目内容的时间不多。而没有项目就意味着没有地位没有好待遇没有发言权。面对这种情况,教授能不浮躁吗?教授还会有心思给本科生上课吗?
科研人员除了上面简单列举的压力外,不少人还从事了行政工作,大会小会天天有,就算是研究中国古典文学,也要学外语,累不累呀?普通人着凉后回通过拉肚子制造更多垃圾,搞学问的人压力太大的时候也会制造垃圾滴。
要想消除学术垃圾,首先还是要消除科研/教育工作者身上过重的压力才行。
17611有些学科给人印象侧重应用,理论方向不好做,并不是不能出成果,而是它的价值不易被人承认,说白了,就是不好发论文,除非是国外最高水平的期刊.但你拿这样的论文评中级和副高,明显亏大了.有时不换研究方向也不行.
17612已知x^2属于{0,1,x},求实数x的值
答案x=-1
x^2可以等于集合里的任何一个元素,-1也是集合里的一个元素。但x^2不等于-1啊
17612没错啊,x=-1,x^2=1,而1恰好就是这个集合中的一个元素啊。此题主要是想考集合中元素的互异性
17612这个题目要求的是X,而不是X ^2,X ^2可以是集合中任一个元素,再由集合元素的互异性,可以求出X来,求出X为-1.
17616大虾们,帮帮忙
176
17好学校,好老师
176
17大家交流一下阿,我的qq是155236604
176
17我也算一个吧
qq:28357
1966
176
17谁来建个群吧:qq308135716
176
17我的QQ:88373130
176
178955563我也加一个
176
17考南开的这么少啊
176
17怎么不存在啊,这个群,Euler
176
17也算我一个吧
我QQ是332449450
EMAIL:name.264@163.com
176
17都不考,我就考(窃喜)!
176
17同志们,有没有有2005年的试题啊,有的话请支持一下,谢谢
jjping@163.com
176
17加我一个
qq88256696
急急!!!!!!!!!!
176
17顶一下!!!!!
南开数学什么专业好
176
17谁来建个群啊!!!顶一下地
176
17大家谁来建一个群呀!!我没有权限
176
17大家是
176
17
| 引用 (whongye @ 2005年09月15日
10时16分) |
顶一下!!!!!
南开数学什么专业好 |
组合数学,微分几何!
176
17南开的分析类怎么样?我想学泛函或调和分析。
176
17概率方向也不错
176
17南开高代数学题是不是很难啊,那考南开就不好考了把
176
17建个群,方便大家交流!希望考南开的同学加入.
群号码:11427359
176
17
| 引用 (Sainter @ 2005年10月16日
11时10分) |
| 怎么不存在啊,这个群,Euler
|
真不好意思,忘了激活了,现在应该可以加入了,欢迎加入讨论!
群号码:11427359
176
17真有胆大的阿
176
18南开金融数学复试时老师会问些什么
会不会问一下宏观经济或微观经济呀??
176
19题一:已知方程ax2+bx+c=0的两根是a,c(ac≠0),则方程9cx2+3bx+a=0的根的情况是
必有一根为1/3(2)必有一根为1/9(3)两根分别为1/3,-1/3(4)必有一根为1/3,-1/3
题二:已知a≠0,b2>4ac, a,b,c是三个常数,ap2+bp+c=0,aq2+bq+c=0,其中p≠q,求pq2+p2q+1的值(用a,b,c的式子来表示)
题三:已知梯形ABCD中,DC∥AB,AC与BD相交与E,S△CDE=m,
S△ABE=n,求梯形ABCD的面积。
176
19这是些什么题 啊?
题2:
p+q=-b/a;
pq=c/a;那么pq2+qp2+1=pq(p+q)+1=-bc/a2+1
题3:
|m-n|
176
19题1 4
176
19第3题2个结果
|m-n|和m+n+2倍根号nm
176
19题1选(4),用韦达定理算一下得
a 2
=1
,分别解出b和c的关系,再用选项中的根代入方程即可解得。
17620
| 引用 (子青 @ 2005年09月06日
13时02分) |
| 这个只能说明你模拟的次数不够
|
因为数据是对方采集来的,不知道对方是否真的是随机产生。
这说明对方不是真的随机抽取吗?
17620那概率肯定是相同的,都是参数为0.42的两点分布
17620
| 引用 (子青 @ 2005年09月05日
23时10分) |
有个概念没说清楚:
什么叫抽到?是指只要抽到一组中的任意一个就算这组抽到还是指具体到某一个数?
|
是指只要抽到一组中的任意一个就算这组
17620有个概念没说清楚:
什么叫抽到?是指只要抽到一组中的任意一个就算这组抽到还是指具体到某一个数?
因为是有放回,并且如果是简单随机抽样的话,那两组应该是一样的,因为是均匀分布,只跟每组中数的个数有关
17620
| 引用 (one @ 2005年09月04日
22时37分) |
| 是什么样的随机抽取?
|
什么样的随机抽取??????
高手莫见笑,我真还不知道随机抽取还有什么什么样的。(这个是放回的)
请说来听听。
因为实际上发现:A组的概率分\密度,比
B组靠前。就是A组概率分\密度大一些。
不知道是什么原因。
因为数据是对方采集来的,不知道对方是否真的是随机产生。
给高手用Matlab检验过,没有看出什么异常,像自然随机。
需不需要我把一些数据上传??
高手请指教~~!
17620同是100个数中的42个,被抽取到概率分布是否一样?实际是否与数据的连续性有关?
100数组成: 即00、01、02……
98、99,共100个
A组42个是:个位0-6,十位0-6,共7*7=49个,在除掉个位、十位重复的,00、11、22…
66,7个,一共42个。
B组42个是:个位7、8、9的时候十位是0-6,3*7=21个;十位7、8、9的时候个位是0-6;3*7=21个,一共42个。
现在在这100个数中随机抽取,抽到后放回。
问:同42个,被抽取到的概率分布是否一样?
请高手指教~
17620A组成员如下:
10 20 30 40 50 60
01 21 31 41 51 61
02 12 32 42 52
62
03 13 23 43 53 63
04 14 24 34 54 64
05 15 25 35 45 65
06 16
26 36 46 56
B组成员如下:
07
17 27 37 47 57 67
08
18 28 38 48 58
68
09
19 29 39 49 59 69
70 80 90
71 81 91
72 82 92
73 83
93
74 84 94
75 85 95
76 86 96
17620A组比较连续,B组比较分散。这个对实际概率分布有影响吗???
17620是什么样的随机抽取?
17620把数据上传:
附件中有2个文件。
一个是只有2行的
另外一个有4行,共可以组成6组2行。
测过其中
百位-十位;百-个;十-个 (剩下3组不是100个为全集的,有的全集才70个)
三组均发现: (题目所指的)A组 比 B组
分布靠前
这是一个古典概率的问题吧~~
搞不太懂,要加把劲~~~~post-
17-1125982034.ibf
17620这个只能说明你模拟的次数不够
17620
| 引用 (子青 @ 2005年09月06日
13时02分) |
| 这个只能说明你模拟的次数不够
|
不是模拟的哦~~~
那岂不是知道答案再去试验。——验证
不是模拟的
一个商业数据
(也不是什么保密叻,担心人家不理解,所以不说是哪方面的叻)
17620
| 引用 (hupo99 @ 2005年09月08日
13时48分) |
| 引用 (子青 @ 2005年09月06日
13时02分) | | 这个只能说明你模拟的次数不够
|
不是模拟的哦~~~
那岂不是知道答案再去试验。——验证
不是模拟的
一个商业数据
(也不是什么保密叻,担心人家不理解,所以不说是哪方面的叻)
|
那两个概率也是一样的,如果按你说的模型的话.
两组数据算出来结果相差很正常,因为你用频率代替概率只是概率的一个估计,有估计就有偏差
17620
引用 (子青 @ 2005年09月08日
17时36分) |
| 两组数据算出来结果相差很正常.
|
是的,如果只是两组,那么数据算出来结果相差也比较正常。因为次数少嘛~~
实际上:不是两组哦~~
一共可以得到 6组 。
其中3组是 A,
3组是B
辛苦编了一个程序,统计过它们的抽取情况。3组A的分布无一列外,都比另外3组B靠前。
这难道只是偶然???
(压缩文件里, 千位-百位,百位-个位,千位-个位,共3种情况。每种情况都有A\B组,一共可以得到 6组 )
17620就是偶然,如果你的数学模型没有搞错的话
17620
| 引用 (子青 @ 2005年09月09日
00时38分) |
| 就是偶然,如果你的数学模型没有搞错的话
|
子青这么说,必然是奠定在多年的深厚数学积累上的;
如果是仔细思考过的,必然是相当有权威性的,一言九鼎。
可是难道这个问题就这么简单??初级概率学就包含了它的一切??
没有涉及到更高级的问题?
相互连在一起占绝大多数的数据(42%),
与零散、极有分散性的相同数量数据,数学性质完全一致?
我就纳闷~~!
17620
| 引用 (hupo99 @ 2005年09月09日
13时52分) |
| 引用 (子青 @ 2005年09月09日
00时38分) | | 就是偶然,如果你的数学模型没有搞错的话
|
子青这么说,必然是奠定在多年的深厚数学积累上的;
如果是仔细思考过的,必然是相当有权威性的,一言九鼎。
可是难道这个问题就这么简单??初级概率学就包含了它的一切??
没有涉及到更高级的问题?
相互连在一起占绝大多数的数据(42%),
与零散、极有分散性的相同数量数据,数学性质完全一致?
我就纳闷~~!
|
我的结论是基于楼主的数学模型的,当然是假设抽样之间是独立的,但是问题在于很多商业数据的抽取其实不是独立的,这个就涉及非抽样误差的问题.
打个比方说,虽然你可能做问卷调查的时候问的每个人是独立的,但是那些人既然有兴趣回答你的问题,就说明他们对你的问题有一定的偏好,也就是说他们有很多问题会选相近的答案.也就是说实际上,你的抽样结果是不独立的。
17620
| 引用 (子青 @ 2005年09月09日
22时00分) |
| 我的结论是基于楼主的数学模型的
|
这个还是请教子青博士: 我的数据真的是 比较简单吗??
我一直都在怀疑这个数据
可能和矩阵模型有关; 只是本科那点《线性代数》实在太简单,那点矩阵知识
根本无法去了解这个数据~~
我正在为此事大费周折、难道它真的只是很简单吗?——这件事情我也在考虑。
因为有迹象表明:数据出现过明显的人为干预:它并不是绝对按着某种仿随机数学模型,(比如一个复杂的矩阵),或自然随机。不过次数不多,究竟它内在规律是怎么走的,也编过delphi去挖掘,不过目前还找不到线索,一点都没有找着。不过发现了它有这个规律,A组比B组概率分布靠前(当然这个A组B组是我们自己为了挖掘数据时分的)。
不知道子青博士有没有挖掘过数据的规律呢?
呵呵,先聊到这里。 再次感谢子青先生~
17621遇到palm Probabilities问题,希望各位能给解释一下这个术语。
17622请高手告诉我
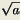
7 -
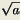
5 与
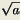
5 -
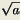
3
哪个大哪个小,老师要我用分子有理化做,但是我连分子有理化什么意思都不懂,希望有高手能告诉我,在此谢过
17622基本的原理:
对于a-b,将其看作(a-b)/1,将分子分母同时乘以(a+b),使分子出现a^2-b^2,这样如果a,b是带有根号的,根号就划去了。
17622做比值
t^7-t^5/t^5-t^3
=t^4-t^2/t^2-1
=t^2=a
a<=1
,left小.
a>1,left大.
不谢(屑)!哈哈.
17623我只见过btt,表示的是可归约性,至于bt是否相同我不敢确定,相信是你朋友捉弄你来着。
17623本人朋友问我:‘你学数学的,知道偏微分方程的BT吗’。‘BT不是下载软件吗,偏微分方程的BT是什么东西”,本人朋友笑着说“偏微分方程的BT都不知道,你在茅厕里学数学的吗”各位大爷,大哥,大姐,救救我吧,什么是偏微分方程的BT????
176262006年研究生招考网上报名时间确定
具体时间安排如下:
9月3日-10日考生查阅招生专业目录,
9月12日-14日全国统一开展网上咨询
考生可登陆http://www.chinayz.com.cn或http://www.chinayz.edu.cn就相关问题与专家进行网上在线咨询。
9月
18日-23日应届本科毕业生预报名
10月10日-31日正式网上报名、填报报考信息。
11月10日-14日考生到指定地点交费并照相。
17629求1+1/3!+1/6!+1/9!+。。。。。。+1/(3n)!+..............
17629考虑1+x^3/3!+x^6/6!+x^9/9!+。。。。。。+x^{3n}/(3n)!+..............
然后求导
17629利用微分方程的知识可以算出这个级数的和S=
1 3
e+2
3 e
-
1 2
cos(3
2
)
17630请教高手解答!post-38-11257543
17.gif
17630这个题目是不是出错了啊!?我找到个是这样的
post-38-1125763349.jpg
17630给出答案:(如下)
可以令M满足
F(x)=[f(x)-f(a)](b-a)-[f(b)-f(a)](x-a)-(x-b)(b-a)(x-a)M/2=0.
①
显然F(a)=0,F(b)=0.
由罗儿定理:比存在a<c1<x,x<c2<b,使的F'(c1)=F'(c2)=0.
F'(x)=(b-a)f'(x)-[f(b)-f(a)]-(b-a)MX+(b-a)(b+a)M/2
代入得,有方程组F'(c1)=0
② F'(c2)=0
③
由②-③即得M=[f'(c1)-f'(c2)]/(c1-c2)=f''©,
c1<c<c2.
代入①,在a<x<b时,①可以变换成需要证明的等式。
17630可以定义函数:
f(x)-f(a)
-------------------------=F(x)
x-a
x=G(x)
可以用cauchy定理!得出
F(x)-F(b)
--------------=F'(

)
x-b
然后,f(a)=f(

)+(a-

)f'(

)+((a-

)^2)f''©/2
把上式代入F'(

)就可以了!
17630高手!解答正确!
17634大学教师写道歉信
(2005-08-29 14:59:09)
8月23日,因为超过一半的学生考试不及格,中国青年政治学院教师杨支柱写了一封道歉信。杨支柱在信里真诚检讨了自己教学的失误,同时也指出了学生学习上存在的问题。
通看道歉信全文,不难看出,杨老师和陈丹青、贺卫生两教授一样,其实也是想通过这种方式表达自己对现行教育体制的观点,尤其是在学生培养上。
杨老师说他的阅卷并不很严格,“不但预先制定的标准答案上没有的内容你们回答得有理的酌情给了分(这是应该的),而且你们普遍存在的词不达意和病句现象我没有扣分”。
那为什么学生还考得这么差呢?杨老师总结是学生们的学习自觉性极为不够,自学能力有限,而他又高估了学生。杨老师上课一般注重讲前沿问题,对于基础问题就让学生们自己去读书中的某些章节,但从没有对学生们看书的情况专门进行检查、监督,毕竟面对的不是中小学生了。没想到学生考试就是基础问题没过关,显然他们无论是平时还是考试前都没有看过书,去理解和消化那些个基础问题,考试能回答出来的是上课听的“似懂非懂而且已经遗忘了不少的那点东西”。
造成这样的结果,杨老师认为一方面是自己的责任,另一方面他在接受《中国青年报》记者采访时说,学生从小缺乏自由的训练,而有些东西在适当的年龄没有学会,是不能补课的。更何况,现在的大学生也都忙于应付英语、计算机、国家司法考试、注册会计师考试等各种“功利性应考”,只做各种试题汇编,而参阅专著。
17634common phenomena
17634年轻的一代已经堕落了
这个老师道歉以后也说明堕落了
中国如此以往是没有什么希望了
大学老师的职责是什么?我认为有3:
1.教书育人(注意除了教书还要育人,育人就是要教会学生具备基本的科研能力,自学能力等等还有一些人的基本品格)
2.捍卫文明:很多学生已经被社会的酱缸浸泡过,眼里全是金钱主义,学什么东西如果不能让他产生经济效益,他是没有什么动力去学的,我的一个学生,他是特困生,他跟我说了一句很让我震撼的话:"我学那些不喜欢的课程,是因为我想拿奖学金,如果我家里条件好的话我绝对不会去努力学的";所以如何守住文明的净土,而不是因为学生的消极而改变自己甚至什么道歉;
3.捍卫学术:我认为这个老师原先做的并没有什么不对,说明他是一个有学术水平的老师,很多人想这么做都做不到,因为学术水平不够.如果不这么做,学术前沿的东西怎么能让这些"天之骄子"们了解呢?又如何激发学生对科学的探索欲望和思想火花呢?不这样做,教出来的学生都是木头,谈不上什么创造力.
所以我认为这个老师正确的做法应该是:不断的宣明自己的观点和主张,坚持自己的做法,要求学生要适应,措施是鼓励学生多发问,多讨论,认真布置习题和批改作业,做好课后辅导工作.
over,以上纯属个人观点
17634现在的考试,不是在考学生,而是在考教师自己。你给他复习要考内容,他过关高兴但看不起你,你让他考得一踏糊涂,他骂你,你还过不了学校那一关。现在呀,你想出一能让大多数学生都能及格的试卷,难呀难呀,你得挖空心思想想,还是一个字:难。
17634某著名人士语录:没有教不会的学生,只有不会教的老师。
有的人是站着说话不腰疼的
17634
| 引用 (huding8099 @ 2005年10月27日
10时42分) |
年轻的一代已经堕落了
这个老师道歉以后也说明堕落了
中国如此以往是没有什么希望了
大学老师的职责是什么?我认为有3:
1.教书育人(注意除了教书还要育人,育人就是要教会学生具备基本的科研能力,自学能力等等还有一些人的基本品格)
2.捍卫文明:很多学生已经被社会的酱缸浸泡过,眼里全是金钱主义,学什么东西如果不能让他产生经济效益,他是没有什么动力去学的,我的一个学生,他是特困生,他跟我说了一句很让我震撼的话:"我学那些不喜欢的课程,是因为我想拿奖学金,如果我家里条件好的话我绝对不会去努力学的";所以如何守住文明的净土,而不是因为学生的消极而改变自己甚至什么道歉;
3.捍卫学术:我认为这个老师原先做的并没有什么不对,说明他是一个有学术水平的老师,很多人想这么做都做不到,因为学术水平不够.如果不这么做,学术前沿的东西怎么能让这些"天之骄子"们了解呢?又如何激发学生对科学的探索欲望和思想火花呢?不这样做,教出来的学生都是木头,谈不上什么创造力.
所以我认为这个老师正确的做法应该是:不断的宣明自己的观点和主张,坚持自己的做法,要求学生要适应,措施是鼓励学生多发问,多讨论,认真布置习题和批改作业,做好课后辅导工作.
over,以上纯属个人观点
|
坚决反对您的观点!!
在这里,我称呼“您”,是对您的尊重。但是,不代表我同意您的观点
1:“教书育人”?
教育是时代的产物,历来是统治阶级利用的工具和方法。如果没有新中国的建立,我们就不会培养“又红又专”的人才。如果没有扩招,就不用把精华想办法变成糟粕后再去喂学生了。可怜的不是我们这些大学教师,而是那些本来可以培养出来但没有机会培养出来的学生!!!!!你难道要把猪变成龙吗?只可惜龙在猪圈里,也变成猪了。这样的“教书”也叫教书?
再看“育人”。你要育人,就要有育人的方向和目标。你想把学生育成什么样子?古典的还是现在的?进年来的“快餐文化”已经把这个社会变化了。教师只是一个职业而已。不教错就可以了。讲完教材就不错了。还提高?你真的认为学生的水平在提高吗?那么为什么现在的高校在招聘的时候不要自己培养的研究生学生?大家心里都清楚这是怎么回事,只是不说而已。如果不信,看看现在的校园,学生亲热你是否管过?!
2:“捍卫文明”:(很多学生已经被社会的酱缸浸泡过,眼里全是金钱主义,学什么东西如果不能让他产生经济效益,他是没有什么动力去学的)。难道这是错的吗?我们为什么不反省自己的教学究竟能给学生带来什么?学校收了学生那么多学费,教给学生无用的东西,不反省自己,反而怪学生?现在就有许多的学生后悔自己上大学!!!“如何守住文明的净土”你难道认为大学是“净土”?你不会是在5、60年代速冻后今天解冻的学者吧?简单一个例子:一个高产的“学者”在一年内居然写出50篇论文,享受国家津贴。一星期一篇,下猪崽子也没那么快!!你以为是个人的事情吗?同济大学的高等数学写得很烂,居然全国都用,你觉得在就是学术的事情?长江中下游气候出现的异常只是因为修三峡工程学术界没有考虑到的原因??
3.“捍卫学术?”。教学是双方面的。教与学是结合的。你能想象给小学生讲什么是共产主义,但现在的实际情况是我们要告诉学生上公共厕所后要冲刷!!国外的留学生公寓就有提示:“中国留学生,用后请冲刷”的警示。你想把原子物理讲给小学生?然后还要考试?不通过交补考费!!沈阳工业大学就是这样创收的。什么叫有学术水平的老师?现在的制度下,能够让学生满意的教师(就是和学生关系好的教师),因为学术水平不够,没关系,我们有事业单位用人体制保护你,外面比你强的人进不来!!你主要会交一本没用的教材就行了。学生懂什么?没学完不知道有没有用、学明白了才知道没用。你主要给及格,学生可以一年不来上课。还激发学生对科学的探索欲望和思想火花?谈什么创造力的培养?
学生比我们现实!!学生比我们先进!!没必要苛求自己,每年因为有责任心而死的老师还少吗?
17634迷时师渡,悟了自渡。修行还是靠个人努力才行:)
令外感觉没必要把学生看的太弱,(虽然他们很多人都很弱),很多人没兴趣那是因为体制的原因导致的,例如无法换专业等。
我胆小,被领导训也不敢顶嘴,我很佩服那些以自己的方式向不合理的事物宣战的人!
17634老师的职责,教书育人。可是教书容易,如何育人呢?我觉着老师这两点必须做好,否则学生好不到那里去的。但是如果学生考试不及格,不能光找教师的原因,还要找学生的原因。因为学生是学习的主体,学生考试不及格首先是自己的原因,其次是外在的原因。可是为此反省的学生多么?现在的学生,学习似乎应付的多些。
17634
引用 (小红帽 @ 2005年09月03日
22时
19分) |
大学教师写道歉信
(2005-08-29 14:59:09)
8月23日,因为超过一半的学生考试不及格,中国青年政治学院教师杨支柱写了一封道歉信。杨支柱在信里真诚检讨了自己教学的失误,同时也指出了学生学习上存在的问题。
通看道歉信全文,不难看出,杨老师和陈丹青、贺卫生两教授一样,其实也是想通过这种方式表达自己对现行教育体制的观点,尤其是在学生培养上。
杨老师说他的阅卷并不很严格,“不但预先制定的标准答案上没有的内容你们回答得有理的酌情给了分(这是应该的),而且你们普遍存在的词不达意和病句现象我没有扣分”。
那为什么学生还考得这么差呢?杨老师总结是学生们的学习自觉性极为不够,自学能力有限,而他又高估了学生。杨老师上课一般注重讲前沿问题,对于基础问题就让学生们自己去读书中的某些章节,但从没有对学生们看书的情况专门进行检查、监督,毕竟面对的不是中小学生了。没想到学生考试就是基础问题没过关,显然他们无论是平时还是考试前都没有看过书,去理解和消化那些个基础问题,考试能回答出来的是上课听的“似懂非懂而且已经遗忘了不少的那点东西”。
造成这样的结果,杨老师认为一方面是自己的责任,另一方面他在接受《中国青年报》记者采访时说,学生从小缺乏自由的训练,而有些东西在适当的年龄没有学会,是不能补课的。更何况,现在的大学生也都忙于应付英语、计算机、国家司法考试、注册会计师考试等各种“功利性应考”,只做各种试题汇编,而参阅专著。
|
教师因材施教,这个老师对自己的学生了解不够,不能把自己的思想强加于学生。你的教学目标够明确吗?学生对这门课又有什么想法,你应该在课程开始就让学生知道课程意义,而不是只为学分(对于学生),对于你,不能只为完成任务,挣课时费。很多大学老师讲课,像是在对付,你敷衍学生,学生也在敷衍你。讲课水平差,还总推卸责任。当然学生有学生的问题,大多数学生还是愿意努力学习,学生对课程的喜爱,不仅源于课程本身,更源于教课老师所给他们带来的影响,从人格到素质,而大多数高校老师却在努力敷衍孩子。老师是否认真备了课,学生是能听出来的,别总把别人当傻子哄。
17634"讲课水平差,还总推卸责任。"???????????
17634呵呵,学生考试不及格老师要负责任啊,我上学的时候我系有个老师给别的系讲《高等数学》,考试的时候不及格率是100%,原因是班级总共53人,平均出勤人数是22人,他们院的院长来求情都
不行,看看现在的要求!!不过如果讲课的时候真的不了解学生的真实状况的话,那还是应该算是老师的失职的,现在的大学生主动性很差的,而且他们经常问的问题就是“这个东西有什么用?”每个人都很实际的,可是现在的大学课程呢,除非你搞研究否则可能一辈子都用不上啊!
17635有七个人同住一间屋,早晨起来没有一个人穿自己的鞋的概率
17635喜欢的话可以用容斥原理
17635可以用加法定理的,复旦大学版的概率统计书,第一本有个战士拿枪的例子与这个例子相同,你可以参考那的
17636见附件,谢谢post-38-1125791043.ibf
17636首先把(sinpx)^2降幂,然后分步积分,就可以!
17636我也用这个方法,可还是做不出来,能否详细一点
17636这个样子吧:post-38-1125847597.ibf
17637

(x^n)*((lnx)^2)
x在[0,1]上是一致收敛的!怎么证明啊!

(x^n)*((sinpix)^2) 在[0,1]上也是一致收敛的吗?
类似这样的问题怎么处理啊??谢谢!
17637考虑n~inf的和函数即可知道
17639见附件!post-38-1125801103.ibf
17639好似叫dini定理
用反证
17639非负有什么用啊??
17640帮我看看啊post-38-112580
1991.gif
17640链式法则求偏导验证
17640可否写过程啊?谢谢!
17641有五个随机数字,求其中最相邻的3个数字。
要求:只能用简单的计算方法得到。
17641我的做法,请大家指正。
取中间数值为基数,取其和其它数值的

最小的两个数值即可。
17641不会,但是帮顶
17642已知一直角三角形ABC,角C等于90度,AC
边上中线所在直线方程为Y=X+3,BC边上中线所在直线方程Y=2X+4,又已知AB=60,求三角形ABC的面积。请教各位高手
17643各位谁有S.I Resnick 写的"Adventures in Stochasti
Processes"习题的答案?能否共享一下?谢谢!
17644When you remove a vertex from a convex ploygon, the remaining
vertices form a convex ploygon. It is equivalent to that if you add a
vertex to a concave polygon, the new polygon is concave.
Please
tell me your idea even if you cannot show it completely.
17644把它翻译成汉语好吗?
顺便把关键词解释一下,好吗?
17645这道题目我怎么看不懂啊?符号都不知道什么意思!tobyiqin,让我佩服,又是我的一个对手。搞的我现在都好累,对手这么多啊!也不知道是研究生还是快毕业的大学生,和我一样是个考研人呢?
17645题目好像不对!
17645?
你这些话我都不懂了,呵呵
我不是什么对手了
再说即使考一个学校也不能说是对手啊
大家以后极有可能是一起学习得好朋友
这里得一种良性竞争
也是为了大家都能考上理想得学校
bless
you
17645如图post-38-1125811010.gif
17645不好意思
等号左边的行列式有下角应该是 Ajl
post-38-1125887306.gif
17645我只对i=k=1,j=l=2的情况给出了证明
其实我们不难看到其他的情况都可以变换成这种情形的
解答如下:post-38-1126087796.gif
17648hhldf相当于没有做吗?
17648

ln(e^x+1)dx
(考研究生填空题)
17648y=-x
原积分=

ln(1+exp(-y))d(-y)
=

ln(1+exp(y))d(exp(-y))
z=exp(-y)
原积分=

ln(1+1/z)dz
=zln(1+1/z)-

z * z/(1+z) *
(-1/z^2)dz
= zln(1+1/z)+

1/(z+1)dz
=zln(1+1/z)+ ln(z+1) + C
z=expx
中午没睡觉,不知道对不对
17648ln(e^x+x)+c这是我的答案
17648ln(e^x+x)的导数我算着不是被积的函数阿,难道我算错了?
17648不好意思,我2楼的解答错了
y=-x
原积分=

ln(1+exp(-y))d(-y)
= -

{
ln[1+exp(y)]-y}dy
=-

ln[1+exp(y)dy]
+ (1/2y)^2
原积分=-原积分+
(1/2)x^2
原积分=(1/4)x^2+C
不知道这个对不对,结果这么奇怪
17648用分布积分法啊!!很简单!!!
17648直接的分布积分法做不出来,
楼上几位兄弟的做法也都有问题。
问题不是像我们想象的那么简单。
17648答案!post-38-1125898699.ibf
17648我5楼的答案
(1/4)x^2+C
很奇怪,但是我不知道什么地方错了,谁能告诉我?
17648
| 引用 (pccq_2002 @ 2005年09月05日
13时47分) |
我5楼的答案
(1/4)x^2+C
很奇怪,但是我不知道什么地方错了,谁能告诉我?
|
原积分=-原积分+
(1/2)x^2
原积分是关于x的,而你后来给出是关于y的,所以两个不是一样的,这和算定积分是不同的。
17648原题目是高数考研题,题目抄错了
17649divu用什么看啊
17649

post-61-1125812236.ibf
17649

post-61-1125812352.ibf
17649

post-61-1125812477.ibf
17649

post-61-1125812610.ibf
17649

post-61-11258129
19.ibf
17649

post-61-1125813066.ibf
17649上传完毕post-61-1125813353.ibf
17649djvu 阅读器
http://www.math.org.cn/forums/index.php?showtopic=8622
17649Very nice. Thank you
17649这年头什么都要分,楼主真是好人,帮你顶一计
17649真是谢谢了。
17649中文版还英文版?
17649非常感谢,刚好图书馆得给人借走了。
17649太感谢了
真是个热心肠的人
17649顶一下
17650怎么入手啊?post-38-1125821540.gif
17650此即函数列的Dini定理,在许多数学分析教材中都有.一般用反证法.
17650先证明函数列点点收敛,再证明在一个领域内一致收敛,然后用有限覆盖定理过渡到在整个区间内一致收敛,最后由一致收敛性推出极限函数为连续函数。
17650henhao de fangfa a
17651看看啊,
17651精彩文章,不容错过
17651刚刚下完,希望能有耐心看完,不管自己能不能看懂
17651绝对精彩
分析了当前的数学发展形势,从多方面对数学进行了详尽的阐述。
欢迎大家下载post-27-1125822545.ibf
17651这么好的文章难道没人看吗?
17651以前看过
17651楼主太好了,感谢楼主
17651re!
thanks
17651好文章
17651体制还是问题啊.
17651谢谢楼主,辛苦了
17651好文章
17651好文章!
17651我也来看看哈
17651好东东!
17651是呀 不管看不看得懂 下来看看
17651强烈支持,这是大家前进的动力
17651谢了!
17651谢谢楼主,自己一直对数学了解太少,这文章能帮到我
请问各位,有不有毕业论文能借我参考一下吗?谢谢
17651好文章收藏,学习,谢谢a
17651谢谢楼主,自己一直对数学了解太少,这文章能帮到我
17651
| 引用 (qinghuas @ 2005年09月04日
16时29分) |
绝对精彩
分析了当前的数学发展形势,从多方面对数学进行了详尽的阐述。
欢迎大家下载
|
兄弟是北师大的弟子吧!
17651为国强而学数
17651谢谢,下载后慢慢看
17651tai 好了
17651楼主太好了,感谢楼主
17651强调了我国学者的工作,但我们是不是也应该放眼全球?
17652英国科学家建立数学求爱模型 重礼有望赢得女孩芳心
(2005-08-
17 11:46:36)
本报讯
如果男人认为他们为了能和女孩子拉拉手而请她们喝酒、吃饭是浪费钱的话,他们最好还是要再想一想。一个由英国科学家建立的数学模型显示,昂贵却又无用的礼物也许对求爱有所帮助。
伦敦大学学院数学系的Peter Sozou博士和Robert
Seymour教授分析了求爱礼物所能起到的作用,并且给出了什么是“好”礼物的定义。研究人员这项有趣的研究工作表明,礼物是能够反映出男人意图的一种信号,选择一件对于男人来说是昂贵的但是对于女人来说却是毫无用处的奢侈礼物,就能解决这个问题。他们发现,昂贵礼物通常能够表达男士对所追求女士的认真态度。
研究人员制作出了一个经过改进的数学求爱模型。这个求爱模型就像一个连续的游戏,也许能够为那些无法吸引年轻女孩子的男士提供一些不同的方法。
Sozou说:“雄性动物赠送礼物是人类求爱和许多物种求偶的一个特征。与雄性动物相比,雌性动物在繁衍后代方面有了更多的付出,因此她(它)必须选择尽可能优秀的伴侣,但是单纯从外观上很难作出判断。”他说,“具体到人类而言,一个女孩不仅希望她的意中人有足够的魅力,而且还希望他能够帮助抚养他们的小孩。对于女人来说,最糟糕的就是遇到一个完事后就付钱走人的男人。说白了就是,她喜欢上了一个男人,而这个男人却让她独自抚养孩子。”
研究人员指出,男人通常对女人有长期相处的兴趣才会送给她们贵重的礼物。而女孩子通常不会对于太廉价的礼物感兴趣。男人可以送给女士昂贵但又没什么用处的礼物,例如,晚餐或者戏票等,这样即使女士拒绝了邀请,男士也没什么损失。女孩子如果发现这个男人没什么魅力,通常也不会接受他的邀请,因为那样就意味着跟一个她不喜欢的人一起浪费时间。Sozou表示,“在另外一种情况下,对于女士来说决定性的因素就是她是否处于性敏感阶段,以及这个男人是否具有较高的社会地位。男人赠送给女士的礼物就包含了能够反映他的社会地位的信息。通常一个社会地位低下的人不可能送给女士十分贵重的礼物。”
研究人员根据以男士是否得到父母的关爱为基础的不同生物学假设设计了这个游戏的两个不同版本。其中引人注意的是人类的求爱,以及男士的社会地位和女士的易于接受成为没有父母关爱情况下的决定性因素。无论在哪种游戏中都包含有二元变量。在游戏中,通过男士和女士是否觉得对方具有魅力这样的要素就可以推测这种交互作用的可能性或者可能的结果。对于每个游戏参与者来说,无论这些要素是积极的还是消极的,都会被记录下来,并且反映在针对他们的决定结果的评分之中。
Seymour说:“我们假设,如果一个男人希望与某个女人仅保持短暂关系的想法是一个积极的因素。但是,如果他发现这个女人具有一定的魅力,值得他多呆一段时间的话,这种积极因素就更进了一步。所以我们就给了他一个高分。”“相反,如果他认为这个女人毫无魅力可言,他刚才的付钱走人行为就因为遗弃而被加重,只能给他比较低的分数。”“这些情节被通过数学的形式表现出来并且加以分析,从而发现每个游戏参与者的最佳策略。”
他们通过研究得出了有关男女之间求爱的“合理”的逻辑。无论生物学假设有何不同,这两个模型具有相同的数学基础结构,同样都推导出相同的结果:男人流行赠送那些贵重但又无用的礼物作为求爱的前奏。Seymour补充说:“通过我们的分析显示,在‘男人烧钱以取悦女孩子’方面,也出现了一些逻辑上的进化发展。”
17652那是不是代表钱是万能的!
17653《九章算术》20年的赴法之旅
“前不久我发现报纸上一个误译:译者把‘南京市长江大桥’,译成了‘南京市长——江大桥’(误以为南京市长姓江,名大桥)”。7月30日,在法国大使馆内举行的《九章算术》中法对照本出版新闻发布会上,席泽宗院士举了一个社会上误译的例子,引起会场上一阵会心的笑声。
席泽宗先生在做科普工作以前,曾搞过几年的翻译工作,因此他很关注翻译工作,也对之有一定的了解。席泽宗认为翻译工作很见功夫,而把古典著作译成外文就更加不易。由于古今思维方式和语法的不同,同一术语古今有不同的含义,古籍版本、标点、错字错句的校勘等问题,要想忠实于原文进行翻译,必须把原书的面貌和内涵搞清。“《九章算术》在这次法文版出版之前,虽然已经有了德、俄、英、日四种文字的译本,但有的只译了《九章算术》的本文,省略了极其重要的刘徽注;有的不考虑版本问题,不校正错误,就根据自己的理解去译,翻译质量可想而知。”
“自
1774年戴震整理《九章算术》以来,《九》的版本十分混乱,错校极其严重”,席泽宗院士说,“郭书春清理了版本演变过程,对全书进行了全面细致的校勘,共写出校勘记
1900余条,从而提出了一部比较准确的《九章算术》底本。此次的法文译本是在郭书春先生(译者之一)20多年研究基础上,他发表了大量关于《九章算术》的学术论文,出版过现代汉语译本和《汇校<九章算术>》等著作才着手译的,可以说水到渠成。”
提起《九章算术》中法对照本的出版过程,郭书春感慨到:“20年零两个月过去了,翻译工作终于完成了,当年我还是年富力强,如今已年逾花甲;林力娜也从一个小姑娘,一晃步入了中年。”
1981年4月,法国女子高师数学系毕业生Kanine
Chemla(中文名为林力娜)来中国科学院自然科学史研究所,师从郭书春学习中国数学史。当时郭书春主攻《九章算术》及其刘徽注已经三四年,基本上弄通了其数学内容,并开始对它的版本和校勘进行深入的研究。《九章算术》是中国古代最重要的数学经典,但国内外学术界对刘徽知之甚少,李约瑟的《中国科学技术史·数学》谈到刘徽的地方还不如杨辉多;美国权威的《科学家传记大辞典》中“刘徽”的释文是一位国际上颇负盛名的中国科学史家写的,实际上是讲的《九章算术》的成就,刘徽本人的成就基本上没有讲,郭书春深感有让国内外认识刘徽的必要。
在郭书春的悉心教导下,林力娜对中国数学史,对《九章算术》及刘徽注有了相当程度的了解。在她结束学习前夕,郭书春建议,在她回国获得博士学位后能够合作翻译《九章算术》及其刘徽注,林力娜欣然同意。林力娜回国获博士学位并进入法国CNRS(国家科学研究中心)工作后。他们获悉,中国科学院和法国CNRS有科学交流合作协议,遂分别向中国科学院和法国CNRS提出合作研究翻译《九章算术》的申请,希望纳入两家的科学合作协议。
1983年,中科院国际合作局与法国CNRS批准立项。从
1984年6月至2004年10月,林力娜三次来华,郭书春数次赴法,切磋琢磨,几易其稿,终于将其付梓。
“这次中法对照本的重要成就是对刘徽注的准确翻译,”吴文俊院士说,“译《九章算术》不译刘徽注等于没有译。”吴院士介绍说,中国由于十进位位值制的发明,使古代数学得到蓬勃发展,超越了其他地区。秦汉之际(公元前2世纪)根据前人成就总结成的《九章算术》和三国(公元3世纪)时刘徽的《九章注》,使中国的算术(即数学)达到高峰。《九章算术》与刘徽注本所代表的中国古代数学与古希腊数学家欧几里德的《几何原本》,成为途径方法大不相同而东西辉映的两大数学体系,欧几里德和刘徽则成为古代东西方两大数学代表人物。在西方《几何原本》与欧几里德妇孺皆知,而数学成就与之相当的《九章算术》却由于中国古文艰涩而鲜为人知。现在由这两位将其译成法文,将使刘徽的成就为异域所理解,并可以推动数学结合东西方优势而蓬勃发展。”
法国科研中心科学史与科学哲学研究所研究员、法国科学史与科学哲学学会委员Sinaceur教授说:“林力娜女士对《九章算术》特定数学语言的翻译问题做了大量工作。建立在案例分析的基础上做出了一个非常详尽的词汇表。比如为了用法语解释清汉语‘意’和‘义’两词,林女士写了6页的篇幅来从语法、语境上进行分析,并给出确切的涵义。”
《九章算术》中法对照本在法国出版后,得到一致好评,第一版印了800册已经售罄。2004年12月31日,法国Kahane院士给吴文俊院士来信,建议与吴先生联合发起一个关于中法对照本《九章算术》的发布会,作为法国文化年的一项活动,吴先生欣然同意。法国CNRS领导也致信中国科学院路甬祥院长,希望得到中国科学院的支持。在多方努力下,2005年7月30日,《九章算术》中法对照本出版新闻发布会在中法文化交流中心召开。会上,法国驻华公使衔参赞郁白先生说:“《九章算术》取得了很高的成就,里面有系统的数学观念,也揭示了法国数学来源的多元性。两位学者历时20多年完成的这部中法文对照本,在中法文化交流和科学合作方面做出了重要贡献。”
(《九章算术》中法文对照本,2004年11月第一版,郭书春、林力娜译,法国DUNOD出版社出版。)
摘自2005年8月4日《科学时报》
1765410年:谱写中国数学史
转自 科学网 (2005-05-26
17:01:54)
历时10余年,厚厚10卷本的《中国数学史大系》去年终于出齐了。这套由吴文俊院士主编的大书,是我国第一部大型多卷本中国数学史专著。全书正卷8卷,按时间顺序论述自远古至清末中国数学发展的历史;副卷2卷,汇集早期外国数学史料和中国算学书目。
对中国数学的一次全面系统总结
中国传统数学源远流长,有其自身特有的思想体系与发展途径,从远古以至宋、元,一直是世界数学发展的主流,但自明代以来,由于政治社会等种种原因,中国传统数学开post-52-1125823553.ibf
17655八卦也要八卦得有点水准吧?拿起直尺圆规研究正十七边形作法,还当场画出来?这只不过是无知之辈的想法而已。
17655好文章
17655一夜解开千年数学难题
转自 数学时空
1796年的一天,德国哥廷根大学,一个
19岁的青年吃完晚饭,开始做导师单独布置给他的每天例行的3道数学题。
青年很有数学天赋,因此,导师对他寄予厚望,每天多给他布置2道较难的数学题作为训练。正常情况下,青年总是在2个小时内完成这项特殊作业。
“咦,怎么今天导师给我多布置了一道?”青年一边打开写着题目的纸,一边嘟哝着。他也没有多想,就做了起来。
像往常一样,前2道题目在2个小时内顺利地完成了。第三道题写在一张小纸条上,是要求只用圆规和一把没有刻度的直尺作出正
17边形。青年没有在意,像做前两道题一样开始做起来。然而,做着做着,青年感到越来越吃力。开始,他还想,也许导师见我每天的题目都做得很顺利,这次特意给我增加难度吧。但是,随着时间一分一秒地过去了,第三道题竟毫无进展。青年绞尽脑汁,也想不出现有的数学知识对解开这道题有什么帮助。
困难激起了青年的斗志:我一定要把它做出来!他拿起圆规和直尺,在纸上画着,尝试着用一些超常规的思路去解这道题……
终于,当窗口露出一丝曙光时,青年长舒了一口气,他终于做出了这道难题!
见到导师时,青年感到有些内疚和自责。他对导师说:“您给我布置的第三道题我做了整整一个通宵,我辜负了您对我的栽培……”
导师接过青年的作业一看,当即惊呆了。他用颤抖的声音对青年说:“这真是你自己做出来的?”青年有些疑惑地看着激动不已的导师,回答道:“当然,但是,我很笨,竟然花了整整一个通宵才做出来。”导师请青年坐下,取出圆规和直尺,在书桌上铺开纸,叫青年当着他的面做一个正
17边形。
青年很快地做出了一个正
17边形。导师激动地对青年说:“你知不知道,你解开了一道有两千多年历史的数学悬案?阿基米德没有解出来,牛顿也没有解出来,你竟然一个晚上就解出来了!你真是天才!我最近正在研究这道难题,昨天给你布置题目时,不小心把写有这个题目的小纸条夹在了给你的题目里。”
多年以后,这个青年回忆起这一幕时,总是说:“如果有人告诉我,这是一道有两千多年历史的数学难题,我不可能在一个晚上解决它。”
这个青年就是数学王子高斯。
有些事情,在不清楚它到底有多难时,我们往往能够做得更好,这就是人们常说的无知者无畏。
17655数学天才――高斯(Gauss)
高斯(C.F.Gauss,
1777.4.30-
1855.2.23)是德国数学家、物理学家和天文学家,出生于德国布伦兹维克的一个贫苦家庭。父亲格尔恰尔德•迪德里赫先后当过护堤工、泥瓦匠和园丁,第一个妻子和他生活了10多年后因病去世,没有为他留下孩子。迪德里赫后来娶了罗捷雅,第二年他们的孩子高斯出生了,这是他们唯一的孩子。父亲对高斯要求极为严厉,甚至有些过份,常常喜欢凭自己的经验为年幼的高斯规划人生。高斯尊重他的父亲,并且秉承了其父诚实、谨慎的性格。
1806年迪德里赫逝世,此时高斯已经做出了许多划时代的成就。
在成长过程中,幼年的高斯主要是力于母亲和舅舅。高斯的外祖父是一位石匠,30岁那年死于肺结核,留下了两个孩子:高斯的母亲罗捷雅、舅舅弗利德里希(Friederich)。弗利德里希富有智慧,为人热情而又聪明能干投身于纺织贸易颇有成就。他发现姐姐的儿子聪明伶利,因此他就把一部分精力花在这位小天才身上,用生动活泼的方式开发高斯的智力。若干年后,已成年并成就显赫的高斯回想起舅舅为他所做的一切,深感对他成才之重要,他想到舅舅多产的思想,不无伤感地说,舅舅去世使"我们失去了一位天才"。正是由于弗利德里希慧眼识英才,经常劝导姐夫让孩子向学者方面发展,才使得高斯没有成为园丁或者泥瓦匠。
在数学史上,很少有人象高斯一样很幸运地有一位鼎力支持他成才的母亲。罗捷雅直到34岁才出嫁,生下高斯时已有35岁了。他性格坚强、聪明贤慧、富有幽默感。高斯一生下来,就对一切现象和事物十分好奇,而且决心弄个水落石出,这已经超出了一个孩子能被许可的范围。当丈夫为此训斥孩子时,他总是支持高斯,坚决反对顽固的丈夫想把儿子变得跟他一样无知。
罗捷雅真诚地希望儿子能干出一番伟大的事业,对高斯的才华极为珍视。然而,他也不敢轻易地让儿子投入当时尚不能养家糊口的数学研究中。在高斯
19岁那年,尽管他已做出了许多伟大的数学成就,但她仍向数学界的朋友W.波尔约(W.Bolyai,非欧几何创立者之一J.波尔约之父)问道:高斯将来会有出息吗?W.波尔
17655除了敬佩,还有什么话说呢!!!
17655
| 引用 (dreams @ 2005年09月06日
00时00分) |
|
八卦也要八卦得有点水准吧?拿起直尺圆规研究正十七边形作法,还当场画出来?这只不过是无知之辈的想法而已。
|
可能是我比较无知,但是这个论坛里就有高斯正
17边型解法。
我没仔细看,但应该使用尺规作出的图形。
17655事实是,高斯用了至少一年来想这个问题,在法国数学家的基础上用了很复杂的方法证的阿!
17655有点神,呵呵
17655前年一遇的天才
17655有意思
17655人才
17655我记得高斯解这个问题不是去画它,它的本质是解一个二项方程,方程总是可解,但做图的可能性取决于次数的性质
并且他的导师看到解答后不是说他是天才,而是不相信他
17655就是就是哈
17655那个故事应该是编出来的,事实上,高斯也只是证明正
17边形
“可以”尺规作出来,但严格的做法,是另外一个小青年作出来的,n长n长的一篇文章。。。。而且,和一般的看法相反,作出正
17边形可能还比较简单,但要说明作出的
17边形确实是正
17边形(也就是证明)却相当麻烦,他的老师也不可能一下子就看出来他的做法是对的,并认为解决了2000年的难题云云~~~
http://mathworld.wolfram.com/Heptadecagon.html
Gauss proved in
1796 (when he was
19 years old) that the heptadecagon is
constructible with a compass and straightedge. Gauss's proof appears
in his monumental work Disquisitiones Arithmeticae. The proof relies on
the property of irreducible polynomial equations that roots composed of a
finite number of square root extractions only exist when the order of the
equation is a product of the form , where the are distinct primes of the
form
(1)
known as Fermat primes. Constructions for the
regular triangle (), square (), pentagon (), hexagon (), etc., had been
given by Euclid , but constructions based on the Fermat primes were
unknown to the ancients.
The first
explicit construction of a heptadecagon was given by Erchinger in about
1800
17655可以画出来的,我知道那是几个根号相套的表达式,只是要想清楚地画好,现实中不好找到那么大的纸,也没那么大的圆规和直尺。但是真的可以画出的,要是谁有几米大的.......
17655好早听过这个故事,听起来挺神的!不过总不是胡乱说的吧!我也相信高斯有那个能力。
佩服!!!
17655越传越神.
17655不管故事是不是编的,他都是天才
17656奥数编写者自编却无力自答
转自
解放网-新闻晨报
奥数教辅编写者“自编”却无力“自答”,难度不仅大大超过了学生的能力,也超过了编写老师的能力。昨天,由政府出面,历时数月的上海市中小学教辅读物问题调查情况正式对外发布,其中小学奥数编写者成为矛头所指。
据悉,在此次抽样调查的
185本数学教辅中,奥数竞赛类教辅多达97本,占52.4%。调查显示,奥数教辅书数量之所以如此之大,是由于许多编写者抄来抄去,“复写本”大量充斥市场。
此外,难度严重超标也成为目前小学奥数教辅读物的另一大问题。“很多小学奥数教辅中题目难度之大,连数学系的大学生都解不出来!”由于目前很多奥数教辅题目都是直接从高等数学中“截取”出来,难度不亚于大学数学测试,并不符合奥数竞赛的思考方法和小学生的认知规律,因此不仅误导学生,也变相加重学生负担。
“奥数教辅编写者很多只是执教一两年的年轻教师,对究竟何谓‘奥数’并不清楚,甚至奉行‘天下文章一大抄’”。在昨天的发布会现场,许多调研人员在接受记者采访时表示,奥数教辅市场鱼龙混杂的背后,是因为现在市场上奥数教辅编写者大量“不合格”。
小学数学教辅读物调查的负责人之一,上海江五小学副校长陈惠珍表示,目前有资格编写奥数教辅的人还在少数,奥数的出题者起码应该有10年以上的带教经验,经过相关的奥林匹克竞赛的培训考核,对奥数比赛有深度了解。“但是目前很多奥数教辅中的题目,是出题者自己都做不来的”。她告诉记者,在她所认识的很多奥数教辅编写“圈内人”都是执教仅一两年的年轻教师,或者从来没有指导过奥数竞赛,对奥数题型甚至一无所知,这就导致了编书过程中往往生搬硬造,很多题目本身存在错误,“无解”或者“根本是无法解”。
但记者了解到,尽管目前沪上小学奥数教辅市场问题重重,可奥数竞赛类教辅仍然热销,特别是小学奥数在语数外主科中异军突起,占到小学数学教辅读物数量的五成以上,此外教辅分布也开始向1、2年级过渡。
盛行的中小学教辅读物质量令人担忧。据了解,此次历时半年以上的调查组织了30余位中小学优秀教师和教研人员,花了数万元从市场上收集了1500余本中小学教辅读物。而市教委教研室公布的调查结果显示,目前的中小学教辅读物从封面到内容、从印刷到发行存在八大问题。
■ 封面自命“灵验”,引诱读者不少教辅书名起得相当巧妙,打出“考试高分,新招高招”或者“名校教师联手打造”的旗号,内容却名不副实。
■ 前言公然鼓吹“应试教育”有些教辅前言里要求学生要“反复演练”,一套题目要做几轮才达到效果,考出高分。
■
作者虚名假名,抬高身价目前有许多教辅编写者不用真名,在虚假姓名的“掩护”下自称是“高考命题组专家”,或者“二期课改编写者”,其实不然。
■
暴利定价,增加负担某语文教辅定价94元,某数学教辅定价
173元。有关专家指出,如此定价完全不合理。
■
习题超标离本,繁难偏旧举某本语文教辅为例,在新课标中已经杜绝概念性的知识在试卷中出现,但是该教辅依然搜罗了语音、字型等选择类、填空类题目1000多道,与新课标完全脱节。
■ 内容重复抄袭、差错屡出教辅互相抄袭现象严重,加上质量低下,导致错误流传。
■ 印刷粗制滥造,质量低下字体太小,纸张质量太差。
■ 发行渠道杂乱,花样百出有的书商甚至直接找到学校的各个教研室,进行回扣交易。
17656这些人简直就是在胡闹
17656这种事情很普遍,不仅是奥数了,我就有师妹师弟去编过什么辅导材料,都是抄
17656唉!!堕落啊
17656瞎搞
17656胡闹 我们口口声声说学老大哥(虽然是过去的事) 为什么老大哥那套全民数学的优良传统倒是没引过来 倒成了南橘北枳
17656我本身是一个高中教师,我很有体会,很少有好的资料,现在都是一骗钱为目的的
17656
| 引用 (pgs @ 2005年11月22日
13时20分) |
| 这些人简直就是在胡闹
|
这些人简直就是在胡闹
17656小学生苦啊~~~~~
17656
| 引用 (VIOSKY @ 2006年03月20日
16时51分) |
| 引用 (pgs @ 2005年11月22日
13时20分) | | 这些人简直就是在胡闹
|
这些人简直就是在胡闹
|
这些人完全是在胡闹
17656 我就是这样一个编辑。一本本劣质教辅经我手出版,个人力量太渺小,无法扭转局面,为自己痛苦,为学生痛苦,更为社会悲哀!
17656
| 引用 (柳林风生 @ 2006年12月28日
16时20分) |
| 我就是这样一个编辑。一本本劣质教辅经我手出版,个人力量太渺小,无法扭转局面,为自己痛苦,为学生痛苦,更为社会悲哀!
|
不要幹了..良心比較重要...
可以多編其它有益的書, 或者匿名投報有關此事, 既然匿名
多加渲染, 至少可以使編寫水準受到顧客的公正挑選, 不要讓家長把錢花在購買虛榮心份上,
=======================================
一念之差
也是善 也是惡
=======================================
17656
引用 (Quillen @ 2007年01月01日
19时59分) |
| 引用 (柳林风生 @ 2006年12月28日
16时20分) | | 我就是这样一个编辑。一本本劣质教辅经我手出版,个人力量太渺小,无法扭转局面,为自己痛苦,为学生痛苦,更为社会悲哀!
|
不要幹了..良心比較重要...
可以多編其它有益的書,
或者匿名投報有關此事, 既然匿名 多加渲染, 至少可以使編寫水準受到顧客的公正挑選, 不要讓家長把錢花在購買虛榮心份上,
=======================================
一念之差
也是善 也是惡
=======================================
|
整个社会都是这个风气,不在这家干,换一家也好不到哪去,经济学上这算是劣币驱逐良币吧——柳林兄也得养家糊口的说。
17656胡闹
令人发指
17656最胡闹的还不是那些胡编的人,而是培养这些人的土壤。
17656
| 引用 (潮音海岸 @ 2007年01月04日
15时42分) |
|
整个社会都是这个风气,不在这家干,换一家也好不到哪去,经济学上这算是劣币驱逐良币吧——柳林兄也得养家糊口的说。
|
知音人啊!人是要生活在社会中的.至少可以让经自己之手的书籍有一点好的变化!
17657丘成桐:为中国培养一流数学人才
据《人民日报海外版》
何雁
现年56岁的丘成桐被公认为“近1/4世纪里最有影响的数学家之一”,他29岁攻克微分几何难题“卡比拉猜想”,轰动国际数学界,因此获得
1982年数学界最高荣誉奖———菲尔兹奖,成为迄今唯一获得该奖的华人。
如今,丘成桐身居海外,却十分关注中国数学事业的发展,“我一生最大的愿望是帮助中国强大起来。”
1979年,30岁的丘成桐应华罗庚邀请第一次回国访问。此后,他不断支持中国的数学研究,在中国先后创建香港中文大学数学所、北京晨兴数学中心、浙江大学数学中心,并出任这3家研究机构负责人。至今,丘成桐培养的50多名博士大部分是中国人,其中一些人回国后成为中国数学的领军人物。
要培养一流人才,研究经费是大问题。为了募集经费,丘成桐四处奔波,用科学家宝贵的研究时间做本来最不屑的应酬。在他的游说下,李嘉诚、郭鹤年、陈启宗等香港企业家先后共募集资金逾一亿元人民币;而他自己在中国任职不收分文报酬,往返飞机票等差旅费都是自己掏腰包。
丘成桐个人生活十分俭朴,可为了培养中国数学新人,他向浙大数学中心一次就捐赠价值50万美元的图书,还在浙大、中国科大设立丘成桐奖学金。他发起召开世界华人数学家大会,该大会自
1998年起已连续举办三届,会议专门设立晨兴数学奖,以奖励45岁以下取得杰出成就的华人数学家。
中国是数学大国,但数学大国不等于数学强国。“中国离数学强国还有相当距离。”丘成桐直言不讳,“这个距离是创新研究的距离,不是考试的距离。”
17658数学心理学
转自 数学中国
数学心理学是应用数学模型来描述心理现象的心理学分支。德国心理学家费希纳在
1860年的心理物理学研究中,最早用数学公式表达了客观物理量和主观感觉强度之间的函数关系。
1927年瑟斯顿在制定心理量表时提出了比较判断率,并用公式来表明两个刺激间的主观距离。这些工作都属于数学心理学的范畴。但是,当时这类工作为数不多,也比较分散,还没有数学心理学之称。第二次世界大战后,由于信息论、控制论、统计决策论及计算机科学的推动,数学心理学才得到真正的发展。20世纪50年代初,埃斯蒂斯、布什和莫斯蒂勒提出的学习模型,是这一新方向的开端。目前实验心理学的许多重要领域,如测量、决策、学习和社会的相互作用等方面,都已制定出大量的数学模型。
一般说来,数学模型的建立,首先是把需要研究的心理现象,如知觉、学习
、决策等等,从复杂的心理活动中分离出来,构成一个特定的集合,把原始资料加工成集合中的客体和关系。然后用代数的、几何的、概率的、公理的形式,或者是计算机程序和方程式的形式,把它们表现出来。在这里,主要的问题是确定研究领域的经验系统
,和表达它的形式系统之间的对应关系。在数学模型建立之后,通过逻辑推理或数学运算可以推导出一定的结果。如果给模型以一定的解释,所推出的结果就可以看作是对经验系统的某种预测。进一步将预测值与实际测试值加以比较,依据二者的符合程度,还可以对数学模型加以修正。用数学模型描述心理现象,其优越性不仅是它比自然语言的描述具有更大的概括性、准确性、演绎力和预测力,更重要的是它便于计算机的模拟,为人工智能的发展创造了条件。
17659挽救陈省身数学奖获得者席南华生命的“生死时速”
远在美国访问的席南华突然被疾病击倒,中国科学院数学与系统科学研究院立即展开救援,在中美两国间“上演”了一场:挽救数学家生命的“生死时速”。
对数学家席南华和他妻子小刘来说,2005年4月16日是一个刻骨铭心的日子。就在这一天,一场悄然而至的疾病突然间改变了他们的生活。3个多月以后的7月31日,席南华在接受记者采访时说:“我还清楚地记得那一天的情景,病来得太突然、太意外了。”
席南华是中国科学院数学与系统科学研究院数学研究所的研究员,我国代数群和量子群研究领域的领头人之一、国家杰出青年科学基金的首批获得者。今年1月,应美国弗吉尼亚大学教授伦纳德·斯科特的邀请,他作为访问教授到该大学访问半年。
疾病突然袭来
4月16日是一个星期六,席南华感到有些疲倦,他想自己可能是太累了,因此还是决定到超市将一周的用品买回家。早晨7点过,他和朋友开车去超市,在路上他觉得越来越没有劲,到超市时都没有下车,朋友帮忙将东西买回,到家时,他觉得呼吸很困难,不能走路了,但他认为也许是感冒了,不要紧,于是就躺在家休息。可是,下午5点多,他发现自己呼吸已严重困难,于是拨通了急救电话“911”。救护车将席南华送到了弗吉尼亚大学医学院附属医院的急诊室,紧急抢救一直持续到晚上10点多。
由于有12小时的时差,弗吉尼亚的夜晚正好是北京的白天。4月
17日早上10点多,小刘在北京的家中接到一个电话,这是一个来自美国的长途电话,弗吉尼亚大学医学院附属医院的医生告诉她,她丈夫席南华呼吸困难,肺部严重感染,正在急诊室抢救,需要做手术,请她立即到美国。小刘万般着急,但她认为丈夫可能是劳累过度生病,做了手术就好了,当务之急是尽快获得签证到美国去照顾他。
小刘4月
18日早晨上班,她将情况向部门领导反映,并请求科学院帮助她尽快获得签证,中科院高技术局领导和国际合作局领导给予了极大的帮助。4月
19日上午10:30,她在美国驻北京大使馆获得签证,下午2:30便登了飞往美国的飞机。
小刘于当地时间4月
19日深夜11点抵达弗吉尼亚,随即赶往医院,她看见病床上的丈夫全身插满了各种管子,呼吸困难,说一句话要费力地喘几口气。当时的诊断是:右肺积水,左肺感染,呼吸困难,而且肺部有气孔。考虑到席南华曾经患过肝炎,医生说还需要做进一步的全身检查。
4月21日下午,医生在病房中向席南华夫妇讲述了诊断结果:严重肝硬化、肝部肝癌早期,右肺积水、左肺感染。小刘说:“当时我们俩人都没有讲话,我惊呆了,万万没想到是这样的结果。”医生说惟一的救治方法是做肝移植,并建议他们回中国治疗,因为在美国肝源非常紧张,做肝移植手术需要等1~2年的时间,席南华的病情不容等待。
小刘对肝癌和肝移植一无所知,她恳求主治的美国医生到中国去为丈夫做手术。医生对她说:“中国医生做肝脏移植手术的经验已很丰富,成功率很高,而且中国的肝源要丰富一些,更有利于席南华的治疗。”
医生还安慰她说,自己的一位美籍华人朋友也是医生,去年到广西做肝脏移植手术,两个月后回美国,现在状况还不错,也许可以和他谈谈。小刘当天晚上和这位美籍华人医生在电话里谈了两个多小时,从他那里得知国内肝脏移植的情况,以及应该如何努力。肝脏移植手术的选择非常重要,直接关系到移植的成功与否,肝脏移植得越早,今后的复发率越低。她决定立即与国内联络,回国治疗。
成立紧急救助小组
4月22日早晨8点左右,中国科学院数学与系统科学研究院数学研究所副所长尚在久刚到办公室,电话铃就响起来,小刘在电话里告诉他:席南华因呼吸严重困难住院,后诊断为肝硬化和肝癌,病情严重,希望能尽快回国做肝移植手术。尚在久感到非常震惊,觉得事情严重,问她是否需要什么帮助。小刘说,在美国暂时不需要,美国的教授对他们照顾得非常周到,请所里在国内帮助联络可做手术的医院。尚在久立即将情况向数学与系统科学研究院党委书记王跃飞汇报。
得知消息,王跃飞十分心痛,他曾担任数学所所长,深知席南华的价值。席南华是国内在代数领域做得最好的几个人之一。
1988年他在华东师范大学获得数学博士学位后来到数学所做博士后,因研究水平很高,在博士后期间就应邀到美国加州伯克利数学研究所访问。
1990年留在数学所工作,同时接到美国普林斯顿大学、德国马普数学研究所和法国高等研究中心的邀请,他在3年的时间里分别访问了这3个世界著名的数学研究所。多位国际著名同行专家对他的工作都有很高的评价,但他在国内默默无闻,因为他从不自动申请经费、申报奖项,15年间只发表了
18篇论文。他痴迷数学,对数学问题有很好的品味,从不在乎外部环境的影响。王跃飞说:“我们拼命也要救他。”
研究院高度重视席南华的病情,立即成立了紧急救助小组,王跃飞任组长,陈敏(研究院副院长)和尚在久任副组长,院办公室主任、医务室主任、物业中心主任等任成员,救助小组成员杨志凌和张洪云分别负责联系医院、机场接机和救护等事宜。王跃飞要求小组成员24小时待命,手机24小时开机。他和尚在久保持与小刘联络,随时了解席南华的情况。他说:“最重要的是做好各种应急准备,让他尽早顺利回国接受手术。”
研究院办公室的杨志凌女士负责联系到了武警总医院,但医院按规定是需要事先看病历和体检后才决定是否住院,杨志凌苦口婆心向院方解释:这是一位非常重要的数学家,国家培养这样一个人才很不容易,他在国外病情危急,回国后需要直接住院。院方被她的话感动,破格决定在没有病历、未做检查的情况下接收席南华入院,并做好了手术的准备。
小刘救夫心切,得知国内进展后决定立即回国,她买了当地时间4月26日清晨6:00的美联航票,并告诉了王跃飞回国的时间:北京时间27日下午2:30。王跃飞立即召集紧急救助小组开会,布置方案,在27日当天兵分两路,一路负责机场与医院的协调,一路直接进入机场停机坪内接人,还有两位同志专门照顾孩子和提取行李。
一切准备就绪,只等席南华归来,但情况突然发生了变化。
情况突然变化
4月26日午夜,睡梦中的尚在久被电话铃声惊醒,小刘在电话中用近乎绝望的声音告诉他,他们不能回来了,因为考虑到席南华呼吸还未正常,美方的3人治疗小组中有2位医生同意他上飞机,但有1位医生不同意,没有院方的证明,航空公司不让他们上飞机。尚在久感到小刘的焦急和无助,也知道手术时间对于席南华生命的价值,而自己却远隔重洋不能伸出援助之手,怎么办呢?情急之中,他想起了中国驻美国大使馆,看能否请他们联络中国民航帮助席南华回国。他立即起身以个人的名义给中国驻美国大使周文重写了一封信。
尚在久向周文重介绍了席南华的病情和乘坐民航飞机受限的情况,他说:“我恳请您是否能够指示有关部门和人员尽快与患者家属、Virginia大学和美国医院取得联系,了解患者的具体困难,给予患者和家属适当的关心,并且提供一些力所能及的帮助;我恳切希望您和驻美使馆能够给予患者及其家属来自祖国的关心和帮助。我们能够想象远隔重洋的患者和家属目前该是如何的焦虑无助。我们单位尽一切可能安排好他们回国后的所有事宜,他们在美期间的有关事宜希望得到您和使馆同胞的关心和帮助。”
他在信中留下自己的办公室和家里的电话以及手机号,4月27日一早通过传真将信发至位于纽约的中国驻美国大使馆。
这天一早,王跃飞与尚在久讨论后,向科学院院部汇报了这一情况,并请求帮助席南华尽快回国。
各方伸出援助之手
美国的医生认为必须控制肺部感染后才能让席南华上飞机。小刘盼望丈夫尽早回国做手术,急得和主治医生争执起来,医生理解她的心情,并和美国肯尼迪航空中心的医生联系,询问如何处理宇航员在空中呼吸受窘的问题。
4月28日,尚在久接到了中国驻美国大使馆教育处给他的传真信,信中写道:
“4月26日您给周文重大使的传真悉。关于你所青年科学家席南华在美国弗吉尼亚患病事宜,我们正全力以赴帮助病人及其家属安排尽快回国。
“周文重大使对席南华罹患重病极为关心,根据周大使的指示,我处公使衔参赞刘川生和管片干部于第二天(27日)专程赴弗吉尼亚看望了席南华研究员,并向病人及其家属转达了周大使的慰问。
“现病人已经出院回到住处休养。根据弗吉尼大学医学院附属医院的出院嘱咐,要求病人休整一周之后,根据复查结果,方可旅行,以确保病人旅途安全。病人家属认为目前病情稳定,已计划于5月4日启程,乘坐中国国际航空公司的班机回国,大学也决定派一名护士随机护理。
“刘川生公参亲自与中国国际航空公司驻纽约分公司总经理联系,介绍情况。民航获悉情况后非常重视,表示一旦病人允许长途旅行,民航会安排机组予以照料。
“我们将继续关注事态进展,直到席南华安全登机离境。”
这天,科学院办公厅也来电话,表示如果确实需要,院部可以与中国民航联系,安排席南华乘坐国航班机尽快回国。
使馆工作人员的看望和帮助给了小刘极大的安慰,她的心略为平静了,开始仔细考虑回国的细节。因为中国国际航空公司到北京的飞机是从纽约起飞,搭乘国航的飞机需要先从弗吉尼亚经10多个小时的陆上交通到纽约,这对病人是不利的,她最后还是决定搭乘美联航的飞机从华盛顿回国。
这时快到“五一”长假期了,王跃飞要求急救人小组的成员一刻不能放松,“五一”期间不可外出,随时待命。他说,那段时间打美国的长途电话就像打市话一样,在家里、办公室随时有情况就打电话。小刘所在单位的领导和中国科学院院部也给予了极大的支持,科学院为出据各种所需证明大开绿灯。
一切都是为了保证病人的安全,每个细节都考虑到了,不能出一点点差错。
“手术非常成功”
5月5日下午2:30,席南华乘坐的班机平稳降落在首都国际机场。在机舱出口处,当周向宇(数学所所长)和尚在久等人看到坐着轮椅出来的席南华时,都拥上前去问候,终于回来了——两周来大家悬着的心也落了地。但是看到席南华虚弱的样子和有些走形的脸庞,大家都不禁难过得要流泪。机场事先安排好的救护车直接将席南华送到了武警总医院,杨志凌早已等候在那里,并安排好了有关住院的所有事宜。
检查结果显示,席南华适合接受肝脏移植手术,待体力恢复并有适合的肝源后即可做手术。医生护士精心地照料他,席南华对治疗满怀信心。在席南华救治期间,研究院和数学所领导数次前往医院探望,王跃飞说:“他在病床上还很乐观,相信自己的病一定能治好,还在给我们谈病好以后做什么样的数学问题的事。”按照计划,席南华负责于六七月份在晨兴数学中心举办一个学术活动,邀请了几位国际著名数学家来华讲学,为使活动能够继续顺利开展,他把这项工作托付给数学所徐晓平和潘建中两位研究员具体负责,在病床上多次就有关问题进行讨论。周向宇告诉他,所里会把这项工作安排好的,请他安心养病。尚在久对席南华说:“你千万不要再想数学的事了,肝病需要好好休息,养好身体是最重要的。”
小刘又面临新的压力。肝脏移植手术费一般在30万元左右,术后病人需要终身服用昂贵的药物,而所有的费用都是自费的。王跃飞安慰她说:“不要担心费用的问题,我们会尽一切可能、想尽一切办法帮助您们。”研究院院领导班子十分关心席南华的病情与救治,院长郭雷院士为此专门召开院长特别会议,讨论席南华的问题,给予了尽可能的帮助,同时研究院还提出为席南华捐款,但被他婉拒,他说:“自己生病已给大家添了太多麻烦,费用的问题自己想办法解决。”
6月8日,武警总医院有中国“肝脏移植第一把刀”之称的沈中阳医生为席南华的手术主刀,手术持续了8个多小时。晚上11点,医护人员将昏迷中的席南华推出手术室,送往重症监护病房。手术成功了,但看着丈夫的模样,小刘说:“太痛苦了,我一个人木呆呆地在门诊大厅坐了半个多小时才回家。”第二天早晨6点一过,小刘就来医院等候丈夫苏醒的消息,早上8点半左右,护士告诉她:席南华醒了。
医生说,手术顺利完成只意味着完成了肝脏移植整个过程的一半,术后的治疗,同样对于是否能最后成功起着重要作用。而术后也要经过很多“关卡”,比如有些病人会出现排斥反应、感染等并发症。一般情况下,术后一个月,病人可以出院回家调养;三个月后基本可以恢复正常工作、适当参加体育运动,这样就可以认为肝脏移植完全成功。
7月6日,席南华回到家中休养,妻子每天为他护理伤口、监督他服药、给房间消毒两次。
冰冻三尺
非一日之寒
对席南华和认识他的人们来说,这场疾病来得确实太突然了。
冰冻三尺,非一日之寒。据武警总医院肝脏移植中心医生介绍,肝癌早期患者是没有任何感觉的,因为肝脏由癌变到出现临床症状之间需要约半年到一年的时间,所以早期的肝癌很难被发现。80%的肝癌患者出现自觉症状后才就诊,但这时病情已经到了晚期。当然,肝癌虽然是恶性度比较高的一种肿瘤,但早期发现可以彻底治愈。因此,定期体检是早期发现的一个有效方法,尤其是肝炎等肝脏疾病的患者,最好每三个月到医院进行一次有针对性的体检。
据称,目前还没有药物可彻底治愈肝炎,过度疲劳、精神压力过大均会加重病情。目前治疗包括肝癌在内的终末期肝病的惟一有效方法就是进行肝脏移植手术。
席南华说,自己早在10多年前被诊断患有乙肝,之后他一直非常注意治疗、饮食、锻炼和休息,也看了许多这方面的书籍,在北京最好的中西医院接受过治疗,也尝试过中药偏方。去年秋天,在去美国之前,他还专门到北京一家医院做肝脏B超检查,没有发现任何问题。仔细分析这次突然发病的原因,他认为是自己对这种疾病的认识有问题:自以为了解,也尽了努力,但实际上还是不清楚的,甚至有些错误的做法加重了病情。妻子则认为,丈夫用脑过度导致抵抗力下降、病情加重。
“不能失去他”
7月25日,第十届陈省身数学奖颁奖仪式在山东省威海市隆重举行,数学家席南华和段海豹获奖。颁奖词介绍:席南华从事代数群与量子群方面的研究,在这一领域取得了一系列优秀的成果。他对仿射A型Weyl群证明了Lusztig关于基环的猜想,是对代数群理论的重要贡献。他是一位杰出的青年数学家,其研究结果受到了国内外同行的关注与高度评价。
席南华的研究得到了国际数学界的承认。
1994年,他在德国施普林格(Springer-Verlag)出版社出版了一本长达137页的专著;2002年,他又在美国数学会出版了一本长达95页的专著。但从
1990年到目前为止,他只发表了
18篇论文。
尚在久说:“尽管席南华已经做出很多重要的工作,但对他来说,前面仍然有更重要的问题在等着他。他有很好的数学品味,从不在乎发表SCI论文,他认为做了重要的工作才写论文。”
从
1994年到2005年的10年间,席南华只申请了一笔经费,即国家杰出青年科学基金30万元的经费和科学院匹配的20万元,共50万元,以后就再没有写过申请书。妻子曾鼓励他申请中国科学院的“百人计划”,他说:“写这些东西太花时间了,不如将时间用在研究上。”他也从不主动申报奖项。
席南华说:“数学是我的乐趣和爱好,很高兴还可以成为谋生的手段。”他认为研究有两件事,一是做好的数学研究,就是要解决领域中现有的问题,或是提出新问题,开辟新的方向;二是带一批学生,让事业后继有人。他在学生身上花了很多精力,曾单独为自己的一名博士生开过两门课
2002年初,科学院在北京中关村为科学家们兴建了一批条件较好的住宅小区,数学所有几个名额,席南华有资格申请,这里的房子对他来说条件实在是太方便了:第一,小区距他的办公室步行只需10多分钟,而他现在从住家到办公室乘车至少需要半个多小时;第二,小孩即将上小学,小学与小区隔街相望,接送孩子非常方便。但他对妻子说:“我是所里最早有三居室住房的年轻人,所领导已经很照顾我了,现在还有不少研究员只有两居室的房子,我不能再申请了。”
尚在久说,席南华的工资其实并不高,但他觉得自己的生活已经很好了,住房也很好了,他从不与别人比较,也从不抱怨。席南华说:“我什么都不求,我只求数学,现在有这么宽松的环境,我很满意了。”
对王跃飞来说,从4月下旬到今天,救助席南华一直是他最重要的工作之一。谈到为什么要这样做时,王跃飞说:“国家培养这样一个杰出的人才不容易,人才是可遇而不可求的。席南华是我院代数学方面的学术带头人,一个学科就是由这几个厉害的人撑起来的,我们难以承受失去他的损失,我们拼命也要救他!”
转自《科学时报》
17659
向习南华和所有帮助的老师致敬!
17659伟大之中的平凡!
17660由中国运筹学会和中国科学院数学与系统科学研究院共同承办的第十一届国际计算和组合会议(The 11-th Annual
International Computing and Combinatorics
Conference,简称COCOON’05)于2005年8月16-
19日在昆明圆满结束。
COCOON是一个每年举办一次的,理论计算机科学方面的高水平的系列国际会议。该会议的规模一般在90左右人,会议的举办地基本上是亚太地区的几个国家或者地区轮流承担。会议的论文集由国际著名的斯普林格出版社作为非常有影响的计算科学系列丛书(Lecture
Notes in Computer
Science简称LNCS)中的一卷出版。COCOON’05的论文集作为LNCS的第3595卷已经正式出版(其中收录了96篇论文,投稿353篇)。
参加COCOON’05的国内外代表近100人,他们分别来自中国(包括香港和台湾)、以色列、意大利、德国、法国、美国、比利时、泰国、匈牙利、新加坡、埃及、日本、加拿大、西班牙、伊朗、捷克、波兰、瑞士、巴西、印度、韩国、澳大利亚和希腊。会议组织了三个大会报告,他们是L.
Valiant讲座教授(Division of Engineering and Applied Sciences, Harvard
University),A. Apostolico教授(Department of Computer Sciences, Purdue
University),Shanghua Teng教授(Department of Computer Science, Boston
University),和90多个分组报告。
COCOON系列会议在国内曾经先后成功地举办过三次,分别是于
1995年在西安,
1997年在上海,2001年在桂林。COCOON’05在国内的成功召开,必将进一步推动国内理论计算机学科的发展(清华大学计算机系图灵奖获得者姚期智教授参与指导的11名研究生也参加了本次的会议)。
COCOON’05的组委会主席是胡晓东研究员(中国运筹学会图论组合专业委员会主任委员,中国科学院数学与系统科学研究院图论、组合与网络研究中心主任),组委会成员包括刘德刚常务副秘书长和秘书胡洁。COCOON’05得到了中国科学院数学与系统科学研究院和中国科学院数学与系统科学研究院应用数学研究所的资助。
COCOON’05的组委会供稿
17661随机图论与网络研讨会在京召开
为期四天的(8月23-26日),由中国科学院数学与系统科学院图论组合网络研究中心与南开大学组合数学研究中心联合举办的随机图论与网络研讨会圆满结束。国内近150多名年青教师和研究生参加了此次研讨会。
会议邀请了国内外多名专家就随机图论、网络和组合的若干研究领域和方向做了专题介绍或者学术报告,其中刘九强教授(美国东密执根大学数学系)做了关于经典的随机图论与概率方法的系列讲座,马志明院士介绍了随机图论在互联网搜索和其它复杂网络方面的应用情况以及他所领导的研究小组在相关领域取得的成果;正在晨兴数学中心访问的国际著名的数学家美国加州伯克利大学数学系的E.
Berlekamp教授(美国科学院院士,美国艺术与科学院院士,美国工程院院士,Fellow of IEEE, Fellow of American
Association for the Advancement of Science)也应邀做了Combinatorial
Games的公众演讲,精彩生动的报告令与会者受益非浅。
会议期间还召开了部分老师和学生的座谈会,就如何学习好相关领域的知识,做好相关领域的研究工作为主题,海内外的老师与学生共聚一堂,开展了充分的讨论;
8月25日下午,与会的老师就国内图论发展的历史、目前的国内外发展的现状以及我们如何抓住机遇,搞好国内图论组合网络召开了座谈会,国家自然科学基金委数理学部和中国科学院基础局的部分同志参加了此次座谈会。
正像本次研讨会的倡议人马志明院士在闭幕上所讲的,本次研讨会是非常成功的,必将极大地推动了随机图论和网络在国内的发展。这表现在四个方面:第一研讨会介绍了一个非常好的研究方向(随机图论和复杂网络不仅有理论研究价值,而且有很强、很广泛应用背景);第二吸引了一大批的年青师生学习和研究这个正在飞速发展的新领域(有大量的未解的问题);第三研讨会得到了多位国内图论组合方面的前辈的关注和支持(其中包括张福基教授,王建方、田丰和陈传平研究员,他们自始至终参加了研讨会的每一项学术和交流活动)。第四研讨会是中国科学院数学与系统科学院图论组合网络研究中心与南开大学组合数学研究中心联合举办的,这是一个成功的尝试,为加强中国科学院的研究所与国内外高校的学术合作与交流积累了很好的经验。
本次研讨会得到了中国科学院数学与系统科学研究院、中国科学院数学与系统科学研究院应用数学研究所、以及南开大学组合数学研究中心的资助,会议的组织得到了中国运筹学会的大力支持。
中国运筹学会图论组合专业委员会供稿
17661Random graphs ,Bela Bollobas
..--2nd ed.
.--Cambridge
:Cambridge University Press,c2001.
17661请楼主指点一下随即图论的教程或者资料!
那里可以定到?
谢谢!
17661版主:我看了 Bela Bollobas 的 Random
Graphs!
觉得看英文的难度有点大。
劳烦介绍一下中文的随机图资料,
以及国内搞随机图的老师和他们的网页!
我觉得他们应该有中文的资料!
17666求助原因:研究作为参考文献
篇号:1
作者:E. GyöriM. D. Plummer
文题:
The Cartesian product of a k-extendable and an l-extendable graph is (k +
l + 1)-extendable
杂志全名: Discrete Mathematics
年份,卷(期): 起止页码:
1992Volume 101, Issues 1-3, 29 May , Pages
87-96
求助者email:yuxi3811495@yahoo.com.cn
建议查询的期刊库:(IE,CNKI......)Sciencedirect
17668请高手解答北大05高代post-38-1125839
185.gif
17668这个可以说是有理标准型的一个简单的特例,解答见附件:post-38-1125846291.ibf
17668对于A^3=I => r(I-A)+r(A^2+A+I)=n ,可用若当矩阵证明
对于A^3=I <=
r(I-A)+r(A^2+A+I)=n,令V1=ker(I-A),V2=ker(A^2+A+I),同时令
T=(I-A)(A^2+A+I)=I-A^3,易知(V1)U(V2)=V,则有T(V)=0,所以T=0,结论成立
17668
| 引用 (蓝戈 @ 2005年09月15日
21时42分) |
| 这下还算完整了!
|
呵呵
当时太懒了
感觉大家想想也好就没再写
有些课本上证明Jordan标准型中根空间分解就是类似的思路
而且也是比较常用的证明直和的方法吧
还有,以后我就像最近一样尽量贴图上来了
最近也习惯这个了
17668
| 引用 (tobyqin @ 2005年09月04日
23时04分) |
|
这个可以说是有理标准型的一个简单的特例,解答见附件: |
to
tobyqin:这个似乎有点问题啊!我感到好象没有说的够详细,可否再发个更具体的?
17668妙哉,说明两个空间是直和,用到多项式来解
f(A)(I-A)+g(A)(I+A+A
^2)=I
若不是直和,设有a, 代入上式,则为0=a,不成立!
17668这下还算完整了!
17668
| 引用 (蓝戈 @ 2005年09月15日
21时00分) |
| 引用 (tobyqin @ 2005年09月04日
23时04分) | |
这个可以说是有理标准型的一个简单的特例,解答见附件: |
to
tobyqin:这个似乎有点问题啊!我感到好象没有说的够详细,可否再发个更具体的?
|
最好你说一下哪里感觉不详细
我好有针对的解释一下
确实我有一些书上反复证明的细节我就没有再写了
是不是要解释那个为什么是直和?
直和只要交是0就可以了
另外dimkerA=n-rankA
对任意的变化A
17668为了大家对这个题目理解得更清楚,我给出它的更一般的结论,若A为n阶矩阵,(f,g)=1,则
f(A)g(A)=0的充要条件是rankf(A)+rankg(A)=n,也可以用线性变换的语言叙述为一个等价命题.详细证明在附件中,先给出其6种证法.post-38-1126794156.ibf
17668下面附件中列举出近年来4个类似考研试题.实际上同类试题非常之多,如幂等阵,对合阵等的类似结论post-38-1126794441.ibf
17668感觉是用丘维声高代中结论:A为线性变换,f,g互素,则ker[f(A)g(A)]=ker[f(A)]+ker[g(A)](注:此处为直和),证明非常之简单.
17668当(f,g)=1时,r[f(A)g(A)]=r[f(A)]+r[g(A)]-n,由此结论,北大那题不证自明(可转化为矩阵语言)
我记得tobyqin曾告诉我说r(BC)>=r(B)+r©-n取等号的充要条件是存在矩阵X,Y使得
XA+BY=E,故若(f,g)=1,上面的结论显然
17668
引用 (hfg
1964 @ 2005年09月15日
22时42分) |
当(f,g)=1时,r[f(A)g(A)]=r[f(A)]+r[g(A)]-n,由此结论,北大那题不证自明(可转化为矩阵语言)
我记得tobyqin曾告诉我说r(BC)>=r(B)+r©-n取等号的充要条件是存在矩阵X,Y使得
XA+BY=E,故若(f,g)=1,上面的结论显然
|
r(BC)>=r(B)+r©-n取等号的充要条件是存在矩阵X,Y使得
XA+BY=E,
这个该怎么证明啊?TOBYQIN
17668加油
17668楼上的朋友是不会证呢,教教我啊
17668个人感觉这类题目有相当简单的解法
给一个俺的(公式编辑太麻烦,仅仅叙述)
(当然就考虑矩阵,这里用个简单的,其他的一样,假设证A的平方等于A
对于2n的大对角矩阵,左上角n阶,为A,右下角也是n阶,为A-E,其余为0阵。
做初等变换(过程就是把A看作是那么大,A-E是那么大-1,用求不变因子的方法,
对于矩阵,乘上初等阵(我的意思是块的初等阵,大家自然知道的),这样
左上角变成
E(对应那么大阵的1),右下角为A的平方-A(对应那么大阵的那么大的平方-
那么大),因为乘的可逆阵,秩不变,依然为n,E的秩为n没什么说的,那A的平方-A为0了
证完。
这道题一样这样证
叙述这么多,其实写成矩阵很简单的。什么空间的东西都没用,大一的同学也可作吧
就当是俺的初等证明吧
17668大家给出了那么多的证法,真是获益匪浅阿!
17668这个六种证明?
176691 若M。是平面点集E的聚点,则在E中存在点列Mr→M。(n )
有些书上就是这样定义的,
2
证明平面点列的收敛原理
先证平面点列收敛等价于分量收敛
176691 若M。是平面点集E的聚点,则在E中存在点列Mr→M。(n


)
2
证明平面点列的收敛原理
谢谢各位大虾指教!
17669引用:
1 若M。是平面点集E的聚点,则在E中存在点列Mr→M。(n )
有些书上就是这样定义的,
2
证明平面点列的收敛原理
先证平面点列收敛等价于分量收敛
1聚点是对于闭集或者开集的描述,如果通过拓扑定义的聚点则可以通过开集构造,构造的过程就得到了那个Mr
2三角不等式应该要用到吧。
17671方法正确,但数据有误。我改正后给出了完整解答。post-38-1126010721.ibf
17671求各位兄弟们帮忙啦,先谢了.
第3题第2小题post-38-1125843054.ibf
17672建议答题区也开设学校专区,便于用户查找,也便于网站管理,筛选并保留有用信息!
17677有那位大侠有关于lzw算法的源程序,请给我一份,小弟急用。
gtttf@sohu.com
谢谢~
17677还是自己写一个吧,别人给的自己也没办法用,应该不难写。
17678reijin的最后一步实现不了。
请再看看。
17678设 A 和 B 为n阶方阵,AB=BA=0,并且 r(A*A)=r(A)
证明:r(A+B)=r(A)+r(B)
17678r(A^2)=r(A)则存在C 使 A=A^2*C,又A^2=A(A+B)=(A+B)A,构造矩阵,应用初等变换:
[A 0 ;0
B] => [A A+B;0 B] => [A^2*C A+B;0 B] => [0 A+B;0 B] => [0
A+B;0 -A] => [0 A+B;0 -A^2*C] => [0 A+B;0 0]
则结论成立
17678renjin的方法很好,下面我再给出一个用相抵标准型+矩阵变换的证明:post-38-1125905724.gif
17678reijin与tobyqin的方法妙极了!
后者更直观。
17678的确最后一不仅仅用初等变换不能说明(貌似没细说明),不过利用r(A)=r(A^2),把[0 A+B;0
-A^2*C]的行向量以线性空间的角度去看就会知道[0 A+B;0 -A^2*C]与[0 A+B;0 -A^2]等秩,最后一步也就实现了
17678属同一个问题。
欢迎再讨论。
17678似乎图方便是没好结果的。-_-
我重新写一次
[A 0 ;0 B] => [A 0;A+B B] => [A^2
0;A+B B] => [0 0;A+B B] => [0 0;A+B -A] => [0 0;A+B -A^2] =>
[0 A+B;0 0]
这里有两个地方
[A 0;A+B B] => [A^2 0;A+B B]
[0 0;A+B -A]
=> [0 0;A+B -A^2]
注意把A的列向量以线性空间的角度去看就会知道这两步可以成立的
17678reijin方法的具体矩阵表达我写了一下,大家看有没有哪里写错了,解答如下:post-38-1126015134.gif
17678这道题让我有了新的体会,谢谢
注意到
A=A(A+B)C
B=A+B-A=(A+B)-A(A+B)C
都有(A+B)的因子
所以
[A 0 ;0 B] => [A A+B;0 B] 以后就可以用初等变换用(A+B)把A,B化为0
17678再补充一点:
reijin的证法中,C是可逆矩阵(可以证明),这样该证法的正确性就又有了一个支撑。
更主重要的是,由此引出了一道很好的习题:
设A是n阶矩阵,则秩(
A
)=秩(
A 2
)的充分必要条件是存在可逆矩阵C,使得
A
=A 2C
.
17678[QUOTE]不过利用r(A)=r(A^2),把[0 A+B;0 -A^2*C]的行向量以线性空间的角度去看就会知道[0 A+B;0
-A^2*C]与[0 A+B;0 -A^2]等秩
怎么用线性空间的角度看啊?要构造另外的一个线性变换吗?
17679若AB幂等 则BA幂等
怎么证明啊?
我见过一道题和这个类似,只不过加了一个条件r(AB)=r(BA)
若加上条件r(AB)=r(A)就可以推出r(AB)=r(BA)
不知道由此证明是不是这个意思
这些题目都是中国科技大学出的线性代数课本上的题
也是我专业课的课本,我从9月份开始从头开始复习考研数学专业,虽然已经很晚很晚了
但是我还是会坚持的,即使我上的本科学校不好,山东理工大学,相信你们没多少人知道
,知道的也不会说是好学校,但我依然要走下去,时间不过,很多题我需要启发,希望大家
多教教我,感谢大家了
17679并由此证明 若AB幂等 则BA幂等
怎么做
17679设A为m*n矩阵,B为n*m矩阵
证明:r(AB)=r(A)的充分必要条件为 存在C 使 A=ABC
并由此证明 若AB幂等 则BA幂等
(A幂等 则 A*A=A)
17679
| 引用 (pccq_2002 @ 2005年09月05日
10时21分) |
设A为m*n矩阵,B为n*m矩阵
证明:r(AB)=r(A)的充分必要条件为 存在C 使 A=ABC
并由此证明
若AB幂等 则BA幂等
(A幂等 则 A*A=A) |
充分性用秩不等式就可以得到了;
必要性见:
http://www.math.org.cn/forums/index.php?showtopic=15916
17679我来给个证明post-38-1125907426.ibf
17679哦,对不起,没有看tobyqin的解答,方法差不多post-38-11259077
19.ibf
17679bless you!
努力就会有好的结果的,为你祝福
我刚刚把P156
T10做了一下
不过没有给出完整的答案
我一会贴在那个问题后面
有问题就发上来
大家共同讨论吧
如果r(AB)=r(A)作为条件而且AB幂等来推r(AB)=r(BA)是不难的:
r(A)=r(AB)=r(A
BA B)
≤ r(BA)
≤ r(A)
17679再给出应用Frobenius秩不等式证明幂等的方法:post-38-1126109162.gif
17680请问如何用VB程序实现整数规划中的单纯形算法
请高手帮帮我把
谢了!
17680我只用c++实现过单纯形算法,不会vb。算法不难,自己看看书也就可以写出来了。
17681哦,谢谢
17681概率、随机变量与随机过程
(美)A.帕普里斯(Athanasios
Papoulis),(美)S.U.佩莱(S.Unnikrishna Pillai)著;
保铮,冯大政,水鹏朗译.
西安:
西安交通大学出版社, 2004
网上只能搜索出邮购信息,我想知道它的读者对象是哪些?希望读过它的仁兄给点建议.谢谢
17681一般这种杂烩型的书都是面向初级读者的
17689如
Ax
=b ,如何用mathemtica来编写程序呢?
这里
A
为矩阵,
x ,b 向量.
17689你的意思是想利用 Mathematica 的 built-in function
求解?还是利用它的编程语言,根据高斯消去法等求解?
如果是前者,可用 LinearSolve;如果是后者,可用 Module
定义函数编程,函数内基本上可以把 C 语言的程序移植过来,也可以充分利用 Mathematica 的 List 计算。
17689我的意思是后者了,最好有个具体的程序
17689给一个简单的例子。3对角矩阵的线性方程组的求解。其中,n 是维数,
a 是对角系数(n 维向量),b,c
分别是下对角和上对角系数(n-1 维向量),
d 是右边系数(n 维向量)。结果给出 n 维向量的解。
triSolve[a_,
b_, c_, d_, n_] := Module[{n1 = n, u, w, z, y},
u = Table[0.0, {i, 1,
n1}];
w = Table[0.0, {i, 1, n1}];
z = Table[0.0, {i, 1, n1}];
y = Table[0.0, {i, 1, n1}];
u[[1]] = a[[1]];
For[i = 2, i <=
n1, w[[i]] = b[[i - 1]]/u[[i - 1]];
u[[i]] = a[[i]] - c[[i -
1]]*w[[i]]; i++];
z[[1]] = d[[1]];
For[i = 2, i <= n1, i++,
z[[i]] = d[[i]] - w[[i]]*z[[i - 1]]];
y[[n1]] = z[[n1]]/u[[n1]];
For[i = n1 - 1, i >= 1, i--,
y[[i]] = (z[[i]] - c[[i]]*y[[i +
1]])/u[[i]]];
Return[y];]
17689你这个程序我还不会用,谅解。不过我受到了启发,自己编写了个追赶
法的小程序,结果良好。但以下的雅克比迭代法却不知道哪里有问题,还望予以指点。谢谢!!post-28-1126682386.ibf
17689While 的用法是 While[test, body]. 所以你的 While 句应改成
While[Norm[y]
> 10^(-6), x0 = x1; x1 = A.x0 + f;
y = x1 - x0; k = k +
1]
你如果是直接在 Notebook 中输入你的命令,分成在不同的 cell 中输入较好。
仅供参考。
17689k=k+1放在里面目的是执行迭代次数。但是程序执行时没有结果,只显示了while语句,及k=1
你的建议我下去试试,谢谢你!!
17689
| 引用 (sol @ 2005年09月15日
12时29分) |
| 你如果是直接在 Notebook
中输入你的命令,分成在不同的 cell 中输入较好。 |
这句话可能给你带来误解。我指的是
A={{0,0.1,0.2},{0.1,0,0.2},{0.2,0.2,0}};
........
y=x1-x0;
等语句和
While 句在不同的 cell 中输入为好。
另外,body 中各个语句用 ; 分开,不能用 , 分开。
在移植 C
的程序时,小心它们的语法不同之处。
我在 Mathematica 中试了一下,改后应该没有问题。
17689再次感谢!忙着上课,还没来得及调试呢。
另外,在mathematica 中,组合数如何计算?我一时还找不到相关命令。
17689刚才调试了一下,只把 k
=k+1 放在了大括号中,一切ok了!!
谢谢你了!!
17689分成在不同的 cell 中输入较好??
这个又该如何做呢?
17689
引用 (小红帽 @ 2005年09月15日
19时42分) |
分成在不同的
cell 中输入较好??
这个又该如何做呢?
|
运行完
A={{0,0.1,0.2},{0.1,0,0.2},{0.2,0.2,0}};
后,再运行
其它的句式即可。
另外,在mathematica
中,组合数如何计算?我一时还找不到相关命令。
请看 Binomial 和 Multinomial 的介绍。
17689明白了,原来是这个了!!多谢多谢!!
17689
引用 (sol @ 2005年09月10日
16时
19分) |
给一个简单的例子。3对角矩阵的线性方程组的求解。其中,n 是维数,
a 是对角系数(n 维向量),b,c 分别是下对角和上对角系数(n-1
维向量),
d 是右边系数(n 维向量)。结果给出 n 维向量的解。
triSolve[a_, b_, c_, d_, n_]
:= Module[{n1 = n, u, w, z, y},
u = Table[0.0, {i, 1, n1}];
w =
Table[0.0, {i, 1, n1}];
z = Table[0.0, {i, 1, n1}];
y = Table[0.0,
{i, 1, n1}];
u[[1]] = a[[1]];
For[i = 2, i <= n1, w[[i]] = b[[i
- 1]]/u[[i - 1]];
u[[i]] = a[[i]] - c[[i - 1]]*w[[i]]; i++];
z[[1]] = d[[1]];
For[i = 2, i <= n1, i++, z[[i]] = d[[i]] -
w[[i]]*z[[i - 1]]];
y[[n1]] = z[[n1]]/u[[n1]];
For[i = n1 - 1, i
>= 1, i--,
y[[i]] = (z[[i]] - c[[i]]*y[[i + 1]])/u[[i]]];
Return[y];] |
你的这个程序我也逐渐看懂了,不过对module这个东西我还没用过呢
17689triSolve[{2, 2, 2,2, 2}, {-1, -1, -1, -1}, {-1, -1, -1, -1}, {1, 0,
0, 0, 0}, 5]
好像运行没结果啊
17689
引用 (小红帽 @ 2005年09月
19日
15时31分) |
triSolve[{2, 2,
2,2, 2}, {-1, -1, -1, -1}, {-1, -1, -1, -1}, {1, 0, 0, 0, 0},
5]
好像运行没结果啊 |
先运行函数定义,再输入运行
triSolve[{2, 2, 2,2, 2}, {-1, -1,
-1, -1}, {-1, -1, -1, -1}, {1, 0, 0, 0, 0}, 5]
结果是
{5/6, 2/3, 1/2,
1/3, 1/6}
这样就没问题。
17689triSolve[a_, b_, c_, d_, n_] := Module[{n1 = n, u, w, z,
y},??
你说的是这个定义么?另外牛顿插值的程序又如何写呢?
17689
| 引用 (小红帽 @ 2005年09月26日
21时46分) |
triSolve[a_, b_,
c_, d_, n_] := Module[{n1 = n, u, w, z, y},??
你说的是这个定义么?另外牛顿插值的程序又如何写呢?
|
是这个定义。因为是自定义函数,使用以前必须先运行。
牛顿插值的程序可参考数值分析的教材,类似编程。
17689谢谢。目前有些程序不是很好编写,过段时间再编写这些程序吧。
17691例如:f(x,y)=atan(y/x) x

[16,31],y杠epsilon [1,x) 用插值的方法拟合 另外:插值点只知道相应的一维函数f(x)=atan(x)的某些点
各位大牛有什么好的方法?
17694
福建师大实变函数
17694真可惜啊,不能下载,仍然谢谢了.
17695两个人A,B,数字为2~100之间的共99个自然数。现找出两个数,把其和告诉A,把其积告诉B。然后问A知道不知道是哪两个数,A说:“虽然我不知道,但是肯定B也不知道。”再问B,B说:“本来我不知道,但是听到A说这句话,现在我知道了。”
A听到B说他知道了,然后就说:“现在我也知道了”。那么这两个数是多少呢?
17695其中一个数是4,另一个数是素数(除2外)。
17695这个问题好像在google或者baidu随便搜索一下就有很多结果了
这个据说是鬼谷子问题,他把数分别给了孙膑和庞涓
答案可能是4和13吧
17695同与华罗庚带帽问题.
17695不错,呵呵,真好。楼上不是有人解决吧
17696不能下载
17696
教学录像
17696不能下载
17696

谢谢!!!
17696不行的
17697有哪位晓得有涉及到n维欧氏空间中区域的几何性质的书么,比如说segment property,
cone property
,strong local Lipschitz property etc,望不吝赐教
17697数分上定义区域为
折线连通的开集。
它应该是闭包完备,内部非空,边缘集为稀疏集...半开集。
17698

点击进入
现在还不全是中文,好像有人正在翻译。不知道是Wolfram公司做的,还是国内有谁与他们合作。
176984.0版有出版的中文书啊,已有一二年了吧。
17698这样看,太费劲了!有什么看起来比较迅速的吗?
17698我都等不急 了
17699我本来想考南开的,但听说南开一半多都是保送的。
没办法!!
17699北大好 啊
17699南开的几何还是很不错的
不过好像没有人搞数论
17699我是学数学的,今年考研究生,想请各位有经验的大侠们指教啦.我想学些关于数论和几何方面的,不知道哪个学校更好呢?
17699其实越好的学校保送的越多!
北大,中科院哪个不是保送过半啊!
中科院的06年估计保送的就已经超过了75%了!
只剩下几个名额是从统考中录取啊!郁闷ing!
不敢游戏的就不要轻易报中科院,那完全是在那前途在赌!
没有绝对的数学优势和比较扎实的英语,考中科院都是泡影!
17699郁闷ing!
谁报中科院啊?苏州大学一个班俩女生06年同时保送中科院,山大有个孩子有被保送了!我们系至少六人
要考
中科院
怎么办?毛了!
17699当然是北大了
17700能否发一下原题?
17700程序老是运行不出来,不是语法问题,都是说模型解不出来,要不就是什么未定义之类的,请高人指点一下,帮我找找问题出在哪儿了?post-28-1125913389.ibf
17700这是我做的题,我觉得模型没有问题,就是程序编出来运行不了,大哥帮忙找找毛病
最大材料数,我估算了1600一个作为他的取值范围,最大天数为到
16 天post-28-1125988489.ibf
17701这个好
17701具体请访问:
http://www.combinatorics.net/conf/CJCDGCGT2005.htmlThe
China-Japan Joint Conference on Discrete Geometry, Combinatorics and Graph
Theory (CJCDGCGT) 2005 is organized by the Center for Combinatorics,
Nankai University, Tianjin, China; Department of Applied Mathematics,
Northwestern Polytechnical University, Xi'an, China and RIED, Tokai
University, Japan
Conference ProceedingsThe proceedings of
the conference will be published as a volume of Lecture Notes in Computer
Science (LNCS, Springer-Verlag). Papers will be strictly refereed in
keeping with the standards of LNCS.
Date and Place
November
18-20, Nankai University (Tianjin)
November 22-24,
Northwestern Polytechnical University (Xi'an)
Sponsored by
Nankai University, China
Northwestern Polytechnical University,
China
Tokai University, Japan
National Natural Science Foundation
of China
Invited Speakers Kiyoshi Ando (The University of
Electro-Communications, Japan)
Guizhen Liu (Shandong University,
China)
Zhiming Ma (Chinese Academy of Sciences, China)
Janos Pach
(City College of CUNY; Courant Institute of New York University;
Renyi
Institute of Hungarian Academy of Sciences, USA)
Jorge Urrutia
(Universidad Nacional Autónoma de México, Mexico)
Fuji Zhang (Xiamen
University, China)
Chuanming Zong (Beijing University, China)
Conference Office Center for Combinatorics, Nankai
University
Tianjin, China
Secretary: Matthew Q. H.
Guo
E-mail: guoqh@mail.nankai.edu.cnpost-32-1125913614.ibf
17701又在南开举行,好!
17701不知道到时有没有机会去
17702同学,我给你解释清楚一点,看起来你没搞清楚随机过程,随机变量和函数变换之间的关系:
你之所以认为求期望出来是个常数,是因为你把D(t),N(t)当做函数变换在做.但是其实是这样的.
假定T随机取到一个值,你先把T带到D(t)里,那么,D(T)到底是个什么东西,是个确定的值还是随机变量.你应该注意到,D(t)是一个随机过程,T取定以后,D(T)是一个随机变量,不是一个常数,也就是说D(t)的不确定性不能由T的确定而消除.所以对N(t)也是一样,D(T)在取定一个随机值以后,N(t)从一个Possion过程变成为一个Possion变量,参数为bT.而不一个确定值.
从期望的角度来看,期望的本质是一个以概率为权的加权平均,连续型就是积分,离散性就是求和.但是你光给出一个E,不说对谁求期望,那你加权的时候是用T的分布函数还是N(T)的分布函数,还是D(t)的分布函数?所以,明显,如果只求一重期望,这个东西出来是个随机的东西,因为你定义成N(D(T),所以,哪怕对T求期望以后把T变成E(T)了,由于D(T)是一个随机变量,导致整个的N(D(T))还是一个Possion过程.
最后给你举一个简单的对比,你对比一下就知了
1.设X~b(p),f(x)=x+1,求E(Xf(X))
2.设X~b(p),两个取值都在0,1之间,
Y是一个混合分布,它有一个参数p(0<=p<=1),Y以p的概率取一个N(0,1)的正态分布,以1-p的概率取一个P(2)的Possion分布,于是我们将Y表示为Y(p),那么让你求
E_X(XY(X)),E_X表示对X求期望
你对比一下这两个期望出来的东西一样不一样,1出来的是一个常数,2出来的是一个随机变量,其中2的求法是用Y|X的条件分布来做的.
17702是对哪个随机变量求期望?这个东西出来是个随机变量不是一个确定的数
17702对关于T的表达式求期望,最后结果应该可以用T的一二阶矩(常数)和D的一二阶矩来表示(关于T的表达式,再代入T的各阶矩),最终的结果应该是一个常数
17702T是一个服从任意分布的随机变量,已知其一二阶矩;N(t)是一个参数为b的Poisson过程,也就是P[N(t)=k]=[(bt)的k次方][e的(-bt)次方]/(k!);D(n)是一个特殊分布,它是线性的,也就是D(n)=nD(1),我们知道它的一二阶矩,甚至可以计算出任意矩。
现在要计算
E[T*D(N(T))]=?
各位高手请出招吧
17703行吧post-38-1129114972.gif
17703应用中值定理中的柯西定理好像可以证出来
17703|f(x)-f(y)|<c(x^(1-a)-y^(1-a)),
这是怎么来的啊????
17703由已知得,存在常数b和c,使得当x属于(0,b)时有|x^af'(x)|<c,|f'(x)|<cx^(-a)
|f(x)-f(0)|<cx^(1-a),由此可证其一致收敛性
17703:)
17703的确我之前也没留意,不过这也简单,换个形式就可以了,根据不等式可得
|f(x)-f(y)|<c(x^(1-a)-y^(1-a)),x,y属于(0,b),一样可证f一致连续
17703我去想想看
17703请解答!post-38-11259
17558.ibf
17703limx^a*f'(x)=C
那么在x=0的某个邻域内
f'(x)>(C-1)*x^(-a)=[(C-1)/(1-a)*x^(1-a)]'
那么是否可以根据微分方程的比较定理来做呢:
存在某个D,再x=0的邻域内f(x)<(C-1)/(1-a)*x^(1-a)+D
请指教
17703的确我之前也没留意,不过这也简单,换个形式就可以了,根据不等式可得
|f(x)-f(y)|<c(x^(1-a)-y^(1-a)),x,y属于(0,b),一样可证f一致连续
x,y属于(0,b) 这样可以吗?
17703
引用 (reijin @ 2005年09月05日
19时41分) |
由已知得,存在常数b和c,使得当x属于(0,b)时有|x^af'(x)|<c,|f'(x)|<cx^(-a)
|f(x)-f(0)|<cx^(1-a),由此可证其一致收敛性
|
此解答似乎有问题啊!f(x)在0处没有定义,而且可能f(x)在0的任何小的领域里是无界的
对于这样的情况是不可以用函数差和导函数的关系的。
17703
| 引用 (reijin @ 2005年09月05日
21时25分) |
的确我之前也没留意,不过这也简单,换个形式就可以了,根据不等式可得
|f(x)-f(y)|<c(x^(1-a)-y^(1-a)),x,y属于(0,b),一样可证f一致连续
|
这个怎么看不懂呢?我进行变换之后不是这个样子,反而还是看不出问题的终结。
17703|f(x)-f(y)|<c(x^(1-a)-y^(1-a)),
因为属于(0,b)内,函数
x^(1-a)一致连续啊!
17705怎么证明?
17705必须是可列集合
17705请问如何证明:对偶定理可以推广到无限个集合?
附问一个:证明的规则是什么呢?我总是怕我的证明不合规则。
17705给我个思路吧,如果不想给我证明就给个思路吧
17705
| 引用 (maxcai @ 2005年09月05日
20时03分) |
请问如何证明:对偶定理可以推广到无限个集合?
附问一个:证明的规则是什么呢?我总是怕我的证明不合规则。
|
定义与逻辑
17705回流大版主:
有没有具体点的细则,我是学计算机的,我想证明是不是和算法一样有些合格的标准?
比如说,有穷性-有穷的部骤
如此等等?
17705没有有穷与无穷的区别,真的是不同于算法
找一本实变的书看看就可以了
17706对于该矩阵有那些教材上有介绍,望告知,不胜感谢!!!
17706好像学数学分析时就讲过一个Jacobian矩阵,不知是不是你说的那个
就是讲多元微分学的时候
17706Jacobian矩阵有几种定义,不知道你问的是哪一个呢?最主要的定义是一个n阶对称三对角矩阵J,且其中
J
i
,i+1
>0,i=1,⋅
⋅ ⋅,n 。
17706最近作论文碰到Jacobian矩阵,我实在不知道,有那位高手请告诉我,或者告诉我看那一本教材。谢谢!!!
17706 请见蒋尔雄的《对称矩阵计算》一书。也可以和我联系,我最近在做关于Jacobi矩阵的反问题。
17706在多元函数论里的隐函数定理中要用到雅可比矩阵,在多元函数积分中积分变量代换中也用到雅可比矩阵了!譬如两个以x,y为二元变量的二元函数f(x,y),g(x,y),那它们的雅可比矩阵就是以两个函数的偏导数为元素的二阶矩阵!
17706Jacobi矩阵一般特指一组多元函数的导数矩阵
记成 D(F1,F2,F3....FN)/D(X1,X2,X3,...,XN)
17706Jacobi-Matrix:=(

f/

x^2,

f/

x

y,

f/

y

x,

f/

y^2)
17706
http://en.wikipedia.org/wiki/Jacobian_matrix自己看看吧
17708见附件:post-38-1125924
183.gif
17709感觉上:
复变函数里零点的孤立性:
不恒为零的解析函数的零点是孤立的
应该可以应用到,而非推广到实数域内。
只须将其中的解析函数换成连续函数即可。
望批评指正!
17709复变中的泰勒展开应是实变中泰勒展开的推广,
当复变函数退化到实变量的实函数时,
即为实变里的泰勒展开
17709那位老兄能告诉我复变里的零点的孤立性能否推行到实数域内,以及复变与实变
里的泰勒展式有何区别,一可导实数域内函数在一条线上的值能否确定整个可导域内的值?在下有些困惑,那位可助一臂之力,感激不尽
!
17713[转帖](8-
19)常用十一大数据库按国家分类详细介绍(
一、美国
(1)Wiley
InterScience(英文文献期刊) Wiley InterScience是John Wiely & Sons
公司创建的动态在线内容服务,
1997年开始在网上开通。通过InterScience,Wiley公司以许可协议形式向用户提供在线访问全文内容的服务。Wiley
InterScience收录了360多种科学、工程技术、医疗领域及相关专业期刊、30多种大型专业参考书、13种实验室手册的全文和500多个题目的Wiley学术图书的全文。其中被SCI收录的核心期刊近200种。期刊具体学科划分为:Business,
Finance & Management (商业、金融和管理)、Chemistry (化学)、Computer Science
(计算机科学)、Earth Science (地球科学)、Education (教育学)、Engineering (工程学)、Law
(法律)、Life and Medical Sciences (生命科学与医学)、Mathematics and Statistics
(数学统计学)、Physics (物理)、Psychology (心理学) 。
(2)美国IEEE (英文文献期刊)
IEEE(Institute of Electrical & Electronics
Engineers)是电子信息领域最著名的跨国性学术团体,其会员分布在世界150多个国家和地区。据IEEE统计,IEEE会员总数2001年比2000年增加3.1%,达到377342人,其中学生会员为65669人,增长12.6%。
随着人们的信息越来越多地来自Internet,IEEE需要为会员提供更加完善和全面的电子信息产品和服务。IEEE应成为IEEE会员获得信息的首选之地。IEEE必须识别正确的信息,并提供对它们的访问方法。实现这个目标的重要一步是通过IEEE
Xplore与IEEE/IEE Electronic Library
(IEL)连接。IEL包括了
1988年以来IEEE和IEE的所有期刊杂志和会议录,以及IEEE的标准,可以通过题目、关键词和摘要进行查阅。
===============================================
(3)美国EBSCO(英文文献期刊)
http://ejournals.ebsco.com数据库简介:
EBSCO公司从
1986年开始出版电子出版物,共收集了4000多种索引和文摘型期刊和2000多种全文电子期刊。该公司含有Business
Source Premier (商业资源电子文献库)、Academic Search Elite(学术期刊全文数据库)等多个数据库。
Business Source
Premier收录了三千多种索引、文摘型期刊和报纸,其中近三千种全文刊。数据库涉及国际商务、经济学、经济管理、金融、会计、劳动人事、银行等的主题范围,适合经济学、工商管理、金融银行、劳动人事管理等专业人员使用。数据库中有较著名"华尔街日报"(The
Walls Street Journal)、"哈佛商业评论"(Harvard Business
Review)、"每周商务"(Business
Week)、"财富"(Fortune)、"经济学家智囊团国家报告" (EIU
Country
Reports)、 American Banker、Forbes、The
Economist等报刊。该数据库从
1990年开始提供全文,题录和文摘则可回溯检索到
1984年,数据库每日更新。
学术期刊集成全文数据库(Academic Search
Premier,简称ASP):包括有关生物科学、工商经济、资讯科技、通讯传播、工程、教育、艺术、文学、医药学等领域的七千多种期刊,其中近四千种全文刊。
640Emuch.NetFjnuZW11Y2geE5
EBSCO内含有两个免费数据库:
ERIC为(Educational
Resource Information Center)
(教育资源信息中心)是美国教育部的教育资源信息中心数据库,收录980多种教育及和教育相关的期刊文
献的题录和文摘,包括250多种EBSCO收录的全文杂志教育文献数据库,数据为
1967至今。
Newspaper
Source (报纸资源)
Newspaper Source收录159种美国地方报纸、
18种国际性报纸、6个新闻专线、
9个报纸专栏,包括基督教科学箴言报、洛山矶时报等
194种报纸的全文。 另 外还收录4种美国全国性报纸的索引和摘要。
Academic
Search Elite 多学科学术期刊 全文
Academic Search Premier 多学科学术期刊 全文
Business Source Elite 商业、管理、财经 全文
Business Source Premier 商业、管理、财经
全文
EconLit 经济学 文摘
Communication & Mass Media Complete (CMMC)
传播和大众传媒 全文
AGRICOLA 农业 文摘
EBSCO Hospital Package 医学、生物医学
MEDLINE 医学 文摘
Biomedical Reference Coll.: Comp. Ed. 生物医学 全文
Health Business Elite 医疗管理 全文
Psychology & Behavioral Sci.
Coll.: Comp. Ed. 心理学和行为科学 全文
CINAHL 医学 - 护理学 文摘
Nursing &
Allied Health Coll.: Comp. Ed. 医学 - 护理学 全文
Cochrane Collection 医学 -
护理学 全文 (IPA) 药学 文摘
SPORTDiscus 医学 - 运动医学 文摘
PsycINFO 心理学 文摘
ERIC 教育学 文摘
Professional Development Collection 教育学 全文
Canadian MAS FULLTEXT Elite 中、小学期刊读物 全文
Scientific American
Archive Online 综合性科技期刊 全文
EBSCO Language & Literature Collection
语言文学数据库集锦
American Humanities Index 人文科学 文摘
MLA International
Bibliography 语言文学 文摘
Cloumbia Granger's Poetry Database 诗歌 全文
MagillOnLiterature Plus 文学 全文
Military Library FullTEXT 军事 全文
MasterFILE Premier 综合性期刊 全文
Newspaper Source 综合性报纸 全文
World
Magazine Bank 综合性杂志 全文
===============================================
(4)美国(umi)ProQuest
博士论文全文 ,是UMI公司的一个分库(我分析之后得来的。)
UMI公司简介:
该公司的全称是UMI,The answser Company
(UMI有问必答公司),成立于
1938年,是全球最大的信息存储和发行商之一,也是美国学术界著名的出版商,它向全球160多个国家提供信息服务,内容涉及商业管理、社会科学、人文科学、新闻、科学与技术、医药、金融与税务等。其出版物包括
18,000多种外文缩微期刊、7000多种缩微报纸、150多万篇博士/硕士论文、20多万种绝版书及研究专集:从
1980年起该公司开始电子出版物的制作与发行:如光盘数据库、磁带数据库、联机数据库等。
UMI提供以下三种数据库:
学术研究图书馆(Academic Research Library,简称ARL)
综合参考及人文社会科学期刊论文数据库,涉及社会科学、人文科学、商业与经济、教育、历史、传播学、法律、军事、文化、科学、医学、艺术、心理学、宗教与神学、社会学等学科,收录2,300多种期刊和报纸,其中全文刊占三分之二,有图像。可检索
1971年来的文摘和
1986年来的全文。
商业信息数据库(ABI/INFORM)
ABI即为Abstracts of Business
Information的缩写,世界著名商业及经济管理期刊论文数据库,收录有关财会、银行、商业、计算机、经济、能源、工程、环境、金融、国际贸易、保险、法律、管理、市场、税收、电信等主题的1,500多种商业期刊,涉及这些行业的市场、企业文化、企业案例分析、公司新闻和分析、国际贸易与投资、经济状况和预测等方面,其中全文刊超过50%,其余为文摘,有图像。
医学电子期刊全文数据库(ProQuest Medical Library)
该数据库收录有220种全文期刊,文献全文以PDF格式或文本加图像格式存储;收录范围包括所有保健专业的期刊,有护理学、儿科学、神经学、药理学、心脏病学、物理治疗及其它方面。
ProQuest博士论文全文检索系统, PQDD的全称是ProQuest Digital
Dissertations,是世界著名的学位论文数据库,收录有欧美1,000余所大学文、理、工、农、医等领域的博士、硕士学位论文,是学术研究中十分重要的信息资
源 ...
http://proquest.umi.com/pqdweb
===============================================
(5)美国Netlibrary(英文电子图书):
http://www.netlibrary.com
NetLibrary处在美国科罗拉多州波尔德尔市,于
1999年成立,是世界上向图书馆提供电子图书的主要提供商。NetLibrary于2002年1月25日成为OCLC联机计算机图书馆中心的下属部门。目前,世界上7000多个图书馆通过netLibrary存取电子图书,其中包括哥伦比亚大学,斯坦福大学,加州大学伯克莱分校,以及世界上其他成千的大小图书馆。
OCLC
netLibrary目前提供400多家出版社出版的60,000多种电子图书,并且每月增加约2,000种。这些电子图书覆盖所有主题范畴,约80%的书籍是面向大学程度的读者。大多数NetLibrary的电子图书内容新颖,近90%的电子图书是
1990年后出版的。
netLibrary是OCLC的一个部门,是当前世界上eBook的主要提供商,它提供来自300多个出版商的50,000多种高质量电子图书,这些电子图书的90%是
1990年后出版的,每月均增加几千种。
==============================================================================
二、荷兰
(1)Sciencedirect: 荷兰Elsevier
Science公司出版的期刊是世界上公认的高品位学术期刊,它拥有1263种电子全文期刊数据库,并已在清华大学图书馆设立镜像站点:ScienceDirect
OnSite(SDOS)。国内11所学术图书馆于2000年首批联合订购SDOS数据库中
1998年以来的全文期刊。
国内镜像:
http://elsevier.lib.tsinghua.edu.cn/ http://www.sciencedirect.com/ http://www.sciencedirect.com/sci http://www.sciencedirect.com/sci http://www.sciencedirect.com/sci
===============================================
(2)荷兰OVID(英文文献期刊),现为Wolters Kluwer集团之一
OVID科技公司是由总裁Mark
Nelson于
1984年创立于纽约,由一人开始营业,扩展
至目前已有将近200人。分公司分布于世界各地,如:雪梨、伦敦、巴黎……等地。
公司名称也从最早的Online Research System改名为CD Plus,CDP echnologies,而至目前的OVID
Technologies,以强调突显Ovid公司与客户及软体间的专业关系。
Ovid是一全球性的资讯公司,以创造容易撷取资讯、独立于平台之媒介为使命。无论我们的顾客使用Dos、Windows、Unix或全球资讯网和Java平台,皆可经由Ovid一般使用者介面轻易地撷取资讯。
公司的发展最初由医学起家,从Medline至目前已包涵人文、社会、科技等近百种资料库。
1984 发展第一代检索界面
1990 发表CDPNet,建立第一套以PC为基础,经由Novell环境检索的网路系统
1991
发表CDPNet Version 2.0,并荣获Information World Review评为年度最佳产品
1992 Beta
version of Ovid 3.0成为Medline第一个Windows界面的产品
1993
发表Unix版系统,并荣获Information Today评为最佳使用界面及检索引擎
1994 1. 并购BRS公司,开启CDP
Online业务
1995 1. 发表Windows和VT-100界面Z39.50相容的Ovid Client/Server
2. 发表Ovid Core Biomedical Collection及Ovid全文系统
3. 荣获Business
Week评为全美排行第14大成长迅速的公司
1996 发表Z39.50相容的Ovid Web Gateway
1997
发表第一套Java检索介面-Ovid Java Client
1998 1. 发表400种STM(Science Technology
Medicine)电子全文期刊
2. 九月份Wolters
Kluwer采购Ovid公司股票,Ovid公司原为检索软体出版公司,现为Wolters
Kluwer集团之一员,因Wolters
Kluwer公司为全球知名900种期刊之出版商,故现今Ovid除了出版检索软体,也是Information Provider。
http://gateway.ovid.com===============================================
(3)Kluwer:含电子图书和期刊.
荷兰Kluwer Academic
Publisher是具有国际性声誉的学术出版商,它出版的图书、期刊一向品质较高,备受专家和学者的信赖和赞誉。Kluwer
Online是Kluwer出版的600余种期刊的网络版,专门基于互联网提供Kluwer电子期刊的查询、阅览服务。
=========================================================================================================
三、英国
(1)英国Ingenta(英文文献期刊)
Ingenta网站是Ingenta公司于
1998年建成的学术信息平台。在几年的发展中,该公司先后兼并了多家信息公司,合并了这些公司的数据库。2001年,Ingenta公司兼并了Catchword公司,近期Ingenta准备将两家公司的信息平台整合为一体。在整合之前,用户可分别从Ingenta.com和Catchword.com查询对方提供的全部信息。整合后可提供全球
190多个学术出版机构的全文联机期刊5,400多种,以及26,000多种其它类型出版物。目前,Ingenta公司在英国和美国多个城市设有分公司,拥有分布于世界各地的10,000多个团体用户和2,500多万个个人用户,已成为全球学术信息服务领域的一个重要的文献检索系统。
ingenta
http://www.ingenta.com/
===============================================
(2)英国Blackwell(英文文献期刊)
(www.blackwell-synergy.com)
Blackwell出版公司是世界上最大的期刊出版商之一(总部设在英国伦敦的牛津),以出版国际性期刊为主,包含很多非英美地区出版的英文期刊。它所出版的学术期刊在科学技术、医学、社会科学以及人文科学等学科领域享有盛誉。
近年来,Blackwell出版的期刊不断发展。目前,Blackwell出版期刊总数已超过700种,其中理科类期刊占54%左右,其余为人文社会科学类。涉及学科包括:农业、动物学、医学、工程、数学统计、计算机技术、商业经济、生命科学、物理学、人文科学、艺术、社会及行为科学等。
180Emuch.NetV5ZW11Y2geE5
Blackwell出版期刊的学术质量很高,很多是各学科领域内的核心刊物,据最新统计,其中被SCI收录的核心期刊有239种,被SSCI收录的有1
18种。
Blackwell-Synergy journals
http://www.blackwell-synergy.com/
=========================================================================================================
四、德国
springer
德国施普林格(Springer-Verlag)是世界上著名的科技出版集团,
通过Springer
LINK系统提供学术期刊及电子图书的在线服务。
Springer公司和 EBSCO/Metapress
公司现已开通Springer LINK电子期刊服务。目前Springer
LINK所提供的全文电子期刊共包含439种学术期刊(其中近400种为英文期刊),按学科分为以下11个“在线图书馆”:生命科学、医学、数学、化学、计算机科学、经济、法律、工程学、环境科学、地球科学
、物理学与天文学,是科研人员的重要信息源。
目前大部分期刊可以阅读全文,但也有一些期刊尚不能阅读全文,一般规律是:显示pdf字样的,可以打开全文,显示remote
pdf字样的,则不能打开全文,目前代理公司正在解决此事。
Springer Link 涵盖的学科范围及种数:
Law
(法律): 5种 Environmental (环境科学): 37 种
Medicine (医学):
179种 Geoscience
(地球科学): 53种 Mathematics (数学): 73种
Life Science (生命科学): 105种
Economics (经济学): 30种 Chemical Sciences (化学): 36种
Engineering
(工程): 58种 Computer Science (计算机科学):45种
Physics and
Astronomy(物理与天文学):61种
附:(1)wiley
和spring可以通过代理注册,注意的是wiley需要激活,而且wiley90天以后必须进入代理续激活。
(2)sd只能通过代理获取相关文献,注册以后也不能脱离代理。
(3)springer搜索完以后,前面有眼镜的是可以直接下载观看的,而那些没有的则是要会费的。
17713thanks
17713Thanks!!!
17713好!
17713感谢了
有了初步的了解
17713thanks
17713不错,介绍的很细。
17714谁有E.Gagliardo Properieta di alcune classi di funzioni in piu
variabili
Rierche Mat (
1958) 102-137这篇论文阿,有的话
加我qq23087808,或者发到我的邮箱alex79123@163.com 作为答谢,本人有拓扑,Sobolev空间,计算数学方面的资料可作交换
17715处理的对象不同,数学分析是主要针对连续函数的,而实变是对可测函数的
17715各位大牛,我刚到美国,一些数学方面的东西都已经忘记了
几个问题求助:
1 数学分析和实分析的联系和不同
2
各位谁知道或有 实分析 拓扑和几何 或者常微分方程方面的书的下载请告诉小弟好吗
感激不尽
17715对了,忘记说了,我的联系方式是 QQ 404690072
或者是 jie_joe@163.com
17716證明﹕n個頂點的多邊形是凸的當且僅當它唯一
177
17證明﹕n (n>3) 個頂點的凸多邊形去掉一個頂點,
剩下的頂點所成多邊形是凸的(=凹
多邊形再加一個頂點所成的多邊形是凹的)
177
18各位大侠帮帮忙,小女子先谢了
177
18去这里下载吧
ftp://elmo.jlu.edu.cn/或
ftp://202.113.29.4/pub2/ScientificComputing/win32/
177
18还有一个好网站
http://mcm.ustc.edu.cn/download1mm/downloa...ownloadppmm.htm
177
18实在太感谢了,多谢了[COLOR=orange][FONT=Optima]
177
18世界原来这么美好!
17720我们知道双曲函数有六个:shx,chx,thx,cthx,schx,cschx.除了直呼其中文名外,请问还有其它读音吗?
17720似乎没有了??
17722Release 14 with Service Pack 3, launched on September 1, 2005,
provides updates to MATLAB, Simulink, and 75 other products. The primary
focus of this service pack is on quality; it also includes new features
for data analysis, large-scale modeling, fixed-point development, and code
generation
目前国内好像没有下载的地方,期待它的出现!
17723大家好,
我现在自学<高等数理统计>茆诗松教师一书,有一个问题请教你们。
请见附件中1.3题,谢谢。post-
17-1125971592.jpg
17723这个这个...可控怎么定义...
哎,我觉得国内的统计都走歪了,路越走越窄,把统计搞成纯数学的东西了.
统计本身和数学就有区别的.我个人觉得统计属于吃钱的学科,钱扔下去,有实验数据了,成果自然出得来,搞纯理论没前途的...何况在应用统计理论的时候,很多东西不是那么well-defined的
17723
| 引用 (子青 @ 2005年09月06日
10时28分) |
这个这个...可控怎么定义...
哎,我觉得国内的统计都走歪了,路越走越窄,把统计搞成纯数学的东西了.
统计本身和数学就有区别的.我个人觉得统计属于吃钱的学科,钱扔下去,有实验数据了,成果自然出得来,搞纯理论没前途的...何况在应用统计理论的时候,很多东西不是那么well-defined的
|
有一定道理,我同意。
17723
| 引用 (子青 @ 2005年09月06日
10时28分) |
这个这个...可控怎么定义...
哎,我觉得国内的统计都走歪了,路越走越窄,把统计搞成纯数学的东西了.
统计本身和数学就有区别的.我个人觉得统计属于吃钱的学科,钱扔下去,有实验数据了,成果自然出得来,搞纯理论没前途的...何况在应用统计理论的时候,很多东西不是那么well-defined的
|
统计不是数学,有自己的sense,把统计变成只把数学当工具的一门学科才是国际上的主流.......
但是也应该有自己的一套基础理论的,否则就不是科学了。
17723可控制结构实际上书上有定义的,说的是所有的概率分布都关于某一

有限的测度是绝对连续的,显然当所有的概率测度是有限或可列时,很容易构造一个出来的,可参考其他的高等数理统计教材,如陈希孺,郑忠国的教材都有涉及
17724
| 引用 |
| 已知f(-x)=-f(x),且 (-x0)=k,则f(x0)=?
|
应该是f'(x0)=?吧
17724我自己思考时,只是想因为f(-x)=-f(x),所以f(x)图形关于原点对称,

(-x0)=

(x0),所以结果也是k,但不知具体要解答里应该怎么处理,请指教,谢谢!
17724已知f(-x)=-f(x),且

(-x0)=k,则

(x0)=?
17724应该是求f'(x0)吧post-38-1125980388.ibf
17724题目应该是f'(x0)否则做不出
用定义作
f'(x0)=lim(f(x)-f(x0))/(x-x0)=lim(f(-x)-f(-x0))/(-x)-(-x0)=f(-x0)=k
画个图也可以做的
17724sorry,写错了。
我看明白了,谢谢zhubin846152、liuqhui你们!
17724不是正确的吗!
17724It's very easy: the derivative of an odd function is
even!!!!!!!!!
17726取
c ij
=
-
b ij
题目就化成标准的Cauchy行列式的计算,具体就是用递推的方法。
17726求解n阶实矩阵M的行列式,其中
m
i ,j
=1
a i
-b
j ,
a
i ,b
j 为互不相同的实数,
i
,j=1,⋅
⋅ ⋅,n .
17726
| 引用 (tobyqin @ 2005年09月06日
10时36分) |
| 取
c ij
= -
b ij
题目就化成标准的Cauchy行列式的计算,具体就是用递推的方法。
|
多谢tobyqin的回答!第一次听说Cauchy矩阵啊!请问Cauchy矩阵有什么性质呢?
17726
引用 (beaver @ 2005年09月06日
17时00分) |
| 引用 (tobyqin @ 2005年09月06日
10时36分) | | 取
c ij
= -
b ij
题目就化成标准的Cauchy行列式的计算,具体就是用递推的方法。
|
多谢tobyqin的回答!第一次听说Cauchy矩阵啊!请问Cauchy矩阵有什么性质呢?
|
我现在知道的也就是一个行列式,被称作Cauchy行列式而已
不过这类行列式看着还是不错的,而且它的逆矩阵可以通过行列式来直接给出来
可以参阅《大学数学解题法诠释》
17728南开今年更难考,我去年栽了。
17728我也想考
顶一下!!
17728我准备考研都半年多了
准备考南开但是听说南开一半多被保送名额占据
我彷徨啊
学习状态进入低谷,怎么办??
考研的人们,你们复习到什么程度了?
考上的大哥大姐们,你们有过这种感觉么?
我现在无助,迷茫。
谢谢回贴
17728me too
17728我也想考南开的,可离报名时间越近,就越犹豫。
我觉得,如果你做好了明年再考的准备,就南开一搏吧。
他就算报送一半,不是还要对外再招一半。
实力决定一切!
17728难考不表示不能考,
可不能临阵退缩哦!
相信自己,准没错.
加油!
17728同是郁闷中人,对人大的概率统计专业不是很了解,有谁了解这个专业怎样?
17728加油,怕他干嘛
17728不要怕学好了考好了自然一切都好了啊!
17728我顶
17728考好了自然一切都好
17728
坚持一天,进步一天,成功多一点
祝你们好运
17728楼主,现在低谷是好事啊,一个多月可以让你再次回到顶峰,如果最后到了元月份出现低谷,那神仙估计就救不了你啊,我都经历过了n多个低谷了,现在虽然不在顶逢,但是也还行,想最后一个月来个猛烈的冲刺,趁这段时间养足精神最重要!
支持你啊,兄弟,考研的都是苦命的孩子啊!
17728谢谢大家
都是考研路上的战友
欢迎你们都考那所学校啊
祝你们考试顺利!!!!!!
17729
http://www.or-reliability.cn/
17729支持!
17730请问这个积分怎么求?post-8-1125977484.gif
17730一种可能的解法post-8-1126166411.gif
17730
| 引用 (Lf832003 @ 2005年09月08日
16时00分) |
| 一种可能的解法
|
顶楼,你这种解法有错误呀!!~~~~~~
I(a)是一个关于a的常数,怎么可以求导呢?
17731continuepost-33-1126082384.ibf
17731为何要解压码呢?咋办啊?
17731太详细了,可以出本书了。一定畅销
17731太好了
17731怎么都要?
17731谢谢搂主!
17731xiexie ,8cuo !
17731楼主万岁!
17731搂主大好人
17731找了很久的东东啊.真是太感谢了.
17731没有积分.只有再支持一次了.希望楼主勿怪.这是我很早就想要的东东了.
17731下得不全.楼主.可以发一份给我吗???
xixu98@163.com
iawfnige@163.com
真是太感谢太感谢您了.二个邮箱都可以的.
17731continuepost-33-11260825
19.ibf
17731不错,谢谢!
17731continuepost-33-1126082675.ibf
17731终于传完了!!!
书上的习题有什么问题大家可以互相讨论呀
再传一份mathenglishpost-33-1126082972.ibf
17731顶
17731谢谢搂主!
17731非常感谢
17731t太棒了
我怎么不能下载那
17731是我电脑不行吗 郁闷 我找了好久了
楼主 你可不可以发打俺邮箱里
zbt31415@163.com
17731感谢楼主!!!!!十分感谢楼主!!!!楼主万岁!!!
17731真的是十分感谢!
我的邮箱:yxtx
1984@yahoo.com.cn
麻烦发到我邮箱里去好吗?
再一次感谢你们的辛勤劳动,致于崇高的敬意!
17731好久就想要这个东东了
谢谢
17731楼主大好人!非常感谢!
17731楼主真是太好了
谢谢阿!
17731楼主万岁就夸张了点,楼主100岁!
17731复旦陈传璋数分答案
下载网址
http://bbs.math.org.cn/dispbbs.asp?BoardID=3...replyID=&skin=1post-33-1125978240.ibf
17731复旦陈传璋数分答案post-33-1125978428.ibf
17731复旦陈传璋数分答案post-33-1125978582.ibf
17731复旦陈传璋数分答案post-33-1125978787.ibf
17731文件大了点,只能分卷压缩
17731就是啊,后面的呢,我们急需后面的!楼主万岁好了,你快发出来,不行万岁万岁万万岁!也要发出来!
17731后面还有很多章,文件分割上传太麻烦了,确实需要的朋友,可以留下邮箱!
17731continuepost-33-112608
1906.ibf
17731continuepost-33-1126082009.ibf
17731continuepost-33-1126082124.ibf
17731继续上传post-33-1126081681.ibf
17731对楼主的做法致以崇高的敬意,楼主万岁!
17731楼主,后面的有吗?谢谢了!
17731楼主真是好人啊!找了好久的东东!
17731我要一份,我的邮箱
guozhiheng590@126.com
谢谢楼主!!!!!!
17731非常感谢呀,
楼主真是太好了
17731谢谢
17731怎么所有的文件夹都一样啊
再给我发一分吧
lyjnsyn@tom.com
谢谢
17731这本书是有习题集买的
是本简装的黄皮小书
我不知道那里有买的
我是从学长那里买到的
17731真的很多,发给:predestan@163.com
非常感谢
17731感谢!!1
17731不错
17731太谢谢了!大大的好人呀!
17731hakeemchoi@yahaoo.com.cn 谢谢楼主
17731谢谢!
17731太感谢了!
17731好好好哈
17731好啊!
17731
太感谢了!太感谢了!
17731谢谢这位老师!您辛苦了!感谢您!我的邮箱是
anzi_
1980@163.com
QQ是10452531
泡泡是anzi_
1980
我想要全部的数分答案,就是复旦大学,陈传章老师的那版的
拜托了!
非常感谢!
17731楼主!非常感谢您啊!呵呵!我下完了,但是解压缩后,是不是都重复了啊?是不是一共就是从ch1~ch22啊?
17731请问楼主我需要打印,可是有密码打不了
能不能帮帮忙
非常感谢楼主!
17731支持楼主!
17731支持!
17731再次感谢
17731真的太感谢了,楼主辛苦了!
向楼主致意!!!
17731楼主 我下载的打不开
能给我把完整的 发到信箱吗 ???? 谢谢
我的信箱号 jhuang
19831116@163.com
17731下载完后放在一个文件夹,后用winrar解压即可,可用pdfreader阅读,Acrobat Reader好象有点问题
17731楼主能不能给我也发一份,littlehorse228@163.com我先谢了!
17731好!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
17731好 非常感谢
17731

怎么才能解压啊
17731谢谢谢谢
17731太感谢了!但是要是不要钱就好了
17731没钱啊
17731麻烦楼主给我发一份陈传璋的数分的答案 E-mail:liujin20032002@yahoo.com.cn
17731向楼主鞠躬
17731楼主,好顶,好顶,万岁万岁万岁~~~~~~
17731十分十分感谢,谢谢楼主了!!!
17731May I have a .pdf version? Thanks. johnzhang1234@yahoo.ca
17731谢谢楼主!
17731太好了!!!
17731精彩 积分难得呀
17731感谢
17731感谢楼主!
17731后面的什么时候能够贴完啊,真是不错啊,省了很多钱买书了!
17731太好 了
17731非常感谢!
17731我要一份,我的邮箱是
kangc
1976@yahoo.com.cn
谢谢楼主!!!!!!
17731我的油箱xifei123@hotmail.com
谢谢楼主
17731很好,加油
17731首先感谢,能发份到我邮箱吗,两个都发一份
yuxianzh@swu.edu.cn
yuxianzhi_penguin@sina.com
第一个可能有点小,我QQ21
195807,可以通过QQ传,交个朋友
17731楼主
为什么我下的打不开啊
能不能发到我邮箱啊
万分感谢哦!!!!!!!!
Qing3386@21cn.com
如果方便的话发到我邮箱吧
谢谢!!!!!!!!
17731真是伟大的行为!
17731在此谢谢了!
17731真是~~~~太好了。我们系里那里mm说过谁要是有这份答案的话就嫁给谁哪。
还有你们那帮让给你们发邮件的无耻的家伙们,难道你们不会自己手工下载嘛。
17731再一次谢谢,解决很大问题哪。谢谢学长。
17731加了密的,不能打印,各位仁兄可有密码
17731好好
17731我的积分 不多!!!!!!!!!!! 55555555555555555555
17731总算搞定了 谢谢了!!!!!!!!!好运
17731解压后用什么工具打开呀!!
17731解压了怎么还是打不开呢??
17731wohuikaode@sohu.com
17731楼住,大好人啊!
17731打不开呀?是怎么会事,是不是你没有上传啊,还是文件已经破寻了!恳请尽快解决,好吗?谢谢了
17731太伟大了,强烈感谢!
17731thankS!
17731楼主我不知道如何感谢你.
17731谢谢拉 谢谢阿
17731我的邮箱是john-ma@163.com 谢谢楼主了
17731那出版的?????!!!!!年份??????!!!!!!!!作者
?????????!!!!!!!!!!!!
谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢谢
17731非常感谢!
17731谢谢这位老师!您辛苦了!感谢您!我的邮箱是
kaoyan2009@163.com
QQ是270136827
我想要全部的数分答案,就是复旦大学,陈传章老师的那版的
拜托了!
非常感谢!
17731好啊
谢谢啦
17731很好 谢谢 就是要好多积分阿
17731吗的,骗人,根本就不能用
17731感谢楼主,这是我搜寻很久的东西。要是楼主能给我密码,那更是感激不尽。
我的信箱是;l-weip@126.com
17731太谢谢了!
17731复旦陈传璋数分答案怎样下载?要用什么软件打开??
17731复旦陈传璋数分答案pdf打不开呀,很遗憾.
17731能打开,得用其他软件!
17731先谢谢啦。
17731非常感谢呀,
楼主真是太好了
17731楼主真是好人啊!找了好久的东东!
17731goodgoodgoodgoodgoodgoodgoodgood!!!!!!!!!!!!!!!
17731要好多积分阿
17731我要一份john-ma@163.com 谢谢楼主
17731楼主,我要一份啊,我的邮箱是beeyzh@163.com
17731Email:golden_chan@163.com
谢谢^_^
17731十万分的感谢
17731hao !~
支持!~
17731请问还有其他有关高代的题解?
谢谢!
17731感谢搂主 ,太厉害了。
17731很好很好。。。。。。
17731xiexiele!
17731我想要一份,我的油箱是nice.dog@163.com非常感谢!
17731楼主,还有吗?谢谢了
17731感谢楼主。向楼主学习
17731复旦的欧阳光中的书也不错
17731多谢 !
17731我的lani1126@vip.sina.com
17731
引用 (kiangb @ 2005年11月10日
17时21分) |
| 要好多积分阿
|
楼主请发到:
hongming6662@163.com
17731guoxue_644@163.com,先行谢谢
17731楼主真伟大,为众多的爱数学的人提供宝贵的资料,向楼主敬礼.烦请楼主给发一份.我的邮箱:markmanid@yahoo.com.cn
17731能否发一份给我nirui
1981@163.com
谢谢了
17731可以给我发一份吗? nk_yt@eyou.com
17731非常感谢,,正在找后几张11111111
17731总是没钱啊,,要下好费劲啊
17731还是谢谢了
17731thank you!!!!!!!!
17731非常感谢!!!
17731东西不错!谢谢搂住!
1773113_22章怎么下不来了?!
前面的怎么都是一样的阿?!
谢谢楼主!非常感谢!!
17731给我一份好吗?谢谢!aalison
18@163.com
17731谢谢!另外,我想问一下:part1,...,part4好象是重复的? 不能打印啊?
17731还有Ch13-22解不开压缩,打不开啊?
17731非常感谢楼主!
17731好东西,多谢了
17731太感激楼主了,人品超好!!我正急用呢!!!!!
17731谢谢,支持
17731为什么只有第一章第一部分的极限初论和第二部分的单变量积分学?别的内容能下载下来,但是无法解压,说什么有下列压缩分卷才能解压,不懂,希望楼主指点迷津.
17731十分感谢楼主。
17731楼主,实在太感谢了。现在都1月份了,不知道现在你还在不在,发到我邮箱来好吗?我邮箱是 kaoyan511@yahoo.com.cn
17731谢谢,我的QQ是88476055,邮箱是xyt0472@163.com,马上就要考试了请帮帮忙尽快给我发过来
17731偶还需努力
17731ksqqxq@163.com
支持楼主
17731太好了,向楼主致意,谢谢,我的qq号:3
1789135
邮箱:liaolixiuming@126.com 再次感谢楼主
17731向楼主致谢,请传一份到 liaolixiuming@126.com 十万火急呀,再次谢谢
17731谢谢楼主 !!!!!!!
我的邮箱 zbwu
1982@163.com
17731
| 引用 (zsumath @ 2005年09月07日
16时39分) |
| continue
|
一个好人啊!
17731
| 引用 (zsumath @ 2005年09月07日
16时44分) |
| continue
|
好人!!!
17731斑竹真是好人呀。
太谢谢你了。
17731听说 今年 北大的高代题很难。
17731能传到我的emil:czhaomeng@163.com.
好么?
17731复旦 陈传璋 数学分析答案怎么要钱, 怎么在网络上挣“钱”呢

17731太感谢了
17731谢谢
17731这种好贴,一定要顶啊。
LZ也请发给我一份,谢谢~~
sjx.wina@gmail.com
17731感谢楼主!!!!!!
17731好人呀,急需要陈传璋的数学答案,
请发到邮箱:liaolixiuming@126.com
17731多谢楼主,不知道哪里有纸版的?
谢谢!
17731非常感谢,楼主真是雪中送炭啊!
17731能否发给我一份?我的邮箱chenxi
1978@126.com,真是急需,十分感谢。
17731多谢呀!!!!
17731楼主不会是自已做的吧?
17731为什么我的钱总是不够呀,晕!!!
17731我的邮箱,cock08@eyou.com,谢谢!!!
17731十分感谢楼主!
17731像楼主这样的好人不多了啊 谢谢了
17731谢谢楼主,我终于找到了!!
17731不够分呀!!!
17731楼主,真是太感谢了!
17731不知怎么解压,谁知,请回复
hft113@163.com,谢了
17731楼主也给小妹来一封吧,谢谢了!!!!
13579f@163.com
17731非常感谢呀
17731多谢楼主!
17731thank you
17731谢谢
17731大哥 很感谢了
17731太好了,好东西.
17731有没有其他数分的解答.
17731十分感谢!请问有没有'科学出版社'孙荣恒的应用概率统计的解答?
17731太感激楼主了,万分感谢!
17731谢谢了
17731我的email
dusuguang@163.com
17731就是啊,后面的呢,我们急需后面的!
17731太感谢楼主了
17731楼主,能不能给我发一份复旦陈传璋数分的答案咯?
我的Email:lengchan@163.com
17731谢谢楼主的帖子
17731楼主能给我发一分吗,谢谢了^^ 我的邮箱foolboy7@swnu.edu.cn
17731楼主能不能给我一份,我的邮箱是caiqing
19841224@126.com
17731楼主,谢谢啊!
17731楼主:
可以给我发完整的吗?
yccycc
19860408@yahoo.com.cn
17731楼主可以给我一份吗?
我的邮箱是sulj1215@yahoo.com.cn
万分感激!!!
17731楼主万岁,楼主是好人
17731多谢楼主,这牛阿!!
好需要!
17731十分感谢楼主~~~~~
顶~~~~~~~~~~~~~~
17731楼主,能给我发吗?好象打不开
wuqianfeng@mail.china.com
谢谢!@#$%^&*(
17731楼主好,我正急需这份答案,我的邮箱是zhaopeng5258@sina.com
谢谢
17731谢谢啊
17731谢谢楼主呀
17731感谢楼主。
我正急需这份答案,我的邮箱是dengvskai@163.com
谢谢。谢谢
17731谢谢楼主,但是加了密,怎样才能打开呢。请发到我的信箱:wudong8866
@sina.com
17731谢谢楼主
可是我打不开
给我发一份好吗!
我的邮箱是
timevsal@126.com
17731给我发一份吧,谢谢楼主!yazhaqu@sina.com
17731好!
17731真是及时雨啊!感谢!
17731多谢楼主啊,我是教数学分析的老师啊,这资料对我太有用了啊,
17731楼主,您是大恩人啊,在解压缩的时候怎么打不开啊
17731谢谢楼主的精神
17731谢谢你的答案!我找了好久了!
17731谢谢!!!!!!!!!
17731谢谢!!!请发给我一份吧!我的邮箱:hs_3@163.com
17731我也 要份完整的答案,我的油箱hebintao@163.com
17731我需要一份完整的答案,请楼主帮忙给我发一份吧.我的油箱hebintao@163.com
17731
| 引用 (shuren @ 2005年09月25日
13时46分) |
| 好 非常感谢
|
搂主这个帖子是相当的好啊,感谢万分
17731谢谢!
17731
引用 (caishuiming @ 2005年09月15日
18时33分) |
| 感谢!!1
|
怎么不能打印啊
17731
| 引用 (djdi58 @ 2006年04月11日
22时47分) |
引用 (caishuiming @ 2005年09月15日
18时33分) | | 感谢!!1
|
怎么不能打印啊
|
能发给我吗??
wanghengxingw@yahoo.com.cn
17731怎么后面的没有呀!!!
17731我也想要,谢谢了!!!!!!!
lwxin001@yahoo.com.cn
17731我的邮箱是 mahaiyan_28@126.com
谢谢楼主了
17731请楼主也给我一份谢谢furuguiqu@yahoo.com.cn
17731bu cuo
17731谢谢!!!!!!!!!
好东东
17731好!!顶一下!!
17731楼主!我想考数学专业的研究生,请你把答案给我完整的发一下吧!!非常感谢!!谢谢!!邮箱 bigeye_mm@163.com
17731太好了
17731真是好人啊
17731我下的怎么不管用呀
17731好东西
17731谢谢啦
17731楼主太好啦
17731我的邮箱是lc407@163.com 现在刚刚把上下册看了一遍 现急需要一套答案来做课后习题 小弟在此万分感谢 谢谢啊
17731无话可说,除了感谢。
17731为什么打不开?谢谢.
[CODE]
17731楼主好人啊,谢谢了。。
17731非常感谢,收下了,
17731不错的东东!呵呵!谢谢楼主
17731太好了
感动呀
17731我的邮箱是 jinannan
18@tom.com
急需答案 非常的感谢搂住
在这先说声谢谢
17731楼主好人啊!!!
17731我是新来的,大家照顾下
17731再次感谢!!
17731谢谢,我想要完全的,liyi433@yahoo.com.cn
17731楼主太好了
谢谢
谢谢
谢谢
我的QQ7786112
我的邮件是xxf8514@126.com
再次谢谢
太伟大了
我找了N久才找到啊
17731用什么程序打开?我解压以后就打不开,请各位帮帮忙
17731我真的很想要,我是读数学专业的,很需要.但却打不开.请楼主发到我的信箱koichicy@126.com,谢谢谢谢!!!!!
17731不好意思,好不容易下载了却解压不开,麻烦楼主给一份完整的,非常感谢
EMAIL:zhengwendeyouxiang@hotmail.com
17731我有个朋友也很需要这个答案,帮帮忙,给我也传一份,先谢谢了,我的邮箱是fangmeilixinqing@126.com。
17731对楼主的做法致以崇高的敬意,楼主万岁!
17731想楼主这样的好人一定会....!!!
我啥也不说了我....555555
17731楼主大好人啊真太谢谢了,你给了我最想的东西
17731麻烦楼主给我发一份复旦大学陈传障主编的数分答案,非常感谢!我的邮箱是abc_xiaoxia@eyou.com
17731楼主,能不能也给我发一份,不胜感激
我 的邮箱: yshl
1985@tom.com
17731我也想要一份:mzhb929@yahoo.com.cn
万分感谢!!!!!!!!
17731非常感谢,lz
17731谢谢楼主,竟然有这么好的东西
17731
引用 (hftenger @ 2006年03月24日
17时01分) |
十分感谢楼主~~~~~
顶~~~~~~~~~~~~~~ |
我也要啊
17731谢谢了!最后那个文件是数学符号的英文表示
17731陈传璋编的《数学分析》怎么要密码才能打开?
谁能告诉它的密码?
17731楼主你好!能给我发一份复旦大学陈传障主编的数分答案吗?万分感谢!我的邮箱是caohongliang0303@sina.com
17731haoren ding
17731谢谢楼主,竟然有这么好的东西 谢谢
17731谢谢分享!
17731lizhijun1
18@163.com
楼主万岁楼主万岁楼主万岁
17731怎么还没有人告诉我那陈传璋的数学分析答案的密码?
17731麻烦楼主给我发一份复旦大学陈传障主编的数分答案,非常感谢!我的邮箱是yangboyhdw@yahoo.com.cn.非常感谢!真是天助我也!
17731太好了 终于找到这个东西了 谢谢楼主
17731楼主真是大恩大德呀,好人总是有好报的.
17731好是不是 苦苦 顶风
17731能不能给我传一份啊 万分感谢 ydlaaa@yahoo.com.cn
17731后面的了?
17731感谢的五体投地呀!3q
17731[COLOR=blue]
非常感谢!但密码是什么呀!
17731非常谢谢
17731还是用邮箱吧我的是 543204446@qq.com谢谢楼主了!
17731好,狂顶!
17731为什么下载后解压失败????
17731楼主是好人啊,我顶顶顶!!!!!!!!!!!!!
17731要怎么增加积分啊?
17731楼主大好人啊
17731可不可以不要积分就下载哟
17731到处找这本书的答案 、就是找不到谢谢了
17731复旦数学分析的那本三导书没多少价值
17731太感谢了,找了很久的!!!!
17731再此感谢,我把它下完了,积分也用光了,很划算的!
17731怎么打不开哟
17731楼住的崇高无法修饰
太好了
17731支持楼主啊~~太好了,找了好久了啊~~~
17731Thank you very
much!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
17731同志们对答案这么感兴趣,等我编完了,让大家爽歪歪。
17731Thanks a lot!!!
17731
顶~!
17731
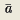
yangna514@163.com~!
thanks~!
17731太好了,这东西太好了
17731感谢楼主!!!
17731没分了
17731为什么啊,又没分了
17731再来
17731楼主你好:
我准备考南开大学数学学院的研究生
他们学校的数分参考书目是复旦大学的那本书
没有答案很不方便
能否帮我拥有想法一份完整版的课后答案?
邮箱:xuekunliu2008@163.com
非常感激!!!
17731我需要一份完整版的答案
xuekunliu2008@163.com
万分感谢!!!
17731陈传璋的数分答案,我急需啊,小妹在这里先谢了.hfz34254@163.com
17731我下载了,也解压了,可是打不开,麻烦楼主该我发份完整的吧,谢谢了
我的邮箱是:whx6_307@163.com
17731楼主,你好
我急要完整的答案,希望你能给我发一份 hubeipjh@tom.com
非常感谢
17731DDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD
17731谢谢了!
17731东西不错,谢谢!
17731谢谢!
17731感谢楼住啊。。雪中送炭啊,,,给我发个全的把。。cgaxj0102@21cn.com
17731楼主
给我发一份吧 谢谢
jiangbinnju@yahoo.com.cn
17731谢谢楼主,好啊!
17731楼主,我急需这个材料啊,可是打不开啊,怎么办,给我发个完整版的啊,谢谢!
yejianhong2000@163.com
17731楼主真是太好了!!!谢谢 !!!!
17731感谢...
17731谢谢LZ,找了好久了
17731说实话,复旦的问题不咋样,也没有收集。记得上海交大的问题有搞头。
17731交大的问题是指什么?
17731谢谢楼主!!
17731谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主谢谢楼主
17731还差一个啊 积分不够 积分不够 积分不够 积分不够 积分不够
17731不全免费阿
17731楼主好 我想打印啊 可是没有密码 能不能告诉我密码 或者再发一份没有密码的到我的邮箱 sunxiaobin_
1783@126.com
17731怎么才能打开下载后的东西?
17731“不全免费阿 ”
还要啥自行车啊!
17731楼主能不能发个完整版的到我的邮箱,多谢了!
邮箱:xueshanmianyun@163.com
17731楼主太伟大了
万分感谢中。。。
17731感谢楼主!当初学得时候好多问题就没搞懂,现在终于有个参考了。再次感谢楼主!
17731楼主,大好人,能不能给我一份啊,我正打算考研呢。急需要啊。
谢谢!
liujuan82@126.com
我想要完整的,再次感谢。
17731

f(x)dx$
MathEndBegin-->
Unknown character Unknown
characterintf(x)dx
17731楼主!我要!wo_shi_caiwen@hotmail.com 先谢了!
17731能否发到我的邮箱:zhangxj2088sina.com,多谢了。(数学分析课后答案)
17731急用,俺知道楼主是个大大的好人,希望有空能早点发到我的邮箱:zhangxj2088@sina.com 再次感谢楼主。
17731真是谢谢楼主了,我找了好长时间啊
17731好
非常感谢11111
17731怎么无法下载啊,快点帮帮忙啊。
17731楼主,能不能有空发到我的邮箱marugs@163.com,我要一整份的,万分感谢!
17731谢谢楼主
17731我要
兄弟
zzxenjoy@163.com
谢谢
17731楼主,可以给我发一份么?我的邮箱jinling_long@sina.com,Thank you very much!
17731感谢楼主[COLOR=orange][SIZE=7]
17731谢谢楼主。
17731hao xiexie
17731我的钱呀 又被剥削了
17731我也想下,谢谢
17731谢谢
17731你真是个大好人啊!
可否帮我传一下所有的答案!
邮箱 xiaoguqinqin@126.com
17731感谢楼主提供好东西啊,是什么格式的?
17731ding
17731感谢感谢,就是花了不少钱 :(
17731下载完成后,解压时,说要有压缩卷才能继续解压,怎么办呢?
17731rayn4
17@163.com 麻烦楼主啦
17731我十分想要,可没分了
17731搂住真好我很需要这个谢谢
17731我的积分又没有了怎么办??钱用得好快呀!!!
17731楼主感谢啊
17731楼主真是太好拉
17731楼主感谢你啊
17731太感谢了!
17731谢谢楼主
17731楼主真好人也!!
17731谢谢.居然是电子版的.
17731谁有陈传章数学分析课本的电子版啊
17731一个好人
17731谢谢,辛苦了
17731怎么的积分啊?
17731怎么解压啊?
17731是呀,怎么解压?我废了老半天都没解开!请告诉一下好吗?要不给我发一份。邮箱:lylmessage@163.com
17731真的太谢谢楼主了!!!
顶!!!!!
17731厉害!!!
17731大家都想楼主致敬吧.万岁万岁万万岁.
祝楼主以后身体健康,工作顺利,万事如意,一切都好.
17731笨蛋啊.解压读不会啊.都放在一起啊.然后释放文件不就可以了.哎
17731谢谢啊 太谢谢了 我正在找呢
17731我感谢得不得了啊
17731非常感谢楼主,我找了好多天终于下到了,向伟大的楼主致敬!!!!!!!!!!!!
17731感谢!!
17731找了好久,楼主真是大好人!谢谢!
17731我想下载,谢谢楼主
17731
虽然已经很长时间了,但我相信此帖是不会衰落的,因为背后有人付出了艰辛!再次感谢楼主,要是也能给我发一份那就更多感谢了!Email:nwy86@163.com顺便给一下解压的方法吧,因为我发现有很多人跟我一样不太会解压的,再次感谢楼主!!!
17731楼主真是太好了 thanks very much
17731怎么还要1分啊,分从哪儿得?
17731谢谢楼主
17731
虽然已经很长时间了,再次感谢楼主,要是也能给我发一份那就更多感谢了!521nk@sina.com顺便给一下解压的方法吧,因为我发现有很多人跟我一样不太会解压的,再次感谢楼主!!!
17731谢谢!我急用!!hhrl
19823@163.com
17731楼主真是好人啊!找了好久的东东!
17731看来很多人都是学的这个教材哈
17731谢谢哈!!!!!!!!!!!!!!
17731感谢楼主,给我传一份复旦大学陈传璋数学分析的答案吧。我的邮箱:fengjianwen2004@163.com 谢谢!!!!
17731谢谢分享!
17731谢谢共享
17731谢谢
17731谢谢
17731我怎么打不开啊,你能不能给我发到邮箱里啊?ning021128@163.com
不胜感激
17731怎么尽快获得积分啊?
17731ding
17731十分感谢
17731多谢楼主共享!
17731积分怎么算的?感觉没有积分了似的,哭
17731谢谢!感谢楼主,给我传一份复旦大学陈传璋数学分析的答案吧。我的邮箱:whzsibuliao@126.com谢谢!!!! !!!
17731
引用 (ning021128 @ 2006年11月16日
17时42分) |
我怎么打不开啊,你能不能给我发到邮箱里啊?whzsibuliao@126.com
不胜感激
|
我怎么打不开啊,你能不能给我发到邮箱里啊?whzsibuliao@126.com
不胜感激
17731楼主真好人也
太谢谢了
17731有没有关于复旦数分二版陈传璋答案这本书,具体书名出版社?
17731楼主帮帮忙
我好象没有看到第三篇关于级数论的答案
17731我怎么打不开啊,你能不能给我发到邮箱里啊?550629264@qq.com
不胜感激
17731非常感谢呀,
楼主真是太好了 !!!!!!!
17731怎么不能打印啊??
17731哪位好心人,能不能麻烦发到我邮箱里,我打不开阿!
不胜感激!
caolihui
1982@sohu.com
好人一生平安!
17731楼主,你简直就是大好人,我的感激之情已经无法用言语来表达!
17731
谢谢
17731希望再接再厉
17731我也要一分
17731v1abnm@163.com感谢楼主
17731楼主好 我想打印啊 可是没有密码 能不能告诉我密码 或者再发一份没有密码的到我的邮箱
v1abnm@163.com
17731shi zai shi tai gan xie liao
17731我想要.我的邮箱是yongjing012@163.COM
17731想要!!可惜啊分分分啊!!
17731楼主牛阿!!楼好高

17731看看我还有多少分!!

17731楼主万岁!
17731经过处理可打印post-38-1168991137.ibf
17731太感谢了!!!!!!!。。。。
不好好学就是辜负您
17731楼主,我也十分急需一份,油箱是asheng65@yahoo.com.cn ,谢谢
17731顺便给一下解压的方法吧,因为我发现有很多人跟我一样不太会解压的,再次感谢楼主!!! asheng65@yahoo.com.cn
17731非常感谢!
17731麻烦楼主给我发一份复旦大学陈传障主编的数分答案,非常感谢!我的邮箱是asheng65@yahoo.com.cn.非常感谢!真是天助我也!
17731马上就考了,有好心的人也给我发一份吧,谢谢了。。。。。。
asheng65@yahoo.com.cn.
17731楼主牛人,很感激
17731有一个怎么打不开呀
17731给我一份v1abnm@163.com
17731太谢谢了!!!!!!!!!
17731谢谢楼主利用宝贵的时间给我们提供这么好的资料!!
17731谢谢 了
17731十分感谢搂主!!!
17731谢谢,太感谢了,眼泪哗哗的
17731何时能够传完整哦。谢谢
17731我也需要一份,楼主能否发一份到我的邮箱:yyww.yq@sina.com
17731太棒了
17731谢谢·改天我也把我手头的电子书贡献一下!
17731楼主,可以给我发一份吗,我搞了好长时间都没弄好,谢谢了
wtf
19850115@126.com
17731谢谢你的数学分析答案,不过最后一个怎么打不开呢?
17731楼主,麻烦你把陈传璋的数学分析的13-22章的习题答案发给我一下好吗?谢谢!我的邮箱是zhang249786339@126.com.真的非常感谢你,因为我是现在才在准备,所以时间比较紧,我很想把这些事情快点搞定.希望你能帮帮我,我将不甚感激!!!!!!!!!!!!!!!
17731我昨天跑遍了重庆的大部分书店,都没有办法买到这本书的解题答案,看到这里有真的是太高兴了.真是非常的感谢你!麻烦你把最后的部分发给我好吗?谢谢!
17731不过就是这个是电子文档,不能转化成WORD打印出来真是太遗憾了,毕竟老是在电脑上看还是很不方便的.请问各位有办法把它转化成普通的文档打印出来吗?请大家帮帮忙,给我出一下主意好吗?谢谢
17731在本站的第一个下载,就能够找到这么好的资料,真是太感谢了!
17731真是经典!所有的页面文字都可以选择的!也就是说不是垃圾PNG转换过来的图片!
17731我要一份!!!先谢啦
wlhuanglin@163.com
17731十分感谢楼主
嘿嘿
17731我也要,太谢谢了!
sarkey102@hotmail.com
17731给我发一份吧,谢谢楼主!
yun27
18@163.com
17731我也想要,谢谢楼主!
yun27
18@163.com
17731我怎么打不开啊
17731真是好人哦,楼主,好人还是好报的!跑遍了长沙的书点也没买到答案,想不到在这看到了,真是
太高兴了,激动!楼主能不能把整本答案也传下我哦,万分感谢!邮箱 jiangling0922@163.com
17731真是好人哦,楼主,好人还是好报的!跑遍了长沙的书点也没买到答案,想不到在这看到了,真是
太高兴了,激动!楼主能不能把整本答案也传下我哦,万分感谢!邮箱 jiangling0922@163.com
17731谢谢,楼主 ,我也想要一份给我发一份吧 ,谢谢 了
qiaojo1228@yahoo.com.cn
17731怎么解压啊
17731真的好无私阿!榜样!!
17731太好了.
17731ou ye lai zhichi yi xia
17731好东东!!!顶。
17731楼主,可以给我发一份吗,
我解压解不开啊,弄了好长时间都没弄好,谢谢了
luochao0927@163.com
17731很需要这份答案,能发到我邮箱吗?liyuanhao10@163.com
非常感谢楼主!
17731去这个邮箱下吧: kaoyanren666@126.com
密码:kaoyan123456
祝大家成功!!!
17731我想要,又想是yangshanbing03@yahoo.com.cn
17731十分感谢!
17731谢谢楼主!代表我和我的同学表示感谢!
邮箱:aaron_04@163.com
17731谢谢楼主 我代表我的同事向您致敬.
向您学习这种无私的精神
17731全不下载下来,然后一起选中,在解压
就可以了
不要一个一个解压,好象是分割的
如果需要的话,发邮件至wangwei.math@gmail.com.我可以给你传
17731感谢楼主
17731给我发一份吧,谢谢楼主
我邮箱是 zhxm84215@163.com
17731z8712@163.com
谢谢
17731十分感谢
17731十分感谢
17731大哥这附件怎么加啊
17731好东西,谢谢楼主。
17731非常感谢
17731谢谢楼主
我的信箱是wbl302@163.com
17731我也要楼主,janzhgy@163.com.谢谢楼主啊。
17731谢谢 楼主!!!
letian99999@126.com
17731请问答案还有吗?
能帮我发一份吗
我邮箱是yfeng-0@163.com
17731我怎么下不成啊,请问楼主还有吗?帮我发一份吧。我的邮箱是yangweixin20082008@163.com谢谢楼主
17731山东龙口伏牛山到访
17731我怎么下不成啊,请问楼主还有吗?帮我发一份吧。我的邮箱是lanzuping_tlmdx@163.com谢谢楼主
17731我也下不了啊,我的邮箱kongxianglin123456@126.com,谢谢楼主
17731可否给我发一份啊?我邮箱是wokonglinglude@163.com.谢谢!!!
17731数学分析-陈传章(复旦) 习题答案
共三部分: email 我,有需要者!
yanbin4@126.com
17731下载不了啊,老说上不了服务器
17731给我的Email发一封吧!下载不了,我有EMAIL:是:
luoqixianglqx@163.com
非常感谢您的帮助!!!!!!!
17731给我的Email发一封吧!下载不了,我有EMAIL:是:
dzhenan2008@163.com
非常感谢您的帮助!!!!!!!
17731下不了,我的邮箱dingyanboo@163.com,发给我一份吧。。。。
17731楼主给我一份吧,太感谢了!wdjzhlbr@126.com
17731你好,我也急需一份,给我发一份吧,十分感谢,等待中:bing463233@163.com
17731darice1234@163.com
谢谢搂主!
17731为什么我下载不了啊
17731我也想要一份,楼主万岁!!!我的邮箱是xiazhiquan2007@sina.com
谢谢咯。。。。。。
17731多谢
17731xionghoushuai@vip.qq.com 发个来 谢谢
17731顶了!
谢谢楼主!
17732我不是:p
17732请问这里有中科院数学方向专业的研究生吗?
17734我今年欲报考中科大的计算数学研究生,请问哪个方向不错? 大型科学计算如何?
17736出来了,在研究生院首页
17736我今年欲考中科大的计算数学,有考中科大数学的可多聊聊啊
17736我现在专业课试题还未找到,谁会想有给点信息啊
17736中科大的《数学分析》、《线性代数》教材上的习题解得怎样?
17736数学分析作得还行主要是后面有答案,线性代数没做。主要我为什么找不到它2000年以后的专业试题啊?
17736还有它的招生简章好象还没出来啊
17736我准备考中科院成都计算所的数学专业,用的
正是中科大的试题,也算我一个吧。
有在系统做科大分析教材后面题的同学吗?
我觉得这本书写得不错。
好像科大分析不单考级数,而是放在函数项级数里面?
多多交流!
17736你是去合肥还是北京?中科院吧?硕士还是博士?
17736何以不考北大,清华呢?
大丈夫难得一博
17736考研究生并不只是为了什么搏一搏,而是对这门学问感兴趣,想从事这方面的研究。
第一,中科大学术气氛还好,人数招的也适当,试想去那些只招一两个人的地方,有什么想法连个讨论的人都没有,未免有些孤独。
其次,中科大处于合肥,城市并不是很发达,清净的环境对外交可能不利,但对学术研究,特别是理科科研究可能就是一个天堂,静以修身嘛。
同时,我们都有自己的想法。我们需要的仅仅是一个空间,一个图书馆,一个朦胧的导向,自由能让我门更大的发挥自己,有了成果才是真正的凤毛麟角。
综上,我认为,中科大是一个比较理想的学习的地方,对于有兴趣想往这方面研究的人来说。
所以,我准备考中科大。
17736不好意思,我今天新来的!我想考中科院数学与系统科学研究所的基础数学专业!他们应是自己出题?不知几位提到的中科大与中科院是什末关系?
17736OK,go together!
17736中科大处于合肥,城市并不是很发达,清净的环境对外交可能不利,但对学术研究,特别是理科科研究可能就是一个天堂,静以修身嘛
17736哦
中科大和中科院的试题是一样的吗??
177371) prove that for every integer n, n^3 mod 6 = n mod 6
2) show
that {1,2,3} under multiplication modulo 4 is not a group but that
{1,2,3,4} under multiplication modulo 5 is a group.
thx
177371)if 2|n,3|n,nothing to prove. so assume that 2|n but 3 not |n, then
n=3k+1 or 3k+2. In the former, k=2m, so n=6k+1, ok; in the latter, k=2m+1,
so n=6m+4, an easy computation gives you everything.
2)Easy. The first,
2\times 2=4=0,so 2 is not invertible. The second forms the
multiplication group of the prime field F_5.
17737just exercise
diy is best
17738清华大学2005数学建模题目post-37-1125988385.ibf
17738到处都可以下
怎么还要积分啊~
17738积分归积分,下归下。这个论坛是为大家提供免费帮助的,是给我们爱好数学的人,开创一片天地。不是商业化的哦!~~~~~~
17738谢谢
17738说的对。
17738其实这次比赛A组
第一题好像在川大的一本书里面有类似的题目
17738第一题好像在川大的一本书里面有类似的题目
17738收到
17738谢谢分享
17738感谢你了
17738谢谢
17738有得下也说这么多真是的,先顶一下
17739求教:我是学几何的,也想考金融方面的博,大家都是了解这一方向的,我想问假如转金融会不会学起来更吃力?因为没有概率或者偏微方面的基础.还有导师们会不会也不情愿收换方向的,几何毕竟和金融联系不太大吧?
17739金融主要还是概率和微积分。
。。。。
17739我也想考金融的博,那些学校要好些-有博点-?
17740
非常感谢 我这样毕考研的 要的就是这个
17740我没钱了,挣钱!!!!!111
17740及议多一些大学的题的解答
!!!!!!!!11
1
17740为什么只有这几个大学的题?
难道只有这几个大学的题材是好的吗?
17740谢谢了!
17740解法简洁,如能举一反三,则可解决一大批类似的题。
17740几道中科院高等代数试题详解(见附件):
2003年第7题,2004年第7题,2005年第4题。post-38-1125989151.ibf
17740每次看都有新的收获,真是温故知新啊!经典的解答才有这样的效果的,大家一定要好好的吸取其中的紧要啊!
17740我来给种证法,不过需利用一个著名公式,如果你对本公式的发现或推导熟悉的话,不难理解
springboshi的方法了.post-38-1126579809.ibf
17740不是计算方向的研,应该不知道吧,没意思
17740我想请问一下,怎么我总打不开?
17740可能是你没有下载AcrobatReader软件
17740ding
17740请问springboshi,第2提的最后一行,也可以
A〈0且b'A-1b〉1啊
A》0,是什么意思啊,是表示正定矩阵,还是说取行列式值》0啊
17740你自己给出了一些符号。
原解答中的
A >0
表示正定。
至于b'A-1b<1,当然不需解释。
17740谢谢了!
17741悟空:
听说你又要考研了,你总是一会儿一个想法.上次,在王母娘娘的蟠桃宴上,我碰到你的时候,你不是说你不考研吗?还说考研这种恶俗的事情你不会做,弄得在场的几个刚刚考上研的仙童很没面子.看你又变卦了不是?
按理说,凭你在取经路上的贡献,应该是能保的,都是你跟
上面的关系处不好.当时不过,师父听说你要考感想,还是很高兴的,毕竟又上了一个档次,对你的发展只有好处没有坏处.你也看到了,现在西天这边大家都在考研,你能认清形势,师父替你高兴.上面给我们取经小组一共两个保研名额,我想就按贡献大小给你和八戒.报上去后,上面对你的意见大得很,尤其是东海龙王意见最大,说你当年借了他的定海神针,现在还不还.光这一条我就没有发言权。你说,现在取经结束都已有300年,你还拿那个棒子有什么用?就是有用需要续借,总得打个招呼嘛。你不打招呼,人家怎么知道你要用,给人家打个招呼,人家肯定会让你续借的嘛。。。。。。有借有还,再借不难。
好了,又扯远了。还是说你保研的事,龙王后来上下活动了一下,最后,你的名额就给了白龙马,虽然你没保上有点遗憾,但给白龙马也算是落到我们小组内,况且白龙马没有功劳也有苦劳,给了也就给了。
再说八戒,人家上面关系处理得好,报上去后,基本没怎么讨论就通过了,面试也放得很松。八戒的导师也不错,是文殊菩萨。现在,人间也重视教育,所以,文殊菩萨的香火很旺,经费也自然就多,今年报她那儿的人最多。你什么都好,就是在神际关系上处理不好,八戒这一点就比你强。
你看,同是一个师父带出来的,人家八戒现在都是研究生毕业,开始带研究生(听说今年第一年招生,可能比较好考,你要不就考八戒那里)。而你现在才准备考,唉!
我也给你介绍一下我最近的研究情况吧。这也是我给你写信的主要目的。其实,我就需要你这样的学生,保过来的几个动手能力太差,还不听话,就知道月底向我要工钱。最近,我刚申请了博士点,从明年起就可以带博士,你要是考这里,我给你一个直博的名额,省得你到时候再考博。最近,我主要研究的课题是“佛界是否应该顺应人间宗教市场的崇拜趋势”。你已经很久没来西天,你不知道我这个课题还是很热的,如来很重视,上次开会,如来还问我课题的进展情况。
我不是刚才跟你说了,人间现在重视教育,你看文殊的身价上去了,重视经济,道教的财神爷人气就很旺,所以,现在伄界也对这个问题重视起来。形成了以观音为首的“保守派”和以108罗汉为首的“革新派”之争。“保守派”认为,佛界应该重修行参悟,不要盲从人间崇拜的大流,应该引导众生慈悲向善,不是一味地迎合大众的口味。“革新派”认为,佛界应该讲市场规律,如果人们都不信佛,我们从哪里来供奉,从哪里来香火?所以,如来给我拨了些经费,让我成立一个课题组,对这个问题进行调研。
我是同意“革新派”的(听口气,如来也是向着革新派),时代不同了,佛界也要与时倶进嘛。最近,我也取得了一些研究成果,我认为应该设新四大菩萨——“吉托菩萨”(主管GR置、TOLLF考试)、“亨通菩萨”(司官运)、“济财菩萨”(相当于财神爷)和“高就菩萨”(主管就业)。
我又扯远了,好了,悟空,废话我也不多说了,还是希望你能考我这里。你聪明,又肯动,我这个课题还得多往人间跑,我觉得你合适,你要是愿意的话,过两天来我这里,我给你画画重点,专业课的题是我出的。至于公共课,出题的几个罗汉我都很熟,帮你打听一下“重点”也可以,免得你报什么“冲刺班”,还不是他们几个在那里讲?好了,废话我不多说了,你好好考虑一下吧。
祝你考研成功!
师父
17741hehe
17741很有意思!!:)
17741不错啊
17741真的有味呢。
17741很有意思,也很能反映现在考研的实际和内幕!!!
17741好笑,厉害
17741现实 理想
17741haha。
17741不错
17741haha
17741haha
17741不错,不错.很好玩的笑话
17741呵呵
17741笑死我鸟
17741这不是海成上面的吗????
17741哈哈哈,好玩!
17741很有意思!
17741!!!!!!!
17741笑过之余是反思,这就是中国现在的现状
17741很有意思.下载试题一定要扣分吗?
17741有些不会扣.
想起某位师姐的保研经历(不是我们学院的,更不是学数学的):她是那种成绩一般但在其他方面都很突出很积极的人,尤其在社交能力上很强.她为了保到北大去,居然与某研究生谈恋爱,借用他的职权改了自己的成绩单.现在已经在北大读研了.
别人可能连想都不会想吧.这就是现实.
17741说什么啊!!晕死!!
17741现实和理想永远有很大的差距
奇怪的是。。有理想的人才会成功,而只有理想的人则死的很惨
总是用与理想相背离的手段来实现理想
17741!!!!!!!!!!!!!!!
17741入木三分
17741看来我也应该申请一个博士点了。
17741呵呵,还真搞
17741强!!!
17741好
17741呵呵,有趣的嘛
17742可以加我呀 QQ64414403
17744就是致密性定理? 我想不出来怎么构造开区间集
17744好长时间不看数分了,是不是存在收敛的子列的定理
用反证法,假设这样的上下界构成闭子集[a,b]
如果不存在这样的子列,必然对于任意的x

[a,b],存在某个邻域O(x0),在这个范围里,只有有限个数。否则,可以构造一系列的邻域O(x0,1/n),这样就可得到收敛于x0的子集.
那么,存在一个开覆盖O(x),其中必然有有限个开集,是紧集的一个开覆盖。而且有定义O(x)中仅有有限个数,这与无限数列矛盾。
17744多谢
17744"那么,存在一个开覆盖O(x),其中必然有有限个开集,是紧集的一个开覆盖。而且有定义O(x)中仅有有限个数,这与无限数列矛盾。"
是什么意思啊??
请指教
17744华东师范大学数分习题解答有证明,很全,那个书很好买
17745有人帮忙介绍一下这本书吗?
17747欢迎光临post-63-1
173549572.ibf
17747我来了post-63-1
173583893.ibf
17747谢谢哈~~~
17748我系应用数学专业今年招一仅十岁的儿童大学生,请各位提供一些著名神童数学家如维纳、哈密尔顿等的成长历程以供参考。
17749衷心感谢楼上的!!!
一切OK!!
17749最近在用Mathematica做数值计算,遇到个难题,请教高手解答!
使用FindRoot函数求解,例如
FindRoot[Exp[x]
== x^2, {x,-0.5}]
得到
{x ->
-0.703467}
将结果直接代入一变量想再次计算,就不能得到近似值了,而是一个公式,不知道为什么??
例如:
mv
= FindRoot[Exp[x] == x^2, {x,-0.5}];
0.8×mv
得到:{0.8 (x ->
-0.703467)}
也就是如何能将FindRoot的结果中的数分离出来??
先谢谢拉!!!!!!!!
17749你的问题是想取出-0.703467值吗?可以这样,
方法1,使用Position命令,或此命令的变通用法[[...]],
mv[[1,
2]] 得到
-0.703467
0.8 mv[[1, 2]]
得到
-0.562774
方法2,使用代换法,将x代换为-0.703467,
x /. mv
得到
-0.703467
0.8x /. mv 得到
-0.562774
177501吉林大学
吉林大学是中国第一“大”学,只因地理位置不佳,宣传力度不够,如果在上海,它不输复旦交大;如果在北京,它可能也仅次于北大清华。超低的学费说明它不只物美分廉,而且物美价廉。
2四川大学
像四川大学这种综合实力排名可挤进前十的分数高于重点线不过十分的大学,真是物美分廉的没话说。
3国防科技大学
只要你拥有鹰的眼睛,狼的耳朵,豹的速度,熊的力量,那么,它是没钱分低的你的最好选择。
4电子科技大学
对于理科学生来说,它很值得考虑,至少毕业之后不愁找不到工作。
5北京中医药大学
如果李时珍当校长,华佗当书记,分数肯定高于北大医学部。想学医尤其是中医的同学一定别错过,将来就等着数钱吧。
6兰州大学
不张扬不代表没水平。
7西安电子科技大学
过了重点线的同学就可以考虑它了。
8西安交通大学
分数虽然不是很低,但看看上海交大,就知道什么是物美价廉了。
9武汉大学
光是游一回公园也值这么多分,更何况是住四年。
10华中科技大学
它的发展很快,富翁的实力,暴发户的分。地理位置怎么说也比中科大好吧,不怕热的去去无妨
17750"只要你拥有鹰的眼睛,狼的耳朵,豹的速度,熊的力量,那么,它是没钱分低的你的最好选择",呵呵,讲的真搞笑.国防科大也没对身体要求那么高啦.而且平均分数也不低.可能因为军校的关系,有的省份录取线不怎么高.但是高分段完全很强.
至于西交也只不过是因为地理的原因.原来当年与哈工横行的时候,哪轮到上交啊.
川大,兰大,吉大就不讲了,理科的实力大家心理都有数.
华科,武大都在武汉,地理位置半好不好的.不过最近几年都还可以,武大老牌子了,校园的确漂亮.华科上升很快,虽然由于武书连的排名弄成众失之的.在网上常常成为被开火的焦点.但还是比较塌实的.
两个电子科技大学我觉得都很好,专业既热门又有历史沉淀.学生毕业很好找工作.
最后的北京中医药大学我就不太清楚了,想来应该不错.
17750hit
17750吉林大学比较不错的.
17750怎么没有哈工大
实力没得说
分也不算高吧
17750武大很美
被称为中国最美的大学之一
17750分析不错
17750是呀!!!
中西部呀!!!
17750顶
17750去了个物不美价不廉的学校啊!!
17750华科,华科,华科,华科,华科,华科,华科!
17750还有我们西南师范大学,分也低的很,要教书得可以考来
17750不错的选择
17750吉林大学很强的 啊
17750吉林很强的啊!
17750顶!
17750我晕.四川大学破落了.
17750haha
17750英语不行 啊
17750hehe
17750还有东南大学,说说啊
17750还有很多呢,军校我是没办法的!
17750不会的,你是哪的?你说的学校我们这没有一个是分数低的,我是济南的。那些学校除了兰州大学,都要比重点线高30分阿,重点线也的600分以上阿,山东真悲惨阿。
17750只要你拥有鹰的眼睛,狼的耳朵,豹的速度,熊的力量,那么,它是没钱分低的你的最好选择!!!
说的真好!!!
17750不清楚
支持一下
17750ai 哎!害死人
17750!!!!!!!!!!!!!!!!!
17750"北京中医药大学
如果李时珍当校长,华佗当书记,分数肯定高于北大医学部。想学医尤其是中医的同学一定别错过,将来就等着数钱吧。"
夸张了吧,我有两个同学在那里,中医的地位在下降啊!他们学的东西不少也是糊弄事的,当然要立志振兴中医的话去也不错,一定要考虑好专业.千万记得学医是超级的累的,绝对比学数学累多了
17750果然是好地方,分析的透彻
17750东南大学今年考研分数很高的哦,呵呵
17750顶!
17750吉林大学是很强
17750我是武汉大学,中山大学的支持者,
17750是对高考的说的吧!
17750感觉中科大也是很尴尬的,在安徽
17750武汉大学,吉林大学都很强啊
17750顶
17750武汉大学还型!
17750支持西部大开发,重庆大学也是不错的选择,分数过线就行
17750好 找一外适合自己的
17750一家之言!
17750武大很美
17750来世再考了~~
17750中西部
17750好
17750武大的综合实力还不错
17750吉林大学文理都很强的,尤其是化学,物理,数学,法学,地质,汽车,医学.....
17750吉林大学数学系一年的学费才3000多,不过宿舍据说极其恐怖。
17750我觉得不管怎么样,选择一个适合自己的学校应该是更重要的!
17750可惜,现在毕业了才知道
17750什么
中国的好大学都被说成了极差的学校
乱七八糟
17750武大很美
被称为中国最美的大学之一
17750是呀,据说有条樱花大道,不知是不是真的。
17750支持吉大
17750怎么没有中山大学??
17750好象山东大学也不错
17750不见得吧
17750兰大已经变成烂大了
17750我是湖北上高中出来的,楼主说的那些学校在我们哪都不低.
武大华科在湖北招6000人,招的最后一名估计排名是8000左右!
而且只要有上武大华科的分,上前5名以外学校基本上都没问题.
我想加几个的是:西北工业大学,东北大学,哈尔滨工业大学.
17750据同学说华科再他们那上升势头很强
17750哪一年都会爆冷门,今年江苏高考中,哈工大、天津大学、山东大学的录取线就是达标线,一分都不多
17750哎,高考的时候太傻了,4年就这样被糟蹋了
考上了研不知道还要多少时间去补救
17750师范类的你们看不起啊?华中师大怎样啊
17750楼主不了解全国的教育形势有很大的地域差异:
要是在河南,你说的过重点10分估计上述学校都别指望了,过40也难说!!!!!!!!
过重点10分上河南师大(二本)可能较大!!!!!!!!
17750楼主说的是不是真的啊~
我想考电子科技大学呢`
照楼主那么说的话,我就没必要过于担心了 哈哈……
17750不错啊!!!!!!!!
17750说的没错!
17750
| 引用 (wyzmaths @ 2005年09月12日
09时01分) |
武大很美
被称为中国最美的大学之一 |
武汉大学也是最黑的学校,人称卖烧饼的“武大郎”。
17750这个这个……就算是黑,也不能就叫武大郎吧……
17750我们河北每各学校分都很高啊
17750我个人认为,分数低的话,是不是就代表生源要稍差一些啊……这样的话,学校慢慢也会走下坡路的……至少我看到的是这个样子,生源好的学校维持其水平确实比这些学校强多了。
17750四川大学是很不错的学校,数学很强,有两位数学院士,在国内没有几所能比,校园很漂亮。成都是西部第一大城市,经济实力比武汉还要强,而且因为四川出美女,美女很多,以后找对象相对容易。
17751同问!
17751知道中科院数学专业复试靠什么吗
17751好象复试不考专业课,因为中科院是要考生的旧三基能够十分过硬。然后才有利于新三基的学习,所以新三基该是在被录取之后系统的学习!
17752请高手帮忙解决二道数分题(1)post-21-1126011
177.ibf
17752我们下载不了你的题目啊!!!
所以帮不了你啊
!!!!
真的不好意思啊!!!哈哈.................
17752下载不了啊!!怎么帮你?
17752看不到,爱莫能助
17754可升级信息系统国际会议将在香港举行
From: Jinli Cao
Date: Fri, 12 Aug 2005 12:34:04 +1000
First International
Conference on Scalable Information Systems (INFOSCALE)
30 May - 1 Jun
2006, Hong Kong
http://www.infoscale.org/ PRELIMINARY CALL FOR
PAPERS
As the data volumes continue to increase and the ways of
information
dispersion across the globe continue to diversify, new
scalable methods
and structures are needed for efficiently processing
those distributed
and autonomous data. Grid computing, P2P technology,
distributed
information retrieval technology, and networking
technology all must be
merged to address the scalability concern. This
forum focuses on this
key merged domain and looks for new integrated
solutions for this
diversifying world of information.
Conference Scope:
Parallel Information Retrieval
Scalable
Distributed Information Retrieval
Scalable Grid Information Systems
P2P Systems
Scalable Mobile/Sensor DB Systems
Index
Compression Methods
Architectures for Scalability
Networking for
Scalable Information Systems
Scalable Information System Applications
(medicine, biology, military, etc.)
Evaluation Metrics for
Scalability
VLDB
Data Mining
Information Security
General Chair
Xiaohua Jia, City University of Hong Kong
17755普林斯顿高等研究院75周年庆典
普林斯顿高等研究院75周年庆典
摘自数学译林2005 年第2期
普林斯顿高等研究院75周年庆典
普林斯顿高等研究院(Institute for Advanced Study,
缩写为IAS)是世界上
理论研究和学术咨询最重要的中心之一。研究院鼓励和支持基础性学识――那些导
致认知进步的原创的、经常是推测的思想。她通过资深教授对年轻的博士后提供指
导,并对在科学和人文科学的宽广领域中可能做出重大贡献的探索性工作提供自由
的空间。
无论从学术上还是从实践上,研究院的教授们和成员们的工作都有不可磨灭的
影响。她有超过5,000人的前成员,他们在美国和(美国)国外有着学术上和科学
上的领导地位。超过12位的Nobel(诺贝尔)奖获得者,还有更多的Wolf(沃尔夫)
奖和MacArthur(麦克阿瑟)奖的得主(曾)是该研究院的教授和成员。在44位
Fields(菲尔兹)奖章获得者中,有32位也(曾)是其教授和成员。
研究院的数学学部是数学和计算机科学的国际研究中心。它的研究集中在一些
可能有深刻和重大进展的数学课题上,并不考虑纯数学和应用数学的人为边界。
数学学部对社会的两个主要的贡献是促进了科学事业和产生了新知识。
IAS建立于
1930年,(注1)
今年是其成立75周年。下一页是研究院各学部目前的
人员情况以及以前的部分人员情况。
在IAS的75周年庆典中,其数学学部于2005年3月11-12日举行了学术报告会,
共有8个报告。这些报告的报告人(及其工作单位)和报告题目如下:
1. Peter
Sarnak(注2)(普林斯顿大学和Courant(柯朗)数学科学研究所),数论,
对称性和Zeta函数;
2. Avi
Wigderson (注3)(IAS), 随机性,对策和计算机;
3. George Dyson,(注4)
Veblen的圈子――早年IAS的数学学部;
4. Michael Atiyah 爵士(注5)
(Edinburgh(爱丁堡)大学),孤子和对称性;
5. Raoul Boot
(注6)(Harvard(哈佛)大学),不与Marston Morse交谈,Hermann
Weyl错过了什么?;
6.
鄂维南(注7) (普林斯顿大学),固体的数学理论――从原子尺度到宏观尺度;
7. Friedrich Hirzebruch (注8)
(Bonn(波恩)大学),
1952-
1954年间我与
Armand Borel的合作工作;
8. Peter
Ozsvath(Columbia(哥伦比亚)大学和Berkeley加州大学),Heegaard
Biagrams和全纯圆盘。
(陆柱家 编译 陆昱 校)
原题:75th Anniversary Celebration for the
Institute for Advanced Study.
编译自:James D. Wolfensohn, Peter Goddard
和普林斯顿高等研究院数学学部教授
会发给王元院士参加该院75周年庆典的邀请函及因特网http://www.math.ias.edu/75/.
James D. Wolfensohn(沃尔芬森),世界银行行长,曾于2002年5月23-30日访问中国。
Peter Goddard,普林斯顿高等研究院现任院长。
注1:
IAS成立及其数学学部的情况请见本刊2003年第1期文章“高等研究院的数学学部”。
――编注
注2: Peter
Sarnak于2005年获得Frank Nelson Cole奖,2002年被选为美国国家科学
院院士和英国皇家学会会员,
1991年被选为美国艺术与科学院院士。――译注
注3: Avi
Wigderson于
1994年获得Nevanlinna奖。――译注
注4: George Dyson,科学史家,Darwin
Among the Machines一书的作者;著名理论
物理学家、IAS自然科学学部教授Freeman J. Dyson的儿子。――译注
注5: Michael Atiyah爵士于
1966年获得Fields奖章。――译注
注6: Baoul
Bott于
1987年获得美国国家科学奖章。――译注
注7:
鄂维南于
1985年在中国科学院计算中心获得硕士学位,
1989年在UCLA(洛杉矶
加州大学)获得博士学位;
1996年获得美国青年科学家和工程师总统奖,
1999年获
得冯康科学计算奖,2003年获得科拉兹奖。――译注
注8: Friedrich Hirzebruch于
1988年获得Wolf奖。――译注
17756舒其望、鄂维南和汤涛教授受聘为中国科学院数学与系统科学研究院杰出访问教授
舒其望、鄂维南和汤涛教授受聘为中国科学院数学与系统科学研究院杰出访问教授
Date: Fri,
19 Aug
2005 16:49:40 +0800 (CST)
From: "=?gb2312?B?em1jaGVu?="
2005年8月
18日,美国布朗大学舒其望教授、美国普林斯顿大学鄂维南教授和香港浸会
大学汤涛教授被聘为中国科学院数学与系统科学研究院杰出访问教授。聘书颁发仪式
由副院长袁亚湘研究员主持,郭雷院长颁发了聘书并赠送了鲜花和礼品,计算数学与
科学工程计算研究所常务副所长陈志明研究员介绍了三位杰出访问教授的学术贡献。
林群院士、崔俊芝院士和计算数学与科学工程计算研究所的同事参加了仪式。
舒其望,
1982年毕业于中国科技大学,
1986年获美国UCLA博士学位,现任美国布朗
大学应用数学系主任、教授。他在计算流体力学,特别是双曲守恒律的计算方向做
出了重要贡献。他是2004年ISI数学类 Highly
Cited Author, 是美国数学会主办的
《Mathematics of
Computation》的主编。他曾获首届冯康科学计算奖,是中国科
技大学长江讲座教授,中国科学院海外评审专家。
鄂维南,
1982年毕业于中国科技大学,
1989年获美国UCLA博士学位,现任美国普林
斯顿大学教授。他在应用数学与科学计算的许多方面做出了重要贡献。他曾获美国
总统青年科学家奖和ICIAM的Collatz奖。曾在2002年国际数学家大会上作45分钟邀
请报告。他曾获冯康科学计算奖,是北京大学长江讲座教授。
汤涛,
1984年毕业于北京大学,
1989年获英国Leeds大学博士学位,现任香港浸会大
学数学系主任,应用数学讲座教授。他在不可压流体和双曲守恒律的计算方法,特别
是自适应移动网格方法等方面做出了重要贡献。他曾获英国应用数学会Leslie Fox数
值分析奖和冯康科学计算奖。
177582005非線性分析國際研討會--數學科學的前景
International
Conference on Nonlinear Analysis:
Prospects of Mathematical Sciences
時間:2005年12月
17日(週六)至20日(週二)
Time: December
17-20, 2005
地點:中央研究院數學研究所(台湾)
Place: Institute of Mathematics, Academia
Sinica
緣起:
中研院數學所多年來積極推動非線性分析在國內之研究。自
1989年已舉辦過多次非線性分析國際會議。
這一系列會議內容涵蓋非線性偏微分方程、變分法,以及流體力學、數學物理、數學生物、化學擴散等
應用科目之數學理論。
本次研討會—數學科學的前景,將涵蓋更寬廣之數學科學領域。物理科學及數學生物之微觀現象為主要焦點。
其目的為一般數學聽眾介紹數學研究新領域之課題。
邀請講員:
Invited Speakers:
Kazuo Aoki (Kyoto University)
Chien Cheng Chang (National
Taiwan University)
Lin I (National Central University)
Reinhard
Laubenbacher (Virginia Bioinformatics Institute)
Wen-Hsiung Li (The
University of Chicago)
Masayasu Mimura (Meiji University)
Robert M
Miura (New Jersey Institute Technology)
Ping Sheng (The Hong Kong
University of Science and Technology)
Yoshio Sone (Kyoto University)
Jane Wang (Cornell University)
Dah-Yen Yang (Academia Sinica -
Taipei)
Shih-Hsien Yu (The City University of Hong Kong)
※ 摘要
及 議程 即將公布。
報名:會議開始前一個月完成報名,請 線上報名 。
(活動中心的房間如不夠分配,將提供台北住宿資訊)
Organizers:
劉太平(召集人) Email: tpliu@math.sinica.edu.tw
劉豐哲 Email: maliufc@math.sinica.edu.tw
李志豪 Email:
leejh@math.sinica.edu.tw
聯絡處:
中央研究院數學所 電話: 02-27851211
轉341 (林玉娟小姐) 傳真: 02-27827432
Email: leejh@math.sinica.edu.tw (Dr.
Jyh-Hao Lee)
yjlin@math.sinica.edu.tw (Ms. Y.J. Lin)
Website:
http://www.math.sinica.edu.tw 一般資訊(交通、住宿....)
中研院位置圖及院區圖
17759Third International Symposium on Neural Networks
Third International Symposium on Neural Networks
May
29-31, 2006, Chengdu, Sichuan, China
Call for Papers
The
Third International Symposium on Neural Networks (ISNN 2006) will be held
in Chengdu, as a sequel of ISNN 2005 in Chongqing and ISNN 2004 in Dalian,
China. Chengdu is the capital of Sichuan (Szechwan) Province in
southwestern China, a modern metropolitan with 2310-year history and rich
cultural heritage, featuring relaxing lifestyle, spicy Szechwan cuisine,
and numerous historic and scenery sites nearby. ISNN 2006 aims to provide
a high-level international forum for scientists, engineers, and educators
to present the state of the art of neural network research and
applications in diverse fields. The symposium will feature plenary
speeches given by worldwide renowned scholars, regular sessions with broad
coverage, and some special sessions focusing on popular topics.
Prospective authors are invited to submit full-length papers (6 pages
normally and 10 pages maximum) by the submission deadline. Potential
organizers are also invited to enlist five or more papers with cohesive
topics to form special sessions. The submission of a paper implies that
the paper is original and has not been submitted under review or copyright
protected elsewhere and will be presented by an author if accepted. All
submitted papers will be refereed by experts in the field based on the
criteria of originality, significance, quality, and clarity. The authors
of accepted papers will have an opportunity to revise their papers and
take consideration of the referees' comments and suggestions. All
papers accepted and presented at ISNN2006 will be published by Springer as
multiple volumes of Lecture Notes in Computer Science which are indexed by
SCI-Expanded.
ISNN2006 has teamed up with the International Journal of
Neural Systems (IJNS), one of the distinguished journals on neural
networks, for publishing a Special Issue on Advances in Neural Networks.
All submitted papers will have opportunities for consideration for this
Special Issue. The selection will be carried out during the review process
as well as at the conference presentation stage. The Editor-in-Chief of
IJNS and the guest editors of the Special Issues will make decisions on
submitted papers based referees' comments and recommendations, as well
as quality and presentation of the papers, and select around twenty five
papers. Authors of selected outstanding papers will be asked to
substantially extend and revise their papers with additional original
materials for further rounds of peer review under the practice of IJNS.
These papers must be extended and updated in a significant and substantive
way so that the amount of overlap between symposium paper and journal
submission is no more than 50%. Prospective authors should submit their
manuscripts directly to the guest editors before the deadline with a copy
to the Editor-in-Chief. Submitted papers must not be under consideration
by any other journal for publication. The final decision will be made
based on peer review reports by the guest editors of the special issue and
the Editor-in-Chief jointly.
Important dates:
Special session
proposal (ISNN2006): November 1, 2005
Paper submission (ISNN2006):
November 15, 2005
Notification of acceptance (ISNN2006): December 15,
2005
Final paper submission (ISNN2006): January 15, 2006
Paper
submission (IJNS Special Issue): June 30, 2006
Notification of
acceptance (IJNS Special Issue): December 31, 2006
For detailed
information, please see
http://www.acae.cuhk.edu.hk/~isnn2006 or
http://cilab.uestc.edu.cn/isnn2006
17760超分辨率成像国际会议将在香港举行
From: Michael Ng
Date: Thu,
18 Aug 2005 22:11:55 +0800
International Conference
on Superresolution Imaging:
Theory, Algorithms and Applications
29--31 August 2005
The University of Hong Kong
http://hkumath.hku.hk/~math/event/Super/home.htm
List of lectures:
Luis Alvarez (University of Granada)
Thierry Blu (Ecole Polytechnique Federale De Lausanne)
Nirmal K.
Bose (Pennsylvania State University)
Raymond Chan (The Chinese
University of Hong Kong)
Tony Chan (University of California, Los
Angles)
Subhasis Chaudhuri (Indian Institute of Technology)
Albert
Cohen (Universit?Pierre et Marie Curie)
Michael Elad (Israel Institute
of Technology)
Jacques Froment (Universit?de Bretagne Sud)
Aggelos
Katsaggelos (Northwestern University)
Edmund Lam (The University of
Hong Kong)
Charles Matson (AFRL/DEBI)
Peyman Milanfar (University
of California, Santa Cruz)
Rafael Molina (Universidad de Granada)
James Nagy (Emory University)
Esmond Ng (Lawrence Berkeley
National Laboratory)
Michael Ng (The University of Hong Kong)
Mila
Nikolova (CMLA ENS de Cachan)
Sung Cheol Park (Samsung Electronics)
Robert Plemmons (Wake Forest University)
Zuowei Shen (National
University of Singapore)
Chong-Sze Tong (Hong Kong Baptist University)
Sabine Van Huffel (Katholieke Universiteit Leuven)
Ding Xuan Zhou
(City University of Hong Kong)
17760现在已经开完会了,如何能得到会议的论文集呢?是否可以发信告知?谢谢!!
yhzhjg@sdu.edu.cn
17761恩,我当成是自己那个求导的方法了,不好意思
大家看看我那个问题吧^_^
17761令
F(x)= \int_{(a+b)/2}^x f(t)
dx,
将F(x)分别在a和b出Taylor展开后相加,再利用介值定理即可。
17761
| 引用 (reijin @ 2005年09月07日
00时47分) |
|
只要二阶导数存在就行了,即使不连续,就是说两个二阶导数之间的任意值都能取到^_^
|
我知道达布定理只需导数存在就行了.问题是f''(x)的可积性,以及积分中值定理怎么办?
17761只要二阶导数存在就行了,即使不连续,就是说两个二阶导数之间的任意值都能取到^_^
17761从这个问题想到了另一个类似的问题:求证

f(x)dx
<从a->b> = -(b-a)^3/12 * f"(e)
其中f(a)=f(b)=0,f二阶导数存在
17761f(x)在[a,b]上连续,且二阶连续可导。f'(a)=f'(b)=0。那么,存在

使得

f(x)dx
<从a->b> = (b-a)(f(a)+f(b))/2 + (b-a)^3/6 * f"(

)
先前漏了连续可导的连续的条件,十二万分地抱歉!
17761
| 引用 (zhubin846152 @ 2005年09月06日
22时03分) |
f(x)在[a,b]上连续,且二阶可导。f'(a)=f'(b)=0。那么,存在  使得 使得
 f(x)dx
<从a->b> = (b-a)(f(a)+f(b))/2 + (b-a)^3/6 * f"( f(x)dx
<从a->b> = (b-a)(f(a)+f(b))/2 + (b-a)^3/6 * f"(
 ) )
|
最后一个系数我怎么感觉应该是1/24呢?!
17761-_-,最后的系数我算到了-(1/12).......而且没用到f'(a)=f'(b)=0.....再研究...
17761进步到-(1/6)了........
17761反复用分部积分法,并注意到积分中值定理及达布定理post-38-1126022005.ibf
17761我用构造函数的方法,和Taylor展开也算到和Hfg
1964一样的答案。
这是我的同学问我的一道数学(一)的考研题目。我一直没做出来。
原来可以分别讨论x=a,x=b的情况,再结合起来。
另外:抱歉!是二阶连续可导。否则可能做不出来了。
17761同理有post-38-1126021267.ibf
17761虽然得到了答案,细心的朋友可能看到,上面解法中需用到f(x)的二阶导函数连续这一条件,方法有待改进,或条件不够?
17761f(x)=f(a)+(x-a)f'(a)+((x-a)^2)*f''(

1)/2
(1式)
f(x)=f(b)+(x-b)f'(b)+((x-b)^2)*f''(

2)/2
(2式)
then,

f(x)dx=

((1式)+(2式))/2dx
17762甲乙两个围棋队各5名队员按事先安排好的顺序进行擂台赛,双方1号队员先赛,负者被淘汰然后负方的2号队员再与对方的获胜队员再赛,负者被淘汰一直这样进行下去,直到有一方队员全部被淘汰时,另一方获胜,假设每个队员的实力相当,则甲方有四名队员被淘汰且,最后胜乙方的概率是多少___
知道的请帮忙写下过程
先行谢过
17762自己想了很久,好像从各方面考虑都比较麻烦,
求助各位拉
17762就是很麻烦的题.题目告诉你实力相当就是说胜负的概率是1/2比1/2.所以这个时候甲剩下一个人,你要算乙剩下1,2,3,4,5人的概率,然后把乙队剩下的人数作为条件,求甲队最后一个人被干掉的概率...然后加起来.
17764复变函数里的零点孤立性在实数域内是否成立?
复变函数里一解析域内函数在某线上的值及在其内的一小区域内的值能否确定其在该解析与内的值?
17764复变函数中的零点孤立性对于实函数是不成立的,例如 实函数
f
(x)=xsin(1
x
),f(0)=0
就是一个反例。
17764实函数 f (x)=xsin(1 x
),f(0)=0在原点并不解析,如果是实解析函数的话,零点孤立性应该还是成立的,本来复变函数中的零点孤立性就是对解析函数而言的。
17764
| 引用 (ccd @ 2005年11月05日
21时52分) |
| 实函数 f (x)=xsin(1 x
),f(0)=0在原点并不解析,如果是实解析函数的话,零点孤立性应该还是成立的,本来复变函数中的零点孤立性就是对解析函数而言的。
|
什么叫实解析?不要乱说,零点定理只对复解析函数成立!
实解析是高维的东西,与复解析有天壤之别
17764其实可以证明,当实函数有无穷阶导数,在某个区域内如果它的Taylor级数收敛到自身,那么在这个区域内零点的唯一性是成立的.不然它的取值为常数0.
17764
引用 (随风 @ 2005年11月12日
15时
17分) |
|
其实可以证明,当实函数有无穷阶导数,在某个区域内如果它的Taylor级数收敛到自身,那么在这个区域内零点的唯一性是成立的.不然它的取值为常数0.
|
一个反例:函数
f
(x)=e
-
1 x
sin(1
x
),f(0)=0,x∈[0,1]
具有无穷阶导数,但是他的零点不孤立。
17765打印复制都不行,只能存在电脑上面看,太累了,那位大虾帮忙看看怎么才能打印下来。万分感谢!
17765try guapdf, but you need a cracked one instead of shareware.
17765你的PDF已经被设置成不能打印和复制了,发过来我帮你改掉这些设置,让它能够打印和复制。请在标题处注明“PDF”
yqs210@163.com
17765Thanks!yqs, I will send to you.
17765能不能给一个破解了的Guapdf呢,或者还有什么别的软件,我也有些pdf文件不能打印
谢谢
17765
| 引用 (jash @ 2005年09月13日
07时52分) |
能不能给一个破解了的Guapdf呢,或者还有什么别的软件,我也有些pdf文件不能打印
谢谢
|
发过来我看看能不能去掉限制。请在标题处注明“PDF” yqs210@163.com
17765这种情况我经常碰到,用一个“Advanced PDF Password Recovery”的软件去掉其密码保护就ok了
17766哪位高人知道非参数回归(nonparametric regression)是哪个学科分支里的?大概讲的是什么啊?谢了
17768下面这道题为面试题(国外的),常规办法似乎不行,那该怎么回答这个问题呢?
问题:
Draw graphs: y
=(sin2x)/x
post-8-1126052674.jpg
17768求y'=0 y''=0 找出拐点 和 最值点 和 渐进线
这个方法不可以么?
17768包络是1/x,在里面话sin(2x)
17768
| 引用 (zyzme @ 2005年09月22日
23时28分) |
求y'=0
y''=0 找出拐点 和 最值点 和 渐进线
这个方法不可以么?
|
可以,但是很复杂,而且面试的时间不够把该题解出来。
177681. 该函数在 x=0 点处的极限值为2, 用圈描出该点.
2. 偶函数只要考虑 x>0 的情况.
3. x ->
0+ 时, 导函数小于0, 单调减.
4. 零点为 k * \PI /2
5. 后面可以类似 y=sin2x 的曲线,
让振幅越来越小.
6. 极值点不是 y=sin2x 对应的极值点,
故图象的每个波峰/谷都不对称(考虑取一个多描几个点,其他做类似处理)
我想这样大致可以确定曲线的图象,虽然不精确但有一定的参考价值。
17768
引用 (xtuyyy @ 2005年09月23日
17时49分) |
1. 该函数在 x=0
点处的极限值为2, 用圈描出该点.
2. 偶函数只要考虑 x>0 的情况.
3. x -> 0+ 时, 导函数小于0,
单调减.
4. 零点为 k * \PI /2
5. 后面可以类似 y=sin2x 的曲线, 让振幅越来越小.
6.
极值点不是 y=sin2x 对应的极值点,
故图象的每个波峰/谷都不对称(考虑取一个多描几个点,其他做类似处理)
我想这样大致可以确定曲线的图象,虽然不精确但有一定的参考价值。
|
方法不错,但若加上包络线就更妙了。
17768支持楼上的!
17769我是因为想找一个在WEB上编辑数学公式的方法,才找到这个论坛的。找了半天,发现真正解决问题的还只有本论坛。
本论坛的方法很好,但总觉得不够方便(对我这样不懂itex的人),因为要有语言的基础,不能随手就上,还要练练。
建议一个:
既然已经能集成部分转换代码的功能,能不能编一个方便的公式编辑器放进来呢?
其实,这是我想做一个网上答疑系统的想法,但我的水平毕竟不如你们。
17769谢谢你的建议,希望能帮你们做点什么。
你所谓的所见即所得的公式编辑器,理论上可以安装。jute论坛商务版可能能解决,不过要money.
本论坛的工作原理参见:
http://aloft.ctex.org/blog/archives/000006.php你还可以改进,比如做分类的符号编辑下拉框,直接仿照mathtype编写成公式符号模块,
用户不必懂tex,即可上手。
另外,国外一些数学物理论坛还有一种较好的解决办法
可能需要服务器将tex命令转化为图片显示。你可以查查看,多多交流。
希望你们成功!
也希望以后多多合作。
17770假设t时刻(分钟),高度为
18-t
圆柱体中的高度为
h(t)={1-[(
18-t)/
18]^3}*V/S
v=dh/dt=(
18-t)^2/6*V/S
V=
18*6*62pi/3=216pi
S=25pi
17770本人有一题,怎么也做不出来,我数学水平不行,谁来帮忙,多谢了.此题如下:溶液从深
18CM,顶直径为12CM的正圆锥形漏斗中漏入一直径为10CM的圆柱形筒中,开始时漏斗中盛满了溶液,此时其表面下降的速率为1CM/MIN,问此时圆柱形筒中溶液表面上升的速率为多少?
17771再一个资料上看到将方阵先进行hosehold变成双对角线阵再通过变形的QR算法迭代最终变成对角阵,小弟对这两种变换都太了解,请哪位大侠帮忙解释一下好么?
17771参见Adaptive filter theory一书 附录F(Simon Haykin著)
17772陕西师范大学的数学系怎么样?有哪位大侠知道请告知,谢谢了!
有没有人要陕西师范大学的试卷和<高等代数解题精粹>啊
http://www.math.org.cn/forums/index.php?sh...107&hl=殁铟軎范
17772挺不错的
而且还是师范类的学校
数学会很强的
17772谢谢!!
17772西安是个不错的地方!!!怀念中。。。。。。
17772数学系的拓扑应该不错,
吴建华老师的方程应该也不错
代数以前也说的过去
不过我从陕师大数学系毕业都6年了,
现在数学系都变成数科院了,
以前的同学都在那做老师了。
17772学费不好解决啊
17772全国排名能进前30名
基础数学挺不错的
17772qinghuas好强啊
都到副教授了
17772请问一下你们有没有陕师大06年的题啊?或是知道怎样弄到的?我是湖北的一名考生。现在急需,我的电话,13487284612 小曾 谢谢
17772数学系蛮强的啊
17772我需要陕西师大的试卷,能不能联系一下我,dingaiwo999@163.com,拜托各位师哥师姐了。
17772还是比较好的
17772很需要陕西师范大学的数学分析和高等代数的历年真题。。帮帮我吧。。。我的邮箱liulizhao_2005@163.com我可以付费
17772陕西师范的题目不难,有没有真题都一样,基本题目熟悉了就可以,但是好像分数线很高,去年我一同学考进去了,370分,比复试线多 5 分
17772数学分析和高等代数的专业真题谁有啊?发一下 我可以付钱的!谢谢啊!
17773已知两条对称切线,切线夹角beta,切点距离L和椭圆底端到线段的距离h,
求,椭圆的长轴半径a和短轴半径b.
post-22-1126060368.ibf
17774请问报考精算师需要修的课程有哪些?
17774小弟以前上网搜到过,有很多门。有兴趣的加我msn。xlwqg@hotmail.com,到时传给你文件。
17774是北美精算师吗?很难啊,有两个阶段考核,总共8门吧
17774科目名称 科目代码 科目名称 科目代码
数学基础Ⅰ 01 生命表基础 06
数学基础Ⅱ 02 寿险精算实务
07
复利数学 03 非寿险精算数学与实务 08
寿险精算数学 04 综合经济基础 09
风险理论 05
科目代码
课程名称 备注
011 保险公司财务管理 必考
012 保险法及相关法规 必考
013 个人寿险与年金精算实务
必考
014 社会保障 选考
015 资产负债管理 选考
016 高级非寿险精算实务 选考
0
17 团体寿险
选考
0
18 意外伤害和健康保险 选考
0
19 高级投资学 选考
020 养老金计划 选考
021 精算职业后续教育(PD)
必修
qq 277363443交流以下
17774考精算师难度好大.
17774听师兄讲,难度确实比较大,做好准备呀!
17774我身边也有考的,不过都铩羽而归,难度是挺大的,呵呵1
17777A是m行n列的实矩阵,b是一个m行1列的实矩阵,证明:线性方程组A'AX=A'b一定有解,其中A'是A的转置,
请将答案写详细些,谢谢!
17777这里有讨论你先看看吧!
http://www.math.org.cn/forums/index.php?showtopic=
17167
17777证明A'A与A'的秩相等!
17779关于定义倒是知道一些,但是这种矩阵的物理意义是什么,从字面上却看不出来。
哪位能详细介绍一下有关的背景啊
另外:正则这个词到处出现
我也无法了解它们的共同点。
17779为虾米没有人啊 555
讲讲正则性的概念也行啊
17781我觉得做计算机挺好的啊,为什么要换做基础数学呢?
17781
我是学计算机的,数学基础很弱,我该选择在清华北大旁听一两年呢还是今年就考一个二流的学校 考上后再补基础呢
?
已经26了很矛盾。。。
17781我是学计算机的 , 数学基础很弱,我是应该选择到名校旁听一两年呢还是今年考一个二流的学校 考上再补基础呢
17782请问北京哪儿可以买到Graph coloring problems(Tommy R. Jensen, Bjarne Toft.--New
York: Wiley, c
1995)这本书?多谢!!!
17782九章没有,我自己去过了,人大附近的国际教育书店也没有,后来在中科院图书
馆找到一本,但借不出来
17782借不出来的话直接在里面复印好了
17782
| 引用 (bnu630 @ 2005年09月09日
16时02分) |
九章没有,我自己去过了,人大附近的国际教育书店也没有,后来在中科院图书
馆找到一本,但借不出来
|
印吧,偶们这里也有很多本,但都是印的。只能这样了。好象买不到。
17786X,Y为一族拓扑空间。Y是X的子空间,
则Y的积空间在X的积空间中强正则当且仅当对Y中每一个拓扑空间都在X中强正则.这是正确的还是错误的请给与指教
17786强正则
定义?
17787这本书旧书市场可能有.
17787听说这套书,学工科和非数学专业理科的学了不错!!跟《微积分学教程》一样经典哦!想拜读拜读!不知道哪位大虾有下啊!?
17787我有全书,但是无电子版。是若干年前特请上海旧书部的先生们收集全的。你可以试一试此法。该书可谓经典之著作。
17787呵呵,这套书在成都的旧书市场就有哦.
17787楼上那位能卖给我吗,联系QQ21
195087
17787我都是特意请人收集并用不菲价格买来的,自然不会转让。到底有无电子版,那就不清楚了。不过,要全部扫描进计算机也非易事。两年前,我查过有关数字图书馆没有看到有,现在不知道是否有了。
17787有吗?我也要!
17787这套书应该至少是物理专业和数学专业的同学们看的.我看过第三卷.而且也弄到了第四,五卷.第三卷是线性代数,复变函数和特殊函数.第四卷是积分方程,变分法和偏微的中级理论.第五卷是实变函数和泛函分析部分.全书的选材很有特点.而且作者也是苏联著名科学院院士.总得来讲.这套书相对《微积分学教程》要全面的多,而且也比较好弄到.但是想一整套一整套的弄到比较麻烦.估计要百来块了.
17787我现在搞到7本还差4本啊!!现在这书真难找的!
17787什么难找啊,我轻易就弄了一套,而且还可以找到的.上周六还得了 数学分析原理一套,微积分学教程的1--7, 只差第八了.
17787在不长的时间里,
我就收集了罗德(很少听说吧)<<高等数学>>一套五册,斯米尔诺夫<<高等数学教程>>一套11册,
<<微积分学教程>>两个不全的(一套7册,一套6册),<<数学分析原理>>两套多一册,
柯朗的<<数学物理方程>>下册, 夏道行的<<实变函数与泛函分析>>一套.......
写在这里不是为了炫耀,只是想告诉各位兄弟,不要只是求,要自己找. 多逛逛旧书店吧.也许你会有收获的.
17787我们这的旧书店可找不到这么经典的书,羡慕啊!!
17787超星里面有全部的
17788比较复杂,
1.求出f(x_1),f(x_2|x_1),f(x_3|x_1,x_2)...这些的条件分布
2.取出x_1~f(x_1)
3.把取得的x_1代入f(x_2|x_1)的条件密度,取出x_2,依此进行得到一个向量
17788
引用 (dingzj @ 2005年09月07日
19时
17分) |
我把
h(X) 的形式也写出来吧:
h(X) = min [( x_i - v_i)^2] ,
其中i是向量下标,v已知,与x是同维的向量。
这样求f(x_1),f(x_2|x_1),f(x_3|x_1,x_2)...就很困难把
同时,即便求出来了,又如何“取出x_1~f(x_1)”,是要计算出累积积分(概率分布函数)再推导吗?
谢谢
|
是的...
17788我把 h(X) 的形式也写出来吧:
h(X) = min [( x_i - v_i)^2] ,
其中i是向量下标,v已知,与x是同维的向量。
这样求f(x_1),f(x_2|x_1),f(x_3|x_1,x_2)...就很困难把
同时,即便求出来了,又如何“取出x_1~f(x_1)”,是要计算出累积积分(概率分布函数)再推导吗?
谢谢
17788rt
已知有服从 f(X) = c * exp (- h(X)) 的高维数据的密度函数,c为常数,h(x)
为关于向量X的一个已知函数,有点复杂
请问如何生成服从这样分布的数据?
请教子青老师
17788用蒙特卡罗抽样方法可以做到吗? 我不懂蒙特卡罗,仅听说过
蒙特卡罗里面有不少抽样方法,MCMC算法,吉
布 斯 采样 。。
等等,这些能不能做到呢?
达人们再给指点一下
17788如果你能把那些条件分布求出来,用Monte Carlo是很方便的
17788
| 引用 (子青 @ 2005年09月08日
11时54分) |
|
如果你能把那些条件分布求出来,用Monte Carlo是很方便的 |
可是这样的条件部分确实不好计算,能不能认为各个随机变量之间相互独立,单维生成数据再合并,这样的数据还符合这一分布吗?
17788
| 引用 (dingzj @ 2005年09月08日
15时53分) |
| 引用 (子青 @ 2005年09月08日
11时54分) | |
如果你能把那些条件分布求出来,用Monte Carlo是很方便的 |
可是这样的条件部分确实不好计算,能不能认为各个随机变量之间相互独立,单维生成数据再合并,这样的数据还符合这一分布吗?
|
肯定不能,除非你能证明各维是独立的.
17788产生高维随机数一般很难。以前我听过Fu. C
,中文名付权(音)
的一个报告讲他提出的一个近似方法我觉得还不错,可能适合你这个问题,
可以在网上搜搜
又你这个分布比较怪,为什么要抽这样的随机数?如果这个分布是由别的分布变换过来的,也可以按照这个变换产生随机数
17788
| 引用 (Fisher @ 2005年09月08日
23时15分) |
产生高维随机数一般很难。以前我听过Fu. C
,中文名付权(音)
的一个报告讲他提出的一个近似方法我觉得还不错,可能适合你这个问题,
可以在网上搜搜
又你这个分布比较怪,为什么要抽这样的随机数?如果这个分布是由别的分布变换过来的,也可以按照这个变换产生随机数
|
我要利用这样生成的数据作试验,验证一个算法的性能
这个分布函数不是来自于其他的变换,原本就这样
更复杂的一个是:
h(X) = sum[(x_i - v_i)^2]/n ....
你说的这个“Fu. C
,中文名付权(音)”能不能再详细些,搜索范围太广了
谢谢!
17788是这个吗:
MICHAEL C. FU (mfu@isr.umd.edu)
Associate
Professor, of Management Science & Statistics and the Institute for
Systems Research
Dr. Fu received his Ph.D. and M.S degrees in
applied mathematics from Harvard University in
1989 and
1986,
respectively. He received S.B. and S.M. degrees in electrical engineering
and an S.B. degree in mathematics from the Massachusetts Institute of
Technology in
1985. Since
1989, he has been at the University of Maryland,
College Park, in the College of Business and Management. Dr. Fu is a
member of IEEE and the Institute for Operations Research and the
Management Sciences (INFORMS). He is an Associate Editor of the ORSA
Journal on Computing and IIE Transactions. He has authored or co-authored
more than 30 journal articles and conference proceedings.
17788不是 James,C,Fu
University of Manitoba,Canada
17788
| 引用 (Fisher @ 2005年09月09日
21时11分) |
不是
James,C,Fu
University of Manitoba,Canada
|
好,谢了
我先搜搜看~~~
17788找到了James C Fu的一篇文章,
A Random-Discentization Based onte Carlo
Sampling Method and its
Application
好像生成高维数据挺有用,但是大部分看不懂撒,
问题比较多,所以都没法细说了,
哪位达人给解释一下阿,拜谢!!
post-
17-1126752943.jpg
17788
引用 (Fisher @ 2005年09月15日
19时26分) |
数学细节你可以不用管了,f是密度函数,support(f)你可以看为使f(x)>0的那些x
的集合.
 (E)是E 的勒贝格测度,可以看成E的体积(面积).
(E)是E 的勒贝格测度,可以看成E的体积(面积). |
谢谢,呵呵,我和同学讨论了一下,基本上
还?#####闶敲靼?但是有一个关键的地方始终还是没搞明白,用它的算法写的程序也就卡在这个地方了
这一点解决我就可以验证这个生成数据的算法到底行不行了
问题在这:

is
the Lebesgue counting measure on S_n(f) ..
这个the Lebesgue counting
measure 到底值得是什么? 前面可见~E_i 应该是可数个点的集合,但 是高维的, 那么它的测度是什么? 0吗? 如果是 0
就没有意义了..
麻烦再给看一下把post-
17-1126792626.jpg
17788数学细节你可以不用管了,f是密度函数,support(f)你可以看为使f(x)>0的那些x
的集合.

(E)是E 的勒贝格测度,可以看成E的体积(面积).
17788应该是指集合内点的个数
17788
| 引用 (Fisher @ 2005年09月16日
10时21分) |
| 应该是指集合内点的个数
|
如果是这样的话, 那都相等了,
因为根据前面的定义,每个~E_i内点的个数都是u,
这样没有什么意义了……
17788
| 引用 (dingzj @ 2005年09月16日
11时29分) |
| 引用 (Fisher @ 2005年09月16日
10时21分) | | 应该是指集合内点的个数
|
如果是这样的话, 那都相等了,
因为根据前面的定义,每个~E_i内点的个数都是u,
这样没有什么意义了……
|
你把全文发给我
我看看xiong@amss.ac.cn
17788我发到你的邮箱了,谢谢撒~~
17791设立如下:
1.考博真题专辑
2.考研真题专辑
3.教科书及著作专辑
17791现在的分类不好么?我觉得已经差不多了。需要的基本上都能找到
17794对不起post-67-1126092809.ibf
17794thank you very much
17794多谢了,呵呵!!
17794Thank you very much !
17794thanks a lot
17795一道分析post-38-1126092968.ibf
17795分两个区间用定义证明,[0,A]的时候用(1-e^(-t/n))约束,[A,inf]时用e^(-t)约束
17795
| 引用 (reijin @ 2005年09月07日
20时54分) |
|
分两个区间用定义证明,[0,A]的时候用(1-e^(-t/n))约束,[A,inf]时用e^(-t)约束
|
什么是约束?
我看的课本上怎么没有啊!
请指教!
17795reijin的约束应该就是不等式的证明的重点!
|sint^3| <= 1
这一点不用去管他
[0,A]的时候,(1-e^(-t/n))*exp(-t)*sint^3 <= (1-e^(-t/n))
-> 0
[A,inf]的时候,,(1-e^(-t/n))*exp(-t)*sint^3 <= exp(-t) ->
0
所以,根据定义,很容易证明是一致收敛与0的
至于,后面题目就比较简单了
17796
17岁女生发现一颗近地小行星
网大首页 > 文教 > 正文 2005-9-7 11:42:
19 新华社
九月四日,杭州高级中学十七岁女学生丁舒珊在介绍近地小行星的运行轨迹。丁舒珊日前发现一颗近地小行星,这一行星已于九月二日零时五十分被国际天文学联合会正式确认,编号暂定为2005QQ87。这意味着丁舒珊成为全球天文史上首位近地小行星的女性发现者,她也是中国第二位近地小行星发现者。高原摄(新华社发)
17796没什么
17796挺有天赋的
17796天才啊。好敬佩哦.
17796我真的不能忍你们了!
这只是个发现!不是发明!更谈不上天才!
为你们的严重糊涂而深刻狂笑中,哈哈哈:)
17796发现是不如发明,但并不是任何人都可以有重大发现的!
17796呵呵,同意楼上的观点呀呵呵,是呀,发现是本来就有吗,只是时间问题
17796天文学很需要运气.
专业的天文学家可能一生一无所获.但是业余的观测者可能无意中发现未被发现的星星.
但不怎样,对天文有着强烈的热爱,那是在天文学上有建树的人的共同之处.
17796强
17796不错不错
17796怎么发现的?肉眼?望远镜?
17796????
居然这么多人嗤之以鼻?
17796她要根据观测数据计算小行星轨道的,
这对一个高中生来说并不算简单,当然这也很幸运。
丁舒珊还挺漂亮哦!post-1-1131096715.jpg
17796少年英才啊,佩服仰慕哦。
17797(1)给定20个人,问在12个月中正好包含2个人生日的月份有4个且正好包含3个人生日的月份有4个的概率是多少??
(2)有5道4选一的单项选择题,有人每道题都选了一个答案.问选对且只选对一个的概率是多少?
17797
| 引用 (79130613 @ 2005年09月07日
20时12分) |
|
问在12个月中正好包含2个人生日的月份有4个,且正好包含3个人生日的月份有4个的概率是多少??
|
3个人生日的月份有4个??? 一个人的生日还至少横跨2个月份乎??
什么意思???
发贴请教
都不管自己的帖子能不能读通~~!! 还真忙啊~~~~
17797
| 引用 (79130613 @ 2005年09月07日
20时12分) |
|
(2)有5道4选一的单项选择题,有人每道题都选了一个答案.问选对且只选对一个的概率是多少?
|
有两种方法。
17797
| 引用 (hupo99 @ 2005年09月09日
00时31分) |
| 引用 (79130613 @ 2005年09月07日
20时12分) | |
问在12个月中正好包含2个人生日的月份有4个,且正好包含3个人生日的月份有4个的概率是多少??
|
3个人生日的月份有4个???
一个人的生日还至少横跨2个月份乎??
什么意思???
发贴请教 都不管自己的帖子能不能读通~~!! 还真忙啊~~~~
|
人家的意思是这样:
比如,1,2,3,4月,这几个月中每个月都有2个人生日;
6,7,8,9月,这几个月每个月都有3个人生日
所以 一共 2*4 + 3*4= 20 ,正好是20人啊,他说的很清楚啊
17797
| 引用 (hupo99 @ 2005年09月09日
00时41分) |
| 引用 (79130613 @ 2005年09月07日
20时12分) | |
(2)有5道4选一的单项选择题,有人每道题都选了一个答案.问选对且只选对一个的概率是多少?
|
有两种方法。
|
第一种,概率的概念:
post-
17-1126243973.gif
17797第二种 可以用概率的乘除公式得到;
慢慢看书吧,最近比较忙啊~~~
17801求助2004南开线性方程组第4题,post-38-1126098311.jpg
17801由于如上的矩阵是基础解系
所以a(1,1)+a(1,2)+...+a(1,n)=a(2,1)+a(2,2)+...+a(2,n)=...=a(n-1,1)+..+a(n-1,n)=0
得到a(i,n)=-(a(i,1)+a(i,2)+...+a(i,n-1))
然后,应该不难得到(-1)^i*Mi都完全相等,可知第一小题中Mi=0,rank(A)<=n-2从而非基础解系
那么就可以解出Mi=(-1)^(i-1)*(1/n)
17801构造一个矩阵[p;A],其中p是n维行向量(1 1 ...1),这样即可很容易得到结果
17801我得想法和reijin的完全一样
添一全为1的行就可以了
第一问可以说就是Laplace展开
第二个就是行列式有n种表示
结果就是zhubin846152给出的
17801首先谢谢各位,
zhubin846152你是如下两位这样想的吗?
我认为是添加一行,a11,a12,.....a1n
则|A|=a11*M1+a12*(-1)M2+...+a1n*(-1)
^{1+N} Mn=0
然后如zhubin846152所说相等
又因为

(-1) ^{i}Mi
=0
所以(-1) ^{i}Mi =0
不知对否?
17801
第二问的答案是:
M
i =(
-1)
in
.
17803事实上,一个基被替换出去后,在紧接着的下一个单纯形表中,它的检验数肯定是负的.
这可以理论证明.
好象可以从线性规划的矩阵表示法入手.
17803人工变量出基后为什么不会再次进基,请高手给我一个理论证明。
17803这个大M法我们刚学完,我只是谈我的想法。别见笑哈!
人工变量就是要出基才是最理想的啊。因为它跳跃式的比较最优解,所以当然回不去了。
它不可能再是最优的拉啊!!!!~~~~~~~~~``
17803我的感觉就是:
水往低处流!
17803推荐看陈宝林的最优化理论
17804Thanks
17804I only have the sixth edition in djvu format. Do you still want it?
17804我想要这本书。 请给我发一份好吗? 非常感谢!
我的邮箱:
swordshining@gmail.com
17804Me too.
ghan8601@gmail.com
Thanks.
17804文件是djvu格式,现存放在RapidShare空间。
于以下连结,搜寻到 Free
按钮后,单击一次,等候半分钟左右,便出现验证密码,输入密码后,单击"Download from Net-Mirror
XXXXX"按钮,便自动下载:
http://rapidshare.de/files/1
1874408/Ross.rar.html请输入以下解压密码:
math.org.cn
17804Fail to download.
Thu Jan 26
17:16:36 2006 Connecting
dl21.rapidshare.de:80
Thu Jan 26
17:16:36 2006 Connecting
dl21.rapidshare.de [IP=130.1
17.156.43:80]
Thu Jan 26
17:16:36 2006
Connected.
Thu Jan 26
17:16:36 2006 GET
/files/1
1874408/274587597/Ross.rar HTTP/1.1
Thu Jan 26
17:16:36 2006
Host: dl21.rapidshare.de
Thu Jan 26
17:16:36 2006 Accept: */*
Thu
Jan 26
17:16:36 2006 Referer:
http://rapidshare.de/Thu Jan 26
17:16:36 2006
User-Agent: Mozilla/4.0 (compatible; MSIE 5.00; Windows 98)
Thu Jan 26
17:16:36 2006 Pragma: no-cache
Thu Jan 26
17:16:36 2006 Cache-Control:
no-cache
Thu Jan 26
17:16:36 2006 Connection: close
Thu Jan 26
17:16:37 2006 HTTP/1.1 404 Not Found
Thu Jan 26
17:16:37 2006 P3P:
CP="ALL DSP COR CURa ADMa DEVa TAIa PSAa PSDa IVAa IVDa CONa TELa OUR
STP UNI NAV STA PRE"
Thu Jan 26
17:16:37 2006 Date: Thu, 26 Jan
2006 22:
17:51 GMT
Thu Jan 26
17:16:37 2006 Connection: close
Thu Jan
26
17:16:37 2006 Accept-Ranges: bytes
Thu Jan 26
17:16:37 2006
Content-Type: text/html; charset=ISO-8859-1
Thu Jan 26
17:16:37 2006
Cache-Control: no-cache
Thu Jan 26
17:16:37 2006 Content-Length:
7905
Thu Jan 26
17:16:37 2006 Error occured!
17804You cannot use any download manager to downlaod the file. The above
link is not a direct link to the file.
Instead, you have to
:
1. Click on the above link.
2. Click on the
"Free" button.
3. Wait for about 30 seconds for a
"password".
4. Type in the "password" in the
space provided.
5. Click on the "Download from Net-Mirror
XXXXX" button.
17804Thanks. It works perfect.
17804谢谢了,还能下载
17804已經不能下載.....可以再發一次嗎?
或寄e-mail給我
cmleeds@hotmail.com
謝謝~~~~~~thanks!!!
17805设数列{Xn}:满足0=<Xm+n=<Xm+Xn,则 Lim Xn/n=inf {Xn/n}
17805《数学分析中的典型问题和方法》P60的题目,我把他的分析贴上:post-38-1126141009.gif
17805题目右边的inf是什么意思啊??
17806谢谢你们的信息哦.
17806有知道那个学校有数量经济学或者博弈论的博士点的大侠帮帮忙,提供一点信息。
17806好像南开有
17806博弈论博士点倒是很少听说
数量经济就多了,首选清华,这是清华经济类唯一的第一
17807谢谢啦!
17807不错不错,就是浅显了点!
17807非常感谢!
17807
http://www.scopen.net/asfroot/scddip/fhfx/第一次发贴,希望大家有用
第一讲 距离空间与拓扑空间
第二讲 赋范线性空间
第三讲 有界线性算子
第四讲
Hilber空间
第五讲 拓扑线性空间
第六讲 距离空间与拓扑空间
第七讲
赋范线性空间
第八讲 有界线性算子
17807非常感谢啊 !!!!!!
17807非常感谢!
17807感谢楼主!!!
17807非常感谢!
17807非常感谢
17807可惜不能下载
17807感谢楼主!!!
17807谢谢
17807不错,看看去!
17807谢谢分享!
17807谢谢!!呀!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
17807多谢!
17807thanks very much
17807我怎么看不到啊,提示说“没有权限”。非常想看泛函分析视频。
17807是哪一本书的哦?
17807thank u very much
17807楼主:
你好.
我们是圈外人.你则是泛函分析方面的专家.
根据附件中的问题和发现,我们写了一篇论文:"比“最大值”还大的值",但没人推荐(编辑部要求),请帮我们引见泛函分析方面的两个专家.先谢了.
我的E_Mail:xishxi987@sina.com
post-69-1140245009.ibf
17807是否有下载?
waveletoooo@163.com
17807一般
17807可以下载的,先现在线看,再从属性里找,再用FLASHGET下载,其实无论地址隐藏的多深,绝大多数是可以下载的,
17807
| 引用 (alaser @ 2006年04月01日
15时35分) |
|
可以下载的,先现在线看,再从属性里找,再用FLASHGET下载,其实无论地址隐藏的多深,绝大多数是可以下载的,
|
请问有地方卖这个内容的光盘吗?
17807thankssssss
17807为什么我没有权限?
17807为什么要再输入用户名和密码,而且输入老是不正确
17807为什么要再输入用户名和密码,而且输入老是不正确
17807好像打不开啊
17807不知道如何打开
17807进不去有什么用,怎么进去看啊,大家给点解释吧,已经看过的人.
17807同问,同问!!!
急!!!
17807我怎么进不去呀。兄弟谁有用户名和密码?
17807用户名和密码是用哪个呀? 我用论坛的登陆不进去哦~
17807我是计算机盲所以下不了,哪位大哥大姐有的话,帮小弟发过来吧!(lleytonhewitt1
18@sina.com).望留下联系方式,本人若考上北师大必有重谢!
17807大哥大姐们,求你们告诉小弟密码呀!!!!!!!!!!!!!!!!!!!
17807
引用 (joeguan2 @ 2006年09月
19日
10时52分) |
| 用户名和密码是用哪个呀?
我用论坛的登陆不进去哦~ |
Me too ! Me too!
17807竟然需要登陆名和密码的,楼主能发一下吗?谢谢了。
17807怎摸下载不了
17807根本又是骗人的,楼主不说用户名和密码等于和没有一样!!!!!
17807有用,谢谢
17807楼上的那位说有用,你倒讲讲它的密码和用户名.
说不出密码和用户名,再说有用,不是等于在放屁!!!!!
这种放屁的话,就少说说!!!!!
17807是啊,要用户和密码呀,请楼主公布.谢谢了
17807看起来不错
17807根本又是骗人的,楼主不说用户名和密码等于和没有一样!!!!!
17807谢谢
17807谢谢
17807楼上有密码吗?多谢!
17807密码用户名是?
17807楼主.我的用户名登入怎么是无效呢
17807密码!
17807偶怎么进不去?
17807re
17807楼上是啥意思呀?若是知道用户名和密码就
17807没有用户名啊
17807用户名和密码是什么呢?
能否告知啊。等着看啊!
17807谢了
17807
| 引用 (johnson_lou @ 2006年11月13日
15时15分) |
用户名和密码是什么呢?
能否告知啊。等着看啊! |
同问!同问!
17807用户名和密码是用哪个呀?
17807太失望了,怎么搞的,好伤心呀,怎么看不了!
17807怎么不行啊>?大哥!!!
17807怎么不行啊>?大哥!!!
17807太好了!我这下有救了。
17807
用户名:student
密码:student
17807楼上提供的用户名和密码又不能登录了。还有谁知道其它用户名吗?先谢了
17807找了5页也没看见用户名密码,
最后student,student也登不上
浪费很多时间了!!!
17807感谢
17807怎么上不去啊?我想参考一下.
17807haohao
17807我也是上不去
总是要求重新登陆
哪位老兄能给个提示
17807好,谢谢!可以用了,就是不能下载!密码:student 用户名:student
17807新手多支持
17807如何下载?
17807照本宣科,讲的不灵活
17807用户名和密码是什么
17807哭求用户名和密码!!!!
17807谢谢拉 我非常感谢你啊
17807skaldjasjflkjlksadjfkasdflkasd
17807怎么还要重新登陆啊,可是我的号怎么无效啊????
17807没有密码的不要问 了
听讲还不如看书呢
讲那么差
17807好人啊!!
17807thfntc rsh ga kbs
17809我在研究一类实用的硬件滤波器设计时遇到一个难题,至今尚未解决,望有兴趣又有数学功底的大侠解决。问题全貌见附件。post-33-1126145438.ibf
17810有那位高手能帮我解决这个微分方程,万分感谢!!!
急,在线等!!!!!
y``-r y` =a y ^{-

} +b y^{-1-

}
17810有没有能做的,我在线等!急!!!!
也欢迎跟贴讨论
17810在附件中,看得清楚一点post-8-1126169333.ibf
17810可不可以用matlab软件做?
如果可以,怎么编程?
17810这个题目最好放到方程版,那里有专门的人来做。
17810好的.谢谢
17811我帮你问问我的老师呵呵,他应该会呀。
17811请问:如何判断四次方程的正根个数???[COLOR=purple]
比如在附件中取b=c=e=1,d=-4时,四次方程的正根有哪几个?post-8-1126
174395.jpg
17811
| 引用 (Twinkle @ 2005年09月11日
22时09分) |
| 试一下画图行不行得通
|
如何画??
17811
引用 (ybyryj @ 2005年09月08日
10时
17分) |
|
请问:如何判断四次方程的正根个数???[COLOR=purple]比如在附件中取b=c=e=1,d=-4时,四次方程的正根有哪几个?
|
b=c=e=1,d=-4的时候很容易判断啊
首先可以分解因式(x-1)为因子
而分解出来的另一部分明显没有正根(系数都不小于0)
17811郁闷!没人帮我?
17811分解因式,有可能根据高等代数的多项式理论
17811
| 引用 (42462257 @ 2005年09月11日
20时21分) |
|
分解因式,有可能根据高等代数的多项式理论 |
分解因式不行吧!我只需要判断其正根的个数,而不需要求其具体值。
17811试一下画图行不行得通
17811可以试试韦达定理,虽然不能解决,但是会有一些指导意义
17811可以用sturm定理解决该问题.不过过程挺烦的!用sturm定理先确定实根个数,在可以进一步判断它所在的大致区间.得出正实根的个数.
关于sturm定理 可参阅<高等代数> 丘维声 实系数多项式一节.
17811
| 引用 (peijun @ 2005年09月15日
08时49分) |
可以用sturm定理解决该问题.不过过程挺烦的!用sturm定理先确定实根个数,在可以进一步判断它所在的大致区间.得出正实根的个数.
关于sturm定理 可参阅<高等代数> 丘维声 实系数多项式一节.
|
能再具体说说sturm定理的内容吗?谢谢!
17811根据符号会有些帮助吧
17811可以用 罗斯判据 判断它在
右半平面根的个数,不过要判断正根个数好像不太容易,peijun,请问sturm定理的内容是什么?谢谢
罗斯判据的内容在:
http://202.1
17.112.33/denglu/system/xuexi/...4/c_4_7_4_1.htm
17811
谢谢!希望能进一步探讨下去!!
17811
| 引用 (yzp471 @ 2005年09月20日
12时57分) |
| 我帮你问问我的老师呵呵,他应该会呀。
|
谢谢!!!!!!!!!!!
17811四次方程一次导数是三次方程,二次导数是二次方程,一导方程的解表示原四次方程的局部极值位置,二导方程的解表示原四次方程在局部极值处的性质(拐点,上凸,下凹),四次方程在各局部极值点处的值配合在原点的函数值,可以讨论四次方程的正实根个数。
过程比较繁琐,但对一般由多项式表示的方程有效。
17811sturm定理到底是哪个定理啊,应用还很广 ,很多学校大纲里都标明了,但书里却没有标明 是不是挺基础的问题哦
17811sturm定理到底是哪个定理啊,应用还很广 ,很多学校大纲里都标明了,但书里却没有标明
是不是挺基础的问题哦
是高等代数里经常用的,就是不知道具体哪个,
原结交数学通路人lengyuyendsk@163.com
17811sturm定理到底是哪个定理啊,应用还很广 ,很多学校大纲里都标明了,但书里却没有标明
是不是挺基础的问题哦
是高等代数里经常用的,就是不知道具体哪个,
17811用来计算多项式零点的。好一点的代数上都有。
17811sturm定理是高等代数里经常用的.一般的教材上是没有的,不过在杨子胥的那本<高等代数习题解>上册里有这个定理!
具体就去看那本书吧
17811我也不记不清楚了,但是我建议你去看看应用这个定理的证明题。或许就是一个特别简单的定理。
17813设A是数域P上的n阶方阵,f(x)属于P[x].已知f(A)可逆.求证:存在g(x)属于P[x],使得
g(A)=f(A)的逆.
谢谢高手的帮助!
17813这些题目最好发到“硕博之路”解答库里面,这个题目有人问过:
http://www.math.org.cn/forums/index.php?show...topic=
17324&hl=
17813证明post-38-1126349092.gif
17813Easy. Let B be the inverse of f(A). Then B=f(A)^{-1}. However, the
inverse X^{-1} of X is a polynomial matrix of X, so B=g[f(A)} for some
polynomial g(x). Thus B=gf(A)=h(A), ok.
17814设
A
∈P n
×n,f(x)∈P[x]
.已知
f (A) 可逆,求证:存在
g
(x)∈P[x]
,使得
g
(A)=f(A)
-
1 .
谢谢高手的帮助!
17814没有太读懂题目的意思,是不是说把一个可逆阵用一个多项式表示出来,如果是这样,就太容易了
17814这个题目有人问过:
http://www.math.org.cn/forums/index.php?show...topic=
17324&hl=
17814Easy. Let B be the inverse of f(A). Then B=f(A)^{-1}. However, the
inverse X^{-1} of X is a polynomial matrix of X, so B=g[f(A)} for some
polynomial g(x). Thus B=gf(A)=h(A), ok.
17815Н Г Чеботарёв “代数函数论”(上册)夏定中 戴执中译 高教出版社
1956年
如有可协商其他事宜,谢谢。
17815
引用 (tzl
1963 @ 2005年09月08日
10时36分) |
Н Г Чеботарёв
“代数函数论”(上册)夏定中 戴执中译 高教出版社
1956年
如有可协商其他事宜,谢谢。
|
我有复印件,要吗?
17815复印件,要多少钱?可否E-mail to me: tzl
1963@yahoo.com.cn thanks!
17815
引用 (tzl
1963 @ 2005年09月15日
10时54分) |
复印件,要多少钱?可否E-mail
to me: tzl
1963@yahoo.com.cn thanks!
|
这部书的下册有电子版,上册没有,只有复印件。如需要上册复印件,请将地址、邮编
和姓名E-mail to me:
hilbert_ru@126.com。全书250页另加邮费共50元。
17815正是此书,如何转让?具体事宜已短信回复。
17815我先把书的品相,来源性质,价格都弄清楚再跟你答复吧.最近弄到不少好数学书.有几本重复了.象复旦
1960年版本的<数学物理方程>,(美)F.W.拜仑
R.W.富勒的<物理学中的数学方法(第一卷),E.C.温特切勒的《概率论》,56年交流讲义的北大的《复变函数论》。M.R.SPIEGEL
的《高等数学的理论与习题》,艾利斯哥尔兹的《微分方程》,方企勤的《多元函数微积分 》,苏步青的《微分几何 》,R.柯朗 F.约翰
的《微积分和数学分析引论(第二卷.第一分册)》,H.H.勃立瓦洛夫
1956年版本的《解析几何学》,王联
王慕秋的《常微分方程定性理论及稳定性理论基础(上.下)》。C.GOFFMAN 史济怀等 译 的《多元微积分》。刘绍学 的《环与代数》
17815是不是H.T.捷波塔辽夫著,夏定中等译 的《代数函数论》(上册)。高等教育出版社
1956年出版的?我想我能弄到。不过可能有点旧的。你有没有兴趣?你还要什么其他的旧书不?
17815我也希望能够有一份,希望有的朋友发给我一份,十分感谢!
jgy_1121@163.com
17816最近学习量子力学,有个超越方程不知在matlab中如何解决,望高手赐教,X=5(1-exp(-x))
17816很简单,使用fsolve函数,示例程序如下(从x0处开始找根,x0可以是复数):
function x=funs(x0)
x
=
fsolve(@(x)x-5*(1-exp(-x)),x0);
运行结果如下(结果出现的其它提示一般不必理睬)
>>funs(1)
>>0
>>funs(2)
>>4.96511423
175243
具体用法请用帮助help
fsolve,这个函数比较好用,方程不是特别复杂时,直接用上面的匿名函数句柄的形式就很方便,复杂的可以另外编写函数返回其句柄。这样简单的方程用命令行就直接可以搞定了,例如x=fsolve(@(x)x-5*(1-exp(-x)),2)就可得到从x0=2处开始找到的根。
178
191+1/3!+1/6!+1/9!+。。。。。。。+1/(3n)!+.......
178
19可能的解法post-8-1126166559.gif
178
19另外提供一个类似的解法
1+x^3/3!+x^6/6!+...=A(x)
x+x^4/4!+x^7/7!+...=B(x)
x^2/2!+x^5/5!+x^8/8!+...=C(x)
A(x)+B(x)+C(x)=e^x
A(1)+B(1)+C(1)=e
A(w)+B(w)+C(w)=A(1)+wB(1)+w^2*C(1)=e^w
A(w^2)+B(w^2)+C(w^2)=A(1)+w^2*=B(1)+w^2*C(1)=e^(w^2)
解方程可以得到A(1)的解
17820 求运算公式:
1-32这32个数字中随机挑出4个数字,
通过什么样的运算公式得到的最终结果可以做到用其他的四个数字使用同样的运算公式得不到同样的结果
要求,计算后得到的结果需要为整数,并且有连续性
举例说明:
随机选择1、4、9、22这4个数字,计算公式为相加,1+4+9+22=36
当然,这个公式是肯定不行的,因为其他的数字使用这个公式同样可以得到36的结果,
如:1+4+10+21=36
可以带括号,甚至对数、函数、指数、微积分都可以
就是要1-36任意4个数字中间的符号加减乘除微积分什么都可以,最后得出的数字必须是唯一的整数
17821难不??网址有没呀??复试都考什么呀??
17822毕业了,再次踏进那个熟悉的校园的时候,一种似是而非的感觉霎时间笼罩心头。正是返校的日子,校园里的路上三三两两提着大包小包的学生一直络绎不绝;人流中,偶尔有一两个似曾相识的面孔,中间偶尔也有几个提前报道的新生,在父母亲友的簇拥下感受着大学生活即将开始时的复杂心情。
我和贾茫无目的的溜达着,路过我住了3年的宿舍楼,看到我住的那屋子亮着灯,心里竟然莫名其妙的一阵温暖;但是随即想到那屋子已经有别人在住着了,这个地方再也不属于我了,惆怅和心酸的潮水哗地一下涌了过来,把那仅有的一丝暖意冲得无影无踪。
“学校不要我们了,我们再也不属于这个地方了....”,
心里这样想着,眼前走过两个报道的新生,突然之间是那样地羡慕他们,甚至有些嫉妒。
不知不觉走到了报亭,贾停了下来,要买份《青年参考》。我站在一边,脑袋里想着天涯海角的事。只见他在那犹豫了一下,掏钱给了摊主,一脸失落地朝我走来。
“唉,毕业了,报纸都得看过期的。”
我无奈地只有摇头苦笑。心里琢磨着这个又苦又酸的黑色幽默,开玩笑说我要是把它发到网上,肯定是2005年最流行句子的top10。
贾说:“太少了吧,才几个字。”
我一想,也是,于是说:“那你就赶紧努力,再说个十句八句的,到时候咱一块发上去。”
拐了一个弯,进了学校正门。迎头一眼望见图书馆的灯似乎一下子都亮了,一股难言的苦闷突然之间梗在喉咙,好像一团稠稠的蜜堵在了心头。
想起在图书馆的那些日日夜夜,想起闭馆时那醉人的音乐,想起那些熟悉的书籍,想起和猴子一起在图书馆找书,现在居然是欲进不能了,眼睛一酸,一声长叹不禁从喉咙深处倾泻而出。
我们就这样无语地走着。任凭时间随脚步一起滑过,远去。
夜幕薄薄的轻纱慢慢地一层一层地垂下,星星也渐渐从深沉的天空渗出来。初秋的夜气透着凉爽,沁人心脾。一轮圆月仿佛伸了个懒腰,缓缓地爬上枝头;心境也就随之沉静、杳远、开阔起来。
一曲上课铃声吹响了晚自习的号角。突然清静了许多,不一会儿,自习的声音和气息渐渐地弥漫了灯火通明地教学楼。但是操场上,依然有不少人在锻炼身体;就在我们经常联系射门的那个门前,几个人在玩抢圈。
校园,似乎永远属于那些朝气蓬勃,活力四射的freshman。
我和贾对望一眼,推了自行车,踏上了归程。
想起现在的工作,难道我们就不是“freshman”吗?想起大学第一年忐忑不安,对未来的那种不确定而又充满希望的心情,跟现在的心情是多么的相似啊。
那时候的我,发愤学习,为了未来;现在的我,努力工作同样是为了未来。虽然校园已经不属于我们,但是青春和未来依然编织着我们的梦想。
只要我们保持一颗“freshman”的心,大学校园就会在我们的生命中永存。
17826g(xi)这类函数怎么编写啊?
哪位仁兄帮个忙
17826具体模型是这样的,哪位兄台帮个忙呢?post-28-1126
180699.ibf
17826请问楼主,
第一式子,在函数的和前面加max是什么意思?
在mathematica中,函数的和可这样定义
Sum[g[xi],
{i, n}]
如果n=2,得到
g[x1] + g[x2]
(注意:式中i是x的下标,在此帖子中无法表达出来。)
第二个式子,s.t.是什么数学符号,我不懂。后面部分的式子可这样表示,
Sum[xi,{i,n}]==a
如果n=2,可得到
x1
+ x2
(注意:i也是x的下标,另“=a”要用“==a”。“=”是赋值符)
第三个式子,可这样表示
Map[(# ≥
0) &, Table[xi, {i, n}]]
如果n=2,可得到
{x1 ≥ 0, x2 ≥
0}
(注意:i是x的下标,(# ≥ 0) &是匿名函数,#是元变量,目的是使后面的xi序列都>=0)
178263楼的朋友,谢谢你!max是表示最大值,s.t.表示“使得”
那是一个数学模型,
目标函数:
max
约束条件:
s.t.
很感谢你能帮我的忙,不过,我对于mathematic是一窍不通,我只会lingo,不知道在lingo怎么编写这样的程序。还望大家多多帮忙。
小弟在此谢过各位!谢谢!~~三楼的朋友!!
17826对不起,第三个式子写错了,应为
Apply[And, Map[(# ≥ 0) &, Table[xi, {i, n}]]]
17826ok!,lingo我不会,帮不上了。
17829已知
~N(0,1),求p{

<2.35}
请将步骤写明白些,谢谢!
17831在非中心卡方分布中,已知分布概率、分位数和n值,如何反求非中心化参数

!
十分急用!
有哪位仁兄知道,希望不吝赐教,万分感激!
17831分布的概率什么意思
17834设Lim An=a ,Lim Bn=b,a<b 证明存在发散数列{Cn},满足An=<Cn<=Bn.(n趋于正无穷)
17834定义Cn:
C(2n-1)=A(2n-1)+[B(2n-1)-A(2n-1)]/4
C(2n)=[B(2n)+A(2n)]/2+[B(2n)-A(2n)]/4
显然n

+

时,C(2n-1)!=C(2n)
17834
a  b,怎么会和夹必定理矛盾呢?可用构造法,
b,怎么会和夹必定理矛盾呢?可用构造法,
构造出来
17834命题不对吧,和夹逼定理矛盾呀
17834
夹逼定理:左右两边的极限都是一样的,这题显然a!=b
17834呵呵,俺没有看清楚,不好意思了
17834这个到简单啊,呵呵!
17834奇数项为An,偶数项weiBn,
17834这是西安交大07年的试题,原题以及详细解答过程在李惜雯那本书上。
17835甲有N+1枚硬币,乙有N枚硬币.双方投掷后进行比较.
求甲掷出的正面数比乙多的概率.若甲有N+2枚硬币有是怎样的结果?
17835提示一下:
甲扔的正面数是一个X~B(n+1,0.5)
乙扔的正面数是一个Y~B(n,0.5)
然后求P(X-Y>0)的概率
17836证明:
P→(Q→R)

(P→Q)→(P→R)
17840我想要啊,我的邮箱是zhouhang751122@163.com
17840我也想要
我的邮箱:henmingz@163.com
谢谢了!
17840我要,谢谢woshiqingqingqing@126.com
17840我要 第5卷 ,其他的我都有,只有第5卷没有下载到
我在国外,网速很慢,请发到我的邮箱里: LHandZX@163.com 谢谢
17840谢谢我要。我的邮箱 supbase@sina.com
17840我也想要,谢谢楼主
tingpuppy@163.com
17840要的。
首先,谢谢你!我的邮箱:penson_lee@yahoo.com.cn
再次感谢!
17840谢谢了,我的mail是
janypow@yahoo.com.cn
17840我有几米的数分题,有需要的吗?1--6本pdf格式
17840我要啊.能不能给我.我的QQ是56016263
17840要的请+81
193590,请注明数学交流,另外请大家把网上收集到的资源共享,最近我发现有人上网弄资料后卖给其他人,这样不是我们学数学的初衷,谢谢!另外本人还有大量数学方面的资料,英语资料,要得请加我qq
17840有阿,谢谢
17840谢谢,我要,我的邮箱是chd12
19@163.com
17840谢谢!我要,我的邮箱是mashouquan@126.com
17840我想收集,邮箱laoqisilo@126.com,谢谢
17840我想邀,我的邮箱是:songyizhuang_323@sina.com
17840我的新浪邮箱
yuxianzhi_penguin@sina.com
第一次上这个论坛,看到大哥的帖子,太感谢了,我是一名在校数学系研究生
希望能把它发到我邮箱,或传QQ:21
195807,每天晚上都要上线,还有中午
17840我加了你了,上次碰到你你也没有理我,不知道什么时候你有空传给我呀
我QQ21195807xiexie
17840我要啊!我的油箱是xie_siwei@163.com.谢谢
17840骗子,根本不理人,大家不要相信他,骗人的,最近搞2个多G的分析方面的电子书,还有两个多G别个还没有给我,一共五个多G,要得给我发邮件
基本所以分析的书都全了,要撒书给我发邮件,QQ21
195087
17840我要第5卷 ,谢谢,suddenly0712@hotmail.com
17840我想要啊!!我的邮箱是maninmatrix-
1924@163.com
17840我也要,谢谢共享我的EMAIL
1985771.student@sina.com
17840我要一份!我的邮箱是chenbohero@163.com
17840发到我的邮箱吧
谢谢你了
googlesever@yahoo.com.cn
17840我加了你我的zhaoleisheng2000@yahoo.com.cn
17840我要3 和5 ,
xjtu_smart@126.com
谢谢
17840我也要,麻烦传一下,谢.我的邮箱yijinxing2005@yahoo.com.cn
17840给我一份 jgli2001@163.com
17840你好,请发一份给我,谢谢
erwinchang@126.com
17840我也要 啊.
beautyblack55555@sohu.com我的邮箱啊 .谢谢了.
17840我也想要,如果可以,请发到我的邮箱 zhoujingyu5@sina.com
17840我也想要,请发hbxlalq@163.com.谢谢啦.
17840麻烦你给我发一下啊,我的邮箱d012109@126.com,谢谢!
17840我也想要,如果可以,请发到我的邮箱
yanglim2001@yahoo.com .谢谢了.
17840给我一份:我的邮箱tiangaorenwofei2006@126.com
我的QQ:506129823
另外我也有一些资料,愿意互相交流的加我共同交流!这是我第一次来这里!谢谢大家!谢谢
17840我想要啊,我的邮箱是dianchenan@21cn.com
17840谢谢,我要,我的邮箱是zhhmjl0828@126.com
17840谢谢!我想要!qq280612933 email fjc1227@126.com
17840要的。
首先,谢谢你!我的邮箱:monk0123456@126.com.cn
再次感谢!
17840要的。
首先,谢谢你!我的邮箱:monk0123456@126.com.cn
再次感谢!
17840致yuxianzhi 兄
可否给我一份?
cheekov@163.com
QQ: 655061
19
跪谢
17840好心的楼主还提供吗?我买了一套,但是放在家里了,暂时看不到。如果方便的话……我的email是dickfisch@hotmail.com
谢谢!
17842请大家帮帮忙看看这个二重积分在【0,1】×【0,1】上为什么累次积分不存在
谢谢各位,急啊
17842
p
x
,q y
是否常数?
17842昨天想了很久终于知道怎么回事了。好长时间不看数分了,都忘了。
谢谢
17846问题如图post-
17-1126
177431.gif
17846第一个就是把两个I乘一下,把一个I中的t换成u,多重微积分里的东西,没看懂回去复习多重微积分
第二个是因为关于y轴对称
17846谢谢指点
17846子青:
我回去看了,第一个问题,我看了多重积分,但这部分没有提到积分的乘法,我不知道看哪了,我是自学的,我看的是高教第五版,还有我第二个问题:书上也是说关于Y轴对称的,但为什么不是post-
17-1126255002.gif
17846第一个是多重积分转化为一维积分
第二个关于y轴对称的是密度函数,你那个
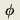
是分布函数
17846
| 引用 (爽歪歪 @ 2005年09月09日
16时36分) |
子青:
我回去看了,第一个问题,我看了多重积分,但这部分没有提到积分的乘法,我不知道看哪了,我是自学的,我看的是高教第五版,还有我第二个问题:书上也是说关于Y轴对称的,但为什么不是
|
1. 没有乘法就把积分的定义,多重积分的定义吃透,就明白了
(两个自变量又没有关系,直接可以还原到各自的积分号下,在把u换为t不就是I^2。。)
2. 关于Y轴对称是指概率密度对称,
分布函数哪能对称?? Fai(x)在-无穷趋进与0,+无穷趋进于1,怎么可能对称? 把
Fai(X)分布函数的定义搞清楚,就明白这个推导了
4.14公式有问题,积分上限因该是x,不是无穷
两个问题建议把定义搞清楚...
(加油)
17846楼上的前辈谢谢了,第二个问题,我已经弄清楚了,把整个
分布函数看成总面积为1就得(4。15)了,
第一个问题,我会按照的指点的方向去继续努力学习的
再次感谢各位
17847武大昨日宣布,接国务院学位办通知,原定2006年推行的研究生培养机制改革暂停实施。该校2006年研究生招生收费方案不变,照以往实行。
17848
可以用反证法吗?
17848设f(x)在(a,+

)上单调上升,lim(xn)=+

(当n

+

)
若limf(xn)=A (当n

+

)
证明:limf(x)=A (当x

+

)
17848显然的
17848解答见附件post-38-1126
183533.ibf
17848可以!
不妨设lim f(x) !=

那么必然存在某个无穷序列y1<y2<...<yn<...
使得lim f(yn)=A !=

显然与lim
f(xn)=

和f(x)单调递增矛盾
17849帮我看看啊 post-38-1126
178931.gif
17849单调函数的间断点必是跳跃点,而导函数正没有此类点
17849把f换成f'的积分形式即可容易看出
17849证明: 因为f(x)在(a,b)可微,故$f

(x)$在(a,b)内有定义.
假设$f

(x)$不连续,则 存在a<x0<b,使得x0为$f

(x)$的间断点.
因为$f

(x)$单调,不失一般性,设为单调增,
可以得到$f

(x0-0) <
f

(x0+0)
$从而$f

(x)$在x0点无定义!
矛盾.从而$f

(x)$为连续函数.
17849这道题目可能会出现在某个学校的试题中,就在06年考数学的人中会有人碰到,我的预感!哈哈
17851如上
17851好象显然,不知道如何证明?请指教。
17851若C为[0,1]上的Cantor三分集,
令S为C与[1,2]的并集,则S不是R上的区间之并
17853通用的方法对特定的题目不同可能更不好用
17853怎样把一般的图形转换成极坐标形式,是否有通用的方法
17853当然,图形的方程需要已知,然后利用直角坐标与极坐标的关系来转化。
17854丘成桐先生近日被意大利林琴科学院(AccademiaNazionaledeiLincei)选为外籍院士。林
琴科学院规定,只有当一位院士去世后,才进行院士增补。此次国际学术界一致推选丘
成桐先生继承已故陈省身先生的意大利林琴国家科学院外籍院士称号,可谓众望所归。
意大利林琴科学院是欧洲最早的科学院之一,
19世纪初正式创立于罗马,而它的前身可
以追溯到
17世纪,著名物理学家伽利略就曾经是林琴科学院的院士。著名数学家陈省身
先生曾于
1988年当选林琴科学院外籍院士。林琴科学院的院士中大多都是国际知名的学
者,其中21位外籍数学院士中有8位费尔兹奖得主,5位沃尔夫奖得主。
丘成桐先生最早把非线性分析系统地引入到微分几何学中,令众多几何、拓扑学的难题
得到解决。他的工作深刻地变革了众多数学分支:微分几何学,非线性微分方程,广义
相对论,代数几何与弦理论,极大地奠基或推动了这些学科的发展,极少有数学家可以
在如此众多的数学领域中都产生巨大的影响。可以说,现代几何分析学的几乎所有研究
方向都深受丘成桐工作的影响。
17854不愧为咱中国人的骄傲!
17854
引用 (caozhq @ 2005年09月14日
19时47分) |
| 不愧为咱中国人的骄傲!
|
自我安慰一下吧!
17854我们这些后辈们不能只是感慨,要多多努力了!!!
17856一次开国内的一个专题研讨会,有位台湾清华大学的教授做报告,本人认为不咋的。
17856只知道台大很厉害;台湾清华也是梅先生创办,可能更贴近他的精神。
17856
| 引用 (wangjh2000 @ 2005年09月08日
20时45分) |
|
一次开国内的一个专题研讨会,有位台湾清华大学的教授做报告,本人认为不咋的。
|
数学教育水平不清楚,但理工科的总体教育水平肯定不会低,否则怎么可能挤入亚洲“四小龙”行列。
17856不咋地,不咋地。
17858rt
它的网站(www.sysengi.com)上提供了tex模版,但无法下载:(
其他相关期刊的投稿模版也可,在这里先谢了。
17862不好意思,请 看附件post-21-1126
187669.ibf
17862先给出第二个题目的证明,第一个再做:post-21-1126
194
183.gif
17862第一题提示:
用数学归纳法,
关键是想办法利用n=1时的情形,将n时的定义域缩短到n-1!
17862
| 引用 (mazl @ 2005年09月09日
06时39分) |
第一题提示:
用数学归纳法,
关键是想办法利用n=1时的情形,将n时的定义域缩短到n-1!
|
呵呵
高手啊
根据提示我给出的解答如下:post-21-1126258064.gif
17862十分感谢tobyqin
17863哪位能将区域满足Lipschitz边界条件具体的写一下啊,谢谢
17865continuous pdf,discrete pmf 什么意思啊
17865第一个是连续概率分布密度函数
第二个pmf应该是边际概率分布吧,discrete是离散的意思.
17865
| 引用 (wang_jh2001 @ 2005年09月08日
22时25分) |
| continuous
pdf,discrete pmf 什么意思啊 |
p.d.f: probability density function.
it is used to describe continuous random variable. eg. Exponential
Distribution M(

) with p.d.f f(t)=

exp(-

t)
p.m.f: probability mass function, used to
describe discrete random variable. eg: Possion(

) P(X=x)=....
17865
| 引用 (cc9hwa @ 2005年09月12日
02时14分) |
| 引用 (wang_jh2001 @ 2005年09月08日
22时25分) | | continuous
pdf,discrete pmf 什么意思啊 |
p.d.f: probability density function.
it is used to describe continuous random variable. eg. Exponential
Distribution M(  ) with p.d.f f(t)=  exp(-  t) p.m.f: probability mass function, used to
describe discrete random variable. eg: Possion(  ) P(X=x)=....
|
谢谢。pdf我后来明白了,但是pmf还是不明白,我想你说得对
17865
| 引用 (wang_jh2001 @ 2005年09月13日
22时28分) |
| 引用 (cc9hwa @ 2005年09月12日
02时14分) |
| 引用 (wang_jh2001 @ 2005年09月08日
22时25分) | | continuous
pdf,discrete pmf 什么意思啊 |
p.d.f: probability density function.
it is used to describe continuous random variable. eg. Exponential
Distribution M(  ) with p.d.f f(t)=  exp(-  t) p.m.f: probability mass function, used to
describe discrete random variable. eg: Possion(  ) P(X=x)=....
|
谢谢。pdf我后来明白了,但是pmf还是不明白,我想你说得对
|
p.m.f 中文是密度函数,比如掷一个匀质筛子 p.m.f is P(X=x)=1/6
1<=x<=6.
17865常用的缩写有:
p.d.f: continuous random variable
p.m.f:
discrete random variable
c.d.f: cumulative distribution function
P(X<=x)
p.g.f: probability generating function
etc, etc.
17866如题,老板要我想想看能不能用metlab解诸如
A1X=C1
XB2=C2
A3XB3=C3
的矩阵方程组,其中(1,2,3)是下标。
已知方程组的解是用已知的系数表示且含有未知变量的表达式,应该用metlab里面的什么啊
求助啊,谢谢!
17866各参数是数字、向量还是矩阵,是要同时满足三个方程还是分别求解,把问题描述清楚嘛。
17866一般的matlab书中都有,采用迭代法来解之
17867今年第一次参加研究生数学建模比赛,以前有参加过本科组的,不知道这有什么差别没有,有谁参加过去年的研究生建模比赛,能否点拨一二?!
17868请问有没有什么方法将一个非线性,多变量,不保凸的函数构成的空间分解成几个子空间啊?
请赐教!谢谢!
17868不知道柱形分解能不能帮你解决问题.
乱猜的.
17870不知道国内哪里能买到这本书:
Introduction to Linear Optimization
by
Dimitris Bertsimas and John N. Tsitsiklis, Athena scientific,
1997.
ISBN:
1886529
191
请告知,谢谢!
17871一.(20分)设 f(x)是定义在[a,b] 上的单调函数
(2)若f(x) 在[a,b] 上不连续,则
f(x)在[a,b] 上的不定积分不存在
请您将答案详细写出!
17871证明:不妨设f(x)单调增,则存在$x0

[a,b]$,使得
f(x0-0)<f(x0+0).
用反证法.假设f(x)的不定积分存在,即有(a,b)上的可导函数F(x),使得
$

f(x)dx =
F(x)+C $
即
$ F

(x) = f(x),
a<x<b $
从而在
$ F

(x0) =
f(x0)$与f(x0-0)<f(x0+0)矛盾.
17871F(x) = f(x), a<x<b $
从而在
$ F'(x0) =
f(x0)
这一步怎么来的,看不明白?
f(x)不是连续的啊
17871根据不定积分的定义,存在可微函数F(x),使得
F^{`}(x)=f(x),
故F(x)的导数应该有定义,可是因为f(x)的间断点不是可去间断点,
所以无法定义F(x).
矛盾!
17872还是不会哦,大哥帮帮忙,说具体点啊
17872
三.(10分)设 D是R ^2 中具有光滑边界的闭区域, f是定义在 [a,b]上的实函数,若
F{(f(x,y)) ^2}dxdy=0 (F{```}dxdy表示在D内二重积分,我打不出符号,抱歉)
则 f在D
中的连续点上的取值为零
17872用反证法啊,容易得出啊!
17872这好象是哪个大学的试题吧,我做过,等我明天回家了之后有自己的电脑了,我打给你看吧,我现在在网吧里,这样具体的打划不来啊!忍两天吧!
17873看不大明白
17873第二种方法好简洁呀
请问蓝戈:
这里的两个积分交换次序是需要什么条件?
17873
最后一题怎么做??post-38-1126224688.ibf
17873我的一个解答,本人做里一套浙江大学数学分析,大脑已经缺氧了,不知道解决这个题目时头脑是否正确运行,大家看哈!post-38-1126253594.gif
17873看看我做的post-38-1126263613.gif
17873问?post-38-1126314977.gif
17873当然要有条件啊,那就是一致收敛,这个对于极限符号的变换十分重要的!
17874第七题第二问怎么利用那个等式证明?
我现在只会利用含参量积分求证,毕竟还不是原题的要求....
17874问题:
1;第5题
2:第7题post-38-1126225003.ibf
17874第七题:
(1)这不是顶积分的定义吗?
(2)由刚推导的式子得出
17874本人用了三个小时,在网上现场做,只是可惜,这个水平太菜了,哎,郁闷,还有一道半没有做出来,大家帮忙想一下,就是最后两题的相关的东西。
估计总分还做不到80分,郁闷ing。post-38-1126250724.ibf
17874蓝戈给出题目的第四题我又做了一下
方法和所给的不同,如下:
bt:原答案少了一个常数倍。post-38-1126458315.gif
17874献丑了,再给出第一题另外的方法:
bt:虽然题目简单,不过个人认为方法可取用于其他题目。post-38-1126459437.gif
17874第八题:post-38-11263
19976.gif
17874牛,兄弟,佩服你啊!你是打算考哪个大学的研究生的呢?
可否加你的qq呢?我的是47394674
17874tobyqin第4题f(x)不一定可导啊,一开始我也犯这个错误了
17874第1题没有看明白post-38-1126522996.gif
17874问:蓝戈
为什么第2题对x,y求完一次偏导以后还要求二次偏导呢,求出来有什么用啊?这里我不大明白啊
17874第6题,题目没有说ak单调啊
17874
引用 (tobyqin @ 2005年09月12日
19时00分) |
引用 (luting5 @ 2005年09月12日
18时55分) | |
tobyqin第4题f(x)不一定可导啊,一开始我也犯这个错误了 |
我知道你的意思
不过你注意第一步没有问题吧?
而下面对f(x)的求导的时候我已经把它表示成可导函数的和了啊
呵呵,这个可不是错误啊
嘻嘻
|
第4题我仍旧不大明白,你不是出现了f'(x)了吗?f'(x)不一定存在的啊
17874问:蓝戈post-38-1126524397.gif
17874
引用 (luting5 @ 2005年09月12日
19时
17分) |
引用 (tobyqin @ 2005年09月12日
19时00分) |
引用 (luting5 @ 2005年09月12日
18时55分) | |
tobyqin第4题f(x)不一定可导啊,一开始我也犯这个错误了 |
我知道你的意思
不过你注意第一步没有问题吧?
而下面对f(x)的求导的时候我已经把它表示成可导函数的和了啊
呵呵,这个可不是错误啊
嘻嘻
|
第4题我仍旧不大明白,你不是出现了f'(x)了吗?f'(x)不一定存在的啊
|
是不是fxxfyy-fxy>0就最小,<0就最大啊?
这边我怎么没有看见过啊,在书上什么地方的啊?
17874问蓝戈post-38-1126525092.gif
17874
引用 (tobyqin @ 2005年09月12日
19时34分) |
做题应该是一点点的得到信息的啊
如果我们得到f(x)为一些可导函数的和那么就是可导了啊
另外那个是在多元微积分的极值问题里出现的
|
哦,第4题我明白了,f(y)是把他看做常数的对吧?
17874哦,果然是高人,你一点拨我先现在茅塞顿开啊,第6题也知道了,不过第5题人就没有能转过弯来
17874第六题证明:
post-38-1126532363.gif
17874可用凸函数方法
17874
第六题蓝戈得做法是对得
17874第七题第一问证明中我们知道那个结论中的下极限可以改成极限的
这样我们就可以通过第一问得到后面的结论了
我给出我得解答,比较长,大家最好保存放大一点看:post-38-1126589154.gif
17874
| 引用 |
牛,兄弟,佩服你啊!你是打算考哪个大学的研究生的呢?
可否加你的qq呢?我的是47394674
|
TO:蓝戈
太高估本人了,在下才疏学浅,还有很多问题请教大家!
17874第七题是 Posisson
积分post-38-1126679
197.gif
17874好!
17875问题是这样的:产生一个8位随机数,产生10W次,重复的概率是多少?只要重复就好,并不是说规定要重复到哪个数!
17875请帮帮我,我不是数学系的,而且大学上概率课都没怎么听,现在碰到问题我都解决不来了!
我再说说我的思路:
只可能是2种可能,一个是不重复,一个是重复!
10W次产生不重复的概率为
a= (1 - 亿分之一)*(1 - 亿分之二)*(1 - 亿分之三)……
一直重复做 (10W - 1)
次
然后产生重复的概率就是 b=1-a
我不懂什么公式,这也只是我的想法,也不知道是不是真确的,我真是虚心求教,等待好人解答!
17875你按什么分布产生这个数
17875首先谢谢您的回复:
然后其实我真的是个数学盲,我不知道什么分布
我先不假设随机8位,数据太大!我们假设随机一个2位数,随机数的范围是0到99,
当你做这样的操作100次后,当然,我们基本可以断定是会产生随机到相同的数了,假如是做101次操作的话,当然那是绝对会产生相同的数,就像抽屉放小球一样,最后不管怎么放,总要有一个抽屉至少有2个球,回到原题,产生到都不一样的随机数也是有可能的,就是从0到99中的数都刚好各随机到唯一的一次,最后产生的结果是0,1,2……,99这样数的组合,这样产生的概率是存在的!
我的想法:
1.产生第1次随机数时,没有什么要求,可以任意
概率设为 100%
2.产生第2次随机数时,要使他都不相同,就必须把第1次产生的随机数排除,所以第2次的概率为
99%
3.产生第3次时也同上,概率为 98%
……
100.这是最后一次产生,他的概率为
1%,因为要产生不同,只有1个数给你选了,选中他的机会是 1%
最后得到都不相同的概率就是前面100次概率的乘积
得到 100%
* 99% * …… * 1%,这个概率很小,当然可以肯定如果产生100次随机的2位数,基本可以确定肯定会重复,我的要求是
假如只产生10次呢?这个概率是不是可以写成 100*百分99*百分98*……*百分91
(也就是要产生多少个数,他不相同的概率就是做几次乘积)
期待您的回复!
17875继续等待答案
17875还没有等到想要的答案啊,继续等待!
17875哎 真晕 ~~~~是太简单了吗?
17875最简单的组合问题
随便翻翻高中课本就知道答案了。
17877刚看还是不怎么懂。回去好好想想呵呵
17877各位,
我现在急需下面的计算公式。
空间直线与球的交点计算公式
空间直线与椭球的交点计算公式
空间直线与圆锥的交点计算公式
空间直线与圆柱的交点计算公式
假设直线的方程,和三维体的方程为已知。
请各位帮忙,给出计算公式。
或相关的参考(最好是电子的)
17878试卷的合理均衡分配
在大学生数学建模竞赛的评卷工作中,M个评委(M个评委来自不同的学校)要完成N份试卷的打分,竞赛试卷来自K个学校,第j个学校有竞赛试卷lj份,N=∑lj(j=1:k)为节省人力,每份试卷只要由其中p(p<M<K<<N)个评委进行打分就行,
1。
根据回避原则,要求评委不能阅自己学校的试卷,请给出试卷合理的均衡分配方案的数学模型,使各评委阅卷工作量均衡;试卷分配均衡分散。
2。
给出试卷合理的均衡分配方案的计算机程序,要求用MATLAB或C语言编写。输入参数为p,M,k,n,输出参数为各评委分别阅卷的号码,就下列实例给出问题的答案。
实例:某省有竞赛试卷568份,32个评委阅卷,40所学校,3<lj<30自己设定,给出问题的答案。
17884我想在我们论坛上搜索一些相关的帖子
请问:怎么操作啊?
回复:点击论他右上侧“搜索”字样,进入搜索页面。
输入关键词,选择搜索范围和时间范围即可。
17886这个问题我已经考虑几天了,也问了教研室很多老师和同学,都解决不了,求高手帮忙!
设从A到B有n条路(S1...Sn)可以选择,m(m小于n)个人同时要从A到B,每个人所走路径不能重复;通过每条道路Si所需时间服从参数为ai(i大于等于1小于等于n)的指数分布;已知道路Si被走的概率为Pi(i大于等于1小于等于n),求m个人从A到B的时间。
求解过程论坛写不下,可发邮件:smartslliu@yahoo.com.cn,非常感谢!
17886这题其实不麻烦的,是一个加权分布:
设第j个人走的时候选的路线是
i j ,所以随机向量:
( i
1,i
2,...i
m)=(i
1,i
2|i
1,i
3|(i
1,i
2),...i
n|(i
1,i
2,i
3..i
n
-1))
所以总时间T
T
=∑ j
=1 m
e(a
i j
)P(i
j|i
1,i
2,...i
j
-1)
公式显示不了下载置顶帖中的插件
17886感谢楼主对我问题的回复!但是帖子上的内容比较简单,而且一些公式看不到,我不是数学专业的,有些东西我一下子理解不了,您能否把这个问题给我一个稍微详细的解答,把解答过程发邮件给我smartslliu@yahoo.com.cn!这个问题是我目前一个无法越过的难题,麻烦!非常感谢!
17886
| 引用 (b964050 @ 2005年09月09日
15时41分) |
|
感谢楼主对我问题的回复!但是帖子上的内容比较简单,而且一些公式看不到,我不是数学专业的,有些东西我一下子理解不了,您能否把这个问题给我一个稍微详细的解答,把解答过程发邮件给我smartslliu@yahoo.com.cn!这个问题是我目前一个无法越过的难题,麻烦!非常感谢!
|
公式显示不了下载置顶帖中的公式插件
这个是个混合分布,最直观的解释,就是以P_i的概率取一个消耗时间为e(a_i)的线路,然后求和就可以了。如果想要严格的解释,是很难说清楚的,如果你连基本的概率知识都没有,那最好先补一下概率的知识,特别是分布函数和随机变量的定义那块
17886感谢斑竹的回复!上面的回复对于从n条道路以不同概率选出一条很有用。但是我认为我的问题应该包含两个步骤:首先要求从n条道路里选择m条出来(m个人要走),其次需要求m条道路时间最长的,因为必须等最后一个人到达B才算结束,即Max(i1,i2,...,im)(ij为第j个人选择的道路)。所以这个问题比一般的加权分布要复杂的多。
斑竹第一次的解答:设第j个人走的时候选的路线是
i j ,所以随机向量( i 1,i 2,...i m)=(i 1,i 2|i 1,i 3|(i 1,i 2),...i n|(i 1,i 2,i
3..i n -1)) ,所以总时间T
T =∑ j =1 m e(a i j )P(i j|i 1,i 2,...i j
-1),不知是笔误还是有其他意思,我认为( i 1,i 2,...i m)应该等于(i 1,i 2|i 1,i 3|(i 1,i
2),...im|(i 1,i 2,i 3..i m -1)), 而且斑竹解答中“所以总时间T,T =∑ j =1 m e(a i
j )P(i j|i 1,i 2,...i j
-1)“因为公式不清楚,所以我也不是很懂。不知斑竹能否给出略微详细的步骤。
这个问题已经困扰我很久了,下午刚同数学系一名副教授讨论了这个问题,他也没有给出合适的解答,只是说要再考虑一下。希望斑竹在百忙中给与解答,非常感谢!smartslliu@yahoo.com.cn
17886不知你有没有下置顶的公式显示插件,装了的话公式应该可以正确显示,只要是IE核心的浏览器.
你定义的m个人的时间原来是m个人里的最大时间啊,那这个就是一个顺序统计量的问题
设
X
i
∼e(a
i) 是第i条路线消耗时间的随机变量.则已知选出
( i
i,i
2,...,i
m) m条路线的情况下:
P
(X
max<x)=∏
j =1
m
P(X
i j
<x)
所以根据全概率公式,设m个人从A到B的时间为r.v. T,则
P
(T<x)=∑
1 ≤i
1≤i
2,...≤i
m≤m∏
j =1
m
P(X
i j
<x)P(i
1,i
2,...,i
m)
17886楼主的答复太笼统了,没有太多可参考性。
我也知道
P
(X
max<x)=∏
j =1
m
P(X
i j
<x)
,但这个公式对于固定的m个求最大非常好解,但是我这里的m条路本身是随机的,这个公式怎么计算?还有斑竹根据全概率公式,设m个人从A到B的时间为r.v.
T,则
P
(T<x)=∑
1 ≤i
1≤i
2,...≤i
m≤m∏
j =1
m
P(X
i j
<x)P(i
1,i
2,...,i
m) ,这个公式我也列的出,关键是怎么往下求呀!斑竹能否详细多给出几个步骤,这个问题我们这边几个工科的博士生以及数学系搞统计的副教授都讨论过,如果很简单我也不会拿到这儿麻烦大家了!非常感谢!
17886思路本来就是用条件分布来做的,用条件分布当然是先对某个固定的m来求,然后再把m放宽成随机.
后面那个P(i_1,i_2,...i_m)计算很烦琐,建议用Monte
Carlo模拟,不要计算真实值,真实值的计算是这样的:
考虑i_1,i_2...,i_m的任意一个不同的排列,为了符号的简单,我们假设排列下来是k_1,k_2...k_m
注意,是排列,不是组合,要考虑顺序,然后在这这组数从这个排列获得的概率是:
∏
j =1
m P
k j
/∏ j
=1 m
(1-P
k 1
..-P k
j ) 这个是一个排列的概率,然后对所有可能取到这组数的所有可能的排列求和,出来的就是抽到这组数的真实概率...很复杂吧...建议建议用Monte
Carlo模拟.简单,快速,模拟次数多了误差也不是很大
17886感谢楼主,mento
Calo模拟到底怎么进行,我是学工科的,基本的数学知识还可以,但是对于这些深层次的数学问题的确是非常困难。你能否将我的问题用你认为可行的方法略微详细的帮我推导一下,我也实在是没有办法,请教了很多人,只在你这边还有点思路!如果搞不定,我现在研究的这一部分就只好放弃了,前一阶段的工作也就白费了!帮忙,斑竹!(如果实在麻烦可以假定各条道路被选择的概率相等,实际上是对我的模型进行简化。)帮忙,拜托!
17886就是写个程序,模拟按你给的概率从n条路中抽取m条,模拟个几千万次,然后用频率代替概率
17886模拟的方法对我好像不是很合适,因为我的问题是根据一个应用所提取的数学模型。楼主能否介绍我一些这个领域的专家,最好告知邮件,我好向他们请教!因为这个问题我实在是绕不过去,可以简化模型来减低问题的复杂度,但是实在躲不过去,谢谢!
17886专家我就不是很清楚了,其实也可以算真实概率,只不过不能手算了,要用计算机算.从1-n中做出所有m个元素的全排列,这个是很基本的算法,找个过了高程的人都能写,然后按前面的公式把真实概率算出来.写个函数.
17887
http://news.sina.com.cn/c/2005-09-09/093
17721370.shtml
17887这也不好啊
17887好啊啊啊啊啊
17887唉,我们的教育部的决策者们啊。。。。
17887好消息,我的选择又多了,真是爽啊!这个消息对于我来说就如同久逢甘露的感觉啊!
17887是呀!!!本科收费已经很多拉,,研究生在收,!!!中国教育就完拉
17887我顶
17887支持!!!!!!!!!!!!!!!!!!!
17887今年还不会收费的,至少是不是全面收费的,要考的快抓紧了。
17887强烈支持~!!
17887总是在报名之前有这要收费的谣言,易影响大家的选择,现在好了,不过收费总会成为趋势的
17888不一定,看学校,师范类一般考多门。
17888不是啊!四川大学初试的时候就要考常微分方程啊!
17888初始,数分,高代
复式,复变,实变
17888对头
复式,一般复变,实变
17888查了几个学校数学专业的考研招生发现就是这样,是吗?概率呢?不在初试考吗?
17888一般是这样,概率应在复试时考试。
17888也不一定呀!!!
17888不一定,要看学校
17888[SIZE=7]一般来说,顶尖的学校会考多门专业课。而且今年和去年可能就不一样。
像北师大今年第一年开始在初试考五门专业课。
17889A(n)=A(n-1)+1/A(n-1)
A(1)=1,他有界吗?极限呢?通项可求吗?
我的思路是平方两边.再叠代放缩但只可证有界.
17889
| 引用 (lixiaohu @ 2005年09月09日
12时12分) |
A(n)=A(n-1)+1/A(n-1)
A(1)=1,他有界吗?极限呢?通项可求吗?
我的思路是平方两边.再叠代放缩但只可证有界.
|
明显无界吧!post-
19-1126245116.gif
17889可以假设有极限,由于单调增,所以极限不会是0,带入即可
17890级数通项为1/n(1+1/2+1/3+...1/n),从n=1,2,....加到无穷.收敛吗?
17890不收敛
注意1+1/2+……+1/n<2lnn
(当n足够大以后)
那么级数就大于1/2nlnn的求和
而后者不收敛
17892感觉工科数学的基础和数学专业的差很远啊.主要是数学思维差.
看定理的推导和证明有些吃力.更别提自己来证明了.
如果需要补基础,大家能推荐一些课程么?
需做的方向是供应链,现在正在上非线性优化的课.
有些晕:(
请大家指点
17892没问题,只要上手就快
17892如果是工程类的,重点放在建模技巧上,了解如何建模便于求解即可。至于模型怎样解出来的,可以有数理科学家去搞定。我自己觉得不是那块料。但对解决实际问题比较感兴趣
17893以前有个地方能下到matlab6.5全套手册,不过现在没了,
请问谁知道哪里有matlab6.5的手册啊??
比如样条工具箱手册,优化工具箱手册...等等
17893
http://lib.verycd.com/2005/04/27/0000048437.html
17894本人很菜的,刚刚接触matlab,不太会用。
想请教各位高手,如何用matlab求极值,是用什么命令command的?
从最基本的开始:
比如,我们都知道y=(x-1)^2的最小值为当x=1时y=0,
那么如何通过matlab编程计算得到上述答案呢?
谢谢了
17894>> fun='(x-1)^2';
>>
x=fmin('fun',-100,100),f=eval('(x-1)^2')
17894谢谢了。小弟会继续努力的
17896很正常啊,你当电脑是万能的?电脑再牛逼也没有人厉害啊,我见得多了!
17896怎么软件也不行了呢?各位帮我算一下,我的lingo软件算不出来哦
程序如下:
model:
sets:
city/1..7/:m,n,t;
link(city,city):c;
endsets
min=@sum(city(i):n(i));
@for(city(i):m(i)/n(i)=d/t(i));
@for(city(i):
@sum(city(j)|j#gt#0:c(i,j)*m(i)/m(j))=1);
d>6;
@for(city:@gin(m));
@for(city:@gin(n));
@for(city:@gin(m/n));
data:
t=6
3 6 5 2 1 2;
c=0 4 5 1 3 0 0
0 0 0 0 0 3 0
0 0 0 1 0 0 0
0
0 0 0 0 0 2
0 0 0 0 0 0 0
0 0 0 0 1 0 0
0 0 0 0 0 0
0;
enddata
end
17896程序来源于下面的模型
post-28-1126260893.ibf
17899类似的区间上的达布连续函数也一定是局部有界的吗?
17899区间上的导函数不一定局部有界,例如
f(x)=(x^2)sin(1/x^2),x不为0时
=0,x为0时.
则f在[0,1]可导,但导函数在x=0(附近)非局部有界.
17900常值函数,斑竹想这个例子有和原有
17900如题
17900这个是数分课本的习题
就是要证明点点极值的必为常值函数
17901如题
改成内闭
一致可微是才对的
17902如题
17903我是搞cs的,具体一点是做ai的,在具体一点是搞知识的表示和推理的。
从我的角度看,这个领域的基础就是各种各样的逻辑,很多研究已经说不上来是数学还是计算机,但是做的深了一定会走到各种各样的数学(集合论,模型论,递规论等等)中去。
有一本书叫“计算机科学中的逻辑”(名字可能不准确),是王元元写的,说他是个数学家应该没什么问题吧。
在这个论坛,我没有找到一个讨论这方面问题的版,所以提出这个建议,请大家讨论。
17903我也是搞CS的,我的当前方向是形式化,经常接触形式逻辑和形式语言,主要是一些非经典逻辑.这些到底是数学还是CS,恐怕没人能说清楚.我赞成你的建议.
我吃惊的是,连经济学和生物学这样的学科在这里都有版面,计算机科学这样的除数学以外最象数学的学科竟然没有版面?---可能是太象了,分不开吧---比如研究算法的可以找"组合"版......等等
我看这里有"图论",应该再开一个"数理逻辑与理论计算机科学".象模型论,各种经典非经典逻辑,计算理论(递归论),形式化,model
checking,automata......等等,都可以讨论.
17903"计算机科学中的逻辑学","面向计算机科学的数理逻辑"
印象中有这两本书
17903
引用 (gzchenyin @ 2005年09月09日
17时50分) |
我是搞cs的,具体一点是做ai的,在具体一点是搞知识的表示和推理的。
从我的角度看,这个领域的基础就是各种各样的逻辑,很多研究已经说不上来是数学还是计算机,但是做的深了一定会走到各种各样的数学(集合论,模型论,递规论等等)中去。
有一本书叫“计算机科学中的逻辑”(名字可能不准确),是王元元写的,说他是个数学家应该没什么问题吧。
在这个论坛,我没有找到一个讨论这方面问题的版,所以提出这个建议,请大家讨论。
|
不知道你关注哪些逻辑.
17904
http://www.math.org.cn/forums/index.php?showtopic=16377
回复:已经警告,谢谢举报!
17905都很重要嘛
17905不是吧,那么概率论树立统计也要考那些实变什么东西啊???
17905还是要学好的,无论是从大处还是小处想----培养能力,复试不定选哪个研究方向,考试就要考到实变,近代之类的
17905我觉得不紧要学,还要学好,尤其是实变函数
我觉得不该为了考验而考验,该把自己的能力培养上去
17905两门都很重要 不要放弃阿
基础阿
17905我相信学实变泛函后会对高代数分理解够好.
但怕厚此薄彼,不如谁便混混算了.
17905这个都是基础的。学还要学好。
17905关键是今后的发展方向,方程类等必须学好泛函$*#@,代数方向则必学数论.
17905一定要学好啊,我自己实变是混过去的,现在非常后悔,基础一定要打好啊
17905我很坚持学习专业课的
不能只为了考研而学习的
17905实变很难
17905当然要学,要不考上后你会后悔的
17905都学比较好
17905如果想有发展,就要学好
17905数学专业的后继课程很重要,尤其是实变函数,泛函分析 拓扑学。学期来是很费劲的
大家好有个准备。
17905以后考研靠综合了,所以都要好好学啊!
17905还是要学吧
17905实变学得不好
17905当然要学
17905当然,不然考上了也是有隐患的
17905一定都要学好的
不然到研究生的时候没法学
17906我想名额上区别大吧.如清大的被保送的几乎完全占了
其次,难度上.
还会有各个学校有各个学校的特色.
还有试题的偏向性.
还有呢??????????????????????
/////////////////????
17906老大,这么有意义的主题怎么不说下去。君是过来人吗?
17906好呀 !!!我也晕拉
17906

逛逛哈
17906哈哈,subject 大而全,而空
17906没懂
17906不能再说一点?
17906努力就有回报!
17906楼主名字....
兰大的?
17906就 这么少 啊
17906干吗呢这是
17908用三根木棒摆成一个比3大比4小的数,怎么摆?
17908用八分之七猜一个成语。
17908大家都来猜猜嘛!
17908切西瓜,九块瓜十快皮,问怎么切???
17908不看
17908有知道的吗。说来听听\
17908第二题
七上八下
17908第二题
七上八下
17908第一题

17911刚刚下完,还没看。谢谢。
17911非常不错的一本书~谢谢楼主大哥~~
17911好好看一下,我是最讨厌数学的人了
17911强烈的顶
17911《给讨厌数学的人》——虽然是小日本写的,但还是值得一看!post-33-1126264980.ibf
17911《给讨厌数学的人》post-33-1126265
192.ibf
17911《给讨厌数学的人》post-33-1126265365.ibf
17911《给讨厌数学的人》post-33-1126265584.ibf
17911《给讨厌数学的人》post-33-1126265859.ibf
17911《给讨厌数学的人》post-33-1126266023.ibf
17911《给讨厌数学的人》post-33-1126266165.ibf
17911《给讨厌数学的人》post-33-1126266298.ibf
17911《给讨厌数学的人》post-33-1126266469.ibf
17911《给讨厌数学的人》post-33-1126266595.ibf
17911好像还需要mathematics.part11.rar...
17911《给讨厌数学的人》post-61-1126274985.ibf
17911《给讨厌数学的人》post-61-1126275088.ibf
17911《给讨厌数学的人》post-61-1126275344.ibf
17911《给讨厌数学的人》post-61-1126275640.ibf
17911《给讨厌数学的人》post-61-1126275751.ibf
17911《给讨厌数学的人》post-61-1126275949.ibf
17911《给讨厌数学的人》post-61-1126276094.ibf
17911《给讨厌数学的人》post-61-1126276306.ibf
17911终于完了,好不好顶一下post-61-1126276436.ibf
17911谢谢,一定看
17911谢谢大哥
17911粗略地看了一下,不错,谢谢
17911非常不错,谢谢~
17911非常感谢。。
17911非常感谢你!
17911谢谢楼主!!我想看看
17911谢谢楼主!
17911数学通俗读物,可以放松地读一下,三可丝.
17911刚下载完,不过还是要顶一下
17911谢谢
17911先表示感谢!
我一定看一看,虽然我不讨厌数学。
17911太感谢了哦!
17911谢谢!!!!!!
17911我爱数学,我爱魔兽,但我讨厌先知。
For the lich king!
17911非常不错
17911谢谢!
17911xiexie!!!!!!!!!!!!!!!!!!!1
17911刚下,谢谢!!!
17911xiexie!
17911mathematics.part07.rar 呢?
17911以前看过
是本好书
不过楼主也分的太多了
呵呵
17911xiexie !!!!!
17911谢谢!
17911谢谢搂住
17911这么大啊!!大哥!!!!!!!!我下一部分来看看
17911十分感谢!
17911谢谢。
17911谢谢,好书,
17911谢谢,科学就是这样普及起来的。
17911


17911好东东,谢谢
17911还没看之前先回一个。看完好看再来thx ;p
17911解压的时候怎么还要第15部分呀?老大,给贡献出来好不好?
17911谢谢楼主!您辛苦了!
17911感谢!感谢!找了很长时间,总算有结果了。
17911好书,正好合用,顶一下~~,谢谢~~
17911先表示感谢!
我一定看一看,虽然我不讨厌数学
17911hehe ,辛苦了》》》谢谢...
17911thank u!
17911太好了!!赞
17911多谢楼主!
17911谢谢楼主。
谢谢
17911谢谢
17911xiexie
17911顶!
17911多谢楼主 呵呵 你一定很辛苦啊 传了这么多 对楼主的努力表示赞赏
17911谢谢楼主,确实不错,正在看。
17911写的挺好的
17911感谢分享,努力学习!
17911时间关系,只下了一部分。
先看看了。
谢谢!
17911虽然还没有看,先感谢了
17911谢谢了,新人报道
17911看过这本书,挺好的,里面好多内容可以用来给学生上课用。
17911谢谢楼主
17911多谢,辛苦了
17911有时间再看
17911thank you
17911just download, though not read, but thanks a lot , hehe!!
17911感谢楼主!!
17911谢谢,一定看
17911非常感谢,可是分的块有点多,呵呵
17911好东东。顶!!!!
17911说来惭愧,我是学数学的,可能学艺不精,所以对大学数学实在谈不上喜欢
下了斑竹上传的文章看看,或许能找到些感觉,谢谢呵
[SIZE=7][COLOR=purple]
17911非常感谢。。
17911非常感谢。。
17911xiexiele
17911谢谢楼主!
17911谢谢楼主
但是,为什么要我们下15个同样的东西呢?
17911先顶一下,以后有空再下载
17911楼主真是大公无私的好人啊!
17911辛苦了,不过我也下载的好辛苦啊
17911不错,楼主辛苦。
17911谢谢
17911谢谢楼主!先来看看。
17911多谢lz
17911请问怎么解压不了啊?
17911谢谢
17911看着那多么包,我都被感动了,谢谢楼主,您辛苦了!!
17911我能不能下载哦新来的?
17911终于下载完了太棒了呵呵
17911请给我一个不下的理由,给我一个不支持的理由吧
17911谢谢你。兄弟
17911谢谢
17911many thanks!
分的部分多了点,好不容易下完了,想必楼主上传的挺辛苦!不要积分更是发扬风格了哈!
17911谢谢了啊,看看,增加点兴趣
17911谢谢啦!!!!!!!!!谢谢分享!!!
17911好啊,下载得好累啊,谢谢楼主
17911绝对是好贴
17911感谢,仔细看看
17911东西不错!!
谢谢楼主
17911很感谢,楼主辛苦了!
17911辛苦了
17911谢谢了
17911~谢谢~
17912为什么?
具体怎么证明?能不能将详细解答写上
17912我怎么没看明白啊!
f(x)=o(x^n)(n

+

) 是什么意思啊?和n


有什么关系啊??post-38-1126265061.gif
17912感觉应该是x->+inf才是,这样的话用反证法即可
17912那
x是什么意思啊?
x,为什么还要

+

啊?
| 引用
|
| 感觉应该是x->+inf才是,这样的话用反证法即可
|
17912准确说是存在趋向无穷的数列{xn},使得结论等式成立
17912题目的条件有错把 首先是 x的绝对之趋于无穷
证明有零点
17912我觉得你是不是把条件弄错了
17912我是新手不会用公式编辑。那个公式编辑必读不能看不然
我一定给你打出来 你是考北航的吗?
17912我认为直接用等价无穷小解!
17912这道题目我也做过,但是没有做出来,感到看不懂是什么意思!
呵呵,真是不知道是考研的卷子有问题还是那些上传卷子的人修改时候搞错了,还是怎么回事~
17912用反证法,再积分几次reijin说的没错
17915只有实变函数的要吗?
17915拜托!<<实变函数与泛函分析>>教案
17915实变函数的也可以!谢谢!
17915大家有的话上传一下,谢谢
17915
http://221.232.129.83/jpkc/whuok/index51.htm
17915我有好多,网络版的,WORD版的,Powpoint版的,你需要哪种?另外,你需要哪本教材的?
17915我也需要<<实变函数与泛函分析>>教案,什么版本的都可以,不过最好是ppt的
17915我要
泛函的课件
zhyi100@yahoo.com.cn
17915我想要实变函数的课件和习题
拜托了
yekai205@126.com
17915
打不开
17915打不开
17915
| 引用 (shengvip @ 2006年02月09日
21时14分) |
|
我有好多,网络版的,WORD版的,Powpoint版的,你需要哪种?另外,你需要哪本教材的?
|
我也想要一份课件,谢谢啦先!
WORD版的,Powpoint版的都可以。如果方便的话把您有的几个版本都发给我吧
wangxu.zju@gmail.com
17915我也需要实变函数的课件!能给发一个吗?非常感谢!
ledongxie@163.com
17915我非常需要,谢谢!mlx0520@sohu.com
17915
| 引用 (shengvip @ 2006年02月09日
21时14分) |
|
我有好多,网络版的,WORD版的,Powpoint版的,你需要哪种?另外,你需要哪本教材的?
|
方便的话我都想要
教案和习题 angel_love_y@163.com 谢谢
17915方便的话我也想要
实变函数及答案
shazi811116@hotmail.com
谢谢!!
17915能不能也给我发一份iagiag@sina.com 谢谢
17915xiexie
17915我也想要一份课件,先谢谢啦!
WORD版的,Powpoint版的都可以。
17915麻烦也帮我发一份他的习题解答!谢谢!我的邮箱:hao.zhi@qq.com
17915我也要,麻烦楼主了
我的邮箱:linboqs@yahoo.com.cn
17915麻烦也给我发一份,woxiangtizuqiu@163.com,多谢!
17915我很想要 谢谢拉 panpanyang2002@126.com
17915
我想要本科实变函数的课件和习题感觉以前学的可以,现在看还是不行
请大侠发我zhaogx
1976@sina.com
17915给我Word版的教案,谢谢!
jhfan00@163.com
17916潘承彪不知道算不算
17916如题 ,不胜感激,若有他的联系方式更好!
17916王元啊 中科院退休了
179
17设函数y=y(x)是由
x
3 +
y
3
-3axy=0(a>0)确定,则lim(x
→ ∞
) y/x=?
179
17怎么没人来帮忙啊
179
17谢谢,不过答案应该是-1吧!!除以x^3,得1+(y/x)^3-3a(y/x^2)=0;
设limy/x=k,则当x->无穷时,有1+k^3-3ak*0=0,得k=-1;
请问是不是呢,我不大清楚呀,谢谢回复
179
17谢谢了,要是没有你的启发,我连做都不会呢,真是惭愧啊,要向你学习,向数学高层进军!!
179
18网址:
http://bbs.putclub.com基本情况:
共有23万多会员.2001年建站.是目前中国最有影响力的英语学习网站之一.
已经做好了贵站的连接.希望得到你们允诺的好消息.:)
by
the way. 我是96级的博士生.也算是和贵站有缘分吧.:)
179
18一直关注贵论坛的发展,合作愉快,已经做好!
希望以后能开展进一步合作!
179
18非常感谢您及时的回复.希望keep in touch! 我想我肯定会从与你们的交往中受益的.
对了我的 email
putclub@163.com
qq
34085856
有空长联系.希望贵站越来越好.能够对大家越来越有帮助.:)
斑竹回复:收到!
17921在此向所有的老师们祝以节日的祝贺,你们辛苦了!!多谢你们的劳动!!
17921各位教师以及即将成为教师的XDJM节日快乐,大家辛苦了.
17921名师寄语
人物素描:郭红松 文字整理:蔡闯
--------------------------------------------------------------------------------
清华大学教授 黄克智
我今年78岁,有52年的党龄,58年的教龄,目前仍在教学科研第一线满负荷地工作。我虽然自己没有博士学位,但是我至今培养了77名研究生和博士后,其中68名已毕
业。
在我们每周的学术讨论班上,对学生们所叙述的问题,我都不放过一点差错和疏漏,容不得马马虎虎,更不允许不懂装懂。讨论到紧要处,我会霍然起身,跑到讲台上和学生一论高下。我们主张身教重于言教。
我这一辈子值得自豪的是 我做了一件事,就是把我的一生奉献给教育事业、奉献给科学和祖国。
北京市通州区培智学校 李银环
17年过去了,为了这些残疾孩子,为了我钟爱的特教事业,我放弃了休闲和享乐,也患上了多种职业病,但我无怨无悔,无比幸福。在电视节目里看到我的学生说儿歌、做表演时,我幸福;被过去教过的学生团团围住时,我幸福;有家长流着泪拉着我的手再三感谢时,我幸福。如今,我教过的近百名残疾儿童中,有的已走上了工作岗位,成为了一名踏实肯干、自食其力的劳动者,有的转入普通学校或升入高一级的学校继续深造,我为他们感到自豪。
北京市第22中学校长 马刚
北京市第22中学是北京市东城区的一所普通的学校,但孙维刚老师的实践告诉我们,在普通学校创造出了不普通的成绩,才更说明他的伟大意义。让普通的孩子也能变得聪明起来,让聪明的孩子变得更聪明起来,才更能说明我们教育的探索具有最普遍的实践意义。我坚信22中学在孙维刚老师教育教学思想鼓励下,会让更多的普通孩子接受“聪明”教育,让更多的家庭、更多的孩子因为我们的工作生活更幸福
更美好 让更多的普通孩子成长为祖国和人民需要的并不普通的人才。
北京市电气工程学校 刘建坡
我们如何将基础差且又缺乏自信的学生教育成为自强自立、社会需要的有用人才呢
答案只有一种,倾注更多更真实的爱,来逐步转变孩子的失败心态,恢复孩子的自信,领他们走向成功
从事了8年的职业教育,让我引以为骄傲的是——经过我们用爱心和责任的精心培育,一批批学生成为现代化建设服务的合格人才,他们在不同的岗位上,回报父母,服务社会。看到他们成功,我倍感光荣与自豪!
北京市密云县太师庄中学 李瑞国
说实在的,我也曾有过动摇,也想过调动工作。但是,每当我走进校园,踏上熟悉的讲台,望着那一双双渴求知识的眼睛,先前的种种想法顿时就消散了。我抱定一个信念
要把毕生心血献给这些渴求知识的孩子们。
我甘愿在山区学校干一辈子,永远做一名扎根山区的英语教师——这是我无悔的选择!
17922同乙
17922各位帮帮忙,谢谢
第6题post-38-1126275073.ibf
17922把增广矩阵的列向量看成一个线性空间,用线性相关和秩的定义即可证明。
17922题中未定义矩阵A。
17922秩A等于1是条件还是要证明的啊?
17922是的,条件描述得不确切,谁有原始版?
17922那个不是r(A)=1,而是r(A)-1
17922应该是“
r
(A
‾)-1
”吧?
17922楼上是说A的增广矩阵的秩减1吧,一样的
17923不好意思,最近复习数分,只怪自己学艺精,不会的题太多,麻烦个为人兄!先谢谢tobyqin
17923复习数分没必要做那本书吧
我想起到的效果不会很好啊
把这两个题目贴一下:post-21-1126358479.ibf
17923附件post-21-1126275423.ibf
17923我觉得现在时间还有,我尽量往后做,如果时间不够,我就不做那本书。
17924
谁知到中科院数学与系统科学研究院计算数学招直博老师的联系方式,告诉我好吗?
17925我们找到两种构件,如用此构件排列的每一层只能按1、1、2、3、5、8、13、21、34、55...的黄金律排列,是不是很奇妙,黄金律是生物方面的规律,比某些纯数学的分形图有意义多了,也许还可以找到更多的构形,大家有兴趣可以找找。

17925有意思
17926楼上说的很有道理
17926
引用 (shenchen @ 2005年12月16日
23时
18分) |
| 数值分析偏向理科,计算方法偏向工科
|
对,前者侧重分析,强调理论。后者侧重算法以及在计算机上实现。
17926数值分析跟计算方法是不是同一种课程?
有什么比较经典的教材?
望高手指教~~
17926在本科的内容上基本上一致!数值分析的说法现在多一些.
17926能不能说的具体点啊
我还是不明白
17926是啊,我希望知道有什么比较好的教材~~
17926数值分析重点是数学推导也就是算法,计算方法重点是计算机实现。
17926数值分析偏向理科,计算方法偏向工科
17928大家好啊,我下周要做报告,关于laplacian图,谱的内容,谁有相关的内容能不能提供一些,我怎么都找不到啊,会被老板批的啊.谢谢各位了
17928如果有什么好的内容能不能发我油箱来,不甚感激,jing165455@126.com
17928你要报告什么内容?我这里有一些论文,要看吗?
17928看看这个post-32-1126508279.ibf
17928楼主是哪个学校的啊
17928谢谢你,我要做的就是关于laplacian图,的报告,可是一直找不到资料,手头只有一份英文的,只能一句句翻译下来了,后天就要上了,豁出去了,
17928我不是图论专业的啊,所以有好多的东西不懂如何翻译,呵呵,
17930我也在学,粗劣看过几本,比较好理解是杨子胥的和华中师大的
17930我刚开始学习近世代数,用的是刘绍学的近世代数基础,还参考了其它一些教材。感觉他的讲法很新颖,但似乎不好理解:一开始就讲对称性的群表示法,而且用到了很多后面的知识。尤其其中的运动群,在其它教材上很少讲到。不知那位高手能指教一二。非常感谢!
17930我这学期也开了《近世代数》用的是张禾瑞的那本书,学着还可以。
17930张禾瑞的那本书做入门书很好
17930刘绍学的书入门的话比较难
看看楼上几位说的那些吧
17930刘绍学先生那本书 精华就在于小字部分 推荐复旦姚慕生的抽象代数做为辅助的入门书
17930我这学期也开了《近世代数》,用的是张禾瑞的那本书。
我觉得有点难入手啊!!!想请教一下学习的方法啊!!
因为我发觉我班很多人都还没有找到学《近世代数》的方法啊!!
他们都为此很伤脑筋的!!!我在这里想请教高手说说学习的方法!!!谢谢!!!
17930不要急于作题,重在历届概念,等概念很熟之后,就会有作题的欲望
17930刘老师的近世代数基础:一开始就讲对称性的群表示法,尤其其中的运动群。
你就当这些内容是介绍近世代数的用途,先了解一下我想就行啦!!等回面的知识够啦,反回来在看,应该就变容易啦!!
17930近世代数有一本是冯克勤编的<<近世代数引论>>,内容好难
17930建议楼主去买一本阮传概和孙伟编著的《近世代数及其应用》(第二版),该书比较容易看懂,由北京邮电大学出版社出版。冯克勤老师的书是专门写给数学专业的人看的,一般很难看懂,我原来看过一本冯克勤老师翻译的《代数学》,把我头都看大了,结果还是搞不懂。
17930张禾瑞的近世代数基础 高等教育出版社
很好的入门书
17930好的!!!
我非常感谢大家给我的意见啊!!
我按你们的方法去做,现在已经找到一点感觉啊!!!
真的非常感谢你们啊!!!!
谢谢啊!!
17930这个暑假我全部用来看武汉大学的那本《近世代数》了,
当时好像懂了,可现在什么都忘了。
17931
计算机科研进展专帖【1】跟贴推荐某个研究方向的经典文献,请注明:作者:Lai
YG,
文题: A numerical -----
杂志全名: Journal of
-----
年份:
然后在附件中粘贴发布,太大的文件压缩一下再上传!
【2】
推荐学术进展的ppt,讲义,您研究的进展,发表的论文题目或摘要
等直接跟贴附件发布【3】
最新学术会议通知和征稿请跟贴发布,或者在本版发布后跟贴给出您发布帖子的链接。
谢谢圈内的朋友老师们的合作,希望大家都抽空奉献一点,这里会成为大家喜欢的交流平台!
应家园成员:zhaoming,gzchenyin等建议,特别开设计算机科学技术研讨班
网址:
http://www.math.org.cn/forums/index.php?showforum=72欢迎大家参与讨论,讨论范围如下:
520
计算机科学技术
520.10 计算机科学技术基础学科
520.1010 自动机理论
520.1020
可计算性理论
520.1030 计算机可靠性理论
520.1040 算法理论
520.1050 数据结构
520.1060
数据安全与计算机安全
520.1099 计算机科学技术基础学科其他学科
520.20 人工智能
520.2010
人工智能理论
520.2020 自然语言处理
520.2030 机器翻译
520.2040 模式识别
520.2050
计算机感知
520.2060 计算机神经网络
520.2070 知识工程(含专家系统)
520.2099
人工智能其他学科
520.30 计算机系统结构
520.3010 计算机系统设计
520.3020
并行处理
520.3030 分布式处理系统
520.3040 计算机网络
520.3050
计算机运行测试与性能评价
520.3099 计算机系统结构其他学科
520.40 计算机软件
520.4010
软件理论
520.4020 操作系统与操作环境
520.4030 程序设计及其语言
520.4040
编译系统
520.4050 数据库
520.4060 软件开发环境与开发技术
520.4070 软件工程
520.4099
计算机软件其他学科
520.50 计算机工程
520.5010 计算机元器件
520.5020
计算机处理器技术
520.5030 计算机存储技术
520.5040 计算机外围设备
520.5050
计算机制造与检测
520.5060 计算机高密度组装技术
520.5099 计算机工程其他学科
520.60
计算机应用
520.6010 中国语言文字信息处理(含汉字信息处理)
520.6020 计算机仿真
520.6030
计算机图形学
520.6040 计算机图象处理
520.6050 计算机辅助设计
520.6060
计算机过程控制
520.6070 计算机信息管理系统
520.6080 计算机决策支持系统
520.6099
计算机应用其他学科
520.99 计算机科学技术其他学科
17931真的希望我们学计算机的在编程之余也关注一下科学,必竟中国的CS还不强,特别是理论---理论这个东西很有用的,比如数学家图灵先在数学上做出了计算机的理论模型,后来才有数学家诺依曼在工程上发明第一台计算机.
17931谢谢!!!
17931不错不错!
顶顶顶!!!
17931顶顶
17931谢谢
17932谢谢,将下栽地址在这告诉我也行,我会过来的,谢谢。
17932真诚求助:
谁有高教出版社刁在筠等四人编运筹学的电子教案?
实在是需要,多谢大侠了!!
发往
gecco@126.com
或 告诉下栽地址(email给我,没时间经常到这来,真的谢谢。)
17932我再什么地方看见过,改天给你把.
17932我也非常需要这个版本的课件和课后习题解答,希望大侠给予帮助,我的邮箱是daixd@hbu.edu.cn
谢了!
17932我也很需要,zhijun1021@yahoo.com.cn
谢谢大侠!!
17933能否详细的告知利用偏微分方程求解二维泊松方程第二类边界条件的线性方程组的矩阵表示?!自己摸索了好一段时间也没有弄出来,找了好几本书也没有详细的矩阵表示,还请多多指教!多谢!
17935天津大学的基础数学初试考的《高等代数与解析几何》其中的解析几何考的知识点是那部分,用的是哪个出版的书?
17935说是高等代数与解析几何
但我看考试大纲里面没有要求解析几何
17935我也是,另外天津大学的复试怎样考,是只考一门吗?别的学校都是考23门!天津大学研究生院上基础数学一栏只写着考实变函数!
17937家园顾问
用户ID: MAT_cxf
所在单位:四川大学数学系
所学方向:常微分方程
学历: 硕士
17937想向管理员请求辞去顾问职务
没有什么时间去回答大家的问题,真是对不住。
回复:接受请求,欢迎常回来看看.
17937有没有讨论的qq群,想加
17937用户ID: penghust
所在单位:华中科技大学力学系
所学方向:振动与噪声
学历: 硕士
17937刚刚来到这里 给大家打个招呼 以后请多关照
17937用户ID: curlyhouse
所在单位:东北林业大学数学系
所学方向:微分方程数值解
学历: 博士
17937北京交通大学
常微分方程 动力系统 生物数学
07122086@bjtu.edu.cn
真诚希望多讨论问题
17937电子科技大学
微分方程 动力系统
真诚希望多讨论问题
17937matheson 你好。我也是动力系统方向的研究生.很想跟你交流下。
浙江师范大学 应用数学 动力系统 生物数学 Email:
satellite35208@126.com
17937curlyhouse,你好啊.我很想认识一下,我是研究动力系统的..你有时间的话可以互相交流一下的.
17937方向:偏微分方程
email:cwww
1984@126.com
17937偏微分方程,
17937方向:稳定性
请教有没有朋友知道3/2稳定性的含义及物理意义,请赐教!
mail:ouyang7425@163.com
17937上海大学数学系,方向 偏微分方程。邮箱3
17458588@163.com
17937pyyabc
1985
方向:常微分方程的边值问题
17937所在单位:天津大学数学系
所学方向:非线性微分方程与动力吸统
学历: 硕士
QQ:305639258
17937上海大学力学所 方向 流体力学 交通流
硕士 邮箱:zcmzip@126.com
17937上海师范大学 PDE
硕士
17938在试题集里发布了,有需要的同志可以看看。
17947将函数互换就是第二个哈
17947我找了好半天post-38-1126322
178.gif
17947我举一个D判别法的例子,A判别法可类似举出:f=sin(x),g=sin(x)/x,则积分发散
17949怎么没有题
不过还是很感谢
17949你好牛!!佩服!
17949顶一下!~强
17949帮忙顶一下
17949去“试题集”下载。
17949帅哥
17949现在好人真是多啊!!!十分感谢楼主!!!
17949谢谢,真的好厉害哦 !还有更多的没有?
17949真厉害!
17949好人
17949请各位诸君下载后顶一下,以便于其他盟军下载。
17949厉害哦!
17949真厉害,帮忙顶一下
17949强烈感谢 呵呵
17949谢谢
17949thanka
17949谢谢
17949顶一下
17949武汉大学2005年高等代数试题详解(见附件)
斑竹回复:十分感谢,图片版推荐到主页。post-38-1126325678.ibf
17949特感谢!
17949谢谢了
17949
| 引用 (yctcjhb @ 2005年09月12日
16时54分) |
| 谢谢
|
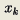
17949
的确物美价廉!
17949你好,,真得谢谢你1
17949thanks
17949牛!
17949谢谢
17949好的
17949顶一下!
太感谢了!
17949十分感谢

17949有没有数分答案呀,大哥!
17949还能说什么呢,只有感谢!
17949强啊,我们老师正要讲这一份试卷啊。谢了。
17949谢谢!
17949无语了!
17949有好东西就该多交流 赞一个
17949烈感谢 呵呵
17949非常感谢!
17949我怎么打不开附件里的资料啊 用什么软件才可以打开它
17949为什麽我打不开呢?
17949我也做了一份不过没你那么清楚,总得说你真厉害!
17949谢谢!!!!!!!!!!!!!!!!!!!!
17949题目没有啊哈哈
17949谢谢上传!
17949谢谢,有原题吗?
17949太谢谢了!
17949厉害,解燃眉之急
17949积分太少,耽误学习。麻烦斑竹撤掉积分
17949谢谢了!!!
永远支持bossh!
17949谢谢了,果然不错
17949不错
17949谢谢,我要买,呵呵!
17949最后一题的那个非零向量为(1,0,...,0).
望斑竹回答
17949终于找到了可打印的试题解答.
17949佩服佩服 !!!
17949xiexielr
17949xiexie
17949谢谢!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
17949有数学分析吗>
17949谢谢
17949多谢
17949xiexiele!
17949xiexie
17949特感谢啊
17949你好牛呀!
17949
| 引用 (yctcjhb @ 2005年09月12日
16时57分) |
| 谢谢
|
真牛!
17949顶一下
17949谢谢了!
17950向大师学习
17950
中国科学院数学与系统科学研究院的数学家呢,数学大本营
17950数学物理学部(共21人)post-52-1126329610.jpg
17950著名数学家:侯振挺
侯振挺,河南密县人,生于
1936年3月。长沙铁道学院教授,数学家。由于解决了数学家们40年来一直探索的Q过程惟一性准则,获得了
1978年度戴维逊奖。这项成果可应用于导弹轨道的计算以及地震预报、气象预报、生物遗传研究工作。他得到的Q过程惟一性定理,被国外学者称为“侯氏定理”。
工作经历
2000-至今 教授 中南大学数学学院概率统计所
1978-2000 教授 长沙铁道学院
1960-
1978 助教 长沙铁道学院
1996-至今 名誉主席 湖南省科学技术协会
1986-
1996 主席 湖南省科学技术协会
1984-2000 副院长 长沙铁道学院
1984-至今 所长
中南大学数学学院概率统计所
主要学术兼职
1990-至今 主编
《数学理论与应用》(《湖南数学年刊》)
1988-至今 理事长 湖南省数学会
1979-
1985 编委
Zeitschrift fur Wahrscheinlichkeits-theorie
教育背景
1955-
1960 唐山铁道学院(现西南交通大学)数力系大学毕业
科研奖励
2002
综合性科技奖励 第三届湖南光召科技奖
2001 马尔可夫骨架过程--混杂系统模型 湖南省科技进步奖一等奖
1998 专著:《马尔可夫过程的Q-矩阵问题》 湖南省科技进步奖一等奖
1988 马尔可夫过程及其相关论题 国家教委科技进步二等奖
1982 马尔可夫过程的唯一性,构造与性质 国家自然科学三等奖
1978 齐次可列马尔可夫过程 全国科学大会奖
1978 齐次可列马尔可夫过程--Q过程唯一性准则(侯氏定理) 全国铁路科技大会奖
1978
齐次可列马尔可夫过程的可逆性 全国铁路科技大会奖
1978 齐次可列马尔可夫过程的理论 湖南省科学大会奖
1978 Q过程的唯一性准则 Davidson奖,英国皇家学会
主要研究领域
马氏过程,
马尔可夫骨架过程,运筹学, 随机过程, 马尔可夫决策过程,数理金融post-52-1126329977.jpg
17950彭实戈教授简历:
1971-
1974年在山东大学物理系读书;
1983-
1986年,在巴黎九大、普鲁旺斯大学读博士,获《数学与自动化》三阶段博士、《应用数学》博士;
1988-
1989年,在复旦大学做博士后研究;
1992年获法国“领导研究资格”证书(即国家博士)。现为山东大学数学与系统工程学院博士生导师,教育部“长江学者奖励计划”首批特聘教授。“倒向随机微分方程理论”的主要开创者,
1995年曾获国家自然科学二等奖。山东大学数学研究所所长,山东大学金融研究院院长。
如今,在诺贝尔奖项的诸多理论研究中,我国与世界水平多有相当的差距,唯有金融数学理论可与国际先进水平比肩,可与国际著名大师们对话,这与彭实戈教授的努力分不开。由于在随机系统控制理论及应用研究中取得许多世界领先的成果,彭实戈教授赢得许多赞誉:国际著名随机控制专家、加拿大教授豪斯曼认为,彭的一般随机最大值原理是当今世界“近十年来随机控制理论的两个最重要贡献之一”;数学界最高奖菲尔兹奖获得者里昂斯教授曾写信给山东大学前校长潘承洞教授说,在倒向随机微分方程理论的研究上,彭“显然是这领域的带头人”、“开创者”。他获得的能应用于一大类非线性偏微分方程的非线性公式被评价为“解决了很多随机专家想解决而一直进展甚微的问题”,他的小周期最优控制奇摄动均匀方法被评价为“理论新颖而结果出人意料,值得为此开创一新领域……”。post-52-1126330243.jpg
17950程崇庆
程崇庆,男,
1956年10月出生,江苏泰州人。现为南京大学教授、博士生导师,教育部长江学者奖励计划特聘教授,国家杰出青年基金获得者。程崇庆教授
1982年1月于南京工学院(现称东南大学)数学力学系力学专业本科毕业,
1984年7月于南京工学院数学力学系一般力学专业硕士毕业,
1988年3月于西北工业大学力学系获博士学位,
1990年进入南京大学天文系博士后流动站从事博士后研究,出站后留校工作,
1992年9月晋升为教授。
1992年5月至
1994年3月受洪堡基金资助赴德国Cologne (科隆)大学进修,
1994年3月赴瑞士ETH-Zurich
(苏黎世高工)访问,
1994年8月回国。后又先后访问美国Northwestern (西北) 大学数学系、瑞典KTH (皇家理工学院)
数学系、香港中文大学数学所、美国哈佛大学数学系。另外,还先后应邀访问美国Princeton (普林斯顿)、法国IHES,
英国Cambridge(剑桥)、 University College
London、德国Augsburg、Mainz等处并作colloquium或Seminar talk.
主要从事于动力系统研究,先后承担并完成国家自然科学基金委青年基金、国家攀登计划 – 非线性科学(首期,二期
)、国家杰出青年科学基金(数学)、教育部优秀年轻教师基金、教育部博士点基金等多项国家、省部级科研项目,目前承担973“非线性科学中的若干前沿问题”(首席科学家助理)、江苏省六大人才高峰“哈密顿动力系统中的KAM理论与轨道扩散”等重大科研项目。
1994年获国家教委科技进步二等奖(第一完成人),
1995年获得国家杰出青年科学基金,
1997年获香港求是杰出青年学者奖(数学),
1998年获得首届Morningside数学奖(银奖),2000年获中国高校自然科学一等奖
( 第一完成人),2001年获国家自然科学二等奖 (第一完成人)。
在承担繁重科研工作的同时,注重培养年轻教师和一批研究生,近年来还一直致力于强化南京大学动力系统研究组的力量,扩展研究面。经过数年的努力,目前研究面已从KAM理论扩展到动力系统的变分方法、动力学不稳定性的研究。
post-52-1126330406.jpg
17950数学科学学院 教授 博士生导师 王诗宬
王诗宬
教授 博士生导师
几何代数教研室
数学所副所长
主要论著
Convering invariant and cohopficity of 3-mfd
groups Proc.London.Math.Soc.68(
1994) 221-242 无
Nonzero degree maps and
surface bunle overs J.Diff.Geom.143(
1996) 789-908 无
On finife group
action on rational homology sphere Topology 36(
1997) 509-5
18 无
Th-injective surface in 3-manfolds Comm.Math.Helv 73(
1998) 499-515
Covering degrees are determined by graph mfds incohed Comm.Math.Heh
174(
1999) 238-247 无
科研项目
起止时间 项目名称 资助来源
1995.1-
1997.12
国家基金委中青年人才专项基金
1998.1-2000.12 国家杰出青年科学基金
所获奖励
获奖时间 所获奖励
1994 第二届中国青年科学家奖
1995 第一届求实科技基金杰出青年学者奖
王诗宬教授主要从事三维流形几何理论的研究,涉及拓扑不动点、几何群论等。获得
1997年度国家杰出青年科学基金资助以来的主要成果有:
⑴开拓和发展了三维流形间的映射这个研究领域,在非零度映射的存在性、有限性、标准型等基本问题上取得突破。(分别与Boileau,Reid,Legrand,Zieschang,周青等合作);
⑵以极小曲面理论为工具,证明了在浸入曲面情形三维流形边界斜率的有界性(分别与Hass,Rubinstein,周青合作);
⑶发现了图的手征性和可平面性的内在联系(与姜伯驹合作),并把几何方法和新的代数不变量结合起来,系统地研究了链环的手征(与姜伯驹、林晓松、吴英青等合作)。
上述研究成果已在《Acta. Math. Sinica》,《 Topology》,《Comment. Math.
Helv.》,《 J. Diff. Geometry》,《 Math. Proc. Camb. Phil. Soc.》,《Math.
Annalen》,CCM等上发表论文11篇次,并被多次引用。
王诗宬教授曾获
1997~
1998年度中国数学会陈省身奖,2000年度中国高校科技进步奖一等奖,2001年度国家自然科学奖二等奖,2001年度长江计划特聘教授。在2000年和2001年分别受聘为《Algebraic
and Geometric Topology》和《中国科学》的编委。
post-52-1126330850.jpg
17950向大师们致敬!
17950我向问一下 可以转贴吗
17950liaobuqi
17950niu
17951[3]闲聊软件工程
关于计算机科学的一些边缘科学我想谈一谈软件工程技术,对于一个企业,推出软件是不是就是几个程序员坐在一起,你写一段程序,我写一段程序呢?显然不是。软件工程是典型的计算机科学和数学,管理科学,心理学,社会学等学科的综合。它使我们这些搞理论和技术的人进入了一个社会。你所要考虑的不仅仅是程序的优劣,更应该考虑程序与软件的区别,软件与软件产品的区别,软件软件产品的市场前景,如何去更好的与人交流。这方面我还在学习阶段,以后这方面再写文章吧,先推荐给大家几本书:畅销20年不衰的《人月神话》(清华大学中文版,中国电力出版社影印版),《软件工程-实践者研究的方法》(机械工业出版社译本),《人件》(据说每一位微软公司的部门经理都读过这本书,推荐老总们和想当老总的同学都看看,了解一下什么是软件企业中的人)以及微软公司的《软件开发的科学与艺术》和《软件企业的管理与文化》(研究软件企业的制胜之道当然要研究微软的成功经验了!)
看完上面的书,结合自己做的一些团队项目,我的一些比较深的体会有这么几点:
1.How important a plan is for a
project development.
2.How to communicate with your team members in a
more effective way.
3.How to solve unexpected situations.
4.The
importance of unification.
5.The importance of doing what you should
do.
6.The importance of designing before programming.
7.The
importance of management.
8.The importance of thinking what your
teammates think.
在软件开发过程中我们应当具有以下能力:
1.Like it if you would
like to do it.
We believe that your attitude toward your work will
definitely makes great effect on the project.
2.The spirit of group
working.
Take myself as an example. I am just a part of the team, just
a little part. You must make it clear that you are just a member of the
team, but your effort will change your project a lot.
3.Passion
With
passion, you can do your job in a more effective way.
4.The ability of
solving unexpected problems.
5.Learning New things in a very short
time
It is the basic requirement for we computer major to learn new
technology.
6.Creativity
The tools are changing. As for us,
what's more important is to use these new tools and technology to
enable people and businesses throughout the world to realize their full
potential.
7.The ability to do your work independently.
Every member
has his own business. In a team, your work cannot be replaced by
others' so you must do your business well in order to assure the
project devel
opment process.
团队开发当中的一些具体精神应当有:
<1>
Success and Failure is not one person's effect.
Your team's
success is not the contribution of a single person. Success contributes to
the whole team. If your project failed, it also is not just because of one
person's poor work. It is also your failure.
<2> Learn from
each other.
Every person has his own specialty. Even Bill Gates cannot
know all the things about software development. We often learn from each
other and gains a lot. The old saying goes like this:
There must be one
out of three who can be your teacher. In our team we say: Every person is
your teacher.
<3> Help those who have problems. Use the group
working spirit to overcome all the difficulties.
There is no need to
explain it. As the old saying: Two heads are better than one. We always
find it difficult to solve all the problems just by oneself.
<4>
Praise them who have got some improvement.
In our team, I always praise
the members when they have finished something or just solved one problem,
and they think that it is interesting and gains a lot. Because they can
see their efforts.
<5> Say something if
needed.
这个是一次软件大赛当中的体会,和大家也做个交流,不过不能再说了,软件工程学说起来写本2000页的书一点也不多,恕我才疏学浅,不再做过多论述了。
[4]谈谈学习态度的问题
关于计算机技术的学习我想是这样的:学校开设的任何一门科学都有其滞后性,不要总认为自己掌握的某门技术就已经是天下无敌手了,虽然现在Java,VB,C,C
用的都很多,怎能保证没有被淘汰的一天,我想.NET平台的诞生和X#语言的初见端倪完全可以说明问题。换言之,在我们掌握一门新技术的同时就又有更新的技术产生,身为当代的大学生应当有紧跟科学发展的素质。举个例子,就像有些同学总说,我做网页设计就喜欢直接写html,不愿意用什么Frontpage,Dreamweaver。能用语言写网页固然很好,但有高效的手段你为什么不使呢?仅仅是为了显示自己的水平高,unique?
我看真正水平高的是能够以最快的速度接受新事物的人。高级程序设计语言的发展日新月异,今后的程序设计就像人们在说话一样,我想大家从xml中应是有所体会了。难道我们真就写个什么都要用汇编,以显示自己的水平高,真是这样倒不如直接用机器语言写算了。反过来说,想要以最快的速度接受并利用新技术关键还是在于你对计算机科学地把握程度。
计算机技术牵扯的内容更为广泛些,一项一项说恐怕没个一年半载也说不清。我只想提醒大家的还是那句话,技术与科学是不能分家的,学好了科学同时搞技术,这才是上上策。犹如英语,原先人们与老外交流必须要个翻译,现在满马路的人都会说英语。就连21世纪英语演讲比赛的冠军都轮不到英语系的学生了。计算机也是一样的,我们必须面对的一个现实就是:计算机真就只是一个工具,如果不具备其它方面的素养,计算机系的学生虽然不能说找不到工作,不过总有一天当其他专业性人才掌握了计算机技术后将比我们出色许多。原因就在于计算机解决的大都是实际问题,实际问题的知识却是我们少有的。单一的计算机技术没有立足之地。
我想是时候指出:学习每一个课程之前,都要先搞清这一课程的学习目的。这一学科的应用领域。据我自身所了解到的同龄同学和低年级的同学的学习状况:他们之中很少有人知道学一个学科的学习目的,期末考试结束了也不知道学这科做什么用。这就失去了读计算机科学的意义。当然这与现存的教育思想不能说一点关系都没有。
总的来说,从教育角度来讲,国内高校的课程安排不是很合理,强调理论,又不愿意在理论上深入教育,无力接受新技术,想避开新技术又无法避得一干二净。我觉得关键问题就是国内的高校难于突破现状,条条框框限制着怎么求发展。我们虽然认识得到国外教育的优越性,但为什么迟迟不能采取行动?哪怕是去粗取精的取那么一点点。我们需要改变。从我们自身角度来讲,多数人4年下来既没有学习计算机科学的学术水平,也没有学习计算机技术的那种韧劲。在我刚上大一时,我的计算机科学入门导师,淮北煤炭师范学院王爱平教授曾经对我说过这样一番话:"当你选择了计算机这一门科学,就意味着你踏上了一条不归路,就意味着你一生都要为之奋斗......你的身后是悬崖,只有向前走,不能往后退。"
有些同学说按照这样学习学的东西太多,有的未见得有用,我想打个形象的比方:学校学出来的人都是一个球体,方方面面的知识都应具备。可是社会上需要球体的地方很少,反而需要的是砖和瓦,即精通某一行的人才。但是对于同等体积的物体,用球体来改造是最方便最省事的。学校的学生很多,为了能够使更多的学生来适应这个社会,学校也就不得以把所有的学生都打造成一个球体,然后让社会对这些学生进行再加工,成为真正能够有用的人才。即使你非常清楚自己的将来要干什么,并且非常下定决心要走自己的路,这一步你也必须走,世界是在不断变化的,你不能预料未来。想清楚,努力去干吧!
必须结束这篇"胡侃"了,再侃下去非我力所能及。其实计算机还有很多基础课都值得一侃。怎奈我造诣有限,不敢再让内行耻笑。计算机科学博大精深,我只是个初学者。最后声明:这些只针对本科阶段的学习。即使把这些全弄通了,前面的路还长,计算机科学需要我们为之奋斗......学习计算机科学需要韧性,更需要创新,需要激情。深刻学习理论知识,勇于接受新技术的挑战,这才是我们这一代人应具有的素质。最后送大家一句话"Wake
up every day with a feeling of passion for the difference technology will
make in people's life!"。
在我大一时无意中找到了南京大学网友sir的帖子"胡侃(理论)计算机学习",这个帖子对我的大学学习起了至关重要的作用,后来也同他进行了一些交流,写这份材料时也引用了其中的不少观点,并得到了sir的支持。再有就是每次和本系司徒彦南兄的交谈,都能从中学到很多东西,在这份材料中也有很多体现。这份材料是我原来在实验学院进行新生在推荐教材方面结合我的学习情况有了较大改变。值得一提的是增加了一些计算机理论的内容,计算机技术的内容结合我国的教学情况和我们学习的实际情况进行了重写。这里所作的工作也只是将各位学长和同学们的学习体会以及我在学习计算机科学时的所
17951全文完
17951[计算机]理论计算机科学漫谈(zz)
reverie 发表于 2004-12-
19 12:11:00
发信人:
sir(sir), 信区: Mathematics. 发信站:
南大小百合
计算机科学和数学的关系有点奇怪。二三十年以前,计算机科学基本上还是数学的一个分支。而现在,计算机科学拥有广泛的研究领域和众多的研究人员,在很多方面反过来推动数学发展,从某种意义上可以说是孩子长得比妈妈还高了。但不管怎么样,这个孩子身上始终流着母亲的血液。这血液是the
mathematical underpinning of computer science(计算机科学的数学基础),--
也就是理论计算机科学。
现代计算机科学和数学的另一个交叉是计算数学/数值分析/科学计算,传统上不包含在理论计算机科学以内。所以本文对计算数学全部予以忽略。
最常和理论计算机科学放在一起的一个词是什么?答:离散数学。这两者的关系是如此密切,以至于它们在不少场合下成为同义词。
传统上,数学是以分析为中心的。数学系的同学要学习三四个学期的数学分析,然后是复变,实变,泛函等等。实变和泛函被很多人认为是现代数学的入门。在物理,化学,工程上应用的,也以分析为主。
随着计算机科学的出现,一些以前不太受到重视的数学分支突然重要起来。人们发现,这些分支处理的数学对象与传统的分析有明显的区别:分析研究的对象是连续的,因而微分,积分成为基本的运算;而这些分支研究的对象是离散的,因而很少有机会进行此类的计算。人们从而称这些分支为“离散数学”。“离散数学”的名字越来越响亮,最后导致以分析为中心的传统数学分支被相对称为“连续数学”。
离散数学经过几十年发展,基本上稳定下来。一般认为,离散数学包含以下学科:
1)
集合论,数理逻辑与元数学。这是整个数学的基础,也是计算机科学的基础。
2)
图论,算法图论;组合数学,组合算法。计算机科学,尤其是理论计算机科学的核心是算法,而大量的算法建立在图和组合的基础上。
3)
抽象代数。代数是无所不在的,本来在数学中就非常重要。在计算机科学中,人们惊讶地发现代数竟然有如此之多的应用。
但是,理论计算机科学仅仅就是在数学的上面加上“离散”的帽子这么简单吗?一直到大约十几年前,终于有一位大师告诉我们:不是。D.E.Knuth(他有多伟大,我想不用我废话了)在Stanford开设了一门全新的课程Concrete
Mathematics Concrete这个词在这里有两层含义:
第一,针对abstract而言。Knuth认为,传统数学研究的对象过于抽象,导致对具体的问题关心不够。他抱怨说,在研究中他需要的数学往往并不存在,所以他只能自己去创造一些数学。为了直接面向应用的需要,他要提倡“具体”的数学。
在这里我做一点简单的解释。例如在集合论中,数学家关心的都是最根本的问题--公理系统的各种性质之类。而一些具体集合的性质,各种常见集合,关系,映射都是什么样的,数学家觉得并不重要。然而,在计算机科学中应用的,恰恰就是这些具体的东西。Knuth能够首先看到这一点,不愧为当世计算机第一人。
第二,Concrete是Continuous(连续)加上discrete(离散)。不管连续数学还是离散数学,都是有用的数学!
前面主要是从数学角度来看的。从计算机角度来看,理论计算机科学目前主要的研究领域包括:可计算性理论,算法设计与复杂性分析,密码学与信息安全,分布式计算理论,并行计算理论,网络理论,生物信息计算,计算几何学,程序语言理论等等。这些领域互相交叉,而且新的课题在不断提出,所以很难理出一个头绪来。
下面随便举一些例子。
由于应用需求的推动,密码学现在成为研究的热点。密码学建立在数论(尤其是计算数论),代数,信息论,概率论和随机过程的基础上,有时也用到图论和组合学等。
很多人以为密码学就是加密解密,而加密就是用一个函数把数据打乱。这就大错特错了。
现代密码学至少包含以下层次的内容:
第一,密码学的基础。例如,分解一个大数真的很困难吗?能否有一般的工具证明协议正确?
第二,密码学的基本课题。例如,比以前更好的单向函数,签名协议等。
第三,密码学的高级问题。例如,零知识证明的长度,秘密分享的方法。
第四,密码学的新应用。例如,数字现金,叛徒追踪等。
在分布式系统中,也有很多重要的理论问题。
例如,进程之间的同步,互斥协议。一个经典的结果是:在通信信道不可靠时,没有确定型算法能实现进程间协同。所以,改进TCP三次握手几乎没有意义。
例如时序问题。常用的一种序是因果序,但因果序直到不久前才有一个理论上的结果……
例如,死锁没有实用的方法能完美地对付。
关键在效率:对付死锁的方法,例如死锁检测,都非常严重地减低效率,以至于得不偿失,因为死锁并不是一种经常出现的现象。所以在全局上,一般都用所谓“鸵鸟算法”,也就是假装什么都不会发生。在局部上,例如你要设计一个访问共享数据的算法,那么你就要证明你的算法在局部上是deadlock
free。至于它会不会导致全局的死锁,就管不了许多了。
17951计算机科学技术学习引论(转帖)
chzhuang发表评论于2005-1-
19 16:09:09
注:有朋友指出本文严重抄袭了Sir的原文,但这篇文章贴在这里,作为参考,还是很不错的。他的文章更全面一点:)
计算机科学与技术这一门科学深深的吸引着我们这些同学们,上计算机系已经有近三年了,自己也做了一些思考,
原先不管是国内还是国外都喜欢把这个系分为计算机软件理论、计算机系统、计算机技术与应用。后来又合到一起,变成现在的计算机科学与技术。我一直认为计算机科学与技术这门专业,在本科阶段是不可能切分成计算机科学和计算机技术的,因为计算机科学需要相当多的实践,而实践需要技术;每一个人(包括非计算机专业),掌握简单的计算机技术都很容易(包括原先Major们自以为得意的程序设计),但计算机专业的优势是:我们掌握许多其他专业并不"深究"的东西,例如,算法,体系结构,等等。非计算机专业的人可以很容易地做一个芯片,写一段程序,但他们做不出计算机专业能够做出来的大型系统。今天我想专门谈一谈计算机科学,并将重点放在计算理论上。
1、计算机理论的一个核心问题--从数学谈起:
[1]高等数学Vs数学分析
记得当年大一入学,每周四课时高等数学,天天作业不断(那时是七天工作制)。颇有些同学惊呼走错了门:咱们这到底念的是什么系?不错,你没走错门,这就是计算机科学与技术系。我国计算机科学系里的传统是培养做学术研究,尤其是理论研究的人(方向不见得有多大的问题,但是做得不是那么尽如人意)。而计算机的理论研究,说到底,如网络安全学,图形图像学,视频音频处理,哪个方向都与数学有着很大的关系,虽然也许是正统数学家眼里非主流的数学。这里我还想阐明我的一个观点:我们都知道,数学是从实际生活当中抽象出来的理论,人们之所以要将实际抽象成理论,目的就在于想用抽象出来的理论去更好的指导实践,有些数学研究工作者喜欢用一些现存的理论知识去推导若干条推论,殊不知其一:问题考虑不全很可能是个错误的推论,其二:他的推论在现实生活中找不到原型,不能指导实践。严格的说,我并不是一个理想主义者,政治课上学的理论联系实际一直是指导我学习科学文化知识的航标(至少我认为搞计算机科学与技术的应当本着这个方向)。
其实我们计算机系学数学仅学习高等数学是不够的(典型的工科院校一般都开的是高等数学),我们应该像数学系一样学一下数学分析(清华计算机系开的好像就是数学分析,我们学校计算机学院开的也是,不过老师讲起来好像还是按照高等数学讲),数学分析这门科学,咱们学计算机的人对它有很复杂的感情。在于它是偏向于证明型的数学课程,这对我们培养良好的分析能力和推理能力极有帮助。我的软件工程学导师北工大数理学院的王仪华先生就曾经教导过我们,数学系的学生到软件企业中大多作软件设计与分析工作,而计算机系的学生做程序员的居多,原因就在于数学系的学生分析推理能力,从所受训练的角度上要远远在我们平均水平之上。当年出现的怪现象是:计算机系学生的高中数学基础在全校数一数二(希望没有冒犯其它系的同学),教学课时数也仅次于数学系,但学完之后的效果却不尽如人意。难道都是学生不努力吗,我看未见得,方向错了也说不一定,其中原因何在,发人深思。
我个人的浅见是:计算机系的学生,对数学的要求固然跟数学系不同,跟物理类差别则更大。通常非数学专业的所学的高等数学,无非是把数学分析中较困难的理论部分删去,强调套用公式计算而已。而对计算机系来说,数学分析里用处最大的恰恰是被删去的理论部分。说得难听一点,对计算机系学生而言,追求算来算去的所谓"工程数学"已经彻底地走进了误区。记上一堆曲面积分的公式,难道就能算懂了数学?那倒不如现用现查,何必费事记呢?再不然直接用Mathematica或是Matlab好了。
退一万步讲,即使是学高等数学我想大家看看华罗庚先生的《高等数学导论》也是比一般的教材好得多。华罗庚在数学上的造诣不用我去多说,但是他这光辉的一生做得我认为对我们来说,最重要的几件事情:首先是它筹建了中国科学院计算技术研究所,这是我们国家计算机科学的摇篮。在有就是他把很多的高等数学理论都交给了做工业生产的技术人员,推动了中国工业的进步。第三件就是他一生写过很多书,但是对高校师生价值更大的就是他在病期间在病床上和他的爱徒王元写了《高等数学引论》(王元与其说是他的爱徒不如说是他的同事,是中科院数学所的老一辈研究员,对歌德巴赫猜想的贡献全世界仅次于陈景润)这书在我们的图书馆里居然找得到,说实话,当时那个书上已经长了虫子,别人走到那都会闪开,但我却格外感兴趣,上下两册看了个遍,我的最大收获并不在于理论的阐述而是在于他的理论完全的实例化,在生活中去找模型。这也是我为什么比较喜欢具体数学的原因,正如我在上文中提到的,理论脱离了实践就失去了它存在的意义。正因为理论是从实践当中抽象出来的,所以理论的研究才能够更好的指导实践,不用于指导实践的理论可以说是毫无价值的。
我在系里最爱做的事情就是给学弟学妹们推荐参考书。没有别的想法,只是希望他们少走弯路。中文的数学分析书,一般都认为以北大张筑生老师的"数学分析新讲"为最好。张筑生先生一生写的书并不太多,但是只要是写出来的每一本都是本领域内的杰作,这本当然更显突出些。这种老书看起来不仅是在传授你知识,而是在让你体会科学的方法与对事物的认识方法。万一你的数学实在太好,那就去看"菲赫金哥尔茨的微积分学教程"好了--但我认为没什么必要,毕竟你不想转到数学系去。吉米多维奇的"数学分析习题集"也基本上是计算型的书籍。书的名气很大,倒不见得适合我们,还是那句话,重要的是数学思想的建立,生活在信息社会里我们求的是高效,计算这玩意还是留给计算机吧。不过现在多用的似乎是复旦大学的《数学分析》,高等教育出版社的,也是很好的教材。
中国的所谓高等代数,就等于线性代数加上一点多项式理论。我以为这有好的一面,因为可以让学生较早感觉到代数是一种结构,而非一堆矩阵翻来覆去。这里不得不提南京大学林成森,盛松柏两位老师编的"高等代数",感觉相当舒服。此书相当全面地包含了关于多项式和线性代数的基本初等结果,同时还提供了一些有用的又比较深刻的内容,如Sturm序列,Shermon-Morrison公式,广义逆矩阵等等。可以说,作为本科生如能吃透此书,就可以算是高手。国内较好的高等代数教材还有清华计算机系用的那本,清华出版社出版,书店里多多,一看就知道。从抽象代数的观点来看,高等代数里的结果不过是代数系统性质的一些例子而已。莫宗坚先生的《代数学》里,对此进行了深刻的讨论。然而莫先生的书实在深得很,作为本科生恐怕难以接受,不妨等到自己以后成熟了一些再读。
正如上面所论述的,计算机系的学生学习高等数学:知其然更要知其所以然。你学习的目的应该是:将抽象的理论再应用于实践,不但要掌握题目的解题方法,更要掌握解题思想,对于定理的学习:不是简单的应用,而是掌握证明过程即掌握定理的由来,训练自己的推理能力。只有这样才达到了学习这门科学的目的,同时也缩小了我们与数学系的同学之间思维上的差距。
[2]计算数学基础
概率论与数理统计这门课很重要,可惜大多数院校讲授这门课都会少些东西。少了的东西现在看至少有随机过程。到毕业还没有听说过Markov过程,此乃计算机系学生的耻辱。没有随机过程,你怎么分析网络和分布式系统?怎么设计随机化算法和协议?据说清华计算机系开有"随机数学",早就是必修课。另外,离散概率论对计算机系学生来说有特殊的重要性。而我们国家工程数学讲的都是连续概率。现在,美国已经有些学校开设了单纯的"离散概率论"课程,干脆把连续概率删去,把离散概率讲深些。我们不一定要这么做,但应该更加强调离散概率是没有疑问的。这个工作我看还是尽早的做为好。
计算方法学(有些学校也称为数学分析学)是最后一门由数理学院给我们开的课。一般学生对这门课的重视程度有限,以为没什么用。不就是照套公式嘛!其实,做图形图像可离不开它,密码学搞深了也离不开它。而且,在很多科学工程中的应用计算,都以数值的为主。这门课有两个极端的讲法:一个是古典的"数值分析",完全讲数学原理和算法;另一个是现在日趋流行的"科学与工程计算",干脆教学生用软件包编程。我个人认为,计算机系的学生一定要认识清楚我们计算机系的学生为什么要学这门课,我是很偏向于学好理论后用计算机实现的,最好使用C语言或C
编程实现。向这个方向努力的书籍还是挺多的,这里推荐大家高等教育出版社(CHEP)和施普林格出版社(Springer)联合出版的《计算方法(Computational
Methods)》,华中理工大学数学系写的(现华中科技大学),这方面华科大做的工作在国内应算是比较多的,而个人认为以这本最好,至少程序设计方面涉及了:任意数学函数的求值,方程求根,线性方程组求解,插值方法,数值积分,场微分方程数值求解。李庆扬先生的那本则理论性过强,与实际应用结合得不太紧,可能比较适合纯搞理论的。
17951[3]也谈离散数学
每个学校本系里都会开一门离散数学,涉及集合论,图论,和抽象代数,数理逻辑。不过,这么多内容挤在离散数学一门课里,是否时间太紧了点?另外,计算机系学生不懂组合和数论,也是巨大的缺陷。要做理论,不懂组合或者数论吃亏可就太大了。从理想的状态来看,最好分开六门课:集合,逻辑,图论,组合,代数,数论。这个当然不现实,因为没那么多课时。也许将来可以开三门课:集合与逻辑,图论与组合,代数与数论。(这方面我们学校已经着手开始做了)不管课怎么开,学生总一样要学。下面分别谈谈上面的三组内容。
古典集合论,北师大出过一本《基础集合论》不错。
数理逻辑,中科院软件所陆钟万教授的《面向计算机科学的数理逻辑》就不错。现在可以找到陆钟万教授的讲课录像,ttp://www.cas.ac.cn/html/Dir/2001/11/06/3391.htm
自己去看看吧。总的来说,学集合/逻辑起手不难,普通高中生都能看懂。但越往后越感觉深不可测。
学完以上各书之后,如果你还有精力兴趣进一步深究,那么可以试一下GTM系列中的《Introduction
to Axiomatic Set Theory》和《A Course of Mathematical
Logic》。这两本都有世界图书出版社的引进版。你如果能搞定这两本,可以说在逻辑方面真正入了门,也就不用再浪费时间听我瞎侃了。
据说全中国最多只有三十个人懂图论。此言不虚。图论这门科学,技巧性太强,几乎每个问题都有一个独特的方法,让人头痛。不过这也正是它魅力所在:只要你有创造性,它就能给你成就感。我的导师说,图论里面随便找一块东西就可以写篇论文。大家可以体会里面内容之深广了吧!国内的图论书中,王树禾老师的"图论及其算法"非常成功(顺便推荐大家王先生的"数学思想史",个人认为了解科学史会对我们的学习和研究起到很大的推动作用)。一方面,其内容在国内教材里算非常全面的。另一方面,其对算法的强调非常适合计算机系(本来就是科大计算机系教材)。有了这本书为主,再参考几本翻译的,如Bondy
&
Murty的《图论及其应用》,人民邮电出版社翻译的《图论和电路网络》等等,就马马虎虎,对本科生绝对足够了。再进一步,世界图书引进有GTM系列的"Modern
Graph
Theory"。此书确实经典!国内好象还有一家出版了个翻译版。不过,学到这个层次,还是读原版好(说实话,主要是亲身体验翻译版的弊端,这个大家自己体会)。搞定这本书,也标志着图论入了门。
离散数学方面我们北京工业大学实验学院有个世界级的专家,叫邵学才,复旦大学概率论毕业的,教过高等数学,线性代数,概率论,最后转向离散数学,出版著作无数,论文集新加坡有一本,堪称经典,大家想学离散数学的真谛不妨找来看看。这老师的课我专门去听过,极为经典。不过你要从他的不经意的话中去挖掘精髓。在同他的交谈当中我又深刻地发现一个问题,虽说邵先生写书无数,但依他自己的说法每本都差不多,我实在觉得诧异,他说主要是有大纲的限制,不便多写。这就难怪了,很少听说国外写书还要依据个什么大纲(就算有,内容也宽泛的多),不敢越雷池半步,这样不是看谁的都一样了。外版的书好就好在这里,最新的科技成果里面都有论述,别的先不说,至少?quot;紧跟时代的理论知识"。
原先离散数学和数据结构归在一起成为离散数学结构,后来由于数据结构的内容比较多,分出来了,不过最近国外好像有些大学又把它们合并到了一起,道理当然不用说,可能还是考虑到交叉的部分比较多。比较经典的书我看过得应算是《Discrete
Mathematical
Structures》了,清华大学出版社有个影印版的。
[4]续谈其他的一些计算数学
组合数学我看的第一本好像是北大捐给我们学院的,一本外版书。感觉没有太适合的国产书。还是读Graham和Knuth等人合著的经典"具体数学"吧,西安电子科技大学出版社有翻译版。
《组合数学》,《空间解析几何》还有那本《拓扑学》,看这三本书的时候是极其费事的,原因有几点,首先是这三本书无一例外,都是用繁体字写的,第二就是书真得实在是太脏了,我在图书馆的座位上看,同学们都离我做得很远。我十分不自然,不愿意影响同学,但是学校不让向外借这种书(呵呵,说起这是也挺有意思,别人都不看这种书,只有我在看,老师就特别的关注我,后来我和他讲了这些书的价值,他居然把他们当作是震馆之宝,老师都不许借,不过后来他们看我真得很喜欢看,就把书借给了我,当然用的是馆长的名义借出去的。)不过收获是非常大的,再后来学习计算机理论时里面的很多东西都是常会用到的。当然如果你没看过这些书绝对理解不到那个层次。拿拓扑学来说,我们学校似乎是美开设这门课程,但是这门课程的重要性是显而易见的,没有想到的是在那本书的很多页中都夹着一些读书笔记,而那个笔记的作者及有些造诣,有些想法可以用到现代网络设计当中。
抽象代数,国内经典为莫宗坚先生的《代数学》。此书听说是北大数学系教材,深得好评。然而对本科生来说,此书未免太深。可以先学习一些其它的教材,然后再回头来看"代数学"。国际上的经典可就多了,GTM系列里就有一大堆。推荐一本谈不上经典,但却最简单的,最容易学的:http://www.math.miami.edu/~ec/book/这本"Introduction
to Linear and Abstract
Algebra"非常通俗易懂,而且把抽象代数和线性代数结合起来,对初学者来说非常理想,我校比较牛的同学都有收藏。
数论方面,国内有经典而且以困难著称摹冻醯仁?邸?(潘氏兄弟著,北大版)。再追溯一点,还有更加经典(可以算世界级)并且更加困难的"数论导引"(华罗庚先生的名著,科学版,九章书店重印,繁体的看起来可能比较困难)。把基础的几章搞定一个大概,对本科生来讲足够了。但这只是初等数论。本科毕业后要学计算数论,你必须看英文的书,如Bach的"Introduction
to Algorithmic Number
Theory"。
计算机科学理论的根本,在于算法。现在很多系里给本科生开设算法设计与分析,确实非常正确。环顾西方世界,大约没有一个三流以上计算机系不把算法作为必修的。算法教材目前公认以Corman等著的《Introduction
to Algorithms》为最优。对入门而言,这一本已经足够,不需要再参考其它书。 深一点的就是大家作为常识都知道的TAOCP了。即是《The
Art of Computer
Programming》3册内容全世界都能看下来的本身就不多,Gates曾经说过"若是你能把这书上面的东西都看懂,请把你的简历发给我一份"我的学长司徒彦南兄就曾千里迢迢从美国托人买这书回来,别的先不说,可见这书的在我们计算机科学与技术系中的分量。
再说说形式语言与自动机。我看过北邮的教材,应该说写的还清楚。有一本通俗易懂的好书,MIT的sipser的 《introduction to
heory of
computation》。但是,有一点要强调:形式语言和自动机的作用主要在作为计算模型,而不是用来做编译。事实上,编译前端已经是死领域,没有任何open
problems,北科大的班晓娟博士也曾经说过,编译的技术已相当成熟。如果为了这个,我们完全没必要去学形式语言--用用yacc什么的就完了。
北邮的那本在国内还算比较好,但是在深度上,在跟可计算性的联系上都有较大的局限,现代感也不足。所以建议有兴趣的同学去读英文书,不过国内似乎没引进这方面的教材。可以去互动出版网上看一看。入门以后,把形式语言与自动机中定义的模型,和数理逻辑中用递归函数定义的模型比较一番,可以说非常有趣。现在才知道,什么叫"宫室之美,百官之富"!
计算机科学和数学的关系有点奇怪。二三十年以前,计算机科学基本上还是数学的一个分支。而现在,计算机科学拥有广泛的研究领域和众多的研究人员,在很多方面反过来推动数学发展,从某种意义上可以说是孩子长得比妈妈还高了。但不管怎么样,这个孩子身上始终流着母亲的血液。这血液是the
mathematical underpinning of computer
science(计算机科学的数学基础),也就是理论计算机科学。原来在东方大学城图书馆中曾经看过一本七十年代的译本(书皮都没了,可我就爱关注这种书),大概就叫《计算机数学》。那本书若是放在当时来讲决是一本好书,但现在看来,涵盖的范围还算广,深度则差了许多,不过推荐大一的学生倒可以看一看,至少可以使你的计算数学入入门,也就是说至少可以搞清数学到底在计算机科学什么地方使用。
最常和理论计算机科学放在一起的一个词是什么?答:离散数学。这两者的关系是如此密切,以至于它们在不少场合下成为同义词。(这一点在前面的那本书中也有体现)传统上,数学是以分析为中心的。数学系的同学要学习三四个学期的数学分析,然后是复变函数,实变函数,泛函数等等。实变和泛函被很多人认为是现代数学的入门。在物理,化学,工程上应用的,也以分析为主。
随着计算机科学的出现,一些以前不太受到重视的数学分支突然重要起来。人们发现,这些分支处理的数学对象与传统的分析有明显的区别:分析研究的问题解决方案是连续的,因而微分,积分成为基本的运算;而这些分支研究的对象是离散的,因而很少有机会进行此类的计算。人们从而称这些分支为"离散数学"。"离散数学"的名字越来越响亮,最后导致以分析为中心的传统数学分支被相对称为"连续数学"。
离散数学经过几十年发展,基本上稳定下来。一般认为,离散数学包含以下学科:
1) 集合论,数理逻辑与元数学。这是整个数学的基础,也是计算机科学的基础。
2)
图论,算法图论;组合数学,组合算法。计算机科学,尤其是理论计算机科学的核心是算法,而大量的算法建立在图和组合的基础上。
3)
抽象代数。代数是无所不在的,本来在数学中就非常重要。在计算机科学中,人们惊讶地发现代数竟然有如此之多的应用。
?
但是,理论计算机科学仅仅就是在数学的上面加上"离散"的帽子这么简单吗?一直到大约十几年前,终于有一位大师告诉我们:不是。D.E.Knuth(他有多伟大,我想不用我再说了)在Stanford开设了一门全新的课程Concrete
Mathematics。
Concrete这个词在这里有两层含义:
首先:对abstract而言。Knuth认为,传统数学研究的对象过于抽象,导致对具体的问题关心不够。他抱怨说,在研究中他需要的数学往往并不存在,所以他只能自己去创造一些数学。为了直接面向应用的需要,他要提倡"具体"的数学。在这里我做一点简单的解释。例如在集合论中,数学家关心的都是最根本的问题--公理系统的各种性质之类。而一些具体集合的性质,各种常见集合,关系,映射都是什么样的,数学家觉得并不重要。然而,在计算机科学中应用的,恰恰就是这些具体的东西。Knuth能够首先看到这一点,不愧为当世计算机第一人。其次,Concrete是Continuous(连续)加上discrete(离散)。不管连续数学还是离散数学,只要是能与我们研究的内容挂上钩的都是有用的数学!
179512、理论与实际的结合--计算机科学技术研究的范畴与学习方法
前面主要是从数学角度来看的。从计算机角度来看,理论计算机科学目前主要的研究领域包括:可计算性理论,算法设计与复杂性分析,密码学与信息安全,分布式计算理论,并行计算理论,网络理论,生物信息计算,计算几何学,程序语言理论等等。这些领域互相交叉,而且新的课题在不断提出,所以很难理出一个头绪来。想搞搞这方面的工作,推荐看中国计算机学会的一系列书籍,至少代表了我国的权威。下面随便举一些例子。
由于应用需求的推动,密码学现在成为研究的热点。密码学建立在数论(尤其是计算数论),代数,信息论,概率论和随机过程的基础上,有时也用到图论和组合学等。很多人以为密码学就是加密解密,而加密就是用一个函数把数据打乱。这样的理解太浅显了。
现代密码学至少包含以下层次的内容:
第一,密码学的基础。例如,分解一个大数真的很困难吗?能否有一般的工具证明协议正确?
第二,密码学的基本课题。例如,比以前更好的单向函数,签名协议等。
第三,密码学的高级问题。例如,零知识证明的长度,秘密分享的方法。
第四,密码学的新应用。例如,数字现金,叛徒追踪等。
密码学方面值得推荐的有一本《应用密码学》还有就是平时多看看年会的论文集,感觉这种材料实用性比较强,会提高很快。
在分布式系统中,也有很多重要的理论问题。例如,进程之间的同步,互斥协议。一个经典的结果是:在通信信道不可靠时,没有确定型算法能实现进程间协同。所以,改进TCP三次握手几乎没有意义。例如时序问题。常用的一种序是因果序,但因果序直到不久前才有一个理论上的结果....例如,死锁没有实用的方法能完美地对付。例如,......操作系统研究过就自己去举吧!
如果计算机只有理论,那么它不过是数学的一个分支,而不成为一门独立的科学。事实上,在理论之外,计算机科学还有更广阔的天空。
我一直认为,4年根本不够学习计算机的基础知识,因为面太宽了,要是真学的话,我想至少8年的学习能使你具有一定的科学素养......
这方面我想先说说我们系在各校普遍开设的《计算机基础》。在高等学校开设《计算机基础课程》是我国高教司明文规定的各专业必修课程要求。主要内容是使学生初步掌握计算机的发展历史,学会简单的使用操作系统,文字处理,表格处理功能和初步的网络应用功能。但是在计算机科学系教授此门课程的目标决不能与此一致。在计算机系课程中目标应是:让学生较为全面的了解计算机学科的发展,清晰的把握计算机学科研究的方向,发展的前沿即每一个课程在整个学科体系中所处的地位。搞清各学科的学习目的,学习内容,应用领域。使学生在学科学习初期就对整个学科有一个整体的认识,以做到在今后的学习中清楚要学什么,怎么学。计算机基本应用技能的位置应当放在第二位或更靠后,因为这一点对于本系的学生应当有这个摸索能力。这一点很重要。推荐给大家一本书:机械工业出版社的《计算机文化》(New
Perspective of Computer
Science),看了这本书我才深刻的体会到自己还是个计算机科学初学者,才比较透彻的了解了什么是计算机科学。科学出版社的《计算科学导论》
(赵致琢先生的著作)可以说是在高校计算机教育改革上作了很多的尝试,也是这方面我受益很大的一本书。
一个一流计算机系的优秀学生决不该仅仅是一个编程高手,但他一定首先是一个编程高手。我上大学的时候,第一门专业课是C语言程序设计,念计算机的人从某种角度讲相当一部分人是靠写程序吃饭的。在我们北京工业大学实验学院计算机系里一直有这样的争论(时至今日CSDN上也有),关于第一程序设计语言该用哪一种。我个人认为,用哪种语言属于末节,关键在养成良好的编程习惯。当年老师对我们说,打好基础后学一门新语言只要一个星期。现在我觉得根本不用一个星期,前提是先把基础打好。不要再犹豫了,学了
再说,等你抉择好了,别人已经会了几门语言了。
[1]专谈计算机系统的学习
汇编语言和微机原理是两门特烦人的课。你的数学/理论基础再好,也占不到什么便宜。这两门课之间的次序也好比先有鸡还是先有蛋,无论你先学哪门,都会牵扯另一门课里的东西。所以,只能静下来慢慢琢磨。这就是典型的工程课,不需要太多的聪明和顿悟,却需要水滴石穿的渐悟。有关这两门课的书,计算机书店里不难找到。弄几本最新的,对照着看吧。组成原理推荐《计算机组成与结构》清华大学王爱英教授写的。汇编语言大家拿8086/8088入个门,之后一定要学80x86汇编语言。实用价值大,不落后,结构又好,写写高效病毒,高级语言里嵌一点汇编,进行底层开发,总也离不开他,推荐清华大学沈美明的《IBM-PC汇编语言程序设计》。有些人说不想了解计算机体系结构,也不想制造计算机,所以诸如计算机原理,汇编语言,接口之类的课觉得没必要学,这样合理吗?显然不合理,这些东西迟早得掌握,肯定得接触,而且,这是计算机专业与其他专业学生相比的少有的几项优势。做项目的时候,了解这些是非常重要的,不可能说,仅仅为了技术而技术,只懂技术的人最多做一个编码工人,而永远不可能全面地了解整个系统的设计,而编码工人是越老越不值钱。关于组成原理还有个讲授的问题,在我学这门课程时老师讲授时把CPU工作原理誉微程序设计这一块略掉了,理由是我们国家搞CPU技术不如别的国家,搞了这么长时间好不容易出了个龙芯比Intel的还差个十万八千里,所以建议我们不要学了。我看这在各校也未见得不是个问题吧!若真是如他所说,那中国的计算机
科学哪个方向都可以停了,软硬件,应用,有几项搞得过美国,搞不过别人就不搞了,那我们坐在这里干什么?教学的观念需要转变的。我们学校现在有一个学弟就专攻CPU设计,平时交流不少,发现他能够将软件的设计思想应用到芯片设计上,我看真的是不错的,比起那些望而生畏的恐怕要强上百倍。
模拟电路这个学科,如今不仅计算机系学生搞不定,电子系学生也多半害怕。如果你真想软硬件通吃,那么建议你先看看邱关源的"电路原理",也许此后再看模拟电路底气会足些。教材:康华光的"电子技术基础"(高等教育出版社)还是不错的(我校电子系在用)。有兴趣也可以参考童诗白的书。
数字电路比模拟电路要好懂得多。推荐大家看一看北京工业大学刘英娴教授写的《数字逻辑》。业绩人士
17951声明:这是一篇讲入门的文章,近几年被多处转载,转贴此文并非赞成其所有观点,仅供参考,仅供讨论.
Sir:胡侃学习(理论)计算机(转载)
庄朝晖
发表于 2005-1-14 23:09:55
发信人: sir(sir), 信区:
Mathematics. 发信站:
南大小百合
记得当年大一,刚上本科的时候,每周六课时数学分析,六课时高等代数,天天作业不断(那时是六日工作制)。颇有些同学惊呼走错了门:咱们这到底念的是什么系?不错,你没走错门,这就是(当时的)南大计算机系。系里的传统是培养做学术研究,尤其是理论研究的人。而计算机的理论研究,说到底了就是数学,虽然也许是正统数学家眼里非主流的数学。
数学分析这个东东,咱们学计算机的人对它有很复杂的感情。爱它在于它是第一门,也是学分最多的一门数学课,又长期为考研课程--94以前可以选考数学分析与高等代数,以后则并轨到著名的所谓“工科数学一”。其重要性可见一斑。恨它则在于它好像难得有用到的机会,而且思维跟咱们平常做的这些离散/有限的工作截然不同。当年出现的怪现象是:计算机系学生的高中数学基础在全校数一数二(希望没有冒犯其它系的同学),教学课时数也仅次于数学系,但学完之后的效果却几乎是倒数第一。其中原因何在,发人深思。
我个人的浅见是:计算机类的学生,对数学的要求固然跟数学系不同,跟物理类差别则更大。通常非数学专业的所谓“高等数学”,无非是把数学分析中较困难的理论部分删去,强调套用公式计算而已。而对计算机系来说,数学分析里用处最大的恰恰是被删去的理论部分。说得难听一点,对计算机系学生而言,追求算来算去的所谓“工科数学一”已经彻底地走进了魔道。记上一堆曲面积分的公式,难道就能算懂了数学分析?
中文的数学分析书,一般都认为以北大张筑生老师的“数学分析新讲”为最好。我个人认为南大数学系的“数学分析教程”也还不错,至少属于典型的南大风格,咱们看着亲切。随便学通哪一本都行。万一你的数学实在太好,这两本书都吃不饱,那就去看菲赫金哥尔茨的“微积分学教程”好了--但我认为没什么必要,毕竟你不想转到数学系去。
吉米多维奇的“数学分析习题集”也基本上是计算型的东东。如果你打算去考那个什么“工科数学一”,可以做一做。否则,不做也罢。
中国的所谓高等代数,就等于线性代数加上一点多项式理论。我以为这有好的一面,因为可以让学生较早感觉到代数是一种结构,而非一堆矩阵翻来覆去。当年我们用林成森,盛松柏两位老师编的“高等代数”,感觉相当舒服,我直到现在还保留着教材。此书相当全面地包含了关于多项式和线性代数的基本初等结果,同时还提供了一些有用的比较深的内容,如Sturm序列,Shermon-Morrison公式,广义逆矩阵等等。可以说,作为本科生如能吃透此书,就可以算高手。后来它得以在南大出版社出版,可惜好像并轨以后就没有再用了。
国内较好的高等代数教材还有清华计算机系用的那本,清华出版社出版,书店里多多,一看就知道。特点嘛,跟南大那本差不太多。
但以上两本书也不能说完美无缺。从抽象代数的观点来看,高等代数里的结果不过是代数系统性质的一些例子而已。莫宗坚先生的“代数学”里,对此进行了深刻的讨论。然而莫先生的书实在深得很,作为本科生恐怕难以接受,不妨等到自己以后成熟了一些再读。
概率论与数理统计这门课很重要,可惜少了些东西。少了的东西是随机过程。到毕业还没有听说过Markov过程,此乃计算机系学生的耻辱。没有随机过程,你怎么分析网络和分布式系统?怎么设计随机化算法和协议?据
说清华计算机系开有“随机数学”,早就是必修课。人家可是工科学校,作为自以为“理科计算机系”出身的人,我感到惭愧。
另外,离散概率对计算机系学生来说有特殊的重要性。现在,美国已经有些学校开设了单纯的“离散概率论”课程,干脆把连续概率删去,把离散概率讲深些。我们不一定要这么做,但应该更加强调离散概率是没有疑问的。
计算方法是最后一门由数学系给我们开的课。一般学生对这门课的重视程度有限,以为没什么用。其实,做图形图像可离不开它。而且,在很多科学工程中的应用计算,都以数值的为主。
这门课有两个极端的讲法:一个是古典的“数值分析”,完全讲数学原理和算法;另一个是现在日趋流行的“科学与工程计算”,干脆教学生用软件包编程。南大数学系的几位老师做了件大好事,把前者的一本极为经典的教材翻译出版了:德国Stoer的“数值分析引论”。如果你能学会此书中最浅显的三分之一,就算没有白上过计算方法这门课!而后一种讲法似乎国内还没有跟上潮流?不过,只要你有机会在自己的电脑上装个Matlab之类,完全可以无师自通。
本系里,通常开一门离散数学,包括集合论,图论,和抽象代数,另外再单开一门数理逻辑。这样安排,主要由于南大的逻辑传统:系里很多老师
17951顶一下!!
17952不懂,不过还是看看吧。等想来再说
17952证明: 级数 ∑ n
=0 ∞
∫ 0
Π
/2
(
-1)
n
(
tanx) n
dx是条件收敛的!
我真是惭愧啊,早上去考时,碰到这题,想了一整天都没做出来,特地来这时向各位高手请教!!
17952可以想办法利用递推公式来解决
17952哪个递推公式呀?
17952那个级数不收敛吧?!
∫ 0
π 2
tan
n xdx =
∫ 0
∞
x n
1 +x
2dx >
∫ 1
∞
x n
1 +x
2dx >
1 2
∫ 0
∞ x
n
-2dx
= + ∞
17952那个n不用考虑嘛?
17952可以假设 I
n
等于那个积分。试试
17952
| 引用 (tobyqin @ 2005年09月15日
22时47分) |
那个级数不收敛吧?!
∫ 0
π 2
tan
n xdx =
∫ 0
∞
x n
1 +x
2dx >
∫ 1
∞
x n
1 +x
2dx >
1 2
∫ 0
∞ x
n
-2dx
= + ∞ |
强
这道题目不错
17952
| 引用 (tobyqin @ 2005年09月15日
22时47分) |
那个级数不收敛吧?!
∫ 0
π 2
tan
n xdx =
∫ 0
∞
x n
1 +x
2dx >
∫ 1
∞
x n
1 +x
2dx >
1 2
∫ 0
∞ x
n
-2dx
= + ∞ |
是否应该是 ∑ n
=1 ∞
∫ 0
π 4
(-1)
ntan n
xdx ?
17952
| 引用 (wangsb @ 2006年01月24日
00时33分) |
| 引用 (tobyqin @ 2005年09月15日
22时47分) | 那个级数不收敛吧?!
∫
0 π
2
tan n
xdx =
∫ 0
∞
x
n 1
+x
2dx
> ∫
1 ∞
x
n 1
+x
2dx
> 1
2
∫ 0
∞ x
n
-2dx
= + ∞ |
是否应该是 ∑ n
=1 ∞
∫ 0
π 4
(-1)
ntan n
xdx ?
|
根据我解答的情况来看,你说的是对的,
17952刚刚说错了
17952
令 t
=tanx,
a
n = ∫ 0
Π
4
( tanx)
n dx
= ∫ 0
1
t n
1
+t 2
dt
= ∫ 0
1
( t n
-2-t
n -2
1 +t
2
)dt
=
1 n
-1
-a n
-2.
即 a
n
+a n
-2=1
n
-1.
由于
a n
单调减,且有下界0,因此
a n
存在极限. 在 a
n
+a n
-2=1
n
-1 两边令
n →+∞
,得 lim n
→+∞
a n
=0.
故 ∑ n
=1 +
∞ (-1)
n a
n 是leibniz级数,而原广义积分的敛散性与无穷级数 ∑ n
=1 +
∞ (-1)
n a
n 的敛散性相同,故收敛.得证.
17952楼上解答的很精彩,谢谢!!!
17953
谁能帮我做做这道高代题目?
17953A*,B*是什么意思?
17953
就是伴随矩阵的意思啊!!!
17953
zhubin846152!我想问问你有有没有各个大学的数分和高代的试卷啊?有的话能不能发几份给我?我今年要考研。
17953好象是浙江大学一硕士生入学试题
其实很简单的,我知道的办法有两种,但写起来很麻烦,好好想想吧
17953如果是伴随阵
那好像是(AB)*=B*A*
以前的帖子里有的,分成奇异和非奇异考虑
另外,我没有什么卷子,都是以前论坛里面下的
17953
麻烦你了,你就做一下吧!!!是的我题目看错了,是(AB)*=B*A*
17953首先,如果AB非奇异
A*=|A|*inv(A)
inv(A)为A的逆阵
[(AB)*](AB)=B*A*AB=|A||B|
如果,A,B存在某个秩<n-1
不妨设rank(A)<n-1
=>
rank(AB)<n-1
A*=0
(AB)*=0
如果,A,B存在某个秩=n-1
(1)rank(B)=n
对于某个初等矩阵P
(PA)*=A*P*
(这应该不难)
B=P1P2...Pn
(A(P1P2...Pn))*=Pn*(AP1P2...P(n-1))*=...=(Pn*)...(P2*)(P1*)A*=BA
(2)rank(B)=n-1
存在P,Q
A=PC,B=DQ
C,D为上三角阵
应该也不难证明该式
17953好帖
17953First of all, the question should be (AB)^*=B^*A^*. The order is
important.
To prove this, let's first assume that both A and B are
invertible, then it's easy to check the equality does hold (since in
this case A^*=|A|A^-1,and so on).
Now let x be a sufficiently large
number such that (A-xI)(B-xI) is invertible, then
[(A-xI)(B-xI)]^*=(B-xI)^*(A-xI)^* by the first paragraph. This equality
holds for infinitely many numbers x and both sides of this equality are in
fact matrices of polynomials in variable x, so it must hold for ALL x. Set
x=0, we are done!!!!!!
Do you get it?????
17953zhubin846152。你实在是太厉害了,小生实在是佩服得五体投地。别人
17953
zhubin846152。你实在是太厉害了,小生实在是佩服得五体投地。别人
17953对不起,我不会编辑数学公式!
17953dododone 的方法是一种很常用的 基本的方法 大家要掌握
17954爱因斯坦将世界视为独立存在于人之外的客观事实,“就像一个伟大恒久的谜,我们的审视至少可以部分解开它。”在玻尔看来,这个事实并不存在,“没有一个量子世界,只有一个抽象的量子物理描述。如果你认为物理学的任务是发现自然是什么,那你就错了。物理学只关心我们能够对自然说些什么。”爱因斯坦采取了笛卡尔在《沉思》中不得不奉行的准则:“凡是我们理解得非常清楚、非常明白的东西都是真实的”。这个准则使我们获得安全感,谁愿意相信自己刚刚塞进嘴里的不是一片面包,而可能是一片棉絮呢?
我投爱因斯坦一票!!!
17954这个量子逻辑不好理解,更让人难接受,这样的量子计算机能造出来吗?
比那个DNA计算难理解多了.
17954姚期智:不可靠的量子计算机
--------------------------------------------------------------------------------
经济观察报记者 覃里雯 黄继新 北京报道 2002-11-26 9:58:01 阅读 2614 次
姚期智
2000年图灵奖得主,普林斯顿大学计算机科学系教授
祖藉湖北孝感,
1946年出生于上海,分别于
1972年和
1975年获哈佛大学物理学博士与伊利诺大学计算机科学博士。曾先后在麻省理工学院、斯坦福大学、加州大学伯克莱分校等美国一流高等学府从事教学和研究。
1986年至今则一直任普林斯顿大学计算机科学系教授。他为美国国家科学院院士、美国人文及科学院院士以及IBM
EC系统研究中心和Xerox Palo
Alto研究中心的顾问。
2000年,他因对计算理论做出了诸多“根本性的、意义重大的”贡献获得计算机学界的诺贝尔奖——“图灵奖”。
在10月份微软亚洲研究院发起的“21世纪的计算”研讨会上,第一个图灵奖华人得主姚期智发现自己没有足够的时间向听众说清自己正在从事的研究。IBM最近做出了量子计算机研制的突破,不过看上去离实际可行的计算机还有很远的距离。量子加密领域的发展比量子计算机要先行一步。
这是真的吗?我们忠实的晶体管说:我要么是0,要么是1;而粒子跳出来说:我可以是0或者1,也可以既是0又是1,我可以在这里或在那里,也可以既在这里又在那里。
这难道不是我们小时候最狂野的梦想吗?在寒冷的冬晨,我们听着窗外呼啸的风声,希望自己能够舒舒服服地躺在床上,让另一个自己代替我们去上学。粒子确实可以办到这一点,它不仅可以既躺在床上又去上学,还可以同时在其他宇宙里干仗,解救被囚禁的奴隶。按照弗莱德金的说法,最小的粒子只需变成一颗bigish星的大小,就可以完全模拟从大爆炸时期到今天的宇宙的演变过程,这个过程只需4个小时。我们可以想象,假如粒子具有思维的话,它会在很短的时间内穷尽存在的可能性,并最终明了上帝的意图。
20世纪20年代,海森堡提出量子测不准原理,他发现不可能同时确定粒子的动量(速度×质量)和位置——这基本上是通过理论推导出来的结论,后来的实验也证明了这一点——一个电子同时穿过了两条缝。
但是爱因斯坦厌恶这个理论,他无法忍受一个创造出不确定存在的上帝。这导致了
1927年那场著名的爱因斯坦-玻尔争论。爱因斯坦相信一定会有一个更深的理论来同时确定粒子的动量和位置,他的后半生大部分花在寻找这个理论上,但他最终也没有逮住那可恶的粒子。
对自然科学家来说,寻找确定性是一项更艰难的工作,比对社会科学家要艰难得多。后者总是按照晶体管的方式来安排自己的观点,是或者不是,耶稣存在过或者没有存在过,特洛伊战争发生了或者没有发生,中国在全球化或者没有全球化——他们最终可以用材料的组织方式来证明自己的观点。假如他们不这样工作,人们会认为他们干得很糟糕。自然科学家在做出结论时则有非常困难的障碍:凡是没有被证实的你就不能下断言。这个证实过程可能是解一批全世界人加在一起10亿年也解不完的方程式,或者是期待一个700年后才出现的天文学发现。
所以才会有这个笑话,一位从2020年回到2000年的未来人告诉现代人:我们生活在量子宇宙中,历史可以同时有不同的状态。已发生的可能从未发生,或者以很多不同的方式发生。“可是我们为什么只有一部历史?”现代人问。未来人说:“因为有天主教学校。”
与传统计算机的二进制原理相比,量子计算机更像是四进制运算——粒子可以同时进行几种不同的运算。其加密涉及的数学问题极为复杂,比传统的数据计算问题要复杂得多。量子加密的方式,简单地说,就是让“偷看”密码的行为干扰?改变?系统,这样,密码是否曾被破译就能检测出来。就好像说,如果你偷看了我的信件,我的信就会留下被改动过的痕迹。
这是因为量子计算机的不可移植性,它同时也给量子计算机的设计带来无穷尽的困难。假如,现在有一个拥有两个位的量子计算机,我们想要从一个位将信息抄到另一个位,也就是用镭射光先去读第一个位的信息,再去写第二个位的信息。如果本来要抄的状态是0或者1,抄过去会和原来一模一样;但是由于粒子的顽皮,第一个位经常可以是一个介于0与1间的状态,这时问题就来了:镭射光会把这样的一个状态变成0或变成1。因此抄过去以后,有一些信息就在这个读取的过程中遗失了。一个本来就不确定的状态是不能复制的,也不能观测而不干扰它。
当有两个以上的位时,粒子还会产生所谓的缠结态
?entangled
states?,你可以想象这是很可怕的状态,就像你本来让几个计算机在进行不同的运算,但是计算机们忽然决定串通一气,都干同一件事情。这些东西都让量子计算机科学家伤透脑筋。
不善于运用比喻和举例的姚期智发现自己很难向外行人解释,自己正在做什么。这使人想起一个肖邦的故事,有人问肖邦他刚才演奏的曲子是什么意思,音乐家一言不发地把曲子再演奏一遍,然后说:“就是这个意思。”同样的,热爱弹奏钢琴的姚期智感到,如果不是原封不动地用那些公式和理论来叙述的话,他不能解释自己工作的内容。对量子计算机给未来世界带来的变化,他并没有科幻小说式的预期。就像那些无处不在的粒子,他的大脑总是考虑各种各样的可能,因此对任何预测未来的问题他都不愿做出结论。他可能不具备戏剧感,但是他从自己的工作中得到令人嫉妒的乐趣。对他而言,同行的理解和尊敬远远比大众的仰慕更让他愉快,虽然后者在不占据太多时间的前提下,也很让他高兴。
爱因斯坦将世界视为独立存在于人之外的客观事实,“就像一个伟大恒久的谜,我们的审视至少可以部分解开它。”在玻尔看来,这个事实并不存在,“没有一个量子世界,只有一个抽象的量子物理描述。如果你认为物理学的任务是发现自然是什么,那你就错了。物理学只关心我们能够对自然说些什么。”爱因斯坦采取了笛卡尔在《沉思》中不得不奉行的准则:“凡是我们理解得非常清楚、非常明白的东西都是真实的”。这个准则使我们获得安全感,谁愿意相信自己刚刚塞进嘴里的不是一片面包,而可能是一片棉絮呢?
但是另一些科学家们更愿意认同于玻尔的看法,他们在科学为自己建筑的平台上舞蹈,而不必考虑平台究竟是虚拟的还是水泥的。说到底,你面前这张报纸很可能并不存在,或者它并一定不是橙红色的,它可能同时还存在于另一个世界,被一个头上长角的生物阅读着,这个采访与量子计算机无关,而是一个爱情故事。
17954人工智能与量子计算机
问:图灵机曾经试图将人的思维量化和逻辑化,这种努力究竟可以进行到哪一步?现在有研究者认为,人脑运作方式与计算机的工作方式非常相像,有可能用计算机来模拟人脑的思维吗?
答:我的想法恰恰相反。现在很少还会听到有人说,人脑可以用图灵机模拟,至少现在好像还没有人相信在可见的未来能够用计算机模拟人脑,至于到底人脑算不算电脑,这还是值得讨论的一个问题。把人脑当成一个计算机,这是一种比较宽泛的概念,和一般我们解决问题的方法不太一样。不过我觉得这是一个非常非常难的问题,到底人脑以怎么样的方式在运作,这个方面需要专门的专家,研究脑、神经的专家,花毕生时间去研究,这是非常非常深的问题。
问:是不是所有计算机科学家都有一个共同的想法,即尽量让计算机像人脑一样思维?
答:在人工智能(Artificial
Intelligence,简称AI)研究的早期,可能有人这样想,仍然觉得这是可能实现的。但是现在好像人们不太有这种乐观的想法,现在人们的目标没有这么高了。
问:那就是说,现在科学家提到的AI,和以前科学家提到的AI,所指的已经不是同一个东西了?不管是在科幻电影中,还是在传统科学家的预想中,AI似乎追求的就是基本上近似于人的智能水平,依您所说,现在我们提到的AI已经不是以前的那个方向和目标了?
答:当然还是有人对这种最基础的概念有研究兴趣,比如说到底什么叫智能。但是就现在来讲,研究AI的科学家都是在一个限定的领域里做研究,现在好像已经没有人还有那种就一般性的模拟智能做研究的想法了。
问:这种对不同研究领域的严格划分是否有点像经济学?现在的经济学越来越多地受到心理学、社会学等其他学科的影响,生物学是不是也会给计算机研究造成这样的影响呢?
答:我想,生物学对计算机最大的影响,是在分子生物学(molecular
biology)里面,因为这个学科有大量的数据需要计算机帮助他们进行处理。我认为,在生物学对计算机发展的刺激上,这就是最大的因素。至于在生物学中有哪个方面能够让计算机去学习和发展成为更好的计算机,目前还不是太明朗。不过确实有些演算法是模仿了生物学的内在特点,比如说有一派人搞的基因算法(genetic
algorithm),他们订立一套规则,让不同的算法去竞争,优胜劣汰,最后得到一个比较优的选择。这些从侧面对计算机科学带来了一些冲击,但不能说它们引起了非常让人吃惊的结果。
问:那您认为目前在科学上比较大的进展是什么?
答:在整个科学界吗?在整个科学界里还是有很多令人兴奋的事情。比如说,大家觉得,我们也许能够找到最基本的理论,可以解释宇宙之间的所有现象,最大的希望是能够有一个理论,我能够解释这个宇宙,这里边有很多漂亮的结果,会引发一些数学上非常重要的发现。
有没有什么是划时代的……一般来讲,每年都会有很重要的结果,但是很难讲谁是划时代的。我想我们想要找到一个像相对论、量子力学这样具有划时代意义的进展,在物理方面可能有比较大的进展,不过这只是我对物理比较熟的缘故,所以我不敢讲在别的领域里边有没有真正划时代的。只是从所发表的学术论文的角度来讲,好像我们没有看到一种真正能够让人的世界观发生根本改变的,譬如沃森和克里克(DNA结构的共同发现者)这样的。
问:那么就计算机科学而言,量子计算是不是已经相当具备划时代性和影响力了?它是不是计算机科学史上最大的一次革命?
答:如果量子计算机能够成功实现的话,那么量子计算将是自图灵以来最重要的发展,因为它的整个架构完全改变了。
问:量子计算机到底是怎么一回事?听说把一些东西装进试管里,它自己就能够进行计算?
答:你说的那个是DNA计算,是另外一回事。计算机从冯·诺伊曼开始到现在差不多有50年左右的历史,基本上没有改变过什么,有技术上的改进,但是基本原理没有改变。你所说的DNA计算,原理也没有很大的改变,与50年代的计算相比差别也不是那么大。比如说现在普通的计算机只有一两个或者三四个进程,DNA计算机则试图在试管里做出很多个进程,但是它的基本原理与50年前还是一样的。
而量子计算则完全不同。它的突破在于,从某个角度来讲,它使用了完全不同的逻辑,已不再是传统的逻辑概念。传统计算逻辑基本上就是0和1,而量子计算的逻辑则是比0和1更为复杂的基本单位,这很难解释的。
可以这样打一个比方,量子计算的原理基本上有一点像光学。在光学上,如果在一个屏风上刺几个洞,光从一个光源出去之后,我们就可以看到后面一个屏风上有明的有暗的,因为光是波,它有消有长,有弯弯曲曲的东西。在光学上,如果不知道上面的针孔形状,那么我们根据光穿过针孔后在后面的屏风上留下的样子,可以猜到针孔之间的关系或者距离。在量子计算上,如果我们手头有一些数据,想用这些数据进行计算的话,那么我可以让这些数据穿过针孔的东西,到后面的屏风上去看它会显出什么样子,然后就能据此说出数据有什么样的性质。所以从这个角度来看的话,量子计算就类似光学系统的计算,不过它跟一般用在光学上的计算机还不是太一样,这只是一个比喻。
问:量子计算机本身离成熟还有多远?
答:这个问题当然不可能有人知道答案,我猜可能要15年,有人甚至说这根本不可能变成现实,至少它非常难是大家都有的共识。
好在美国政府这几年来对量子计算这方面的研究经费投入较多。当然,多半的钱都给了做物理的,是他们在研究怎样实现量子计算。这些人本来都是很不错的物理学者,如果量子计算的研究完全没有希望的话,他们不会改变研究方向、花宝贵的时间来做这件事。一直以来我们有一个发现:如果说一个技术不是一定不能做到的话,那么最终它都是可以实现的。现在,大家都没有想出一个真正的理由来证明量子计算确实做不到。七八年前,物理学家就认为有一些困难是不可能克服的,但是最近七八年都克服了这些非常关键的问题。
问:目前硬件的发展遵循摩尔定律,而软件的发展却似乎跟不上硬件的发展速度,我们经常谈论的是如何让软件最大限度地调动起硬件的潜能来。对您来说,软件会不会出现概念上的大突破,最终使人类的计算发生本质上的变化?
答:我不是一个软件方面的专家,但是我的印象是,没有人觉得很快就能够解决我们以前不能够解决的问题。基本上,怎么样写一个大的软件程序,这种事情没有人知道怎么样做。大家有一些听起来不错的想法,但是好像还没有听说过一种大的系统是完全没有bug的。
问:就是说,人们现在还没有看到软件方面会有像量子计算这样的突破?
答:量子计算能够实现很大突破,主要原因在于它的整个基础理念都完全不同以往。很难想象软件方面能够出现一个新的观念,突然之间就让所有的问题都不见了,除非完全改变软件的内在特点,如果说软件还是这样一行一行地写的话,很难想象(它会发生很大突破)……一般来讲,你在错综复杂的大系统下面决定要具体做什么事情,这就已经很困难了。你得想出一个方法,告诉自己到底想要做什么事情,写成白纸黑字,这就已经是一个很巨大的工作了。像Windows这样的一个系统,你要把它的整个构思、每个要求都全部写下来的话,我相信在写的过程中就一定会有错。
科学家:自我尊重与公众尊重
问:从二战后到80年代,是科学非常显赫的时期,科学家非常受人尊敬和关注。但是这之后,科学的发展逐渐变成了理所当然,没有人再去奇怪科学的进步,科学家受到的关注也远不如前。尽管90年代IT业发展非常迅猛,但计算机科学家受到的关注并没有因此增加。包括荣获了图灵奖的科学家,受到的关注也不比以往。对您来说,这种变化有没有什么影响?它会不会影响到您投入研究的热情?
答:我个人的意见是,你所追求的是自我尊重(self
respect)和自我实现。在这个过程中,你可能会得到同行的尊重(peer respect),如果你得到了公众的尊重(public
respect),从一个角度来讲,也是会影响到你自己,但那是虚荣心方面的东西。
问:那就是说,不管外界对科学家的关注到什么程度,对科学工作者本身来说,公众尊重总是影响力最小的?
答:每个人会不一样,有些人比较在乎,有些人比较不在乎,我想这会因行业而异。
问:那是不是说,同行的尊重更能够给您激励?
答:(笑)当然,得到公众的尊重也很好,我不能说我不喜欢这个。
问:比如说,像我们这样的人,我们都非常地尊敬您,但是什么都不懂。
答:(微笑)人都是有点虚荣心,(得到公众的尊重)这当然是很好的事情。但基本上这不是影响你决定做科学家的因素。我在决定成为一名科学家时,不会是因为将来能够得到公众的尊重才去做。
基本上,做科学家是一件很舒服的事情。我想,不光是做科学家,每个人能够发现自己最能够去做的事情,而且还有机会去做,那都是最舒服的事。在美国,有相当好的条件和舒适的生活方式让你去做研究,我自己都有点不好意思,我就觉得生活不应该会这么好。
问:您没有觉得很辛苦吗?
答:好像没有,因为基本上是自己在驱动自己,你自己愿意去做,你有足够的意志力去做。
问:你小时候最想成为什么样的人?
答:我想很多的中国家庭都希望自己的孩子做一个学者,这是最好的职业,比较独立的,不会太受环境的影响。所以,我从小就是想要做个科学家,但是我不晓得做什么样的科学家。比较好的是,因为我们那个时候信息比较缺乏,不需要你去担心太多。很自然,运气好的话,碰到一些事情你是能够做到的,运气不好的话,你就进入你不喜欢的行业。所以也没有烦恼,我想跟中国父母对孩子的期望一样:上最好的中学,考进最好的大学,以后能够留学。
问:对你影响最大的人是谁?
答:我想是爱因斯坦。
问:在哪些方面对你影响最大呢?
答:主要是他的作品。在高中的时候,读过Eddington写的介绍爱因斯坦的一本书。以前在我们那个时候,台湾还相当穷,只有美国新闻处有这种洋书。我去那里借了一本书,虽然是写给大众看的读物,但是因为相对论是非常难的理论,要看很久才能看懂。但是那天看懂的时候非常非常高兴,从来没有过这种感觉。后来读量子力学也有这种感觉,这种激励感好像是世界上最值得追求的一个东西,希望自己将来即使做不到这样伟大的事情,但是也要向这个方向前进。所以我做科学家,读这几个学说对我的影响最大。
问:您刚才提到,作为科学家最重要的是自我尊重,其次是同行尊重和公众尊重。当然了,它们都很重要。
答:(笑)最好都有。
问:因此,我们知道,科学研究最重要的驱动力来自于自我(self
drive)。二战之前,人们都是因为个人兴趣而投入科学研究。但到了战后,情况发生了变化,科学家从完全自发的、出于兴趣的研究,变成了政府、商业机构或非商业机构投资的、以任务为导向的研究。人类在科学研究上的这样重大转变,不知道对科技工作者来说有没有影响?
答:我想这是没有办法的,因为现在科学研究的重要项目都需要很多很多人。所以没法说这种事情是好是坏,这是无法避免的。最重要的要留下生存空间,让那种想要享受生活的、独立的思想者有机会发展。这两个事情是冲突的,但是在很多情况下,最大的发现并不是因为有很多钱才得到的,而是个人做的。很多事情都是偶然的决定。
问:公司或者政府组织的研究,非常容易造成研究组织之间的壁垒,也就是所谓的商业机密或者国家机密,您觉得这对现在的科学研究会不会造成很大的阻碍?
答:我不太清楚中国的情形,但我知道美国的情形。在美国,学校还是一个很重要的研究力量,在学校里面做研究的人,通常钱都是从政府里来,而不是被某一个公司赞助。一般来讲,像自然科学基金这样的研究机构,他们基本上还是相当公正的,他们的钱还是给了正确的人去做正确的事。学校里甚至有教授和赞助的公司争执的情形,我觉得这是一种平衡力量。公司愿意出钱,这当然是好事,研究当然是做得越多越好。
问:研究成果是否公开?……在这方面IBM、HP都做了很重要的贡献。
答:我觉得是很难的问题。就拿生物技术公司来说。一般来讲,你需要给个人以激励,他才会有投入,才会去冒这个风险,有发财的机会,也有完蛋的机会。不然,药厂不研究新药的话就没有人出得起这么大笔的研究款项了。所以需要在所有权上激励他们。至于说怎么样把握这件事情,我反对完全开放这样的做法。我是觉得不能走极端,但是现在的情况确实不错。
问:您在研究当中碰到最困难的时刻是什么?
答:好像不太有什么不太美好的回忆,我好像只能记得好的事情。困难的时刻其实也很多,但都是很正常的现象。比如说有个问题你想不出来,想一想后又放弃,然后再想一想再放弃,很多年想不出来,有一天突然就想通了。我在做复杂性理论(complexity
theory)的研究时,就需要知道做一件事怎么样才是最好的方法,需要去证明不会有更好的方法了。
问:这是不是有点像偏执狂:我要去证明一件事情不可能再得到改进了。这种偏执心态会导致花很长时间去证明。对您来说,您做研究,最让您兴奋的是哪一件事?
答:在我刚刚开始做研究的时候,即使获得了一些不太重要的结果也会让我感到兴奋。到后来标准越来越高,只能拿一两个星期时间来兴奋,接着就要做下一个课题。通常来讲,你所做的比较重要的结果做完了以后,自己当时是会有感觉的,你自己知道这个东西将来会变得很重要。所以,一般来说,最重要的结果做出来的时候就是你最高兴的时候。
问:就您来说,哪一次研究结果是最令您兴奋的?
答:我想
1982年的论文可能是我最满意的。那是一个关于密码学的研究成果。它所做的事情基本上是研究什么样的序列才能算是随机序列。它的影响是两个;一个就是说,它提出了一个新观念,这个观念解决了当时的很多困难;第二个是说,这个东西对密码学后来的发展很有影响。这个东西实在是太技术了,很难讲得很仔细。
( 本报记者 覃里雯 黄继新 北京报道 02-11-11 82 )
17954不可小视量子计算机,如果设计成功,NP问题都能在多项式时间内解决啦!
17954楼上说的是,这是量子计算理论方面,这个层面的工作做完了吗?剩下的问题是不是计算的量子实现?盼高人解答.
17954量子通信虽然处于试验阶段,但是已经可以在50公里内传输数据啦。
17955看不清,楼主能不能整理一下。
17955对
f `
(x)-f(x)
用介值定理即可。
或者定义g(x)= f
(x)e
-
x 再用零值定理+Rolle定理
17955题目:
设函数f(x) ∈ C[a,b]
∧ D(a,b) ,且f(a)
• f(b)>0,f(a)
• f[(a+b)/2]<0,求证:在区间(a,b)内至少存在一点 ξ ,
 (
ξ )=f( ξ );
(
ξ )=f( ξ );
希望大家帮我顶一下呀,让我有动力继续上传一些崭新的且是经典的题目给大家品尝,
谢谢!!
17955 | 引用 (tobyqin @ 2005年09月10日
21时48分) |
对
f `
(x)-f(x)
用介值定理即可。
或者定义g(x)= f
(x)e
-
x 再用零值定理+Rolle定理
|
谢谢,你的解答,你真是很聪明呀,我怎么样才能有你那样的思维呢?
179564,
有十道相互关联的选择题叫你选择,如下:
、第一个答案是b的问题是哪一个?
(a)2;(b)
3;(c)4;(d)5;(e)6
2、唯一的连续两个具有相同答案的问题是:
(a)2,3;(b)3,4;(c)4,5;(d)5,6;(e)6,7;
3、本问题答案和哪一个问题的答案相同?
(a)1;(b)2;(c)4;(d)7;(e)6
4、答案是a的问题的个数是:
(a)0;(b)1;(c)2;(d)3;(e)4
5、本问题答案和哪一个问题的答案相同?
(a)10;(b)9;(c)8;(d)7;(e)6
6、答案是a的问题的个数和答案是什么的问题的个数相同?
(a)b;(b)c;(c)d;(d)e;(e)以上都不是
7、按照字母顺序,本问题的答案和下一个问题的答案相差几个字母?
(a)4;(b)3;(c)2;(d)1;(e)0。(注:a和b相差一个字母)
8、答案是元音字母的问题的个数是:
(a)2;(b)3;(c)4;(d)5;(e)6。(注:a和e是元音字母)
9、答案是辅音字母的问题的个数是:
(a)一个质数;(b)一个阶乘数;(c)一个平方数;(d)一个立方数,(e)5的倍数
10、本问题的答案是:
(a)a;(b)b;(c)c;(d)d;(e)e。
我只想知道怎样用手工推理解决这道题目?
盼高手解答。
附:本人用计算机穷举得到的唯一解cdebeedcba
179561,
五五谜题
文章收藏, 软件技术
既瑜 发表于 2005-3-16
17:05:49
内容:
1. 有5栋5种颜色的房子
2. 每一位房子的主人国籍都不同
3.
这五个人每人只喝一个牌子的饮料,只抽一个牌子的香烟,只养一种宠物
4. 没有人有相同的宠物,抽相同牌子的烟,喝相同牌子的饮料
已知条件:
1. 英国人住在红房子里
2. 瑞典人养了一条狗
3. 丹麦人喝茶
4.
绿房子在白房子的左边
5. 绿房子主人喝咖啡
6. 抽PALL MALL 烟的人养了一只鸟
7.
黄房子主人抽DUNHILL烟
8. 住在中间房子的人喝牛奶
9. 挪威人住在第一间房子
10. 抽混合烟的人住在养猫人的旁边
11. 养马人住在抽DUNHILL烟人的旁边
12. 抽BLUE MASTER烟的人喝啤酒
13. 德国人抽PRINCE烟
14. 挪威人住在蓝房子旁边
15. 抽混合烟的人的邻居喝矿泉水
179562,
小光,小强二人都是王老师的学生,王老师生日是x月y日,两人都知道x月y日是下列10天中的一天,王老师把x值告诉了小光,把y值告诉了小强,王老师问他们二人知道他的生日是那天吗?
3月4日 3月5日 3月8日 6月4日 6月7日 9月1日 9月5日 12月1日 12月2日 12月8日
小光说:如果我不知道,那小强肯定也不知道
小强说:本来我不知道,但现在我知道了
小光说:哦,那我也知道了
王老师生日应该是哪一天呢?
179563,据说难倒上亿人的一道智力题
罪犯抓黄豆
1-5号5个罪犯按顺序在装有100颗黄豆的袋子里抓黄豆,每人至少抓一颗,抓得最多和最少的人将被处死,他们之间也不能交流,但抓的时候可以摸出剩下的黄豆数。问他们中谁活下来的可能性最大??
提示:
1,5个人都是聪明人
2,5个人都是要先求保命,再多杀人
3,100颗黄豆可以分完,也可以不分完,这一点对5个人不做要求
4,如果几个人一块最多或最少,一并处死
17956我认为是9月1日
说说你的解法
17956好几道题以前都见过
179562.老师的生日为6月4日
17956很有意思
17956我顶!
17956楼主能不能把"十道相互关联的选择题"的破解代码给我啊?
我想参考一下
谢谢
17956不好意思,我转的贴子,忘注明了...
搜一下看看吧...
17956第2道题显然不是6月4日,应该是9月1日
推理如下:
由已知1,可得,如果X未知,则由Y无法确定X,也就是说甲已经能确定Y不是2或7,因为2或7只出现一次,所以如果Y为2或7则乙可以直接知道答案,所以乙可以知道X不为6或12,因为2和7出现在6月和12月,所以X只能为3或9,而Y只能为1、4、5、8,这里就可以排除6月4号了
由已知2,乙在确定X为3或9时,就知道了答案,那么Y就不可能是3月和9月中都出现了的5,而只能是1、4、8
由已知3,甲也由已知2排除了Y为5,但是X如果为3的话,甲仍然无法确定Y为4还是8,所以,X只能为9,而Y只能为1。
所以答案为9月1日
17956第4题没有找到好的手工解法,所以用DELPHI写了个穷举程序:
答案唯一:cdebeedcba
| 代码 |
function lg_test(k:array of
integer):boolean;
const
d3:array [0..4] of
integer=(1,2,4,7,6);
d9:array [0..4] of
integer=(7,6,4,8,5);
var
i,j,p,b,c,d,e:integer;
begin
result:=false;
j:=-1;
for
i:=0 to 9 do
begin
if k[i]=1 then
begin
j:=i;
break;
end;
end;
if
k[0]<>j-1 then
exit;//1
j:=0;
p:=-1;
for i:=0 to 8 do
begin
if k[i]=k[i+1] then
begin
inc(j);
p:=i;
end;
end;
if
j<>1 then exit;
if k[1]<>p-1 then exit;
//2
if
k[d3[k[2]]-1]<>k[2] then exit;
//3
j:=0;
for i:=0 to 9 do
begin
if k[i]=0 then
begin
inc(j);
end;
end;
if
k[3]<>j then exit;//4
if
k[9-k[4]]<>k[4] then exit;
//5
j:=0;
b:=0;c:=0;d:=0;e:=0;
for
i:=0 to 9 do
begin
case k[i] of
1:inc(b);
2:inc(c);
3:inc(d);
4:inc(e);
else
end;
end;
p:=4;
if (k[3]=b)
then p:=0 else
if (k[3]=c) then p:=1 else
if
(k[3]=d) then p:=2 else
if (k[3]=e)
then p:=3;
if p<>k[5] then exit; //6
if
abs(k[6]-k[7])<> (4-k[6])
then exit; //7
if
(k[3]+e)<>(k[7]+2) then exit;
//8
if
(d9[k[8]]+k[7]+2)<>10 then exit;
//9
result:=true;
end;
procedure
TForm1.Button1Click(Sender:
TObject);
var
i,j:integer;
s:string;
k:array
[0..9] of integer;
begin
for i:=0 to 9 do
begin
k[i]:=0;
end;
while
k[0]<5 do
begin
//
if
lg_test(k) then
begin
s:='';
for i:=0 to 9 do
s:=s+chr(97+k[i]);
memo1.Lines.Add(s);
end;
//
inc(k[9]);
for i:=9 downto 1
do
begin
if
k[i]>4 then
begin
k[i]:=k[i]-5;
inc(k[i-1]);
end
else break;
end;
end;
application.MessageBox('完成','提示',MB_OK);
end;
|
17956第1题:
1 挪威 黄 猫 矿泉水 DUNHILL
2 丹麦 蓝 马 茶 混合
3 英国 红 鸟 牛奶 PALL
MALL
4 德国 绿 咖啡 PRINCE
5 瑞典 白 狗 啤酒 BLUE
MASTER
方法
拿一张纸列一个5*5的矩阵,然后连线,最后排除就可以了,笨办法,花点时间而已。
17956第3个是个博弈问题。应该写个深度搜索算法能够解决。
偶先休息休息。
17956第3题结果为第2个人活下来的可能性最大
五个人活下来的可能性分别为 0 93 0 0 0
代码如下:
| 代码 |
function
lg_value(level:integer;k:array of
integer):integer;
var
i,imax,imin:integer;
begin
result:=0;
imax:=0;imin:=100;
for
i:=0 to 4 do
begin
if k[i]>imax then
imax:=k[i];
if k[i]<imin then
imin:=k[i];
end;
if
(k[level]=imax) or (k[level]=imin) then
exit;
for i:=0 to 4 do
begin
if
(k[i]=imax) or (k[i]=imin) then
inc(result);
end;
end;
function
lg_test(level,num:integer;var k:array of
integer):integer;
var
i,v0,v1,j:integer;
begin
j:=1;
v0:=0;
for
i:=1 to num-(4-level) do
begin
k[level]:=i;
if level<4 then
lg_test(level+1,num-i,k);
v1:=lg_value(level,k);
if v0<v1 then
begin
v0:=v1;
j:=i;
end;
end;
k[level]:=j;
end;
procedure
TForm1.Button1Click(Sender:
TObject);
var
i,j,level:integer;
s:string;
k,v:array
[0..4] of integer;
begin
level:=0;
for i:=0 to 4
do v[i]:=0;
for i:=1 to 100-(4-level) do
begin
k[level]:=i;
lg_test(level+1,100-i,k);
for j:=0 to 4 do
begin
if
lg_value(j,k)>0 then
begin
inc(v[j]);
end;
end;
end;
for
i:=0 to 4 do
begin
s:=s+'
'+inttostr(v[i]);
end;
memo1.Lines.Add(s);
end;
|
17956我要的书
递归论
1 Anil Nerode, Richard A. Shore合著的《Logic for
applications》,Springer出版社
1997出版
2 Nigel Cutland在
1980年写的《Computability:
an introduction to recursive function theory》,Cambridge University
Press
3 Robert I. Soare
1987年写的《Recursively enumerable sets and degrees
:a study of computable functions and computably generated
sets》,Springer出版社
1987出版
4 Piergiorgio Ddifreddi写的《Classical recursion
theory :the theory of functions and sets of natural numbers》(North-Holland
1989年)
5 Rogers, H.写的《Theory of recursive functions and effective
computability》
模型论
6 C.C.Chang和H.J.Keisler合著的《Model
theory》,North-Holland
1973年出版
7 David Marker在2002年刚出版的《Model theory :an
introduction》
该书是Springer出版社的GTM丛书中的一本
集合论
8 Kenneth
Kunen的《Set theory :an introduction to independence
proofs》,这本书是North-Holland出版社在
1980年出版的书
9 Thomas Jech的《Set
theory》(Springer,
1997出版)
10 On Formally Undecidable
Propositions of Principia Mathematica and Related Systems (Basic Books,
1962)
我的Email:chenshi23@tom.com
手机:013509932656
17956第3个是博弈问题,但我认为:5个人抓豆的数目必收敛于一条水平直线,结果5人全死
17956如果5个人全死的话,就不会有这个题目了:)
17956
| 引用 (kk2 @ 2006年03月12日
00时33分) |
|
如果5个人全死的话,就不会有这个题目了:) |
会的,
如果第一个人抓N(N<=20)棵,第2到5个人也都会抓N的,原因很简单,只要有一个人抓M棵,后边的人只要抓一个介于M和N之间的数就得救了,而抓M的人仍必死,跟据先自保再多杀人的原则,他不会这样做,所以,所有人都是N,也就是
17956
我的算法错了,推理如下:
如果第1个人A抓<=20,则后面4人必然会和他抓的相同,或比他少抓1,这样大家都得死;
如果A抓>20且<=49,则B必然会抓A-1,则C、D、E中必然有人少于A-1个,B必然生,A必然成为最多的人,必死;
如果A抓>=49且<96,则B会抓100-A-3个,则C、D、E必然每人只能抓1个,B必然生,A必然成为最多的人,必死;
如果A抓96个,则B、C、D、E每人只有1个,大家都得死。
所以正常而论,在A没有被B贿赂的情况下:),zhaoming应该是对的,是全死
17957好像判断一个不定积分是不是初等的有刘维尔定理
大家能告诉我记载这个定理的书籍吗?
17958题目叙述不清
17958已知
Ψ
(χ) 满足
Ψ
(0) =0,
Ψ
`
(0) =0,且
∫ τ
Ψ (χ)
ydx+[sinx-
Ψ `
(x) ]dy的积分与路径无关,求
Ψ (χ)
?
17958我也记不清了,那天把大部分精力发在做题上,可能题目记错了,但好象觉得是这样的呀,没错呀,请问不清楚在哪一个细节呢?
17958对函数有什么要求吗?
17958算了,这题大家就不要做了呀
17958编辑的都看不清楚哦!
17959武汉大学数学系博导联系方式post-60-1126337500.ibf
17959谢谢了!正需要呢
17963标 题: 阿米尔·伯努利: 把时态逻辑引入计算机科学 zz
发信站: 小百合BBS (Thu Apr 28 07:02:36
2005)
发信人: ccapp (ccapp), 信区: CompLang
标 题: 阿米尔·伯努利 ——
把时态逻辑引入计算机科学
发信站: 南京大学小百合站 (Sun Dec
19 20:09:55 2004)
阿米尔·伯努利
——把时态逻辑引入计算机科学
1996年度的图灵奖授予了一位以色列学者,著名的以色列魏茨曼学院(Weizmann Inst
itute Of
Science,位于圣城耶路撒冷西北约50 km的雷霍沃特)应用数学系教授阿米尔·
伯努利(Amir
Pnueli),以彰显他把时态逻辑引入计算机科学所做的贡献。
伯努利于
1967年在魏茨曼学院获应用数学博士学位,后留校任教。他的主要研究方向
是时态逻辑或叫时序逻辑(temporal
logic)。时态逻辑是非经典逻辑中的一种,它研究如
何处理含有时间信息(现在、过去、将来;之前、之后等)的事件的命题和谓词。时态逻辑
体系包含的要素有:
1.基本符号:事件e,关系或谓词r,时间区间i(interval)等。
2.时态谓词:after(e,r),before(e,r)等。
3.时态事件演算规则:初始规则、终止规则等,如holds(before(e,r)):—termin
ates(e,r)表终止规则,意为若事件已使谓词r失效,则在e之前且r成立的一段区间中r为
真。
4.时态逻辑运算:时态区间的并、交,时态谓词的与、或、非等。
1977年,伯努利把时态逻辑引入计算机科学,把它作为开发反应式系统(reactive sy
stem)和并发式系统(concurrent
system)时进行规格说明(specification)和验证(verifi
cation)的工具,取得了极大的成功,在软件工程界引起轰动,被认为是软件工程中的一场
革命。伯努利也因此而声名大振,他曾被美国斯坦福大学、哈佛大学等著名高等学府聘为
客座教授或进行讲学。
伯努利和他的同事曼纳(Z.Manna)共同开发的时态逻辑系统叫“命题线性时态逻辑系统”
(Proposition
Linear Temporal
1ogic,缩写PLTL)。PLTL包含可数无穷多个命题变元,逻
辑联结词“否定”┐,“合取”∧,“析取”∨,“蕴含”
,“等价”≡;时态算子□
,意为“任一时刻”;◇,意为“某一时刻”;○,意为“下一时刻”;μ,意为“直到
”。合式公式(well-formed
formula)在PLTL中的定义如下:
(1)命题变元P是合式公式;
(2)若w、w1和w2是合式公式,则┐w、w1∧w2、w1∨w2、w1
w2、w1≡w2都是合式公式;
□W、◇W、○W和w1μw2也都是合式公式;
(3)每个合式公式均可通过有限次应用(1)、(2)获得。
PLTL中包含10条公理和3条推理规则,它们是:
公理1:┐◇w≡□┐w
公理2:□(w1->w2)
-> (□w1->□w2)
公理3:□w ->
w
公理4:○┐w≡┐○w
公理5:○(w1->w2) ->
(○w1->○w2)
公理6:□w -> ○w
公理7:□w ->
○□w
公理8:□(w->○w) -> (w->□w)
公理9:(w1μw2) ≡
(w2∨(w1∧○(w1μw2)))
公理10:(w1μw2) ->
◇w2
推理规则1(重言规则):若u是命题重言式(tautology),则├u
推理规则2(假言推理规则):若├u
v且├u
,则├v
推理规则3(口引入规则):若├u,则├□u
应用上述公理和推理规则,经过有穷步骤,可推导出一系列合式公式,即PLTL的定理。
显然,PLTL是对普通命题逻辑(propositional
lohic)的扩充,但这一扩充却意义重大,
因为这使系统具有了处理随时间变化而改变其值的动态变元(称为时序或时态变元)的能力
。在时态逻辑中,时间的结构可以有线性、分支、离散、连续,基于时间点或时区的这样
几种不同情况,可视具体应用背景而定。PLTL采用线性、离散,且与自然数同构的时间结
构。它的语义解释是一个无穷状态序列σ=S0,S1,S2,…,每个Si都是对命题变元的一个赋
值。若令σ(i)=Si,si+1,si+2…,且用σ|=w表示时态公式w在解释σ下为真,则各时态
算子的含义如下:
σ|=□w当且仅当对任意i≥0,均有σ(i)|=w
σ|=◇w
当且仅当存在i≥0,使σ(i)|=w
σ|=○w当且仅当σ(i)|=w
σ|=w1μw2当且仅当存在i≥0,使σ(i)|=w2且对任意j(0)≤j<(i)均有σ(j)|=w1
由于程序的行为是一种动态现象,其状态是随着时间的推移而不断改变的,而这种改
变又可能反过来影响其外部环境。并发反应式程序的这种持续的动态行为无法用经典逻辑
描述,由著名的逻辑学家霍恩(A.Hom)于
1951年提出,因而用他的名字命名的至多包含一
个正文字的Hom子句所组成的霍恩逻辑也不能描述。而伯努利的PLTL则凭着它的极强的表达
能力,填补了这一空白,成为研究并发程序尤其是持续不终止的反应式程序(如操作系统,
网络通信协议等)的强有力的形式化工具,可充分表达程序的安全性、活性和事件的优先性
等,成为程序规约(specification)、验证(verification)等的有力工具。
值得指出的是,我国科学家在伯努利工作的基础上,将时态逻辑用于计算机科学的研
究大大地向前发展了一步。伯努利只把时态逻辑用于程序规约和验证,而我国科学家唐稚
松(中科院院士,软件所研究员)在20世纪70年代末、80年代初把时态逻辑用于软件开发的
整个过程,包括需求定义、规约、设计、证实、验证、代码生成和集成,并开发了世界上
第一个可执行时态逻辑语言XYZ/E和一组相应的CASE工具,在国际上引起强烈反响。
1979
年,时任美国加州大学伯克利分校计算机科学系主任的布卢姆(M.Blum,计算复杂性理论
奠基人之一,
1995年图灵奖获得者)曾致信唐稚松本人,称:“在美国,很有一些最重要的
计算机科学家知道您及您的工作,他们都对您的研究工作作了高度评价”。伯努利本人也
同唐稚松建立了联系,并成为朋友。
1995年8月,为庆祝唐稚松70寿辰,举办了一个名为“
逻辑和软件工程”的国际专题讨论会,伯努利和他的老搭挡曼纳带了一篇新的论文“有时
钟的变迁系统”(Clocked
Transition System)来北京参加了这个讨论会,并亲自编辑出版
了会议论文集(Logic and Software
Engineering:International Workshop in Honour
Of Chih-Sung
Tang,Singapore:World Scientific
Pr.,
1996)。在论文集的前言中,伯
努利高度评价了唐稚松的工作。
伯努利主要从事教学和研究,但也和国外绝大多数教授一样,不限于“纯学术”工作。他
和别人一起在美国马萨诸塞州的布灵顿(Burlington)办了一个公司:i—Logix
Inc,他任
该公司首席科学家。
伯努利的著作反映了他的研究成果,主要有:
《反应式系统和并发系统的时态逻辑:规约》(The Temporal Verification of Reac
tive and
Concurrent Systems:Specification,Springer,
1992)
《反应式系统的时态验证:安全》(Temporal Verification of Reactive
Systems:
Safety,Springer,
1995)
伯努利现任施普林格出版社(Springer
Verlag)著名的系列丛书kecture Notesin Com
puter Science的编委,也是有关领域的不少杂志如Acta
lnformatica、Science Of Comp
uter Programming、Notes On Computer
Science的编委。
伯努利的电子邮箱为: amir@wisdom.weizmann.aC.i1
17963以色列在计算机方面比较强
17963不知道楼主在线性时态逻辑方面搞的怎么样
想找点有关这方面的中文资料可以么
谢谢
xinyonda@163.com
17964发信人: yogaII (过期龙井), 信区: CompSci
标 题: 天文学,计算机科学和汽车工程
发信站: 小百合BBS
(Tue May 24 07:36:44 2005)
简短而言:
1。
天文学和望远镜的关系:
望远镜是研究天文学的工具。 没有望远镜, 很多天文发现都
是不可能;
CS和computer的关系: computer也是CS的工具,
给足够多的时间, 任何计算机能
解决的问题, 纸和笔都能解决。 没有计算机,
很多CS领域也不可能。
2。
汽车工程是研究造汽车的, 谁说汽车工程没有科学? 只不过有另外的学科而已,
力学
热学之类的东西;
计算机工程是研究如何让计算机成为更好的工具而已, 同样也需要计算机科学作为一门
科学来进行指导,
计算机科学也许可能可以作为数学的一个分支, 同样很多做CS的人
做的偏工程,所以有时也有computer
engineer这个系。
不过在老D讲这句话的时候他当然是从pure CS来讲的。
17964顶一下!
17965引言:
形式化方法可以分为形式化描述和建立在形式化描述基础之上的形式化开发。形式化的描述就是用形式化的语言(具有严格的语法语义定义的语言)做描述。形式化的软件开发,就是用形式化的语言来描述软件需求和特征,并且通过推理验证来保证最终的软件产品是否满足这些需求和具备这些特征。这样的验证当然得建立在严格的语法语义的基础之上的。在实际应用中,这是不容易做到的。形式化方法研究的目的就是希望能够提供更好的理论、方法和工具,扩大形式化方法的应用范围和使用价值。
形式化方法的意义在于它能帮助发现其它方法不容易发现的系统描述的不一致,不明确或不完整,有助于增加软件开发人员对系统的理解,因此形式化方法是提高软件系统,特别是safety-critical系统的安全性与可靠性的重要手段.最早的形式化方法是逻辑与逻辑推理,它的目标是使推理机械化.从广义上讲,这一目标受到许多挫折.比如说逻辑系统的不完备性(incompleteness)、逻辑系统的不可判定性(undecidability)、自动推理的难处理性(intractability).但是在一些实际应用上,逻辑方法和自动推理还是起着非常大的作用.
早期形式化方法在软件验证的应用是串行程序的验证,后来随着软件研究和应用的发展,逐渐多样化.比如用逻辑和代数方法描述软件,用逻辑推理来验证软件(即描述软件的这些逻辑公式)的性质.又比如用进程代数描述并发软件,用模型检测方法验证这些软件的性质.近年来,由于认识到形式化方法重视的是严谨性,而这些方法与常用的软件方法差别很大,逐渐有许多结合图形化软件方法、面向对象方法和形式化方法的工作.以上所述几个方面(即程序验证,定理证明,模型检测,图形化方法和形式化方法相结合)的内容虽然不尽一样,但密切相关.定理证明与模型检测互为补充,各有所长.对于复杂的软件系统的验证,最好是能够结合多种方法的使用.这些方法对高可信软件开发方法的探索和应用都极为重要。
形式化方法与软件可靠性:
随着软件的广泛应用,特别是软件在尖端领域的应用,软件可靠性成为一个非常重要的问题。软件的可靠取决于两个方面,一个是软件产品的测试与验证,另一个是软件开发的方法与过程。对简单的软件开发,我们的经验是先有对软件的要求,然后对软件进行设计,然后是编写程序,最后是对程序进行测试,如果测试出错则对软件进行修改,然后再测试,直至对程序满意为止。对复杂的软件系统,总的过程基本还是这样,只是各个阶段也相应复杂一些。比如说,软件的要求可能需要从多方面进行描述,软件的设计需要从多方面考虑,程序的编写需要分成多个单元,对于测试来讲也就有单元测试和总体测试的分别。有些软件的要求难以一开始就完全清楚,而更改软件要求会对软件设计以及其他大量已经完成或正在进行的工作产生很大的影响,因此有些软件开发方法和过程就需要提供反复修改软件要求的便利。
形式化方法在软件开发中能够起到的作用是多方面的。首先是对软件要求的描述。软件要求的描述是软件开发的基础。比如说一般非形式化的描述很可能导致描述的不明确和不一致。如果描述的不明确和不一致导致设计,编程的错误,将来的修改所要付出的代价就非常大了。如果导致的错误没有被发现,则影响程序的可靠和使用。形式化方法则要求描述的明确性,而描述的不一致性也就相对易于发现。其次是对软件设计的描述。软件设计的描述和软件要求的描述一样重要。形式化方法的优点对于软件要求的描述同样适用于软件设计的描述。另外由于有了软件要求的形式化描述,我们可以检验软件的设计是否满足软件的要求。对于编程来讲,我们可以考虑自动代码生成。对于一些简单的系统,形式化的描述有可能直接转换成可执行程序,这就简化了软件开发过程,节约了资源和减少了出错的可能性。另外,形式化方法可以用于程序的验证,以保证程序的正确性。对于测试来讲,形式化方法可用于测试用例的自动生成,这可以节约许多时间和在一定程度上保证测试用例的覆盖率。
形式化方法原则上就是用数学与逻辑的方法描述和验证软件。从描述上讲,一方面是系统或程序的描述,另一方面是性质的描述。这些可以用一种或多种语言来描述。这些语言包括命题逻辑,一阶逻辑,高阶逻辑,代数,状态机,并发状态机,自动机,计算树逻辑,线性时序逻辑,进程代数,
π-演算, μ-演算,特殊的程序语言,以及程序语言的子集等。从验证来讲,主要有两类方法,一类是以逻辑推理为基础,另一类则以穷尽搜索为基础。逻辑推理有
natural deduction, sequent calculus, resolution 以及Hoare-logic
等方法。穷尽搜索方法统称为模型检测。这类方法与系统或程序以及系统性质的表示有很大的关系,比如说符号模型检测,其基本原理是用命题逻辑公式表示状态转换关系,用不动点算法计算状态的可达性以及这些状态是否满足某些性质。
形式化方法的应用在电路设计和协议设计上都取得了很大的成绩。但是对于软件来讲还有很多没有解决的问题。软件的描述要比电路和协议复杂。一个软件描述所包含的状态空间通常来讲可以是无限的。因此验证的难度很大。逻辑推理的不足之处在于推理的难度。对于稍微复杂的系统,自动化的推理就难以胜任。人为的推理有很大的缺点,除了费时费力外,比如说一个定理推不出来,并不能说明这个定理不成立,很可能是推理方法和策略应用不当。模型检测的好处在于它有全自动化的检测过程,并且如果一个性质不满足,它能给出这个性质不满足的理由。我们即可据此对我们的系统描述进行改进。模型检测的困难首先是它所能检测的是有限状态模型。这样对于一般软件来讲,需要有一个从任意状态到有限状态的建模过程。并且这样的一个模型的状态空间会面临组合爆炸的问题。
研究内容:
形式化语言:怎样描述软件系统及其行为模式。
更好地刻画软件系统的性质,比如说,通讯、分布、开放、移动。
各种语言的应用、比较。语言与语言之间的转换。
开发相应的软件工具。
形式化验证:怎样验证软件系统符合给定的行为模式。
更有效地验证软件系统的性质,比如说,自动化、速度快、内存需求少。
各种方法的应用、比较。
开发相应的软件工具。
形式化方法的出发点是数学逻辑方法。其目的是开发可靠的软件产品。从软件开发来讲,形式化方法目前并非软件开发的主流。从软件发展看,早期的软件是用于数值计算,程序语言侧重于函数和算法的描述。后来数据库的应用和数据结构逐渐变得重要。现在的软件更为复杂,因此,对象、组件、接口、通讯、开放等成为非常重要的概念。从软件工程方法来讲,有一套描述这些概念的办法,比如说用图形、表格、逻辑、自然语言等,交叉使用以描述一个系统的各个方面。因此换一个角度来考虑,我们也可以以目前常用的软件开发方法为出发点,研究怎样将这些方法形式化,使软件系统的描述精确化,以减少可能的误解所带来的问题;或以目前常用的软件开发过程为出发点,研究怎样在软件开发过程中增加一些形式化方法的应用,以提高软件的可靠性。
http://lcs.ios.ac.cn/~zwh/projects/xshff.html
17965支持一下!
17965ding ~~~
期待下文[COLOR=purple][FONT=Arial]
17965不知道国内目前此方面的研究情况怎么样,做的人多吗?
17966[本篇全文] [回复本文] [本篇作者: Einstein] [本篇人气: 56]
发信人: Einstein (A.M.C. -
Abel's Majia-Cluster), 信区: Theoretical_CS
标 题: [合集]量子计算动摇了丘奇-图灵论点吗?
zz
发信站: 小百合BBS (Fri Apr 29 05:16:41
2005)
--------------------------------------------------------------------------------
发信人:
minde (明德), 信区: Theoretical_CS
标 题: [转载]
量子计算动摇了丘奇-图灵论点吗——兼纪念图灵逝世50
发信站: 南京大学小百合站 (Mon Dec 6 09:50:26
2004)
【 以下文字转载自 LectureHall 讨论区 】
【 原文由 minde 所发表
】
量子计算动摇了丘奇-图灵论点吗——兼纪念图灵逝世50周年
郝宁湘 郭贵春
1930年代初提出的丘奇-图灵论点,是判定什么是计算、什么问题是可计算的、什么问
题是不可计算的这一切问题的最根本原则或标准。电子计算机诞生后,丘奇-图灵论点还成
了刻画电子计算机计算能力的最基本的理论依据。70年过去了,尽管新型的计算范例不断
涌现,如神经网络计算、遗传计算、进化计算、DNA计算等,但它们除了在计算复杂性方面
(计算效率)较优,并没有从根本上动摇丘奇-图灵论点。
1990年代以来,一种全新的更具挑战性的计算范例——量子计算机出现了。它是不是超
越了丘奇-图灵论点的界限呢?是不是可以计算丘奇-图灵论点认为不可能计算的问题呢?对
此人们产生了不同的看法,一种看法认为量子计算并没有超越丘奇-图灵论点的界限,只不
过量子计算有着电子计算机不可比拟的计算效率;另一种看法认为量子计算超越了丘奇-图
灵论点的界限,量子计算机能够计算电子计算机或图灵机所不能计算的一些问题。
笔者认为,理解量子计算机的本质需要一个过程,因为这里面有些关键的问题不是靠哲
学思辨能够解决的,而需要严格的数理逻辑证明。另外,在理解量子计算机本质的过程中
,必然涉及到量子力学本身以及它与经典力学关系的一些问题,而对这些问题的认识,至
今都有众多分歧。馕抟稍黾恿死斫馍系睦?选?
计 算 的 实 质
为了回答本文的基本问题,首先要对计算的本质有个明确界定,以及对近些年不断涌现
的新的计算范例在计算理论上的意义有个正确的评价。
丘奇-图灵论点,即凡是可计算的函数都是一般递归函数(或是图灵机可计算函数等),
这一论点标志着人类对可计算函数与计算本质的认识达到了空前的高度,它的提出确立了
计算与可计算性的数学含义,是数学史上一块夺目的里程碑。正如莫绍揆教授所言,有了
这个论点后,就可以断定某些问题是不能能行地解决或不能能行地判定的。对于计算机科
学,丘奇-图灵论点的意义在于它明确刻画了计算机的本质或计算能力,确定了计算机只能
计算一般递归函数,对于一般递归函数之外的函数,计算机是无法计算的。许多新型计算
,除了计算效率较优外,并没有从根本上动摇丘奇-图灵论点。
那么应该怎样理解或评价这些不断涌现的新的计算范例在计算理论上的意义呢?对此,
笔者已在《理解计算》(见:科学,2004,55(4):33)中有过论述,基本思想是:这些新
的计算范例的不断涌现是计算方式不断进化的表现。计算方式是一种历史的结果,而非计
算本性的逻辑必然。也就是说,计算之所以为计算,在理论层面上只在于它具有一种根本
的递归性,或在于它是一种可一步一步进行的符号串(信息)变换操作。至于这种符号变换
的操作方式如何,以及符号的载体或其外在表现形式如何,都不是本质性的东西,它们无
不是一种历史的结果,无不处于一种不断进化的过程之中。新型计算机的不断涌现只是计
算方式不断进化及其多样性的表现(至少在目前如此)。其次,计算方式的历史性、多样
性反观了计算本性的逻辑必然性、统一性。由丘奇-图灵论点所揭示的计算本质,不仅包括
数值计算、定理推导等不同形式的计算,还包括了DNA计算机、量子计算机等新型计算机的
计算。这说明不同形式的计算、不同“计算器”的计算,在计算本质上是一致的,这就是
递归计算或图灵计算。
笔者认为,丘奇-图灵论点对计算本质的抽象,有着极其高度的普适性。这种高度的普
适性根源于可计算理论本身是一门高度抽象的形式化的数学理论。大家不要忘了,以丘奇
-图灵论点为基石的可计算性理论是在电子计算机诞生之前的
1930年代提出的,即它不是在
对任何具体的计算机进行总结与抽象的基础上提出的,而是从纯粹的数理逻辑的角度提出
的。笔者相信,让众多科学家惊叹的“数学在自然科学中那不可思议的有效性”在计算机
科学中也会有同样的体现。
最后还要强调这样一种认识:计算的实质只是一个理论层面上的问题,即与现实没有直
接关系的一个形式化的数学问题,它超越于任何现实的具体计算,是对各种具体计算高度
的数学抽象。相反,计算方式则是一个现实层面上的具体问题,它与任何具体的计算设备
直接相关,是一种历史的结果,并且随着历史的发展而不断进化。从现实层面上讲,计算
包括两方面的内容:信息的表征和信息的加工。而从理论层面上讲,计算就是一个方面的
内容——符号或信号的变换。笔者认为,这两个不同层面上的问题不能混为一谈。而事实
上,在人们谈论量子计算是否动摇了丘奇-图灵论点时,是有着混淆两类不同层面问题之嫌
的。
量子计算的特点
下面来分析一下量子计算的实质与特点。简单地讲,量子计算机就是实现量子计算的机
器。量子计算机是以量子态作为信息的载体,其信息单元是量子比特,它是两个正交量子
态的任意叠加态,实现了信息的量子化。直观地讲,一个简单的量子比特是一个双态系统
,如半自旋或两能级原子:自旋向上代表0,自旋向下代表1;或基态代表0,激发态代表l
。与经典比特不同,量子比特不但可以处在0或l的两个状态之一,而且一般地可以同时处
于两个态的叠加态,即
|?渍>=c0|0>+c1|1>,|c0|2+|c1|2=1。经典比特可以看成量
子比特的特例(c0=0或c1=1)。由L个量子位组成的量子寄存器能够一次存储2L个“数字”
,即量子寄存器随着位数的增加能够指数地增加存储的数据量。信息一旦量子化,量子力
学的特性便成为量子信息的物理基础,信息的演变遵从薛定谔方程,信息传输就是量子态
在量子通道中的传送,信息处理(计算)是量子态的幺正变换,信息提取便是对量子系统实
行量子测量。
那么到底什么是量子信息呢?它是一种本质上不同于经典信息的信息吗?还是仅为信息的
量子表征呢?对此笔者之一已撰文指出:量子信息实质上就是信息的量子表征,而不是本质
上不同于经典信息的另一种信息。人们所谓的量子信息与经典信息有着本质的区别,只能
是在信息表征方式意义上而言。
从现在的研究状况来看,笔者认为,量子信息就是用量子态表示信息。量子信息单元的
叠加态并不能或并没有反映出信息本质的区别。量子叠加态只是能表示多个数(即它可以同
时表示0和1),对量子叠加态的操作,也只是意味着对多个数同时多路操作运算,即所谓“
量子并行计算”。说得更具体点,对于一个L个物理比特的存储器,若它是经典存储器,则
它只能存储2
个可能的数当中的任一个,若它是量子存储器,则它可以同时存储2L个数,
而且随着L的增加,其存储量子信息的能力将指数上升。另外,量子计算机在实施一次的计
算中可以同时对2L个输入数进行数学运算。其效果相当于经典计算机要重复实施2L次操作
,或者采用2L个不同的处理器实行并行操作。由此可见,信息的量子表征只是在信息的存
储、处理(计算)以及传输方面区别于并优越于信息的经典表征。由此也进一步看到,信息
的表征方式是多种多样的,既可以是经典的,也可以是量子的。但信息的本质是不因表征
方式的变化而变化的。当然也不可否认,量子信息与经典信息相比,由于它的表征方式发
生了重大变化,因而具有了许多量子力学的特性,如量子纠缠、量子不可克隆、量子叠加
性等。
正如经典计算机建立在通用图灵机基础之上,量子计算机亦可建立在量子图灵机基础上
。量子图灵机可类比于经典计算机的概率运算。通用图灵机的操作是完全确定性的,用q代
表当前读写头的状态,s代表当前存储单元内容,d取值为L,R,N,分别代表读写头左移、
右移或不动,则在确定性算法中,当q,s给定时,下一步的状态q′,s′及读写头的运动
d完全确定。我们也可以考虑概率算法,即当q,s给定时,图灵机以一定的概率(q,
s, q′
, s′, d )变换到状态q′,s′及实行运动d。概率函数X(q, s, q′, s′, d
)为取值[0
,1]的实数,它完全决定了概率图灵机的性质。
量子图灵机非常类似于上面描述的经典概率图灵机,现在q, s,
q′, s′相应地变成了
量子态,而概率函数X(q, s, q′, s′, d)则变成了取值为复数的概率振幅函数X(q, s,
q′,
s′,
d),量子图灵机的性质由概率振幅函数确定。正因为现在的运算结果不再按概
率叠加,而是按概率振幅叠加,所以量子相干性在量子图灵机中起本质性的作用,这是实
现量子并行计算的关键。说得简单点,量子计算机能做到如此高效,得益于量子叠加效应
,即一个原子的状态可以同时是l和0,更确切地说,原子可处于0和l的概率各为l/2的叠
加态。采用L个量子位可以一次同时对2L个数进行处理,一步计算完成了电子计算机2L个数
计算。由于量子态具有叠加性,一个幺正操作同时作用在各叠加态上,从而达到并行计算
的效果。这里各叠加分量在统一的操作下以各自的路径独立演化,每一个分量上完成的变
换就相当于一台传统计算机的工作。最后,各分量之间通过不同概率将结果同时输出。因
而一台量子计算机等价于多台传统计算机的功效。也就是说,量子计算机的计算本质依然
是图灵计算或递归计算,在这一点上,量子计算机与电子计算机有着共同的计算本质。
为什么有人认为量子计算动摇了
丘奇-图灵论点
那么为什么现在有人认为量子计算动摇了丘奇-图灵论点呢?他们的理由是什么呢?或者
说他们有些什么样的具体实例呢?目前有人提到的实例主要是以下三个:(1)有人认为,
1989年在纽约IBM研究所建成的量子计算机就完成了一件图灵机所不能完成的任务——量子
密码术。(2)也有人认为,量子计算机中实现的随机数是真正的随机数,是传统计算机无
法实现的,传统计算机实际上产生的是伪随机数。(3)超距传送的量子计算实现是另一个
实例。至于为什么这三个实例就表明量子计算动摇了丘奇-图灵论点,则均没有一个合理的
说明,更谈不上严格地证明它们是一种非递归问题。因此,如今认为量子计算动摇了丘奇
-图灵论点的人,无不是一种想当然的观点,其原因主要是把现实问题与理论问题混淆了,
把量子力学本身的特点强加给了理论计算。
在回答“量子计算是否动摇了丘奇-图灵论点”这个问题时,一定要明确它只是一个理
论层面上的问题,而不是现实层面上的问题。在现实层面上,由于计算复杂性的原因,量
子计算机确实可以计算一些由传统的电子计算机所不能计算的问题。笔者认为,在理论层
面上,量子计算能否动摇丘奇-图灵论点,关键在于能否证明它可以计算非递归函数。能,
则表明量子计算超越了丘奇-图灵论点的界限;不能,则表明量子计算依然受丘奇-图灵论
点的制约。因此,任何声称量子计算超越了丘奇-图灵论点界限的人,都必须严格证明量子
计算机解决了一个非递归性的问题,否则这种声称就是无意义的或值得怀疑的。自丘奇-图
灵论点提出后,人们不是已确证了许多不可计算的问题吗?如一阶逻辑的判定问题、丢番图
方程的整数解问题、群论上的字问题、四维流形的同胚问题等。如果哪一天量子计算机能
够解决这么一个非递归问题,那么人们一定会接受量子计算动摇了丘奇-图灵论点的观点。
可是目前还没有。
下面分别讨论一下那三个实例的实际意义。量子密码术是密码术与量子力学结合的产物
,它利用了系统所具有的量子性质。首先想到将量子物理用于密码术的是美国科学家威斯
纳(S.Wiesner)。他于
1970年提出,可利用单量子态制造不可伪造的“电子钞票”。量子
密码术并不用于传输密文,而是用于建立、传输密码本。根据量子力学的不确定性原理以
及量子不可克隆定理,任何窃听者的存在都会被发现,从而保证密码本或加密信息的绝对
安全。也就是说,量子密码并不是一种加密算法,它只是通过公开信道,借助量子力学原
理来建立只有A、B双方才知道的随机数序列的一种手段(如果有人窃听,A、B可以通过某些
手段知道)。这里完全不是一个算法的问题,根本谈不上对丘奇-图灵论点的动摇,而只是
实现了经典技术不能实现而由量子技术实现的一种通信手段。
有人认为量子计算机中实现的随机数是真正的随机数,是传统计算机无法实现的,传统
计算机实际上产生的是伪随机数。笔者认为,即便这一说法是正确的,它也没有构成对丘
奇-图灵论点的动摇,因为传统计算机无法实现的并不等于图灵机不能实现。前者是一个现
实层次上可否实现的问题,后者是一个理论层次上能否实现的问题。传统计算机(电子计算
机)实际上产生的是伪随机数,并不等于图灵机在理论意义上不能产生真正的随机数——如
果产生真正的随机数是一个递归问题。另外,如何理解量子计算机中实现的随机数,其实
也是一个问题,因为对量子力学的不确定性或随机性的认识至今还是有争议的。
超距传送的量子计算被看作是动摇丘奇-图灵论点的另一个案例。笔者认为这也是一个
误会,超距传送的量子计算并不是一种新的算法,而是实现量子通信的一种新的量子技术
——利用量子纠缠加速经典信息的传送,它实际上就是量子态的超距传送,即实现量子态
从一个粒子到另一个粒子的转换。按照贝内特(C.Bennett)提出的方案,其基本思想是:
为实现传送某个物体的未知量子态,可将原物的信息分成经典信息和量子信息两个部分,
它们分别经由经典信道和量子信道传送给接收者,经典信息是发送者对原物进行某种测量
而获得的,量子信息是发送者在测量中未提取的其余信息。接受者在获得这两种信息之后
,就可以制造出原物的完美的复制品,在这个过程中,原物并未被传送给接受者,它始终
留在发送者处,被传送的仅仅是原物的量子态,发送者甚至可以对这个量子态一无所知,
而接受者是将别的物质单元(如粒子)变换为处于与原物完全相同的量子态,原物的量子态
在发送者进行测量及提取经典信息时已遭破坏,因此,这是一种量子态的隐形传送。最终
恢复原物量子态的粒子也可以不必与原物同类,只要它们满足相同的量子代数即可,由于
经典信息对量子态的隐形传送是必不可少的(否则将违背量子不可克隆定理),而经典信息
传递速度不可能快于光速,因此,量子隐形传送也不会违背相对论的光速最大原理。
由上论述可见,我们尚不能断言量子计算动摇了丘奇-图灵论点。其实在笔者与一些从
事量子信息、量子计算研究的人士的通信中了解到,他们大都认为:“大量的问题需要讨
论,有些问题过早下结论可能不是太妥。”
有的人直接指出:量子计算机不可以解决图灵
机原则上所不能解决的问题。量子计算可以针对某些特殊的难解问题来加速计算。经典图
灵机理论上也可做这类问题,只是从计算资源(解决问题所用的时间和空间资源)上来讲,
要随问题的难度指数上升。对于图灵机所不能解决的问题,量子计算机同样不能,它只能
解决“可计算的函数”问题。至于有人说量子计算机可以解决经典图灵机不能解决的问题
,应该正是指那些用目前的经典算法来算会随问题难度增加而呈现指数加速的问题。
最后应提到的是,
1990年以后,有研究者开始另辟蹊径,不局限于传统的逻辑手段,而
开始尝试“以自然为基础”的探索工作,研究方法除了借助计算机外,还引进了量子物理
和生物学的“自然机制”,试图将“计算”的概念从经典的图灵可计算概念进一步拓展,
倡导一种“自然机制+算法”的研究模式,采取一种新的方法论策略:将能够归约到算法层
面的问题,采用算法来实现,不能归约到算法层面的问题,采用某种自然机制实现。大家
知道,计算或算法是有严格的数学含义的,它是以递归函数、丘奇-图灵论点为基础的。但
笔者不知道这里所说的“自然机制”是一个什么概念,它具有什么样的数学含义?如果它
没有严格的数学含义,或只是一个思辨性的哲学概念,那么它就不是一个与计算相关联的
科学概念。如果是这样,那么又如何能运用它“将计算的概念从经典的图灵可计算概念进
一步拓展”?至少目前世人还没有看到超越丘奇-图灵论点的一种新的“计算”。
17966该文很有见解,支持!
17966量子计算动摇的是现代版或叫做复杂性版的丘奇-图灵论题。
而对于量子可计算问题,Deutsch在他的量子图灵机中已经证明与图灵机的能力相同。
17966顶!
17966想想也是,丘奇-图灵论题是说什么的?图灵的计算理论是说什么的?
可以说是对计算机的理论上的计算能力(计算极限)的刻划,也有人说是对"计算"这种现象的本质的一种认识.
怎么说"计算"也处在数学层面,量子则在物理层面,抽象级别都不一样.
物理定律能颠覆数学定理吗?这个可能吗?
问题太大,个人想法,不一定对
17966此文毫无见识,呵呵(模仿上面一位兄弟的说法)
如果只是字面上理解‘量子计算动摇了丘奇-图灵论题’这句话,那么结论当然是不可能。正如我们都知道爱因斯坦的广义相对论表明,现实世界并不是严格的欧几里德几何空间;但在欧几里德几何公理的体系之内,它仍然是绝对正确的。这是数学的特点,在一定前提下,他的结论是逻辑的结果,是绝对的。但是知道在‘欧几里德几何’之外,还有不同的几何存在,难道不是伟大的发现吗?
我觉得在‘量子计算和丘奇-图灵论题’这个问题上,完全可以类比。现在我们都知道在自然数集上,丘奇-图灵论题是一个绝对的结论。那么是否在更一般的集合上也有类似的结论?有没有和一般递归函数相似的一类函数?更一般地,所谓量子系统在数学上能不能有一个形式化的描述。。。
我觉得在这些问题上,最好的回答仍然是:“还需要等待”。
17966

17966好文章
但是观点太机械了
问题的本质好像不在于计算
而是在于信息
信息的本质是当然不因表征方式的变化而变化的,
但是问题是:并不是所有的信息都有经典的表征,除了经典的信息,还有量子信息,量子信息和经典信息是否有完全相同的属性?
显然不是。
存在着没有经典表征的量子信息,量子系统的所能表征的信息当然可能超过任何经典系统的能力。
图灵的计算说的是对经典信息的处理。量子计算就是对量子信息的处理,
有些本质上是量子的信息和对他们的处理是无法用图灵的理论去描述和刻画的。
若不考虑信息的属性,从信息的处理这个角度,对量子信息的处理和经典信息的处理在数学结构上可能是一样的。
图灵考虑的是数论函数
量子计算考虑的除了数论函数之外,还有连续函数,可微函数,等等
图灵考虑的只有加减乘除
量子计算考虑的除了加减乘除,还有微积分,富立叶变换等等
所以:量子计算必然超越但不是证伪了丘奇-图灵论点!
17966现在看来,计算不应该仅仅理解为递归性,
能够机械操作的计算(具有固定的收敛的算法的处理过程)可以归结为递归性,
递归性的本质在于每一步的“细节”都是清楚的,
但是量子计算(量子递归)更像一个黑箱子。
17966利用"自然机制”进行计算其实不难理解。如形式主义观点所说,数学不过是符号间的操作和研究运算与关系的科学,人所能理解、施行的操作都是有限离散的(图灵型的),比如给计算机输入只能是有限串。但自然界却有许多“连续”操作。比如,人(计算机)无法计录一个连续变化函数的每一点,因为有实无穷个信息,但大自然却“可以”,例如最简单的例子就是,调变阻器记录一个电流表和电压表间示数的关系,可以直用摄象机录制。这例子有些牵强,但道理已经说出来了,大自然计算机可以处理实无穷信息。还可以想象一个更牵强的例子:宇宙中存在一个怪异的机器,输入一个数后立即就能将它分解因子,虽然这一过程的存在不能超越丘-图框架但也还是有意义的,因为它改变了计算的速度,许多原本因需要分解大数的程序现在可以用了,可以多项式归约到该类程序的程序也可用了。(我举不出自然些的例子,我也不是专门研究这方面的,而且我对大自然现象了解也不多)
至于作者的问题,自然计算没有数学上的定义,因为可以进行哪些计算完全取决于大自然,及我们对大自然的了解。最困难的步骤自然是如和把大自然的天然过程以人们所想的方式利用,这就是那些人研究的目标,这相当于计算理论上的归约,想想Np完全问题,只要编好解决其中一个问题的程序其它程皆可归入其中。至于最让人关心的问题,大自然计算机,对离散模型的计算是否超越图灵框架,好像至今还没有发现有这样的过程。
利用自然机制计算也可理解为计算理论中的“谕示”。数学上也可以举出“谕示”的其它例子。比如解微分方程时,人们允许作变数变换、求反函数、求函数方程组的解等一系列操作,用它们来得到解。但没有什么说明这些操作比“解出某个方程”这个操作理论上更特殊,虽然它们在数值计算上可能更方便一些。也就是说人们研究的不过是解方程这一操作和其它那些操作间的关系。但以上这些操作都是“不可计算的”。更广泛地说,在某个问题中,一些操作由于某些因素而被允许,而另一些则不被允许。但这一规定往往是人为的,被允许的操作也常常是不可计算的,而被允许的操作只是相对被允许的操作可计算。一般的图灵机可以看作是被允许的操作必须是“可查表的”(这也完全是人为规定,至于这么规定的原因,众所周知)。
17967充要性是否成立,
还有类似的结论能否推广到广义积分?
17967呵呵,弄错了
应该是
绝对收敛级数加条件收敛级数还是条件收敛级数
17968通项收敛于零的级数的收敛 当且仅当
存在一个N,,对级数加括号使得每一括号里的项不多于N,则加括号的级数收敛?
另外,是否有:
若存在一列的Ni,
对每一个Ni,对级数加括号使得每一括号里的项不多于N,则加括号的级数收敛,
则原级数收敛?
17969每一点都不为零的向量场的积分曲线是否都是单射?
如何证明
17969呵呵。
由
向量场和积分曲线的定义,
简单性和正则性是互不蕴涵的
直观的理解,可以认为向量场就是空间中一点的运动。
比如考虑空间中一点的匀速圆周运动,显然它的运动是光滑的,但它不是简单的(单射)
17969不一定
17969如果是光滑的向量场呢?
17969豁然开悟
17969我想问2维球面上的任一光滑切向量场必有一个奇点,怎么理解
17970军事运筹学的学习好地方
http://edu.xjtudlc.cn/webkc/Xjtu/Jpkejian/.../JSLL/index.htm
17971发信人: starfish (好好学习,天天向上), 信区: Algorithm
标 题: Three Problems
in Computer Science
发信站: 南京大学小百合站 (Tue Jul 8 00:23:26
2003)
Three Problems in Computer Science
LESLIE G.
VALIANT
Harvard University
We describe three problems
that each have a history of research that
goes back to the early
days of computer science. These past efforts,
which we do not
review here,have succeeded in uncovering some the
essence of these
otherwise elusive challenges, and make it possible to
focus on
these questions more clearly now. Difficult as they may
appear to
be, they are well-posed scientific questions, we believe,
and
therefore will be solved eventually. While their solutions can
be
expected to have mathematical content, the problems as we state
them
are not purely mathematical. In each case, a part of the
solution
would be the emergence of some consensus on the nature of
the right
mathematical formulation.
1. Characterizing
the Power of Computation
The aim here is to achieve a theory of
practical resource bounded
computability that is as satisfying as
the theory of general
computability developed by Turing[
1936] and
his contemporaries. In
particular, the goal is to fully
characterize what can be computed in
practice in the physical
world.
First, we need one characterization of the class of
computations that
can be computed in the physical world in
practice. In this pursuit, we
embrace the polynomial resource
cutoff that has proved so fruitful to
date for articulating the
limits of what is currently understood. We
therefore call our class
PhP, the class of physically constructible
polynomial resource
computers. This class PhP certainly contains P,
the class of
problems computable in polynomial time by deterministic
Turing
machines, and also, we believe, the class BPP of problems that
can
be computed in polynomial time by classical randomization.
The
question of whether the quantum class BQP [Bernstein and
Vazirani
1997] is contained in PhP, we consider to be open, since
there is no
practical proposal for realizing these machines for
which scalability
has been demonstrated beyond reasonable doubt. In
principle, PhP could
be smaller than, equal to, larger than, or
incomparable with BQP.
Once we settle on a characterization of
PhP from such a physics
viewpoint, it will remain to understand the
scope of this class with
respect to its computing power, as
compared, in particular, with the
known fundamental complexity
classes such as NP, #P and PSPACE (see
Papadimitriou [
1994] for
definitions.) Numerous significant
computational problems are
complete for various of these classes, and
it is clearly important
to resolve whether these are computable
in
practice.
When all this has been done, and we have a
full characterization of
PhP, then we should have a good
understanding of which problems can be
computed in practice, and
which not. What we are doing here is, of
course, simply folding in
with the question of which basic
computational processes physics
allows, with the several central
problems of complexity theory that
have emerged since the discovery of
the NP-completeness phenomenon
three decades ago [Cook
1971; Karp
1972; Levin
1973]. However, it
is the interplay between these two
disparate modes of thinking, and
the possibility of bringing these
together to phrase a single
question, the full characterization of
PhP, that lends significance
to both. Since a positive solution to
almost any component of it
may give powerful new computational methods
for almost all domains
of computing, this single question appears at
this time to be
scientifically the most fundamental in
computer
science.
2. Characterizing a Semantics for
Cognitive Computation
The aim here is to identify a way of
looking at and manipulating
commonsense knowledge that is
consistent with and can support what we
consider to be the two most
fundamental aspects of intelligent
cognitive behavior: the ability
to learn from experience, and the
ability to reason from what has
been learned. We are therefore seeking
a semantics of knowledge
that can computationally support the basic
phenomena of intelligent
behavior.
The force of this formulation is that we place at the
fore the
question of semantics, and posit that, if we get this
right, then
algorithms and architectures for intelligent systems
will follow. The
formulation brings into focus the dilemma that
while both learning and
reasoning have been widely studied within
computer science, and are,
in some senses, well understood, they
have been formalized with
irreconcilably different semantics.
Formulations of learning appear to
require a statistical component,
as in the PAC model, while those of
reasoning, such as the standard
Tarski semantics of predicate
calculus, do not.
The
question of semantics is, of course, integral to much work
in
artificial intelligence, though often only implicitly. As far as
more
explicit proposals, the one that has been pursued the furthest
is that
of adopting the semantics of the predicate calculus
[McCarthy
1959]. There has been much discussion on whether this
approach is
inherently limited, and much commentary on where it
falls short. The
strength of formal logic can be expected to be
most visible in domains
that lend themselves to axiomatization,
where it ensures principled
deduction. In other domains, and
particularly in areas related to
commonsense knowledge, its
tendency to take a position in situations
that are uncertain or
unknown appears to be a liability. Alternative
starting points that
still offer principled deduction on the basis of
some form of
axiomatization are probability theory (e.g., Carnap
[
1950] and
Pearl [
1988]), and probabilistic logics (e.g.,
Halpern
[
1990]).
The requirements for a semantics to be
adequate for commonsense
knowledge appear to be quite subtle and
not fully realized by the
above mentioned systems. Some discussion
can be found in Valiant
[2000]. One set of requirements is that it
should support integrated
algorithms for learning and reasoning
that are computationally
tractable and have some nontrivial scope.
Another requirement is that
it has a principled way of ensuring
that the knowledge base from which
reasoning is done is robust, in
the sense that errors in the
deductions are at least controlled.
The main suggestion made in that
paper is that the way to make
reasoning robust enough to be viable in
a world as complex and
ill-understood as this one, is to have the
knowledge base
constantly checked and updated against real world
experience. In
turn, this leads to the idea that the semantics of PAC
learning may
be an adequate semantics since in that field performance
is
measured by goodness of fit with real world experience.
This
contrasts with the standard semantics of logic, where there is
a
presumption that a precise formalization of the knowledge
is
possible. In practice, human designers who attempt to
axiomatize
knowledge in complex commonsense domains fail to foresee
all the
necessary possibilities or eventualities, and the resulting
reasoning
systems that use these knowledge bases turn out to be
brittle.
The technological consequence of success here may be
the final
emergence of computer systems that can interact and cope
with complex,
uncertain and incompletely understood environments
much as humans
appear to be able to do.
3.
Characterizing Cortical Computation
The aim here is to describe
how knowledge is represented in the brain
and what the algorithms
are for computing the most basic behavioral
tasks. The first
challenge is to obtain explicit computational
accounts of such
basic functions as memorizing a scene, recalling an
event, deducing
a consequence of two facts and simple supervised and
unsupervised
learning. Only after this has been done need one proceed
to more
complex phenomena.
In order to achieve this one first needs a
model of computation that
describes the essential capabilities and
limitations of the brain for
computing such functions. Models of
the activity of single cells are
probably too low-level, just as in
a digital computer the bit level is
not right for describing the
corresponding level of
functionality. However, some biological
facts about single cells may
be crucial in determining what the
right high-level model is. In our
study [Valiant
1994], we
concluded that the following biological
questions may be
particularly informative in guiding one to the right
model: the
strength of synapses, the accuracy of timing mechanisms,
the
existence of state not just at synapses but also globally in
a
cell, and the numerical parameters of cell interconnectivity. It
was
shown there that sufficiently positive answers to these four
questions
are enough to support the set of basic tasks, such as
memorization,
that we listed above. In the absence of such positive
answers, it
appears much more difficult, we believe, to account for
such a breadth
of cognitive phenomena. Mathematical proofs of
impossibility are,
however, lacking and clearly offer a possible
avenue for future
enquiry.
On the biology side, it would
appear that questions about cortical
cells such as the
above-mentioned four, are resolvable by experiment
in the
foreseeable future. Consensus can then emerge on the
needed
high-level model of computation. Some facts about the brain,
such as
the stylized nature of the spikes in the long range axons,
and the
apparently huge increase in size of the brain as humans
evolved in the
last several hundred thousand years, suggest that
the computations may
share some simple underlying algorithmic
processes, and hence that
this overall endeavor of understanding
the brain through its basic
computational capabilities might be
viable.
Cortical computation may well turn out to be the
science that speaks
to us most directly about our experience as
humans.
REFERENCES
BERNSTEIN, E., AND VAZIRANI, U.
V.
1997. Quantum complexity theory,
SIAM J. Comput.,
1411--1473.
CARNAP, R.
1950. Logical Foundations of
Probability. University of
Chicago Press, Chicago,
Ill.
COOK, S. A.
1971. The complexity of theorem proving
procedures. In
Proceedings of the 3rd ACM symposium on Theory of
computing. ACM, New
York, 151--158.
HALPERN, J. Y.
1990.
An analysis of first-order logics of
probability. Artif. Int., 46,
311--350.
KARP, R. M.
1972. Reducibility among combinatorial
problems. In
Complexity of computer computations. R. E. Miller and
J. W. Thatcher,
Eds. Plenum Press, New York,
85--103.
LEVIN, L. A.
1973. Universal sorting problems. Prob.
Inf. Trans., 9,
265--266.
MCCARTHY, J.
1959. Programs
with commonsense. In Teddington conference
on the Mechanization of
Thought Processes. HMSO, London, England.
PAPADIMITRIOU, C. H.
1994. Computational Complexity. Addison-Wesley,
Reading,
Mass.
PEARL, J.
1988. Probabilistic Reasoning in Intelligent
Systems:
Networks of Plausible Inference. Morgan-Kaufmann, Los
Altos, Calif.
TURING, A. M.
1936. On computable numbers, with
an application to the
Entscheidungsproblem. Proc. Lond. Math. Soc.
42, 230--265. Also 43,
(
1937), 544--546.
VALIANT, L. G.
1994. Circuits of the Mind. Oxford University Press,
New
York.
VALIANT, L. G. 2000. Robust logics. Artif. Int., 1
17,
231--253.
Journal of the ACM, Vol. 50, No. 1, January
2003.
--
Computer science is no more about computers
than astronomy is about telescopes
---- Edsger
Dijkstra
17971十几位图灵奖得主对下50年计算机科学提出新世纪的若干核心问题,其本意是想效仿当年Hilbert所为.
发信人:
starfish (好好学习,天天向上), 信区: Algorithm
标 题: Problems and Projections in CS
for the Next 49 Ye
发信站: 南京大学小百合站 (Tue Jul 8 02:12:05
2003)
Problems and Projections in CS for the Next 49
Years
JOHN MC CARTHY
Stanford University, Stanford,
California
Projection 50 years ahead is difficult, so I
have eased my problem by
offering problems and projections for only
49 years. My projections
concern areas in which I have
worked---artificial intelligence,
mathematical theory of
computation, and computer systems. However, I
am surely not
uptodate in any of these areas, so some of what I
project for the
future may have already happened. I also talk about
the problems
caused by the way computing and computer science are
practiced. We
shouldn't exaggerate. The computer has caused big
changes in
society, but these probably aren't as great as those caused
by
the automobile.
The future is a continuation of the past, so we
treat progress in
areas of computers and computer science as a
continuation of their
histories.
1. The Personal
Computer.
Let's begin by dating some facilities provided
by com puters. In each
case the first date is when some people had
the facility and the
second date when it was
widespread.
1.1 Computer Cost of Writing and Email becomes
Marginal.
By the late
1970s for some people and by the
1990s
for almost all,
computer power for writing and for email did not
have to be rationed.
1.2 Online All the Time at Home or at
Work.
For a few (me) this started in
1968. By the
1990s, it
was
widespread. The obvious culmination is that via a computer
attached to
clothing or even built into the body, one will be
online all the
time. It seems to me that the main payoff has
already been achieved
with computers at home and in the office. The
additional time a person
spends doing something with a computer
through having it all the time
will be a small fraction of what he
is doing already.
1.3 Email to Worldwide Destinations.
1970 to
1990s
1.4 Point and Click.
1980s.
1.5 Pocket
Computer.
1990 to ?.
They aren't good enough for me yet.
Surely we'll soon have rollable
pocket displays or head mounted
displays good enough so that one can
wear them continuously. Having
the computer facilities of one's desk
computer or laptop always
at hand will be nice, but it will be a minor
Author's address:
John McCarthy, Computer Science Department, Stanford
University,
Stanford, CA 94305. email: jmc@cs.stanford.edu. url:
http://wwwformal.stanford.edu/jmc/. improvement,
because the reason
one is away from one's computer is to engage
in some noncomputer
activity.
1.6 Online Buying and
Selling via the Web.
1990s.
This has a lot further to
go.
1.7 Search Engines.
1980s to present.
Google is
the first reasonably adequate web search engine. It
can't
answer questions but can often find an adequate
humanreadable source
of information.
In several
important respects, the use of computers is more difficult
than it
was in the
1970s and
1980s. The complexity of basic facilities
like
editors and operating systems and application programs has
grown
now that limitations on RAM and disk have enormously
relaxed.
Point and click has made it very difficult, even for
programmers, to
customize their environments. It has encouraged the
authoritarian
tendencies of people who design systems for other
people to
use. Another difficulty arises from the Microsoft and
Apple basic
software being proprietary and secret. Linux has made a
minor
improvement. Now the ordinary computer user needs the
services of
system administrators who do no programming but know
how the
facilities are connected together.
Perhaps this
situation can be relieved by programs that can understand
the
features of system programs and can connect them in order
to
achieve goals specified in interaction with the user. Doing this
right
involves some AI but much less than humanlevel
AI.
Here are some areas with problems to solve and
opportunities for
progress
2. Programming Languages.
In some important respects, recently developed languages, for
example,
Java, are a step backward from Lisp. For example, while
Java does
include automatic garbage collection (which its ancestor
C++ did not),
it still doesn't include functions as firstclass
objects (like Lisp
lambdaexpressions); these facilitate the
creation of programs which
themselves inspect, synthesize, or
otherwise manipulate programs [and
this has many important
applications]. A Lisp program can look at its
own internal
structure and modify itself or create new Lisp program
and
interpret it right away. A Java program could modify itself at
run
time only by reference to the byte code, not the source code.
Lisp
also benefits from its in ternal form being list structure
with the
lead word saying what the expression is, for example, an
assignment
statement is (setq ...). To recognize an assignment
statement, a Java
program must search for =. The Java program can
also have used a Java
parser to parse itself into a suitable data
structure.
In the next 49 years, programs that extend
themselves at run time will
become important.
I see
opportunities for improvement in regarding inputoutput
as
consisting of speech acts. Thus, computers can make requests
or
promises to people or other computer systems. They can also
ask
questions and give truthful and responsive answers to the
questions.
The proper performance of speech acts gives new
specifications for
programs. For example, we can ask whether a
program keeps its promises
or at least intends to keep them. The
speech acts can be represented
in machines as strings, or as XML,
or (better) Lisp ######pressions, but
they will have an abstract
syntax and semantics at a higher level, and
promise (proposition,
person) can be a program statement meaning to
promise to person
that propostion will be true. See
http://wwwformal.stanford.edu/jmc/elephant.htmlfor
some ideas that
are still not at the level of concrete
proposals.
3. Mathematical Theory of Computation.
The mathematical relations of computer programs, computable
functions
and data structures.
3.1 Computability and
Computational Complexity.
This is the one area in which
computer science has developed deep
mathematical questions, for
example, P = NP. I trust others will
characterize what may be
expected from it in the next 49 years.
3.2 Channel
Capacity?
Here's a problem whose solution would be as
impressive as the
discovery of NPcompleteness: Is there a
computational analog of
Shannon's channel capacity theorem for
communication? Shannon's
theorem says that it is possible to
transmit information over a
communication channel at a rate
arbitarily close its channel capacity
with an arbitrarily low
probability of error. A corresponding theorem
for computation would
say approximately that a computer of speed V
would be able to do a
computation of size X in time X/V given
enough
memory.
3.3 Proving Correctness of Computer
Programs.
In principle, noone should pay money for a computer
program until its
specifications are expressed formally and the
program is proved to
meet them and the prove is mechanically
checked. Considerable progress
was made in the
1960s and
1970s, the
outstanding achievement being the
BoyerMoore interactive theorem
prover. While progress continues, it
has been slowed by demands for
shortterm payoffs.
Today there is already great emphasis on
computer programs that
interact with people or other programs.
Therefore, specification and
verification of such programs will
become increasingly important. As
early as the
1970s, there was
work on specifying text editors and
proving that they met their
specifications.
The inputs and outputs of interactive programs
are often well regarded
as speech acts as discussed in Austin
[
1962], Searle [
1969], and
McCarthy [
1996]. Speech acts include
promises, requests, acceptances
and denials of requests, questions,
answers to questions, and
pronouncements. Each of these, as
discussed in McCarthy [
1996], has
conditions for its correct
execution, e.g. promises should be kept and
answers to questions
should be true and responsive. These aspects of
programs will
become increasingly important.
4. Artificial Intelligence.
The long term goal of artificial intelligence research should
be
humanlevel AI, that is, computer programs with at least
the
intellectual capabilities of humans. There are two main
approaches to
seeking this goal.
The biological approach
builds agents that imitate features of the
physiology or psychology
of humans. Most cognitive science agents
imitate humans at the
psychological level; connectionist systems and
their neural net
relatives imitate at the physiological level.
For progress, the
biological AI researchers need to figure out how to
represent facts
independent of their purpose, to make systems capable
of sequential
behavi or and to figure out what information to build
into their
systems corresponding to the rich information that human
babies are
born possessing.
The engineering approaches to AI regard the
world as presenting
certain kinds of problems to an agent trying to
survive and achieve
goals. It studies directly how to achieve
goals. The logical approach
is a variety of the engineering
approach. A logical agent represents
what it knows in logical
formulas and infers that certain actions or
strategies are
appropriate to achieve its goals.
The logical agents of the
next 49 years need at least (1) continued
existence over time, (2)
improved ability to reason about action and
change, (3) more
elaboration tolerant formalisms, (4) the ability to
represent and
reason about approximately defined entities, (5)
enough
selfawareness and introspection to learn from the successes
and
failures of their previous reasoning, (6) domain-dependent
control of
theorem provers and problem solvers, and (7) identifying
the most
basic commonsense knowledge and getting it into the
computer. This
must include knowledge that people use without being
able to formulate
it verbally.
The classical AI
problems---the frame problem, the qualification
problem and the
ramification problem [Shanahan
1997]---have been
solved for
particular for malisms for representing information about
action
and change. However, these currently known
representation
formalisms are unsatisfactory in various respects.
Improved ways of
representing action and change may present new
versions of the frame,
qualification and representation
problems.
It's a race to humanlevel AI, and I think the
logical approach is
ahead. Why? The logical approach to AI has
faced and partly solved
problems that all approaches will face
sooner or later. Mainly they
concern identifying and representing
as data and programs information
about how the world works. Humans
represent this information
internally, but only some of it is
verbally accessible. The logical
approach also has the advantage
that when we achieve human-level AI we
will understand how
intelligence works. Some of the evolutionary
approaches might
achieve an intelligent machine without anyone
understanding how it
works.
What are the problems faced by logical AI? Here are a
few.
4.1 Facts about Action and Change.
This has
been the major concentration of work in logical AI.
Present
formalisms are pretty good for representing facts about
discrete
sequences of actions and their consequences. Programs
exist for the
automatic translations of planning problems so
described into
propositional theories, and the propositional
problem solvers are
often adequate to solve the problems. The
situation is not so good for
continuous change, concurrent events,
and problems involving the
actions of several agents. We can hope
for progress in the next 50
years.
4.2 Elaboration
Tolerance Including the Frame Problem.
Existing AI systems,
including both logical and biological, are
extremely specialized in
what in formation they can take into
account. Taking into account
new information, even information not
contradicting previous
knowledge, often requires rebuild ing the
system from scratch.
Logical AI has studied elaboration tolerance, a
special cases of
which is the presented by the frame problem and the
qualifi cation
problem. The frame problem involves the implicit
specification of
what doesn't change when an event occurs, and the
qualification
problem involves elaborating the sufficient conditions
for an event
to have its normal effect. [Shanahan
1997] treats
elaboration
tolerance and there is also my
http://wwwformal.stanford.edu/jmc/elaboration.html.
4.3
Nonmonotonic Reasoning.
Humans and machines usually reach
conclusions on the basis of
incomplete knowledge. These conclusions
may change when new knowledge
becomes available. Probability theory
is applicable to a part of the
problem, but more general
nonmonotonic logics seem to be also
required.
4.4 The
Three Dimensional World: Approximate Knowledge.
The knowledge
available to a person or robot of its three
dimensional
surroundings and of the objects it needs to manipulate
is almost
always very approximate, though sometimes precise
geometric models
like rectangular parallelepiped approximate real
objects well
enough. Logical AI needs a general theory of
approximate objects.
4.5 The Relation between Appearance and
Reality.
We and any robots we may build live in a world of
threedimensional
objects built up from substances that are, in
turn, made of
molecules. Our direct information about this world
comes directly from
senses like vision and hearing that only carry
partial information
about the objects. We, even babies, are built
to infer information
about the three dimensional objects from
observations and from general
information about what kinds of
objects there are.
Machine learning and most AI have treated
classifying appearances but
don't go beyond appearance to the
reality. I have a puzzle about
this
(http://wwwformal.stanford.edu/jmc/appearance.html). I think
the
relation of appearance and reality will be an important topic
of AI
research in the next 49 years.
Logical AI has
faced the above phenomena. Other approaches haven't
faced them
explicitly. Maybe it will turn out that they don't have to,
but
I have seen no arguments to that effect.
My views on many of
the specific problems are in articles published in
various
journals; almost all are to be found on my web page
http://wwwformal.stanford.edu/jmc/. There is no
complete summary,
but
http://wwwformal.stanford.edu/jmc/whatisai.html
and
http://wwwformal. stanford.edu/jmc/logicalai.html
express the
logical AI point of view. [Shanahan
1997] covers much
of the logical
AI approach.
No approach is close to
humanlevel AI and or within development
range. No one can
convincingly say that given a billion dollars he
could reach
humanlevel. A critical level of AI will be reached, as
Douglas
Lenat pointed out, when an AI system has enough basic common
sense
information to be able to get more information by reading
books.
Humanlevel intelligence is a difficult scientific
problem and
probably needs some new ideas. These are more likely to
be invented by
a person of genius than as part of a Government or
industry
project. Of course, present ideas and techniques are
sufficient for
many useful applications.
Still we can
ask for a subjective probability that humanlevel AI will
be reached
in the next 49 years. In the past, I have said that
humanlevel AI
will take be tween 5 and 500 years. I'll guess 0.5
probability
in the next 49 years but a 0.25 probability that 49 years
from now,
the problems will be just as confusing as they are today.
4.6
What if We Get HumanLevel AI
in the Next 49 Years? The current
speculation about the consequences
of getting humanlevel AI is
mostly beside the point, because it
concentrates on the possible
personalities of the intelligent agents.
Present ideas about what
humanlevel AI will be like seem to come from
sciencefiction.
Consequently discussions of policies concerning AI are
presently
beside the point.
Because of the speed of computers,
qualitatively humanlevel AImeans
quantitatively superhuman AI. Its
immediate applications will be to
get advice relevant to decisions
of what to do. Even here the
speculation, especially science
fiction, is beside the point. In the
typical story, the human asks
what to do, the machine answers, and
taking the machine's
advice has unexpected and unpleasant
consequences. The proper use
of an AI advisor is to ask it the
consequences of many possible
courses of action and to give the
reasoning leading to the
machine's opinion.
The main danger is of people using AI to
take unfair advantage of
other people. However, we won't know
enough to regulate it until we
see what it actually looks like. I
would hate to see the American
presidential candidates in 2004
asked for their positions on AI.
5. Quantum Computers.
I believe they will be made to work. There are many physical
phenomena
being tried and the discovery of quantum error correction
makes
getting a general quantum computer a finite task. On the
other hand,
there is still only Shor's factoring algorithm as
an example of a
spectacularly useful quantum algorithm. The next 49
years will surely
tell us what quantum comput ers are good for.
I'll conjecture that
factoring will turn out to be a
paradigmatic example.
6. Economics of Information.
Many costeffective improvements in the way information is
handled are
not done, because society is not organized to pay for
them
properly. We can hope for improvements in economic
organization of in
formation in the next 49 years. Here are some
examples.
(1) Since about
1970, it has been economically
feasible to put the
world's lit erature, approximately the U.S.
Library of Congress, on
line and make it available worldwide. It is
now rather cheap, but John
Ockerbloom's library catalog
www.digital.library.upenn.edu lists only
about 20,000 freely
available books. The situation was made worse by
the extension of
copyright from 75 to 95 years. The economic interests
of publishers
have dominated those of authors and readers. There is
more money
available than ever before to pay authors for their talent
and
work. This will get even better if the pub lishers can be
squeezed
as the new technologies warrant. Technologically, there is
still a
little ways to go before everyone can sit in his bathtub with
a
waterproof flat screen and browse the world's
literature.
(2) The world would benefit from a lot more
manpower going into free
software. The volunteer efforts associated
with the Free Software
Foundation could use ten times the manpower.
We need a way of paying
for it out of public funds and for
encouraging new volunteer
efforts. Alternatively, the same result
might be obtained by some
improvement in the economics of
commercial software.
(3) The previous sections of this article
have described goals for
computing and computer science for the
next 49 years. How fast these
goals are achieved depends
significantly on the attitude of the
researchers and the agencies
that support research. A large fraction
of computer science
research in industry and academia over the last 20
years has been
wasted, because the projects have had too short a time
scale. For
example, major researchers in program verification have
spent
almost all their time on verifying successive parts
of
microprocessors and have had little support for research in
the
general theory of verification.
One result has been
many academic projects and Silicon Valley
companies pursuing
essentially identical minor ideas. This is likely
to continue
during the next 49 years. Big advances will not come from
a
succession of 25 two year projects. The rush to patent has
resulted
in patenting trivial improvements. Among the sciences
computer
science has been particularly badly off. One reads all the
time about
physics and astronomy projects with ten and twenty year
completion
times.
What long term projects are worthwhile
in computer science? For one,
there needs to be more longterm
projects to develop automatic
interactive theorem provers, better
computer algebra systems, a Lisp
better than scheme. It is
important to choose experimental domains
designed to be
informative, rather than to emphasize short term
goals. The
geneticists have worked with Drosophila since
1910, and yet
the
fruit flies of today are no better than the fruit flies of
1910.
Couldn't the geneticists at least have bred them for speed so
we
could enjoy fruit fly races? The ``practical'' types
sneer at ``toy
problems,'' but these are the
Drosophilas.
To summarize, here some problems I
see.
(1) Humanlevel AI and how to get there;
(2)
Getting AI to where programs can learn from books;
(3)
Specifying programs that interact with people and other
programs;
(4) Making formal proofs that programs meet
specifications part of
contracts.
(5) Giving users full
control of their computing environments,
i.e. devising ways for
users to reprogram their environments without
their having to
understand more than necessary.
(6) Giving programming
languages primitives for the abstract syntax of
the language
itself.
(7) Proving a computational analog of the Shannon
channel capacity
theorem.
REFERENCES
AUSTIN,
J. L.
1962. How to Do Things with Words, Oxford.
MCCARTHY, J.
1996. Elephant 2000
http://wwwformal.stanford.edu/jmc/elephant.html
Stanford Formal Reasoning Group, available only as
http://wwwformal.stanford.edu/jmc/elephant.html.
SEARLE,
J. R.
1969. Speech Acts, Univ. Press, Cambridge, Eng.
SHANAHAN,
M.
1997. Solving the Frame Problem, A Mathematical
Investigation of
the Common Sense Law of Inertia. M.I.T. Press,
Cambridge,
Mass.
--
Computer science is no more about computers
than astronomy is about telescopes
---- Edsger
Dijkstra
17971看了30行
17971呵呵,大家都看过了最后一句。
17971
引用 (justlikethewind @ 2005年09月22日
17时25分) |
| 呵呵,大家都看过了最后一句。
|
是的,计算机科学不等于计算机,就象天文学不等于望远镜.
17971看不了啊啊啊 啊
17971
| 引用 (primenumber @ 2005年09月23日
21时11分) |
| 看不了啊啊啊 啊
|
太长了,看不完
17971顶
17972感谢感谢
17972
点集拓朴近世代数初等数论
17972
真是好东西啊。非常感谢。
17972是个不错的东西。现在,这样的真是很少。
17972
微分几何
17972非常有用,谢谢
17972very good,do u have Functional
17972好东西,谢谢
17972非常感谢楼主!!!!!!!!
17974$\alpha$$\beta$
滤波器用于匀速直线运动,但是为什么速度估计值是发散的呢?
不知在哪个板块,请教!
17974$\alpha\beta$滤波器用于匀速直线运动,但是为什么速度估计值是发散的呢?
不知发在哪个板块,请教!
17974具体把滤波器说一下吧.
还有,输入公式的时候要在两面加[math][杠(/) math]
17975我们老师是湖南人,上课我听不懂她的湖南口音,谁有比较详细的常微分方程答案,中山大学那本,谢谢!
17977我上次做美国mcm2005a题时,碰到啦这个难题,一至到现在还没解出来,有那位大哥会的话,帮小弟一下,我的邮箱是
jacker_0828@163.com
17977
!,
!- )!(. ) .#)
!! ( #
(*)
!,
!! )!(,( / .)
!- ) +. !*
!-
) 01 ( ) 0 ) & ( #
(,)
如果那位大哥大姐会求解的话,请帮小弟一下,小弟不胜感激,我的邮箱是:jacker_0828@163.com
17980请问什么是“the method of moments”?
回复:
The method of moments equates sample moments to
parameter estimates. When moment methods are available, they have the
advantage of simplicity. The disadvantage is that they are often not
available and they do not have the desirable optimality properties of
maximum likelihood and least squares estimators
17980用样本矩代替总体矩,然后解方程估计总体未知参数的一种点估计方法
17981up
17981wonderful!
17981网址:
http://idwhiz.vicp.net/whizzebooks/00/cate...tegory-0091.xml
17981好象打不开啊。
17981太好了,就需要你这样的帖子,好久没有看到这么好的帖子了,楼主太强了,交个朋友
QQ21
195807
yuxianzh@swu.edu.cn
西南大学数学系
17981果然是个好网站啊
谢谢楼主
17981打不开!
17981果然打不开
17981打不开啊。是不是只白天、晚上开啊
17981thx a lot!
17981太好了啊
17981谢希腊,不错的的好地方,
17981为什么要安装fireworks ?
太不人道了
17981真是十分的感谢!
very good!!
17981要安装fireworks 太不人道了
17981不错,不错.
17981要Firefox来支持
资料不错
较全
17981谢谢, 真心的~~~
17981非常感谢啊!
17981不错.
17981真是十分的感谢!
very good!!
17981顶!
17981请教楼主:
1、如何下载?
2、PS格式的文件用何种软件打开?
谢谢!
17982感觉权函数的定义很难理解,权函数有什么性质啊?
17982用距离来理解
因为是从几何上抽象得出的
17982那种权函数,是不是用来求某种平均值的函数?
17982权函数也叫衡重函数,顾名思义,衡量某个重要性的函数,“权”也是指“重要性”的意思。这个“权”与政治上的那个“权”意义相同。权重者自然重要哦!
比如作函数逼近,是否在所指的定义域内都有一样的重要性?如果是,只需取权函数等于1即可,如果不是,在域内某些地方较重要,那么,就要找一个表示这个重要性的函数乘以给定的被逼近函数(或离散点集)。有时,权函数的引入,非但不使问题变得复杂,还有可能变得简单。当然,还没有普适的构造权函数的办法。权函数的引入使数学家们把问题描述得更加精细,甚至更易解,是很绝妙的。
17982楼上的已经描述的非常清楚了,从权重的角度理解是比较好懂的,或者就想想百分比或所占有的份额吧,都可以帮助你理解权函数的概念
17982很想听听2楼在距离上是怎么理解的!希望你能讲解一下!谢谢
17983想传播数学,科普读物是少不了的,大家都来介绍一些好的数学科普读物吧
17983《数学家的眼光》
《数学万花镜》
《天才引导的历程》
17983我下次在来看
17983能不能提供一些下载的地方,电子书
17983我曾经在家园的数学史话中上传了几部科普书
可以去下的word 版的
17984计算数学对计算机的知识要有多少了解?
不会像计算机专业的学生那样精通吧.
17984说法太广了,还是不清楚。
说说那个更有用?
17984差不多
17984应用数学主要搞一些应用方面的东西
解决实际问题等等
主要是建模把
计算数学应该是算法之类的东西
17984我学的是数学专业,想考个研.
不知道要自己往那方面发展比较好........,各位有什么建议给我提提啊?
应用数学与计算数学分别学些什么啊?
17984计算数学就搞计算机了,算法的研究,应用数学就广了.
17985中国科协主席周光召认为做官与科研不可兼得留心胜留人
(新华社记者王建刚,人民网记者许秀华)
中国科协主席周光召在正在乌鲁木齐举办的中国科协2005年学术年会期间指出,做官和从事科学研究是两种不同的人生价值取向。一个人如果选择做官,就不宜再继续搞研究。如要从政,就应不夹杂任何私心杂念地为大家服务。
对于目前盛行的科研与行政比照待遇引发的一些问题,如,一些有职权的人相对容易获得课题和科研经费;一些研究人员心思不在科研上,只想在仕途上发展;一些地方以行政级别吸引目标人才等现象,周光召认为,科技界出现官本位现象是极不正常的。科研管理机构应尽早建立一种以业绩和个人才干为标准的科研经费和课题分配机制,让有真才实学的科研人员充分施展自己的才华,而不要为是否能得到课题以及科研经费过分牵扯精力。
对于目前课题分配机制中用年龄做标尺搞“一刀切”,客观上造成部分老科技工作者和中青年科学家之间的收入和待遇差距加大,“奉献越早,回报越少”等不正常现象,周光召指出,我国科研制度改革仍在不断摸索之中,这种现象很值得注意。老科技工作者同样具有创新精神,不能让这部分科研资源白白浪费掉。
对于新疆老科技工作者深表忧虑的新疆人才外流问题,周光召认为,引进人才要讲究策略,关键人才要引进,同时还应该注重本地人才的使用和培养,“留心更胜留人”。
中国在这方面可以借鉴韩国的做法。韩国在70年代也曾有大批青年赴发达国家学习,但上至总统下至普通百姓对他们出国后都给予极大的关心,鼓励他们努力学习,学成之后回国效力。韩国学生出国学习后,韩国有关部门便开始密切跟踪他们在国外的学习情况,每当他们学业或工作中获得骄人的成绩,政府有关部门都会发信表示祝贺。
同时,韩国政府鼓励年轻人到企业中去工作,企业经历对年轻人非常重要,在国外大公司中工作,不仅可以学习先进的技术,还可以学习国外先进的创新理念和管理理念,这对于发展中国家尤为重要。
因此,韩国留学生归国比率非常高,而那些决意留在国外工作的人同样心系祖国,当他们在国外有一定的实力和影响力后,首先会考虑在韩国进行投资和选择合作伙伴,为本地提供巨大的发展机会。
周光召认为,引进人才必然会涉及到待遇和福利的提高,不仅会对本地人才造成心理冲击,也会加剧财政压力。因此,引进人才一定要引进关键人才,而不是不加区分的盲目引进。地方政府在努力提高人才物质待遇的同时,一定要设法做好感情留人。
周光召认为,要讲究用人策略,即关键或不可或缺的人才从外部引进,而承担大量基础性研究工作的只能依靠大批本地人才。如何通过人才引进大规模培养本地人才,提高本地整体科研水平,也许正是西部科研管理部门在人才引进方面急需考虑的问题。
(新华社记者王建刚,人民网记者许秀华)
17986“尺子”是怎样坏掉的
科学时报
“SCI现象”引起了科研界广泛的关注。有人称它是一把已经坏掉的尺子。既然是“已经坏掉的尺子”,也就说明它原先并不“坏”。于是,尺子是怎么坏掉的,就具有了思考的价值。
把SCI引进我国科研评价体系,作为评价科研人员之科研水平的一把尺子,不过是20年左右的时间,该算是一个新事物,然而,我们就有这个能耐,在这短时期中冒出一批“SCI大师”。被SCI收录的论文,有的10年500篇,有的干脆就一天一篇。采用的方法大同小异,按新语丝网站负责人方舟子的说法,就是到一些影响因子极低,发论文非常容易的刊物上刊登小论文,论文的内容都大同小异,用相同的简单的方法不停地测不同化合物的晶体结构。
以论文的被引用率作为衡量论文作者和发表论文的期刊的影响因子及其水准的客观依据,也算是一个新事物,连“影响因子”这个词汇都能使局外人耳目一新。然而,又马上就有人为制造“影响因子”的高招:论文作者自己引用自己的论文,此所谓“自引率”。宁波大学那位已有130余篇论文被SCI收录的郑岳青教授,平均每篇论文的被引用率为6次多一点,“自引率”就高达4次。
面对如此“低投入高产出”的“科学研究”,笔者好有一比:室内温度是由室内的温度计测量的。提高“室内温度”的最简捷的办法,就是给这支测量室内温度的温度计加温。只需一盏酒精灯或一支蜡烛,也就能使温度计中的水银柱直线上升。至于室内温度是否真有升高,大可弃之不顾。
采用此类投机取巧之手段获取名利,最突出的其实还在政界。以“政绩”考核干部,本来也是很科学的一种方法。看一个干部能不能提拔,只看思想不行、只看学历不行、只看年龄也不行,惟有政绩,方是各种因素的综合。然而,应付政绩考核的办法也跟着出现,或是将政绩简化为GPT,或者干脆就弄一些专供上级领导看的“政绩工程”——这种以急功近利、弄虚作假和形式主义为显著特点的“政绩工程”如今已经成了一大公害。与此相比,SCI的变味走样,也就小巫见大巫了。
这就难怪,在“郑岳青现象”被新语丝网站披露之后,宁波大学校方居然会认为郑岳青的做法“没有什么不正常”,校内职工的反应也“非常平静”,而网上也会有人为他喊冤,说他还是“比较老实的一个人”。平心而论,说郑岳青“比较老实”是有参照系的,至少他没有剽窃别人的成果,没有弄虚作假偷梁换柱;说“郑岳青现象”“没有什么不正常”也是有参照系的,整个社会都有人在用升高温度计的水银柱来替代提高气温,不正常的已经变得非常正常,怎么能独独苛求SCI甚至是一个年轻的教授呢?何况,据有关权威人士说,“SCI指标可以量化、易操作,经过10多年的应用,已经成为科研系统中一项重要的‘政绩工程’”。
在我们中国,一直以来似乎总有某种“元素”,就像能使金属失去原有光泽的氧元素一样,使任何新事物——不论是进口的还是国产的——变味走样。太多的欲望使人贪得无厌,几乎是与生俱来的惰性又使人不想付出相应代价。于是就有人——包括权势者和想获得权势的人——投机取巧,使原先有益于社会的新事物渐渐地适合于他们的口味而成为社会的弊端。曹操首创的九品中正制,隋唐时期出现的科举制,作为不拘贵贱地评价和选拔人才的机制,起初都不啻是新事物,以后又都成了一把坏掉的尺子,或许就有这种“元素”在起着作用。
SCI成了一把坏掉的尺子。仅仅将它归咎于现行科研评价体制的弊端,不去找一找社会与文化方面的原因,笔者以为是很不够的。你想想,在那种能使任何新事物变味走样的“元素”相当活跃的时候,即使如有些专家所说,科研评价以同行评议为主了,同行评议会不会蜕化为圈子中人的评议,恐怕还很难下定论呢!
美国人类学家本尼迪克特认为,人类文化有罪感文化和耻感文化之分。西方文化为罪感文化,做错事的人有一种原罪性的罪恶感,东方文化为耻感文化,做错事的人只有被发现时才有耻恶感。然而,当社会评价失衡以至于头足倒置,许多不正常的事情反而变得正常的时候,不要说人的诚信与良知,就是那种只有在“被发现时才有”的“耻恶感”也会荡然无存。
17987受益颇深!谢谢!
17987大师往往很幽默
科学时报
一
科学大师不乏幽默者。
有人问法拉第,研究电磁现象有什么用?
法拉第反问:“新生婴儿有什么用?”
二
财政大臣问法拉第,电有什么用?
法拉第答道:“总会有一天,您可以向它征税,大人。”
三
在科学领域,爱因斯坦是一位蔑视权威的“叛逆者”。
就此,爱因斯坦说:“为了惩罚我对权威的蔑视,命运使我本人成了权威。”四
1954年,美国管工工会授予爱因斯坦荣誉会员称号。
因为,在这一年的11月
18日,报上刊登了爱因斯坦的答记者问,他表示,为了得到“目前环境下还允许的那一点点独立性”,宁愿去做水管工或小贩。
五
爱因斯坦以幽默的语言说明,“好奇”与“怀疑”对科学发现是多么重要:
“我的智力发展得比较晚,以致成年之后才对空间和时间感到好奇和疑惑,而正常人在童年时就想过这些东西了。”
六
在纳粹德国,有一百名教授写了一本书,说爱因斯坦的理论是错误的。有人问爱因斯坦对此作何感想,他答道:“如果是我错了,一个教授就足够了。”
七
1945年,广岛、长崎遭到原子弹轰炸的消息传来,爱因斯坦痛心地说,当初致信罗斯福提议研制核武器,是他一生最大的错误和遗憾。他甚至懊悔当初从事科学研究,说:“早知如此,我宁可当个修表匠。”
不知为何美国修表匠工会没给爱因斯坦来个荣誉称号,或许是根本没有这么个工会?
八
伦琴的幽默也颇让我们深思:
“我喜欢离开人们常走的小路,而走荆棘丛生的山路……如果我迷失了,不要在大道上找我!”
九
薛定谔是科学家,还是诗人,请看他的幽默:
“在很多情况下,逻辑思维在引导我们到达某一点后,就丢下我们不管我们的死活了。”
十
有人要达尔文写一份自传,达尔文是这样答复的:“我先是学习,尔后是环球旅行,然后又是学习。这就是我的自传。”
十一
“是谁在驾驶?”地面控制中心问。
“我想,现在是牛顿在驾驶。”
阿波罗指令长在返航途中的回答也极其幽默。
十二
冯卡门是航空、航天领域的元老。他曾说,科学家预言未来是要冒风险的。但是
1962年他却出来“展望未来”,为什么?冯卡门泄露天机:“我年已81岁,就这点来说,预言20年还是相当安全的。因为到了回头验看预测结果的时候,我早已远离尘世了。”
十三
杨振宁曾经写诗称赞陈省身:“千古存心事,欧高黎嘉陈。”对于把自己与欧几里得、高斯、黎曼、嘉当并列,陈省身报以幽默:“上中学时,体育不好,百米跑不过女生;学化学做不好实验,还经常把试管打碎,所以只好学数学。”
十四
“儒商”可能很幽默。
有记者问一位成功的企业家,你赚了多少钱?
这位男性企业家答曰:“对女人不要问有多大岁数,对男人不要问有多少钱。”
十五
艺术大师也许更多幽默。
有人问侯宝林,里根曾是演员,你也是演员;可为什么人家当了总统,你还在说相声?
侯宝林妙语评说:“因为他是二流演员,我是一流演员。”
里根的演员职业不算成功,他没有得过奖,仅仅拿到一个“最糟糕终生成就奖”,这是个搞笑奖。
十六
足球大师也幽默。
有人问米卢,中国足球队与巴西对阵,结果会怎样?
米卢答道:“足球场上,什么事都可能发生。”
有人请他预测,中国足球队在世界杯的表现,米卢说:
“足球的魅力在于不可预测。”
十七
书法大师很幽默。
66岁那年(
1978年),启功《自撰墓志铭》自嘲曰:“中学生,副教授。博不精,专不透。名虽扬,实不够。高不成,低不就……”为了对付太多上门求字的人,老人称病不写字,就在门外贴个条子:“大熊猫病了”。
十八
大师的幽默让我们认可一位英国人的判断:
“幽默的人必定是机智的人。”
十九
幽默对自己、对大家都“有用”,包括“有用之用”,以及“无用之用”。爱因斯坦去布拉格演讲,欢迎者说了一大堆好话,这使科学大师很不自在。轮到爱因斯坦讲话了,他却举起了小提琴:“女士们,先生们,这里气氛太严肃了,让我先为大家演奏小提琴吧,那将更愉快、更容易理解。”听众皆笑,兴致盎然。你说幽默没用还是有用?
让我们都学着幽默起来。
17987
薛定谔是科学家,还是诗人,请看他的幽默:
“在很多情况下,逻辑思维在引导我们到达某一点后,就丢下我们不管我们的死活了。”
这句话我喜欢。
17987就是幽默!
17987我顶
17987我们需要幽默,我们更要教会我们的学生幽默!
17987给我一个支点,我可以撬起地球
17987幽默是天生的,是学不来的。
17987大师的风范
17987很好的人生态度
17987好多幽默的人都不是大师
17987但不幽默的大师就不能称为大师
17987大师就是大师,不过没有深刻的理解是无法幽默的
17989我也留下个脚印,这学期教高数,还有数学分析,一周12节呢
17989我教高数与点集拓扑。qq15154343,还希望能与你们多多交流
17989
自己先来吧,我教《高等数学》,嘻嘻
17989
本学期刚参加工作的新老师,你好,在此报个到,看看你教什么科目??
17989线性代数,我们共同讨论
17989高数与概率 最近很困惑!
17989高数与工数,我才郁闷呢!!!
17989我也来报个到
17989学生太难伺候!!!!!!
17989不是本学期刚刚参加工作不过,是第一次讲课,呵呵,也应该算在这里的吧,我教《高等数学》和《高等数学实验》我也比较郁闷,学生完全没有语言基础,我又不能以软件的使用为主,因为数学实验的目的还是“用数学”,哪位老师有经验可以交流一下,另外通过两次实验课的学习学生反映都题目比较困难,我都不知道后面的内容到底以什么为主了!!
17989工科数学
17989我也报个到吧。
教了两个周的高等数学,现在很愁。
对于课堂上如何控制速度,如果吸引学生的注意力很不清楚。
认真的就很认真,不认真的就很不认真。
也许是我讲话并不吸引他们吧
据一些认真听课的学生的反映,说我讲课太快了,
可是一对着ppt,就不自觉的越讲越快,压制不下速度来。
想要慢点讲,又害怕在规定学时内无法完成课堂内容,
真的是不清楚应该怎么办:(
17989我是本科的呵呵,我教的是高一呵呵
17989我的第一个学期上的课程不少:
数学系二年级的数学分析三,
每周六节,用的是复旦的教材,我觉得这本教材很好比原来学的华东师范大学高教社的那本好。这门课不轻松,特别是隐函数,曲面积分以及含参变量积分中的很多问题都不轻松。
另一门是计算机科学系二年级的常微分方程,每周四节,这门课比较容易,理论少,主要理论来自于线性代数,其他就是解题技巧了。
17989wojiao 我叫高等数学和工程数学/一起讨论//42462257/313368392QQ联系我
17989都写上QQ号码,我们就可以联系了
17989我上高等数学和实变函数,难啃!
17989我是去年当老师的,已经有三个学期了,共上了高等数学、线性代数、C语言程序设计、实变函数、数学建模等课程,每个学期都有新任务,导致自身学习处于停滞状态,郁闷!
17989我也是刚刚教学. 线性代数/概率 概率太累人
17989daishujihe 代数几何,学生没有兴趣,郁闷
17989我教大学工程类专业科,学生
17989我教高数与微分几何。哈
17989想多上几门课,可就是不让上。
17989我下半年参加工作,带的是复变函数,以前本科的时候学的就不好,郁闷!还只让带一门.
17989我也来报道:概率与统计,难
17989首先声明,我不是教师,我还是学生,在读研究生,不是读数学的,但对数学很感兴趣,曾给本科生上过课。感觉有一点就是特不喜欢用ppt来讲课,我还是喜欢板书,而现在几乎所有院校都用ppt来讲课。其实这很不好,第一你事先已经把ppt做好了,上课就那样照着ppt讲,很没激情,学生也没激情,第二,留给学生许多不好的地方,像放电影一样的闪来闪去,根本就没有理解,其次给他们造成另一种懒惰的习惯,因为现很多本科生都有电脑,上课的时候不好好听,反正有电脑下课把课件铐回去自己看,但往往回去是不看的,因为他们还要打游戏,看帖子,聊qq。
179892005年九月开始教书的
到现在为止教的课有:高等代数(还在教,也将继续教),线性代数,还有一个学期的文科高等数学,空间解析几何。
17989教文科高等数学,还有一门专业课:计算机辅助几何设计。
17989那位教微分几何的兄台,如何联系,我也教微分几何和高等数学,可以交流一下啊
17989解析几何,计算方法,数学分析选讲
17989我也是今年新参加工作的教师
我教物理专业的《高等数学》、数学系二年级的《数学建模》
下学期教数学系三年级的《运筹学》
我们多交流啊
17989数学分析三、高等数学本科和专升本的学生,每周11大节课。
17989呵呵,我也来报个到,这学期没上课,下学期要上偏微分方程数值解法
17989我教线性代数,复变函数.工科的,还可以.
1798906年本科毕业,
现在,在一个高职学院教高数,下学期想改成经济数学,估计相差不大
QQ.60
18
18884
17989我是下半年才上课的。。。我我教微积分
17989我也是新教师.我建了一个关于高数以及大学数学教学的群欢迎各位数学教师加入我们可以一起交流. 群号:41256981.希望大家多多宣传!
17989我也是的高等数学和工程数学
qq393062166
17989我也来报到.这学期教高等数学和计算方法
感觉自己还是没有教学经验,表达能力还不够好
17989
| 引用 (lsqmath @ 2005年12月07日
14时23分) |
我的第一个学期上的课程不少:
数学系二年级的数学分析三,
每周六节,用的是复旦的教材,我觉得这本教材很好比原来学的华东师范大学高教社的那本好。这门课不轻松,特别是隐函数,曲面积分以及含参变量积分中的很多问题都不轻松。
另一门是计算机科学系二年级的常微分方程,每周四节,这门课比较容易,理论少,主要理论来自于线性代数,其他就是解题技巧了。
|
学校领导好器中你啊,刚上班就派了重头课给你,牛
17989我上学期教的工科的《复变函数》和数学系大三的《微分几何》,这学期是《微积分》和《高等几何》
17989讨论数分教学的QQ群:446
17504,欢迎加入!
这学期我教数学分析II和数学史.
17989不错不错
17989我教高一数学
17990请教各位大侠:
在下刚刚发现这个数学的家园,敢问各位如何在博士论坛上获得积分,有些帖子要积分才可以看。
回复:http://www.math.org.cn/forums/index.php?showtopic=10
17990thanks
17991
http://203.66.125.77/twocw/strang-
1806
17991那么多,很好啊,谢谢了
17991那个线代的怎么下啊?好像缺很多啊!能不能给具体点啊?万分感谢!
17991新东方的那个看不见阿 。能给我发来吗 ?谢谢了 。beautyblack55555@sohu.com非常感谢。
17992若有f(x)=0,
为何有f(A)=0?
17992上边的A为n*n距阵
17992f(x)为多项式,把A代进去就是A的矩阵多项式啊,一维的和n维的一样的啊
就象为什么初中做题目,有f(x)=0,x

R,则我随便取个1就变成f(1)=0
你问的意思我估计是不是f(x) 是A的特征多项式啊,那么有f(A)=0,而不是你的一开始的条件就是
f(x)=0
17992特征多项式
17992
| 引用 (iii @ 2005年09月11日
09时50分) |
若有f(x)=0,
为何有f(A)=0? |
没有这么说的
若f(x)为非零多项式,A为方阵
f(A)=0当且仅当f(x)可表为h(x)*g(x),其中g(x)为A的最小零化多项式
17994有高手知道郭雷院士招收博士的要求吗?请指点迷津
17995在学石生明的《近世代数初步》,请教各位大虾,这本书有习题解答么?
请回贴!
17996明天要叫卷子,这个约束条件用lingo编写不出来了。各位大哥大姐们,帮小弟个忙吧!!要用lingo编写,而且要是线性的。post-28-1126407455.ibf
17996sets:
row/1..7/:m;
col/1..7/;
matrix(row,col):c;
endsets
@for(col(j):@sum(row(i)|i
#ne# j:c(i,j)*m(i))=m(j));
17996不行啊!我全部的程序如下:
model:
sets:
city/1..7/:m,n,t;
col/1..7/;
row/1..5/;
cost(city,row):l;
link(city,city):c;
endsets
min=@sum(cost(i,k):l(i,k)*n(i));
@for(city(i):m(i)*t(i)=d*n(i));
@for(col(j):@sum(city(i)|i#ne#j:c(i,j)*m(i))=m(j));
!这个语句应该是对i求和的,@for(city:@gin(m));
可这样一编写,却成了对j求和了;
@for(city:@gin(n));
@for(city:@gin(m/n));
data:
t=6
3 6 5 2 1 2;
c=0 4 5 1 3 0 0
0 0 0 0 0 3 0
0 0 0 1 0 0 0
0
0 0 0 0 0 2
0 0 0 0 0 0 0
0 0 0 0 1 0 0
0 0 0 0 0 0 0;
l=71
27 34 37
18 33
17
30
18
17 13 12 28 23
7 9 0 7 6 5 11
4 3 0 4
2 0 2
1 3 1 0 2 5 6;
enddata
end
17996该句应该没有问题,@for(col(j):@sum(row(i)|i #ne#
j:c(i,j)*m(i))=m(j));
@for(col(j)是对每个j
而@sum(row(i)|i #ne#
j是对不等于j的i求和
17996可是为什么我一运行,它就说:该程序出错,即将关闭!我运行一次,就给我关一次,弄的我都没语言了。
反正我也管不了那么多了,我把它交我们老师,让他去郁闷吧
谢谢你!~~
17996可是为什么我一运行,它就说:该程序出错,即将关闭!我运行一次,就给我关一次,弄的我都没语言了。
反正我也管不了那么多了,我把它交我们老师,让他去郁闷吧
谢谢你!~~
17999hehe,这个问题还有人问,已经有很多范文发表了!!!!!!!!!!!!!!
17999求解一个数学建模题.(泄洪问题)
求解解题思路
题目见附件post-37-1126409624.ibf
17999在什么上有这问题的答案?
18000好的,谢谢了
18000问题一:
在看离散型随机变量的时候,不理解“可列无限多个”的含义。是不是属于某个区间内的这种变量?
问题二:
附图中,第一个红色部分,什么叫做“严格单调增加”,为什么一定要强调这个“严格单调增加”?
问题三:
附图中,第二个红色部分,我自己推出的结果不一样,想不出为什么?
我的结果是-f[-h(y)][-h'(y)]
post-
17-1126416380.gif
18000爽歪歪:
你的第一个问题作如下解释:可列无穷多个是指"可以排成一列(如数列),且为无穷多个"
第二\三个问题我看没有必要正面回答你:你完全不必记住定理的最后结果,只需弄清其证明思路,遇到类似问题如此推演即可.
好了吗?
18001我想考北科的数学系的研究生,请问这里有研一或研二的师兄,师姐吗?
请留言与我联系好吗??
18002
| 引用 (tobyqin @ 2005年09月11日
23时36分) |
楼上的对角线的元素不够大啊
:) |
随您的需要,在这里够解答问题并且简单就行了
18002mazl
的例子是对的,是经典的对角线方法的一个应用
这个例子不仅可以说明无限个无穷小的积不一定还是无穷小,还可以以此构造一个例子说明即使把一个数列分解成无数个子列的并,并且每一个子列均收敛到相同的极限,但原数列不收敛。
18002
引用 (yuanxuehan @ 2005年09月12日
17时02分) |
谢谢各位。
可是我没有看懂。如果是对的话,应该有一个逻辑的推理过程。如果是错的话,可以举个反例吗?
能不能再详细一点呢?
|
mazl 的例子中每一行构成一个无穷小量
但他们的乘积为1,故不是无穷小
18002我明白了!
小学生在这里谢谢各位初中生、高中生、硕士生、博士生,谢谢你们!
下次有问题再向你们请教。
18002谢谢各位。
可是我没有看懂。如果是对的话,应该有一个逻辑的推理过程。如果是错的话,可以举个反例吗?
能不能再详细一点呢?
18002各位:
高等数学书上有提到:有限个无穷小的积仍是无穷小。
请问:无限个无穷小的积还是无穷小吗?如何证明呢?
如果有证明过程,希望您能将证明发至我的邮箱:yuanxuehan@sohu.com
谢谢!
18002不一定
18002肯定是,这样吧把前面有限个保留,后面无限个乘积每一个绝对值确定范围1,也就是扩大,然后前面有限个趋于0,这个界趋于0,当然收敛于0了
18002提示:
考虑二重序列,在对角线上打主意!
18002见附图post-21-1126533440.ibf
18002是呀,没仔细看,我只看了前面几个元素
18002对不起,
我将序列重新改写了,谢谢诸位
18002
| 引用 (mazl @ 2005年09月12日
21时59分) |
对不起,
我将序列重新改写了,谢谢诸位 |
没什么对不起的
大家一起讨论一下
争取给大家满意的答案是共同目标
18003例如
if y <= a
x'= A y + B
else
x'= C y
+ D
end
或者
if y >=0
x' = A y
else
x' = 0;
end
这种情况的,如何用一个方程(组)表达呢?
18004假设有一顶点个数为$n$的完全图,从里面抽取三角形,每抽取一个三角形,就去掉相应的三条边(但是顶点保留),一直到没有三角形为止,目标是使最终每个顶点剩下的边数中最大者最小,问在最好的抽法中这个最小能小到什么程度,比如不倚赖$n$的常数,或$n$的无穷小或$n$的常数倍(倍数当然小于一)。不胜感激!
18006

18006没信誉
18007回家之后我就十分有机会来这里做题目了,我要大开杀戒了,好久没有在这里争着去做题目了啊!心里总是感到是一滩死水,没有生气!
18008小弟,新来到专科院校教书,求北大编著的高等代数视频可见
18008已经有人发上来了,你找找。我下了一部分,到二次型那章的!正在找之后的我QQ10452531
18008
http://61.128.234.241/search.asp?keyword=%...%C8%B4%FA%CA%FD
18008骗人,必须要是注册学员
18008北师大的应该好些吧。
18008当然是北师大的好啦!
18009大家好:
请问数学金融有哪些研究方向啊?
特别是彭实戈先生的研究方向?
18010www.china-pub.com
18010我知道的有"九章书店","天元书店"
但还是有很多好的数学书买不到.我想有很多的数学爱好者与我有同样的困惑.
不过如果大家一起来分享自己所知道的书店的话,那么我们都会从中获益的.
所以请推荐.
18010北京九章图书有限公司,全国最大的数学书书店,可以邮购,网上还可以查阅目录及相关信息!
18010
Math
6
18 的几何世界 主页右下角有
18010
| 引用 (sophisticated000000 @ 2005年09月12日
12时56分) |
| www.china-pub.com
|
这个挺不错的
18010九章的书还是太少了,外文的很少,哪里最好有买外文数学专业书的复印盗版就好了,这样便宜我们学生好好
18010同意楼上看法
18010如上所说
www.china-pub.com
确实不错,我就办理过,送货上门
18010
| 引用 (sophisticated000000 @ 2005年09月12日
12时56分) |
| www.china-pub.com
|
支持,有很多新书!而且办理代办邮购,送货上门。
18010我买的书基本上都是在当当网上买的,挺全。
18010
http://shop34502100.taobao.com天元书店全部书籍邮购
18010如果想买老的经典可以上孔夫子,推荐几个不错的书店,口碑都好。不过要先注册,很快的,不差那么点时间。打开页面后,在左下角的“分类浏览”里点选“理科、工程技术”条目即可。
貘的书屋:http://www.kongfz.com/star/2509/
(店主很专业,数学、物理类经典很多都能在这里见到,价格也合理)
商周书店:http://www.kongfz.com/star/
1712/
(老板是个好人,书也相当不错,定书超过50元还免费给你邮挂)
麓山特价旧书店:http://www.kongfz.com/star/3225/
(真正的特价,特便宜,同样超过50元免费给你邮挂)
精诚书坊:http://www.kongfz.com/star/3701/
(最近有一批俄文理科图书放出来)
振明书店:http://www.kongfz.com/star/3458/
(一匹黑马,先前有段时间放出大批物精、价平的数学物理类经典,最近比较少见了)
泳燕书屋:http://www.kongfz.com/star/3134/
(世图那批经典的外文影印偶尔有量,而且一般在5折以下,还全新的,T_T)
和平书社:http://www.kongfz.com/star/5669/
(也是一匹黑马)
九龙轩:http://www.kongfz.com/star/5375/
(黑马中的黑马,经常出其不意的放出你意想不到的好书)
18010补充两个兄弟书店
阆苑书斋:http://www.kongfz.com/star/4845/
阆阆书社:http://www.kongfz.com/star/4736/
阆苑书斋
好像暂时歇业。
买书之前请仔细阅读公告,利用好短消息功能与店主沟通。本人只是爱好书籍,所以把觉得不错的书店推荐给大家,但并不负任何连带责任。
18011是,这里用到微分方程里比较典型的求解方法
最后结果是Y/y+C
18011可我把式子越化越复杂
就是求不出来
18011
| 引用 (mimi8112 @ 2005年09月12日
09时51分) |
可我把式子越化越复杂
就是求不出来 |
那我把我做的贴一下好了:post-38-1126541095.gif
18011一道分析题
是不是要先利用p对x的导数等于q对y的导数求出值
第二曲线几分
post-38-1126446355.ibf
18011最后求原函数是不是应用积分与路线无关,现在0-x上对dx积分在对0-y上对dy积分呀。因为按上法,有可能那个常数c中含有与该积分变量无关,与另一个积分变量相关的项呢,这样积得就不对了吧
例如 (x^2+2xy-y^2)dx+(x^2-2xy-y^2)dy
望高人指点!!!
18011
| 引用 (my3555941 @ 2005年09月12日
23时22分) |
最后求原函数是不是应用积分与路线无关,现在0-x上对dx积分在对0-y上对dy积分呀。因为按上法,有可能那个常数c中含有与该积分变量无关,与另一个积分变量相关的项呢,这样积得就不对了吧
例如 (x^2+2xy-y^2)dx+(x^2-2xy-y^2)dy
望高人指点!!!
|
谢谢提醒
我已经在原帖进行了修改
18011我以前也用过那个方法,后来看好像不对。才注意到这个问题的。共同探讨共同学习共同进步吗
18011我的一个参数变换后的解法,不用考虑微分方程的东西,就直接做!post-38-1126756289.gif
18013你是要考06年大工研究生的吧
我是大工的
需要帮助的话加我qq:8
17121
18
18013顶一下
沉了都
18013呵呵,不应该哦!
18015是这样的,我考虑错了,但是我有更简单的证明。
post-21-1129048
192.ibf
18015
引用 (superyyzg @ 2005年10月09日
18时12分) |
| 似乎第一道题不需要nan单调那个条件 |
如果没有单调的条件,请讨论如下定义序列{a_n},
在n=m^3时,令a_n=1/m^2,其他情形a_n=1/n^2
.
18015请高手解决二道数分题(2)谢谢!post-21-1126486362.ibf
18015先解决其中一个问题:post-21-1126500787.gif
18015第一个题目解答:post-21-1126513082.gif
18015楼上的倒数第2行最后的趋于0是怎么来的哦,好象不成立
18015似乎第一道题不需要nan单调那个条件
18016
| 引用 (子青 @ 2005年09月12日
12时52分) |
|
把X_(1)和X_(n)的密度函数求出来,然后做减法的变换 |
谢谢。
18016向大家请教一题,见附件post-
17-1126489131.jpg
18016把X_(1)和X_(n)的密度函数求出来,然后做减法的变换
180
19[1] D. Gabor, “Theory of communication,” J. Inst. Elec. Eng.
(London),vol. 93, pp. 429-457,
1946.
[2] J. Daugman, “Uncertainty
relation for resolution in space, spatial frequency. and orientation
optimized by two-dimensional visual cortical filters,” J. Opt. Soc. Amer.
A, vol. 2, pp. 1160-1169, July
1985.
180
19没人回应自己顶一下!
180
19Too old, hard to find!
18020苏步青院士:负志争光为中华
苏步青院士,数学家,浙江省平阳县人。
1927年毕业于日本东北帝国大学,
1931年获该校理学博士学位。
1948年选聘为中央研究院院士。他曾任复旦大学教授、名誉校长,中国数学会名誉理事长。主要从事微分几何学和计算几何学等方面的研究,被誉为“东方第一几何学家”。早期在仿射微分几何学和射影微分几何学研究方面取得出色成果,其后在一般空间微分几何学、高维空间共轭理论、几何外型设计、计算机辅助几何设计等方面取得突出成就。
1955年选聘为中国科学院院士(学部委员)。
步青到达日本,是
19
19年重阳时节。一踏上岛国,就得选择投考的学校。当时,春季招生的只有东京高等工业学校。这是一所名牌大学,考生多,竞争激烈,中国学生没有一年的准备是不敢报考的。可是到日本三个多月后,苏步青满怀自信地走进了东京高等工业学校的考场。考数学时,试题包括算术、代数、几何、三角共24道,要求三个小时内做完。苏步青呢?只用了一个小时,就准确地演算完了全部试题,第一个交了卷,第一个离开考场。他的快速,连监考的老师也感到吃惊。
苏步青以优异的成绩考取了东京高等工业学校,又以优异的成绩毕了业。临毕业前,学校训导长把苏步青叫去,交给他一封信:“苏先生,你有数学才能,应当得到深造。我写了一封信,你拿着到东北帝国大学找数学系主任,我祝你成功。”苏步青真的找到了东北帝国大学数学系主任。在办公室里,系主任客气地迎接了他,并说:“苏先生,我们欢迎您!本校是非常重才的,希望先生能来到本校。”苏步青明白这位系主任的意思,他必须以自己的才智来推开这所学府的大门。
1924年,东北帝国大学数学系招收9名学生,报考的90人中,只有苏步青一个是中国留学生。谁将名列前茅?这是勇气和才智的竞赛。考试结果,苏步青的微积分和解析几何都以100分的优异成绩而名列第一。东北帝国大学的门洞开了,苏步青踏着坚实的脚步,向数学的高峰攀登。在这里,白天他埋头于图书馆,夜晚在昏暗的灯光下演算。
樱花雪花,春去冬来。这时期,国内政局动乱,有时根本没有钱汇寄给在外的留学生。身处异国的苏步青,只好利用星期六晚上,当家庭教师的办法,挣钱来维持贫寒的学习生活。有的同学曾劝他:“苏兄,何必如此拼命,毕业后有碗饭吃就行了。”早先,苏步青也曾有过读书找职业的想法,但来日本后,为中华民族争气的决心像一颗种子,在他心里生了根发了芽。他对同学说:“让我们想想受凌辱的祖国,为了祖国奋发学习吧!”不久,苏步青发表了第一篇数学论文《某个定理的扩充》,轰动了东北帝国大学,为中国人民争了气。这以后,他又连续写了三十余篇论文,在微分几何方面取得卓著的成就,获得了博士学位。(阿素)
摘自2005年8月28日《大众科技报
18021中国科学院研究生院2006年硕士研究生招生网上咨询通知
2005年9月12日~14日(9:00-20:00),中国科学院研究生院将参加2006年全国硕士研究生招生网上咨询活动。届时将由中科院研究生院招生办公室负责人解答有关2006年中国科学院系统各单位招收硕士学位研究生的有关问题,欢迎各位考生提问和咨询。中国科学院研究生院也是报考点之一,有关报考点的相关问题也欢迎广大考生咨询。
网上宣传咨询活动将在中国研究生招生信息网进行,网址是, http://www.chinayz.com.cn 和
http://www.chinayz.edu.cn 。
18021中国科学院研究生院与中科院数学所等到底有什么区别啊???
18023这是本人最近所授初等数论课程的考核试卷及其答案与评分标准
教材为
闵嗣鹤,严士健[/COLOR[COLOR=blue]]《初等数论》(第二版)斑竹回复:感谢!post-68-1126502437.ibf
18023有用!!
18023顶了
18023支持
18023不错!!
18023很不错!!!
18023谢谢楼主提供
18023Ding
18023值得顶!!
18023谢谢
18023支持一下
18023楼主真是好人啊,真是忒好的东西了啊
18023谢谢
18023thanks
18023谢谢了哦!
18023顶一个
18023顶了啊
18023真的不错
18023支持一下 呵呵
18023太好的东西!我喜欢!
18023thanks
18023xiexie
18023谢谢
18023谢谢!!!
18023先保存下来再说,谢谢了
18023谢谢!
18023DING
18023顶
ding
18023Problem A1 设p是素数,则p是某个整数边长的直角三角形的斜边的边长当且仅当p≡1(mod4)
Problem A2
设d≡3(mod4)是奇自然数,则
Pell型不定方程x^2-dy^2=-1 没有整数解。
Problem A3
试证:不存在自然数n,满足同余式
10^n≡9(mod79)Problem
18023要是作者添加上参考答案,那就是锦上添花了!
期待……
18023江西师范大学2006年初等数论专业课程考核试卷
所用教材:柯召,孙琦《数论讲义》(第二版)
18023要是有答案就好,谢了,好人哦。
18023没答案吗,要是有答案就好了。
18023有无答案啊
18023还有没有多点的考试题目,谢谢
18023没有答案的啊,可不可以再传一下啊
18023
2007年初等数论课程考核模拟测试试卷(***)问题1
试证:不存在自然数m和n满足不定方程2006m^2+m=2007n^2+n,而且m-n是完全平方数。
问题2
(0513)设a,b,c是正整数,且
9
+8cos20
0
=(a+bsinc
0 )
2 试证: max{
(
a+b)/c
}=
1 /10 问题3 试用两种方法证明二次平面曲线 x ^{2}-3y ^{2} =2
上没有有理点。Hint:点P(x,y)称为曲线f(x,y)=0上的有理点,如果点P满足曲线方程,且两个坐标分量都是有理数。
问题4
试求三次同余式5x^3+7y^3≡3(mod11)的所有不相同的同余解。
问题5
(1)设奇素数p满足p≡5(mod12),则同余式x^4≡9(modp)没有解。
(2)设奇素数p不满足p≡5(mod12),则同余式x^4≡9(modp)有解。
问题6 试证:inf{n/
φ
(n) :n是自然数}=1
问题7
问题8
18023什么时候把答案作出来咯!
18023
好东西,有答案吗?
18023贵
18023楼主只有试题没有答案的吗?
18023对啊!有没有答案?
18024楼上请多来和大家交流哦:)
180241、 NoteExpress多国语言版
10.6MB,性能最好的文献管理软件。支持Amazon,Pubmed等检索,具有笔记,全文等管理功能,可以在word中快速格式化输出引文列表。能管理的文献数量多达百万数量级。强烈推荐!
下载地址:http://www.scinote.com/support/cgi-bin/download_chs.cgi
2、JaniSearch 0.2
3M,是CMBI自主开发的一种高效、快速、智能的搜索软件。它可以调用数十种搜索引擎进行工作,其搜索的查全率、查准率和搜索速度都较常规搜索引擎有成倍的提高
JaniSearch中包含了16个医学、生物学相关的搜索引擎, 可以对文献、会议、基因、蛋白等数据进行查询。 并且作者还将继续添加新的引擎。
下载地址:
http://www.mirror.ac.cn/biosoft/down/JaniSearch02.zip
3、ica32t.exe
1.8M,
中科院上海文献情报中心推出的中国生物学文献数据库检索客户端软件,下载安装后,便能进行普通生物学、细胞学、遗传学、生理学、生物化学、生物物理学、分子生物学、生态学、病毒学、微生物学、免疫学、植物学、动物学、昆虫学、人类学、生物工程学、药理学及与生物学相关的科学技术领域相关中文文献的检索。
下载地址:http://www.mirror.ac.cn/biosoft/down/ica32t.exe
4、PathDB检索程序2.0
18M,PathDB是NCGR(National Center for Genome
Resource)提供的代谢途径数据库,,储存了丰富的与代谢途径、酶、反应、生物化学物质有关的信息。所有数据均按照分类法进行分类存放。PathDB储存了大量与代谢有关的信息,NCGR提供了这个Java语言编制的检索程序。
下载地址:http://www.mirror.ac.cn/biosoft/down/pathdb2-win-jre.zip
5、PubCrawler 1.8
88K,Perl语言写成,需要安装ActivePerl-5.6.0.6
18才能运行,8.7M,而安装ActivePerl需要先安装MsiInstaller,1.4M(Windows2000不需要安装),是一个免费的“警示”软件,可以检索NCBI
Medline文献库与GenBank核酸序列库每日更新的内容,使科学家获得其研究课题相关的科研方向的最前沿文献与信息。安装较为麻烦,而且使用也需要到原始网站仔细学习其ABC三步使用方法,不是很方便,但使用熟练后会非常有用。可以先到原始网站熟悉一下在线检索。
原始网站。
下载地址:http://www.mirror.ac.cn/biosoft/down/WinPubCrawler.exe
ActivePerl-5.6.0.6
18:http://www.mirror.ac.cn/biosoft/down/ActivePerl-5.6.msi
ActivePerl:http://www.mirror.ac.cn/biosoft/down/InstMsi.exe
6、npbook.exe
1.4M,国图网上图书浏览器插件。阅读网上图书馆的图书,需下载专用的国图网上图书浏览器插件,该插件支持 IE 和 Netscape
浏览器。有大量生物类书籍可在线阅读。
下载地址:http://www.mirror.ac.cn/biosoft/down/npbook.exe
7、PDGReader
1M。超星图书本地阅览器。比原官方的浏览器器要好多了,增加了一些小功能,阅读的时候不用老用鼠标拖来拖去了。该版本带有安 装界面,非常方便。
下载地址:http://www.mirror.ac.cn/biosoft/down/PDG%20Reader.exe
8、NetRose 1.3
1.7M。专门下载国家图书馆八个大类12000余本图书的免费下载软件,下载后使用超星浏览器浏览。多线程,多任务,支持断点续传。可以下载超星3.52版本所有图书的软件。其配套的PDG格式浏览器NetRoseBrowser
1.3,228K。
下载地址:http://www.mirror.ac.cn/biosoft/down/netrosev13.exe
NetRoseBrowser 1.3:http://www.mirror.ac.cn/biosoft/down/browserv13.zip
9、Book Express 1.03d
509K。是专门用于超星数字图书下载的工具软件。超星数字图书让网虫们足不出户也能逛逛国图,可是超星图书阅览器却只能提供在线阅览方式,它自带的付费下载功能有诸多限制且不稳定。Book
Express 可以大大节省我们的上网费用,把图书下载到硬盘上让你看个够。
下载地址:http://www.mirror.ac.cn/biosoft/ ... oft/down/ENDemo.EXE
10、中国数图浏览器beta 1.01标准版与增强版
2M与4M。增强版带OCR功能,中国数图网是网上看书的又一选择,下载中国数图浏览器安装后,便能在网上阅读大量的图书,其生物图书馆中的书似乎比超星图书馆新些。安装此软件需要系统安装有IE4.0以上版本。
标准版:http://www.mirror.ac.cn/biosoft/down/Nlc_reader.exe
增强版:http://www.mirror.ac.cn/biosoft/down/NLC_reader_ocr.exe
11、中国数图欺骗程序 0.8beta
6,上述软件的配套软件,可以让你用中国数图浏览器随心所欲地下载图书而无需买读书卡。本软件为Java语言写成,需要Java 2 Runtime
Environment支持,可以到java.sun.com下载。
下载地址:http://www.mirror.ac.cn/biosoft/down/d-cheat.zip
12、D-Library 1.1.0
60K,中国数图下载软件,可以下载中国数图的图书随意观看。找到你要的书,点“阅览”,数图的阅览器会出来,会显示出书的地址,把它复制到d-library的地址栏内,接下来就可以下载了。
下载地址:http://www.mirror.ac.cn/biosoft/down/d-lib110.zip
13、书生之家浏览器精简版与全字库版 3.30 Build588版
分别为3.3M与13.6M,精简版含有基本的字库,
可实现您的基本阅读功能,全字库版含有全部字库, 可实现您的原版阅读功能。下载后需在本机运行安装,方能使用书生之家数字图书馆,又一个网上看书的好地方。
精简版:http://www.mirror.ac.cn/biosoft/down/SMALLINS.EXE
全字库版:http://www.mirror.ac.cn/biosoft/down/INSFULL.EXE
14、百博阅读软件 VV2.30 Build 1030
1.84M,又一个网上看书的网站,不过没有什么生物类书籍可看。
第一个有可*的版权保护功能的中文数字图书阅读软件。专用于阅读百博版的数字图书,具有书架管理、图书分类、图书查找、全文检索、书签、笔记以及直接上百博网上书城下载数字图书等丰富功能。百博版数字图书文件比超星、博库版小得多,特别适合在线下载。语音阅读插件,9.5M。
下载地址:http://www.mirror.ac.cn/biosoft/down/bbrsetup231030.exe
语音阅读插件:http://www.mirror.ac.cn/biosoft/down/SpeechSetup.zip
15、Book Reader for NLC 1.0 Build 13
380K,数字图书(NLC)阅读器
1、只有一个bkreader.exe文件, 绿色软件 2、批量打印功能 3、键盘滚动、换页 4、鼠标拖动 5、全屏幕阅读(COOL)。
下载地址:http://www.mirror.ac.cn/biosoft/down/bkreader.zip
16、MiniViewer V1.58b
v1.59a5.exe
1.3M和583K,Brill大侠编写的功能强大并很有特色的一個数图浏览器,支持在线和离线浏览,支持在线检索(检索出的图书信息可以复制到剪贴板),支持鼠标拖动、自动滚屏(速度可调),支持全屏浏览、前景背景色调整、可浏览或下载图书的概览,以及支持代理服务器等等。使用前请下载ltkrn12e.zip(140K)解压后覆盖MV目录下的同名文件。
V1.58b:
http://www.mirror.ac.cn/biosoft/down/mv158b.exe
V1.59a5:
http://www.mirror.ac.cn/biosoft/down/mvexe159a5.exe
ltkrn12e.zip:http://www.mirror.ac.cn/biosoft/down/ltkrn12e.zip
17、CompressIt V2.0
4.8M,提供JBG(NLC)<->JPG转换功能
先要把*.nlc改为*.jbg->选browse->在左边框中选你要的文件->按Add->加入右边框中->按Compress->选择各种选项。
下载地址:http://www.mirror.ac.cn/biosoft/down/compressit.exe
18、维普浏览器OCR版
维普浏览器简化版
6.5M和1.8M,查看免费的维普期刊全文数据库专用软件。维普期刊全文数据库是一个免费的期刊全文数据库,如果不能上中国期刊网,这是一个很好的选择。不知免费能到什么时候。
OCR版:
http://www.mirror.ac.cn/biosoft/down/VipBrowserOCR.exe
简化版:http://www.mirror.ac.cn/biosoft/down/VipBrowser.exe
19、Dlib1.58b
1M。weberyap大侠的Dlib1.58b的出现,基本上可作为中国数图浏览器的一种替代(除了OCR)。可直接下载数图图书,不再需要图书的IP地址。下载后的图书自动添加到本地列表中(需要等到下一次打开),双击可以浏览。Dlib1.58b下载功能强大:支持书目列表、书目在线更新及排序,支持多线程下载,支持广义续传,支持在线检索(并能显示全面的图书信息),同时支持对检索结果的直接下载,支持代理服务器。浏览方面也极有特色:支持滚轮鼠标,支持鼠标拖动,支持方向键,并且以上三项均支持速度可调,另外还支持前景和背景色。
下载地址:http://www.mirror.ac.cn/biosoft/down/DLib_158.exe
20、nlcdownload 0.9.9
1.7M。国图图书下载系统,共享软件。专门为下载国家图书馆的电子图书而设计。以下是本软件的几个主要特点:
多线程下载国家图书馆电子图书10余万册。 直观的树状列表,显示图书书目。
采用数据库暂存技术,存储访问的历史记录,加快重复访问速度。共享软件,有限制。 可以用100天,但最多只能下载一本书的150页。
下载地址:http://www.mirror.ac.cn/biosoft/down/nlcdownload.exe
21、医网打尽 4.0版
140K。“医网打尽”主要用于生物医学类和普通类搜索,集成了google,百度,Pubmed,37C,Bio.com等著名搜索引擎,使其本地化。而且有在量的离线和在线搜索技巧。应该很好用吧,尤其对搜索生物方面内容很有帮助。
下载地址:http://www.mirror.ac.cn/biosoft/ ... wn/JaniSearch02.zip
22.
通用医学搜索软件2001
434K,中文共享软件。是一个专业的医学搜索程序,提供了国外20多个专业的医学搜索引擎的搜索,同时为了方便医学人士的使用,还加进了8个常用英文搜索,8个常用中文搜索。非常棒。
下载地址:http://www.mirror.ac.cn/biosoft/down/ms2001.exe
看完了,觉得有用,别忘了顶一下,鼓励一下积极性。。。。。
18024好久不来了,一来就看到这么有用的东西,我顶!!!!
18024好贴,顶!
180243x
18024不错的东西,有些不能下载了,要是能够更新就好了,:))
18024thanks
18025请问高等代数中的Sturm定理是什末?在哪本书上有?另极限和范数那本高代教材上有?谢谢!
18025蓝以中《高等代数简明教程(下)》、清华大学出版社的《高等代数学》上都有,还有在研究生代数学书上很常见。
18025今天才看到,多谢!
18026有人使用过或是研究过gabor函数吗,像这个下面的公式:
g
(x,y;σ
x
,σ
y
,Ω
x
,Ω
y
)=1/(2*π*σ
x
*σ
y
)*exp((-1/2)*(x
2
/σ
x 2
+y
2
/σ
y 2
))*exp(j*(Ω
x
*x+Ω
y
*y))
其中
Ω
x
=Ω 0
*cosθ,Ω
y
=Ω
0
*sinθ
我想把上面的公式应用到纹理图像中,其中涉及到的三个参数
σ x
,σ y
,Ω
0
应该根据什么进行选择才更科学?
18026你是做图形学的吧,要不就是数字图像.这个公式我不懂,不过,
"x 2 /σ x 2 +y 2 /σ y
2"---请问这句什么意思,没输入错吧?怎么突然多了4个新变量?有x2,没有x1....?我不懂,问一下.
18026可能是输入的问题,不是新变量,是x的平方,y的平方,带2的都是指原来变量的平方!
18027各位大侠帮帮忙,我想往国际期刊投稿,听说国外的审稿时间比较短还不收审稿费,可不可以给本人推荐几个关于计算机方面的?谢谢,欢迎回贴!
18027你上网上查一下期刊的投稿细则,有些可以电子邮件,有些则必须邮寄。计算机方面的在www.sciencedirect.com上有很多的。
18031假设一设备在任何长为t的时间内发生故障的次数N(t)服从参数为

t的泊松分布P(

t)。求相继2次故障之间的间隔时间T的分布函数。
18031
| 引用 (思考的蚂蚁 @ 2005年09月12日
15时26分) |
假设一设备在任何长为t的时间内发生故障的次数N(t)服从参数为 <!--Math $ $
MathEndBegin--><!--End Math-->  t)。求相继2次故障之间的间隔时间T的分布函数。
t)。求相继2次故障之间的间隔时间T的分布函数。 |
the interval time ,
W,has
exponential distribution M(

). therefore, the c.d.f of
W
is
F(w)=1-exp(-

w)
The proof is quite
straightforward.
Let time interval between to events is w.
P(W>w) if and only if there is no event accurs during this time
interval. Since number of events during w, N(w), has Possion distribution
P(W>w)=P(N(w)=0)=exp(-

w)
Hence, the cumulative distribution
function is
P(W<=w)=1-P(W>w)=1-exp(-

w)
any question, please ask.
18031
引用 (cc9hwa @ 2005年09月13日
19时24分) |
| 引用 (思考的蚂蚁 @ 2005年09月12日
15时26分) |
假设一设备在任何长为t的时间内发生故障的次数N(t)服从参数为 <!--Math
$ $ MathEndBegin--><!--End Math-->
 t)。求相继2次故障之间的间隔时间T的分布函数。
t)。求相继2次故障之间的间隔时间T的分布函数。 |
the interval time , W,has
exponential distribution M(  ). therefore, the c.d.f of W
is F(w)=1-exp(-  w) The proof is quite
straightforward. Let time interval between to events is w.
P(W>w) if and only if there is no event accurs during this time
interval. Since number of events during w, N(w), has Possion distribution
P(W>w)=P(N(w)=0)=exp(-  w) Hence, the cumulative distribution
function is P(W<=w)=1-P(W>w)=1-exp(-  w) any question, please ask.
|
I am sorry that you have made a mistake!
you
said :"Let time interval between two events is w. P(W>w) if and
only if there is no event accurs during this time interval."
if
the w is between two events, there will never be a event during the time
w! So,P(W>w) must be equal to 1.it's wrong obviously.
and
now i have solved the problem after thinking for two days .anyhow, your
rezult is right.
you'd better think again what is the meaning of
w.that is important.
thank you all the same.
18031晕过之后才有豁然开朗:)
18031
| 引用 (思考的蚂蚁 @ 2005年09月14日
12时01分) |
| 晕过之后才有豁然开朗:)
|
that's good you can make progress on you own.
there is no error in my statement, which really depends on how to
understand variable and constant.
There is one more point worth
mention. Possion process has a very important property which is
memoryless.
Finally, please be careful with your manner.
18031我说的是我晕过之后才有豁然开朗,不要误会。
顺及,无记忆性是指数分布的性质,泊松分布好像没有。
18032学华师大的<<数学分析>>吧。
我就在学这本书。
18032北大出的《数学分析新讲》也不错的!另外《数学分析习题集题解》也很经典啊!
18032分析我觉得北大的数学分析解题指南很好。教科书都差不多!
18032苏联的菲赫金哥尔兹的(微积分教程)很好,不过挺难学的。而且现在也不容易买到啊!
18032Rudin的<<数学分析原理>>很不错的.
18032上面的我都有,不过苏联的菲赫金哥尔兹的(微积分教程)是很老的版本了,Rudin的<<数学分析原理>>现在有中文的了吗?刚开始我觉得还是看中问的比较好,可以慢慢在看英文的。
18032
引用 (mathseu @ 2005年11月
18日
18时47分) |
|
上面的我都有,不过苏联的菲赫金哥尔兹的(微积分教程)是很老的版本了,Rudin的<<数学分析原理>>现在有中文的了吗?刚开始我觉得还是看中问的比较好,可以慢慢在看英文的。
|
能不能卖给我一套菲赫金哥尔兹的(微积分教程)吗?或者介绍几个卖家~~不要太贵~~
18032到bossh_math@163.com
密码123456找找看
上面有很多好书的
我觉得,如果想好好学的话,复旦大学的数学分析(陈纪修或者陈传璋)都是很好的
当然,如果觉得太难,复旦童裕孙的高等数学一书也不错,另外同济四版式很不错的辅导书
18032诸位,如果要考研过初试只要把华东师大那本数分和北大那本高代弄熟就没问题了,何必找那么多的资料,劳神又费力
18032我是数学系大一新生, 感到数学分析和高等代数很难,想寻求好的辅导书和各位师哥师姐好的学习方法.在这里先谢谢了.
18032我用的是复旦陈纪修版的<数学分析>感觉不错.
高代是用自己学校出的(挺不爽的),自已学时是以北大的为蓝本的
不好意思,没看清题意^_^
数分我们老师总是和我们说他们那一代人,每人都把吉米多维其翻烂了,虽然很多人不建议看,不过确是一本好书
高等代数一值在用一本山东科技出版的的习题解-_-!
还有就是有很精典很精典的
菲赫金歌尔茨著的<微积分教程>
18032菲赫金歌尔茨著的<微积分教程
18032季米多惟其习题集也不错
18032分析中的反例也很不错.
18032钱机林的书也很好.
18032今天刚从王府井井买了几本书:<数学分析新讲>张筑生。当把放在一起的众多分析书对比时,文盲也会爱上这本书,但印刷不是很好,尤其是第三册,简直是六十年代年代的感觉。我犹豫了好久,还是禁不住放弃其它印刷好的,买了这本;<数学分析解题指南>林源渠,新讲的配套题,一起买了。
<高等代数><高等代数教程习题集>王萼芳。。
七八十年代编的书比现在的有吸引力。感受到作者的认真。花了100两,呵呵。
18032小红帽 同志,你能给我推荐一本好的《数学分析》书吗?
18032一般就是复旦的《数学分析》,我们原来用的就是这个了。再就是你可以看看《托马斯微积分》这本书,经典的权威书籍。
18032rudin 数学分析原理
18032数学分析书籍很多,各自有自己的特点,学习应该多读几本书
18032你可以使用华东师范大学版的数学分析,配套答案,效果不错!我当年就是这样子读的!
需要答案的话加我qq26
1990224!
18032有好书通知我一声..
我都很需要.
18032陈纪修的数分
18032想多学点经典分析可以依次看Rudin的三本分析,其中写的最好的是 Baby
Rudin;国人套路,陈纪修等的数学分析(有配套习题详解)或张祝生的加方企勤的习题集,南开的实变写的简要,时间多的话,可以看周民强(有辅导书)或徐森林的,接下来是张恭庆的范函。俄罗斯教材选译也有几本好书尤其那本函数论与范函分析简明教程,布尔巴基学派的现代分析教程写得太牛了不大好念。
18034
在阅读文章时,我遇到了如下的公式:
d = arg min
{1/2x'Gx-cx}
其中,d,x,c,G 都是矩阵或向量.
那位大虾能为小弟解释一下符号 arg 的含义,
谢谢!
18034表示幅角
18034幅角主值!
Arg表示幅角!
18034应该是使得这个函数最小的x的取值
18034我看到的资料是说对后面那堆东西的最小估计
18034如果c,G
是常量的话,那就是使后面这个式子达到最小估计的x的取值,我看到文献中基本上都是表示这样的意思,建议你找一些优化方面的英文书查一下
18034argmin这个表示取到函数最小值的x的值
而argmax表示取到函数最大值的x的值
所以单纯的说arg得看后面的是什么函数:min
or max
18034arg是元素(变元)的英文缩写.argmin表示取到函数最小值的x的值
18035啊呀
真是奇怪了
你向人家请教
怎么要买帖子呢?
这个样子怎么会有人帮你呢
18035

请教:关于排列组合的题目!!
题目:以表g(n,k)示把n件相异的物件发给k个人,使得每人至少分得一件物件的不同分法,求证:g(n+1,k)=k*g(n,k-1)+k*g(n,k)
( 注"* "表示普通的乘法) 这是上组合数学课时候老师布置的一个题目,我怎么想都想不出来,请各位高手赐教,
18035初次在这里面发帖子,不知道那个 买帖子是什么意思..所以....哎...现在知道规则了...希望有人相助..
18035
| 引用 (妞妞虫 @ 2005年09月12日
21时34分) |
| 初次在这里面发帖子,不知道那个
买帖子是什么意思..所以....哎...现在知道规则了...希望有人相助..
|
那你就在原来的帖子上编辑一下
取消那个卖贴吧
18035设有n+1个物品,先将n个分配给k个人,剩下的一个称为W,有两种情况(1)这k个人都拿到了物品,一共有g(n,k)种情形,再将W给其中的一个人,共有k*g(n,k)中方法;(2)有1个人没有拿到n个物品中的任何一个,也就是说将n个物品分给了k-1个人,有g(n,k-1)中方法,在将W给没有物品的人(有k中可能),得k*g(n,k-1).
两者相加就得到g(n+1,k)=k*g(n,k)+k*g(n,k-1).
18037谢谢了!
18037lindo手册post-37-11265
17
197.ibf
18037谢谢了
18037不错不错
十分感谢
18037谢谢。
18037Thank you very much!
18037Thank you!!!!
太感谢了!我刚开始接触数学建模,急需要一个lindo的教程,太感谢了!!
18037very good thank u a lot
18037谢谢!
18037ho好,谢了阿!
18037这个还是以前DOS版本的说明书!!怎么就没有windows下相应的说明书哪?
帮助文件可以解决一切问题
18037谢谢!呵呵!
18037bu xie
18037Thank you!
18037怎么没有windows版本的手册啊
18037严重的好啊!!!
18037内容丰富,非常感谢!
18038德国数学家大卫·希尔伯特(
1862~
1943)是20世纪最伟大的数学家之一.他对数学的贡献是巨大的和多方面的,研究领域涉及代数不变式,代数数域,几何基础,变分法,积分方程,无穷维空间,物理学和数学基础等.他在
1899年出版的《几何基础》成为近代公理化方法的代表作,且由此推动形成了“数学公理化学派”,可以说希尔伯特是近代形式公理学派的创始人.
1900年希尔伯特38岁时在巴黎举行的第二届国际数学家大会上作了题为《数学问题》的著名讲演.在讲演中,他根据
19世纪数学研究的成果与发展趋势,以卓越的远见和非凡的洞察力,提出了新世纪所面临的23个问题.这23个问题涉及现代数学的大部分重要领域(著名的哥德巴赫猜想就是第8个问题中的一部分),对这些问题的研究有力地推动了20世纪各个数学分支的发展.
本文介绍关于希尔伯特青年时代的两个小故事.
一、老师在课堂上现想现推
1880年秋天,
18岁的希尔伯特进人家乡的哥尼斯堡大学,他不顾当法官的父亲希望他学习法律的愿望,毫不犹豫地进了哲学系学习数学(当时的大学,数学还设在哲学系内).希尔伯特发现当时的大学生活要多自由有多自由.意想不到的自由,使许多年轻人把大学第一年的宝贵时光都花费在学生互助会的传统活动饮酒和斗剑上,然而对希尔伯特来说,大学生活的更加迷人之处却在于他终于能自由地把全部精力给予数学了.
大学的第一学期,希尔伯特选学了积分学,矩阵论和曲面的曲率论三门课.根据规定。第二学期可以转到另一所大学听课,希尔伯特选择了海德尔堡大学,这是当时德国所有大学中最讨人喜欢和最富浪漫色彩的学校.希尔伯特在海德尔堡大学选听拉撒路·富克斯的课.富克斯是微分方程方面的名家,他的名字和线性微分方程几乎成了同义语.他讲课确实与众不同,给人的印象很深.课前他不大做准备,对要讲的内容,在课堂上现想现推.于是常常发生这样的情形,某个问题在黑板上推不下去了,这时他就再想另外一种方法,有时一连要换好几种方法,但他最后总能推导出结果来.他就是这样,习惯于在课堂上把自己置于危险的境地.这样的课学生们如何看呢?他的一位学生后来回忆时写道:这样的课,使学生们“得到一个机会,瞧一瞧最高超的数学思维的实际过程.”我们可以想象,善于思考和学习的希尔伯特肯定会从中领悟到一个数学家是如何思考问题的,这种包括几经碰壁终于找到解法的探索过程在教科书上无论如何是看不到的.把思考问题的实际过程展现给学生看,这样做实际上是非常富于启发性的.我国著名的数学方法论专家徐利治教授认为这一点对希尔伯特的成长肯定起过很好的作用.我想这一点对我们今天也很有启发.学习数学不仅要学会这道题的解法,而且更要学会这个解法是如何找到的.即学会思考.
二、苹果树下的例行出步
希尔伯特在海德尔堡上了一学期以后,接下来的一个学期,本来可以允许他再转到柏林去听课,但他深深地依恋自己的家乡,于是他又回到了哥尼斯堡大学.再下一个学期——
1882年春天,希尔伯特仍决定留在哥尼斯堡.
这时赫尔曼·阅可夫斯基从柏林学习了三个学期后也回到了哥尼斯堡大学.闽可夫斯基从小就数学才能出众,据说有一次上数学课,老师因把问题理解错了而“挂了黑板”,同学们异口同声叫道:“闭可夫斯基去帮帮忙!”在柏林上学时,他因为出色的数学工作曾得到过一笔奖金.这时,年仅
17岁的阅可夫斯基正沉浸在一项很深奥的研究之中——解巴黎科学院出榜征解的一个问题:把一个数表成五个平方数的和.一年后,
1883年春天,
18岁的阅可夫斯基和英国著名的数学家史密斯共享巴黎科学院的这项大奖.这件事轰动了整个哥尼斯堡.希尔伯特的父亲因此曾告
诫自己的儿子不要冒冒失失地去和“这样知名的人”交朋友.但由于对数学的热爱和共同的信念,希尔伯特和比他小两岁的闽可夫斯基很快成了好朋友.
1884年春天,年轻的数学家阿道夫·赫维茨从哥廷根来到哥尼斯堡担任副教授,年龄还不到25岁,在函数论方面已有出色的研究成果.希尔伯特和闽可夫斯基很快就和他们的新老师建立了密切的关系.他们这三个年轻人每天下午准5点必定相会去苹果树下散步.希尔伯特后来回忆道:“日复一日的散步中,我们全都埋头讨论当前数学的实际问题;相互交换我们对问题新近获得的理解,交流彼此的想法和研究计划.”在他们三人中,赫维茨有着广泛“坚实的基础知识,又经过很好的整理,”所以他是理所当然的带头人,并使其他两位心悦诚服.当时希尔伯特发现,这种学习方法比钻在昏暗的教室或图书馆里啃书本不知要好多少倍,这种例行的散步一直持续了整整八年半之久.以这种最悠然而有趣的学习方式,他们探索了数学的“每一个角落”,考察着数学世界的每一个王国,希尔伯特后来回忆道:“那时从没有想到我们竟会把自己带到那么远!”三个人就这样“结成了终身的友谊.”
正如徐利治教授所指出的,良师益友间的互相切磋讨论对希尔伯特的成长发展也起了十分重要的作用,可以想见那段时间是希尔伯特才、学、识获得迅速成长的重要阶段,假如没有这段经历,那么希尔伯特在
1900年竟能在许多重要领域中一次提出那么多著名难题,倒是不易想象的了.
有关希尔伯特散步的这个小故事告诉我们,师生除了在课堂上的活动以外,师生在课外的交流以及同学间的课外交流,也是一种重要的学习方式,对数学学习非常有益。而且,在散步中交流因为没有书本,也不用纸和笔,因此没有繁琐的推导和计算,只能交谈那些能用话“说出来”的东西,即对问题的理解,分析总是中的思想和方法,挖掘统帅形式推导的灵魂,......而这些对学好数学非常重要。同学们不妨经常邀几位要好的同学一起散步交谈,肯定会其乐无究的。
18039假设一设备在任何长为t的时间内发生故障的次数N(t)服从参数为kt的泊松分布P(k t)。求相继2次故障之间的间隔时间T的分布函数。
18039好像服从2阶爱尔朗分布。
18039嗯,没错
18040" Let H be the group opposed to G" G is a group.
请问这个 H
是怎样一个群?也就是问这个 H 是如何定义的,谢谢!
18040the opposite group of a group
一个群的反群,可能是把一个群的乘法定义成原来群的乘法的反运算所构成的群,a*b:= b*a ,猜的,不一定对.
18040关键oppose是怎样定义的
书中给出了例子没有?
18040楼上的说的很对,应该同反代数差不多
18040是在以群G的乘法为基础定义新运算的G,乘法为a.b=ba
18040好象不应该,没有必要。还是建议看上下文
18040假设群G为<G,.>,则H(<H,*>) 的运算*可以这样:a*b=b.a
18040
| 引用 (cryse @ 2005年11月24日
12时14分) |
|
假设群G为<G,.>,则H(<H,*>) 的运算*可以这样:a*b=b.a
|
是个人理解还是查的
18041lim[1/n +1/(n+1)+

+1/(2n)]
n


18041ln2
利用:
lim
(
1+1
2
+⋅ ⋅
⋅+1
n
-lnn)→
常数。
18041我把tobyqin的写的好点post-38-1126525632.gif
18041
引用 (luting5 @ 2005年09月12日
19时47分) |
| 我把tobyqin的写的好点
|
谢谢
我刚才都编辑好了
只是发现那时候我这里没法贴附件和图的
18041看成积分的求和形式也可
18041
| 引用 (reijin @ 2005年09月12日
20时04分) |
| 看成积分的求和形式也可
|
不过还是要夹逼一下吧
:)
我错了
我理解成另外的意思了
呵呵
我习惯称为积分的定义没注意
18041用吗?
原式=lim[1/n*sum(1/(1+k/n))]=

1/(1+x)=ln2
x属于[0,1]
18041我想至少得说一下可积吧!
这道题目的方法很多的
18041谢谢!!
18041利用1/n+1/(n+1)…………1/2n-lnn收敛于欧拉常数可以,积分也可以!不过直接用它大于[1/2n+1/2n+……+1/2n]n=n/2不就可以了吗?
18042章新胜:大学要与科研院所及企业合作
--------------------------------------------------------------------------------
教育部副部长章新胜在第二届中外大学校长论坛上接受记者采访时表示,大学要进一步加强与科研院所、企业的合作,在支持、服务国家和大学所在地的发展中发展自己。
章新胜说,法、美等国的许多国家实验室都放在大学里,利用大学的人才、学科交叉优势,获得一些原创性科研成果。大学像河流,人才经常流动、知识不断更新;科研院所像水库,储蓄了大量的人才、设备等科研资源。综合性大学汇集了众多的学科,大学天然易于学科交叉,大学培养的硕士、博士研究生几年一茬,大学具有天然的人才流动优势。国内大学与科研院所结合的规模、层次等还不够。章新胜认为,大学与企业的结合尚有巨大潜能。企业的技术提升和革新需要大学支持,其人员需要到大学深造,大学可以利用企业的资源,达到自己“瘦身”、精筒的效果,同时获得科研成果转化的更多机会和更多的经费支持。
(摘自人民网2004年8月)
18043中国软件业有望在几年内赶上印度的发展
政府采购决定中国软件业的发展
倪光南院士认为,“政府采购就应该考虑保障自己国家的利益和安全,”政府采购优先本国软件不违反WTO规则,政府采购花的是纳税人的钱,就应该为本国的产业发展服务。
倪光南院士表示:“中国应当向发达国家学习,用国家资源大力支持自主创新。目前各级政府在这方面做得还远远不够,例如在2004年政府软件采购中,在本国软件能够使用的情况下仍大量采购外国软件,这显然不符合政府采购法。而如果没有政府的支持,尤其是没有政府来带头使用国产基础软件,那么中国的基础软件是不可能发展起来的。”
在不久前的“政府采购事件”和《政府采购法管理条例》中关于“非国内软件企业采购目录”引发的争议中,倪光南院士认为,近几年政府给予了国产软件很多方面政策支持,但软件产业是自然垄断的产业,大企业会越来越大,小企业会越来越小,特别是在操作系统和办公套件这些方面,事实上已经形成了垄断。“在我们国家没有出台《反垄断法》的情况下,政府采购和行业采购是我国软件企业对应国际软件企业垄断,获得发展的一大希望所在,意义非常巨大。”
“持续发展要靠发展核心技术”
倪光南院士曾强调说:“软件产业必须强调自主知识技术,强调知识产权,这是因为它在很大程度上决定着一个国家信息安全和综合国力。公司无论大小,都有可能应时制宜、因地制宜地进行创新,这正是中国成为信息强国的希望所在。
反之,如果不讲技术,不搞创新,一味跟随模仿,只能处处被动、永远落后,不可能成为信息强国。”
“建立自主、完整的软件体系将增强我国软件的国际竞争力,促进外加工业务发展,而且还可摆脱发达国家利用市场和标准方面的优势扼杀我们的创新能力,实现跨越式发展。”
他指出,中国软件企业在核心技术领域的话语权缺失,只能在国外核心技术基础上实现面向用户的应用开发。
“中国软件业有望三五年内赶上印度”
倪光南曾在济南一次会议上表示:“如果考虑到自主知识产权开发、销售市场、教育等方面的因素,我个人认为中国软件产业完全有望在三、五年内整体上赶上印度。”他表示,“中国和印度国情的最大不同在于,印度没有很大的内需市场,而中国有很大的内需市场,这是中国的重要优势。如果我们将中国软件产业的主攻方向放在外包方面,而将国内市场拱手送给外国软件公司,这显然是不明智的。”
倪光南院士指出:“印度软件产业的一个弱点就是没有自己的基础软件,缺乏自主发展能力,无法建立自主的软件产业体系,印度的模式则是承接美国软件业的外包加工,这种模式我们不能照搬。为了满足软件产业作为中国的一个战略产业的需求,中国只能依靠自主创新,发展包括基础软件在内的全部软件,逐步建立中国自主、完整的软件产业体系,最终使中国成为一个软件大国、软件强国。”
摘自2005年7月5日《大众科技报》
18043我看不太可能,中国的科学氛围和语言方面的优势远远不如印度
18044哈哈
谢谢大家支持啊
18044楼主发的好贴子.
18044韩国科技起步晚于中国10年为何反超
《瞭望东方周刊》
中韩两国产业技术创新五年规划70%的发展目标相同,但是,韩国企业的科技竞争能力早已经挤进了全球前五强,创新能力源于民族精神。而中国科技发展,在官本位思想的长期腐蚀下,创新能力让位于政府公关能力;民间科技创新能力受制于传统的官僚管理体制。客观上造成了:科技管理部门提供的资金越多,科研部门主动创新能力就越小;经济越发展,民族创新的能力反而越弱的怪相。
韩国科技起步晚中国10年
漫步韩国街头,举目四望,韩国品牌的汽车招摇过市。可是在中国,街头最豪华的汽车都是外企或合资企业的产品。当许多人沉浸在中国成为世界工厂的兴奋之中时,韩国在科技领域已远远地走到前头。
科技部副部长尚勇6月在深圳公开对上百家企业代表说:“韩国科技起步比我们晚10年,为什么在很多领域韩国远远领先?很重要的一点是韩国有很强的民族精神,并把创新形成了国家的意志。”
在举办足球世界杯期间,韩国全民的亢奋状态让全世界的球迷们深有感触。但是,仅有民族狂热显然是不够的,韩国科技主管部门把民族的精神变成了促进科技发展的动力,并且在各个部门、各个环节形成了有机的整体,把扶持和发展本国高科技企业当成使命,形成国家和地方经济的评价体系。当我们热衷于市场换技术的时候,韩国人早已把发展科学技术,提高民族的创新能力上升为国家意志,并且制定了具体的法律制度。
朝鲜半岛大规模军事冲突结束以后,韩国百废待兴。在吸收美国和其他国家的先进技术之后,韩国在很短的时间内重建了自己的工业体系,并且把科技发展作为自己的立国之本。面对外国企业提出的诱人合作条件,韩国企业始终不放弃自有品牌。经过几十年的辛勤培育,韩国在汽车、半导体、高速铁路、核电站等项目上都拥有了领先世界的技术,并且成功地将知识产权转化为生产力,继续推动韩国的产业革命。
可是在中国,土地换技术、市场换技术的发展模式,长期成为许多地方发展经济的首选。有些地方政府官员为了在短期内出政绩,甚至默许纵容科研单位利用虚假材料申报科研项目。
韩国的经验告诉我们,技术的模仿并不可怕,可怕的是满足于模仿他人,而缺乏民族气节,失去创新的能力。比较中韩两国产业技术创新五年规划,在70%的领域两国发展目标相同,但是,韩国企业的科技竞争能力早已经挤进了全球的前五强,可中国企业仍然徘徊在门外。
中国并非没有优秀的科技工作者
民族精神不是一句空洞的口号,而是民族品质的集中体现。从功能上来看,民族精神首先体现为一个民族的凝聚能力,从价值上来看,民族精神体现为一个民族的创新能力。如果一个民族缺乏凝聚力,那么纵然有许多科技工作者投身于创新事业,由于不能够形成合力,整个民族的创新能力仍然无法体现。
在中国并非没有优秀的科技工作者,但是在条块分割的官僚体制下,优秀科技工作者的创新能力难以得到充分的发挥。在某些地方,由于官僚主义作风盛行,科技工作者不但不能享受应有的待遇,反而由于缺乏人际关系处理能力,而陷入困境。
如果没有良性的促进科技创新机制,没有通过民主改革而形成的凝聚力,那么,中国的科技工作者得不到创新的动力支持。
韩国的科技创新能力培养,不是自上而下,而是自下而上。在韩国,企业是创新的主体,每一个企业经营者都深刻地意识到,如果缺乏自主知识产权,就不会得到政府的支持,更不会得到民众的理解和欢迎。因此,在韩国拥有自主的品牌,成为创业者最原始的动力。
而在中国,科技创新仍然源于政府推动。在政府主导下,科技经费的发放、科技成果的评估、科技成果的推广乃至科技人员的奖励都严重依赖政府。这样的科技促进体制,容易滋生官僚主义,容易产生苦乐不均的现象,容易培养伸手向上的惰性,甚至容易扼杀民间科技创新活动。
爱国主义教育必须注入科技创新内容
提高中国科技创新能力,必须从改变中国的科技管理体制入手,通过重塑民族精神,鼓励民间自主创新。至少应做好以下几方面的工作:
首先,必须建立全国科技统筹委员会,广泛吸收社会民间人士参加科技规划和资金分配工作。科技统筹委员会由总理直接领导,通过召开一年一度的科技统筹委员会,制定中国科技规划;根据规划合理分配财政资金。政府不再组织科技评审、不再组织项目验收、不再直接管理科技经费。科技统筹委员会可以通过民主决策的方式,确定未来中国长期、中期和短期科技发展目标,可以通过投标招标的方式,公开科技资金的分配情况。
其次,在爱国主义教育中必须注入科技创新的内容。爱国主义教育不等于革命教育,更不仅等于革命先烈教育。爱国主义教育必须宣传科技创新人才,必须把推动历史前进的科技工作者放在优先的地位。
第三,必须改变“损不足以补有余”的科技管理体制,将有限的科技资金,通过公开透明的方式拨付给最基层的单位。当前这种“对花浇水,根部缺乏水分”的现象,再也不能继续下去了。
18044感慨啊
18044说的太对了,官本位嘛,这篇帖子不止应该出现在这里
18044其实,官本位仅仅是扼杀了中国的科技吗?中国的死气沉沉和缺乏创造性思维的坚强品格,恐怕也与官本位不无关系。
中国的学生缺乏创造力,这是为什么呢?要说学校是批量生产的工厂,可那个国家不是这样呢?要保证全民受教育,除此更有它法吗?给每人请个家教?针对个人情况因材施教?前者难以做到,可后一种方法看来不错,但是,因材施教就能培养创造力吗?我看未必,只要你所施教的对象还在不停的保先、只要领导在时打扫一尺见方的教室还看得见全体年轻教师一拥而上、只要领导走后若干人等一哄而散,留下垃圾一地、只要全体高校教师还为职称而不得不。。。只要现目今的政治制度不调整,就不会有创造力!可以说,正是我们伟大的、地大物博进口石油的、坚强的、每年经济以10%递增的、贪污腐败盛行的、年轻人过日子看眼色的、以前无古人的方式作假和后无来者的手段搞形式主义的、让无数爱国志士抛头颅撒热血的中华人民共和国,造成了这一切。又或者,只要我因为写了这些东西就被压迫的事实还存在,中国就不会有创造力!
当然,有人说应该实行教改,应该提供学生更生动形象的、更贴近现实的教材,加上先进的教学设备、最接近国外一流大学的管理方式、高薪聘请最一流的科学家。。。。。。,总之,把学校按国外的先进方式整个修改,这样一定可以培养出创造力!我要说的是,这样也能培养创造力,西边就会出太阳了!理由其实同上,只要在这个学校里的老师和学生继续做上述各项事情,那么刻板和闭锁就仍然是该校不死的幽灵,至于创造力,绝对是癞蛤蟆想吃天鹅肉,想也别想。更糟糕的是,也许若干年后,该造学校的人离开了,发誓杜绝所有形式主义的人退休了,这学校就因为条件一流而成了某某大官的某某侄子的私人会所,届时他将拥有学校的多处房产,他的三姑六婆将占据学校的食堂经理、后勤董事、财务处处长等职,实在没文化,也可以承包学校围墙边的商店、大门看守、扫地工、单车棚等等。也许诸位看到的现在的某些中国大学,正是这样一步步演变来的呢。
18044分析透彻呀!!!
哈哈!!
18044说的好啊
18044好帖!!发人深省!
18044有些问题是不能深入讨论的!不然会发掘出重大问题·!!
18044听听"董存瑞"或者张楚的歌放松一下
18044说得好!可是我们又能做些什么呢?无奈啊!
18044
引用 (李世民 @ 2005年09月25日
18时14分) |
其实,官本位仅仅是扼杀了中国的科技吗?中国的死气沉沉和缺乏创造性思维的坚强品格,恐怕也与官本位不无关系。
中国的学生缺乏创造力,这是为什么呢?要说学校是批量生产的工厂,可那个国家不是这样呢?要保证全民受教育,除此更有它法吗?给每人请个家教?针对个人情况因材施教?前者难以做到,可后一种方法看来不错,但是,因材施教就能培养创造力吗?我看未必,只要你所施教的对象还在不停的保先、只要领导在时打扫一尺见方的教室还看得见全体年轻教师一拥而上、只要领导走后若干人等一哄而散,留下垃圾一地、只要全体高校教师还为职称而不得不。。。只要现目今的政治制度不调整,就不会有创造力!可以说,正是我们伟大的、地大物博进口石油的、坚强的、每年经济以10%递增的、贪污腐败盛行的、年轻人过日子看眼色的、以前无古人的方式作假和后无来者的手段搞形式主义的、让无数爱国志士抛头颅撒热血的中华人民共和国,造成了这一切。又或者,只要我因为写了这些东西就被压迫的事实还存在,中国就不会有创造力!
当然,有人说应该实行教改,应该提供学生更生动形象的、更贴近现实的教材,加上先进的教学设备、最接近国外一流大学的管理方式、高薪聘请最一流的科学家。。。。。。,总之,把学校按国外的先进方式整个修改,这样一定可以培养出创造力!我要说的是,这样也能培养创造力,西边就会出太阳了!理由其实同上,只要在这个学校里的老师和学生继续做上述各项事情,那么刻板和闭锁就仍然是该校不死的幽灵,至于创造力,绝对是癞蛤蟆想吃天鹅肉,想也别想。更糟糕的是,也许若干年后,该造学校的人离开了,发誓杜绝所有形式主义的人退休了,这学校就因为条件一流而成了某某大官的某某侄子的私人会所,届时他将拥有学校的多处房产,他的三姑六婆将占据学校的食堂经理、后勤董事、财务处处长等职,实在没文化,也可以承包学校围墙边的商店、大门看守、扫地工、单车棚等等。也许诸位看到的现在的某些中国大学,正是这样一步步演变来的呢。
|
精辟
18044
引用 (baixueli88 @ 2005年10月
17日
17时06分) |
|
有些问题是不能深入讨论的!不然会发掘出重大问题·!! |
也是一家之言
18044因为韩国人贱!
18044是好贴.不过发错地方了吧.
18044楼主好贴!几篇跟帖也非常不错!
其实大家对中国此方面的问题都有所觉悟,但多数人只是敢怒不敢言,偶尔发下牢骚而已。
可叹泱泱大国,人才凋零;百足之虫,死而不僵
18045呵呵,原因不是唯一的呀
18045信心不足妨碍中国自主创新
转自
科学时报
以自主创新、构建创新型国家的战略抉择为主题的“第四届中国科学家论坛”今天在京举行。中国科协主席周光召院士出席论坛开幕式并作关于自主创新的主题演讲,全国政协副主席、两院院士王选作了书面发言。
周光召说,现在科技界的自信心不足将妨碍我国的自主创新。比如有了一个新想法,就会有人问:外国有没有?如果外国没有,就要接着问,我们干吗要做?这是一种缺乏自信心的表现。只有环境变得宽松一些,让大家能够开展严肃的学术争论,才会真正有利于新的思想、新的看法涌现。
周光召认为,现在社会上宽容失败的氛围还没完全形成,创造一个什么样的创新文化和创新环境应该进行专门研究。中国人很聪明,但从小就受到应试教育和传统观念的束缚,崇尚权威。不过,在创新的这个问题上应该没有权威意识才行,要敢于向权威挑战,敢于开展严肃的学术争论,发展学科交叉和融合,促使新的思想不断涌现、新的人才迅速成长。自主创新要改变观念,通过制定发展战略和规划形成创新的文化和氛围、组成创新的团队、采取积极的创新措施,这样,我国的自主创新能力就一定能很快达到世界前沿。
记者潘锋根据王选院士在第四届中国科学家论坛上的讲话整理:
要有超过外国人的决心和信心
去年仙逝的数学大师陈省身说过:“一般中国人觉得我们不如外国人,所以我要把这个心理给改过来。”杨振宁先生认为,他一生中最大的贡献也许不是获得了诺贝尔奖,而是帮助中国人改变了一个看法,那就是“中国人不如外国人”的看法。对此我深有同感。有人问过我:“你在从事激光照排研制过程中,最大的苦恼是什么?”我立刻回答说:“最大的苦恼就是大多数人不相信中国的系统能超过外国产品,不相信淘汰铅字的历史变革能由中国人独立完成。”
1980年前,对于我们跨越式发展的独特技术方案,大多数人的评价是“根本做不出来”;
1981年激光照排原理性样机鉴定后,直到
1989年前,多数人的估计是“即使做出来,也无法与外国产品竞争”。其实,在高新技术领域,赶超外国产品的机会是很多的。
设法比外国同行更早得到最前沿的需求刺激
“未来的市场需求”和“现有技术的不足”是创新的源泉。恩格斯说过:“社会一旦有技术上的需要,则这种需要就会比十所大学更能把科学推向前进。”我们在研制激光照排过程中,由于汉字字数多,迫使我们比西方同行更早地采用了字形轮廓描述方法;汉字笔画多,促使我们于
1975年最早提出用附加信息指示横宽、竖宽,保证了字形变大、变小时依然匀称。由此可见,只要能准确地预测未来市场需求,找到满足这种需求的新技术,我们就有可能在技术和产品上领先于国外同行。
近年来,中国的信息产业市场发展迅速,正是得益于这种市场需求的刺激。获2004年国家科技进步一等奖的“多业务统一网络平台”就是很好的例证,这一平台在世界上首次实现了在一个统一的承载平台上,同时提供语音、数据、互联网、视讯会议、可视电话等多种业务网络。
找准市场的切入点
一个企业在创业方面选择方向时,总是面临国内外已有产品的竞争压力,如何选准和研发有竞争力的产品切入市场,从而积累继续发展的资金,成为首要问题。
中星微公司是海归创业最成功的企业之一,研制的获得2004年国家科技进步一等奖的数字多媒体芯片,在国际市场上销量第一,是我国惟一大量占领市场的自主创新的芯片。中星微成功的原因很多,但重要的一点是市场切入点选得非常好。中星微成功地选择了技术含量高、市场前景广阔、尚处于群雄混战局面、没有强势企业和产品的多媒体芯片。在找准方向后开足马力、奋力拼搏,占领了技术和市场的制高点。
国外杂志经常提到,在激烈的竞争中,找到薄弱环节切入,吃下一块市场。我非常赞同这种做法。
在国外最先进技术的基础上进一步创新
美国一家制药公司发明了一种抗癌新药,但治疗效果并不理想,最终未获批准上市。我们中国上海三维生物技术公司的研究人员,在仔细分析和试验了这一新药之后,变换思路并首次提出将肿瘤细胞溶解释放的抗原信息全息地呈递到免疫系统,以激发特异的体内肿瘤免疫,实现了个性化治疗。这样,注射一处肿瘤,全身其它部位的肿瘤也可能缩小或消失,疗效大为提高。目前,这一新药已经经过三期临床试验,这一在美国专利基础上的重大创新,即将获得国家药监局的批准。
同样,在通信领域的不少核心技术也被外企专利所垄断,中国企业不得不为此付出专利费。华为是中国申请和取得发明专利最多的企业之一,其创始人任正非的一段话很有意思:“好比一座山,山顶已被外商专利占领。华为就大力发展山脚下的专利,把山脚围起来。当从山顶下山时,就必须经过这些专利,我们就用山脚下的专利来换取山顶上的外商专利。”
对中国低成本的渴求是创新的动力
我从事激光照排研制时中国还比较穷,印刷厂渴望淘汰铅字,但又无法承担高昂的设备更新费用。
1981年,日本东芝公司报价2000万美元,愿为中国某大报提供整套照排系统,但被否定。根据我们的调查,一套照排系统的报价应在70万元人民币左右,加上其它附属设备,总价格应控制在200万元人民币。
正是这种对性能价格比的强烈追求,使我们创新。首次设计出了提高字形产生速度的专用芯片,降低了成本,不仅体积小,而且比国外同类系统起码高十几倍。首次使输出逼真大样的印字机,与精密照排机共享一个字形发生器和控制器,显著降低了成本,这一技术保持了多年的领先地位。现在,日本很多报业集团也都采用了方正日文出版系统。
从预测未来到发明未来
1987年,当MS
Windows只有1.0版本时,我的博士研究生郑民敏锐地感到Windows的强大生命力。他当时认为Windows不仅提供了友好的图形用户界面,更重要的是提供了良好的软件集成环境。这一颇具前瞻性的观点深深地打动了我,当即决定今后的软件均在MS
Windows上开发。20世纪90年代后期,方正研发的第一个基于MS
Windows的日文杂志编排系统和日文报纸组版系统,分别在日本投入使用。
1997年,微软一位高级副总裁与我会面,当他得知中国多数较大的报社已经采用了基于Windows的客户机和服务器架构时大为吃惊,说美国报社尚未达到这样的水平。
预测未来的最高境界是发明未来。20世纪70年代初,计算机终端大多为打字机,显示器尚未普及。而此时施乐公司PARC研究中心的一批科学家,在无拘无束的自由环境和浓厚的学术氛围中,创造了一系列里程碑式的成果,其中包括今天广为流行的鼠标和图形用户界面。其主要发明人Alan
Kan有一句名言:“预测未来的最佳途径是发明未来。”
发明未来的另一个光辉榜样是袁隆平院士。20世纪60年代,国内外农学家并不相信水稻杂交有产量优势,所以不可能预测到杂交水稻将成为主流作物。袁隆平院士独具慧眼发明了杂交水稻,使之成为主流作物。袁隆平院士又从杂交稻到超级稻,不断地发明未来。我国年轻一代科学家应以袁隆平院士为榜样,做出一批称得上“发明未来”的重大成果来。
18045关键是体制啊
18046看过了.
18046呵呵,很有道理呀。说的真好呀
18046借“伽利略的手指”指点伟大的科学想法
科学时报8月31日讯
现代科学登上历史舞台以来,被从无数个科学家头脑中产生的伟大科学想法推动着不断进步。什么是伟大的科学想法?一个科学家眼中的科学想法是怎样的?牛津大学化学教授彼得·阿金斯,也是著名的通俗科学作家,近日带着他的新书《伽利略的手指》来到中国北京,和一群年轻人坐在科技咖啡馆中,分享他心目中科学史上最伟大的10个思想。
伽利略是对近代科学产生了推动性影响的科学家,他的一只手指现正保存在意大利佛罗伦萨的密封容器中。正是他的手,指点人们走出中世纪的愚昧,揭开关于宇宙、世界和我们自身的秘密。新华社国际部科技编辑室副主任毛磊说,伽利略的手指象征着西方近代的科学知识、科学的魅力,甚至可以说是科学的魔力,借用这个比喻,象征着科学家发现和发扬了这些伟大的科学想法。
阿金斯声称,任何受过教育的人,都应该熟谙这些现代科学的核心思想。他说,一个科学的想法到底好不好,有两个很简单的标准。
首先,这个想法应该特别简单。作为一个科学家,在观察周围世界的时候,会看到世界的纷繁复杂和美丽多姿,然后还能用非常简单的原理对这个世界加以分析。科学家就是要在复杂之中追求简洁。当然,一个想法不能光是简单,这远远不够,简单的想法有可能只是愚蠢的想法而已。所以,除了看起来简单以外,另一方面,科学的想法还要有丰富的内涵,能够囊括各种现象,就像一个能够窥见丰富科学世界的小小的窗口。
在阿金斯心目中,能称得上推动人类科学进步的10个伟大科学想法包括:自然选择导致进化;DNA包含遗传代码;能量守恒;一切变化都是能量和物质趋于耗散所导致的后果;物质由原子构成;对称性限制、引导并推动事物发展;粒子与波相生相形;宇宙膨胀说;时空弯曲;协调一致的算法是不完善的。10个想法一出,立刻引起了年轻人的好奇,尤其是最后一个想法,指出了数学这一科学工具的局限性。
面对疑问,早有所准备的阿金斯说,科学研究离不开数学,数学能帮助我们形成并应用科学的想法。如果数学出了错,它可能会对科学产生严重的影响。而著名的哥德尔不完全性定理证明,数学这个在所有科学中最抽象的一门(如果它算是科学的话),在揭示任何知识的形式系统的结构时可能都存在着限制,即命题本身和它的否定在该系统中都不可证。所以在比较深层次上看,人们对科学的信心是有一定局限性的。基于这个原因,阿金斯就把它包含在10个伟大的科学想法中。
激烈讨论之外,阿金斯向人们透露,他最喜欢的一个科学想法就是热力学第二定律。尽管没有细说,但看看该定律产生的过程就能明白原因何在。热力学理论的奠基者是
19世纪的法国工程师萨迪·卡诺。在研究瓦特蒸汽机的过程中,他最关心的是热能与机械能的转化问题。他发现,除热能转化为机械能这一主要过程之外,还有许多辅助过程。而正是这些辅助过程阻碍了人们对能量转化进行深入研究。于是,卡诺决定舍弃这些辅助过程,采用一种抽象的数理分析方法,着重探讨热能与机械能的转化。经过长时间的理论分析和实验,最终,卡诺奠定了热力学第二定律。显然,热力学第二定律的故事,是科学家从纷繁复杂的现象中追寻简洁原理的典型。
“如果你想当科学家,就必须先找出非常简单的原理,但这并不是说世界的复杂不能引起你的兴趣,实际上,真正的科学家非常享受这种复杂带来的美。”作为一位科学家,阿金斯的话无疑道出了伟大的科学想法的魅力所在。
18047
引用 (hfg
1964 @ 2005年09月13日
10时28分) |
| 我没有看到原题
|
我把题目再贴一下:post-38-1126582888.gif
18047大家都来做啊!我相信通过大家的共同努力一定能把这道题做出的
18047我没有看到原题
18047tobyqin你看北师大第三题能否用Dini定理判断一致收敛,然后逐项积分?期待回复!
18047不懂你的意思啊
你所说的Dini定理是那个要和函数连续的吗?
但是和函数的连续性怎么确定的
最多知道在开区间上成立吧,这不是Dini的条件啊
Dini定理应该要求闭区间的
18047Dini的主要定理的一个条件是函数列的单调性
18047好像不可以用Dini定理,不过,似乎只要用比较收敛定理应该就可以了证明f(x)一致收敛了吧!
18047首先证明sum(2^(-n)cos(2^nx))一致收敛于f(x)。
应该不难证明f(x)在x=0附近连续且可导
lim(f(x)-f(0))/x=f'(0)=-sum(sin(2^n*0))=0
可不可以这样做?最近好长时间不碰数学了,不知道做得对不对?
tobyqin帮忙看看
18047我也感觉不可导啊
18047
引用 (zhubin846152 @ 2005年09月13日
18时52分) |
首先证明sum(2^(-n)cos(2^nx))一致收敛于f(x)。
应该不难证明f(x)在x=0附近连续且可导
lim(f(x)-f(0))/x=f'(0)=-sum(sin(2^n*0))=0
可不可以这样做?最近好长时间不碰数学了,不知道做得对不对?
tobyqin帮忙看看
|
f(x)在x=0附近好象不可导呀
18047设 _x{n}= 2^{-n}
f(+0)=f( x_{n} )n趋于无穷大
则原式= [sum 2 ^{-n} cos1-
sum

2^{-n}
]sum2^{n}
=cos1-1
18047如何证明f(x)可导啊请求给予回答。。。。。。。。。。。。。。。。。。。。。。
18047这个题太难拉,我一直就没想出来那位高手给予指导我将不胜感激
18047这个题目似乎没有得到完美解答!
18048[COLOR=purple]
多谢个为了
18049分形、小波应用性也很强
18049多谢各位了!
18049方程方面吧,我想的(因为方程有定性分析,数值分析。从应用角度说,许多实际问题的数学模型都是方程)
18049灰色系统
18049呵呵,这个我也想知道。看过之后也增加了见识,谢谢,
18050
怎么证明一个无穷集合 A 必有一子集 A*
与之等价, 且 A-A* 是可数集?谢谢。
18050分两种情况讨论:
若A是可数集,作其一排列,令偶数项全体为A*即可
若A是不可数集,任意去掉一可数子集即可
18050thank you .
18051本人今年准备考研,只是不知道数学的5个专业:基础数学、应用数学、计算数学、概率论与数理统计、运筹学与控制论
有什么不同,虽然专业介绍得很好,可是我还是看不懂???
请问,这几个专业毕业后大都干了些什么?哪个专业显得更好一些!!!
18051谁又能搞清楚呀!!
18059
过几天就要研究生建摸大赛了,大家有没有什么好的建议这几天提供点好吗?我第一次参加,还真有的点怕怕的,要是都不会怎么办,还有建议带点什么资料进去比较好呢?
18060对不起,我学经济的,数学比较菜,学习中遇到了凸集合方面的问题,想问。
斑竹回复:凸集理论--数学系称为凸分析,你可以去
http://www.math.org.cn/forums/index.php?showforum=21
具体金融问题可以去
http://www.math.org.cn/forums/index.php?showforum=35
18061怎样给导师写自荐信,是有关图论的,谢谢
18067呵呵,有点像初等数论。让我想想呵呵
18067a.证明对任意n>1,(1/1)+(1/2)+(1/3)+...+(1/n)不是整数
b.证明对任意x>0,1/(x)+1/(x+1)+1/(x+2)+...+1/(x+n)不是整数
GGJJ都来看看~~~
18067不妨设n=2^s+b,b<2^s
1+1/2+...+1/n中的分母的2的最高因子为k
不难证明k=s
从而至少分母中有2的因子
第二题应该用2作因子也可以解
18067谢谢了~~~~
18067(1/1)+(1/2)+(1/3)+...+(1/n)=
p\q
且p,q互质,那么只须正q!=1.
以下过程明显.
18067楼上的,能不能讲得详细一点,为什么显然。能不能把具体步骤公布出来大家一起参详一下呢
18067能不能用归纳法证明啊
18067由点意思!!
18067
| 引用 (韩清风 @ 2005年09月13日
11时39分) |
a.证明对任意n>1,(1/1)+(1/2)+(1/3)+...+(1/n)不是整数
b.证明对任意x>0,1/(x)+1/(x+1)+1/(x+2)+...+1/(x+n)不是整数
GGJJ都来看看~~~ |
第二题,当x为正整数,可以用二楼zhubin846152君的方法做。当x为正的实的超越数,命题显然是对。对于一般的代数数,命题不一定成立,例如:记f(x,n)=1/(x)+1/(x+1)+1/(x+2)+...+1/(x+n),固定某个n使的f(0,n)>3,则f(x,n)是x的在正实轴上的连续函数,它的值域包括(1,
3),即有某个正的代数数a,满足f(a, n)=2。
18068请问对偶空间和共轭空间的概念是不是一样的?有区别吗?
18068一样的,一个是dual 一个是conjugate
叫法不一样,定义是相同的
18068有时不一样的,有时一样
在不同的理论中,有不同的用法,
有的理论中可以用来区分不同的但性质相仿的空间。
18068
| 引用 (流形 @ 2005年09月15日
16时51分) |
有时不一样的,有时一样
在不同的理论中,有不同的用法,
有的理论中可以用来区分不同的但性质相仿的空间。
|
能不能详细解释一下?
18068名称上的东西不必太较真
比如:
设X,Y为任意数域K上的
拓扑线性空间,若存在一个非奇异的弱内积F:X*Y-->K.
则称X,Y互为共轭空间.
18069大家请帮帮忙,我急需信息论与编码学的英文课件!要完整的!谢谢!感激不尽!
18070我是个数学外行,最近写图形程序需要用到空间网格变形。
我选用了rbf研究了一段时间,经过我调试,我发现公式里的那个插值宽度值设定对最终结果影响很大,我现在采用的是预定义的,但在经过连续几次变形的时候,网格位置就会异常出现很大/很小的值。
向请问这里的专家,如果用公式确定插值宽度,对应不同选用的基函数时候又要对这个值进行修改??
求助,谢谢了。
18073有没有人知道 关于 北京理工数学专业 考试与录取比例或者分数情况???
18074我发现用PPT学习好啊,一本概率论书要一两百页,而我现在学的PPT才80页!每天看10页一周就学完。
18074那能叫"学"吗?
18074是啊,你看得懂吗
18075不会有这个会议吧!我只知道12月14日-12月
18日在中科院信息安全重点实验室有个年度会议,只是请了几位国外的学者而以,也算不上什么国际会议啊!而且国内密码学界几乎所有的权威都去,怎么会有空去厦门开你说得那个会议呢?还是好好学习吧!就算有消息也首先会通知我们学校去参加,因为少了我们学校的密码会议绝对不权威!
18075大家好,我是无线网络专业的,
遇到很大的安全问题,请各为密码学大师给于合作
,我想做关于网络安全方面的东西,
有没有什么好的建议,
特别求密要管理的.
谢谢大家!!!!
18075这~~
让人怎么跟你联系呢
18075对不起,好久没上来看看了,最近在做密钥管理的,有点难度.谁有好的建议呢!12月14日在厦门有国际密码学会议,我要参加,各位有吗?有可以到时候交流交流啊
18075楼上的是哪个学校的,小弟刚刚接触密码学,想了解一下中国这方面的学校,都有什么优势,能给我介绍一下吗
18075我也想知道楼上哪个学校的?我要不要把通知全发一遍你才相信啊:
国际重要的信息安全学会------IACR()主办,"The
4th international conference on crytology and network
security"将于2005年12月14日至16在厦门举行.由英国伦敦大学Yvo
G.Desmedt教授和澳大利亚Macquarie大学的王华雄博士担任程序委员会主席.
其他不说了,费用:500美元,学生400美元
18075我知道楼上说的那个会议,是关于无线网络安全等计算机方面的吧,我已经收到邮件了,不过于厦门会议冲突,所以只能选一者.
18075我是解放军信息工程大学的,欢迎大家来我校交流!我校拥有全国惟一的密码学国家重点学科(2002年国家教育部颁发),军队密码学重点学科(2001年解放军总部)!我校立足国防信息安全,已经拥有近70年的密码研究历史,曾在抗日战争,解放战争,抗美援朝战争及当今国家情报中发挥了不可磨灭的密码破译做用!
18075欢迎大家参加每两年一次的中国密码学会学术会议!2006年9月在山东大学召开第九届中国密码学会学术会议,这是国内密码学和信息安全级别最高的会议,每次我校都将帅大队人员参加!
18076Keermogeluofu
柯尔莫哥洛夫,..
(
1903~ )
[] 苏联数学家。
1903年
4月25日生于中亚的顿巴夫,
1920年入莫斯科大学学习,
19岁从师..卢津'"
class=link>..卢津时就构造了一个勒贝格可积函数,其傅里叶级数几乎处处发散,这对解决卢津问题作出了重大贡献。
1931年任莫斯科大学教授,
1933年任该校数学所所长,
1939年起任苏联科学院院士。他对开创现代数学的一系列重要分支作出了重大贡献。
柯尔莫哥洛夫建立了在测度论基础上的概率论公理系统,奠定了近代概率论的基础,他也是随机过程论的奠基人之一,其工作包括:20年代关于强大数律、重对数律的基本工作;
1933年在《概率论的基本概念》一文中提出的概率论公理系统;30年代建立的马尔可夫过程的两个基本方程;用希尔伯特空间的几何理论建立弱平稳序列的线性理论;40年代完成独立和的弱极限理论;经验分布的柯尔莫哥洛夫统计量等。
柯尔莫哥洛夫在动力系统中开创了关于哈密顿系统的微扰理论与Κ(柯尔莫哥洛夫)系统遍历理论。他把经典力学与信息论结合起来,在50年代解决了非对称重刚体高速旋转的稳定性和磁力线曲面的稳定性。在他的工作的基础上..阿诺尔德和J.K.莫泽完成了以他们三人名字的字首命名的KAM理论。
他在动力系统与遍历理论中引进的K熵,对具有强随机性动力系统的内部不稳定性问题的分析起了重要作用。
50年代中期,他开创了研究函数特性的信息论方法,他对距离空间的集合引进了熵,他的工作及随后阿诺尔德的工作解决并深化了希尔伯特第13问题(用较少变量的函数表示较多变量的函数)。60年代以后他又创立了信息算法理论。
1980年由于他在调和分析、概率论、遍历理论及动力系统方面出色的工作获沃尔夫奖。
此外他在信息论、数理逻辑算法论、解析集合论、湍流力学、测度论、拓扑学等领域都有重大贡献。
他的工作在数学的一系列领域中,提供了新方法,开创了新方向,揭示了不同数学领域间的联系,并广泛深入地提供了它们在物理、化学、生物、工程、控制理论、计算机等各学科的应用前景。
他十分重视数学教育,在他的指引下大批数学家在不同领域内取得了重大成就,其中包括 ..盖尔范德'"
class=link>..盖尔范德,..阿诺尔德,..西奈依等人。同时,他也非常重视基础教育,甚至还领导了中学数学教科书的编写工作。
柯尔莫哥洛夫是20世纪最有影响的苏联数学家。还是美、法、意、荷、英、联邦德国等国的院士或皇家学会会员,是三次列宁勋章的获得者[SIZE=1][SIZE=7][COLOR=purple][COLOR=purple]
18077第t年j行业k岁m性别在职“中人”参保人数ZRCBRS(t,j,k,m)
请问这条语句,在matlab里面怎么实现啊 ?
18077如果各数据值都是数字,那么同二维、三维数组一样定义
如果各数据值不都是数字,那么使用结构存储
18078钱吉林的书上 28 题
中科院 2000年
不是很明白,能否帮忙解释一下
或者给从新证一下,详细些
18078题目如下post-38-1126603377.gif
18078Ck(x)=[(x-x1)/(xk-x1)]...[(x-x(k-1))/(xk-x(k-1))]*[(x-x(k+1))/(xk-x(k+1))]..[(x-xn)/(xk-xn)]
为满足条件的多项式
g(x)=Ck+C(k+1)也是n-1次的函数,他们的导数也连续
根据rolle定理不难得到,((xk-1),x(k+2))中只有一个或两个导数为0
(1)((xk-1),x(k+2))中只有一个导数为0
显然得到((xk-1),x(k+2))中只有最大值
(2)((xk-1),x(k+2))中只有两个导数为0
((xk,x(k+1))中至少有一个点导数为0,下证明只有一个
否则((xk-1),xk),(x(k+1),x(k+2))中没有导数为0
显然g'(xk)>0,g'(xk+1)<0
接着,如果,存在两个不同的u<v

[xk,x(k+1)]
g'(u)=g'(v)=0
显然,u=v矛盾,否则存在t

(u,v),使得g'(t)=0
那,不难得到g(x)在x

[xk,x(k+1)]内恒大于1
所以g(x(k))~g(x(k+1))中只有一个点的导数为0,且函数值全大于1
g()
18078简化的证明:
用一下代数学基本定理和Rolle定理。post-38-1126632010.gif
18078但是x1,...,x(k-1) x(k+1)... xn是零点,只有n-2个,但是如果另一个零点落在xk,
x(k+1)之间呢
18078两个都看不懂,不好意思
能不能再解释一下
x1,...,x(k-1) x(k+1)...
xn是零点,但是另一个在什么地方能确定吗
为什么((xk-1),x(k+2))中只有一个导数为0,就是最大值,
18078
| 引用 (zys @ 2005年09月14日
12时59分) |
两个都看不懂,不好意思
能不能再解释一下
x1,...,x(k-1) x(k+1)... xn是零点,但是另一个在什么地方能确定吗
为什么((xk-1),x(k+2))中只有一个导数为0,就是最大值,
|
不是说次数最多n-1吗?而且知道了n-1个零点自然就可以确定多项式了
在零点间的函数值如果大于0
那么导数为零的点就只能是极大值点
否则就会有至少两个导数为零的点
这和我题目中的解释矛盾
18078
| 引用 (zys @ 2005年09月14日
14时06分) |
但是x1,...,x(k-1)
x(k+1)... xn是零点,只有n-2个,但是如果另一个零点落在xk,
x(k+1)之间呢
|
x1,...,x(k-1) x(k+1)... xn
这是多少个数?!
18078写错了
应该是x(k+2)
x(k+1)不是零点
18078
| 引用 (zys @ 2005年09月14日
16时54分) |
写错了
应该是x(k+2)
x(k+1)不是零点 |
那在我上面的解答中说得很清楚了啊
你再仔细看一下就好了
18079构造一个在0,1之间每一点都取有限值,但在任何点的任何邻域内都无界的函数
帮忙解释清楚些,THS
18079f(x)=q 如果,x=p/q,(p,q)=1,且x!=0
f(x)=0 如果,x为无理数,或者x=0
18079能不能证一下
18079对于任意的点x,
那么在每个领域中有无穷多个有理数,显然,存在分母m->

否则说明存在最大分母,换句话说,其中只有有限个真分数,这与有无穷个有理数矛盾
x的任意领域中必然由某个分母->

18081S=

1/ n^n ?
(无限和)
18081f(x)=x 在(0 pi) 和(-Pi 0)展开为fouier级数
18081我知道它小于2
18081是

^

/6,但不晓得怎么算的?
18081用幂级数怎么解?
18081用傅立叶级数做
18081
| 引用 (iii @ 2005年09月13日
21时52分) |
是
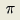 ^ ^
 /6,但不晓得怎么算的? /6,但不晓得怎么算的?
|
这个的答案绝对不是你所说的,应该比这个还要小,要用到含参数的级数的知识,我有个积分不会,大家把这个做出来了就解决了!post-38-1126692343.gif
18081答案是 六分之pi的平方
18081绝对是

^

/6,用傅立叶级数,而且有的习题书上经常用到这个结论.快考试了,我好怕哦,同志们,无尽的恐惧```
18081kankanpost-38-1126697380.gif
18081难道就没具体的方法吗?
18081我晕,这个题目我对求导还是不怀疑的!
现在只想知道tobyqin你是考哪个大学的研究生?可否告之一下啊?
我想做个参考!
18082我的英语不是很好,现在正在复习着华东师大的数分,北大的高代。但不知道报什么好
18082上海比较难考,如果你的专业课不错,英语也还行不妨试试
18082楼上帖子的内容是:
上海比较难考,如果你的专业课不错,英语也还行不妨试试
18082这样的一句话也要卖,真不知道这人怎么想的。
18082上海那边很注重英语,得要加强哦!
18082我建议你可以考一些小学校
其实都一样
找工作的只注重你是否拿着什么样的文聘
18084代数几何,华师最好,但它每年要多少?有几个这个方向的导师哪?好象就一个呀
18085浙大首届丘成桐数学英才班开办
来源:浙大新闻办 时间:2005-09-12 12:45:16
--------------------------------------------------------------------------------
9月10日,备受关注的浙大丘成桐数学英才班在数学研究中心举行开办仪式,14名热爱数学、综合素质优秀的学生正式成为英才班的首届学员。
正在数学中心讲学的中科院院士、原中科院数学研究院院长杨乐,浙大副校长褚健、娰健敏出席开办仪式并讲话。杨乐希望英才班能不断地培养出高水平、高质量的人才,并劝诫英才班的同学要勤奋学习,多思考、多动手。
娰健敏在讲话中直呼英才班为“丘成桐大师班”,强调学员们既要成为数学学科的佼佼者,也必须在综合素质的培养上下更大的功夫。
褚健在最后的讲话中对英才班的14名同学表示祝贺,要求他们在学习和研究中能够发挥丰富的想象力,具备创新精神;希望通过教师和学生的共同努力,加快浙大数学学科的发展。
此前,14名英才班的学生已经体验了一周的大学生活,除了基础公共课,学员们还聆听了学校专门安排的许以超、王斯雷、沈一兵等代数、分析、几何领域的专家主讲的课程。据悉,今后学校还将逐步安排一些研究生的课程。
英才班创办人之一、浙大数学中心执行主任刘克峰,学校有关部门负责人和全体数学系教师参加了开办仪式。
(石楠)
18085令人兴奋,使人鼓舞!!!!
18086[东方时空]丘成桐:冷说奥数热
来源:央视国际 时间:2005-09-12 10:
19:05
--------------------------------------------------------------------------------
解说一:2005年7月
18日,在刚刚结束的第46届国际数学奥林匹克竞赛上,中国队以总分235分的成绩获得团体总分第一名。这一消息使得原本已经有所降温的“奥数热”再度升温,也使此前曾多次对国内奥数补习热现象提出批评的数学家丘成桐先生甚为忧虑。
记者:现在很多地方都叫停了数学奥校的培训课程,但是很快换了个名字,换了个地点一些培训班又开始了您听说吗?
丘成桐:我批评奥数的问题影响到很多人赚钱的一个途径。
记者:有没有人对你有意见。
丘成桐:我想一定很多,不过我个人的利益的关系在里边,我开始讲的我晓得会接触到很多人利益的问题,所以我一定受到很多攻击,可是我觉得是整个国家的问题,我觉得我受不受人攻击可能是一个,他当然希望我不要讲。
解说二:事实上,早在2003年,丘成桐先生就多次在不同场合提出,“数学奥林匹克竞赛无法成就数学大国的梦想”“奥数培训打击并遏制了孩子们的好奇心”。对此,丘先生给我们讲述了一段令人惋惜的经历。
记者:您为什么会反对数学奥林匹克学校培训这样的方式?
丘成桐:我考过一般中学生他们是很高分的,他们除了做题目以外其他什么东西不要讲不懂,不能讲不懂就是没有兴趣,完全没有兴趣,因此他们学到的是很假的一个小的部分,遇到其他实际上题目他们会很彷徨。真正数学的目标,是发现深的题目,去将深的题目解决,而做所谓汪洋里边的题目,基本上都是人家提出来的。
记者:他们完全为了围绕这个考试的要求在决定自己学什么,在这些题目的您看过吗,您做过吗?
丘成桐:我不一定做得出来,就是很狭窄方向的题目,可能钻牛角尖钻的很厉害,我不见得考的出来。
记者:您都不一定能做的上来?
丘成桐:我不一定能够考的出来,但我最后能做得出来,可是我不见得就说做它两遍一下子一看就做出来。
记者:这说明什么?
丘成桐:说明它是钻牛角尖,不是真真正正对数学有很大深度的了解,他们这个奥运数学的训练对基本数学的贡献并不大。
记者:我还想问一个关于奥校的问题,毕竟多做题目对喜欢数学的孩子是有好好处的,您觉得做奥校的题目会打击好奇心,遏制他的好奇心这是为什么?
丘成桐:一个孩子他花很多工夫去做,做最后他觉得很烦没有兴趣了,这个小孩子全部给他打掉了,他看得望而生厌,就是看到很不好,我不想再看这是一个问题,第二个问题奥赛的孩子拿了金牌了很大的荣耀,一下子已经衣锦荣归就是这个全校全社会拍掌,他们前途很可悲,因为他们压力这么大以后谁能够保持学习而不受到这个压力的影响这种小孩子很少,我举个例子给你出来我有一个博士后,发了疯,事情是这样子,我发觉他从小就没有朋友,谁都不跟交流,我很害怕很多很早成名的小孩遇到的同样困难,他们变成社会上一个特殊分子,很年轻,还没有受到真真正正的成熟,而得到社会上很大的荣誉,这会对他们不是很好的事情。
解说三:现任美国哈佛大学讲座教授,中国科学院晨兴数学中心主任的丘成桐曾师从著名数学家陈省身先生,在美国加州大学伯克利分校学习并获得博士学位。
1976年,27岁的丘成桐完成了卡拉比猜想的证明,这一成就在世界上引起轰动。
1983年,34岁的丘成桐荣获世界数学领域诺贝尔奖---菲尔兹奖,成为至今为止唯一获得该奖项的华人。
记者:您对数学的兴趣和喜欢,好像是从青年的时期甚至少年时期就确定了。
丘成桐:对。
记者:您在刚刚入门的时候有没有像现在的孩子这样面对汪洋的题海在里面挣扎?
丘成桐:我从中学开始就做题目,一路做到研究生我都做题目,题目是觉得重要的,因为你不做题目,觉得你工具也好,你的想法做好也好,没有办法做题目就废话,所以题目是决定要做的可是题目不是总结,题目是帮忙你去考虑,帮忙你使得你晓得你学的工具真正是怎么意思,
解说四:除了数学领域的研究之外,丘成桐的视野开阔,兴趣广泛。他精通《史记》,擅长用古文写作,在丘成桐看来,文学、历史等方面的知识有利于提高数学修养,因此,对于那些身处奥数培训热当中的孩子们,他给出了一个独特的建议。
记者:您曾经说与其让孩子们做那些没有的题目还不如多找几本数学大师的传记来看一看,这是为什么?
丘成桐:你看看数学家,数学大师他走过的路,你从里面慢慢了解一个学家是怎么想问题的,这样子等于你念大学数学的传记的时候,你这样数学提升到到里边去,数学的真髓就找到了,因为很多事情大数学家的创造,他们创造的过程就看得出来这整个数学的内容在哪里,
解说五:如今,丘成桐频繁往返于美国、香港和祖国大陆之间,除了专业研究之外,丘成桐把更多的时间和精力花在了发展祖国数学事业上。而对诸如奥数培训热等一些不合理现象进行批判,正是他关注祖国内地数学事业发展的一个着力点。
记者:作为某一个领域的专长家,是不是也可以就说我只做不说关起门来搞学问,对社会的问题不加评价。
丘成桐:我从小长大的家庭是对中国这个民族觉得有一个很重要的一个责任感的,我不知道会做到这个地方,除了对数学的贡献兴趣以外,我最大的志愿是期望能够替中国做些事,做不做成功,我没法讲我是尽了自己的心力,我觉得我对我的国家有这个义务,我只尽我的义务而已。
CCTV.com消息(东方时空-人物)2005年08月09日
18087"设f(x)=tanh( \alpha
x),x*为任意实数,E1>0是常数,则存在另一个只依赖于E1的常数0<E2<1,使得:对所有x>E1,都有:|f(x+x*)-f(x*)|<E2|x|"这个命题成立吗?
18090怎么证明第2题的23问??
18090题目应该没问题!
出自《数学分析中的典型问题与方法》
185页
是南开
1981年的题
谢谢高手指点!post-38-11266
17128.ibf
18090自己看一下教材,教材上有第2题呀
18090第一题化为积分形式,再用施罗乌滋法则
第二题用taylor定理,在a+b/2处展开
18090用定积分定义来做,证明过程中用中值定理,这是一道常见试题的应用。
18090第一题大家给个具体的解题过程吧,不怎么看的懂是怎么做的
谢谢了啊!
18090
引用 (蓝戈 @ 2005年09月14日
17时40分) |
第一题大家给个具体的解题过程吧,不怎么看的懂是怎么做的
谢谢了啊! |
如下:
对于为什么可以那么做我就不写了
那个很容易得到的post-38-1126699001.gif
18090我晕哦,这么简单,我当时就是一味的在用stolz公式,哎,郁闷,原来是在用L'Hospital法则做,糊涂!
thanks
to tobyqin!!
18090
| 引用 (slhzyx @ 2005年09月13日
21时08分) |
| 谁能帮我求解!
|
第二个题目是错误的
你把前面的二阶导数的绝对值给漏了
希望大家提问的时候最好给出问题的出处啊
到上面来求助毕竟不是给大家出题的
18090请问 tobyqin : stolz不是要求分母是单调增的么
18090把n换成x可以么
18090函数在[a,b] 中存在点c使

©
= (

(a)
+

(b)
)/2
成立否啊
18090就是题目转化为求x的函数啊,它的极限就是序列的极限
18090那么你用的00是什么公式啊?(不要郁闷啊)
18090
引用 (iii @ 2005年09月
18日
18时
19分) |
|
那么你用的00是什么公式啊?(不要郁闷啊) |
Stolz公式有两种吧
一个是
∞
∞ 型
一个是
0
0 的
18090第二题
怎么做啊??那个说明常数4是最好的
还有第2问都怎么做啊??
18090关于第二大题的第一问!post-38-1127221072.gif
18090其实如果不是常数,就利用如果要结论不成立,就一定可以推出函数不可导!
关于第二问的解答思路!
其实要试着去尝试用连续函数的逼近原理来思考,思路放才可以清晰!
18090还是不懂
18090构造比次数比2大函数即可区间为[-1,1] f(x)=x(2+c) ()里为次数且为奇数
18090第三个问可以用导数的介值性.证明f ^{x} =a.(a不为零.)跟 f^{a+b/2}=0. 矛盾.
18092买一本巴!
18092谢谢
18094考研想考金融数学,牛人能否给些建议。
顺便介绍一下现在世界金融数学界的情况如何。比如说国内外那些学校在这个方向比较前沿。
18095[COLOR=blue]博弈论
市场失灵与政府调节讲义。
[COLOR=red]向斑竹申请加分post-35-1126624211.ibf
18096哪位有菲赫金哥尔茨著《微积分学教程》可否共享下?到我邮箱吧
shunfengren2003@yahoo.com.cn
18096论坛上有的,你仔细找找看吧
你或者到bossh_math@163.com
password:123456
看看,我帮你传上去
18096这个书那里有得买啊
我也要需要买一本看
请指教
18096论坛上有的
18099求关于粒子滤波的相关资料,最好是中文:)多谢!
18099...没概念,是量子加密那方面的么?
18100多谢多谢!!!!!!!
18100
怎样产生随即序列u(n),可以服从均匀分布,也可以服高斯分布,其幅值、均值与方差可以由输入数来调节!!!!!!!!!!!!!多谢!!!!!!!
18100...什么意思?没看懂?怎么可能又服从均匀又服从正态?
18100我记得复旦的<概率论教程>上有这样一个例题,不过那里好象不是高斯分布而是正态分布,只要稍加修改应该就行了.
18101事件A、B满足P(B/A)=1时A

B,对吗?
原题中还有个答案P[A-AB]=0这个我也认为是对的,但上面这个答案我也认为是对的,不知道为什么不对,请指教,谢谢!
18101
| 引用 (xzdrainbow @ 2005年09月14日
10时29分) |
事件A、B满足P(B/A)=1时A
 B,对吗?
B,对吗?
原题中还有个答案P[A-AB]=0这个我也认为是对的,但上面这个答案我也认为是对的,不知道为什么不对,请指教,谢谢!
|
why not

?
18101
| 引用 (xzdrainbow @ 2005年09月14日
10时29分) |
事件A、B满足P(B/A)=1时A
 B,对吗?
B,对吗?
原题中还有个答案P[A-AB]=0这个我也认为是对的,但上面这个答案我也认为是对的,不知道为什么不对,请指教,谢谢!
|
你那个既不是一个充分条件,也不是必要条件
18101P(B/A)=1是指事件A发生时事件B肯定发生吧?那是不是就能说A

B
18101Fisher:您好!
请问是不是这样的啊
18101Fisher:谢谢您!
18101事件 A: 3< x
事件 B: 3< x+1
推翻了

简直扯淡
18101
引用 (xzdrainbow @ 2005年09月15日
18时45分) |
P(B/A)=1是指事件A发生时事件B肯定发生吧?那是不是就能说A  B B
|
P(B/A)=1所以P(B)=1,而(A-AB)
B=
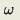
即得到书中答案P(A-AB)=0
而如果取
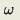
=[0,1],P为
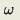
上勒贝格测度,A={
0.5},
B=
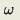
中全体无理数的集合,
则P(B/A)=1但A

B不成立
概率论里的很多事实不能靠想当然,概率为零的事还有可能发生那 呵呵
18102请各位帮忙,regret-matching algorithm. Lagrangian hedging
algorithm
no-regret algorithms如何翻译啊?
18102损失匹配算法??
18102多谢多谢啊
18103题目post-38-1126669152.gif
18103见下:post-38-1126669963.gif
18103是否可以用复数做
A(z)=z^3/3-z^6/6+...
B(z)=z-z^4/4+z^7/7-...
C(z)=-z^2/2+z^5/5-z^8/8-...
A(z)+B(z)+C(z)=ln
(1+z)
A(1)+B(1)+C(1)=ln 2
A(w)+B(w)+C(w)=A(1)+wB(w)+w^2C(w^2)=ln
(1+w)
A(w^2)+B(w^2)+C(w^2)=A(1)+w^2B(1)+wC(1)=ln
(1+w^2)
w^3=1
解方程可以得到答案
18104请教:辗转相除法所依据的数学原理
18104整除性,余数,没别的了吧。
18104几乎每一本《高等代数》都有证明,不妨自己看一看
18104辗转相除法运用的原理就是除数和被除数的最大公因式等于除数和余数的最大公因式!可以证明的!因为被除数是除数和余数的组合,同时余数又是被除数和除数的组合!所以同时整除除数和被除数的因子也同时整除除数和余数!
18104f(x)=q(x)g(x)+r(x)

(f,
g)=(g,r)
18104
| 引用 (xxt @ 2005年09月27日
21时28分) |
|
辗转相除法运用的原理就是除数和被除数的最大公因式等于除数和余数的最大公因式!可以证明的!因为被除数是除数和余数的组合,同时余数又是被除数和除数的组合!所以同时整除除数和被除数的因子也同时整除除数和余数!
|
就是这样的了
18104
| 引用 (xxt @ 2005年09月27日
21时28分) |
|
辗转相除法运用的原理就是除数和被除数的最大公因式等于除数和余数的最大公因式!可以证明的!因为被除数是除数和余数的组合,同时余数又是被除数和除数的组合!所以同时整除除数和被除数的因子也同时整除除数和余数!
|
就是这样!自己小心点应该没有什么问题!
18104自己找本数论书看看吧!
18104除数和被除数的最大公因式等于除数和余数的最大公因式
18105
http://scholar.lib.vt.edu:8765/index.html?...nh=10&lk=1&rf=0--------------------------------------------------------------------------------
18106我也想要一个!
18106求救于各位大虾,谁有linux下的matlab
license.dat文件麻烦传一个,或者发到hniychenwei@sina.com邮箱也行,先行拜谢!!
以前这个论坛有个一个,但是已经失效
18106Here it is.post-28-1129610143.ibf
18106顺便请问大侠有没有Windows下的license.dat? 谢谢了!
18106xp下 的注册码post-28-1129972071.ibf
18107问茆时松<概率论与数理统计教程的>怎么样?
18107
| 引用 (diguomengxiang @ 2005年09月14日
13时14分) |


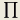 问茆时松<概率论与数理统计教程的>怎么样
问茆时松<概率论与数理统计教程的>怎么样 |
听说写得不错
18107一般,感觉有点乱,不如原来魏宗舒那本
18107概率部分还比较直观,统计部分(的部分)有点繁,不过,我觉得这本书对于学过的人来说非常有帮助
,因为他把理论结合实际很紧密,不过统计部分不适合初学者(纯属个人意见)!!!!!!!
18107名家写的书大都不错,关键是你要仔细读!!!
18107是不是扉页上写纪念魏宗舒教授的那本?我个人觉得还不错,他的风格基本承袭魏老(如分布函数的右连续等)。比较翔实,证明比较明了,但是有些内容没有涉及(比如完备性等)。
一家之言,止增笑耳
18108见附件!post-33-1129
180521.ibf
18108闵嗣鹤的《初等数论》上有证明
18108好是很好,但冗长了些。
有初等证明,见《数学分析纵横谈》一书。
数学与我们同在!
18108楼主要证的是pi是无理数啊
18108这个证明不太好吧,,,
18108证明啥呀,无理数就是无理数,就像1+1等于2一样。证这些有啥子用。
18108证明

是无理数?最好不要说他是超越数所以是无理数??
18108华东师大的数分书第六章微分中值定理第三节有
18108e=1+1+1/2!+1/3!+...+1/n!+1/(n+1)!+...
若e=p/q(p,q互质)是有理数,则q!e=A+1/(q+1)(q+2)...,其中A是正整数,
导致矛盾!
18108sorry,不是俄e,是pi=3.1415926.....
18108

也可以展开成级数吧。
18108pi/4=1-(1/3)+(1/5)-(1/7)+...
pi^2/6=1+(1/2)^2+(1/3)^2+...
然后,用以前写过的证明e,sqrt(3)的方法,就可以了。
18108“Pi 是无理数”的一个新证明,见附件习题00004的证法2post-33-112952
1874.ibf
18108pi/4=1-(1/3)+(1/5)-(1/7)+...这不是初等数学能直接解决的吧。
欧拉解决过大家可以吗??
18108把问题证明的更简单有什么意义呢??
18108
引用 (wdcyc @ 2005年10月
19日
14时33分) |
pi/4=1-(1/3)+(1/5)-(1/7)+...这不是初等数学能直接解决的吧。
欧拉解决过大家可以吗??
|
你的想法是寻找只用中学数学知识水平的初等证明吗?这个恐怕我办不到!
18108要用初等数学的知识来证,那么在初等数学里

是怎么定义的
哦?
好像是用园的周长和半径比定义的吧?
那就得画图根你比划了
18108<<初等数论>>闵嗣鹤编写的,P
183页上就有.
18108
| 引用 (magic9901 @ 2005年10月21日
10时22分) |
引用 (wdcyc @ 2005年10月
19日
14时33分) |
pi/4=1-(1/3)+(1/5)-(1/7)+...这不是初等数学能直接解决的吧。
欧拉解决过大家可以吗??
|
你的想法是寻找只用中学数学知识水平的初等证明吗?这个恐怕我办不到!
|
可以的,应该是。当时我看完证明和评价时才上初中。
那本书我现在再找找,好长时间没看了。
18108等一下吧,那书不是很好找了
18108
1761年就已经解决了
18108我也想看看,谁能传上来啊?记得有个式子把e,i,pi,都联起来的,具体的忘了。谁能传个。
18108
引用 (strife @ 2005年12月
17日
22时32分) |
|
我也想看看,谁能传上来啊?记得有个式子把e,i,pi,都联起来的,具体的忘了。谁能传个。
|
e^(pi*i)=1
???
18108这个证明很常见吧,在一般的数论书里多有给出。
《四大普适常数》上也有证明,跟上面一些数友的证法相近。
18112运行MATLAB,命令窗口就重复出现下面的信息
Exception occurred during event
dispatching:
java.lang.ArrayIndexOutOfBound######ception
at
com.mathworks.mwt.MWClipboardMonitor.actionPerformed(MWClipboardMonitor.java:94)
at com.mathworks.util.Timer.notifyListeners(Timer.java:426)
at
com.mathworks.util.Timer$TimerEvent.dispatch(Timer.java:543)
at
com.mathworks.util.QueueEvent$QueueTarget.processEvent(QueueEvent.java:67)
at java.awt.Component.dispatchEventImpl(Unknown Source)
at
java.awt.Component.dispatchEvent(Unknown Source)
at
java.awt.EventQueue.dispatchEvent(Unknown Source)
at
java.awt.EventDispatchThread.pumpOneEventForHierarchy(Unknown Source)
at java.awt.EventDispatchThread.pumpEventsForHierarchy(Unknown Source)
at java.awt.EventDispatchThread.pumpEvents(Unknown Source)
at
java.awt.EventDispatchThread.run(Unknown Source)
每次已注销就好了,到底怎么回事呢,各位帮忙了
18112同问,我也经常会出现这样的现象。
18113
求问ing:郑州大学随机分析方向是哪位教授带的?
http://www.math.org.cn/forums/index.php?sh...c=36487&hl=觯鳊考郑州大学数学系研究生的同学与我联系好吗?同肩奋战!
我的邮箱lucuihong_xz@126.com
18113我是报考的数学系 你报的是那个专业呢?
18113
今年是马建国老师.
马老师非常和善.
18114
| 引用 (mazl @ 2005年09月16日
05时58分) |
| 引用 (renzhazero @ 2005年09月15日
21时55分) | | 要是可数集合的所有子集够成的集合还是可数集合。以自然数集合为例。那就是认为2的“阿列夫0”(正整数集合的基数)次幂也是可数集合的基数了。而2的“阿列夫0”次幂等于实数集合的基数“阿列夫”。这样就违反了连续统假设了吧。讲得不清楚请高手多加指教。 |
如果你是在用反证法就不对了。
因为“可数集的所有有限子集之集为可数集”的否定是
“可数集的所有有限子集之集为不可数集”,
而不是“可数集的所有子集之集为可数集”。
另外,本问题一般在讨论不可数集之前就会出现了。
|
mazl兄.你看看楼主的问题"最好能够指出为什么所有子集情形不一样,二者的区别再哪?"我只是对这一段做一个反例.自然数集合是可数集,其所有子集的集合(族)的基数是2的“阿列夫0”(阿列夫0是可列势)次幂.而一般来讲"2的“阿列夫0”(阿列夫0是可列势)次幂"等于实数的势.这样就是一个反例的构成.
流形兄说的对.我这段话有些地方讲得多此一举了.下回注意!
18114怎样证明可数集合的所有有限子集构成的集合是可数集合?
最好能够指出为什么所有子集情形不一样,二者的区别再哪?
18114要是可数集合的所有子集够成的集合还是可数集合。以自然数集合为例。那就是认为2的“阿列夫0”(正整数集合的基数)次幂也是可数集合的基数了。而2的“阿列夫0”次幂等于实数集合的基数“阿列夫”。这样就违反了连续统假设了吧。讲得不清楚请高手多加指教。
18114对可数集合的有限子集按基数分类
对任意的自然数n,基数为n的有限子集为可数个(可一一对应与0到1之间的有理数的一个子集(有限小数))
这样的话,
由于可数个可数集合的并为可数集,
全体有限子集自然可数
18114
| 引用 (renzhazero @ 2005年09月15日
21时55分) |
| 要是可数集合的所有子集够成的集合还是可数集合。以自然数集合为例。那就是认为2的“阿列夫0”(正整数集合的基数)次幂也是可数集合的基数了。而2的“阿列夫0”次幂等于实数集合的基数“阿列夫”。这样就违反了连续统假设了吧。讲得不清楚请高手多加指教。 |
如果你是在用反证法就不对了。
因为“可数集的所有有限子集之集为可数集”的否定是
“可数集的所有有限子集之集为不可数集”,
而不是“可数集的所有子集之集为可数集”。
另外,本问题一般在讨论不可数集之前就会出现了。
18114
引用 (流形 @ 2005年09月15日
17时39分) |
对可数集合的有限子集按基数分类
对任意的自然数n,基数为n的有限子集为可数个(可一一对应与0到1之间的有理数的一个子集(有限小数))
这样的话,
由于可数个可数集合的并为可数集,
全体有限子集自然可数
|
没有回答“为什么所有子集情形不一样,二者的区别再哪”呀.
由有限子集构成的集族中的任意两个成员的交中只有有限个元素.
而如果取所有子集构成的集族, 那么其中成员的交集就可能会有无穷多个元素, 这样就使得有很大一部分子集被排除在由所有有限子集构成的集族之外了
18114
| 引用 (renzhazero @ 2005年09月15日
21时55分) |
|
要是可数集合的所有子集够成的集合还是可数集合。以自然数集合为例。那就是认为2的“阿列夫0”(正整数集合的基数)次幂也是可数集合的基数了。而2的“阿列夫0”次幂等于实数集合的基数“阿列夫”。这样就违反了连续统假设了吧。讲得不清楚请高手多加指教。
|
没有违反连续统假设甚至说该问题与假设无关
假设是说载可列势与实数的势之间不存在其他的势。
18114
引用 (流形 @ 2005年09月15日
17时39分) |
对可数集合的有限子集按基数分类
对任意的自然数n,基数为n的有限子集为可数个(可一一对应与0到1之间的有理数的一个子集(有限小数))
这样的话,
由于可数个可数集合的并为可数集,
全体有限子集自然可数
|
对基数n有可数有限子集,那么n+1不也成立吗?这样对任意的n不都成立了吗?这不是对可数子集也成立了吗?
18114不是的
你那不是归纳法
呵呵
有限个有理数的和石有理数,但不能说可数个有理数的和一定是有理数
18114楼主,我想起来了,你的问题好象是熊金城的<点集拓扑讲义>上的习题.原题好象是问"设X是一个无限可数集,证明其幂集为不可数集合,但由X中所有有限子集构成的集族为可数集"
18114mazl兄.你看看楼主的问题"最好能够指出为什么所有子集情形不一样,二者的区别再哪?"我只是对这一段做一个反例.自然数集合是可数集,其所有子集的集合(族)的基数是2的“阿列夫0”(阿列夫0是可列势)次幂.而一般来讲"2的“阿列夫0”(阿列夫0是可列势)次
18114mazl兄,我还不怎么习惯bossh上的公式编辑.多谢你的建议.楼主的问题其实是个很基础的东东.很多书上都有类似的习题或者讨论.
18114
| 引用 (renzhazero @ 2005年09月21日
13时45分) |
| mazl兄.你看看楼主的问题"最好能够指出为什么所有子集情形不一样,二者的区别再哪?"我只是对这一段做一个反例.自然数集合是可数集,其所有子集的集合(族)的基数是2的“阿列夫0”(阿列夫0是可列势)次幂.而一般来讲"2的“阿列夫0”(阿列夫0是可列势)次 |
我的确没注意小字排印的这段话,抱歉.
但是我想还是要提醒你一下,
注意标点符号的使用,
否则的话,别人可能无法正确地理解你.
另外,关于
“可数集的有限子集之集与所有子集之集的区别”
这一问题想说两句,
注意到集合
A = {1/2^k:k为自然数}
可数,
A的每个有限子集之和都是[0,1]中的有理数,
而区间[0,1]上的每个实数x都存在着
A的一个子集A(x)使得该集元素之和为x.
因为有理数集Q可数而[0,1]不可数,
这就看出了两者的区别.
18115我也想知道呢
但是哦,如果用CAJView打开,再用专业版的Acrode
Reader打印,就成了,可以打印了,只是CAJView打开后的PDF文件效果都不好的
18115前几天从这儿下载了陈传璋的数学分析习题解答(pdf格式),现在想打印,发现原来加了密码,不能打印。请好人做到底,给发个密码吧。现在上课正好用,谢谢
18115请以上两位把它发到我的邮箱里来,我把它的密码除掉,然后再发回来就可以了。yqs210@163.com
18115我也想请楼主把它的密码除掉, 我昨天把它发到你的邮箱yqs210@163.com ,可是不成功,被退回来了啊? 请楼主帮忙.谢谢.
18116为什么数学编辑公式不能用了
斑竹回复:什么意思?
181
17请问tobyqin:
蓝戈做的没错啊,秩为s未知数为n的方程,基础解组的秩不就是n-s么
181
17结论我知道,可我不知道怎么表达post-38-1126695894.gif
181
17这道题目好象很 基础啊!post-38-1126701431.gif
181
17我的解答:
post-38-1126710549.gif
181
17这道题我用一个很简单的方法做出来了,可是我不会用数学编辑公式,没法写出来
设原来的向量组生成一线性空间V,令W等于V的补空间,取W的一组基,再令A是由这组基
按照行排成的一个矩阵,则AX=0即满足题意
181
17还是不懂哦
Y的秩不就是n-s么,方程的基础解不就是有s个么,X线性无关,不就是基础解么??不懂,555```
181
18看上去简单,可我弄了半天也没有证明出来,请高手帮忙post-38-1126696159.gif
181
18靠!!!!!!!!!!!!!!!post-38-1126700853.gif
181
18没理由可以交换呀
181
18当然可以交换了
(E-A)(E-B)=E说明E-A,E-B互为逆矩阵,当然有(E-B)(E-A)=E
181
18这题我发完贴就想到了,不知道我先前脑子是怎么了,嗨,有点滞涨
181
18一般么环中有此结论,当然在全矩阵环中亦然
181
19我想知道应用怎么样
181
19想去南开读数学,不知道是分析还是代数强一些?知道的请说一下,谢啦!
181
19组合数学,微分几何!
18120不会post-38-1126696611.gif
18120我的解答!post-38-1126698594.gif
18120差不多,利用若当阵可得知0特征根的重数就是ker(V)的维数,知道这点能轻易证明
18120这么也可以:post-38-112671
1739.gif
18120蓝戈的,n=2也可以
18123实在找不到这篇文章, 请各位兄台帮忙找找.谢谢
作者: J. B. Robertson
文题: On wandering
subpsaces for unitary operators
杂志全名: Proceedings of the American
Mathematical Society
年份,卷(期): 起止页码:
1965, 16,
233-236
求助者email:bmyuu@hotmail.com
18124目前做一个项目,里面需要用到文本聚类,文本聚类里有一种方法叫做LSI(潜在语义索引),核心就是对文档矩阵进行奇异值分解,然后取若干个大的奇异值,这段时间在试这个算法,有几点不太明白,特请教大家
(1)奇异值分解的理论基础是什么?分解出来的三个矩阵的特点两边的是各代表行和列的,中间是奇异值对角矩阵
(2)我觉得有点类似多元统计里因子分析和主成分分析,但是好像也不完全是。
(3)关于取奇异值个数的问题,如何选取,觉得没有头绪。
谢谢大家了
18125有上海师大研究生学长吗,我想了解一下数学系研究生情况
18126请大家多多指教
见附件post-33-1126713882.ibf
18126解答:post-33-1126716146.gif
18126谢谢楼上的大师
18128李开复博士写给中国大学生的第一封信
华裔美国科学家、微软中国研究院院长李开复是一位在语音识别、人工智能、三维图形和国际互联网多媒体等领域享有很高声誉的年轻人。他的成功经验和治学精神引起了我国许多青年尤其是大学生的广泛关注。在与我国年轻人的交往过程中,李开复归纳出了一些大家共同关心的问题,并结合自己的学习和工作经历,坦诚相见,直抒胸臆,写成了一封给我国学生的长信。
今天全文刊载这封信件,相信对大学生和青年朋友在如何对待机遇、如何对待学业、如何对待工作、如何对待他人
、如何对待自己等诸多方面会有一些有益的启示。
我在中国的这两年来,工作中最大的享受是到国内各高校与学生们进行交流。这些访问和交流使得我有机会与成千上万的青年学生就他们所关心的事业、前途等问题进行面对面的沟通。中国学生的聪明、好学和上进给我留下了非常深刻的印象。
在与这些青年学生的交流过程中,我发现有一些问题是大家都十分关心的。那些已经获得国外大学奖学金的学生,大都希望我谈一谈应该如何度过自己在美国的学习生涯;那些决定留在国内发展的学生,非常关心如何确定一个正确的方向,并以最快的速度在科研和学业方面取得成功;还有那些刚刚踏进大学校门的学生,则希望我能讲给他们一些学习、做人的经验之谈。最近,更有一些学生关心网络信息产业的发展,希望了解美国的大学生是如何创业和致富的。看到这么多双渴求知识、充满希望的眼睛,我突然产生了一种冲动,那就是给中国的学生们写一封信,将我与同学们在交流过程中产生的一些想法以及我要对中国学生的一些忠告写出来,帮助他们在未来的留学、工作或者创业的过程中能够人格更完美,生活更顺利,事业更成功。
坚守诚信、正直的原则
我在苹果公司工作时,曾有一位刚被我提拔的经理,由于受到下属的批评,非常沮丧地要我再找一个人来接替他。我问他:“你认为你的长处是什么?”他说:“我自信自己是一个非常正直的人。”我告诉他:“当初我提拔你做经理,就是因为你是一个公正无私的人。管理经验和沟通能力是可以在日后工作中学习的,但一颗正直的心是无价的。”我支持他继续干下去,并在管理和沟通技巧方面给予他很多指点和帮助。最终,
他不负众望,成为一个出色的管理人才。
与之相反,我曾面试过一位求职者。他在技术、管理方面都相当出色。但是,在谈话之余,他表示,如果我录取他,他可以把在原来公司工作时的一项发明带过来。随后他似乎觉察到这样说有些不妥,特作声明:那些工作是他在下班之后做的,他的老板并不知道。这一番谈话之后
,对于我而言,不论他的能力和工作水平怎样,我都肯定不会录用他。原因是他缺乏最基本的处世准则和最起码的职业道德:“诚实”和“讲信用”。如果雇用这样的人,谁能保证他不会在这里工作一段时间后,把在这里的成果也当作所谓“业余之作”而变成向其他公司讨好的“贡品”呢?这说明,一个人品不完善的人是不可能成为一个真正有所作为的人的。
在美国,中国学生的勤奋和优秀是出了名的。曾经一度是美国各名校最欢迎的留学生群体,而最近,却有一些变化。原因很简单,某些中国学生拿着读博士的奖学金到了美国,可一旦找到工作机会,他们就会马上申请离开学校,将自己曾经承诺要完成的学位和研究抛在一边。这种言行不
一的做法已经使得美国一部分教授对中国学生的诚信产生了怀疑。应该指出,有这种行为的中国学生是少数,然而就是这样的“少数”,已经让中国学生的名誉受到了极大的损害。另外,目前美国有些教授不愿理会部分中国学生的推荐信,因为他们知道这些推荐信根本就出自学生自己之手,已无参考性可言。这也是诚信受到损害以后的必然结果。
我在微软研究院也曾碰到过类似的问题。一位来这里实习的学生,有一次出乎意料地报告了一个非常好的研究结果。但是,他做的研究结果别人却无法重复。后来,他的老板发现,这个学生对实验数据进行了挑选,只留下了那些合乎最佳结果的数据,而舍弃了那些“不太好”的数据。我认为,这个学生永远不可能实现真正意义的学术突破,也不可能成为
一名 真正合格的研究人员。
最后想提的是一些喜欢贪小便宜的人。他们用学校或公司的电话打私人长途、多报销出租车票。也许有人认为,学生以成绩、事业为重,其他细节只是一些小事,随心所欲地做了,也没什么大不了的。然而,就是那些身边的所谓“小事”,往往成为一个人塑造人格和积累诚信的关键。一些贪小便宜、耍小聪明的行为只会把自己定性为一个贪图小利、没有出息的人的形象,最终因小失大。中国有“勿以恶小而为之”的古训,很值得记取。
生活在群体之中
与大多数美国学生比较而言,中国学生的表达能力、沟通能力和团队精神要相对欠缺一些。这也许是由于文化背景和教育体制的不同而造成的。今天,当我们面对一个正在走向高度全球化的社会时,生活在群体之中,做出更好的表现,得到更多的收获,是尤为重要的。
表达和沟通的能力是非常重要的。不论你做出了怎样优秀的工作,不会表达,无法让更多的人去理解和分享,那就几乎等于白做。所以,在学习阶段,你不可以只生活在一个人的世界中,而应当尽量学会与各类人交往和沟通,主动表达自己对各种事物的看法和意见,甚至在公众集会时发表演讲,锻炼自己的表达能力。
表达能力绝不只是你的“口才”。哈佛大学的Ambady教授最近做过一个非常有趣的实验,他让两组学生分别评估几位教授的授课质量。他把这几位教授的讲课录像带先无声地放两秒钟给一组学生看,得出一套评估结果。然后与那些已经听过这几位教授几个月讲课的学生的结果进行对比,两个小组的结论竟然惊人的相似。这表明,在表达自己思想的过程中,非语言表达方式和语言同样重要,有时作用甚至更加明显。这里所讲的非语言表达方式是指人的仪表、举止、语气、声调和表情等。因为从这些方面,人们可以更直观、更形象地判断你为人、做事的能力,看出你的自信和热情,从而获得十分重要的“第一印象”。
对于一个集体、一个公司,甚至是一个国家,团队精神都是非常关键性的。微软公司在美国以特殊的团队精神著称。像Windows2000这样的产品的研发,有超过3000名开发工程师和测试人员参与,写出了5000万行代码。没有高度统一的团队精神,没有全部参与者的默契与分工合作,这项工程是根本不可能完成的。
以前我在别的公司时却也曾见到过相反的现象。一项工程布置下来,大家明明知道无法完成,但都心照不宣,不告诉老板。因为反正也做不完,大家索性也不努力去做事,却花更多的时间去算计怎么把这项工程的失败怪罪到别人身上去。就是这些人和这样的工作作风,几乎把这家公司拖垮。
为了培养团队精神,我建议同学们在读书之余积极参加各种社会团体的工作。在与他人分工合作、分享成果、互助互惠的过程中,你们可以体会团队精神的重要性。
在学习过程中,你千万不要不愿意把好的思路、想法和结果与别人分享,担心别人走到你前面的想法是不健康的,也无助于你的成功。有一句谚语说,“你付出的越多,你得到的越多”。试想,如果你的行为让人觉得“你的是我的,我的还是我的”,当你需要帮忙时,你认为别人会来帮助你吗?反之,如果你时常慷慨地帮助别人,那你是不是会得到更多
人的 回报呢?
在团队之中,要勇于承认他人的贡献。如果借助了别人的智慧和成果,就应该声明。如果得到了他人的帮助,就应该表示感谢。这也是团队精神的基本体现。
做一个主动的人
三十年前,一个工程师梦寐以求的目标就是进入科技最领先的IBM。那时IBM对人才的定义是一个有专业知识的、埋头苦干的人。斗转星移,事物发展到今天,人们对人才的看法已逐步发生了变化。现在,很多公司所渴求的人才是积极主动、充满热情、灵活自信的人。
作为当代中国的大学生,你应该不再只是被动地等待别人告诉你应该做什么,而是应该主动去了解自己要做什么,并且规划它们,然后全力以赴地去完成。想想今天世界上最成功的那些人,有几个是唯唯诺诺、等人吩咐的人?对待自己的学业和研究项目,你需要以一个母亲对孩子那样的责任心和爱心,全力投入,不断努力。果真如此,便没有什么目标是不能达到的。
一个积极主动的人还应该虚心听取他人的批评和意见。其实,这也是一种进取心的体现。不能虚心接受别人的批评,并从中汲取教训,就不可能有更大的进步。比尔·盖茨曾经对公司所有员工说过:“客户的批评比赚钱更重要。从客户的批评中,我们可以更好地汲取失败的教训,将它转为成功的动力。”
除了虚心接受别人的批评,你还应该努力寻找一位你特别尊敬的良师。这位良师应该是直接教导你的老师以外的人,这样的人更能客观地给你一些忠告。这位良师除了可以在学识上教导你之外,还可以在其他一些方面对你有所指点,包括为人处世,看问题的眼光,应对突发事件的技能等等。
我以前在苹果公司负责一个研究部门时,就曾有幸找到这样一位良师。当时,他是负责苹果公司全球运作和生产业务的高级副总裁,他在事业发展方面给我的许多教诲令我终身受益。如果有这样的人给你帮助
,那你成长的速度一定会比别人更快一些。
中国学生大多比较含蓄、害羞,不太习惯做自我推销。但是,要想把握住转瞬即逝的机会,就必须学会说服他人,向别人推销自己或自己的观点。在说服他人之前,要先说服自己。你的激情加上才智往往折射出你的潜力,一个好的自我推销策略可以令事情的发展锦上添花。
例如,有一次我收到了一份很特殊的求职申请书。不同于已往大多数求职者,这位申请人的求职资料中包括了他的自我介绍、他对微软研究院的向往、以及他为什么认为自己是合适的人选,此外还有他已经发表的论文、老师的推荐信和他希望来微软作的课题等。尽管他毕业的学校不是中国最有名的学校,但他的自我推销奏效了。我从这些文件中看到了他的热情和认真。在我面试他时,他又递交了一份更充分的个人资料。最后,当我问他有没有问题要问我时,他反问我,:“你对我还有没有任何的保留?”当时,我的确对他能否进入新的研究领域有疑虑,于是就进一步问了他一些这方面的问题。他举出了两个很有说服力的例子。最后,我们雇用了这名应聘者。他现在做得非常出色。
挑战自我、开发自身潜力
我在苹果公司工作的时候,有一天,老板突然问我什么时候可以接替他的工作?我非常吃惊,表示自己缺乏像他那样的管理经验和能力。但是他却说,这些经验是可以培养和积累的,而且他希望我在两年之后就可以做到。有了这样的提示和鼓励,我开始有意识地加强自己在这方面的学习和实践。果然,我真的在两年之后接替了他的工作。我个人认为,一个人的领
18128写的真好,对我是一个极大的鞭策与激励
18128写得很好啊啊啊
18130学概率统计的一般都做什么工作?
18131如题post-8-1126748040.jpg
18131注意:你利用的是柱面坐标,z的取值不是从极点引线来确定的,(球面坐标才是的),应该平行z轴引线来与区域相交确定,而r的取值其实就是就该是区域投影到xoy面上的区域,当作二重积分极坐标取值的方式来确定,该题的投影就是一个圆,那么r就只该与

有关,不可能与z有关了
18133噢,明白了,偶找了好多地方没点头绪的来着,太感谢了流形版主!以后有空一定多多支持贵论坛!
18133
| 引用 (aireaplane @ 2005年09月27日
15时10分) |
很久没得时间来上网,差点耽搁流形版主一腔热情的回复,还有个问题继续问一下:
"这样的过程不是极限过程(没有度量或拓扑),无法由对任意有限的N成立,得到对所有的集合的并成立。"
请问关于"极限过程"的内容可以参考哪方面的书籍呢?谢谢喽!
|
找拓扑教材就可以
建议看一些科普著作,或者介绍结构数学和数学史的书
18133最近看实变,发现其中一个关于外测度的证明很不可思议:
书中说假定外测度具有有限可加性,则可以证明外测度也将具有可数可加性,然后举出了一个反例说明可数可加性不成立,从而说明外测度不具备有限可加性也不具备可数可加性
在由有限可加性证明可数可加性时,书中的方法感觉很难理解,给人感觉好像所有满足有限可加的东东按照它的方法都可以推至可数可加似的.
请问哪位大虾可以解释一下有限可加在满足什么条件的情况下可以推至可数可加,是否可以举出满足有限可加但却不满足可数可加的具体例子?
18133仅限于实变课本介绍的范围讨论问题
首先外测度的定义域为R^n的幂集所形成的可测空间
如果假定外测度满足有限可加性,由外测度的定义确实可以证明可数可加性
而事实上外测度仅有次可加性。
你的第一个问题好回答,
对于外测度(由定义自然满足次可加性),
次可加性+有限可加性就蕴涵可数可加
测度的定义就要求可数可加性
存在定义于可测空间上的有限可加但不可数可加的非负集函数,
可测空间上的有限可加非负集函数是可数可加的的
充要条件是集函数具有下连续性
18133多谢版主热心回答,但还是不理解两个地方:
1.
它由有限可加推到可数可加的过程,我感觉照它的推法根本不需要用次可加性也可推出,课本是这么推的:
第一步:左边N个集合并的外测度等于右边N个集合中每个集合的外测度的和 ----->
左边无穷大个集合并的外测度大于右边N个集合中每个集合的外测度的和(由外测度的性质二) ----->
将右边N趋于无穷大,即得左边无穷大个集合并的测度大于右边无穷个集合中每个外测度的和.
第二步:由于外测度具有次可数可加性,综合一二步最后推出可数可加性.
而我认为保持第一步不变,再将第一步反过来推一次,即右边无穷大个集合中每个集合的外测度的和大于左边N个集合并的外测度,最后令左边的N趋于无穷大,推出右边无穷大个集合中每个集合的外测度的和大于左边无穷大...,综合一二推出可数可加性.
请问这样有何不妥?是否问题出在将N趋于无穷大时出错了?
2.集函数具有下连续性是嘛意思?咋偶的书上从来没见到过捏?
文字哆嗦了点,抱歉还没整过公式编辑器,先这么发啦,谢谢版主和热心回答者!
18133第一步:左边N个集合并的外测度等于右边N个集合中每个集合的外测度的和 ----->
左边无穷大个集合并的外测度大于右边N个集合中每个集合的外测度的和(由外测度的性质二) ----->
将右边N趋于无穷大,即得左边无穷大个集合并的测度大于右边无穷个集合中每个外测度的和.
第二步:由于外测度具有次可数可加性,综合一二步最后推出可数可加性.
对,
左边无穷大个集合并的外测度大于右边N个集合中每个集合的外测度的和
这是外测度的单调性
将右边N趋于无穷大,即得左边无穷大个集合并的测度大于右边无穷个集合中每个外测度的和.
这是利用
外测度的非负性,有单调有界原理,右边的和存在且小于左边
而我认为保持第一步不变,再将第一步反过来推一次,即右边无穷大个集合中每个集合的外测度的和大于左边N个集合并的外测度,最后令左边的N趋于无穷大,推出右边无穷大个集合中每个集合的外测度的和大于左边无穷大...,综合一二推出可数可加性.
请问这样有何不妥?是否问题出在将N趋于无穷大时出错了?
第一步是反不过来的
右边无穷大个集合中每个集合的外测度的和大于左边N个集合并的外测度,这由外测度的非负性是可以得到的并且对任意一个有限数N都对,但关键在于
,最后令左边的N趋于无穷大,推出右边无穷大个集合中每个集合的外测度的和大于左边无穷大...,
这是行不通的.这样的过程不是极限过程(没有度量或拓扑),无法由对任意有限的N成立,得到对所有的集合的并成立。
集函数具有下连续性是嘛意思?咋偶的书上从来没见到过捏?
如果是讨论任意可测空间上的任意测度的话,为了刻画测度的一些要紧性质而提出的概念,找一本一般测度论的树就可以找到。
下连续性一般是指对可测空间任意一列单调下降的可测集列,当他们的极限为空集时,若对应的集值函数值极限为零,则称这样的可加集函数具有下连续性,这是最一般的定义。
类似的还有上连续性,
在一些具体的理论中,有时统称为连续性
18133很久没得时间来上网,差点耽搁流形版主一腔热情的回复,还有个问题继续问一下:
"这样的过程不是极限过程(没有度量或拓扑),无法由对任意有限的N成立,得到对所有的集合的并成立。"
请问关于"极限过程"的内容可以参考哪方面的书籍呢?谢谢喽!
18133自己顶一下!
18135概率统计专业的金融数学方向和应用数学专业的金融数学方向有什么区别?
18135你要考吗?我觉得差不多把,学金融数学,概率肯定是重中之重!
我也想考这方面,我对金融也比较感兴趣!
18136设A,B是n级复矩阵,且AB=BA.求证:存在一个n级可逆矩阵P,使得
P - 1 AP与P-1BP 都是上三角矩阵.(P-1表示P的逆).
数学编辑公式现在怎么用不上了?
18136
引用 (iii @ 2005年09月
19日
08时42分) |
| 为什么说至少有一个公共的特征向量呢??
请指教 |
这个结论可用特征子空间的知识给予证明。
18136为什么说至少有一个公共的特征向量呢?? 请指教
18136请问::::该怎么证明呢???post-38-1127026390.ibf
18136北京大学的教材中习题.方法是先证A,B至少有一个公共特征向量,然后用归纳法.这类试题建议自己查找解答.
18136我粗粗的做了一下post-38-1127040960.gif
18136谢谢 书上是有,,谢谢.
18137学科、专业名称(代码) 研究方向 招生规模 考试科目 备 注
数学:基础数学(070101) 泛函分析 模糊数学 代数 低维拓扑学
随机过程 解析数论 几何函数论 偏微分方程 30 ① 英语或俄语② 政治③ 数学分析④ 高等代数
数学:计算数学(070102)
微分方程数值分析 数值逼近 精算学 计算机图形学 计算与应用小波分析 神经网络 20 ① 英语或俄语② 政治③ 数学分析④ 高等代数
数学:应用数学(070104) 微分方程反问题 泛函微分方程及其应用 应用几何 小波分析及其应用 常微分方程稳定性理论及其应用
18 ①
英语或俄语② 政治③ 数学分析④ 高等代数
数学:运筹与控制论(070105) 控制理论 最优化理论和应用 应用概率统计 10 ①
英语或俄语② 政治③ 数学分析④ 高等代数
18138但我想,核函数的概念应该是一致的。
18138我以前在SVM中看到过核函数的概念,现在在看一篇关于注视的调制模型中,又由有关核函数的内容。
对于这个概念,我一窍不通。请教各位大虾:它是属于哪个数学范畴的,概念是什么。大致有什么应用!
谢谢您的关注!感激不尽
18138是Kernal
Functions?
这是散点平滑里面的概念,它是在估计某一点的函数时用这一点周围的几个点,根据这几个点到这一点的距离给予不同权重的函数,你在讲平滑的书里很容易找到
18138楼上的谈的可能也对,但积分方程中也有核函数的概念。不知道你要的是那一种???
18138Definition of The Kernel Function: The kernal function is a weighting
function used in nonparametric function estimation. It gives the weights
of the nearby data points in making an estimate. In practice kernel
functions are piecewise continuous, bounded, symmetric around zero,
concave at zero, real valued, and for convenience often integrate to one.
They can be probability density functions. Often they have a bounded
domain like [-1,1].
18138我想楼上说的同SVM相关的核函数应该是以下这种吧
核k是一个函数,这个函数对所有x,y 属于
X(输入空间),满足
k
(x,y)=<φ(x),φ(y)>
其中
φ 是从输入空间到特征空间(内积空间)的映射
18139各位高人能提供一些概率论与数理统计的习题集吗,和复旦概率论基础一个难度的,那书上的习题没有解答,做了也不知道对错的.请热心人指点
18139怎么都没有人理我啊:(
18139各位大虾都是只看书不做题的吗,汗
18139学这种基础课做题非常重要,我记得我以前用过一本苏联的概率论习题集不错,
有答案和例题。也有些很难的题目。“概率论习题集”特罗高夫切夫等,
1989上海翻译出版公司
18139学数学要学会自己判断对错
18139谢谢Fisher老师了,不过我总是觉得做了题不知道答案没有成就感,然后也就没有动力去做了,光看书没有做题来检验看的效果,也是很不爽的=.=
18140如下post-38-11267579
18.gif
18140这个好象是中科院的05年的高等代数中的一个题目吧!post-38-1126758466.gif
18141看你学什么,你一定要把所有点(值)放在一起,那就不是函数了,单值或多值函数都要化成单一映射的,不会一个值"确实"对应2个点.所以在处理后是函数.
18141多值函数是否函数?数列的项数是否一定为无穷?
18141多值函数是否函数是函数:函数就该分单值和多值函数
数列的项数是一定为无穷,由定义:对应任何正整数n都有一个确定的书xn
18143如下图片中错了,是等于六分之一 [MATH]$

$[\MATH] 的平方post-38-1126762687.gif
18143其实这个题目也可以用一致收敛性来做,也比较好做,大概会比fourier级数要计算简单一些吧!
我没有去做,想想应该是可以的,而用fourier级数好象是书本上的知识,有的!
18144
具体参见:
http://www.math.org.cn/article.php/161
18145博士数学预印库论文,请勿删除!post-44-1127133306.ibf
18146我见过中南大学2000-2002的试题,怎么那么难啊?最近几年还是那样吗?
18146怎么会很难呢?老第你不是开玩笑吧.中科院的都不怎么难呀.
18146应该不会太难吧!
18146各个学校出题都有偏向的,多有针对性的练练就好了。
18146请问楼上的各位知不知道中南大学
复试都考哪些方面的知识啊
静侯佳音啊
18146中南的是很难哦 ```
18147pdf版post-44-1126766160.ibf
18148求助
设f是[0,1]上全体是函数所构成的集合
证明 f的基数为 2的c次幂
18148还是作个附件传上来吧post-21-1126791590.ibf
18149A,B,U,V是n阶实矩阵,且满足:AU=B,VB=A,证明:存在可逆阵T满足AT=B
18149靠,真是晕哦post-38-1126770467.gif
18149那么这样的线性变换或矩阵T该如何构造呢?????
18149这个我倒是没有想过,因为我认为这个是理论上比较有用点,而在计算上没有什么好的用处,所以就没有去想,也懒的去想。
18149这个好像还很重要哦!
理论上没有这个结论啊,难道是俩个列向量空间是同构的????
18149我给个构造性的证明:
post-38-1127035956.gif
18149蓝戈说的是,若有两n个列的矩阵A,B,他们的秩相等,则有T,使得A=TB,这个是不正确的。
18152我最近看的一篇文献里面牵涉到核函数。请教各位,什么是核函数?有什么性质?属于哪个数学范畴?
特别是有没有什么好的书介绍一下!感激不尽!
18152我知道统计里面有核函数kernal function,
但是其他的数学分支里面也可能有
这一样的名词但意思不一样,不知道你指的是哪个分支里的定义
18152kernal
function.偶在这里的定义蛮模糊的。我看积分方程的时候,有积分方程的核。还有统计里也有核函数。还有积分变换里的核的定义,甚至我在看代数的时候好象不记得在什么地方也遇到了核的定义。你看的文献是哪一方面的?
18152是不是位势核?
位势论里有这么称呼的
18152我自己也不太清楚,是关于生物方面的一篇文章,讲得是注视(attention)的调制作用。
里面讲得是optimal linear
transfer fuction (kernel)。
好像是说通过核函数K,将两个变量联系在一起R=K*M,请教各位了
18152核函数在偏微分方程里讲过吧
这么课我学的不怎么好
就是隐约有点印象
18152
| 引用 (zhubin846152 @ 2005年09月15日
23时44分) |
我自己也不太清楚,是关于生物方面的一篇文章,讲得是注视(attention)的调制作用。
里面讲得是optimal linear
transfer fuction (kernel)。
好像是说通过核函数K,将两个变量联系在一起R=K*M,请教各位了
|
应该就是了
位势核积分其实就是 一般的积分变换
如拉普拉斯变换,富里叶变换,等等
18152恩,想必就是积分变换里的核函数定义了。学了不少核函数的定义,不知道在不同的课程中这些定义能不能统一?至少我觉得积分方程里和积分变换里的核函数定义比较相似。
18152那统计里的核函数是什么意思啊?请教各位。谢谢。
18153鄙人在该论坛第一贴
相关系数怎么就代表了两个变量的相关性?
似乎仅仅是在两个极端的情况符合人们的直觉:两个完全相同的变量相关系数为
1,完全不相关的变量,相关系数为0
我觉得这个东西是个有点莫名其妙的量,迷惑中
望高人指点,最好能深入浅出
18153如果你学过向量代数和空间解释几何
就可以把相关系数理解为
两个向量在多维空间的夹角的余弦值
夹角为90度,相关系数 = 余弦值 = 0
夹角为0度,相关系数 = 余弦值 =
1
夹角为
180度,相关系数 = 余弦值 = -1
18154如题
18154见图post-21-112678
1978.jpg
18154谢谢,简单明了
顺便请教一下,函数列的积分的 一致收敛性是否蕴含一致可积性?
18154我没看懂“函数列的积分的 一致收敛性是否蕴含一致可积性? ”
能否叙述一下相关概念的定义。
18154能说得再清楚一点吗?
18154
| 引用 (mazl @ 2005年09月15日
22时10分) |
我没看懂“函数列的积分的
一致收敛性是否蕴含一致可积性? ”
能否叙述一下相关概念的定义。 |
我只是把数分的概念和实变的概念作了一个联系
函数列的积分的
一致收敛性是否蕴含一致可积性
不好意思应该改一下:
一列黎曼绝对可积的函数,他们的积分一致收敛(广义积分),
是否可推出该列函数一致可积?
18154第n个函数为在(0,1/n)上为n,其他点皆为0。
18154不是反例吧
这样的函数列是一致可积的
18154请问一致可积的定义
18154
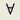

,
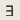
绝对可积F(x)>=0,使得对任意的n,
∫ E
[|fn(x)|≥F(x)]
|fn(x)|dx <

18154
引用 (mazl @ 2005年09月15日
17时59分) |
| 见图
|
不好意思,
能否讲一下你这个例子真的是一致收敛的么?
18154
引用 (流形 @ 2005年09月
17日
17时00分) |
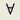
 , ,
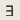 F(x)>=0,使得对任意的n, ∫ E
[|fn(x)|≥F(x)]
|fn(x)|dx <
F(x)>=0,使得对任意的n, ∫ E
[|fn(x)|≥F(x)]
|fn(x)|dx <  |
照此定义,取 F(x)=1/x
即可.
另外我抄了一个定义,见附图
post-21-1127002708.jpg
18154呵呵,你给的性质我们称之为积分等度连续性
他还有一个更弱的定义
我上面的定义中F(x)要求可积,发贴的时候漏了,
呵呵
我的定义是来自北大周民强的书一致可积性,有的测度论上也是如此定义的
记得数学辞海的定义也与我上面的定义类似
18154你们讲的太深了吧,我不懂!
郁闷!
18154
引用 (流形 @ 2005年09月
17日
14时07分) |
不是反例吧
这样的函数列是一致可积的 |
您认为
“第n个函数为在(0,1/n)上为n,其他点皆为0”
这样的
“函数列是一致可积的”,意味着
您已经对这个函数列
找到了一个绝对可积函数F(x).
请教F(x)是如何定义的?
18154
引用 (PlayBoy001 @ 2005年09月
17日
18时35分) |
引用 (mazl @ 2005年09月15日
17时59分) | | 见图
|
不好意思,
能否讲一下你这个例子真的是一致收敛的么?
|
f_n(x)的图像是
用过点(0,1/n)与|x|的图像相切的圆的小弧替代其下方的折线
得到的.
18159我在使用piecewise定义过程时,如果自变量含有sin项,则piecewise过程失效。
例如以下代码:
f:=(x)->piecewise(x<0,x-a,x>0,x+a,0);
f(aa*sin(x1+bb));
convert(%,piecewise,x1); <-失败
这是不是Maple软件的限制,有没有什么好的解决方法。
18159首先,你要给定aa和bb的值,
否则基本上无法判别x1在取什么值的时候,
asin(x1+bb)是小于0还是大于0。
其次,Maple对于处理分段函数的,
由于三角函数具有周期性,
因此不予处理。
18162谢谢了!
18162thanks
18162线性和非线性最优化理论、方法、软件及应用post-37-1126777432.ibf
18162谢谢!
18162谢谢,中秋快乐
18162谢谢!
18162多谢了,仔细研究!
18162thanks
18162谢谢
18162谢谢
18162谢谢
18162谢谢lz贡献!!
18162謝謝您!很受用
18162谢谢
18162感谢拉,很实用
18162不错,好东东
18162谢谢啊
18162谢谢了啊
18163是啊,科大的人多了点吧!
181632003 年发表的概率论与数理统计论著目录
1. Hu, T., Khaledi, B.-E. and Shaked, M.
(2003). Multivariate hazard rate orders.
“Journal of Multivariate
Analysis”, 84 (1),
173-
189.
2. Yuan, M., Su, C. and Hu, T. (2003). A
central limit theorem for random fields of negatively
associated
processes. “Journal of Theoretical Probability”, 16 (2), 309-323.
3.
Belzunce, F., Hu, T. and Khaledi, B.-E. (2003). Dispersion-type
variability orders.
“Probability in the Engineering and Informational
Sciences”,
17 (3), 305-334.
4. Hu, T., Ma, M. and Nanda, A. K. (2003).
Moment inequalities for discrete ageing families.
“Communications in
Statistics, Part A---Theory and Methods”, 32 (1), 61-90.
5. Hu, T.
and Zhu, Z. (2003). Stochastic comparisons of order statistics from two
samples.
“Southeast Asian Bulletin of Mathematics”, 27 (1),
89-98.
6. Bai, Z.D., Miao, B.Q. and Yao, J.F. (2003). Convergence
rates of spectral distributions of
large sample covariance matrices.
“SIAM Journal on Matrix Analysis and Applications”,
25 (1), 105-127.
7. Bai, Z., Chen, Z. and Wu, Y.H. (2003). Convergence rate of the
best-r-point-average estimator
for the maximizer of a nonparametric
regression function. “Journal of Multivariate
Analysis”, 84, 3
19-334.
8. Wei, L.S. and Chen, J. (2003). Empirical Bayes estimation and its
superiority for two-way
classification model. “Statistics and
Probability Letters”, 63, 165-
175.
9. Hu, Z.S. and Su, C. (2003).
Limit theorems for the number and sum of near-maxima for medium
tails. “Statistics & Probability Letters”, 63 (3), 229-237.
10.
Wu, C.Q., Zhao, L.C. and Wu, Y.H. (2003). Estimation in change-point
hazard function models.
“Statistics & Probability Letters”, 63,
41-48.
11. Wang, Y.B., Yan, J.G., Cheng, F.Y. and Su, C. (2003). The
strong law of large numbers and the
law of iterated logarithm for
product sums of NA and AANA random variables. “Southeast Asian
Bulletin of Mathematics”, 27, 369-384.
12. 韦来生, 袁家成 (2003).
指数分布定数截尾情形失效率函数的经验 Bayes 检验问题.《应用概率统计》,
19, 130-138.
13. 王小明、赵林城
(2003). 方向数据密度核估计的对数律. 《数学学报》, 46, 865-874.
14. Zhao, L.C. and Zhang,
H. (2003). Model selection for log-linear models of contingency tables.
"Journal of Systems Science and Complexity“, 16 (2),
249-259.
15. Zhao, L.C. and Xu, J.F. (2003). Weak convergence of
weighted empirical cumulative quantile
regression functions.
《应用概率统计》,
19, 161-166.
16. 缪柏其、赵林城、谭智平 (2003).
关于变点个数及位置的检测和估计.《应用数学学报》, 26 (1), 26-39.
17. 苏淳、胡治水、唐启鹤 (2003).
非负分布重尾程度的刻画. 《数学进展》, 32 (5), 606-614.
18. Su, C. and Tang, Q.H.
(2003). Characterizations on heavy tailed distributions by means of
hazard rate. 《应用数学学报》(英文版),
19 (1), 135–142.
19. 雷鸣、缪柏其、宁静 (2003).
运用生存模型对上证指数与成交量的研究--兼论股市的政策效应 《数理统计与管理》,6,46-50.
20. 潘婉彬、缪柏其 (2003).
加权分布模型测算个股VaR. 《微计算机信息》,8, 90-91.
21. 牛惠芳,缪柏其 (2003).
课堂教学评估中权重的制定方法探讨. 《数理统计与管理》,22 (5), 34 -37.
22. 缪柏其、肖婕、宁静 (2003).
教学数据的统计分析与建模. 《教学理论研究与实践》, 2, 33 -35.
2002 年发表的概率论与数理统计论著目录
1.
Dorea, C. C. Y. and Zhao, L. C. (2002). Nonparametric density estimation
in
hidden Markov models. "Statistical Inference for Stochastic
Processes", Vol. 5,
55-64.
2. Zhao, L. C. (2002). Strong
consistency of M-estimates in linear models.
"Science in
China" (Ser. A), Vol. 45, No.11, 1420-1427.
3. Zhao, L. C. and
Peng, L. M. (2002). Model selection under order restriction.
"Statistics & Probability Letters", Vol. 57, 301-306.
4.
Hu, T. and Xie, H. (2002). Proofs of the closure property of NBUC and
NBU(2) under
convolution. "Journal of Applied Probability",
Vol. 39, No. 1, 224-227.
5. Wei, G. and Hu, T. (2002). Supermodular
dependence ordering on a class of
multivariate copulas.
"Statistics & Probability Letters", Vol. 57, No. 4,
375-385.
6. Su, C., Hu, T. and Liang, H. (2002). On the logarithmic law
for strictly
stationary and negatively associated arrays.
"Theory of Probability and
its Applications", Vol. 46, No.
2, 369-379.
7. Lin, M. and Wei, L. S. (2002). The small sample
properties of the principal
components estimator for regression
coefficients. "Communications in Statistics
--Theory and
Methods", Vol. 31, No. 2, 271-283.
8. Bai, Z. D., Miao, B. Q. and
Tsay, J. (2002). Convergence rates of the spectral
distributions of
large wigner matrices. "International Mathematical Journal",
Vol. 1, No. 1, 65-90.
9. Su, C. and Hu, Z. S. (2002). The asymptotic
distributions of sums of record
values for distributions with
regalarly varying tails. "Journal of Mathematical
Siences",
Vol. 111, No. 6, 3888-3894.
10. Tang, Q. and Su, C. (2002). Ruin
probabilities for large claims in delayed
renewal risk model.
"Southeast Asian Bulletin of Mathematics", Vol. 25, No. 2,
735-743.
11. Boland, P. J., Hu, T., Shaked, M. and Shanthikumar, J. G.
(2002). Stochastic
ordering of order statistics II. In "Modeling
Uncertainty: An Examination of
Stochastic Theory, Methods, and
Applications" , Kluwer Academic Publishers,
pp. 607-623.
12.
王立春、韦来生(2002). 刻度指数族参数的经验 Bayes 估计的收敛速度. "数学年刊",Vol.
23A,
No. 5, 555-564.
13. 胡治水、苏淳、王定成 (2002). 对数正态型分布纪录值之和的渐近分布.
"中国科学"(A辑),
Vol. 32, No. 7, 603-612.
14. 吴成庆,赵林城 (2002).
马可夫链中密度函数核估计积分绝对偏差的指数界. "中国统计学报, Vol. 40, N0. 2, 215-2
18.
15.
Chen C. and Zhao L. C. (2002). Detection of the rank of regression
coefficient
matrix by M-method. "应用概率统计", Vol.
18, N0. 1,
43-50.
16. Zhao, L. C. and Diao, G. Q. (2002). Strong convergence of
modified partitioning
estimates of nonparametric regression functions.
"应用概率统计", Vol.
18, No. 2,
192-
196.
17. 林明、韦来生 (2002).
回归系数 Stein 压缩估计的小样本性质. "应用数学学报", Vol. 25,
497-504.
18.
Su, C., Jiang, T. and Tang, Q. (2002). Extension of some classical results
on
ruin probability to delayed renewal model. "应用数学学报"
(英文版), Vol.
18, No.
4, 675-680.
19. Liang, H. Y., Chen, Z. J. and
Su, C. (2002). Convergence of Jamison-type weighted
sums of pairwise
negativly quadrant dependent random variables. "应用数学学报"
(英文版), Vol.
18, No. 1, 161-168.
20. 王定成、苏淳、章劲松 (2002).
NA序列广义Jamison型加权和的几乎处处收敛性. "应用数学学 报", Vol. 25, No. 1, 77-87.
21. 蒋涛、缪柏其 (2002). 终极破产概率的双边界. "应用概率统计",Vol.
18, No.
2,161-166.
22. 刘东海、缪柏其、彭衡 (2002). M-估计下误差密度估计的相合性.
"应用概率统计",Vol.
18,
No. 2,125-134.
23. 苏淳、童铁军 (2002).
一类特殊Weibull分布纪录值之和的中心极限定理. "高校应用数学学报" (A辑), Vol.
17, No. 1,
83-90.
24. Wu, C. Q. and Zhao, L. C. (2002). Limit theorem for
integrated square error of
orthogonal series density estimators.
"中国科学技术大学学报", Vol. 31, No.4,
407-411.
25. Zhang, H. and
Yuan, M. (2002). Entropy-based test for exponentiality under
interval
censorship. "中国科学技术大学学报", Vol. 32, No. 1, 70-78.
26. 蒋涛、缪柏其
(2002). 复合混合Poisson模型中的破产概率. "中国科学技术大学学报",Vol.
31, No.
4,400-406.
27. 王立春、韦来生 (2002). 刻度指数族参数的渐近最优的经验 Bayes 估计.
"中国科学技术大学学报", Vol. 32, No. 1, 62-69.
28. 缪柏其、宁静、肖婕、戴小莉
(2002). 评估数据的统计分析与修正. "中国科学技术大学学报" Vol. 32, No. 1,56-61.
29.
周开国、缪柏其 (2002). 应用极值理论计算在险价值(VaR)--对恒生指数的实证分析,"预测", Vol. 21, No.
3,37-41.
30. Lei, M., Miao, B.Q. and Ning, J. (2002). Study of
Shanghai stock index and the
polices effort with survival analysis and
extremum theory, 金融学前沿问题探讨,
第9届全球金融年会
(GF2002)论文选编,北京大学光华管理学院编,北京大学出版社,962-971.
31. 缪柏其、牛惠芳(2002).
非线性主成分在课堂教学评估体系中的应用,"中国高等教育评估",
52(3),53-55.
32. Wang,
D.C., Su C. and Hu, Z.S. (2002). Precise deviation for random sums of
random walks with dependent heavy-tailed steps. "Far Eastern
Mathematical Journal",
Vol. 3, No. 1, 34-51.
33.
苏淳、江涛、唐启鹤、梁汉营 (2002). NA结构的安全性. "应用概率统计", Vol.
18, No. 4,
400-404.
2001 年发表的概率论与数理统计论著目录
1. Zhao L.C. and Wu C.Q.(2001).
Central limit theorem for integrated square error of
kernel estimators
of spherical density.《中国科学》(Ser.A), 31(1):
18-27(中文版);
44(4):474-483
(英文版).
2. Zhao L.C. and Zhang H.(2001). A Central Limit Theorem for
Testing Exponentiality.
“Communicationsin Statistics:Theory and
Methods”, 30(6):1163-1
170.
3. Zhao L.C., Wang X.N. and Wu Y.H.(2001).
Inference on the rank of the growth curve
model using model selection
method.“Journal of Systems Science and Complexity”,
14(2):
2
18-224.
4. Zhao,L.C., Dorea, C.C.Y. and Goncalves,C.R.(2001).On
determination of the order of
a Markov chain."Statistical
Inference for Stochastic Processes",4:273-282.
5. Wang X.M. and
Zhao L.C.(2001). Laws of the iterated logarithm for kernel estimator
of density function of spherical data.《系统科学与数学》, 21(3): 264-273.
6.
Hu, T., Zhu, Z. and Wei, Y. (2001). Likelihood ratio and mean residual
life
orders for order statistics of heterogeneous random
variables.“Probability in
the Engineering and Informational Sciences”,
15(2): 259-272.
7. Hu, T. and Wei, Y.(2001). Stochastic comparisons
of spacings from restricted
families of distributions.“Statistics
& Probability Letters”,53(1): 91-99.
8. Hu, T. and Wei,
Y.(2001).Multivariate stochastic comparisons of inspection and
repair
policies.“Statistics & Probability Letters”,53(3): 315-324.
9. Hu,
T. and Zhu, Z. (2001). An analytic proof of the preservation of the up
shifted likelihood ratio order under convolutions.
“Stochastic
Processes and Their Applications”, 95(1): 55-61.
10. Su, C., Hu, T.
and Liang, H. (2001). On the logarithmic law for strictly
stationary
and negatively associated arrays. “Theory of Probability and its
Applications”(Teoriya Veroyatnostej i ee Primeneniya), 46(2):397-407 (in
Russian).
11. Hu, T., Kundu, A. and Nanda, A.K. (2001). On generalized
orderings and ageing
properties with their implications. In“System
and Bayesian Reliability”(Eds:
Y. Hayakawa,T.Irony and
M.Xie),Vol.5--Series on Quality, Reliability and
Engineering
Statistics (Essays in Honor of Professor Richard E. Barlow on His
70th
Birthday), World Science Publication, pp.
199-228.
12.
Bai,Z.D.,Miao,B.Q. and Tsay,J.(2001) Convergence rates of the spectral
distributions of large wigner matrices. “Intern. Math. Journal”,1(1):
65-90.
13. Wu, S.S. and Miao, B.Q.(2001). Statistical inference for
contamination
distribution."Journal of Systems Science and
Complexity",14(3).
14.
谭志平,缪柏其(2001).分布变点模型的非参数检验和区间估计.《数学年刊》22A(5):6
17-626.
15.
缪柏其,谭智平(2001). 二阶随机控制变点的Kolmogrov型体健和估计(英).《应用概率统计》,
17(2).
16.
蒋涛、缪柏其(2001).复合混合Poisson模型中的破产概率.《中国科学技术大学学报》,
31(4):398-406
17.
Su, C.,Tang Q. and Jiang T.(2001).A contribution to large deviations for
heave-tailed
random sums,"Science in China", Ser.A
(中国科学,英文版,A辑),44(4):438-444.
18. Tang Q.,Su C.,Jiang T.and Zhang
J.(2001). Large deviations for heavy-tailed random
sums in compound
renewal model."Statististcs & Probability
Letters",52(1):91-100.
19. Liang H.Y., Su C. and Wang Y.B.(2001).
Convergence rates in the law of logarithm
of random elements.
"Acta Mathematicae Applicates Sinica",
17(1):98-106.
20.
Tang Q. and Su C.(2001). Note on large deviations for heavy-tailed random
sums
in compound renewal model. "Far Eastern Mathematical
Journal", 2(1):53-57.
21.
江涛、苏淳、唐启鹤(2001).I.I.D.随机变量部分和之随机和的极限定理.《中国科学技术大学学报》,2001,
31(4):394-399.
22. 韦来生(2001). NA 样本情形概率密度函数核估计的相合性.《系统科学与数学》,
21:79-87.
23. 方兆本、吴硕思 (2001). 带约束条件的 AGARCH 模型.《应用概率统计》,
17(3).
24. 缪柏其、肖婕、宁静(2001).脂肪肝及其影响因素分析——中国科学技术大学体检专向调查.
《数理统计与管理》,20(3).
25. 肖婕,宁静,缪柏其,戴小莉,宋昌耐(2001).影响学生成绩各因素的评价.《中国高等教育
评估》,46(1).
26.
宁静,肖婕,缪柏其,戴小莉,宋昌耐(2001).高考成绩与大学成绩的相关性研究,
《高等理科教育》,37(3).
27.
宁静、肖婕、缪柏其、戴小莉、宋昌耐 (2001).我校近十年生源质量呈现攀升之势.《教育与现代
化》,61(4):73-76.
2000 年发表的概率论与数理统计论著目录
1. Wang,Q.Y.,Jing,B.Y. and Zhao,L.C.(2000).The
Berry-Esseen bound for Studentized
statistics."Annals of
Probability", 28: 511-535.
2. Zhao, L.C.(2000). Some
contributions to M-estimation in linear models.
"Journal of
Statistical Planning and Inference", 88:
189-203.
3. Qin Y.S. and
Zhao L.C.(2000).Empirical likelihood ratio confidence intervals for
various differences of two populations.《系统科学与数学》(英),13: 23-30.
4. Wang
X.M., Zhao L.C. and Wu Y.H.(2000). Distribution free laws of the iterated
logarithm for kernel estimator of regression function based on
directional data.
"Chinese Annals of Mathematics", Ser.B,
21: 489-498.
5. Hu, T. and He, F.(2000). A note on comparisons of
k-out-of-n systems with
respect to the hazard and reversed hazard rate
orders."Probability in the
Engineering and Informational
Sciences". 14(1), 27-32.
6 Hu, T. and Pan, X.(2000). Comparisons
of dependence for stationary Markov
processes."Probability in
the Engineering and Informational Sciences".
14(3), 299-315.
7 Hu, T.(2000). Negatively superadditive dependence of random variables
with
applications.《应用概率统计》.16(2),133-144.
8 梁汉营、苏淳、胡太忠(2000).
B-值独立随机元重对数率收敛速度的一般形式.《应用数学学报》 (中文版). 23(3),455-465.
9 Yuan M. &
Su C.(2000). Weak convergence for empirical processes of
Negatively
associated sequences.《应用概率统计》,16(1):45-56.
10 Yuan M. and Su C.(2000).
Weighted weak convergence for empirical processes
of Negatively
associated sequences.《应用概率统计》,16(2):
199-207.
11 秦永松,苏淳
(2000).含附加信息时条件分位数的估计及其渐进性质.《应用数学学报》,
23(1):56-62.
12 秦永松,苏淳
(2000). 条件分位数的经验似然置信区间.《数学年刊》(A辑),21(2):231-240.
13 苏淳, 梁汉营,王岳宝(2000).
IID随机变量两两乘积之和的Hsu-Robbins型定理(I),
《数学学报》, 43(5):875-886.
14 苏淳,
梁汉营,王岳宝 (2000). IID随机变量两两乘积之和的Hsu-Robbins型定理(II).
《数学学报》,
43(6):1041-1052.
15 Liang H. and Su C.(2000). Strong laws for weighted
sums of random elements.
"Statistica Sinica",
10:1011-10
19.
16 Wang Y.,Su C. and Liang H.(2000). Equivalent
conditions of complete convergence
for m dimensional products of iid
random variables and application to strong law
of large
numbers."Science in China" (Ser.A),43(11):1144-1153.
17
韦来生(2000). 错误先验假定下回归系数 Bayes 估计的小样本性质,《应用概率统计》,
16:71-80.
18
黄元亮,陈桂景,韦来生 (2000).广义G-M 模型参数估计的相对效率,《数学研究与评论》,
20(1):103-108
19
韦来生(2000).刻度指数族参数的经验BAYES检验问题:NA样本情形.《应用数学学报》,23: 403-412.
20 Singh,
R.S and Wei L.(2000). Nonparametrioc empirical Bayes procedure,
asymptotic
optimality and rates of convergence for two-tail tests in
exponential family.
"Nonparametric Statistics",
12:475-501.
21 缪柏奇,戴小莉,韦来生等(2000).课堂教学评估问卷的统计分析,《中国高等教育评估》,
2:31-35.
22 谭智平,缪柏其(2000).关于分布变点的非参数统计推断,《中国科技大学学报》,30(3)
23
彭衡,缪柏其(2000). 随机变量分量负(正)相依变点问题的统计推断.《中国科技大学学报》,31(1)
24.
缪柏其,戴小莉,韦来生,彭衡,汪晓峰,关于课堂教学评估问卷的统计分析.
《中国高等教育评估》. 43(2).
25.
缪柏其,宁静,肖婕(2000).主成分分宜和因子分析在体健数据中的应用.《数理统计与管理》.
19(6).
26.方兆本、吴硕思
(2000). 非对称广义自回归条件异方差的新模型.《应用概率统计》,16(4).
1999 年发表的概率论与数理统计论著目录
1. Liang, H.Y. and Su, C. (
1999). Complete convergence for weighted sums
of NA
sequences. Statist. & Prob. Letters, 45: 85-95.
2.
Shao, Q.M. and Su, C. (
1999). The law of the iterated logarithm for
negatively
associated random variables. Stochastic Processes and Their
Applications,
83:139-148.
3. 韦来生.(
1999).
一类线性模型中参数的经验Bayes检验问题.《数学年刊》 20A: 6
17-628.
4. 韦来生.(
1999).
误指定模型中回归系数混合估计的小样本性质.《中国科技大学学报》
29: 253-259.
5. Wei, L. (
1999).
Asymptotically optimal empirical Bayes estimation in one-way
ANOVA
model. System Sciences & Mathematical Sciences. 12: 13-22.
6.
Zhang, S.P. and Wei, L. (
1999). A note about convergence rates for
empirical
Bayes estimation of parameters in multi-parameter
exponential families.
Commum. Statist.-----Theory Meth., 28:
1273-1291.
7. Hu, T. and Pan, X. (
1999). Preservation of multivariate
dependence under
multivariate claim models. Insurance:Mathematics
& Economics,25:
171-
179.
8. Hu, T. and Hu, J. (
1999). Sufficient
conditions for negative association of
random variables. Statistics
& Probability Letters. 45: 167-
173.
9. Hu, T. (
1999). A proof for
two conjectures on distributions with logistic
conditionals.《中国科技大学学报》29: 394-399.
10. Hu, T. and Wu, Z. (
1999). On
the dependence of risks and the stop-loss
premiums.
Insurance:Mathematics & Economics,24: 323-332.
11. 胡太忠、方兆本(
1999).
《大学生数学解题诠释》“第十一篇:概率论”,安徽教育出版社。
12. Bai, Z.D., Miao, B.Q. (
1999).
Remarks on the convergence rate of the spetral
distributions of Wigner
matrices. Journal of Theorectical Probability.12:105-110.
13. Liang,
Q.W. and Miao, B.Q. (
1999). The relationship between the rates of
employment increasing and economic developing.《数学季刊》, 14:105-110.
14.
Z.D.Bai, C.R. Rao, Y. Wu, M.M. Zen , L.C. Zhao. (
1999). The
simultaneous
estimation of the number of signals and frequencies of
multiple sinusoids
when some observations are missing: I. Asymptotics.
Proc. Natl. Acad. Sci. USA. 96:11106-10.
15. 吴耀华、赵林城(
1999).
线性模型中随机加权自助法的大样本研究.《中国科学》(A辑),
29:616-624;英文版, 42:1066-1074.
16.
Dorea, C.C.Y. and Zhao, L.C. (
1999). Convergence of a random algorithm for
function optimization. Num. Funct. Anal. & Optimiz. 20:
825-833.
17. 张曙光 (
1999). Pricing of European call option on corporate
bond.
《应用概率统计》,15:63-67。
1998 年发表的概率论与数理统计论著目录
1. 吴耀华、赵林城
(
1998). 线性模型随机加权自助法的渐近有效性.《科学通报》,43:586-588;
英文版, 43:711-71.
2.
秦永松、赵林城(
1998). 两样本分位数差异的半经验似然比检验.《应用数学学报》,21: 103-112.
3.
秦永松、赵林城(
1998). 有偏模型中一类统计泛函的经验似然比估计及其渐近性质.
《应用数学学报》,21: 428-436.
4. Miao, B.Q., Wu, Y. and Zhao, L.C. (
1998). On strong consistency of a
2-dimensional frequency estimation algorithm. Statistica Sinica,
8:559-570.
5. 缪柏其. (
1998). 《概率论基础》,中国科技大学出版社。
6. Hu, T. and Hu, J.
(
1998). Comparison of order statistics between dependent
and
independent random variables. Statist. & Prob. Letters, 37: 1-6.
7. Wei, L. (
1998). Convergence rates of empirical Bayesian estimation in a
class of linear models. Statistica Sinica, 8: 589-605 .
8. Wu,
Y.H. (
1998). The power function of a maximum studentized range test in
a two-way design. Statist. & Prob. Letters, Vol. 38.
9.
吴耀华、蔡新中、吴之强..(
1998). 一种夫妻联合养老金(附死亡)保险的计算.
《中国科技大学学报》,Vol. 28(4).
10. 苏淳、迟翔 (
1998). 非平稳NA序列中心极限定理的一些结果.《应用数学学报》, 21:9-21.
11. 苏淳、迟翔
(
1998).随机变量序列最大部分和之矩的二阶估计式及其应用.《科学通报》,
43:2049-2053.
12.
王岳宝、苏淳(
1998). 不同分布NA列加权和的强极限定理及其在线形模型中的应用.
《应用数学学报》, 21:571-578.
13. 王岳宝、苏淳、刘许国(
1998). 关于两两NQD 列的若干极限性质. 《应用数学学报》,21:404-414.
14.
王岳宝、刘许国、苏淳 (
1998).独立加权和的完全收敛的等价条件.《中国科学》(A辑),
28:213-222.
15.
王岳宝、周斌、苏淳(
1998).关于NA 序列部分和上升的阶.《应用概率统计》,14:213-2
19.
16.
丁克跃、苏淳(
1998).于DRCE 随机矩阵列的若干极限性质.《数学杂志》,
18:241-248.
17.
苏淳、王岳宝(
1998).同分布NA 强收敛性.《应用概率统计》,14:131-140.
18. 梁汉营、苏淳(
1998).NA
序列对数律的收敛性.《科学通报》, 43:
19
19-
1925.
19. 张曙光(
1998).A note on the selection
of equivalent martingale measure.
《中国科学技术大学学报》,11.
20. Zhang,
S.G.(
1998).Generalized BSDs and nonlinear Neumann boundary value
problems.
Probability Theory & Related Fields.110: 535-558.
21. 方兆本、鲁炜、张曙光(
1998).《现代金融之迷-----浅谈金融风险管理、金融工程与
金融数学》,中国环境出版社。
22
方兆本等 (
1998). <<淮河和长江中下游旱涝灾害年表与旱涝规律的研究>>. 安徽教育出版社.
1997
年发表的概率论与数理统计论著目录
1. Block, H.W., Chhetry, D., Fang,Z. and Sampson,
A.R.(
1997). Metrics on permutations
useful for positive dependence.
“Journal of Statistical Planning and Inference”.
62, 2
19-234.
2.
秦永松、赵林城 (
1997). 两总体分位数差异的经验似然比置信区间.《数学年刊》,
18A: 687-694.
3. Zhao, L.C.,
Bai, Z.D., Chao, C.C. and Liang, W.Q. (
1997). Error bound in a central
limit theorem of double-indexed permutation statistics."Annals of
Statistics".
25(5): 2210-2227.
4. Bai, Z.D., Miao, B.Q. and
Tsay, Jh. (
1997). A note on the convergence rate of the
spectral
distributions of large random matrices.“Statistics & Probability
Letters”,
34: 95-101.
5. Fang, Z. and Hu, T. (
1997). Developments
on MTP2 properties of absolute value
multinormal variables with
nonzero means.《应用概率统计》(英), 13: 376-384.
6. Tamaschke, S., Trenkler,
G. And Wei, L.S. (
1997). Mean square error matrix properties
of Bayes
estimation for incorrect prior information under misspecification.
“Journal of the Italian Statistical Society”. 6(3): 273-284.
7.
韦来生、杨亚宁 (
1997). PC 准则下回归系数的一类线性估计的优良性.《应用概率统计》,
13:225-234.
8.
苏淳、秦永松 (
1997). NA 随机变量的两个极限定理.《科学通报》, 42(3): 243-246[42(5):
356-359
(英文)].
9. 迟翔、苏淳 (
1997). 同分布 NA 序列的一个弱大数定理.《应用概率统计》,13(2):
199-203.
10. Su, C., Zhao, L.C. and Wang, Y.B. (
1997). Moment inequalities and weak
convergence
for negatively associated sequences. 《中国科学》(英), 40(2):
172-
182.
11. 胡太忠 (
1997). The class of sum-geometric infinitely
divisible distributions of
order k.《数学研究》,30:355-363.
12. 张曙光
(
1997). Option pricing in a constrained incomplete market.《中国科学技术大学
学报》,27(3).
13. 韦来生 (
1997). 方差分析模型中参数的经验 Bayes估计及其优良性问题.《高校应用数学学报》,
12A:163-
174.
14.苏淳、王岳宝(
1997).B值随机变量完全收敛性的进一步探讨.《数学物理学报》,
17(1):74-80.
15. Rao, C.R.
and Zhao, L.C.(
1997). A limiting distribution theorem. "Festschrift
for
Lucien Le Cam: Research Papers in Probability and
Statistics",Ed.Pollard,D.,
Torgersen,E.,and Yang,
G.L.,Springer-Verlag, New York,pp.325-335.
作者:胡太忠 日期:2001-8-27 下午
09:02:36 更新:2004-2-24 下午 06:59:
19 访问:46
18
18163你这个都是科大的人发的文章吧?
18167
设级数 a(n)=f(1/n)>0。且 f(x)在零点右极限为0。 f'(x)在x=0的右邻域存在。
设limx*f'(x)/f(x)=G 其中x趋于0正。
为什么当 G>1 级数收敛??
G<=1 级数发散??
18167见附件
post-38-1126782313.ibf
18167恩。。看了。。不错的方法啊。。。
谢谢啦。。
18168大纲里的参考教材我觉得复旦大学的有点内容。05年的最后一题,怎么下手呀!请指教。
18168
引用 (bromn006 @ 2005年09月15日
18时50分) |
|
考中科院数学的同志们,你们的代数都参照谁的教材呀,上面提供的教材为什么不涵盖考试大纲呢?
|
两本参考书:一本北大的,另一本比较老:《线性代数》蒋尔雄等编 人民教育出版社
1978
18168我好象没有什么规定的教材,有什么教材看什么教材,没有想过专门买中科院指定的教材,我现在手上已经没有一本教材了!
18168考中科院数学的同志们,你们的代数都参照谁的教材呀,上面提供的教材为什么不涵盖考试大纲呢?
18168杨子旭编的<<高等代数题解>>(如同数分的机米多惟其习题集)
18168其实有些教材知识都不全,使用前看看前言
18168有些内容要看一些计算方法,矩阵论的书!顺便问问以下概念:极大极小原理
rayleign商
18168大纲好象是按照科大的高代编的吧,但是一般都没超过北大的高代内容
18
172全国大学生数学建模竞赛组委会
2005年9月修订
word附件,免费。post-37-1126787723.ibf
18
173MIN
-0.5833X11-0.5833X21+X31-0.3333X41+0X51+0X61-0.5X71-0.5X81
-0.8333X12-0.3333X22+0.5833X32-0.5X42-0.0833X52+0.0833X62-0.4167X72-0.5833X82
-1.5X13-X23-0.25X33-X43-0.75X53+0.25X63-X73-0.75X83
-1.0833X14-0.8333X24+0.3333X34-0.75X44-0.3333X54+0.0833X64-0.6667X74-0.5833X84
ST
X11+X21+X31+X41+X51+X61+X71+X81>=1
X12+X22+X32+X42+X52+X62+X72+X82>=2
X13+X23+X33+X43+X53+X63+X73+X83>=2
X14+X24+X34+X44+X54+X64+X74+X84>=2
X11+X12+X13+X14=1
X21+X22+X23+X24=1
X31+X32+X33+X34=1
X41+X42+X43+X44=1
X51+X52+X53+X54=1
X61+X62+X63+X64=1
X71+X72+X73+X74=1
X81+X82+X83+X84=1
END
INT32
:GO
18
173Min:-5.0833
参数最优解为:
x11: 0
x21: 0
x31: 0
x41:
0
x51: 0
x61: 0
x71: 1
x81: 0
x12: 0
x22: 0
x32: 0
x42: 0
x52: 0
x62: 1
x72: 0
x82: 1
x13:
1
x23: 0
x33: 1
x43: 0
x53: 1
x63: 0
x73: 0
x83: 0
x14: 0
x24: 1
x34: 0
x44: 1
x54: 0
x64:
0
x74: 0
x84: 0
18
173应该没问题的
看看是不是变量限制
18
175图片下载之后不好打印
18
175大家还是都把题目和解答都搞成图片形式发到论坛了吧,那样又清晰又直接,
大家只要在MathType5.0中编辑,然后在保存的时候选择保存的文件格式是gif,则就是图片了,然后在上传,其实是很方便的!
我看到论坛里有些题目都没的办法了,看了都不想看,都不知道在说什么,光看题目都够费脑筋。
如果大家有这个软件就直接用吧,如果某些人没有,可以在网上搜索一下,很容易找到的
18
175我提供一个下载mathtype5.2的地方
http://www1.skycn.com/soft/16216.html
18
178如何求不规则图形的面积??? (本人只有小学学历所以请在座的各位博士们为我稍微动一下脑筋)谢谢!
18
178剪剪拼拼喽!
我上幼儿园的外甥女教我的。:D
18
179如果只有米尺怎样测量操场的面积
18
179用勾股定理应该可以做到,如果是刻度尺的话
首先,用刻度尺找到弧的中点和弦的中点,利用勾股定理就可以解出那部分弧包围的面积
18
182拓扑学的书,我推荐罗嵩龄等人翻译的Munkres 的《拓扑学基础教程》。很好的经典!
18
182请问:要学〈抽象代数〉和〈实分析〉,除了知道微积分和线性代数之外,还要掌握什么数学?像偏微分方程,空间解析几何也要学吗?
我现有一本74年的<Algebra>由Thomas
W. Hungerford写的,另一本68年的<Real
Analysis>第2版由H.L.Royden写的,还有一本80年的由Walter Rudin写的<Function Theory in
the Unit Ball of
C^n>。本本书年龄皆比我大,这三本原版书放在陈年的书柜里积了一层灰,现想起不看可惜了,便来问一问。那本Walter
Rudin写的球面几何想起比较难,所以打算做好准备之后,先看前两本,最后看Rudin。
18
182实分析一般就看些点集拓扑学和集合论,加上数学分析的较深基础就可以开始了。抽象代数在高等代数学了之后就可以开始了。只要这些基础打得好,开始学实分析与抽象代数也没有什么麻烦的。不过最好是去跟班听课吧,这样比自学要快得多。你想看的书<Algebra>--Thomas
W. Hungerford,<Real
Analysis>第2版--H.L.Royden,都是名著,不过我没有看过。如果英文基础好的话,直接开动英语的书当然好,要不就先找些中文的书看看吧。比如《实分析》就用北大周民强的,或者是上海科技87年出版的《实变函数与应用泛函分析基础》的前三章。两本书各有侧重点,都很不错。至于抽象代数,我还没有开始看,听说北大莫宗坚的《代数学》写的挺不错的。还有就是中科院冯克勤的《近世代数引论》,这书入门挺好的。
18
182
| 引用 (renzhazero @ 2005年09月16日
20时21分) |
|
实分析一般就看些点集拓扑学和集合论,加上数学分析的较深基础就可以开始了。抽象代数在高等代数学了之后就可以开始了。只要这些基础打得好,开始学实分析与抽象代数也没有什么麻烦的。不过最好是去跟班听课吧,这样比自学要快得多。你想看的书<Algebra>--Thomas
W. Hungerford,<Real
Analysis>第2版--H.L.Royden,都是名著,不过我没有看过。如果英文基础好的话,直接开动英语的书当然好,要不就先找些中文的书看看吧。比如《实分析》就用北大周民强的,或者是上海科技87年出版的《实变函数与应用泛函分析基础》的前三章。两本书各有侧重点,都很不错。至于抽象代数,我还没有开始看,听说北大莫宗坚的《代数学》写的挺不错的。还有就是中科院冯克勤的《近世代数引论》,这书入门挺好的。
|
看样子《抽象代数》只需要线性代数即可开始学习。
而〈实分析〉的要求要高一些。我从来没有读过数学专业,也不知道什么是〈数学分析〉,到网上搜了一下,发现它比我所学的微积分要系统得多。以下是我找到〈数学分析〉的大纲:
复旦大学数学类基础课程
《数学分析》教学大纲
(Mathematical Analysis)
2
18.003.1
数学分析( I ) 学分数5 周学时4+2
总学时96
(讲课64,习题课32)
2
18.003.2 数学分析( II )
学分数5 周学时4+2
总学时96
(讲课64,习题32)
2
18.003.3 数学分析( III ) 学分数4
周学时3+2
总学时80
(讲课48,习题32)
课程性质与基本要求
课程性质:数学分析是数学系最重要的一门基础课,是许多后继课程如微分几何,微分方程,复变函数,实变函数与泛函分析,计算方法,概率论与数理统计等课程必备的基础,是数学系本科一、二年级学生的必修课。
本课程总学时为272学时,其中讲课为
176学时,习题课为96学时,共分三学期完成,分别为数学分析(
I ),数学分析( II ),数学分析( III
)。
基本要求:通过系统的学习与严格的训练,全面掌握数学分析的基本理论知识;培养严格的逻辑思维能力与推理论证能力;具备熟练的运算能力与技巧;提高建立数学模型,并应用微积分这一工具解决实际应用问题的能力。
教学内容,教学要求与学时分配
学时(含习题课)
数学分析( I )
第一章 集合与映射 8
§1.集合
§2.映射与函数
本章教学要求:理解集合的概念与映射的概念,掌握实数集合的表示法,函数的表示法与函数的一些基本性质。
第二章
数列极限 16
§1.实数系的连续性
§2.数列极限
§3.无穷大量
§4.收敛准则
本章教学要求:掌握数列极限的概念与定义,掌握并会应用数列的收敛准则,理解实数系具有连续性的分析意义,并掌握实数系的一系列基本定理。
第三章 函数极限与连续函数 16
§1.函数极限
§2.连续函数
§3.无穷小量与无穷大量的阶
§4.闭区间上的连续函数
本章教学要求:掌握函数极限的概念,函数极限与数列极限的关系,无穷小量与无穷大量阶的估计,闭区间上连续函数的基本性质。
第四章 微 分 15
§1.微分和导数
§2.导数的意义和性质
§3.导数四则运算和反函数求导法则
§4.复合函数求导法则及其应用
§5.高阶导数和高阶微分
本章教学要求:理解微分,导数,高阶微分与高阶导数的概念,性质及相互关系,熟练掌握求导与求微分的方法。
第五章 微分中值定理及其应用
21
§1.微分中值定理
§2.L'Hospital法则
§3.插值多项式和Taylor公式
§4.函数的Taylor公式及其应用
§5.应用举例
§6.函数方程的近似求解
本章教学要求:掌握微分中值定理与函数的Taylor公式,并应用于函数性质的研究,熟练运用L'Hospital法则计算极限,熟练应用微分于求解函数的极值问题与函数作图问题。
第六章 不定积分
9
§1.不定积分的概念和运算法则
§2.换元积分法和分部积分法
§3.有理函数的不定积分及其应用
本章教学要求:掌握不定积分的概念与运算法则,熟练应用换元法和分部积分法求解不定积分,掌握求有理函数与部分无理函数不定积分的方法。
第七章 定积分(§1 —§3) 11
§1.定积分的概念和可积条件
§2.定积分的基本性质
§3.微积分基本定理
期末考试
数学分析( II )
第七章 定积分(§4 —§6)
15
§4.定积分在几何中的应用
§5.微积分实际应用举例
§6.定积分的数值计算
本章教学要求:理解定积分的概念,牢固掌握微积分基本定理:牛顿—莱布尼兹公式,熟练定积分的计算,熟练运用微元法解决几何,物理与实际应用中的问题,初步掌握定积分的数值计算。
第八章 反常积分
9
§1.反常积分的概念和计算
§2.反常积分的收敛判别法
本章教学要求:掌握反常积分的概念,熟练掌握反常积分的收敛判别法与反常积分的计算。
第九章 数项级数
21
§1.数项级数的收敛性
§2.上级限与下极限
§3.正项级数
§4.任意项级数
§5.无穷乘积
本章教学要求:掌握数项级数敛散性的概念,理解数列上级限与下极限的概念,熟练运用各种判别法判别正项级数,任意项级数与无穷乘积的敛散性。
第十章 函数项级数
21
§1.函数项级数的一致收敛性
§2.一致收敛级数的判别与性质
§3.幂级数
§4.函数的幂级数展开
§5.用多项式逼近连续函数
本章教学要求:掌握函数项级数(函数序列)一致收敛性概念,一致收敛性的判别法与一致收敛级数的性质,掌握幂级数的性质,会熟练展开函数为幂级数,了解函数的幂级数展开的重要应用。
第十一章 Euclid空间上的极限和连续
9
§1.Euclid空间上的基本定理
§2.多元连续函数
§3.连续函数的性质
本章教学要求:了解Euclid空间的拓扑性质,掌握多元函数的极限与连续性的概念,区分它们与一元函数对应概念之间的区别,掌握紧集上连续函数的性质。
第十二章 多元函数的微分学(§1—§5) 21
§1.偏导数与全微分
§2.
多元复合函数的求导法则
§3.Taylor公式
§4.隐函数
§5.偏导数在几何中的应用
期末考试
数学分析( III )
第十二章 多元函数的微分学(§6—§7)
7
§6.无条件极值
§7.条件极值问题与Lagrange乘数法
本章教学要求:掌握多元函数的偏导数与微分的概念,区分它们与一元函数对应概念之间的区别,熟练掌握多元函数与隐函数的求导方法,掌握偏导数在几何上的应用,掌握求多元函数无条件极值与条件极值的方法。
第十三章 重积分
19
§1.有界闭区域上的重积分
§2.重积分的性质与计算
§3.重积分的变量代换
§4.反常重积分
§5.微分形式
本章教学要求:理解重积分的概念,掌握重积分与反常重积分的计算方法,会熟练应用变量代换法计算重积分,了解微分形式的引入在重积分变量代换的表示公式上的应用。
第十四章 曲线积分与曲面积分 28
§1.第一类曲线积分与第一类曲面积分
§2.第二类曲线积分与第二类曲面积分
§3.Green公式,Gauss公式和Stokes公式
§4.微分形式的外微分
§5.场论初步
本章教学要求:掌握二类曲线积分与二类曲面积分的概念与计算方法,掌握Green公式,Gauss公式和Stokes公式的意义与应用,理解外微分的引入在给出Green公式,Gauss公式和Stokes公式统一形式上的意义,对场论知识有一个初步的了解。
第十五章 含参变量积分 12
§1.含参变量的常义积分
§2.含参变量的反常积分
§3.Euler积分
本章教学要求:掌握含参变量常义积分的性质与计算,掌握含参变量反常积分一致收敛的概念,一致收敛的判别法,一致收敛反常积分的性质及其在积分计算中的应用,掌握Euler积分的计算。
第十六章 Fourier级数 14
§1.函数的Fourier级数展开
§2. Fourier级数的收敛判别法
§3.
Fourier级数的性质
§4.
Fourier变换和Fourier积分
§5.快速Fourier变换
本章教学要求:掌握周期函数的Fourier级数展开方法,掌握Fourier级数的收敛判别法与Fourier级数的性质,对Fourier变换与Fourier积分有一个初步的了解。
期末考试
考核方式
闭卷考试
教材和参考书
教材:《数学分析》(上,下), 陈纪修,於崇华,金路编
高等教育出版社
(上)
1999年9月,(下)2000年4月
参考书:
(1)《高等数学引论》(第一卷),华罗庚著
科学出版社(
1964)
(2)《微积分学教程》,菲赫金哥尔兹编,北京大学高等数学
教研室译,人民教育出版社(
1954)
(3)《数学分析习题集》,吉米多维奇编,李荣?译
高等教育出版社(
1958)
(4)《数学分析原理》,卢丁著,赵慈庚,蒋铎译
高等教育出版社(
1979)
(5)《数学分析》,陈传璋等
高等教育出版社(
1978)
这个大纲说的〈数学分析〉从第11章到最后第16章所说的东西,我都接触得很少。我打算找一本〈Advanced
calculus>或者直接找一本〈数学分析〉学习。
至于拓扑学方面,我只有一本〈拓扑空间论〉的中译本,这本书是由日本人儿玉之宏,和,永见启应写的。书上说这是一本点集拓扑学的经典,前言说只要知道大学低年级的集合论的基本内容即可读懂这本书。
跟班听课对我几乎不可能,所以只能自学。我还是先看那本<Algebra>--Thomas
W. Hungerford,和数学分析的部分章节,以及〈拓扑空间论〉。
对楼上的renzhazero赞一个!
18
182最好学一下数学分析与高等代数,不过你要是抽象理解能力强,直接读近世代数与测度论好象也行.
18
182呵呵,刚才没有讲完就不小心发了,再贴一楼!
FOURIER分析在实变函数与泛函分析上都有极为重要的意义.所以一定要有基础.初等的基础就看看北大和复旦的数学分析课本就可以了,有一本很精悍的写FOUROER的小书--<富里埃级数> (英)G.H.哈代,
W.W.洛戈辛斯基著,徐瑞云,
王斯雷译.这本小书是英国现代数学大师G.H.哈代在剑桥用过的相关课程讲义.观点较高,也很易读,可以拿来一看.一般在图书馆有借.(我买到一本,很幸运:-)
至于<抽象代数>这门课程.我还是建议看完高等代数再说.就用北大丘维生的那套书.有两本.上册是线性代数,下册是多项式环,线性空间等东东.你已经学了线性代数的话.就直接看下册的好.要是可以弄到这套书高等教育出版的第一版最好,比较详细.新的一版的下册删除了好几章.我用的是第一版的,高等教育96年出版的.虽然有些东西在抽象代数里会讲,不过预先看一下还是很好的.尤其你想看的是Thomas
W.
Hungerford的<Algebra>那本.那书是研究生的课本.比较"高".必须先有本科数学系的高等代数基础.
而你想看的另外一本书H.L.Royden的<Real
Analysis>也是研究生的标准课本.(不记得是美国哪个知名大学的了,好象是哈佛用的)所以数学分析的扎实基础是必须的.
关于拓扑的基础.用那本(日)儿玉之宏的<拓扑空间论>也可以,说是说可以"大学低年级"的学生看.我看只了前3章.后面就省了.那些集合论哪有那么简单的.还是先找点集合书打下基础的好.我推荐你用J.L.凯莱的<一般拓扑学>的集合论基础.就是这本书的开头一章和附录部分.总共才60多页.先看完这些集合论初步,了解了势啊.基数啊,选择公理等再去看(日)儿玉之宏的<拓扑空间论>,而且那本书也只要看到前3章就"绰绰有余"了.(当然这里我说的有余是对于学实分析和泛函的)
说些题外的话.W.RUDIN的书都是极好的.尤其是那本<数学分析原理>是高等分析的入门好书.还有就是他的<泛函分析>,<实分析与复分析>都是很好的教材.推荐读读!
另外自学是很辛苦的事,不过有兴趣是最大的动力!楼主加油啦!
就说到这里了,有不全面的地方还请各位网友多多指教.
18
182楼主列举的大纲〈数学分析〉上从第11章到最后第16章所说的内容,在美国一般叫做高等微积分.有些参考书可以直接用来学这部分的.(我最早就是用的这套复旦的教材)--<多元函数>(美)W.弗列明著
,庄亚栋译 .人民教育出版社,
1981出版.这书用的人很少.不过观点比较高,讲的主要是多元函数那些东东.但是难度就现代观点来讲一般.在图书馆有借.可以看看. 还有就是--<微积分和数学分析引论>的第二卷. (美)柯朗(R.Courant),(美)约翰(F.John)著;
张鸿林,周民强译.这本书最近几年有新版,科学出版社出版的.很经典.直观而且也比较严密.推荐一读!这个第二卷主要也是多元微积分的,还有一些FOURIER分析和微分方程,变分法以及复变函数初等.要是你没有学过的话,看看这本书就行.
另外在实分析和泛函分析上用的比较多的就有FOURIER
18
182
引用 (樱析光 @ 2005年09月
18日
11时29分) |
|
最好学一下数学分析与高等代数,不过你要是抽象理解能力强,直接读近世代数与测度论好象也行.
|
行,明天到书店里去买《数分》。
18
182哇,不愧为高手,谢谢!最近就在这里看常庚哲和史济怀写的数学分析,感觉还是从头看起吧,因为到底是数学专业的书,很多东西不一样,比如第2章函数的连续性就讲了李天岩和yorke的“周期3蕴涵混沌”的定理,还有像bezier曲线,Van
der Waerden方法,很多很多,听到名字就使我认为cool的东西。:D
想必高等代数也有很多东西不一样,那个多项式环就没听说过。
在书店里看到一本英文的高等微积分,觉得还是跟数学分析有出入,除了重积分,多元函数,傅立叶级数,这本高等微积分讲了跟线性代数有关的微积分,复数、复平面的微积分,后来更主要讲了向量积分。最后是常和偏微分方程。全书700页。这与数学分析好象差别还是不小的。
楼上的读了这么多书,真是很幸福!觉得你推荐的J.L.凯莱的<一般拓扑学>的集合论基础入门甚是好,下次去找找。
今天想那个椭圆内部反射问题,想了5个多钟头,写了上千字,头都晕了!具体在几何那一栏:
http://www.math.org.cn/forums/index.php?show...=0&#entry105570都是一些想法,没有能力去证明。
18
182《近世代数》只要高等代数的知识就够了。不过前者的起点更高更抽象,需要对高代有系统深刻的理解。
18
182顶一下!!
18
191一个矩阵集合{A1,A2,...Ap}是紧集有什么含义,能不能具体解释一下,其中p可以是无穷,麻烦各位,最好能给个例子,我不是学数学的,弄不明白,麻烦知道,谢谢了
18
191没见过这种提法,
应该把背景 说一说才好理解
18
195难道只看影响因子?
每一个行业都有几个比较牛地杂志,为什么称为牛那?同行地评价吗(不同人还有不同看法那)?
都为SCI,确实有差距。但是谁能说哪个杂志就强啊。
18
196A为s*n阶实矩阵,XY均为s元实向量,求证:A'AX=A'Y一定有解
我的思路是构造一个解,以证明解的确存在,但我并不知道该如何下手构造,有技巧么?入手点在哪里?多谢赐教:)
18
196我给个构造:post-38-1126854368.gif
18
196这好象是广义解
18
196tobyqin的分块技巧虽好,不过我觉得此题如下证之更简单:
r(A'A,A'Y)<=r(A')=r(A'A),故有解。
杀鸡焉用牛刀?
18
196请指教:::为什么说
S行满秩,则SS’可逆????
18
196to :tobyqin
还是不懂,看谁的解空间啊??讲清楚点好么??
18
196
引用 (iii @ 2005年09月
17日
18时02分) |
to
:tobyqin
还是不懂,看谁的解空间啊??讲清楚点好么??
|
呵呵,可以
不过听着你的口气好郁闷
若 xSS'=0 ⇒
xSS'x'=0 ⇔
xS(xS)'=0 ⇒
xS=0
由于S行向量线性无关,故x=0
18
196原来如此啊。这种方法和证明r(A)=r(AA’)有些相似哦,西西
18
196是我没看清楚提问者的意思,有点答非所问了,还是tobyqin的方法好
18
196提问者最好能将过去的帖子浏览一下。
记得我曾经(时间并不太久)解答过这一题。
18
196
引用 (springboshi @ 2005年09月
17日
20时46分) |
提问者最好能将过去的帖子浏览一下。
记得我曾经(时间并不太久)解答过这一题。
|
是的
18
197楼上的学长,问了老师吗?
还有我发现同济5版的教材上有些证明不严谨,甚至是错误的
18
197有空帮你问问我们学校的老师呵呵
18
197我是大一的新生,正在学习高等数学,发现集合与映射的证明很有趣,不知道版里有没有相关的题目,
俺想做做
18200Satanophany:"提问:这样由C点反射回来的线段,会不会又与点B相交,最后又与点A相交,如此循环呢?"
Satanophany,你这问法我觉得怎麽看都是有问题的……
另外,“从椭圆上某点出发的射线经过焦点后于椭圆相交,经过反射后必过另一焦点。”是可以证明的,所以请不要在这上面找错误,这不是数学研究的方法……
我说一个证明或否定的思路,设初始的射线长为a1,反射后为a2,之后再为a3……,
我们可以对椭圆的一些初始数据进行一般化的设定(比如说设长轴为m等……),利用解析的方法可以探求an,a(n+1),a(n+2)间的关系……
不过很显然这是一个很麻烦的方法……
18200
| 引用 (gauss @ 2005年09月24日
23时37分) |
引用 (流形 @ 2005年09月16日
18时16分) |
不一定
有可能是循环的,也可能是混沌还可能什么都不是 |
一定的
证明也不难
|
既然不难,那就证明,开开眼界,忠心感谢!:)
18200光线是可逆的
从而出现单调严格减的情形的概率极小
相反却有可能出现某种周期或循环
就像在一个三角形中的光线那样,
实际计算光线的轨迹太复杂了。
也可用图形的对称群作,光线的运动和和图形的镜像变换对偶。
不过我也不确定答案最终是什么
还指望高手给出严格的讨论,自己是没有哪个能力
18200关于椭圆内部反射问题:
我记得高中解析几何里说过:“从椭圆上某点出发的射线经过焦点后于椭圆相交,经过反射后必过另一焦点,请问,经过这样无数次后,它(此直线)的极限是否于长轴同一
18200不一定
有可能是循环的,也可能是混沌还可能什么都不是
18200直观上看是一定的
18200怎么看都不一定
18200能够说得清楚一点吗,我画了很多都是啊,只是无法证明
18200注意光线是可逆的
题目是很有意思,不过也不简单,呵呵。
18200
对,这个题目比较好玩!左想右想,想找一个反例。但下面这个反例与楼主说的“从椭圆上某点出发的射线经过焦点后于椭圆相交,经过反射后必过另一焦点。”相矛盾,
如果楼主说的没错的话,下面这个反例是不成立的。令椭圆长轴在X轴上,短轴在Y轴上,椭圆中心与坐标原点重合。将焦点F1和椭圆与Y轴的一个交点B相连成一线段,并从焦点F1延长这条线段直到与椭圆相交,令交点为A。则线段AB可以看成为光线从A射出,经焦点F1后与短轴交于B点。接着由B点反射,经焦点F2后与椭圆交于C点。显然,AB=BC
提问:这样由C点反射回来的线段,会不会又与点B相交,最后又与点A相交,如此循环呢?
如果是循环的话,那么此线段的极限都不等于长轴的长。
我这个菜鸟认为,要证明循环,必须计算C点的斜率,如果刚好与反射线BC垂直,那么由C点反射回来的线段必与点B再次相交。则可以证明这是一个循环。
这个楼主去参考吧。
另外,一般情况下,我菜鸟觉得在椭圆内部经焦点反射初期阶段,反射线或者射线的长度变化很不稳定,有时减少,接着又增加。如果将反射线或者射线的长度值排成一个数列的话,则此数列是有界数列,而且由于初期阶段的不稳定性,使得这个数列不是单调数列。这个数列有极限,且等于长轴,所以这个数列是有界的收敛数列。根据Cauchy收敛原理,这个数列是一个基本列。
还有,当初始入射点比较靠近长轴时,则第一条入射线比后面接下来的若干次的反射线都要长。且在初期反射过程中,会有若干个反射点比初始入射点更接近短轴。经过很有限次的初始反射过程,反射点的位置将比入射点更接近长轴。我菜鸟称,当反射点比初始入射点更接近短轴的时期叫蓄势期(即初始反射阶段);反射点的位置将比入射点更接近长轴的时期叫耗损期。
通过粗略地画图,我菜鸟发现,当初始入射点离长轴越近时,则接下来发生的蓄势期会越长;当初始入射点离长轴越远时,则接下来发生的蓄势期会很短,会更快地进入耗损期。以上面的椭圆为例,过焦点F1作垂直于长轴的垂线,并与椭圆交于M点和N点,当椭圆上的初始入射点离长轴很远,且比M点或者N点离长轴还要远时,则接下来的反射现象不会发生蓄势期,直接进入耗损期。可见与焦点F1对应的M点和N点是蓄势期和耗损期的临界点。
菜鸟直觉判断,在进入耗损期后,所产生的长度值变化数列是有界的严格递增的收敛数列。(
这个不知道对不对,哪位高手能证明?我菜鸟定重谢!)而且,进入耗损期产生的第1根反射线比初始入射线的长度要长,这也是进入耗损期的标志,而蓄势期产生的线段没有一根比初始入射线的长度要长。在蓄势期所产生的长度值变化是不稳定的,所以我菜鸟也喜欢把这个阶段叫做“
上帝调整期”。由于人为地指定了一个初始入射点,为了进入耗损期,天才的数学家上帝便事先来进行调整,所产生的不稳定,便是上帝这位老家伙捣的鬼。
Let's
go!让我们来调戏一下上帝,累死它!由于“上帝调整期”(即蓄势期)的菜鸟定义是:当反射点比初始入射点更接近短轴的时期叫蓄势期。那么,我们设想,如果初始入射点无限地接近于长轴时,则反射点将轻易地比初始入射点更接近于短轴。也就是说只要

>0,且

属于实数,初始入射点与长轴的距离L1总小于预先设定的

。但问题是经过多次调整,也不能进入耗损期。也就是说,经过N次调整之后,所产生的反射点与长轴的距离L2,由L2-L1总小于预先设定的

。
我对这个有两种说法:1,如果初始入射点无限地接近于长轴时,只发生“上帝调整期”(即蓄势期),不发生耗损期,即可使这个线段的极限等于长轴。
2,如果初始入射点无限地接近于长轴时,只发生耗损期,即可使这个线段的极限等于长轴,且长轴与椭圆的两个交点也是蓄势期和耗损期的临界点。
个人菜鸟认为两种说法都可行!:)这里有个问题:如果初始入射点无限地接近于长轴时,经过“上帝调整期”的n次调整,当n趋于

时,是否可以进入耗损期?这似乎要用到基数来证明证明...
其实椭圆的蓄势期和耗损期还是有一定的物理意义的。比如,玩橄榄球。橄榄球要踢得远,我们选择踢球的腹部,因为腹部的伸缩性好,质地软,弹力大,踢出的球较稳定。我们知道踢橄榄球的两个尖端部分时,
会感到脚疼,因为伸缩性差,质地硬,弹力差,踢出的球不稳定。我们还知道,当把橄榄球扔到地上时,橄榄球触地反弹,经过多次反弹后,橄榄球静止在地面,略加统计可以知道,橄榄球腹部肚皮触地的次数比两个尖端部分触地的次数多得多。即上帝总在找橄榄球最脆弱的地方,让最脆弱的地方触地更多次。我菜鸟把橄榄球腹部叫做“蓄势带”(最脆弱的地方),两个尖端部位叫做“耗损带”。
按照这个逻辑,椭圆内部的两个凹陷向外突出的部分即为“耗损带”,即是与长轴方向平行。离短轴较近的区域,没有凹得那么厉害的,即为“蓄势带”。有心者可以用上面提到的M点和N点来严格定义“蓄势带”和“耗损带”。
上面的橄榄球只能粗浅地说明椭圆外部的情况,而椭圆内部的情况与外部截然相反。“耗损带”是椭圆内部最脆弱的地方,“蓄势带”是相对坚固的地方。
设想,椭圆内部有一个无限能量的弹子球,在椭圆内部经焦点不停地反弹,经过蓄势期,最后上帝会指引它,在椭圆的“耗损带”(最脆弱处),不停地来回反弹,这也体现了上帝想尽快打破现有平衡体系的思想,看样子上帝也是一个喜新厌旧的角色!:D另外,天才的小鸡一般是从蛋壳的“耗损带”钻出来的,这个应该符合力学原理。
我菜鸟认为,具体研究“上帝调整期”及后面的耗损期应该借用特定的数学软件就比较直观和精确。我们可以进一步探讨内部反射线段的变化规律,看看在某个特定的椭圆里面,调整的次数和初始入射点的位置到底是个什么关系,是否有数学公式可以将其充分描述。我猜想,如果有的话,应该跟分形几何和混沌有关。:P
注意:以上名字“蓄势期”,“上帝调整期”,“耗损带”,等等属于我菜鸟自己编出来的专有名词,可能再也不会在任何一本书上找到。大家只看我说的有没有道理即可,如有任何错误,请指教!菜鸟在感激中.....
18200
引用 (流形 @ 2005年09月16日
18时16分) |
不一定
有可能是循环的,也可能是混沌还可能什么都不是 |
一定的
证明也不难
18200我也觉得是一定的,不过目前不会证明,哪位帮我证明一下吧,谢谢
18200Satanophany:"从椭圆上某点出发的射线经过焦点后于椭圆相交,经过反射后必过另一焦点。希望楼上的能够帮菜鸟证明这条性质,我跪谢+裸谢之....哈哈"
大至的思路是,先设定一个椭圆,考滤其上任一点,写出过该点的切线,再将此点与某一焦点相连作直线,再在切线上做出法线,然后把另一焦点的坐标写下,证明此点在反射线上(此反射线的解析式显然可求)……
你懂了吗?细节你自己补充吧……
18200
| 引用 (andychen @ 2005年10月15日
12时11分) |
Satanophany:"提问:这样由C点反射回来的线段,会不会又与点B相交,最后又与点A相交,如此循环呢?"
Satanophany,你这问法我觉得怎麽看都是有问题的……
另外,“从椭圆上某点出发的射线经过焦点后于椭圆相交,经过反射后必过另一焦点。”是可以证明的,所以请不要在这上面找错误,这不是数学研究的方法……
|
对,表述得不好。我这么想是因为,在我的高中课本上,似乎没有明写反射的这条性质,想证明这条性质又觉得好象我不会证,故想找一个反例,以确认这个性质是正确的。我后面的讨论都是在这个性质正确的基础上展开的,如果这个性质不正确,我的那千把字不白写啦!
从椭圆上某点出发的射线经过焦点后于椭圆相交,经过反射后必过另一焦点。
希望楼上的能够帮菜鸟证明这条性质,我跪谢+裸谢之....哈哈
楼上讲的一般化的设定,再加解析的方法,我不清楚。对于这个问题,这里还没有人证出来呢!用麻烦的方法证出来也是很不错吗!
18200
引用 (andychen @ 2005年10月
17日
10时02分) |
大至的思路是,先设定一个椭圆,考滤其上任一点,写出过该点的切线,再将此点与某一焦点相连作直线,再在切线上做出法线,然后把另一焦点的坐标写下,证明此点在反射线上(此反射线的解析式显然可求)……
你懂了吗?细节你自己补充吧……
|
楼上的方法和思路很明朗,但是计算不是一般的繁!因为椭圆上任一点的表达式,就是椭圆的标准方程,那个方程本来算起来就不是很简单,后面为了算法线与入射线的夹角和法线与反射线的夹角相等,又要用到两直线的夹角公式。那个法线、入射线、反射线都是通过椭圆的标准方程的变换表达出来的,代入夹角公式显然是繁上加繁!
待我菜鸟再算几天,然后再一并跪谢楼上的,看在是我自己算的份上,裸谢就免了吧。呵呵。
18200我推了好久,这个斜率K的表达式写不出来,因为计算超繁!所以无法证明K趋于0。Let me cry!
18200经过无穷次一定是的攻轴的,可以用反证法的嘛。
因为每次这直线的K是单调严格减的,
如K!=0,则可推出矛盾的嘛,EASY
不过这个IDEA很好~~
嘿嘿
18200
| 引用 (stefine520 @ 2005年10月28日
14时24分) |
经过无穷次一定是的攻轴的,可以用反证法的嘛。
因为每次这直线的K是单调严格减的,
如K!=0,则可推出矛盾的嘛,EASY
不过这个IDEA很好~~
嘿嘿
|
光线是可逆的
18200嗯!?不懂,说清楚一点吧,不过人家是无穷次啊
极限就不一定了啊
你光线可NI只是有限路程啊
18200设光线第n次经过焦点(设为F1)时前进方向与 F
1 F
2⇀
的夹角为 θ n
,易得递推关系
Cos θ n
+1=Cos
θ
n-a1
-aCosθ
n ,这里 a
=2
e1
+e
2 ,e为偏心率。令 Cos θ
n=Tanhβ
n , a
=Tanhα ,递推关系变为 Tanh β
n
+1=Tanh(
β
n-α
) ,即 β n
+1
=β
n-α ,因此 limit n
→∞
Cosθ
n=limit n
→∞Tanh(
β
0-nα
)=-1 ,
θ n
→π 。
18200怎么证的呀?
dreams写的我看不懂,特别是那个递推关系看不懂,没办法。
楼主既然基本证明出来了,能否把基本方法说一下吗?
18200多谢各位,这个我基本上已经证明了。
18200我直觉上认为是对的,可以证明!!
18200画了一个图,椭圆的长轴为蓝线表示。入射初始点为梅色方点,经过4次反射,产生5条线段,第5条线段的末端与椭圆交于梅色圆点。
令每条线段与蓝色长轴右下角的夹角为
α ,
α 1 以图中红字角1表示, α 2
以角2表示,依次类推。
已知三角形外角1等于两个橘红色内角之和,根据对顶角关系,其中一个内角等于角2,角2又等于两个蓝色内角之和,其中一个蓝色内角等于角3。则有下列递推关系:
α k =
α k
+1 +
B k
其中
B k 表示另一个内角,这个内角的顶点总是在椭圆的曲线上。
由于“从椭圆上某点出发的射线经过焦点后于椭圆相交,经过反射后必过另一焦点”,则任何反射点不会与两个焦点在同一直线上,任何反射点永远不会落在长轴上(除非入射点本身就落在长轴上),所以,但这个内角
B k 永远存在,即
B k >0。这也证明上面的递推关系是成立的。
由于 B k
>0,则有下列关系:
α 1 >
α 2 >
α 3 ...> α k
-1 >
α k >
α k
+1 ...
其中, α k
=[0, b k
],k ∈
N * ,且MAX(
b k )
≤ Π 。
怎么样?这使人联想到闭区间套定理,同时,我想也可以用SHARKOVSKII’s
theorem(萨尔可夫斯基定理)证明其中的反射线角度和长度变化应属混沌现象,因为SHARKOVSKII’s
theorem本身就是闭区间套定理的延伸,证明SHARKOVSKII’s
theorem也是以闭区间套定理为基石。
令每条线段与蓝色长轴右上角的夹角为S,即用来表示斜率的那个夹角。由于数列
α k 是单调递减的数列。同理可证,
S k 是一个单调递增的数列。而数列
B k 也是单调递减数列。
根据上面的递推关系,如果数列 B k
比数列 α k
递减的速度要慢,则当k →
∞ ,
α k
+1 只可能
→ 0,而不趋于比0大的任何数。
于是要证,
B k
- B k
+1 -(
α k -
α k
+1 )<0
原式= B k
-B k
+1-(α
k
+1+B
k)+α
k
+1=-B
k +1
<0
所以当k
→
∞ ,
α k
+1
→ 0.则无穷次反射后的线段的长度极限等于长轴的长度。
所用的都是高中数学,当然我菜鸟也只有这种水平!post-22-11364335
17.jpg
18200有点意思
18200还是没证出来,过几天再来。
18200一个简单例子:圆 是振荡的
一般定理:只要反两次不过短轴顶点,极限一定是长轴
证明: 反射点离短轴顶点, 越来越远
18200来,接着上次的证明继续证一证:
前几天的证明得出如下递推关系:
α k =
α k
+1 +
B k
其中
B k 表示另一个内角,这个内角的顶点总是在椭圆的曲线上。
由于 B k
>0,则有下列关系:
α 1 >
α 2 >
α 3 ...> α k
-1 >
α k >
α k
+1 ...
其中, α k
=[0, b k
],k ∈
N * ,且MAX(
b k )
≤ Π 。
由上面关系可以知道数列 α k
是单调递减有界数列,所以此数列必有极限。
那么只要证明 lim k
→∞
α
k=0 ,即可得出椭圆反射线趋于长轴的结论。
与上次那个愚蠢的证明不同的是,这次用反证法证明 lim k
→∞
α
k=0 。
于是,假设 lim
k
→∞
α
k≠0 ,而等于a(a
≠ 0,且 a
∈(0,π)
).
那么也就是说角 B k
仍然不等于0,那么仍然存在角B、角
α 和角S组成的斜三角形,则仍有上面的递推关系
α k
= α k
+1 +
B k
则仍有 α k
+1
<α k
。
说明,当 k
→∞,α
k→a
时,仍有 α k
+1 <
α k ,故与题设相矛盾。
所以 lim
k
→∞
α
k=0 。
所以k →
∞ ,
α k
→ 0.则无穷次反射后的线段的长度极限等于长轴的长度。
证毕啦!完蛋啦!哈哈!
GG
18200恭喜恭喜
18200这是一个好问题,有意思!
18201对于任何一个流程,是否都可以用一个共同的数学模型来描述呢?
有人告诉我用有向图来描述,但是流程中每一个节点的属性有怎么实现,而且这些属性需要在流程动起来的过程中不断的修改。
18201画流程图了
18202借大量数据的0-1规划 要用到两层西格玛累加的目标函数 ,这个该怎么表示呢:???
18202得具体看,用@sum做,我会lingo不是很会lindo
18203多谢
能否给出一个紧的非序列紧的拓扑空间?
18203见《拓扑空间中的反例》第1
18页
18203那个太复杂了。看来是没有简单的反例了
18203?
18203 [
0,1]
[
0,1]
18203如题
18203余可数拓扑空间是紧的当且仅当其只包含有限个点
18203必要性可以说说证明思路么
18203否则, 可取可数个不同的点
x 1
,x
2,⋅ ⋅ ⋅
, 令
A
i
=X∖{x
j|j≥i}
, 则
{
A
i|i∈ℕ}
是开覆盖没有有限子覆盖.
18203多多指教!
18203只有一个点的空间
18204如题
18205如题
18206??
18206这问的是什么名堂啊?不懂!
18206行列式的值非零 当且仅当 列向量线性无关
很基本的,
不过不好证
18206
| 引用 (流形 @ 2005年09月16日
21时32分) |
行列式的值非零 当且仅当
列向量线性无关
很基本的,
不过不好证 |
打洞了
这个就算是定义吧
行列式的定义就是规范反对称n重线性函数
所以这些定义的性质可以用的
:)
18206必要性是可以用反证法证明
利用反对称性和线性性
但由线性无关证明值非零,却不显然.
我还得好好想一想,要是按反对称n重线性函数理解可能要用到函数在基上的值,
18207设A对称矩阵,则对任意自然数k,存在矩阵B,使得B^k=A
呵呵,刚开始复习高代,还真有不少问题,向各位请教
18207这个问题似乎是你自己想的吧!呵呵post-38-1126867702.gif
18207强烈同意蓝戈的说法!
18207
引用 (蓝戈 @ 2005年09月16日
18时48分) |
| 这个问题似乎是你自己想的吧!呵呵
|
错了,
应该是设A对称矩阵,则对任意自然数k,存在矩阵B,使得B^k=A
18207取

i的K次根就可以啊
18207所有的B是相同的
18207请问:不是实对称的矩阵,而光是对称矩阵,就能对角化吗???
18207
引用 (iii @ 2005年09月
17日
18时37分) |
| 请问:不是实对称的矩阵,而光是对称矩阵,就能对角化吗??? |
(
1
0 0
-
1)
+ (
0
1 1
0
)i
这个就不能用实可逆方阵对角化
18207
引用 (tobyqin @ 2005年09月
17日
11时36分) |
引用 (流形 @ 2005年09月
17日
11时25分) | | 所有的B是相同的
|
他说得就是满足题意得
:)
|
呵呵,注我只假定A是对称的,并没有说是对角阵
iii的答案好象还差个相似变换
18207设A对称矩阵,则对任意自然数k,存在矩阵B,使得B^k=A
这是我的原问题。
我觉得他没有解决这个问题
18207
引用 (流形 @ 2005年09月
18日
17时54分) |
设A对称矩阵,则对任意自然数k,存在矩阵B,使得B^k=A
这是我的原问题。
我觉得他没有解决这个问题
|
我就在蓝戈的基础上加一步解决你的问题:post-38-1127037942.gif
18207呵呵,明白了
18207可是我还是不懂,既然不是实对称,那么就不一存在蓝戈说的化法啊??
18207
请指教::蓝戈你说的‘有用的证明’应该怎么证明啊??
就是那个对任何对称矩阵的?麻烦告诉我好不拉
18207还有我觉得只有实对称矩阵才能够存在正交矩阵使它对角化?哪道任何数域上都可以吗?
高手请帮忙解决一个问题:为什么实对称矩阵都可以对角化?书上只是带过,没有具体证明?能给出具体证明吗?谢谢!!
18209一个小于1的偶数等于一个小于1的偶数?
对吗?
一个小于1的偶数等于一个小于1的素数?
对吗/
一个小于1的偶数大于等于一个小于1的偶数?
对吗?
一个小于1的偶数不等于一个小于1的偶数?
对吗?
一个小于1的偶数不等于一个小于1的奇数?
对吗?
1等于一个小于1的偶数?
对吗?
18209呵呵,我这里没有条件,不是推理.只有命题,幕状词,和等词的性质.
有点钻牛角尖的意味,不过确实很重要
18209不明白
18209这个属于逻辑基础中的东西
可归结为以下两个原则的可接受性:
1 数学允许讨论一个其存在性未知的对象的性质,
2 逻辑是不关心实在和意义,逻辑是纯形式的规则,逻辑可以讨论任意的假定
数学和逻辑的发展历史支持这两个原则
18209莫名
18210我在自学近世代数时遇到了难题,左看看看不懂,右看看也看不明白,虽然参考其他的书时,也有这方面的内容,但讲法不一样。我想求助于大家,希望得到你们的帮助!
书名:《近世代数引论》(冯克勤,李尚志等)(中国科大出版社2002)
P.50
。。。进一步,对K中每个元素

,G中就有一个等式f(

)=1G,K中有多少元素,G中就相应有多少关系。。。
这一段都不是很懂,特别上一段看的特别不明白。。。。。
哪位仁兄知道帮忙一下,我在这里感谢你了!很急。
18210我已明白了!
18214计算机高手们,小弟请你们帮帮忙!!!!请问Qbsic如何编制程序?????谢谢!!!1
18215大家好!我第一次到这个园地寻求你们的帮助.我目前在意大利,由于需要求解微分方程,但在这儿找不到相关的程序供参考,请有该子程序的朋友帮助.感谢你的帮助
18215我也一样,急需
18215
http://www.happycampus.com.cn/pages/2004/0...13/D127651.html这个网页中有微分方程数值解的程序源码,可惜需要金钱.不知道谁能提供
18215没有人有啊??
18216迪厄多内的那本《现代分析基础》怎样
想自己看,大家给点意见
谢谢
18216只见过下册,很复杂,没有基础的话看起来没什么帮助,初学的话不适合
18216但是关于近代的分析真的找不到什么特别好的书啊
要不版主推荐几本我去看看吧
18216迪厄多内的<现代分析基础>观点"高"啊.我看了第一册的第一章,后面就没有继续了.觉得自己的数学基础还不够.还要更多的学习.这套书把好几门课程统一了.而且继承了布尔巴基的严密与体系化.完全用现代的观点讲数学分析.以后有机会一定读读.不过那也是在完成拓扑,实变和泛函之后再说.楼主你学完这些课程了吗?学完了就应该可以开动了.还有W.RUDIN的<实分析与复分析>不错,也是串着讲.可以看看.另外一本书,可能简单了一点,并且只有上册翻译过来了.是(法)施瓦茨(Schwartz,L.)著;
张明梁 译 的<分析教程> 高等教育出版社,
1987年出版的.看了一下,也是用现代的方法讲数学分析的.不知道楼主有没有兴趣一读.应该在图书馆有借.
总之,法国的数学教材(尤其是函数方面的)一般都是同类教材里最难的,他们好象很喜欢用现代的观点讲古典分析.就象邹应的那套<数学分析>号称是国内编的最难的数学分析一样,他那套书也是来自于法国的体系.当年武汉大学中法基地班的学生想必受了不少"折磨":-)
18216自学的话,最好多看一些,只有看了才知道好不好
可能有的书适合自己有的不适合,多看总是好的
18216
引用 (流形 @ 2005年09月
17日
11时32分) |
|
只见过下册,很复杂,没有基础的话看起来没什么帮助,初学的话不适合 |
哥们肯定没看过,这套书共8卷,堪称经典。我只看过第一卷,好象其他几卷没有中译本,或许有但我没见过。这套书的起点并不太高,只是要求的数学素养很高。这套书不讲黎曼积分,作者认为随着历史的发展理曼积分将失去它的地位。作者更崇尚一般状态下的积分。
如果有足够的耐心、细心和数学修养这套书是很值得读的。
18216不知道那位大侠可以提供电子版的下载地址,谢谢!!
182
17无穷大量与无穷小量中有个定义:
设f(x)=0(1),且g(x)=f(x)+0(f(x)) x rightarrowX
则称
x rightarrowX
时,f(x)是g(x)的主部.
对于那个"0(f(x))"我不太了解,
它是指某一未知值呢?还是与
g
(x)f
(x)
=0(1)有关???
麻烦各位高手指教,很感谢!!
182
17再请教!如这性质:
设f(x)在 x
→X 时的极限是
∞
,且g(x)的主部是f(x),则g(x)在 x
→X 时的极限为
∞
,且g(x)~f(x).
证明:
由于g(x)=f(x)+0(f(x))
( x
→X )
则lim
g
(x)f
(x)
=lim[1+
0
(f(x))f
(x)
]=1
(lim下都有
x →X )
(问题1:怎么计算
0
(f(x))f
(x)
的?等于0?)
由于局部保号性:
g
(x)f
(x)
≥
1 2
( x
→X )
当limf(x)=
∞ 时,lim|f(x)|=+ ∞
,由
|g(x)|
≥
1 2
( x
→X )
知lim|g(x)|=+ ∞
,即limg(x)=
∞
,且g(x)~f(x).
证明完毕.
(问题2:
g
(x)f
(x)
≥
1 2
怎么得到的???)
编辑好了!!请指教!!谢谢!
182
17无穷大量与无穷小量中有个定义:
设f(x)=0(1),且g(x)=f(x)+0(f(x)) ( x
→X
)
则称 x
→X 时,f(x)是g(x)的主部.
0(f(x))的意思是若lim
g
(x)f
(x)
=0,则称
x →X 时, g(x)相对于f(x)是无穷小量,简记为g(x)=0(f(x))( x
→X ).
按这样说0(f(x))当
x →X 时是g(x),g(x)有可能为一函数也有可能为一常数,若为一函数,不能成为主部吗?还可以忽略不计?
0(f(x))到底是一常数还是函数式??
而
0
(f(x))f
(x)
又如何比较呢??
182
17本人数学不太好,麻烦指教!谢谢!!
182
17
引用 (tobyqin @ 2005年09月
17日
15时56分) |
引用 (wasyzvivian @ 2005年09月
17日
15时26分) | |
本人数学不太好,麻烦指教!谢谢!! |
o(f(x))什么意思为什么你不看看书呢?
知道极限的意思就应该知道你的问题了
这个不是数学好不好的问题!
|
抱歉...请你不要生气..
因为我只有一本书,书上说得也不太清楚..
我会去找找的.
谢谢你了.
182
19作者声明:此篇记的是真人真事
182
19我想在我的数学历程上,我逐渐变成了一个懦夫.
----题记.
1.解开第2颗扣子
很明显,各位看到这个题记的时候便会想到我曾经是一个所谓的数学高手吧.不错,那时我在读高中,眼界很狭窄,于是自以为自己就是传说中的数学王子.各位,请拍我吧.不过听我说下去先.
故事从高1开始,那时开的课是代数,立体几何.现在想起来,曾经我对数学是全没开窍的,同一般成绩好的人一样,我小学得过市智力竞赛一等奖,奥数全国2等奖,初中得过2个市竞赛3等奖.要是你以为我是在说我的小小战绩那你就错了.可以说恰恰是这些所谓的丁点小奖蒙蔽了我的双眼.因为在那个阶段,我应该算是从未理解过数学的.
数学是什么?我开始尝试自己去诠释.高1下学期的时候,我自己定义了一种坐标,称为分点坐标.一个定义下了之后如何去展开呢,这无疑是个挑战数学直觉的问题.当然,在那时我已经了解平面解析几何了,于是我想仿照其中的理论结构建立我这种坐标的理论体系.
首先应求出定比分点坐标公式.求倒是求出了.不过写出来的形式显得不直观.不管这些了,写出来就好了.其次当然是求两点距离公式了.这个有点难.放到高2下学期我才给出了很好的答案.那么你们会问:高2下学期之前我在干嘛呢.
我在玩.不知谁说的,数学问题放一段时间再去做说不定会有奇效.你要是觉得我是把那个问题故意放一段时间后在去做那你就错了.我自从卡在距离公式上之后就忘了这个烦人的定义.就好象我解了一位MM的领扣之后再也解不下第2颗扣子就放弃去玩别的了.
总之高2下学期时我因为上课认真听讲很好的理解了平面解析几何理论结构,思维便开始躁动了,发现用过余弦定理之后距离公式唾手而得了.可惜我所给出的距离公式的形式还是太繁且不对称了.不过解开了这第2颗扣子让我发现了一些美丽风光--乳沟之美.我充满了好奇,毅然决定要从头探索到底.于是我的高3生涯从此多事了.
2.关于CUP
不用说了,象我这样的人暑假是闲不住的.我虽说过我在玩,但我高1暑假也学了一些
微积分的知识,尤其是线形代数的知识.高2暑假更不用说了,鬼都知道我下面要做的事是直线方程.还好有了定比分点公式就有了直线方程.我又求直线平行的条件.接着求的是点到直线的距离公式--这涉及到3点确定的三角形的面积公式.读者应该记得在直角坐标系中的三角形的面积公式那个行列式吧.我猜出了分点坐标中的3点面积公式--也是一行列式.这个公式形式优美结构坚固后来我称它为分点坐标的3大基本公式之1.
面积除以底边即得点到直线的距离了.这时需要求的是底边上的2点确定的直线的方程---根据面积等于0便可写出直线上的任意点满足的方程.这个当然是小CASE.我早在求直线方程的时候就给出了直线的2点式截距式还有自定义的特殊式,后来我也给出过比例式参数式.
接着平行直线的公式太明显了.然后攻垂直条件了.TMD这就是那第3颗扣子了.我万万没有想到这个时候是距离公式在起决定作用.
1.距离公式被我简化了很对称.当然是根号下的什么东东了.
2.余弦定理求夹角的余弦值涉及3个距离平方.最终整理后有点向量内积的味道.(向量在此是一伏笔)
3.夹角正切值求出了.于是斜率公式与垂直条件俱得.
有了求角的公式后我无疑相当于解下了MM的第3颗扣子.不好意思,我看到了CUP
我惊叹于数学之美.是不是上过之后,终身难忘呢?那要看我的本事了.
3.奥数的功绩
内行的读者一看便知我的理论架子是打了.但未经实践解题,难免沦于空谈而且没实用价值.为了追求理论的进一步优化,我决定小试牛刀.
我有买奥数书的习惯,到高3时我约买了7本了吧.这种书多多益善,我刚转新华书店,发现南京大学马传渔教授的一本积高中奥数之大成的书,如获至宝.有了8本书上的平面几何题,我的确精进了不少.有几大发现:
1.使我的所有公式都简洁对称形式优美结构坚固.
2.关于三角形的五心我可给出简洁对称的坐标.提示:我的坐标是3元的(pqr)恰好与三角形的3边3角保持对称.如外心<sin2A,sin2B,sin2C>.
3.欧拉定理是明显易证的.
4.我的坐标证题的本质是三角恒等式.
我开始从新分章节写出我的这套理论和编它的题典.终于写了2章.很严密,因为我的公式都用于过解题的验证.而且理论形式都如直角坐标差不多简洁.
之后我开始了比较工作,写出了分点与直角坐标的互化公式.这个公式是分点坐标的3大基本公式之2.
4.脱去上衣的苦恼
哎,我差点没耐心.高考形势逼人呐.
班主任批评我的成绩一落千丈.数学老师说我越来越马虎.我只得辩解我资质愚钝嘛.你不可能要求人人都那么行撒.我对付老师老是这一套,我不想跟他们浪费时间辩解.高考前一月时,我曾寄希望与他们能帮我发表,数学老师只是说原来论文是这样写的,这可以算是一篇本科生的优秀论文吧,你以后上了大学会有很广阔的发展空间的,目前来讲这是个无底洞.班主任跟数学老师问过,也只是对我说现在高中没有这种空气,好好高考才是正经.
可是MM的上衣都没脱,你说他们来给我聒噪什么.
我看准了圆可能在其中的理论表现.马上又写了一章圆的解析.我趁此证明了所有的古典平面几何的定理.如托勒迷,牛顿,拿破仑,茉莉,费马最短,史坦纳,莱默恩,塞瓦,西模松定理...关于圆的参数方程我一直都找不到.这给我这种坐标解析圆虽没带来什么烦恼.但本人终是不爽.暂且打住.
圆锥曲线的麻烦我一直没感惹,现在都是.
我的理论再怎样发展呢?我记得我打过一伏笔.说起过向量.海明威说,如果小说开始
出现了一把猎枪,那么这把枪就应该在什么时候响一下.现在枪响了,也就是说我终于抓住了MM的上衣.哈哈,开始脱了...
5.春色无边
人说学了欧氏空间才算真正学了线形代数.我说写了向量才算写出了分点坐标的精髓.
内积外积上我做了与直角坐标无数的对比工作.互化公式可谓用的炉火纯青.内积公式是分点坐标的3大基本公式之3.求法就是用余弦定理.这样把余弦角公式的等式右边的各个距离代入整理.看其中的形式给出向量的定义和内积的定义.于是运用混合积的公式推出外积的可能形式并证明.
有一个问题:为什么不直接定义外积呢?我发现外积的形式究竟怎样得由向量的性质说了算.但这里的向量不是可分解到几个轴上的结果我就郁闷了.外积与内积够成混合积且具有轮换性我就先承认了.没想到借此就求出了外积的模.剩下的是外积的方向了.这是空间的问题了.于是我打住.无疑关于空间的分点坐标我会再写一本理论的.
6.看来往下脱有点难
实在是要琢磨琢磨对付高考的事了,才剩2个月了.
终于考完了我从数学老师那里要回我叫给他的2个本子.一本平面分点坐标.一本空间分点坐标,后都附题典.
家里是从不给我压力的,不过才考上中南民族大学我觉得很没面子.偏偏华师百年校庆堆渣了大堆人,结果我高武大一分的报的华师却少了一分.天呐,你错堪贤愚枉做天.
长长的3个月为通知书奔波就耗了一个月.剩下的时间我就在研究怎样脱裙子的问题.
既然平面的空间的都写了,那么现在的关键是优化再优化.不卖关子了,我引入了点的向量表示法,所以向量就再也不是有方向的量了,对点讲它的称呼失去了意义.那么向量即是点,点即是向量,此即为最高境界.
我特地研究了外心作为一个点的向量特性,写了传说之中神奇的一章:外心性质.就平面来讲,它有效的简化了五心的运算.一眼道破所谓的IMO试题.
我在学射影几何的过程中了解到了圆锥曲线的理论结构形式.我没有写了.因为我的坐标从射影的角度谈它的话内容丰富,但谈起度量,是不如直角坐标能保持圆锥曲线的对称性的.也就是说我的坐标研究三角对称,而直角坐标研究轴对称.
不过我引入了直线方程的另一表达式却或多或少的增加了分点坐标在运用是的技巧性.
至少可一笔即解99年高中数学联赛第2试的几何题.
有时要自己命题难自己,各位数学同道做研究是也有这样的心得吧.
我命了一些题.总之在编题典的同时我学会了作研究的条理性.在写理论的同时我理解了严密性.看来我已修成正果.可以往下脱了.
最光彩的是我写出了空间中,四面体的内心与外心的距离公式.据说康脱早就求出过.看来他也擅长脱MM.
7.可以享受她吗
都脱光了.我就交给了我的大学解析几何老师.这位老师不太冷.
他说20年未见有过如此之作.寄给了北京科技大学叉叉人.后来经过叉叉天收到了电子邮件.说我的东西实际应用价值不强不予刊登.稿不退.老师一边感叹世风日下一边叫我投于他处.我说哎太麻烦了.又把我那磁盘里的东东打印了2分.一分自藏,还一分糊里糊涂的交到华师托门卫给我递上.又经过叉叉天,杳无音讯.后来我弃了磁盘和自藏的那份.
现已是大3了,我忆及此事,尤现于昨日.从那以后我就没有学数学了,一直整整一年.我至今耿耿于怀.故为斯文,以为忘却的纪念.好以后彻底相忘.在没有数学的这一年,我作为一个数学专业的学生,当然没挂科.正是这一年,我主攻英语过了4,6级.算是无何遗憾.
现在大3我又开始搞数学了,但我觉得我只是简单的为了考研而学了.说不定我哪天考上上交大或是中科院.因为我的独立思考能力是很强的.但我觉得在数学的路上我已经衰败了.我现在已无当初的热情了,MM脱光了,我也不会反应了吧.
我可以这样规划我的人生:我以后会继续搞数学,当个老师,过平静的生活.
我觉得我一年没搞数学,忘掉的东西很多了,现在剩下的只是一些思想.各位注意了,我将点出数学教育的真谛了:你忘了所有的数学知识点,然后剩下的只是思想方面的东东,这个东西就是你学了那么多年数学数学留给你的教育吧.
我想这个教育一定教导了你;过平静的生活.
我只想过平静的生活了.我想在我的数学历程上,我逐渐变成了一个懦夫.
由于高中一女生勤学好问(现已读大2),总以为我就是那传说中的数学高手,虚心向我讨教做研究的过程与经验.有感于她的苦心,写此文亦为与她共同交流学习经验.从午夜1点半写到了5点.
182
19好文……
不过题目说是答大2女生
怎么后面成了高中的了?
182
19你忘了所有的数学知识点,然后剩下的只是思想方面的东东,这个东西就是你学了那么多年数学数学留给你的教育吧.
呵呵,记得爱因斯坦也说过类似的话
182
19
引用 (lixiaohu @ 2005年09月
17日
04时53分) |
1.解开第2颗扣子
4.脱去上衣的苦恼
5.春色无边
6.看来往下脱有点难
7.可以享受她吗
|
总想着脱掉她的衣服,却不知道她有血有肉有感情。
1、格调不高,境界不高,未曾接触过真正的数学。
2、学数学最不该的就是想从中获得数学之外的一些什么。
3、所谓的民间数学家多数只想借数学成名而已,数十年钻研只为一朝成名,只为名动天下。这正是民科被专业人士瞧不起的原因,因为他们根本不懂数学,亦不知所做问题的意义所在,只是想籍此证明自己绝顶聪明。
4、许多学数学的人都会问:数学有什么用?多年的经验告诉我这个问题实际是:数学对我有什么用?能赚钱吗?能出名吗?万物皆有数,数学的用处无处不在。数学推动科学的发展,推动技术的进步,推动人类文明的进程。但对个人而言,我实在不知道它有什么用,除非它是个人的兴趣所在。
182
19其实数学也有不少实际的用途。
比如我现在学的计算机图形学,理论上的研究结果都是用数学符号表达的。同时,各种方程,算法的推导也是需要很多数学知识。所以自己在恶补数学。
我相信除了作为纯粹的兴趣,应该只有象我这样迫切需要将数学作为工具使用的人才会认真去学习她。然而真正喜欢数学的人只是少数,所以,我觉得普及数学的关键还是让大家了解数学在各个领域上的应用,从而了解数学的力量,进而一定程度上喜欢数学。
182
19不坐评论
182
19真的假的?
182
19写了这么多
不管是不是真的
还是顶一下
182
19其实还是有点水平的
182
19要多多关照
182
19
有些许共鸣,我在高中也差不多这样,
做自己喜欢的却并不要紧的数学。
当时最得意的事:
独立地用三角方法证明了平面几何中的Morley定理。
182
19经历与你很相似.
不同的是我依然深爱数学.
数学与我们同在!
182
19和我经历有些像,我才发现中学时精力过剩的人真不少
我是初二时推广了二项式定理为多项式定理,发现了多项式的像杨辉三角一样的系数排列模型,高中时给老师看,大一才发现那个定理早有了,不过那个系数模型可能还是我发现的
我本想去北大哲学系,差一点没考上,现在在中国农业大学数学系,我不要选择平淡,我要学得扎实,我还有梦
北京的朋友可以联系我,我qq:253014224,请告诉我你是这个论坛的人
182
19

顶一下
182
19感谢楼上凑热闹
182
19原来数学人也如此幽默
182
19你牛!!
182
19

没人关照!!

182
19高高,你别这样撒,好不好~~~~~~~~~~~~谢谢你SURPPORT
182
19总是以为自己很牛,其实啥也不是
182
19写出不容易!支持!
182
19我们的经历相似啊,只不过没发表,也谈不上发表,因为在我做出什么东西后不久就会在教科书上发现它们。在初三做了关于割圆多项式的计算与在微分方程的特征多项式计算上的应用,以及一些初等的东西。高中时主要在微分方程,解析几何等上做了一点,纯碎当练习,推出了伏朗斯基行列式以及解析几何的不变量等。我倒没想到要发表,那么明显的东西肯定有人早做了。现在在学数学,更多的考虑一些真正的数学了。
其实学习这个东西倒没有必要去追求什么具体的东西,只要喜欢就行了,当然也要考虑以后的生存。顺便说一句,我的学习普通,可没有获什么大奖啊!
182
19顶一个,赞!
182
19读完了,写的不错
虽然还是觉得你的文章可能没什么价值,不过你真是投错了地方了……
我约莫能猜出来你投给谁了……
182
19我也做过,不过我的兴趣是历史,所以把数学放下了
没有想你这样把宝贵的饿时间都浪费了
其实你陷入误区了
想罗布切夫斯基一样傻
不是职业人
是一个倒霉的愤青
发育过早了
没有专门的人的指导
182
19我大惊
18221金融数学涵盖的应用领域是比较广泛的,你得说说你问的是哪个领域的吧。比如,风险管理,衍生品定价,资产组合管理等等。大类中有分小类,又是哪一个呢?
18221请问各位大侠,现在金融数学研究的前沿问题是什么?
用什么数学工具?
18221楼上看来是牛人,问个问题
国内外这个领域那些院校比较牛
18221北美的情况和欧洲不太一样.我对美国知道的比较少,对英国知道的多一些.
英国:Oxford, Cambridge, Warwick,
Imperial College (University of London), Birkbeck College (University of
London), City University (London), ISMA Centre (Reading), LSE (University
of London), LBS (University of London), UCL (University of London),
University of Lancaster, University of
Strathclyde. 都是有金融数学或者金融工程专业的学校,有几个是属于没有此专业但有这方面老师的学校。
另外在欧洲大陆的瑞士的ETH,斯德哥尔摩经济学院,赫尔辛基商学院,阿姆斯特丹大学,比利时的鲁文大学都有不少牛人,当然在法国,德国,意大利也有一些这方面很好的学校,由于本人的局限性不能一一列出了.欢迎知道的同仁写也几笔。
回头有空再写。
18221我想做定价的,用随机过程或者是方程!
有没有那位大侠,可以上传一下,国外的文献啊?
18221How about structured finance or structured credit?
By the
way, in terms of good FE program in Europe, how about ZTH??
You
guys forget Philipp J. Schönbucher??
18221
引用 (witness11 @ 2005年09月
19日
07时36分) |
|
金融数学涵盖的应用领域是比较广泛的,你得说说你问的是哪个领域的吧。比如,风险管理,衍生品定价,资产组合管理等等。大类中有分小类,又是哪一个呢?
|
请教您讲得这几个方面各有什么不同呢?
有没有金融数学方面的综述性的文章可以看看?
18221
引用 (losemind @ 2005年11月20日
17时34分) |
引用 (witness11 @ 2005年09月
19日
07时36分) | |
金融数学涵盖的应用领域是比较广泛的,你得说说你问的是哪个领域的吧。比如,风险管理,衍生品定价,资产组合管理等等。大类中有分小类,又是哪一个呢?
|
请教您讲得这几个方面各有什么不同呢?
有没有金融数学方面的综述性的文章可以看看?
|
/*************************************
现在国内谈得最多的金融数学事实上大部分是指产品定价的那部分。
Arbitrage
Pricing主要是在一些假设下通过解SDE or PDE(Analytically or Numerically or Hybrid
Methods)来近似找出的衍生品的价值。比如:Barrier Option, Digital Option, American Option,
Multi-underlying Option, Swaps, Compound Option, Credit Derivative,
Insurance Claim and etc.当然还有FX, FI的产品的定价和价格联系的发现.
Evolutionary
Pricing是另一个派别,主要是发现产品的内在价值和应有的中长期价值.
**************************************/
/**************************************
资产组合管理主要是研究怎么有效地管理一篮子资产在控制风险的条件下取得更高的收益.
风险管理是近十五年来的新领域,主要是研究怎样数量化地量度,控制和转移不同类别的金融风险.
**************************************/
18221我感觉金融数学的前沿是围绕着热点业务做数学模型(即使是对原有模型的修正与改进),把手里的数据发挥到极点,能够相对准确地做出预测,可以是宏观的,也可以是微观的,具体的业务热点可以参考两本的《金融热点研究》,好象是金融出版社的。其他的都是外围研究,如工具、方法等。
18221金融数学模型作数据分析可以,但是千万别用在作预测上,就算你做了预测也没有人会相信
18221小弟我想写点风险管理的(VAR),不知有无文章可看,请各位大侠指教
18221我是做可转债定价的,感觉自己对国内的市场不熟悉,挺盲目的,就是照抄别国的,有哪位大虾能帮帮介绍吗?不慎感激。
18227我的方法是:
fn(x)=x*f(n-1)(x)然后求n阶导数,然后用证明:f
(n-1)(x)的n阶导数为(n-1)!/x
很麻烦的!大家有没有好的方法啊??post-38-1126927932.gif
18227我的解答post-38-1126951381.gif
18227zhubin846152的解法很简单,我给一个递推的做法:post-38-1126955727.gif
18227好像第一问的证明过程可以简单点
先对f(x)的求一阶倒数得到两项的和
再对这两项求n-1阶倒数
带入
很容易证明相等的
18227的确,如果知道了一阶导的递归式子了,就很容易知道怎么做了!
18227
| 引用 |
好像第一问的证明过程可以简单点
先对f(x)的求一阶倒数得到两项的和
再对这两项求n-1阶倒数
带入
很容易证明相等的
|
好!简单!
18228是这样的。一方面给“家园”提升人气(因为这个网站办得很有意义),另一方面通过深入讨论也增添些许学术氛围。
18228springboshi说的"仅有最小多项式相等不一定相似",肯定不错!!!!
不过我们上面是由特别(!!)的最小多项式相等可以导出所有的不变因子相同,故相似.
可以举例说明某些最小多项式相等时就相似:
例如:当阶阵A与B的最小多项式都是(x-a)^(n-1)时,可证A与B相似;
例如:当阶阵A与B的最小多项式都是(x-a)^n时,可证A与B相似
因为不知springboshi是否认为我上面的证法有问题,故举例说明之.我认为原题用不变因子最简单,仅两句话而已.
182282000post-38-1126928110.gif
18228

矩阵是等价的!
18228其实用若当矩阵容易知道该矩阵对应的若当矩阵是个矩阵块,而且由它是幂零矩阵,所以特征值都是0!于是就容易得到结论。
18228能算出其最小多项式为

^(n-1),于是

矩阵相似拉
18228
引用 (springboshi @ 2005年09月
18日
17时59分) |
| 我给出一个较详细的解答。
|
昨晚的解答有一点笔误,已经修正。
18228懒哥的理由不充分(特征值全为0的矩阵未必相似),三个i的方法好,用最小多项式=第n个不变因子,说明这类矩阵的不变因子一定相同,都是1,...1,x,x^(n-1)
18228
引用 (iii @ 2005年09月
17日
18时30分) |
能算出其最小多项式为
 ^(n-1),于是 ^(n-1),于是
 矩阵相似拉 矩阵相似拉
|
怎么算亚?
18228
引用 (hfg
1964 @ 2005年09月
17日
20时31分) |
|
懒哥的理由不充分(特征值全为0的矩阵未必相似),三个i的方法好,用最小多项式=第n个不变因子,说明这类矩阵的不变因子一定相同,都是1,...1,x,x^(n-1)
|
我的理由不充分吗?我怎么没有看出来啊,就是那样嘛,如果这个矩阵存在非0的特征多项式,就不可能是幂零矩阵,而又它是n阶n-1次幂零矩阵,所以它的若当矩阵就只可能是一个矩阵块啊
于是就知道了啊。这样的一个若当矩阵是唯一的啊。
18228tobyqin说的没错,从我给的不变因子即知,有两个若当块.如果A的幂零指标为n,就一个若当块了,即Frobenius块
18228我给出一个较详细的解答。post-38-1127090566.ibf
18228对于两个n阶矩阵,仅有最小多项式相等不一定能推出矩阵相似。
具体有(可以证明或举反例)下述结论:
设A,B是n阶方阵,则
当n=2时,A相似于B的充分必要条件是A与B的最小多项式相同;
当n=3时,A相似于B的充分必要条件是A与B的特征多项式相同,且最小多项式也相同;
但n=4时,即使A,B的特征多项式相同,最小多项式也相同,但A不一定相似于B。
18230有没有答案啊,我是初学者
18230一些简单的题目
我写出来给大家练练兵post-38-11269299
17.gif
18231有界线性泛函必然连续,谁能举出一个不连续的线性泛函?不连续的线性泛函肯定是无界的,它们是一些什么样子的泛函。如狄拉克函数&(x)=0
,x≠0;∞,x=0,是无界的,但它显然是非线性的,也就是线性条件到底把泛函限制(约束)到了什么程度?这个条件是否就是Riesz表现定理描述的?
18231没有不连续的有界线性泛函
赋范空间上线性泛函或线性映射有界与连续等价
设Ei为空间的一族可数基,F(Ei)=i,i=1,2,3,...n,...
无界线性
18231设T是作用在一阶可微函数空间上的可微算子,即若x(t)是一阶可微函数,
则T(x(t))=x'(t),于是T是线性算子,但是T不是有界算子。
18231可微函数空间上的可微算子是否有界?
看C∞[a,b]即光滑函数空间上,T:C∞[a,b]->C∞[a,b]是微分算子,f属于C∞[a,b],f的范数定义为||f||=sup{|f(n)(x)|:n=0,1,2...,a≤x≤b},则||Tf||=sup{|f(n)(x)|:n=1,2,...a≤x≤b},
显然,||Tf||≤||f||,所以T是有界的。
我的证明是否准确?
另外,如T:C1[a,b]->C1[a,b],是微分算子,则显然如分段线性函数f,Tf根本不属于C1[a,b](而是属于L[a,b]).我的看法是否准确,请多指点。
18231
| 引用 (chl @ 2005年10月24日
09时30分) |
可微函数空间上的可微算子是否有界?
看C∞[a,b]即光滑函数空间上,T:C∞[a,b]->C∞[a,b]是微分算子,f属于C∞[a,b],f的范数定义为||f||=sup{|f(n)(x)|:n=0,1,2...,a≤x≤b},则||Tf||=sup{|f(n)(x)|:n=1,2,...a≤x≤b},
显然,||Tf||≤||f||,所以T是有界的。
我的证明是否准确?
另外,如T:C1[a,b]->C1[a,b],是微分算子,则显然如分段线性函数f,Tf根本不属于C1[a,b](而是属于L[a,b]).我的看法是否准确,请多指点。
|
微分空间C1[a,b]是C[a,b]的子空间,微分算子是映C1[a,b]到C[a,b]的无界算子,
范数
x
=max{x(t)的绝对值:t

[a,b]}
取xn(t)=sin(nt),则f(xn(t)=ncos(nt),[a,b]=[0,2pai]
xn
=1,
f(xn)
=n

f是无界算子
18231线性赋范空间上的线性算子的连续性依赖与线性赋范空间上范数的定义,在有限维Banach空间中,所有范数等价,而对于无穷维的Banach空间,上面可以定义不等价的范数,所以线性算子是否连续则会依赖于范数的定义。本质上,范数(度量)也就是定义了空间上的开集结构,而函数的连续性是完全依赖于开集定义的(即拓扑结构的)。所以,微分算子是否连续,也就要看C∞[a,b]上到底定义了什么样的范数,所以也就可能有不同的结果了。
这个看法应该是正确的。
18232IQ题:超难数学题
摘自 新浪网
一天有个年轻人来到王老板的店里买了一件礼物,这件礼物成本是21元,
结果是这个年轻人掏出100元要买这件礼物,
王太太当时没有零钱,用那100元向街坊换了100元的零钱,
从中找给年轻人82元,误以为礼物
18元.
这时年轻人发现82元都是假钞,要求换真的,王太太说没有零钱了,
年轻人只好掏出8元(真币)连同那82元说,那我就再买5件,共90元,老板娘照办了。
但是街坊后来发现那100元是假钞,过来退,说你的零钱还是假钞呢!
双方争执不休中,王老板从外面回来,协商后,退给街坊50元.
现在问题是:王老板在这次交易中到底损失了多少钱???
18232损失了1
18块钱啊!
是不是太简单了,还是我想的太简单了啊?
18232这个很简单啊
18232成本21作何解?本钱21卖多少不一定?还是卖21,进货价格不定?
18232我觉得是损失了147元!如果说物品进货价21的话!
18232给邻居五十,给年轻人五件物品,共损失155元,只得到年轻人的8元真钞票!(其他都是假的,不考虑)155-8=147
18232年轻人拿走了六件吧!
18232第一次就做错了
18232年轻人拿走6件付8元真币,王老板又付给邻居50元,故赔了21*6-+50-8=168元
18232到倒数第三行止,年轻人用8元真币买走6件商品。陪了21*6-8=1
18元,这时假设100元假钱还归他所有。
但是,他又等价于用100元假钞骗了邻居82元假钱+
18元真钱(如果是真的话)。即得利
18元。
但是后来他又白给邻居50元。
上面两个过程损失50-
18=32元。
共150元。
所以在上面假设下,陪150,但是
另外,他的实际销售价格未知,按照经济学原理,他损失应该是(售价-21)*6+150。
大家看严密否
18232有点数学游戏的味道了! 旁门左道
18232难啊
18232是全部零钱是假的还是只有那82哦?
18232小学数学竞赛的常见题.很有意思.
18232应该是147元吧!!!
18232大家的答案不尽相同啊。
18232如果假定街坊给的100零钱全是假的
则年轻人赚1
18,王老板赔168,街坊赚50
如果假定街坊给的82是假的,
18是真的话
则年轻人赚1
18,王老板赔150,街坊赚32
18232不会做
18232是一个很老的题目了!!
18232有趣...
18234问渠哪得清如许,为有源头活水来
——谈狄拉克符号法的美
·叶万渝·
关于美是什么的论题,历史上有诸多不同见解,至今也没有定论,然而从最
朴素的直觉出发,美是能给人以感情的寄托和精神的充实和愉悦的事物,是某种
和谐的存在。而在科学方面,追求和谐的理念集中体现在“奥卡姆剃刀原则”,
即“如无必要,勿增实体”。有基于此,简单性和对称性作为通向和谐和真理的
重要途径,历来为科学工作者所孜孜以求:从古希腊关于地球是球体、毕拉哥拉
斯的黄金分割率理论到近代的日心说、行星运动三定律,现代的量子力学、相对
论理论,无一不是追求简约工作的结晶。作为量子力学的标准语言,狄拉克的符
号法在量子理论方面早已得到广泛应用,而后继理论工作的深入拓展也相当程度
上实现了他的期望:“在将来它(符号法)变得更为人们所了解,而且它本身的
数学得到发展之时,它将更多地被人们所采用。”(1)
狄拉克符号法的美是毋庸置疑的,然而首先不得不承认的一点是它首要的美,
即它带给人的如闻天籁的喜悦的源泉是不可言说的:这正是所谓的“大音希声,
大象希形”。这一事实的本质原因在于不同人的经历、底蕴、物理直觉各不相同
——这同时也是美之难以定义的一大原因。海森堡这样描述他创立量子力学时的
感受:“我窥测到一个异常美丽的内部,当想到现在必须探明自然界如此慷慨地
展开在我面前的数学结构的这一宝藏时,我几乎晕眩了。”(2)狄拉克也承认:
“我和薜定谔都极为欣赏数学美,这种对数学美的欣赏支配了我们的全部工作。”
(3)但时代的特定性和大师的天才决定了后世人身上难以重现那种得以窥得天
机,创立一个自洽的理论体系的激情,而他们对量子力学美的认识相应也将有所
不同,如朗道曾感叹自己生不逢时,未能为量子理论的原创工作做出贡献,而他
对其中之美的感受自当不同或说不如,而一般人则更加难以体会。这与欣赏名画
有些相似:内涵深刻的作品将立刻给人鲜活的第一印象。看到毕加索的名作“格
尔尼卡”,战争的悲剧将通过种种扭曲的意象迅速攫取你的心,梵高的“星夜”
则给人以挺拔向上之感,然而这些美感通常只在第一次见到画作时才有最深刻的
体验,也只有具备一定修养,懂得如何欣赏之人方能领会。
本质性的美同时也是无法向他人传达的。美感有时类似于灵感,只有在特定
状况下才能产生。当公式的推导终于成功,或是忽然看懂一种繁难的理论,那一
时刻的强烈感受不仅难以重现,也是不可转述的。晚唐的贾岛是有名的苦吟诗人,
和韩愈共同推敲“僧敲夜下门”之句并结为忘年交之事自古传为佳话,然而他还
有一句更是苦吟了数年:“独行潭底影,数息树边身”。对于此句他自称“二句
三年得,一吟双泪流。知音如不赏,归卧故山秋”,然而后世却有人认为此句
“有何难吟”,稀松平常。这里自然也有文化底蕴的差别,但美感之难以传递也
是极重要的原因,是以诗人自己也说“知音”方才能赏。
因此,对狄拉克符号法的美的讨论存在某种局限性,且通常只能针对个别、
表层的特点——大概这也可以称之为“表象”,即其本质之美的外在体现。
那么符号法的美究竟体现在何处?
首先,作为物理学的重要分支,符号法将q数的对易关系与经典力学泊松括
号类比,从而建立了量子力学与经典力学的对应关系,揭示了自然规律的简洁性。
同时,它将矩阵力学纳入哈密顿公式体系,从而很好地统一了之前的薜定谔表象
和海森堡表象:两种学派曾因不同的数学形式争论不休,后来薜定谔发现它们是
殊途同归的,而狄拉克则运用他的符号法所建立的变换理论使这一证明变得优美
凝练。此外,狄拉克坚信符号法的特殊数学能够继续发展并得到更广泛的应用,
而事实上这一点已经部分地由范洪义教授的IWOP方法实现。纵观人类科学发展史,
每一个重要的理论体系无不为其后继理论留下相当的拓展空间,如牛顿力学之于
理论力学,狭义相对论之于广义相对论,符号法良好的拓展性同样使它得以而且
必将成为一个完备、严整的理论体系。
同时,符号法给以强烈的数学美感。狄拉克坦陈数学美“是我们的一种信条,
相信描述自然界的基本规律的方程都必定有显著的数学美”(4)。与此相应地,
历史上狄拉克有好几次慢于其他科学家做出重要工作,然而同样的结论,狄氏的
文章往往更注重数学的简洁,也就是杨振宁先生所说“秋水文章不染尘”(5)。
符号法关于物理抽象的表述,态矢的归一化及薜氏,海氏表象的统一无不体现着
这些特点。如果按杨的说法,数学与物理犹如两片向不同方向生长的树叶,大多
不重叠,只有末端有一小块重叠,那么狄拉克对于这一小部分无疑拥有极敏锐的
洞察力。这也使得他的符号法得以“性灵出万象,风骨超常伦”(6)。
符号法的美还表现在对事物本质的描述之中:它在概念上与哲学颇有关联。
这一相通集中地体现在表象与本质的定义上。西方经典哲学认为事物背后存在本
质,本质通过表象部分地呈现出来,而本质本身并不为人所见,只能通过表象对
它加以认识;任何对本质的认识都是不全面的,即相对真理;真正完善、全面的
认识(绝对真理)不可达到。符号法中的表象同样是作为认识事物的本质(体系
状态)的方式而存在,态矢本身是抽象的、本质的,它的物理意义只有具体投影
到某一特定表象,才能为人们加以观察。这与老子哲学也有一定相似之处:老子
认为“道”是客观世界自然法则和万物物质实体的总和,具有形而上的特点,没
有确切的形体,无法用感官去直接感触:“视之不见……听之不闻……搏之不得”
(7);“道”是一种永恒的存在,它是世间万物的本原:“可以为天地母”
(8),“渊兮,似万物之宗”(9);“道”作用于外界,产生纷繁芜杂的现象
(表象):“道生一,一生二,二生三,三生万物”(10),因此具有无穷的潜
在力和创造力,是自然界生命活力的象征。态矢是否也与“道”有些相似之处呢?
下面再谈一谈符号法的通感美。通感是自然科学之美的重要形式,科幻小说
里对于仪器的描述:“温暖的电流在一瞬间流遍了那巨大的躯体……在它的电子
意识中,整个世界是极其简单的。”(11)就是典型的通感。对符号法而言,通
感之美首先表现在它与诗歌的相似性上:它们都追求简单、和谐与对称,是特定
时刻的灵感结晶。薜定谔就是一个很好的诗人,他把荷马史诗译成英文,自己会
用德、英文写诗,还出版过诗集。而狄拉克对数学之美有一种特殊的执著,这使
得他的符号法逻辑严密,论述清晰,如诗歌般工整美丽。同时,物理学家与诗人
往往都是富于想象力的理想主义者,愿意为追寻梦想奉献一生。诗人苦吟而至于
“吟安一个字,捻断数根须”,这与物理学家为推导公式、完善理论而数十年如
一日地努力,甚至夜不能寐、寝食难安何等相似!符号法的尘埃落定,无疑也是
“看似寻常最奇崛,成如容易却艰辛”。
符号法被杨振宁先生评价为“用了简单清楚的逻辑推理,经过他的讨论以后,
你就觉得非这样不可。”“他的每一步跟着下一步,都有他的逻辑,而他的逻辑
与别人的逻辑不一样,但是非常富有引诱力,跟着他一走以后,你就觉得非跟着
他走不可。”(12)正是这种鲜明的层次感和循循善诱的推理最后导致简洁的理
论和诸多方面的应用,使大量问题得到妥善的解决。这个过程立刻令人想起刘鹗
《老残游记》里对说书的描写(请恕我全段引用,否则难以尽显其妙):
“王小玉便启朱唇,发皓齿,唱了几句书儿。声音初不甚大,只觉入耳有说
不出来的妙境:五脏六腑里,像熨斗熨过,无一处不伏贴;三万六千个毛孔,像
吃了人参果,无一个毛孔不畅快。唱了十数句之后,渐渐的越唱越高,忽然拔了
一个尖儿,像一线钢丝抛入天际,不禁暗暗叫绝。那知他于那极高的地方,尚能
回环转折。几啭之后,又高一层,接连有三四叠,节节高起。恍如由傲来峰西面
攀登泰山的景象:初看傲来峰削壁千仞,以为上与大通;及至翻到傲来峰顶,才
见扇子崖更在傲来峰上;及至翻到扇子崖,又见南天门更在扇子崖上:愈翻愈险,
愈险愈奇。那王小玉唱到极高的三四叠后,陡然一落,又极力骋其千回百折的精
神,如一条飞蛇在黄山三十六峰半中腰里盘旋穿插。顷刻之间,周匝数遍。从此
以后,愈唱愈低,愈低愈细,那声音渐渐的就听不见了。满园子的人都屏气凝神,
不敢少动。约有两三分钟之久,仿佛有一点声音从地底下发出。这一出之后,忽
又扬起,像放那东洋烟火,一个弹子上天,随化作千百道五色火光,纵横散乱。
这一声飞起,即有无限声音俱来并发。那弹弦子的亦全用轮指,忽大忽小,同他
那声音相和相合,有如花坞春晓,好鸟乱鸣。耳朵忙不过来,不晓得听那一声的
为是。正在撩乱之际,忽听霍然一声,人弦俱寂。这时台下叫好之声,轰然雷
动。”(13)
这一段精辟的描写若用以形容符号法是何等贴切,传神!符号法与文学作品
的通感之美实已尽现其中,毋须多言。
符号法与音乐。毕达哥拉斯认为美妙的音乐之所以动人心弦,是因为它符合
数学的规律,是数学和谐的反映,而符号法亦如此,狄拉克更认为创作符号法之
时,数学美“对我们像是一种宗教。信奉这种宗教是有益的。这是我们多次成功
的基础。”(14)这种创作方式令人联想到亨德尔和他的清唱剧《弥赛亚》。罗
曼·罗
18236求Duffing方程的数值解法程序,谢谢
gdutsaj005@tom.com
qq:9067648
18240这,快要决定应该去哪里了,可我还没定下来,踌躇于大连理工和南开之间.
我学习班里前一二名的.我们的学校虽不是211,但也比某些211的学校强.
想求教大家,能不能给出个主意.本人在山东,女,为未来计,不想远行.
实在是谢谢大家了.大家就算没主意,帮忙顶一下也好.
18241受益非浅!
18241请教高手!post-38-1126947511.gif
18241看看我这么做是不是清楚,准确:post-38-1126952446.gif
18241争取早日作高手:)
祝大家中秋节快乐post-38-1126952748.gif
18241十分感谢!&Happy mid-autumn day!
18241第二种解答看不懂,怎么推出最后一行的啊??
18241zhubin846152兄,可不可以说一下你解法最后一行:怎么由f(x)的连续性说明M(Cn)-->M©
(c->无穷)?
谢谢!
18241这是华师课本的一道课后题,解答上的答案很简单!分区间!
18241第二种做法中,不能不妨设!因为左侧极限不存在和右侧极限不存在是不太一样的!
1824216pt???
18242如题,敬请赐教,谢谢.
18242我都来也出了这个问题,上不了主菜单,弄得我还没办法了
18242
引用 (小红帽 @ 2005年09月
19日
14时46分) |
|
我都来也出了这个问题,上不了主菜单,弄得我还没办法了 |
在ctex论坛上, 一网友建议我用“
word宏的安全性设置为最低即可 ”,
可是我没试成功, 希望这个问题能得到更多高手指点.
18242看来只有卸掉office,重装了,晕
18242后来发现,该软件已和公式编辑器合成一个了。点击
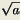
,出来的就是mathtype 5.2c,呵呵
18242
| 引用 (小红帽 @ 2005年10月08日
21时37分) |
后来发现,该软件已和公式编辑器合成一个了。点击 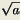 ,出来的就是mathtype 5.2c,呵呵
,出来的就是mathtype 5.2c,呵呵 |
这是对的, 但是用不上其中的宏, 例如一篇用16pt敲的上课讲稿,
要想转换为28pt的课件
就不能用宏命令, 整篇一次转换完成.
18242是因为word的startup文件夹里没有相关mathtype的命令引导文件,找到后复制进去就ok了!我也遇到过,就这样解决的。
18242重新安装M就可以啦,但是需要输入注册码,网站上有的,耐心找一会就可以了。
18242
引用 (lwhay @ 2005年12月30日
18时09分) |
| 出售内容
|
你这个方法谁不知道?
我的还没解决呢
把钱退了吧
18245我知道一个方法,但很难想到,大家有没有好的方法啊?post-38-1126954002.gif
18245我的解答post-38-1126955524.gif
18245可以利用Taylor展开来做:post-38-1126957249.gif
18245不知道zhubin的是不是和我的一样,贴出来大家看哈post-38-1126958350.gif
18246是否可以用stolz定理啊?为什么我求出的是1/

???post-38-1126954244.gif
18246不能用,否则根据奇偶性应该是正负1/a。所以可见不能用Stolz公式。因为Stolz公式仅在极限存在时才能使用
这道题目用比较法
显然分子的绝对值<n^(a-1)就可以了
18246综合上面两位的解答就是这个题目的完整解答了!
18246stoltz公式要分母从某项开始单调上升
应该不能用了
18247爱数学
18247因为热爱,所以要学数学!
18247“爱因斯坦在读大学本科的时候数学水平就已经超过世界一流重点大学博士毕业的水平了”?不是这样吧!
18247
| 引用 (spiceoil @ 2005年09月29日
13时45分) |
得数学者得天下
思维锻炼出来了,其他的领域便很容易攻破.
|
强烈支持!!!
18247
引用 (一点点 @ 2005年10月11日
19时44分) |
| 引用 (spiceoil @ 2005年09月29日
13时45分) |
得数学者得天下
思维锻炼出来了,其他的领域便很容易攻破.
|
强烈支持!!!
|
同意!!!!
决定跨专业考北大数学!
182471、计算机之父、博弈论之父---著名数学家---冯·诺伊曼,布达佩斯大学数学博士,普林斯顿大学数学系终身教授。冯·诺伊曼著过《博弈论与经济行为》一书,从而成为博弈论的奠基人。冯·诺依曼在30年代撰写的《量子力学的数学基础》,奠定了量子力学的数学基础。同时他还参加曼哈顿计划,被美国总统任命为国家弹道导弹委员会主席。冯·诺依曼对科学做出的最大贡献当然是在计算机领域。
2、控制论之父---著名数学家----维纳。40年代后期,维纳将先前在数学、通信工程、自动控制、计算技术和神经生理等方面的成就综合在一起,于
1948年出版了《控制论》一书,标志着控制论的创立。控制论提出了划时代的崭新思想方法,对人类思维和科学研究产生了广泛而深远的影响。
3、通信科学的奠基人、信息论之父、“通信的数学原理”作者---数学家香农。香农
1936年毕业于密歇根大学并获得数学,
1940年获得麻省理工学院数学博士学位。
1941年他加入贝尔实验室数学部。
1956年他成为麻省理工学院客座教授,并于
1958年成为终生教授。从
1948年6月到10月,香农在贝尔系统技术杂志上连载发表了影像深远的论文《通讯的数学原理》,香农被称为信息论之父。
4、非合作博弈论的创始人、
1994诺贝尔经济学奖得主---著名数学家-约翰。纳什。纳什
1951年在美国普林斯顿大学获得数学博士学位,曾任麻省理工学院数学教授,他提出著名的纳什均衡的概念,从数学上证明了n人非合作博弈的纳什均衡解的存在性,从而奠定了博弈论的数学基础,彻底改变了人们对竞争的观念,动摇了西方经济学的基石,纳什被称为非合作博弈论之父。
5、莱因哈德·泽尔腾,德国波恩大学教授,德国科学院院士,欧洲经济学会主席,美国经济学会名誉委员,
1994年诺贝尔经济学奖获得者。于
1951年到
1957年在德国法兰克福大学学习数学,
1957年获得硕士学位后,
1961年获得数学博士学位。
6、麦克斯韦,
19世纪伟大的英国物理学家、数学家。15岁就发表过数学论文,16岁时进入爱丁堡大学,
1850年转入剑桥大学研习数学,
1854年以优异成绩毕业于该校三一学院数学系,并留校任职。他抱着给法拉第的理论“提供数学方法基础”的愿望,决心把法拉第的天才思想以清晰准确的数学形式表示出来。他在前人成就的基础上,对整个电磁现象作了系统、全面的研究,凭借他高深的数学造诣接连发表了电磁场理论的三篇论文,将电磁场理论用简洁、对称、完美数学形式表示出来---麦克斯韦微分方程组。
7、狄拉克,诺贝尔物理学奖获得者。在布里斯托尔开始时学的是电气工程,但不久就转向纯数学方面了。
1923年考入剑桥大学圣约翰学院当数学研究生,
1932到
1969年,狄拉克任剑桥大学数学教授。狄拉克对物理学的主要贡献是发展了量子力学,提出了著名的狄拉克方程,狄拉克的数学水平很高,思维十分敏捷,人们称他“象牙之塔”式的科学家。
在诺贝尔经济学奖的获得者当中80%都是数学家,有很多都是纯粹的数学家。
国际计算机最高奖---图灵奖的获得者中基本上都是学数学出身的计算机科学家。
微软公司的首席科学家基本上都是数学家。
像牛顿、霍金这样的理论物理学家就不用说了,已经是驰名世界的数学大师。爱因斯坦在读大学本科的时候数学水平已经超过世界一流重点大学博士毕业的水平,他比牛顿幸运的是广义相对论是建立在黎曼几何的基础之上,而黎曼几何在爱因斯坦之前就有人做出来了,所以爱因斯坦不用像牛顿独立创立微积分那样去创立黎曼几何,但尽管这样,爱因斯坦还是专门花费了好几年专门研究数学,从这个意义上讲,牛顿比爱因斯坦更伟大,因为他是微积分的创立者之一。
中国的举两位:
中国航天事业的奠基人、中国航天之父、两弹一星功勋奖章获得者、中国系统科学和工程控制论的奠基人---钱学森(
1939年在美国加州理工学院获数学博士学位)。
北大方正的开创者,被誉为当代的毕升、“汉字激光照排系统之父”、“中国现代汉字印刷革命的奠基人
”、“中国迎接知识经济挑战的先驱”---王选(北京大学数学力学系获计算数学学士学位,他提出轮廓描述和参数设计的数学方法,从而使汉字印刷彻底告别铅与火,迈入光与电的时代)。
如果你想在科学上有大的贡献,要想在科学、工程领域开创一番天地,扎实的数学基础十分重要,因为你要做出原创的理论,让所有的人跟着你跑,而不是你在别人的路上能走多远,这才是真正意义上的领先!问渠哪得清如许,为有源头活水来!现在有很多学工科的人数学功底比较差,也就算个工匠,很难做出大的成绩。所以不要为了几个钱就把自己搞得晕头转向,对于那些想在科学上有所建树的同学,一定要打好坚实的数学基础!
数学是自然科学的王冠,是真正的科学、美学、哲学!
18247说的好
我也要确定自己得数学了!!
18247支持数学,热爱数学
18247爱!
18247非常感谢!
18247看来可以给我的学生们讲讲
18247计算机的创始人---著名数学家-冯。诺依曼
18247计算机的创始人---著名数学家-冯。诺依曼
18247计算机的创始人---著名数学家-冯。诺依曼
18247计算机的创始人---著名数学家-冯。诺依曼
18247得数学者得天下
思维锻炼出来了,其他的领域便很容易攻破.
18247我永远热爱数学~~~
18247dingding
18247楼主说地赞啊!既然选择了走数学这条路,就要不回头,坚定不移地走下去。
18247数学,仅仅是为了心智的荣耀;我们不企求数学在自然科学中会有多大的作用。
18247
| 引用 (wenbaoyu @ 2005年10月24日
22时12分) |
|
数学,仅仅是为了心智的荣耀;我们不企求数学在自然科学中会有多大的作用。 |
可惜事不如你所愿,这个世界上真正NB的事情(特别是推动社会进步的重大科学成果)基本上都是数学家干的!
18247
| 引用 (matrix594 @ 2005年10月25日
14时46分) |
| 引用 (wenbaoyu @ 2005年10月24日
22时12分) | |
数学,仅仅是为了心智的荣耀;我们不企求数学在自然科学中会有多大的作用。 |
可惜事不如你所愿,这个世界上真正NB的事情(特别是推动社会进步的重大科学成果)基本上都是数学家干的!
|
nod.比较遥远的说,要是没有微积分,现在世界会是什么样
没有数学的发展,经济学家们还在掰手指头
18247把数学看成纯粹精神和理念的东西数学中的是典型的伯拉图主意,这种观点最早由伯拉图发展,但很快就成为他的学生亚里世多德反对的对象。他的明言“我爱我师,但我更爱真理”在很大程度上就是在批判伯拉图的数学思想。
18247每次必顶
18247爱数学,学数学!
18247给学数学人以信心和力量!
18247为了明天,学好数学
18247
计算机应该是图灵,博弈论倒是冯诺依曼,数学学到他们那份上,实际上
不容易,普通人学数学不是为了成为数学家,数学家毕竟是少数。
18247爱
美
自由
18247我不大擅长比喻,但我试图先打个比方。
甲第一次要拧螺丝的时候(遇到问题),先学习螺丝刀的用法(为解决问题学习
相应的工具及其用法),之后,他就会使用不同尺寸和力臂的螺丝刀拧不同的螺
丝,甚至对这个问题发生兴趣的人会进一步顺藤摸瓜地学习了杠杆原理(变通),
最后联想出起子、滑轮等一系列工具解决相应的问题(这就是大部分搞研究的人
搞的研究)。
从这个例子,我们可以看到,学习过程总是沿着遇到问题->为解决问题学习->融
会贯通->发明创造这个步骤的。再看下面一个比方
甲之前没有接触过螺丝,但他学习了成千上万种工具的原理和用法,当他第一次
要拧螺丝的时候,他在大脑数据库中搜索相应的工具,最后他没找到,他得出一
个结论,学工具很重要,我就是工具没学好,所以不懂拧螺丝。
你一定会说甲有问题,他不是没学好工具,而是他的学习方法有问题。
当然,不排除有这么少数人,他们无师自通,第一个发现了螺丝刀可以用来拧螺
丝,这些一般就是留名千古的学者了,即使这样也离不开一个事实,发明工具
(或者说发现工具用法)的人往往是遇到问题的人,并且明确问题本质所在的人。
其实,把数学说得再神,他极其量是一门工具课,而不是自然科学课。现在不少人
“搞研究”,看别人的论文,遇到数学的地方看不懂,就得出一个结论,唉,自己
数学没学好。那我要先问一句,数学要学到什么程度才算学好了?熟悉微积分算学
好没有?熟悉线性代数、微分方程、概率论算学好了吗?熟悉现代数学呢?如果真
这样说下去,你就一辈子学数学吧。
上现代数学时马老师就举过爱因斯坦的例子,说他发表相对论时早就有了该方面的
思想,只是找不到工具表达出来,最后花了一年多时间学习数学,才得以成功。这
个例子就说明了,真正的发明创造,是先有思想,再有数学的。学数学就像学用工
具一样,是要有针对性的。相反,数学家懂很多数学,但相对论最终不属于他们。
也许很多人在看论文时发觉别人将几条式子变两变,就出了一篇文章,十分感慨。
排开欺世盗名,没有实质成果的变换式子做数据的这部分论文不说。虽然你看到的
是他通过几个式子得出结论,但你可曾知道人家在变换时已经明确知道为什么要这
样变法,这样变法目的是要改进一些什么、得到一个怎样的结果。也就是写论文的
人早就知道这样可行,只是用数学将他表达出来而已;而不是毫无目的地变两变,
最后什么都不知道就出个结论。我们看文章看不懂数学方面固然是一个原因,但不
是问题的关键所在,问题关键在于你不理解作者下一步(下一条式子)将要企图做
些什么!你连问题的真正所在(问题是什么)都不知道,而去看问题的表达形式
(数学),当然一无所获。
如果你明确了问题所在,知道自己要解决些什么,下一步就是像爱因斯坦一样,
在相关的数学领域上下苦工了。真到了那个时候,自己不懂应该学哪些数学,应该
怎么办?那这时候就要像爱因斯坦一样,拜访一下其他数学家,让他们指条路你行了。
但事实上,现在“搞研究”的人远远没有做到“有思想”这一步!!
说了那么多,只是为了说明一点,无论是搞什么研究,关键是在于明白到底是要搞
些什么,也就是“有思想”。
18247说得真好
18247当实那个离证出那个命题只有0。01秒,但是四分之一柱香之后我决定穷我一生去研究数学,因为我发现了一个绝好的证明方法。它使我爱上了数学。
18247找回了一些信心
18247学怕了
18247因为爱,更要学好数学,学好数学英语,走遍天下都不怕
18247因为要学,所以热爱!
18247数学的魅力所在啊
支持!!!
18247学数学没有必要一定成为数学家,但数学确实可以成为我们的帮手,让我们的思想更加缜密。
18247是啊,成为数学家的终究是少数,但有了数学的思维,很多的问题就会更容易的解决.而且学数学的人都爱思考,不喜欢接受现成结论,这是对应试教育的挑战
18247学数学不是一定要有用才学。其实好些东西刚开始是一点用都没有的,但是正如全世界的人民都想在奥运会上争夺金牌一样,是一个国家实力的证明,100米你能跑多快有什么用还不是想证明人类的极限,数学也是,不一定马上就有用,我们去证明一些猜想也是一样。
有意思的是,在清朝末年,日本和中国都向欧美派了大量的留学生,中国的主要攻读工科技术类的,而日本的学生主要攻读数学和物理等基础性的学科。后来的历史表明,中国并没有在工程技术上比日本强。我们可以从中的出一点启示。
18247就是数学好难呀
18247说实话,大家
18247可惜国内太浮躁了,没有几个人能净下心来学习数学,学习资源也少,一本数学手册都是几十年不变,现代数学还没进入到大学教学中来
18247
引用 (ustc2007 @ 2006年03月16日
16时
17分) |
|
学数学不是一定要有用才学。其实好些东西刚开始是一点用都没有的,但是正如全世界的人民都想在奥运会上争夺金牌一样,是一个国家实力的证明,100米你能跑多快有什么用还不是想证明人类的极限,数学也是,不一定马上就有用,我们去证明一些猜想也是一样。
有意思的是,在清朝末年,日本和中国都向欧美派了大量的留学生,中国的主要攻读工科技术类的,而日本的学生主要攻读数学和物理等基础性的学科。后来的历史表明,中国并没有在工程技术上比日本强。我们可以从中的出一点启示。
|
强烈支持,人类智力的最高成就,智慧女神的化身。
18247想静下心来也不容易啊,又有几个圣人呢,还是得看环境。
而现在大多数人都把数学看成不实际的东西,又能有多好的环境呢。
不过我觉得实不实际得由各人自己看,学数学,有足够的资料,有支笔、现在得再加上
台电脑就够了,要那么多又有什么用。
能考上研究生就好了,起码环境就不用愁了
18247数学在未来的作用必将进一步加强
18247后悔当初没学好数学
18247受益匪浅
18247我对陈凌云的观点真心支持,学习是学思想,学方法,学做人。国家需要的是对国家有贡献的人才,有益的人,而不是高学历但总想牟私的人。
18247
| 引用 (fanny409 @ 2005年09月22日
21时16分) |
| 支持数学,热爱数学
|
观点一样
18247颇有感触了啊!
18247我有了一种看数分的冲动。。。
18247因为要为以后着想所以要考研 努力加油
18247现在有很多学工科的人数学功底比较差,也就算个工匠,很难做出大的成绩。
震撼!!!
18247非常支持
18247有了底气!~
18247数学是科学之父!是其他学科的基础!
18247好
增强信心
18247因为热爱,所以学习。
18247我看自己没有哪个实力啊,而且有几人会有呢
18247热爱数学
数学创造财富
18247数学简直太好了 要想作出大的贡献,数学不好是不幸的,也是不行的
18247好!支持!!!!!
18247我顶[SIZE=14]
18247理论研究数学很重要
那如果工作的话数学怎么起作用呢?
18247大师,冯康绝对大师。
18247很有道理!
呵呵!
18247决定考数学
18247要教育好后代,好好学习数学.
18247得数学者得天下
思维锻炼出来了,其他的领域便很容易攻破.
18247这管用吗?
18247楼主说得到位!
强烈支持!
18247那些都是成功者,但是你知道有多少的失败者吗很多学数学的很难就也,吃都吃不饱呢
18250非常感谢 真的很需要
18250厉害
18250我怎么下不来
18250万分感谢!
18250数分答案有么?
18250高手,偶像
18250不错
18250顶
18250好东西,谢谢楼主!!!
18250谢谢LZ!~
18250“顶”力相助
18250好厉害啊!
楼主一定是数学博士吧?
18250谢谢!真强!!
18250he
18250牛叉!
18250中国科学院2005年高等代数试题详解
斑竹回复:奖励60分!post-38-1126960748.ibf
18250好棒,这些解答都是楼主完成的吗?太厉害了
18250顶!
建议斑竹放到首页!
18250赞!!
为什么没数分
18250对,为什么没有数分?强烈建议!
18250太厉害了!!!!谢谢
18250多谢
18250好好学习
18250强!
18250强~~~
18250太感谢搂主了!
顶!
18250弓虽
18250为了更多的同道下载,望诸君“顶”力相助。
斑竹放假了,若能贴到主页就更妙了。
18250怎么没有试题啊,是我没找着?!
18250非常感谢!
会不会有数分的答案出来
期待
18250强~~~
18250请PHIL到中科院数学所的网站去下载全部试题(免费)。
18250厉害呀
我顶
18250我就是在首页下的!
18250
这是谁做的啊 我想认识一下!!1
18250太好了
18250太感谢了
不过还是自己先做一下。
18250太好了,谢谢
18250楼租牛啊
18250自己先做一下。
18250好厉害!
18250下不了啊
18250太厉害了!
感谢楼主!
18250thanks.
顶顶顶顶顶顶 顶 顶
顶 顶 顶
顶 顶顶顶顶 顶顶顶 顶顶顶 顶 顶
顶 顶 顶 顶 顶
顶 顶 顶顶
顶 顶 顶 顶 顶 顶 顶 顶 顶
顶 顶 顶 顶顶 顶 顶 顶 顶 顶
18250顶!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
18250最后一题的的 那个“容易证明的不等式”“在倒数第5行” 是怎么证明的???????
18250可用数学归纳法。
先观察p=2,3的情形,则不难得证。
也可参看有关不等式的书籍。
18250可不可以把 答案贴出来,好不拉,本人搞了半天摸不着头脑
18250太厉害了!!!!谢谢
18250好好好
18250是啊,很想要数学分析的考研资料
18250
| 引用 (iii @ 2005年09月24日
22时28分) |
| 最后一题的的
那个“容易证明的不等式”“在倒数第5行” 是怎么证明的??????? |
To
iii
主要是录入太麻烦了,证明见附件。post-38-1127734301.ibf
18250顶顶!!!!!!
18250谢谢
18250Ding!
18250很棒!谢谢。
数学与我们同在!
18250ding!!!!!!!!!!!!!
18250多谢,楼主!
18250顶顶顶
18250非常感谢
18250不知道怎么有乱码,重新发一遍,佩服!
18250非常感谢!
18250确实太厉害了
18250非常感谢!
18250中科都考些什么
182503小时作出来真是强人,这当中许多题目是成题,
在书上查到了,除了最后一题。
当时功力尚浅,也是无可奈何!!
18250太感谢楼主了。
不知道其他往年的试题答案能不能也传上来呢,现在自己做的完全没有把握,而且也有一些题目不会作。
182503ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks3ks!!!!!!!!!!!!!!!!
18250佩服
18250kiss!还想要04年的高代解答,其他不要了,有吗?我给你加999999999999999分!!
18250谢谢??!!!
18250顶,辛苦了。
18250厉害
18250太感谢搂主了!
顶!
18250漂亮与赞!!!
18250佩服
18250真得很棒!
18250对呀,很期待数分的答案。
18250楼主太厉害了,佩服佩服!
18250thanks!
18250xiexie
18250谢谢精彩解答!
18250长达6页的解答真不简单呀,值得敬仰和学习这是我的目标!!!
18250楼主真是一个好人
18250谢谢啊,好人哪
18250为什么没有数分?
18250gan xie
18250不错!
18250很好!
18250感谢搂主了
18250非常有帮助。
18250谢谢楼主了啊
18250看的有一些困难呐!
叫我怎么做?
强人!!!!!!!!
18250
引用 (wangzhiquan @ 2005年09月24日
18时08分) |
thanks.
顶顶顶顶顶顶 顶
顶
顶 顶 顶
顶 顶顶顶顶 顶顶顶 顶顶顶 顶 顶
顶 顶 顶 顶 顶 顶 顶 顶顶
顶 顶 顶 顶 顶 顶 顶
顶 顶
顶 顶 顶 顶顶 顶 顶 顶 顶 顶 |
ding
18250太强了,继续啊.
18250能做出最后一题,的确不一般,高手!
18250相比高代 数分太简单了
这位兄台实在是太强了
谢谢
18250你可真厉害!感谢!
18250左边的还是没出来啊D1没大于等于的不等式啊
18250请问下题目在哪里?
只有解答没有题目啊...
18250我最爱美女,除非没有数学.
18250非常感谢!!!
18250谢谢楼主
18250好呀
18250谢谢!!!!
18250谢谢!!!
18250好啊
18250Lz强
18250多谢楼主
18250给点数学分析!
182529月
18日-23日,应届生预报名
10月10日-31日,正式报名
11月10日-14日,现场确认
18254补充一下,对于g(Ii)的做法实际上对了g(y)的有理点处的函数值做了一个一一映射,但是g(y)是单调函数,那么它的不连续点至多可列个,我们可以将映射修改一下,即(x1,x2,y1,y2,x3,y3,...)x1,x2表示不连续点,y1=f(x1),这样的话即可以作出一个一一映射了
18254首先 R上的单调函数f(x)=arctg f(tgy)
=g(y),这样g(y)是开区间上有界的单调函数,并且f到g的映射是一一的。
假设我们考虑单调增函数g(y),y属于[0,1],这里可以在0,1点赋予g(y)适当的值
不妨设g(y)属于[0,1].我们一次将[0,1]n等分记所得的闭区间为Ii,那么g(y)在对应的Ii上的函数值也是包含于[0,1}的闭区间记作g(Ii),那么每一个单调函数就对应着这么可列个g(Ii)(i=1,2,...)这样就做出了一个g(y)到可列个闭区间的一个一一映射,剩下的推导就简单多了,最终讨论的结果是具有连续势
问题的关键是如何将原问题简化,首先是对于定义域和值域的简化,其次是对于单调函数的表示上,我现在也准备看实变泛函,有什么问题我们可以多多交流,qq=23087808
上面的证明可能有些繁琐,有些地方不严密,不过时间有限,也不想再去想了,应该可以简化和严密一些
18254设用m表示负无穷到正无穷上一切单调函数所成的集合,讨论它的势。
初学实变函数,觉得好难啊~~
bow
182542^C吧
18254每个常值函数对应一个实数,所以|m|>=|power set of
N|
而每个单调函数的值域可以用值域中的有理数来表示
就是单调函数集对应有理数的全部子集
|m|=<|power set
of N|
18254但是要是值域是( -

,

)怎么用有理数表示呢??bow
18254每个单调函数的值域可以用值域中的有理数来表示
不对吧
若是连续函数可以的,单调的不可以
18256以下就是一个规划问题:请大家多提出意见和观点,能解的尽量帮我解一下,谢谢!!!,好急呀
model:
sets:
aa/1..100/:c;
bb/1..20/:d;
link(aa,bb):x,a;
endsets
min=@sum(link(i,j):x(i,j));
@for(bb(j):@sum(aa(i):x(i,j)*a(i,j))<=d(j));
@for(aa(i):@sum(bb(j):x(i,j)*a(i,j))=3);
@for(link:@bin(x));
data:
d=8
1 22 10 8 40 40 1 8 15
19 20 10 2 5 8 30 10 8 38;
a=
0 0 2 0 0 0 9 1
0 5 7 0 0 8 0 3 6 0 0 4
1 0 9 0 0 7 0 0 4 0 0 2 0 6 3 0 0 8 5 0
0
6 0 0 0 7 0 0 0 0 0 4 1 3 8 0 2 0 9 5
0 0 0 0 4 0 7 6 0 0 3 1 0 5 9 0
8 0 2 0
5 0 0 0 0 4 7 0 0 9 0 0 3 0 2 8 6 0 1 0
4 0 6 0 0 8 0 5 9
0 0 3 0 0 1 2 0 0 7 0
0 0 6 3 0 0 1 2 8 0 4 0 0 0 0 5 0 0 9 7
3 0
0 0 0 0 0 8 0 0 7 9 1 2 0 6 0 5 4 0
0 3 2 9 0 0 7 5 0 6 0 0 0 0 1 4 0
8 0 0
7 0 0 0 0 0 0 6 0 1 4 2 0 0 0 0 5 3 0 0
0 0 4 0 0 0 0 1 0 2
8 0 3 0 5 0 0 6 7 0
0 8 0 0 4 0 7 0 0 6 2 0 5 3 9 0 0 0 1 0
8 0 0
0 0 5 0 0 2 0 0 9 3 0 6 0 4 0 1 7
7 0 9 0 0 3 0 0 0 0 0 4 6 0 0 1 2 5
8 0
4 0 0 0 0 0 1 0 2 7 6 5 0 0 9 0 3 0 0 8
3 0 9 0 0 0 6 1 2 0 4
0 0 0 0 0 7 8 5 0
2 7 0 1 0 0 5 4 0 0 0 0 0 8 0 0 3 6 0 0
7 5 0 0
0 0 1 0 0 0 3 0 9 0 0 4 8 2 0 6
0 5 0 0 0 7 0 3 0 0 8 0 0 0 2 6 1 0 4
0
0 0 9 0 4 2 7 0 1 8 0 6 0 0 0 0 0 0 5 3
0 0 7 4 0 5 0 0 3 8 0 0
2 0 1 6 0 0 0 0
0 4 2 0 6 0 1 0 0 0 3 5 0 7 0 8 0 0 0 0
4 3 0 0 0
0 0 0 7 9 5 1 2 0 8 0 0 6 0 0
5 0 9 0 0 0 6 3 0 0 1 0 2 0 7 0 8 0 4 0
6 5 0 0 0 0 0 0 0 8 0 0 7 0 2 4 1 9 3 0
6 8 1 0 0 5 0 3 0 7 0 0 9
0 0 2 0 4 0 0
7 1 0 0 8 3 5 0 0 2 0 4 0 9 6 0 0 0 0 0
0 0 0 7 2 0
3 6 1 4 0 0 5 0 8 9 0 0 0 0
0 7 0 4 5 0 0 1 0 8 0 6 2 0 0 0 0 0 0 3
0 0 1 0 0 0 0 4 3 7 8 0 0 6 0 5 2 0 0 0
0 0 0 0 0 5 3 6 2 4 0 0 8
7 0 1 0 0 0 9
7 0 2 3 6 0 0 0 5 8 0 0 4 0 0 1 0 0 0 0
0 1 0 0 0 0
0 0 8 0 5 7 4 0 0 0 0 6 3 2
3 0 0 0 0 0 8 0 4 5 6 0 1 7 0 0 9 0 0 2
0 5 4 0 8 0 6 0 0 0 0 0 7 0 2 0 3 0 0 1
0 0 4 0 0 0 8 5 1 0 2 0 0
0 0 6 7 0 3 0
3 0 4 8 0 5 0 0 0 0 2 1 6 0 0 7 0 0 0 0
0 4 2 0 0 0
0 5 9 7 1 0 0 3 0 0 0 0 8 6
0 0 0 0 0 0 6 0 1 4 0 5 0 7 2 0 8 3 0 0
6 5 2 4 9 0 0 1 0 0 0 0 0 0 7 0 8 3 0 0
6 4 5 0 0 0 0 8 0 2 0 7 0
0 9 0 0 1 3 0
4 0 0 3 0 0 5 0 0 0 0 0 0 2 1 8 7 0 0 6
9 0 0 0 0 0
0 3 4 8 0 6 0 7 1 0 0 5 2 0
3 0 0 2 8 5 0 0 0 0 0 9 0 4 0 0 6 7 1 0
4 0 0 0 3 2 8 0 9 0 7 0 0 0 5 0 6 0 1 0
4 0 9 6 0 7 0 3 5 0 0 2 0
1 0 0 8 0 0 0
0 0 0 0 2 1 0 0 0 0 3 0 0 8 7 0 6 4 0 5
0 0 5 0 0 6
1 0 3 0 0 0 0 2 0 0 8 7 0 4
7 4 6 0 3 0 8 0 0 5 0 0 0 2 0 0 0 0 1 0
1 0 0 5 2 3 0 0 0 0 0 0 6 0 0 4 0 7 0 0
9 0 2 0 0 6 7 0 0 0 5 0 0
4 0 8 1 3 0 0
1 0 0 2 4 0 0 8 0 0 7 0 0 0 3 0 5 0 0 6
7 0 0 0 0 0
4 6 0 2 0 5 0 8 3 0 0 0 1 0
0 3 0 0 4 0 2 0 0 7 6 1 8 0 0 9 5 0 0 0
1 0 0 2 6 0 0 3 0 0 0 0 0 0 5 4 0 7 9 8
0 8 1 6 0 0 0 5 0 2 0 0 0
0 7 0 0 3 4 0
0 5 0 0 2 0 1 3 0 4 6 9 0 0 0 0 0 8 7 0
9 8 0 0 0 0
0 0 6 0 0 0 2 3 0 4 1 7 0 5
0 0 0 0 7 2 3 0 0 0 8 0 0 5 0 6 9 1 4 0
2 7 0 0 0 0 3 0 5 1 9 0 4 0 8 0 0 6 0 0
0 0 9 2 0 0 6 5 0 0 0 3 0
7 4 8 1 0 0 0
6 2 0 1 9 0 0 0 0 0 7 3 0 8 5 0 0 4 0 0
6 0 2 0 0 0
0 0 8 0 3 0 4 7 5 0 0 1 0 0
7 0 8 2 0 1 0 3 0 0 0 0 5 0 6 0 0 9 0 4
0 0 0 0 0 0 0 0 1 0 3 4 5 0 7 0 0 6 0 2
4 5 0 2 0 0 6 8 3 1 7 0 0
0 9 0 0 0 0 0
0 0 6 0 1 7 0 0 0 3 0 0 0 0 5 0 0 2 8 4
9 0 0 1 0 3
7 0 4 6 0 0 2 0 8 5 0 0 0 0
3 8 0 0 0 9 0 0 0 2 7 0 5 0 0 4 0 6 1 0
1 0 3 6 0 8 4 5 0 2 0 9 0 0 0 0 0 7 0 0
0 0 0 7 3 0 0 0 2 8 5 0 0
6 0 0 4 1 0 0
0 0 0 0 0 3 0 6 9 1 0 2 0 4 0 8 0 0 7 5
0 4 0 0 0 0
0 0 8 1 2 0 0 5 9 0 3 7 0 6
0 0 0 1 0 0 0 6 0 0 3 8 0 0 2 0 4 0 7 5
6 0 4 0 8 0 0 0 3 7 0 5 1 0 0 2 0 0 9 0
2 3 1 0 9 0 0 8 0 7 4 0 5
0 0 0 0 0 6 0
0 0 4 0 8 7 0 0 0 2 0 0 6 0 1 0 0 3 0 5
8 2 3 0 0 0
0 4 0 0 0 0 0 7 9 1 0 6 5 0
0 0 0 0 5 0 1 8 0 0 0 9 6 4 0 0 7 0 2 3
0 0 8 7 0 2 0 1 0 0 0 0 3 6 5 4 0 9 0 0
0 9 0 6 0 2 0 0 0 7 4 1 0
3 5 0 0 0 8 0
9 0 0 0 0 0 3 2 0 0 7 4 1 5 6 8 0 0 0 0
4 0 2 0 6 1
0 5 9 3 0 0 0 0 0 8 0 0 0 7
4 0 7 0 0 3 0 2 0 5 0 0 8 0 6 1 0 0 0 0
0 0 0 4 0 0 1 0 0 6 5 0 0 0 8 0 2 0 3 7
0 0 1 6 0 4 0 7 0 8 2 0 0
5 9 0 0 3 0 0
0 0 0 0 1 3 0 0 6 5 8 2 9 0 0 4 0 0 7 0
0 9 0 2 1 0
0 0 0 6 0 8 0 4 7 0 3 0 5 0
3 0 8 0 1 2 0 0 0 7 9 6 5 4 0 0 0 0 0 0
0 6 5 8 0 3 0 7 0 0 4 2 9 0 1 0 0 0 0 0
0 0 2 8 5 0 6 0 1 0 3 0 0
7 0 9 4 0 0 0
8 7 0 0 0 6 0 5 0 0 0 2 0 0 1 4 3 0 0 0
3 8 6 0 4 1
0 0 2 0 0 7 0 9 0 0 5 0 0 0
3 0 6 2 0 4 7 8 0 1 0 0 9 5 0 0 0 0 0 0
0 0 0 6 5 0 1 7 2 0 3 0 8 0 0 0 0 4 9 0
0 9 6 0 0 4 0 7 1 0 0 0 0
0 5 0 3 0 2 8
7 1 0 0 8 9 0 0 6 0 4 2 0 3 0 0 0 0 0 5
1 0 0 0 0 2
7 0 0 4 0 0 0 6 0 8 0 3 5 0
0 1 4 0 6 0 5 0 9 0 8 0 2 3 0 0 0 7 0 0
0 0 0 5 4 0 0 7 1 6 0 0 0 0 0 3 8 2 0 0;
enddata
end
18257数列极限的定义:先定义极限点(数列{Xn}的某一个子列收敛的数值),然后所有的极限点构成一个集合,这个集合中的最大值就是上极限,最小值就是下极限,当二者相等时,就说数列有极限。
仿照上述模式能否这样定义集合的极限:
集合A1、A2、…An…中,某一个子集合列收敛于集合Ai,这个集合看作为一个极限点,然后所有的极限点构成一个集合,这个集合中的最大值就是集合A1、A2、…An…上极限,最小值就是下极限…
能否这样定义呢?我觉得这样定义容易理解
可教科书的定义是:
集合的上极限:{x,有无穷多个n,x属于An}
集合的下极限:{x,有有限个n,x不属于An}
两种定义是一样的吗?表面上看差距太大了,理解不了:(
望高人指点,谢谢
18257没有拓扑你怎么定义子列的收敛性
不过确实可以定义单调子列的收敛性
你的定义和书上的定义是不同的
在拓扑空间中,集列的极限还有其他的定义,在集值映射
的研究中很有用
18257所谓集合收敛于是什么意思呢
你说的那个收敛的定义其实有另外用交并来表示的形式
那个就很好理解,而且看懂了之后你会知道集合与数列极限之间的定义有什么不一样了
18257谢谢,明白了.关键是集合之间的"距离"没有定义:)
18259考研心理素质真的很重要啊!我现在才深深的体会到了啊!
18259本来感觉学的不错了,但是做了一些题,感觉还不如以前了,真是倒退了!看 来还要继续努力啊!
18259是啊。数学这个东西必须经常练习才行。
你一不做题目就会生疏了!
18259继续努力吧
18259是啊我也有同感啊
有没有好的学数学的方法啊 做题是一方面啊 有时一道题解不出来真是烦人啊
我自从高中时就做十分多题
可是太累了啊 有没有取得成功的捷径啊
18259继续努力啊
18259学数学是需要感觉和激情的,那是一种平静的激情和心如止水的感觉!我们都需要继续努力!正如马爷爷说:要从"暂时的方面去理解一切事物",一切皆过程!
18260居我观之
要做完季氏数分习题集.
和杨子婿边的高代习题集.
另外,老2那本高代复旦的(姚文僧编的)讲了一些什么特征直的估计,谱...值得去看,以求能更好把握高代.
友情提示:高代特难,有超纲的知识点,要看一些特别书籍辅导.
18260中科院的高代真的很难?我虽然手头上有一些其考试题目,可至今还没好好看呢。假如真的那样难,那我得看一些研究生的代数学方面的书了,谢谢提醒呀!
18260得好好准备
18261
“勒贝格的工作是20世纪的一个伟大贡献,确实赢得了公认,但和通常一样,也并不是没有遭到一定阻力的.
”──克兰
“对许多数学家来说,我成了没有导数的函数的人,虽然我在任何时候也不曾完全让我自己去研究或思考这种函数. ”
──勒贝格
勒贝格是法国数学家.
1875年6月28日生于博韦;
1941年7月26日卒于巴黎.
勒贝格在博韦读完中学后,于
1894年入巴黎高等师范学校攻读数学,并成为博雷尔的学生,
1897年获该校硕士学位.
毕业后曾在南希一所中学任教.
1902年在巴黎大学通过博士论文答辩,取得哲学博士学位.
1902—
1906年任雷恩大学讲师.
从
1906年起先后在普瓦蒂埃大学、巴黎大学、法兰西学院任教,
19
19年晋升为教授.
1922年当选为法国科学院院士.
1924年成为伦敦数学会荣誉会员.
1934年被选为英国皇家学会会员. 他还是前苏联科学院的通讯院士.
勒贝格是20世纪法国最有影响的分析学家之一,也是实变函数论的重要奠基人.
勒贝格的成名之作是他的论文《积分,长度,面积》(
1902年)和两本专著《论三角级数》(
1903年)、《积分与原函数的研究》(
1904年).
在《积分,长度,面积》中,第一次阐明了他关于测度和积分的思想.
他的工作使
19世纪在这个领域的研究大为改观,特别是在博雷尔测度的基础上建立了“勒贝格测度”,并以此为基础对积分的概念作了最有意义的推广:即把被积函数f(x阿)定义的区间分成若干个勒贝格可测集,然后同样作积分和,那么原来划分子区间方法的积分和如果不收敛,则现在划分为可测集的方法就有可能收敛.
于是按黎曼意义不可积的函数,在勒贝格意义下却变得可积.
他在《积分与原函数的研究》中还证明了有界函数黎曼可积的主要条件是不连续点构成一个零测度集,因此从另外一个角度给出了黎曼可积的主要条件.
要想从一个不太抽象的角度,用几句话就能概括勒贝格测度和勒贝格积分的概念及其在近代数学中的巨大作用,是极为困难的.
可以这样说,大家熟知的黎曼积分有如下若干缺点,严重地限制了积分概念在自然科学中的应用.
第一,黎曼积分中的被积函数只能是定义在实直线R的闭区间上(或Rn的闭连通区域上)的实值函数,但实际上有用的函数f
,其定义域可以是R或Rn的某些适当的子集. 第二,黎曼可积的函数类甚为狭小,基本上是“分段连续函数”构成的函数类.
第三,许多收敛的黎曼函数序列,其极限函数却不是黎曼可积的,即使是黎曼可积的,但积分与求极限的过程也不是随便可交换的.
这些缺点不仅在泛函分析中导致严重困难,而且在无穷级数的逐项积分这种简单问题上也导致了严重的困难.
正是勒贝格在20世纪初开创的这些工作为扫除这些障碍提供了理论工具.
按照勒贝格意义下的积分,可积函数类大大地扩张了;积分区域可以是比闭连通域复杂得多(R或Rn)的子集;收敛性的困难大大地减少了.
勒贝格曾对他的积分思想作过一个生动有趣的描述:“我必须偿还一笔钱.
如果我从口袋中随意地摸出来各种不同面值的钞票,逐一地还给债主直到全部还清,这就是黎曼积分;不过,我还有另外一种作法,就是把钱全部拿出来并把相同面值的钞票放在一起,然后再一起付给应还的数目,这就是我的积分.
”
勒贝格积分的理论是对积分学的重大突破.
用他的积分理论来研究三角级数,很容易地得到了许多重要定理,改进了到那时为止的函数可展为三角级数的充分条件.
紧接着导数的概念也得到了推广,微积分中的牛顿—莱布尼茨公式也得到了相应的新结论,一门微积分的延续学科—实变函数论在他手中诞生了.
勒贝格的理论,不仅是对积分学的革命,而且也是傅里叶级数理论和位势理论发展的转折点.
勒贝格还提出了因次理论;证明了按贝尔(Baire)范畴各类函数的存在;在拓扑学中他引入了紧性的定义和紧集的勒贝格数.
他的覆盖定理是对拓扑学的一大贡献.
美国数学史家克兰(kline)说:“勒贝格的工作是本世纪的一个伟大贡献,确实赢得了公认,但和通常一样,也并不是没有遭到一定的阻力的.
”例如,数学家埃尔米特曾说:“我怀着惊恐慌的心情对不可导函数的令人痛惜的祸害感到厌恶.
”当勒贝格写一篇讨论不可微曲面《关于可应用于平面的非直纹面短论》论文,埃尔米特就极力阻止它发表.
勒贝格从
1902年发表第一篇论文《积分,长度,面积》起,有近十年的时间没有在巴黎获得职务,直到
1910年,才被同意进入巴黎大学任教.
勒贝格在他的《工作介绍》中感慨地写道:“对于许多数学家来说,我成了没有导数的函数的人,虽然我在任何时候也不曾完全让我自己去研究或思考这种函数.
因为埃尔米特表现出来的恐惧和厌恶差不多每个人都会感觉到,所以任何时候,只要当我试图参加一个数学讨论会时,总会有些分析家说:‘这不会使你感兴趣的,我们在讨论有导数的函数.
’或者一位几何学家就会用他的语言说:‘我们在讨论有切平面的曲面.
’”但到了20世纪30年代,勒贝格积分论已广为人知,并且在概率论、谱理论、泛函分析等方面获得了广泛的应用.
勒贝格具有基于直观几何的深刻洞察力. 他的工作开辟了分析学的新时代,对20世纪数学产生了极为深远的影响.
他的论文收集在《勒贝格全集》(5卷)中.
在数学中以他的姓氏命名的有:勒贝格函数、勒贝格测度、勒贝格积分、勒贝格积分和、勒贝格空间、勒贝格面积、勒贝格准则、勒贝格数、勒贝格点、勒贝格脊、勒贝格链、勒贝格谱、勒贝格维数、勒贝格分解、勒贝格分类、勒贝格不等式等,而以他的姓氏命名的定理有多种.
18262欢迎下载及提供其它高校05年试卷,注意WORD中还有图片,打开可能很慢,要有耐心呀!这些都是大家提供的,为了方便下载,我把它们合并起来了post-60-1126975773.ibf
18262北大2005高等代数与解析几何post-60-1126977
184.ibf
18262南京理工大学2005年高等代数试题post-60-1126977248.ibf
18264请问哪里有专门介绍大数定理的书或电子资料?谢谢。
18264
引用 (ipv6 @ 2005年09月
18日
01时54分) |
|
请问哪里有专门介绍大数定理的书或电子资料?谢谢。 |
极限理论方面的书籍即可。
18265各位谁有实分析和拓扑方面的教材和习题集请告诉小弟好吗,我急作题.....谢谢
膜拜....
发给我willberain@163.com
qq 404690072
MSN jie_joe@hotmail.com
多谢多谢
18265本论坛的网络资源屋就有!
Buffalo_hua 提供了一很好FTP站点
ftp://math:math@202.103.207.135/mathbook
18269用SPSS对一组数据进行K-S检验,得到关于正态分布,均匀分布和指数分布的结果
关于正态分布的结果为:
One-Sample
Kolmogorov-Smirnov Test
VAR00001
N 6
Normal Parameters Mean
10.1667
Std. Deviation 10.83359
Most Extreme
Absolute .246
Differences Positive .246
Negative
-.
199
Kolmogorov-Smirnov Z .602
Asymp. Sig. (2-tailed) .861
a
Test distribution is Normal.
b Calculated from data.
关于均匀分布的结果:
One-Sample Kolmogorov-Smirnov Test 2
VAR00001
N 6
Uniform Parameters Minimum 1.00
Maximum
27.00
Most Extreme Absolute .423
Differences Positive
.423
Negative -.167
Kolmogorov-Smirnov Z 1.036
Asymp. Sig.
(2-tailed) .233
a Test distribution is Uniform.
b Calculated
from data.
指数分布的结果:
One-Sample Kolmogorov-Smirnov Test 3
VAR00001
N 6
Exponential parameter.Mean 10.1667
Most Extreme
Absolute .244
Differences Positive .244
Negative -.
193
Kolmogorov-Smirnov Z .599
Asymp. Sig. (2-tailed) .866
a
Test Distribution is Exponential.
b Calculated from
data.
请问这组数据是服从哪种分布???
为什么???
18272请高手帮忙解决二道数分考研题post-21-1127006549.ibf
18272我觉得那本书上的题都很难
老师说八几年的考研题没有半个小时是做不出来的
有心无力啊
当初我也就只是吧例题都做完而已啊
18272谢谢各位大虾的帮忙!
18272第一个题目是错的,第二个现在还没有解法:post-21-1127043921.gif
18273wo xuyao
18273Thank you very much!
18273信箱密码已经被改了吧,我上不去,下载不了,谁能共享一下阿
我的邮箱bluemyosotis@eyou.com
18273将文档转到“ 收 件 箱”就可以下载了!!!
我已经转了!!
太谢谢了!
18273郁闷啊,怎么能上传的文件大小这么小啊.所有答案都放在下面邮箱的草稿箱里面,需要者可自行下载.
E-MAIL:
bohemian_l@126.com 密码:bohemian.
呼呼同学,我的这个帖子是否可以算个精华贴呀,可要多给我点奖励啊,呵呵
回复:奖励100分!另:大的附件论坛无法承受,建议上传到你的这个邮箱共享!中秋快乐
18273
引用 (bohemian @ 2005年09月
18日
09时23分) |
郁闷啊,怎么能上传的文件大小这么小啊.所有答案都放在下面邮箱的草稿箱里面,需要者可自行下载.
E-MAIL:
bohemian_l@126.com 密码:bohemian.
呼呼同学,我的这个帖子是否可以算个精华贴呀,可要多给我点奖励啊,呵呵
|
收到, 可是怎么给你加分呢? 我愿意给你加100分!
18273太强了, 请问您还有其他课程的教案吗? 比如: 实变(程其襄), 常微分(??), 复变.
最好有 实变
18273
引用 (bohemian @ 2005年09月
18日
09时23分) |
郁闷啊,怎么能上传的文件大小这么小啊.所有答案都放在下面邮箱的草稿箱里面,需要者可自行下载.
E-MAIL:
bohemian_l@126.com 密码:bohemian.
呼呼同学,我的这个帖子是否可以算个精华贴呀,可要多给我点奖励啊,呵呵
|
如何下载啊??
18273非常感谢,不过答案2解压后不能用!?
18273很是感谢!!!
18273感谢阿感谢!!!
18273多谢了,呵呵!!
18273非常感谢
18273thank u very much!
18273非常谢谢!!!
18273很是感谢!!!
18273Manymany Thanks!


18273在陕西师大出版社出了这个的书,可以买嘛,在网上下怎么下得完,600多页呢!!!1
18273非常感谢!!!!
18273好东西呀,我已经下载收藏了,谢谢楼主的热心!!!!
18273谢了
18273thanks a lot.
18273kiss
18273谢谢!
18273太强 了!
18273谢谢了
18273可以呀。谢谢了
18273非常感谢楼主。
18273怎么是空箱啊?
18273有这么好的大哥!!!多谢呀!!!
18273信箱空了,不知道谁删了
18273非常感谢
18273还有没有
18273加分!!!

18273好样的 !不错我所需要的东西!
18273你的答案太好了,希望多往上面放点呀
18273好像没有了吗
18273被人删除了啊,那位大哥可以发我邮箱吗?谢谢
cumtzhyq@163.com
18273真可惜,被谁删了,楼主能不能再发一下
18273哪个家伙不仗义,居然删了楼主的东西!楼主能不能重发?
18273怎么不能进去阿,哪位好心人能给我一份吗?我的E-mail:huangxing9
19@tom.com
谢谢!!!!
18273楼主,好象邮箱里没有耶?干脆你发到我邮箱里来吧,楼主你真是大好人馁!
我邮箱是
kaoyan511@yahoo.com.cn
谢谢啊。。。
18273里面是空的,楼主再给我发一个吧 wskpl220@163.com
谢谢了
18273里面是空的,楼主再给我发一个吧 khfangli@163.com
谢谢了
18273我也需要,好心人给我发一份吧
hzmtom@163.com
18273是空的拉 ,那个好心人给共享一下阿
aceviolet@163.com
18273去了126信箱,怎么没有啊。如果可以,给我也发个答案吧。
liushui_888@hotmail.com
谢谢!
18273是不是有人给删了啊,里面什么也没有了
18273是啊。我想要啊。楼主。可不可以发到我邮箱里:
huanglikun@gmail.com
谢谢!!!!!!!
18273我想要啊。楼主。可不可以发到我邮箱里:
oybp
1979@gmail.com
谢谢!
18273楼主,邮箱打不开耶?你发到我邮箱里来吧,求你拉, 楼主你真是大好人馁!
我邮箱是
windvoice@126.com
谢谢啊。。。
18273求 数学分析参考答案(华东师大版) 答案
跪求楼主发去我的邮箱 windvoice@126.com
18273发给我一份吧,多谢了
chungang_zhu@yahoo.com.cn
18273楼主,你是大好人.往我油箱里发一份吧
cyyaao@yahoo.com.cn
各位有的也可以发呵
不胜感谢!
18273谢谢
18273跪求楼主发去我的邮箱
beyondhe2008@163.com
18273
我去了那个邮箱,进不去呀
楼主,你是大好人.往我邮箱里发一份吧
yyh_
1977@eyou.com
各位有的也可以发呵
不胜感谢!
18273我最近急需该书的答案,希望得到大家的帮助。告诉我下载的地址。如果你有的的话,也可发送到
我的邮箱lxd230@eyou.com。在此,我先谢谢各位了。拜托,兄弟姐妹们。
18273求助华东师大版数学分析答案
18273楼主,你是大好人.往我油箱里发一份吧
chengji306@163.com
各位有的也可以发呵
不胜感谢!
18273不错,
18273楼主好,各位楼上的好:
我来晚了啊,看不到资源了啊,有好心人能不能帮我发一下,我的邮箱是
jianmowww@yahoo.com.cn,谢谢各位了!!!
18273非常感谢啊。
我在网上找了好久了。
泪。。。
18273很久没有登录那个邮箱了,今天发现我也没法登录了,呵呵,承蒙哪位仁兄看的起,令小弟受宠若惊!由于文件过大,需要的兄弟轻耐心等候,我再去申请个大点的邮箱,或者哪位兄弟有比较好的ftp也可以,望告知!
回复:
bossh@56.com
请大家把需要交流的电子资源发到此信箱,斑竹会定期整理发布.
您可以在网速较快的时间下载共享.
56邮箱容量为:2g
附件:15m 速度挺快的
注册地址为: http://www.56.com/bossh
18274但是x^(1/2)在x=0的时候,值是有限的。
如果,在x->a,f(a)存在且有限,那么也应该是一致收敛的
18274蓝戈里边::令
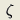
=

^(-1/2),便得到差值>1/2,对任何

,都有x>
时````好基本哦
18274函数的一阶导数在无穷处有有限极限是函数一致收敛的必要条件吗post-38-1127007230.gif
18274!!!post-38-1127008984.gif
18274函数一致连续不一定一阶导数在无穷处有极限
eg.f(x)=sinx (0,+

)
18274此处导数在x->

的时候趋于正无穷,所以是不一致连续的。这一点用导数的定义就可以证明了。
至于,如果,导数趋近于无穷,或者,当导数的振荡越来越大的时候,我觉得不是一致收敛的
18274X^1/2 在[0, +infer )
上一致连续但导数趋于无穷在零点附近
18275请问一下:在VC编写的软件中可以调用lingo做规划吗??
怎么调用有没有相关的教程..谢谢
18277没有思路!post-38-1127013965.gif
18277存在两个点列分别趋近与正负无穷大,使它们的

极限为零,则存在一点

'为零
18277用反证法,如果不存在这样的点,则f'(x)是单调的,从而容易知道若
f'(x)=0不恒成立就有f(x)无界,如果f'(x)=0恒成立,自然就存在f''(x)=0,产生矛盾,所以就得到了证明了!
18279求post-38-11270
17526.gif
18279存在点列趋于无穷时,

为零,则根据

(x)-

(y)
=

'(z)(x-y)
<M
x-y
,得怔
18279是不是可以这样啊?post-38-11270
19540.gif
18279
| 引用 |
iii
存在点列趋于无穷时, 为零,则根据
(x)- (y) = '(z)(x-y) <M x-y
,得怔
|
有问题吧,只是证明一致连续!而不是符合cauchy收敛定理!对不对啊?
18279是地拉,我错地一塌糊涂
你会做嘛,还问
18279刚想出来,呵呵
18280求助:
model:
sets:
man/1..100/;
dvd/1..20/:c,d;
links(man,dvd):a,b;
endsets
min=@sum(links:a*b);
@for(links:@bin(b));
@for(dvd(j):@sum(man(i):b(i,j))<=c(j));
@For(man(i):@Sum(dvd(j):b(i,j))=3);
data:
c=@file('D:\file1.txt');
b=@file('D:\file2.txt');
d=3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
3 3 3 3;
enddata
end
看看是否有问题啊
18280有的
不能运行
好象是条件不够
18282已知S集合{1,2,3....99,100}
若它的一个10元子集中的元素由小到大排列呈奇偶相间的排列则称该子集为交错集
求S集合中有几个交错集
希望那位GGJJ帮忙,非常感谢
18282这样做对不对?
首先,两两相邻数之间的差是一个奇数,且这些奇数的和小于等于99
不妨设,这9个奇数为(2k1-1),(2k2-1),(2k3-1),...,(2k9-1)
得到k1+k2+...+k9<=54,ki>=1
用隔板法,在54个空间内插9快板,将其分为10各部分,k1~k10
k1,k2...,k9>=1,K10>=0
满足条件,所以答案是不是C(54,9)
18282楼上的果然是个强人呀。
18283日,没我们学校
18283路过,没决定呢,就怕考不上!
18283我报太原科技大学的应用数学,刚成立2年
18283天津大学应用数学
18283我想报北师大啊!
今年北师大改革了,要考高代,数分,复变,常微,概率统计。
小郁闷!
有没有战友啊?
18283哪里啊?!
大家一起努力吧。希望大家都能考上!
18283我报的是中山的运筹,好难啊。大家一起努力吧
18283楼主,我报的是系统所里面的复分析。
18283你们好牛啊!又是中科院,又是复旦浙大,偶为了和女朋友一起考上同一所学校,选个不太好的!:(华中科技5555555555555555555555555555555
18283大家都写出自己报考的学校吧,那样估计更有利于大家复习。知道自己在报考自己的那个学校的人中的地位。
我先说吧,我报的中科院!中科院的数学与系统科学研究院!报考的方向是:数学物理方向的研究生
努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力努力
18283我思来想去,报了复旦的概率与数理统计(是管院和数学系一起开的)
18283我想考浙江大学概率论与树理统计,好怕哦```
18283我想考北京理工的运筹学与控制论
18283为什么看的那么多,没有几个回帖子的呢?是有什么原因吗?
还是懒得写那么几个字呢?
晕哦
18283因为这里没那么多牛人,不好意思撒!
18283大家继续啊!
怎么没有人写呢?
18283牛人面前安敢放肆!
18283努力!
18283我考中山,计算数学!
18283我包得学校咋没有
18283武汉大学概率统计
18283中大◎_◎
18283我想报中科院上海光机所,不知道有没有战友一起呢?不认识导师,不了解情况,好害怕考不上,有战友的话,大家交流一下经验啊!!我的邮箱:chenlei820902@126.com
18283我报中山大学,基础数学
18283我上次看了看,没投票啊!怎么说我已经投过票了????
18283
| 引用 (whongye @ 2005年09月28日
10时23分) |
| 我报南开,急寻战友
|
我也报南开 QQ 7152471 寻战友
18283我想考中科院系统科学学院的基础数学研究所的集合论
18283牛人太多,真是不敢多说!我想报山大!!但是他们又都指定自己的学校编的书,真郁闷!!
18283我想想还是报苏州大学,那些好学校压力实在太大
18283哈工大
18283毕业学校不好,加上感觉自己底子比较弱,准备报考一个小点学校,
18283我怎么记得是10月8号
18283浙大运筹
18283实力有限啊!我报考西华师范大学!!!不要笑我啊
18283我考北大!
(我不考了,很抱歉投票了)
18283路过看看
18283我报南开,急寻战友
18283感觉到了自己的压力之大了,这里有几位还没有露面的考中科院的老兄!
真晕,我都露了这么多了!看来不能够再来这里了,没有想到有许多高手都不屑于来这里!
我也开始自己忙自己的去了,懒得在这里瞎忙乎
18283呵呵,我也考中科院数学所!
看来这里考中科院的也不少啊!
郁闷,是不是都有把握哦?我知道我笨,不过也想追求一下,要考就考最好的,最难考的!呵呵,初生牛犊不怕虎!
18283我要考浙大的基础数学,希望可以成功,大家祝福我吧!
18283浙大数学研究中心也不错,丘成桐办的那个,里面全是不错的导师,都是从美国的大学聘请的,丘成桐也亲自挂帅
18283我要回家,所以我要考华中科技大学,考概率与数理统计,战友加QQ:
181292407
18283哎呀!@
考华东师大运筹学与控制论 拉!
有同行吗?qq103373429




18283看来这里的朋友中考北大的和中科院的人比较多啊!
呵呵,我倒是想知道今年有几个能够圆梦!哎,也不知道如果那些考中科院和北大的人如果考不起打算干什么呢?我现在一直被这个问题困惑着,如果我考不起中科院,我会后悔死了,如果心不高,随便报个稍微差些的学校,应该是可以稳上的!哎,真他妈的晕!
想象高考自己报的北京航空航天大学,准备致力于中国航天事业,却没有考取,之后被这个二类大学录取了,心里就想,如果考武汉大学,我就肯定可以上了,只是自己的心太高,要求太多,所以才会有这样的后果,来到这样的二类垃圾学校混日子,搞得自己越来越没有什么优势了!
不知道这里的朋友有几个会像我高考那样的感觉呢?到明年的三月份看吧,那个时候就什么都知道了!参加复试的,就是成功了一大半,没有资格参加的,就等待去这样思考吧,或者家里有资本,可以玩个一年,重新来过,只是可惜我家里穷,必须今年考取,要不然工作就不好找的!
努力,努力!
呵呵,我现在的复习效果还行,基本上数学和英语没有什么问题了,主要就是政治了,十一月份开始正式搞政治了,英语希望自己可以突破到70分以上!
18283有谁报
18283因为懒得计较来计较去!恰好南开的教材和我的一样!虽然自己很"菜",但是还是考南开吧!只有拼死了!
18283如今大家有改变志愿的吗?都已经确定了吗?还有不到半个月的时间就什么都定了,再也改不了了啊!
呵呵!我希望看到最终大家都是什么个去向,反正我现在知道有几个朋友的志愿是改了,一个已经保送了,一个从中山改为了考北大,而且这位朋友是铁了可以上了!
18283
| 引用 (czy @ 2005年10月14日
04时33分) |
我想报北师大啊!
今年北师大改革了,要考高代,数分,复变,常微,概率统计。
小郁闷!
有没有战友啊?
|
我考啊
lee_vincent@163.com
多多提携我啊。
18283大家都好有志向呀!以前高中想学工学,志向是华科,结果选择拉理学,所以我现在选择拉武大计算数学,为完成自己的梦想去奋斗吧!大家加油!
18283各位师兄,现在的学校太差,不知在07年中科院有无希望?
18283
引用 (zhubin846152 @ 2005年09月
18日
14时08分) |
|
我思来想去,报了复旦的概率与数理统计(是管院和数学系一起开的) |
一定要逼开你这样的大牛呀~~~
18283我报华科的非线性发展方程,这个方向怎么样?
18283思考了很久很久,报了西安交通大学的信号与信息处理,准备硕博连读得了!!
18283我第二专业学的是数学,准备当几年老师后考北大数学!!
18283浙大数学系在全国高校排名怎么样??
18283相当之靠前!
18283走过路过,顶下
18284lingo中怎么实现不等于约束?
a!=b 用一个语句约束
18285小弟初来, 数学一般,被这样的一道题难住了
如果0<=x , x是真数(real number),而且x<=e
,所有的e>0,
证明 x=0
18285real number 是实数,不叫真数,
用反证法,几乎是显然的
呵呵
18285楼主不懂国语
18287RT.
18287
引用 (wenheping @ 2005年09月
18日
16时09分) |
| RT.
|
histogram?
probability plot?
18287把数据录入eviews,3秒就搞定
18288RT
18289RT.
18289先产生(0,1)随机数u1
u2
正态
x1=(-2lnu1)**(1/2)*cos(2*u2*2*pi)
x2=(-2lnu1)**(1/2)*sin(2*u2*2*pi)
18289matlab里有 现成的产生正态随机数的函数
18291设A,B为两等价的线性无关向量组,(基数有限)
任意交换A,B中的两向量得到向量组C,D
证明或否定以下结论:
1
A等价于B等价于C等价于D
2 C,D的向量个数相等
不要利用线性方程组的结论
18291我认为都不正确!
e1=(1,0,...,0)'
e2=(0,1,...,0)'
...
en=(0,0,...1)'
------------------------------------------------------
a1=(1,0,...,0)'
a2=(0,1,...,0)'
......
a(n-1)=(0,0,...,1,0)'
an=(1,0,...,1)'
e1和an交换以后,是不是就C,D的个数不相等啊!
18291你还
没看懂题意
18291好像B与C未必等价(上面的例子可以说明这个)
C与D的个数相等好像没什么问题
现在需要看的就是C与D是不是等价了
18292a,b 为两向量组,均线性无关且个数相等
证明:a中每一个向量都不能由b线性表出当且仅当b中每一个向量都不能由a线性表出
18292不对吧
取b={(1,0,0,0),(0,0,0,1)},a={(1,1,0,0),(1,2,0,0)}
那么a中的向量都不能由b中向量线性表出
但是b中向量可以由a中向量线性表出
:)
18292是呀,我在改一下原题
18292
引用 (流形 @ 2005年09月
18日
17时59分) |
| 是呀,我在改一下原题
|
我也同样改了一下反例
好像你还得改原题
:)
18292hehe ,不改了
18293已知{

1,

2

,

n}线性无关,且可由{

1,

2,


n}线性表示
证明:存在某个

k,使得{

k,

2,

3,

,

k}线性无关。
18293这就是有名的替换定理
用反证法证明
18293呵呵,
是呀,好像是楼主弄反了
把
β 和
α 换一下
就是替换定理了
18293
那样不一定行
由题干,两向量组等价
只要且应该取{

1,

2

,

n}中不同于杠alpha
1的向量即可,显然那样的向量是存在的(当然有条件n>2)
当n=1是显然成立的
18293呵呵。我发的太早了。你再看上帖
18293设两向量组除编号不同外,元素相同

1=

2
不就相关了?
只要且应该取{

1,

2 ,

n}中不同于杠alpha
1的向量即可
18293看来都误会了,你的意思是向量组中个数为1的情况,大于1 的时候那样就不一定对了
18293清高手将详细过程写出来,谢谢!!
18293我看不懂你们说的!谢谢各位大侠,给处答案
18293这道题目不是那么难啊!!!!!!大家都怎么回事啊?????post-38-1127039379.gif
18293没有问题,它是天津大学2003的高代考研题
18293太感谢啦!!!
18293有问题,不能有蓝戈说的。它们只是线形无关,没说都A可用后面的B向量表示(对不起,我这里不能显示符号,这里用A,B
代替)
反正法:
有N个式子,最后可以消去后面的N-1个B向量,得到前边的A是线形相关的这,是不成立的。
18293这就是替换定理:若向量组I

1,

2,...
,

n线性无关,向量组II

1,

2,...
,

m也线性无关,且
可由I线性表出,则必存在

k,
使得

k,

2,...
,

m也线性无关且m<=n.
反证法: 若不然,则向量组I可由

2,...
,

m线性表出,又

1可由向量组I线性表出,从而

1可由

2,...
,

m线性表出,即向量组II
线性相关,与题设矛盾.
为证m<=n,反证,设 m>n,于是又第一步的逻辑可逐步替换,得到线性无关组

1,

2,...
,

n,

n+1,...
,

m.
而

n+1,...
,

m均可由

1,

2,...
,

n线性表出,与线性无关矛盾. 证毕
18293进一步的能否有:
对向量组I,II,
存在

i,

j,使得交换两向量得到的向量组I',II'同时线性无关?
更进一步的能否有:
存在

i,

j,使得交换两向量得到的向量组I',II'分别和向量组I,II
等价?
诸如此类
18295同意你的观点!
努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!努力,热身!
18295矩阵A,B可交换,求证:R(A)+R(B)〈=R(A+B)+R(AB)其中R(A)表示A的秩.
望用矩阵的变换得到解答.
18295?????post-38-1127040988.gif
18295堪称绝啊!
佩服佩服!不过你的这个矩阵变换好象十分特殊,不好想到啊,没有足够的洞察力是无法想到你这样的变换方式的!
18295一般教材上对分块矩阵的运算以及分块初等变换讲得稍弱了一点,
考研复习时要有针对性地加强练习和“热身”。此乃一已之见!
18295这下好象没有用题目中的可交换的结论,不知道是否这个条件是否多余的!post-38-1127049257.gif
18295再补一点!post-38-1127050
193.gif
18295题目贴错了,要证明的结论应为:
R(A)+R(B)
≥
R(A+B)+R(AB)
附件是我的解答。post-38-1127055704.ibf
18295谢了,兄弟们
18295蓝戈的解答我看不懂,是不是错了?
18296如果在最大流问题中,多个边容量受线性约束,比如其中某两条边的容量C1,C2,满足:k1C1+k2C2=A,其中k1,k2,A都为常数,在这种边容量受线性约束可变情况下,有没有较好的求解最大流的方法?
如蒙赐教,不甚感激。
18296可以转化为线性规划求解。
这个方法笨一些。
不过我想不出别的好办法。
你最好把原题写出来,也好看的懂。
18296我最近也在看和最大流有关的论文
primal-dual+FPTAS
可否一起交流?
QQ:361006247
18296
真这有趣,我也想参加,
我是即将搞最优化方面的,最字对我来说,特别的敏感,
我希望大家以后多聊聊有关最优化运用方面的,谢谢。
18296觉得用线形规划是个好办法,可以这样算法就不是一个组合的算法了
18298需补充条件:A是实矩阵。
18298r(A)=r(A*A的转置)
18298同解
另外,求这个问题的几何解释
18298同解,什么意思?同志们快帮忙看看啊,顶一下
18298
引用 (jjping @ 2005年09月
18日
21时50分) |
|
同解,什么意思?同志们快帮忙看看啊,顶一下 |
xA=0 <=> xAA'=0
这就是同解
18298另外,求这个问题的几何解释
18298矩阵轮的书好象有
18298谁能给具体证一下
18298这是丘维声编《高等代数》中的一个命题,详细的证明过程见:丘维声编《高等代数》(上册)p.
184,命题4.5.1的证明.
18298令W={X,AX=0},V={X,A'AX=0},则可证W=V,从而秩A=秩A'A=秩AA'
18298这是很常用的一个结论
我才复习了一个星期,也会:)
18298上面的说的很正确,不过我想一般现在的研究生考试是很少考这样重要结论的题目的,不过也说不准!
18299感谢
18299
引用 (蓝戈 @ 2005年09月
18日
21时41分) |
| 第一问的解答!
|
这步我做不出post-38-1127109997.ibf
18299见下:post-38-1127048834.ibf
18299第一问的解答!post-38-11270509
18.gif
18299第二问的!post-38-1127051100.gif
18300我是山大信息安全的学生,我想考中科院,一个是本部,一个是软件所,分别要考近世代数,另一个是密码学,网络安全计算机安全。我想问一下考近世代数的会不会很多?
18302!!!!!!!!!!!!post-38-1127060444.gif
18302裴礼文《数学分析中的典型问题与方法》post-38-1127059882.ibf
18302第二问证明求和式极限为2/(1+x^2)在0~inf的积分式即可,结果大概是pi吧
18302第二题应该用
π t∏ n
=1 ∞
(
1+t
2 n
2
)=sinh(
πt ) ,两边取对数再求导即得
1 t
+∑
n =1
∞
2
tt
2 +n
2=πcoth(
πt )
18302看见第二种方法了^_^,大家继续
18302拜托高手能不能写详细些!
谢谢!
18303请辞中级顾问:tobyqin
理由:来了快四十天了,想出去走走,不能为大家解答什么题目了,头衔也就名不副实了
在这里认识了一些朋友很开心,特别要感谢 呼呼
的支持和帮助!
btw:自删贴至100以示纪念(基本都是在不该灌水的论坛上灌水的文章)
我回来了
有空会常来得!
不过得过了这个寒假
后天回家
回复:希望常回来看看!保留顾问头衔。
183111,If 0 ≤ x ∈ R and x ≤ ε for every ε > 0, prove that x =
0
2,Let x ∈ R. Prove that sup{r ∈ Q|r < x} = x
18311第一个:不妨设x>0,产生矛盾!!
第二个:由实数的稠密性可得!!
18311实数集R是一个具有最小上界性的有序域,以上两个问题都可以利用这一性质加以证明
18311同意浅尝辙止的解答,建议去看看戴德金的实数分割理论
18313欢度中秋,勿忘国耻
月圆神州情
勿忘国耻恨
9.
18
中秋何处月最美
中秋赏月是我国传统的民间习俗。中秋之夜,明月高悬,边赏月边闲聊,其景融融其乐也融融。华夏神州赏月绝佳之地有40多处,择其最负盛名之地供您品味。
平湖秋月
位于西湖白堤西侧。中秋之夜,坐在伸入湖面的平台上,静候明月渐上中天,放眼湖中,但见湖平如镜,清辉似泻,清风拂面,桂花飘香,正是“万顷湖面长似镜,四时月好最宜秋”。
三潭印月
在杭州西湖小瀛州“我心相印”亭前,有3座石塔,塔身内空,均呈球形,其壁各有5个小孔。每当皓月凌空,人们在石塔内点燃烛光,烛光透过小圆孔投进深潭,在湖面上映出无数个小月亮,与倒映在湖上的明月相映成趣。
象山夜月
在广西桂林象鼻山,象鼻和象身中间有一水月洞,江水从洞中横贯而过。中秋之夜,乘小舟作江上游,驶入水月洞,便见“水底有明月,水上明月浮,水流月不去,月去水还流”的绝妙景观。
太清水月 登上青岛崂山太清宫东边的山顶,烟波浩渺的大海立刻展现在眼前。天上月与海上月交相辉映,水生光,月更明,恍如置身于仙镜之中。
石湖串月
石湖位于苏州西南郊,湖上有座行春桥,桥有9个环洞,洞洞相连,倒映水中,美妙神奇。每年农历8月
18日,是观赏“石湖串月”的极佳时光。是时,月光皎洁,映入行春桥桥洞中的月影如串,映于湖面,煞是好看。
二泉映月
在无锡市西郊惠山山麓、二泉池畔。此地古木参天,并有“二泉亭”、“漪澜堂”、“景微堂”等建筑,都是品泉赏月的极佳位置。每届中秋之夜,观赏那汩汩清泉之中映出一轮皎皎明月,楚楚倒映,恍如身临广寒之宫。
卢沟晓月
北京丰台永定河上的卢沟桥,是秋夜赏月的佳地,为燕京八景之一,但由于永定河时盈时涸,此景已不易见到。而由此南行50公里,还有一处“胡良晓月”,为河北涿州八景之一。
二十四桥月夜
在驰名中外的扬州二十四桥赏月,确实别有意境。月明之夜,驻足桥头,举头望月,俯首看水,会使人油然想起唐朝诗人杜牧“二十四桥明月夜,玉人何处教吹箫”的名句。
华严月色 在江苏镇江市东北长江中的焦山华严阁观赏长江月景,可见天地间空明一片,明月高悬,大江奔腾东去,极为壮观。
洞庭秋月 “潇湘八景”
之一,最佳观赏地在湖南岳阳市的岳阳楼。中秋夜,明月渐上中天,此时于岳阳楼前放眼湖中,只见湖平如镜,月光似泻,令人心旷神怡。
~~~~~~~古今多少事,都付笑谈中~~~~~~~
九一八事变简介
1931年9月
18日,日本驻中国东北地区的关东军突然袭击沈阳,以武力侵占东北的事件。
19世纪末至20世纪前半叶,日本逐步确定了征服世界必先征服中国,征服中国必先征服“满蒙”的战略方针。
1930年,世界资本主义经济危机波及日本,为了转移日益激化的国内阶级矛盾,日本加快了武力侵华的步伐,于
1931年7月和8月在东北制造了“万宝山事件”和“中村事件”。9月
18日,日本又制造“柳条湖事件”,发动了侵略中国东北的战争。
当晚10时许,日本关东军岛本大队川岛中队河本末守中尉率部下数人,在沈阳北大营南约800米的柳条湖附近,将南满铁路一段路轨炸毁。日军在此布置了一个假现场,摆了3具身穿中国士兵服的尸体,反诬是中国军队破坏铁路。日军独立守备队第二大队即向中国东北军驻地北大营发动进攻。次日晨4时许,日军独立守备队第五大队由铁岭到达北大营加入战斗。5时半,东北军第七旅退到沈阳东山嘴子,日军占领北大营。战斗中东北军伤亡300余人,日军伤亡24人。这就是震惊中外的九一八事变。
18313正不巧啊
18314感觉没有什么优势啊。
如果真的说是有的话,就是多见过几个数学符号吧1
18314数学系的同学理论比较强,但解决实际问题的能力有待提高,而且软件使用的不是太好!
18314数学系学生参加数学建模有多少优势?
18314感觉没有很多优势。
18314没有优势!
18314如果matlab用得也很好的话是很有优势的
但现在我国的教学跟不上啊,还是在心笔为主...应该改革
18314没有优势的!除非在应用数学领域有一定的造诣
18314优势还是有的,至少理论上要强
18314这么说来,数学系的人岂不是有点点。。。。
不过
再给我一次机会 我还是会选择数学的!!!
18314理论优势,
但是,数学建模还需要理论联系实际!
未曾清贫难成人
不经打击老天真
自古英雄出炼狱
从来富贵入凡尘
醉生梦死谁成器
拓马长枪定乾坤
挥军千里山河在
立名扬威传后人
nothing is impossible !just do it !
18314都一样的
本科生还能有多大的差别?
其他专业也都没什么优势可言!
18314数学院的学生思维无人可比
18314等到了大三优势就明显了,不过好像迟了.
数学系的人应该有更大的动力,毕竟以后要用的.
18314
| 引用 |
| 数学系的同学理论比较强,但解决实际问题的能力有待提高,而且软件使用的不是太好!
|
你又看到过多少数学系的学生?
18314优势是有的,就是没有老师培训自己找本书来看就可以去竞赛了。
18314理论基础扎实,选择方法明显有优势;能独立解决问题
18314没有优势怎么叫数学建模?
18314数学专业的到了大三才能有点优势,但我们学校一般只要大二的学生参加全国赛和美国赛
18314应该很有优势,只有扎实的数学基础才能运用自如,当然也得掌握软件及其他方面的知识。
183
18 作者:青铜豌豆 提交日期:2005-9-6 09:40:00
应试教育就是用考试的办法衡量教育的成绩。现在
183
18上2位都回过我的帖子.不胜荣幸.
要真有46级就好了.可以浓厚数学学习的风气.为那偏数学的人提供水平认可.
183
18教育应该以人为本,可我们现在还做不到
现在是制度为本加考试为本
183
18这个建议我喜欢
不过考数学4 6级 怎么考呢
考微积分
??
183
18支持
183
18此议不妥!
183
19《孙子定理和大衍求一术》读过没,这本书是由万哲先院士编的,其目的是用近代数学的语言和符号向青年读者介绍我国古代数学的两项重要大成就:孙子定理和大衍求一术,并揭示它们对近代数学的影响和它们与近代数学的某些内在联系。
183
19没读过!楼主介绍介绍!
183
19是啊
18320当然.但只是过去式了.
18320哥廷根真是数学家的摇篮,我发现20世纪许多著名数学家都出自那里。
18321兴趣是数学家成功的必要条件但不充分
18321兴趣对于数学家成功起多大作用?
18321要是对数学没有兴趣的话,又怎么能下工夫学数学并有一番成就呢?
18321兴趣对任何一门学科都很重要啊
18321我对篮球感兴趣,可惜进不了nba;我对足球感兴趣,可惜参加不了世界杯;我对数学感兴趣,希望将来能够参加一把世界数学家大会.
18321Michael23nba 你可以的。
come on!!!
18322这两个都挺强的
18322这是刘自己发的帖子吧?:)
18322
引用 (target4234 @ 2005年09月
19日
13时31分) |
| 川大的数学家谁最有名
|
以前是柯昭,现在是刘应明。
18322川大的数学家谁最有名
18322继柯昭,刘应明之后好像是李安民。而且他研究的东东都是国际热门。
18322现在应该书副校长刘应明吧
18322不好意思,走错门了,对这个我不了解,可不可以给小弟我介绍一下川大的数学家有哪几个啊!谢!
18322感觉是李安民,虽他现在没有刘有名,但他是川大数学里最与国际接轨的一个,研究的东东都是国际的热门.
18322有时有名的人不一定现在就强,很多趁果是年轻时搞的,现在不一定行.
18322顶
18322我!
嘿嘿,希望20年后实现
18322我觉的张世清很牛,再等是十年可能川大就是他的天下了.
18322顶 ,这确实是位好老师
18322刘应明很强
记得中国的有个什么科学家词典
数学家有两个入选
一个是他
另一个就是吴文俊了
18322什么词典都是假的,张世清老师牛,我终生佩服他
18322刘应明
18323楼上的朋友的方法很不错!
其实这个题目可以转化为求一个连续可导函数的极值的问题来做,也容易做!大家试试,我没有去做!
18323附件post-38-1127108377.ibf
18323归纳:post-38-1127110029.ibf
18324用Google或百度输入“Ansoft工程电磁场有限元分析”即可找到。
如:
http://www.dearbook.com.cn/book/viewbook.a...x?pno=TS0030109http://yydz.phei.com.cn/
18327请问大家谁知道武汉大学的数学专业课数学分析、高等代数的大纲?
若有,可否告知一下?
18329设A为s*n矩阵,B为n*m矩阵,证明:秩(AB)>=秩(A)+秩(B)-n
(北大高代第4章补充题第10题,我没有答案书)
18329不知道推理是否有问题,大家看哈!post-38-1127120853.gif
18329可用几何方法证:
dim ran(g*f)>=dim ran(g)+ dim ran(f)-n
利用dim
ran(g)+dim ker(g)= n
dim ran(f)<=n
即可
18329在蓝哥的第四行中,,Q1是m*m矩阵吧,P是s*s矩阵吧,,那么这两个矩阵怎么能相乘呢????
18329用矩阵分块:post-38-1127393467.gif
18329你们好像题目都没看清哦,那个TOBYQIN怎么没来啊,或许他会做哦
18329他很忙,没时间来了吧
找本书就有答案的
还可以考虑分块矩阵的初等变换做
18329俺手上啥书都没哦,你说的那些书和定理都没听说过哦
要么就把答案贴出来,急四人了,哼``````````````
18329除以上所说教材的证法外,再介绍两种:其一,是数学的实践与认识上的一篇论文,见附件命题2post-38-1127314116.ibf
18329还有下面附件中的推论4,如果你学过代数中的模论的话,就没任何问题了.不过,你如果看不懂的话,可以把"除环"理解成"数域",把"左向量空间"理解为"线性空间"即可post-38-1127314392.ibf
18329
to iii
我的证明有问题吗?请明示.
18329通过句阵变换,或者通过研究方程的解的维数可得
18329lchw:
你的第2行矩阵中,,B是n*m,不是n*s,,不过是小问题,改过来就可以了,你的是正确的证法。hfg
1964谢谢你啊
18329iii,你应该先查查资料,许多教科书(除北大外)中都有该定理,称为Sylvester不等式,还有更一般的Frobenius不等式.至少有如下几种方法可以证明:
1.秩的降阶定理(见复旦教材)
2.分块方法(见清华张贤科教材)
3.线性映射(注意:是指同态映射,不是线性变换)的方法,自己就可以把矩阵转化为线性映射,用线性映射的核的维数证;
4.用商空间及同态方法.
还有n种方法没想到.
18330
引用 (chenhhycc @ 2005年09月
19日
16时55分) |
|
大家好!你们能否告诉我什么是门限参数?切盼赐教!非常感谢!
|
我在其他领域见过门限参数,不知道是不是你想知道的这个.具体讲来如下:
一般来说,对函数F(X)而言,一个X就会有一个函数值与之对应,但是如果我们设置一个门槛
A,令X-A<0的时候F(X)不存在或者为0,当X-A>0时F(X)才按照正常的定义取值.那么这个A就
是一个门限参数.
如果不是这种参数,那我也就不知道了.
18330是不是一种域值,根支撑集有关。例如,对示性函数I[SIZE=1](-

,

)(x),此时的

不就是门限函数。
18330大家好!你们能否告诉我什么是门限参数?切盼赐教!非常感谢!
18330时间序列里面的东西
18330谢谢,不过有没有具体的定义
18331楼上的想法也是没错的,只是一时之间没有想到将求和改成一变量:
2+6+12+...+n(n-1)=

i*(i+1)=

i^2+

i
这本来就是公式(高中出现过)
话说回来,若考虑到了这一点,你可能也会倒回去干脆这样做了:
1*n+2(n-1)+...+n*1=

i*(n+1-i)
18331附件post-38-1127127045.ibf
18331我晕,这一步踏踏实实的去求是很容易知道的啊!
你尝试着把这个当作一个独立的题目来做,我想对于大学生来说应该是没有什么问题的啊!
18331这位朋友误会我的意思了,如果你这样想的话,看来我百说了!
对于我,谁如果这么说,就会让我上进,而不会考虑别人不会我会而自我安慰!
别人会的我也要会!呵呵!看来我理解错了,不是所有人和我一样!
不好意思啊,我向“是不是考研人”说sorry!post-38-1127132246.gif
18331不过用高中排列组合,也可以巧妙的求出来!呵呵!
18333谁可以告诉我,每50个人中肯定有两个人的生日在同一月的同一天吗??如果可能几率大于85%吗?还有方便的话,顺便告诉我抛物线的公式是多少??
18333可以看看<<概率论与数理统计教程>>,魏宗舒,高教出版社中的第20页
主要是把365天看成了
365个房间
接下来按分房问题解决
18334大家好;
我是学习小波分析的博士 ,主要研究的方向是框架理论和采样定理,希望结交从事理论研究的学友,可以共享一些资料。
qQ:149432645 Email: archang-0111@163.compost-54-1127128915.ibf
18334149432645,email:xbw2004@163.com同样在学习小波和框架
18334我也是学习小波的,不过毕业了,现在感觉小波好像没有什么可以写的了,希望向各位仁兄学习 QQ597323435
18334
引用 (jiaosy @ 2007年05月26日
09时
18分) |
|
我也是学习小波的,不过毕业了,现在感觉小波好像没有什么可以写的了,希望向各位仁兄学习 QQ597323435
|
低维小波理论已经比较完全了,高维的还有很多的东西需要做吧
18334小波分析已经很完善了吗?
我是学调和分析的,现在想学小波分析,不知要看一些什么书(关于小波分析,以前从没有接触过)?请楼主不吝指教!!谢谢
18334我也学小波,不过现在小波确实是没有什么新东西可做,lian jie-ao,qiang
qingtang,也好久时间不出文章了,高维得有点看不懂啊,转应用吧
18334师兄呀,附件怎么下载下来,是0 K呀,不能打开
18334
引用 (lwg02
18 @ 2007年11月05日
22时59分) |
|
我也学小波,不过现在小波确实是没有什么新东西可做,lian jie-ao,qiang
qingtang,也好久时间不出文章了,高维得有点看不懂啊,转应用吧 |
我也学小波,不过现在小波确实是没有什么新东西可做,lian
jie-ao,qiang qingtang,也好久时间不出文章了,高维得有点看不懂啊,转应用吧
18335直径有限
18335在度量空间中,定义度量
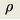
,有界是如何定义的??
18335谢谢楼上的!!
18336最近遇到这个概念:矩阵的根,不知道它是怎样定义的!!
18337请教一个菜问题:什么是双对数曲线、半对数曲线?怎么在数学手册上查不到
18343我校没有专门的数学系,有一个相关专业(信息与计算科学)教授1,副教授9个,中级及以下30多个把,没有突出之处,也没有权威,大多数数学老师在写论文时也只能写与计算机相关的,能写存数学又有水平的基本没有吧.
个人认为目前这种大学各自自主招生,教育产业化就是比较失败的,为了成综合大学,什么专业都在申报,都在招生,也不管能不能培养这方面的人才.其结果是大多数学校把自己以前王牌专业,特色专业给丢掉了,一味的最求综合,结果什么专业人才都在培养,什么专业人才都没培养出来.赞成楼主的集中培养制,各学校集中优势,发展特色
18343最近个人有点疑问,想做以下简单调查,请配合!先多谢!
贵校有多少名数学教授\副教授\专业研究人员?
贵校数学在哪个方向比较著名,或具权威?
你认为贵校数学研究水平如何?教学水平如何?
你认为学生质量如何?学生课外研究如何?
有这样一种说法:借鉴20世纪波兰数学的振兴,把中国数学专业集中在某些数学水平较高的学校,也即其他学校只需要公共数学教学教师即可!把这些学校建成数学专业数学学校!以其集中中国的数学精英,大量学生生员,不减少现今中国各高校数学专业学生人数!或许对中国数学有点贡献!
你认为如何呢?
18343我谈一下中南民族大学的吧.也就是说我认为它是可代表数学做的差的学校的情况.各位可以看一下它差到哪种成度.
1.我们数学系学生数学素质很差.即使有的很用工,但学校的教育培养不了他们独立思考的能力.
2.师资.如果有一个很会写论文的学生出现在这个系.下场多是被埋没.因为老师的眼界有限.评定不了他们的文章.
3.学风.50人中有10来个搞一搞数学学习吧.多数人认为无用.不如学点计算机.
18343谈谈我校吧,地质方面是具有权威的,但是在该学院对数学的学习风气很差,根本就找不到数学素质好的学生,院领导也没有什么反省。大家都埋在英语四、六级中,毕竟四六级通过率是评价学校好坏第一个重要指标。
可是,想想觉得不妥,每天发大部分时间学英语,哪来的时间创新。天天想着引进国外的技术成果,可是以现在科技发展的速度,哪怕天天跟着别人的尾巴也学不完呀,哪来的创新。算算大家单单在学习英语上就落了外国人十几年啊?凭这些人就能出个诺贝尔??但是,这并不是说就不需要引进了。
难道大家就不能配合一下,分工一番:一部分人,多学外语
引进国外成果。
另一部分人:不要浪费时间在学习英语上,多学基础学科,才能创新呀。头脑里没有广阔的知识面怎么来新思路。
何况,并不是每个人都有学习英语的天分,甚至有些人本该有很好的成绩,却在外语方面的失意而~~~~
18343我也谈谈我们学校——东莞理工学院,只有个数学教研室。我想我这比上面那些还要不理想。说起来很多副教授和博士,但都是只能上高数和线代的,有的副教授连概率统计都讲不来。每个新学期就见他们抢高数和线代。至于难一点的概率统计,复变函数与积分变换之类的都是我一个人去上。好在没成立系,不用上专业数学,不然累死我。真不知道她们当年怎么混来的职称和学位?
18344我们有道题目是用Mathcad验证中心极限定理,先计算随机变量y样本值(Xi的和),然后画出y的PDF
我程序是这么编的
p:=runif(10000,0,10)
q:=runif(10000,0,10)
y=p+q
yy=hist(20,y)
请问接下去怎么打出直方图呢?我按insert
- graph - x-y plot 然后就不会了,偶无论输入yy还是hist(20,y)都是没反映的红色的,急死我了
18344没有看懂你的意思,是说要这种效果吗?
post-28-1131468251.jpg
18354很多年学校什么表示都没有,今年破天荒系里发了500元。穷啊
18354600元
18354偶们800
18354工会200元券
18354我们好一点点拉.国庆\中秋\教师节一起:学校200,工会100,学院400
18354
| 引用 |
| 自己先来:教师节,中秋节,加上国庆节,学校发购物卡100元,月饼“无”,其它“无” |
教师节真的是教师们的节日么?
18354我来这个学校两年了,过教师节都是一共300元,国庆等节假日学校一分钱不发。系里偶尔给100块钱的卡
18354惨啊
偶发了1000元的超市卡,还不如换成现钱
18354偶也惨啊!!!!
欧来这学校两年了,上一年是150,今年是300,月饼无!!!还说是教师节,中秋节和国庆节一共的福利!!!!
18354同2楼类似,只缺少了学院的400,哈哈。
教师节,该上课的老师还是要上课,该搞科研的还是要搞科研。能收到学生送的一束花、一张卡片、一个电话或者是一条短讯,你就念“阿弥驮佛”吧。打赏你100你就老老实实地收着,买上10来斤肉把嘴巴堵上,别说话!
18354我顶
18354
| 引用 (中子星05 @ 2005年09月21日
15时14分) |
惨啊
偶发了1000元的超市卡,还不如换成现钱 |
不要给我吧,我要。我们只发了200元啊,还是中秋后发的!!
18354大洋:0000元;物品:00000件;其他:无!
18354300元的卡
18354教师节,中秋节,加上国庆节发了500吧,不记得了,没发月饼。过年要发个笔记本电脑吧,不过自己要出点钱,2000
18354高中国家级贫困县重点中学300
18354教师节发了3000,中秋节汤圆2包,国庆节3000,元旦2000。
18354教师节600,中秋节鸭蛋1箱,过年1000圆的油肉米面。我是个可怜的中学教师
18354其实还算不错了
18354我们钱没有多少(不超过100),而且还得不到休息(往往要演一些文艺节目。为演好这个节目还要提前训练N天)。
18354大家的都不错
18354我来这个学校 5 年了,过教师节、国庆一共300元,其他节假日学校一分钱不发。
18354中学老师,教师节1000,国庆+中秋300
18354500元
18354楼上哪个学校?待遇不错哦
183543000,2000,3000的牛啊?那个学校的?羡慕。我们教师节去年500,今年1000,中秋国庆无
18354三节发500,去年三节600。越来越少。没有月饼。
18354高校,教师节600,中秋节啥也没发,学校真抠。
18354偶认为教师节给教师最好的礼物是多多的money和假期
18355我也是一个丢番图方程的爱好者。
18355我比较喜欢指数DIOPHANTINE方程和连立PELL
1835730*30的矩阵,画折线图是怎样的情况,能说的更具体些吗?
18357我有个30*30的矩阵,想把它画成三维折线图(横纵交错,最基础的那种就行)
似乎可以先定义一个Array,然后再把所有数据装入到数组中,然后再ListPlot3D
但30*30个数据要是写在命令行里就太多了
有没有什么比较好的办法?
(最好能给代码,我是新手)
多谢了
18358我先来考试,抛砖引玉post-38-1127
177326.ibf
18358哈哈!post-38-1127
174
199.gif
18358很棒的一种方法,还可以有至少一种方法可以做!继续!看大家能够用多少方法解决
~!
18358ms还可以用反证法。
如果,命题不成立,那么,必然存在{xn}趋于正无穷的时候,{An}趋于正无穷。
那么,对,任意的

村在某个

,只要找到An>1/

对应的xn,在该点就不满足一只收敛
想得比较粗糙,不知道对不对
18358此命题是否可以更加精确呢?
18358怎么看不到第一种方法的解答过程啊.
18363帖子很不错
不过是不是不同的学校得用不同的书呀
不是所有的都适用呀
18363就是
18363我来加一本高等代数的书,《高等代数常用方法》,这本书绝对是一本学习高代的好书,只不过这本书是在89年出版的,现在市面上是买不到的,只能去图书馆借,也可以去超星里看。
18363谢谢
18363我本科学的教材是刘玉琏的数学分析,个人觉得对于底子不好的人还是不错的,知识点很全面,而且习题不难,这样对理解知识有帮助。这本书对仪新手入门我认为还是不错的!
18363xie xie
18363

我添一本,华东师大编的
数学分析习题精解 单变量部分和多变量部分 科学出版社
18363数学分析还是华东师范大学的
高等代数就用由北京大学编写的出版的
18363好呀
18363
注:红色的是我认为最好的!资料只是作为参考,学数学独立思考很重要!一、数学分析:
1、复旦大学的教材(欧阳光中等编,高教社)
2、数学分析中的典型问题与方法(裴礼文,高教社)
3、数学分析题解精粹(钱吉林,崇文书局)4、数学分析习题集(北大林源渠、方企勤、李正源、廖可人编,高教社)
5、数学分析解体指南(北大林源渠、方企勤)
6、数学分析习题课讲义
7、数学分析经典习题集解
8、数学分析习题精解
9、数学分析导教.导学.导考(复旦第二版)
二、高等代书:
1、高等代书新方法(王品超,矿业大学出版社)
2、高等代数习题解(杨子胥,山东科技)3、高等代数题解精粹(钱吉林,中央民族大学出版社)
4、代数学词典(钱吉林)
5、北大教材
6、高等代数解题方法与技巧
7、高等代数(北大.第三版)导教.导学.导考
三、实变函数与泛函分析
实变函数与泛函分析概要(郑维行、王声望,这本书很适合初学者!)
实变函数论的典型问题与方法
张喜堂
实变函数与泛函分析习题精解 宋国柱
18363好东西哦,我顶
18363我想补充以下几本:
一 数学分析
数学分析习题全解指南 陈纪修
数学分析选讲 王戈平
数学分析讲义练习题全解
刘玉琏
二 高等代数
线性代数导引 郭聿琦
高等代数选讲 陈利国
高等代数学 张贤科
三
实函
实变函数论的典型问题与方法 张喜堂
实变函数与泛函分析习题精解 宋国柱
18363支持.数学分析题解精粹(钱吉林编),确实是好东西.我看了以后,收益非浅.上面有历年各学校的考研数学分析试题.
18363请问
实变函数论的典型问题与方法 张喜堂
实变函数与泛函分析习题精解 宋国柱
在哪里可以买到?
谢谢
18363好介绍.谢谢了.
18363刘玉涟的挺好的,不是很难,但是涵盖知识面很全,题目也较典型~~
18363
引用 (fbdfbd8055 @ 2005年09月25日
17时05分) |
|
刘玉涟的挺好的,不是很难,但是涵盖知识面很全,题目也较典型~~ |
我当时学的时候用的也是刘玉琏的,现在再看看,觉得还不错,例题很经典,习题也还8错滴~
18363Is anybody 读过蒋尔雄的线性代数(
1978)的请举手!交流经验!
18363高等代书新方法(王品超,矿业大学出版社)
哪里有卖?
18363请问<常微分方程>有什么好的参考书?
18363我来加一本书里面含有数学分析和常微分方程的内容,机械工业出版社
,李心灿,季文铎,余仁胜得主编的,大学生数学竞赛试题研究生入学考试难题解析选编!这本书相当好啊!难度应该超过了裴礼文的那本啊!
18363wo ding !!!!
18363巴斯的<数学习题>不错吧?!!!
18363我也顶!!!
18363数学分析习题全解指南 陈纪修
在那里可以买到
18363谢谢了
18363不错的意见,一定照办!
18363
1978复旦大学的线性代数很好的
还有王品超的高等代数书
18363高等代书新方法(王品超,矿业大学出版社)
2、高等代数习题解(杨子胥,山东科技)
这两本在哪能买到啊?我在沈阳
18363这本在哪买啊????
18363高等代数辅导与习题解答 黄光谷 华中科技大学出版社 很好的,适合同步辅导
18363我也顶!
看了大家所说的书感觉考研要学的还有好多哦!
向时间要生命吧!
18363好!
18363、高等代数题解精粹(钱吉林,中央民族大学出版社
18363再补一本高等代数,《高等代数》上下,丘维生,高等教育出版社
看完了概念特别清晰,习题够量,质量也好。
18363我要考华中科技大学的数学系,请大家给我推荐用什么参考书好一点,谢谢!
18363
| 引用 (xor @ 2005年10月30日
01时34分) |
再补一本高等代数,《高等代数》上下,丘维生,高等教育出版社
看完了概念特别清晰,习题够量,质量也好。
好像有点简单!
|

18363太谢谢您了
18363请大家帮忙推荐“数学分析”和“高等代数”教材各一套,注明作者和出版社。谢谢大家了。
18363数学分析:华东师范大学的。
高代。我用的是高教的,感觉很好的
18363好东西!
183633Q
18363我也要去看看这几本书哈
18363邱维声写的高等代数真的很不错,一看就喜欢了.
18363复旦大学最新版本的《数学分析》,2002年不错啊!
18363裴的书高教刚刚出了第二版!!
18363那些资料都很不错,不过我觉得总不能全看的,要有重点的选择,数分高等每门选上两本就不少了,资料太多了也不好的。
18363书是好书,全部学完学精恐怕要几年工夫,还是早准备好
18363高等代书新方法(王品超,矿业大学出版社)
学校附近的书店应该有卖的!我也用着本书
,是从我门学校这边的书店买的!你可以去书店问一下,或者让店员帮你顶一本啦!
18363买了一本数学分析中的典型问题与方法(裴礼文,高教社),可惜题目没答案!
18363《常微分方程讲义》王柔怀
1978,书很经典!
书上的习题答案谁有?哪里能弄到!联系我39891242
18363复旦陈纪修的数学分析非常不错!!我用的就是这本教材!现在习题解答高教社也出版了!!!
18363那么,在那里能买到这些书呢?
18363数学分析题解精粹(钱吉林,崇文书局),,是很不错,,不过不适合那些刚进入复习阶段的朋友使用
18363钱吉林的《数学分析方法选讲》题目不错,不过里边的解答有很多错误和漏洞
希望大家在看得时候一定要小心,因为有些错误很难看出来。不要把错误结论和
方法当成正确的,以免得不偿失。
18363个人建议:书在精!!!
很幸运,我们老师就是王品超那本书的编者之一,它的笔迹很不错,但我感觉我在一些小的细节方面还醉在问题!
钱吉林那两本书数分不错!但有错误!高代简单了些!
大家加油还有16天了!
18363我不太赞成吉米的书,那书适合工科,裴的 书交好,一致连续与一致收敛比较难,有《一致连续与一致收敛》人教版可以看以下
18363钱吉林的《数学分析方法选讲》??
哪个出版社?啥时出版的?
18363
| 引用 (liuxiaowei @ 2005年09月29日
07时50分) |
|
支持.数学分析题解精粹(钱吉林编),确实是好东西.我看了以后,收益非浅.上面有历年各学校的考研数学分析试题.
|
那个好吗?
18363xie
18363好,我也来添一本啊,<<数学分析习题课讲义>>(谢惠民等,高教出版社)有上下两册的啊.
18363我在看姚慕生的<高等代数学>,因为是复旦大学的硕士书目.不过跟北大那个好象不是一个思路~~~~~我们老师说用北大那本就足够了.至于我们的辅导课用的是中国矿业大学出版社王品超的<高等代数新方法>.学校统一定的,当时我们还以为是因为主讲老师有份参与编写所以才引用,呵呵,看来是以小人之心度君子之腹了
18363谢谢大哥们提供的资料!
18363北大出的《数学分析解题指南》不错,不少题的解法很有特色。
18363有个山东科技大学出版设出版的高等代数的辅导书很不错,我们好多同学都借来看
18363好!很有启发!
18363不错,谢了.
18363谢谢啊,我顶!
18363好多呀。。搞得有点目不暇接。。又不只改选什么了。。
我想考北大该用哪几本呢?各位学长给个建议。。。
谢谢了
18363太多了
183631、高等代书新方法(王品超,矿业大学出版社)
2、高等代数习题解(杨子胥,山东科技)请问哪本难度大一点
18363很感谢呀!
18363
| 引用 (huahuaandmeimei @ 2005年09月29日
21时53分) |
Is anybody
读过蒋尔雄的线性代数(
1978)的请举手!交流经验! |
蒋尔雄是计算数学大家
18363王品超的书好象过于偏了啊?
18363好东西啊
18363数学专业的研究生考试中,
18363
| 引用 (matrix594 @ 2005年09月20日
10时10分) |
注:红色的是我认为最好的!资料只是作为参考,学数学独立思考很重要!
一、数学分析:
1、复旦大学的教材(欧阳光中等编,高教社)
2、数学分析中的典型问题与方法(裴礼文,高教社)
3、数学分析题解精粹(钱吉林,崇文书局)
4、数学分析习题集(北大林源渠、方企勤、李正源、廖可人编,高教社)
5、数学分析解体指南(北大林源渠、方企勤)
6、数学分析习题课讲义
7、数学分析经典习题集解
8、数学分析习题精解
9、数学分析导教.导学.导考(复旦第二版)
二、高等代书:
1、高等代书新方法(王品超,矿业大学出版社)
2、高等代数习题解(杨子胥,山东科技)
3、高等代数题解精粹(钱吉林,中央民族大学出版社)
4、代数学词典(钱吉林)
5、北大教材
6、高等代数解题方法与技巧
7、高等代数(北大.第三版)导教.导学.导考
三、实变函数与泛函分析
实变函数与泛函分析概要(郑维行、王声望,这本书很适合初学者!)
实变函数论的典型问题与方法
张喜堂
实变函数与泛函分析习题精解 宋国柱 |
非常的不错啊,要是能够把这些书的搞成电子书就再好了啊,就不用花钱去买了~
18363谢谢!!
介绍的书很好!!
我想对我会有很大的帮助的!!!
18363难道吉米多维其的《数学分析习题集》不行吗 ?
偶感觉挺好的 》》》》
18363我觉得高教的数学分析习题课讲义(上下两册)真的挺不错的,隆重推荐!
18363数分的解题方法一般技巧性很高,想要把方法变成自己的惟有多作多思!
18363用以前的书考研行不行呀,请高手指教了
18363好东西呀!呵呵
18363谢谢!
18363请问 数学分析题解精粹 钱吉林的 哪里有卖的?
18363其实一本做透就够了
18363很不错!!!!!!!!!!!!我是一名专科生,数学专业,想考研,但是英语,专业课,有很长时间没有学了,我如何完成复习??况且工作时间很紧!!!!!!!!!!!!我的QQ:402957836,想考基础数学,或者应用数学方向!!!!!!!!!!!给予帮助!!!!!!!
18363好,谢谢了!
18363很多都不好买到!呵呵!去九章买也是。一本足以了。呵
18363感激不尽
18363谢谢了
其实就一本书足以
18363
引用 (twins @ 2006年03月05日
09时
18分) |
难道吉米多维其的《数学分析习题集》不行吗 ?
偶感觉挺好的 》》》》
|
这个书跟上课是同步用好
18363中科院推荐的教材是什么啊?
18363最经典的数学分析参考书应该是菲赫金哥尔茨的微积分学教程
---------------
不知道那能买到这样的书啊?
18363我也介绍几本我曾经用过的书:
数学分析 姚允龙(是参考书)
高等代数解题方法 许甫华
高等代数解题技巧与方法
黎伯堂刘桂真
复变函数学习指导书---钟玉泉
复变函数全程学习指导与解题能力训练(2001)刚家泰谭欣欣
18363非常感谢!

18363机米的平时看还好,考的时候就当字典了吧!还是看学校要求的吧!
18363

顶
18363不知道再哪里可以买到那些书
18363华东示范的数学分析行吗,考南开还用买复旦的数分吗
18363
引用 (luminator @ 2005年11月21日
17时20分) |
| 裴的书高教刚刚出了第二版!!
|
还是第一版,封面换了
18363谢谢楼上各位!
18363
引用 (JeffreyBlue @ 2006年03月20日
19时09分) |
引用 (luminator @
2005年11月21日
17时20分) | |
裴的书高教刚刚出了第二版!! |
还是第一版,封面换了
|
请问:在哪儿看到的? 请告诉我好吗?
18363吉米多维奇的 <数学分析习题解>很好啊
18363我还知道有一本高代的资料书,安徽大学出版社,《高等代数解题法》,赵礼峰编,还可以的。现在重点是书后面的习题要全部搞清楚
18363数分的用斐礼文的典型例题与方法和钱吉林的都可以
18363顶!
18363沙发,顶一个!
18363Thanks
18363根据我们偏微分方程老师的意见,北大的那本数学分析解题指南相对较难,高教社出版的与华东师大教材配套的那本学习指导书比较好。
18363听说钱吉林的数分和高代都不错,可以找来看一下
18363遇到知音啦,我认为钱吉林编的数分,高代都不错,就是版本旧了点
18363各位高手,考验的过来人
可不可以推荐几本比较基础的参考书,我觉得裴礼文这样对刚开始复习似乎太难了,想先把基础打牢一点,特别是高代,我真的不知道有什么参考书,学的时候就只是看课后题
18363谢谢各位指教
18363
引用 (tananxulei @ 2005年10月13日
18时06分) |
 我添一本,华东师大编的
数学分析习题精解 单变量部分和多变量部分 科学出版社 我添一本,华东师大编的
数学分析习题精解 单变量部分和多变量部分 科学出版社 |
是本不错的好书,比较适合边学边看。我正在用。
18363好东西!!不过有的学校不是用的这些书!!
18363谢谢
我很喜欢这个帖子
18363请问各位前辈,小弟乃大三学生,面临考研,在选择参考书方面,有些茫然。不知是钱吉林的数分和高代还是杨子胥和裴礼文的好。
请大家赐教。
18363我添一本,复旦大学的陈纪修的数学分析也不错!
18363复旦大学的教材欧阳光中德在那儿有卖?
18363目前数分我在用苏大老师们编的《数学分析习题课讲义》,很扩展知识面,但有些内容好象考研不可能考到。。。高代啥辅导资料都没买,到是买了丘的教材,有点郁闷,比较难啊。
18363数学分析经典习题解析 孙涛 也蛮不错的
18363篮以中的<<高等代数简明教程>>不错啊!
18363对于考研来说,大家觉得目前最全面、最深入的是哪一本啊?
我推荐北大蓝以中的《高等代数简明教程》。
18363北京大学的《高等代数》,经典教材。知悉体会。
18363
| 引用 (chuhaifeng123 @ 2006年04月05日
10时35分) |
|
北京大学的《高等代数》,经典教材。知悉体会。 |
同意
18363经典
18363丘维声
18363丘维声的高等代数和解析几何都是非常经典的教材!!!!
18363
| 引用 (matrix594 @ 2005年09月20日
10时10分) |
注:红色的是我认为最好的!资料只是作为参考,学数学独立思考很重要!
一、数学分析:
1、复旦大学的教材(欧阳光中等编,高教社)
2、数学分析中的典型问题与方法(裴礼文,高教社)
3、数学分析题解精粹(钱吉林,崇文书局)
4、数学分析习题集(北大林源渠、方企勤、李正源、廖可人编,高教社)
5、数学分析解体指南(北大林源渠、方企勤)
6、数学分析习题课讲义
7、数学分析经典习题集解
8、数学分析习题精解
9、数学分析导教.导学.导考(复旦第二版)
二、高等代书:
1、高等代书新方法(王品超,矿业大学出版社)
2、高等代数习题解(杨子胥,山东科技)
3、高等代数题解精粹(钱吉林,中央民族大学出版社)
4、代数学词典(钱吉林)
5、北大教材
6、高等代数解题方法与技巧
7、高等代数(北大.第三版)导教.导学.导考
三、实变函数与泛函分析
实变函数与泛函分析概要(郑维行、王声望,这本书很适合初学者!)
实变函数论的典型问题与方法
张喜堂
实变函数与泛函分析习题精解 宋国柱 |
代数学词典(钱吉林)
它并不适合于考研复习
18363高等代书新方法(王品超,矿业大学出版社)
在哪可以买到啊
18363王品超的那本高代挺不错的!
18363对数学分析和高等代数的复习各位有什么好的建议,可否交流一下?谢谢
18363我们学校数分学的是华东师大的版本.高代是北大的版本.
不知道如何复习.
望各位学长不吝赐教.
谢谢.
18363高等代数新方法是王品超的没错,但是好像是山东科技出版社的
18363最经典的数学分析参考书应该是菲赫金哥尔茨的微积分学教程
18363谢谢斑竹啊,呵呵,很有用的!
18363大哥;
谢谢你介绍那么多的好书让我门参考,可是我觉得自己好像要考我们数学专业的研究生是不是那些资料题目太少了啊,我不知道,希望你可以帮帮我,我现在是大二的
,很想考个很好大学的研究生(概率统计)的,呵呵!
指点我一下好吗?谢谢了!!!!!!!!
俊杰[COLOR=blue]
18363
| 引用 (ljg99 @ 2005年09月23日
14时00分) |
我想补充以下几本:
一
数学分析
数学分析习题全解指南 陈纪修
数学分析选讲 王戈平
数学分析讲义练习题全解 刘玉琏
二
高等代数
线性代数导引 郭聿琦
高等代数选讲 陈利国
高等代数学 张贤科
三 实函
实变函数论的典型问题与方法
张喜堂
实变函数与泛函分析习题精解 宋国柱 |
谢谢你啊
18363不错我也在用那几本书.
18363考武汉大学的复分析要看余家荣的复变函数或路见可,钟寿国(余家荣的弟子,武大的教授)的复变函数
实分析要看侯友良的实变和刘培德的泛函(研究生必修课,而且就是他上的)
18363谢谢
18363我学数学分析用的是钱吉林《数学分析》题解精粹,感觉不错
18363谢谢!
18363高校经典教材配套考研辅导系列
数学分析
题解精粹
钱吉林 等主编
崇文书局
ISBN7-5403-0652-1/G.443
定价:28.8元
各位有什么好书也可在此处推荐一下,OK?
OK
183631、高等代书新方法(王品超,矿业大学出版社)这本书哪有卖的啊????
这书行么??
2、高等代数习题解(杨子胥,山东科技)
人家
18363我觉得 湖南科技出版社 出版的《数学分析中的典型例题与解题方法》也相当不错。
18363呵呵,都是好东西啊,哪里有下载的吗?
18363好东西呀
18363谢谢
183631裴礼文的那本数学分析
2、数学分析题解精粹(钱吉林,崇文书局)
3、2、高等代数习题解(杨子胥,山东科技)
4高等代书新方法(王品超,矿业大学出版社)
王品超的那本高等代数是曲阜师范大学数学系编的
18363数学这东西说难就难,说难就不难,
不过,那个高等代数那个东西是死的,不灵活,
数学分析就不同了,我们这里用的钱吉林高等代数和数学分析,
以及王品超的高代新讲,
还有裴礼文的数分,这几本书真的不错,
有考华南理工的同道中人.我和你们交朋友,以及共享信息,
及学习体会.
18363说半天原来一广告!呵呵!
18363高等代数习题解(杨子胥,山东科技)
18363我想知道比如一些大学初试时还要考其它科目的参考书
谢谢
18363都很好啊,斐礼文的数分也不错啊
18363中科大常庚哲的数学分析 苏大的数分习题课讲义很不错 至于数分的三导我觉得不怎样 高代的三导很好
18363以我的经验,我觉得
数学分析比较好的是
华东师大编的
高等代数是
北京大学编的
人只有一个脑袋,学好这两本书足够了。
18363请问,南开出的数学分析书有答案书吗?
18363最好多看几本教材,博得所长
18363好多书是很好,可是不好买
18363我对这些都不懂的,多谢指导,倡导此类帖子多发
18363书是好多的。有没有更精华的?
18363裴礼文的那本书很经典
18363
| 引用 (choulaorui @ 2006年05月15日
22时40分) |
| 裴礼文的那本书很经典
|
是本好资料啊
18363钱吉林的那本也不错
18363发现了那本金圣叹编的考研试题精选,石化出版社,感觉不错
18363复旦大学的陈传璋等编著的《数学分析》还是相当好的,可以看一看。
18363新华书店就有的卖哦
可是就是有点儿贵。
18363我推荐一本《高等代数学综论》王卿文
无敌棒,不过很难找到这本书。
18363数分:
数学分析习题解(吉米多维奇)
数学分析题解精粹(钱吉林)
数学分析(陈纪修)复旦大学
高代:
高等代数习题解(扬子胥)
高等代数题解精粹(钱吉林)
高等代数(北大)
矩阵分析(杨奇译)从美国译过来的
里面好多和矩阵有关的不等式
还有科学出版社的好像市数学分析中的典型问题和方法和高等代数中的典型问题和方法也特别不错
裴礼文的那本书也很经典
18363我添一本,华东师大编的 数学分析习题精解 单变量部分和多变量部分 科学出版社
18363帖子很不错
不过是不是不同的学校得用不同的书呀
不是所有的都适用呀
18363感觉这书挺好的,准备复习完基础知识后认真研究一下,对知识的扩充的思维的提高有不少益处。大家有什么好的经验交流一下?
18363谢谢 各位的指点
18363比较公正
18363[COLOR=green]中山大学编的概率统计谁有啊?我想买!
18363高等代数新方法哪儿有卖的?不过方企勤,林源渠的数学分析解题指南我看过,相当不错!向大家推荐
18363谢谢,太好了
18363裴礼文的书很好,知识点很全,方法也很好,唯一的缺点是习题没有答案
18363[COLOR=red]请问:
金圣叹编的考研试题精选(石化出版社)
在哪个网站能下在载到
18363我觉得不错,数分中裴礼文的数学分析的典型问题比较难了,高代的我还是觉得杨子胥那本比较好
18363我还是觉得那个《数学分析习题课讲义》有点偏呀,和很多学校的考试都没有很大关系!不过对于数学分析水平提高还是很有帮助的啊!!
感谢师兄提供的这些资料啊!!
18363hao xiexie
18363wo ye ding
18363高等代数新方法(上册)在哪里买?谢谢各位!
18363钱吉林的那个有很多印刷错误
18363好书啊~
去看看
18363谢谢了,开来还是人多力量大
18363不错
18363裴礼文的不错!!就是题目有点难.谁有答案啊!
18363北大周明强的数分教材我觉得非常不错的,比较难,有深度,适合考研用吧!
18363钱吉林的书很不错的!值得一研究呀!
18363书很不错,不过要有购书方式,地址,就更好了
18363今天去新华书店,好多都没得卖了...
要买都得上网买了
18363顶,东部一般高校和西部较强高校研究生哪个更容易上?
18363高等代数综合题解(蔡剑芳等编著)也很好
18363谢谢
18363那么多啊.哪些跟好呢?
18363实变函数论的典型问题与方法 张喜堂
实变函数与泛函分析习题精解 宋国柱
强烈推荐!!!
18363《高等代数新方法》中国矿业大学出版社出版的,王品超编的,王品超就是我们学校的代数老师,今年我们学校高等代数,报他的辅导班的很少最后系里取消了。主要是王老师年龄大了,讲一节课需要休息半节课。今年我们没用他的那本资料,不过那本书真的太好了,初学者最好耐住心漫漫看。
《数学分析典型习题方法》裴礼文的这本书真的太好了,本人感觉最好配合着钱吉林的那本《数学分析习题精粹》看更好
18363给大家介绍个买专业书的网站
www.welan.com里面书还是比较多 ,还是不错的
18363顶 书都不错啊 就是没时间啊
18363因人而异
18363顶楼主啊
18363支持,而且我已经买了,确实不错
18363非常好谢谢阿!
18363不错,我觉得仔细研究完一本就很不错,没那么多时间啊
18363ding
183632007年中科院数学所考研(群
17465471)!!!快来呀!!
心得体会任意畅谈!!!
18363我不知道什么数学资料书好啊?
谢谢了啊 |!!
18363转贴
一、中文的:
最难的3套书:
1、《数学分析新讲》(1、2、3册),张筑生,北大版
2、《数学分析》(1、2、3册),方企勤,北大讲义
3、《数学分析》(1、2、3册),中科大常庚哲等,江苏教育版
最抽象的教材:
《数学分析》(上、下册),邹应,武汉大学数学基地班教材
二、国外的书
好书太多,菲赫金哥尔茨的《数学分析原理》太老了,他的那套《微积分学教程》3卷(共
8本)才是他的成名作,不过也太老了。。。
美国的好书:
1、W.Rudin的《数学分析原理》
观点很高,1—7章(单变量部分)绝对经典,拓扑味很浓,写得很深(除非你资质太高,
否则大一别看这本书),后面多变量部分也写的不错,不过过于急促了;
2、R.Courant的《微积分和数学分析引论》
绝对的经典,推荐必读,该书无论单变量还是多变量部分都写得很深,尤其是第二卷多变
量部分,很早就引入了若当测度,n维欧氏空间的微积分,微分流形、外微分等现代分析的
基本概念,写得非常详尽,尤其值得一提的是习题很不错,有相当的难度(此书在国外用
的并不普遍,因为难度过高,常被当作参考书);
3、Apostol的书
1)、《微积分》1、2卷,难度低于courant的书,入门很合适;
2)、《数学分析》,难度略低于RUDIN的书,也很不错
1)+2)基本上等于courant+rudin的难度,不过最难的绝对是前2套书;
4、spivark的《流形上的微积分》
主要是在流形上讲述微积分学,有很浓的拓扑味,一般结合RUDIN的书看,正好补充RUDIN
的书后面几章的缺陷,他还写过一本《calculus》据说也不错(我没看过);
俄罗斯的书:
70年代以后的书观点都很高,不过翻译过来的很少,国内常见的有2套:
1、B.A卓里齐的《数学分析》
2、尼可尔斯基的《数学分析教程》
据说新近出的书还要难,不过国内很少见!!!
法国的书:
法国的数学分析教材据说全球最难、最抽象,国内很少见,我只见过3套:
1、迪斯米挨的《大学数学教程》不知有几卷,一开头就是拓扑、实分析等抽象的东西,如果
你实在够牛可以看看;
2、《普通数学》1—6卷,法国大学头2年的数学教材,看完这套可以看看Dieodonne的9卷
本《现代分析基础》;
3、Bourbaki的《数学基础》有6门核心课程(到现在为止不知出了多少卷了)可以说是近
代数学的一个“最小工具箱”,可惜没有中文版,绝对超一流的难,绝对经典现代(该书
在不断的修订)
此外还有德国的书难度介于我过最难的数分和法国数分教材之间,就不再多说了!
18363这个内容我在很多网站上都看到过
确实还不错!
不过我觉得找到各个学校的历年真题也还是很重要的!
18363xiexie
18363
引用 (cat
19
19 @ 2005年10月25日
15时54分) |
高等代书新方法(王品超,矿业大学出版社)
2、高等代数习题解(杨子胥,山东科技)
这两本在哪能买到啊?我在沈阳
|
我在我们学校商业区的书店里买到的
18363好东西哦,我顶
18363钱吉林的书试题太杂,没有征对性,而且有个别错误,个人以为没必要买这本书作参考。
18363
| 引用 (huahuaandmeimei @ 2005年09月29日
21时53分) |
Is anybody
读过蒋尔雄的线性代数(
1978)的请举手!交流经验! |
我在okhere.net里看到有这本书的复印版,很贵要48元,估计这本书在市面上已经绝版了。
18363那个精粹确实好
18363即使不同学校要求的参考书不同,多看几套教科书还是不错的!
18363邹应的数学分析习题集,大本的,绝对是有志搞研究的好参考书,很大很厚,才100多道题,题题很难,可是会一道,说明你又有了很大的进步
18363邹应得书不搞研究没必要看,考研根本没必要看,包括数分中的典型问题和方法,如果不靠名校,没必要看了,我只是说针对考试,要是学好的话还是要仔细研究的。看了耽误时间,现在考研出题方向变了,不太注重考难题了,都是些基础知识,把书看透,课后题做好,做一本中等难度的习题就可以了。
18363钱吉林的好 我也同意
18363
引用 (苦海无边 @ 2006年06月
17日
22时30分) |
[COLOR=red]请问:
金圣叹编的考研试题精选(石化出版社)
在哪个网站能下在载到
|
哪个金圣叹
18363山东科学技术出版社出过一本书,题为:研究生入学考试指导(数学分析),作者:裘卓明等.是一本好书,可惜没有看到新的版本.
18363没有见到特别好的书啊,都是一些教材。我觉得最好的办法就是找点考试题和标准答案来。
18363hao
18363钱吉林的书好,我们班同学都买他的
18363等我的书编好后,老钱的书就BB了
18363如果哪位仁兄有《实变函数与泛函分析概要》(第一册)王声望 郑维行
的电子版,请发给我好吗?这是我的邮箱:qianshourentu@126.com
十分感谢!!
18363大家好!敬请大家介绍一下:最好的数分和高代习题集是什么?特别是适合复旦数分或华东师大数分的,以及适合北大高代教材的习题集分别是什么?敬请大家积极的回答,小妹在此万分感谢!
18363请问:
1.北大的高等代数是这一本吗:http://www.china-pub.com/computers/common/info.asp?id=732202

2.我现在快大2了(但不是数学系的),做吉米多维奇的数学分析习题集应该还来得及吧?
18363
| 引用 (zdyzhj @ 2006年08月22日
20时51分) |
| 等我的书编好后,老钱的书就BB了 |
吹多啦会叫人讨厌的
18363我也要告诉大家一本好书
清华大学出版的
丘维声的高等代数学习指导
18363顶···
18363不知道有没有PDF版的
18363好介绍.谢谢了
18363这些复习书容易买到吗?到哪能买到啊?
18363可以的
18363请大家推荐几本概率论与数理统计的教材和习题参考书
我考数学专业概率统计方向,但是在书店里没找到合适的书,
书店里有很多非数学专业的概率论与数理统计教材
18363谁能提供下载
18363请问有人知道实变函数、概率论和数理统计、常微分方程的好参考书吗?
18363数学分析习题集(吉米多维奇)仍然是一本不可缺少的参考书,好多试题出于该书.
18363数学分析题解精粹(钱吉林编),我看过 .还可以吧
18363非常感谢非常感谢
18363好贴
18363大家有没有考几何的啊
解析几何是哪个版本最好
18363
补充一本
高等代数学习指导 2005 丘维声 清华大学出版社
18363好贴,谢谢
18363我想这些书够用了。
我想再说一下:数学分析的裴礼文的书好像太难了。好像不太适合。
我是只用了:钱吉林的数学分析和高等代数就行了,但是这两本书一定要熟练,最好要背一些东西。
然后就是独立的做一些个高校的考研试题,
课本要熟练,这是最主要的。
我的同学,看的就是钱吉林的书,取得了不错的成绩。
18363没有什么最好的习题集,适合自己才是最重要的.
我使用的是
数分:裴礼文的典型题解
高代:杨子胥的高代习题解
18363我顶阿
我觉得裴礼文的那本书最好啊
18363高等代数新方法(王品超,矿业大学出版社)
哪个有电子版的啊 传一下啊!
感谢了
18363我有钱吉林的数学分析解题精粹,还有他的高代解题精粹,很好用
18363现在在用钱吉林那本,不过对我来说,唯一不好的是,答案就在题下面,我有时就忍不住诱惑,就看看答案了。
发现做题什么的提高不是很快。
裴礼文是不错的。
不过我觉得那书还是挺难的。
18363刘玉琏版本挺好的!
18363好贴2...顶顶顶...
18363为什么没有人做几米多维其的啊
18363你说的是他的数分讲义,还是讲义指导?我看了他的讲义指导,觉得不错.有的地方很细致.
18363刘玉琏版本的,我用过他编的习题解答,不错的.
18363斐礼文的有解答吗
18363请问华东师范大学的 数学分析的解答在那里可以买到啊
有电子板的吗
作者是谁啊
谢谢
noargu99@yahoo.com.cn
18363这里列出的书我全部有。
18363好帖!
18363顶~顶~顶~!
18363xie xie
受益不浅
18363谢谢,去看看哦
18363这个书好像书店里面很少看到
18363复旦大学的教材(欧阳光中等编,高教社)
数学分析中的典型问题与方法(裴礼文,高教社)
高等代数解题方法与技巧
这三本书非常不错,仔细揣摩很有必要
18363用华师大的教材代替复旦的行不行?复旦的教材是那种很老的吧?80年代的
18363我觉得南开的那本书学分析也不错呀
18363谁有南开版数学分析的课后习题答案?
18363支持!
18363
| 引用 (matrix594 @ 2005年09月20日
10时10分) |
注:红色的是我认为最好的!资料只是作为参考,学数学独立思考很重要!
一、数学分析:
1、复旦大学的教材(欧阳光中等编,高教社)
2、数学分析中的典型问题与方法(裴礼文,高教社)
3、数学分析题解精粹(钱吉林,崇文书局)
4、数学分析习题集(北大林源渠、方企勤、李正源、廖可人编,高教社)
5、数学分析解体指南(北大林源渠、方企勤)
6、数学分析习题课讲义
7、数学分析经典习题集解
8、数学分析习题精解
9、数学分析导教.导学.导考(复旦第二版)
二、高等代书:
1、高等代书新方法(王品超,矿业大学出版社)
2、高等代数习题解(杨子胥,山东科技)
3、高等代数题解精粹(钱吉林,中央民族大学出版社)
4、代数学词典(钱吉林)
5、北大教材
6、高等代数解题方法与技巧
7、高等代数(北大.第三版)导教.导学.导考
三、实变函数与泛函分析
实变函数与泛函分析概要(郑维行、王声望,这本书很适合初学者!)
实变函数论的典型问题与方法
张喜堂
实变函数与泛函分析习题精解 宋国柱 |
好东西,支持!!!!!!!!!
183633q
18363
引用 (静轩路 @ 2006年08月08日
17时06分) |
《高等代数新方法》中国矿业大学出版社出版的,王品超编的,王品超就是我们学校的代数老师,今年我们学校高等代数,报他的辅导班的很少最后系里取消了。主要是王老师年龄大了,讲一节课需要休息半节课。今年我们没用他的那本资料,不过那本书真的太好了,初学者最好耐住心漫漫看。
《数学分析典型习题方法》裴礼文的这本书真的太好了,本人感觉最好配合着钱吉林的那本《数学分析习题精粹》看更好
|
是不是曲阜师范大学????
听说你们学校数学系的老师和学生都很强!
18363谢谢了.
18363我在做一本《高等数学解题技巧与方法》。这本书也不错,有很多试题缘于数学分析,是高等数学竞赛辅导书。具有相当难度。
18363补充一点:实变函数教材和辅导资料:
实分析与泛函分析(经典!!!!!)
作者:徐胜芝
出版社:复旦大学
注:可供研究生或本科生使用的一本辅导书。
实变函数教程
作者:刘培德
出版社:科学
注:研究生或本科生使用教材
函数论与泛函分析初步 (顶!!!)
作者:A.H.柯尔莫戈夫
出版社:高等教育
注:研究生或本科生使用教材
实变函数内容.方法与技巧
作者:孙清华,孙昊
出版社:华中科技
泛函分析(第2版)有英文版
作者:Walter Rudin
出版社:机械工业
研究生教材
实变与泛函基本原理与思相方法
作者:吴炯圻,周戈
出版社:厦门大学
18363高等代数优秀教材和资料补充:
高等代数
作者:姚慕生
出版社:复旦大
《线形代数》中国科技大学。李尚志、冯克勤
《高等代数》高等教育出版社,丘维声
《高等代数学》许浦华,张贤科,清华大学
《线形代数》熊全淹,武汉大学
高等代数学习指导与习题详解
作者:杨振华,李志慧
出版社:陕西师大
高等代数学习指导与习题解析
作者:李星
出版社:华中科技
高等代数学习方法与解题指导
作者:李晓奇,王晓敏,王书田
出版社:东北大学
高等代数辅导及习题全解(下册)
作者:田国华,董志伟
出版社:人民日报
高等代数辅导及习题全解(上册)
作者:田国华,董志伟
出版社:人民日报
数学分析优秀教材和资料补充:
《数学分析新讲》张筑生〈1〉〈2〉〈3〉北京大学
《数学分析》高等教育,陈纪修
《数学分析》 方企勤 ,周明强,上海科技
《数学分析》 姚允龙
复旦大学
数学分析习题演练(第一二册)
作者:周民强
出版社:科学
数学分析学习指导书(上下册)
作者:吴良森,毛羽辉
出版社:高等教育
数学分析的思想与方法
作者:明清河
出版社:山东大学
分析中的基本定理和典型方法
作者:宋国柱
出版社:科学
数学分析(一元函数部分)例题解析及难点注释(上)
作者:李惜雯
出版社:西安交大
18363数学分析习题集(北大林源渠、方企勤、李正源、廖可人编,高教社),
这本可能找不到,也邮购不到,不知道到哪里邮购????
18363山东科学技术出版社不也出了几本吗
18363谢谢
18363
| 引用 (dudu_215 @ 2005年09月23日
14时13分) |
请问
实变函数论的典型问题与方法
张喜堂
实变函数与泛函分析习题精解 宋国柱
在哪里可以买到?
谢谢
|
在南开大学西门的书店里就有,好找啊,一般书店都有 ,因为这是好书啊 !
18363xie xie
18363数学分析题解精粹(钱吉林编)里面错误太多不仅仅是印刷错误,难有大家之风范.
高代题解精粹(钱吉林编)
很多是高数的内容.
裴礼文的那本是题目很是经典 不过有些太老了.
建议打基础的同学应该看看吉米多维奇的习题解还有是杨子胥的高代习题解.
18363高等代书新方法(王品超,矿业大学出版社)
不好,题的解答有误
18363实变函数与泛函分析概要(郑维行、王声望,这本书很适合初学者!)
这本书从哪儿能下载?
18363数学分析华东师范大学编的很好啊,高代北大的不错。
18363华东师大的数学分析过于简单了
有的也不通用
总之还是好好学好自己的书做适当的题就行了
18363我觉得复旦大学编的数学分析也比较好。
18363好的 谢谢
18363考研复习实变和泛函有什么好的书么??推荐几本 谢谢
18363数学分析中的典型问题与方法(裴礼文,高教社,第二版)
高等代数题解精粹(钱吉林)
这两本书很不错的,要考浙江大学的请高度注意
高代这本书每年都有原题
18363不过好像现在很多都用华东师范大学编的呀
18363好东西啊,谢谢!!!!!!!!
18363高代还是北大的好。数分复旦的不错!
其实最权威的微积分书还是俄罗斯的《微积分教程》
18363还是要注意书本把
最少要看5边
18363
| 引用 (dudu_215 @ 2005年09月23日
14时13分) |
请问
实变函数论的典型问题与方法
张喜堂
实变函数与泛函分析习题精解 宋国柱
在哪里可以买到?
谢谢
|
这两本书好吗?我怎么不觉得啊,周明强的书很好,强烈推荐!!!
18363
| 引用 (wangyinxikeda @ 2007年01月13日
14时35分) |
华东师大的数学分析过于简单了
有的也不通用
|
你看了这本书吗?估计也就是大致的看了下吧,后面的习题你做了吗?估计是没做吧,如果你把后面的习题一个个都做了,都弄明白了,我想你考研应该是没太大的问题的,这本书是一本好的书,要是说难的书那就是中科大的了,不过没必要!
18363多谢\\\\\\
18363我支持。这几本参考书的确很好。
18363谢谢啊,真好
18363常微分方程,抽象代数,实变函数,泛函分析,复变函数和拓扑学,大家帮忙推荐几本好的参考书和资料书哈,谢了!
18363楼上的
常微分方程的参考书可以参考高等教育出版社的常微分方程学习
指导书,很不错的
配套东北师范大学的常微分方程课本
个人觉得各位大虾的观点都有各自可取的地方
不过还是那句老话只有适合自己的才是最重要的
欢迎各位与我交流探讨
我们共同努力哈
我的油箱:wangyinxikeda@163.com
本人09考
18363都不错呀,哪一本只要吃透了都行的
18363书是不错!
不过我个人觉得考研与这关系不大。
中国目前的教育制度还不能对此有很好的区分。
而且这些参考书更应该在当初学的时候就看,体会才深。
考研是一种带有功利性的行为,最好不要因此失去对数学的兴趣——就像一些国际数学奥赛的金牌选手们似的就不好了。
18363都不错,我想请问一下概率与数理统计方向有没有什么好的参考书介绍
18363
| 引用 (materzj @ 2005年09月30日
14时50分) |
高等代书新方法(王品超,矿业大学出版社)
哪里有卖? |
曲师大本校就卖王品超的高代。
18363
| 引用 (wangcz85 @ 2007年04月28日
12时36分) |
书是不错!
不过我个人觉得考研与这关系不大。
中国目前的教育制度还不能对此有很好的区分。
而且这些参考书更应该在当初学的时候就看,体会才深。
考研是一种带有功利性的行为,最好不要因此失去对数学的兴趣——就像一些国际数学奥赛的金牌选手们似的就不好了。
|
说得对阿
18363是吗
18363谢谢
18363请问你现在在哪就读?
18363黄洛生,高等代数原理和方法,福建人民出版社,福州(
1994)
强烈推荐!!!
18363支持
18363高等代书新方法(王品超,矿业大学出版社)
这本书哪里有啊?我们这里好象没卖
18363[COLOR=purple][SIZE=7][I]
考哪个学校 就应该买这个学校的教材
必须吗
18363很好的指导材料
谢谢
18363谢谢!
18363支持!不过数学分析题解精粹(钱吉林编)我看不怎么好,里面有很多的错误(印刷的,解答本身的错误),那本书我没全看!不知道大家怎么看?
18363谢谢搂主
18363大家提的建议都很好啊!再次深表感谢啊
18363史明仁的<<线性代数600题>>是好东西,我强烈推荐!
18363谢谢了!
18363请问各位学长,考华东是大的数分和高代用哪本参考书好啊
18363数学分析习题精解 单变量部分和多变量部分 科学出版社 也是很好的书
18363顶!!!
确实是好东东。
18363书目好全 谢谢
18363
| 引用 (huahuaandmeimei @ 2005年09月29日
21时53分) |
Is anybody
读过蒋尔雄的线性代数(
1978)的请举手!交流经验! |
我学过,还不错。适合计算方向的读者,有点像数值代数。
18363推荐刘玉涟的...,你是谁,是狒狒吗?
18363前吉林的书里的错误实在太多
18363钱的书中的错误都是很低级错误的,很容易看出来,不影响大局.
18363复变那一本比较好啊?
18363不错啊,谢谢
18363
| 引用 (huahuaandmeimei @ 2005年09月29日
21时53分) |
Is anybody
读过蒋尔雄的线性代数(
1978)的请举手!交流经验! |
读过点,来我们学校进修过。只看了最后一章
18363小弟有志于报考数学专业研究生,苦于消息闭塞参考资料极少,请大家帮忙,为小弟推荐一本比较好的高等代数参考书,拜谢
18363怎么没人说
吉米多维奇的数学分析习题集
与
菲赫金哥尔茨的微积分学教程
经典啊
18363数学分析题解精粹(钱吉林,崇文书局有没有啊
18363好帖 顶!
18363ding
18363顶!
18363顶啊 !!!
18363我觉得西北工业出版社出版的《高代-北大第三版--考研教案》也 不错,值得一看啊!
18363卓里奇的《数学分析》和柯斯特利金的《代数学引论》怎么样?
18363
| 引用 (铸剑为犁 @ 2008年03月08日
14时38分) |
怎么没人说
吉米多维奇的数学分析习题集
与
菲赫金哥尔茨的微积分学教程
经典啊
|
作吉米多维其纯属浪费时间
18363哪里有卖钱吉林的高等代数啊!
18363哪里有卖钱吉林的高等代数啊!
18363不错,很好的论坛
18363谢谢版主
18363谢谢!
18363读书不必太多,每门课精选一本,从头到尾一道不剩地专一做通就行。最要不得的是这本也想看,那本也手痒,都一知半解,马马虎虎,松松垮垮。考研朋友们切记:脚踏实地下苦功夫是唯一的决窍。任何一本书只要不太滥都有独特之处,全神贯注地读下去做下去!
裴礼文先生的书绝对是经典,没有任何材料可以超过它。一览众山小。
钱吉林的书是应试之作,缺乏系统,错误很多,题目参差不齐,劝诸位不要为其所误。
以下诸书值得推荐
清华张贤科、许甫华的《高等代数学》教材和解题方法。
《常微分方程习题集》,庄万主编,山东科技出版社。
《概率统计习题集》,南开周概容编。
《实变函数解题指南》,周民强编,北大社。
18363
| 引用 (liuxiaowei @ 2005年09月29日
07时50分) |
|
支持.数学分析题解精粹(钱吉林编),确实是好东西.我看了以后,收益非浅.上面有历年各学校的考研数学分析试题.
|
我也有同样的感受
18363有了很好的参考书,同时也要有好的方法
18363吉米多维奇数学分析习题集
我觉得很好
18363很好啊,谢谢了!
18363很好啊,谢谢了!
18363恩,不错 准备准备了
18363bu cuo!!!
18363我觉得钱吉林的那本《数学分析题解精粹》出的不是很好,
自我感觉考研复习用不大合适。
18363
18363个人感觉高代考研教案很好,里面方法归纳的很全面 !!!
我朋友用这本书考武大都没问题了
18363
| 引用 (matrix594 @ 2005年09月20日
10时10分) |
注:红色的是我认为最好的!资料只是作为参考,学数学独立思考很重要!
一、数学分析:
1、复旦大学的教材(欧阳光中等编,高教社)
2、数学分析中的典型问题与方法(裴礼文,高教社)
3、数学分析题解精粹(钱吉林,崇文书局)
4、数学分析习题集(北大林源渠、方企勤、李正源、廖可人编,高教社)
5、数学分析解体指南(北大林源渠、方企勤)
6、数学分析习题课讲义
7、数学分析经典习题集解
8、数学分析习题精解
9、数学分析导教.导学.导考(复旦第二版)
二、高等代书:
1、高等代书新方法(王品超,矿业大学出版社)
2、高等代数习题解(杨子胥,山东科技)
3、高等代数题解精粹(钱吉林,中央民族大学出版社)
4、代数学词典(钱吉林)
5、北大教材
6、高等代数解题方法与技巧
7、高等代数(北大.第三版)导教.导学.导考
三、实变函数与泛函分析
实变函数与泛函分析概要(郑维行、王声望,这本书很适合初学者!)
实变函数论的典型问题与方法
张喜堂
实变函数与泛函分析习题精解 宋国柱 |
好帖,顶!
18363

精看参考书再加本好点的习题集,不错
18364关于图的同态我最近有些不明白,请问
(1)图的同态映射是不是满射?
(2)若G同态于H,若在图H中添加若干条边得新图M,那么是否G也同态于M?
按照现在很多文献上同态的定义就应该这样,但也有一些书中定义不是这样的,如
在哈拉里的书中同态定义。
拜请明白者告知,多谢!!!
18364谢谢!
18365如下:post-38-1127
184051.gif
18365先说一个一维问题,设一元函数g(x)二次连续可微,且g(0)=g(1)=0,则

g(x)=g''(e)/12(具体证明这里就不说了)
回过来看本问,令h(z)=


f(x,y,z)dxdy,则h(z)符合上述一维问题中的g(x)条件,则有



f(x,y,z)dxdydz=h''(z)/12
接下反复用两次类似做法即可得到结论^_^
18365
牛!牛!牛!
18365
| 引用 (reijin @ 2005年09月23日
23时51分) |
先说一个一维问题,设一元函数g(x)二次连续可微,且g(0)=g(1)=0,则  g(x)=g''(e)/12(具体证明这里就不说了)
g(x)=g''(e)/12(具体证明这里就不说了)
回过来看本问,令h(z)= 
 f(x,y,z)dxdy,则h(z)符合上述一维问题中的g(x)条件,则有
f(x,y,z)dxdy,则h(z)符合上述一维问题中的g(x)条件,则有


 f(x,y,z)dxdydz=h''(z)/12
f(x,y,z)dxdydz=h''(z)/12
接下反复用两次类似做法即可得到结论^_^
|
先说一个一维问题,设一元函数g(x)二次连续可微,且g(0)=g(1)=0,则

g(x)=g''(e)/12 怎么证明这个等式???
18365哈哈,好办法
18365楼上的,该怎么证明啊??一维时??
18366请问2005年数模竞赛成绩什么时候公布?在什么地方可以第一时间查到的结果?
18366全国奖一般在12月份,省里会早一些。
18366大学生在一般在11月底,研究生赛要晚一个月左右。
18369mathematica中 Bessel 函数如何使用?
各位有没有遇到含有Bessel函数的方程,如何解呢?
18370请教我现在遇见一道挺难的递归题:
T(n) = 2*log(n) * T(n/log(n)) +
n^2.
请各位给些解法, 我想了挺长时间, 但就是没思路. 谢谢!
18370不好意思, 应该是
T(n) = (log(n))^2 * T(n/log(n)) + n^2
18370数学里面有什么方法可以消除递归吗?没听说过...
我是学计算机的,这用计算机我想也解不了吧...
18370老实说这是计算机的一道算法题. 题目是
T(n) = (log(n))^2 + T(n/log(n)) + n^2
当然base case 是 T(n) = 1 如果 n<=1.
我想计算出这题的running time. 听老师说.
这题最后的running time 会在一各常量区间内.
18370这可以用数据结构里面的递归吧 时间复杂度可以分开考虑 最简单的是你先举几个例子 然后再考虑一般的情况
18372近距离接触费马大定理证明者-怀尔斯公共报告纪实
(转自《科学时报》,胡惊雷)
在发表费马大定理的证明十年之后,普林斯顿的数学系教授安德鲁·怀尔斯2005年8月29日首次来到中国,并站在了北京大学的讲台上。
“我的方法是现代的”
安德鲁·怀尔斯(Andrew
Wiles)中国首行的第一站是北京,逗留3日后又将马不停蹄地前往香港领取2005年度的“邵逸夫奖”。此间最受国内媒体和数学爱好者关注的是他首次对中国学生作的公共报告。
8月30日在北大英才交流中心,记者有幸聆听了这次报告并目睹了大师的风采。
下午3点30分时,交流中心内较好的位置已被占据。到4点整怀尔期入场时,过道上已经站满了听众。
怀尔斯伴随着热烈的掌声缓缓走上讲台。他个子很高,身材瘦削,举止文雅,身着深色西装,里面是一件天蓝色的休闲衫衣,灰黄而稀疏的头发盖在略微有点秃的额头上,大概是由于总和比他个矮的人对话,他的背总是微微弓着,他才52岁。在后来的采访中记者可以清楚地看到他聆听问题时从镜片后射出的孩子般的单纯眼神。这单纯背后蕴含着惊人的意志,支撑着他在完全保密的情况下独立完成了最初7年的工作。而回答问题时常带着典型的英国式含蓄微笑,偶尔露出不太整齐的两排牙齿。他说话慢条斯理而缺乏抑扬顿挫,尽管生于剑桥,并分别在牛津大学和剑桥大学完成本科和博士学业,但有着很难和清晰、优雅的牛津(剑桥)腔联系起来的浑浊嗓音,加上现场音响设备的原因,以至于坐在后排的听众很难听清他演讲时说的大部分话。
怀尔斯以一系列有关毕达格拉斯定理和费马大定理的手稿复印件开头,缓缓地介绍了这个数学上“最臭名昭著的三个难题(另外两个分别是‘黎曼猜想’和‘歌德巴赫猜想’)”之一的历史,然后用充满数学公式表达的幻灯片展示了他的极少部分证明过程——一系列即便是资深数学家也很难全部理解的符号和推理,当中没有忘记提醒大家:“我认为费马极不可能如他所说的那样,在
17世纪已经解决了这个难题。”在演讲结束后的受访中他再次谈到,“现在这一领域的数学家们都很难相信可以用基础的数学方法来解决这一难题……数学家们花了350多年时间想尽基础的数学方法,但所有的努力几乎都失败了……我的方法是现代的”。
怀尔斯一成不变的声调使得这场公众报告起到了专业报告的部分作用——进行到约40分钟时,一些原本期待着高潮的同学开始走神、退场,绝大部分同学仍然坚持着,毕竟聆听这位过去十年来最吸引媒体的数学家的讲座的机会毕竟不多。
坚持下来的同学终于有了回报,当报告历时近一个半小时结束时,接下来的提问时间前后维持了40多分钟,这是同学们和怀尔斯交流的难得机会。
“再多花5年时间我也不在乎,因为这是我想做的”
问:是否从前人证明费马大定理的努力中得到任何线索?
怀尔斯:我十几岁的时候的确这样认为过,但这之后我再没有,数学家们花了350多年时间想用基础的数学方法解决这个难题,但所有的努力几乎都失败了,所以我必须用现代的方法。
问:为什么您会选择这样一个困难的问题来解决?
怀尔斯:不是我选择了它,而是它选择了我。我很小的时候就想过解决这个问题,但数学家们用
19世纪的方法进行的尝试已经失败了,当我最后暂时抛下这个命题后,我很不情愿再回头来解决这个问题,太容易就耗尽一生而一无所成,直到我看到了突破,就再也忍不住回头来解决它了。
问:您在解决过程中最大的困难是什么?
怀尔斯:最困难的问题是要盘算自己能否在有生之年解决它。我们通常相信绝大多数难题都是可以解决的,但这个问题是否属于那绝大多数呢?有关费马大定理的一个让人头疼的事实是,没有人知道解决它需要多少时间,所以你必须要足够确信这个问题可以在有生之年解决,可以被现存的方式解决,你不会想去解决一个在下一百年也无人可以解决的问题。所以你必须要有信念,在我有生之年被解决的信念。必须要有这种态度,否则你无法投身其中。在真实生活中,我也抱着相似的态度。
问:您是否认为数学是一门神秘的学科?
怀尔斯:和绝大多数数学家一样,我不是哲学家(听众迸发出笑声)。我们做数学因为我们爱做数学,我们几乎不考虑为什么。很多哲学家会问这样的问题:数学是自在的并由数学家发现的,还是数学原本不存在而是由数学家发明的?我所知的每一个数学家都相信数学是自在的,我们只是发现者,但哲学家们可能穷尽一生追问我们是发现了还是发明了数学。
问:您是否认为一些基本数学理论如数论、拓扑学等的训练对各种专业的学生都是有意义的?
怀尔斯:我认为数学对任何人来说都是有益的训练,它是对理性思维和逻辑思维的训练,同时,它培养直觉,要求一定的心理素质。因此,我尤其认为每一个政客都应该学习数学。
问:在发展证明手段方面,您对大学生们有什么建议吗?
怀尔斯:老实讲,我的证明手段很老式,纸和笔,我的同事们能熟练地借助计算机来做演算,但对我来说计算机还是个有点神秘的东西。
问:有什么建议可以给一个爱好数学的人?
怀尔斯:尽可能多地听各种各样的课,最后锁定你喜欢的研究范围,因为你不可能在并不喜欢的领域里耗上八年时间。
问:您选择独立完成这个证明。为何没有让你的学生和你一起做?是因为没有学生吗?
怀尔斯:我每年至少有三四名学生,但他们有他们的研究方向。数学家只是干自己喜欢的事。
问:您认为单独干比合作更好吗?
怀尔斯:我也有过一些合作,但证明费马大定理时我选择单独干。因为我决定把一生都投入进去,而我的合作者也许在两年后看不到成果就离开了,或者他会同时做多个项目,不管怎样我感觉单独干比较好控制……现代数学更需要合作。
问:那你每窗体顶端
天花多少时间研究费马大定理?
怀尔斯:我没有计算过,但一醒来我就想到费马,这也通常是我上床以前想过的最后一个问题。
问:您申请了经费吗?
怀尔斯:我悄悄地做研究,所以经费都是在外出讲学时申请的旅行补贴。
问:您在证明的最初7年间没有研究结果,普林斯顿没有给你施加过压力吗?在中国每个教授都能感到发文章的压力。
怀尔斯:美国的大学教授也会有一定发文章的压力。我在那期间的确没有成果,但之前我有很多文章,于是我攒着没发,而在那7年间陆续发出来,在这点上我有些小技巧。
问:您想过放弃吗?
怀尔斯:放弃吗?没有,我总感觉到我在不断接近,再多花5年时间我也不在乎,因为这是我想做的。
问:您怎样评价费马大定理和它的证明的意义?
怀尔斯:这个难题本身不重要,重要的是因为解决它而产生的数学方法。这些方法对日常生活当然没有直接的意义。”
(他在数年前接受美国公共电视网PBS的“新星”〈NOVA〉节目采访时也曾说道,“一个数学问题的好坏几乎全取决于它产生的数学的好坏,而不在于其本身的好坏”。代数数论本来是作为费马大定理的一个解决方案才粉墨登场,而现在其自身却发展成了一个目的——它的创立被认为是
19世纪代数学上最大的成就。难怪20世纪最伟大的数学家希尔伯特称费马大定理是一只会产金蛋的鹅。而对于这只鹅本身的价值,怀尔斯的英国同胞和剑桥老学长、当代著名数学家约翰·康威曾评价说,“并非所有的数学难题都毫无用处,但费马大定理是真的一无是处,它不会有任何实际价值”。)
问:您怎样看待数学的未来?或者说数学的哪个领域将会成为热点?
怀尔斯:数学领域需要解决的问题很多,现存的问题到下个世纪也解决不完,这对数学工作者是个利好消息,而解决这些问题我们需要数学各个分支的思想,如几何、分析、表示论和拓扑学等等,因为它们是互相联系的。
“数学和莎士比亚是相通的”
由于怀尔斯旅途疲惫和紧张的行程安排,记者无法专访他,他得为两天之后的香港之行储存体力和脑力以应付接踵而来的专访。记者能够继续追问他的时间只有短短几分钟——在他走完从英才交流中心到北大数学院楼上的几十米路程之前。
“您在大学学到的单一最重要的东西是什么?”
他在沉思。时间一分一秒在过去,那意味着要有两个问题将来不及问。终于他答道:“我认为最重要的恐怕是发现自己有太多更多的东西需要学习。”他的步子迈得越来越快,给他引路的老师们提醒记者马上就得结束。
“您可以为中国的大学生推荐几本自己喜欢的书吗?”
他在沉思。脚下却没有丝毫停顿。“对数学研究者我可以推荐几本书,但我并非全才,对其他领域很难推荐。如果是对所有大学生,我得说数学和莎士比亚是相通的。”
“那就是说你从文艺中获得过灵感?”记者追问。著名华人数学家丘成桐曾说他对数学的理解与他自幼就有的对文史的兴趣是分不开的。
他笑了起来:“就数学而言是的,但就证明费马大定理而言,我从未从文艺中获得灵感。”他的手已经放到了楼梯扶手上,北大数学系的老师提醒记者和跟随而来的同学“到此为止”。就在他们匆忙上阶梯的当头,记者追问了最后一个长问题:“证明费马大定理之后你对生活的意义是否有不同看法?”“是的!”他给了一个坚决的答复,人已经上完一半阶梯了。“有何不同?”记者大声追问,得到的答复是从二楼传来的爽朗笑声。
怀尔斯无疑是本世纪最引人瞩目的数学家之一,放在历史的天平上,他该如何评价自己呢?这是记者想问而没有来得及问的问题。以他的克制,他也许会回答说“我只是个追求儿时梦想的数学家而已”,也许会说“和那些开辟新领域的数学大师们比起来我做的工作很有限”,也许这个评价本身就不该由他自己做出。
“你在证明黎曼猜想吗?”这是另外一个记者关心而没来得及问的问题。他曾经承认费马大定理被证明之后有一种“伤感”,一种很难再找到挑战的伤感——如果他的目标就是想证明一个又一个猜想的话。“黎曼猜想”是他提到过的在费马大定理之后为数极少的有挑战性的难题。但是,这将是个没有答案的问题,因为即便他真的在为黎曼猜想努力,出于和证明费马大定理同样的原因,他也不大可能让人知道。
也许就在结束采访的那一刻,在世界的某个角落里已经有一个黎曼猜想终结者诞生了。某一天,他(她)会说出和安德鲁·怀尔斯同样的话:“这是我儿时的热望,任何事都无法取代。我有着极少人才拥有的特权和恩赐,去追求儿时的梦想。倘若在成年后你能实现它,带来的回报会超越一切想象。解决这个难题让我有失落感,但也让我感到广袤的自由。八年里,我从早到晚为它着魔,这段长期的漂泊终于结束了。我的心灵归于平静。”
18372太好了,这个对我很有用
18372费马大定理的证明不是不完美吗?
18372被他和Taylor补上了
18372好贴
18372顶!
18372向牛人致敬
18372hao!!!!!!!!!!!
18374在一本教科书的例题中有
∫ (
0,0)
(
x,y)
(2y-x)dx+(2x+y)dy=∫
0 x
(-x)dx+∫
0 y
(2x+y)dy.
怎么都不明白为什么不等于
∫ 0
x
(2y-x)dx+∫
0 y
(2x+y)dy.
请好心人指教
斑竹提示:请将公式编辑中的“杠”字替换为“\”,就成功编辑公式了。
18375复变函数中用z=x(t)+iy(t)表示曲线,数学分析中用
x=x(t),
y=y(t)表示曲线。但无论何种表示形式,在定义光滑曲线时都要求
x(t)与y(t)均连续可导,且不同时为零,不知“不同时为零”
在几何直观上是什么,为什么要这样定义?求!
18375保证每一点都有方向
18375且不同时为零,是没必要的
不得不承认,有些编书人就是水平不怎么样,,把简单的东西搞得很啰嗦复杂
18375
引用 (primeshu @ 2005年09月21日
17时58分) |
| 保证每一点都有方向
|
是保证每一点都有唯一的切方向吗?如何保证的?能否详细一点呀?多谢!
18375曲线的方向是x'(t)+iy'(t),如果同时为零,该点的方向不存在,曲线的很多好的结论都得不到
18376兄弟姐妹们!我发现了一个免费视频有数学专业的
http://www.hebjpk.com.cn/class.asp其中有近世代数 高等代数
数学分析
18376
引用 (yyshuxue @ 2005年11月03日
19时13分) |
| 能下载吗?????????
|
能下载吗?????????
18376不是免费的亚
18376概率论与数理统计 视频点拨
http://www.nwpunec.net/vod1/kj/gll/gll.asp
18376
http://2
19.144.245.36/vod/vodsx.php?PHPSES...63a258806cb3d5e·几何基础
·数学分析
·高等代数
·近世代数
·数学发展史
18376我顶
18376帮你顶
18376能下载吗
18376thank you
18376非常感谢!
18376帮忙顶
18376上不了
18376楼上的,打不开呀
18376非常感谢!能下载吗
18376是陕西广播电视大学的!
18376没法打开呀!!
18376上不了!!!
18376谢谢了!!
18376好!谢谢![COLOR=green]
18376thanks
18376楼上的,打不开呀
183763QU
18376怎么不能下,要燕山大学的帐号
18376打不开阿
18376打不开了,遗憾
18376谢谢!非常感谢!
18376怎么打不开呢?
18376非常感谢!
18376we can't see it
18376好像载不了了,试试下面的
http://www.abab123.com/bbs/down.asp?html=981351
18376打不开
18376被防盗链了....
18377产生这种现象的原因在于对于一般信源信道的信源信道联合编码,老的容量已无意义,如果非要比较,才会出现这种情形,即脱离信源单纯衡量信道容量是没有意义的。
18377非常想知道:Te Sun HAN的文章“an information spectrum approach to joint source
channel
coding"中提到:“有一些情况下即使信息传输率>信道容量,也可能实现可靠的通信传输”。这与香农说的“当信息传输率>信道容量,错误率一定大于一个正数”是矛盾的,那么香农的这个说法是错误的吗?应该如何来理解这个问题呢?
18377谢谢,但是我还是不太明白。
此时信道容量又该是怎样计算呢?是不是就是用信息谱的方法得到的?
您能不能说得详细点,稍微深点我理解起来就比较困难了。不好意思。
18378与微分方程模型有关的问题都是开放性的,不是吗
18378请问到哪里可以找到微分方程方面的开放性题目,或者能不能有人整理一下发出来?
18380已经知道五种不同的解答了,sigh
18380那是由于取法的分布不确定造成的
18380现在南开,北大的数学专业用的概率论教科书,大百科全书,以及中文期刊上对此问题一直无定论。但如果在明确题目条件:圆内点是均匀分布,任意弦做法(圆内随机取两点做弦,还是其他),以及弦是不可重取到,问题中的那些等可能性和其他一些条件的默认,选取符合具有变换群的不变性的测度,结合随机过程积分的判断敛散性等,那么Bertrand's
paradox 就象布丰投针问题应有正解,反之无正解。以上拙见,恳求赐教。
18381Yale Mathematics Department
The department is saddened with
news of the death of Serge Lang, who passed away Monday September
12.
塞尔日·兰(Serge
Lang,
1927年5月
19日–2005年9月12日)是美国数学家,因他在代数的工作和他编写的多本教科书(包括影响颇大的Algebra)而闻名。他的教科书定位于纯数学,以习题原创闻名。根据一个
1970年代在普林斯顿大学数学社群流传的逸闻,他的教科书至少一本是因为打赌而在一个周末写成。他是布尔巴基小组成员。
兰教授给人的印象是热心与学生交流。他获得美国数学学会的Leroy
P Steele Prize for Mathematical Exposition (
1999)。在
1960年,他获得第六个Frank
Nelson Cole Prize in Algebra,嘉许他的论文Unramified class field theory over
function fields in several variables(Annals of Mathematics, Series 2,
volume 64 (
1956), pp. 285-325)。那年Maxwell A.
Rosenlicht也获奖。他逝世时是耶鲁大学的数学荣誉教授。
他在
1951年由埃米尔·阿廷指导,获得普林斯顿大学的博士学位。
他除了是数学家,也花很多时间参与政治。最为人注意的是,他认为有人为了达到他们目的错用科学或数学,他会揭露出来。
1986年他挑战政治科学家Samuel
P.
Huntington的国家科学院院士提名,声称他的研究含有“伪装成科学的政治意见〕。他的挑战成功了。
兰把他的政治通信“存档”,一部分在他的书Challenges(ISBN
03879486
19)出版。post-52-11272
19357.jpg
18381痛悼
18381读过他的一点algebra,不知道他学问怎么样,至少书写的不错,
不是那种专搞自己学问而不懂得传授给别人的数学家。
18381
GMT中很多本他写的书.
18381值得我尊敬和学习的数学家!
18383
能谈谈strum定理(有关多项式的)吗?谢了!
18384我不是研究数学的,但数学知识需要很多。各位帮帮忙,解释一下jordan分解,jordan链的概念。
18385国际数学家大会和新世纪的数学问题
国际数学家大会和新世纪的数学问题
北京师范大学张英伯
一
四年一度的国际数学家大会于2002年8月20日至28日在北京召开,正如奥运会是国际体育界的一件盛事,国际数学家大会也是数学界的一件盛事,受到全世界数学工作者和数学家的关心与瞩目国际数学家大会能够在某一个国家申办成功有很多因素,其中该国在数学研究和数学教育方面的水平无疑是一重要因素。自
1897年开始,国际数学家大会已经举办了23届,除了由于两次世界大战有所中断外,每四年召开一次,会议的举办国有瑞士、法国、德国、意大利、美国、加拿大、挪威、荷兰、英国、瑞典、苏联、芬兰、波兰、日本,都是经济发达或比较发达,数学研究十分活跃的国家,主要集中于北美和中、北欧,在亚洲仅有
1990年的东京大会。
90年代初,著名数学家陈省身先生和他的学生,惟一的华裔菲尔兹奖得主邱成桐教授向国家主席######建议,中国可以申办世界数学家大会,借以提高我们在国际数学界的地位,促进我们的数学科研和教学。自此中国数学会开始了长达数年的申办工作。当时的中国数学会理事长是杨乐教授,他向国际数学家联盟提出了办会的申请。
我国是
1986年正式加入国际数学家联盟的,现在的国际数学家联盟(IMO)是各国数学会联合组织的机构,成立于
1952年,是世界数学家的一个松散的组织,
19世纪末成立,通常由五六个人组成的执委会主持日常工作。联盟的一项最重要的工作是确定国际数学家大会的地点和程序委员会。联盟执委会下设一个选址委员会,接收各国的申办请求并通过实地考察向联盟召开的成员国代表大会提出他们的推荐意见。联盟还负责确定国际数学家大会的程序委员会,该委员会全权决定大会的学术工作。经过中国数学家坚持不懈的努力,
1997年5月,选址委员会通过了推荐中国为2002年大会举办国的决定。
1998年8月15日,国际数学家联盟成员国代表大会在德国的历史名城德雷斯顿举行,来自世界59个国家和地区的159名数学家聚集在这里。上午十一时,当时的国际数学家联盟主席Mumford将选址委员会的推荐提交全体代表讨论。挪威代表首先发言,她说2002年正值挪威数学家Abel诞生200周年,因此挪威希望举办该次大会,尽管选址委员会推荐中国为候选国,但挪威不打算放弃申办,并要求作为候选国一起参加投票。挪威代表的发言得到丹麦、瑞典等国的支持,瑞典代表还就西藏问题向中国代表提出了责难。还有一些国家的代表对中国政府发放入境签证提出质疑。当时的中国数学会理事长、北京大学数学系教授张恭庆代表中国代表团发言,阐明中国申办2002年大会的动机、立场以及筹备情况,经过长达一个多小时的辩论终于开始了投票表决。公布表决结果时会场一片肃静,Momford主席一字一句地读道:中国99票,挪威23票,中国当选为2002年大会举办国。全场长时间热烈鼓掌,掌声未停,挪威代表走到麦克风前,向中国的当选表示祝贺,至此选址工作尘埃落定,中国数学会历经两届理事会申办世界数学家大会的努力终于获得了成功。世界数学家大会历时一百多年,第一次在一个发展中国家举行,21世纪国际数学界的第一次盛会在中国举行,这是中国数学界的骄傲和光荣。
2002年世界数学家大会组织委员会主席由现任中国数学会理事长,中国科学院数学与系统科学研究院马志明教授担任;下设大会秘书处和联络委员会,由中国科学院负责;科学委员会和服务委员会,由北京大学负责;会议论文集出版委员会,由复旦大学负责;筹款委员会由南开大学负责;资助委员会由北京师范大学负责;大会前后约有30个左右卫星会议,由中科院负责。大会开幕式定于2002年8月20日在人民大会堂举行,会址定在位于亚运村的国际会议中心。自
1998年确定2002年大会在北京召开,大会组织委员会进行了紧张的筹备,许多中国数学家为筹备大会做了大量工作。会议得到了我国政府的大力支持,国家主席######说:“中国政府支持2002年在北京召开国际数学家大会,并希望借此契机力争在下世纪初(此处是指21世纪初——本刊记者注)将中国的数学研究和人才培养推向世界前列,为中国今后的科技发展奠定坚实雄厚的基础。”财政部为大会提供了充分的经济保障,大会新闻发布会已于2001年8月16日下午四时在人民大会堂举行,各大电视台和报刊进行了报道,向全国人民宣布这一消息。
二
国际数学家大会近年来规模在3000~4000人,会期十天,主要内容是进行学术交流和颁发两项数学奖。
第一项数学奖是菲尔兹奖,
1936年始发,授予40岁以下成绩卓著的青年数学家,每届2人,后来增至4人,迄今为止共有42人获奖,此奖项在数学界声望甚高,被誉为数学界的诺贝尔奖。另一项为内万林纳奖,
1982年开始颁发,用来奖励计算机科学方面的学者,每届1人。
学术交流的形式很多,主要是由大会程序委员会(与组织委员会无关)邀请的大会报告和分会报告,大会报告俗称为“一小时报告”,由做出重大贡献的数学家介绍重要研究方向上的最重要的成就。会议还按相近学科分成十几个分组邀请若干名在近四年中作出突出研究成果的数学家作分会报告,介绍该领域中各个方向上的重要进展。因为历届委员会都是由在学术上有权威地位的数学家组成,他们提名邀请的报告从整体上看十分精彩。
由于我国直到
1986年才加入国际数学家联盟,也由于我国的数学研究曾遭受过严重的干扰和破坏,我们中国大陆的数学家尚未得到过菲尔兹奖,也没有作过一小时邀请报告,受到邀请作45分钟报告的有冯康、吴文俊、张恭庆、马志明。
在
1999年浙江大学举办的一次研讨班上,我曾遇到过上海同济大学陆洪文教授,他是华罗庚先生的弟子。大家都知道华先生解放初期回国,创建中科院数学所,在函数论、典型群、数论三个方向培养了十几名研究员,撑起了我国数学研究的一片天,陆先生说华老60年代中期就建议数论专业的学生们研究模型式,后来的事实表明,这是证明费玛大定理的主要工具。陆先生开玩笑说,如果不是文化大革命,证出费玛大定理的应该是中国人,遗憾的是,科学没有“如果”,失去的机会不会再来。
可喜的是,改革开放以后,我国的数学研究空前地发展壮大,研究论文和专著成十倍地增长,在许多数学分支,中国的科研队伍成为不可忽视的力量,在各种国际会议上,中国人应邀作报告已屡见不鲜。尽管在重大的研究领域内,我们与国际先进水平仍有较大的差距,但中国数学家已经迅速地进入了国际数学大家庭。鉴于中国数学家的努力,也出于对东道国的尊重,大会程序委员会特别请中国组委会推荐中国自己的45分钟报告人。因此,在2002年的国际数学家大会上,我们有11名左右的数学家作45分钟报告。这是一个了不起的数字。
特别值得大书特书的是,改革开放后80年代走出国门,赴欧美求学的年轻学子们,今天已有一批人成为优秀的数学家,成为许多重大数学领域的学术带头人,在世界各地的大学,特别是世界名校的数学家中,都有中国人担任重要教职,我
1999年在加拿大访问时听到国外同行开玩笑说:“六七十年代美国、加拿大每个学校的数学系都有印度或巴基斯坦教授,八九十年代每个系都有中国教授,90年代后期每个系都有原苏联和东欧教授。”在2002年的大会上,美国麻省理工学院的田刚教授作一小时大会报告,田刚曾是南京大学数学系的本科生,北京大学张恭庆先生的硕士生,邱成桐教授的博士生,在几何分析方面做出过重大贡献,他也是中国大陆出去的数学家中第一个一小时报告人,他至今仍保留着中国国籍,并每年回北大讲课。除此之外,还有14位海外华人及港澳台数学家作邀请报告,其中3位华人数学家被邀请作一小时大会报告,他们是程序委员会在世界数学家的平等竞争中推选出来的,正是由于海内外华人数学家的共同努力,中国数学才有了今天的国际地位。
特别应该指出的是,这些杰出的数学家生于中国,长于中国,在中国接受了中小学教育。中国存在着广大的青少年人才资源,中国的中等教育在国际上享有盛望,这从历届国际奥林匹克数学竞赛获奖情况可见一斑。尽管由于我们的经济尚欠发达,大学太少,高考压力过大,中等教育存在着种种不尽如人意的地方,但中等教育的主流是好的,广大中学教师是称职尽责的,中等教育的传统应当发扬光大。
北京师范大学数学系的教师们感到特别高兴的是,我们这里有两位教授光荣地当选为45分钟报告人,一位是师大的概率论专家陈木法教授,另一位是数学系聘请的长江学者,美国Rugerst大学的戎小春教授,后者曾是北京师范学院的学生,梅向明老师的硕士生,在美国获得博士学位,目前是国际上格拉莫夫几何的年轻学术带头人。
三
众所周知,在
1900年20世纪初召开的第二届世界数学家大会上,数学泰斗Hilbert教授提出了影响整个20世纪数学研究的23个数学问题,那么,什么是21世纪的数学问题呢?由谁来提出影响21世纪研究方向的数学问题呢?
2000年5月24日,在巴黎法兰西学院举行了一次特别活动(巴黎曾经是100年前Hilbert提出23个数学问题的地方)。Clay数学促进会在那里宣布了七个数学问题,并允诺对每个问题的解决者给予100万美元的奖励。Clay数学促进会是由美国实业家LandonClay组建的私人非赢利基金会,旨在传播数学知识,Clay认为“数学体现了人类知识的精华”,研究所的科学顾问由四名当代顶尖级的数学家组成,他们来自法国高等科学研究院,哈佛大学、普林斯顿大学和普林斯顿高等研究院,其中包括证明费玛定理的AndrewWiles,这一委员会选择了七个多年没有解决的重要的经典问题:
1.P与NP问题:一个问题称为是P的,如果它可以通过运行多项式次(即运行时间至多是输入量大小的多项式函数的一种算法获得解决,一个问题是NP的,如果所提出的解答可以用多项式次算法来检验。P等于NP吗?
2.Riemann假设:Riemannzeta函数是复变量S有函数,定义于实半平面R(s)>1上,表示为一个绝对收敛的级数
它可延拓到整个复平面上,这一函数在负偶数-2,-4,…有零点,称为平凡零点,Riemann猜想ζ(s)的非平凡零点的实部等于1〖〗2Riemannzeta函数由括号内给出的欧拉公式与素数分布问题紧密相连,如果Riemann假设不成立,将引起素数分布理论的崩溃。除此之外,Riemann假设还与其他一些数学领域的理论基础密切相关,因此很多数学家认为,Riemann假设是今天纯数学中最重要的未解决问题,
19世纪德国的天才数学家Riemann(黎曼),只活到39岁,留下的论文不多,但篇篇都是经典,为后人留下了一个半世纪未能解开的数学之谜。
3.Poincaré猜想:任何单连通的闭三维流形同胚于三维球面。该命题当n≥4时已被证明,也就是说,如果Mn是n≥4的可微同伦球面,侧Mn同胚于Sn,当n=3时在基本群方面遇到了本质性的困难。Poincaré是与Hilbetr同时代的法国数学家,
1900年Hilbert在第二届世界数学家大会上宣
18385顶!!
18386著名数学家陈景润纪念馆
http://cjr.netor.com/
18386顶!!
18386好!
18387A: Highway Traveling time Estimate and Optimal
Routingpost-37-1127226265.ibf
18387B题 空中加油问题
post-37-1127226443.ibf
18387C题 城市交通管理中的出租车规划
post-37-1127227738.ibf
18387D题 仓库容量有限条件下的随机存贮管理
post-37-1127228115.ibf
18388怎样解题,数学的发现,数学与猜想的下载
哪位有,帮忙一下
18388ding
18388进超星图书馆,这三本书都有。
18388可惜就是超星这几本书的扫描质量都不怎么好.这三本书都属于数学教育的书吧.干脆去图书馆复印的好,又便宜,又比较清楚.买的话有点贵.
18389
试构造一个3阶矩阵$A$,并要求满足下面条件:
1. $A$是奇异矩阵;
2.A可以写成$A=M-N$的形式,其中M是满秩矩阵.
3.$M
^{-1}N$的特征值的绝对值小于1,即谱半径小于1.
万分感谢!!!
18389
| 引用 (sonjaw @ 2005年09月20日
23时11分) |
试构造一个3阶矩阵$A$,并要求满足下面条件:
1. $A$是奇异矩阵;
2.A可以写成$A=M-N$的形式,其中M是满秩矩阵.
3.$M
^{-1}N$的特征值的绝对值小于1,即谱半径小于1.
万分感谢!!! |
这样的矩阵不存在。
理由如下:
A
=M-N⇒M
-
1A=I-M
-
1N 从而如果
|M -
1A|=0⇔|I-M
-
1N|=0
故不存在这样的矩阵。
18390正定矩阵A,B,A>B,又有正定矩阵C,求证:AC>BC,是否还要别的条件?谢谢
18390
引用 (kinga
1981 @ 2005年09月20日
23时20分) |
| 正定矩阵A,B,A>B,又有正定矩阵C,求证:AC>BC,是否还要别的条件?谢谢
|
应该要求A,B都与C可交换
否则那个大于号没有定义吧
18390不好意思,是这样的一个问题,要求证ACA〉BCB
18391请问各位:中科院数学与系统科学研究院与北大数学科学院哪个好些 读研生来看:)
18391看你是选择啥方向,北大拓扑很牛。中科院代数,数论方面很牛。
18391随便上哪个都好啊!还分什么啊!
18391呵呵 被这两个地方都录取了 最后可能选择去北大:)
18391总的来说,北大比中科院好。我有一个朋友03年烤北大,分差一点,调剂到中科院,可他没去,又在家复习了一年,还是考到北大去了。我一个同学他哥前年考浙大,由于名额有限,被调剂到中科院。别看中科院名气响,但要是读研还是北大好。工作时可选中科院。
(只代表了自己的观点,请供参考)
18391北大强呀!!!!!!!
18391如果是考研求学的话就到北京大学,要是工作的话就去中科院
18391北大好!北大好!北大好!北大好!北大好!北大好!北大好!北大好!北大好!
18391那究竟是北大难考,还是中科院难考呢?我去年参加过北大的考试,感觉不是很难啊,要是我去年认真复习的话,我估计早就考上了!不知道是不是去年是否是个特殊的一年!
感觉北大不是太难考啊!难道我的感觉是错误的?
18391你有北大的试题吗,求!
18392一道高代题目post-38-1127240322.gif
18392这个题目考的是正交基的知识,下面是解答,不过向量写的不严格,行向量列向量没加区分,不过这个不是主要问题,请自行整理,bless:
ps:对于欧氏空间证明成立;对于一般的正如springboshi所说。对springboshi表示感谢!
post-38-1127261135.gif
18392
对于实矩阵 A
1 ,上述解法可以;
但若 A
1
是复矩阵,则结论是错误的。
例如,考虑n=3,且
A 1
=(1,i,0),
则可取 α
1 =α
2=⋅ ⋅ ⋅
=(1,i,0)
T
,
所以
A 1
,A
2,⋅ ⋅ ⋅
是无穷序列。
18399y'=e^x*lnx*cosX
y''=e^x*lnx*x^{-1} *(-sinX)
=-e^x*lnx*x^{-1} *sinX
y'''=e^x*lnx*1/x*(- x^{-2}
)*(-cosX)
=e^x*lnx* x^{-3}
*cosX
y''''=e^x*lnx*1/x*(- x^{-2}
)*(-1)*(-2)*x^{-3}*sinX
=-2*e^x*lnx* x^{-6}
*sinX
y'''''=-2e^x*lnx*1/x*(-6)*x^(-7)*cosX
=12e^x*lnx*x^(-8)*cosX
y''''''=96*e^x*lnx*x^(-9)*sinX
然后大概可以用归纳法作出求Y的N阶导数
18399也可以用数学归纳法证明一下.post-8-1127278706.gif
18399你强,向你学习~!!!
18399Y=e的X次方 *sinX
求Y的N阶导数.post-8-112727
19
18.ibf
18399用莱不尼茈公式或者把sin x用欧拉公式表示
18399呵呵,这是数学分析课本上得的习题哈,有现成的答案
18400我是一个新手,请教各位怎样才能获得积分?
回复:参见http://www.math.org.cn/forums/index.php?showtopic=10
18401matlab下一个奇异的伴随矩阵怎么求啊?
18401利用A*A^=det(A)*E,则A^=inv(A)*det(A)
18402平面上的一组点集 ,是否“存在重心”这一说法,若有怎么定义的,有什么书可以参考吗 ?
18402我想是不是这么定义的:D是点集,

_D
(x,y)dm2(x,y) 为其重心, m2为2维
勒贝格测度
18402贴一篇老文章
发信人: etikenol (其实应该倒过来的), 信区: Mathematics
标 题: Re:
问题二:测度和重心的问题
发信站: 北大未名站 (2004年03月12日22:48:43 星期五),
转信
问题提的不是很严格,不过粗略的说,在某种意义下,测度存在能推出重心存在.
粗略的说,一个集合存在重心,指某种作用在全空间上的效果与在重心这点的作用效果
等价.但想一想就知道,这种作用不可能有太大的任意性,只能加一些诸如线性之类的
限制才能成立,这样要重心有定义,我们自然需要在空间上加个线性结构.如果空间是
无穷维,直观上看只加线性的条件还是任意性太大,于是自然要求这个集合有拓扑.
在上述思想的指引下,我们可以引入如下定义:
设A是一个局部凸线性空间中的一个紧凸子集,m是A上的一个Borel概率测度.如果存在
一点b\in
A, 使得对所有连续线性泛函f, f(b)=\int_A fdm,
则称b为A关于m的重心.
可以证明,在上述条件下,重心存在唯一.
详情可见Phelps, Lectures on
Choquet's theorem.
【 在 einstain (:)) 的大作中提到: 】
:
对于一般的欧式空间里的点集我们可以定义测度也可以定义重心
: 问题
: 测度存在的点集和重心存在的点集是否一致?
18404a1+a2+...an= 2^n-1求a1^2+a2^2+.....an^2=?
18404Sn=2^n-1
An=2^(n-1)
Bn=An^2
B(n+1)/Bn=4
a1^2+a2^2+.....an^2=Tn
Tn=(1-4^n)/(1-4)=(4^n-1)/3
不知是否考虑周全了
18409熊金成写的电集拓扑课件
18411假设有N个正态分布的随机变量b_1,b_2,...b_N,他们的均值a_1>a_2>...>a_N,现在我每次取最大的三个数,我的目标是每次都能取到b_1,b_2,b_3.(即均值最大的前三个数)。假设我正确的取到了b_1,b_2,b_3,那么false
alarm rate
(FAR)就是0,假设我只正确取到了其中的两个,FAR就是1/3,如果是只取到了一个,FAR就是2/3,....现在要求E(FAR)。谢谢赐教
18411参见顺序统计量的内容
18411哪里能弄到?给个连接或是书名,万分感谢
18411我的问题里随机变量分布是不同的,我查了一下order statistics,
没有看到分布不同的随机变量排序。另外我对概率不是太数,能不能详细的告知解题过程?谢谢
18411...恶,均值不同...这个就比较难办了...方差也不同么?
18411这些正态变量互相独立?方差分别是多少?
你这个问题可化成求正态变量在一个区域里取值的概率,可以写成一个高维积分,
一般积不出来,可考虑数值算法
18411这些变量互相独立,如果近似的话,可以假设前三个的分布一样,后(N-3)个的分布一样,如果这样近似的话,有没有可能解出来?
18411那就好办,先算后n-3个的最大顺序统计量,再算前3个的最小顺序统计量,再求两个差的分布
18413求救:Matlab 7.0的安装方法!!
我已经下完了。总共1.3G,解压后不会安装,求救!!怎么安装???
18413在里面先找到安装文件就行了,没有什么特殊之处
18414
引用 (casio24 @ 2005年10月09日
16时
17分) |
*Science网上杂志找文章。对中国人完全免费!
请问网址是什么?
|
可能日期已经过了。网上找找入口,很多的
18414谢谢搂主共享
18414谢谢
18414
搞研究的人离不开文献, 一下是获得最新专业资料的一些途径:
*根据作者E-mail地址,向作者索要。
这是最有效的方法之一,可以直接向作者索取原文,但一定要简洁!如果作者有自
己的主页,可以去作者的主页看看。不过一般查找作者的主页倒不容易!记住信箱尽量
大一点,否则一些大的文件搞不定!
Dear Mr./Mrs.: ________(Author name)
I am a graduate
student of XXX(您的学校) in China. I major in "__
______"(您的专业).
Recently, I found one of your articles, titled
&qu
ot;__________" (Title)in XXX(). I found it may help me
achieve my goa
ls in this research field. This would make a really
positive contribution to
my work. I would like to be able to read the
full text of this article. The
abstract makes the article sound very
interesting. I know there is usually
a fee required to obtain the full
article from XXX; however, as a student, m
y only income is a small
scholarship which is about U S $30.00 per month. I
wonder if you
would consider sending me the full text by Email. Perhaps you
would
consider this as an act of friendship between our two countries.
Thank you for your kind consideration of this request.
Sincerely:
___________(your name)
My Email address is: ____________________
(your email)
Date:Month/day/year
*利用一些软件NoteExpress,reference manager等等
这些软件的demo版本网络里面都可以有下载,一般自己会收录一些引擎,不妨自己
试一试,而且作学术这些软件至少要有些了解啦!
noteExpress简明教程:
http://www.scinote.com/supportcn ...
/576-NoteExpress.ra
r
免费下载地址:
http://www.scinote.com/support/cgi-bin/dow...ownload_chs.cgi
*利用搜索引擎:
英文采用著名的搜索引擎,如Lycos,HotBot,Yahoo,输入详细的关键词(一定要
具有特征性,防止搜索出太多的东西),末尾加PDF可能效果更好些。要是觉得不方便就
到www.5566.org进入后点搜索,里面收集了十多个引擎,足够你查的,不过一般百度和
google比较好!Lycos也不错。关键词很重要,要掌握一些技巧,否则不是漏检就是眼前
是个文件的海洋,捞不到针!
下面补充一些重要的学术引擎:
综合通用
英文
AltaVista>http://www.altavista.com
LYCOS >http://www.lycos.com
YAHOO! >http://www.yahoo.com
EXCITE >http://www.excite.com
INFOSEEK >http://www.infoseek.com
HOTBOT >http://www.hotbot.com
EVLAST >http://www.evlast.com
GALAXY >http://www.galaxy.com
NORTHERNLIGHT >http://www.northernlight.com
OPENTEXT
>http://pinstripe.opentext.com
中文
Sohu >http://www.sohu.com
Yahoo>http://www.yahoo.com.cn
综合科技
Scicentral &
SciQuest >http://www.sciquest.com
Martindale’srefrence
>http://www-sci.lib.uci.edu/HSG/REF.html
EEVL >http://www.eevl.ac.uk
英文期刊的搜索可以用 citeseer来搜.他有很多相关性比较和引用.很不错.
*
按部就班,根据文章出处,去图书馆查找原文。
这个自然不用多说,大家都会。
*付费中文全文数据库
中文文献,大多需要买。中文文献价值一般欠高!不建议个人购买!(个人意见)
万方数据库(万方系统中有1000余种电子期刊,以理工科技类为主,全部是国内出
版的中文和英文期刊,比印刷版略晚。CNKI、999都是全文,花钱吧就没价值了。这里面
查的时候注意到里面分为很多小的库,不要漏查!很多可以直接得到文字资料,但很多
没有全文,尤其是一些镜像站点的库!
CNKI(CNKI:中国期刊网提供三种类型的数据库,题录数据库、题录摘要数据库和
全文数据库,其中前两者属参考数据库类型,只提供目次和摘要,可在网上免费检索,
全文数据库需付费。)中“期刊题录数据库”是免费的。和重庆维普资讯公司有一定的
相似性,但是看起来舒服一些,一般是近年来的。没有重庆维普资讯公司的年代久!查
的时候还有重复文献。可以识别得到文字资料,英文的或者一些符号会有错误要自己修
改。
重庆维普资讯公司(收录有中文报纸1000种,中文期刊12000种,外文期刊4000种,拥
有固定客户2000余家。维普有两种注册用户,一种是可以查阅全文的,这种是要收费的
。另外就是一般注册用户,是使用免费资源的,比如全文检索,讨论版等等。
收费用户
中采用包库方式的机构用户或个人,我们将在年末附送期所包库的光盘版作为保存用。
流量计费的用户在累计一定金额后,我们将增送使用时间或是光盘版。同时提高其会员
级别,将获得更优惠的使用费用。)可以识别得到文字资料,英文的或者一些符号会有
错误要自己修改。
超星图书馆(若要文章,可通过超星图书馆,从网易上下载超星图书馆专用下载器
即可免费下载了!极好!您可免费下载十万种书,否则你也可以直接阅读。)有些学校
购买过就不要钱。一般书比较大,建议有用的可以刻光盘!
好医生网站、37C提供部分全文。
对了前面四个是中文查新必查的四大中文文库,可见其重要性!
这里只是介绍几个常用的啦!还有很多规模没有这么大,但是也很好。
积累一些常常去的网站
网络上的东西很多,数据库就更多。各个专业不同,目前生物化学医药的数据库分
类明确,非常多,有专业化的趋势,比如有各种专业的图谱库,序列库,微生物库等等
,有免费,有部分免费都是我们要得到的!:)下面举两个例子。
*Science网上杂志找文章。对中国人完全免费!
High Wire Press
网站,斯坦复大学主办,文献量十分大,而且free!斯坦福大学H
ighWire出版社的电子期刊斯坦福大学HighWire
Press是著名的学术出版商,目前已成为
全世界最大的、能够联机提供免费学术论文全文的出版商之一。它提供免费检索目次和
摘要的期刊为
192种,主要包括物理、生物、医学和社会学领域的核心期刊,其中有90种
可以得到全文。该站点上列出了所有可供检索的期刊名称,右边标识为free
site的期刊
是完全免费的期刊,可以看到数据库里任意卷期的全文;标识为free
trail的期刊是免
费试用的期刊,在一段试用期内可以免费得到期刊全文;标识为free
issues的期刊是指
不能看到最新出版卷期的论文,但可以回溯几个月以前或1到2年以前所有的过刊文章。
http://intl.highwire.org/Medline在Medline
18414hao
18414*Science网上杂志找文章。对中国人完全免费!
请问网址是什么?
18414不错,很好
18414henhao
18414很有帮助啊,谢谢了!
18414多谢楼主了
18414Thanks!
18414谢谢楼主,我们最需要学会查找文献资料了,要想做的好,做的快,做的东西不落后,文献资料的查找非常重要,我对这点很有体会,在做硕士毕业论文时要是我能找到某篇文章,那么我的论文早就做完了,也不用现在还来做一些重复的工作.
18414多谢
18414顶一个~~
18414很好!!
18414Very good!
18414Marvelous!
18414xiexie
18414谢谢楼主啦 偶看第一个还差不多 其他的就不用了
18414顶一个~~
18414thanks a lot
18414thank u
18414thanks!
18415到底该不该作大量习题?是做?还是尽可能去了解更多的前沿知识。学新的。有时真觉得。自己一天天在题海中,可能在做无用的事。关键是将来要出成果,而题却怎样做也不算多
18415我个人的经验是,找到你想从事的方向,然后有重点的学习相关领域的数学。
让应用指导你的学习方向。
另外,本科阶段的话,前沿技术需要做一般性的了解,不需要太过深入。把本科的计算机基础课程都精通了,才有可能真正掌握前沿技术。
当然,研究生那就是另外一回事了。
华罗庚曾经说的“初高中就去学量子物理的话,连微积分都不懂,是不可能学好的。”
同样的,本科阶段去非要钻研需要更多数学,计算机基础的高级课题,也是非常不适合的。
18415 | 引用 (justlikethewind @ 2005年09月21日
23时30分) |
我个人的经验是,找到你想从事的方向,然后有重点的学习相关领域的数学。
让应用指导你的学习方向。
另外,本科阶段的话,前沿技术需要做一般性的了解,不需要太过深入。把本科的计算机基础课程都精通了,才有可能真正掌握前沿技术。
当然,研究生那就是另外一回事了。
华罗庚曾经说的“初高中就去学量子物理的话,连微积分都不懂,是不可能学好的。”
同样的,本科阶段去非要钻研需要更多数学,计算机基础的高级课题,也是非常不适合的。
|
有理
18415也不好说,我觉得就是找方法,有了一套适合自己的方法就行,这个要靠摸索,生搬硬套别人的方法未必好~~
18415有理,顶
18416刚刚接触复变函数的知识
有些概念不太理解,望高手指教!
可去奇点的定义是洛朗展开中n<0时的系数为零。那不就意味着是幂级数了吗?
差一个常数不应该影响幂级数的收敛性,那不就意味着是解析函数了吗,怎么会是
奇点呢?
18416在收敛圆盘中心z补充f(z)=a后展式确实解析了~所以“可去”嘛~。
18416
引用 (樱析光 @ 2005年09月25日
18时26分) |
|
在收敛圆盘中心z补充f(z)=a后展式确实解析了~所以“可去”嘛~。 |
如果定义f(z)=b(不等于a),不是也解析吗?
18416f(z0)=a0,a0为级数“首项系数”。
184
17什么是edgeworth展开?
184
17分布函数或密度函数的高阶展式 可参考一些讲渐近统计方面的书
184
17能否帮我具体推荐几本,我这里资料不是很全
184
17我所知道的详细讲这个的书不多,有
Feller,An introduction to probability theory,Vol
2,section 16.2,
1971,
Jensen ,Saddlepoint
approximations,
1995
Hall,The bootstrap and Edgeworth
expansion,
1992
Pace,Salvan,Principles of statistical inference,
1997
184
17感激!
184
18用光滑样条方法求出变系数模型:
y=x^b(t)+e where b(t) is coefficient function
varying with t
e is the error
term
中系数函数b(t)的估计bb(t)后,
我们即可得出模型的偏差 x^b(t)-x^bb(t)
请问,该偏差均方
||x^b(t)-x^bb(t)||^2的数量级是多少?(n^{-1/2}??)
有谁见过相关的文献吗?
184
18没看懂,你是说收敛速度?这个没一般的结论吧,要具体分析
184
18可参见我师兄的书 变系数模型 科学出版社 2004
18422想自学解析数论,不知学长有何指教,哪位大哥有解析数论方面的入门书,能否发我一本.谢谢
primeshu@yahoo.com.cn
18422请问冯克勤那本什么书
18422先学复变函数与抽象代数啦~,科学出版社,冯克勤那本不错。代数解析数论合一本,还有一部分赋值论的内容。(还是去买一本书看吧)
18422科学出版社那本很厚的不错,适合自学!
18422《代数数论》,冯克勤,科学出版社。20元左右一本,大的书店应该有。电子版的没有。
18422多谢了,不知其他还有什么建议
18431全体代数数构成一可数集,进而证明必存在超越数。
顺便问一下什么是超越数?
18431利用代数方程只有可数个
18431超越数就是实数中除去代数数剩余的部分,是不能被表示成代数方程解的数
18432来这里的有没有大连理工的?报考的或者已经考上的
18434
∫ 0
π
arccos(a•cos(x)+b)dx
∫ 0
π
arccos(a•cos(x)+b)•cos(x)dx
以上两个积分如何求解,其中a,b是实数与x无关且 a
•cos(x)+b
的值满足arccos的定义域
既然有说看不清楚的,我就用文字叙述一遍
第一个积分的被积函数是arccos(a*cos(x)+b),
第二个积分的被积函数是arccos(a*cos(x)+b)*cos(x),
其中x是积分变量,积分区间是[0,Pi]
a,b与x无关,作为常数
谢谢各位高手帮助
18434看不清楚哦!
18434看来解析解是弄不出来了,只好做泰勒展开求近似解了
18435牛人呀!
18435谁能告诉我,以下两种期刊是哪个国家的,它的全称or网址!
Comput.Methods Appl Mech
Eng
Int J numer.methods.eng
谢了!
18435
| 引用 (cool_smile @ 2005年09月21日
20时52分) |
谁能告诉我,以下两种期刊是哪个国家的,它的全称or网址!
Comput.Methods Appl Mech Eng
Int J
numer.methods.eng
谢了! |
1) Notice du
Périodique
Computer methods in applied mechanics and engineering
Titre abrégé: Comput. methods appl. mech. eng.
ISSN: [0045-7825
(0374-2830 annulé)]
CCN:
Cote: P154
Editeur: North-Holland,
Amsterdam
URL Editeur:
Collectivité:
Historique:
Etat
Collection:
1978(vol 13) --
1982(vol 35)
Lacunes:
URL Sommaire:
http://www.elsevier.nl:80/locate/inca/505645 URL
Textes:
http://www.elsevier.nl:80/locate/inca/505645 Autre
URL
http://www-mathdoc.ujf-grenoble.fr/cgi-bin...?issn=0045-7825
2)
Notice du Périodique
International journal for numerical
methods in engineering
Titre abrégé: Int. j. numer. methods eng.
ISSN: [0029-5981]
CCN:
Cote: P125
Editeur: Wiley,
Chichester, New York
URL Editeur:
http://www.interscience.wiley.com/ Collectivité:
Historique: Titre en relation : Communications in numerical methods in
engineering [1069-8299]
Etat Collection:
1969(vol 1)-
Lacunes:
URL Sommaire:
http://www.interscience.wiley.com/jpages/0029-5981/
URL Textes:
http://www.interscience.wiley.com/jpages/0029-5981/
Autre URL
http://www-mathdoc.ujf-grenoble.fr/cgi-bin...?issn=0029-5981
18435太牛了佩服
18437诺贝尔经济学奖与数学
1975
1975年的诺贝尔经济学奖授予苏联数学家Leonid
Vitaliyevich Kantorovich(
1912-
1986) 和美籍荷兰裔经济学家Tjalling C.Koopmans
(
1910-
1986),以奖励他们对资源最优配置理论的贡献。
所谓“资源最优配置问题”就是研究怎样利用有限的资源,使其取得的效益最大。它是经济学中最基本的问题,甚至还有人认为经济学就只研究资源最优配置。这类问题一般可以表达为一个约束极值问题。Kantorovich较多地利用线性规划技巧来研究资源配置,而Koopmans则更多地把它表达为变分学或最优控制问题。如所周知约束极值问题可以用Lagrange乘子法来处理。而Kantorovich和Koopmans都发现问题中的Lagrange乘子(在线性规划情形下,Lagrange乘子就是对偶问题的解)都有特殊的经济意义,并由此提出新的经济概念。Kantorovich对此用的仍然是数学名词“解乘子”,而Koopmans则把它们称为“影子价格”。这些概念现在都已经成为经济分析中的经典。Kantorovich是前苏联的一位大数学家。他14岁就进入了列宁格勒大学数学系,
17岁解决了实分析大家Lusin提出的一些难题,并于
1930年被邀请参加全苏数学家大会。22岁晋升为正教授。他在实分析、泛函分析、计算数学等许多领域都有开创性工作。他的许多著作都曾被译成中文〖如《高等分析中的近似方法》(
1936,与V.I.Krylov合著)、《半序空间中的泛函分析》(
1950,与B.Z.Vulich,
G.Pinsker合著)、《赋范空间中的泛函分析》(
1959与G.P.Akilov合著)
等都有中译本)〗,对我国数学界有很大影响。他在泛函分析和计算数学方面的成就使他获得
1949年的斯大林奖金。
1939年起Kantorovich开始关心研究生产计划和经济问题,并出版了《生产计划和组织的数学方法》一书(也有中译本)。这是最早应用线性规划来研究生产问题的经典文献。后来他逐渐转入以研究经济问题为主,领导一批苏联数学家共同研究。为此他又获得
1965年的列宁奖金。
Koopmans虽不是专业数学家,但他在荷兰的大学学习期间却是先学习数学,后又转向理论物理。再后来,他又对马克思经济学感兴趣。最后,才开始追随他的同胞、
1969年第一届诺贝尔经济学奖得主Jan
Tinbergen学习数理经济学。他在数学物理系得到博士学位,但是提交的论文却是一篇Tinbergen指导下的经济学论文。二次世界大战期间,他移居美国,逐渐成为经济活动分析和最优经济增长理论研究的带头人。他的许多研究工作都可以看作属于运筹学范畴,因此,运筹学工作者对他也都相当熟悉。
1976
1976年的诺贝尔经济学奖授予美国经济学家Milton Friedman (
1912-),
以奖励他在消费分析、货币史和货币理论以及他对稳定化政策的复杂性的论证。
Friedman以作为主张经济自由放任的货币主义芝加哥学派的创始人而著称。他对货币史、货币在通货膨胀中的作用、货币政策的影响的研究极为深刻。对此,他回顾了
1867-
1960年的美国货币史,并构造数学模型,考察货币供应量与由此引起的收入和价格的变化之间的关系。他的“货币主义”结论,粗糙地说,就是政府在经济方面只要管好货币政策,其他都不必管。这当然在学术上引起很大争论。尽管如此,货币主义理论对欧美各国的中央银行的货币政策的影响仍然是极为深远的。
1950年以后,他更是鼓吹他的学说,积极推进基于自由汇率的国际货币体制。但是人们认为他在学术上更有意义的贡献是更新基于“持久收入”假设、而不是基于逐年收入假设的消费理论。也就是说,他用统计分析指出,人们的消费习惯确实更多地是从“终生”来考虑,而较少出于“今日有酒今日醉”。同时,他还提出经济政策中的“观察延迟”、“决策延迟”、“效应延迟”来表达某些以前被忽略的基本问题,由此可更确切地来为商情周期中的稳定化程度定时。这一观点也被一些国家的中央银行在一定程度上所接受。
Friedman出身于美国纽约州的一个东欧移民家庭。他大学时代开始时学的是数学,其志向是通过精算师考试,到保险公司工作。由于他的有些考试没有通过,他又开始对经济学感兴趣。研究生学习阶段,他同时收到了Brown大学的应用数学专业和芝加哥大学经济系的录取通知。最后他选择了去芝加哥大学,师从计量经济学家H.
Schultz。后来他又在Schultz的介绍下去哥伦比亚大学向H.
Hotelling学习。Hotelling使他受到了严格的数理统计和数理经济学的训练。这些经历都使Friedman的研究带有浓厚的数学色彩。
1977
1977 年的诺贝尔经济学奖授予瑞典经济学家 Bertil Ohlin (
1899—
1979) 和英国经济学家 James
E. Meade(
1907—
1995), 以奖励他们对国际贸易和国际资本运动的突破性贡献。
Ohlin 的最重要的贡献是他于
1931 年出版的《区间贸易和国际贸易》。在这本专著中,他用一般经济均衡的框架发展了 Heckscher 在
19
19
年发表的《外贸对收入的影响》的一文中的思想,而形成今天的国际贸易理论中的经典 Heckscher-Ohlin
定理。这一定理阐明什么因素确定外贸模式和国际分工;同时,也指出外贸对资源配置、价格关系和收入分配的效应。Meade 的主要著作则是
1951-55
年出版的《国际经济政策理论》,其中他论述了外贸经济政策的效应,并剖析了“开放”经济 (极为依赖外贸的经济)
的稳定化政策问题。他的分析尤其集中于内外均衡的必要条件,并指出成功的稳定化政策不但要考虑对商品和劳务的总需求水平,也要考虑价格和费用的关系。
Ohlin
和 Meade 的学说都相当数学化。在上述的 Meade 的著作中, Meade 甚至还专门写了两个相当长的数学附录。Meade 在
1952
年出版的一本专著的标题还被称作《国际贸易的几何学》。他们的理论自然都需要实证分析支持。但是在 20 世纪 50
年代以前,这种实证分析很难进行。而到了 60
年代以后,一方面由于经济体系的全球化,另一方面也由于计算技术的大发展,他们的理论就变得越来越受重视,实际验证也越来越多。
1978
1978 年的诺贝尔经济学奖授予美国德裔经济学家Herbert A. Simon (
1916—),
以奖励他对在经济组织内部的决策过程的先驱性研究。
Simon
的学术贡献远远超出经济学范围。他对决策过程的研究影响遍及政治学、管理学、心理学、运筹学、信息科学等。他在
1947
年出版的《管理行为》一书是一本划时代的著作。在这本专著以及以后的一系列论文中,尤其是在
1960 年出版的《管理决策的新科学》一书中,Simon
提出了一种与传统的微观经济学研究极为不同的观点。传统的观点不区分企业与企业家,并总假定他们“完全理性”地去追求一个目标:利润最大化。而实际上,随着企业的规模越来越大,企业的所有权与经营权越来越分离,企业内部的组织管理就越来越重要。他把企业描绘为一个物理的、个人的和社会成分的自适应系统,企业家被取代为许多相互合作的决策者。面对着未来的不确定性和当前搜集信息的费用,这些决策者们不再有“完全理性”,而只有“有限理性”。他们不再追求“最大”,而只追求“满意”。每个部门决策者在考虑到别人的情况后,力求对自己的问题求出“满意”解答,使得整个企业不再追求利润最大,而只寻求问题的可接受的解答。这样的思想在今天已经变成管理科学的基本观念。
Simon
年轻时就立志成为一名“数学社会科学家”。他认为社会科学应该与自然科学同样严格,同样有数学根底。因此,他在芝加哥大学学习时,向许多名家学习数理统计、计量经济学、数理经济学、政治学、逻辑学、数学生物物理、科学哲学等等。他在计量经济学方面也有不少出色的工作。投入产出矩阵有正解的存在性定理在今天称为
Hawkins-Simon
定理就是一个例子。他的管理理论带来许多数学问题。为此他发展了动态规划的技巧,导出了对于不确定性条件下的确定等价最优决策定理等等。同时,他的研究还紧密结合算法和计算机程序,并使他曾把认知过程的计算机模拟作为他的中心研究课题。因此,他也是人工智能方面的一位先驱者,并且还曾荣获计算机科学奖。总之,他确实已经成为一位当代影响最大的“数学社会科学家”。
1979
1979 年的诺贝尔经济学奖授予美国经济学家Theodore W. Schulz (
1902—
1998)
和出生于英属西印度群岛的英国经济学家 Sir Arthur Lewis (
1915—
1990)
以奖励他们对经济增长的先驱性研究,特别是对发展中国家的经济增长研究。
Schultz 和 Lewis
的研究都是非常具体的。Schultz 以一名农业经济学家而著称,而作为一位黑人学者,Lewis
更关注发展中国家的贫困问题。尽管他们着眼的都是各种经济历史资料,但是要上升到经济增长理论,仍然使他们不得不求助于数学思维和数学模型。 Schultz
对农业发展潜力的分析基于非均衡方法。运用这样的方法,Schultz
在不同的背景下对发展中国家的工业化政策和她们对农业的忽视提出详尽的批判。他首先系统分析教育投资是如何影响农业生产率和整个经济。作为一阶近似,他还定义了教育中的累计投资之和来衡量教育资本的大小。这些教育投资的成本的大部分构成就业所得在求学期间的损失。这样的观点在国家和个人两方面都能应用。在经济发展的模型中把人力资源或人力资本作为重要因素也是自
Schultz 及其学生开始的。Lewis
在研究发展中国家的经济时,提出两个著名的模型。第一个模型基于发展中国家的双重本性。一方面是首先基于自给自足的按传统运作的农业部门,它们占用了人口中的极大部分劳力;另一方面是现代市场定向的部门,主要是工业部门。经济的驱动力来自后一部门,它不断向农业部门提出无限制的劳力需求,而工人则接受对应农村中的低生活标准的低工资。现代部门中的利润使储蓄增长,形成扩张的资本积累。
Lewis
的另一个基本模型是把发展中国家和发达国家之间的贸易看成原材料和农产品与工业产品之间的贸易。在模型中有两组国家,每一组国家生产两种产品,其中一种是公共的,那就是食品。另外两种产品,在模型中称为“钢”与“咖啡”,是进行贸易的。Lewis
指出,怎样在规定的条件下,贸易取决于发展中国家和发达国家的农业生产率。
总之,他们两人的研究不但为经济增长理论作出重要贡献,并且也为如何用简单的数学模型来抓住经济现象的本质以及用实际统计数据来进行验证,作出经典性的范例。
1980
1980
年的诺贝尔经济学奖授予美国经济学家 Lawrence R. Klein (
1920—),
以奖励他创立经济模型,并把它们应用于经济波动和经济政策的分析。
Klein 是宏观经济计量模型的大师。他复兴了
Tinbergen (
1969 年首届诺贝尔经济学奖获得者) 在 20 世纪 30
年代开始的宏观经济计量分析,但是他使用不同的经济理论和不同的统计技巧。其追求的目标也有所不同。Tinbergen 针对的是商情状况和价格运动,而
Klein 则期望建立一个预测商情波动的发展和研究经济政策度量的效应的工具。
1950
年他发表了某些战争期间的美国经济的数值模型,以后又沿着同样的路线继续研究,提出更多的计量经济模型,其中最著名的是他与 Arthur
Goldberger 合作的模型,它已经在计量经济学中成为经典。
Klein
早期的论文主要是方法论性质的。例如他的第一个美国经济模型只有 6
个变量,没有任何实用价值。然而,他后来提出的一些模型就越来越有实用目的。他曾与英国、加拿大等许多国家都合作建立过计量经济模型。20 世纪 60
年代以后,他又领导过“Brookings- SSRC 项目”(SSRC
是“社会科学研究委员会”的缩写),为美国建立计量经济模型用于预测美国经济的短期发展。后来他在宾州大学创立的 Wharton 计量经济预测协会以一系列
Wharton 计量经济预测模型闻名于世。其规模虽然未能与 Brookings
模型相比,却有极好的声誉。至今人们还用它们来预测国民生产、进出口、投资、消费等等的波动,以及研究税收、公共支出、石油价格的提高等等的变化对这些变量的效应。后来他又领导更大的研究计划
LINK。这一计划的目标是协调世界各国的计量经济模型,其中包括各石油输出国家、前苏联和东欧社会主义国家以及中华人民共和国。为此 Klein 于
1980 年还带领许多美国经济学家来中国讲学。这次讲学几乎成了中国计量经济学研究的开端。
Klein
的这些宏观经济计量模型研究的影响是不可估量的。正是他把建立宏观经济模型成为一个投资巨大 (一个大型宏观计量经济模型可能耗资几亿美元)
的行业,使得世界各国政府、研究机构、公共管理部门,以至银行、大企业等都年复一年地运转计量经济模型。虽然他本人始终从事非盈利的研究工作,但是他的许多门徒开办的经营经济计量模型的公司都收入颇丰。一个宏观经济模型涉及的变量要上千个,甚至几十万个。要驾驭如此之多的变量的统计特性自然引起许多数学问题。Klein
在他的自传中特别强调数学教育对他一生的影响。正是因为他在大学期间同时修了经济学和数学,才使他进入当时方兴未艾的计量经济学领域,并成为这方面的领袖人物。
1981
1981 年的诺贝尔经济学奖授予美国经济学家James Tobin (
19
18--),
以奖励他对金融市场及其与支出决策、就业、生产和价格的关系的分析。
Tobin
的成就覆盖了许多经济学研究领域,其中包括计量经济学方法、严格的形式化的风险理论、居民和厂商行为理论、一般宏观经济学理论、应用经济政策分析等。对于数学工作者来说,首先会想到计量经济学中有
Tobit 模型。这起源于Tobin
1958
年关于耐用消费品的研究。消费者有欲望去购买耐用消费品必须在其它基本需求已得到满足时才有可能。为刻划这样的需求,必须在模型中引进特殊的定性变量。这类模型就是所谓Tobit
模型。Tobin 也被认为是 Markowitz (
1990 年诺贝尔经济奖获得者)
证券组合选择理论的奠基人,并且把它广泛地应用到居民和厂商的投资行为理论中去。他实际上最早提出二基金分离定理,即每一有效的投资组合都可由两个有效组合来生成,从而投资者面对众多证券进行组合与只对银行帐户和某一有效的基金进行组合是一样的。但是
Tobin
对经济学最重要的贡献是为凯恩斯经济学提供了最为严格的数学模型基础,并使宏观经济学与货币经济学的逻辑紧密结合。他把证券组合选择理论的观念引进对于金融资产和实在资产的一般经济均衡理论,由此来分析金融市场和实在商品市场之间是如何交互作用的。他强调金融事件对实在资产的
(投资和消费)
需求的影响,并得出两方面的基本结果:首先是所谓“传输机理”:税率变化、中央银行买卖政府债券和国库券的变化之类的货币政策和财政政策是如何影响国民收入的。其次是由货币政策和财政政策所引起的产量和价格水平的变化是怎样成为名义国民收入变化的因素。为此
Tobin 还提出工资形成问题等等。他的一系列研究对西方在 70
年代以后关于货币政策的影响、政府预算赤字的后果、一般的经济稳定化政策等研究都起着奠基作用。
1982
1982 年的诺贝尔经济学奖授予美国经济学家George J. Stigler(
1911--
1991),
以奖励他对行业结构,市场功能以及公共监管的起因和效应的系统研究。
Stigler 被认为是“信息经济学”(这也是他于
1961
年出版的专著的标题)
与“监管经济学”的创始人,是经济学与法学的交叉研究的先驱者。传统的经济学在阐述市场过程时,都有很强的假定,使得许多个别市场现象无法解释。例如,一般均衡的市场理论断言,市场上的每一种商品都只能有一种价格。但实际情况并非如此,除了没有考虑运输费用等以外,信息的不完备是一个主要原因。研究信息在市场中的作用就是信息经济学的主题。Stigler
是首先对市场上同样的商品会有不同的价格作出深入分析的经济学家。一个典型例子是人们在购买房屋、汽车、家用电器之类的耐用消费品时,会发现价格分歧很大,而消费者也会广泛收集有关信息,来使自己买到最合用的商品。
Stigler 把这样的问题模型化为效用函数的变量中还有信息变量。这一数学观念很快就被广泛运用。虽然 Stigler
本人的研究是从线性规划、价格理论的实证分析等与数学关系很密切的课题开始的,但是他关于信息经济学的工作总的来说并不很数学化。然而,他的理论框架显然为如何为它们数学建模提出许多问题。信息论在其中肯定大有用武之地。在带不确定性的一般经济均衡模型中引入信息结构,在激励机制模型中引入信息传递等等也都受到
Stigler 的影响。至于“监管经济学”更多地是与法学相联系,但是 Stigler
仍认为,经济学分析的有力工具,尤其是效用最大化的行为理论,仍能给出非常成功的预测。
1983
1983 年的诺贝尔经济学奖授予美籍法裔经济学家Gerard
Debreu (
1921--), 以奖励他把新的解析方法引进经济理论以及对一般经济均衡理论严格重新叙述。
Debreu
完全是在第二次世界大战期间由法国的 Bourbaki精神培养出来的数学家。
1946
年,当他作为数学家在法国国家科研中心工作时,他开始对一般经济均衡的数学理论发生兴趣,从此使他一生都献给了数理经济学。他甚至被认为是现代数理经济学的奠基人,因为他把Bourbaki
的公理化方法引进了经济学。他在
1959
年发表的对一般经济均衡的公理化叙述的专著:《价值理论》被认为是现代数理经济学的划时代著作。
一般经济均衡价格的存在问题是亚当.斯密以来的微观经济学的基本问题,即各经济活动者是如何通过价格体系来互相协调经济活动的。
1874 年,法国经济学家
L.Walras
把这一问题表达为数学形式:假定一个经济体中有若干种商品,若干个消费者,若干个生产者。消费者追求消费效用最大,生产者追求生产利润最大。由此引起的消费需求和生产供给都是商品价格的函数。那么是否在一定条件下,存在一个所谓一般均衡价格体系,使得供给与需求相等。Walras
认为这可归结为由供给等于需求决定的方程组的求解。但是 Walras
没有意识到他面临的方程组是一个非线性方程组,而只是简单地比较方程个数与未知量的个数来断定方程有解。这一错误很快就被人们所意识到,以至变为经济理论中的悬案。几十年来许多经济学家和数学家都对此进行过探索。
1954
年 Arrow (
1972 年诺贝尔经济学奖获得者) 和 Debreu
第一次给出了一般经济均衡的严格叙述和存在证明,其中尤其是引进了集值映射、凸性、不动点定理等数学工具。这使得 80
年来,一般经济均衡理论真正开始成为严格完整的理论体系。而《价格理论》又进一步使这一理论体系变为公理化体系。从此,数学公理化方法成为经济学研究的基本方法。
Debreu
后来还有一系列在数学上相当深刻、经济学上影响很大的研究。其中之一是他于
1970
年为了研究一般均衡的局部唯一性,提出了“正则经济学”的概念。其基本思想是把价格规范化以后,n 维价格向量可看作 n
维单位球面上在第一卦限上的向量,而超需 (需求减去供给) 映射作为价格的 n
维映射,由于它要满足财务平衡的要求,必须与价格向量正交。这样超需映射可看作n
维单位球面上的向量场,以至一般均衡存在问题变为该向量场是否有零点的问题。 Debreu 为此应用了Sard 定理和 Poincare-Hopf
定理,指出“极大多数”经济都是“正则经济”,而“正则经济”必定存在有限个一般均衡。有关研究后来引起
1960 年 Fields 奖得主
S.Smale的极大兴趣,使他后来发表了一系列题为“大范围分析与经济学”的论文。另一个问题是 Walras 均衡与 Edgeworth
均衡是否一致的问题。所谓Edgewarth
均衡是在一个不带生产者的纯交换经济中交易者们通过互利谈判最后达到的商品交换均衡。它与一般均衡价格体系下达到的 Walras均衡是否一致被称为
“Edgeworth 猜想”。
1963 年他与 H.Scarf 联合发表的论文指出,当交易者越来越多,使得同样的商品交换的机会越来越多时,
Edgeworth 均衡会趋于 Warlas 均衡。这一研究引起了对“大 (large)经济”的系统研究。其中尤其引入注目的是
1964 年
Aumann 用无原子测度空间来表示交易者全体以及
1972 年 D.J.Brown 和非标准分析的创始人A.Robinson
用非标准无限大来表示交易者的个数。后者是非标准分析历史上第一个非标准数学模型。
1974 年,Debreu
应邀在温哥华的国际数学家大会上作报告。由此也可见Debreu 的工作对数学的深远影响。
1984
1984 年的诺贝尔经济学奖授予英国经济学家 Richard Stone(
1913--
1991),
以奖励他对发展国民经济核算体系从而大大改进了经验经济分析基础的基本贡献。
Stone 从
1940
年起就开始为英国设计国民经济核算体系,使各生产部门的产出和资源消耗一目了然。由此推进了非常广泛的统计研究。他的工作很快就被推广到早年的国联和后来的联合国,使后来国民经济核算体系国际化,非常便于比较不同国家之间的经济状况。
Stone
的出发点是要在居民、企业、公共部门、世界各国之间建立起交易关系来。问题在于如何把浩瀚的个体汇总成若干个部门,并且要使汇总后的部门间的交易关系对于国民经济核算来说是有意义的。简单的归并显然不行。这就需要经济学上的考虑以及数学和统计上的处理。
Stone
的著作甚丰。可以说,他的所有研究都围绕如何用数字来度量和表示经济状况。他在他的自传中说到,他小时候热衷于做火车、轮船之类的模型,而成年后却总做数学模型。除了他的大量有关国民经济核算的著作外,他还发表了诸如《社会核算和经济模型
(
1959)》、《经济增长的可计算模型 (
1962)》、《
1920-
1938 年英国的消费支出和行为的测量 (
1967)》、《人口核算和建模
(
1970)》等专著。由这些题目我们都可看到数学建模对 Stone
的经济研究的关键作用。
1985
1985 年的诺贝尔经济学奖授予美籍意裔经济学家Franco
Modigliani (
19
18-), 以奖励他对储蓄和金融市场的先驱性分析。
对于家庭储蓄问题,Modigliani
与他的英年早逝的学生 Brumberg 于
1952-
1954
年期间用数学模型提出“生命周期假说”。在这个模型中,他们假定人们储蓄就是为了自己的一生
(特别是包括收入较低的退休期),而不是为了留给后代;他的消费只依赖于他毕生的收入,而与他当前的收入无关。于是就可得出短期储蓄取决于其毕生平均收入与当前收入的差异以及终生消费分配效用的最大化。这样的模型与实际非常符合。尤其是它能用来合理解释国民收入增加并不使储蓄率提高,穷人的储蓄率通常比富人高等现象。同时,如果这样的“生命周期假说”成立,就要得出征收消费税比征收当前收入的所得税更合理,而试图用临时性所得税来抑制或刺激消费需求是不能成功的。
对于金融市场问题,他与
Miller (
1923-,
1990 年诺贝尔经济奖获得者) 在
1958 年提出的 Modigliani-Miller
定理已经成为公司财务理论的基础。我们在介绍 Miller 时已经提到过这一定理。这里可再进一步介绍的是MMT
是用“无套利假设”通过数学推导而得到的第一条金融市场方面的定理。由此后来形成一整套套利定价理论,它是数理金融学的最重要的组成部分。除了这些得奖工作外,
Modigliani 在 60
年代一直为美国联邦储备银行负责设计大规模的美国经济模型。直到现在这些模型还在使用。
1986
1986
年的诺贝尔经济学奖授予美国经济学家 James McGill Buchanan Jr.(
19
19—),
以奖励他对政治决策和公共经济学理论的贡献。
Buchanan 所研究的理论称为“公共选择学 (Public Choice)”或
“新政治经济学”。传统经济学研究的是消费者和生产者如何在市场上根据各自的利益在生产、消费、投资、就业上作出抉择;而 Buchanan
则把政治行为理解为类似于市场行为那样来研究政治决策。政治过程由此就变成一种为达到互利的目的的合作手段。但是这种过程的结果依赖于“游戏规则”,即各种法规。这样,制订各种法规和法制改革的可能性就变得特别重要。
Buchanan
的研究中使用数学论证不多。甚至他对某些脱离经济内容的数理经济学研究有相当强烈的批评。例如,他对与公共选择学基本上研究同样问题的“社会选择学
(Social Choice)”就明确表示不满意。社会选择学可以说就是“数理公共选择学”。其奠基定理——Arrow 不可能性定理是
1972
年诺贝尔经济奖得主 K. Y. Arrow 完全用数学公理化方法来陈述和证明的。但是 Buchanan
认为,因为人们的价值观念并不能完全用社会福利函数这种数学形式来表述,这样的研究是有缺陷的。对于一些公共选择学问题的对策论研究他也持类似的态度。总之,他认为数学对于经济学来说,只是提供了一种语言上的补充,而不是全部。尽管如此,我们仍然可以看到
Buchanan
对数理经济学研究非常熟悉,并且在理解上更为深刻。因此,他对某些无视经济学实质的数理经济学研究的批评确实一针见血。这与某些对数学一无所知、却要全盘否定数学方法在经济学中的作用的来自经济学界的批评是截然不同的。此外,我们还可以看到,Buchanan
的论述就像一些法学家那样,显然隐含着一种与数学一样的强大的逻辑力量。
1987
1987
年的诺贝尔经济学奖授予美国经济学家 Robert M. Solow (
1924--),
以奖励他对经济增长理论的贡献。
长期来,经济增长理论都是经济学研究的中心论题。Solow 的贡献之一在于他在
1956
年为新古典主义经济增长理论建立了一个数学框架,使得各种经济因素在经济增长中的作用既可在理论上、也可在实际度量上得到阐明。这一数学框架是用微分方程来刻画的。
考虑技术进步时,由此可推出,对长期经济增长来说,资本、劳力和产出趋向于有同样的增长率。如果进一步考虑技术进步,那么可导出实际收入的增长将取决于技术进步。随后,Solow
又在两篇分别题为《技术变更和总量生产函数》和《投资和技术进步》的论文中进一步论证技术进步在经济增长的作用,在理论上和实际统计数据分析上都指出,经济增长中只有很小的比例可用资本和劳力的增长来解释,相当大部分的增长应归功于技术进步。Solow
的数学模型和由此给出的分析对经济增长理论和实际经济分析产生了极为巨大的影响。
Solow 在 Havard
大学攻读博士学位时,师从投入产出分析的创始人 W. Leontief (
1973年诺贝尔经济学奖得主);后来他在麻省理工学院任教时又与大经济学家
P. Samuelson (
1970 年诺贝尔经济学奖得主) 共事。这两位诺贝尔经济学奖得主都以用数学方法研究经济学而著称,对 Solow
自然都有很深的影响。Solow 的在Havard 大学荣获 Wells 奖的博士论文就用 Markov 过程来研究工资收入的变化。而他与
Samuleson 和 Dorfmann 合作于
1958
年出版的《线性规划与经济分析》一书在数学界也很受重视。此外,他还长期从事统计学和计量经济学的教学,可见其数学修养是非常全面的。
1988
1988
年的诺贝尔经济学奖授予法国经济学家 Maurice Allais
(
1911—),以奖励他在市场和资源的有效利用理论中的先驱工作。
Allais 最著名的工作莫过于他在
1953 年所提出的
Allais
悖论。这个悖论是针对所谓期望效用函数理论的。所谓效用函数是衡量消费者满意程度的函数。在确定性的市场环境下,效用函数是商品向量的函数。在不确定的市场环境下,效用函数又是随机商品向量的函数。在数学上,一个自然的数学假定是:随机商品量的数学期望的效用应该等于随机商品量的效用的数学期望。由此出发,人们列出了这种所谓
von Neumnn-Morgenstein
期望效用函数的公理体系,并证明在至多相差一个仿射变换的意义下的,期望效用函数是唯一的。于是对于不确定市场环境下的经济行为 (尤其是金融市场行为)
,就可用期望效用函数来刻画。这样的理论曾风行几十年,谁也没有提出怀疑。而正是 Allais
首先构造了一个例子,并广泛征求人们的判断,使人们发现,上述数学假定与人们日常的判断是不一致的。从数学上来说,随机变量的数学期望有线性性,而要求这种线性性在期望效用函数理论中仍然保持,就会引起与人们对风险态度的不相符。Allais
悖论提出以后,引起了大量的研究,至今仍然方兴未艾。在数学上它导致与经典概率论截然不同的不确定性理论,尤其是可提出非线性的数学期望理论。这方面的研究目前似乎更多的是经济学家在参与。
然而,Allais 获得诺贝尔经济奖主要并非因为 Allais 悖论,而是他对 Walras
的一般经济均衡理论的贡献。一般经济均衡理论是数理经济学的核心。法国经济学家 Leon Walras (
1834—
1910)
也因此被认为是数理经济学的创始人。诺贝尔经济奖获得者有许多人都是因为在一般经济均衡理论研究中有重大贡献而得奖。
1983 年获奖的 Gerard
Debreu (
1923—) 就是其中之一,他正是 Allais 的学生。Allais 的贡献则在于他于
1943 年和
1947
年出版了两本长达八、九百页的巨著,在数学上严格论述一般经济均衡理论。这就为 Debreu
最终严格证明一般经济均衡的存在性奠定了基础。
Allais 的学识极为广博。首先他也是一位著名的运筹学家。他于
1957
年发表的采矿研究论文获得
1958 年的 Johns Hopkins 大学和美国运筹学会Lanchester
奖。同时,他还是一位物理学家,在地球物理方面发表过不少重要论文,并于
1959 年获得法国天文学会的 Galabert
奖和美国重力研究基金会奖。此外,他还是一位历史学家,在 60 年代出版过一本题为《文明的兴起和衰落——经济因素》的专著。此后 20
年间不断修订再版。
1989
1989
年的诺贝尔经济学奖授予挪威经济学家 Trygve Haavlmo (
1911—),
以奖励他澄清计量经济学的概率论基础以及他的联立经济结构分析。
Haavelmo
的突破性贡献被称为计量经济学的概率论革命。计量经济学研究开始于本世纪初。当时的计量经济学只使用一些很原始的想法和很简单的回归分析。例如,根据商品的价格和消费的数据,来确定商品需求与价格的关系。这样的研究就像处理物理实验数据,很难对经济现象作出较深刻的结论。Haavelmo
在他发表于
1944
年的博士论文《计量经济学的概率方法》中指出,为了使经济理论可以用实际数据来检验,必须用概率论来陈述;这是因为经济现象涉及大量个体和厂商的行为,各种总量关系必然表现为带有随机“干扰”,以至需要对随机项的分布作一定的假定。于是统计推断理论就可得到应用,并且由此可对经济现象作一定的预测。与此同时,Haavelmo
还指出,在经济现象中各个经济变量之间的关系错综复杂,决不是简单的回归分析可以解决问题,而需要变量间的联立方程组来构造计量经济学模型。这点后来成为一本计量经济学教科书与一本实用数理统计教科书的主要数学区别。Haavelmo
后期的工作是把他的计量经济学方法运用于经济成长理论和投资理论。在这两个研究领域他都是先驱者。Haavelmo
对计量经济学所进行的概率论革命不是偶然的。事实上,概率论与数理统计也正是在本世纪 30 年代才开始严格化。Haavelmo
的早期学术生涯更多地是作为一名统计学者而出现。在概率论与数理统计现代化的影响下,他用现代数学工具来改造计量经济学正是一种必然趋势。他后来还当过挪威驻美国使馆的商务参赞,挪威工商部、财政部的官员。这使他后期就更关心现实的经济学。
1990
1990 年的诺贝尔经济学奖授予三位美国经济学家:Harry M. Markowitz (
1927—),
Merton H. Miller (
1923—) 和 William F. Sharpe (
1934—),
以奖励他们在金融经济学理论中的先驱工作。
Markowitz 得奖是因为他在
1952 年开始提出的投资组合选择 (portfolio
choice) 理论。他考虑这样的问题:如果一名投资者为减少风险而同时对多种股票进行投资,那么怎样的投资组合 (portfolio)
将是最好的?为此,Markowitz 把投资组合的价格变化量视为随机变量,以它的均值来衡量收益,以它的方差来衡量风险 (从而 Markowitz
理论又称均值──方差分析);把投资组合中各种股票之间的比例作为变量,那么求收益一定的风险最小的投资组合问题就被归结为一个线性约束下的二次规划问题。Markowitz
又进一步指出,把收益作为参量,它与求得的最小风险相应的标准差之间的关系,形成双曲线的一支;再根据投资者的偏好,由此就可进行投资决策。
Markowitz 的理论后来被誉为“华尔街的第一次革命”。
Sharpe 得奖是因为他对金融资产的价格形成理论 (
即所谓“资本资产定理模型 ( Capital Asset Pricing Model, CAPM)”) 的基本贡献。其思路起因于 Markowitz
的投资组合的风险计算涉及各种股票的价格变化之间的协方差计算,计算量极大。为简化这一计算,改用投资组合 (或更一般的资本资产)
的价格变化与“市场投资组合” 的价格变化之间的回归系数来衡量股票交易的风险。这里 “市场投资组合” 是刻划股市总体状况的量,理论上可由
Markowitz 的分析得到,实际计算时可用股市指数来得到。由此可导得每种资本资产的收益与市场收益之间的一个线性关系,它就是资本资产定价模型。与
Markowitz 理论一起,这也被看作“华尔街第一次革命” 的一部分。
Miller 得奖是因为他对公司财务
(corporate finance) 理论的基本贡献。其中以他与另一位诺贝尔经济奖获得者 Modigliani从
1958
年起提出的所谓Modigliani-Miller 定理 (MMT)
为代表。他们断言,在一定条件下,公司的市场价值只依赖于它的利润流,而与它的资本结构无关,即与债权与股权之间的比例无关,从而也与它的分红策略无关,即与债权者和股权者之间的利润分割无关。这些定理目前已经成为公司财务的理论和经验分析的基础。
这三位经济学家的工作显然都是非常数学化的。尤其是
Markowitz 更是常被看作一位运筹学家。事实上,他在
1989 年还获得过美国运筹学会颁发的 von Neumann
奖。除奖励他的投资组合选择理论外,还奖励他在稀疏矩阵计算与 SIMSCRIPT 程序语言方面的贡献。
1991
1991 年的诺贝尔经济学奖授予在美国工作的英国经济学家 Ronald H. Coase
(
1910—),以奖励他发现、澄清交易费用和产权对于制度结构和经济职能的重要意义。
Coase
认为,传统的基本微观经济学是不完全的,因为它只考虑生产和运输的费用,而忽略了执行合同与管理机构的费用。后一类费用就是所谓交易费用,它们在经济中的资源的总体利用中占有相当大的份额。一旦把交易费用考虑在内,企业的存在、不同的法人形式、合同安排中的变化、金融系统中的结构、甚至法律制度的基本特点等,都可以得到相当简单的解释。结合不同的交易费用类型,Coase
为系统分析制度在经济体系中的重要意义铺平了道路。
如果把财货和生产要素本身代替为使用财货和生产要素的权利,那么 Coase
也指出,这样的分析的力度和精度都可加强。这种权利在经济分析中称为“产权”,它可以包括完全的所有权,以及由合同条款或机构内部条例所规定的各种使用权或特殊的、有限的决策权和处置权。Coase
指出,如果交易费用很低时,每一种给定的个体间的产权的分布,都会趋向于有利于各方的重新配置,并且制度的重整会多于合同的出现。由法庭和立法者所作出的法律条文的修改也以这种重整为指针。产权因而变为经济制度结构分析中的基本成份。
Coase 甚至把它们比作经济体系中的“基本粒子”。“法律与经济”(不是“经济法学”) 形成为一门新学科是与 Coase
分不开的。
与多数诺贝尔经济学奖获得者不同的是:Coase
不喜欢数学。在他的学生时代,就是因为不喜欢数学而从理科转向商科。他的著作也是非数学化的。有趣的是,后来的研究者以及在许多微观经济学的教科书中,Coase的理论总是被赋予相当数学化的形式。他的理论要点被概括为可用数学表达的所谓
Coase 定理:如果发生外部条件的交易,那么成交过程将导致与产权配置无关的有效结局。他的关于垄断的研究被陈述为需要证明的 Coase
猜想:垄断者并无垄断权。至于在他的企业理论影响下而形成的委托──代理 (principal-agent) 理论更是完全数学化的。
1992
1992 年的诺贝尔经济学奖授予美国经济学家 Gary S. Becker (
1930-),
以奖励他把 微观经济分析的研究范围拓广到人类行为 (包括非市场行为) 及相互作用的广阔领域中去。
Becker 曾借用萧伯纳
(Bernard Show)
的话来描述他的方法论:“经济是造成生活的极大部分的艺术”。他利用微观经济分析通常的人类合理行为假定,即人的行为总是试图最大化其某个特殊的目标函数,研究了四大类问题:人力资本、家庭或住户的行为、犯罪学、市场上对劳力和商品的歧视。其中最令人注目的是他关于人力资本的研究。所谓人力资本研究即人类竞争中如何投资的研究。他对此提出了一个基本理论框架,并由此导出劳动收入的分布以及所谓人力资本所得函数。这些不仅可用来研究教育和在职培训的回报,也可研究工资差别和工资图景随时间的变化,以至研究经济增长、移民、健康部门的投资和所得等等问题。
Beker 对此在理论上和实证分析上都有很大贡献。在家庭和住户行为的研究中,Beker对住户构造了一系列类似 “小工厂”、“半制造商”
之类的模型,以此来解释家庭中人们如何分配工作和闲暇的时间,实际工资的增加如何使家务劳动专业化,越来越多的已婚妇女走出家庭成为职业妇女,同时还引起离婚率的提高等等,父母收入的提高如何使他们增加对子女的教育投资和减少子女的个数,由此来解释工业化国家的节育历史倾向以及不同国家、
不同地区的不同生育率。同样,
Beker 仍然从人类的合理行为假设以及人力资本观点出发,来研究犯罪学和经济歧视。不同于传统的看法, Beker
认为犯罪是一种带不确定性的合理行为,而种族、性别以及商品上的经济歧视都有其自身的经济学原因。
Beker
的这些研究都是相当数学化的。这是与他中学时代热爱数学,并希望把数学用到社会问题研究中去是分不开的。在 Princeton
大学上学时,他系统学过近世代数、微分方程等课程,在芝加哥大学当研究生时,又听过 Savage
的主观概率和统计基础的课程。正如他在自传中说,由于他在数学上的巨大投资,使他能很好地不断增加数学在经济中的应用。
1993
1993 年的诺贝尔经济学奖授予美国经济学家 Robert W.
Fogel (
1926-)和 Douglass C. North (
1920-),
以奖励他们通过应用经济理论和定量方法阐明经济和制度变化来更新经济史研究。这两位经济学家是所谓“新经济史学”或“计量经济史学
(cliometrics)”的前驱者。他们把经济理论、定量方法、假设检验、反向因素替代和经济史学的传统技巧结合起来,来解释经济增长和下降。他们的工作在研究如何、为何以及何时发生经济变化的基本领域中,大大加深了人们的认识。
Fogel
的突破性贡献是他在
1964年发表的关于铁路在美国经济中的作用的著作。在这著作中,Fogel提出所谓反向因素替代的历史学方法(counterfatual
historiography),
即把事件的实际过程与假设事件没有发生来作比较,以评判事件的重要性。与人们的直观印象相左,他的结论是铁路系统对于美国的经济发展并非是绝对必要的,它对美国的国民生产总值
(GNP) 的贡献小于3%. Fogel
为此广泛地运用数学模型和数理统计方法,并且有专门的程序员为他编程和处理浩瀚的数据,耗费了在当时相当昂贵的大量上机时间。Fogel
的另一项极有影响的工作是关于历史人口学的研究。他尤其是研究了几百年来的人类死亡率变化与生活标准的变化的关系。这项研究是跨学科和跨国界的。Fogel
的结论是人类死亡率降低一半以上可以用饮食标准的改善来解释,而主要不是因为现代医学的突破。对此,Fogel利用了近40000名美军的一生的健康资料,以及构造了一个超过15000个变量的数学模型来刻划这些人的一生的健康状况。
North于
1961
年提出一个影响极大的
1790-
1860
年的美国经济增长的数学模型。其中他分析了棉花种植如何引起其他部门的发展,以及如何导致专业化和地区间的贸易。随后他又在一系列著作中对他的模型强调制度对经济的作用,以至被誉为
“新制度经济学派” 的代表人物。在
1990
年发表的著作中,他进一步提出有关经济变化、技术发展和制度条件之间的联系的基本问题,指出只考虑财富或效用最大化的新古典主义经济学对于解释经济增长是不够的,创新、技术进步等只是经济增长过程自身的一部分,而有效的经济组织才是经济变化的关键。与
Fogel 相对比,Fogel总是利用大量数据来进行计量经济论证,而 North
则是一位理论家,他不断提出新的观念和思想,迫使经济学家重新考虑各种经济基本问题。但是他们都被称为是“计量历史学家 (cliometrician,
Clio 是希腊神话中的历史女神)”,即用数学来研究经济史的学者。
1994
1994
年的诺贝尔经济学奖授予美籍匈牙利经济学家 John C. Harsanyi (
1920—),美国数学家 John F. Nash (
1928—)
和德国经济学家 Reinhard Selton(
1930—),
以奖励他们在非合作对策论中的平衡分析方面的先驱工作。也就是说,这次诺贝尔经济学奖是奖给了一个数学分支──对策论。
对策论
(Game Theory) 开始是研究诸如下棋、打牌之类的游戏 (如所周知,game的原意是游戏或博弈。“对策论” 有时也译为 “博弈论”)
中的各方的策略的交互作用。早在本世纪初,数学家 Zermelo, Borel, von Neumann 就已着手研究对策的数学陈述。
1928
年,von Neumann 提出的两人零和对策的极小化极大定理通常被认为是对策论奠基的标志。而到了
1939 年,经济学家Morgenstern
与数学家 von Neumann 开始合作研究用对策论来进行经济分析,才使对策论开始成为经济学家手中的有力武器。他们在
1944
年出版的《对策论与经济行为》一书被认为是划时代的著作。Nash 的重要贡献在于他首次区分了合作对策和非合作对策,并且提出了非合作对策的所谓 Nash
平衡的概念。Nash 在
1948 年进入 Princeton 大学攻读数学博士学位。他在
1950
年通过的博士论文题目就是《非合作对策》,随后其主要结果就发表在
1950 年的美国科学院报告上和
1951 年的《数学纪要 (Annals of
Mathematics)》上。后来人们才发现,Nash 平衡的观念,早在
1838 年的法国数学家和经济学家 Cournot 关于双头垄断
(oligapoly) 的著作中就已经出现过。Selton 的主要贡献是他首先对于分析动态策略交互作用深化了 Nash
平衡的概念。而Harsanyi 则指出,怎样的不完全信息的对策可以分析,从而为极为活跃的研究领域──信息经济学提供了理论基础。他在
1967—
1968
年发表的论文题目是《具有不完全信息的由 Baysian 局中人所进行的对策》。
这里再提一下 Nash
这位带传奇色彩的数学家。他后来虽然在对策论研究上还有不少贡献,但不久就进入核心数学的研究。在数学界中,他更以其 Riemann
流形嵌入定理、Nash-Moser
叠代法等著称。可惜他很早就得了精神病,直到现在。在诺贝尔经济奖的授奖会上,他也显出语无伦次的病态。
1995
1995 年的诺贝尔经济学奖授予美国经济学家 Robert E. Lucas,
Jr.(
1937—),以奖励他发展和应用合理期望假设,从而改造了宏观经济分析以及加深了人们对经济政策的理解。所谓合理期望,是指人们在经济决策时都会考虑对未来的期望。例如,在工资形成问题中,人们会考虑今后的通货膨胀和今后的劳动需求。而这样的工资形成反过来又会影响今后的通货膨胀和劳动需求。用普通语言来表达合理期望的作用,使人常常不得要领。实际上,合理期望假设对经济学的影响是使经济数学方法发生根本性的变化。从
1989 年 Lucas 与 N. Stokey
合作发表的《动态经济学中的递归方法》一书中我们可以看到,由于应用合理期望假设使得他们所用的主要数学方法将是随机动态规划(从将来的期望最优出发来推导当前的决策),而不再是通常的微分方程或差分方程(从目前的状态来推测未来)。所谓
“Lucas 批判”几乎对传统的计量经济学给以致命的打击。以前人们认为,根据以往的数据建立的计量经济模型可以用来分析经济政策的作用。而 Lucas
认为,由于人们对当前的经济政策所产生的对将来的合理期望,使得根据过去的数据建立的数学模型将发生结构上的变化,以至这样的分析是无意义的。
Lucas
在他的自传中特别强调数学对他的研究的作用。当他在芝加哥大学念大学本科时,曾翻来覆去地学习 W. Feller
的《概率论及其应用》,从而也激起了他对计量经济学的兴趣。在 Carnegie 工学院(Carnegie-Mellon
大学的前身)工作的第一年他花了大量时间来学习动力系统理论和动态最优化理论,这为他的合理期望研究打下了数学基础。在后来几年中,他又为学习一般经济均衡理论而学习泛函分析和概率论。最后在
1970 年才用他这些年来积累的数学功底,把 John Muth 提出的合理期望思想发展成为一套成熟的经济理论。
1998
1998 年的诺贝尔经济学奖授予印度经济学家 Amartya Sen
(
1933--),以奖励他对福利经济学的贡献。
Sen
可以说又是一位经济学家中的数学家。他对福利经济学中有多项关键贡献:社会选择的公理化理论,福利与贫穷指标的定义,饥荒的经验研究。其中社会选择的公理化理论研究几乎可以说是“纯数学”的。所谓社会选择理论就是研究如何由个体选择来导出集体选择。
最为人们熟知的集体选择规则是“少数服从多数”。但是著名的“投票悖论”
指出,“少数服从多数”规则在三个以上的候选人时选举可能出现不满足传递律的情况。例如,有 A, B, C
三个候选人,对他们中的任何两人进行投票选举。那么就有可能出现 A 比 B 的票多,B 比 C 的票多,而 C 又比 A
的票多,以至无法对他们三人排出次序。Arrow (
1972 年诺贝尔经济奖获得者)
由此还建立了更一般的著名的不可能性定理,它指出,由个体选择不可能得出满足许多“应该”满足的原则的集体选择规则。早期的社会选择理论几乎都是否定性结果。而
Sen 则致力于社会选择理论的肯定性结果。例如他与 P. Pattanaik 一起提出了消除
“不传递律”的“少数服从多数”规则的充要条件。不过他也把 Arrow
不可能性定理进一步深化。他从个体权利要求出发来讨论社会选择问题,发现要得到满足个体权利最低要求的集体选择规则也是不存在的。Sen 在
1970
年出版的《集体选择和社会福利》一书影响极为深远,其中他作出杰出贡献的论题除了上面提到的以外,还有关于个体福利信息的可接受性问题,由此可讨论社会选择的不平等性。
Sen
对福利经济学的研究并未停留在纯理论分析上。他从五条合理假定的公理出发,导出下列贫穷指数: P=H×[I+(1-I)×G], 其中H
是贫困线以下的人口份额,G 是 Gini 系数 (收入不平等程度的度量),I
是收入分布的度量;后两者都只是对贫困线以下的人口来计算的。这一指数比单纯用 H
来衡量贫穷程度更深入,从中可比较出“穷中之穷”。与此类似,他又从另一些公理出发,提出福利指标: y×(1-G),其中 y
为人均国民收入。这也比单纯的人均收入要进一步。 Sen 强调指出,仅仅用人均收入来衡量社会福利是不够的,它还依赖其它因素
(例如,健康等)。许多其它福利指标,如联合国人类发展指标等都以这种思想来构造。
作为一位发展中国家的经济学家,Sen
更关心贫穷地区的经济问题。
1981 年他出版了一本名著:《贫穷与饥饿:关于赋权和剥夺的随笔》,其中他对缺粮是饥荒的最重要的 (甚至是唯一的)
原因的观点提出挑战。基于他对
1940
年以来印度、孟加拉、撒哈拉国家等地的饥荒精心作出的各种经济和社会因素的全面数量分析,他发现饥荒地区有时粮食并不短缺,甚至还有出口;例如,
1974
年的孟加拉的饥荒并非缺粮,而是由于洪水使粮价提高、农民收入锐减等引起的。
1999
1999 年的诺贝尔经济学奖授予加拿大出生的美国经济学家Robert A. Mundell
(
1932—),以奖励他对不同汇率体制下的货币政策和财政政策的分析以及对最优货币流通区域的研究。
Mundell 最重要的贡献是在
60 年代后期作出的,当时他在芝加哥大学工作。他对有资本完全流动性的小开放经济提出下列三个均衡条件:
Y
= G +Λ(Y,r,e ) (1)
D + R = L(Y,r
) (2)
R = r*
(3)
第一个方程指出国民收入等于政府公共支出G和个人需求Λ之和,而个人需求又正向依赖于国民收入和反向依赖于国内利率 r,
e是汇率,它确定国内商品和国外商品之间的相对价格;通过净出口,个人需求也正向依赖于 e 。第二个方程的左端是中央银行持有的政府债券D和外汇储备R,
右端是个人货币需求,它正向依赖于国民收入,反向依赖于利率。在均衡时,这两端相等。由于假定资本的完全流动性,国内与国外的金融资产是可完全替代的,因而在第三个方程中提出国内利率
r 等于国外利率r*。政府和中央银行可以控制G(财政政策)和
D(货币政策),而汇率e和外汇储备R依赖于汇率体制的类型。在固定汇率体制下,中央银行必须捍卫汇率,使其维持一定的水平。这时,形式上 e 是外生变量
(自变量),R是内生变量 (因变量)。而在浮动汇率体制下,汇率是由市场来确定的,于是形式上R是外生变量,而 e是内生变量。对此, Mundell
以代数形式和几何形式作了非常清晰的分析。值得注意的是在 60 年代,采用浮动汇率制的国家还极为稀少。而 70
年代以后,随着布雷顿森林体系的崩溃,采用浮动汇率的国家越来越普遍,这与 Mundell 以及另一位作了类似分析的经济学家 M. Fleming
的研究显然是紧密相关的。上述模型目前通常称为 Mundell-Fleming 模型。
Mundell
还在此基础上建立了所谓货币动力学,其中他强调了不同市场的调节速度的差异,并提出有效市场分类原理,指出汇率是如何可临时“超越”某些干扰。最优货币流通区域是他在
1961
年提出的一个带根本性的问题。他提到“公共通货”在国际贸易中的好处,例如低交易费用,低不确定性等。这一研究无疑对近年来欧元的出现有巨大影响。
Mundell
的研究把数学形式的分析、直观解释和直接政策应用的结果有机结合起来,并且以不寻常的、几乎是预言般的精度来预告国际货币布局和国际资本市场的未来发展,充分体现了基础研究的价值。
2000
2000年的诺贝尔经济学奖授予两位美国经济学家James
Heckman (
1944-)和Daniel McFadden
(
1937-),以奖励他们发展广泛应用在经济学以及其他社会科学中对个人和住户的行为进行统计分析的理论和方法。尤其是,对Heckman奖励他对分析选择性样本的理论和方法的发展,对MacFadden奖励他对分析离散抉择的理论和方法的发展。
这两位经济学家所从事的学科领域可称为微观计量经济学。如所周知,早年计量经济学主要都用在宏观经济学上,即主要研究以国民经济为主体的经济行为。微观经济学问题,即个人、住户和企业的经济行为问题;例如,决定个人在教育、就业、住房等方面选择的经济因素是什么,不同的劳动市场和教育计划对个人收入和就业有什么激励影响等等。这类问题以前很少有人研究。其原因之一是这方面的统计数据不容易找到。近三十年来,微观统计数据开始越来越丰富,使得微观计量经济学研究就有了可能。但是这里有许多新的统计上的问题要解决。例如,个人或住户行为的统计样本不一定是随机的,从而不一定有代表性;影响个人行为的某些特征是不可观察的等等。
Heckman的主要贡献是提出对统计数据的选择偏差进行纠正的简单可行的理论和方法。所谓选择偏差是指在样本选取时因数据的局限或取样者的个人行为而引起的偏差。例如,考虑受教育程度与个人收入之间的统计关系问题。一般来说,数据来源总是有偏差的。教育程度高的人群的数据容易得到,而教育程度低的数据就不容易得到,因为他们的工作可能不固定,甚至常常失业。这样仅仅以搜集到的数据来作统计分析,受教育程度对个人收入的影响就会被低估。Heckman
为此提出著名的 Heckman
修正法。这种方法分为两个步骤。第一步先构造一个基于经济理论的工作概率模型,并由此对每个个人预测其工作的概率。第二步再把这些预测概率加到原来的模型中去,作为新的解释变量,由此就得到更确切的受教育程度与个人收入之间的统计模型。Heckman
用这样的方法处理了许多类似的问题;例如,失业者再就业的时间间隔问题 (观察到的数据往往带有个人特征的影响),职业培训的估价问题
(未经职业培训的个人数据不易得到,Heckman 得到的结论是许多职业培训的作用被高估)
等。
McFadden的所谓离散抉择分析是指个人在有限种可能中作出抉择的行为分析。例如,个人对职业、住地、交通工具等等的选择,都是有限的离散抉择。在McFadden以前,对这种抉择的研究都缺乏经济理论基础。McFadden的理论从经典的微观经济学出发,即个人都有一个以备选物为自变量的效用函数,抉择的原则是使效用函数达到极大。但是由于人们不可能观察到影响抉择的所有因素,因此,统计数据也都是有偏差的。McFadden意识到观察上具有同样特征的个体群中还有随机变化,于是在模型中作了处理。由此可以预测人口中选择不同的备选物的人群比例。McFadden更为系统的贡献是他发展了所谓条件logit分析理论。这一理论可以用下列例子来说明。假设人口中面临若干种备选物,例如,备选的是交通工具:自行车、汽车、公交车、地铁等。每种备选物都有一定的特征,例如,各种交通工具的费用、所需时间等等;每个个人都有一系列特征,例如,年龄、收入、教育程度等。有关数据都可以通过统计调查得到。但此外,还有一些不可观察的特征被处理为随机“误差
项”。McFadden假定这些随机误差都有一些特殊的分布特征。在这些条件及其他技术假定下,McFadden证明,第
类人 (年龄、收入、教育程度在某范围的人) 选择第种备选物 (交通工具) 的概率可记作下列形式:
= ,
其中 代表第
类人对第 种备选物的效用, 代表第 种人对第种的某种评价,
代表第种人的某种一般评价。其他都是通过统计来确定的参数。McFadden用同样的方法研究过许多社会经济需求问题,例如,中年人对于住房、能源、电话服务等的需求问题。旧金山市的BART
(湾区快速转移) 系统的设计就用到了McFaddend的方法。
Heckman和McFadden显然又都是经济学家中的数学家。事实上,Heckman有数学学位,而McFadden有物理学位。他们的研究工作即使从数理统计的角度来看,也都有重大突破。就如Tobin
(
1981年诺贝尔经济奖获得者)
因为在宏观计量经济学中提出一种估计方法以后,就出现了Tobit这个术语,Heckman修正法也被后人称为Heckit法。它与McFadden的条件logit分析都已经成为计量经济学和数理统计学中的经典。
18437顶!
18437赞
18437顶!!
18437不知道今年那位数学家会问鼎!
18437受益良多,不知最近的资料是否贴出?
18437希望不久会有中国人或此殊荣
18437顶!
18437受益良多,不知最近的资料是否贴出?
18437
| 引用 (rg9903 @ 2006年05月06日
16时16分) |
| 受益良多,不知最近的资料是否贴出?
|
感动
18437为何这些人基本都是美国(籍)的
18437数学是一门科学,也是一门艺术。
18437顶!
18439我参加了呀,不过那个题有好的处理方法吗?
我的QQ:249065472.
shuynxust@yahoo.com.cn
18439那个题从头到尾我就没写出一个公式,全是用matlab统计出来的图表.
唯一可以算是公式的就是后面用来预测未来的拟合函数
18439我今年大三,参加了高教的数学建模比赛,做的是A题!!!
做得头晕...
有参加的来跟贴
18440分析post-38-11273108
17.ibf
18440我晕哦,怎么这么简单的题目我做的这么复杂,而且答案匪夷所思!
大家具体给个简单的方法吧!post-38-1127314038.gif
18440很明显他那个ds是标量,积分不可能是零。曲面是个倒立圆锥体的表面,积分为
∫ 0
1
z
2*2πz*2
dz+∫
0 1
r
2*2πrdr=π
2 (
1+2
)
18440我只有答案,是 (


2)(1+ 杠sqrt{2} )
18440如下:post-38-1127377
178.gif
18440我也知道我的错误了,可是就是不知道为什么错误了!
18441碰到一个问题需要求解多项式方程组。
用Grobner基和吴方法对系数的精度要求很高,有哪位大虾对此有研究,有数值求解的程序,或者提供下载地址,谢谢了呀。
18444求书:《生物数学》(《Biology Mathematics》
18444me too
18444www.china-pub.com
网上购书,送书上门,很方便的,如果等电子版的话可能是没戏了,有6、7百页。
我买过一本,一般的书店是没有的。原价120
18444我也想要一份,十分感谢!!!!!!!!!!!
我的邮箱:jgy_1121@163.com
18445请高手解决二道数分题(2)谢谢!post-21-11273487
17.ibf
18445好久不来了
贴个解答吧:post-21-1127373697.ibf
18445好就不见!谢谢tobyqin的解答。
18446看附件post-38-1127389683.ibf
18446请问大家,“若f(x)在区间I上为凸的,则f(x)在任一内点x上连续”,为什么连续呢?
由凸性只能知道 左导数小于右导数啊。
18446还有就是,在该点的导数不存在吧?
为什么一定是在内点,端点没有这样的性质么?
18446用反证法容易证明啊!其实如果函数的导数单调,就一定可以推出函数是连续的!
而如果是不可导的凸函数,通过连续性的定义也容易知道必须是连续的!如果不连续就会违背凸函数的性质!
18446这是我的小小见解,希望有用!!post-38-1127364271.ibf
18446若f(x)在区间I上为凸的,可证f(x)左(右)导数都存在,故f(x)既左连续,又是右连续的,则f(x)在任一内点x上连续.
不过,要证f(x)的单侧可导,还是有点困难的,可以参考北师大"微积分教程"第2册,其它许多教材中也有,或者习题中有提示.
注意:仅能得到左(右)导数都存在,但左(右)导数未必相等.
18446用反证
18446那个小小见解的好像是错的哦
18446请明示我的错误。!!
18446是小于啊,不是大于啊!!
其实还有一种方法做的,跟这个类似的
18446另f(x)= x ^2
18446
引用 (hfg
1964 @ 2005年09月22日
15时13分) |
若f(x)在区间I上为凸的,可证f(x)左(右)导数都存在,故f(x)既左连续,又是右连续的,则f(x)在任一内点x上连续.
不过,要证f(x)的单侧可导,还是有点困难的,可以参考北师大"微积分教程"第2册,其它许多教材中也有,或者习题中有提示.
注意:仅能得到左(右)导数都存在,但左(右)导数未必相等.
|
对
凸函数为绝对连续函数
18446
| 引用 (dudu_215 @ 2005年09月22日
09时01分) |
请问大家,“若f(x)在区间I上为凸的,则f(x)在任一内点x上连续”,为什么连续呢?
由凸性只能知道 左导数小于右导数啊。
|
由凸性可以得到左右导数存在,从而在内点左右连续,因此也就连续
18446班竹的解答不错呀
18446裴礼文的<<
数学分析中的典型问题与方法>>中有证明,而南开的<<数学分析>>下册第一章里有它的推广形式,你可以看一看
18446前面的同学基本上把问题解决了
至于在端点处,我们可以把在端点处连续的凸函数改变端点处的函数植,让它还是凸的但不连续就可以
左右单侧可导,你可以作一个图,接着证连续的后面观察图形,用夹逼定理可以得到
我顺便问一个简单问题,有的书上分上凸和下凸函数,有的书上是凸、凹函数(这种分法我总是记不住,分为上凸和下凸函数就好记了。:) )
现在比较标准的说法是怎样的?
184464654post-38-1130304587.ibf
18447
| 引用 (snail2046 @ 2005年09月22日
09时53分) |
|
小弟是研一的新生,是应用数学方向的,最近学习严加安<<测度论讲义>>,太难了,请教一下学长们,有没有课后习题可以参考,或者请教一下怎样学这本书.小弟不胜感激!!!
|
没有这方面的习题解答,不过你可以问网上有朋友。人多力量大。哈哈。
18447小弟是研一的新生,是应用数学方向的,最近学习严加安<<测度论讲义>>,太难了,请教一下学长们,有没有课后习题可以参考,或者请教一下怎样学这本书.小弟不胜感激!!!
18447
好象没有专门的习题解答,你可以问一问北大的老师.我听过他们讲的这门课,感觉不错!
18447这个版里面不是有答案么。人家都发了,你自己注意啊
18448本人初学计算数学,是用的复旦大学出版社出版的<微分方程数值解法>其中提到"边界轨迹法"不知是什么方法,不知哪位大虾肯指教,或推荐一本好的参考书,本人不胜感激.
18449俺想看的的就是这个推导哈,谢谢!
18449求和:
1^m
+2^m+3^m+4^m+.....+k^m=?
其中m,k均为正整数。
请问有这样的求和公式么?
18449没有所谓的公式不公式的,只有所谓的结论!
如果你可以对于任意的m求出一个关于m,n的和函数,那就是个公式!
如果没有一个很美的和函数,那就没有什么所谓的公式了要依情况来确定的
18449没有,但可以自己推导
18449coolless::怎么推导啊??比如m是3的情况,,m是4的情况
18449不要指望这里有几个人可以做出来!
如果可以做出来的话,早就有数学研究的工作者把它当作公式推倒出来了,就没有必要我们在这里推导了!
这个如果真的可以有个公式,那么这将是一个很好的论文题材!
18449这个推导还好了,就是裂项相消,然后用到低阶得到的公式就可以了:
ps:依次给出k=2,3,4的推导。post-38-1127388536.gif
18449还有一种通法,这类数列{k^m}的求和式是关于n的m+1次多项式,所以可以用待定系数法把求和式弄出
18449怪哉,居然没多少人知道。
http://mathworld.wolfram.com/BernoulliNumber.html第(39),还有(35),
ζ (
2n
)=∑
i =1
∞
1
i 2
n 也可以用伯努利数写出来。
18449谢谢大家的回复!真的很感谢!
^_^
18449
| 引用 (maths @ 2005年09月22日
10时29分) |
求和:
1^m
+2^m+3^m+4^m+.....+k^m=?
其中m,k均为正整数。
请问有这样的求和公式么?
|
好像存在这样的公式
并且是用泰勒公式得到的
我再找找
18450各位高手,能帮忙推荐几本随机过程和测度论的好书吗?我是学金融统计方向的
谢谢
18450随机过程用ross的,测度论用halmos的
18450[日]伊藤清的《概率论》,科学出版社出版。里面讲概率论联系了随机过程。还有他也有一本《随机过程,上海科技出版社,
1961.9出版,刘璋温译
。是当年日本出的[现代应用数学丛书]中的一本。比较薄,但写得挺好。伊藤清研究随机过程,被视为随机分析的创立者。并因其在概率论方面的奠基性工作而获
1987年Wolf奖。
至于测度方面的书。就halmos的最有名,而且也有中文翻译版。但是看起来可能有些困难。实在不行就先看看朱成熹的《测度论基础》,科学出版社,
1983出版的。另外在一些现代概率论的书里应该可以找到测度的章节及其在概率中应用的内容。
18450建议看测度论之前先看实变函数
18450谢谢!刚刚接触测度论感觉太难了,我们学校用的是《测度论讲义》严加安写的科学出版社出版的,自己看不懂呀。随机过程我们学校使用的教材是张波写的《应用随机过程》人大出版的也是很薄的一本小册子。因为这两门课都是基础课,所以很着急!尤其是测度论!
18450张波那本凭心而论还是不错,几乎哪方面都涉及到了,是本不错的书.如果觉得测度论太难,可以先看实变函数前面的部分,或者看Halmos那本,严加安的那本貌似是面向研究生的,Halmos那本是经典的本科测度论教材...
18450可以看严世键他们写的 概率论基础 啊,包括了学统计需要的测度论的内容,而且
也不难,用不着专门去学一门测度论
18450
引用 (zhouhui @ 2005年09月24日
17时06分) |
随机过程我们学校使用的教材是张波写的《应用随机过程》人大出版的也是很薄的一本小册子。
|
张波这本就免了吧
错误太多
还不如林元烈 老师那本呢
18451lgx/lg2=x/2
怎么解?什么叫超越方程 ?
18451这个不需要超越方程的知识的,就是一个函数题目,如下:post-8-1127373364.gif
18451好
18451楼上的观察能力厉害!
本题作辅助函数f(x)=lnx/x-ln2/2来做也很简单!
18452求助啦,matlab 中柱状图如何改柱的宽度?
18454一道高代题目post-38-1127364698.gif
18454把A变换成对角阵考虑即可
18454详细点,谢谢你
18454这类题目都是一个模式,都要通过对A进行正交或相似化成简单的形似来考虑
18456中国运筹学会2006年学术年会
征文及第一轮通知
由香港运筹学会和中国运筹学会共同协助承办的2006年INFORMS
(Institute for Operations Research and Management
Science)国际学术大会将于2006年6月25-28日在中国香港举行(详情请见会议网站http://www.informs.org/Conf/Hongkong06/)。为了配合2006年INFORMS学术大会,《中国运筹学会2006年学术年会》将于2006年6月30日-7月2日在深圳召开,会议主题为:中国运筹学面向世界。
大会主席
袁亚湘(中国运筹学会理事长)
组织委员会
主
任:张汉勤(中国运筹学会秘书长)
副主任:刘德刚(中国运筹学会常务副秘书长)
委 员:胡洁、吴凌云、
程序委员会
主
任:胡晓东(中国运筹学会学术交流工作委员会主任)
副主任:修乃华、杨晓光(中国运筹学会学术交流工作委员会副主任)
委
员:曹炳元、曹晋华、程 兵、郭田德、龚循华、韩继业、胡毓达、胡智全、简金宝、刘宝碇、刘 斌、刘光中、刘
克、刘彦奎、李建平、李少远、唐国春、邢文训、闫桂英、张 峰、张汉勤、赵云彬
大会特邀报告
q Mark S.
Daskin讲座教授
(INFORMS当选主席;美国西北大学,工业工程与管理科学系)
q David D.
Yao讲座教授
(美国哥伦比亚大学,工业工程与运筹系)
q
陈光亚研究员
(中国科学院数学与系统科学研究院)
专题特邀报告
本届年会还将邀请参加2006年INFORMS大会的一些国际知名学者和专家分别针对五个领域做专题报告:金融工程、物流管理、随机规划、数学规划、离散优化,介绍国际上相关研究方向的发展状况和最新成果,以提高国内运筹学研究和应用的水平。
希望国内从事运筹学领域研究和应用的科技工作者和研究生,踊跃投稿和积极参加本次学术交流活动,抓住这次与国内外同行进行学术交流的难得的机会。
投稿注意事项
1.
提交的论文应未在其它学术会议论文集或者期刊上公开发表过。
2.
来稿请在注明通信作者的详细工作单位、通信地址(邮编)和电子邮件地址,及联系电话和传真。
3.
论文以中英文撰写均可(中文文章须附英文摘要,英文文章须附中文摘要)。
4.
论文限用CCT-LaTex或MS-Word两种软件排版,格式可在中国运筹学会网站(http://www.orsc.org.cn/)上下载。
5.
提交的论文由标题、作者、摘要、关键词、正文和参考文献构成。论文全文应不超过6页。
6.
投稿时必须提交论文的电子版和两份打印稿。论文电子版请通过电子邮件发到orsc2006@amt.ac.cn,打印稿请通过邮局寄到:
胡洁,中国运筹学会,北京2734信箱,北京100080。
7.
提交的论文将由相关专业方向的专家评审。所有被会议接受的论文将收录到由正式出版社出版的论文集中(论文集在会议期间发给作者)。被接受的论文的作者必须到会上报告自己的论文。
会议收费说明
1.
会议注册费:注册费须通过邮局用电子汇款汇寄给胡洁。
代表类别 提前注册(2006年5月26日前汇款)
正常注册(2006年5月26日以后)
会员 450元 550元
非会员 550元 650元
研究生 220元 320元
2.
版面费标准:每篇论文360元(最多6页;每增加一页加收60元);另外,采用MS-Word排版格式的,每页加收10元。版面费于2006年5月26日前汇寄给胡洁(请注明文章编号及作者;逾期未收到版面费,论文将不能收录到会议论文集中)。
3.
收费收据:会议注册费和版面费都将开正式发票,并在会议期间发给缴费人。
重要日期
1.
提交论文截至日期:2006年4月14日。
2. 发布论文录用或拒绝通知截至日期:2006年5月5日。
3.
提交论文修改稿和版面费截至日期:2006年5月
19日。
4. 提前交纳注册费截至日期:2006年5月26日。
5.
会议报到日:2006年6月29日。
6.
会议时间:2006年6月30日-7月2日。(30日晚召开理事会全体会议。)
其它事项
本通知未说明的事项(如会议的举办地点,住宿安排等),待第二轮通知说明,并刊登在国运筹学会网站2006年学术年会专栏上。
中国运筹学会
二零零五年九月十日
18460
引用 (icie @ 2005年10月08日
19时15分) |
线性=齐次性+可加性
齐次性:y=f(x) => f(ax)=ay
可加性:y1=f(x1) y2=f(x2) =>
f(x1+x2)=f(x1)+f(x2)=y1+y2
|
这两条对非其次线性方程好像不太对哦
18460俺数学不好,但对数学很感兴趣,以前数学没学好,想现在补一补!
我所知道的线性方程就是行列式、矩阵等,但什么是线性,一直没有弄明白。希望各位不要因为我提的问题太原始而不屑一顾。
18460线性,通俗的讲,就是在映射下保持代数式系数不变,“平直”的变换。
18460对于线性我认为就是各个量之间是成比例的!
18460线性=齐次性+可加性
齐次性:y=f(x) => f(ax)=ay
可加性:y1=f(x1) y2=f(x2)
=> f(x1+x2)=f(x1)+f(x2)=y1+y2
18460“线性”关于线性方程组表现为未知量的一次性,关于映射则表现为加法和数乘的保持(或icie所言齐次性和可加性)
18460我们说可以视为线性空间的集合的元素具有线性性质……
注:线性映射是可以看做向量的,Hom(V1,V2)表式V1到V2上的线性映射全体,
是一个线性空间……
18460就是“平直“的变换
18460所谓"线性变换"就是把一个"直"映射成"直"的.
18460所谓线性就是小学时候学过的加法和乘法的分配律,
18460Definition:
Let T:V->W be a mapping over field K
T is linear
if it satisfies:
1)T(v1+v2) = T(v1)+T(v2), for any v1,v2 in
V
2)T(kv) = kT(v), for any v in V, k in
K
Exercise:-)
T:R^2->R linear mapping,
T(1,1)=3,T(0,1)=-2
Find T(a,b)
184611。let X1,x2,...be a sequence of independent random variables.Suppose
that Xn is uniformly distributed on (0, n^2)
calculate P( ∑Xk∕n→∞)
k from 1 to n
2.Let X be a random variable with a continuous
distribution function F. Derive the formul
EX^2=?(1-F(√x)+F(-√x))dx
(积分从0到无穷)
3。let X1,X2,...be a sequence of independent identically
distributed random variables taking value 0 and 1 with probability p and
1-p repectively
consider Y=2∑Xn3^(-n) (n从1到无穷的和)
calculate
EY and E(Y^2)
18461第一题看不明,似乎一般P的括号内应是一个应满足的条件。
第二题见附件。post-
17-1127489
189.jpg
18461Y=2∑Xn3^(-n) (n从1到无穷的和)
calculate EY and E(Y^2)
第三题:
E(Xn)=0*p+1*(1-p)=1-p
D(Xn)=p(1-p)
E(Y)=E[2∑Xn3^(-n)]
=2∑E[Xn3^(-n)]
=2∑[3^(-n)E(Xn)]
=2∑[3^(-n)(1-p)]
=2(1-p)∑3^(-n)
=2(1-p)/2
=1-p
E(Y^2)=(E(Y))^2+D(Y)
=(1-p)^2+D[2∑Xn3^(-n)]
=(1-p)^2+4∑[3^(-2n)D(Xn)]
(因为各Xn独立)
=(1-p)^2+4∑[3^(-2n)p(1-p)]
=(1-p)^2+4p(1-p)∑3^(-2n)
=(1-p)^2+4p(1-p)/8
=(1-p)(1-p/2)
18461严重十分感谢!!!
18463现有:
A1 A2

An
..................... Ai

0
B1 B2

Bn
..................... Bi

0
有什么公式可以计算A和B的"相似程度"?
请赐教!谢谢!
184631,做相关,看相关系数
2,做Kolmogorov-Smirnov
检验,检验两组数是否属于同一分布.在matlab里面用kstest2。(我想你的“相似”是想找内在联系)
18463用关联度分析!
18463将两组数进行福立叶变换,然后看能量谱
18471有道理!支持编号。
18471建议把题目编号,比如:
今天是九月二十二号,求解一道高等代数试题,是否可编号为:0922高等代数0X。
这样有利于跟踪过去的贴子,增添“讨论”的氛围,把一些解法引向深入。另外,有时候诸位未必有空或者有兴趣把每一贴都浏览到。
此乃一已之见,供版主与诸君参考。
回复:谢谢,这需要大家的配合与版主的辛苦劳动。
18471支持!!!!
关键是版面要改进,每一贴要有一个号码,每个问题有一个总汇,点右键就可查到。
有的论坛就是这样啊!
我希望bossh成为最最好的论坛!
18471支持,强烈支持
18472找一个高中(初中)生,让他分区间讨论一下就行了!
18472要求的数学表达式如下,其中"[x]"是一取整函数, 表示不大于x的最大整数 (譬如 [1.3]=1,
[-0.3]=-1)
f(x)=[1/6(x-1)+1/2([(x+1)/2]-[x/2])]]
还是看下面的图吧,清楚些post-33-1127390477.jpg
18472
取为整数,
当2n-1<=x<2n时,[(x+1)/2]=n,[x/2]=n-1,整个式子就化为(x-1)/6+1/2;
当2n<=x<2n+1时,[(x+1)/2]=n,[x/2]=n,整个式子就化为(x-1)/6。
请指正。
18476请教大家一个问题:
在测度论中讲到的环,域与近世代数中的环,域是同一个概念吗?
谢谢!!!!!
18476由于讨论范围不同,不能等同视之。一般与特殊的关系。抽象代数讲的是最一般的代数系统,哪里都适用。实变只是借用了一下抽代的定义的思想方式,即集合运算的“封闭性”。
18476非常感谢 !!!!!
18478偶正在学习
谢谢大家
18479
∫ 0
2
f(x)dx
post-38-1127395241.ibf
18479怎么,这道是不是很难啊,怎么没人做
18479利用对称性!post-38-1127482908.gif
18479谢谢你了,没想到这么简单,
18480在附件里,谢谢post-38-1127396806.ibf
18480令wi
(i=1,2,3,4)是方程x^4+x^3+x^2+x+1=0的四个根,则有
f(1)+wi*g(1)+wi^2*h(1)=0
所以函数f(1)+x*g(1)+x^2*h(1)有四个0根,则必有f(1),g(1),h(1)均为0,结论得证
18480!!!!post-38-1127399769.gif
18480谢谢,各位高手哈
18481怎样用最少的时间求出n以内的所有素数,希望获得最快的算法.
18481
| 引用 (asdf @ 2005年09月22日
21时46分) |
|
怎样用最少的时间求出n以内的所有素数,希望获得最快的算法. |
筛选法 ?
18482在附件里,谢谢post-38-1127397673.ibf
18482好复杂啊!
18482令f11=f1/(f1,f2,f3),f22=f2/(f1,f2,f3),f33=f3/(f1,f2,f3),利用
u1f11+u2f22=(f11,f22)
v3(f11,f22)+u3f33=1
v1u1+v2u2=1
自己凑合一下就可以得到问题所求的6个多项式了
18482答案不唯一(简直有无穷多个!没办法,只能告诉你1种,礼轻情义重嘛!)post-38-1127406275.ibf
18482谢谢哈
18483在附件里,谢谢哈post-38-1127400254.ibf
18483题目没错的,是你放缩过头了,注意f(i/n+x)-f(i/n)<=Mx
18483好风格
18483妙极了 采用变量代换法哈
18483那个x怎么处理成1/2呀,搞不懂,能讲细点吗
18483!!!post-38-11295
17003.gif
18485已证明了是条件收敛
绝对收敛性判别求帮助解答
感激!post-38-1127401005.gif
18485注意exp(cos(x))sin(sin(x))是周期函数且在[0,pi/2]上有sin(x)>(2/pi)x,此积分非绝对收敛
18485没明白过来
不好意思能不能说详细一点
感激!
18485了了
谢谢呵
还有把exp上的cos改成sin,其他不变,结果是发散的
两题一起的顺便提一下
18485利用上面所说,考虑该函数在[npi,(n+1)pi]上的绝对值积分,可得其积分值大于k*(1/(n+1)pi),其中k是一个常数,据此可知其不绝对收敛
18486通分后用Stolz公式, 得出答案1/2,
很简单.
可是, 我想将此极限化为"定积分"来做, 却无从下手.
还望高手赐教! (请写出过程, 谢谢)
post-38-1127402267.gif
18486lchw的方法好!
18486用梯形公式及其误差估计。
18486利用下结论:post-38-1127433478.gif
18486再次向lchw兄表示真诚的感谢!
我为啥就没想到把Taylor公式展至二阶余项呢?
从最终结果来看,"中矩公式"的精确度要比"右矩公式"高出一阶。post-38-1127544759.gif
18486那个公式,一开始我连看都看不懂,
而lchw居然能够信手拈来,佩服!
Thanks
a lot.
18486这个公式怎么来的啊
18486很多书上多有类似的命题,下给一种证明;post-38-1127463130.gif
18486等于1/2,,通分后用stolz公式证
18486不好意思没看清问题,,好方法
18486我想知道这书有没有习题解
18486
见《裴礼文》例 4.1.8
另外, 受帖子
http://www.math.org.cn/forums/index.php?showtopic=
18090
第一题的启发,
那里f(x)=1/(1+x),
我联想到一个类似的问题, 敬请高人指点!post-38-1127483
174.gif
18486如下:post-38-1127492214.gif
18487就是Douglas R.Stinion的个人网站,兄弟找不到,据说上有关于密码学论文的很多连接啊
18487是不是Douglas Robert Stinson?
http://www.cacr.math.uwaterloo.ca/~dstinson/
18487恩,就是这个.
谢谢你了.
18488当1+2+

+n=n(n+1)/2是奇数时,由于改变+-号不影响其奇偶性,所以和不可能为0,
a(n)=0
当1+2+

+n=n(n+1)/2是偶数时我只能证明一定存在,具体a(n)的个数不好求
不难得出a(4k)

2*C(2k,k) k

1
a(4k+3)

4*C(2k,k) k

1
18488在1,2,…,n数前添上+-号,使其和为0,问有几种添法?
例如,n=3,
+1+2-3,-1-2+3,
则有a(3)=2种;
又如a(12)=70*2=140种,求a(n)的母函数.
18488a(n)能否求出来还是个问题呢?
就相当于你能否求出 int (cos(x)*cos(2x)*
......cos(nx),x=0..2Pi)
易得 上面这个值乘以2^n,就是要求的a(n).
其母函数是不是初等函数也是个问题啊
18488
引用 (hhhh31415926 @ 2005年10月
19日
19时15分) |
a(n)能否求出来还是个问题呢?
就相当于你能否求出 int (cos(x)*cos(2x)*
......cos(nx),x=0..2Pi)
易得 上面这个值除以2^n,就是要求的a(n).
其母函数是不是初等函数也是个问题啊
|
怎么会这样呢,不懂的
18488可不可以用图形的直观形式表示出来的
18490想请教一下,计算的基本单位是什么? 计算的本质是什么? 像信息都有基本的度量单位比特,计算的度量单位有吗?
18490这个问题问得有问题,对于计算采用的算法,我们只能谈论它的速度和所占用计算机内存,为些有复杂度的概念,它说的是在最坏的情况下,一种算法的速度和所占内存,常称为"时间复杂度"和"空间复杂度",并采用数学上的量的比较的计法来表示,例如问题的规模为n时,可用O(n)表示算法的规模与n成比例,等
18491想请教一下正在读博 或者要读博的同学们:
如果不想留在学校搞学术,那么有必要读完硕士就直接拿下博士学位吗???
现在单位招聘基本上都要求工作经验,那么读了博士却一直没有工作,是不是使自己
的就业面太窄了!
困惑中,请大家帮忙,谈谈你们的看法
18492国际上数值模拟软件发展呈现出的趋势特征
http://www.sciei.com/bbs/dispbbs.asp?board...rdid=34&id=1082
来源:SDU VNC
a. 由二维扩展为三维
早期计算机的能力十分有限,受计算费用和计算机储存能力的限制,数值模拟程序大多是一维或二维的,只能计算垂直碰撞或球形爆炸等特定问题。随着第三代、第四代计算机的出现,才开始研制和发展更多的三维计算程序。现在,计算程序一般都由二维扩展到了三维,如LSDYNA2D和LSDYNA3D,AUTODYN2D和AUTODYNA3D,但也有完全在三维基础上开发的,如MSC.DYTRAN,就没有二维功能。
b. 从单纯的结构力学计算发展到求解许多物理场问题
数值模拟分析方法最早是从结构化矩阵分析发展而来,逐步推广到板、壳和实体等连续体固体力学分析,实践证明这是一种非常有效的数值分析方法。近年来数值模拟方法已发展到流体力学、温度场、电传导、磁场、渗流和声场等问题的求解计算,最近又发展到求解几个交叉学科的问题。例如内爆炸时,空气冲击波使墙、板、柱产生变形,而墙、板、柱的变形又反过来影响到空气冲击波的传播……这就需要用固体力学和流体动力学的数值分析结果交叉迭代求解,即所谓“流—固耦合”的问题。
科研中国SciEi.com。
c. 从单一坐标体系发展多种坐标体系
数值模拟软件在开始阶段一般采用单一坐标,或采用拉格朗日坐标或采用欧拉坐标,由于这两种坐标自身的缺陷,计算分析问题的范围都有很大的限制。为克服这种缺陷,采用了三种方法,一是两个程序简单组合,如CTH—EPIC,爆炸与侵彻由不同的程序分开计算;二是在同一程序中采用多种坐标体系,如DYNA3D中早期采用的是拉格朗日坐标,而LSDYNA3D的最新版除原有类型外,新加了欧拉方法以及拉格朗日与欧拉耦合方法,而最近几年才发展的DYTRAN则是拉格朗日型的LSDYNA3D(
1988版)与欧拉型的PISCES的整合体;三是采用新的计算方法,如SPH等,SPH法不用网格,没有网格畸变问题,所以能在拉格朗日格式下处理大变形问题,同时,SPH法允许存在材料界面,可以简单而精确地实现复杂的本构行为,也适用于材料在高加载速率下的断裂等问题的研究。
d. 由求解线性工程问题进展到分析非线性问题
随着科学技术的发展,线性理论已经远远不能满足设计的要求。诸如岩石、土壤、混凝土等,仅靠线性计算理论就不足以解决遇到的问题,只有采用非线性数值算法才能解决。众所周知,非线性的数值计算是很复杂的,它涉及到很多专门的数学问题和运算技巧,很难为一般工程技术人员所掌握。为此,近年来国外一些公司花费了大量的人力和投资,开发了诸如LSDYNA3D、ABAQUS和AUTODYN等专长于求解非线性问题的有限元分析软件,并广泛应用于工程实践。这些软件的共同特点是具有高效的非线性求解器以及丰富和实用的非线性材料库。
e. 增强可视化的前置建模和后置数据处理功能
早期数值模拟计算软件的研究重点在于推导新的高效率求解方法和高精度的单元。随着数值分析方法的逐步完善,尤其是计算机运算速度的飞速发展,整个计算系统用于求解运算的时间越来越少,而数据准备和运算结果的表现问题却日益突出。在现在的工程工作站上,求解一个包含10万个方程的有限元模型只需要用几十分钟。但如果用手工方式来建立这个模型,然后再处理大量的计算结果则需用几周的时间。可以毫不夸张地说,工程师在分析计算一个工程问题时有80%以上的精力都花在数据准备和结果分析上[14]。因此目前几乎所有的商业化数值模拟程序系统都有功能很强的前置建模和后置数据处理模块。在强调“可视化”的今天,很多程序都建立了对用户非常友好的GUI(图形用户界面—Graphics
User
Interface),使用户能以可视图形方式直观快速地进行网格自动划分,生成有限元分析所需数据,并按要求将大量的计算结果整理成变形图、等值分布图,便于极值搜索和所需数据的列表输出。
科研中国SciEi.com。
f. 与CAD软件的无缝集成
与通用CAD软件的集成使用,即在用CAD软件完成结构设计后,自动生成有限元网格并进行计算,如果分析的结果不符合设计要求则重新进行构造和计算,直到满意为止,从而极大地提高了设计水平和效率。今天,工程师可以在集成的CAD和数值模拟软件环境中快捷地解决一个在以前无法应付的复杂工程分析问题。所以当今所有的商业化有限元系统商都开发了和著名的CAD软件(例如AutoCAD、Pro/ENGINEER、Unigraphics、SolidEdge、SolidWorks、IDEAS等)的接口。
科研中国SciEi.com。
g. 工作平台多样化
早期的数值分析软件基本上都是在大中型计算机上开发和运行的,后来又发展到以工程工作站(EWS,Engineering Work
Station)上,它们的共同特点都是采用UNIX操作系统。PC机的出现使计算机的应用发生了根本性的变化,工程师渴望在办公桌上完成复杂工程分析的梦想成为现实。但是早期的PC机采用16位CPU和DOS操作系统,内存中的公共数据块受到限制,因此当时计算模型的规模不能超过1万阶方程。Microsoft
Windows操作系统和32位的Intel
Pentium处理器的推出,为PC机用于有限元分析提供了必需的软件和硬件支撑平台。因此当前国际上著名的有限元程序研究和发展机构都纷纷将他们的软件移值到Windows平台上。最新高档PC机的求解能力已和中低档的EWS不相上下。
为了将在大中型计算机和EWS上开发的有限元程序移值到PC机上,常常需要采用Hummingbird公司的一个仿真软件Exceed。这样做的结果比较麻烦,而且不能充分利用PC机的软硬件资源。所以最近有些公司,例如ANSYS、MSC.software等开始在Windows平台上开发有限元程序,大多采用了OpenGL图形编程软件,同时还有在PC机上的Linux操作系统环境中开发的有限元程序包。
科研中国SciEi.com。
h. 软件开发强强联合
由于数值软件的开发是一项长期而艰巨的任务,开发一个通用软件是十分困难的,各家开发的软件由于应用背景的不同而各有千秋,随着数值模拟软件商业化的进展,各数值模拟软件公司为扩大市场,追求共同的利润,出现了强强联合的局面。典型的如ANSYS与LSDYNA3D联合,MSC.software软件公司对ABAQUS、LSDYNA3D及PISCES等的购买。
18492顶!
18493真不知道自己大学是怎么过来的,现在想想真的好危险啊!
网上无美女是真的么?看来以后要少上QQ了。
18493哈哈哈,我顶
18493真经典!!
18493真经典!!
18493我也有同感,但是我不想那么多不要,我有我自己的路
18493还是有例外的,没有绝对的说法。
18493永远不要参加任何社团招新,除非它让你作社长。任何社团存在的理由,就是增加社团负责人的竞争资本。
永远不要指望哪个plmm没有男朋友,不排除有mm这么说,这是因为她的男友太多了,她数不过来。
永远不要指望踢足球能够吸引mm的注意,在学校,你踢得再好,也只有你的对手知道,mm只会在帮男友看衣服的时候,送你两眼。
永远不要买电脑,虽然你的初衷是用来学习,但最后你会把它改装成你的游戏机。
永远不要指望食堂里的服务员的小学数学学得有多好,他们会通过两位数加法的正确率不会高于百分之40。
永远不要到看上去心情不好的食堂服务员窗口打菜,他会让你的酸菜鱼成酸辣汤,宫保鸡丁成炒花生米。
永远不要指望每个大学人的素质都和你一样高,记住三分之一的人本来分数只配……虽然,他们很多人将来就是保研一族。
永远不要去学校对面的网吧玩游戏,它会让你提早享受程序员的生活,让你知道钱的重要性,让你走上永远堕落的生活。
永远不要把英语给忘了,英语四六级越往后越难过,给四六级委员会捐钱是小,无形的心理压力会让你有了报复社会的想法。
永远不要到校门口饭店吃饭的时候看他们是怎么洗碗的,他会让你……让我吐完先。
永远不要在放假的时候把很多书带回家,你怎么带回家就会怎么带回学校,一定是原封不动。假期就是用来休息的,你放假前作的种种学习设想永远只是设想。
永远不要相信网恋,美女是不上qq的,上的话也是隐身。只有和你有同样需求的女生才在网聊上乐此不彼。不要把自己的光阴花在无谓的投资上。
永远不要买大家都用的手机型号。从摩托罗拉到诺基亚,再到三星,它会让你显得很没有个性。
永远不要看重手机的其他功能,除非你有偷拍mm的恶习。记住,你买手机的最大用途是为了收发短信。
永远不要指望当一个风靡万千少女的文艺青年,你再出名也是一个叫得很响的蚂蚱,蹦不来几天。何况,还要冒着被绝大多数人骂成sb的风险。
18493哈哈
18493我顶
18493哈哈哈,有道理!
18493“咬定青山不放松,任尔东南西北风”我顶啊。
18493长见识了.不顶对不住.
18493厉害,是不是还得用数学分析一下啊?
18493好!!!
18493不错
18493狂赞!深有同感!特别是4、6级和带书回家两条,真tmd有道理。
另外,我发现用qq真是不好,天天有无聊的人问我:激情视频吗?我晕
18493精辟,深刻
18493永远不要把英语给忘了,英语四六级越往后越难过,给四六级委员会捐钱是小,无形的心理压力会让你有了报复社会的想法
实话是说啊
再过几天还的靠六级
已经第n次了
n>=3
18493痛感!
18493jingdian!
18493不错啊,总结的很经典,想想,大学好像就是昨天的事情。
18493用学数学分析训练出来的思维分析一下吧!我可不全同意哦!!!我女友就经常去看我踢球啊!!!
18493顶!
18493顶!!!!!
18493说得真的很中肯,强烈顶住!
18493当快上完大学时,才有如此感慨!
18493哈哈
18493说的实在,顶
18493同感
18493上了大学才知道玩游戏是要通宵的
上了大学才知道手机是用来追女生的 上了大学才知道人渣都是大学培养的
上了大学才知道原来大学和养老院是差不多的
上了大学才知道馒头一捏就能变汤圆的
上了大学才知道所有的课都能跷,只有体育课是不能跷的
上了大学才知道打水是用来泡面的
上了大学才知道开学校原来是那么赚钱的
上了大学才知道二锅头是用来干的
上了大学才知道刻苦学习的,都是穷得交不起补考费的
上了大学才知道一门课一学期可以就考试那天去一次的
上了大学才知道一头猪是可以供食堂吃几天的
上了大学才知道原来理想只是高中以前才有的
上了大学才知道大学里是学不到东西的
上了大学才知道自习室是用来谈恋爱的
上了大学才知道生活还是糜烂的
上了大学才知道电脑是用来玩游戏
大学生=吃饭+睡觉+谈恋爱
猪=吃饭+睡觉
所以:大学生=猪+谈恋爱
以上推出大学生-谈恋爱=猪
18493顶一下吧!
18493顶
18493考研!!1
18493宁可信其真,不可信其无。。。
18493差不多就是这样吧!大一第一天被人骗过!~妈的!
18493
| 引用 (ljb @ 2006年04月07日
12时37分) |
上了大学才知道玩游戏是要通宵的
上了大学才知道手机是用来追女生的 上了大学才知道人渣都是大学培养的
上了大学才知道原来大学和养老院是差不多的
上了大学才知道馒头一捏就能变汤圆的
上了大学才知道所有的课都能跷,只有体育课是不能跷的
上了大学才知道打水是用来泡面的
上了大学才知道开学校原来是那么赚钱的
上了大学才知道二锅头是用来干的
上了大学才知道刻苦学习的,都是穷得交不起补考费的
上了大学才知道一门课一学期可以就考试那天去一次的
上了大学才知道一头猪是可以供食堂吃几天的
上了大学才知道原来理想只是高中以前才有的
上了大学才知道大学里是学不到东西的
上了大学才知道自习室是用来谈恋爱的
上了大学才知道生活还是糜烂的
上了大学才知道电脑是用来玩游戏
大学生=吃饭+睡觉+谈恋爱
猪=吃饭+睡觉
所以:大学生=猪+谈恋爱
以上推出大学生-谈恋爱=猪 |
幽默不失沉稳.
不过最后几句过头了点.
18493支持,很有道理。
18493有点意思
18493有点意思,不过大家都要过啊
18493恩呢。
18493哈哈,我顶了
18493得顶顶喽~!
谁让我还得度过余下两年的大学生活呢...
18493很有道理啊!
18493说得好
18493宝贵的经验
18493说得好.
18493生命诚可贵,
爱情价更高,
若为只有古,
二者皆可抛。~~~~~
我顶!!!!
18493顶
18493我也有同感,走自己的路
18493
引用 (zhubin846152 @ 2005年11月24日
11时
17分) |
狂赞!深有同感!特别是4、6级和带书回家两条,真tmd有道理。
另外,我发现用qq真是不好,天天有无聊的人问我:激情视频吗?我晕
|
哈哈
18493经典呀,真的好经典,我顶!!!!!!!!
18493果然有道理
哈哈
18493说的真好!
18493哈哈
18493
| 引用 (jsyangli @ 2005年09月23日
09时50分) |
永远不要参加任何社团招新,除非它让你作社长。任何社团存在的理由,就是增加社团负责人的竞争资本。
永远不要指望哪个plmm没有男朋友,不排除有mm这么说,这是因为她的男友太多了,她数不过来。
永远不要指望踢足球能够吸引mm的注意,在学校,你踢得再好,也只有你的对手知道,mm只会在帮男友看衣服的时候,送你两眼。
永远不要买电脑,虽然你的初衷是用来学习,但最后你会把它改装成你的游戏机。
永远不要指望食堂里的服务员的小学数学学得有多好,他们会通过两位数加法的正确率不会高于百分之40。
永远不要到看上去心情不好的食堂服务员窗口打菜,他会让你的酸菜鱼成酸辣汤,宫保鸡丁成炒花生米。
永远不要指望每个大学人的素质都和你一样高,记住三分之一的人本来分数只配……虽然,他们很多人将来就是保研一族。
永远不要去学校对面的网吧玩游戏,它会让你提早享受程序员的生活,让你知道钱的重要性,让你走上永远堕落的生活。
永远不要把英语给忘了,英语四六级越往后越难过,给四六级委员会捐钱是小,无形的心理压力会让你有了报复社会的想法。
永远不要到校门口饭店吃饭的时候看他们是怎么洗碗的,他会让你……让我吐完先。
永远不要在放假的时候把很多书带回家,你怎么带回家就会怎么带回学校,一定是原封不动。假期就是用来休息的,你放假前作的种种学习设想永远只是设想。
永远不要相信网恋,美女是不上qq的,上的话也是隐身。只有和你有同样需求的女生才在网聊上乐此不彼。不要把自己的光阴花在无谓的投资上。
永远不要买大家都用的手机型号。从摩托罗拉到诺基亚,再到三星,它会让你显得很没有个性。
永远不要看重手机的其他功能,除非你有偷拍mm的恶习。记住,你买手机的最大用途是为了收发短信。
永远不要指望当一个风靡万千少女的文艺青年,你再出名也是一个叫得很响的蚂蚱,蹦不来几天。何况,还要冒着被绝大多数人骂成sb的风险。
|
透彻
一番话道破大学人生
18493哈哈,楼主太厉害了,不过那四六级很对的,我都快气爆了
18493有道理哎,我在虚度光阴
18493真办事!!!
18493
我看了,好东西啊!
18493顶顶顶顶
18493好有趣啊,有些还是挺有道理的
18494lindo实用手册post-26-112744
1776.ibf
18494楼主是个好人
18494谢谢
顶
18494好!
18494谢谢啊,不过很奇怪,怎么我下的都打不开
新手上路N多问题的
18494好东西,正要找一个这样的文章呢
18494谢了,有没有for window的?
18494thank you
18494谢谢
184943x
18494非常不错,谢谢
18494谢谢你的东西
18494谢谢!
18494非常感谢!我是新手,希望多谢学习.
18494谢谢
18494顶!谢谢!
18497我学到了多元微积分时感到了有困难啊 有谁愿意帮助我 谢谢啦
十分感激啊 怎样求二重极限啊 你一元难多了啊
有没有与罗必达法则对应的方法啊
18497求二重极限一般方法是化成二次极限,利用定积分方法来完成。
18499实数的稠密性:任何两个不相等的实数之间必有另一个实数,且既有有理数也有无理数!
请问:怎样构造两实数之间的无理数.
18499sqrt(ab)就是一个构造啊!
18499
楼上显然错了哈,可以这样
(a,b)中, c=a+e/n (n为足够大的整数)
18499有更好的构造方式么?
18500
18500谢谢!!!
18500
| 引用 (古月西风 @ 2005年09月28日
20时09分) |
引用 (wzxyz49 @ 2005年09月28日
19时43分) | | 古月西风确有古道貌热肠!
|
你让我想到了道貌岸然!!!
|
是呢,笔误哦!
18500非常感谢!!!!!
18500近世代数的习题答案,谁有啊,敬请相告!谢谢
回复:去电子资源版的信箱里找找。
18500电子版的post-67-11274810
18.ibf
18500张禾瑞近世代数习题解答post-67-1127481270.ibf
18500张禾瑞近世代数习题解答post-67-1127481443.ibf
18500张禾瑞近世代数习题解答post-67-1127481615.ibf
18500
引用 (wzxyz49 @ 2005年09月28日
19时43分) |
| 古月西风确有古道貌热肠!
|
你让我想到了道貌岸然!!!
18500古月西风确有古道貌热肠!
18500谢谢!!!!!
18500真是太太太感谢了!雪中送炭啊!
18500你的近世代数的答案为什么本能解压啊 能不能帮帮我
!!!!!!!!!!!!!!!我急用 !!!! 谢谢!!!!
18500怎么才能购买阿?新手请指教!
18500不错,谢谢了
18500太感谢您了啊!
18500怎么打不开呀,楼主
18500多谢了,正要用呢!
18500太感谢!!!
18500Thanks!!!
希望别挂了
18500呵呵,热心人辛苦了
18500support!!
18500刚好需要
考博参考书
救命的东西啊
谢了
18500thanks
18500怎么解不了
18500全下完就可以解压了
18500我有解密了的,找我啊,QQ443436
185
18500thanks
18502不好意思,偶已有了这本书,请问您还有什么数学方面的书要处理!!
18502谁有张奠宙的<20世纪数学经纬>这本书,从图书馆借过,觉得真的不错,想收藏一下,不知哪位大哥能帮小弟一下!!多谢啦!!
18502我有,正在转行准备卖。我的E-mail:dinghuay@163.com
18503有人问了我一个问题,怎么用matlab求幂级数的和函数,没想出来。求助。
18503可以把你的问题说明的详细点么:)
18503例子
>> syms x t k
>>
symsum(x^k*t^k/factorial(k),k,0,inf)
??? Error using ==>
fix
Function 'fix' is not defined for values of class
'sym'.
Error in ==>
D:\MATLAB6p5p1\toolbox\matlab\specfun\factorial.m
On
line 14 ==> if (length(n)~=1) | (fix(n) ~= n) | (n <
0)
查帮助后知道,该这样
>>
symsum(x^k*t^k/sym('k!'),k,0,inf)
ans =
exp(x*t)
18506在一个盒子里有15个白球,15个黑球,
17个红球。现在从中随机取100次(取出放回),请问100次中有30次白球,35次黑球,35次红球的概率怎么计算?
工作几年,大学学的概率论快忘了,哪位兄弟帮忙写一个计算公式?
18507to 快乐的思考:
谢谢你的回复,但我有点不懂,请问第2个不等号是如何得来的
18507
| 引用 (永理 @ 2005年09月28日
23时20分) |
to 快乐的思考:
谢谢你的回复,但我有点不懂,请问第2个不等号是如何得来的 |
因为正弦值是小于1的
只要取邻域的时候x比较小就可以了,其实直接写4/3还更好点
18507在附件里,谢谢了
18507在附件里post-38-1127458938.ibf
18507这道题挺麻烦的
18507劳驾
18507用定义来讨论就可以了:post-38-1127780534.gif
18507谢谢了
18507ok,明白
18508天津没有南大的光辉啊
18508天大和南开的数学系那个更好一点
18508天津大学数学方面那个更好一些?
大家来谈谈
[专贴]天津大学试题
http://www.math.org.cn/forums/index.php?show...pic=12388&st=0&天大数学有没有内部辅导班
http://www.math.org.cn/forums/index.php?sh...topic=20564&hl=关于天大数学考完的感受
http://www.math.org.cn/forums/index.php?sh...topic=23852&hl=
考天津大学有戏吗
http://www.math.org.cn/forums/index.php?sh...topic=25246&hl=天津大学的基础数学怎么样
http://www.math.org.cn/forums/index.php?sh...topic=30036&hl=求助天津大学复试资料
http://www.math.org.cn/forums/index.php?sh...topic=42154&hl=
请教大家一个关于天大数学考研的问题?
http://www.math.org.cn/forums/index.php?sh...topic=
17935&hl=
18508不知道这位先生什莫意思呀
您是天大毕业的嘛?
天大数学里面 控制论比较好一些
18508真郁闷
我准备考天大数学系
那么烂
18508我是湖南大学数学系毕业的,去年考湖大的基础数学研究生,考了408分,但是因为我本科时欠学费没毕业证不让我读,所以我今年还得考,准备考浙大的,不知道有没有同路的,QQ:775
1885
大家多多交流一下,谢谢.
18508我要报考天大
那个方向好一些
谢谢 请高人指点一二
18508天大数学发展很快哦...
18508猛然发现还有这么多关于天大的帖子,去年我考时咋就没发现呢。其实天大的数学就是起步比较晚,没形成气候,但是这两年确实发展很快,导师也挺强。
18511急求: Brezis,H & Strauss,W.A.的73年文章:
Semi-linear
second-order elliptic equations in L^1
发表在:J.Math.Soc.Japan 25
(
1973), 565-590.
请各位帮忙,如果有请发到:alongwei@163.com,谢谢!
18513求购fortran90(9X)软件(含序列号),小弟不忘大恩!!!
18513哪个平台上的?如果是 Linux 上的话,请到 Intel 的网站,有 Noncommerical License
的 Intel
Fortran for Linux 的免费下载。
18513在网上能找到fortran95(V 6.5)我用的还可以,就是不支持中文目录。
我用的就是这个版本,师兄04年春给我的
18513我有vfortran版,但太大,无法上传,如果需要,等春节后我给你用QQ发过去
404834577
18513我有Microsoft Fortran
PowerStation,96MB,FOR90标准。
qq:410660408
需要的话就传给你。
我们上学期学FORTRAN程序设计,老师给的这个版本。
18513
我也需要一个linux系统下的For90或95,
18513
我也需要一个linux系统下的For90或95,
请问哪里可以下载?或者谁可以提供,小弟先谢了!
18513我举报,awakeawake 采用欺骗的方法获取积分。
18516那位师兄师姐是吉林大学的啊?能给我介绍一下那边的研究生保送情况吗?
以及导师情况吗?
他们的试题有何特点?
谢谢!谢谢!
18516吉大本校保送的挺多的,但每年都招不满。
搞方程的有几个老师很牛。比如尹景学。相当厉害。应用方面高文杰老师很好。
李勇老师搞动力系统的,近几年作的很好。
18516计算方面有一些老教授都很好的。
概率方面好老师走了挺多的,都去大连理工,还有北京的一些学校了。所以这个方向好像不太好了。
吉大还是计算方面比较强。新任院长是搞方程的,所以。。
历年试题都是考数分,高代,实变,常微的,和平时上课老师强调的重点差不多。
题目看上去不太容易,但把老师的思路理解透了就相当顺手了。
18516吉林大学保送的在50%左右吧,不过每年过初试分数线的都没有招收的名额多
试题初试今年只考数分高代了
18520v是n维欧式空间,,在它中至多有n+1个向量,,它们之间夹角大于90度
18520用数学归纳法!
18520夹角大于90度
和小于90度 有何区别?
18520等价于内积小于零与大于零。
18520证明!post-38-1127482371.gif
18520n=1时,在一维欧氏空间中,任意3个向量必有2个向量的夹角为0
18520错的哦
18520我觉得不太对,,在一维空间要正至多有2个,,而你证的是任意3个向量有2个,,不合适
18521你好!我是常熟理工学院的学生,想考浙江师范大学的研究生!
我学的是数学专业,今年想考你们学校的研究生,我知道时间也不多了,所以现在也比较急,看好了学校就想赶紧找资料!
<我个人感觉浙江师范大学挺不错的,所以想请你帮帮忙!
能不能帮我找到历年数分高代的复习资料?
如果可以的话我将不胜感激!!!(如果要钱买的话我也可以接受)
18521我是浙师大的,05年的数分试卷我想你已经有了,答案应该也有了。我这里有我们出题老师的上课笔记,你可以联系我。有分析选论和高代选论,非常有用的。13505795730
18521老兄,你这个电话号码到底可不可靠呀
咱们都是爱好数学的人,我想你也是讲诚信的人!
我相信你
我想我们邮件联系比较好
我的是satellite35208@126.com
18522我正在努力做中ing
不过要看你相不相信我的答案了 ^_^~~~~~~~~~~
18522
各位大虾有没有谁知道那里有《数学分析中的典型问题与方法》这本书的习题答案买吗?
有的话请告诉我。十分感谢!!!!!!!!!
18522大侠,这个估计是没有的。
18522这本书不会有什莫答案的
还是自己看吧
18522还是自己看吧
18522美答案,自己做
18522估计没有答案的
18522现在出了个第二版,比第一版充实多了,贵都要贵10多块,给出很多习题得解答,九章有卖,只是不打折哟
18522难找啊,
只能自己慢慢想啊
18523如题
18523国内的张文鹏
18523山大好象有个刘建亚,据说是长江学者,是博导!水平挺不错的
18523山大搞数论也不错的,校长展涛
18523广州大学的王学理
18524数论
18525求助概率统计(浙大3版)、复变函数(西安交大)积分变换(南京工学院)课件
急!急!急!
18526用"[x]"表取整函数, 即表示不大于x的最大整数 (譬如 [1.3]=1, [-0.3]=-1)
这个函数的英文名叫 floor function
有没取整函数的运算法则呢?
譬如:
[a/3]+[b/6]-[c/2]=?
18526取整函数的运算经常是用一些不等式表达的,例如
[
2x]+[2y]≥[x]+[y]+[x+y]
等等。
18527请问哪位大哥是华东师大数学系的,我想问一下张奠宙老师的邮箱或其他联系方式!多谢啦
18527这个不知道
去学校网站上查啊
18527办公通讯地址:
上海市中山北路3663号
华东师范大学数学系
邮编:200062
电话:
086-021-62233120
传真: 086-021-62238105
电子邮件:dzzhang@math.ecnu.edu.cn
18527够狠的话,谁还用找导师的联系方式啊!好好学,到哪里一样吃得开!
1852812珠子仅有一颗不同,用天平称3次,找出不同者,如何设计程序,请教!!
18528有十二个乒乓球特征相同,其中只有一个重量异常,现在要求用一部没有砝码的天平称三次,将那个重量异常的球找出来.
这道和你的题目一样,在下帖中,我说算法.
1852813个球分成A,B,C,3组,并编号:
A1,A2,A3,A4, B1,B2,B3,B4,
C1,C2,C3,C4,C5
第一次:A和B比较,可能观察到三种结果:
1,若天平平衡,则A1=A2=A3=A4=B1=B2=B3=B4,在这八个球中任取一个,放入C
组,剩下的问题就是:已知一个球重量正常,其它五个球有一个异常,四个正常,称两次
找出重量异常的球
2,若看到A组较重,则说明C1=C2=C3=C4=C5,且此时有两种可能:
A组四个球有一个重 或者 B组四个球有一个轻:
此时,第二次比较:
在C组任取一个球(记为C,肯定是重量正常),加上A,B两组,共9个球,分3组:
第一组:A1,B1,C
第二组:A2,A3,B2
第三组:B3,B4,A4
第一.二两组比较,结果有三种情况:
(1)一=二:说明B3轻或B4轻或A4重,那么:
第三次比较:B3和B4,若相等,说明A4重,若不等,轻的就 是我们要找的球.
(2)一组重,二组轻:说明A1重或B2轻,那么:
第三次比较:C和A1,若相等,则B2轻,若不等,则A1 重
(3)二组重,一组轻:说明A2重或A3重或B1轻,那么:
第三次比较:A2和A3,若相等,则B1轻,若不等,则重 的就是.
最后,考屡"已知一个球重量正常,其它五个球有一个异常,四个正常,称两次
找出重量异常的球"
方法是:设六个球为A1,A2,A3,A4,A5,C,其中C重量正常.
第一次:A1,A2比A3,C,若
1,相等,则A4或A5异常,
第二次:C比A4,相等,则A5异常,不等,则A4异常
2,A1+A2>A3+C,则A1重或A2重或A3轻,
第二次:A1比A2,相等则A3轻,不等则重的就是
3,A1+A2<A3+C,则A1轻或A2轻或A3重,
第二次:A1比A2,相等则A3重,不等则轻的就是
18528有了算法,再写程序就好办了.
上帖我是用自然语言描述算法的,把它改用C++描述,就是程序了.
18529rt
18529设Q表示有理数集合,它是可数的,记为Q={r1,r2,...rn,...},在R-Q(即无理数集合)中分出一个可数子集合,记为X={x1,x2,...,xn,...},作映射f如下,在R-Q-X中自身对应到自身,而X与X
Q之间有一一对应,合起来便得到映射f,它是从无理数到实数的一个双射!
18529妙极!
佩服!!
18530100囚徒难题
有100个无期囚徒,被关在100个独立的房间,互相无法通信。
每天会有一个囚徒被随机地抽出来放风.随机就是说可能被抽到多次。 放风的地方有一盏灯,囚徒可以打开或者关上,除囚徒外,没有别人会去动这个灯。每
个人除非出来防风,是看不到这个灯的。
一天,全体囚徒大会,国王大赦,给大家一个机会:如果某一天,某个囚徒能够明确表示,所有的囚徒都已经被放过风了,而且的确如此,那么所有囚徒释放;如果说错了,那么所有的囚徒一起死!
囚徒大会后给大家20分钟时间讨论,囚徒们能找到被释放的方法么?如果能,他们还要被关多少天?有没有能更快被释放的方法?
18530讨论时开过灯的总数确定,以后在总数上每个都往后加1,来过第2次及以上的不再加,直到一个没开过的看到99这个数.
18530?如何看到99这个数字?不明白,好像每个囚徒之间不能通信的阿,怎么知道谁是第一次去的?
18530感觉很难
18530我有一个办法可以确保最后一个人确定所有囚徒都被放过风,但是不能给出确定的时间消耗,但是我所感兴趣的是你的问题从那来的?
njx77971m@sina.com
18530
国王给囚徒们20分钟商量的时候,囚徒们作如下决策——
1、挑选一个最年轻的囚徒作为
计数员(考虑到这个过程可能非常漫长)
2、交换信息了解目前 灯 处于什么状态。我们且假设目前处于 灯亮
状态。
3、灯的开关规则:对于非计数员来说,每个人在第一次看到灯亮的时候
把灯置为熄灭,也就是说每个人只有一次操作灯的机会;计数员在看到灯为熄灭状态的时候需要把灯重置为“亮”,并且在脑子里的计数器上+ 1
,如果看见灯亮则不做任何操作。
这样,当计数员数到99个数的时候,说明所有囚犯都已经放风过了
18530
| 引用 (木精灵在树梢 @ 2006年11月14日
13时48分) |
国王给囚徒们20分钟商量的时候,囚徒们作如下决策——
1、挑选一个最年轻的囚徒作为
计数员(考虑到这个过程可能非常漫长)
2、交换信息了解目前 灯 处于什么状态。我们且假设目前处于 灯亮
状态。
3、灯的开关规则:对于非计数员来说,每个人在第一次看到灯亮的时候
把灯置为熄灭,也就是说每个人只有一次操作灯的机会;计数员在看到灯为熄灭状态的时候需要把灯重置为“亮”,并且在脑子里的计数器上+ 1
,如果看见灯亮则不做任何操作。
这样,当计数员数到99个数的时候,说明所有囚犯都已经放风过了
|
不错,是个可行的办法
18530真厉害 我怎么连个怎么解决的影像都没有呢?
18530更快的办法:
申请6盏灯,共7盏
二进制7位可以表示100
每个人第一次来时将灯代表的数字加1直到1100100
18530计数员是一个可行的办法,不过要求计数员被抽到99次,这样得要多少年的时间啊,怪不得犯人们会商量选出最年轻的一个人来当技术员。
18530对于上面那个确定的方法,由于等待的时间实在是太长了,很有可能又有的罪犯都已经老死了都不得解,因此可以考虑采用概率的方法来解。先给一个粗略的估计:
事件A:100个人,每天随机抽取一个人,m天之后,全部人都至少被抽到一次。
事件B:100个人,每天随机抽取一个人,m天之后,至少有一人未被抽到。
事件C:100个人,每天随机抽取一个人,m天之后,恰好有一人未被抽到。
B包含C,所以P(B)>P©,P(A)=1-P(B)<1-P(C),而P(C)很容易计算
P(C) = 100*[(99/100)^m]
m=500时,P(C)=65.7%;
m=1000时,P(C)=0.43%
也就是说,到了1000天的时候(3年不到的时间),至少有99.6%的可能性,所有囚犯都已经放过一次风了。这时候,做一次很有把握的冒险是值得的。
实际计算的结果P(A)是小于这个数值的。mathematica程序:
count
= 0; M = 1000; For[i = 0, i < M, i++, If[Length[
Union[Table[Random[Integer, {1, 100}], {M}]]] < 100, count++]]; count/i
18531数学专业的概率统计方面有哪些好的习题集或参考书?请大家推荐几本吧。另外我想询问一下,工科的概率统计与数学专业的概率统计,有什么区别呀
?谢谢各位!
18531我用过一段时间的苏联老习题书<概率论解题指南>--(苏)史威斯尼珂夫,计度生, 朱锡斌译 上海科学技术出版社,
1965.1出版.一般在图书馆有借.这书还是挺全面的,不过稍微有点厚:-)教材我当时用的是复旦大学
李贤平的<概率论基础>,高等教育出版社,
1997出版.很不错的书.数理统计是北大 陈家鼎的<数理统计学讲义>
是高等教育出版的.最近有新的印刷版本,我那时买的印刷质量不敢恭维.还有推荐可以看看
(美)费勒的<概率论及其应用>,有上下两册.科学出版社出版的.老版本可以在图书馆借到.
至于工科的概率和理科概率的区别.大概就是教材上简单一些.还有应用成分大,对于概率的公理化体系和做为现代概率基础的测度等方面不会讲多少.
18531谢谢这位仁兄,没想到您能回复的如此详细,真是很感激!
18532正在找答案啊
太感谢了哦!
18532感谢楼主!!!
18532套用一句感激的话:
“啥也不说了,眼泪哗哗的!”
18532谢谢
18532多谢呢!
18532好人哪
18532习题1.2、习题2.1、习题2.2、习题2.3、习题2.4、习题2.5、习题3.1、习题3.4
习题4.1、习题4.2部分、习题5.1、习题5.2、习题5.3、习题习题post-67-1127482669.ibf
18532王高雄版《常微分方程》部分习题解答post-67-1127482764.ibf
18532非常感谢,希望多出这类好贴!
18532谢谢!我现在就需要答案。
18532谢谢!
要是有一些历年的各个学校历年的考研试题就好了!
18532多谢!!
18532Thank your
18532谢谢了,我也正需要呢。
18532真是太感谢了!
185323ks
18532非常感谢
18532小弟初来乍到,古月兄的附件怎么打开啊?
18532
| 引用 (古月西风 @ 2005年09月23日
21时35分) |
习题1.2、习题2.1、习题2.2、习题2.3、习题2.4、习题2.5、习题3.1、习题3.4
习题4.1、习题4.2部分、习题5.1、习题5.2、习题5.3、习题习题
|
neng fou ziji ba ta buchongwanzheng
18532王高雄版《常微分方程》部分习题解答 很好
18532王高雄版《常微分方程》部分习题解答 很很好
18532实在是太感谢啦!!!!
18532谢谢,非常谢谢
18532thanks a lot
18532好人啊好人
18532太好了
18532真是好!!!虽然我不要,但我的同学问过我!!!
18532谢谢楼主大公无私的精神.
18532thanks
18532

,再全点就好了!不过还是谢谢了!
18532跟本就不是,我要向斑竹举报!!!!!!!!!!!!!!!!!!!!!!!!!!
18532大学生”古月西风“发了一帖王高雄常微分方程习题答案。本人下载与课本后的习题进行对照,发现题目与答案完全不符,真不知道大学生“古月西风”是有意欺骗大家捞取积分,还是工作马虎,引起大家空欢喜一场。本人作为一位受害者,特向斑竹举报,也希望大学生“古月西风”给大家一个合理的解释!!
18532真是太感谢了!
18532谢谢常微分
18532向古月西风抱歉,我发现这个答案的还是正确的只是习题的题目没有对上。
18532谁有王高雄版<<常微分方程>>(第二版)习题答案.
18532
| 引用 (deepnorth @ 2006年03月20日
15时55分) |
|
向古月西风抱歉,我发现这个答案的还是正确的只是习题的题目没有对上。 |
呵呵!小事而已!
其实这个题解本来就不全,有空帮他补全了
18532谢谢了,这次我可以给同学发过去,帮她参加复试了
18532thanks.斑竹!!!
18532顶!
18532十分感谢!!!
18532非常感谢楼主,我买不到书快考试了很麻烦呢!
18532搂住辛苦了。谢谢
18532谢谢
18532非常感谢楼主
18532正需要着 谢谢
18532谢谢了
18532非常感谢
不知道有没有《常微分方程》的电子书?
18533姜启源(第三版)数学建模课件post-67-1127483302.ibf
18533数学建模课件 姜启源(第三版)post-67-1127483483.ibf
18533数学建模课件 姜启源(第三版)post-67-1127483579.ibf
18533数学建模课件 姜启源(第三版)post-67-1127483711.ibf
18533数学建模课件 姜启源(第三版)post-67-1127484238.ibf
18533数学建模课件 姜启源(第三版)post-67-1127484338.ibf
18533数学建模课件 姜启源(第三版)post-67-1127484684.ibf
18533数学建模课件 姜启源(第三版)post-67-1127484853.ibf
18533好像不能解压
怎么回事?
18533我也解不开啊
18533不会吧?
18533可以解压
18533支持啊!!!
18533把全部文件放在同一文件夹下,运行解压,应该OK。
18533绝对可以用
18533nice
18533非常好用,谢谢
18533好东西
感谢了
18533谢谢拉
18533ppt格式,很好
18533可以解压的,HOHO!!
18533
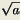
,楼主辛苦了!
18533楼主辛苦了!谢了!
18533十分感谢呀
18533太好了,谢谢楼主!
18533很感谢呀
18533谢谢,支持你,
18533感谢楼主
18533很好,内容很丰富
18533谢谢了
18533此等好贴,不顶对不起楼主.
18533学习了,谢谢
18533谢谢楼主,回去好好研究
18533好东西,谢谢
18536共勉
莫为潮落空自愁,酷夏过后又金秋.
效那葵花逐红日,不占鳌头誓不休.
古有破釜沉舟事,八千子弟掘秦冢.
卧薪尝胆百余日,小虾化龙大江游.
18536与为自己理想目标奋斗着的兄弟共勉
18536这是谁的诗?不会是你自己写的吧?!
18536是小弟乱写的
贻笑大方了
18536共勉
18536明天你是否会想起,食堂里川流不息
明天你是否还惦记,水房里不堪拥挤
老师们都已想不起,下课前猴急的你
你也是偶然翻笔记,才发现是复印我的
谁抓住逃课的你,谁安慰补考的你
谁叫醒死睡的你,谁经常借钱给你
那时侯你总很小心,政治课戴着耳机
你也曾无意中说起,最怕考英语四级
有时候你也很早起,为占座费尽心机
你总说时间很充裕,可踢球人难凑齐
谁记得考试前熬夜的你,谁表扬经常打水的你
谁把成绩寄到家里,谁把它丢在风里
从前的时光都远去,我们又有新的问题
我亲爱的姐妹兄弟,你们都在哪里
无论工作多忙,一定要保重身体
18536好诗文,共勉之.
哈
18536加油
18537这个题目我认为简单,但是就不知道该怎么表述,希望朋友们给个推理的理由,一步一步的去证明!
呵呵,如果要求跳跃我都觉得是个直观的结论似乎就没有必要证明!post-38-1127486950.gif
18537又是研题,有没有创意啊。是南大的题
18537楼上的!给个具体的解答吧!现在什么时候了啊!也没有闲工夫自己找题目出上来了!
18537如下post-38-1127533408.gif
18538这个题目也是简单的题目,希望大家给个具体的推理过程!要理由!post-38-1127487060.gif
18538如下:post-38-1127554014.gif
18539这个类型的题目大家给个具体的解题思路!一个还算系统的!post-38-1127488742.gif
18546是英文版吗?
18546谢谢了!
18546
Rudin《数学分析原理》希望对大家有用。
18546谢谢
18546Thanks a lot
18546谢谢楼主,可以看
18546在哪呢
18546我也想要一份,十分感谢!!!!!!!!!!!
我的邮箱:jgy_1121@163.com
18546看不了啊???
18546我也看不到阿,在那里?有电子版能给我发一份么?我的信箱是jinling_long@sina.com
18546麻烦给我一份,hitseven@163.com
18546我也看不到呀,可以的话也给我发一份呀,谢谢了
ruiyi@hqu.edu.cn
18546
引用 (ruiyi @ 2006年08月04日
18时29分) |
我也看不到呀,可以的话也给我发一份呀,谢谢了
lizhiyuan.cn@163.com
|
| 引用 (coDavid @ 2005年09月24日
11时24分) |
| 这样就方便多了,哈哈
|
谢谢,呵呵。
18560顶一下
18560顶
18560太好了,感谢感谢!呵呵
18560好东西共享!!!
18560xiexie
18560兄弟,今年B题用到那中方法啊!
18560Thank you so much!!
18561优化问题变量有连续的、离散的、整数。目前有这样的优化软件吗?
这个方面的研究达到了什么水平?世界上哪个科研机构又是谁走在最前沿?
在目前,有哪些软件最适合于二次开发用于混合变量优化?
18562求助!!!求助
各位高手谁有组合数学方面的题目呀!!!
18562你要哪方面的?
18563第三大题,怎么做?post-38-1127542349.ibf
18563怎么个一致收敛呢??
请你把答案贴出来,好不拉??
18563怎么个一致收敛啊??用什么判别法呢
18564我们这学期开设了 数学物理方程
刚刚开始讲课 就觉得很是麻烦
物理知识和数学的相互转化 很难把握
要是纯粹的解方程
那倒还没有什莫了
不知道各位当时是怎莫学习这门课程的
谢谢各位的赐教
感激不尽
18564首先要有对方程涉及的物理问题有直观印象,想热传导方程,弦的振动等等。对这们课程中等物理基础是必要的。在数学系,这门课叫偏微分方程,主要是讲三类方程:波动方程,热传导方程,位势方程。并且根据名字有其代表性的物理模型。此外就是加上一些变分法和广义函数。而在数学物理方程课里,可能还有一些积分方程等内容。这些还是数学的成分大一些。比起常微分方程。这门课还要好学一些。只要多做题就行。对三类主要问题求解的熟练是很必要的。至少它涉及的定理大概就极值原理啊,柯西-柯瓦列夫斯卡娅定理等几个。要是偏微分方程的话可能会多不少。
18564要学好数学物理方程,首先要学好数学分析,复变函数,常微分方程,这些课程,要不然里面有些东西看不明白,还有物理学上的一些知识。
18564我这学期也开始学数学物理方程,感觉非常难,有没有人指教一下应该怎么轻松学习啊
18564如果是数学系的课程,物理推导不重要.关键是数学部分
把多元微积分,曲面,曲线积分学好.还有其他的相关知识:傅立叶级数,傅立叶变换,复变函数,高等代数中的二次型.关键是基础要熟练掌握.
18564悟
别老是做题。
多元微积分和场论学的好的话,数学物理就不难
最好结合泛函分析学
一般情况下,不要期望能够学的很好
思想成熟了,不用学也会
18564我个人感觉这门课程的数学部分还可以解决,
应该值得注意的是对其中的物理背景肯定要熟悉,
要不然数学模型建立不起来,解决问题就无从说起了.
18564请问谁有姜礼尚的《数学物理方程讲义》的习题答案或习题集? 请与我联系
zhou
1920@126.com
不胜感谢!
18565亟需SAS
18566是科院2005年博士入学试题.
我也是很疑惑,如果简单地处理是不是误会他们的意思了?
多谢了post-38-1127551079.jpg
18566只要令Gk(X)为N维向量X到它的第K个分量的映射就行了。
18566
依照楼上的说法,岂不是
f(x)=Sum(x_k*x_k,
k=1..n)= |x|^2 ?????
哈哈
18566
题目给人感觉怪怪的,哪来的?post-38-1127613
184.gif
18566
是不是原题还要求 g_k亦可微
呢?
这样该题还有些意思,
不过我尚无法确定修改后结论是否仍然成立。
发帖请务必注明出处!
18566
| 引用 (uranium @ 2005年09月25日
10时28分) |
是不是原题还要求 g_k亦可微
呢?
这样该题还有些意思,
不过我尚无法确定修改后结论是否仍然成立。
发帖请务必注明出处!
|
我感觉你构造的函数对于(x _{1},x _{2,

,x _{n}
}并非普遍成立,因为你是对于基本固定的点来构造的.不知道我的理解对不对.
感谢你的帮助!
18566用拟微分平均值定理来做,得到逐点定义的函数:post-38-1127694069.gif
18566
| 引用 (walterwind @ 2005年09月26日
08时00分) |
我感觉你构造的函数对于(x
_{1},x _{2,  ,x _{n}
}并非普遍成立,因为你是对于基本固定的点来构造的. ,x _{n}
}并非普遍成立,因为你是对于基本固定的点来构造的. |
请言其详,谢谢。
我只是逐点定义g_k而已。
"快乐的思考"的做法应该是出题者的本意。
18566
| 引用 (快乐的思考 @ 2005年09月26日
08时21分) |
|
用拟微分平均值定理来做,得到逐点定义的函数: |
请问拟微分平均值是怎么回事?没有接触过呀.
这种分解是标准的吗? 是否使用了Fourier变换?
18566这个题目应该属于硕士研究生考试的题目吧!post-38-1127802229.gif
18566
| 引用 (蓝戈 @ 2005年09月27日
14时23分) |
|
这个题目应该属于硕士研究生考试的题目吧! |
蓝戈的解法应该就是他们要求的,
偶已经扔下数学很久了,呵呵,都忘光了.
再次表示感谢!!!
PS.
怎么修改标题呀? 我想让斑竹给蓝戈加分!
18566我个人比较欣赏uranium的方法,"另类"得恰到好处,有创意!
18567怎么编写入口命令?
18567不是F95标准都有了么??
matlab可以调用fortran程序的,只是需要编写接口。
18567手上有几个前人开发的Fortran77程序,原码还在,可以修改输入、输出。
但我现在想以MATLAB为主开发计算(优化)软件,又想最大限度利用前人开发的FOrtran77程序。
是否可以在MATLAB中直接调用由FORtran77编译得到的EXE执行文件呢?是否还有其他好的方法呢?
本人在网上找了很久,也没找到更高级的Fortran了,只有fortran77
18567查Matlab帮助
搜索Fortran
18567请问您的FORTRAN77源代码有没有数值计算方面或最优化计算方面的,如果有的话能不能给我一份,我现在在用fortran
编程做最优化方面的计算,想借鉴一下。谢谢。我的邮件地址:fengyun
19@21cn.com
185682005考研数学复习心得与体会post-38-1127555652.ibf
18568看看先!!
18568我顶
18568厉害,得了满分
无法超越你,希望能和你打个平手
努力达到你所说的居高临下
谢谢
18569见附件post-38-1127555977.ibf
185691.f(x)在无理数点取有理数,在有理数点取无理数,证明:f(x)不是连续函数
证明:显然f不是常值函数,故我们容易得到f在无理数上的像也非常值。
不妨设f(x)=a<b=f(y),x<y为无理数,a,b为有理数。
由于f连续,故f([x,y])包含[a,b],故对于[a,b]上的无理数是被映满的,这
于f的定义矛盾。
2.f(x)在除一可数集外,f'(x)>0,证明:f(x)为严格增函数
证明:由于f’(x)是Darboux连续的,故对所有的x,f’(x)不小于零。
故f递增,若f不是严格递增,那么存在区间,f在其上恒为零,矛盾。
18572如果矩阵的特征值是两个共轭复数,重数为2。例如:

1=1+j,

2=1-j,

3=1+j,

4=1-j.
那么,它的jordan形如何为求取?
谢谢!
18573对一

矩阵进行初等变换,
我变化的结果是:
对角线,其对角线上元素为:1,1,1,1,

(

-2)

2,(

-2)

3
而,答案是1,1,1,

,(

-2)

2,(

-2)

3.
18573上一问题的具体描述见附件,谢谢post-23-1127558796.ibf
18576设Fn=R-Gn(N=1,2,.....),则Fn为I的开覆盖,由有限覆盖定理,存在F(k1),....F(km)覆盖I,则I-F(ki)=G(ki)的交集为空集!!
18576符号错了吧?
18576这是紧性的等价定义,拓扑中常用
18576
| 引用 (jxnfhxh @ 2005年09月28日
20时52分) |
|
设Fn=R-Gn(N=1,2,.....),则Fn为I的开覆盖,由有限覆盖定理,存在F(k1),....F(km)覆盖I,则I-F(ki)=G(ki)的交集为空集!!
|
Fn在题目中是闭集,到这里怎么又全都变成开集了?
是不是符号用错了?
18576二楼的证明很漂亮!
18576
证明:I 是一有限闭区间,Fn 是其闭子集,若
Fn (n=1,2,3...)的交为空集,则必然存在正整数 N ,使 Fn (n=1,2,3...N)的交集为空集.
18577对啊。我也想知道,我帮你顶一下,让他发一下。
18577[SIZE=1][SIZE=7]我在考研网里面看到大连理工明年数分高代分别有加试实变和近代
18577在哪里看到的呀??
18577有吗?
18577明年是那一年?
18577明年当然是2006年了,那天在考研网看到了。
18577是真的吗?
我在大工招生网上没看到有什么改动?
你是在哪看到的?
把具体信息粘到帖子里吧
18578pw4ever兄,很想和你交个朋友
我是一个刚刚开始学习拓扑学的人,很想和你交流一下学习拓扑学的经验
我得QQ:308515507
盼复!
18580有那位仁兄对模糊拓扑环有研究的,小弟将虚心向您请教
18582设有半径为R的定球,另有一半径为r的变球与定球相割,若变球的球心在定球的球面上,使问r等于多少时,含在定球内的变球部分的表面积最大,并求最大表面积。
18582请教各路高手哈
18582
http://www.math.org.cn/forums/index.php?showtopic=13895
18584W怎么证明的是V的子空间啊,W是n*1列向量,V是m*1列向量,怎么搞成子空间的啊
18584在附件里,谢谢post-38-1127569984.ibf
18584显然 BX=0的解空间V1 是 ABX=0的解空间V2
的子空间
V1的基{a1,...,as}可以扩展成V2的基{a1,...,as,a(s+1),...,ar}
证明
B*a(s+1),...,B*ar 是W的基
18584谢谢你的回复,我明白了
18584不客气,请问你今年考研吗?
18584对啊,专业就是数学,你呢,也是吗?
18584请链接:
http://www.math.org.cn/forums/index.php?showtopic=
18690
18584BX=0的解空间V1 和 ABX=0的解空间V2 n*1的向量空间啊
我也考数学,请问楼主考什么学校
18584我给个具体的解答吧!post-38-1127815169.gif
18584跟我的做法一样的吧
18584要证明后面的秩的关系,谁不会啊!真是的,哪来的子空间哦
18584北京师范,你考哪,复习的如何了
18585开始,我看到这样一道题目
任给2005个互不相等的数,是否总可以将它们排成数列a1,a2,...,a2005,使得对任意
的
1<= i < j < k <= 2005 都有 2aj ≠ ai + ak ?
当这些数为 1).整数 ,
2).有理数 , 3).实数 , 4).复数
时,分别有怎样的结论?
我觉得很有趣,所以在空闲的时间好好的考虑了一下,得出一个解答:
1.1,2,3...,n可以无等差错排(用数学归纳法)
2.任意的n个整数可以无等差错排(把他们放到若干个连续的整数中考察即可)
3.任意的n个有理数可以无等差错排(通分就转化成2)
4.任意的n个实数可以无等差错排(利用实数的Hamel基分解,就可以把它转化成3,不
过我
觉得利用细分法然后利用3也可以做)
我并没有就此打住,接着又考虑了下面的问题
问题1
给定一个实数列an,任意两项互不相等,是否存在一个它的重排数列bn,使得对任意的
整数i
,j,k,1<=
i < j < k 都有 2bj ≠ bi + bk
?
问题2
是否存在实数集的错排f(x),使得对任意的x<y<z,都有2f(y)≠f(x)+f(z)?
问题3
对任意一个赋予全序的群A,是否都存在一个A的重排f(A),使得对任意的元素x<y<z,
都有2
f(y)≠f(x)+f(z)?
但
问题3由于提得过于一般化,竟存在反例
反例
令A=Z3={0,1,2},但是其中任取两元相加必等于第三者自加:
0+1=2+2=1
0+2=1+1=2
1+2=0+0=0
而
对于1.如果an有无穷的等差子列cn
,可以证明相反的结果:对于cn的任意重排bn ,可
将全体
正整数划分为三元子集{ui<vi<wi}使得对于每个i,
bui,bvi,bwi
成等差数列.
所以,我修正了一下问题:
如果问题1限制an没有无穷等差数列不知道是不是就可以了?
遗憾的是上面的问题也有反例
例如
0;
sqr(2),
2*sqr(2), 4*sqr(2), 8*sqr(2), ...
sqr(3), 2*sqr(3), 4*sqr(3), 8*sqr(3),
...
sqr(5), 2*sqr(5), 4*sqr(5), 8*sqr(5),
...
...
无论怎么排,0前面只能有有限多个,有一行全在0的后面,这一行无法做到。(一个
更简单
的例子:1,2,3,5,9,...,2k+1,...)
对于有无穷等差数列的数列,有下面的结论
所有正整数的任何排列都必定包含一个递增的3项等差数列,但存在一个排列,它没
有单调
的5项等差数列.是否对任意的排列总有4项等差数列,这还是未知的.
后来又有了新的进展:
关于2.全体正整数的集合N*上可以规定一个无三项等差的全序.
接着又推广到整数集上,即全体整数的集合Z上可以规定一个无三项等差的全序.
下面很自然的问题就是问是否可以在实数集上定义一个无等差的全序.
而我得出这样的一个结论:
如果能够给出有理数集上的无等差全序的话,我马上可以给出实数上的全序.
所以问题的关键就转化成了现在这个问题.
当然我想解决的是最一般的问题:对于什么样对加法封闭的赋有全序的集合可以定义无等差全序
.要一个简单的充要条件.
18585不错,做研究就应该有这种精神啊,我现在做什么之前都会首先考虑
这个东西能不能发文章,呵呵,但也没办法。祝你成功!
18585
引用 (Fisher @ 2005年09月26日
19时25分) |
不错,做研究就应该有这种精神啊,我现在做什么之前都会首先考虑
这个东西能不能发文章,呵呵,但也没办法。祝你成功!
|
务实也不错啊
呵呵
18586在附件里,谢谢post-38-1127574873.ibf
18586解答post-38-1127638438.ibf
18586谢谢了,我也觉得这个题面熟,但实在是忘了在哪做过,
18587李敖清华大学演讲文字实录
曾子墨:等了非常长的时间,今天我们终于等到了这样的机会,下面请大家用热烈的掌声来欢迎李敖先生,以及清华大学人文社会科学院院长李强先生和凤凰卫视董事局主席兼行政总裁刘长乐先生走上主席台。
从清华大学师生们的掌声中大家已经感受到非常热情的欢迎的气氛,作为主人家的代表,此时此刻清华大学人文社会科学学院院长李强先生要为我们致一段欢迎辞,有请李强先生。
李强:尊敬的李敖先生,尊敬的刘长乐先生,尊敬的各位来宾,老师们,同学们,大家上午好。
为了把更多的时间留给演讲会,我只讲三点:第一,非常欢迎李敖先生作客清华并发表演讲。李敖先生涉猎广泛,此次,清华师生能有机会与李敖先生面对面交流,我相信,这对双方都颇有益处。我也希望李敖先生在清华的演讲会对弘扬中华文化,对促进海峡两岸的交流和统一产生积极的影响。
第二,感谢刘长乐先生和凤凰卫视,因为他们的努力,使得本期世界大讲堂特别节目能够安排在清华。以往清华师生只能在电视上和书本上看李敖,听李敖,读李敖,此次有了面对面直接交流的机会,这很有意义。李敖先生阔别56年之后,重返大陆,此次神州文化之旅使得他能够有机会直接的看大陆,听大陆,读大陆。相信,他对大陆的了解也会更加全面、准确、深刻。
最后,祝愿李敖先生的神州文化之旅取得圆满成功。
曾子墨:非常感谢李强院长的第一二三,此时此刻,各位老师,各位同学和我一样都在期待着世纪大讲堂的这期特别节目,首先请李强先生以及刘长乐先生在台下就坐,谢谢两位!
今天的大讲堂我们为大家请来一位特殊的嘉宾,说他特殊,首先因为他有着多重的身份,他是历史学家、还是作家,还是台湾的立法委员。说他特殊,还因为他阔别了大陆56年之后第一次,回到北京,他说他不希望自己被当做是一个客人,他不过是一个归队的老同志。而且说他特殊,因为他在公众心目中的形象,最近有一个调查就显示,在大陆,有4成以上的网友都认为,他是狂人。今天来到我们的大讲堂我们这个归队的老同志到底有什么样的话来说?下面我们用热烈的掌声欢迎李敖先生为我们演讲。
李敖:刚才被美女抱了一下,浑身发热,我可以脱外衣吗?你们各位也可以宽衣,因为这屋好象热了一点,不要客气,不要见怪。
「清华是中国的清华」
毛泽东主席说,辛亥革命没有完成,但我到了贵校以后,发现真的没有完成,这不是大清帝国吗?大清帝国在清华,这说起来有点政治性的含义,我已经听到大陆的一句话,叫做大清帝国北大荒。刚刚我已经被嘱咐,不要奚落北大,所以今天虽然我在清华,我决定放北大一马。
各位,就在三年七个月以前,美国帝国主义的总统布什就站在这儿向大家说了一个谎话,大家看到布什的讲演稿没有?他说,清华大学是美国支持下建立的,等于是美国捐赠的。他说,清华大学是透过我国(美国)赞助建立的,布什总统讲了一句谎话。
大家想想看,当年一群爱国的中国人,可是他们给我们国家闯了祸,就是义和团,闹着八国联军,八国联军到今天只有一个奥匈帝国没有了,其他七个国家还在,尤其是那个可恶的小日本都在,当时八国联军以后,叫中国人赔钱,中国人赔不起钱。我们以甲午战争做例子,中国人赔日本人,赔的是两年全国的总收入,相当于日本三年的全国总收入,中国人赔垮了,所以日本小孩子用中国人的钱受了很好的教育,中国人没有钱办教育。到了八国联军的时候,要赔钱,美国也开出价码来,说我很客气,你们赔我军费就好了,结果账单开出来以后被一个聪明的中国人发现了,这个人叫做梁诚,是当时驻美国的公使,相当于大使。他就仔细算这笔军费,发现美国人多算了两倍半,梁诚就很聪明地向美国的国务卿海约翰商量说,你们既然说是要赔军费,怎么可以报出来这么多,多了两倍半,美国人又爱里子又爱面子,搞得国务卿很不好意思,说怎么办?聪明的中国大使梁诚说,钱捐出来好不好?办一个大学好不好?后来美国人就同意了,这就是今天的清华大学。所以清华大学钱的来源是因为美国人故意冒领钱,被我们逮到被我们追回,今天又愣又笨又凶又恨的美国总统小布什,居然说是他们送给我们的大学,当然,我要撕他的讲稿,大家觉得我做得对吗?
我们中国在过去一直有觉得有外国人,为什么我们盖长城呢?盖长城就是挡外国人,挡胡人,各代都挡,现在长城说起来不是秦始皇的长城,也不是孟姜女哭倒的长城,它是以一个旧的为根据盖出来的一个新城。可是我们想到,隔了半天,发现隔了这些人,到了和英国人
1840年、
1842年打仗的时候,才发现那是真正的外国人,过去长城挡的,或者东征西讨打的这些人都是自己人,到了英国人出来以后,我们才知道什么是真的外国人。那个时候我们出现了一个民族英雄就是林则徐,鸦片战争以后,林则徐被定了罪,给他发配新疆,在路上林则徐写了一封秘密的信给他的好朋友说,和英国人打仗,关公岳飞出来都束手无策,他们都没有办法,为什么?他说我们看不见敌人,敌人就打到了我们,为什么?他们有大炮,我们绝对打不过他们。他说,可是我写给你这个真相的这封信不能发表,发表以后,大家说我林则徐不爱国,这个真相一出来,会影响我整个的名誉,所以这件事情用我们北京话说起来,就是要把它“眯”(音)下来,不能讲。为什么发生这个现象?因为真的发现洋人来了,我们真打不过他,这时候中国就一路挨打。中国面临两个问题,就是如何避免挨打和挨饿,如何避免挨打?经过这么多年下来,最后香港也收回了,现在没有人敢打我们中国了,我在这里公开和大家说,只有一个党能够做到这个现象,就是中国*。
「*治国堪比汉唐盛世」
大家以为我喜欢骂人,不晓得我也喜欢捧人,该属于谁的就是属于谁的,我必须说刚才这个结论是正确的。刚刚有人说了你在北京这样讲,大家忘了我在中国的一部分台北也是这样讲的,告诉大家这个功劳是*的。我们的确富强起来了,当时穷的时候,日本人奚落我们的外交部长陈毅,说你们中国人穷得裤子都没有穿的,你们还要造原子弹,虎虎有生气的陈毅外长说,我们光着屁股,没有裤子穿也要造原子弹,我觉得这个气势是很了不起的。可是谈到没有穿,这件事情是真的还是假的?是真的,要不要怪*?我们把帐要算一算。
大家记得不记得唐朝的诗,来抓兵了,壮丁跑掉了,老头子也跑掉了,三个儿子也被抓走了,家里面剩下老太太,她和抓兵的这些官说,我家里没有人,“室内更无人”,只有吃奶的孙子、吃奶孙子的妈妈还在,不能见你们,为什么?因为没有裤子穿,没有裙子穿,“室中更无人,唯有乳下孙。有孙母未去,出入无完裙”,各位,中国人没裤子穿从唐朝就开始了,叫*负责任负到唐朝未免远了点。
我看过30年前的一个报告,一群人到甘肃去考察农业,大家口渴了,到农家要水喝,进了农家以后,农民很客气地招待他,他们在喝水的时候看到床上有一个棉被,棉被底下人在动,他们很好奇,就问这位农夫,说有人在睡觉吗?农夫说,没有睡觉,那说没有睡觉蒙着棉被干什么?农夫说,不瞒你们说,她是我女儿,你们是客人,她不能出来,她没有裤子穿。
这没有裤子穿的事我到处听说,台湾有我一个好朋友李庆华,他的爸爸就是李焕,在党政府里面做过“行政院长”,他亲口告诉我们,在西北行军的时候家里只有一条裤子,看到农夫出来,家里人都在家里面光着屁股,农夫的老婆出来裤子给她穿,农夫在家里光着屁股。我们中国是这么穷,这个账不能算在*头上。可是我们必须说,从
1949年以后有账目我们要和*说,*是不是要负责,可是49年*所接受的摊子是什么摊子?是国民党,国民党把能带走的全带到台湾走了。我带走了500本书,国民党带走了全中国国库里的黄金,当时的黄金折成美金是3亿美金,现在不算什么,可是当时是全中国的钱,国民党把这个钱带走了,能带走的全带走了。
大家看到莎士比亚的剧本,那个皇帝最后要跑的时候就讲了一句话,说一匹马,一匹马,我整个的王权用它来换一匹马,因为只有一匹马能够救他的命,国民党最后跑的时候能拿走的全拿走了,留给中国大陆的是一穷二白,国库掏空了,能破坏的桥都炸掉了,能带走的东西全部带走了,并且留下了300万的坏分子捣乱,土匪、国特留下在了大陆,所以引起*的紧张,又穷又要解决这些治安的问题,我们是在这种情况下成长的,今天大家知道吗,现在是中国自汉唐以来所没有的一个盛世。
我在中学时候写文章批评一个教授,他后来写信,他很谦虚地给我回信,这个教授你们都不认识,可是他给中国大陆,给北京大学留下了一个有趣的记录,就是“未名湖”三个字是他起的名字,这个人叫钱穆。他常常讲的一句话就是“汉唐以来所未有也”,汉朝唐朝以来从来没有的事情,他希望这个局面出现,今天告诉各位,我李敖亲眼看到了。
大家要知道,我们取得这么一点点的成绩,付出了多少代价呢?不但是千万人头落地,而且是多少愚昧的代价我们付出来了。在鸦片战争的时候,中国有名的思想家死掉了,他的名字叫余振界,他是替中国妇女受到不人道的待遇讲话的。他写了一篇文章说外国人什么样子,他说,外国人的生理结构和我们中国人是不一样的,他说中国人的心有七个窍,洋鬼子只有四个窍,我们中国人的肺只有六片,洋鬼子只有四片,我们中国人的睾丸有两个,洋鬼子有四个。所以,大家想想看,中国第一流的思想家在鸦片战争刚开始的时候,对外国人的了解是这样子的可怜和单薄,所以真正打起仗来的时候我们打不过它,所以我们尽各种方法和洋鬼子和他们周旋,可是我们所得到的都是打败打败,屈辱屈辱。到了后来,
1949年终于到了,中华人民共和国成立了,穷是我们最大的一个威胁,当时一个笑话,苏联关系还好的时候,当时有一个笑话挖苦毛泽东和苏联的统治者赫鲁晓夫说,老赫鲁晓夫给我们粮食,我们穷,没有粮食,给我们面包,赫鲁晓夫回电给毛泽东说,毛同志,没有粮食,你们只好拿勒紧裤腰带,毛主席第二个电报打给赫鲁晓夫说,请送给裤腰带来。
「这里是我的国家,我要使它自由」
大家说我的掌声没有连战多,因为我讲得太精彩了,你们都来不及鼓掌了,我讲演很多次,可是我最怕这种讲堂,为什么?大家知道吗?因为它是个半圆形的,礼貌上我们要照顾每一个人,头要从左边到右边,右边到左边,就觉得自己像是一个电风扇。
报告刘老板讲到目前为止还安全吗?外面谣言说我和凤凰的情缘已尽。我告诉大家,胡扯!
当年,胡适先生在北京大学,当时北京大学有*和国民党的学生,当时为了一件事情在礼堂里面吵起来了。胡先生出现在礼堂的时候,*的学起来说,汉奸!指着胡适在骂。胡先生是教育家,心平气和苦口婆心说,这个房屋里面没有汉奸。
今天在我们的祖国大地上面,没有谁不爱中国,没有谁是要捣你的乱,和你过不去,乱出反动言论,影响民心士气。可是有的人说你们言论有问题,这就是邓小平同志所讲的,有些同志思想需要慢慢的改过来,我愿意等待!不过大家不要忘记,我已经年过70了,我已经等不久了,希望大家要改,要快一点。
各位,今天我和大家讲,大家都以为我是自由主义者,你到了北京,过去你骂国民党,你骂民进党,你骂老美,你骂小日本,你到了北京,你敢不敢骂*?我会问我自己,我敢不敢骂*?我该不该骂*?
我告诉各位,如果有可骂之处我会骂,大家发现我不但没有骂*,我现在放弃了我自己的东西,就是自由主义。大家觉得太奇怪了,你李敖说自己是自由主义者,我的朋友
18587好像跟数学没什么关系啊!
18587聊聊天了,嘿嘿
18587李敖北大演讲全程录像
上半段
http://bbmedia.qq.com/media/news/200509/09...1liaobeida1.wmv
下半段
http://bbmedia.qq.com/media/news/200509/09...1liaobeida2.wmv
18587怎么这个也有啊!
18588在附件里,谢谢post-38-1127575132.ibf
18588不要沉了,小弟谢了
18588原题中要证明的式子好像还是有个地方写反了,我的解答:post-38-1127748638.gif
18589在附件里,谢谢post-38-1127575697.ibf
18589郁闷啊,做得这么不自然,大家对付看吧:post-38-1127582052.gif
18589没看明白你的计算过程,能详细点吗?
18589呵呵,懂了,谢谢哈
18590如图post-8-1127576820.gif
18590我的解答,可能不十分准确,希望有所启发:post-8-1127585276.gif
18593
http://www.nosta.gov.cn/dongtai/zrnew11.htm
包括:
复旦 陈恕行
高维非线性守恒律方程组与激波理论
科学院大气所: 曾庆存 王会军 等
气候数值模式模拟及气候可预报性研究
福州大学 范更华
Hamilton圈及圈覆盖理论
南开大学:
张伟平
Atiyah-Singer指标理论的若干研究
上海天文台: 景益鹏
宇宙结构形成的数值模拟研究
18594
http://www.cdgdc.cn/yxbslw/pxjg/2005/tmxk.htm
数学科学的提名论文包括 :
大学/ 学生/ 导师/ 论文名称
北京师范大学 刘普寅 李洪兴
模糊神经网络理论及应用研究
南京大学 宋永忠 沈祖和 解奇异线性方程组的迭代法
西安交通大学 吴伟志 张文修
粗糙集近似算子与随机集理论研究
中科院(数学与系统科学研究院)朱书尚 汪寿阳 多阶段投资组合选择及其风险控制
18595Fifth International Conference on Scientific Computing and
Applications
May
18-May 21, 2006
Banff, Alberta, Canada
Short
Course on Multigrid Methods, May 22, 2006
http://www.ualberta.ca/~sca2006/ This will be
the fifth of a sequence of conferences on Scientific Computing and
Applications held in the Pacific Rim region. All of them have the goal
of
bringing together mathematicians, scientists and engineers working
in the field
of scientific computing and its applications to solve
scientific and
industrially oriented problems and to provide a forum
for the participants to
meet and exchange ideas of common interest in
an informal atmosphere.
The focus of this particular conference
will be on the problems and methods
related to image processing,
financial applications and modelling of multiphase
flows. The goal of
the conference is twofold. The theoretical areas of interest
include
fundamental methods and algorithms for solving PDE's and linear
systems
of equations. On the other hand, it will try to attract the
attention of the
applied community, in particular the oil sands
industry, banking and medical
imaging, to present and discuss the
applications of scientific computing to
practical problems. The
theoretical topics of interest are (but not limited
to): Finite
Element, Finite Volume Element and Finite Volume Methods for
partial
differential equations, splitting techniques and stabilized methods,
iterative solvers and preconditioning techniques for large scale
systems,
methods for systems with a special structure, parallel
algorithms and
performance analysis.
Organizing committee:
W. Allegretto, Y. Lin, P. Minev and Y. Wong
Contact person:
Peter Minev, e-mail: minev@ualberta.ca,
phone: 1 780 492 3398,
fax: 1 780 492 6826.
Student support:
Limited funds are
available for supporting students and postdoctoral fellows to
attend
the conference or the Short Course. For details please contact the
organizers.
Plenary speakers:
Tony Chan, UCLA
Zhiming
Chen, Chinese Academy of Sciences
Ivar Ekeland, Pacific Institute for
the Mathematical Sciences
Olivier Pironneau, University of Paris VI
Invited speakers:
P. Bochev, Sandia National Laboratory
R.
Chan, Chinese University of Hong Kong
T. Choulli, University of
Alberta
K. Deng, University of Louisiana at Lafayette
R. Elliott,
University of Calgary
J.-L. Guermond, Texas A&M
B. Guo,
University of Manitoba
Q. Huynh, Naval Surface Warfare Center, USA
O. Mehdizadeh, Pratt & Whitney Canada
M. Noga, University of
Alberta
T. F. Russell, National Science Foundation, USA
D. Sheen,
Seoul National University
S. Sivaloganathan, University of Waterloo
& Fields Institute
W. Sun, City University of Hong Kong
X.-C.
Tai, University of Bergen
T. Tang, Hong Kong Baptist University
P.
Vassilevski, Lawrence Livermore National Laboratory
F. van de Vosse,
Eindhoven University of Technology
J. Wang, National Science
Foundation, USA
J. Wang, Northeastern University at Qinhuangdao
J.
Zhu, Laboratorio Nacional de Computacao Cientifica, Brazil
J. Zou,
Chinese University of Hong Kong
Date: Wed, 24 Aug 2005 11:
18:00 -0600
(MDT)
From: Y Wong
18596"冯康科学计算奖" 评奖委员会通告
http://lsec.cc.ac.cn/fengkangprize/index.html
2005年第六届``冯康科学计算奖"评奖委员会今年共收到13份申请, 其中海外8人,
国内(包括香港)5人.
经过二轮通讯投票及一次评委会会议, 在对全体参选人员进行
严格评选, 反复讨论的基础上, 考虑到今年若干国外候选人科研实力强, 对国内计
算数学发展的贡献大等非常特殊的情况, 委员会一致同意增加一个国外获奖人名额,
由一名增至二名. 现将获奖人名单公布如下:
国内: 黄云清, 湘潭大学;
国外(按拼音字母为序): Wei CAI(蔡伟), 美国 North Carolina
大学,
Qiang DU(杜强), 美国宾州州立大学.
授奖仪式定于2005年10月
17日在大连举行的全国高校计算数学年会
(http://math.dlut.edu.cn/meeting/index.jsp)的开幕式上进行.
特此公告.
第六届``冯康科学计算奖"评奖委员会
2005年9月2日
18597中国科大潘建伟教授获“求是杰出科学家”百万大奖
中国科大潘建伟教授获“求是杰出科学家”百万大奖
新华社8月20日电
2005年8月20日在乌鲁木齐举行的中国科协2005学术年会开幕式上,中国科协和求是
基金会对本年度获得求是科技大奖的专家进行表彰,潘建伟获得“求是杰出科学家
奖”,朱碎焕、王传福等
19位科学家获得“中国科协求是杰出青年奖”。
求是科技基金会出资人查济民亲自为获得“求是杰出科学家奖”的中国科技大学教授、
合肥微尺度物质科学国家实验室量子物理与量子信息研究部主任潘建伟颁发了获奖证书
和奖金100万元人民币,表彰其在量子科学领域的杰出成就
35岁的潘建伟教授在量子信息论和量子论基本问题等世界学术前沿领域取得的一系列开
创性成果,这些研究成果被中国科学院、中国工程院评为2003年、2004年年度中国十
大科技进展,并先后7次被欧洲物理学会和美国物理学会评为年度世界物理学重大进
展。
“求是杰出科学家奖”由香港求是科技基金会创设,这一基金会由查济民及其家族于
1994年捐资2000万美元设立。基金会特邀陈省身、杨振宁、周光召、李远哲、简悦威、
何大一6位国际知名学者为顾问,对在数学、物理、化学及生物医学等科技领域有突
出贡献的中国科学家进行奖励。自2000年起,“求是杰出科学家奖”颁奖典礼在每
年举行的中国科协学术年会开幕式上举行。
同时颁发的还有“中国科协求是杰出青年奖”,这个奖项分为实用工程奖和成果转
化奖:王传福、张明海、饶晓雷、熊翔四人获得中国科协求是杰出青年成果转化奖;
朱碎焕等15人获得中国科协求是杰出青年实用工程奖。
18598管理科学前沿问题研究
光明日报 2005年9月20日
人类社会作为一个复杂的组织系统,其维系和发展必须依赖于管理及其相关科学;而现代社会的发展又给管理科学提供了更多的现实问题和发展可能。进入21世纪,随着社会的进步和组织体系的完善,人们在逐步意识到管理重要性的同时,也开始越来越多地思考管理在社会实践中所面临的新问题,管理科学在面对机遇和挑战时表现出新的可能。这是社会发展的必然,同时也是管理学自身发展的需求。所以对于管理学学者来说,思考管理科学的前沿问题就显得尤为重要。
管理与管理科学
什么是管理?我们认为管理就是实践。在实践中要讲究科学,要以知识、理论作为基础。管理具有鲜明的时代特征,具有动态的性质。现代的管理是将多变的客观环境(宏观、中观、微观)视为一个复杂系统,为有效地实现系统目标(产生社会效益、经济效益或提高效率或使企业价值最大化等)而激活人的智力,优化配置系统中各种资源,并改变资源产出的一系列决策、措施、办法(包括思想、理念、观点、规章、制度、机制、模式等)。管理的作用是营造一个好的环境或者说一种好的氛围,使之能激活组织中成员的智力,而使组织跳跃式发展;或者说管理的作用是将科学技术转化为生产力,促进经济发展;或者说将资源从生产力和产出较低的领域转移到较高的领域,产生新的增长。管理的实质是创新的行为,是改变已有资源创造财富的潜力的行为。简单一点,创新就是改变资源及改变资源的产出。这有三层意思:改变已有资源;改变已有资源创造财富的能力;改变资源的产出。如在经济行为中,购买力是一种最重要的资源,管理就是获得购买力资源。管理在社会、经济中占有重要的位置,其重要性小在提高一个企业的效益,大在改变一个行业的命运,以至一个国家国民经济的状况。
管理有两个层次:第一是战略决策,它包括宏观战略决策,如国家区域的规划,宏观政策的制定等;中观战略政策,如投资项目的选择,大型工程项目的决策等;微观战略决策,如新产品开发决策、企业的营销策略等。第二是职能管理,它又分为两个层面:第一层包括工商管理、工程管理、金融管理、国际贸易(它们属于盈利的),以及公共资源管理、科技管理等(它们属于非盈利的);第二层面包括人力资源管理、生产管理、市场营销管理、财务管理、信息管理等。
什么是管理科学?
这里说的管理科学是广义的。管理科学是探索人类管理活动规律的一门科学,是管理的知识,它包括管理的思想、理论、理念,以及管理者指定决策的科学的、富有逻辑的、合理的方法。管理科学是一门科学,也是一门艺术,是自然科学与社会科学的交叉融合。可以说:管理科学=管理的科学+管理的艺术=定量分析+定性分析
我们说管理科学是管理的科学,是因为它应用定量分析的计算方法研究管理的决策问题。包括资源配置、人力资源、项目规划、财务、时序、选址等类问题,这些解决方案的定量计算方法,是研究制定最优化决策的科学方法,如,线性规划、目标规划、决策分析等;是研究改善决策制定的一种合理的、富有逻辑的分析和思维,具有科学性。管理科学定量计算的基础是:统计学;运筹学(数学优化、组合优化);智能信息处理;复杂科学。
我们说管理科学是管理的艺术,是因为它应用定性判断的思维模式,研究环境及其针对变化的环境,管理应该做什么、怎样做、怎样把该做的事情做好。判断的思维模式来自于管理的实践,是对经济、技术、人的行为进行分析的结果;是对管理者的经验、智慧、理念进行分析、归纳、总结的结果,具有艺术性。定性分析的基础是:经济学;组织行为学;心理学;社会学。
管理科学的理论基础是:经济学——决策的依据;行为学——对人的心理、人的行为进行定性分析的基础;数学——定量计算分析方法的基础;计算机科学——智能计算的基础,它为定性分析提供了智能信息处理方法;复杂科学——为使人们在研究管理问题时,有一种新的思维模式——以整体观为核心的系统思维模式。
管理科学与管理之间有着密切的关系,这种关系体现为理论与实践的关系。管理是应该做什么,怎样才能做好?这就要靠管理科学(管理思想、管理理论)作指导。而管理科学的研究,提出的管理思想、管理理论、管理方法均来自于管理的实践,是管理科学家深入实践,观察、分析,进行案例研究,总结、提炼管理的实践经验的结果。正因为管理的实践,才丰富了管理科学。
21世纪的管理:管理的变革
我们将现在和未来的管理与以前的管理进行比较,可以看到21世纪的管理面临管理的变革。表现在:管理思想方面,以前的管理思想是科学管理、以人为本、战略竞争、日本式管理技巧;现在和未来出现了新的管理思想,他们是学习型组织和复杂科学管理。在管理模式方面,以前的管理模式是橄榄型,即只注重生产制造,不注重研究开发和市场营销,而且知识对人、财、物的管理;现在和未来的新的管理模式是哑铃型,即注重研究开发和市场营销,而且是知识管理,是使显性知识与隐性知识结合,产生知识资本创新增量的经营管理模式。在管理理念方面,以前的管理理念是一味的竞争,只是停留在为顾客服务上;现在和未来的新的管理理念是竞争—合作,而且不只是停留在为顾客服务上,而是引领顾客创新,形成顾客资本。在组织机构方面,以前的组织机构是纵向的,一般都是实体;现在和未来的新的组织结构是扁平化和虚拟型组织。在资本观和资源观方面也有了很大的变化,关于资本观,以前的资本观认为有形资产和无形资产,且更重视无形资产——知识资本。关于资源观,以前的资源观认为自然资源就是资源,现在和未来的新的资源观认为,不仅自然资源是资源,社会资源(网络)、文化资源(文化、科技)、体制资源(制度、机制)、人力资源(劳力、资力)、购买力资源等等都是资源,而且是十分重要的资源。在增长方式方面,以前的经济增长方式是拼资源,用消耗资源获得经济增长;现在和未来的新的增长方式是用智慧、电子推动经济发展。在组织形式方面,以前的组织形式是工厂,现在的和未来的新的组织形式是科技园区。在决策方面,以前的决策是凭经验,现在和未来的决策是知识化、科学化。如此等等。可以说,21
世纪的管理在进行一场管理的变革。
21世纪:管理科学前沿问题
面对管理的变革,管理科学有许多新的问题需要研究。我们在这里提出管理科学需要研究的两方面的前沿问题:管理科学的理论、方法和管理科学的应用研究。
随着相关学科的发展,尤其是软科学、复杂科学的兴起与发展。给管理科学的发展创造了很好的条件和机会。管理科学可以借助相关学科的成果,发展自己的理论和方法,以适应管理的需要。因而,当前管理科学的理论和方法前沿问题主要是管理科学与软件科学相融的研究和复杂科学与管理科学相融的研究。
软科学是社会科学、自然科学、科学技术的有机结合,是高新技术。高新技术是人们在探索科学前沿的过程中派生出来的技术,而软科学技术是人类探索人的智慧派生出来的高新技术,即是模拟人的思维、智慧的高新技术(如CIMS、专家系统、人工智能等)。管理科学面临的都是复杂的大系统,管理科学与软科学相融的研究,就是利用软科学技术(如人工智能)研究管理科学中的复杂的决策问题,支持管理者决策。如,利用人工智能技术研究产品定价决策、新产品开发决策、投资项目的评价决策等等。
复杂科学是研究复杂系统(包括生物、物理、社会、经济等等)的科学。复杂科学对传统的经济学提出了挑战。传统经济学认为经济是市场稳定和供求均衡的结果,复杂科学则认为是互相作用的个体在不稳定的状况下不断调整关系的结果,暂时平衡再不断地演化。复杂科学管理改变了我们的思维模式,即从分割式思维模式转变为系统思维模式;复杂科学也改变了我们观察问题的角度,即由单向看因果转变为环状看因果。复杂科学与管理科学相融的研究,就是依据新的思维模式、新的观察问题的角度,来研究管理思想、管理理论、管理方法。它包括:视组织为系统思维的大脑的复杂科学管理的管理思想;基于信息技术的战略管理理论;基于投资者行为的投资组合理论、资本资产定价理论;基于知识管理的项目管理理论和方法;定性定量结合的方法;基于数据挖掘的预测与决策技术,等等。以适应复杂的管理系统。复杂科学管理的研究将成为管理科学理论前沿的一个重要研究领域。
随着管理实践的需要,管理科学的应用研究愈来愈宽泛,它包括的领域很多,主要有:知识管理、知识资本、企业的核心竞争力、中小企业集群发展、中小企业融资的实证研究、学习型组织、企业家精神、企业文化、企业领导力、基于顾客资本的营销模式研究、用数据挖掘技术进行购买者行为分析、创业管理、技术管理、风险管理、科技园区、风险投资、传统产业高科技改造、高新技术产业化、资本市场、投融资研究等等。
18599老科学家讲给年轻人的创新故事
科学时报 9月14日
金秋时节,中国科学院又迎来了万名莘莘学子,他们将成为科研队伍的生力军。9月8日,固体力学家、中科院力学所研究员白以龙院士和中科院数学院研究员陈锡康来到中科院研究生院中关村园区的创新案例讲座会场,通过现场与视频传输结合的方式为2000多名新生做了精彩的演讲。
会猜会做
40年前,白以龙院士作为研究生进入中科院,不知道自己能干什么。听师兄们讲,在研究方法上要会猜会做,将来就能做出一些国家很需要、又很像样的工作。
“会猜会做”给当时的白以龙留下了深刻的印象,他还清楚地记得一位师兄说过的两句话:“只会做不会猜,是瞎写真算,没有方向地在地上乱爬行。只会猜不会做,则会是一时聪明,最后落得一场空。”
当了研究生的白以龙开始学习“猜”和“做”。“猜”的阶段,就是对整个问题的预估。在这个前提下,结题前的两三年或者更长的时间,是一个既要不断地猜又要更踏实做研究的过程。他回想起在学校里学到的两种治学方法的争论:胡适提倡要“大胆假设,小心求证”,20世纪50年代被批判;于是郭沫若提议要“小心假设,大胆反证”。其实两种方法都强调了“假设”(猜)和“求证”(做)两个环节,但是在提法和分寸把握上则有不同。看来,“猜”和“做”的问题是有普遍性的。
白以龙认为,要猜得准、做得好,就必须熟练掌握基础知识、熟练掌握思维方法。因为猜着一点或猜得似是而非并不太难,但真正猜得准、做得对,能下科学结论,绝非易事。他提醒年轻人在学校学习阶段要注意积累知识,并指出应当如何训练思维方法:首先要掌握唯物辩证法的重要法则;其次是具体设计实验,观察现象,用具体的定律、方程和公式拟定算法,整理数据,去找未知的规律或精确的答案;再次,要牢牢把握实际对象的质和质的变化、特征量和量的界限,用合适的尺子来“去粗取精”。
猜错了怎么办?有些学生猜错了之后就对自己表示怀疑,是不是自己不适合做研究?白以龙鼓励研究生们说,做研究工作经常会猜错,但是一定要认真地纠正,如此不断地猜、做、猜、做,最终,必然能尝到“会猜会做”的味道。
因“挨饿”产生的重大成果
自
1980年起,陈锡康连续25年成功预测了全国粮食产量,提前期为半年以上,平均误差为1.9%,为国家相关部门制定有关农业和粮食政策提供了科学依据,多次获得中央领导肯定和好评。陈锡康等科研人员在编制和应用农业投入产出表过程中,针对其存在的问题在国际上首先提出了新的投入占用产出技术。说到这项成果,他告诉在场的研究生们,这是在国家重大需求下产生的。
1957年,陈锡康到中国科学院工作。
1959年,根据中央指示,研究人员要下放锻炼,陈锡康被派到四川省。当时农村的粮食非常紧缺,社员常说:“能吃饱饭就是共产主义了。”从
1959年到
1961年,中国粮食歉收导致全国大面积饥荒。由于出生率降低、死亡率增高,
1960年和
1961年两年中国人口减少约4100万人。陈锡康深切地体会到粮食生产和粮食预测的重要性。
20世纪70年代末,原中共中央书记处农村政策研究室和国务院农村发展研究中心委托中国科学院系统科学所进行全国粮食产量预测,并对此项预测提出两项要求:为便于及早安排粮食的消费、存储和进出口,要求预测提前期为半年左右,如果8~9月份发现当年粮食歉收,再到国际市场买粮,粮价已大幅度上升;要求预测精度高,误差一般在3%以下,发达国家谷物产量预测的误差通常为5%以上。
陈锡康等人承担了这项任务后了解到,国际上预测粮食产量方法主要有三种:气象产量预测法、遥感技术预测法、统计动力学生长模拟法。但是这三种方法的预测提前期都比较短,一般都是两个月左右。经过长期研究,新思路应运而生:不仅从气象因子,而且从社会、经济、技术和自然因子(气象及非气象)出发,提出以投入占用产出技术为核心的系统综合因素预测法进行预测,采用定性与定量相结合的综合集成方法,建立了多方程预测模型。
陈锡康等人进行的全国粮食产量预测工作,已经起到了对国家重大农业决策的咨询作用。
18600抛硬币,抛出正面的概率是p,一直到抛出到反面、反面、正面为止。求所抛次数的的数学期望。
拜托会的同志指教一下,我实在不知从何入手。
18600记p(k)为恰在第k次成功的概率,P(k)则为在第k次已成功的概率。
则有
p(k)=P(k)-P(k-1)
显然P(0)=P(1)=P(2)=0,
P(3)=qqp
对于k>3有
P(k)=P(k-1)+[1-P(k-3)]qqp
(见前面回肖邦的贴)
故有
P(3)=qqp
P(4)-P(3)=qqp
P(5)-P(4)=qqp
P(6)-P(5)=[1-P(3)]qqp
.....
P(k)-P(k-1)=[1-P(k-3)]qqp
各式两边相加就得
P(k)=[(k-2)-(P(3)+P(4)+....+P(k-3))]qqp
现在我们来求E(X)
记I(k)=0*p(0)+1*p(1)+2*p(2)+....+k*p(k)
因为p(0)=p(1)=p(2)=0
I(k-2)=3*p(3)+4*p(4)+...+(k-2)*p(k-2)
=3*P(3)+4*[P(4)-P(3)]+5*{P(5)-P(4)]+...+(k-2)[P(k-2)-P(k-3)]
=P(k-2)-[P(3)+P(4)+....+P(k-3)]
代入上面就有
P(k)=[(k-2)(1-P(k-2))+I(k-2)}qqp
我们有P(k)的递推公式知道它在k很大时趋于负指数函数形式,故k趋于无穷大时不但
1-P(k-2)趋于零,而且(k-2)*[1-P(k-2)]也趋于零。
显然在k趋于无穷大时,P(k)趋于1,(k-2)*[1-P(k-2)]趋于0,I(k-2)趋于E(X),故有
1=E(X)qqp
E(X)=1/(qqp)
18600谢谢赐教
只是我不太明白为什么p(k)=P(k)-P(k-1)
还有为什么P(k)=P(k-1)+[1-P(k-3)]qqp,我没找到
还望指教
18600一、如果事件A和事件B的并集等于C,而A和B的交集为空,则P©=P(A)+P(B)。显然,到第k-1次已成功和在第k次首次成功这两件事的并集就是第k次已成功这件事,而前两件事又是不相容的,故P(k-1)+p(k)=P(k)。
二、在第k次首次成功这一事件等价于第1次不成功,第2次不成功,....第k-1次不成功,第k次成功这k个事件均发生。记这k个事件分别为A1,A2,....Bk。则
p(k)=P(A1A2A3....Bk)
它既可以写成
P(A1)P(A2A3...Bk|A1)
也可以写成
P(A1A2)P(A3A4...Bk|A1A2)
....
P(A1A2A3...A(k-1))P(Bk|A1A2A3.....A(k-1))
当然也可以是
P(A1A2...A(k-3))P(A(k-2)A(k-1)Bk|A1A2...A(k-3))
其中P(A1A2...A(k-3))就是前k-3次均不成功,即到第k-3次仍未成功的概率,就是1-P(k-3)
P(A(k-2)A(k-1)Bk|A1A2...A(k-3))就是在第k-3次仍未成功的条件下,最后3次是“反、反、正”的概率qqp,因为先是两次“反”,故不可能在这两次已成功,故这就是在第k次首次成功的概率,即p(k)=P(k)-P(k-1),故有
p(k)=P(k)-P(k-1)=(1-P(k-3))*qqp,即
P(k)=P(k-1)+(1-P(k-3))*qqp
18601请问EI中的Full Coverage,Patial Coverage和TOC only分别是什么意思?
18607是不是可以这样啊?大家看看啊??
还有没有其他的方法啊?post-38-1127623210.gif
18607这样的题目,分成两部分
[0,1-d]
[1-2d,1]两个区间分别讨论,就可以得到一致收敛了
不过,有一点值得注意,这两个区间必须有非空的交集
18607
| 引用 |
这样的题目,分成两部分
[0,1-d]
[1-2d,1]两个区间分别讨论,就可以得到一致收敛了
不过,有一点值得注意,这两个区间必须有非空的交集
|
可否详细解答一下啊?谢谢!
18607x趋于1时,由于f连续且趋于0, x^n有界小于1,则g(x)一致趋于0;前边不含端点1的任意开区间g(x)都是一致收敛于0的。
18607当然在[0,

]上是一致收敛的,那么在[0,1]上呢?
18607不是说了吗,,分成两部分,分别一致收敛,前一部分利用f(x)在1连续...
18608对每个n,fn(x)在[a,b]上都是连续的,fn(x)收敛于f(x),而且f(x)在[a,b]上是连续的,那么
fn(x)在[a,b]是一致收敛的吗?
大家找出个反例啊?
18608用反证法想想就知道这是个正确的命题拉
18608若正确,请给个证明过程啊
18608构造{fn}:fn连续,满足n>2时
fn(x)=nx+f(x) x

[0,1/n]
=1-nx+f(x) x

[1/n,2/n]
=f(x) x

[2/n,1]
fn(1/n)-f(1/n)=1
在每一个[0,1]的点x,存在某个N(x),n>N(x)使得,fn(x)->f(x),但是他不一致收敛
如果画图的话就像有一个锯齿不断靠近0
这个函数他不满足Dini定理,仅仅是点态收敛,不知道构造的对不对
18608对的!
18608
| 引用 (zhubin846152 @ 2005年09月25日
22时11分) |
构造{fn}:fn连续,满足n>2时
fn(x)=nx+f(x) x  [0,1/n]
[0,1/n]
=1-nx+f(x) x  [1/n,2/n]
[1/n,2/n]
=f(x) x  [2/n,1]
[2/n,1]
fn(1/n)-f(1/n)=1
在每一个[0,1]的点x,存在某个N(x),n>N(x)使得,fn(x)->f(x),但是他不一致收敛
|
明显fn(x)不连续哦
18608只要知道zhubin846152那个意思就行了,单边锯齿函数
18608楼上的,俺才不知道单边``哦,你能给出具体的来么???
18609zhubin846152
我想了一下,可能有时候x(n+1)/xn,在n足够大的时候,也不是界于某个区间内的,可能是无穷的
比如:
x(2n+1)=x(2n)+1
x(2n+2)=n*x(2n+1)
是不是啊?也可能我钻牛角尖了,呵呵,望指教!
18609除了cauchy收敛定理外,没有其他的方法吗?post-38-1127624667.gif
18609首先,当n足够大的时候,1 < x(i+1)/xi < 2
1-(x(i)/x(i+1)) >
[(x(i+1)/xi)-1]/2
级数sum[1-(x(i)/x(i+1))]收敛 =>
级数sum[(x(i+1)/xi)-1]收敛
等价于sum(ln(x(i+1)/xi))收敛,矛盾
利用了sum(ln(1+an))~sum(an)
其中an>0
的性质
18609
| 引用 (zhubin846152 @ 2005年09月25日
21时27分) |
首先,当n足够大的时候,1 <
x(i+1)/xi < 2
|
谁说非要小于2的呀,
18609我也认为有问题
当lim(x(n+1)/xn)!=1时,级数显然发散
当lim(x(n+1)/xn)=1时,原级数和

((x(n+1)/xn)-1)的敛散性相同
后者可以证明发散.
没有用编辑公式,呵呵!
18609为什么有问题,可能我想得太简单了
如果,不是小于2,那么,存在无穷多个大于2的x(n+1)/xn
换句话说,就是有无穷多个(1-xn/x(n+1))
> 1/2
这难道,不说明发散吗
请楼上的指教
我这样做,主要是为了凑到(1+an)的形式
18609zhubin846152
你这样说我明白了,如果大于2,肯定发散的!
呵呵,之前没注意
18610正项级数

an收敛,在an单调递减的情况下 ,有limn*(an)=0
若没有递减的条件,什么情况下上述极限不为0,有反例吗?
18610n!=2^k时an=1/n^2,n=2^k时an=1/n,
18610我怎么感觉这个题目我都看不转啊,好象有问题,比方an=1+(1/n)就是单调的,而limn*an!=0啊!
不知道是我的误解还是什么啊!
18610反证法:
如果,存在limn*an=a<>0
立马可以退出矛盾,sum(an)>=(a/2)sum(1/n)
从N开始
另外,提供一个公式
sum(an)与a1+a2+2*a4+4*a8+...+2^(k-1)ak同收敛或发散
利用这个公式,就很显然了吧
另外,to
蓝戈
你的数列,求级数不收敛
18610呵呵,不好意思,我把题目都看错误了啊!
反证法就很容易证明了啊!
呵呵,现在大脑总是出窍!
18611最好是详细的解答,谢谢post-38-11276265
17.gif
186113.lim(f(x)/(x^2))存在,x趋向于0
18611三题用柯西收敛准则
四题作拉格朗日函数求极值
18611能不能详细写下,我在解答过程中感觉有些东西很麻烦的
谢谢
18611我的解答,帮忙看看post-38-1127653325.gif
18611我觉得第一替补拥着么复杂,用taylor公式展开一下就可以了
18611第三题不需要那么麻烦吧
不知道用Taylor展开这么做有问题没?
大家看看:post-38-1127655689.gif
18611谢谢楼上的答案,的确是好方法。我的方法的确麻烦了,抱歉
18611楼上的正解
浙大04年数分第二题和这题类似,只是二阶变成了三阶
18612帮忙post-26-1127626781.ibf
18612我改了一下最后三个约束具体表达式,看一下!post-26-1127632426.ibf
18612非常感谢Lf832003的帮忙谢谢
18612谢谢lf832003,你可帮我解决大问题了,要不然我的论文就泡汤了:)
18614给年轻人共6件商品,成本21

6共126元,给邻居50元,得到年轻人8元,合计损失168元。
18616lim(x-o)tan4x/x的极限
请求高手解答,先谢谢大家了.
18616limsin4x/(cos4x*x)=lim(4sin4x/4x)*(1/cos4x)=4
或学过罗必达法则后用罗必达法则=lim4sec4x^2=4/cos4x^2=4
18616大哥,多谢了.我完全明白了.以后有不会的题还要多多帮忙
18616第一个重要极限即可
18616记住这个 sinX/X=1 tanX/X=1 (X->0)
18616等价无穷小!tanx~x(x趋于0时)
18621各位高手:
现在想求助 在LINDO软件求解LP问题时,如果想知道迭代的详细过程应该怎么做啊?
谢谢!
18622急救
帮忙看看这个模型的问题---程序里面有错误post-37-1127637078.ibf
18623数分题目2详细点
谢谢post-38-1127637085.gif
18623怎么感觉第一题有问题啊?
18623我的解答post-38-1127651327.gif
18623我觉得第一题x应该趋于无穷,不然就不用做了
18623如果x->正无穷
用夹逼法则,答案应该是1/T

f(t)dt
(0->T)吧
18623to
zhubin846152第二个题目没有说f二阶可导,所以凹函数那个等价命题不可用吧,我用另外一个等价命题(解答中已证)来证明,另外我的解答完全是用你的贴子修改的,侵权请见谅,:)
下面给出两个题目的完全解答:post-38-1127692880.gif
186252003年美国数学竞赛post-7-1109315022.gif
18625请问怎么打开这些试题啊!
18625
| 引用 (zhouence @ 2005年01月07日
14时04分) |
| 请问怎么打开这些试题啊!
|
图片格式的,鼠标放在上面,直接保存。
18625谢了
18625图片显示不了啊!
18627证明:I 是一有限闭区间,Fn 是其闭子集,若
Fn (n=1,2,3...)的交为空集,则必然存在正整数 N ,使 Fn (n=1,2,3...N)的交集为空集.
18627证明:I 是一有限闭区间,Fn 是其闭子集,若
Fn (n=1,2,3...)的交为空集,则必然存在正整数 N ,使 Fn
(n=1,2,3...N)的交集为空集.
证明:取U为开集,并且包含I,令Un=U-Fn,则
Un的并集为U包含I,故存在有限个开集Um,m=1,2……,n使得他们的并包含I,故此时Fm,m=1,2……,n的交为空集。
18627thank you !
18628請問.X^666-1=
1999的倍數,
1999為質數,求X的所有值解?(列出1到
1999之間的值即可)
像這類的題目(X^n-1=Pk,P為質數,P-1為n的倍數),是否有特別的求X值方法呢?
或是有方法可推算X值解有多少個呢?(指1到P之間的X值)
另外想請教會程式設計的人,這類題目能否撰寫程式
18634weibull分布函数的三个参数怎样计算?有没有什么软件可以算?谢谢了!
18635各位大虾给看看小弟编的程序,
可以运行,但不知道是否有错误之处。post-26-1127650610.ibf
18636陈纪修,数学分析答案,电子版,谢谢
18636http;//math.fudan.edu.cn/math783/math_anal/
有所有题目的解答!
18637华中科技大学2004年《数学分析》试题解答post-38-1129005766.ibf
18637太好拉 不只怎么说好拉 就是非常感谢[COLOR=purple]
18637谢谢!!!!!!
18637谢谢
18637我瞧了一下tangshan0315关于华东师大的解答,前面两个填空题好像不对
18637谢谢!:)
18637mqh9015先生,这是你作的解答吗?好象是我以前的解答呀.
18637thank you
18637我的几道题目.希望有人能够给出详细的解答post-38-1127651371.ibf
18637过几天再把高等代数的贴出来...
18637不错的说~谢谢了
18637多谢 !
18637dfg
18637
| 引用 (baixueli88 @ 2005年10月11日
12时51分) |
| 谢谢!:)
|
真牛!
18637
| 引用 (tangshan0315 @ 2005年09月25日
20时29分) |
|
我的几道题目.希望有人能够给出详细的解答 |
好象你的第一题不对哦
不是用"洛毕塔法则"吗?我算出来是0哦
不知道对不对,已经很久没有碰过这东西了
18637不错
18637tank you very much
18637楼主是好人
18637好人啊
18638数列通项为 1/2ln2+1/3ln3+1/4ln4+。。。+1/nlnn-lnlnn ,证明这个数列收敛。请问怎么证明,谢了。
18638lnlnn=sum(lnlnn-lnln(n-1))=sum(ln(lnn/ln(n-1)))
ln(1+n)/lnn=ln(1+1/n)/lnn+1=1+1/nlnn+o(1/nlnn)
ln(lnn/ln(n-1))=1/nlnn+o(1/nlnn)
利用积分判别法,不难证明sum(1/nlnn)收敛,所以sum[o(1/nlnn)]->0
从而知收敛
证明的比较粗略,不知道对不对
18638给个taylor展开的证明:post-38-112766
19
19.gif
18638我再给一种证明.post-38-1127702349.gif
18638
| 引用 (yysnn @ 2005年09月25日
20时50分) |
| 证明: 数列
1 2
ln2
+1
3
ln3+1
4
ln4+⋅
⋅ ⋅+1
nln
n-lnlnn
收敛. |
lnln
(k+1)-lnlnk=ln[lnk+ln(1+1
k
)]-lnlnk<ln(lnk+1
k
)-lnlnk=ln(1+1
k
lnk)<1
k
lnk⇒
x n
≡∑ k
=2 n
1
k
lnk-lnlnn>∑
k =2
n
[lnln(k+1)-lnlnk]-lnlnn=lnln(n+1)-lnln2-lnlnn>-lnln2 ;
lnln
n-lnln(n-1)=lnlnn-ln[lnn+ln(1-1
n
)]>lnlnn-ln(lnn-1
n
)=-ln(1-1
n
lnn)>1
n
lnn⇒
x n
-x n
-1=1
n
lnn-lnlnn+lnln(n-1)<0⇒
x n
-1
>x n
>-lnln2 .
单调递减有下界的数列 x n
收敛.
上述证明中,
用了熟知的对数不等式:
引理 当 t >-1
时, 有
ln
(1+t)≤t
,
等号成立当且仅当 t =0
.
18638与{1/1+1/2+...+1/n-ln n} 的收敛性类似。
18640题在附件中。post-23-1127655366.ibf
18640我的解答post-23-1127659138.gif
18640我的证明:post-23-1127666132.gif
18640楼上的解法好优秀,可用于解决x^2+x+1不是平方数.
18640
| 引用 (快乐的思考 @ 2005年09月26日
00时35分) |
| 我的证明:
|
佩服佩服!
18641有的时候想为集合定义赋文本值的属性,但系统报错。是否LINGO的变量只能是数值?
18642证明:有限域上的自同构都为 Fp-自同构。
18643???
18643贴出来,看看。我也想要偏微分方程的算例。
18643各位同仁,鄙人最近写了一个解偏微分方程的小程序,但是不知结果对否,诸位可有有结果的算例,有的话请联系我,QQ:50871090,感激不尽!感激涕泠!感激万分!多多交流
18643贴出来啊
18643
∂ 2
U/∂t
2 =
∂ 2
U/∂x
2
其中(0<x<1,t>0)
边界条件是:U(t,0)=U(t,1)=0其中(t>0)
初值条件是:U(0,x)= sin
(Πx)
; ∂
U/∂t(0,x)=0
其中
0
≤x≤1
18643
| 引用 (shwfang @ 2005年11月06日
14时30分) |
∂ 2
U/∂t
2 =
∂ 2
U/∂x
2
其中(0<x<1,t>0)
边界条件是:U(t,0)=U(t,1)=0其中(t>0)
初值条件是:U(0,x)= sin
(Πx)
; ∂
U/∂t(0,x)=0
其中
0
≤x≤1
|
这个方程如何解呢?能否写出其程序?
18645附件中有我的问题的简单描述,请各位帮忙想一下,如何推导Tn的方差。 多谢了!!post-
17-1127688353.ibf
18645一般来说,你那个Tn在整个R上积分,不会是有限的,
建议把dx,dy分别改为dF_X(x),dF_Y(y).这样积分就有限了。
考虑其极限行为要借助经验过程的理论。
你这个问题是要做类似拟合优度检验的东西吧?
18645
引用 (Fisher @ 2005年09月26日
19时40分) |
一般来说,你那个Tn在整个R上积分,不会是有限的,
建议把dx,dy分别改为dF_X(x),dF_Y(y).这样积分就有限了。
考虑其极限行为要借助经验过程的理论。
你这个问题是要做类似拟合优度检验的东西吧?
|
当时我看到lz的问题也觉得很奇怪,但是如果改成dF_x(x)就没有意义了,出来肯定是1,两个减一下出来就是0.一般来说求估计偏至少也要加绝对值或者取平方
18645多谢两位的回复。我又继续尝试了一下,附件中是我导出的一点进展,请帮忙再看看对不对。基本思路是进行变量代换,这样定积分的区间就变成了[0,1]。然后用brownian
bridge的理论近似。但是我不知道如何求covariance。post-
17-1127745634.ibf
18645
引用 (子青 @ 2005年09月26日
19时50分) |
引用 (Fisher @ 2005年09月26日
19时40分) |
一般来说,你那个Tn在整个R上积分,不会是有限的,
建议把dx,dy分别改为dF_X(x),dF_Y(y).这样积分就有限了。
考虑其极限行为要借助经验过程的理论。
你这个问题是要做类似拟合优度检验的东西吧?
|
当时我看到lz的问题也觉得很奇怪,但是如果改成dF_x(x)就没有意义了,出来肯定是1,两个减一下出来就是0.一般来说求估计偏至少也要加绝对值或者取平方
|
你的意思是

(Fn(x)-F(x))dF(x)=1恒成立?
好象不对吧,如果F处处连续,

F(x)dF(x)=1/2.
而 0


Fn(x)dF(x)

1
18645
| 引用 (liuleo @ 2005年09月26日
22时40分) |
|
多谢两位的回复。我又继续尝试了一下,附件中是我导出的一点进展,请帮忙再看看对不对。基本思路是进行变量代换,这样定积分的区间就变成了[0,1]。然后用brownian
bridge的理论近似。但是我不知道如何求covariance。 |
我不懂经验过程,不知道你怎么能把积分从R变到[0,1]上的
这个极限分布肯定与X,Y的相关性有关的,如果这点未知,那你要算的东西
肯定得不到
18645
| 引用 (Fisher @ 2005年09月27日
11时25分) |
引用 (子青 @ 2005年09月26日
19时50分) |
引用 (Fisher @ 2005年09月26日
19时40分) |
一般来说,你那个Tn在整个R上积分,不会是有限的,
建议把dx,dy分别改为dF_X(x),dF_Y(y).这样积分就有限了。
考虑其极限行为要借助经验过程的理论。
你这个问题是要做类似拟合优度检验的东西吧?
|
当时我看到lz的问题也觉得很奇怪,但是如果改成dF_x(x)就没有意义了,出来肯定是1,两个减一下出来就是0.一般来说求估计偏至少也要加绝对值或者取平方
|
你的意思是 
(Fn(x)-F(x))dF(x)=1恒成立? 好象不对吧,如果F处处连续, 
F(x)dF(x)=1/2. 而 0 
 Fn(x)dF(x)
 1
|
我以为你改成
∫ d(F
n(x)-F(x))
18645
| 引用 (Fisher @ 2005年09月27日
11时30分) |
我不懂经验过程,不知道你怎么能把积分从R变到[0,1]上的
这个极限分布肯定与X,Y的相关性有关的,如果这点未知,那你要算的东西
肯定得不到
|
这个当然。X 和 Y 的相关性可以用它们的joint distribution
来描述(我们可以假设已知,至少是可以估计的)。
根据两位的启发,我已经导出了“答案”,现在就等跟导师确认了。
18648英文```
_杠Phi
18649一般只能复印啦。我就没有在旧书市场上见过这书。
18649有意的可以联系:
wyd
1982212@163.com
18649北京五道口有买,
18650我也正想找这本书.太感谢了
18650如题,急求,感激不尽!
(或尼柯尔斯基的《分析学教程》)
18650到此网站上找
http://elmo.jlu.edu.cn/数学书籍——分析与函数——中文图书——数学分析
肯定有
18650你给的网页上都下不了啊,怎么办
18650
引用 (caojing @ 2005年09月29日
19时44分) |
| 你给的网页上都下不了啊,怎么办
|
不会的,我刚刚还下载了,文件太大
不然我就发上来
18650
| 引用 (古月西风 @ 2005年09月29日
22时55分) |
引用 (caojing @ 2005年09月29日
19时44分) | | 你给的网页上都下不了啊,怎么办
|
不会的,我刚刚还下载了,文件太大
不然我就发上来
|
可以下,十分感谢!!
18650这本书不好读,我在图书馆借了第二册,没有看过第一册,发现就没法读了,因为前面的一些术语都不知道.
18651请教斑竹及各位大侠mathematica中怎样实现分步积分,我看到过上说可以自己定义法则,但不知道该如何做?谢谢各位!
18652刚刚看到的计算机教育新方案,通俗地说是这样的:计算机本科专业被分为三种类型:
计算机科学(CS),计算机工程(CE),信息技术(IT),分别对应研究型,工程型和应用型.
各学校任选其一.但,少数学校的学生学习CS,多数学校的学生学习IT,但专业名称不变,都还叫"计算机科学与技术"
CS就业意向是基础科研部门;CE是企业产品研发部门,IT是社会各行各业需要使用计算机的采购使用与维护部门.
这样学计算机的就不至于混乱了,你是学的CS还是CE?还是IT?学习的内容可是天壤之别啊---三种学习分别侧重的是:科学,核心技术,技术的使用.
比如学CS的学生学的主要是"算法学","可计算性"一类的理论课程,学CE的主要是"计算机组成原理","软件工程"一类的软硬件课程,而学IT的可能是.NET一类的流行工具.
18652我个人觉得这个不错,学IT的都去高校和企业研究院的确不是好事,学CS的到一家单位做电脑操作员也不合适---市场应该把他们二者反过来.
18652不应该!士别三日,即更刮目相看
18652这和水平没关系,只是说你学的侧重点不同.
就象学数学的人一样,有基础数学,有应用数学,难道谁比谁高一等吗?
既然市场需要少量CS大量IT,干嘛都学CS,结果学术也没学深,技术也没学精,使用又不会用,不如分几种类型搞.
18652个人看法:计算机要发展,还要靠CS
18652同意楼上的,我认为,没有CS就没有IT
18652没有 CS 的学校的计算机系是不入流的计算机系,再厉害充其量最多也就只能算是3流的
18655怎么这么多考川大的
18655准备考基础数学的研究生。很想以后研究低维拓扑。但报考的学校没有低纬拓扑方向。和低纬拓扑研究方向最近的只有点集拓扑,微分几何两个研究方向。想问一下,我考哪个方向,方便以后搞低维拓扑?也即点集拓扑和微分几何哪个和低维拓扑最接近?多谢。
18655北大有低维拓朴专业
现在好象专门研究点拓的应该不多吧,还是应该学微分几何,和拓扑关系比较近,
可以自己学点低维拓扑的书
18655多谢, 北大我哪敢考。。。 ,就听你的了考微分几何。
18655楼上那位仁兄,不知你考的是不是川大?
18655不是呀,呵呵,离四川比较远。考个近点的。
18655考微分几何,因为低维拓扑用到许多几何的技巧.
另:北大的王诗晟是作低维拓扑的,2002年ICM作过45分钟报告.
华东师大在这个方向也是很强的
18658本人在看用小波分析气温变换周期时,不知道怎样从小波变换系数矩阵的等值线图中看周期,请高手指教,谢谢!
18659同意Fisher的说法
18659弱弱的问 ,F-1(y)=sup{x|F(x)<y}中的sup是什么意思?
18659最小上界
18659设X

U(0,1)求
-1(X)的分布
解:记Y=
-1(X),,则F(y)=P{Y

y}=P(
-1(X)

y)=P(X

(y))=
(y)
书中解答是这样的,但是我觉得应该是P(X

(y))=
[
(y)]啊,请高手帮助,不胜感激
18659
引用 (xxxx_ffff @ 2005年09月26日
19时38分) |
设X
 U(0,1)求 U(0,1)求
 -1(X)的分布
-1(X)的分布
解:记Y=  -1(X),,则F(y)=P{Y
-1(X),,则F(y)=P{Y  y}=P( y}=P(
 -1(X) -1(X)
 y)=P(X y)=P(X

 (y))= (y))=
 (y)
(y)
书中解答是这样的,但是我觉得应该是P(X 
 (y))= (y))=
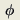 [ [
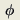 (y)]啊,请高手帮助,不胜感激
(y)]啊,请高手帮助,不胜感激
|
注意X

U(0,1)所以对任意t,0<t<1,
P(X

t)=t,
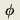
(y)就是这里的t
18659晕人傻掉了,居然想的是正态分布......
18660拜托!post-38-1127737777.ibf
18660很明显这个积分不收敛吧=v=
18660不好意思,写错了!post-38-1127740977.ibf
18660我的解答,好像还有别的方法:post-38-11277427
17.gif
18660好像还是不收敛哦,
18660这次没事的,含参量积分求导后也可以用微分方程求解
18662lim(x-0)arcsinx/x的极限???
18662答案是1
18662用L'Hospital法则求即可
18662arcsinx~x(x

0),所以=1
18662用等价无穷小替换
x->0
arcsinx ~ x
所以答案是1
18662楼上的等价无穷小替换用的好,我也是才学的,谢谢了
18663或者两个可交换的对称方阵能否同时相合于对角型吗?
18663请问,是否存在正交矩阵,使得,两个可交换的规范方阵同时相合于对角型.
多谢!
18663请问规范型方阵是具备什么性质的矩阵?请问兄台说的同时相合于同一个对角型还是分别相合于不同的对角型?
18663满足N'N=NN'的矩阵称为规范阵,规范阵好象只有两种:
对称阵 N=N' 或者 斜对称 N'=-N
或者 对称与斜对称的和
同时相合于对角型:只需要满足于相合于不同的就行了.
多谢!
18663这位老兄的关于矩阵的提法(斜对称、相合)很奇特。
任何方阵都可写为一对称阵与一这位老兄所说的斜对称阵的和。
可交换的对称方阵是可以同时相合(若你说的相合就是通常的合同的话)于一对角阵
18663抱歉,忘记注明,上面的对称阵限于实数域
18663
| 引用 (arthurlee @ 2005年09月26日
21时12分) |
请问,是否存在正交矩阵,使得,两个可交换的规范方阵同时相合于对角型.
多谢!
|
对呀 存在
规范变换在标准正交基下的矩阵为规范矩阵,反之也对
规范矩阵必可对角化(酉相似)。
规范方阵至少有三个等价定义。与伴随变换可交换,像于伴随变换的像模相等,可表为对称变换和反对称变换的河,酉相似于对角阵,酉相似于上三角形,任意不变子空间的正交补子空间为不变子空间,等等。
正交相似于实对角阵的变换等价于对称变换。
还有很多结论,请大家补充,关于分解等等
18663能否提问题时把概念提得明确一些,相合是否就是合同?你的名词有些特殊
18664中外数学家南开纪念陈省身94岁诞辰
人民网天津10月28日电
今天是已故国际数学大师陈省身先生的94岁诞辰。来自中、美、德三国的数十位数学家来到南开大学省身楼,参加一年一度的京津几何工作营,以学术会议的方式纪念这位数学领袖。
由南开数学研究所主办的2005年京津几何工作营于10月27日-29日召开。中国科学院院士丁伟岳以及特邀代表德国马克思-普朗克研究所教授
18664南开大学的BBS有一个专门纪念陈老的专题,看了很多关于陈老的报导,才知道什么叫做为人治学皆大师。
18664
http://chern.math.org.cn/姓名:陈省身
生辰:
1911年10月28日
祭日:2004 年12月3日
籍贯:浙江嘉兴秀水县
地区:天津
国家:美籍华人
职业:数学家
民族:汉post-71-1127741065.ibf
18664他给我们留下的实在是太多太多了
让我们永远的纪念他
*********************************
陈省身,男,1911年10月28日生于浙江嘉兴秀水县,美籍华人,20世纪世界级的几何学家。少年时代即显露数学才华,在其数学生涯中,几经抉择,努力攀登,终成辉煌。他在整体微分几何上的卓越贡献,影响了整个数学的发展,被杨振宁誉为继欧几里德、高斯、黎曼、嘉当之后又一里程碑式的人物。曾先后主持、创办了三大数学研究所,造就了一批世界知名的数学家。晚年情系故园,每年回天津南开大学数学研究所主持工作,培育新人,只为实现心中的一个梦想:使中国成为21世纪的数学大国。
18664敬仰啊!!!
18664陈省身:他提升了“大师”的内涵
文/dacien
在未识陈省身先生以前,总喜欢跟着媒体把“大师”二字冠之以在某些方面做出杰
出贡献的人,可是自从见到陈省身先生后,我才知道什么叫做大师,真正的大师。从此
我不敢轻易把一些成名成家的人叫做大师了。大师,不仅仅体现在学术造诣和所做出的
成绩上,更体现在人品修养和道德境界上。
陈省身,他提升了“大师”的内涵。
“这也是中国人的骄傲啊!从那个时候开始,他就在我心目当中是一个非常受到我
尊敬的偶像。”
-中国科学院院士王元
真诚的爱国者
陈省身少年时就读于南开大学,这所由伟大爱国者,教育家严范孙和张伯苓创办的
学校历来坚持爱国敬业创新乐群的理念,张伯苓校长不但本人身体力行,更是不遗余力
的向学生们灌输这种思想。陈省身便是在这样的环境中成长并走向数学之路的。
1937年,战争的烽火四处燃烧。此时在国际数学界已崭露头角的他并没有眷恋外国
的优美环境和丰厚待遇,而是千方百计地回到了自己的祖国,任教于国立西南联合大
学。在联大,有一段日子,他甚至连自己的生活都不能保障,一家三口在吴有训家里吃
住一月有余。
1971年5月23日,陈省身组织数百名华裔学者和学生连署,在美国《纽约时报》刊登
广告。抗议日本政府占领历来属于中国的领土-钓鱼岛!这便是中国人的第一次保钓。
1972年,中美关系刚刚解冻,他就迫不及待的回到了魂牵梦萦的祖国,与时任中国
社会科学院院长的郭沬若商谈中国数学的各项事宜。他表示他要为中国的数学事业做出
贡献。
1984年,一向不爱担任行政工作的陈省身欣然接受了中华人民共和国教育部的聘
任,出任南开大学数学研究所所长。出任所长时他曾立下誓言:“为南开数学所我要鞠
躬尽瘁,死而后已。”
在以后的日子里,他每年选择一个主题,聘请国内国外一流专家学者来到南开,为
中国的数学家们开办学习班,这样的“学术年”
在连续11年的时间内举办了12次。终使
中国数学的平均水平迅速接近了世界先进水平。
1988年,陈省身提出了“中国应该成为21世纪数学大国”的观点,这被称为“陈省
身猜想”。“陈省身猜想”点燃了国人数学大国的梦想。
2000年,陈省身定居南开大学,终于叶落归根。
2001年,陈省身对将要出任香港科技大学校长的女婿朱经武说:“应该为理想做点
事,为中国人做点事。”
2002年,由陈省身和丘成桐提议并推动的国际数学家大会在北京召开,这是国际数
学家大会成立一百多年来首次在发展中国家召开。在大会上,陈省身宣布:“中国成为
数学大国的梦想已经实现,我们要做数学强国!”
2003年,在南开大学新生入学大会上,陈省身向03级本科和硕士生讲述当年日本侵
占南开的历史,号召大家勿忘国耻,奋发有为,为国求学。
2004年12月3日,陈省身逝世
。“不要忘记中国数学事业的发展!”这是弥留之际
的陈省身给南开大学校长侯自新说的最后一句话,也是他留给这个世界的最后一句话。
“他自己一个人就影响了所谓二十世纪下半世纪数学的发展!”
―――2003年中国国家最高科学技术奖得主吴文俊
数学史上的天才
陈省身小学只上了一天,中学连跳二级,15岁考入大学,大三成为老师助手,24岁取
得博士学位,26岁担任西南联合大学教授,32岁便证明了高斯-博内公式,发现“陈
类”理论,将微分几何和拓扑学有机地结合了起来,从而奠定了整体微分几何的基础,
也奠定了他在数学史上的地位。
1984年5月,陈省身获世界数学界最高奖
-“沃尔夫奖”。该奖项上写到:此奖授于
陈省身,因为他在微分几何上的卓越成就,其影响遍及整个数学。
陈省身,微分几何之父,数学史上的里程碑!
陈省身是20世纪最伟大的数学家,他在微分几何方面的成就尤为突出。
陈省身是欧几里得、高斯、黎曼、嘉当的继承者与开拓者。杨振宁曾赋诗一首,单道
陈省身先生的伟大贡献和他在数学史上的地位,诗的最后两句便是“千古寸心事,欧高
黎嘉
陈省身发展了高斯-博内公式,为陈氏示性类,被命名为"陈氏级理论",成为经典
杰作。他
1946年提出了微分纤维丛理论,这与杨振宁30年后提出的规范厂理论殊途同
归。该理论的影响遍及数学的各个领域。他创立的复流形上的值分布理论,包括陈-Bott
定理,影响及于代数数论。他为广义的积分几何奠定基础,获得基本运动学公式。他所
引入的陈氏示性类与陈-Simons微分式,已深入到数学以外的其他领域,成为理论诸如规
范场等的重要工具。他先后发表过数学论文158篇、《陈省身论文集》4卷以及《陈省身
文选》等著作。
陈省身把一生都献给了数学。93岁高龄的他还整日里思考着数学问题,他逝世前的
一个月还为南开的师生们讲解了自己在“彭家勒猜测的新处理”、“六维球面上的复结
构问题”、“外微分系统”、“芬斯勒几何”四大研究方向的观点和见解。而这四个题
目中的任何一个都足够耗费一个年轻人大量的时间和精力,有的甚至要用一辈子来研
究,陈省身在如此高龄却在同时考虑解决这4个重大问题!这怎能不让世人敬重?
美国著名数学家布莱恩特在评价陈省身时说:“他比天才要优秀,我的意思是说,
世界上有很多优秀的数学家,但并没有很多陈省身,他是唯一的!”
1979年,陈省身从美国加州大学伯克力分校退休时,从世界各地赶来的300多名数学
家一起用歌声颂扬起他的丰功伟绩:
“向陈省身致敬,数学的伟人!
他使得高斯博内公式家喻户晓,
他发现了内蕴的证明,
他的真理传遍了世界,
他给我们陈类,
还有第二不变量,
纤维丛和层,
颁布和叶形,
让我们向陈省身欢呼致敬!”
“朝闻道,夕可死,有的时候是你简直无法想像的!”
――-第三世界科学院院士张伟平
令人爱戴的贤师
陈省身的职业是老师,一位数学老师。作为老师的他教出了许多优秀的弟子:丘成
桐、吴文俊便是其中的代表;作为老师的他无时无处不在想着数学,他的家叫几何之
家,他的客厅里挂着的是一块大大的黑板;作为老师的他在清华教过书,在西南联大教
当过教授,在普林斯顿搞过研究,在芝加哥大学带动了美国数学的复兴,在南开大学把
中国的数学事业推到了一个新的高峰。
丘成桐本科就读于香港中文大学数学系,因一门课程没有及格从而无法毕业。陈省
身得知后,便将其破格收到美国加州大学伯克利分校自己的门下直接攻读博士。27岁,
丘便做出了令世人瞩目的成绩。丘成桐在各种回忆恩师的采访中说到:“先生对我的的
影响和意义是无法用语言来述说的。”
不光是丘成桐,现在在国际数学界微分几何领域取得一定成绩的人基本都是陈省身
的亲传弟子。“得天下之英才而教育之,是我一生的幸运”。他曾这样表示他教书育人
的渴望。同样,有谁能得到这样一位老师的传道授业可以说是三生有幸。
陈省身的讲课艺术十分高妙,再难处理的东西到了他的手里也能十分简单地处理,
而且,他的几乎每一句话都让学生有一种如拔乌云见晴天的感觉。杨振宁在描述陈省身
的授课艺术时这样说到:“陈先生讲课让学生们很惊讶。同学们都觉得他好像在变戏
法,妙不可言。”
“朝闻道,夕可死,有的时候你简直是无法想像的!”陈省身的关门
弟子张伟平在回忆与恩师探讨学问时这样说到。
在美国有个“陈省身讲座”。这个讲座既不是什么大财团设立的,也不是什么富人
出资的,而且这个讲座的设立连陈省身事前也丝毫不知。原来这是他的一个名叫乌米尼
的学生自己出资设立的。有次乌米尼买彩票中了2200万美元,于是他便拿出一部分钱在
伯克利设立了“陈省身讲座”。
“我喜欢上他的课。”乌米尼说。他觉得陈省身讲授的大学本科的微分几何课程,是
如此令人感到刺激和振奋,以至“在课程结束时我曾想成为一名微分几何学家”。而这
便是其中全部的理由。
在陈省身的教学中,他鼓励学生们不妨“狂妄”一点,拿出自己的想法,不管是否
于主流一致。他教育学生的态度就是让其自然发展。不牵制其思维。
陈省身先生去世时,南开师生3000多人集聚新开湖边,手持蜡烛,唱着校歌为他送
行;全国许多高校BBS的进站画面改成了缅怀大师的图案;大洋彼岸的伯克利也为他降半
旗表示哀悼,而国际数学界则陷入了一片悲痛。
“陈先生不仅仅是数学大师,他也是文学上的大师!”
―――中国科学院院士葛墨林
博学多才的智者
陈省身先生不仅仅是一位数学的大师,他在其它方面亦有很深的造诣。
2002年国际数学家大会在北京召开,陈省身担任本次大会的名誉主席,组委会于是
给各国记者们安排了一个专场进行采访,当91岁高龄的陈省身在接受媒体一个半小时连
续不断的提问后略现疲倦。想要就此停止可各媒体依然不停发问,组委会无计可施。而
这位睿智的老人却提出了一个巧妙的建议:“我提问一个历史上的问题,如果你们回答
出来,我就继续回答问题,如果你们回答不出来,采访就到此为止。”结果,他的“司
马迁是怎么死的?”让各国的记者们目瞪口呆。大家面面相觑,无人知晓,于是陈省身
微笑着离席而去。
走近陈省身的书房,你会惊奇的发现那里不仅仅是数学书,电视机旁摆着的是《孝
庄秘史》的碟片,一堆数学书中间夹着《红楼梦》,《老子》,《庄子》,古典诗词,
围棋,医学和金庸的全套小说。而他的床头则放着一本相当新的《尘埃落定》,茶几上
放着《嘉兴市市情小册子》,饼干盒上的则是《张爱玲文集》。陈省身最喜欢的当数老
庄哲学,除此之外,他还十分喜爱陶渊明和李商隐的诗,尤其喜欢李的那首《锦瑟》。
陈省身不光会写数学论文,他还写诗。
飘零纸笔过一生,
世誉犹如春梦痕。
喜看家国成乐土,
廿一世纪国无伦。
这首《回国》便是他
1974年二次回国时写的。而《论清太宗孝庄皇后》这样的评论文
章也可以在他的《陈省身文集》里看到。
在接受东方之子采访时,他举了一个炒西红柿和炒苜蓿肉的例子来解释一个复杂的问
题,2003年底,他还亲手设计了一份挂历,叫“数学之美”。他想通过这种形式向同学
们普及数学知识。
与陈省身有过交往的不仅仅是爱因斯坦,计算机之父冯诺依曼,原子弹之父奥本海默
嘉当,杨振宁,李政道等科学家,不仅仅是邓小平,######,美国总统福特,以色列总统
哈伊姆•赫尔佐克这样的政治精英。他亦曾与范曾论画,与叶嘉莹谈诗,与金庸“武”
与聂卫平对弈,与季羡林有交。
陈省身曾说:“一个中国数学家不可以没有中华文化的涵养。”这大概就是他为什
么于
1963当选美国人文与自然科学院院士的缘由吧。
“陈先生是一位豁达、和善的老头儿。”
-南开数学所博士生苏广想
平凡质朴的长者
陈省身虽然是国际数学大师,却没有一点架子,平易近人,说话幽默,生活简朴几
乎是每个见过他的人对他做出的评价。正如南开数学所博士苏广想所说的那样,他是一
个和善的老头。
陈省身最爱与青年学生打交通,他生前南开数学院的许多学生都来过他的家里,数
学系的许多同学还有他亲自签名的照片。不但与学生,他还和几家大饭馆的大师傅打过
交道,和南开工地上的一些工人有过交情,当年为了盖南开谊园,他亲自为施工人员敬
酒。
2004年陈省身在浙江大学演讲时,浙大学子向陈省身提问他问问题,对话如下:
学生:我知道您早期在天津扶轮中学,
1926年的时候发表过一首诗叫《纸鸢》。
陈:这诗,很惭愧(听众笑)
学生:那首诗表明您是一个追求思维自由的人
陈:我那时候完全不知道我会是搞数学(听众笑)
学生:那我觉得从那首诗上来看,您是一个对思想自由比较看重的人
陈:我就是做那首诗,就是一个朋友他是编辑,他叫我写点东西,我后来写了那么一
个,不好。(听众笑)
这则故事表现出来的不仅是陈省身幽默的言语,更是他谦逊的为人。
陈省身生活简朴可是出了名的,粗茶淡饭的过了一生。其夫人郑士宁更是有名的简
朴,早在西南联大时期,一件旧袍子穿了老长时间都不肯换。最后还是其好友趁她不在
将衣服剪烂,最后郑士宁不得不换。
陈省身夫妇生活美满,相敬如宾。他们六十多年没吵过一句架,2000年,郑女士在宁
园去世,这对陈省身来说是难以接受的。郑女士逝世后,骨灰就放在宁园内,陈省身对
后人说,有一天他也去了,就把他和郑女士的骨灰埋在一起。
“数学没有诺贝尔奖是数学的幸事。”
-陈省身
淡泊名利的隐者
许多中国人,包括一些老师和学生甚至都没有听说过中国有这样一位伟大的人物。
的确。陈省身的一生没有大起大落,没有跌宕起伏,没有罗蔓缔克,没有绯闻。他的成
长是天才式的,一帆风顺,他的婚姻是别人介绍的,古老而美满。他的一生只是在做着
数学。
他甚至不愿意接受媒体的采访,他曾对前来采访的记者说:“我不愿意在北京、在
上海,我要找个安静一点的地方,安安心心做工作。我在南开也不顶清静,你还来找
我,有时候不能避免就是了。”
不仅如此,他还号召数学家要淡泊名利,做出好的数学来。在获得沃尔夫奖时他曾
说:“我趁此希望大家欣赏数学的美,减少竞争心理。”2004年11月20日,他向出席天
津市数学学术年会的100余名研究人员及天津各大、中学的数学教师发表演讲时说:“数
学家主要看重的应该是数学上的工作,对社会上的评价不要太关心。”
2004年10月28日,陈省身93岁生日,这天,国际小行星组织正式向世界公布,将中
国国家天文台发现的永久编号为
1998CS2号小行星命名为“陈省身星”,以表彰他为全人
类所做出的杰出贡献。当记者问及他对于这项荣誉的感受时,陈省身说:”陈省星小的
不得了,得了荣誉,觉得热闹热闹,见到几个有名的人,也有意思,好玩。不怎么要
紧。”这就是陈省身的对待荣誉的做法。
当年爱因斯坦邀请陈省身做统一场论,可是他认为这个没道理,所以最后并没有接
受爱因斯坦的邀请。这类数不胜数的轶事陈省身很少向人提起,因为他害怕被炒作从而
影响他的工作。
对于名誉他从来没有在意,他的名誉数不胜数。同样,在物质方面,他也从不计
较。
2004年10月,陈省身在万人瞩目中登上了邵逸夫奖的领奖台,可是有谁知道,他身上
的西装是他唯一的一套西装,而他脚上的皮鞋则是问女婿朱经武借的。
早在南开数学所刚刚成立之际,陈省身便把他获尔夫奖的5万美元奖金全部捐奖给了
南开数学所,随同捐赠的还有五辆名牌汽车。
1988年,陈省身把他在美国休斯敦授课所
得的两万美元捐给了数学所,到了21世纪,他为南开数学所设立了上百万美元的基金,
其中大半出自他的积蓄,他不仅捐献出国家给的津贴、学校的补贴、奖金,甚至他连自
己的生活费也捐了出来。
2004年,他又把邵逸夫奖的100万美元奖金和南开奖给他的100
万美元全部拿了出来,捐给了国内外的许多高校和研究机构。自己一分未留。
至于他捐献出来的图书,杂志及其他零星的东西,已经无法精确估计了。
陈省身曾于夫人郑士宁合约立下遗嘱:把仅剩的财产分作三分,留给子女各一份,另
一份则留给了南开数学研究所。
他还嘱咐后人:死后就埋在南开,和夫人的骨灰葬在一起。丧事从简,不立墓碑,墓
前栽几颗小树,树上挂一块黑板,以供后人演算数学。
2004年12月3日,陈省身在南开逝世。享年93岁。
让我们铭记这个伟大的姓名和他为人类所做出的杰出贡献。向他致敬,向他学习;
让我们让我们在“陈省身星”照耀下向着科学前行,抛确名利,丢弃虚荣;让我们遵照
他的遗言,为把中国建为世界数学强国而不懈努力!
附:不完全统计陈省身先生的荣誉式简历:
1948年中央数学研究所正式成立,陈省身任代理所长,主持数学所一切工作。并入选
中央研究院第一届院士。时年仅37岁。
1948年底,陈省身应原子弹之父欧本海默邀请,前往美国普林斯顿研究所。
1950在美国坎布里奇举行的第十一届国际数学家大会上作一小时演讲。
1951年,印度数学会名誉会员。
1958年,在爱丁堡举行的第十三届国际数学家大会上作30分钟的发言。
1961年被美国科学院推举为院士,这是美国科学界的最高荣誉职位。
1963,美国人文与自然科学院院士。
1969年,香港中文大学名誉法学博士,芝加哥大学名誉理学博士。
1970年,在法国尼斯举行的第十六届国际数学大会上作一小时演讲。
1971年,汉堡大学名誉理学博士,巴西科学院通讯院士。
1975年,获得美国国家科学奖。美国总统福特亲自为其颁发。
1981年退休后,担任美国数学科学所第一任所长,任期三年,后任名誉所长。
1982年获德国洪堡奖。
1983年获美国数学会“
体成就”斯蒂尔奖。
1984年中华人民共和国教育部聘请陈省身担任南开大学数学研究所所长。
1984年5月,获世界数学最高奖之一的“沃尔夫奖”。奖金50万美元。
1985,当选为英国皇家学会外籍会员。
1985年,接受南京大学名誉教授,中国科技大学名誉教授,北京师范大学名誉教授,
浙江大学名誉教授,名誉博士。
1986年,接受杭州大学名誉教授,复旦大学名誉教授,上海工业大学名誉教授。伦敦
数学会名誉会员,意大利西西里paloritani学院通讯院士。
1986年中国数学会常务理事设立“陈省身数学奖”,该奖由香港亿利达(ELITE)工业
发展集团有限公司提出倡议并捐资的。
1988年当选为意大利马林琴科学院外籍院士。
1989年当选为法兰西学院外籍院士。美国哲学会会员。
1989年当选纽约科学院终身名誉院士,天津大学名誉教授,日本东北大学名誉教授
1991年,受聘西安交通大学名誉教授。
1993年,中国科学院研究所名誉教授。
1994年,当选中国科学院首批外籍院士。
2000年,受聘天津科学技术馆名誉馆长。受聘清华大学名誉教授。
2001年,当选俄罗斯科学院外籍院士。
2001年1月9日,天津科技馆为陈省身竖立半身铜像正式揭幕。
2003年,美国数学科学研究所(mrsi)决定将扩建的摩天楼命名为“陈省身楼”
(chern hall)
2003年11月7日,获香港科技大学名誉博士。
2004年9月,获有东方诺贝尔之称的“邵逸夫奖”。奖金100万美元。
2004年10月28日,陈省身93岁生日,这天,国际小行星联合会小行星中心正式向世界
公布,将中国国家天文台发现的永久编号为
1998CS2号小行星命名为“陈省身星”,以表
彰他为全人类所做出的杰出贡献。
2005年,南开大学数学研究所命名为“省身楼”,这是继范孙楼和伯苓楼之后,南
开用校友命令的第三座建筑。
邓小平同志生前三次会见陈省身。######,李鹏等同志多次会见陈省身教授,其中
89年党和国家主要领导分别会见并宴请规格很高。
陈省身为第三世界科学院创始人之一
注:由于在举世闻名的诺贝尔奖中没有数学一项,“沃尔夫奖”和“菲尔兹奖”便成为
两个世界最高水平的数学奖。在华人中,陈省身和他的学生丘成桐分别是这两个奖项的
得主。迄今为止,获此殊荣的华人还只有他们两位。
18664
[东方时空]吴文俊忆陈省身
央视国际 (2005年09月13日 16:37)
CCTV.com消息(东方时空):
解说:今年86岁的吴文俊院士,至今还记得半个世纪前,与恩师陈省身的第一次见
面。
吴文俊:那是我第一次见到陈老,这次见面对我一生的工作,带有决定性意义的。
解说:抗战爆发后,吴文俊被迫中断了自己钟爱的数学研究,在上海租界的一所中
学教书,
1941年由于日军侵入上海租界,吴文俊一度失业,全家生活也处于困顿之中。
为生计所迫,半年后吴文俊再上讲台,繁重的教务工作,令他有五年半的时间没搞数学
研究。
吴文俊:那是因为抗战,所以没法搞数学,而且生活上面也有问题了,所以主要是
在一些初中教授兼职教务员这样维持生活,根本谈不上搞数学,数学全部都丢光了。那
时候忙于谋生。
解说:
1946年,抗战刚刚结束,吴文俊迫不及待地在上海临时大学恢复了自己的研
究工作。然而,他没有想到,自己孤独一人摸索的结果,却是陷在数学名词的倒来倒去
之中,钻进了牛角尖。更加强烈的精神痛苦每时每刻都在折磨着他。正在这时,一个机
缘使他结识了刚从北平清华大学到上海组建中央研究院数学研究所的陈省身。陈省身当
时在国际数学界因为完成了“高斯—博内公式”证明及构建陈氏理论而闻名遐迩。
吴文俊:西南联大的同学就陪我一起去到陈省身家里,那是我第一次见到陈老,我
记得我带了我写的自学的东西给他看。他认为,我提纲上面也有,说我的方向不对,指
的路子不对。这个对我有很大的影响的,你搞数学,挑些什么样的道路,走方向是很重
要的,搞的方向不对,一辈子也没有什么前途啊。那个时候我自己学习拓扑学了,我因
为从学校里面一步一步走上去,自然而然搞的这个拓扑学是点结拓扑学,这个比较专门
了。陈省身认为,你走的点结拓扑学这条路不对,你应该走代数拓扑学这条路。不能搞
点结拓扑,点结拓扑就是来回倒这没意思。
解说:一句方向不对,让吴文俊大梦初醒。与此同时,一个更加大胆的从师念头在
吴文俊心头升起。
吴文俊:记得当时我就提出来,我知道他是在中央研究院办数学研究所,我说是不
是可以到你的研究所来学习?他当时没说,到后来我走了,在门外,告别的时候,他说
了一句,他说你的事我放在心上。
解说:走出陈先生大门没有多少日子,吴文俊就接到了中央数学研究院的通知。
吴文俊:他叫我到那里去上班去。这是我到那个地方去做他的学生了。我数学放弃
不是心甘情愿的,这是苦闷了好些年了,没有办法只好丢掉了。这是违背自己的愿望的
,后来等于是从火坑里面逃出来了。
解说:此时的吴文俊,内心充满了阳光。不仅数学研究方向得以明晰,生活状况也
因为成了陈省身的学生得以改善。他每天泡在图书馆里如鱼得水,研究工作突飞猛进。
吴文俊:他把我安排到图书馆里面。我是非常高兴了,放到图书馆里面我可以随便
,书架子上面的书可以随便拿过来看。对我是最合适的。我在图书馆里东看西看,除了
陈先生指的我教我学的以外。因为我那个全部的书都包在里面,杂七杂八看得多了。有
一次因为经常提到一个叫纤维从(音),我就不知道怎么回事。有一次我见到他,我就
问了他一下,什么叫纤维从(音)?陈先生非常高兴,因为陈先生很大的成绩,就是因
为在纤维从(音)他上面的,他作出的贡献。使得这个陈先生的名字全世界都知道,这
个比较概念,比较难懂了,所以他在讲课的时候也没有提到。我现在主动去问他了,什
么叫纤维从(音)。他非常高兴。
解说:在中央研究院数学研究所,吴文俊有很多时间和机会向陈省身当面求教,而
陈省身也渐渐喜欢上这个勤奋的年轻人。随着和陈省身越来越多的接触,吴文俊更加感
觉到他在数学领域超强的能力。
吴文俊:他有一个能力,我觉得是别人很难做到的。他能够很快就把你带到最前沿
,正在大家都在共揭(音)的地方,所以你就可以比较快的前进了。一般人是做不到的
。他跟你磨咕,跟你上课,教这个教那个,教了一大堆的东西,然后慢慢一步一步跑到
接近前沿。他可以很快,一下子送到你前沿。所以我在中央研究院,我是前后不过一年
,我就可以一直跑道纤维从(音)了,就是刚才说的纤维从(音)了,他就是有这个本
事啊。
解说:
1947年,陈省身推荐吴文俊到法国留学,师从当年陈省身留学时的导师嘉当
的儿子小嘉当,可安排他去的地方却不是巴黎,而是法国边境的斯特伦斯堡,这让吴文
俊有点纳闷,为什么要送他去那么一个名不见经传的小地方。直到几十年后,陈省身回
国定居天津南开,这才把吴文俊当年的纳闷解开。
吴文俊:安静,这是可以说,那的确是很安静。
解说:去清静的地方,专心致志做学问。陈省身的许多方式在当时可能会让人摸不
着头脑,但事后如梦初醒,感觉到实实在在的温暖。此后几十年,在大师的指引下吴文
俊不仅对数学的主要领域-拓扑学做出了奠基性贡献,70年代后期又开创了崭新的数学机
械化领域,建立了“吴公式”、
“吴方法”、“吴中心”,更在国际数学界形成了“吴
学派”。近代数学史上第一次由中国人开创的这一新领域,吸引了各国的众多数学家前
来学习。
吴文俊:我想他是非常能帮助人的。乐于助人,并不是对我这样,对许多人他都帮
助人,受到他帮助的人不计其数。我是其中受他帮助之一,假定说没有人推荐到我他家
里面,我可能还到什么中学里面去继续教书。当教职员,当一辈子,教学工作。
解说:陈省身,中国科学院外籍院士。他在整体微分几何上的卓越贡献,影响了整
个数学的发展,是享誉国际的“微分几何之父”。2004年12月3日晚7时14分,93岁的国
际数学大师陈省身因病医治无效,在天津南开大学与世长辞。这个消息传来的时候,86
岁的吴文俊简直不相信自己的耳朵,因为就在两周前,他刚刚去天津看望过陈省身先生
。
吴文俊:主要都是他讲,精神好得很。他精神非常好根本没有想到他会突然病。
解说:手指着跟恩师的合影,吴文俊无声地缅怀自己的恩师。对于一位已经86岁的
老人来讲,悲痛在这个时候似乎并不浓重,重要的反而是在思考恩师走后,给这个世界
留下了什么?
吴文俊:到90多岁了他还在那儿钻研一些比较艰深的问题,这个精神我觉得应该大
家都学习的。我经常说外国的数学家都是早熟早衰,我非常反对。早熟没什么不好,当
然好了,但是也不能早衰。60岁以后是工作的黄金时代,他比较成熟了,应该最可以发
挥的时代。
解说:一位已经86岁的老人,谈着自己已经永远93岁的恩师。岁月在他们研究的数
学领域,似乎走得太慢。可也许正因如此,他们的人生精神,才能始终保持着一种永远
的年轻。
吴文俊:中国有句话是潜移默化,有些是无形之中的,对你思想上面,工作方法上
有影响。不是说很具体的实实在在,是潜移默化。
18664纪念微分几何之父 南开大学命名“省身楼”
人民网天津8月24日电
今日,南开大学隆重举行仪式,将国家投资兴建的南开数学
研究所新大楼命名为“省身楼”,以彰显杰出校友、“微分几何之父”陈省身先生(
191
1-2004)的伟大科学成就、高尚情操和对南开的杰出贡献。
这是南开校内目前第三幢以校友命名的建筑物,前两者分别以创始人严范孙和张伯
苓的名字命名。“省身楼”三字由陈省身生前亲笔题写。这座宏伟的数学建筑,是这位
大数学家留给南开和数学界最后的物质遗产。
“省身楼”南依津河,分为主体大楼和配套专家公寓两部分,总建筑面积20680平方
米,建筑风格庄重大方,朴实无华。楼内拥有数学教室、图书馆、教授办公室,以及多
个学术报告厅,可承办高水平的国际会议,接待大量访问学者。在每层楼道内都有一面
黑板,便于师生随时记下数学灵感——这一带有“陈式风格”的精心设计,凝聚着陈省
身先生最后的心血。
陈省身生前曾说过:“国家投巨资建设这么大规模的一流数学中心,实际是给我们
一个责任,那就是数学家要在这里为中国和世界的数学做一些工作。南开数学研究所要
放眼世界,要为中国的数学走向世界做更大的贡献。”陈省身的弟子、南开数学所所长
张伟平说,恩师的嘱托言犹在耳,南开人一定会继承先生遗志,充分利用“省身楼”来
服务南开、服务全国、服务世界。
为更好地完成先生遗愿,南开数学所2005年推出访问学者计划,国内外数学家纷至
沓来。客人们对新大楼极为赞赏,认为这是世界上最大、最好的数学建筑之一,在全世
界都很罕见。(张国
赵婀娜)
来源:人民网 (责任编辑:王金雪)
18664江泽民同志视察南开数学研究所
9月27日上午,江泽民同志来到南开数学研究所视察工作。陪同视察的有中共中央政治局
委员、天津市委书记张立昌,中共天津市委副书记、市长戴相龙,中共中央办公厅副主任
、中央警卫局局长由喜贵,市委副书记、市人大常委会主任房凤友,市委副书记邢元敏,
市委常委、市委秘书长王文华,市委常委、市委教卫工委书记陈超英,副市长张俊芳,南
开大学党委书记薛进文,校长侯自新,副校长陈永川,原副校长胡国定,南开数学研究所
所长张伟平,以及国家和天津市有关部委负责同志。
九月的南开园,秋风送爽,天高云淡。上午8时50分,南开大学省身楼前一片欢腾。
江泽民同志一下车,立即来到列队迎接的南开数学研究所师生身边。在持久而热烈的掌声
中,他面带微笑与学校领导和教授代表们逐一握手。
成立于
1985 年的南开数学研究所,由国际数学大师陈省身提议创办并担任首任所长
。江泽民同志一直关心和支持南开数学所的发展,曾多次听取陈省身等的汇报。
1994年视
察南开大学期间,他曾专程来到数学所,世界一流的省身楼也是在他的亲自批示下建成的
。
“我是来还愿的”
在师生的簇拥下,江泽民同志信步走入宽敞明亮的一楼大厅,目光被迎面而来的一桢
巨幅照片所吸引。这幅摄于
1990年代的照片,留下了他与陈省身亲切握手的珍贵镜头,寄
托着人们的崇敬与思念。江泽民在像前驻足良久,凝神端详,与陪同人员一同忆起拍摄时
间,感慨地说:“记得当年陈先生的双腿还很健康,身材高大。”
来到二楼贵宾厅,江泽民同志和蔼地招呼:“大家坐下谈吧。”厅内墙壁上悬挂着多
幅照片,其中有一张江泽民接见2002年国际数学家大会数学家的合影。他的昔日同窗、著
名数学家胡国定教授对照片作了说明,并由衷地称赞:“您亲自出席国际数学家大会,使
我们很受鼓舞。”江泽民真诚地说:“我是来还愿的。”环视四周,他动情地说:“陈省
身先生是我的好朋友,也是老朋友,我很敬重他。他是当代最杰出的数学家,始终心系祖
国,最后叶落归根在中国定居,这是很不容易的。他的两大心愿一是把中国建成数学大国
、二是办好南开数学研究所,我们很支持他。我想我一定要来看一看,圆他的梦。”
接着,江泽民同志深情地回忆起了他与陈先生多年的友谊。多次接见陈省身先生及其
夫人、出席2002年国际数学家大会、批复陈省身与胡国定先生关于建设数学大楼的申请、
与陈省身先生交谈数学问题……往事如昨,江泽民指出,陈省身先生的溘然离世令人无限
伤感,但他建设数学大国和创办南开数学所的夙愿已偿,足以告慰陈先生。“你们做得很
好。”
“要把南开数学所办成世界一流的研究所”
薛进文、侯自新、胡国定、张伟平等人汇报了陈省身先生的晚年生活与工作,以及南
开大学、南开数学研究所的发展现状。江泽民同志一边倾听,一边点头。他问:“哪一位
是现任所长?”
张伟平所长站起身来。胡国定笑着向江泽民介绍:“您上次来曾经见过他的。”侯自
新补充说,张伟平是我国杰出的青年数学家,曾在南开师从陈省身先生攻读博士,随后被
推荐到法国留学,学成归国任教已10余年,并被推选为第三世界科学院院士。
1994年江泽
民视察南开数学所时曾见过张伟平并称赞他“为中华民族争了光”。
见到当年的年轻人已经成长为著名研究机构的所长,江泽民高兴地勉励道:“很好!
你的任务很重,要继续努力,在南开做好数学。”张伟平点头称是。他又关心地询问数学
所有多少名教师,多少名学生,了解教学科研工作。听说全所已有师生员工60余人,他高
兴地说:“有那么多人做研究,很不错。”江泽民还问起教师们的年龄结构。当获悉所里
以中青年骨干居多,有3位著名学者均为41岁,他赞赏不已:“你们大有希望,祝你们成
功。”说着,他又转过身去,风趣地对胡国定说:“你80多岁了还在搞数学,也希望你顺
利完成课题,取得新的成绩。”
谈及数学,江泽民同志的兴致更浓了:“昨晚,我和胡国定谈了一个多小时的数学,
我似懂非懂,但认为数学很重要。我一直在思考中国科学的发展问题。我们的应用科技在
短时间内赶上世界发达国家并不容易,因为需要实验室,需要大量的投入。但是数学可以
不用投入那么多。数学是众多学科的基础,中国有优良的数学传统,古代就诞生过祖冲之
等数学家。”
“中国,应该能够把数学搞好。”江泽民同志顿了一顿,话语中饱含自信与期待:“
我希望你们越办越好,多出人才,多出成果。要把南开数学所办成世界一流的研究所。”
谈话间,侯自新等汇报了省身楼投入使用的情况。今年8月投入使用以来,这里已经
举行了“理论物理中的微分几何方法”等国际顶级学术会议,国内外数学家纷至沓来。这
座建于津河之畔的数学建筑,朴素大方,雄伟壮观,受到国际科学界的高度评价,被认为
是体现中国政府对基础科学重视与支持的经典之作。此时,张伟平送上一份媒体有关报道
的资料,江泽民认真地翻阅着,脸上露出欣慰的笑容。
张伟平代表数学所向江泽民同志赠送了校党委宣传部所编的画册《南开之子陈省身》
等纪念品,江泽民仔细地翻阅,露出高兴的笑容。在众人的陪同下,江泽民参观了大楼内
部设施。当看到学术报告厅内正在播放纪念陈省身先生的纪录片,他来到前排就座,兴致
勃勃地招呼大家一同观看。胡国定说,大楼的选址和设计都是陈省身先生亲自确定的。江
泽民称赞陈先生的眼光:“这是一块宝地。在这里选址很好,风景好,设计好,有水有灵
气,学术气息浓厚,适合做学问。”他回头对张立昌说:“这是一块宝地。在这里建数学
楼,体现了天津市的支持。”
“我好羡慕你们,年轻人!”
9时30分许,江泽民同志来到位于四楼的南开数学图书馆。这里是我国最大、最好的
数学图书馆之一。像往常一样,师生们正在忙着查阅文献,馆内一片安静的学习氛围。
在大家欢迎的掌声中,江泽民在一张阅览桌前停下了脚步,亲切地问候:“同学们都
在读书啊!”不远处是陈省身先生捐赠的4个书架的藏书。2005级硕士研究生胡双威手中
的一本陈先生的著作《微分几何讲义》引起了江泽民的兴趣。他接过来一边浏览,一边询
问:“是陈先生的书?是不是你们都学?”同学们七嘴八舌地回答:“是陈先生的。”“
微分几何在数学和物理上都很重要。”
有人搬来椅子,江泽民坐下来。这次吸引他的,是身旁2005级硕士研究生牛晖面前摊
开的两本书,英文版的《李群表示论及其应用》与《李群表示理论和特殊函数》。江泽民
饶有兴致地翻看,问牛晖:“你学什么专业?”
牛晖答:“数学物理。”身旁有人纠正她:“是理论物理专业。”
江泽民笑了,用英语提问:“能否告诉我数学物理与理论物理的区别?”
2004级硕士研究生周晓婷抢先用英语回答:“二者的目的不一样。”牛晖接着补充:
“数学物理更依赖数学,而理论物理更关注物理。”
江泽民微笑颔首,接着用英语问:“你多大年龄?”
牛晖流利的英语脱口而出:“保密!”讲完后,她意识到对年龄“保密”只是西方人
的习惯,有些不好意思了。
江泽民笑着解释说:“对不起,我只是随便问问。”
牛晖红着脸回答:“我今年22岁。”
江泽民问道:“在读研究生之前,有过工作经验吗?”
“没有。我是按部就班一直读书的。”在同学们眼中,江泽民同志是一位和蔼、慈祥
、睿智的长者,有一种说不出的亲切感,因此,谈话轻松又自然。
侯自新校长的研究方向恰好是李群理论,江泽民与他兴致勃勃地谈论起来,胡国定、
张伟平等也加入讨论,场面十分热烈。当再次看到那本《微分几何讲义》时,江泽民情不
自禁地回想起自己的大学生活:“记得我上大学二年级,考过微分方程的。”
在了解同学们的学习、科研和生活情况后,江泽民语重心长地说:“我好羡慕你们哪
,年轻人!”
另一群“年轻人”——南开数学研究所教授陈永川、龙以明、方复全、扶磊也在人群
中。江泽民听了校党委书记薛进文的介绍后,与他们一一握手交谈。陈永川是美国麻省理
工学院博士、陈省身先生的弟子,龙以明是美国威斯康星大学麦迪逊分校博士,方复全是
我国自主培养的数学家,36岁的扶磊已是南开数学所副所长。几位教授风华正茂,均为长
江学者或国家杰出青年,处于事业的黄金时期。见到龙以明的头发已灰白,江泽民问他:
“你是‘少白头’啊!是不是想问题想得太多了?”一句幽默的话语,使气氛更加欢快而
融洽。
走出图书馆,胡国定介绍说,由于创始人陈省身先生的伟大成就和号召力,南开数学
所在国外一般被称为“陈省身数学研究所”。江泽民听后,欣然应邀在宣纸上挥毫签名:
“江泽民 二〇〇五年九月廿七日
于陈省身数学研究所”。题毕,他对大家说:“我
回去再正式写一幅吧。”
不知不觉,一个小时多过去了。临别之际,江泽民同志来到楼前,与众人合影留念。
张伟平汇报说,墙上镶嵌的“省身楼”三个大字由陈省身先生亲笔题写。江泽民听后,踱
到老友的字迹前,久久地凝望着。
在南开师生的目送下,那熟悉的身影乘车远去。但是,亲切的关怀,谆谆的教诲,殷
殷的期望,却像一股清冽的甘泉,流淌在每个南开人的心田。
post-71-1128776271.jpg
18664世界日报:江泽民访南开大学 赞扬陈省身 (2005-10-07)
促建数学大国
【本报香港讯】现年79岁的江泽民,上周前往天津的著名学府南开大学,参观已故数学大师陈省身生前创办的数学研究所,表示要为陈省身“圆梦”。江泽民高度评价陈省身的人格、学问,并强调要建设“数学大国”。
据香港太阳报报导,江泽民于9月27日来到南开大学数学研究所。这是江泽民在9月3日出席抗战胜利60周年纪念大会后首次公开露面。天津市委书记张立昌、市长戴相龙、中央警卫局局长由喜贵等陪同视察。
报导指出,在陈省身的画像前,江泽民表示,陈省身是他的老朋友,“陈先生有两大心愿,一是把中国建成数学大国,二是办好南开数学研究所,我们很支持他。我想我一定要来看一看,圆他的梦。”
据报导,江泽民赞扬陈省身是当代最杰出数学家,始终心系国家,最后叶落归根,很不容易。他回顾自己与陈省身多次见面的情景。江泽民表示,陈省身溘然离世令人无限伤感,但夙愿已偿。谈及数学,江泽民兴致甚浓,他承认自己对数学“似懂非懂”,但认为数学很重要。江泽民指出,数学是众多学科的基础,中国有优良的数学传统,古代就诞生过祖冲之等数学家。
江泽民还到图书馆与学生交谈。离开前,他应邀挥毫:“江泽民2005年9月27日于陈省身数学研究所”。
(来源:美洲《世界日报》2005年10月3日
18664向数学大师学习!!!!
18664陈 省 身 演 讲:中 国 的 数 学美 籍 华 裔 数 学 家、 中 国 南 开 大 学 数 学 研 究 所 所 长 陈 省 身 教
授, 在 庆 祝 自 然 科 学 基 金 制 设 立 15 周 年 和 国 家 自 然 科 学 基 金 委 员 会 成 立 10 周 年 之 际,
以 《中 国 的 数 学》 为 题 发 表 讲 演。
以 下 是 这 篇 演 讲 的 全 文, 特 此 刊 出, 以 飨 读 者。
中 国 的 数 学
几 件 数 学 新 闻 和 对 于 中 国 数 学 的 一 些 看 法
陈
省 身
张 存 浩 先 生 要 我 讲 点 数 学, 这 么 短 的 时 间, 而 数 学 这 么 大, 只 好 举 几 个 要 点
谈 谈。 数 学 是 什 么? 数 学 是 根 据 某 些 假 设, 用 逻 辑 的 推 理 得 到 结 论, 因 为 用 这 么 简 单 的 方
法, 所 以 数 学 是 一 门 坚 固 的 科 学, 它 得 到 的 结 论 是 很 有 效 的。 这 样 的 结 论 自 然 对 学 问 的 各
方 面 都 很 有 应 用, 不 过 有 一 点 很 奇 怪 的, 就 是 这 种 应 用 的 范 围 非 常 大。 最 初 你 用 几 个 数 或
画 几 个 图 就 得 到 的 一 些 结 论, 而 由 此 引 起 的 发 展 却 常 常 令 人 难 以 想 象。 在 这 个 发 展 过 程
中, 我 认 为 不 仅 在 数 学 上 最 重 要, 而 且 在 人 类 文 化 史 上 也 非 常 突 出 的 就 是 Euclid 的 《几
何 原 本》。 这 是 第 一 本 系 统 性 的 书, 主 要 的 目 的 是 研 究 空 间 的 性 质。 这 些 性 质 都 可 以 从 很
简 单 的 公 理 用 逻 辑 的 推 理 得 到。 这 是 一 本 关 于 整 个 数 学 的 书, 不 仅 仅 限 于 几 何 学。 例 如,
Euclid 书 上 首 先 证 明 素 数 的 个 数 是 无 穷 的, 这 便 是 一 个 算 术 的 结 论。 随 着 推 理 的 复 杂
化, 便 有 许 多 "深 刻" 的 定 理, 需 要 很 长 的 证 明。 例 如, 有 些 解 析 数 论 定 理 的 证
明, 便 需 几 十 条 引 理。 最 初, 用 简 单 的 方 法 证 明 几 个 结 果, 大 家 很 欣 赏, 也 很 重 要。 后 来 方
法 发 展 了, 便 产 生 很 复 杂 的 推 理, 有 些 定 理 需 要 几 十 页 才 能 证 明。 现 在 有 的 结 果 的 证 明 甚
至 上 百 页, 上 千 页。 看 到 这 么 复 杂 的 证 明, 我 们 固 然 惊 叹 某 些 数 学 家 高 超 的 技 巧 和 深 厚 的
功 力, 但 心 中 难 免 产 生 一 些 疑 问, 甚 或 有 些 无 所 适 从 的 感 觉。 所 以 我 想, 日 后 数 学 的 重 要
进 展, 在 于 引 进 观 念, 使 问 题 简 化。
先 讲 讲 有 限 单 群 的 问 题。
1. 有 限 单 群
我 们 知 道, 数 学 的 发 展 中 有 一 个 基 本 观 念 -- 群。 群 也 是 数 学 之 中 各 方 面 的
最 基 本 的 观 念。 怎 样 研 究 群 的 结 构 呢? 最 简 单 的 方 法 是 讨 论 它 的 子 群, 再 由 小 的 群 的 结 构
慢 慢 构 造 大 一 些 的 群。 群 中 最 重 要 的 一 种 群 是 有 限 群, 而 有 限 群 是 一 个 难 极 了 的 题 目, 需
要 有 特 别 的 方 法, 特 别 的 观 念 去 研 究。
命 G 为 群, g ∈ G 为 一 子 群, 如 对 任 何 g
∈ G, g -1 H g ∈ H, 则 称 H 为 正 规 的 (normal)。 正 规 子 群 存 在, 可 使 G 的 研 究 变 为 子
群 H 及 商 群 G / H 的 研 究。 这 样 就 有 一 个 很 自 然 的 问 题, 有 哪 些 有 限 的 单 群 (simple
group)? 单 群 除 了 它 自 己 和 单 位 元 (identity) 之 外, 没 有 其 他 的 非 平 凡 的 正 规 子 群
(normal subgroup)。 数 学 上 称 其 为 简 单 群, 其 实 一 点 也 不 简 单。
有 限 群 论 的 一
个 深 刻 的 定 理 是 Fei-Thompson 定 理: 非 交 换 单 群 的 阶 (数) (即 群 中 元 素 的 个 数) 是 偶 数。
更 不 寻 常 的 是 除 了 某 些 大 类 (素 数 阶 循 环 群 Zp, 交 错 群 An (n>=5), Lie 型 单 群) 外,
后 来 发 现 了 26 个 零 零 碎 碎 的 有 限 单 群 (散 在 单 群, 离 散 单 群), 现 在 知 道, 最 大 的 散 在 单
群 的 阶 是
241 320 59 76 112 133
17
19 23 29 31 41 47 59 71 =
808,0
17.. = 1054
这 是 很 大 的 单 群, 由 B. Fisher 和 R. L. Griess 两 位 数 学 家 所
发 现, 数 学 家 称 它 为 魔 群 (怪 物, Monster)。
单 群 的 权 威 数 学 家 D.
Gorenstein 相 信 有 限 单 群 都 在 这 里 了, 这 当 然 是 数 学 上 一 个 很 好 的 结 果。 把 单 群 都 确 定
了, 就 像 化 学 家 把 元 素 都 确 定 了, 物 理 学 家 把 核 子 的 结 构 都 确 定 了 一 样。 可 这 里 有 个 缺
点, Gorenstein 并 未 将 证 明 定 出 来。 他 讲 若 将 证 明 写 出 来 至 少 有 1,000 页, 而 1,000 页
的 证 明 无 论 如 何 很 容 易 有 错 误。 可 是 Gorenstein 又 说, 不 要 紧, 若 有 错 误, 这 个 错 误 一 定
可 以 补 救。 你 相 信 不 相 信? 数 学 界 有 些 人 怀 疑 这 样 的 证 明 是 否 必 要。 现 在 计 算 机 的 出 现,
许 多 问 题 可 以 验 证 到 很 大 的 数, 是 否 还 需 要 严 格 的 证 明, 已 变 成 数 学 上 一 个 有 争 论 的 问
题。 这 个 争 论 看 来 一 时 无 法 解 决。 段 学 复 先 生 是 我 的 老 朋 友, 是 有 限 群 论 的 专 家, 也 许 我
们 可 以 问 一 下 他 的 意 见。 我 个 人 觉 得 这 个 问 题 很 难 回 答。 不 过 数 学 家 有 个 自 由, 当 你 不 能
做 或 不 喜 欢 做 一 个 问 题 时, 你 完 全 不 必 投 入, 你 只 需 做 一 些 你 能 做 或 喜 欢 做 的 问 题。
2. 四 色 问 题
把 地 图 着 色, 使 得 邻 国 有 不 同 的 颜 色, 需 要 几 种 颜 色? 经
验 告 诉 我 们, 四 色 够 了。 但 是 严 格 的 证 明 极 难。 这 就 是 有 各 的 四 色 问 题。
地 图 不
一 定 在 球 面 上, 也 可 在 亏 格 高 的 的 曲 面 上 (一 个 亏 格 高 为 g 的 曲 面 在 拓 扑 上 讲 是 球 面 加
g 个 把 手; 亏 格 为 1 的 曲 面 可 设 想 为 环 面)。 可 惊 奇 的 是, 这 个 着 色 问 题, 对 于 g>=1 的
曲 面 完 全 解 决 了。 可 以 证 明: 有 整 数 χ (g), 满 足 条 件: 在 亏 格 为 g 的 曲 面 上 任 何 地 图 都
可 用 χ (g) 种 颜 色 着 色, 使 邻 国 有 不 同 颜 色, 且 有 地 图 至 少 需 要 χ (g) 种 颜 色。 这 个 数 在
g>=1 时 可 以 完 全 确 定。 我 们 知 道 χ (1) = 7, 即 环 面 上 的 地 图 可 用 七 色 着 色, 四 色 不
够。
令 人 费 解 的 是, 证 明 地 球 上 四 色 定 理, 困 难 多 了。 现 有 的 证 明, 需 要 计 算 机 的
帮 助, 与 传 统 的 证 明 不 同。 而 我 们 觉 得 最 简 单 的 情 况, 即 我 们 住 的 地 球 球 面 上 的 着 色 问 题
反 而 特 别 复 杂。 把 扩 充 的 问 题 解 决 了, 得 到 了 很 有 意 思 的 结 论。 但 是 回 到 基 本 问 题, 反 而
更 难。 这 种 现 象 不 止 这 一 个, 还 有 很 多, 一 个 例 子 是 所 谓 的 低 维 拓 扑, 即 推 广 的 问 题 更 简
单, 而 本 身 核 心 的 问 题 反 而 不 易 克 服, 这 确 是 数 学 神 秘 性 的 一 面。
3. 椭 圆 曲 线
最 近 的 数 学 进 展, 最 受 人 注 意 的 结 果 就 是 Fermat 大 定 理 的 证 明。 Fermat
大 定 理 说: 方 程 式
xn + yn = zn , n > 2
没 有 非 平 凡 的 整 数 解 (即 x y
z < > 0)。 这 个 传 说 了 300 年 的 结 果 的 证 明, 最 近 由 Princeton 大 学 的 教 授
Andrew J. Wiles (英 国 数 学 家) 给 出。 但 证 明 中 缺 一 段, 是 由 他 的 学 生 Richard Taylor
补 充 的。 因 此, Fermat 定 理 现 在 已 经 有 了 一 个 完 全 的 证 明。 整 个 文 章 发 表 在 最 近 一 期 的
"Annuals of Mathematics" (Princeton 大 学 杂 志,
1996, 第 一 期), 整 个 一
期 登 的 是 Wiles 与 Taylor 的 论 文, 证 明 Fermat 定 理 (Wiles 为 此 同 Robert Langlands
获 得 了
1996 年 的 Wolf 奖 与 National Academy Science Award in Mathematics)。
有 意 思 的 是, 证 明 这 个 定 理 的 关 键 是 椭 圆 曲 线。 这 是 代 数 数 论 的 一 个 分 支。
有 以 下 一 则 故 事: 英 国 的 大 数 学 家 G. H. Hardy (
1877-
1947) 有 一 天 去 医 院 探 望 他 的 朋
友, 印 度 天 才 数 学 家 S. A. Ramanujan (
1887-
1920)。 Hardy 的 汽 车 号 是
1729。 他 向
Ramanujan 说, 这 个 数 目 没 有 意 思。 Ramanujan 说, 不 然, 这 是 可 以 用 两 种 不 同 方 法 写 为
2 个 立 方 之 和 的 最 小 的 数, 如
1729 = 13+ 123 = 93 + 103
这 结 果 可 用 椭
圆 曲 线 论 来 证 明。
我 们 知 道, 要 找 一 个 一 般 方 程 的 解 不 容 易 的, 而 要 找 一 个
系 数 为 整 数 的 多 项 式 方 程
P (x, y) = 0
(传 统 上 叫 Diophantine 方 程) 的
整 数 解 更 困 难。 因 为 普 通 的 解 不 会 是 整 数, 这 是 数 论 中 的 一 个 主 要 问 题。
需
要 说 明 的, 在 Wiles 完 成 这 个 证 明 之 前, 我 有 一 位 在 Berkley 的 朋 友 Kenneth A.
Ribet, 他 有 重 要 的 贡 献。 他 证 明 了 一 日 本 数 学 家 Yutaka Taniyama 的 某 一 个 关 于 椭 圆
曲 线 的 假 设 包 含 Fermat 定 理。 于 是 可 将 Fermat 定 理 变 为 一 个 关 于 椭 圆 曲 线 的 定 理。
Wiles 根 据 Ribet 的 结 果 又 继 续 经 过 了 许 多 步 骤, 以 至 达 到 最 后 的 证 明。 即 在 复 平 面 内
得 到 曲 线。 由 复 变 函 数 论 知 道, 复 平 面 内 的 曲 线 就 成 为 一 个 Riemann 曲 面。 Riemann 曲 面
为 定 向 曲 面, 它 可 以 是 球, 也 可 以 是 球 加 上 好 多 把 手。 其 中 有 一 个 最 简 单 的 情 形, 就 是 一
个 球 加 上 一 个 把 手, 即 一 个 环 面。 环 面 是 个 群, 且 为 可 交 换 群。 所 谓 椭 圆 曲 线, 就 是 把 这 个
曲 线 看 成 复 平 面 内 亏 格 (genus) 等 于 1 的 复 曲 线。 亏 格 等 于 1 的 曲 线 有 一 个 非 常 深 刻 而
巧 妙 的 性 质。 即 它 上 面 的 点 有 一 个 可 交 换 群 的 构 造。 两 个 点 可 以 加 起 来, 且 有 群 的 性 质。
这 是 很 重 要 的 性 质。 椭 圆 曲 线 与 椭 圆 无 关。 原 因 是, 若 所 有 曲 线 的 亏 格 大 于 1, 相 当 于
Riemann 曲 面 有 一 个 Poincare 度 量, 它 的 曲 率 等 于 1, 所 有 曲 面 若 其 曲 率 等 于 - 1, 则
叫 做 双 曲 的。 亏 格 等 于 1 的 叫 椭 圆。 亏 格 等 于 0 的 叫 抛 物 线。 椭 圆 曲 线 的 研 究 是 数 论 中 非
常 重 要、 非 常 有 意 思 的 方 面。 最 近 一 期 的 科 学 杂 志 (Science), 有 位 先 生 写 了 一 篇 关 于 椭
圆 曲 线 的 文 章。 椭 圆 曲 线 在 电 报 的 密 码 上 有 应 用。 而 中 国 也 有 很 多 人 在 做 代 数 几 何 与 代
数 数 论 方 面 的 工 作。 最 近 在 黄 山 有 一 个 国 际 性 的、 题 为 "代 数 几 何 与 代 数 数
论" 的 会 议, 由 冯 克 勤 先 生 主 持。
从 这 个 定 理 我 们 应 认 识 到: 高 深 的 数 学 是
必 要 的。 Fermat 定 理 的 结 论 虽 然 简 单, 但 它 蕴 藏 着 许 多 数 学 的 关 系, 远 远 超 出 结 论 中 的
数 学 观 念。 这 些 关 系 日 新 月 异, 十 分 神 妙, 学 问 之 奥, 令 人 拜 赏。
我 相 信, Fermat
定 理 不 能 用 初 等 方 法 证 明, 这 种 努 力 是 徒 劳 的。 数 学 是 一 个 整 体, 一 定 要 吸 取 几 千 年 所 有
的 进 步。
4. 拓 扑 与 量 子 场 论
1995 年 初 的 一 天 晚 上, 我 在 家 看 晚 间 电
视 新 闻。 突 然, 我 听 到 自 己 的 名 字, 大 吃 一 惊。 原 来 加 利 福 尼 亚 发 一 种 彩 票, 头 彩 300 万 美
元, 若 无 人 中 彩 的 话, 可 以 积 累 到 下 一 次 抽 彩。 我 从 前 的 一 个 学 生, 名 Robert Uomini, 中
了 头 彩 美 金 2,200 万 元。 他 曾 选 过 我 的 本 科 课, 当 时 还 对 微 分 几 何 很 有 兴 趣。 他 很 念 旧,
以 100 万 美 元 捐 赠 加 州 大 学, 设 立 "陈 省 身 讲 座"。 学 校 决 定, 以 此 讲 座 邀 请 名
学 者 为 访 问 教 授。 第 一 位 应 邀 的 为 英 国 数 学 家 Sir Michael Atiyah。 他 到 中 国 不 止 一
次。 他 是 英 国 影 响 最 大 的 数 学 家, 剑 桥 大 学 三 一 学 院 的 院 长, 卸 任 的 英 国 皇 家 协 会 会 长。
Atiyah 很 会 讲 学, 也 很 博 学, 他 的 报 告 有 很 大 的 吸 引 力。 他 作 了 八 讲, 讲 题 是 "拓 扑
与 量 子 场 论"。
这 是 当 前 一 个 热 门 的 课 题, 把 高 深 的 数 学 和 物 理 联 系 起 来
了, 导 出 了 深 刻 的 结 果。 现 在 拓 扑 在 物 理 上 有 非 常 重 要 的 应 用, 这 跟 杨 振 宁 的
Yang-Mills 场 方 程 有 很 密 切 的 关 系。 杨 先 生 喜 欢 说, 你 们 数 学 家 写 的 东 西, 我 们 学 物 理
的 人 看 不 懂, 等 于 另 外 一 种 文 字。 我 想 我 们 搞 数 学 的 人 有 责 任 把 我 们 的 结 果, 写 成 不 是 本
行 的 人 也 至 少 知 道 你 讲 的 是 怎 么 一 回 事。 物 理 学、 量 子 力 学, 尤 其 是 量 子 场 论 与 数 学 的 关
系 其 实 并 不 复 杂。 说 到 数 学 的 应 用, 讲 一 下 矢 量 空 间, Euclid 空 间 就 是 一 个 矢 量 空 间。 再
进 一 步, 多 个 矢 量 空 间 构 成 一 个 拓 扑 空 间, 这 就 是 所 谓 的 矢 量 丛, 即 一 束 这 样 的 空 间。 这
样 的 空 间 有 一 些 简 单 的 性 质。 比 如 说, 局 部 来 讲, 这 种 矢 量 空 间 是 一 个 chart, 是 一 个 集,
可 用 坐 标 来 表 示。 结 果 发 现 矢 量 丛 这 种 空 间 在 物 理 上 很 有 用。 物 理 学 的 一 个 基 本 观 念 是
"场"。 最 简 单 的 场 是 电 磁 场, 尤 为 近 代 生 活 的 一 部 分。 电 磁 场 的
"势" 适 合 Maxwell 方 程。 Hermann Weyl 第 一 个 看 出 这 个 势 不 是 一 个 确 定 的
函 数。 它 可 以 变 化。 这 在 物 理 上 叫 做 规 范 (gauge, 不 完 全 确 定 的, 可 以 变 化 的), 这 就 是 物
理 上 规 范 场 论 的 第 一 个 情 形。
物 理 上 有 4 种 场: 电 磁 场、 引 力 场、 强 作 用 场 和 弱
作 用 场。 现 在 知 道, 这 些 场 都 是 规 范 场。 即 数 学 系 上 是 一 束 矢 量 空 间, 用 一 个 线 性 群 来 缝
住 的。 电 磁 场 的 重 要 推 广, 是 Yang-Mills 的 规 范 场 论。 杨 先 生 的 伟 大 贡 献 就 是 在 SU(2)
(special unitary group in two variables) 情 形 下 得 到 物 理 意 义 明 确 的 规 范 场, 即
同 位 旋 (isospin) 规 范 场, 这 种 将 数 学 现 象 给 以 物 理 的 解 释, 是 件 了 不 起 的 工 作, 因 为 以
往 的 Maxwell 场 论 是 一 个 可 交 换 的 群。 现 在 变 为 在 SU(2), 群 是 不 能 交 换 的。 而 实 际 上,
物 理 中 找 到 了 这 样 的 场, 这 是 科 学 上 一 个 伟 大 的 发 展。 数 学 家 可 以 自 豪 的 是, 物 理 学 家 所
需 的 几 何 观 念 和 工 具, 在 数 学 上 已 经 发 展 了。
杨 先 生 之 所 以 有 这 么 大 的 成 就, 其
中 一 个 很 重 要 的、 很 了 不 起 的 原 因 是 除 了 物 理 的 感 觉 以 外, 他 有 很 坚 实 的 数 学 基 础。 他 能
够 在 这 大 堆 复 杂 的 方 程 中 看 出 某 些 规 律, 它 们 具 有 某 种 基 本 的 数 学 性 质。 Yang-Mills 方
程 的 数 学 基 础 是 纤 维 丛。 这 种 观 念 Dirac 就 曾 有 过。 Dirac 的 一 篇 基 本 论 文 中 就 讲 到 这
种 数 学。 但 Dirac 没 有 数 学 的 工 具。 所 以 他 在 讲 这 种 观 念 时, 不 但 数 学 家 不 懂, 就 连 物 理
学 家 也 不 懂。 不 过, 其 中 有 一 个 到 现 在 还 未 解 决 的 物 理 含 义, 即 有 否 磁 单 极 (magnetic
monople)。 可 能 会 有。 就 是 说, 有 否 这 样 的 场, 它 的 曲 率 不 等 于 0 (曲 率 是 度 量 场 的 复 杂
性 的)? 物 理 上 要 是 发 现 了 这 种 场, 会 是 件 不 得 了 的 事 实。 这 些 观 念 的 数 学 不 简 单。
Yang-Mills 方 程 反 过 来 影 响 到 拓 扑。 现 在 的 基 础 数 学 中, 所 谓 低 维 拓 扑 (二 维,
三 维, 四 维) 非 常 受 人 注 意。 因 为 物 理 空 间 是 四 维 空 间。 而 四 维 空 间 有 许 多 奇 妙 的 性 质。 我
们 知 道 代 数 几 何、 曲 线 论、 复 变 函 数 论 等 许 多 基 础 数 学 理 论 是 二 维 拓 扑。 而 现 在 必 到 四
维, 四 维 有 spinor 理 论, 有 quantum 结 构。 四 维 与 物 理 更 接 近。 它 的 结 构 是 Lorentz 结
构, 而 不 是 Riemann 结 构。 这 方 面 有 很 多 工 作 可 做。 根 据 Yang-Mills 方 程, 对 于 四 维 拓
扑, Atiyah 的 学 生 英 国 数 学 家 Simon Donaldson 有 很 重 要 的 贡 献。 其 中 有 一 个 结 果 就 是
利 用 Yang-Mills 方 程 证 明 四 维 Euclid 空 间 R4 有 无 数 微 分 结 构 与 其 标 准 结 构 不 同。 这
一 结 果 最 近 又 由 Seiberg-Witten 的 新 方 程 大 大 的 简 化 了。 这 是 最 近 拓 扑 在 微 分 几 何、 理
论 物 理 应 用 方 面 最 引 人 注 意 的 进 展。
二 维 流 形 的 发 展 有 一 段 光 荣 的 历 史, 牵 涉
到 许 多 深 刻 的 数 学, 可 以 断 言, 三 维、 四 维 流 形 将 更 为 丰 富 和 神 妙。
5. 球 装 问 题
(Sphere Packing)
如 何 把 一 定 的 空 间 装 得 最 紧, 显 然 是 一 个 实 际 而 重 要
的 问 题。 项 武 义 教 授 最 近 在 这 方 面 做 了 很 重 要 的 工 作。 这 里 先 介 绍 一 个 有 关 的 问 题: 围 着
一 个 球, 可 以 放 几 个 同 样 大 小 的 球? 我 们 不 妨 假 定 球 的 半 径 为 一, 即 单 位 球。 在 平 面 情 形,
绕 一 单 位 圆 我 们 显 然 可 以 放 6 个 单 位 圆。 而 在 三 维 空 间 的 情 况 则 更 为 复 杂。 如 果 把 单 位
球 绕 单 位 球 相 切, 不 难 证 明, 12 个 球 是 放 得 进 的。 这 时 虽 然 还 剩 下 许 多 空 间, 但 不 可 能 放
进 第 13 个 球。 要 证 明 这 一 结 论 并 不 容 易。 当 年 Newton 与 Gregory 有 个 讨 论。 Newton 说
第 13 个 球 装 不 进, Gregory 说 也 许 可 以。 这 个 争 论 长 期 悬 而 未 决。 一 直 到
1953 年, K.
Schutte 和 B. L. van der Waerden 才 给 了 一 个 证 明。 这 个 证 明 是 很 复 杂 的。
一 个 更 自 然 的 问 题 是 怎 样 把 一 个 立 方 体 空 间 用 大 小 相 同 的 球 装 得 最 紧。 衡 量 装
得 是 否 紧 凑 的 尺 度 是 密 度 (density), 即 所 装 的 球 的 总 的 体 积 和 立 方 体 空 间 的 体 积 的 比
例。 Kepler 于 1611 年 提 出 了 一 个 猜 想: 他 认 为 立 方 体 的 球 装 的 密 度 不 会 大 于 π /
(
18^1/2)。 项 武 义 说 他 证 明 了 这 个 猜 想。 可 是 有 人 (Gabor Fejes Toth) 认 为 他 的 证 明
不 完 全, 甚 至 有 人 (Thomas L. Hales) 说 是 错 误 的。 "Mathematical
Intelligencer" 这 个 杂 志 上 (
1995 年), 有 关 于 这 一 问 题 的 讨 论, 项 武 义 有 个 答
复。 Toth 是 匈 牙 利 数 学 家, 三 代 人 搞 同 一 个 课 题。 匈 牙 利 数 学 很 发 达, 在 首 都 布 达 佩 斯 有
个 200 多 人 的 几 何 研 究 所。 我 不 知 道 几 何 中 是 否 有 这 么 多 重 要 的 问 题 需 要 这 么 多 人 去
做。 最 年 轻 的 Toth 在 "Mathematics Reviews" 中 有 篇 关 于 项 的 文 章 的 评 论。
他 说 项 的 文 章 有 些 定 理 没 有 详 细 的 证 明。 天 下 的 事 情 就 是 这 样。 做 重 要 工 作 有 争 议 的 时
候, 便 产 生 一 些 有 趣 的 现 象。 不 过 他 觉 得 项 的 意 思 是 对 的。 不 但 项 的 意 思 是 对 的, 甚 至 表
示 这 个 意 思 他 从 前 也 有。 最 近 项 武 义 抒 他 认 为 没 有 的 证 明 都 有 写 出 来 了。
最 主
要 的, 我 要 跟 大 家 说 的 是 立 体 几 何 在 数 学 中 是 很 重 要 而 因 难 的 部 分。 即 使 平 面 几 何 也 可
能 很 难。 到 了 立 体 时, 则 更 为 复 杂。 近 年 来 对 碳 60 (C60) 的 研 究 显 示 了 几 何 在 化 学 中 的
应 用。 多 面 体 图 形 的 几 何 性 质 对 固 态 物 理 也 有 重 大 的 作 用。 球 装 不 过 是 立 体 几 何 的 一 个
问 题。 立 体 几 何 是 大 有 前 途 的。
6. Finsler 几 何
最 近 经 我 鼓 励,
Finsler 几 何 有 重 大 发 展, 作 简 要 报 告 如 次:
在 (x,y) 平 面 上 设 积 分
S = F (x, y, dy / dx) dx
其 中 y 是 x 的 未 知 函 数。 求 这 个 积 分 的 极
小 值, 就 是 第 一 个 变 分 学 的 问 题。 称 积 分 s 为 弧 长, 把 观 念 几 何 化, 即 得 Finsler 几 何。
Gauss 看 出, 在 特 别 情 形:
F2= E (x, y) + 2F (x, y) y'
+ G (x,y) y' 2, y' = dy / dx
其 中 E、 F、 G 为 x, y 的 函 数, 几 何 性 质
特 别 简 单。
1854 年, Riemann 的 讲 演 讨 论 了 整 个 情 形, 创 立 了 Riemann-Finsler 几 何。 百
余 年 来, Riemann 几 何 在 物 理 中 有 重 要 的 应 用, 而 整 体 Riemann 几 何 的 发 展 更 是 近 代 数
学 的 核 心 部 分。
Riemann 的 几 何 基 础 包 含 Finsler 几 何。 我 们 最 近 几 年 的
工 作, 把 Riemann 几 何 的 发 展, 局 部 的 和 整 体 的, 完 全 推 广 到 Finsler 几 何, 而 且 很 简 单。
因 此, 我 觉 得 以 后 的 微 分 几 何 课 或 Riemann 几 何 课 都 应 该 讲 一 般 情 形。 最 近 有 几 个 拓 扑
问 题。 最 主 要 的 一 个 是 Riemann 流 形 的 一 个 重 要 性 质, 即 英 国 数 学 家 Hodge 的 调 和 积 分。
现 在 有 2 个 年 轻 人, 一 个 是 David Bao, 另 一 个 是 他 的 美 国 学 生, 抒 这 个 Hodge 的 调 和 积
分 推 广 到 了 Finsler 情 形。 这 将 是 微 分 几 何 的 一 块 新 园 地, 预 料 前 景 无 限。
1995 年 夏 在
美 国 西 雅 图 有 一 Finsler 几 何 的 国 际 会 议。 其 论 文 集 已 于 今 年 由 美 国 数 学 会 出 版。
Finsler 几 何 在
1900 年 有 名 的 Hilbert 演 讲 中 是 第 23 个 问 题。
7. 中 国
的 数 学
数 学 研 究 的 最 高 标 准 是 创 造 性: 要 达 到 前 人 未 到 的 境 界, 要 找 着 最
深 刻 的 关 键。 从 另 一 点 看, 数 学 的 范 围 是 无 垠 的。 我 愿 借 此 机 会 介 绍 一 下 科 学 出 版 社 从 俄
文 翻 译 的 《数 学 百 科 全 书》, 全 书 5 大 卷, 每 卷 约 千 页。 中 国 能 出 版 这 样 的 巨 著, 即 使 是 翻
译, 也 是 一 项 可 喜 的 成 就。 这 是 一 部 十 分 完 备 的 百 科 全 书, 值 得 赞 扬 的。
对 着 如
此 的 学 问 大 海, 入 门 必 须 领 导, 便 需 要 权 威 性 的 学 校 和 研 究 所。 数 学 是 活 的, 不 断 有 杰 出
的 贡 献, 令 人 赞 赏 佩 服。 但 一 个 国 家, 比 较 可 以 集 中 某 些 方 面, 不 必 完 全 赶 时 髦。 当 年 芬 兰
的 复 变 函 数 论, 波 兰 的 纯 粹 数 学, 都 是 专 精 一 门 而 有 成 就 的 例 子。 中 国 应 该 发 展 实 力 较 强
的 方 面。 但 由 百 科 全 书 的 例 子, 可 看 出 中 国 的 数 学 是 全 面 的。 这 是 一 个 可 喜 的 现 象。
中 国 的 财 富 在 "人 民"。 中 国 的 数 学 政 策, 除 了 鼓 励 尖 端 的 研 究 以 外,
应 该 用 来 提 高 一 般 的 数 学 水 平。 我 有 两 个 建 议: (1) 设 立 数 学 讲 座, 待 遇 从 优, 其 资 格 可
能 是 对 数 学 发 展 有 重 大 贡 献 的 人; (2) 设 立 新 的 数 学 中 心, 似 乎 成 都、 西 安、 广 州 都 是 可
能 的 地 点。 中 心 应 有 相 当 的 经 费, 部 分 可 由 地 方 负 担, 或 私 人 筹 措。
近 年 因 为 国
家 开 放, 年 轻 人 都 想 经 商 赚 钱, 当 然 国 家 社 会 需 要 这 样 的 人。 但 是 做 科 学 的 乐 趣 是 一 般 不
能 理 解 的。 在 科 学 上 做 了 基 本 的 贡 献, 有 历 史 的 意 义。 我 想 对 于 许 多 人, 这 是 一 项 了 不 得
的 成 就。 在 岗 位 上 专 心 学 问, 提 携 后 进, "得 天 下 之 英 才 而 教 育 之", 应 该 是 十
分 愉 快 的 事 情。
一 个 实 际 的 问 题, 是 个 人 应 否 读 数 学。 Hardy 说, 一 个 条 件 是 看
你 是 否 比 老 师 强。 这 也 许 太 强 一 些。 我 想 学 习 应 不 觉 困 难, 读 名 著 能 很 快 与 作 者 联 系, 都
是 测 验。 数 学 是 小 科 学, 可 以 关 起 门 来 做。 在 一 个 多 面 竞 争 的 社 会 中, 是 一 项 有 优 点 的 职
业, 即 使 你 有 若 干 能 力。
中 国 的 数 学 有 相 当 水 平。 近 年 来 政 治 多 变, 达 此 情 况, 足
风 中 华 民 族 的 勤 劳 本 质。 从 前 一 个 数 学 家 的 最 高 标 准, 是 从 国 外 名 大 学 获 得 博 士 学 位。 我
们 国 家 现 在 所 必 需 做 的, 是 充 实 各 大 学 的 研 究 院, 充 实 博 士 学 位, 人 才 由 自 己 训 练
18664
数学陶冶我一生
陈省身
早年在中国所受的教育
我于
1923年1月进天津扶轮中学。那是一所四年制的高级中学,我获准插班入一年级就读
第二学期。该校的数学课程有:
(1)第一年,算术,使用中文课本;
(2)第二年,代数,使用 Hall 与 Knight 的课本;
(3)第三年,几何,使用 Wentworth 与 Smith 的课本;
(4)第四年,三角学和高级代数,分别使用
Wentworth-Smith 及 Hall-Knight 的课本。
我的老师都很有能力,又极富献身精神,我做了大量习题。到第四年,我已能做许多 Ha ll-Knight
的书中引用的剑桥大学荣誉学位考试的题目。
1926年我从扶轮毕业;同年我进南开大学,实际上是跳了两级,因此我从未上过解析几何课。更糟的是,我必须参加南开大学的入学考试,其数学试题中解析几何占很重的份量。考试前的三个星期,我自学了
Young 与 Morgen 的《数学分析》(Mathematical analy
sis)如果记得不错的话,我的考卷位列第二。不过在很长的一段时间内,「圆锥曲线的焦点」这一概念令我大伤脑筋,直到几年后学了射影几何学我才茅塞顿开。
进南开大学后,我很快就发现自己做实验笨手笨脚,于是数学便成为我唯一的选择。我有幸得姜立夫教授为师-他
19
18年获哈佛大学哲学博士学位,导师是
J. Coolidge,论文题目是关于非欧几里得空间中线球接触变换的。因此,我在大学第四年,花了许多功夫学几何,所读的书中有 Coolidge
的《非欧几何学》(Noneuclidean Geometry) 与《圆和球的几何学》(Geometry of the circle and
sphere),Solmon 的《圆锥曲线》(conic sections) 与《立体解析几何》(Analytic Geometry of
Three Dimmensions),以及 Castelnuovo 的《解析几何与射影几何》(Analytic and Projective
Geometry) 等。尤其使我着迷的是 Otto Staude
的二卷本着作《线构造》(Fadenkonstruktionen)。二次超曲面的几何是数学中优美的篇章。我很高兴看到 J. Moser
1979年在可积哈密顿系统和谱理论的研究中继续这方面的工作。(参见3)甚至在今日,研究 Salmon 的东西可能仍是有价值的,至少在我看来是有趣的。
1930年我从南开毕业,去北平清华大学从孙? 注1
教授工作。孙先生在当时是中国发表数学研究论文的唯一的数学家。孙的研究领域是射影微分几何,他曾是芝加哥大学 E.P.Lane 的博士生。这个主题由
E.J. Wilczynsky
于
1901年创立,是那时已经支配几何学近一世纪的射影几何的一个自然产物。我熟悉了这方面的文献,并写了几篇论文,其中包括我的有关射影线几何的硕士论文。继
Plücker 与 Klein 之后,线几何一直是几何学家们喜爱的主题。事实上,Klein 的学位论文就是关于二次线体的,即 Plücker
坐标下的二次方程所确定的线轨 (line loci)。二次线体具有许多背景中也有许多线几何的内容。
我的论文研究线汇,即线的二维子流形以及它们的通过二次线体的密切 (osculation)。
在我的研究生学业接近结束时,即大约
1934年左右,我开始认识到整体微分几何(当时称
为大范围微分几何)的重要性。我的主要灵感来自 W. Blaschke 的关于微分几何的那些著作。
很清楚,代数拓扑是整个领域的基础。而代数拓扑本身当时还处于发展阶段。Veblen 于
1922年发表的 analysis situs
注2 引进了「同调不变量」(homology characters) 即根据关联矩阵得出的 Betti 数和挠系数。Lefschetz
的《拓扑学》于
1930年出版,但该书对初学者进入这个领域并无裨益。我曾听过 Emanuel Sperner 的讲课(
1933~
1934年)。当时
Sperner 正在北京大学访问,他的课包含有对 Erhard Schmidt 关于约当曲线定理的证明的严密而详细的论述。我也听过江泽涵讲授的以
Lefschetz 的书为蓝本的「位置分析」课,江是 Marston Morse 过去的学生,曾担任 Lefschetz
的助手。而我当时的感觉是我只是刚刚站在代数拓扑这座伟大殿堂的门口。到
1934年 Seifert-Threlfall 的书和
1935年
Alexandroff-Hopf 的书问世,情况才有了巨大的变化。
1932年春季,Blaschke
访问了北平,作了关于「微分几何中的拓扑问题」的系列演讲。这是真正的局部微分几何。他采用全体微分同胚构成的伪群取代经典微分几何中的李群,并研究了局部不变量。我能跟上
Blaschke 的演讲并去阅读发表在汉堡大学数学讨论会论文集 (Hamburger Abhandlungen)
及其它杂志上的包含在这同一个总标题下的许多论文。这个主题现在称为网几何 (web geometry)。由于有此接触,之前又已掌握 Blaschke
的微分几何书中的知识,所以当
1934年获得一笔奖学金时,我决定去汉堡留学。
欧洲的留学生活
1934~
1936年我在汉堡,
1936年获理学博士学位;并曾在巴黎随 Elie Cartan
从事一年博士后研究,去汉堡的选择实属幸运之举。汉堡大学有一个很强的数学系,Blaschke、Artin 以及 Hecke
是那里的教授,较资浅的成员包括 E. K?hler、H. Petersson 和H. Zassenhaus。
那时 Blaschke
的数学兴趣正从网几何转向积分几何。
1934年9月我刚见到他时,他给了我一大叠关于网几何的抽印本。我开始对网的秩的概念和具有最大的秩的网产生了兴趣。大家知道,Rn
中一个余维是 1 的 d 网由处于一般位置的 d 个超曲面叶结构组成。设 x1,...,xn 是 Rn
的坐标,叶状结构由方程给定。形如的方程被称为是 Abel 方程。线性无关的 Abel 方程的最大个数被称为是这个网的秩。如果 d-网由 Rn
空间里的 d 类代数曲线的超平面定义,它就具有这样的 Abel 方程,它们是将 Abel 定理应用于 Abel 微分获得的。因而这个
d-网的秩至少是该曲线的亏格 (genus)。在一篇短文中我确定了 Rn 中所有余维为 1 的 d-网的最大秩 。根据 Castelnuovo
的一个定理,这个整数等于 n 维射影空间 Pn 里不属于任意超平面 Pn-1 的 d
次代数曲线的最大亏格。值得注意的事实是,并非所有具有最大秩的网都是由上述方式描述的具有最大亏格的代数曲线给出的;这里存在怪异的具有最大秩的网,这些网的叶并非都是超平面。这些
Abel 方程本质上是函数方程,因为在经典情形中,这些方程变成众所周知的超越函数的加法定理。在平面上 (n=2),曲线的 5-网的最大秩为
6,而且存在一个怪异网(Bol网),这个网的 Abel 方程含二重对数。
1978年 Griffiths 和我研究了 Rn 中具有最大秩 且余维为 1
的 d-网问题,但我们没有获得最后结果。我认为确定这样的怪异网是一个非常有趣且很重要的问题。
1934~
1935年间我的主要精力用于参加 K?hler 的讨论班。讨论班以
K?hler刚出版不久的著名小册子《微分方程组理论导引》(Einführung in die Theorie Systeme von
Differentialgleichangen) 为基础。主要成果就是后来所称的 Cartan-K?;hler 定理。所有的人,包括
Blaschke、Artin 与
Hecke,都出席了首次讨论会,每人还得到一本上述的小册子。但参加者减少得很快,我是坚持到底的极少数人之一。我把这一理论用于 R2r 中 r
维子流形的 3-网。Blaschke 和 K?hler
都认为这个结果与我先前关于最大秩的结果已足够写成一篇学位论文了。到
1935年底我的学位论文已准备就绪。
Blaschke
及其学派主要关心积分几何,Blaschke 开过积分几何的课程。这一主题最漂亮的结果是由 L.A. Santalò
发现的。一个结果是用正项的无穷和表示平面凸曲线的等周亏量,其中每个正项均具几何意义。Santalò
的工作使他成为积分几何方面的世界级领袖。他原籍西班牙,后来移民到阿根廷。
我的另一位学友是代数几何学家周炜良,他为了跟
Hermann Weyl做研究从芝加哥来到哥廷根。但是哥廷根乃至整个德国政局的变化使这一愿望成为泡影,他又转往莱比锡随 Van der
Waerden 工作。由于某种原因,他住在汉堡,有时来参加讨论班。周炜良当时正在发展他的「配型」(zugeordnete
Formen),即后来所称「周氏坐标」。周是一位有创见的数学家。他对代数几何作出了重要贡献,包括他的紧子簇定理和相交理论。周出身于中国一个高层官宦家族,它很早就认识到西化的必要,因此这个家族出了不少杰出人物。周习惯夜间工作。当他来访时我就得牺牲一些睡眠,但却学得一些数学。
无论如何,只要可能,我就去听 Artin 的讲课。二年间他开过的课包括复变函数论、代数拓扑、相对论和丢番图逼近等。我还听过
Hecke 主要按他的书讲的代数数论课。我在汉堡的学术生涯是很理想的,但是政局不允许这种生活继续下去。
1936~
1937年我可从事一年博士后研究。当我征求 Blaschke 的意见时,他建议我或继续留汉堡跟 Artin
研究数论,或去巴黎跟随 Elie Cartan。这两个方案都有吸引力,我最后选择了后者。
这一抉择非常理想。那年 Cartan
开了一门外微分系统的课程;讲义后来以书的形式出版了。那些后来成为 Bourbaki 的「年轻的」法国数学家开始活跃起来。他们组织了一个「Julia
讨论班」,每二周聚一次,致力于对每年选定的一个专题进行研究。
1936~
1937年的专题是「E. Cartan 的工作」。
Cartan
是位极好的导师。他提出的「小」问题,有些成为我论文的主题。大概由于我对他所提问题作的解答,他允许我大约每二周去他家一次。见面后的第二天我通常会收到他的信,信中往往说:「你走后我又考虑了他的问题。……这问题似乎很有趣……」这一年过得有趣而令人难忘。
我还听过 Montel 有关多复变的讲课,参加过 Hadamard 在法兰西学院举办的讨论班。在每次讨论班结束时 Hadamard
总会作总结,它通常比讨论班上的演讲本身更清楚更丰富。
在获悉中日战争爆发的消息后,我怀着沉重的心情于
1937年7月10日告别巴黎返回中国。
数学上与世隔绝
1937年夏我离欧返华时,本打算去北平就任清华大学教授之职,由于中日战争之故,十年后才达到此目的。当时清华大学先搬到长沙,
1938年又迁至昆明,在那儿一直滞留到
1945年夏战争结束。
昆明是座美丽的城市。虽然处于战事中的国家物资匮乏、局势动荡,但在生活的其它方面倒是愉快的。清华大学与北京大学、南开大学联合,组成了西南联合大学,昆明立刻成为战时中国知识界的中心。我的数学同仁包括华罗庚和许宝?。我开了代数拓扑、李群、球几何及外微分系统等方面的课程和讨论班,吸引了一批学生。主要的不便是此地与外界的联系被切断了:有段时间连「缅甸信道」也关闭了,与外界的联系只有靠空运。我有个私人小书库。起初,我做了以前想做而没时间做的事:读了些书,思考些问题,还觉得有趣。但挫折很快就降临了,而且必须克服。我将此情信告
E.
Cartan,他寄给我许多他的抽印本,包括一些过去的论文。我花了大量时间研读这些论文,考虑其内涵及应用。这确实使我受益匪浅。在30年代,人们已开始认识到
Cartan 的工作的重要性,如 Weyl、Blaschke 和 K?hler,但几乎没有人去读 Cartan
旧时的论文(有关李代数的论文除外)。我很幸运能因环境之故把这些论文都遍读无遗。
驻华盛顿的中国大使胡适博士空邮来一本
Hurewicz-Wallman
写的有关《维数论》的书。现今习惯于静电复印的人也许很难想象我把除最后一章外的整本书抄了一遍。在最后一章中,作者是在没有正合序列概念的情况下处理正合序列的问题,我觉得很难理解。其实当时读论文作笔记是很普通的。复印大量资料并不能说明自己取得了多少进步。
我开始有了一些学生,其中有王宪钟和严志达。王后来对拓扑学作出了许多贡献,尽管他最出名的成果是王序列。严最早给出所有例外李群的
Betti 数的正确值。
回首往事,我并不认为自已对作为整体的数学有完善的见地。我清楚自己的某些不足并渴望得到充实。我的数学实力在于我能算。至今我不在乎繁复的计算,直到数年前我做这样的计算还很少出现差错。这方面的训练现在不大流行,也得不到鼓励,但在处理许多问题时它仍有很大的好处。
Gauss-Bonnet
公式曾使我着迷,我知道它的最概念化的证明是通过结构方程来表示联络形式的外微分。当
1943年我去普林斯顿时,它已为为我在数学工作中最得意的一篇论文开了题。
普林斯顿阳光灿烂
我于
1943年8月抵达普林斯顿。气氛的变化令人难忘。那段日子高等研究院很清静,大多数人已离去为战事服务。Hermann Weyl
对我的工作很感兴趣。我访问之前他曾为《数学纪事》(Annals of Mathematics)
审阅过我一篇有关迷向曲面的论文,并写了一个很长的给予好评的报告。这件事是他亲自泄露给我的。报告提出了改进的建议,这说明他仔细地看了全文。我们经常交谈。Weyl
的深刻洞察之一是预言代数几何有非常美好的前景。
Andre Weil 那时在附近的 Lehigh
大学,我们很快就见了面并有好多可谈的内容。当时Weil 刚刚发表与 Allendoerfer 合作的关于 Gauss-Bonnet
公式的论文,它立刻成为我们讨论的话题。根据我对二维情况的埋解,我知道正确的证明应该建基于我们现在称之为超度 (transgression)
的概念之上。困难则有两个:1)当时我对关于向量场的奇点的 Poincare-Hopf
定理不甚清楚;2)超度必须在单位切丛中而不是在主丛中实现,这就涉及到一个不平凡的技术困难。这两个困难我都在短时间克服了,事情有了一个满意的结果。我仍认为这是我做得最好的工作。
其后自然要把这个结果扩展到 Stiefel-Whitney
类。那时即使在普林斯顿,谈起纤维丛也必得从定义开始。那时没有矢量丛,只有球丛。我注意到复示性类较简单,容许局部曲率表示。这项工作不难,但它并非那个时代拓扑学的时尚课题。
我虽是高等研究院的成员,但很多时间是在普林斯顿大学的范氏大楼 注3 度过的。Chevalley
那时正在写他的有关李群的书。Lefschetz
则固执己见,他不愿用当时盛行的常规方法研究微分几何。当时请我为《数学纪事》审阅一篇论文而建议退稿后,他让我担任该刊的副主编 (associate
editor)。
普林斯顿的环境与工作节拍令我十分惬意。我对数学的看法成熟多了。留居普林斯顿的日子使我感到极大的乐趣。近年来科学竞争已使科学家的生活大煞风景,尽管在数学方面的情况要好得多。我认为没有非要如此快地出成果的必要,我也不为电子邮件的发现所动。
1945年底我告别普林斯顿回中国。踏上故土立即受命组建中国的科学院,即中央研究院的数学研究院,其时二次大战虽已结束,中国却由于内战而处于分裂状态。我向
Hermann Weyl 发出访华邀请,他欣然接受。但是中国当时的形势使这一访问未能实现。
1948年底南京政府处于崩溃之中,感谢高等研究院主动安排我离华。
1949年冬季学期我在高等研究院,是 Veblen
的微分几何讨论班的主讲人。讲稿两年后补写出来,流传甚广。这些讲稿现收录在已出版的我的《论文选集》第四卷内。主要结果是 Weil
同态。这是陈类从酉群到任意李群的一个推广。
1944年我在写有关复示性类的论文时就知道这个结果;由于未熟练掌握李群,当时未能证明它。Weil
通过考虑联络族,提供了一个关键性的思想。我把这个结果称为 Weil 同态。朋友们认为我应该分享这一荣誉,对此我自然不持异议。
数学上进入不惑之年
二次大战后,Marshall Stone
应召重组芝加哥大学数学系,并任系主任。他最早发出的两份聘约分别送达 Hassler Whitney 与 Andre
Weil,这是他洞鉴数学与数学界的一个证明。Whitney 谢绝了,而 Weil 经过数次协商后接受了。
我在中国时 Stone
就曾写信给我谈起要在芝加哥为我提供一个讯问职位的事。
1949年我来美国后,芝加哥大学数学系决定长期聘我。我认为芝加哥大学是美国唯一的其主要目标是「知识进步」而非教育的大学。我有许多朋友在那里的数学系;
1949年夏我成了该系的成员。由此引出了一段愉快而有益的合作。
1949~
1950学年我开了一门名为「大范围微分几何」的课程,有一批才华横溢的学生。我自己正在开辟自己的道路,我的学生及时更正了我的许多错误和疏忽,这是生气勃勃而又有趣的结合。我还记得
Arnord
Shapiro,他曾主持许多这样的讨论。回想起来,当时我对微分几何的了解还是初步的。这门学科中一些争论问题至今未决,也许正反映了它的力量之所在。例如,曲面是什么?是嵌入还是浸入,或是由可能有奇点的方程所定义的?另一方面,我的课上涉及的许多课题,也获得了新的多方面的发展。
我与 Weil 联系密切。他随时都有准备,随时都可合作。在与我讨论过数学的众多数学家中,Weil
是极少数能迅速抓全我的思想并给予有益的评说的数学家之一。我们常沿着密执安湖畔长时间的漫步,这在当时还很安全。
我对代数拓扑也感兴趣,偶尔开一门这方面的课。我与 Ed Spanier 在球丛的研究上进行过合作。所获结果之一是把 Gysin
的工作写成一个正合序列。Rene Thom 把它做得更明白化了,这个结果现在通常称为 Thom 同构。
我觉得芝加哥和汉堡都非常令人愉快。我认为两者的规模都很合适。不幸的是数学的发展已使一切都膨胀了。
在西海岸定居
1960年我迁往伯克利
(Berkeley)。对我来说这地方并不陌生。我在中国的老师姜立夫教授就是在伯克利获得理学学位的。
1946年和
1949年我曾两度驻足伯克利并在伯克利数学系呆过一段时间。伯克利数学系是第一流的,它由
G.C. Evans 创建。Evans 曾在若干场合询问过我对去伯克利有无兴趣。Evans
的兄弟曾是天津著名的西文书店的老板。我曾在那儿买过一些课本,而书价一般贵得吓人。
Evans
要退休了,我去伯克利工作的事变得认真了,确实,我有时想到,自己年纪大了,伯克利较温暖的气候很有吸引力。当然,伯克利数学系在扩展,空运的发达已使加利福尼亚不再像从前那么孤立等因素,亦促成了我的这次迁居。
伯克利一直在提高它在数学界的地位,吸引着许多优秀的学生。在我指导下有31名研究生获博士学位,当然我还影响其它一些学生。我开始以「第二作者身份」注4
与年轻人合作撰写论文,如与 Bott,Griffiths、Moser,以及 Simons
等合作就是如此。在这种情况下我感觉责任较轻。生活越来越觉舒畅。
与我在学术上交往密切的同事有 Hans Lewy 和 Chuck
Morrey,他们都是有创见、能力很强的分析学家。Lewy 和对 R6
中的三维黎曼度量的局部等距嵌入问题进行过一段时问的研究。它把我们导向三次渐近锥面的研究,我们弄清楚那是双曲的,但仅止于此。
数学中的微分的作用很奇妙。通常人们倾向于认为代数和拓扑是数学的两根支柱。但是事情并非那样简单;牛顿和莱布尼兹玩的是绝技。这一时期已经看到微分几何汇入了数学的主流。
老耄之年的消遣
我的生命历程正在接近终点,我唯一的考虑是怎样度过这段时光。答案很简单,我将继续摆弄数学。体育运动我从来就不在行,现在就更不用说了。听音乐对我一直是浪费时间,偶尔介入此道,纯粹出于社交之故。所幸的是整体微分几何还有许多基本问题,尽管在其发展中我很可能仅是一名观众。
我认为,研究对象限于光滑流形只是由于技术上的原因,也是不能令人满意的。不仅很自然地存在着非光滑的流形,而且即使从光滑流形开始,诸如包络这样一些几何构造也将导致非光滑流形,Whitney
引进了分层流形 (Stratifiad manifold) 的概念,它允许有奇点并可应用无穷小分析。最近 Robert McPherson
的工作又带来了新的希望。Cheeger-Goresky-McPherson 相交同调和 McPherson 陈类已揭示出这一概念的本质。(见2)
对我来说,Riemann 结构是否像最新的进展所表明的那样基本还不清楚。毕竟 Riemann
在那篇历史性的论文中,允许他的度量是一种 4 次形式的 4 次根。更一般情形现在称之为 Finsler 度量。我在最近的一篇注记4
中指出,只要采取适当的观点,Finsler 几何可以很简单地加以展开。进一步的发展则是必然的。
正如 Griffiths
曾注意到的,我之所以喜欢代数手法起因于我的经历。局部微分几何需要这样去作,但是要得到漂亮的局部性定理是困难的。很清楚,前面讨论过的有关最大秩的网的问题是很重要的问题,它将受到我的关注。
数学仍在不断地陶冶着我。
18664纪念南开数学研究所成立20周年
1985-2005
—暨陈省身先生逝世一周年纪念
2005年12月3日-5日 天津
南开大学
纪 念 活 动 日 程 安 排
12 月3 日 上午10:00 举行纪念大会
12 月3 日 下午2:00-3:00 请吴文俊院士介绍陈省身先生的生平和工作情况(暂定)
12 月3 日
下午3:30-5:30 同时举行三个座谈会:
A )南开数学所学术委员会成员及与会院士
B
)与会的求是科技基金会杰出青年学者奖、长江特聘教授及国家自然科学基金委
杰出青年科学基金获得者
C
)与会的各兄弟院校领导及各校数学院(系)领导
座谈会宗旨: 缅怀陈省身先生,探讨南开数学所在新时期如何更好地为全
国数学界服务
12月4日 - 5日 举行求是学者报告会,请历届获得过“求是杰出青 年学者奖”的代表
做学术报告。
18664向大师致敬!!!!!!
18664致敬,鞠躬
18664向大师致敬!!!!!!
18664怀念陈老!
18664
怀念大师!向大师致敬!向大师学习!
18664怀念
18664令人敬仰!
向数学大师致敬!
咬定青山不放松,任尔东南西北风!
18664敬礼!!
18664景仰陈老先生,他光辉的一生照亮了。。。。
18664这样一生也值了
18664纪念陈省身先生特稿:指标定理在中国的萌芽
来源: 南开新闻网 发稿时间: 2006-10-28 09:23
--------------------------------------------------------------------------------
张伟平(南开大学陈省身数学研究所所长)
今年的10月28日,是陈省身先生诞辰95周年。长久以来一直想写些什么作为纪念,但苦于找不到适当的题目。前几天与一位多日不见的朋友聊天,谈起陈先生及其对中国数学的贡献,朋友提起说陈先生为《阿蒂亚(Atiyah)论文全集》的中国大陆发行本撰写的前言似乎还没有中文翻译,何不翻译出来交《数学译林》发表?这突然提醒了我,是啊,指标定理及相关理论在中国的萌芽和发展,陈先生不正是最初的先驱者和后来的推动者吗?就写写这个吧。
1.指标定理简介
这里所谓的指标定理,是指由阿蒂亚、辛格(Singer)于
1963年证明的,以他们的名字命名的定理。它被公认为是二十世纪最重要的数学成就之一。有不少人认为如果在二十世纪中挑选出两个最伟大的数学定理,那么其中之一就应该是阿蒂亚-辛格的指标定理(另一个是外尔斯(Wiles
)证明的费马(Fermat)大定理)。它的大意是说:对一个封闭的弯曲空间上的一类微分算子(称为线性椭圆微分算子),可以定义两个整数:一个是用分析办法定义的,称为分析指标;另一个是用拓扑办法定义的,称为拓扑指标。在这个情形下,阿蒂亚-辛格指标定理可以叙述为:“对任何一个线性椭圆微分算子D
,下面的公式成立:
D的分析指标=
D的拓扑指标。”
从这个定理的字面上就可以大致了解,本质上它在数学的两大领域-分析与拓扑-之间建立起了一座内在的桥梁。像这样的将两个看似无关的领域紧密结合起来的结果,其重要性及应用的广泛性是显而易见的。从另外一个角度讲,"D的分析指标"是通过分析的方法决定的一个"整体"的不变量,而"D的拓扑指标"经由所谓的陈省身-魏依(Chern-Weil)理论可以有一个"局部"的表达式。这样上述的公式就可以有另外一种更抽象同时也更具哲学意味的形式:
“整体=局部的叠加”。
这里尽管"局部"的量可以任意的变化,但是通过"叠加"
(积分)后得到的整体量却是固定不变的!这种"万变不离其宗"的要旨体现出惊人的美感,给人以强烈的震撼。
如此优美并显然有重要意义的定理在数学中的地位自然举足轻重。例如它就包含了当时微分几何学、拓扑学以及代数几何学中的诸多大定理如高斯-博内特-陈省身(Gauss-Bonnet-Chern)定理、希策布鲁赫(Hirzebruch)符号差定理、希策布鲁赫-黎曼-洛赫(Hirzebruch-Riemann-Roch
)定理等等为其特例。无怪乎我国指标定理专家虞言林教授感叹:指标定理像个大太阳,许多大定理都围绕着它转。而著名数学家哈尔莫斯(Halmos)在其综述报告《数学的进展慢下来了吗?》中的评论或许更能说明问题:"这项工作的成果是最深刻和最广泛的。对作为报告人的我来说,它是这份报告中最铁的部分。它们不仅是一个定理,而且是一种理论、一个领域、一种观点,这种观点进入数学的许多部分,同时也受它们的影响。在写到过去50年来微分几何的惊人成就时,奥瑟曼(Osserman)称阿蒂亚-辛格指标定理为'分析、拓扑与几何的美妙综合,特别导致对高斯-博内特定理的新看法:不是作为孤立的结论,而是一大群事物中的一个'."指标理论的创始人阿蒂亚、辛格理所当然地获得了国际数学界的褒奖:阿蒂亚获得了
1966年的菲尔兹奖;阿蒂亚和辛格共同获得了2004年的阿贝尔奖。
2.中国数学家的先驱性贡献:高斯-博内特-陈省身公式及其发展
中国数学家对阿蒂亚-辛格指标定理的形成做出了先驱性的贡献。其中最突出的就是陈省身先生于上世纪四十年代中期的一系列开创性工作,特别是上面已经提到的高斯-博内特-陈省身定理,还有就是陈省身示性类的提出和研究。陈先生自己说过,他一生最好的工作就是高维高斯-博内特公式的内蕴证明。有鉴于此,更由于高斯-博内特-陈省身定理的突出的历史地位,我们先对这个定理的来龙去脉作一个简略的回顾。
事实上,陈省身先生的工作可以追朔到著名的古希腊欧几里得(Euclid)的《几何原本》中的一个基本定理:"平面上任何一个三角形的内角之和等于
180度".这个定理到
19世纪中叶被德国数学大师高斯推广到球面上弯曲三角形的情形,而高斯的定理又被法国数学家博内特推广到多边形的情形。高斯和博内特的定理后来在理论和实际中都有很大的发展和应用,成为二维微分几何中最重要的定理之一。
到了
19世纪下半叶,由于研究物理学特别是电磁学的需要,同时也由于数学内部发展的驱动,高斯的学生,大数学家黎曼提出并研究了高维微分几何(例如我们所处的空间是三维的),后来成为爱因斯坦(Einstein)发展广义相对论的重要工具。由于高斯-博内特公式在二维微分几何中的重要性,一个自然而然的问题就是能不能把它推广到高维微分几何中去。二十世纪著名的几何和拓扑学家霍普夫(Hopf)就在上世纪20年代撰文认为这个问题是当时微分几何中最重要的未解决问题。而陈省身先生顺应历史潮流,于上世纪40年代彻底解决了这个问题。现在文献中都把这个高维情形下的定理称为高斯-博内特-陈省身公式,充分肯定了陈先生的贡献。然而,陈先生的伟大贡献不仅仅限于此。它还反映在以下几个方面:其一,他利用了从他的老师,法国大几何学家嘉当(E.
Cartan
)那里学到的独特技术,采用了完全创新的方法,给出了此问题的一个出人意料的处理,对后来发展产生了深远的影响;其二,由他的方法出发,陈先生意识到"用微分形式来表示拓扑不变量"应该在微分几何中起非常重要的作用。正是由这个原理出发考察当时已经知道的不变量,并且推陈出新,陈先生定义了现在以他的名字命名的示性类(现通称陈示性类,Chern
class
)。
陈示性类的提出和发展,掀开了微分几何的新篇章。上面提到过的大数学家霍普夫评论到:"微分几何由此进入了一个新的时代".而多年后,年轻一辈的微分几何代表人物辛格(即阿蒂亚-辛格指标定理的作者之一)写到:"对我们来说,陈就是现代微分几何".具体到阿蒂亚-辛格指标定理这个伟大的成就,从以下的两个方面可以看出正是陈先生的工作奠定了它的基础:
(i
) 高斯-博内特-陈省身公式可以看成是第一个在任意维数都成立的指标定理的一个特例,是指标定理的先驱;
(ii)
指标定理中的拓扑指标本身就是用陈示性类来定义的,这反映了陈示性类的不可或缺的基本重要性!
由上面简短的历史概述也可以体会,杨振宁先生脍炙人口的诗句"千古寸心事,欧高黎嘉陈"
,赞颂陈先生在几何学中的历史地位直追欧几里德、高斯、黎曼和嘉当,是十分到位的。
对指标定理的形成做出先驱性贡献的另一位中国数学家是吴文俊先生。希策布鲁赫在其
1956年的名著《代数几何中的拓扑方法》的导言中指出,是吴文俊最早猜出了4维流形的符号差公式的形式,后来由托姆(Thom)予以证明的(苏联数学家洛赫林(Rokhlin
)也独立地证明了这个公式)。而希策布鲁赫这本名著的主要定理之一就是把吴文俊猜到的公式推广到任意维数的情形。
后来的发展证明,希策布鲁赫在这本书中证明的定理以及使用的方法(即由托姆发展起来的配边理论)对阿蒂亚-辛格指标定理的最终提出和证明有本质性的启示。
托姆于
1958年获得了菲尔兹奖,希策布鲁赫后来获得了沃尔夫奖。陈先生获得了沃尔夫奖和2004年颁发的首届邵逸夫数学奖,吴文俊先生获得了2001年首届国家最高科学技术奖和2006年的邵逸夫数学奖,这些都反映了数学界对上述工作的高度赞扬。
3.指标定理研究在中国的萌芽
尽管指标定理从一开始就被公认为数学中的伟大成就,但由于其牵涉面广,用到的知识多而且深刻,所以要完全弄懂它并不是一件容易的事情。因此虽然国内在60年代就影印出版了帕莱斯(Palais)编著的《阿蒂亚-辛格指标定理讨论班》(这本书是国际上第一次包含指标定理完整证明的正式出版物),但真正理解指标定理的人几乎没有。而作为国际微分几何领袖的陈省身先生,自然知道它的分量。因此,
1972年中美关系解冻后他第一次回国就在中国科学院数学研究所以《纤维空间与示性类》为题做学术报告,"描绘了阿蒂亚-辛格指标定理的全貌".陈先生的报告显然在数学所的青年数学家中间产生了影响。例如当时才三十出头的虞言林就投入到高斯-博内特-陈省身公式的研究,写出了好几篇颇具匠心的论文。他
1983年发表在《拓扑学(Topology)》杂志上的论文成功地将高斯-博内特-陈省身公式推广到组合流形的情形,是我国大陆数学家第一次在这份著名的杂志上发表论文。
另一方面,陈先生利用他与阿蒂亚的友谊,积极推动在大陆刊印《阿蒂亚论文全集》,并亲自撰写前言,希望此全集"不要成为书架上的摆设"
(此前言的译文见附录)。
后来,陈先生接受吴大任和胡国定两位先生的邀请,回母校南开大学创立南开数学研究所。在筹备
1986-
1987学年南开数学所的几何与拓扑学术年活动时,陈先生再次强调要学习和研究指标定理,并语重心长地指出"即使出不了文章,也要搞阿蒂亚-辛格指标定理".这深深鼓舞了同是筹备委员会成员的虞言林。虞言林后来回忆,陈先生的上述讲话"体现了一种期待、一份'偏袒'
、一项号召。这句话对我的文章的完成起了决定性的影响".这里所谓"我的文章"就是指虞言林关于狄拉克(Dirac
)算子的局部指标定理的工作。在这个工作中,虞言林将印度天才数学家帕托笛(Patodi)的方法推广到旋量丛情形,给出了关于狄拉克算子的阿蒂亚-辛格指标定理的直接的热方程证明。这是我国大陆数学家在改革开放后对指标定理所做的第一项坚实的工作,它独立于西方同期的工作,可以被认为是文化大革命以后中国指标定理研究的奠基石。
到了
1986年南开数学所的几何与拓扑学术年正式开始时,虞言林以他的上述工作为基础,开设了阿蒂亚-辛格指标定理的课程。这对指标定理在国内的普及和发展起了非常巨大的作用。很多年轻的参加者都是第一次接触到纤维丛、示性类、狄拉克算子、热核等概念,他们正是通过虞老师的课程,还有其他的类似课程,迈入了现代数学的殿堂。笔者自己有幸在那个时候成为虞老师的硕士研究生,跟随虞老师学习指标定理,并在虞老师的指导和直接参与下,同当时正在南开数学所做博士后的拉法堤(Lafferty)一起,将虞老师的工作推广到带群作用的情形。我们三人合作的论文后来发表在《美国数学会会刊(Transactions
of AMS
)》上。
附录:陈省身先生为《阿蒂亚论文全集》大陆发行本所写的前言(据英文原文翻译)
当阿蒂亚在接受《数学人》杂志(
1984年第6卷第9-
19页)采访,被问及谁是他最钦佩的数学家时,他说"我想这很容易回答。我最钦佩的人是外尔(Hermann
Weyl)。他对群论、表示论、微分方程、微分方程的谱性质、微分几何、理论物理都有兴趣;而我做的几乎每件事情从精神上讲都是他做过的。同时我也完全赞同他的数学理念,以及关于哪些是数学中有意思的东西的看法。"我们发现上述关于数学的理念与精神在这套全集中被保留和延续了下来。
我建议我的中国同行和学生们将这套全集当成高等"教科书".无论关于某项工作的新论述有多大的改良和改进,关于此工作的原始文章往往更直接和到点。在我年轻的时候,我听从建议去读庞加莱(Henri
Poincare)、希尔伯特(David Hilbert )、克莱因(Felix Klein )以及胡尔维兹(Adolf Hurwitz
)等的著作,并从中获益。而我自己对布拉须克(Wilhelm Blaschke)、嘉当(Elie Cartan )和霍普夫(Heinz
Hopf)的著作更为熟悉。其实这也是中国的传统:在中国我们被教导要读孔夫子、韩愈的散文以及杜甫的诗歌。我真诚的希望这套全集不要成为书架上的摆设,而是在年轻数学家的手里被翻烂掉。
18664致敬!!
18664指標定理是給出一般的幾何-拓墣關係,但是為推廣此定理而做研究,就有一點不夠味道
18664怀念大师!
18665种群生态学现在发展成什么样子了?现在的方法是什么呢?需要看什么样 的书籍呢?
18665一些资料,也许有用:http://www.eedu.org.cn/Article/ecology/ecologyth/Populationeco/Index.html
招生专业:生态学(071012)
研究方向:群落生态学
群落生态学研究方向研究农业生产格局变化对生物群落的影响、农业生物灾害预警与控制机理及策略。该研究组自
1982年成立以来,一直从生态学与有害生物控制技术研究,先后承担国家自然科学基金、国家“七五”至“九五”科技攻关、中科院、国际合作和省级科研项目
18项,先后获国家、中科院、省科技进步奖8个,其中2等奖3项,3等奖5项,发表论文150余篇,其中专著6本,SCI收录4篇,CSCD收录30余篇。
已完成主要科研项目:湖南省重大科技项目“湖南农业害鼠生物学特性和防治技术研究”;国家“七五”科技攻关“长江中游稻作区褐家鼠黑线姬鼠种群动态及综合治理技术研究”、“八五”国家科技攻关专题“洞庭湖稻区东方田鼠黑线姬鼠发生规律、控制策略及技术研究”、“九五”科技攻关专题“长江流域稻区主要害鼠成灾规律及综合防治技术研究”和“东方田鼠实验动物化与抗日本血吸虫感染机理的研究”;国家自然科学基金项目“洞庭湖东方田鼠种群特性和成灾原因研究”;中科院重大课题“复方灭鼠剂研试与开发”,中科院项目“大型水利工程和湖泊沼泽化与东方田鼠暴发成灾关系的研究”和“重要害鼠成灾机理及其持续控制”,国际合作FIP-6项目“鼠类野生种群控制:摄食和繁殖行为机制的基础与应用研究”。
目前承担的科研课题:中国科学院知识创新项目(KSCX2—SW—103)专题“东方田鼠种群暴发和崩溃机理的研究”;中国科学院知识创新项目(KZCX2—407)专题“不同农林复合生态系统中鼠类群落结构及其行为生态学研究”,中科院农办项目和湖南省自然科学基金项目“洞庭湖区退田还湖工程对生态环境的影响”等。
招生对象:生物学与植物保护专业的大学本科毕业生
通讯地址:湖南省长沙市马坡岭
邮政编码:410125
联系人:王勇0731-4615229
wangy@isa.ac.cn
18665当然还有景观生态学,单这些和种群生态学分支不同,种群生态学以研究种群动态及其数量规律为主
18666大家真的都是同感啊,到了报考就怕报错了学校。
18666之前的踌躇满志到现在的惴惴不安
18666先考一次实在不行,明年继续一次啊!
18666自己看着办
18666研究生入学考试报名开始了,你准备好了么?
18666懂的感觉太少,心里没底
18666同感啊
18667各位大哥,谁有吉米多维奇数学分析习题集题解,在下万分感激!!!!
chd12
190@163.com
18667
http://elmo.jlu.edu.cn/Link/MathTools/show.asp?id=66到这里去下载吧:)
18667不错的地方
18667大哥:无法下载的!
18668g(x)是[0,1]上的 连续函数,f(x)是周期为1的连续周期函数 证明 在(0,1)上n

无穷
lim

g(x)*f(nx)==

g(x)*

f(x)
18668看裴礼文得书2
17和2
18
18668大哥 你说说过程吧
18669钱兄的书好像很不错哦.问一下.大家有没有电子书.,给我一本,,呵~~~~
18669P是一些方阵得集合。。若A属于P,B属于P,则AB属于P,且AB得三次方等于AB 求证:
AB=BA
18669I think that your question is wrongly formulated.Here is an
counterexample: A=(1,0), B=(1,0)',then AB=1=(AB)^3. but it's
nonsense to ask that AB=BA!
18669楼上能不能说得清楚点吗?我有个疑问:(且A,B互换有-----2(BA的三次方等于AB的三次方)怎么互换啊?
如果有这样的互换结果.就可得BA的三次方等于AB等于AB的三次方等于BA了.何必
(AB=BA的三次方=AB的三次方的三次方(即AB的九次方)=AB的三次方=BA)呢?
18669题目条件是:
"P是一些方阵的集合"
所以楼上的反例是错的!
18669这个题目似乎是错误的,好象条件写错误了,我把错误的那个条件改过来了!
这个题目我曾经做过的!post-38-1127995962.gif
18669为什么说E是属于P的。。。。楼上的谢谢。。。你说一下。。。条件是我弄错了。。。。
好象如果E属于P的话。。。还有一问
等几天在问你们
18669是AB的三次方等于BA吧!
18669因为AB三次方等于BA,所以以A的平方代B得
---1(A的九次方等于A的三次方),且A,B互换有-----2(BA的三次方等于AB的三次方)!-----------------所以AB=BA的三次方=AB的三次方的三次方(即AB的九次方)=AB的三次方=BA
第一个等号由2得,第二个等号由1得.
18669呵.呵.刚没看清楚.
18669duide
钱吉林的书上有
证明AB=BA=(AB)^9
18669bossh_math@163.com
密码:123456
18669都是以前讨论过的一些题了.只要有心把这个论坛里的老贴挖个遍.会有收获.
呵呵.不过太费时了.
18669钱吉林的书上有
证明AB=BA=(AB)^9 ,是的,
我也看过了,,
没想到楼上的作法更简装啊!!
18673对
如果是大图就不好那样算了
18673给定一个G 的 Line Graph, 应该如何找到 G
呢?
想了很久都没有眉目
不知道应该按照怎样的思路好
18673如果用定义返回来一条一条找, 小图就无所谓, 但当 degree 有 6 以上的时候就变得很混乱, 根本无法找到. 你自己随便画一张
E(G) >= 12, |G| >= 6 的图然后画出 line graph, 再返回来找就知道有多麻烦了
更何况,
这种东西应该会有一条思路或者算法, 最后可以用程序来实现的.
ACM 那里倒是有一篇论文讲解这个算法,
可惜我没法看
据说是用 clique 来推出原图
现在才刚刚有时间回来考虑这题
18673这个
应该可以按照Line graph的定义
返回去做
不行吗?
18673bascially, I solved it...... lol
18674把长度为a的线任意折成3条,问能折成一个三角形的概率是多少?
呵呵~~挺简单的吧~~~
18676请问在马尔可夫决策过程中,Now let Π be the set of partial transitions which
correspond to events that happen outside the control of the
application
server. These transitions are followed instantaneously by
a
decision transition which is in the control of the
application
server.
其中partial transitions,decision transition是什么意思啊
18677f= exp {- t^{2} } 它的全变分为什么等于2。请问如何求解?谢谢
18678浙大2001post-38-1127787349.gif
18678先求y(0)然后求导求出y'(0)post-38-1127792502.gif
18679我是一个刚学习高数的菜鸟,学习过程中有些问题不懂,想请教一下!
在数列的极限中,数列极限的定义是:对于任意给定的正数K(无论多小),总存在着正整数N,使得对于n>N时的一切Xn,不等式
|Xn-a|<k
都成立,称a为数列的极限
疑问:在此定义中如何体现了数列无限接近于极限k,就算再取一个正数k',让它小于k,收敛半径的确不会超过以前的半径,但是如何它不会等于以前的收敛半径.
18679如下:post-8-1127806688.jpg
18679感谢这位仁兄的解答
那在

趋近零时,如何能保证 n
趋近无穷大
18679数列有无穷多项,自然n就是趋无穷的,这里的关键并不是n,而是正整数N,我们的目的是要找到这样一个N,这个 N是可以用

表示出来的,使得n>N之后的所有Xn都能满足定义中的不等式,也即是N之后的所有Xn与a的距离都能比

小
18680请高手们尽量多提供些解题的方法,不胜感谢!post-38-1127787705.gif
18680中山大学数学分析教材(邓东皋教授写的那个书)里面有相关的例题,你可以参考一下
18680可是我没有那个书啊,还请liuqhui不辞辛劳的把那个书上的解法发上来,不胜感激!
18680能不能提供一份2001年试题
king_0577@hotmail.com
18681我想是应该p在(0,1/2]上发散,在(1/2,1]上条件收敛,在(1,无穷)上绝对收敛
当p>1时很好证明的,可是在(1/2,1]上我实在是弄不出来,还请高手帮忙了post-38-1127788393.gif
18681把符号相同(即[n^0.5]=k)的和式看成一个整体考虑,可知当p>0.5时级数收敛,相应也可得出其内闭一直收敛性
18681不明白,reijin,你能否详细点,或者把过程写出来吗?
18681其中有些步骤需要完善,思想大概就是这样了!post-38-1127798
192.gif
18682谢谢你们。 yyshuxue是正在学《非线性泛函》吗?我也是,我怎么觉得有点不透气,感觉思路不清晰,你们怎么学的?讨论吗?
18682有研究郭大钧《抽象空间常微分方程》或《非线性泛函分析》的吗?可以交流一下。我现研二方向是时滞微分方程,又同方向的可以交流.
18682时滞微分方程?你可以看hale的Differential Functional
Equations
当然可以作方程组。
可惜我没看《抽象空间常微分方程》这本书
18682《非线性泛函分析》正在学习当中,还没搞得怎么明白
18685姓名:宋立新
住宅电话:847099
17
办公室电话:84708351-8606
电子邮箱地址:lxsong@dlut.edu.cn
主要学历及工作经历:
1985.9-
1989.2 吉林大学数学系,本科
1989.2-
1990.9 吉林大学数学所,硕士
1990.9-
1993.7 中国科学院系统科学研究所,博士
1993.7-
1996.5 吉林大学数学系,讲师、博士后
1996.5-2000.1 吉林大学数学系,副教授
2000.1-2004.1 吉林大学数学系,教授、博士生导师
2004.1- 大连理工大学应用数学系,教授、博士生导师
主要学术及社会兼职:
中国数学会概率统计研究会理事
中国现场统计学会理事
《东北数学》编委
研究领域(研究课题):
①非参数统计
②统计判决理论
③时间序列的统计分析
④金融数学中的统计推断
⑤风险分析与费率厘定
指
18686复旦大学2001年的数学分析证明!想了好久都想不出来!那位大哥帮小弟一下!post-38-1127797705.gif
18686我的答案post-38-11278
17167.gif
18686可以用ln(1-y)的Taylor展开,和楼上兄弟的方法类似:post-38-1127832355.gif
18687^_^post-38-1127929688.gif
18687谢谢大家
springboshi的解法不错,不过从P(A+B)Q=(Er 0)+(0
Es)推出
PAQ=(Er 0)
PBQ=(0
Es)的过程我没看懂,能不能详细说说
这道题我开始做的时候是这么想的
取定Vm,Vn的基,则由 A,B可以确定出
Vm到Vn的两个线性映射
Im(A+B)属于ImA+ImB,所以
dim(Im(A+B))<=dim(ImA+ImB)=dim(ImA)+dim(ImB)-dim(ImA与ImB的交)
<=dim(ImA)+dim(ImB)=dim(Im(A+B))
所以,dim(ImA与ImB的交)=0,ImA与ImB的交={0}
Im(A+B)=ImA和ImB的直和
请问,我以上做的对不对,以后该怎么做啊
18687能否用矩阵理论和几何理论分别解答post-38-1127797823.jpg
18687不好意思少打了几个条件
r=rank(A)
s=rank(B)
r+s<=min{m,n}
18687还是不继续了,就用一种方法证明算了!该题在解答过程中有许多省略!post-38-11278
18374.gif
18687主要是证必要性。
我的解法看看行不行?post-38-1127830883.ibf
18687貌似倒数第二步只说明了P(A+B)Q能表示成那两个对角阵的和,还没有说清楚为什么PAQ,PBQ分别就是那两个对角阵吧
18687一起都贴出来了
我自认为打洞做的很经典
细节请自行补出来吧
我大都都是用语言描述的:post-38-1127964435.gif
18687
| 引用 (reijin @ 2005年09月27日
22时58分) |
|
貌似倒数第二步只说明了P(A+B)Q能表示成那两个对角阵的和,还没有说清楚为什么PAQ,PBQ分别就是那两个对角阵吧
|
我也是这个感觉
18688市面上好多呢,买一本巴
18688急求北大高等代数习题答案
18688我也需要呀,E-MAIL li_bin100@sina.com
18688西北工大出了一本!
18688有电子版的话,也给我一份,邮件地址:najia01@sina.com
多谢!
18688市面上到处都有卖的,我都买了两本不同版本的拉,我有丘维生的电子版本,需要的加我QQ21
195807,注明要书
18689最近在学SAS,但是很多宏命令看不懂,那位大侠能指导指导啊?我的QQ:79152356。多谢!
18692请教诸位高手:
Maltlab中是否有这样的模块可以直接解决以下问题:
对偏微分方程采用矩形网格剖分,并采用双3次Lagrange型有限元进行离散.
如果Matlab不行,其他软件是否可以办到,比如,Ansys?
盼指教.
18693不太难,最后一题是不是打错了
18693求几道高代的详细解答.post-38-1127813374.ibf
18693不好意思啊....我不给出具体解法,但是就以第三题来说,从已知条件你不难写出A在那一组基下的矩阵啊!(不然你就回去再把高代看一遍吧!)由此可以计算行列式得到A的特征值.你可以证明矩阵多项式的特征值等于矩阵特征值的相应多项式啊!第2问不就解出来了?!对角化矩阵再不会的话,那就没药可救了.....呵呵.....>>>>>>
18693不是没有做出来,而是想找个标准答案,或者更好的方法,所以呢,题目全部部分都贴了出来post-38-1127814835.jpg
18693有些东西并不是因为不会才发上来,而是想看下自己解答的缺陷,或者更好方法
因为这些题目都是没有答案,所以来讨论一下
谢谢post-38-1127815207.jpg
18693帮我解答一下.谢谢了
自己手头没有标准答案
18693其实这些题目都简单啊,应该怎么做都是标准答案吧!
18694求两道数分的详细解答post-38-1127814530.jpg
18694谁可以帮我解答一下,谢谢
18694第一问我有点对fourier级数的结论不熟悉,只知道如果导k次之后再讨论就方便多了!
对于第二问必要条件是显然的,很容易证明。
对于充分性则要利用到实数的有理数子集是稠密子集,所以只要证明在有理点连续就可以了。而这个正好是那个条件的等价,所以就容易获得证明思路了!
18694第一题详细写有些烦琐,而且在很多教材或参考书上都有详细解答。
第二题的充分性是一致收敛极限函数的性质,故不需证明。
我的解答:
post-38-1127868616.gif
18695硕士研究生入学数学考试历年是考生们感到很棘手的问题,很多考生由于数学没考好而痛失深造的机会。尤其对于文科改考理工科或经济类学科的考生来说,数学这门课的难度可称为所有科目中最大的,也是最让人担心的。 自从
1997年数学考试大纲进行了一次较大的调整以来,考生们普遍反映试题越来越难了。数学几乎成了相当部分考生难以逾越的“关口”。在这种情况下,部分考生“病急乱投医”,盲目参加各种辅导班,结果花费了大量的时间精力,效果却不好。
从
1987年至2001年这十五年的数学录取线差不多总是统考的三门基础课( 数学、英语、政治)中最低的。为什么会出现这种情况呢?有专家分析:一是考研数学试题的题量和难度与现行高校期末考试的差距较大,很多考生反映即使在大学时代数学学得不错,但在考研中如果不认真对待,不好好复习一番,也难以取得好的成绩,甚至上不了及格线。二是现在的硕士研究生数学试卷相对其它课程来说,所考内容多,知识面宽,综合性强,技巧性较高。如果只掌握知识而不掌握解题方法和技巧是很难考出水平的。
相比以前,2002年的数学考试大纲做了部分调整,而且2003年数学也发生了变化,统考数学将归入专业一科目中,数学一、二、三、四也由各招生单位按照有利于选拔人才和适应培养要求的原则自选。这意味着数学考查的方向将是更加注重对考生在掌握好基础上的综合运用能力的考查。如何复习好数学,可以说是报考理工类和经济类考生整个考研复习的关键。复习得好,你可以将别人拉得很远;复习的不好,就会吃苦头,甚至因此而失去机会。
考研的数学内容包括三个部分:微积分、线性代数、概率论与数理统计;同时还分为四个类别,即数一、数二、数三和数四,报考不同的专业要求考核不同的类别,这四种类别虽然考查的难度和侧重点不同,但作为数学学科特点是一样的,复习的方法也大体一样,而且数学相对英语来说,只要方法得当,提高非常快。所以只要掌握了正确的复习方法,就能事半功倍。下面的备考经验也许能给考生以启发。
数学备考一定要有一个复习时间表,也就是要有一个周密可行的计划。按照计划,循序渐进,切忌搞突击,临时抱佛脚。
数学是一门基础性学科,其解题能力的提高,是一个长期积累的过程,因而复习时间就应适当提前,循序渐进。根据往年的考试经验,不少考生大致在三月开始着手进行复习,当然数学基础差的考生可以将复习的时间适当提前。复习一定要有一个可行的计划,通过计划保证复习的进度和效果。一般可以将复习分成四个阶段,每个阶段的起止时间和所要完成的任务考生应给予明确规定,以保证计划的可行性。
根据历年高分考生的经验,大体可分为以下几个阶段:第一个阶段是按照考试大纲划分复习范围,在熟悉大纲的基础上对考试必备的基础知识进行系统的复习,了解考研数学的基本内容、重点、难点和特点。这个时间段一般划定为六月前。第二个阶段是在第一阶段的基础上,做一定数量的题,重点解决解题思路的问题。一般从七月到十月。这个阶段要注意归纳总结,即拿到题后要知道从什么角度,可以分几步去求解,每道题并不要求都要写出完整步骤,只要思路有了,运算过程会做了,考生可以视情况而灵活掌握,这样省出时间来看更多的题。所选试题可以是历年真题,也可以是书上的练习题,但真题一定要做,而且要严格按照实考的要求去做,把握真题的特点和解题思路及运算步骤。第三个阶段是实战训练阶段,从十一月到十二月的中旬,这也是临考前非常重要的阶段。考生要对大纲所要求的知识点做最后的梳理,熟记公式,系统地做几套模拟试卷,进行实战训练,自测复习成果。在做模拟题前先要系统记忆掌握基本公式,做题要讲究质量,既要有速度,又要有严格的步骤、格式和计算的准确性。最后阶段是考前冲刺,从十二月下旬到考试。针对在做模拟试题过程中出现的问题作最后的补习,查缺补漏,以便以最佳的状态参加考试。
考生们应该明白,学好数学是一个长期的过程,来不得半点的投机取巧,所以考前突击,临时抱佛脚的做法是不足取的,只有按照自己的计划,踏踏实实的进行准备,才能以不变应万变,只要自己的综合能力提高了,不管考试如何变化,都能取得好的成绩。
吃透考试大纲要求,准确进行复习定位。
考研大纲是教育部颁发的,指导命题和考生复习的纲领性文件,是命题的根本性依据。它严格划定了各类专业考生应考的范围和难度要求,这也是考生制定计划的依据。首先要认真阅读考试大纲,并结合近三年来的考研试题,实际了解本专业类数学考题的题型、类别和难度特点,进行复习的准确定位。考生应切记,与考纲无关的内容坚决不看,以免浪费时间,得不偿失。其次,考生要对大纲进行逐条分析,潜心研究,把握大纲的所进行的调整和命题的变化。
大纲实际上就是教育部为考生所划定的复习范围,考生应参照大纲,全面复习,不留遗漏,这是复习的基本对策。通过复习比较系统地理解数学的基本概念和基本理论,掌握数学的基本方法。要想在研究生入学考试中取得好成绩,必须做到"知己知彼"。"知己"首先是了解自己的优势和弱势,从而在学习和复习中有的放矢。“知彼”就是要研究近几年命题的特点和趋势,从而找到解答的方法。这项工作就要靠研读大纲和历年试题来完成。比如新出现的知识点一般情况下是命题的重点,而且经济类数学考试的特点之一是新知识点连考2--3年,所以,在复习中应紧紧结合大纲及真题,做到"知己知彼"。
通过分析大纲,考生在复习时要突出重点,同时紧紧抓住考试热点。一般地说,大纲中要求理解的内容,要求掌握的方法就是考试的重点,而近几年的考试中重复出现的内容就是考试热点。在对概念、定理和公式进行系统复习的基础上再对重点、难点及热点部分作重点复习,但不要专门去做偏题、难题、怪题,正式考试基本上没有什么偏题和怪题。开始全面复习之前抓住重点章节及常考部分非常关键,因为全面复习并不等于把精力和时间平均地分摊在所有的知识点上,而是要在全面复习的基础上,抓住重点、难点、热点和主要考试点。多年经验表明:各科的重要常考考点一般占其考试大纲的60%--70%。抓重点难点考点可使复习针对性增强,加快复习进度并节省大量时间,提高考研竞争优势,为考场取得高分打下坚实的基础。
就各课的特点来说,高等数学是考研数学的重中之重,所占分值较大,需要复习的内容也比较多。另外高等数学还有跨章节乃至跨科目的综合考查题,近几年出现的有:级数与积分的综合题;微积分与微分方程的综合题;求极限的综合题;空间解析几何与多元函数微分的综合题;线性代数与空间解析几何的综合题等。这种类型的题目考生要联系其它数学课程的知识才能做好。线性代数的内容纵横交错,环环相扣,知识点之间相互渗透很深,因此不仅出题角度多,而且解题方法也是灵活多变,需要在夯实基础的前提下大量练习,揣摩思路。而且2002年的大纲中适当增加了数学二的线性代数的考试内容,加大了难度,同时还提高了线性代数在试卷二中的占分比例,从原来占总分的15%提高到现在的20%,考生在复习时就要加大这一部分的复习力度。 概率论与数理统计是考研数学中比较难的部分,近几年这部分试题得分率普遍较低。与微积分和线性代数不同的是,概率论与数理统计并不强调解题方法,也很少涉及解题技巧,而非常强调对基本概念、定理、公式的深入理解。
事实证明,最新的考题与往年的考试非常类似的占5
0分左右,这些考题大部分改变一种说法,但解题思路几乎一样。所以对考生来说,一是要注意年年被考到的内容,对往年考题要全部消化巩固;二是注意那些多年没考到而大纲要求的内容。这样,通过准确的定位,抓住复习的重点和热点,提高复习的效率和效果。
三.重视基础,重视和加深对基本概念、基本定理和基本方法的复习和理解,
考生要重视对基本概念、基本定理和基本方法的复习,打好基础。数学是一门演绎的科学,首先要对概念有深入理解(要做到用自己的语言叙述出来),若不然,做题时难免会所答非所问,甚至是南辕北辙。其次要把定理和公式牢牢记住,每一道题都是由基本的定义、定理和公式构成,它们的不同组合就形成了不同的问题,多层次的组合形成不同复杂程度的问题。所以这些定义、定理和公式是解题的基础,而熟练掌握和深刻理解这些内容就成为解题成功的关键.
可以说,掌握了定理和公式就等于找到了解题的突破口和切入点。对近几年数学答卷的分析表明,考生失分的一个重要原因就是对基本概念、定理记不全、记不牢,理解不准确,基本解题方法掌握不好
为了熟练掌握,牢固记忆和理解所有的定义,定理,公式,一定要先把所有的公式,定理,定义记牢,然后再做大量的练习基础题。做这些基础题时如能达到一看便知其过程,这样就说明真正掌握了基础习题的内容。这些题看起来简单,但它们能帮助我们熟悉和掌握定义、定理、公式,所以考生不能因为这些题简单而不去看它,不去重视它。打个比方,如果把整个习题看成一座大厦,则定理,定义,公式等就好比砖瓦,而基础习题就是由砖瓦垒起的一面墙,可见熟练掌握基础习题对考生来说有着重要的意义。另外,考生还要注意定理和公式成立的条件,应用范围及变形,在理解的基础上灵活运用。近几年综合性试题、实际应用性试题越来越多,考生要特别注意。
俗话说"拳不离手,曲不离口"才能达到精妙的境界,学数学也是如此,只有把基本功打扎实了,才有进一步提高解题能力的可能性。比如高等数学中的最主要的基本功是极限、导数和积分。线性代数中主要基本功是矩阵的初等变换、线性方程组的解法、矩阵特征值、特征向量的求法。概率中主要是事件概率的求法、二维随机变量的分布、随机变量的数学特征等。把这些最基本的掌握住了,才谈得上掌握解题方法和技巧,否则所谓技巧只能是无本之木、无源之水。谈到基础,一些考生也许会不以为然,认为这与实际考试难度相比相差甚远。这里有一个对试题难度的认识问题,只要对历年考题认真分析就可以看出,试题难就难在对大纲划定的基础知识的延伸较深,对基本概念、基本定理和基本方法的综合应用较多较灵活,并不存在多少技巧性很强的偏题、怪题,2002年的试题从深度上说试题仍然体现了以考察数学的基本概念、基本理论、基本方法为主。只要考生的基本概念、基本理论、基本方法掌握扎实,是不难回答的。一些中间偏难的题,最终也是从基本概念基础上延伸转换中求解的。只不过在对基本概念、基本理论、基本方法的理解和运用上,强调了多方位多角度。考生应该认识到虽然仅打好基本功还得不到高分,但这是取得好成绩的基础和前提。历年都有相当多的考生考后的估计分与实际成绩差距很大究其原因就是基本功不扎实,该得分的得不到分,直接影响到“上线”。
对于基础差的考生来说,更要注重基础,最好能把课本通看一遍,在看的过程中牢记一些重要的概念,公式和定理,并结合课后练习题理解、消化这些公式、定理,前面已经说过,定义、定理和公式是基础的基础,基础较差的考生要想提高自己的解题能力,就必须在这上面多下功夫。
基本训练要反复进行。学习数学,一定要做一定数量的题。提倡精练,即反复做一些典型的题,做到一题多样,一题多变,要训练自己的抽象思维能力。对一些基本定理的证明,基本公式的推导,以及一些基本练习题,要做到“熟能生巧”。通过基本训练巩固对基本概念、基本定理和基本方法的理解。
“眼高手低”是很多考生在复习数学时易犯的错误,很多考生对基础性的东西不屑一顾,认为这些内容很简单,用不着下劲复习,还有的考生只是“看”,认为看懂就行了,很少下笔去做题,结果在最后的考试中眼熟手生,难以取得好的成绩。所以,在复习数学时一定要脚踏实地,一步一个脚印,就像下象棋,要取敌方老帅,就要老老实实战败所有兵卒,稳扎稳打,步步为营,这样的话,才能以不变应万变,在最后的实考中占据主动!
基础的重要性已不言而喻,但是只注重基础,也是不行的。太注重基础,就会拘泥于书本,难以适应考研试题。打好基础的目的就是为了提高。但太重提高就会基础不牢,导致头重脚轻,力不从心。考生要明白基础与提高的辩证关系,根据自身情况合理安排复习进度,处理好打基础和提高能力两者的关系。一般来说,基础与提高是交插和分段进行的,在一个时期的某一个阶段以基础为主,基础扎实了,再行提高。然后又进入了另一个阶段,同样还要先扎实基础再提高水平,如此反复循环。考生在这个过程中容易遇到这样的问题,就是感觉自已经过基础复习或一段时间的提高后几乎不再有所进步,甚至感到越学越退步,碰到这种情况,考生千万不要气馁,要坚信自己的能力,只要复习方法没有问题,就应该坚持下去。虽然表面上感到没有进步,但实际水平其实已经在不知不觉中提高了,因为在这个时期考生已经认识到了自已的不足,正处于调整和进步中。这个时候需要的就是考生的意志力,考研本来就是一场意志力的比赛,不仅需要丰富的知识和较高的能力,更要有坚强的意志力。只要坚持下去,就有成功的希望。
四.加强综合解题能力的训练,熟悉常见考题的类型和解题思路,力求在解题思路上有所突破。
考研试题与教科书上的习题的不同点在于,前者是在对基本概念、基本定理、基本方法充分理解的基础上的综合应用,有较大的灵活性,往往一个命题覆盖多个内容,涉及到概念、直观背景、推理和计算等多种角度。因此一定要力争在解题思路上有所突破,要在打好基础的同时做大量的综合性练习题,并对试题多分析多归纳多总结,力求对常见考题类型、特点、思路有一个系统的把握。许多考生在做完教科书上的习题后,往往对考研题难以适应,其突出感觉是没有思路,这正是考生考前准备应解决的突破口。考生要掌握住各种题型的解题方法和技巧。考虑到数学学科的特点,要求考生自己将所有的解题思路都琢磨出来是十分困难的,这方面通常可以通过求教有经验的老师,参加有较好信誉的辅导班,或者阅读有关的辅导书解决。另外在做题时,不必每道题都要写出完整的解题步骤,类似的题一般只要看出思路,熟悉其运算过程就可以,这样可以节省时间,提高做题的效率。
在选择习题时,考生要注意,最好先不要做模拟题,应该把真题先做一遍。因为真题的错误率比较低,而且最接近实际的试题。有的模拟题出得刁钻古怪,没有可做性。如果先做模拟题,假如选的模拟题不好则白白浪费了时间,而且对自己的解题思路也有着负面影响。通过做真题,考生可以真切的体会到考研的重点,难点,重要的是掌握了各种常考的题型。在做完真题之后再做模拟题就会感觉自己的解题思路有了质的提高,对数学认识也有了新的变化。很多考生往年的经验都证明了这一点。
考生在做题的同时还要注意各章节之间的内在联系,数学考试会出现一些应用到多个知识点的综合性试题和应用型试题。这类试题一般比较灵活,难度也要大一些。
考生要注意对综合性的典型考题的分析,来提高自身解决综合性问题的能力。数学有其自身的规律,其表现的一个重要特征就是各知识点之间、各科目之间的联系非常密切,这种相互之间的联系给综合命题创造了条件,因而考生应进行综合性试题和应用题训练。通过这种训练,积累解题思路,同时将各个知识点有机的联系起来,将书本上的知识转化为自己的东西。
考生在备考时还要多做例题,而不仅仅是练习题。做例题时应遵照下面的方法,也就是在看第一遍之前一定要遮住答案,自己先认真做;无论做出与否都要把自己的思路详记于空白处,尤其是做不出的,一定把自己真实的思考方式记录在案,留待日后分析,而不是对了答案就万事大吉,这样做可以迅速的找到做题的感觉。总之,考生在做题目时,要养成良好的做题习惯,做一个"有心人",认真地将遇到的解答中好的或者陌生的解题思路以及自己的思考记录下来,平时翻看,久而久之,自己的解题能力就会有所提高。对于那些具有很强的典型性、灵活性、启发性和综合性的题,要特别注重解题思路和技巧的培养。数学试题千变万化,其知识结构却基本相同,题型也相对固定,往往存在明显的解题套路,熟练掌握后既能提高解题的针对性,又能提高解题速度和正确率。
当然,一味的靠做题来提高数学能力也是不足取的。曾有一个考生,平时的解题能力很高,但最后的考试成绩却不是很理想,谈到自己失利的原因时,他说,自己平时几乎全部靠做题来提高水平,而对知识点缺乏更高层次上的把握和运用,导致遇到陌生的题目时,得分率严重下降。所以考生不能为做题而做题,要在做题时巩固基础,提高自己对知识点更高层次上的把握和运用。要善于归纳总结,对数学习题最好能形成自己熟悉的解题体系,也就是对各种题型都能找到相应的解题思路,从而在最后的实考中面对陌生的试题时能把握主动。
考前的强化训练应注意的问题。
加强考前强化训练,做几套模拟试卷必不可少。在规定的时间内做几套模拟试卷一是可以了解一下自己对所考的知识点究竟掌握到什么程度,同时可以了解到自己的薄弱环节从而抓紧时间补上。再者通过平时的练兵可以给应试时提供点临场发挥的经验。有相当一部分考生的经验证明,如果考生能够通过做题将所遇到的各种题进行延伸或将试题的变式做到融汇贯通,一定会在考试中运用自如超常发挥,取得好成绩。根据往年的情况,许多考生往往看得多,练得少。有些考生在考后抱怨题太多,做不完或做错。其原因就是平时缺少练笔的机会以及考前没有进行强化训练。所以建议考生在限定时间里系统做几套模拟题或样题,然
后对照答案自己分析总结。在做模拟题时,应注意以下几点:
1.注意答卷时时间的分配。一定按照实考那样严格限定做题。时间只有平时养成良好的习惯,考试的时候才能做到心中有数,不至于张皇失措。
2.数学公式必须在做题前就牢记住,这样在使用时才会得心应手,
3.举一反三,不只是为做题而做题,注意知识点之间的联系。
下面再说一下考生在答题过程中应注意的事项,也就是一些做题经验。
考研数学的难度是越来越大,但根据往年的情况,一般会有50分左右的基本题。要想及格,这50来分一定要抓住。历年考题中计算题的前4-5题,差不多所有填空,选择题就属于这一类。因而考生在安排答题顺序时,应该先答填空题,因为这部分是最简单的概念和运算,得分比较容易,当然试题中如果有计算题或者证明题与平时看书或者参加辅导班老师所讲的例题类似的也可以先做。然后答证明计算题。答计算证明题时应先答与习题模拟题类似的,然后答没有见过的。最后答单项选择题,因其综合性太强不易做对,而且有些单项选择题概念性非常强,计算技巧也比较高,所以不易在做完填空后立即做,以免自信心受到打击。
求解单项选择题一般有以下几种方法:
推演法:它适用于题干中给出的条件是解析式子。
图示法:它适用于题干中给出的函数具有某种特性,例如奇偶性、周期性或者给出的事件是两个事件的情形,用图示法做就显得格外简单。
举反例排除法:排除了三个,第四个就是正确的答案,这种方法适用于题干中给出的函数是抽象函数的情况。
逆推法:所谓逆推法就是假定被选的四个答案中某一个正确,然后做逆推,如果得到的结果与题设条件或尽人皆知的正确结果矛盾,则否定这个备选答案。
赋值法:也就是说将备选的一个答案用具体的数字代入,如果与假设条件或众所周知的事实发生矛盾则予以否定。
慎选辅导用书。
必须强调的是,辅导班或辅导书只是学习的一种手段,最终解决问题还要靠自己动手动脑。目前市场上一些考研辅导材料将数学(一)至数学(四)不同要求的内容不加区分地混编在一起,甚至超纲,考生应注意识别,考纲不要求的内容坚决不要看,不必因此耗费许多宝贵的时间和精力。考研参考书层出不穷,如何选择是每个考生都会遇到的问题。有专家向考生提了以下几点建议:首先要选择那些有归纳和总结,在方法上高屋建瓴,有具体方法的指导并以题型为纲的辅导书。这种辅导书是以题型为纲,而不是搞题海战术。数学题目浩如大海,要想都做遍是不可能的。而数学的题型是有限的,要掌握和理解它们的解法是可以达到的。考生们在复习时应抓住题型,最好背过它们。其次,应选择有超前性前瞻性的书。书中应有作者精心讲解的方法和技巧,可以用来解决将来考研中的试题。考生不必选择太多的书,但是所选的辅导书中一定要有重要的概念定理和公式,有题型的归纳总结。那么怎样才能了解众多作者编写的书是否具备这两大特点呢?考生可以通过三个途径去了解。一是自己到书店去多翻阅几本进行比较;二是到在读的研究生中去了解情况;三是到网上咨询、了解信息。
考生在利用辅导书时,要明白复习参考书是为了大多数人的需求而编写的,具体到每一个人身上,书中肯定有不适合或对他来说浪费时间的地方,因此复习时一定要做书的主人,根据自身情况对书中部分进行取舍。只要这样才能把有限的精力充分加以利用。另外,考生在看这些辅导书的时候应以例题当习题,做完后想想做对(错)的原因到底是什么,然后回头看提示,紧紧抓住题型。
辅导班的利用
选择一个好的辅导班对数学基础不是很好的考生来说还是有必要的。一是可以凭借辅导机构和辅导专家的专业优势以及丰富的辅导经验,帮助考生把握考点、重点、难点、各知识点的考查方式和题型;二是可以“逼迫”考生进行经常性的复习,提高复习的效率;三是可以提供准确的考验信息和珍贵的内部资料等等。根据往年的参加过辅导班而取得好成绩的考生的经验,报辅导班一般选择春季班或暑假班,这依个人的能力不同而取舍。如果个人的数学能力较强,则可以不报春季班而选择暑假班或直接选择冲刺班;如果基础不好,能力较差则最好报一下春季班,因为春季班相对来说讲得比较慢,比较详细,主要是帮考生打基础。这时候课下跟着看辅导书,效果会比较好,对于自学能力差一点的同学来说,可以提高复习的效率。
在上辅导班时,最好能在每次课前预先看一下老师要讲的内容,否则很可能跟不上老师的思路,影响听课的效果;在进行课后复习时尽量把老师讲过的解题步骤完全弄懂,有不懂的地方也没关系,注上标记,作为日后复习的重点。
对于自制力较强,学习很有规律的同学,可以报暑假班。一般来讲,暑假班的听课效果要优于春季班。经过考生自己几个月左右的复习,完全可以把数学中的三部分系统地看一遍,这样上课时就不会被某些生僻的概念或公式难倒,从而可以随老师一同思考。
在参加辅导班后,考生先期应在熟悉大纲的基础上,对考试必备的基础知识进行系统地复习,这个过程应在上辅导班之前完成。然后在上辅导班时,要及时跟进,消化老师讲课内容,并注意归纳条理。在上完辅导班后,根据老师归纳的各种题型的解题思路,有意识地看书做题,在一定数量基础上,进一步归纳总结,解决思路问题。
有的考生也许比较关心辅导班的选择问题,因为参加辅导班的考生已经把自己的复习计划和辅导班的进程联系在一起,如果所选的辅导班不适合自己或质量较差,很可能导致整个复习的失败。往年已有考生因为辅导班的问题而影响最终的考试。那么如何选择一个适合自己的同时质量又比较高的辅导班呢?有专家向考生建议,在选择辅导班时,首先要对自己的能力有一个较准确的评估,从而选择何种类型的班,比如基础班或强化班。其次,考生要从辅导学校的师资力量,辅导材料,学校的声誉以及服务多方面综合考虑。可以向上一届刚考完研的学长打听,他们因为有亲身体验,往往能够提供比较准确的信息。当然,如果有几个班都不错,可以几个人合作,一个人报一个。这样既可以节约财力和精力,又能多接受些知识和信息。
考生们应该明白,不管是辅导书还是辅导班,都只是辅助你复习的工具,决不能迷信哪本书或哪个辅导班。许多考生的经验都证明,好的考试成绩的取得最终还是靠自己动脑动手,仅靠听几个班,多看几本书是不会有好效果的。
数学考试不光是考数学知识,也是对考生综合素质的考核,比如心理应战能力,分析问题、解决问题的能力,难题化简的能力等等。有不少考生平时学得很好,基本功很扎实,但考试时把握不住“战机”,所以考不出理想的成绩。还有的同学考前乱“投医”,结果本来已经掌握的东西却被搅成一团麻。所以考前几天对考生来说是非常重要的。在这几天的安排合理与否将直接影响考生在考场上的发挥。对此考生要注意以下几个方面:
一.考前一两天不要再做模拟题,因为答不好会容易打击自己的自信心。这时候应多做一些基本的常考题型,多想想这些题型的解题思路,多想想自己平时解题时易犯的错误。有一个考生的经验值得大家借鉴,他把自己平时解题时犯的错误都记在一个小本子上,这样在考前翻看,就可以提醒自己不再犯类似的错误。
二.临近考试前不要天天抱着类似《考前冲刺》之类的书看,这些书里没有解题的方法和技巧,只有一些模拟题,在临近考试再做这些模拟题对考生来说意义不是很大。而且,有的所谓冲刺题出题角度和真题相差很大,做这些题只会给考生的解题思路带来负面影响
。
三、如果所看的参考书中某一个例题的解法特别繁琐,而且再没有其他简单的解题方法(而不是作者故意繁琐化),这种题一般就不会考,就不要在这种题上浪费时间。
四、对于基础不太好的考生来说,不要认为上了辅导班,习题会做了就掉以轻心。数学和其他课不同,其他课通过一段时间的学习获得提高就可以了,而数学要经常练习,尤其对一些基础性的运算要非常熟练。因为任何的解题方法和技巧都建立在内容熟悉的基础上,只有非常熟悉基本理论,解题技巧才有发挥的余地。所以在考前这些考生应根据自己的情况,再去看一看书本,想想各种题型基本的解题思路。
五、临考前最好不要再看新的参考书,把原来的参考书吃透就行了。一是时间不允许,二是每本书都有自己的解题方法和思路,吃透一本就行了,多了反而不好。另外,要好好总结一下过去参加各种考试的经验,这很重要。
六、考试时思想一定要放松,情绪要平静下来,尤其是当见到一些平时没见过的题目时,千万要镇定,不要乱了方寸。对于比较有把握的题,要争取完全做对,千万不要东做一点西做一点影响得分。对于非常陌生的题,如果有会的部分一定要写出来,在考试时应“分分计较,每分必争”。如果某题你做出的结果很复杂,就应该马上否定自己,重新再做一遍。
相信经过有计划的复习,每个考生都可以使自己的综合解题能力有一个质的提高,从而在最后的实考中坦然的面对试题的变化,考出好的成绩。
18695
虽然不是数学专业的,但也相通,值得借鉴!
18695分析的很多,很全面啊。
18695太长了呀!!!
有点启发!!!
18695这是说非数学专业的吧?
18695收到
18695对数学专业的学生来说,考研还是卡在英语上。有没有介绍如何念英语的。这个想必对数学或非数学专业的学生都是有用的。
18696使用Stolz定理可以得到结论。
18696没想出来
post-38-11278
19393.gif
18696利用柯西不等式
sum(1/pn)sum(pn)>=n^2
18696能不能详细点,谢谢!
18696左

右,不需要pn单调递增啊??
18696这个是《数学分析中得典型问题与方法》中的例题,我把解答贴一下:post-38-1127872609.gif
18700973计划项目《高性能科学计算研究》被正式批准立项
From: Zhiming Chen
<zmchen@lsec.cc.ac.cn)
Date: Thu, July 14, 2005 5:57 pm
国家973计划项目
《高性能科学计算研究》介绍
2004年11月9日上一个973计划项目《大规模科学计算研究》以优秀的成绩完成结题评估
以后,中国科学院计算数学与科学工程计算研究所、中国科学院大气物理研究所、北京
应用物理与计算数学研究所、北京大学、大连理工大学的部分专家即着手进行新一个
973计划项目的申请准备工作。2004年12月初成立了以石钟慈院士为组长的新一个973
计划项目的申请筹备组,在征询了众多专家意见的基础上,我们于2005年3月14日向科
技部提交了新一个973计划项目《高性能科学计算研究》的申请书,2005年4月21日进
行了复评答辩,2005年6月8日进行了综合评审答辩。2005年6月23日接到科技部通知,
我们新一个973计划项目《高性能科学计算研究》被正式批准立项。
《高性能科学计算研究》项目的总体目标包括二个方面。在科学计算的共性问题研究
方面,项目将在基于后验误差估计的并行自适应有限元方法和复杂流动问题的并行自
适应移动网格方法形成既有算法理论、又有程序实现、且有具体应用的完整的创新体系。
在应用目标研究方面,项目将完成千万自由度的完整气候模式的研制;进行千万自由度
三维多介质大变形高温高压流体力学数值模拟;建立能够处理几百个原子的实空间第一
原理计算方法,以该计算方法为基础,在原子和纳米尺度上通过结构设计实现量子调控;
建立非周期(随机)结构的、适用于材料服役行为分析的、从纳米、介观到宏观多个尺
度的多物理多尺度耦合模型和计算方法。
根据上述总体目标,《高性能科学计算研究》项目设立了四个课题组,它们是:
1.创新计算方法的基础理论研究
课题组长:陈志明、许学军
主要研究内容和目标:并行自适应算法与理论,
保结构方法的理论与应用
大规模高速集成电路中电磁信息计算
2.
大规模并行计算研究
课题组长:张林波、莫则尧
主要研究内容和目标:发展系列的高效可扩展并行算法与并行实现技术;
建立2~3个并行数值模拟支撑软件框架
3.复杂流动问题的高性能算法研究
课题组长:王斌、江松
主要研究内容和目标:地球系统模式中的高性能算法研究及应用,
高维多介质大变形流体动力学计算方法研究
4.材料物性的多物理多尺度计算研究
课题组长:张平文、龚新高
主要研究内容和目标:基于第一原理计算新方法探索
材料物性的多物理多尺度计算模拟
围绕上述项目总体目标的实现,2005年6月26日项目专家组根据各组组长的提名,
投票选出了新一个973计划项目《高性能科学计算研究》的55位正式参加成员。专家组
成员一致希望,新一个973计划项目的成员能在两期国家攀登计划项目和上一个973项
目的良好基础上,为完成本项目的总体目标努力工作,推动我国科学计算事业不断向
前发展。
陈志明
中国科学院计算数学与科学工程计算研究所
2005年7月13日
附:973计划项目《高性能科学计算研究》专家组成员名单:
石钟慈、沈隆均、王兴华、郭本瑜、陈志明、张林波、王斌、张平文、张洪武
首席科科学家:
陈志明
18702数学与系统科学研究院成立统计科学研究中心
科学时报2005年7月7日文章
“虽然我国经济奇迹般发展,其距离与美国正在缩小,但我国的统计研究水平却与美国
差距拉大。由于种种原因,我们的统计队伍和研究水平还远不能满足社会对统计科学的
大量需求,就与纵向相比,我们现在的统计水平恐怕还不如20年前。统计教学与研究的
危机一直存在着。”这是海外华人学者、美国普林斯顿大学教授范剑青7月6日在中国科
学院数学与系统科学研究院统计科学研究中心成立大会上所讲的。
据悉,该中心由中国科学院数学与系统科学研究院目前从事统计科学理论与应用研
究的科研人员和海外知名统计科学家组成,主要从事统计科学方法、理论及应用研究。
范剑青出任中心主任,美国哈佛大学教授刘军、英国伦敦经济学院教授姚琦伟、中科院
数学与系统研究院研究员陈敏和副研究员邹国华任中心副主任。
在中心成立的同时,为期3天的“统计科学前沿问题国际研讨会”同时举行。
统计学是量化科学的中心
统计学是一门研究数据收集、表达、整理与分析的科学,与社会生活的方方面面
密切相关。范剑青说,统计学源于2000多年前的古希腊,我们的祖先对统计的重要性
早就有深刻的认识,改革家商鞅在公元前390年就曾说过:“强国需知十三数。”但
在当今信息年代,十三数早已无法满足社会发展的需求。
传统的统计学主要指官方统计、工业统计和现场统计。现代统计学则注重挖掘数
据包含的信息,让数据说话。范剑青说,今天,计算速度的指数增长、计算费用的大
幅下降给统计科学带来了巨大的影响,技术革命给数据的收集带来了许多便利,互联
网使统计学家获得了大量的信息,但对这些数据进行分析遇到前所未有的复杂挑战,
统计学重要性因此日益彰显。如今,统计学正迅速地渗透到许多尖端科技的研究前沿,
被广泛应用于机器学习、资讯工程、医学、生物学、经济学、金融学、风险管理、心
理学及社会学等许多领域,成为量化科学的中心,在许多交叉学科研究中起着桥梁作
用。他认为,尽管许多科学领域如生物信息与计量金融学所关心的问题很不一样,但
其本质的统计问题、数学问题却是相通的。
陈敏介绍,统计有很强的预测功能,可为政府决策提供依据。比如,当SARS2003
年突然在中国部分地区出现时,数学与系统科学研究院对SARS在北京地区的发展进行
了统计预测,他们提出了在采取最好的防护措施的情况下,一定时期内被感染人数的
最高值和最低值,以及何时可能会降到最低值,为政府决定调动多少人力、物力、财
力应对疾病的流行提供了依据。
最后的事实证明,他们的预测是成功的,SARS病人的实际数量正好在他们预测的
区间内。
范剑青说,为了满足日益增长的统计需要,美国于
1991年成立了国家统计科学研
究所(NISS),其宗旨是寻找、促进、鼓励和培养与统计科学相关的、具有巨大影响
的交叉学科的前沿研究。欧共体也不甘落后,于
1997年成立了EURANDOM研究所,其任
务是研究随机现象。为了进一步促进统计与数学科学在科技前沿的合作,美国于2002
年成立了“统计与应用数学研究所(SAMSI)”,与此同时,许多大学增设统计系或生
物统计系。美国数学会的研究报告指出,统计与生物统计的硕士、博士毕业生占数学
科学研究人员的1/3。由此可见,国际社会对统计的重视是不言而喻的。反观我国,虽
然经济奇迹般发展,与美国正在缩小差距,但我国的统计研究水平与美国的差距却在
拉大。
千里之行 始于足下
范剑青分析了中国目前统计学水平不如人意的种种原因。他说,20年前,正值国
内改革开放后不久,一批有志于统计学的学者全心致力于统计学研究,当时中国科学
院应用数学研究所和系统科学研究所分别有20多位这方面的专家,力量较强,但由于
毕业后学生们一方面到金融、证券部门工作,一方面又大批留学海外,现在国内统计
科学领域的发展出现了青黄不接的现象,而且由于教学水平跟不上要求,培养的学生
质量也有问题。
但是20世纪80年代出国的学者如今已经成长起来,在海外形成了强势力量。陈敏
认为,在所有的学科中,华人统计学家在美国的力量是最强的。在美国主要大学统计
学领域的重要岗位基本上都有华人学者,他们分布在各个重要岗位。他说,美国为表
彰在统计学界做出杰出贡献的统计学家,联合世界上5个著名的统计协会在
1981年设
立了考普斯“总统奖”,每年只颁奖给一名40岁以下的学者,该奖已成为国际统计学
界的最高荣誉,有“统计学诺贝尔奖”之称,目前已有6位华人学者获得此奖。
在海外已有成就的华人学者也有强烈的愿望为祖国做贡献,同时国家也急需统计
学人才,陈敏介绍说,“成立这个中心就是为了搭建平台,让年轻的学生在国内就可
直接接触到世界统计学领域的前沿,与最优秀的学者对话,了解他们是怎么思考问题
的。”
“千里之行,始于足下”,范剑青希望让中心这个平台发挥桥梁作用,将国外最
优秀的学者请到中国讲学,与国内学者、学生进行深入的讨论,并将国内的学者和他
们所做的工作介绍给国际学术界。他说:“学术的竞争是文化和人才的竞争,最重要
的是人才,培养人才是我最大的愿望。”他在成立大会上提出两点恳求:“有十几位
国内外的统计名人在中心兼职,我恳求你们在百忙之中每5年为中心培养一名博士生,
改善中国统计高级人才供不应求的状况;中心机构成立了,我恳求研究院的领导制定
一套有弹性的提职政策,减缓统计人才外流,同时用一些优惠条件招聘优秀的统计人
才。”
范剑青梦想中心能揭开中国统计学研究的新篇章,为中国建立一支高水平的研究
队伍,为社会培养更多的高级人才,并以此为核心,将统计学辐射到其它学科。他鼓
励海外学者为祖国做贡献:“当统计科学发展了,数学也就得到了发展,数学在社会
中的作用也会得到更高的承认,到那时,中国的数学界会感谢你们,会赞赏你们的远
见。统计学的发展势必增进量化技术的开发,给尖端科技赋予更有力的工具,使中国
成为科技强国。到那时,中国的科技界会感谢你们,炎黄子孙感谢你们。”
18703数学小说: Mathematical Fiction
世界上存在相当数量的数学小说。显然,在科幻小说(Science
Fiction)中经常有
一些富含数学内容的作品,比如Greg Egan[1]和Stephen
Baxter[2]的作品。不过
在流行的主流小说中也存在一些这样的作品,比如, The Curious Incident of
the
Dog in the
Night-Time这部相当优秀的小说[3]中就有一些关于Conway的Soldiers问
题[4]的讨论,而在戏剧Tom
Stoppard[5]则经常出现严肃的数学内容。但是,如果你
想要一份全面的数学小说的列表,不妨看看这里[6]。
Ref:
[1]
http://gregegan.customer.netspace.net.au/[2]
http://en.wikipedia.org/wiki/Stephen_Baxter[3]
http://www.randomhouse.co.uk/childrens/gro...ngbooks/curious/
[4]
http://plus.maths.org/issue12/xfile/[5]
http://www.siam.org/siamnews/04-99/play.htm[6]
http://math.cofc.edu/faculty/kasman/MATHFICT/all.php
18705人生目标不明确,考研方向有问题。要知道出国深造或考验是你研究的延伸和提高,如果不喜欢这个方向就不要往里走,否则做到一定深度会很痛苦。不要根据出国或考验本身为目的来选泽专业,要根据自己将来想做什么和喜欢做什么来选择
18705请教,研究生读什么方向比较容易出国或到中科院读研。
谢谢,欲考吉林大学,我是女生:)
18706急用!
18707有好多方法啊,最简单的就是上面说的定义。
其他的方法也挺多的,根据题目的不同用不同的方法。
18707请问如何证明f(x)可导啊。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。请求给予回答
18707用可导的定义证啊!
18708这是习题解答,不是教案啊
18708谢谢!!!
18708去年教这门课,自己参考别的答案整理的,欢迎批评指正
发现自己能上传附件太小了,请问可否直接发到博士信箱
有复变函数与积分变换的答案、教案,还有几份试题
18708答案第一部分post-67-1128787240.ibf
18708答案第二部分post-67-1128787423.ibf
18708答案第三部分post-67-1128787548.ibf
18708答案第四部分post-67-1128787638.ibf
18708答案第五部分post-67-1128787722.ibf
18708答案最后一部分post-67-1128787899.ibf
18708欢迎 教案
18708为方便大家修改,发个word的教案和大纲post-67-1128834125.ibf
18708大纲post-67-1128834394.ibf
18708从别的地方下载的哈工大的卷子(1)post-67-1128834690.ibf
18708第二份试卷
post-67-1128834933.ibf
18708第三份试卷post-67-1128835166.ibf
18708jash 怎么那些答案解压不了啊???
我解压时出现错误的!!!
你能不能帮我啊??
18708不会吧,把那几个压缩文件下全了,直接解压第一个就行了阿
如果不行请发email:
jash_sdu@hotmail.com
或用以上email msn联系
18708十分感谢,
18708十分感谢你啊!!!!
18708感谢啊。
18708我可以解压了!!!
jash谢谢你!!!
谢谢!
18708谢谢
18708辛苦了,楼主
18708谢谢
18708可能是你的解压软件版本底了,下载个版本高一点的重装一下应该就可以了.我现在用的是winara3.51版的
18708谢谢楼主
18708太感谢了
18708谢谢分享
18708多谢了
18708jash谢谢
好人啊
18708可以解压的。
谢谢分享。
18708十分感谢你啊,谢谢分享
18708呵呵,谢谢,好人,收下了,
18708
| 引用 (zxzcumt @ 2006年12月07日
15时57分) |
多谢楼主,可否由doc格式。
多谢。 |
我有doc文件的,如果需要可以和我联系
htqisd@163.com
18708谢谢!
18708请问怎么解压啊
就救我把
18708
引用 (nudtlxw @ 2006年04月
19日
09时24分) |
| 呵呵,谢谢,好人,收下了,
|
有课件吗?
18708谢谢好人呀
有课件吗?
187083块肉
18708声明一下:俺没有复变函数的课件啊,都是直接板书的
18708谢谢
18708真的谢谢呀
18708谢谢
18708很好的东西
看来楼主是很费心思了
18708谢谢你!
18708多谢楼主,可否由doc格式。
多谢。
18708谢谢楼主分享 辛苦了.
18708thanks,你辛苦了
18708哈,谢谢ing!!!
18708多谢,真是救人于水火啊
18708thanks,你辛苦了
18708好人啊!!谢谢啊!!
18708多谢分享,
但里面好像没有第六章的习题答案
18708近期有发email索要答案doc格式的文件,我将其压缩放在91files上
有需要的可直接去下载
复变函数doc格式
http://www.91files.com/?P1Q8F2KX3M2Z7L7O8KWO复变函数pdf格式
http://www.91files.com/?BRNKY3HN6E08B08ARPG2积分变换doc格式
http://www.91files.com/?EMZS37C9L70PMYOU6K1I积分变换pdf格式
http://www.91files.com/?RPGSKOKFLCF5EL0ZXBP8
18708jash谢谢
好人啊
18708很好,谢谢了!
18709向各位请教, Mathematica软件学生版与专业版的主要区别在哪?解决问题能力的限制还是其他方面?
18709
http://www.wolfram.com/products/student/ma...html#difference
Q&A about Mathematica for
Students
Technology and Capabilities
Q: How is
Mathematica for Students different from the professional version of
Mathematica?
Mathematica for Students is a fully functional version
of Mathematica but at a low student price. It runs at the same speed,
produces the same output, and is identical in functionality to the
professional version of Mathematica. Its distinctions include the
following:
Mathematica for Students is for exclusive sale to
students enrolled at accredited educational institutions for use on their
own personal computers. Proof of enrollment is required at the time of
purchase.
Registration and a password are required to use
Mathematica for Students. To register Mathematica for Students and to
receive an activation password, students must go to the Wolfram Research
product registration page or contact Wolfram Research via phone, email,
fax, or postal mail.
Mathematica for Students includes The
Mathematica Book as an electronic version in the online documentation
found under the Help Browser. The professional version of Mathematica
contains a hard copy of this book in addition to the online documentation.
A printed edition of the book is available from the Mathematica bookstore.
Mathematica for Students has an encoded footnote that prints at
the bottom of every document page. This "Printed by Mathematica for
Students" footnote cannot be eliminated.
Note: Information on
the technical differences between the student and professional versions of
Mathematica is available on our Technical Support website.
也就是说,除了帮助中的mathematica书籍是否有离线硬盘版外,使用上已经没有区别了。
18710晕,设arcsinx=y不就可以了
18710求arcsin
x/
x在x趋于0时的极限,不能用求导的方法.
18711请问大侠:
“利用阿贝尔等式变换可证明
lim[(n*an)*sum(1/i)]=0
(i=1....n)”是怎么证明的啊?
18711test!
post-38-1127901279.gif
18711已知,an>0,sum(an)收敛,n*(an)单调,证明:lim(n*an*lnn)=0
18711
http://www.math.org.cn/forums/index.php?showtopic=
18015
18711不错[CODE]
18711之前居然没看到那个贴!◎_◎
我说另一种思路
sum(an)=sum((n*an)/n)
利用阿贝尔等式变换可证明
lim[(n*an)*sum(1/i)]=0
(i=1....n)
而sum(1/i)~ln(n),可知结论成立
18712扔骰子赌钱 :起点是0元。
1。 扔到3,加 3元, 玩家决定 A)继续
B)不玩了,拿钱走人。
2。扔到4,加 4元, 玩家决定 A)继续 B)不玩了,拿钱走人。
3。 扔到5,加 5元,
玩家决定 A)继续 B)不玩了,拿钱走人。
4。扔到6,加 6元, 只能继续 ,玩家 不可以拿钱走人。
5。扔到2,
加2元,停。 不能继续, 拿钱走人。
6。 扔到1,回到起点0。玩家不能继续,两手空空走人。
编个程序 .
定一个退出标准, 找出 最大化玩家期望值的策略。 算出那个期望值
那位高手解答一下,多谢
18713一道数分题目post-38-1127837768.jpg
18713标准的
ε ∼N
语言就可以了
18713这个题目其实这样做是正常的思维方式,如果注意在处理不等式的时候可以适当应用放缩法是非常不错的!post-38-1127852987.gif
18714谢谢了
18714在附件里,谢谢post-38-1127838498.ibf
18714这个题目其实就按照定义下手就可以!post-38-1127855623.gif
18715错这么多,我真服了出这道题的人了,不管如何,还是要谢谢你
18715我感觉第一个问,是不是属于号的方向反了post-38-1127839338.ibf
18715我晕,这个题目的两个问都错误了,第一问方向改反,和改为交
第二问的直和符号应该改为交的符号!
下面是我贴的我改了之后的正确命题!post-38-1127854905.gif
18715
| 引用 (蓝戈 @ 2005年09月28日
05时01分) |
我晕,这个题目的两个问都错误了,第一问方向改反,和改为交
第二问的直和符号应该改为交的符号!
下面是我贴的我改了之后的正确命题!
|
有点乱呀~~看得我晕晕的
18715to 蓝戈:
你好,你的解答过程我有一步不懂,就是在证明第2问的时候,"f1(A)x=0,g1(A)x=0 =>
( f1(A),g1(A) )x=0".好象已经主观上承认了第2问的结论,再去证明第2问的结论,谢谢.
18715呵呵,其实蓝戈的解答是有点跳,
f1(A)x=0,f2(A)x=0=>f1(A)-g(A)f2(A)x=0,f1(A)=g(A)f2(A)+r(A)
如此辗转就会知道存在rn(A)=(f1(A),f2(A))=1,使得rn(A)x=0,即x=0
从而就获得了证明了!关键还是辗转相除法的应用!
18715To 永理:
你的题抄错了,这是北大的一道题。
只需把
(
f(A),g(A))
改为
(
f(A)g(A))
即可。
18716有一数学公式不了解(看不懂, 关于常数e的.
是关于一篇计算自动索引方法里的一种;---统计学方法:
1.设
TFij 为短语Tj在文章Di(0<i<=1000,共N=1000篇文章) 出现的频率, 比如: 短语
啊呀(Tj)
在<<论绿茶的由来>>这篇文章(Di)出现的频率为 2%.
2.
设DFj为在N(N=1000)篇文章出现了短语Tj的频率, 比如: 短语
啊呀(Tj)在1000篇文章出现的频率为
43%.
结论1: DFj的反转频率 (inverse frequency)为: log(N/DFj)
结论2:
短语Tj在文章Di中的权重(weight) 为:TFij*log(N/DFj).
哪位知道这是为什么吗?
为什么会得出结论1,2 ? 在这里为什么,用导数就能解决问题? 这里的导数应该是自然导数吧?
谢谢指导!!!
18716问题太简单? 太复杂?
请给个说法,大家,好吗?
18716

你该给个参考文献啊什么的,至少题目说的周全点吧。

18716这里回答问题该给个奖励吧??斑竹看那???
187
17如果大家把论文看成了负担,那就完全可以不写。学术研究成了这一个样子,还有什么意义呢?如果觉着国内研究不行而出去干,那么这是个人的权利,但是对国家来说,这个人完全可以起个带头作用,带个好头,而不是出去!
个人意见,权当讨论。
187
17
My Webpage退学前曾在清华大学计算机系软件所就读,主要进行集成电路布线算法的研究。
四川大学97级本科毕业,报送到清华大学计算机系直博。
2004年左右发表《完全用linux工作》和《写给支持和反对<完全用Linux工作>的人们》的文章,在中国的计算机和linux阵营引起极大轰动效应,成为水木清华linuxapp版和中国多个linux社区的偶像级人物。
2005年,王垠为第一作者的论文参加IEEE/ACM
Asia and South acific Design Automation Conference (ASP-DAC
2005)国际学术会议中获得Best Paper Award。这是自ASP-DAC会议举办以来大陆论文首次获奖。
论文,论文,还是论文
王垠:说到paper我就痛心。我的方向上我至今还没有看到几篇我觉得像样的文章。我主要进行集成电路布线算法的研究。看起来高深,其实是很简单的问题,一个平面上有一些点是电路里的电极,现在需要用铜线把它们连起来,怎么样让连线的长度或者时延最短?
我的导师就是以前写了一篇这样的paper发到IEEE
transactions。已经毕业的一个师兄就在他研究的基础上修改来修改去,发了好几篇paper。英文的不够还翻译成中文,投到国内的期刊。后来一个师姐又在这个师兄的基础上进行修改,又发了好多篇。可是在我看来,他们的论文纯粹就是炒冷饭,没有什么创新。 >>>详细
突然间醒悟,paper的奥秘
清华研究生谈论的重点是什么?是paper。吃饭的时候谈,喝茶的时候谈,睡觉的时候也谈。隔壁的同学在进校第一年就为paper惶惶不可终日,说:"你知道吗,他们要求我们发SCI,怎么办呢?我几个师兄都是因为没有paper延期毕业的。"这恰好就是那个为后10%淘汰惶惶不可终日的同学。他的老师是个院士,可是他在手下就干一些写word文档之类的杂活还忙得要命,根本没有时间思考问题。>>>详细
该清醒了,博士无产阶级
学校没有能力评价学生的水平,就拿文章数来衡量。这样的毕业标准造就的是怎样的学生,怎样的实验室呢?难道导师真的没有能力判断paper的好坏吗?有些是,但是有些不是。即使他知道你的论文没什么价值,也会叫你发表。paper可以带来基金,可以在美国买小车洋房,没有基金就让学生干活吧。一个月几百块钱吊着一条命在那里为你拼命,谁叫他们想要那个博士学位呢!>>>详细
告别清华的博士学位
我准备放弃清华的博士学位,出国找个好老师,进行真正的研究。博士第4年了,做出这样的决定真是不容易。有人告诉我不要放弃,你知道有多少人正在羡慕你?你知道一个清华的博士学位有多么值钱吗?但是我不能这么沉默下去了! >>>详细
清华梦的“诞生记”
小时候,妈妈给我一个梦。她指着一个大哥哥的照片对我说,这是爸爸的学生,他考上了清华大学,他是我们中学的骄傲。长大后,你也要进入清华大学读书,为我们家争光。我不知道清华是什么样子,但是我知道爱迪生和牛顿的故事。清华,大概就是可以把我造就成他们这种人的地方吧。我说我要实现这个“清华梦”。这就是清华梦的诞生。
研究,让我其乐无穷
我的生命中出现了这样一门课程。它改变了我对老师的看法,让我觉得上课原来也可以如此有趣。这就是计算几何。上课的人很少,只有十来个人。因为听说这门课很难,很多同学都没有选。但是我就是那种知难而进的人。老师上课的方式跟别的课程很不一样,大家坐在一个小教室里,老师有精美的幻灯片,有动画,不时还冒出大哲学家的名言。
说真的,这门课太有趣了,我就只逃过一次课。但是还是有时候人数不到一半,因为其他课程压力太大,有人都去复习别的课程了。但是邓老师从来不点名,还对逃课的同学表示同情。还问我们在座的有没有其他课特别紧张的,下次课可以不来。真是让人感动。
出名是因为一篇《完全用Linux工作》
我写了一篇文章叫做《完全用Linux工作》,放在主页上。矫枉过正,确实写的有点偏激,结果引起网上linux界轩然大波。后来我又发现几乎全校的论文都是word排版的,那些公式质量太差,看起来头痛,才发现很多学生害怕数学的原因之一。所以又写了文章宣传TeX,希望中国产生更多漂亮的数学书。
这下子我出名了,真没想到,出名不是因为我的研究成果,而是因为这些业余的东西。我起初不希望我因此出名,但是看到旁边的人都用上了TeX,我觉得我还是做了一件好事,至少让论文看起来漂亮了一些。>>>详细
187
17王垠文中称,导师招学生,是为了“财源”,而paper可以带来基金。他说,自己厌烦了国内所谓的“学术”。准备放弃清华博士学位,出国找好老师,进行真正的研究。随后记者在BBS上看到一自称是王垠同一教研室的人发的帖。在该帖中,作者对王垠成就是否是其个人努力的结果进行了质疑:“他利用了本来应该用来给教研组工作的时间和精力来建立自己的名声,从很大程度上说他的知名度是依赖于清华给他的宽松环境。
完全用Linux工作,抛弃windows
我已经半年没有使用Windows的方式工作了。Linux高效的完成了我所有的工作。
GNU/Linux不是每个人都想用的。如果你只需要处理一般的事务,打游戏,那么你不需要了解下面这些了。
我不是一个狂热的自由软件份子,虽然我很喜欢自由软件。 >>>详细
王垠:我安静的等他说完。真像是一场闹剧,一场梦。他平息下来之后,我说了一声“再见”,然后默默地走出了办公室。你们要退学申请?这里就是我的退学申请。
187
17对于王垠来说,能够摆脱这种环境,到国外去追求理想,那是太好不过,但是大多数人还是不得不面对毕业论文的发表问题。很无奈,但不得不。假使我们也因此取消论文这一硬条件,让导师决定你能否毕业,那么又会有更多新问题出现,比如只要和导师搞好关系,即使一头猪可能也能拿到博士学位,如果得罪了导师,估计在中国的环境下,爱因斯坦估计都不一定能拿到学位哦。所以个人认为,在没有更好,更合适的办法出来前,论文作为硬条件还是必要的
187
19化成x的2/5次方,指数乘到系数上,再把指数减1
187
195倍根号下X的平方怎么变成5分之2倍X的负5分之3次方?有什么公式转换么?
187
19楼主表述是否有问题哦,看样子大概是 x的平方在开5次根号 吧,求一次导数就可以了
187
19咋求呢?因为本人已经不接触数学很多年了,早就把原来学的忘了,请高人指点一下
18721用特征函数证明一下看.用反证
18721Show that it cannot be the case that U=X+Y is uiformly distributed on
[0,1] and Xand Y are independent and identically distributed. You cannot
assume X and Y are continuous. It should be applied to all cases.
18722汪林的<<实分析中的反例>>,科学出版社,以及
<<分析中的反例>>(美)盖尔鲍姆(B.R.
Gelbaum),(美)奥姆斯特德(J.M.H. Olmsted)著 上海科学技术出版社
18722多谢了
18722我想买本《实分析的反例》,但不知道作者,出版社等一些信息,希望知道的朋友可以帮助一下。谢谢!
18722倒想看看
18722
| 引用 (primeshu @ 2005年09月28日
16时39分) |
汪林的<<实分析中的反例>>,科学出版社,以及
<<分析中的反例>>(美)盖尔鲍姆(B.R.
Gelbaum),(美)奥姆斯特德(J.M.H. Olmsted)著 上海科学技术出版社
|
<<分析中的反例>>(美)盖尔鲍姆(B.R. Gelbaum),(美)奥姆斯特德(J.M.H. Olmsted)著
上海科学技术出版社
这本书可能已经没有纸质的买了,不过可以复印,网上有电子版的。
18722好象《拓扑空间中的反例》还有的买。
18723设f(x)在[a,b]上定义,对于任意闭区间[c,d]包含于[a,b],对介于f©与f(d)之间的任一常数l,方程f(x)=l有且仅有有限个解,证明f(x)在[a,b]上连续.
18723这个就是应用一下定义就可以了:post-38-1127873572.gif
18725如果
x
∈R
n,G(x)=(x⋅∇u)∇u-12|∇u|
2x+1p|
u|
p|
x|
a+n
-2n
u∇u
,那么
div
G(x)=?
18725怎么是乱码啊?有时行有时不行,郁闷
18728请问各位硕博:
随机过程中,小概率事件发生以后的随机过程是怎么样的?是否有人研究?
查找什么资料?
请各位帮忙!
可以通过电子邮件联系.
18731[转帖]全文下载的行业标准网站
全文下载的行业标准网站
主要是:CB、JB、HG、SY等
http://irnfc.hbsti.ac.cn/biaozhun/index.html
18731不错,谢了!
18731rhf i gc ka ?
18734利用琴生不等式
18734若f在[a,b]上连续,且f(x)>0,则ln(

f/(b-a))>=

lnf/(b-a)
18735设一军列有装备m种。其中M1有A1件;M2有A2件;M3有A3件………
Mm有Am件。送到装车线上的铁路平车,依次为K1型有B1辆;K2型有B2辆……
Kf型有Bf辆。定义:
Xij为第i种装备使用第j种装法的次数。P(i,j)为第i种装备在j种装法下所装载的件数。
对装备的约束条件:
∑∑P(i,j)Xij=Ai
对铁路平车的约束条件:
X11+X21+……………………………………………+Xm1<=B1
X12+X22+……………………………………………+Xm2<=B2
……………………………
X1f+X2f+……………………………………………+Xmf<=Bf
非负及整数约束条件:
Xij>=0且Xij为整数
(i=1,2……m;j=1,2,…n)
目标函数:∑Xij=min
请问如何用VB编程解决这个具体问题。
请VB高手帮帮我,谢谢!
18736需要规划的保障资源的种类有:保障设备\供应保障\训练及训练保障\技术资料
某一项如何作用于保障效果的模型,就是单位资金投入到其中一项所产生的效益问题?
我已经被这个问题弄晕了!
求各位高手能予以援手!
18737需要规划的保障资源的种类有:保障设备\供应保障\训练及训练保障\技术资料
某一项如何作用于保障效果的模型,就是单位资金投入到其中一项所产生的效益问题?
我已经被这个问题弄晕了!
求各位高手能予以援手!
18739有数学分析的视频么?复旦大学数学系那版本的!谢谢拉各位老师们
18740北大数学力学系那版本的
18740
http://210.45.208.115/gdds/index.html到这个上去下载吧!
18741北大的数分教案
18742让我想象
18742掷一颗匀称的筛子n次,设M与m分别表示所得点子的最大值与最小值,求P(m=2,M=5).
高手指教谢谢
18742顺序统计量的基本内容,你的概率书上应该有
18742汗.能不能稍微具体点啊,我还是不会,请继续指教,谢谢
18743有两个函数,分别是
f(x,y), g(x,y)
想直接用matlab对 函数 h(f,g) 进行运算,比如说对 x
求导
该怎么做呢?
找了半天帮助命令,也不得要领.
18743如果进行符号运算推荐使用Maple,毕竟符号运算不是Matlab的强项
如果是纯数值运算且对结果精度要求不高,就按差分计算好了
如果对结果要求较高又非用matlab不可的话可以看一些matlab的工具书,如《Matlab命令大全》和《Matlab工程数学应用》等等,上面讲的很详细
18743这是我用matlab做的一个例子,可以参考一下。总之结论是matlab中的符号计算表达方式还是和matlab的数值计算表达方式一样的。要显示地表示f(x,y),
g(x,y), h(f,g),还是要mathematica或者maple这样的专业符号计算软件
>> syms x
y
>> f(x,y)=x^2+x*y+y^2
??? Conversion to double from sym is
not possible.
>> f=x^2+x*y+y^2
f =
x^2+x*y+y^2
>> g=x^3+2*x^2*y-y^3
g =
x^3+2*x^2*y-y^3
>> h=f*g-f+g
h =
(x^2+x*y+y^2)*(x^3+2*x^2*y-y^3)-x^2-x*y-y^2+x^3+2*x^2*y-y^3
>> diff(h,x)
ans =
(2*x+y)*(x^3+2*x^2*y-y^3)+(x^2+x*y+y^2)*(3*x^2+4*x*y)-2*x-y+3*x^2+4*x*y
>> diff(h,y)
ans =
(x+2*y)*(x^3+2*x^2*y-y^3)+(x^2+x*y+y^2)*(2*x^2-3*y^2)-x-2*y+2*x^2-3*y^2
18744按照书上介绍的先建mmff1函数然后再添加到M-file function name 文本框中为什么总是出错?
Undefined
variable 'mmff1' or class 'mmff1.m'.
Error in
==>
C:\MATLAB6p5p1\toolbox\fuzzy\fuzzy\evalmf.m
On
line 64 ==> y = eval(evalStr);
Error in ==>
C:\MATLAB6p5p1\toolbox\fuzzy\fuzzy\plotmf.m
On
line 62 ==> y(:,mfIndex)=evalmf(xPts,mfParams,mfType);
Error in
==>
C:\MATLAB6p5p1\toolbox\fuzzy\fuzzy\mfedit.m
On
line 1156 ==>
[xAllMFs,yAllMFs]=plotmf(fis,varType,varIndex,numPts);
Error in
==>
C:\MATLAB6p5p1\toolbox\fuzzy\fuzzy\mfedit.m
On
line 680 ==> mfedit #plotmfs
??? Error while evaluating patch
ButtonDownFcn
18745欧拉问题。
18745
有一所监狱其中的牢房被布置成8*8的矩形框的样式。每间牢房都有上下左右四扇门与上下左右的牢房相通。监狱的狱典长对一名关在角落牢房里的罪犯说:“如果你能通过监狱里的每间牢房且不能两次进入相同的牢房到达与你相对的那个角落的牢房就释放他。”请问怎么样才能帮他获释?
小弟愚顿,百思不得其解,请网友帮我解答一下。(画一下路线图)
18745这的确是一个欧拉问题
但是并不只仅仅是图论问题
可以用递归法编写程序求解
不过时间与空间的开销会比较的大
18749我今天也上了高数的函数极限,和你一样学生基本不懂。作业一塌糊涂,很多年了都是这样过来的
18749但我们教学主任说,外系的数学也就是指高数是只重计算技巧而不重


证明的。我都不知该怎么讲,习题有很多证明,而例子又没多少,而且又没有个大纲可以参考。请问你们讲课有大纲吗?没有的话,以什么为标准?
18749我的意见:讲
18749慢慢来。主要教会学生这么求N?要说清楚几何意义
18749那么我想问一下,上高数用不用讲很多的


语言,对他们怎么要求,书上没怎么用,但是习题却有很多要用它证明的,那怎么办?希望各位大虾讨论!
18749我今天上了三节的高数,是讲数列的极限,就是用定义证明数列的简单极限,又讲了数列收敛的性质。可是上下来,学生们普遍反应听不懂,各位说说该怎么讲???我这里先谢谢各位了!!!
18749那该怎么办呢?
各位大虾怎么只看不留言啊!!
18749想办法,由浅入深了。必须开头让学生弄懂,讲慢点儿都可以。作业题要及时处理的。
18749我今天也讲了数列的极限,感觉也是学生发蒙.回想我上学时,也是不懂,但是自己学了一段时间后也明白了.所以学习还得靠自己.就是得靠学生他们自己努力才行!
18749要把学生讲的都明白,基本上是不可能的,定义给他,然后讲题吧,先让学生会做题,再让他们自己慢慢去理解吧,
18749我这里还行,让他们依样画葫芦,六成的同学没问题。
先让他们理解什么是“无穷小”(按照小孩子比大比小的游戏来理解)
把数列极限的几何意义讲清楚(数轴上的点;作为整标函数的图象)
最后把定义的几个要素说清楚。
个人理解,欢迎讨论。
18749我马上就要讲完第一章函数与极限,可是学生的反映确实不是那么理想,主要问题也是集中再极限概念上,他们总觉得像高中那样,不管极限为什么是那个样子,只要会求就可以了,因此在心理上就有抵触情绪,试问这样的心理状态又怎么能学的好,还有一些学生认为这样的问题(极限定义证明)讲那么长时间实在无趣,都已经放弃定义的证明了,而跑去后面先自学去了,实际上如果极限定义不明确的话,后面的很多知识和概念在理解起来都是有困难的,真的是不知道怎么办才好啊!
18749真的有这么夸张吗?
我觉得要想让学生明白,首先要自己很清楚的知道这部分的内容,可以不客气地说,讲这一部分,需要老师在讲课的时候不需要看课本,也不参照讲义,全凭自己的理解(当然必须正确),这当然有一定难度,尤其对年轻老师,。其次,讲这种抽象的问题,条理性特别重要,一旦条理性失去,可以说这节课你白上了。个人觉得这一部分最好先让学生在头脑之中形成一个模块,就是熟练掌握证明语句,其实就那几句话,实在不行就让他们背!
18749有道理,也许真的是我自己没有把问题讲透,我刚刚工作没有多久,所以对于课程的关键之处可能没有吃透。
18749这个内容本来很抽象,我想学生听不懂是正常现象.
我讲课的时候,一般把思想讲的尽可能清楚,例如讲极限的概念,关键在于我们如何定义极限,也就是需要给定一个数列(或函数)与一个常数的接近程度,
记epsilon ,这和人的主观程度有关,因此既有任意性也有确定性,就像物理中定义的误差范围一样.......等等.仅供参考,我的个人意见.
18749唉,同感,现在学生的思想越来越僵化,稍微有点变化就跟不上,一句话,都是应试教育的结果...
18749极限的概念是很抽象的,还有就是学生在以前的数学思维都是静态的,而极限是一个动态的概念,所以思维方式的转变也是一个主要的因素.
根据我教学两年的经验,除了土木系和物理系的学生,其余专业都不讲证明,也不要求学生用定义证明,因为这个门槛实在是太高了,等讲了导数以后,学生已经习惯了这种动态的思维方式以后再适当的讲讲效果还是不错的.
over
18749我上了两年高数了,我觉得你上数学课.不能只讲数学.你有时要用人文科学的例子去比喻数学.虽然在这种情况下的例子不一定严格.另外以前西师陈重穆老先生的观点可以用的.那就是做了再讲.先让学生从直观上做一些练习.有一定的熟练程度后再说严格的定义.这种观点在欧阳光中的数学分析中有一定的体现.我对学生说的是.第一遍你可以不懂,第二遍你可能还是不懂.但首先你要会模仿.在模仿中体会.
18749我上了两年的经济数学,对此深有体会,经济类专业对数学的要求比起理工科的来,难度又降低,极限的定义对于他们来说理解起来更是困难,有些课本根本不用


来叙述,我的方法就是淡化极限概念,重视极限的计算。
18749
| 引用 (mathcontro @ 2005年11月03日
22时00分) |
| 我上了两年高数了,我觉得你上数学课.不能只讲数学.你有时要用人文科学的例子去比喻数学.虽然在这种情况下的例子不一定严格.另外以前西师陈重穆老先生的观点可以用的.那就是做了再讲.先让学生从直观上做一些练习.有一定的熟练程度后再说严格的定义.这种观点在欧阳光中的数学分析中有一定的体现.我对学生说的是.第一遍你可以不懂,第二遍你可能还是不懂.但首先你要会模仿.在模仿中体会. |
这应该是一种办法。
要让学生认识到,
1.
在大学之前的中学数学教育基本上都是前近代数学的内容。
2.
极限概念基本上可以说是近代和古典数学的分水岭。掌握了极限概念,就从思想上跨入了现代数学的殿堂(哪怕只是第一步)。
3.
现代极限的概念实际上是众多数学家几十年合力完成的结果,这些概念在当时即使是最伟大的数学家都会在这里那里搞错。(安慰学生即使一时不能领会也不要灰心)
4.
告诉学生,学习前人的成果,其实是最有效益的一件事情,因为这相当于用一两个星期,甚至几个月就可以掌握前人包括天才花了几百人年才完成的工作。
5.
学习不要怕难。容易的东西不值得上大学来学。对于一个概念的掌握,有“渐悟”和“顿悟”之分,但都需要持之以恒。
6.
如果文字暂时不懂,就强记背诵。多做练习,模拟书上的做法。光在岸上学游泳是不行的,扔到水里呛两次水反而学得更快。(因为人更容易通过互动而不是一味被动来学习。)
在教学上,我认为应当深入浅出地介绍极限的思想,而不是一味纠缠于
ε
-δ 的概念。
我个人的理解,极限概念对于初学者的难度在于它那一堆绕口的复合句条件:"对于...存在...使得..."每一个子句的意义都需要理清,再在头脑中组合起来理解,对于初次接触的人确实很难。因此要求学生在短时间内掌握有些困难。极限的思想是数列对一个数的无限逼近,而那些复杂的形式定义有三重目的:
1.
绕开“无限”这个词;
2. 严格地数学地刻划“逼近”;
3.
使得验算成为可能(虽然几乎没人用原始定义来确定极限的存在性).
另外,我觉得概念的讲演应该多用实例,而且最好每个单独的概念用一个实例(正例或者反例)突出。
比如讲对极限的无限逼近,不要光用什么{1/n}这种平凡的例子(学生会觉得没用),使用一个有理数序列逼近无理数(甚至超越数)的例子应该更为有力。
18749如果仅听一次课就能让绝大部分学生理解“极限的定义”,可以说,你可以不用再上课了,因为你的学生对高数的学习已经没有障碍了!
18750大家看看附件里的文章罢
虽然与工作关系不是很大 还是很有参考价值的
对准备进行学术研究的同学
会有些许的帮助的post-71-112789
1940.ibf
18750我也写过长的文章.怎么说也顶一下.但我不理解搞研究怎么会是一种合作讨论.
18750有意思,这个社会就是这样捉弄人,我想读清华还考不起,还有人要退学,唉,社会呀,真不公平呀
18750
引用 (yuxianzhi @ 2005年10月21日
17时37分) |
|
有意思,这个社会就是这样捉弄人,我想读清华还考不起,还有人要退学,唉,社会呀,真不公平呀
|
是啊
人比人气死人
18750了解了,中国5000年封建思想还在持续延续中
悲哀。。。。。
18750我相信许多人的聪明,但那篇文章我觉得是有水分的
18750
| 引用 |
| 有意思,这个社会就是这样捉弄人,我想读清华还考不起,还有人要退学,唉,社会呀,真不公平呀
|
这正是我想说得
18751我06年想考研,估计在北大考(不是考北大的研究生),试题是北大出的!
包括数分和高代!
两门课合成一张卷,150分!
我想请教一下各位师兄,老师
给点建议,觉得很迷茫!
我本科时学的不是很好!
18752有没有人对计算机网络的入侵检测理论与技术感兴趣.比如对IDS各方面的研究内容.
应该不一定都基于密码学和密码协议吧.
18752关注。。。
18752计算机网络的入侵检测也不容易
用的比较多的方法比如数理统计学,随机过程,人工神经网络,数据挖掘...
总之,用了很多种数学和计算机科学的方法,不过效果都很难令人满意.
想想也是,只要几台计算机物理上连接,高明的黑客就总能找到入侵方法,
你用什么样的模型和算法去监测他?用一个有效的算法去检测出各种各样的黑客的五花八门的入侵,何况黑客还是有智商的人,他会和你的算法斗智!.---寻找这样的算法是最难的,至于找到了模型和算法后,再根据模型和算法写出监测程序,那就非常简单了.
18752和寻找更优更有效的入侵检测算法相比,写程序的难度只是高阶无穷小,因此完全可以忽略不计.
18752最近在看一本相关内容的书,很多内容是讲snort的,但是看得有些蒙蒙的,可能要结合实际操作比较好理解吧.
18753subjective probability?主观概率?
btw:我也是新手,有错勿怪
18753各位老师好,初来乍到,想请教一个问题。因为在工作过程中遇到一个术语,personal probability,不知道该如何翻译?谢谢!
18754有人对"对等网络"(P2P)感兴趣吗?
有人对网格计算感兴趣吗?
计算机网络与分布计算的面太宽,一个人学不完,希望能讨论一下,特别是研究方向的前沿.有哪些进展?有哪些算法与协议?
18754现在好像比较热衷于多方安全计算,在计算中涉及到很多密码协议。
18754楼上说到网络安全,不错不错,不知道多方安全计算是否有安全协议,是否经过形式验证,有空能不能介绍一下.
听说QOS和网络安全都很热,我最近对入侵检测的形式化技术有兴趣,对P2P也有兴趣,可惜学不完.
18754安全多方计算是一种分布式协议,在这个协议中n个成员P1,P2,...,Pn分别持有秘密的输入X1,X2,...,Xn,试图计算函数值(Y1,Y2,...,Yn)=f(X1,X2,...,Xn)。其中f为给定的函数,安全的含义指既要保证函数值的正确性,有不暴露任何有关各自秘密的输入信息。
常用的安全多方计算协议主要有:
基于OT的安全多方计算协议,可验证的秘密共享子协议,基于同态加密的计算协议,基于mix_match的计算协议。
安全多方计算发展方向:
一般化的安全多方计算协议的裁剪
安全多方计算的形式化定义
安全计算协议的构造方法
安全多方计算协议生成器
18755@max 函数一般都会导致模型求解很慢,或者找不到解
我一般是不用的,用一个足够大的固定值作为上限代替它就是了
18755MODEL:
SETS:
Aux_const/1..5/: B;
SERIES/1..500/: U,
ZNORM,
Demand, Parts, Labor,
Profit;
Aux_var(SERIES,
Aux_const):Y;
ENDSETS
DATA:
average_Dem=15000;
dev_Dem=4500;
Parts_min=800; Parts_max=1000;
Price=2490;
Fixed_cost=10000000;
B=43,44,45,46,47;
ENDDATA
!
Generate a series of Normal, Uniform and
Discrete distributed random
variables ;
! First uniform is arbitrary;
U( 1) = @RAND(
.1234);
! Generate the rest recursively;
@FOR( SERIES( I)| I
#GT# 1:
U( I) = @RAND( U( I - 1));
! Generate some...;
@FOR( SERIES( I):
! Normal deviates...;
@PSN( ZNORM( I)) = U(
I));
! ZNORM may take on negative values;
@FREE( ZNORM( I))
);
! Demand in first year;
@FOR(SERIES( I): Demand( I)=
dev_Dem*ZNORM( I)+average_Dem);
! The cost of parts in first
year;
@FOR(SERIES( I): Parts( I)=
Parts_min+(Parts_max-Parts_min)*U(I));
! Labor ocst in first
year;
@FOR(SERIES( I): Labor( I)=
@SUM(Aux_const( J):
B(J)*Y(I,J));
Y(I,1)=@IF( U(I) #GE# 0 #AND# U(I) #LT# 0.1, 1, 0);
Y(I,2)=@IF( U(I) #GE# 0.1 #AND# U(I) #LT# 0.3, 1, 0);
Y(I,3)=@IF( U(I)
#GE# 0.3 #AND# U(I) #LT# 0.7, 1, 0);
Y(I,4)=@IF( U(I) #GE# 0.7 #AND#
U(I) #LT# 0.9, 1, 0);
Y(I,5)=@IF( U(I) #GE# 0.9 #AND# U(I) #LT# 1.0,
1, 0)
);
! Profit in first year;
@FOR(SERIES( I):
Profit( I)=
(Price-Labor(I)-Parts(I))*Demand(I)-Fixed_cost;
@FREE(
Profit( I))
);
! Other outcomes in first year;
Profit_mean=@SUM( SERIES( I): Profit( I))/@SIZE( SERIES);
Profit_dev=(@SUM( SERIES( I): (Profit( I)-Profit_mean)^2)/@SIZE(
SERIES))^(1/2);
Number_loss=@SUM( SERIES( I): @IF( Profit(I) #LT# 0,
1, 0));
Prob_loss=Number_loss/@SIZE( SERIES);
Profit_max=@MAX(SERIES( I): Profit( I));
Profit_min=@MIN(SERIES( I):
Profit(
I));
END
在以上程序中,最后四行之任意一行加入就没可行解了。怎么回事?
这个程序是分析风险利润的模拟程序。@MAX应该用对了吧。
18756作变换!
18756楼上的会做吗?给个具体的解答吧!谢了
18756我还是慢了,:)
还是都发上来吧:post-38-1127914604.gif
18756第一题post-38-1127913941.gif
18756虽然没有怎么看懂,不过还是谢谢!
18756很是郁闷,好多做不到的!post-38-1127901135.gif
18757反证法不是显然的么,另外此命题可作很重要的推广
18757
| 引用 (流形 @ 2005年10月09日
20时37分) |
|
反证法不是显然的么,另外此命题可作很重要的推广 |
在连续统假设之下显然。
18757
| 引用 (yeslijing @ 2005年10月10日
20时42分) |
这里应该不需要用到连续统假设吧
cardianl的加法应该不需要连续统的保证吧
|
要的不然逻辑不通
18757可以用连续假设证明吗?
可数基数与连续基数之间是否有其他基数不还没有被证明吗?
18757这里应该不需要用到连续统假设吧
cardianl的加法应该不需要连续统的保证吧
18757呵呵,多谢提醒.
没怎么考虑
记得在集合论上有类似的定理
18757证明: A 并 B 的基数为 c ,则 A
,B 至少有一个基数为 c .
18757FANZHENFA
18757提示:
将A并B看作全平面,考虑A和B在横轴和纵轴的投影。
18757这样说,可以吗?post-21-1128828789.gif
18757大学生就是比中学生强
18757
| 引用 (luowan2000 @ 2005年10月09日
11时33分) |
| 这样说,可以吗?
|
Good. 这正好是周民强的实变的第3版的第一章例
19
证明简直一模一样
18757
| 引用 (luowan2000 @ 2005年10月12日
12时07分) |
可以用连续假设证明吗?
可数基数与连续基数之间是否有其他基数不还没有被证明吗?
|
可以用.
甚至可以将连续统假设放到ZFC公理系统中,以丰富我们的数学.
连续统假设与ZFC公理系统是相互独立的,已经由美国数学家科恩证明.
18757
引用 (高来源 @ 2005年10月
19日
14时12分) |
可以用.
甚至可以将连续统假设放到ZFC公理系统中,以丰富我们的数学.
连续统假设与ZFC公理系统是相互独立的,已经由美国数学家科恩证明. |
我的意见是:
对于连续统假设的使用还是慎重点好.
而且对用上连续统假设就“丰富”了数学的观点,也不敢苟同.
就像一定要用“第五公设”,就不可能出现非欧几何一样,
很可能给自己局限在一个更窄的范围里面,能说是"丰富”吗?
很显然,如果我们在欧氏几何中证明的某个定理时没有用到
“第五公设”,那么这个结论就更具有普适性。
因为这个命题不需要连续统假设,所以
即便是在连续统假设不成立的公理系统中,结论也是对的.
18757
引用 (mazl @ 2005年10月
19日
21时01分) |
引用 (高来源 @ 2005年10月
19日
14时12分) | 可以用.
甚至可以将连续统假设放到ZFC公理系统中,以丰富我们的数学.
连续统假设与ZFC公理系统是相互独立的,已经由美国数学家科恩证明. |
我的意见是:
对于连续统假设的使用还是慎重点好.
而且对用上连续统假设就“丰富”了数学的观点,也不敢苟同.
就像一定要用“第五公设”,就不可能出现非欧几何一样,
很可能给自己局限在一个更窄的范围里面,能说是"丰富”吗?
很显然,如果我们在欧氏几何中证明的某个定理时没有用到
“第五公设”,那么这个结论就更具有普适性。
因为这个命题不需要连续统假设,所以
即便是在连续统假设不成立的公理系统中,结论也是对的.
|
支持
18759函数f(x)在(a,b][b,c)上都一致连续,那么他在(a,c)上也一致连续,这我们知道,现在如果f(x)在(a,b),(b,c)上都一致连续,那么他不在(a,c)上
一致连续,怎么早一个反例呀,清高手指点
18759随便一个分段函数就可以了把
18759就象你说的,在b的一个小领域内不一致收敛即可.
18759
引用 (shanmao10 @ 2005年09月28日
19时08分) |
|
函数f(x)在(a,b][b,c)上都一致连续,那么他在(a,c)上也一致连续,这我们知道,现在如果f(x)在(a,b),(b,c)上都一致连续,那么他不在(a,c)上
一致连续,怎么早一个反例呀,清高手指点 |
这个题目好像只能在b点不连续的函数才可以吧
否则在b有个闭邻域连续故一致连续
然后三段一看在(a,c)上必然一致连续的
18760请问一下,保送研究生可以跨专业吗 ?多谢!!
18761自相似性与地震
摘自《基础科学动态监测快报》2005年7月15日 第14期
自相似性与地震
西班牙巴塞罗那自治大学的物理学家Alvaro
Corral发现了地震循环时间的结构,即连续地震之间的时间间隔,它类似于在临界点发生相变时物理系统的空间结构。研究显示,连续地震之间的时间间隔与以前地震之间的时间间隔相关。尽管这是统计结果,但却有利于改进风险估计。
自然界中的临界现象包括相变和自相似性.AIvaro Corral
发现了不同尺度的自相似性也发生在地震的时间间隔内。所以,如果我们注意观察大时间周期的给定区间内己经发生的不同地震,可以发现其聚集特性。最令人惊讶的是,如果关注一个较长的时间周期,地震群自身还会进行更大的聚集。任何时间周期、任何级别的地震无论发生在何处,都会出现同样的情况。所以,人们可以从临界角度,而不是从混沌的角度来考虑地震。
Corral
证实,作为地震之间的相关性,自相似结构的存在肯定非常重要,地震之间的间隔一定以非常确定的方式依赖于以前发生过的地震。但这并不表示当下一次地震将要发生时,研究人员能据此进行预测。不过明确的统计依赖性有助于改进风险估计。
18762章祥荪认为急功近利不利于交叉学科发展
章祥荪认为急功近利不利于交叉学科发展
(转自科学网)
十届全国政协常委、中国科学院数学与系统科学研究院研究员章祥荪日前在接受记者采访时说:“以前生物学主要是靠实验,在人类基因组测序完成后,生物学数据如洪水般涌现,生物学研究越来越需要借助数学方法和计算机工具来建立数学模型。数学在21世纪生物学的时代将发挥非常重要的作用,年轻的数学家最敏感,他们应该是数学与生物学交叉领域中最活跃的身影,可是据我所知,在今天的中国,转入生物学研究的数学家不仅人数非常少,而且主要是老同志,急功近利阻碍了交叉学科的发展。”
章祥荪目前主要从事应用数学、运筹学的研究。他说,随着人类基因组计划等大型国际项目的实施与迅速发展,分子生物信息研究成为一个研究热点和前沿领域。早在七八年前,国外就成立了与生物学交叉的研究中心,但目前这一领域在我国的发展仍然很慢,一是因为转入该领域的中青年数学家很少,二是因为经费投入不足。
中科院数学与系统科学院的生物信息学研究中心成立于2003年。章祥荪说,他们曾千方百计地鼓励中青年数学家投入生物学的研究,数学中的统计、优化理论和算法与生物学的关系很密切,这是一个非常有前途并有希望做出突破性工作的领域,但到目前为止,转到该中心工作的中青年数学家仍然很少。因为从一个成熟的学科转入新领域,要重新做学生,要花很大的精力从头开始学,还有风险,在短时期内不一定能出成果,需要提职称、申请经费的中青年同志可能承担不了这个风险;对老同志来说,已经没有了职称等的压力,所以反而容易些。此外,因为导师可以要求自己的博士生转入交叉学科领域,所以目前在该中心工作做得最好的还是博士生,但他们面临毕业后的问题。新领域相对于成熟领域来说,出成果慢一些,现在大学招聘教授都要考虑SCI论文的发表数量;另一方面,尽管我国现在有很多生物技术公司、制药公司,可是它们似乎没有这方面的人才需求,所以这些博士生的求职压力很大。
章祥荪认为,国家在鼓励交叉学科发展的同时,相应的科研教育制度改革也应该与时俱进,创造出有利于交叉学科培育和发展的环境。
(转自科学网)
18763不唯学历职称“小人物”也将问鼎国家科技大奖
不唯学历职称“小人物”也将问鼎国家科技大奖
申报国家科技大奖,一直是高学历、高职称科技工作者的“专利”。有技术创新的工人、推广农业适用技术的农民能不能评奖?在“两会”上,全国政协委员、科技部副部长程津培表示,从今年开始,国家科技进步奖有重大变化,不唯学历职称,技术工人、技术农民也能摘取国家大奖。
程津培说,国家科技进步奖在应用推广科技成果方面发挥了重要作用,成为目前成果最多、数量最大的国家科技奖项之一。但是,随着市场经济的发展,能够被市场认可的成果越来越多,政府奖励的激励导向应该有所调整。为此,科技进步奖除将科普成果纳入奖励范围之外,还将在创新和推广先进适用技术上做出突出贡献的“小人物”纳入国家科技进步奖。
“科技创新不仅仅是原始性的发明创造,还应包括量大面广的适用技术的创新及推广。”程津培说,科技创新在涉及广大工人农民群众的各行各业无处不在,像桥吊技术、农业大棚和地膜技术等先进适用技术的创新和推广,都对经济和社会发展起到了重大的推动作用。这些一线技术人员,在工作中有许多发明创造,有的已产生了重大影响,但是因资历、学历不够,或者成果的学术水平不高,被排斥在科技奖励之外。“此次对科技进步奖的奖励范围进行改革,突破了以往的成果和人才评价标准,更重要的是有利于激励和引导全民性的科技发明创造。”程津培说。
“对我国产业有重大影响的企业自主技术创新和技术的集成创新也将纳入国家科技进步奖。”程津培说,许多企业在自主创新道路上“披荆斩棘”,推动了行业的技术进步;有些创新在单项指标上可能并不突出,但把各种相关的单项技术创造性地集成起来,形成新的产业技术,可能对行业进步产生重大作用。为这些集成性创新设立相关奖项,也正在考虑酝酿之中。
程津培介绍说,今年中科院的院士评选工作与往年不同,被评价人除了提供论文发表、专利数量等文字材料外,还要陈述自己在该成果形成中的作用以及对学科领域的贡献和影响,以供评委全面准确把握情况。“定量与定性评价有机结合是今后科技评价改革需要关注的重要问题”,程津培说。
18763爱迪生是什么学历?
18763这是好变化,令人感到鼓舞啊!
18764关于自主创新和科研时间保障的几点思考
中国科学院 院刊
一 中科院如何能更好地自主创新
自主创新可有如下几种类型:
人对自然界的探索本性。王竹溪先生在其《热力学》引言中曾说,热力学是由于人对热的本质的追求。爱因斯坦的相对论是他从事科学活动中对自然规律的总结和发现。人的思维是自由的,没有任何功利目的的科学研究,是自主创新的最高境界。
大环境的压力。新中国成立以后,帝国主义的封锁以及中苏关系的破裂,迫使中国只能自力更生、独立白主地发展科学技术。中国的“两弹一星”就是自主创新的最好的例子。在当时的条件下,作为个人来说,他的聪明智慧不能随自己的意志,而要服从一个大的目标。
还有一种就是个人的压力。改革开放以来,在科学工作者中引入了竞争机制。如果没有申请到项目,就不能上岗,不能升研究员、教授。于是为了能申请到项目,就找一个容易做的热门小题目,每年出几篇文章,这样就能达到上岗、升教授的目的。这种情况下,就毫无自主创新可言。
现在为什么要强调自主创新?主要属于第二类的情况:大环境的压力。当前,中国经济、科学技术发展很快,引起了国际上的重视。西方国家开始警觉,认为高新技术输入中国太多,对他们造成了威胁。另一方面,西方国家的大企业出于商业利益也加紧了技术封锁。温家宝总理说过:“真正的核心技术是买不来的。只有拥有强大的科技创新能力,拥有自主的知识产权,才能提高我国的国际竞争力,才能享有受人尊重的国际地位和尊严。”
另一方面,基础研究方面的情况也不容乐观。改革开放20多年来,基础研究重大成果较少,相反炒作的东西很多,也就是昙花一现。国家自然科学奖一等奖多年短缺就是一个明证。国家科学技术最高奖都是奖励以前的成果。这是由一些科研管理的短期效应引起的,就是上一段的第三种情况。在基础研究方面要自主创新,做出国际上先进的成果,只有创造一个宽松的环境,达到上面所说的第一种境界。
如何自主创新?自主创新是每一个科研工作者义不容辞的责任。但是是否能做出自主创新的成果,还决定于集体、环境、政策等多种因素。作为个人来说,需要淡泊名利,安于寂寞,生活上不与别人攀比,静下心来做研究工作。
首先保证科研人员有足够的研究时间。在文化大革命以前,中科院有条规定:保证科研人员有5/6的工作时间,1/6用来政治学习。这一规定非常好,到现在还是有现实意义。请问现在的科研人员,不论是年纪大的,还是年轻的,你有5/6的研究工作时间吗?回答多数是否定的。有的甚至连1/6工作时间都没有。请问这样的条件下,能做出自主创新的工作吗?研究生倒是有5/6工作时间,但是他的基础不够。如果导师不过问,他们就“放羊”了,上网或学英语。
必须强调的是,要做出自主创新的成果,需要有长期的科学积累,厚积薄发。只有基础越深厚、宽广,才能做出自主创新的成果。中科院这几年为什么能承担并且比较好地完成国家重大任务,就是由于中科院的研究所自解放以后的几十年,几辈科研工作者辛勤劳动成果的积累。如果不看到这一点,就会产生急功近利的思想,以为只要给一大笔钱,就能出一个大成果,而忽视了长期、持久的科研投资,保持一支稳定科研队伍的重要性。特别是有些长远的科研目标,如生物科学、信息科学等,需要从现在就开始抓起,埋头工作十几年、几十年,最后才能达到高峰,而不能要求在某位领导的一个任期内就出什么大成果。
领导的指
18765极限式刚好就等于f(x)在0处的右导数
18765在附件中post-8-1127909224.gif
18765这我知道啊
现在就转化为求sinx+sin2x+sin4x+........sin2^nx=?????
哪位高手帮帮忙啊
18765f'(x)在0处连续,不就=f'(0)吗
18765好像不是吧
只知道右连续而已
18765f(x)导数处处连续
18766国际学术刊引用排行
国际学术刊引用排行 《自然》和《科学》分列第三和第四
转自《科学时报》
1994年~2004年国际学术期刊“引用总数”排行榜日前出炉。美国《生物化学杂志》以引用
1740902次位居首位。
美国科技信息研究所(ISI)日前公布了它所统计的从
1994年1月到2004年10月、11年间所有领域期刊被引用次数的排行榜。其中,内容以发表生物医学领域论文为主的美国《生物化学杂志》排名第一,综合类期刊《美国国家科学院院刊》以1338
191次排名第二;英国的《自然》杂志与美国的《科学》杂志则分别以1
190768次和1
17
1920次位居第三、四名。
基础生物医学领域与临床医学领域最具盛名的两种期刊——《细胞》、《新英格兰医学杂志》则分别名列第六名与第十名。不过从
1994年到2004年间,这两本期刊都仅仅发表了四千多篇文章,虽然在论文发表总数上远远低于其它期刊,但仍在“引用总数”中跻身前十名,这充分说明《细胞》、《新英格兰医学杂志》的单篇论文引用率是相当惊人的。影响力与《生物化学杂志》相近的《免疫学期刊》则排名第九。在物理领域方面,由美国物理学会出版的《物理评论快报》与《物理评论》分别以773
192次和600702次名列第五与第八。在化学领域方面,美国化学学会的《美国化学学会期刊》以606533次位居第七名。
一篇论文质量的好坏,可以根据该论文发表后被引用的频繁程度来判断,通常被引用次数越多的文章往往代表了其数据质量与原创性也相对较好,所以被引用文章越多的期刊则说明其在该领域具有较强的影响力。不过这项排名并不能完全评价期刊质量的优劣排名,毕竟期刊的发行间隔、每期收录的论文篇数各有不同。每期收录论文篇数较多的期刊可能因为较容易获得引用次数,而在统计总引用次数上具有优势。
18767修养的价值大于知识
人民日报 9月23日
知识与修养,是立身之本,也是成事之基。知识与修养的关系,是一个永恒的话题。
知识是人们在改造世界的实践中所获得的认识和经验的总和。观念形态的知识以语言、文字、图表等形式固定下来以后,就具有了可传承性和习得性,成为人们在生产、生活、工作中经常运用的一种工具。修养则指的是人们在思想道德、品质品格和精神境界等方面经过锻炼和培养而达到的一定水平。一个人的修养如何,一个重要的方面就是看他如何运用所掌握的自然知识和社会知识去对待生活、对待工作、对待他人。
知识就是力量。人类从刀耕火种、结绳记事发展到新科技革命和知识经济时代,知识发挥着重要的、不可替代的作用。作为自然知识重要表现形态的科学技术,在当代更发展成为推动社会进步的“第一生产力”。然而,人类知识的积累、科学技术的发展从来都具有两面性:运用得好,能为人类自身造福;运用不当或为恶人所用,则可能导致知识的“异化”,成为祸乱之源。例如,人类对核能的开发,开辟了利用能源的新途径;但核武器的出现,却使人类笼罩于自身制造的死亡阴影之下。近年来渐趋成熟的克隆技术,同样带有鲜明的双刃剑特征。就个人而言,知识既可以成为完善自身、服务社会的手段,也可能成为欺世盗名、违法犯罪的工具。目前社会上存在的形形色色的“学术腐败”、“高科技犯罪”,就说明了这一点。由此可以看出,仅有知识是不够的。不断提高思想道德修养,正确运用所掌握的知识,对现代社会的公民尤其是知识分子来说,显得愈益重要。从一定意义上可以说,修养的价值大于知识。
丰富知识是一种学识积累,加强修养是一种品德历练。这两者都是一个艰苦的过程。然而,人类社会发展进步的过程表明,同知识的获得相比,修养的提高似乎难度更大。大概也正是由于这个原因,我国古人十分强调正确处理修养和知识亦即“德”与“才”之间的关系。儒家所谓的“三不朽”:“太上有立德,其次有立功,其次有立言”,就把德行修养作为最高追求。北宋政治家、史学家司马光认为,“才者,德之资也;德者,才之帅也。”也就是说,才是德的基础,德是才的灵魂,二者密切联系,但德是第一位的。显然,这并不是简单地重德轻才,而是在深刻把握修养与知识的内在关系后得出的结论。在我国学术思想史上,固然有心口相背、言行不一的“乡愿”,但真正为后人所景仰的大家,肯定不仅仅是因为他们“才高八斗”、“学富五车”,而更多地是因为他们既具有广博的学识,又具有高尚的情操。
近现代以来,社会分工日趋复杂,学科分类日益精细。很多分支学科都从哲学这个大而全的“母体”中分离出来,分门别类地发展壮大。人们认识和改造世界的深度和广度、能力和水平,都远非古人可比了。知识的传承和拓展,也不再如亚里士多德所说的只是“闲暇者的一种嗜好”,而成为学者赖以谋生的一种职业。学科研究的精细和学术的职业化,也达到了前所未有的程度。与此同时,某些背离人们初衷的负面效应也渐渐显现:一些学者终其一生都在一个非常狭窄的学科范围内开展研究,对此之外的学问知之甚少。他也许能成为某个知识领域的“专家”,却未必具有必备的人文道德素养。学术职业化在客观上带来了工具理性与价值理性的紧张关系,知识和学问在一些人眼中只是一种“为稻粱谋”乃至沽名钓誉的工具,而消解了正义、良知等价值理性的神圣光环。特别是在有关机制制度不健全的情况下,学者工具理性的膨胀往往容易引发急功近利、剽窃造假、以“学”谋私等“学术浮躁”和“学术腐败”现象,进而导致学术研究和道德水平的双重退化。有鉴于此,许多有识之士大声疾呼:学术研究须注入人文关怀,确立学术规范,加强道德自律。这也提示我们:知识与修养的关系在新的时代条件下具有了新的内涵;“修养的价值大于知识”,应当成为一种共识。
18767修养与知识!!!
18767德才兼备,德是第一位的.
18768媒体总结近期中国教改动态 六大关键词成为热点
(转自中青在线)
2005年3月以来中国教育动态的6大关键词:
1、教育收费
中国社会科学院发布的《2005年社会蓝皮书》中的调查显示,子女教育费用在居民总消费中被排在第一位,超过养老和住房;而中国人民银行2004年第四季度关于“储蓄目的”的调查也显示,“攒教育费”是居民储蓄的首要目的,接下去是“养老”、“买房装修”和“预防意外”,比例分别为
18.9%、14.1%、11.8%和10.7%。让教育不再昂贵,成为许多学生家长对“两会”的期待。
2、教育公平
一份有关“中国高等教育公平问题研究”的报告,在两会上引起又一次震荡。报告说,“各地通过缴纳赞助费、择校费进入高中的学生比例几乎超过了10%,通过缴纳赞助费、择校费进入城市重点高中的比例达到25.2%。”报告同时显示城乡之间的巨大差距成为我国最主要、最显著的教育差距。对此,全国政协委员朱清时疾呼教育公平亟须制度保障。
3、大学生就业
迅速发展的中国需要大学生,而大学毕业生却就业困难。由于大学生就业率低而导致的新读书无用论,甚至已波及中小学教育发展。面对这个全社会关注的问题,全国人大代表们认为现在,高校的专业设置和专业调整往往不是面向市场需求,而是单纯地根据主管部门要求和自身师资条件,考虑社会需求明显不够。这必然造成有些专业的学生大量过剩,而现实急需的创新型人才和技能型人才却十分稀缺。这种结构性矛盾,已成为导致大学生就业难的重要原因。
4、农村义务教育
两会前夕,中国青年报、中青在线进行了一次网上调查,请网友选择“两会”期间关注的问题,农村义务教育是最受关注的问题之一。国务院总理温家宝在十届全国人大三次会议上作政府工作报告时表示,从今年起,免除国家扶贫开发工作重点县农村义务教育阶段贫困家庭学生的书本费、杂费,并补助寄宿学生生活费。到2007年在全国农村普遍实行这一政策,使贫困家庭的孩子都能上学读书,完成义务教育。与会的全国人大代表、政协委员报以热烈的掌声。
5、四、六级考试改革
教育部决定,从今年6月起,教育部考试中心正式参与大学英语四六级考试组考。与此同时,从2007年1月起,大学英语四六级考试将只接受在校生报名。今后,考试报名和考场安排、监考员培训、试卷接收、运送和保管由教育部考试中心负责,口试由大学英语考试委员会负责实施。考试中心将和省级教育考试机构共同承担组考任务。这是继上月宣布今年6月开始大学英语四六级考试将采用710分记分制,不再设及格分数线后的又一重大变革。
6、新版普通高等学校学生管理规定
教育部3月29日正式公布了新修订的《普通高等学校学生管理规定》,15年未修改的旧《规定》大变脸,体现出与教育法、高教法等有关法规的承接,学校规章逐步与相关法律“接轨”。针对考试作弊、大学生婚恋、学校自主处分权,被称为当前高校管理的“三大难题”分别作出了明确规定。据悉,这两个新版的规定将于今年9月1日起正式实施。
(转自中青在线)
18768实事求是吗!!!
18769西方理性数学的倡导者——泰勒斯
转自 数学中国
泰勒斯(Thales,前624-前547),古希腊学者,出生在小亚细亚的米利都城的一个奴隶主贵族家庭。家庭政治地位的显贵、经济生活的富足,泰勒斯均不屑一顾,而是倾注全部精力从事哲学与科学的钻研。在年轻时,他四处游学,到过金字塔之国,在那里学会了天文观测、几何测量;也到过两河流域的巴比伦,饱学了东方璀灿的文化。回到家乡米利都后,创立了爱奥学派,后成为古希腊著名的七大学派之首。泰勒斯素有“科学之父”的美称。
泰勒斯有名名言:“水是万物之本源,万物终归于水。”他否定了神创造一切的观点,开创了从世界本身来认识世界的正确道路。在科学上,他倡导理性,不满足于直观的感性的特殊的认识,崇尚抽象的理性的一般的知识。譬如,等腰三角形的两底角相等,并不是指我们所能画出的、个别的等腰三角形,而应该是指“所有的”等腰三角形。这就需要论证、推理,才能确保数学命题的正确性,才能使数学具有理论上的严密性和应用上的广泛性。泰勒斯的积极倡导,为毕达哥拉斯创立理性的数学奠定了基础。
泰勒斯在数学方面曾发现了不少平面几何学的定理,诸如:“直径平分圆周”、“三角形两等边对等角”、“两条直线相交、对顶角相等”、“三角形两角及其夹边已知,此三角形完全确定”、“半圆所对的圆周角是直角”等,这些定理虽然简单,而且古埃及、巴比伦人也许早已知道,但是,泰勒斯把它们整理成一般性的命题,论证了它们的严格性,并在实践中广泛应用。据说他可以利用一根标杆,测量、推算出金字塔的高度。
泰勒斯在天文学方面也曾有不同凡响的工作,据说他曾测知公元前585年5月28日的一次日全食。当时正值战争之际,泰勒斯向世人宣告,若不停战,到时天神震怒!到了那天下午,两派将士仍激战不已,霎时间,太阳在天空中消失,星辰闪烁,大地一片漆黑。双方将士见此景象,砍太阳神真的发怒了,要降罪于人类,于是立即罢兵休战,从此铸剑为犁,和睦相处。
另据传说,泰勒斯醉心于钻研哲学与科学,且可谓清贫守道,而遭市井嘲笑。他不以为然地说,君子爱财取之有道。他在对气候预测的基础上,估计来年油料作物会大丰收,于是垄断了米利都和开奥斯两地的所有油坊,到季节以高价出租。有了钱,科学研究可以做得更好。
这两则传说,如果是真实的话,那么泰勒斯确实不愧于其墓碑上所镌刻的颂辞:“他是一位圣贤,又是一位天文学家,在日月星辰的王国里,他顶天立地、万古流芳。”不过,这也是一则传说,因为泰勒斯生活的年代离我们太久远了,没有确切可靠的资料。
18771N人站成一列,重新站队时,各人都不站在原来的位置上,有多少种站法?
18771google搜索"错排问题"即可
没本教科书都有的例题了
18771为方面表述,将题目改为有n个顺序编号的位置和n个顺序编号的人,问所有的人都不站在对号的位置上有多少种排法。
记此排法数为I(n)。
现在看一下加如第n+1个人的情形。
先让他站在自己的第n+1号位置,然后对前n人n位的每一中符合规定的排发,让第n+1人依此与在第1,2,3,...n位置上的人换位,如此构成n*I(n)中符合规定的排法。
再让前n人中有1人站在自己号数的位置,其他人均不对位。对位的人依此是第1,2,..n人,故有n*I(n-1)种排法,然后让第n+1人与对位的人对调,有产生了n*I(n-1)种符合规定且与前面n*I(n)种一起两两不同的排法。
故有I(n+1)>=n*I(n)+n*I(n-1)
另一方面。对I(n+1)种排法中的没一种,将第n+1人与在第n+1位置的人对调,结果是前n位n人中,或无一对号,或有1人对号,故又有
I(n+1)<=n*I(n)+n*I(n-1)
两式一起变得
I(n+1)=n*I(n)+n*I(n-1)
即[I(n+1)-(n+1)*I(n)]=-[I(n)-n*I(n-1)]
令J(n)=I(n)-n*I(n-1)
则上式就是J(n+1)=-J(n)
故有
J(n)=-J(n-1)=J(n-2)=.....
=(-1)^(n-2)
*J(2)
=(-1)^n
*[I(2)-2*I(1)]
因I(1)=0,I(2)=1
故J(n)=(-1)^n
即I(n)=(-1)^n +
n*I(n-1)
=(-1)^n + n*(-1)^(n-1)+n*(n-1)*I(n-2)
......
=(-1)^n
+(-1)^(n-1)*n+(-1)^(n-2)*n*(n-1)
+.......+n*(n-1)*....*3*I(2)
后项变前项就得
I(n)=n!/2!-n!/3!+n!/4!.....+(-1)^(n-1)
*n!/(n-1)! +(-1)^n *n!/n!
18771这是概率中经典的匹配问题, 很多教科书以此作为例题, 比如
复旦大学出版社的新出的概率论书第
19页例1.2.11
18771这是一个经典的问题!!
18773请教高手!post-38-1127914653.gif
18773dsjflkpost-38-1127915463.gif
187732,变换t=1/x
18773这个证明方法好象有问题吧!
sqrt(sinx)<sqrt(x),所以1/sqrt(sinx)>1/sqrt(x),所以还是不能够证明啊
右边的可积,左边的不一定啊!
第二题变换之后又怎么考虑呢?还是不会!好象变了没有什么用!
18773楼主理解有错误
用的是阶的估计法
18773
| 引用 (footprint @ 2005年09月29日
00时23分) |
楼主理解有错误
用的是阶的估计法
|
什么意思?我没有搞懂,什么阶的估计法?没有听说过!
18774怎么放缩啊?>?post-38-1127914835.gif
18774
http://www.math.org.cn/forums/index.php?showtopic=14746
18775i为奇数,则f(i,j)=f(i-j-1,j+1)+ f(i-j-2,j+2)+ f(i-j-3,j+3)+ ……+f
[i-(i-1)/2,(i-1)/2]+(i-1)/2-j
i为偶数,则f(i,j)=f(i-j-1,j+1)+ f(i-j-2,j+2)+
f(i-j-3,j+3)+ ……+f
[i-(i-2)/2,(i-2)/2]+(i-2)/2-j
i,j∈N,且i≠0,
对于函数f(i,j)而言i>j,
若f(i,j)无法继续迭代则f(i,j)=0,
求f(i,0)=?
例子:f(15,0)=f(14,1)+
f(13,2)+ f(12,3) + f(11,4)+ f(10,5)+ f(9,6)+ f(8,7)+7
=1+3+2+5+1+4+2+1+7
=26
因为,f(14,1)=f(12,2)+ f(11,3)+ f(10,4) +
f(9,5)+ f(8,6)+5
f(12,2)=f(9,3)+ f(8,4)+ f(7,5) +3
f(9,3)=f(5,4)+1
f(11,3)=f(7,4)+ f(6,5)+2
f(13,2)=f(10,3)+ f(9,4)+
f(8,5) + f(7,6)+4
f(10,3)=f(6,4)+1
f(12,3)=f(8,4)+ f(7,5)+2
f(11,4)=f(6,5)+1
18777求:科学出版社黄玉民版的〈数学分析〉课后习题答案
请问哪位有科学出版社黄玉民版本的〈数学分析〉课后习题答案?
发一份给小弟好吗?急需。谢谢谢谢!邮箱:
[email]zlhahaha@eyou.com 再次拜谢!!
18777我也需要!!!
18777我也需要 谢谢!
pingguo-1001@163.com
18777这个东西……大家不用求了,我知道有三份:黄玉民老师那里一份,李成章老师那里一份,李军老师那里一份……
书上的题目还是建议大家做做,不论是正在上这个课,还是自学,或者是准备考研,书写的很经典,题目也是非常不错的,自己做了才是自己的知识。
有些题目过难的大家可以参考一下其他书,很多难一点的题目可以在别的书上找到,比如裴礼文的《数学分析中的典型问题与方法》。
我用的一本《数学分析题解精粹》(注意是数学分析,市场上更多的是一本微积分题解精粹,封面一样,内容可大不同),里面很多题是南开《数学分析》课后题,而且讲解不错,建议大家参考书,不过可惜内容只覆盖了上册的。
18777我也要!better1102@126.com 谢过了!
18777能给我一份好吗?邮箱:janh2813@sohu.com
18777可以给我一份吗?非常感谢!
邮箱地址:
deepfish2005@163.com
18777看来 只能是自己做了
18777我個人認為,這本教材是寫的最好的.......
18777请问《数学分析题解精粹》这本书是哪个出版社出的,作者是谁?按妳的描述应该不是钱吉林那本.
18778反证法,利用Riemann积分的定义就可以导出矛盾
18778小第对这道题目不知道
什么处理
各位博士,硕士
可以帮帮看看吗?
18778谢谢!哦,第一次发贴,忘了,是浙江大学的2004年数学分析
18778你能不能把题目贴出来啊??
18781数学科普作家来沪演讲
数学科普作家来沪演讲
城就数学的趣味进行演讲。去年,由中国科学院院士张景中主编的一套科普系列丛书“好玩的数学”由科学出版社出版。连续10个月的热销使数学家和科学普及作家们意识到孩子们对待趣味数学的期待,于是开始了这次全国巡回演讲。在现场,谈祥柏就“冰雹猜想”、“水仙花数”等话题与孩子们进行交流。话题看似枯燥,但百位中小学生仍然乐在其中。
18782
美国著名数学家学术界斗士泽奇-朗逝世
美国数学家泽奇·朗
国际在线消息:美国数学家泽奇·朗日前撒手人寰,享年78岁。纵观朗先生的一生,我们会惊奇地发现,这位倔强的数学家名声雀起的原因,并不仅仅局限在几何以及数论等学术性研究方面,对于政治以及社会公共事业的关心,也让人们感受到一位科学家的伟大人文关怀。
据《纽约时报》日前报道,朗生前曾经在美国最为知名的大学耶鲁数学学院担任了30年的教授工作,而逝世的消息也是由耶鲁大学数学学院发布的。
永远在质疑的朗博士
在忙忙碌碌的一生中,朗博士一直致力于对伪科学以及科学领域内的失真现象的斗争。朗曾经表示,科学领域内对于权威的盲目崇拜已经变得日益严重,任何相反的创新意见最终只能不了了之。和其他人不同,朗博士在对待伪科学的过程中使用了十分有趣的手段。在
1977年之后,朗采取了一系列激进的斗争方式。亲自撰写一篇篇战斗檄文,甚至购买报纸上的广告栏目,登载自己的研究报告,挑战那些所谓的不可动摇的权威力量。
与此同时,朗博士还积极地向美国的议会部门取得学术证明,并且将这一系列收集到的资料通过邮件的方式发送给其他科学家、媒体记者,甚至政府部门。加州伯克利大学数学教授肯斯先生表示:“朗先生将这些主要的文件展示给每一个人,让人们用自己的眼睛和头脑去思考,毫无疑问,这种做法收效非凡。”
朗所挑战的最为有名的教授,要数哈佛社会科学家萨谬尔·P·亨特顿了。亨特顿曾经在
1986年得到了美国国家学院院士提名。然而朗博士仍然表示,在亨特顿有关经济发展以及政治不稳定性的论文中使用的数学公式,属于“伪科学”,并且“毫无意义”。朗曾经尖锐地指出:“亨特顿的论文中使用了相似于科学的假相,但是其实质上什么都不是。”这也导致了亨特顿两次院士提名的最终落选。
在上世纪90年代中期,朗博士再次与艾滋病病理学怀疑主义者站在了同一战线,对目前公认的观点——艾滋病源于人类免疫能力缺乏,提出了质疑,表示目前所得的科学证据并不能在艾滋病与人类免疫能力缺陷之间建立强有力的联系。
实际上,一直到去世之前不久,朗先生都没有停止自己的战斗。在去世的前一周,朗发出了最后一封邮件,其中包含了亲自撰写的有关艾滋病问题争论的平信和电子邮件,该邮件主要针对之前曾经被美国国家科学院院报驳回的两篇论文。
传奇的学术生涯
朗于
1927年生于法国巴黎,并且在青年时期就随着家人来到了美国加州。
1946年从加州科技学院毕业后,朗来到了美国数学最高学府普林斯顿,并且在
1951年顺利的得到了数学博士学位。随后的时间,朗先生任教于芝加哥大学,并且在
1955年哥伦比亚大学获得教授职称。
1971年,因为哥伦比亚大学反战游行等问题,朗先生毅然决然地放弃了教授职称,并且在
1985年获得美国国家科学院院士的称号,顺利地晋级为美国数学协会的成员。
1996年,朗先生从美国数学协会辞职,原因是数学协会周刊上拒绝发表他撰写的有关艾滋病的文章。
在一生的研究工作中,朗博士的方向主要集中在数论以及代数几何方面。并且在
1960年的时候,凭借代数方面独到的见解,获得了美国数学协会颁发的柯尔代数奖。
在科学生涯的最初期,朗博士被视为美国最顶尖的基础数学家,利用几何性质来研究数论问题,并且最终成为了一位极具创新性的教育家。与此同时,朗博士还是一位多产的作家,迄今为止已经撰写了40本有关数学的教材和研究专题论文,而发表的研究性文章已经超过了百篇。(国际在线独家资讯
李远)
18783哥们,一个实系数二次型对应着一个实对称矩阵,求这个矩阵的一组线性无关的特征向量组并进行单位正交化就行了(施密特方法),通过单位正交化后的特征向量组所成的矩阵就是一个正交变换的矩阵
18783麻烦大家看一下附件中的正交变换 ,将二次型化为标准形,并写出其标准形.谢谢!post-23-1127958
179.ibf
18784数学建模大赛有了文科参赛者
2005-09-28
在人们的印象中,数学建模竞赛从来是理工科学生的天下,最近在全国同时开赛的“2005高教社杯全国大学生数学建模竞赛”出现了令人惊奇的现象:来自北京师范大学、北京语言大学、上海外国语学院、北京第二外国语学院的文科类学生出现在报名参赛的队伍中。
这次大赛全国组委会副主任、北京理工大学的叶其孝教
授对此并不惊奇,他告诉记者,早在几年前就有武汉大学图书馆系的学生报名参加这一赛事。他说:“虽然文科学生参赛并不具有普遍性,但是这种现象说明一种趋势,即数学在文科的教学与研究中正在发挥越来越大的作用。”
大赛北京赛区组委会副主任、北京师范大学的刘来福教授告诉记者,他们学校的对外汉语学院由于无法算出汉语研究领域中的很多数学指标,因而到数学系请一些本科生去帮忙。还有一位英语的博士生导师向学校提出能否从数学系选一名研究生到英语系工作,以帮助研究英语里的数学问题。刘教授对记者感叹道:“看来数学正在渗透到社会的各个领域。”
全国大学生数学建模竞赛创办于
1992年,目前已发展成为全国高校规模最大的课外科技活动,今年更是吸引了全国788所高校8443个队的2万5千多名大学生参赛。建模大赛的竞赛题目都是来自社会、经济、工程领域的热点问题,以启发同学运用数学、计算机技术及其他学科的知识以数学建模思想来解决实际问题。今年的参赛题目是,甲组:长江水质的评价和预测、DVD在线租赁;乙组:雨量预报方法的评价。
18785请大家帮忙解决,不胜感谢!
18785谢谢各位大虾!post-21-11279582
17.ibf
18787收敛post-38-1127958991.ibf
18787你等一会,我下载个mathtype就帮你把解答发上去
18787行了post-38-1127960240.gif
18787非常感谢
1878805年post-38-11279595
18.ibf
18788呵呵,这个题目可以当作含参数积分的题目来做,要证明是常数,就去尝试证明导数是0就可以了!利用含参求导法则去做!然后简化了利用周期性的条件!
18788我知道求关于t的导数为0
可就是不会用周期
18788如下:post-38-1127977966.gif
187892005年10月4日, 天气晴朗,北大未名湖风景非常优美,聚会如期举行,
十点开始,在未名湖南侧东部。
参加人员包括
数学中国 www.mathchina.com 管理员流体中文网 www.cfluid.com 版主,数学中国/矩阵论坛
http://数学中国.com ,
http://www.madio.net
管理人员,人鱼网 www.renyu.com 超级版主,湍流中文网 www.turbulence.cn/BBS/ 管理员






另见:
http://www.aoxue.org/cgi-bin/bbs/topic_sho...915&pg=2#723947即
http://2005.mypku.com (该页中有很多照片)
18789十.一聚会,多论坛联合会聚,十月四号上午十点在北大未名湖
------
仅仅是个建议,觉得好顶一下
---------
十一各位来京朋友,是否想聚一下,一个论坛的人数少,我们在几个论坛同时建议:
博士家园,清洁能源,傲雪,流体中文,仿真互动,动力学与控制技术,数学中国,同时希望更多论坛加入。
希望大家多提建议,参加组织,有可能参加的朋友请跟贴写明参加的可能性。
时间定在十月四号上午十点至十一点在北大未名湖,十一点钟愿意参加聚餐的前往聚餐,AA制,
聚会能达到什么目的要靠大家,我们只是建议个时间地点,失望不要抱怨。
刚刚从以下网页查到十月四号北京天气晴朗,万一遇雨则推辞一天,
http://www.weather.com/activities/travel/b...topnav_business进一步,以后各论坛增加联合活动,发展成更有组织的论坛联盟,
版主支持的话
顶一下本贴,固顶更好,聚会一下增加论坛凝聚力!
附:SIMWE论坛会员上海聚会:
http://www.simwe.com/forum/post/view?bid=1...1&age=30#5
19868http://www.simwe.com/forum/post/view?bid=1...ds=%BE%DB%BB%E1yuxin
(于欣)
BITZHANGJIE (张杰)
18789顶!!
18790有没有搞安全协议的形式化分析的?
18790密码协议和安全协议完全一样。
18790我看到的形式化分析都是博士生、博导做的,好像特别抽象,有什么串空间、模态逻辑、状态机什么的,我是根本不懂啊!
18790感谢2楼,
3楼的,形式化分析无非是数学一点罢了,就象你说的,形式逻辑,或者自动机,或者其它的形式语言,形式模型来描述,它的好处是严密的地分析验证网络协议和网络安全协议的性质.
也不一定是博士生,几年前我读硕士时,就搞过形式化分析,当然不是网络安全协议,而是对软件的形式化分析.
18790
| 引用 (zhaoming @ 2005年12月13日
16时46分) |
感谢2楼,
3楼的,形式化分析无非是数学一点罢了,就象你说的,形式逻辑,或者自动机,或者其它的形式语言,形式模型来描述,它的好处是严密的地分析验证网络协议和网络安全协议的性质.
也不一定是博士生,几年前我读硕士时,就搞过形式化分析,当然不是网络安全协议,而是对软件的形式化分析.
|
道理是对的,但不容易搞出来。敢问阁下现在在做这个方面的研究吗?
18793希望给予指教
18793嘿嘿.
Schwarz的分析.
这可是分析...不包含微积分的计算内容
18795A,B为 n Xn矩阵 r(A)+r(B) <=n. 证明存在可逆阵M使AMB=0.
18795如下:post-60-1127973595.gif
18796X,Y,Z三个随机变量,他们之间互相独立,其中X和Y的概率分布相同,若X,Y,Z三者中最大的两个为X和Y的概率是多少,最大的两个概率为Y和Z的概率是多少?
这个概率怎么计算
Thanks
18796X,Y为最大的概率P(X

Z,Y

Z)=Ez P(X

z,Y

z|Z=z)
=Ez
P(X

z)P(Y

z)
=

P(X

z)P(Y

z)
F(dz)
F为Z的分布函数
18797我老师曾经讲过,但是我给忘了。这种说法课本上课时没有的讲呀
18797对分块矩阵施行初等变换后得到的矩阵含有零子矩阵,即含有一个洞,因此我国证明数学家华罗庚将分块矩阵的初等变换称为矩阵打洞.
18797楼上说得对,但我要补充一句:打动技巧经常用在求分块矩阵的逆
18798设yn=(1/k*lnk )-ln(ln(n)) ,则{yn}收敛
18798证明yn递减有下界即可.
18798利用单调有界原理即可得证
18798你的题中少写一个连加符号
18798积分的方法
18798你的k有啥子用嘛?
18799数学分析 中各种形式的极限环需所需的条件:
1 函数列极限的连续性
条件1函数列连续
2函数列局部一致收敛(内闭)
2 函数里曼积分与极限的换序
条件 1函数列的里曼可积性 2函数列一致收敛性
3
函数求导与极限换序
条件1 函数列的可微性 2导函数的局部一致收敛性 3函数列在一点收敛
3
函数牛顿积分与极限的换序
条件 1函数列的牛顿可积性
2函数列内闭一致收敛性
以上各种情况也是适用于连续参数情形
参数常义积分和广义积分的连续性可微性可积性
待续
18799我感觉级数和积分的一致收敛问题的求解和证明很难 那么多判别法 怎么能记住啊 哪位高手可以告诉我一个好的方法 谢谢
18799没啥技巧。哎,级数一致收敛啊,那是有点难,不过劝你还是先记下来,再多做点题,不要偷懒。
18799一般的书上的条件都是太强的
我有很弱的条件,可以说是数分框架下最弱的条件有时间贴上去
不过还没有和实变联系起来,估计很难联系起来
18801sinx+sin2x+sin4x+……+sin(2^n)x=??
18801可以用复数证明:
sinx+sin2x+sin4x+……+sin(2^n)x是e^(ix)+e^(2ix)+……+e(2^nix)的虚部
而设e^(ix)=t,则后式=t+t^2+……+t^(2^n)
后面好象不好做了
:(
188012*sin(x/2)*(...)/(2*sin(x/2))
可以分析他的有界性!是不是这样的啊?
18801这个题目是不是可以尝试着多导几次呢?感觉好象可以和矩阵运算挂钩!
18801我不是已经作出来了吗?!为:
cos(1/2)*x-cos[(n+1)/2]*x!
18801随着新内容的引入,三角部分在中学里被淡化了,和差与积的互化好象已经不要求了.
18804qq9513267 email crsinbar◎163.com
18804202.
198.71.
195
math
math2004
应该有.
18805设A,B都是n阶方阵,C=AB-BA,CA=AC,CB=BC,证明:存在正整数m,使得C^m=0
18805我做的方法似乎无法继续下去,还是删除了吧!
18805特征值可能为复数。(也需要删去)
18805我的解答,开始都想麻烦了:
ps:to 我是傻瓜 我在原来贴子里解答了你的问题;to
windvalley,呼呼已经给我技术加分了,我比较主动的,贴子几乎都贴过去了,谢谢。post-38-1128042274.gif
18805to:快乐的思考!
我有点搞不懂,我也尝试过你的那条路,不过我走不懂一个推理
A0=P^-1AP,B0=P^-1BP为什么就是对角阵呢?
我在不断的尝试证明的过程中总是不会推这个!
可不可以给个具体的推理过程?谢谢!:)
18805快乐的思考,我怎么为你申请技术分啊??
18806各位大虾们,出来捧场啊
18808这个事情,我比较熟悉,所以说明一下。
首先,湖南省属理科实验班的成绩是全国公认的,不止43枚金牌,在每年各个学科的全国冬令营中,湖南代表队基本上都是金银牌,有时候出现铜牌,那很有可能是高一高二的学生:)极盛时期,也就是大概95--03年,每年五科的国家队都会有湖南选手,而且全部是金牌,在数学上,连续好几年湖南有两枚金牌,占总数1/3。
其次,理科实验班的学习并不尽如这个报道所说,比如长沙一中邓老师说的,要求实验班学生成绩在年级前150名,实际上,如果学生竞赛成绩特别突出,往往受到竞赛导师特别培训,不参加正常教学,更不参加教学计划内考试,一般在高二下学期和高三上学期,为了准备高三最后一次学科竞赛,往往有好几个月的时间停止一切课程,参加竞赛培训。
另外,为了把两年的时间挤出来,实际上各校实验班并没有开设如历史、地理、政治、音乐、美术、劳动技术、研究性学习等课程,三年只有语文,数学,英语,物理,化学,生物,体育,计算机八门课程,其余时间节约下来用做竞赛培训。
然后要说的是,湖南理科班的成绩,是与大量的群众基础和大量的专业训练离不开的,但是最近几年情况出现了改变,最主要是很多优秀的辅导教师因为各种原因离开湖南前往北京上海广州等地学校就职,大量优秀金牌教师的流失产生一个很大的一时无法补上的空缺,所以最近两年湖南的竞赛情况并不乐观,虽然每年仍然有三枚以上的金牌,但已经能够感到疲软的气息。
************************注意!*************************
最重要的一点,也是所有报道没有提到也不会提到的就是:
基于很明显的利益关系,四大学校根本不会放弃理科实验班的底子,也不会浪费现有资源,虽然教育部和省教育厅直接下文要求停办,但实际上,四大中学都有自己的名办附属学校,湖南师大附中有广益实验高中,长沙一中有湘一实验中学,雅礼中学有长雅实验中学,长郡中学有湘钧实验中学,这四个学校是自主招生的,于是,在今年五到七月份,四个学校分别以夏令营,参观学校活动,特长班等各种名义为一个名字不是实验班但性质是实验班的班级做招生选拔工作,对象是湖南全省应届高中毕业生。各校已在8月之前完成招生。
在各校对各自的班级说明中,都有提到,任课教师为原理科实验班原班人马,意思很明显,来这个班,最适合就是搞学科竞赛。
也就是说,虽然名义上停止了,但实际上的理科实验班仍然在各种公文的夹缝中生存,但和以前相比已经有了下面的改变:
一、以前是全省统一命题,统一招生考试,任何学生只能报考一个学校,现在各校分别招生,只要时间上不冲突,学生可以参加多个学校的招生考试,这样实际上更能控制有用人才的流失。
二、最初的湖南省理科实验班学生是享有直接保送资格的,后来随着政策的改变,只有竞赛拿到省级一等奖以上才能取得保送资格,虽然这一项变的苛刻,但实验班仍然可以名正言顺的享有很多有利资源,比如图书馆,免费的竞赛培训等,这些都是对文中所说的贫困学生很有帮助的。但是,以后的各校自己办的实验班,都是属于名办中学,收费是自由的,虽然在竞争的压力下不会有哪个学校的学费特别突出,但如果处于一个高而且平衡的状态,对学生的选拔,公平性和广泛性大打折扣。很多地区来的学生,以前考入理科实验班,每期只用交最低要求学杂费(每期1100左右),就可以在自己心目中的学校上课,听自己心目中名师的竞赛培训,但以后这种状况会怎么样,我们还得共同关注。
*************************注意!************************
由于我自己就是这个班级出来的学生,因此对它怀着一种特殊的感情,一方面我深知这个班级的弊端,另一方面,这个班级对于选拔特殊人才,培养特殊人才,都有不可磨灭的贡献和伟大的意义。如果你很了解以前的事情,就会知道网大总裁黄沁等人和理科实验班是有渊源的。
总之,湖南省理科实验班,这个有着十几年光荣历史的集体,在名义上已经消失了,但是关于这样一个班级的争议,关于学科竞赛的争议,关于特长教育的争议,还会继续……
1880843枚国际奥赛金牌救不了湖南理科实验班
精英教育被迫为素质教育让路
43枚国际奥赛金牌救不了湖南理科实验班
基层中学一片欢呼,贫寒学子家长在校门口直哭
(转自《中国青年报》)
今年湖南长沙高中招生,一条政策的出台激起了万千波澜:湖南师范大学附属中学、长沙市一中、长郡中学、雅礼中学4所省级示范高中的理科实验班从今年起停止招生。
上世纪80年代,湖南的基础教育工作一直享有盛誉。湖南省教委决定在上述4所中学开设理科实验班。经过十几年的风风雨雨,理科实验班要退出历史舞台。这让不少家长慌乱和震惊,也在湖南省教育界引发了争论和思考。
两大因素促成“理科实验班”散学
这4所中学在湖南省甚至全国都是大名鼎鼎。因为4校在国际奥林匹克各科竞赛中共获得43枚金牌,使湖南在国内各省中奖牌数名列前茅。获奖学生全部被保送到重点大学。
赢得了如此优异的成绩,功勋卓著的理科实验班为何还要取消呢?
湖南省教育厅基教处负责人王玉清向记者阐述了原因:一是去年教育部要求停办,但当时省内的招生工作已经完成了,因此又维持了一年。
另一个重要因素则是出于湖南的实际情况。
据王玉清介绍,湖南的理科实验班成绩尽管在全国是数一数二,可是也存在着不少负面影响。为了在竞赛中获取奖牌,不少学生重理轻文,有偏科倾向。这对全面推行素质教育是一大冲击。而且,郴州、怀化等地市区的某些学校从小学开始,就办起了重点班、实验预备班等,社会上出现的“奥赛”经济愈演愈烈。孩子们的负担变得非常沉重。“学生减负是一方面,教育均衡也迫使我们不得不这样做。”王玉清说,理科实验班的这群孩子一直享受着最好的教育资源和待遇,而获奖学生又往往能保送到北大、清华这类名校,让不少普通班的学生抱怨不公平。
另外,由于理科实验班是面向全省招生,虽然每年只招收320名学生,但涌入这4所学校参加考试的尖子生都高达数千人,入学比例基本达到了20∶1,优秀生源流走让许多地方学校意见很大。
遵循“因材施教”教育应该尊重个体差异
那么这群理科实验班的学生究竟享受到了什么样的教育资源呢?
湖南师范大学附属中学校长助理郑定子认为,每个学校的平台和经验差异,注定了教育资源的不均衡。就该校而言,在举办理科实验班时,他们坚持走让学生得以全面发展的教育之路。
他指着该校一座名叫“奥林匹克之光”石碑上刻着的第一个夺奖人“郭早阳”的名字告诉记者,他们是
1993年开始办理科实验班的。但在
1991年、
1992年时,学校的学生已经在竞赛中夺得金、银大奖了。
并且,学校普通班和实验班的学生一样,只要学习成绩好,同样可以参加奥林匹克竞赛。即使现在停办了理科实验班,他相信拿奖牌的名字还继续会在碑上刻下去。
据郑定子介绍,社会上很多人认为,理科实验班的孩子只会机械性地做题,其实这是误解。他举例,在
1994年的奥赛当中,该校一个名叫彭建波的男孩,在参赛时指出了教研老师翻译试题时有误。“如此过硬的英语成绩,能证明他偏科吗?”
长沙市一中教研室主任邓立新与郑定子看法相同。
邓立新说,在理科实验班教学中,为防止学生偏科,招生时学校规定:学生在初中学校里面的每期考试当中,年级排名每次必须是在前150名以内。
另外,学校为实验班配备的班主任都是文科老师,即使到了高三,学校都还会为学生们开设阅读课、音乐课、美术课及形体课,从一定程度上扼制了偏科的情况。
对于外界所质疑的精英教育模式,邓立新解释为他们在遵循“因材施教”的教育理念。
他说,孩子的智力水平存在个体差异,在同一个教室里,老师一节课讲的内容,对于智力超常的孩子来说也许太少,但对于接受能力差的孩子来说却跟不上。曾经,学校让一个普通班的优秀学生到理科实验班听课,仅念了3个月,该生就主动申请回原班学习。原因是感觉过于吃力。因此,每个人的教育不能使用一把尺子,那样容易耽误孩子们的发展,也不利于社会对精英阶层高端人才的培养。
贫寒学子进入名牌高校因此面临难题?
在不少老师看来,取消实验班另外的损失是无法估量的。郑定子说,停办理科实验班虽是实现教育均衡的需要,但也使一些贫寒学子失去了就读名校的机会。邓立新也称,他们学校举办了12年的理科实验班,其实还是一部分贫寒学子争取进入名校就读和读完高中课程的一个重要途径。“知道这个消息后,许多家长都在学校门口哭了,不少是从外地赶来的。但学校不能破例呀。”一中学负责人无奈地说。
据邓立新反映,由于理科实验班是面向全省招生,它是许多长沙市以外的学生取得进入长沙市4所名校就读的机会,就在80名学生中间,就有60%以上的学生是来自贫寒家庭。
为了使这些贫困生能顺利读完高中,各个学校都采取了措施。师大附中、长沙市一中都采取了设立奖学金、助学金及借助社会力量等方式进行救助,帮助学生解决困难。也就是说,4所学经济实力雄厚,他们有能力资助贫寒子弟读到大学,而如果这些孩子仍在地方学校学习,他们有可能因为贫困而无法继续求学。
而这批贫寒的学生大多不负众望。
据长沙市一中统计,理科实验班95%的学生能考上重点大学,80%的学生所考学校都是排名前10名的优秀高校,40%的学生拿到了出国留学的资格。
面对即将失去优秀生源的难题,据了解,部分学校也找到了应对的方法:邓立新说,长沙一中计划拿出200万元资金,在其所主办的民办中学湘一学校,面向全省招收约80名贫寒学子,对于这些贫寒学子,湘一学校采取免收择校费,并按公立学校规定收取相关费用。
基层学校一片欢呼资源集中影响公平
对取消理科实验班,在湖南的各地州市教育机构,记者听到的是一片欢呼声。
衡阳市一中一位资深教师告诉记者,实验班的收益远远比不上它带来的破坏效果。
他指出,在实验班开设后,省会城市长沙与各地对优秀人才的争夺明显加剧,在前几年甚至达到了恶化的程度。不少地方都实行了方法不一的抵制行动。而此次停办实验班后,阻断了对地方生源的抢夺。“就先天条件而言,我们承认与那些学校相比在一些方面有差距,但不能因此就把最优秀的人才都集中给他们,差点儿的孩子就该让我们这些学校来教。这难道算是教育公平?”
这位老师称,在教学上,实验班学生“应试”的成分很大,大题量的测试基本是家常便饭。许多学生在理科实验班实际上基本学完了大学的课程。由于精力的限制,即使是天才学生,其他科目的学习也不可能不受影响。
并且,取得了好成绩的学校因为学生进入了名牌大学而声誉更高,政府管理部门势必会对实验班的软硬件方面增大投入,更加拉大了它们与其他学校的差距。“在地方上,更是上行下效。少数人的精英化教育替代了普教原则”。他说。
(转自《中国青年报》)
18808教育,永远不能放弃精英主义
18810明白了,谢谢!!!
我再整理一下。
18810明白了,谢谢!
我再好好整理一下。
18810也就是说Jordon标准形中有0块或对角线为0的Jordon块就可以了
18810怎么说?能不能具体一点,谢谢!!!
18810已知:矩阵A乘以矩阵A的伴随矩阵等于0矩阵
求:矩阵A的Jordon标准形。
18810这个题目我不知道是在考什么!真晕!
post-38-1127992941.gif
18810为什么说行列式为0就一定有一个0Jordan块?要是它的初等因子是

2的呢?
18810我觉得楼上说的有道理,应该只要对角线有0的Jordan块都满足.
18811已知A,B,A-B,为实正定阵,AA-BB是否正定。
18811如果A+B与A-B乘积可交换就可以.
18811除非附加条件,否则该命题不一定成立的
18811我给一个二阶的反例好了:post-38-1128053547.gif
18811需要附加条件!
18813A正定,则存在C正定使的A=CC
18813A正定那么A与I合同即:存在可逆阵C使得:A=c'Ic=c'c!
18813
| 引用 (mathguy @ 2005年09月29日
20时46分) |
|
A正定那么A与I合同即:存在可逆阵C使得:A=c'Ic=c'c!
|
题目要求c是正定,
18813A 正定 那么存在正交矩阵Q 使得 A=Q'diag(a1,...,a2)Q a1,..,a2为A的特征值 均大于0
记
c'=Q'[squ(a1),..,squ(an)]Q 即得
18815设f(x)在[a,b]上一阶可导,在(a,b)上二阶可微,且f(a)=f(b)=0,f'(a)f'(b)>0
证明:(1)存在


(a,b
),f(

)=0
(2)存在
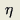

(a,b),f"(
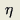
)=f(
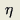
)
第一问我已经证出,请各位高手指点第二问!谢谢
18815第二个题目用反证法,如果是恒大于的话,从左边分析起,容易知道第一问不成立
如果恒小于的话,从右边分析起,也容易知道第一问不成立!
18815反证法可能不行,因为没有说二阶导数连续
我觉得应该构造函数做,有没有那位大侠有好方法,共享一下
18815其实这个题目是完全可以用反证法做的,下面我给个另外的解答方法!
令
A(x)={t|f''(t)>f(t),a<t<x},
B(x)={t|f''(t)<f(t),a<t<x},
a<x<b
则A(x),B(x)至少有一个不为空,
不妨假设A(x)不为空,
则supA(x)是有上界的,
如果supA(x)=b则容易知道会和条件f'(a)f'(b)>0矛盾
如果supA(x)<b,就可以证明在x=supA(x)处就有了f''(x)=f(x)
18815了解了!谢谢!
188
19我想了解一下哈尔滨工程大学数学系,谢谢!!
18820师大概率王风雨陈木法很强
18820我今年研二,读的是概率论方面的,以后准备向无穷粒子系统方向发展。我打算想考北师大,请各位给点建议和信息吧!非常感谢!
18821对一个图 G(V,E) 进行 k-coloring
顶点着色(也就是说只有k种颜色),然后求最小冲突(M)的着色方案。这里的冲突的意思的对于相邻的节点u, v,两个节点颜色相同。
这应该是NP-hard问题,有人可以给出证明吗,呵呵
18822本人想跟位最牛的导师??请问国内搞材料科学建模和计算的谁是最牛的人???
如果出国的话,这方面国外有那些牛人??谢谢!!!
18822材料科学建模?
有搞固体的,有搞流体的,有搞液晶的,有搞高分子的,你问什么?
18825
| 引用 (鬼哥 @ 2005年09月29日
23时06分) |
无穷大到底是个什么东西,是数吗,它到底是怎么定义的
还是它仅表示一个符号
向各位高手求教
|
定义很简单,数学课本上都有
关键是理解概念,形成一种表象
18825无穷的量你就看成是过程的量,不是定量
这样考虑的话就会清晰许多
因为是这样的一个不断趋向的量,所以任何的定量(任意大/小的数)都不会是它的界
真正做些题就会更清楚了
18825关于无穷“大”是什么,是变量还是数?
关于无穷“小”是什么,是变量还是数?
区别在于其称谓,无穷大数是数,是客观存在的数,在客观现实中有它的对应事物。不要因为它有无穷的位数就不认为它不是数,就像无理数一样,有着无穷的位数,却仍然是数。而无穷大量是变化的量。
我们的课本没有对此进行严密区分,以致于很多人学完微积分后搞不清什么是微分,因为其定义中用到了无穷小量。
欲知详情,建议可以看一些近代的关于分析基础的书,对此有详尽论述。
18825无穷大到底是个什么东西,是数吗,它到底是怎么定义的
还是它仅表示一个符号
向各位高手求教
18825无穷大是数列或函数的一种趋向特征。
当然也可以将它理解成有限数的一种推广。
比如说,+

是一个大于任一给定正数M的数。
—

是一个小于任一给定负数M的数。(
这两个数都是不定数!)
当数列即有子列趋向+

又有子列趋向—

时,
我们说该数列趋向于

。
当然,这只是我的一点粗浅理解,若有不对之处,还望指正。
18826在附件里,谢谢post-38-1128006529.ibf
18826解答:post-38-1128047830.gif
18826谢谢 ,
18828方程有解a1*x1+a2*x2+---+an*xn=N当且仅当(a1,a2,---,an)整除N。
如果方程有解:记N=d*t
先求出x1,x2,---,xn的最大公约数d=(a1,a2,---,an)
再确定y1,y2,---,yn,使a1*y1+y2*x2+---+yn*xn=d
则t*y1,t*y2,---,t*yn
为方程a1*x1+a2*x2+---+an*xn=N的一组解。
数学与我们同在!
18828求解:x1+x2+.......+xn=N 且 xi>=0
18829一份中国学科分类国家标准,看看,就一个数学中的一个分支一个人一辈子都研究不完。其中也说明了,应用数学归为每个具体应用学科里面。除了专门数学专业的,其他专业的也只是学了其中在本学科需要的一小部分而已。
110
数学
a.. 110.11 数学史
b.. 110.14 数理逻辑与数学基础
a.. 110.1410 演绎逻辑学
亦称符号逻辑学
b.. 110.1420 证明论 亦称元数学
c.. 110.1430 递归论
d.. 110.1440
模型论
e.. 110.1450 公理集合论
f.. 110.1460 数学基础
g.. 110.1499
数理逻辑与数学基础其他学科
c.. 110.
17 数论
a.. 110.
1710 初等数论
b.. 110.
1720
解析数论
c.. 110.
1730 代数数论
d.. 110.
1740 超越数论
e.. 110.
1750
丢番图逼近
f.. 110.
1760 数的几何
g.. 110.
1770 概率数论
h.. 110.
1780
计算数论
i.. 110.
1799 数论其他学科
d.. 110.21 代数学
a.. 110.2110 线性代数
b.. 110.2115 群论
c.. 110.2120 域论
d.. 110.2125 李群
e.. 110.2130
李代数
f.. 110.2135 Kac-Moody代数
g.. 110.2140 环论
包括交换环与交换代数,结合环与结合代数,非结合环与非结
合代数等
h.. 110.2145 模论
i.. 110.2150
格论
j.. 110.2155 泛代数理论
k.. 110.2160 范畴论
l.. 110.2165 同调代数
m.. 110.2
170 代数K理论
n.. 110.2
175 微分代数
o.. 110.2
180 代数编码理论
p..
110.2
199 代数学其他学科
e.. 110.24 代数几何学
f.. 110.27 几何学
a.. 110.2710
几何学基础
b.. 110.2715 欧氏几何学
c.. 110.2720 非欧几何学 包括黎曼几何学等
d..
110.2725 球面几何学
e.. 110.2730 向量和张量分析
f.. 110.2735 仿射几何学
g..
110.2740 射影几何学
h.. 110.2745 微分几何学
i.. 110.2750 分数维几何
j..
110.2755 计算几何学
k.. 110.2799 几何学其他学科
g.. 110.31 拓扑学
a..
110.3110 点集拓扑学
b.. 110.3115 代数拓扑学
c.. 110.3120 同伦论
d..
110.3125 低维拓扑学
e.. 110.3130 同调论
f.. 110.3135 维数论
g.. 110.3140
格上拓扑学
h.. 110.3145 纤维丛论
i.. 110.3150 几何拓扑学
j.. 110.3155
奇点理论
k.. 110.3160 微分拓扑学
l.. 110.3
199 拓扑学其他学科
h.. 110.34
数学分析
a.. 110.3410 微分学
b.. 110.3420 积分学
c.. 110.3430 级数论
d.. 110.3499 数学分析其他学科
i.. 110.37 非标准分析
j.. 110.41 函数论
a..
110.4110 实变函数论
b.. 110.4120 单复变函数论
c.. 110.4130 多复变函数论
d..
110.4140 函数逼近论
e.. 110.4150 调和分析
f.. 110.4160 复流形
g.. 110.4
170
特殊函数论
h.. 110.4
199 函数论其他学科
k.. 110.44 常微分方程
a.. 110.4410
定性理论
b.. 110.4420 稳定性理论
c.. 110.4430 解析理论
d.. 110.4499
常微分方程其他学科
l.. 110.47 偏微分方程
a.. 110.4710 椭圆型偏微分方程
b.. 110.4720
双曲型偏微分方程
c.. 110.4730 抛物型偏微分方程
d.. 110.4740 非线性偏微分方程
e..
110.4799 偏微分方程其他学科
m.. 110.51 动力系统
a.. 110.5110 微分动力系统
b..
110.5120 拓扑动力系统
c.. 110.5130 复动力系统
d.. 110.5
199 动力系统其他学科
n..
110.54 积分方程
o.. 110.57 泛函分析
a.. 110.5710 线性算子理论
b.. 110.5715
变分法
c.. 110.5720 拓扑线性空间
d.. 110.5725 希尔伯特空间
e.. 110.5730
函数空间
f.. 110.5735 巴拿赫空间
g.. 110.5740 算子代数
h.. 110.5745
测度与积分
i.. 110.5750 广义函数论
j.. 110.5755 非线性泛函分析
k.. 110.5799
泛函分析其他学科
p.. 110.61 计算数学
a.. 110.6110 插值法与逼近论
b.. 110.6120
常微分方程数值解
c.. 110.6130 偏微分方程数值解
d.. 110.6140 积分方程数值解
e..
110.6150 数值代数
f.. 110.6160 连续问题离散化方法
g.. 110.6
170 随机数值实验
h..
110.6
180 误差分析
i.. 110.6
199 计算数学其他学科
q.. 110.64 概率论
a..
110.6410 几何概率
b.. 110.6420 概率分布
c.. 110.6430 极限理论
d.. 110.6440
随机过程 包括正态过程与平稳过程、点过程等
e.. 110.6450 马尔可夫过程
f.. 110.6460 随机分析
g.. 110.6470 鞅论
h.. 110.6480 应用概率论 具体应用入有关学科
i.. 110.6499
概率论其他学科
r.. 110.67 数理统计学
a.. 110.6710 抽样理论 包括抽样分布、抽样调查等
b..
110.6715 假设检验
c.. 110.6720 非参数统计
d.. 110.6725 方差分析
e..
110.6730 相关回归分析
f.. 110.6735 统计推断
g.. 110.6740 贝叶斯统计 包括参数估计等
h.. 110.6745 试验设计
i.. 110.6750 多元分析
j.. 110.6755 统计判决理论
k..
110.6760 时间序列分析
l.. 110.6799 数理统计学其他学科
s.. 110.71 应用统计数学
a..
110.7110 统计质量控制
b.. 110.7120 可靠性数学
c.. 110.7130 保险数学
d..
110.7140 统计模拟
t.. 110.7
199 应用统计数学其他学科
u.. 110.74 运筹学
a..
110.7410 线性规划
b.. 110.7415 非线性规划
c.. 110.7420 动态规划
d..
110.7425 组合最优化
e.. 110.7430 参数规划
f.. 110.7435 整数规划
g..
110.7440 随机规划
h.. 110.7445 排队论
i.. 110.7450 对策论 亦称博奕论
j..
110.7455 库存论
k.. 110.7460 决策论
l.. 110.7465 搜索论
m.. 110.7470
图论
n.. 110.7475 统筹论
o.. 110.7480 最优化
p.. 110.7499 运筹学其他学科
v.. 110.77 组合数学
w.. 110.81 离散数学
x.. 110.84 模糊数学
y.. 110.87
应用数学 具体应用入有关学科
z.. 110.99 数学其他学科
18835关于不等式证明的
post-38-112804
1913.ibf
18835好象不成立啊
只要b充分大,就不成立
18835是大连理工05年的一道题
18835呵呵,解答:post-38-1128044238.gif
18838这是一个CSP问题求解软件,先谢谢了
18840我很喜欢计算数学,就
18840当今数学必须应用到实际中去,以解决实际问题为主,因此计算数学非常有用.有志考计算数学专业的研究生,毕业后很好找工作
18840的确
18840计算数学有意思吗?论文好写吗?将来从事什么工作?教学吗?大连理工其他专业好吗
18840计算数学当然有意思,想想看,你可以用你所学的数学知识解决实际问题,成就感不强吗?
论文好不好写要看你的要求怎么样,高水平的需要高手来写了,混的文章很好写.
毕业后可以从事IT,教育,军队,公务员,各种行业.
大连理工偶不熟悉
18840很强,全国第一
18841这题原来帖过,但是没人解答出来.重新帖出,供大家讨论.
设e^(e^x)=

an*x^n
求证:
an

e(

*log
n)^(-n)

是大于e的常数
18841me想想看!:)
18842各位大侠:sas软件如何编非线性方程组的回归在sas的那一部分可以找到,
或者用那些函数可以实现。请各位大侠多多指教,小弟得靠它毕业了。
小弟在这里祝各位大侠:
工作、学习顺利
身体健康
18843Let me try.
我只学过BASIC语言,也不知道能否做出来。
但我会努力的。
数学与我们同在!
18843我是一名程序员,数学学得不好,我先介绍一下我这个问题的背景,我们公司是做娱乐类产品的,接到一个国外客人的单,但是他要求要按照他的想法来写程序,我解决不了,所以来求救于大家了。
问题:有两圈跑灯,程序控制跑动的哪种,内圈为红色同绿色两种LED灯,每一个灯可以用程序控制显示成红色,也可以用程序控制显示成绿色,共有24个这样的灯;
外框是固定的24个动物,第一个为鼠,依次为牛,虎,兔,羊,鸡,剩下的还是按照这个排列重复排列3次,组成24个动物。
有12个按键,分别为红色鼠,绿色鼠,红色牛,绿色牛,红色虎,绿色虎,红色兔,绿色兔,红色羊,绿色羊,红色鸡,绿色鸡。
游戏步骤:1。程序给出内圈的颜色(每次都不一样,是不是要随机给出?)
2。每个按键前面给出一个倍率(也是要程序给出)
3。玩家可以选择任意一个按键,按一下1分,可以按多次,可以按任意组合,同时最多8人可以同时游戏。
4。玩家按按键的总分数,跟玩家赢去的总分数,在一段时间内,比率要为100%。
不知道有没有办法解决?我不知道怎么弄这个才好,请各位大侠帮帮我,要是需要报酬也可以发邮件给我!谢谢!
cool_dream12000@yahoo.com.cn
18843呵呵,我也不知道呀,呵呵,看看哪个大虾比较历害呀
18843不知道
18848中科院考解析几何吗
18848好象从来不考
18849谢谢楼主!!
18849好站
18849向大家推荐一个数学学习网站,希望大家喜欢
中国数学资源网
18849谢谢楼主,这个网站不错
18849谢谢了
18849多谢
18849不错!!!谢谢楼主.
18849去看看
18849的确很一般
18850我有黑龙江的结果!!!!
不过我是陕西赛区的学生,结果再等几天呀.post-37-11290129
18.ibf
18850关于公示2005年全国大学生数学建模竞赛湖南赛区成绩评审结果的通知
各普通高等学校教务处:
2005年全国大学生数学建模竞赛已经结束。湖南赛区共有33所高等学校355个队报名参赛,经湖南赛区组委会组织专家评选,共有138个队被评为优胜队,其中一等奖27个队,二等奖41个队,三等奖70个队。
以上结果请学校予以张贴公示。任何单位或个人若有异议,请以书面形式,并加盖单位公章或签名,向湖南省教育厅高教处提出。异议期截止日期为10月30日。
附件:2005年全国大学生数学建模竞赛湖南赛区成绩评审结果
学校名称 队员1 队员2 队员3 指导教师 题型 获奖等级
国防科技大学 曹华阳 王怀晖 王啸天 指导教师组 A 一等奖
国防科技大学 张硕 张磊 王艺敏 指导教师组 A 一等奖
国防科技大学 王小强 黎渊 王友瑞 指导教师组 A 一等奖
国防科技大学 李旭 韩岗 周文亮 指导教师组 A 一等奖
国防科技大学 张杰 续志明 刘磊 指导教师组 A 一等奖
国防科技大学 邹颖 王章 赵伟 指导教师组 A 一等奖
国防科技大学 张子文 李毅 张文 指导教师组 A 一等奖
国防科技大学 徐新海 胡耀鹏 荀长庆 指导教师组 A 一等奖
国防科技大学 蒲世兵 罗章 谢波 指导教师组 A 一等奖
国防科技大学 彭拯 高山 孙亚男 指导教师组 A 一等奖
中南大学 吕诗良 申俊 李文龙 易昆南 A 一等奖
中南大学
张海明 杜香刚 贾承林 易昆南 A 一等奖
中南大学 李平衡 封朋成 周佳 秦宜云 A 一等奖
湖南商学院 贺雅丽 陈志华 黄含其
尹向飞 A 一等奖
怀化学院 伍红亮 朱红红 陈欢春 舒晓惠 A 一等奖
国防科技大学 高梅勇 徐涛 郑振南 指导教师组 A 二等奖
国防科技大学 江荣 胡灏 郭良益 指导教师组 A 二等奖
国防科技大学 林一松 姚铎 李祐国 指导教师组 A 二等奖
国防科技大学 王全镇 周伟 霍广城 指导教师组 A 二等奖
国防科技大学 沈思淇 刘尧 赵四海 指导教师组 A 二等奖
国防科技大学 马俊 韩威 牛新 指导教师组 A 二等奖
国防科技大学 杨晶 赵耀峰 高绪刚 指导教师组 A 二等奖
国防科技大学 陈波 孙小兵 王华 指导教师组 A 二等奖
国防科技大学 张长旺 易成龙 韦中伟 指导教师组 A 二等奖
国防科技大学 夏晓 罗磊 王攀 指导教师组 A 二等奖
国防科技大学 韦官余 黎永强 张羽丰 指导教师组 A 二等奖
中南大学 邓练波 仇洁婷 刘健 张鸿雁 A 二等奖
中南大学 郑巧霞 云春凤 吴礼嘉 刘建华 A 二等奖
湖南大学 李连伟
王松 蒋雅琴 数模指导组 A 二等奖
湖南大学 张晓昱 尚小莉 林惠敏 数模指导组 A 二等奖
长沙理工大学 樊渊文 张宴 陈烨
张弘强 A 二等奖
长沙理工大学 卯升义 李世青 曾利强 杨东 A 二等奖
湖南科技大学 袁思明 陈润娟 李萍萍 谭敏 A 二等奖
湖南科技大学 王金苏 郭强 张聪尊 肖艳清 A 二等奖
湖南科技大学 张中健 钦强 毛盛文 侯进军 A 二等奖
吉首大学
王俊 张权明 覃孟龙 数模组 A 二等奖
湖南城市学院 刘昭魏 姚美玲 刘勇 指导教师组 A 二等奖
国防科技大学 陈思伟 王磊
周晓松 指导教师组 A 三等奖
国防科技大学 王珏 任永敏 王坤 指导教师组 A 三等奖
国防科技大学 林金茂 周晗 付浩
指导教师组 A 三等奖
国防科技大学 彭国宝 冯洪涛 张广军 指导教师组 A 三等奖
国防科技大学 廖洋 毛朝 钟水和 指导教师组
A 三等奖
国防科技大学 王彦桥 龙潭 陈思安 指导教师组 A 三等奖
国防科技大学 王富强 杨波 胡世元 指导教师组 A 三等奖
国防科技大学 刘华柏 张强 周旭峰 指导教师组 A 三等奖
国防科技大学 韩彪 刘晓东 任洪广 指导教师组 A 三等奖
国防科技大学 李骞 张志华 董欢 指导教师组 A 三等奖
国防科技大学 杨绍武 王雷 杨稳竞 指导教师组 A 三等奖
国防科技大学 孙仕海 康冬冬 解培岱 指导教师组 A 三等奖
国防科技大学 肖俊 董能 丁超 指导教师组 A 三等奖
国防科技大学 刘瀛翔 朱志军 罗有敢 指导教师组 A 三等奖
国防科技大学 张慧 廖振明 侯苏宁 指导教师组 A 三等奖
国防科技大学 曾令李 邓镭 高永明 指导教师组 A 三等奖
国防科技大学 马京旺 徐建国 随昆明 指导教师组 A 三等奖
国防科技大学 刘承兰 范崇祎 李娜 指导教师组 A 三等奖
中南大学 郑巍 龚勋 廖小娟 张佃中 A 三等奖
中南大学 黄锋
谭乐 袁名举 张鸿雁 A 三等奖
中南大学 蔡芳娜 瞿安娜 孙亚星 胡朝明 A 三等奖
中南大学 文斌 徐东升 焦栋梁 侯木舟 A
三等奖
中南大学 李宗明 王晓冰 章宗长 何伟 A 三等奖
中南大学 徐亚兰 车晶晶 赵保华 何伟 A 三等奖
湖南大学
孙学胜 胡敏 王毅 数模指导组 A 三等奖
湖南大学 鲍宇 罗致 杨贵志 数模指导组 A 三等奖
湘潭大学 刘聪 甘茂仁 邓国兴
李成福 A 三等奖
湖南师范大学 贺艳焱 时佳妮 李淑娟 邓汉元 A 三等奖
长沙理工大学 张丽琴 姜云卢 韩国胜 周富照 A
三等奖
南华大学 肖湘 范成林 谭文志 欧阳自根 A 三等奖
湖南科技大学 檀传华 艾谨 肖契志 侯进军 A 三等奖
湖南科技大学 李小红 孙喜堂 李杰 彭振赟 A 三等奖
湖南农业大学 卓力 刘琦 赵芳 李绪孟 A 三等奖
湖南理工学院
姜建妹 吴建华 杨真 周岳斌 A 三等奖
湖南文理学院 李立华 韩锋 涂振翰 指导教师组 A 三等奖
湖南文理学院 严茂林 曾科
宾霞 指导教师组 A 三等奖
湖南城市学院 刘寿发 夏志华 秦海涛 指导教师组 A 三等奖
国防科技大学 余鹏奇 单荣 李军
指导教师组 B 一等奖
国防科技大学 李蓬蓬 朱小满 解炜 指导教师组 B 一等奖
国防科技大学 李宝娟 张云安 刘健 指导教师组
B 一等奖
国防科技大学 黄雅静 余博超 罗群 指导教师组 B 一等奖
国防科技大学 李冬 张鹏 杨乾明 指导教师组 B 一等奖
国防科技大学 张能 李骁 李俊玲 指导教师组 B 一等奖
中南大学 周仕飞 陈中祥 李黎明 秦宜云 B 一等奖
湘潭大学
唐荣 王北战 郭枚花 李成福 B 一等奖
中南林学院 谭文科 李注滋 周军 指导教师组 B 一等奖
国防科技大学 周悦 巨金川 张超
指导教师组 B 二等奖
国防科技大学 刘忠训 邢世其 龚航 指导教师组 B 二等奖
国防科技大学 朱晓香 魏艳艳 黄祖文 指导教师组
B 二等奖
国防科技大学 何元 吴舜晓 吕太权 指导教师组 B 二等奖
国防科技大学 黄震 邹丹 李劲 指导教师组 B 二等奖
国防科技大学 赵晓慧 欧阳琦 王嘉伟 指导教师组 B 二等奖
国防科技大学 黄石生 黄开兴 倪忠堂 指导教师组 B 二等奖
国防科技大学 张礼廉 黄丽娟 袁博 指导教师组 B 二等奖
国防科技大学 林蓉芬 吴伟 解金刚 指导教师组 B 二等奖
湖南大学 高俊鑫 符达明 彭富德 数模指导组 B 二等奖
湘潭大学 周玉鼎 万海波 李志婧 梁开福 B 二等奖
湘潭大学
陈谛 龚明 谢佳 刘红良 B 二等奖
湘潭大学 胡凯 黄玺 赵永红 梁开福 B 二等奖
湖南理工学院 古钱刚 何少林 郑菲 周小强
B 二等奖
国防科技大学 何蕾 卢文波 董德帅 指导教师组 B 三等奖
中南大学 谢晓慧 吴敬凯 陶学良 张飞涟 B 三等奖
中南大学 黄高辉 郭跃键 黄志强 秦宜云 B 三等奖
中南大学 郑强 王小捷 陈典银 张鸿雁 B 三等奖
中南大学 艾小冬
周晔 王磊 刘诚 B 三等奖
湖南大学 陈荣亮 黄超 罗向龙 数模指导组 B 三等奖
湖南大学 吴敏 李广迪 周志顺 数模指导组 B
三等奖
湘潭大学 颜志飞 左莉霞 周聪 刘红良 B 三等奖
湘潭大学 黄俊 朱发文 刘爱华 刘树人 B 三等奖
长沙理工大学
李远梅 谷瑜婷 卢丽霞 全宏跃 B 三等奖
长沙理工大学 石介平 刘海峰 邓铸辉 周富照 B 三等奖
南华大学 程林飞 赵庆峰
吴川七 王奇生 B 三等奖
南华大学 肖斯龑 李奇甫 唐宜斌 刘亚春 B 三等奖
湖南科技大学 谢湘中 王鹏 宋辉 肖艳清 B
三等奖
吉首大学 陈峻孝 李杰 王峰 数模组 B 三等奖
吉首大学 张礼 张伟 张鸣雁 数模组 B 三等奖
湖南农业大学
徐建军 黎钊 袁波 周建军 B 三等奖
株洲工学院 曹江 谭应华 李X东 余波 B 三等奖
湖南文理学院 张锐锋 王可为 龚林
指导教师组 B 三等奖
湖南文理学院 罗灿 曾更明 陈国清 指导教师组 B 三等奖
湖南工程学院 万杰 韩勇 郭建召 指导教师组 B
三等奖
湘南学院 周刚山 潘治位 刘博硕 刘智刚 B 三等奖
湖南人文科技学院 蒋文峰 夏森林 陶晖 梁金珑 B 三等奖
湖南科技职业学院 李亚林 龙志文 伍华华 周密 C 一等奖
湖南省第一师范学校 曾鹏 盛立 王和华 田祖伟 C 二等奖
湖南交通职业技术学院 罗德强 莫军 李中洲 张岸扬 C 二等奖
湖南理工学院 陈强 张子腾 陈兵 苏卡林 C 三等奖
湖南人文科技学院 黄涛 聂清标 朱克全 陈庆平 C 三等奖
湖南建材高等专科学校 贺荣 兰芳 李宇 指导组 C 三等奖
湖南科技职业学院 周智远 刘积英 陈小林 黄光清 C 三等奖
湖南建材高等专科学校 严术骞 郭亮 夏程 指导组 D 一等奖
湖南大学衡阳分校 李洪光 董婷 黎翔 指导组 D 一等奖
湖南建材高等专科学校 罗祝良 金文章 王飞虎 指导组 D 二等奖
湖南化工职业技术学院 石佳梁 胡银娟 刘志惠 陶盈 D 二等奖
湖南交通职业技术学院 查结盛 唐立强 郑凡 吴磐献 D 二等奖
长沙学院 蒋丁旺 李佳军 谢恩 谭义红 D 三等奖
湖南省第一师范学校 张毅 唐凤 谢金英 唐懿 D 三等奖
湖南省第一师范学校 田桉 周顺美 刘琛 唐懿 D 三等奖
湖南建材高等专科学校 陈利阳 旷利平 曾祥寿 指导组 D 三等奖
湖南大学衡阳分校 万君 陈罗 胡平科 指导组 D 三等奖
湖南交通职业技术学院 戴婷 陈代辉 陈冬梅 吴磐献 D 三等奖
全国大学生数学建模竞赛湖南赛区组委会(代章)
二○○五年九月二十九日
.
18850山东赛区post-37-1128052128.ibf
18850浙江赛区post-37-1128052425.ibf
188502005全国大学生数学建模竞赛湖北赛区成绩评奖结果
本科组一等奖(排名以学校笔划为序)
序号 学校 队员
指导教师
1 军事经济学院 李 元 黎 森 周志国 黄金明
2 华中师范大学 吴 玲 桂婵娟 蒋立兵 唐向阳
3 华中科技大学 王
琬 何 东 袁 涛 数模指导组
4 武汉大学 许美兰 李大龙 宋 锐 指导组
5 武汉大学 延永东 刘顺强 徐小丽 指导组
6
武汉大学 温建忠 江隆盛 刘晶乐 指导组
7 空军雷达学院 冯哲铭 万建岗 韩国成
数模指导组
本科组二等奖(排名以学校笔划为序)
序号 学校 队员 指导教师
1 华中师范大学 王启明 胡建敏 舒元刚
李书刚
2 华中师范大学 魏梅娟 顾世勇 赖心铭 严国政
3 华中师范大学 杨 鹏 钱建贞 张瑜瑜 李书超
4 武汉大学 李尚盛
杨道坡 叶 超 指导组
5 武汉大学 陈 颖 申 茜 胡天玉 指导组
6 武汉大学 何子键 李 辉 洪 威 指导组
7 武汉大学
郑 慧 李彦强 晏 琦 指导组
8 武汉理工大学 李昭华 袁裕鹏 熊 巍 童仕宽 等
9 武汉理工大学 王雨春 张立民 程惠芳
朱华平
10 空军雷达学院 刘小双 吕奇辰 曹 栋 数模指导组
11 海军工程大学 陈 博、潘梦京、黄汉阳 数模组
12
海军工程大学 潘 华、张明元、王 钰 数模组
13 湖北大学 马 亮、朱理飞、李 玲
数模组
大专组一等奖(排名以学校笔划为序)
序号 学校 队员 指导教师
1 黄冈师范学院 杨豆花 李 华 胡佳文 廖小勇
等
2 湖北经济学院 施金利 毛志鹏 王 沛 数模组
大专组二等奖103名(排名以学校笔划为序)
序号 学校 队员
指导教师
1 孝感学院 陈凤华 邹 利 冯 浩 胡付高
2 黄冈师范学院 汪 飞 孙永清 谢文友 库在强 等
3 湖北职业技术学院
邵峻岭 袁 梦 蒋凤华 刘学才 等
18850哈哈,这是湖北的吗?好象是03年的成绩呀
18850有没有四川的?
18850已经公布评阅结果的赛区如下:
山东赛区,详情请到shandong.shumo.com查阅。
浙江赛区,详情请到zhejiang.shumo.com查阅。
湖南赛区,详情请到www.shumo.com
首页查阅。
黑龙江赛区,详情请到heilongjiang.shumo.com查阅。
河北赛区,详情请到hebei.shumo.com查阅。
陕西赛区,详情请到shaanxi.shumo.com查阅。
吉林赛区,详情请到jilin.shumo.com查阅。
18850天津赛区太没效率了!
18850江苏赛区结果
post-37-1131332081.ibf
188502005年“高教社杯”全国大学生数学建模竞赛
四川赛区获奖名单(学校排名不分先后)
全国一等奖(14队)
甲组11队
学 校 参赛队员 指导教师
四川大学 朱湘禅 朱蓉禅 李武劲 陈 琼
四川大学 潘利蒙 袁晓洁 田 野 刘晓石
电子科技大学
黄 宇, 彭 波 张艳妮 陈绍刚
四川师范大学 张永乐 刘星江 李 娇 赵 凌
四川师范大学 宗 萌 张 建 陈 涛 马邦勤
成都理工大学 叶际阳 王明华 郭雨非 教练组
成都理工大学 刘远清 王迪海 余国家 教练组
成都理工大学 谯程骏 张东辉 张
敏 教练组
成都信息工程学院 安忠锋 勾 娟 陈 挺 刘启宽
西南科技大学 钟武律 朱 毅 黄兴中 卢 谦
西南科技大学 张
毅 黄志新 侯延荣 蒋建军
乙 组3队 成都大学 蔡映梅 田 逍 刘彩霞 教练组
成都电子机械高等专科学校 王 婷 王爱儒 赵小龙
指导小组
西南交通大学峨眉校区 李蒙赫 韩琨明 王子兰 徐昌贵
全国二等奖(31队)
甲组
19队 学 校 参赛队员 指导教师
电子科技大学 张小欢 王俊彦 陈碧仙 高 晴
电子科技大学 傅俊伟 刘 怡 孙竟飞 张 勇
西南交通大学 陈崇双 刘存青
胡雪伟 杨 晗
西南交通大学 杨端午 邬鸣笛 王春鹏 何 平
西南交通大学 吴培栋 李宗杰 王青元 王 璐
四川师范大学 黄
爽 肖勃飞 李雪梅 赵 凌
成都信息工程学院 且丽莎 王 俊 陈和金 周玉谦
成都信息工程学院 严 波 蒲存伟 李玉辉 方国敏
成都理工大学 黄 涛 张 拓 高 波 教练组
成都理工大学 王春天 李坤明 杨 帅 教练组
四川理工学院 雷直苡 文 昌
吴发洪 刘自山
西南财经大学 谢迟鸣 冯世杰 蔡 晨 丁 川
西南财经大学 杨红强 弓 宇 徐 翔 刘 丽
西南财经大学
杨茂娟 胡 笛 李 路 戴 岱
西南科技大学 程君岭 曹华彬 曲 林 苏 英
西南科技大学 苏 丹 杨 博 康 飞 彭 煜
西南科技大学 杨春宇 张川燕 郭海涛 卢 谦
成都理工大学工程技术学院 王中宝 陈远亮 罗雪瑜 教练组
内江师范学院 秦飞龙
邓 琴 邹维丽 牟廉明
乙组12队 成都大学 胡 娟 刘 强 王 阳 教练组
成都大学 任 建 谢 勇 陈小单 教练组
成都大学 王 聪 张 红 贺光凯 教练组
成都电子机械高等专科学校 宋雷先 屈成炳 高志超 指导小组
成都纺织高等专科学校
黎梏楗 常庆玲 李 磊 陈 仅
达县师范高等专科学校 何 强 张富强 刘 燕 苟 格
四川交通职业技术学院 何 毅 党哲飞 梁 增
钟 韬
西南科技大学 谯惠平 张艺龄 徐忠群 郑 斌
西南科技大学 吕福强 贾建全 杨 锐 杨学南
武警成都指挥学院 罗永济
李 荣 周遵仁 数模组
西南交通大学峨眉分校 黄 梅 李 忠 白海军 符 伟
西南交通大学峨眉分校 陈 峰 李四光 刘 萍 张 跃
四川省一等奖(64队)
甲组46队 四川大学 向 伟 刘 松 张先毛 陈 琼
四川大学 潘 宇 王 辉 郑小凤 邓 瑾
四川大学 夏 超 曹 天 芦 珊 舒慕增
四川大学 刘鸿鹄 马 波 栾 颖 谭英谊
四川大学 范久瑜 郑 刚 李 锴 韩会磊
四川大学 陈 瑶 张仔鸿 钟崇光 邓 瑾
四川大学 李 静 古 博 寇 波 刘晓石
电子科技大学 罗冠华 刘朝生 张 锴
覃思义
电子科技大学 张宏涛 曾维亮 梁春生 杜鸿飞
电子科技大学 侯永兰 聂茂文 谢 川 张 勇
电子科技大学 彭小帆 曾
毅 黄林根 高 晴
电子科技大学 侯德彬 常晓剑 贾世功 覃思义
电子科技大学 王 曦 欧开日 周成刚 高 晴
电子科技大学
李 伟 冯 涛 胡方靖 陈绍刚
西南交通大学 张 波 康晓莉 吴治德 何 平
西南交通大学 张利凤 黄宇涵 樊鹏英 薛长虹
西南交通大学 周登波 温坤华 杨国标 叶建军
西南交通大学 钟科桢 肖鸿威 王选钢 薛长虹
西南交通大学 武晓毅 何增辉 姚
懿 王 璐
西南交通大学 王娟娟 李 霞 杨 韬 袁 俭
四川师范大学 邱长平 游晋峰 王 珊 吕王勇
作者: 涪江
2005-11-28 12:14 回复此发言
2005年高教社杯全国大学生数学竞赛结果
成都理工大学 彭 祥 张国涛
颜雯娟 教练组
成都理工大学 唐资昌 连碧应 郭 彬 教练组
成都理工大学 叶昌炜 罗耀耀 张月梅 教练组
成都信息工程学院
彭洋阳 董小兵 高鹤梅 胡延庆
成都信息工程学院 郭 淳 许文涛 许 甜 王世平
西华大学 肖红强 郭 伟 彭志山 蔺大正
四川理工学院 陈 莉 李凌宇 赵建军 李作安
西南财经大学 曾 文 金 闯 管 微 孙疆明
西南财经大学 刘飞虹 王楚安 谭
明 孙云龙
西南财经大学 金 刚 刘 倩 李 远 孙疆明
中国民航飞行学院 高浩然 贾志宏 朱晨光 数模组
西南石油学院 王
泉 魏 丹 李泳志 李铁军
西南石油学院 王 娟 路 平 何家欢 吴小庆
西南石油学院 咸会雨 李超平 李亮亮 肖辞源
西南石油学院 李 珍 陈方方 詹 华 刘小华
西南石油学院 周俊杰 何良泉 唐京辉 钟仪华
西南石油学院 张玉勇 谢 骏
冯利娟 李玲娜
西南科技大学 罗启铭 胡 成 杨宁刚 林 军等
西南科技大学 鲁 彪 连 杰 马 骏 蒋剑军
西南科技大学
赵 俊 黄敏敏 吴玲瑕 杨学南等
西华师范大学 陈时效 刘 静 谭邹卿 孙 海
西华师范大学 齐宝平 黄永红 王 佼 陈友军
乐山师范学院 罗修金 赖 林 汪中友 汪天飞
内江师范学院 毕庆博 袁道秀 冯力秀 吴开腾
内江师范学院 陈兴海 代锦春
唐明会 吴开腾
乙组
18队 西华大学 熊玲丽 徐 黎 袁 冬 胡 明
西华大学 刘伯东 袁小琼 王 咏 李克俊
四川理工学院
徐 俊 钟 涛 吴应丰 高 尉
中国民航飞行学院 李秋云 严传利 邱艳红 数模组
中国民航飞行学院 钱 戈 尹岚钰 闵燕均 周亚军
西南科技大学 杨国荣 端木晖 王 东 郑克龙等
西华师范大学 陈加伟 赵优秀 周小刚 郑伯川
攀枝花学院 李平生 蹇清平 刘
伟 李思霖等
成都纺织高等专科学校 李莉花 杨 燕 张志杰 袁 勋
成都电子机械高等专科学校 李如权 孔祥生 柳 卿 指导小组
宜宾学院 曾维利 李仁铸 王 敏 教练组
武警成都指挥学院 高 睿 王 鹏 赵 波 数模组
达县师范高等专科学校 李 德 彭
勇 郭 娟 苏海军
达县师范高等专科学校 王 勇 庞 亮 鞠光炳 苏海军
达县师范高等专科学校 辜泽强 封贵阳 何梦雯 苟 格
四川工商职业技术学院 江成伟 陈 香 张 松 华 剑
成都理工大学工程技术学院 罗凌波 罗超全 张卫军 教练组
四川电力职业技术学院 王 飞 汪 维 王小文 指导小组
四川省二等奖(80队)
甲组 56队 四川大学 姚 经 巩 杰
陈永恒 邹述超
四川大学 李世泽 廖爽爽 纪 亮 陈 琼
四川大学 唐海云 叶 星 徐翔宇 邓 瑾
四川大学 徐 堃 满 欣
龙 巧 周 杰
四川大学 姚 赟 黄 磊 杨 轩 李 珊
四川大学 赵 明 雷 一 高 飞 舒慕增
四川大学 何 健 周晓阳
何姜江 陈敬敏
四川大学 黄 晶 易 兰 张 林 陈敬敏
四川大学 杨 羿 张 路 刘宗钰 李 珊
电子科技大学 马 涛 李
川 张晛譞 覃思义
电子科技大学 鲁文龙 王 雄 郑 宇 杜鸿飞
电子科技大学 倪 威 李俊龙 郝英楠 杜鸿飞
电子科技大学
张 超 杨 帆 吕信江 覃思义
西南交通大学 于贺威 李发智 张鸿春 薛长虹
西南交通大学 陈清爽 李 想 苏渊 叶建军
西南交通大学 马果垒 王恒佩 赵武英 杨 晗
西南交通大学 胡 俊 汤 义 李 芳 杨 晗
西南交通大学 王 雷 邱 峻 叶
佳 蒲 伟
西南交通大学 郦 彦 杨 倞 廖中文 蒲 伟
四川师范大学 付 蓉 张 翼 钟 珍 熊清泉
四川师范大学 徐 哲
项怡熹 郭振华 熊清泉
四川师范大学 邱 诚 李世浩 姚 洪 李昌勇
四川师范大学 余 爽 何成泰 邹 涛 赵 凌
四川师范大学 龚靖婷 赵 姗 冯春霞 吕王勇
成都理工大学 任继奎 邱垂锐 王双丽 教练组
成都理工大学 吕彩丽 苏 伟 刘
瑞 教练组
成都理工大学 邓安嫦 邹 辉 冯胜辉 教练组
作者: 涪江 2005-11-28 12:14 回复此发言
3 2005年高教社杯全国大学生数学竞赛结果
成都理工大学 胡耀军 王施人 彭 雷 教练组
成都信息工程学院 熊 俊
文丽琼 王 蕊 吴泽中
成都信息工程学院 辛 亮 汪开元 范修宏 杨 韧
成都信息工程学院 陈 行 刘 星 何向东 何蓉华
西华大学 查振华 莫邕毅 严海杨 蒲 俊
西华大学 王 谊 彭 文 张 珂 裴 峥
四川理工大学 张 剑 陶 燕 兰晓峰
黎克麟
西南财经大学 郑时雨 王文娟 车春梅 孙疆明
西南财经大学 朱局凯 陈 懿 魏绪仲 孙疆明
西南财经大学 张晋杨 付
强 张小江 李绍文
西南财经大学 李 林 杨 柳 覃 磊 丁 川
西南财经大学 汪昊旻 李毓灵 杨 捷 李绍文
西南民族大学
李世全 张 丹 陈湘柏 黄天云等
西南科技大学 郭利平 白 松 张 锐 郝金华
西南科技大学 杜正军 刘 强 周 亮 林 军等
西南科技大学 胡红波 李庆斌 傅成元 肖光灿
西华师范大学 李嘉浩 刘子丽 戴文娟 潘大志
西华师范大学 林友岳 郭 娜
段玉娟 熊 华
西华师范大学 王 颖 肖 军 郑鸿燕 冯长焕
西华师范大学 刘红波 杨 红 邓小华 陈豫眉
西华师范大学
刘德虎 罗 艺 曾 云 李云飞
西华师范大学 胡利强 周小丽 翁志超 肖胜超
成都大学 周佳杰 王 梅 倪林红 教练组
成都大学 张永辉 凌世波 薛 凌 教练组
西南交通大学峨眉校区 韩金刚 杨 璨 范 翊 张兴元
西南交通大学峨眉校区 向活跃
王 磊 钱 瑶 徐昌贵
西南交通大学峨眉校区 黄方圆 马晓昕 涂友军 田俐萍
内江师范学院 任志强 范瑞雅 陈 丽 牟廉明
达县师范高等专科学校 王 海 杨孝勇 梁远银 冯向东
乙组24队 成都信息工程学院 夏 强 李才明 刘照宇 徐 琼
西华大学
田世中 肖 曦 唐露梅 王 平
西南民族大学 张雪梅 王 鹏 田 伟 宋建成等
西南民族大学 钱春君 罗国镇 孟凡淇 宋建成等
西南民族大学 胡珍珍 陈海雪 冯 钊 宋建成等
西南科技大学 龚 超 屈 鹰 殷 瑛 郑克龙等
四川农业大学 邓立国 毛 弛
邓其兰 程 莉
四川农业大学 田晓刚 李凌江 赵 文 邓阳春
攀枝花学院 '陈滇军 王晓桥 刘承浪 丁耀青等
成都纺织高等专科学校 张进军 许伦成 邹 义 张步林
成都电子机械高等专科学校 潘友智 李锡宏 吴海军 指导小组
宜宾学院
涂玉莲 冷应斌 李海林 教练组
成都航空职业技术学院 黄义忠 陈思涛 张 娟 教师组
四川职业技术学院 刘虹伟 陈 群 李 明
建模组
四川职业技术学院 赵世伟 杨 慧 何加林 建模组
四川工程职业技术学院 王元刚 姜丽苹 赵 斌 指导小组
四川工程职业技术学院 王 燕 何 平 杨清雄 指导小组
四川建筑职业技术学院 舒之伟 罗建男 张济之 黄非难
四川工商职业技术学院 邓 娇 吴昌明 邬 艳 杨培辉
四川电力职业技术学院 冯 昆 刘 旭 周隆霞 指导小组
宜宾职业技术学院 李姣艳 刘晓焱 杨 洋 阮杰昌等
宜宾职业技术学院 邵晓超 李晓青 程辉 兰华龙等
成都理工大学工程技术学院 符 林 朱兴国 羊春香 教练组
四川天一学院 蒋君正 谢 聪 蔡武强 贾克裕
四川省三等奖
甲组56队 四川大学 伍泽东 刘亚东 申春梅 韩会磊
四川大学 陈章友 彭灵芝 但唐强 周 杰
四川大学 黄朝东 肖龙帅
刘婷婷 韩会磊
四川大学 许 鹏 程贤坤 马 楠 陈敬敏
电子科技大学 伍 捷 蒋其梦 武 鹏 张 勇
电子科技大学 陈 伟
甄树慧 陈苏超 张 勇
电子科技大学 林 宵 赵彦辉 孙 宁 杜鸿飞
西南交通大学 晏 阳 赵万平 于 浩 徐跃良
西南交通大学 游家训 栾春旭 何常红 赵联文
西南交通大学 王柄达 李 华 周宇明 何 平
西南交通大学 刘加利 申 宇
张栋科 王 璐
西南交通大学 陈月梨 方 萍 高晓玲 袁 俭
西南交通大学 施丽丽 景 丽 覃小春 袁 俭
四川师范大学 康
胜 余有彬 王艳华 李昌勇
四川师范大学 周 正 冯伦进 刘 锐 孙峪怀
作者: 涪江 2005-11-28 12:14
回复此发言
4 2005年高教社杯全国大学生数学竞赛结果
四川师范大学 张 婷 莫 艳 孙 峰 冯 山
成都信息工程学院
黄颖秋 余 兢 姜明富 梅志红
西华大学 景 雯 陈 坚 魏再平 张朝伦
西华大学 严有均 刘兴燕 伍 利 张朝伦
西华大学
赵 金 朱树英 林雪梅 华 巍
四川理工学院 付伯承 杨 健 文 枭 兰恒友
四川理工学院 王田堂 李海军 沙元贺 张新华
四川理工学院 谢 普 智蒋力 卿 琳 陈德勤
四川理工学院 余光蓉 史晓红 常少健 高 尉
四川理工学院 杨继东 杨云亮 颜
萍 谢 巍
四川理工学院 康小兵 阚思洋 杨 岩 叶 俊
四川理工学院 王 平 任海龙 向中贵 柏宏斌
四川理工学院 江建华
宁广源 陈厚杞 柏宏斌
西南财经大学 罗少军 胡晨 何淼阳 孙云龙
西南财经大学 林水仙 周俊斌 柳利花 龚金国
西南民族大学 李 鹏 胡 晓 王军华 黄天云等
西南民族大学 李 颖 潘照辉 刘栋梁 黄天云等
中国民航飞行学院 孙 莉
吴萃平 胡宗凤 数模组
中国民航飞行学院 杨 哲 李 鹏 李艳莉 数模组
西南石油学院 陈 伟 王 帅 桂林燕 刘志斌
西南石油学院 李剑波 周继烽 张 义 刘建兴
西南科技大学 王洪魁 汤历平 王仲恒 彭 煜
西南科技大学 姚若鹏 冯力天
倪海涛 彭 煜
西南科技大学 孙英福 金燕飞 谢文龙 鲜大权
西南科技大学 李 林 邓 勇 蒋林秋 郑克龙等
西华师范大学
刘汉光 孙 林 申芳华 陈 强
西华师范大学 邓 娟 李福香 罗 俊 谭代伦
四川农业大学 马文彬 杨 勇 何 东 潘 杰
成都大学 王毅峰 郑 杰 袁子建 教练组
成都大学 马 奔 罗 英 熊 斌 教练组
成都大学 肖春亮 蒲 涛 谷 菲 教练组
攀枝花学院 周靖东 方 超 杨代英 罗 淼等
西南交通大学峨眉校区 熊恒武 李跃旭 黄立文 符 伟
西南交通大学峨眉校区
陈兴魏 曹 野 李朝东 徐昌贵
西南交通大学峨眉校区 曾侧伦 赖柏林 陈 强 万美凯
内江师范学院 黄海果 黄小艳 冯祥永 牟廉明
内江师范学院 邓光毅 王加友 张红霞 吴开腾
内江师范学院 邢红卫 程抒曼 余小艳 王凡彬
宜宾学院 李 华 申 丽 李玉莲
教练组
达县师范高等专科学校 赵崇江 谢天强 李明星 冯向东
成都理工大学工程技术学院 田丰年 王 明 贾玉鑫 教练组
乙组24队 成都信息工程学院 黄 维 王子丹 范余茂 徐 琼
四川理工学院 高 翔 陈川江 张 莉 雷远民
四川理工学院 郭
陈 邹海玲 姜黎黎 张新华
四川理工学院 李阳春 罗 莉 甘 珏 陈德勤
西南民族大学 张春雨 武亚萍 于素强 宋建成等
西南民族大学 王吉强 阳 岚 冯亚娥 宋建成等
中国民航飞行学院 刘 鹏 郑 冉 杨晓君 数模组
四川农业大学 张民勇
母培松 张晓林 邓阳春
四川农业大学 唐 波 张 渊 吕 瑶 刘旭东
攀枝花学院 张 珍 易 平 段 超 林宗兵等
成都电子机械高等专科学校 廖新梁 任金平 张明忠 指导小组
宜宾学院 徐文龙 杨 雄 邓良军 教练组
绵阳师范学院 徐 丹
田程香 潘志刚 任秋道
绵阳师范学院 赵 芳 卢 敏 舒 勇 宋曰聪
武警成都指挥学院 陈俊屹 张 驰 张齐飞 数模组
武警成都指挥学院 丁 琛 陈 晶 李佳昊 数模组
武警成都指挥学院 李 强 祝亚林 徐仕哲 数模组
阿坝师范高等专科学校
廖海军 欧 阳 曾泽英 蒋自国
成都航空职业技术学院 刘益秀 文 军 彭洪超 教师组
成都航空职业技术学院 李正林 李 建 马春雨
教师组
四川工程职业技术学院 魏俊恒 舒 菲 李 科 指导小组
康定民族师范高等专科学校 游 燕 田 玲 付 勇 潘家鑫
宜宾职业技术学院 赵春旭 王俊梅 张 未 王立平等
四川天一学院 张 武 宋晓明 周 钊 毛小英
18854
| 引用 (climbercai @ 2005年09月30日
15时07分) |
|
概率分布偏态中的微偏怎么判定?有没有相关的经验规则,望告知,多谢了! |
不太明白你说的微偏指的是什么意思?是不是偏态的程度不是很大?如果是偏态程度,这个有一个专门的指标来衡量分布的偏态程度,你应该知道的哦.
18854概率分布偏态中的微偏怎么判定?有没有相关的经验规则,望告知,多谢了!
18854
| 引用 (978301 @ 2005年10月15日
08时08分) |
| 引用 (climbercai @ 2005年09月30日
15时07分) | |
概率分布偏态中的微偏怎么判定?有没有相关的经验规则,望告知,多谢了! |
不太明白你说的微偏指的是什么意思?是不是偏态的程度不是很大?如果是偏态程度,这个有一个专门的指标来衡量分布的偏态程度,你应该知道的哦.
|
就是,有一个偏度的定义,跟相关系数一样,好象小于0.3属于微偏
18857排序 大专院校名称 合计 发明 实用新型 外观设计
1 清华大学 527 454 73 0
2 上海交通大学 332 302 30 0
3 浙江大学 321
184 134 3
4 天津大学 165 111 53 1
5 武汉大学 163 114 48 1
6 华南理工大学 153 91 62 0
7 西安交通大学 131 104 27 0
8 华中科技大学 125 57 68 0
9 四川大学 111 91 20 0
10
东南大学 102 60 42 0
(教育部科技发展中心供稿)
188581、清华
18
1、浙大
18
3、哈工大14
4、天大11
5、上海交大10
5、北航10
5、东南大学10
8、西安交大9
9、华中科大8
9、北京理工8
11、中国科大7
11、大工7
11、中南大学7
14、西北工大5
15、北大4
15、吉大4
15、同济大学4
18、四川大学3
19、南大2
18859学校 2004-TO-PRESENT 2005-TO-PRESENT
清华大学 138篇 20篇
上海交大
103篇 9篇
西军电 47篇 4篇
哈工大 31篇 13篇
浙江大学 30篇
4篇
复旦大学 23篇 5篇
东南大学 24篇 3篇
北邮 22篇 5篇
成电 22篇
1篇
西安交大 20篇 2篇
华中科大 20篇 5篇
北京大学 13篇 1篇
武汉大学
11篇 4篇
天津大学 9篇 3篇
科大 3篇 0篇
南京大学 2篇 0篇
北航 1篇
1篇
同济大学 1篇 0篇
18859哈哈
挺强的
18860当然不是计算了,只有基础没有招够
18860问大连理工计算数学报送的多么?
18860听说大连理工大学去年没招够
18860真的吗?哪个专业没招够!
18860没招够是真的
可那不代表没人考
大连理工大学的题出的比较难
上线的人没够
18861请问我这个证明错在哪
正确结论是:紧空间的任一闭子集是紧的
我却得出任意子集都是紧的post-21-112807
1940.jpg
18861考虑闭区间[0,1]的子集(0,1),覆盖为{(1/n,1)},n∈N
另外,很难理解“有X任意开覆盖得不到A的任意开覆盖
”的真确含义。
18861你的证明的逻辑顺序不对
符号不好打
有X任意开覆盖得不到A的任意开覆盖
18861
| 引用 (流形 @ 2005年10月08日
21时20分) |
你的证明的逻辑顺序不对
符号不好打
有X任意开覆盖得不到A的任意开覆盖
|
谢谢,
是这里错了
18865我现在学习泛函分析,感觉自己独立思考很困难,总得看习题的答案,但来得快去得也快,当时看明白了,很快就忘记了,但不看答案自己又不会,总感觉做题找不到思路,请问该怎么办呢?
谢谢!
18865我想可从容易的题目做起,一步一步打好基础.或者先把实变的基础打好.
18865看书吧
看多了就发现只要用证明定理的手段
一般的题目都好弄
推荐:巴拿赫空间引论
这本书较易自学
18865完全浸入式学习原理对自学困难课程很有效
理解证明关键就是理解证明的要紧点和命题的重要性,
用康德是的思维理解证明:这是如何可能的
18865我一个教随机过程的老师曾告诉我们,拿到总看不下去的书,最好方法多看,拿笔在纸上边看边记,一个内容这样5到6遍,直到你都背下来,这样你就从心里接受他的内容和思想,这大概叫洗脑吧
没办法的办法.作题也如此.
18867好帖,不知道有没有招收生物信息学博士的专业,比如研究生物信息的组合算法?
18867目前生物数学属于应用数学专业, 因此招收生物数学博士的导师很多. 但主要是: 微分方程动力系统和生态系统两个方向.
我所知道的情况现列举如下:
1) 陈兰荪(大连理工大学)
2) 马知恩(西安交通大学)
3)
陆征一(温州大学, 博士招生挂靠在中科院成都计算机应用研究所)
4) 王稳地(西南师范大学)
5)
李自珍(兰州大学)
6) 靳祯(中北大学)
其他,宋新宇, 宋国华, 徐瑞, 唐云, 等等. 一时记不起来了.
以后再续.
18867另外,再补充一点,本来生物数学在我国学科分类中是属于应用数学的,但在中科大生物则直接是二级学科,详见http://gradschool.ustc.edu.cn/ylb/xk/xwsq/bsdyl.htm,只是生物数学的带头人蒋继发教授现在同济大学。
18867其实,凡是跟招收微分方程与动力系统的教授都可以做生物数学研究的。
中科院动物所,植物所都有这方面的专家。
但,据我所知国内最牛的一所大家是鞍山师范学院,数学系只有6个教授,但6个教授全是搞生物数学的。这恐怕是国际领先的了!!!
另外,从目前就业来看,生物数学名称不见得比微分方程与动力系统好!
谢谢。
18867最近中科院成立了上海生物计算研究所,但不知道有没有招博士
18867陆征一教授也招生物数学?好像是招计算类的吧!
188680.375
18868应该是3/4吧
18868是

,所以是0.375,即3/8,最直观的方法就是画个图
18868这是几何概率问题,答案是边长为10的正方形的八分之一,即0.125
18868是不是0.125?
1886825%
18868有两实数
a
,b(a∈(0,10);b∈(0,10)
且a>b)
求
a
-b≤5
的概率是多少。
18868It's clear enough if you draft this problem.
The answer is 3/4
.
18868是3/4?
18869计算机数学与计算机代数系统
计算机科学技术的迅猛发展对数学科学产生了巨大的冲击, 对数学研究的观念及研究方法都产生了深刻的影响.
引发这场冲击波的最主要的数学事件是“四色定理”的证明.
1976年,美国Illinois大学的两名年轻数学家和一位计算机专家利用计算机成功地解决了困扰数学界长达近两百年之久的著名的四色定理,
这一成果震惊了整个数学界. 众所周知,数学问题只能通过严格的数学逻辑推理才能得到证明, 但四色定理的结果则是借助计算机技术并运用归纳法而得,
因而在当时有一大批数学家不承认这是一个证明. 经过长时间的争论,这一结果最终还是被数学界接受了,
并由此引发了数学家们的思考,从而产生了“数学实验”这一新的数学研究方法.
在此后的数十年,数学科学中的一个新的具有极大生命力的分支---计算机数学得到了人们广泛关注并有了长足的发展,
其主要组成就是数学实验.
所谓数学实验, 简单地说,
就是用计算机代替笔和纸以及人的部分脑力劳动进行科学计算、数学推理、猜想的证明以及智能化文字处理等.
科学计算包括两类:一类是纯数值的计算,例如求函数值、方程的数值解等;另一类是
符号计算, 又称代数运算,这是一种智能化的计算, 处理的是符号, 符号可以代表整数、有理数、实数和复数,
也可以代表多项式、函数,还可以代表数学结构如集合、群等.
我们在数学的教学和研究中通常用笔和纸进行的数学运算多为符号运算.
数学计算常常是一项非常繁琐的工作,
事实上,人类很早就意识到在解决实际问题时对于数学特别是“计算”(包括数值计算,逻辑运算,符号计算,图形计算等)的极端重要性,并致力于“计算”的机械化及计算机械的发明创造(如算盘,对数计算器,计算尺,加法机,Leibnitz演算机,差分机,
等等). 直到计算机的出现和发展才逐步 解决了数值计算中的困难. 从计算机发明到现在五十多年间, 用计算机进行的科学计算主要是数值计算,
如天气预报,油藏模拟,航天等.
而用计算机进行符号计算是数学和计算机领域的一个新的发展方向.
长期以来,数学家和计算机科学家梦想用计算机代替人脑进行代数符号运算以及数学的各种处理, 使数学走向“机械化”的道路, 从而也使计算机本身更加智能化.
我国著名数学家吴文俊院士首先提出的“吴方法”为数学处理在计算机上的实现奠定了理论基础, 并在几何定理机械证明,方程组求解, 微分几何, 理论物理,
机器人学, 计算机图形学等数学和高科技领域相继获得了广泛的应用.
20世纪80年代以来, 用计算机进行符号计算的研究在国外发展非常迅速,
涉及的数学领域不断地扩大, 出现了多种符号运算方法,计算程序和系统, 如符号运算,符号和代数运算,符号处理,计算机代数等等.
这是一个以构造性数学为核心, 以计算机实现为目标,以实用的算法为研究内容,
以实用程序或软件为成果的研究领域,这个领域被称为计算机数学.计算机数学的发展逐步产生了一些独立的计算机程序库,称为计算机代数系统.
一部分计算机代数系统发展成为完整的专用或通用的计算机数学软件, 如美国的Mathematica, Matlab,
加拿大的Maple等.
根据计算机代数系统的用途, 将其分为两类:专用系统和通用系统.
专用系统主要是为解决物理和数学某些分支中的特殊问题而设计的, 专用系统在符号和数据结构上都适用于相应的领域而且多数是用低级语言编写的,
因此专业人员使用很方便, 计算速度也较快, 它们在专业问题的研究中起着重要的作用;通用系统具有多种数据结构和丰富的数学函数,
应用领域广泛.
总之, 计算机数学是数学研究领域的新方向,计算机数学的产品---数学软件在不断地发展、提高和完善.
计算机代数系统为数学的教学、研究和应用开辟了新天地, 既使数学实验成为可能, 又使数学成果直接为实际服务以及使数学的大众化成为可能.
18869我也在自学数学,以前也是个程序员,在华为开发,测试都干过。现在离职在家,决心是搞计算机代数系统的研究与开发。再具体一点,就是研究如何在用计算机作为符号计算的工具,来进行数学研究。我选择的数学方向是代数学的群论,群表示论等内容的计算机代数研究。
我的数学基础有一点,那是因为我是四川大学数学系毕业后转行搞IT的,现在又想回头转到数学中去。为了能用让这近十年来的IT工作经验积累的东西,同时又能进行我心爱的数学研究,所以选择了搞计算机代数系统这个方向。
现在我最迫切需要的是要有人与我讨论关于群的计算机代数系统,例如:GAP(这是国外专门针对群论的计算机代数系统),我自己也在搞。感觉目标有点不明确。我研究计算机代数系统的深层目的是将数学家的思维在计算机中表达出来,而不只是在论文中以文字的方式来表达。那样的表达方式太抽象,计算机表达就可以生动得多。
目前我自己也开发了一个用JAVA写的用于群计算的程序。基于以上思想,我在程序中实现的功能包括:在一个画布上显示一个群的所有元素,并且可以将群的元素对称地分布在画布上,并且可以根据一些运动规则,让群中的元素动起来,以期达到更好地理解群的某些概念的目的。
18870计算机数学研究领域一个重要内容是计算机辅助分析(推理、证明、求解), 这是近20年来国内外计算机科学、计算机数学研究中的重要课题,
也是我国重点基础研究(973)资助的课题(《数学机械化与自动推理平台》, 《数学机械化及其在信息科学中的应用》).
事实上,
不论是机器代替体力劳动, 或是计算机代替某种脑力劳动, 其所以成为可能, 关键在于所需代替的劳动已经“机械化”. 所谓机械化, 简单地说,
就是“刻板化”或“规格化”. 数学问题的机械化, 要求在运算或证明过程中, 每前进一步之后, 都有一个确定的、必须选择的下一步,
这样沿着一条有规律的、刻板 的道路, 一直达到结论. 这正是计算机辅助分析的本质.
另一方面, 我们可以简单地将数学研究分为两类:
存在性数学与构造性数学. 存在性数学在于研究数学对象的存在性以及它们的性质和之间的相互关系, 它是近代数学发展的主流.
而构造性则为数学的应用提供支撑, 也是计算机辅助分析的基础.
计算机辅助分析的基本内容主要有两方面:
一方面,将传统数学中可以算法化求解、求证的问题利用计算机及数学软件完成或实现; 另一方面, 实现计算机辅助分析首先要将问题转化为可算法化问题,
然后按照MAP思想, 即Model (模型)+Algorithm (算法)+Program} (程序), 确定正确的具有操作性的算法,
再选择适当的平台设计相应的计算机程序实现计算机辅助分析. 也就是:
问题→小问题→数学问题→算法→伪码→程序→计算机实现
由此可见,
计算机辅助分析的基础是算法设计和程序设计.
实践证明, 计算机辅助分析是分析问题, 解决问题的有效途径,
特别是解决数学研究中常常出现的超大规模的计算问题的有力工具, 因为我们根本无法想象手工去进行成千上万项多项式的计算问题,
而这则是现代数学研究中常见的问题.
18871这个我好像明白了
因为Ee[e|X]=0
所以明白了
18871实际上,X是回归分析中的数据矩阵,e是总体中的一个假设正态的扰动(好像就是白噪声),在这里,可以不用深究
X和e
是否确切为向量或者只是两个一维变量
在一本计量经济书中,原文为:
E[e|X]=0,那么就是说Cov[X,e]=0.由于叠期望定理
Ex{E[e|X]}=E[e],我们可以把这个写为
ExEe[Xe]=...(省略号是将e的表达式代入)
18871Ex{E[e|X]}
是否可以等价于
ExEe[Xe]
当X给定的时候,e的条件期望和Xe直接对e求期望是一回事情?
虽然道理上好像一样,可是结果也是一样的么?
18871Xe什么意思?e是下标还是什么?
18872设f(x)在R有定义且恒不为零,f'(x)存在且对任何x,y
都有f(x+y)=f(x)*f(y),求f(x),f'(x)
18872f(x) 恒等于1,导数为0
18872一种解法!post-8-1128831434.gif
18875不可以说浪费自己的青春。
18875
[SIZE=1] 是选择一所自己十分有把握的学校呢?
还是挑战自己,报考顶尖的学校呢?今年不行,明年再考一次呢。
苦恼呀!马上就要报名了。
想听听大家的想法!
谢谢!
18875我也正为此苦恼呢!
18875选个自己喜欢的学校最好,毕竟顶尖的学校不好考,
考不上又浪费自己的青春。
考上的人是少数啊,选个自己觉得能考上的名牌也不错啊
18877太好啦!我又可以找资料
18877十一长假期间,网络接入,数据库等一直在调整,所以出现暂时无法登陆,
现在恢复正常,希望大家继续关注博士家园论坛!
对于耽误大家的讨论交流深表歉意!
博士家园管理委员会
18877回来当然高兴了
就是一直不知道什么时候能登陆,很是郁闷啊
要是能在之前给个通知就好了
ps:你的QQ是不是换了?
18877
| 引用 (tobyqin @ 2005年10月08日
16时13分) |
回来当然高兴了
就是一直不知道什么时候能登陆,很是郁闷啊
要是能在之前给个通知就好了
ps:你的QQ是不是换了?
|
抱歉啊,一般会给出通知,但此次正值十一长假,所以没有及时通知.
QQ:290699606
18877啊呀
终于通了
可是把我给别坏了
呵呵
18877能进来真高兴,希望网站永葆活力
18878解答post-38-1128763797.gif
18878该命题是否正确呢?如果是正确的证明它,如果不是正确的给一个反例!post-38-1128759
181.ibf
188781211post-38-1128759202.ibf
18878时隔八天第一贴:post-38-1128759560.gif
18882顶一下
18882顶一下
18882a,A(a),A^2(a),...成为a生成的循环子空间
设A是数域F上n维线性空间V的线性变换,如果存在非零向量a属于V,使得a生成的循环子
空间等于V,则称A为循环变换。
帮我做一下吧
18882第三题用若当标准形,第四题用数学归纳法。
18882什么是循环变换??
18882请帮我做一下把
18882请帮我做一下把
188821.设A是数域F上n维线性空间V的线性变换,如果存在非零向量a属于V,使得a生成的循环子 空间等于V,则称A为循环变换。
如果A的最小多项式等于A的特征多项式,则A为循环变换
2.如果数域F上n维线性空间V的线性变换A的二次幂A^2为循环变换,则A本身也是循环变换
3.如果方阵A的特征值全是1。证明方阵A的任意次幂都于A相似
4.如果方阵A是n阶可逆方阵,且A和A^k相似,k是正整数,证明:方阵A的特征值都是单位根
18882请大家帮忙做做看
18882帮你顶
18887佩服!佩服!
回去努力喽。
数学与我们同在!
18887美国的《科学杂志》(《SCIENTIAMAGNA》)是一份比较有影响的专业学术杂志,在美国用英文出版,全球发行,它上面的文章一经发表就编入全球论文索引(ISSN),内容包括数学、哲学、语言学等专业论文,全球学者都可以投稿。
可是谁又会想到这份知名美国杂志的编辑部却坐落在我市西北大学数学系张文鹏教授的办公室,张教授是它的主编。
怎样工作———
“我所做的工作主要是审稿,全球各地的学者可以通过电子邮件、信件等各种形式把他们的论文寄给我,然后我编辑审阅通过后,再以电子版形式传给美国研究出版社,他们再在美国用电子版和印刷版公开出版发行。”张教授大概给记者简单介绍了自己的这份特殊工作。
教授其人———
为什么一个美国专业学术杂志找一个中国学者当主编?这和张教授在自己研究的数学领域所取得的巨大成就是分不开的。张文鹏教授今年47岁,是西北大学数学系的博士生导师,我国知名数学家,他在数论学分支中的解析数论和组合数论的研究中处于国际领先位置。
怎样受邀———
问起怎么当上了这个主编,张教授说自己以前就经常给这家杂志投稿,还给他们提过好多建议,所以美国研究出版社在这本杂志今年改版后,想到请他来当主编。他也很乐意当这个主编,“我当这个编辑是没有工资的,美国的研究出版社就是把杂志编辑的冠名权给了西北大学,注明由西北大学编辑,这是对我们大学的极大宣传。再者编辑了这个杂志,我们国内的优秀论文就有了一个和国际接轨的平台,把我们的研究成果以最快速度介绍到世界去,目前第一期印刷版马上就出版了,可在印刷版出版前,我们杂志的电子版在国际互联网上已经发表,国内一个学者的一篇论文,已经有美国学者看到后给它写了评论,这在以前是不可想象的。”其实张教授这个免费义工还是有“私心”的,“我们学生的论文发表也多了一个园地,还可以增强学生研究的国际视野。”张教授笑着说。
记者了解到张教授在培养学生上也成绩显著,目前他的学生中硕士、博士在全国知名学术刊物上发表研究成果的比比皆是,今年他的在读博士刘华宇还获得了第七届钟家庆数学奖,是该奖项设立以来西北首位获得此项殊荣的在读博士。
188882楼已经基本上解答了,确实是高人。
另外n!是不正确的答案……
18888第1题好象很简单,数学归纳法,n!,怎么没人回啊
188882n个数,n个1,n个-1组成一个2n长的数列
要求前k项之和>=0
对所有的(0<=k<=2n)的k满足
问这样的数列共有几个
有A、B、C三个药瓶,瓶A装有
1997片药,瓶B和瓶C都是空的,装满时可分别装97和
19片药,每片药含100个单位有效成分,每开瓶一次该瓶内没片药
18888第1题学过Catalan数的话就好做了.
18888第2题是97年冬令营(CMO)的第6题,相当有难度,但主要还是很麻烦,光答案就写了不止一页纸!!
18888好难啊!
18888好难!
18888不要搞这么难的,一般的题目拿来探讨就好!
18890请问大家在数论学习中采用哪些教材!!
18890柯召,孙绮的<数论讲义>不错, 不过题目有点难, 但是, 怕做难题的话就别学数论了, 呵呵!
18890华罗庚的<数论导引>是一本不可多得的自学好书
18890GTM教材: A Classical Introduction of Medern Number Theory
18890柯召的《数论讲义》是很好的
潘承栋 潘承彪的《初等数论》
也挺好的
18890不会只采用这几本吧!研究生课程一般采用哪些 啊!
18891我怎么没发现呢,要不大哥你把网址发过来吧
18891好,谢谢,我去看看去,我记得好像没这本书!!看看再说
18891去南开数学学院ftp下载!我下了,太大,没法给你传!
18891最近学习解析数论,需要用到华老的<堆垒素数论>,请问哪位大哥有这本书的电子版,能传小弟一份,小弟不胜感激!!我的邮箱:w.xinghu@gmail.com
多谢啦!!!
18891对不起了,兄弟!我看错了,我原来下的是数论导引,pdg格式的!
18891你在哪个学校学解析数论,交个朋友。我的qq271690275
18891自学,明年进中科院或山大!考进去的话
18891华罗庚先生的数论著作的各种版本
[1] 华罗庚. 堆垒素数论. 北京: 科学出版社,
1957年. 158页.
俄文本:Хуа
Ло-Кен. Аддитивная теория простых чисел. Труды Математического института
им. В. А. Стеклова 22(
1947) ,
179с.
英文本:L.-K. Hua, Additive theory of
prime numbers, Translations of Mathematical Monographs, Vol. 13, American
Mathematical Society, Providence, Rhode Island,
1965.
德文本:Hua,
Loo-Keng,. Additive Primzahltheorie. Leipzig,
1959.
174 S.
[2] 华罗庚.
指数和的估计及其在数论中的应用. 北京: 科学出版社,
1963年. 134页.
俄文本:Хуа Ло-ген. Метод
тригонометрических сумм и его применения в теории чисел. Перев. с
англ.-М.: Мир,
1964.-
187 с.
德文本:Hua Loo-Keng.Abschätzungen
von Exponentialsummen und ihre Anwendung in der Zahlentheorie. - 2.,
völlig neubearb. Aufl. Leipzig: Teubner.
1959.
[3] 华罗庚. 数论导引.
北京:科学出版社,
1979年.
英文版:Hua Loo Keng: Introduction to Number Theory,
Springer–Verlag, Berlin–New York,
1982.
18891请问楼上的有没有电子版?
18892
| 引用 (helend @ 2005年10月09日
21时11分) |
超星的图书要吗?
告诉我邮箱,我下载后,给你发到邮箱去! |
好的,多谢,
但是不知道超星下载之后在我这里是否能打开,你先发过来再说吧。
我的email:xubiaohuaibei01@163.com(最好是这个)
或者:xubiao123@gmail.com
18892超星的图书要吗?
告诉我邮箱,我下载后,给你发到邮箱去!
18892王松桂的<线性模型的理论及其应用>,安徽教育出版社,
1987.这本书怎么才可以得到,
如果有电子版发个过来,多谢.qq:352615671
18893求《常微分方程边值问题和sturm比较理论引论》 华中师大出版社 邓宗琦
万分感谢
18894我们刚开拓扑,学得好吃力,看到这么漂亮的图形,才又给了我一点对拓扑的兴趣咯!
18894同感
18894拓扑真的很有意思啊!!!!]
18894点集拓扑还是代数拓扑?
18894应该是点集拓扑
18894代数拓扑也挺有意思
不同的边界,不同的同调群!
18894怎么我看不到图啊。
18894學習拓墣 不要花太多時間在 metrizability 問題 也就是各種 T1 T2 T3 T4 T5 條件和可賦距問題, 看懂緊致性,
連續 , 開閉集 就可以, 趕快先去學 基本群 和 拓墣流型的性質, 以及同調群 同倫群 及其應用. 就可以. 所謂的 點集拓墣或是 general
拓墣 , 不需要花太多時間就可以唸完 (兩個星期吧)...真正的拓墣在後面 代數拓墣或是微分拓墣
18897恭喜贺喜
18898可以用连通图的知识来解吗?
18898不难,用抽屉原理,在李乔写的《走向数学丛书--拉姆赛理论》的第六也可以找到
18898任意给定一含 n^2+1项的实数序列(各项互不相同).证明:一定可以从这个数列中找出一含n+1项的单调子列
18898兄弟,你的题意不明确阿
18899大会报告:
http://www.icm2006.org/scientificprogram/p...lenarylectures/分组报告:
http://www.icm2006.org/scientificprogram/s...ectionlectures/下面是大会一小时报告人具体名单
Percy Deift
Courant Institute of Mathematical Sciences, New
York University, New York,
USA
Jean-Pierre Demailly
Université Joseph Fourier, Grenoble, France
Ronald DeVore
University of South Carolina, Columbia, USA
Yakov Eliashberg
Stanford University, Stanford, USA
Étienne Ghys
École Normale Supérieure de Lyon, Lyon, France
Richard Hamilton
Columbia University, New York, USA
Henryk
Iwaniec
Rutgers University, Piscataway, USA
Iain Johnstone
Stanford University, Stanford, USA
Kazuya Kato
Kyoto
University, Kyoto, Japan
Robert V. Kohn
Courant Institute of
Mathematical Sciences, New York University, New York,
USA
Ib
Madsen
Aarhus University, Aarhus, Denmark
Arkadi Nemirovski
Technion - Israel Institute of Technology, Haifa, Israel
Sorin
Popa
University of California, Los Angeles, USA
Alfio
Quarteroni
École Polytechnique Fédérale de Lausanne,
Lausanne, Switzerland
Oded Schramm
Microsoft Corporation,
Redmond, USA
Richard P. Stanley
Massachusetts Institute of
Technology, Cambridge, USA
Terence Tao
University of
California, Los Angeles, USA
Juan Luis Vázquez
Universidad
Autónoma de Madrid, Madrid, Spain
Michèle Vergne
École Polytechnique, Palaiseau, France
Avi
Wigderson
Institute for Advanced Study, Princeton, USA
18899晕...
就一个大陆学者.
上一次2002北京数学家大会有一堆国内数学家获得邀请...
18899一个大陆数学家也无!悲哀!
18899哪个Terence Tao 是个华裔 不过不会说汉语
18899这就是差距阿
同志们,努力啊
18899
近日中科院数学与系统科学研究院陈志明研究员收到国际数学家大会组委会的邀请,
将于2006年8月在西班牙马德里举行的第二十五届国际数学家大会上作45分钟邀请
报告。
陈志明研究员现任中科院数学与系统科学研究院计算数学与科学工程计算研究所常
务副所长,科学与工程计算国家重点实验室副主任。主要研究领域为数值分析与科
学计算,重点为非线性偏微分方程的有限元自适应方法和多孔介质中渗流问题的多
尺度计算方法。近年来在椭圆变分不等式的后验误差分析、非线性对流扩散方程的
自适应有限元方法、波的散射问题的自适应PML技术和多孔介质中含机井奇性问题
的多尺度计算等方面获得多项重要成果。他曾于
1999年入选中国科学院“百人计划”、
2000年获国家杰出青年科学基金、2001获冯康科学计算奖 。
18899中国数学还需不断努力啊!
18899为什么么没有中国??
美国 法国 西班牙 瑞士 丹麦 日本
18899同志们:难道你们不觉得悲哀么?
快拿出行动为中国的数学事业而努力吧!
18899呵呵,现在才看到。了解了一下。
18899不行,兄弟们不可以认输,我们一定要让老外看看我们中国人的数学
18899
| 引用 (wyzmaths @ 2005年11月16日
16时50分) |
这就是差距阿
同志们,努力啊
同志们:难道你们不觉得悲哀么?
快拿出行动为中国的数学事业而努力吧!
|
我怎么不觉得这是“悲哀”。
老外做出来的东西不管好不好,国人都有看的。
国人做出来的东西一旦用汉语发表,不管好不好,你能指望有几个老外看?
人家不了解你凭什么请你?
18899
| 引用 (iceflower @ 2006年04月01日
09时21分) |
| 引用 (wyzmaths @ 2005年11月16日
16时50分) |
这就是差距阿
同志们,努力啊
同志们:难道你们不觉得悲哀么?
快拿出行动为中国的数学事业而努力吧!
|
我怎么不觉得这是“悲哀”。
老外做出来的东西不管好不好,国人都有看的。
国人做出来的东西一旦用汉语发表,不管好不好,你能指望有几个老外看?
人家不了解你凭什么请你?
|
国人的成果如果是很优秀的,应该拿到国际著名的刊物上发表,那好像也是要用英文发的。
18899
| 引用 (iceflower @ 2006年04月01日
09时21分) |
| 引用 (wyzmaths @ 2005年11月16日
16时50分) |
这就是差距阿
同志们,努力啊
同志们:难道你们不觉得悲哀么?
快拿出行动为中国的数学事业而努力吧!
|
我怎么不觉得这是“悲哀”。
老外做出来的东西不管好不好,国人都有看的。
国人做出来的东西一旦用汉语发表,不管好不好,你能指望有几个老外看?
人家不了解你凭什么请你?
|
国人也都是用英语发啊。
18899数学家是搞研究和跟上时代反映时代精神的.少点政治,让数学家有精力在学术上放光彩才是真正最重要的
18899我怎么不觉得这是“悲哀”。
老外做出来的东西不管好不好,国人都有看的。
国人做出来的东西一旦用汉语发表,不管好不好,你能指望有几个老外看?
人家不了解你凭什么请你?
傻鸟,你以为数学是文学吗?
数学可是全世界统一标准的
咱们的水平本来就不行
18899环境有很大的关系,
国内是职称害人!我觉得应该在有些方面要做点改革。
18899在中华人民共和国是有数学高手的。现在还不是公布的时机。如果现在公布,其创立的数学新途径将只有头没有脚。让我们等待吧!或许在06年9月,或许还要几年。
18902计算机数学,我想的话,应该先在理论上有所突破吧。只要理论搞好了,发展是势在必行的事情!
18902计算机数学绝对是个新兴的边缘学科,数学研究中更多的问题由于过于复杂而无法手工推演,借助计算机是势在必行。计算机数学中的热门----定理自动推证其实隶属于人工智能,人工智能当然是计算机学科的了,但这并不能说所有搞计算机研究的牛人都可以做定理机器证明,相反,目前国内搞这方面研究的人基本上都是数学出身。仔细想想,道理很简单,做计算机学科研究的人更多的精力花在计算机学科本身的研究上了,而很少有人思考数学问题。
不信?你试试,说不定你是下一个牛人了呀!
哈哈哈
18902
| 引用 (SUPER-2005-WANG @ 2005年10月10日
12时08分) |
其实,现代科学发展的一个重要标志就是学科间的界限越来越不明显了。楼上的兄弟所说的问题确实存在,但是有句俗语您应该听说过:数学是一切科学与技术的基础!!!
计算机数学研究的基础是构造性数学,理论保证是存在性数学,终极目标是计算机实现。
而计算机科学与技术学科研究的重点似乎不是这些东西??
数学机械化丛书是973项目成果的汇编,不仅有应用成果总结,也有理论基础研究。
|
数学是科学之母,计算机科学更是从离散数学发展来的,CS主要研究的是形式化的算法。因为形式算法保证了计算机的能行性;构造性数学是它的理论基础,因为计算机算法都是构造性的。
计算理论是对计算机的本质的抽象描述,它也是理论计算机科学的核心内容;而非数值的组合算法是计算机的灵魂,也是计算机能应用广泛的根本保证,(它把世间万物的逻辑关系做了高度的数学抽象,形成算法类,程序就是基于这些算法类的),所以它是计算机科学的核心内容;相对而言,数值计算方法对CS就次要的多,它更多是科学计算的需要。
18902其实,现代科学发展的一个重要标志就是学科间的界限越来越不明显了。楼上的兄弟所说的问题确实存在,但是有句俗语您应该听说过:数学是一切科学与技术的基础!!!
计算机数学研究的基础是构造性数学,理论保证是存在性数学,终极目标是计算机实现。
而计算机科学与技术学科研究的重点似乎不是这些东西??
数学机械化丛书是973项目成果的汇编,不仅有应用成果总结,也有理论基础研究。
18902说到数学机械化,我看到有一套"数学机械化学术著作",其中还有一本是关于计算理论,连这个也是计算机数学了?如果这样划分成立的话,理论计算机科学也成了计算机数学的真子集了.看来计算机不仅是这种数学的工具,也是这种数学的研究目标了.这样说计算机数学是不是太广义了?
楼主说到张景中院士,搞的自动定理证明正是人工智能的重要目标之一.
18902最近,看到有朋友发帖谈到“计算机数学”,其中有句话“计算机数学就是数值计算”,似觉得不妥。
20世纪80年代以来,
用计算机进行符号计算的研究在国外发展非常迅速, 涉及的数学领域不断地扩大, 出现了多种符号运算方法,计算程序和系统,
如符号运算,符号和代数运算,符号处理,计算机代数等等. 这是一个以构造性数学为核心, 以计算机实现为目标,以实用的算法为研究内容,
以实用程序或软件为成果的研究领域,这个领域被称为计算机数学.计算机数学的发展逐步产生了一些独立的计算机程序库,称为计算机代数系统.
一部分计算机代数系统发展成为完整的专用或通用的计算机数学软件, 如美国的Mathematica, Matlab,
加拿大的Maple等.
不知各位是否明白??
18902to:SUPER-2005-WANG
哈哈, 洗耳恭听!

18902写的非常好
计算机数学的范围是非常广的
从数值计算到编程算法实现
从逻辑运算到代数结构
等等
是一个非常庞大的体系
18902计算机数学不只是数值计算,更多是非数值计算.
说到符号处理,我想到人工智能和数学自动化,基于符号的智能碰到了很大的困难,基于连接的智能也不能超出图灵算法的形式逻辑约束,难啊......
楼主的帖子不错,我也洗耳恭听.
18902楼上的过奖了,小弟不才,对计算机数学略知一二。
我在讨论班班务里发了个帖子,试图搞个计算机数学讨论班,欢迎大家共同来讨论。
谢谢。
18902其实,在我国,计算机数学研究领域非常活跃,当然主要科学家还是集中在中科院数学与系统科学研究院,以吴文俊院士为带头人,973首席科学家为高小山,此外还有刘卓军,李洪波,刘木兰,等等。除此之外,还有中科院成都计算机应用研究所的张景中院士,杨路教授(也是华师大软件学院特聘教授),陆征一教授(工作单位:温州大学数学学院),以及华师大的李志斌教授(计算机系)与曾振炳教授(软件学院),另外大连理工大学的张鸿庆教授,宁波大学的候效荣教授,当然还有一位大家是北京航空的长江学者王东明教授,中科大陈年来教授,除了候教授不知道是不是博导外,其余当然全是博导了。
中国是一个数学大国,但近代原创的在国际上有影响的只有吴方法,这也是吴院士为什么是第一位国家科技功臣的原因。目前的计算机数学领域主要还是在吴的领导下做研究,即数学机械化。
18902楼上的这位就是搞这方面的, 大家可以和他讨论.
18902计算机数学理论上的突破最重要的一点就是多元多项式消元法了,目前,国际流行的消元法主要有子结式链消元法,GROEBNER基消元法和吴方法,而消元的过程中最困难的问题就是项数膨胀问题。
因此,如何有效利用计算机硬盘存储中间过程可能是很重要的一件事情,或许这个很简单,但目前依然是一个难点。
我不知道能不能仿效某些下载软件的临时存贮功能,就是这次可能才下了一部分,下次开机还能继续上次的下载。
多谢各位讨论,特别是计算机界的朋友的参与。
18902最近我们这个论坛的人怎么会这么少呀?
大家都跑那个去玩了呢?
18902支持 大家应该多讨论
18902克努特有一本《具体数学》,就是计算机中所用到的数学知识。当然,不是全部。大家可以看一看,毕竟克努特是大师级的人物
18902
引用 (SUPER-2005-WANG @ 2005年10月16日
18时08分) |
计算机数学理论上的突破最重要的一点就是多元多项式消元法了,目前,国际流行的消元法主要有子结式链消元法,GROEBNER基消元法和吴方法,而消元的过程中最困难的问题就是项数膨胀问题。
因此,如何有效利用计算机硬盘存储中间过程可能是很重要的一件事情,或许这个很简单,但目前依然是一个难点。
我不知道能不能仿效某些下载软件的临时存贮功能,就是这次可能才下了一部分,下次开机还能继续上次的下载。
多谢各位讨论,特别是计算机界的朋友的参与。
|
看你的帖子很有收获
18902谢谢
18902这个帖子引出来的讨论真是太精彩了。
好帖啊。顶一下。
各位继续哈
18902克努特那本《具体数学》我看了中文版中前一点点,大师的写作风格就是不一般啊,吸引人往下读。
18902现在我最迫切需要的是要有人与我讨论关于群的计算机代数系统,联系方式:liugb0414@sohu.com,QQ:815880595
我在自学数学,以前是个程序员,在华为开发,测试都干过。现在离职在家,决心是搞计算机代数系统的研究与开发。再具体一点,就是研究如何在用计算机作为符号计算的工具,来进行数学研究。我选择的数学方向是代数学的群论,群表示论等内容的计算机代数研究。
我的数学基础有一点,那是因为我是四川大学数学系毕业后转行搞IT的,现在又想回头转到数学中去。为了能用让这近十年来的IT工作经验积累的东西,同时又能进行我心爱的数学研究,所以选择了搞计算机代数系统这个方向。
例如:GAP(这是国外专门针对群论的计算机代数系统),我自己也在搞。感觉目标有点不明确。我研究计算机代数系统的深层目的是将数学家的思维在计算机中表达出来,而不只是在论文中以文字的方式来表达。那样的表达方式太抽象,计算机表达就可以生动得多。
目前我自己也开发了一个用JAVA写的用于群计算的程序。基于以上思想,我在程序中实现的功能包括:在一个画布上显示一个群的所有元素,并且可以将群的元素对称地分布在画布上,并且可以根据一些运动规则,让群中的元素动起来,以期达到更好地理解群的某些概念的目的。
18902
引用 (SUPER-2005-WANG @ 2005年10月09日
19时04分) |
楼上的过奖了,小弟不才,对计算机数学略知一二。
我在讨论班班务里发了个帖子,试图搞个计算机数学讨论班,欢迎大家共同来讨论。
谢谢。
|
强烈同意,发现自己的方向被bossi给BS了,哈。为什么没有符号计算的讨论班呢,在吴文俊先生的影响下,在中科院KLMM的影响下,中国的数学机械化在世界上还是有一定地位的。而且,计算机代数应该是目前符号计算机数学做的比较成熟的一个方向,应该多讨论呀!
18902一直都比较有兴趣。今儿个来看,开了眼界了。。。。
18902正在看MIT的这个课。
http://www.core.org.cn/OcwWeb/Electrical-E...eHome/index.htm
18902很想结识对符号计算有研究的朋友。
软件的积分post-72-1212160965.jpg
18902求导post-72-1212161043.jpg
18902有愿意交流或希望了解该软件研发的进展,可与七重天联系,邮件地址:qizhongtian@sina.com
因式分解post-72-1212161388.jpg
18902简化三角函数post-72-1212161594.jpg
18902楼主说出了一部分问题的关键。
顺便说下,大家注意haskell和functional programming。
18902看来搞计算机的数学必须得好啊。
18903可对角化有几个充要条件,如最小多项式无重根,n个无关特征向量等!具体描述那些可对角化是不容易的!
18903顶一下
18903如题
18904浙大杰出校友、宾夕法尼亚大学著名数学家杨忠道先生不幸去世
惊悉,浙江大学杰出校友、著名数学家杨忠道先生因病于近日不幸去世,享年82岁。杨
忠道先生早年就读浙江大学,曾长期担任美国宾夕法尼亚大学数学系主任,
1968年当选
为台湾“中央研究院”院士。杨忠道先生曾多次来浙江大学访问讲学,非常关心我校数
学学科的建设与发展。他生前曾多次表示,非常希望来浙江大学为大学生开基础课。他
的去世是国际数学界的重大损失,也是浙江大学数学学科的重大损失,在此表示沉痛哀
悼。
沉痛悼念杨忠道教授
惊悉杨忠道学长病逝,在温中和浙大时,他是我的高年级同学,更是我的辅导老师,他
对几何学的浓厚兴趣,我深受教益和感染,后来他还使我了解到拓扑学和代数学的重要
作用。他为人忠厚诚恳,主持正义,爱祖国,爱家乡,道德足为后人楷模。失此良师益
友,我不胜悲痛。学生时期的影响,
1949年的远别,
1972年的重逢,及此后在宾州家中
的多次接待,2002年在温州的最后面叙,六十多年的深情交往,我都历历在目,永记不
忘。他的数学贡献将永载史册,他将永远活在朋友们和学生们的心中。
谷超豪
2005年9月
著名数学家杨忠道先生简介
杨忠道(Chung-Tao
Yang),著名拓扑学家。
1923年5月生于浙江省平阳县;
1942年毕业于浙江省立温州中学高中部;
1946年毕业于国立浙江大学数学系;
1946-
1948年在浙江大学数学系任助教;
1948-
1950年在中央研究院数学研究所担任助理研究员;
1949-
1950年任台湾大学讲师;
1952年获美国Tulane大学数学博士学位;
1952-
1954年任Illinois大学研究助理;
1954-
1956年在普林斯顿高等研究所访问;
1956-
1991年在宾夕法尼亚大学数学系任教
1978-
1983年间曾担任美国宾夕法尼亚大学数学系主任;
1968年当选台湾中央研究院院士;
1972年入选美国Who
is
Who名人辞典。
杨忠道先生在射影几何学,一般拓扑学,代数拓扑学,李群等领域中做出了重要的贡
献,证明了著名的Dyon猜想,在一般拓扑学中有著名的杨忠道定理。他的儿子Deane
Yang是美国Polytechnic大学数学系教授。
杨忠道院士访谈
张海潮老师
访问,叶德财
纪录
(2000年1月17日)
「做数学要有一股傻劲和拼劲。」----杨院士给后学
我是在浙江省平阳县一个乡下地方长大的。现在属浙江省苍南县平等乡。那时候平阳县
很落后,全县没有一所初级中学,小学也不多。不过当地有一所私立初小,所以我自然
地在那里就读到四年级。上五年级时附近就没有学校了,最近的离家五里。天天走那么
远去上学非体弱的我所能做到,何况乡下多泥路,一下雨不好走,所以上高小时我就住
在学校的宿舍里,到周末才回家。
上四年级时,数学教师黄仲迪先生利用逻辑方法,讨论鸡兔同笼的问题,激发起我对数
学的兴趣,我喜爱数学,从此就开始了。仲迪先生是一位十分难得的小学教师。他家境
清寒,只读了半年初中就辍学了。不过他努力自修,以教小学谋生,调教出来不少好学
生。他给学生们的印象是口才好,而且智识丰富。
1983年我回故乡探亲,他得到消息
后,特地到我弟弟家找我,互谈半个世纪中的演变。
1991年我在回家乡探亲时,县教育
委员会安排我对数十位中学数学教师讲学一星期。我乘机提出邀请仲迪先生为贵宾,参
加讲学前的典礼。在典礼中我介绍仲迪先生是我读数学的启蒙老师,希望大家以后以他
为榜样。
因为当时平阳县没有初中,我上的初中在别的县里,离开家约一百四十里。乡下的交通
很不方便,从家里去学校须换舟车近十次,得花十五小时,所以一学期中难得回家一
次。父亲是地主的后代,到他当家时只有足以餬口的田地,对我上初中的费用负担的很
辛苦。所以我初中毕业后没有让我考高中,但是停学在家不是办法,于是安排我在当地
初小教二年级,继续让我用自己赚来的钱先去上高中,再看以后如何。因为失过学,我
成熟多了,也感到求学的可贵,所以在高中三年中,我的成绩总在班上前三名,因此得
到公费,使我完成高中学业。读高中时我的数理化都不错,以数学被老师及同学们认为
最出色。文科的成绩不坏,但是那都是靠死背强记得来的。
在艰苦的生活下,父亲知道祖产不能凭,也知道他年纪大了必须我去赡养他,因此他鼓
励我去念工科。当时我很喜欢数学,也是理化的好学生,于是去向数学教师陈仲武先生
请教。仲武先生早就了解我,而且有他个人的判断。他没有犹豫的说:「你当然去念数
学,如果连你也不去念,还有什么人该去念呢﹖!」凭仲武先生这一句话,我就义无反顾
去读数学了。
那时候平阳县的教育虽然很落后,但是出了两位数学家。第一位是姜立夫教授,他于
19
19年获得美国哈佛大学数学博士学位,是中央研究院数学研究所第一任所长。第二位
是苏步青教授,他于
1931
年获得日本东北帝大数学博士学位,是台湾大学理学院第一任
院长。两人都是中央研究院第
一届的院士。我从小就听过他们的大名,但到四十年代才
认识他们。
高中毕业会考,我的成绩不错,可以保送进国立大学就读。当时我决定进浙江大学,从
苏步青先生学习现代数学。抗战期间许多地方被日军占领,浙江大学已迁到贵州去了。
所以大学一年级我是在浙大龙泉分校念的,到第二年才到贵州去。
当时浙大数学系在贵州省湄潭县,步青先生是系主任。说起来很难使现在年轻人相信,
那时候系里没有职员,系主任必须总管系里大小事务。幸亏全系师生的总人数只有三四
十人,非有要事不会去麻烦系主任的。步青先生对学生亲如子女,照顾得很周到。我是
他的小同乡,觉得他对我更好些。
步青先生的努力,大概没有第二个人可以及得上,这是由下述的事实见到的。
1944年步
青先生家里有七个小孩,最大的上高一,最小的刚出生。那时候教授的薪水不高,他没
有办法顾人帮忙。一家九口的家事靠师母一个人做,事实上不可能,所以步青先生和大
的几个小孩都得帮忙。那时候数学系没有办公室,师生门有事情找他只好直接去他家。
因为没有电话,无法预先约定时间,所以白天和晚上,随时有人登门拜访。在那种情形
下,他不但处理系务、教课,而且继续作他自己的研究工作,也指导年轻教师做研究。
每年总有几篇论文发表在外国数学杂志上,真是谈何容易。步青先生很能利用他的时
间,好多次到他家时,见到他一只手抱小孩,同时阅读数学书籍,还用另一只手写笔
记。说他一个人做两三个人的工作,不算太过分吧!有这样一位老师摆在前面做榜样,想
偶而偷点小赖也找不到借口了。
四十年代浙大数学系的课程和现在台大数学系的课程大同小异。我读过的课程,在一年
级时有微积分和微分方程,在二年级时有高等微积分、级数概论、立体解析几何及选修
的数论和偏微分方程,在三年级时有综合几何、近世代数和复变量函数,在四年级时有
微分几何、实变量函数和数学研究。在浙大我没有念过泛函分析、拓朴学,原因是没有
教师能教授这两门课。据记忆,在大学四年中,我的数学课的成绩没有低于九十分者,
好像每学期的总平均都高过九十分。我让步青先生惊讶的不是这些高分数却是在二年级
读理论力学时得九十分。理论力学是数学系学生的必修课程,但可待至三四年级时去
读。这是一门出名难读的课程,数学系好学生去读时,有时也很困难,甚至不及格须补
考,使数学系很不满意。怪不得步青先生见到我的高分时,笑着对我说:「数学系多年
来的怨气,给你一下子出光了。」事实上物理系学生读这门课同样有困难,和我一起读
理论力学的同学有十多人,及格只有五人,而且都是数学系的。
上三年级的综合几何课是步青先生亲授。他鼓励学生阅读课外参考书籍,因此我读了一
本的德文版射影几何。也许他认为我还能担当一些工作,于是指派我义务替数学系管理
图书杂志,也能就近翻阅易懂的数据。因此我上四年级时,自己找题目完成一篇论文。
步青先生觉得还不错,结果那篇论文在美国发表(《Duke
J. of Math.》,
1947
)。大
学毕业后,我留在系里任助教,两年中又自己找题目作论文,除在国内发表的外,又有
一篇在美国数学杂志上发表,再有一篇在阿根廷数学杂志上发表。如何去找题目,求解
答,主要是受步青先生的训练,当时不够深入。文章虽然可以刊登出来,到后来再看,
太肤浅了。
1947年起政局相当混乱,想在学校里安心做研究工作事实上不可能,于是我征得步青先
生的同意,于
1948年夏天,去中央研究院数学研究所,从代所长陈省身教授学习代数拓
朴。目的是希望在两三年中,学到一些新的
知识,再回到浙大数学系。
没有料到去了中央研究院后,时局急转直下,数学研究所的研究活动完全停顿,同时陈
省身教授决定接受邀请,去美国普林斯顿高等研究院做研究。接着教育部发表历史语言
研究所博斯年所长将继任台湾大学校长,于是他提议将中央研究院迁往台湾。但是可以
想象,如物理研究所、化学研究所等有实验室设备的研究所根本不可能考虑搬迁,所以
最后决定搬迁的只有历史语言研究所和数学研究所,而且只准许部份人员去台湾。
根据我的了解,数学研究所的安排是所长姜立夫先生和代所长陈省身先生共同决定的,
一方面保全图书杂志,另方面保全部份研究实力,以备来日东山再起。随数学研究所到
台湾的研究工作人员,除立夫先生外,有副研究员王宪钟先生和胡世桢先生及助理员三
人,即廖山涛、陈杰和杨忠道。王、胡两位先生曾在英国得数学博士学位,打算到台湾
后在美国觅教职(后来都是中央研究院院士,已过世)。至于三位助理员,将协助他们
去美国留学。我知道有一位助理员要求去台湾被拒绝了,我是到所最晚的助理员,为什
么被挑中,则非我所知了。
到了台湾后,院方告诉数学所四位单身人员,没有办法安排我们在台北居住,暂居的地
方是杨梅镇。到了杨梅,才知道居住的地方是在一仓库里。历史语言研究所书籍很多,
堆积在杨梅的一所仓库里。临时把两个书箱排在一起,在上面摆一个塌塌米,就做为我
们每个人的床铺了。仓库的建设,并没有准备在里面住人的,窗户小,而且高逾一丈。
屋顶很高,只有近屋顶地方,才有几盏昏暗的电灯。大门一关,黑暗的很。加上杨梅镇
风大,非关大门不可,所以几天后大家都知道白天非出去不可。杨梅只是一个小镇,没
有图书馆,没有公园,一条小街上只有几间小铺子,进去后若不照顾生意,两三分钟就
得出来,所以我们四人决定必须自己设法回台北找居住地方。经过努力,也透过私人关
系,我们四人在台北厦门街台湾大学一个招待所里,找到了一间六塌塌米大的房间。因
为没有壁橱,四个人睡在四角落,让皮箱堆在中央。虽然如此,比在杨梅镇好多了,至
少在白天可以上公园、逛街、逛书店。那时候想找一个地方坐下来写一封信都不容易,
更谈不到做什么工作。
后来我知道师院附中(即后来的师大附中)急需一位数学教师,教高二三班的大代数,
于是去向立夫先生请示。
他说反正目前无法工作,先利用这机会解决眼前的困难再看
吧!所以我决定接那份教职,但是有条件的,就是说必须有单身宿舍可以住。因此我在师
院附中执教了一学期。
到
1949
年夏天,生活情况好多了,但人事上有变化。立夫先生去了广州,决定留在那里
帮岭南大学创办数学系。王、胡两位先生在美国找到教职,离开了台湾。陈杰因惦念未
婚妻,取道广州回四川。廖山涛和我两人正式在台大数学系兼任讲师,而且有宿舍可
住。由
1949至
1950,我教一班土木系的微积分和一班机械系的微分方程,其中许振荣先
生去美国进修,他的高等几何课也由我代授。记得那班上的同学有王典荣(已在香港中
文大学退休)和吴青木(已在淡江大学退休)。又在微分方程班上的吴达森同学,后来
转读数学系,留美而成为美国大学的教授
。
1950年王、胡两先生帮我获得Teaching Fellowship,去美国Tulane University
(Louisiana)读博士学位,旅费是中央研究院给的,到那时我才知道,这个安排在数学
研究所搬迁到台湾之前,已经取得院方同意。同时,廖山涛亦去美国留学,也受到同样
的待遇。
初到美国时,我的英语不好(后来也没有好过,只是能够应付而已。这一点我觉得去美
国留学的人必须注意!),一天到晚羞于开口。也许在十多位数学系的研究生中,我是唯
一的非美国人,所以大家对我都很照顾。第一学期我选了四门数学课及一门阅读报告。
其中一位授课老师是
A.D. Wallace 教授,也是我博士论文的指导教授,他教课的方法
是他的师祖 R.L. Moore
创造的,将课程内容分做许多小命题,预先发给学生。上课时
他要学生上台去证明,他自己坐在台下听。一个学生没完成时叫第二个上去,一个小时
没有完成就留到下一小时再继续,他自己绝不帮忙。我的英语虽然不好,在他的课中表
现得不错,所以一开始就给他一个好印象。他对学生们很友善,常常在课余时到研究生
的办公室,谈谈数学,也讲笑话。见到我的时候,总要提出或大或小的数学问题,嘱我
多想想。第二个学期一开始,他嘱我去读法国数学家H.
Cartan
在哈佛大学教授代数拓
朴的讲义。
第一学年结束后系里给我生活费,嘱我在暑期中好好用功。Cartan讲义中一个主要成果
是“For
compact Hausdorff spaces, certain two cohomology theories are
equivalent”在 Wallace 教授的课程中,我学到了fully normal
spaces的概念。经过
几个星期的思考,我觉得 Cartan讲义中那成果可以被扩充到 fully normal
spaces。当
我向Wallace教授提起这一发现时,他十分惊讶,于是抽空和我讨论我的构想。几星期后
他逐渐相信我的构想很可能是对的,可以作为我的博士论文,于是他开始筹划我的前
途。Tulane
University是美国南方一所好大学,在全美也称得上二三流学校,不过数学
系在我之前只出过不到十位的博士,于是Wallace教授通过系主任请研究院给我一个例外
待遇。得博士学位照惯例必须修满二十个学分,但Wallace教授觉得为我,为数学系,反
不如早点给我博士学位,而且推荐我去研究活动多的地方,求进一步的发展,所以系里
特许我于第二学期不选课,专心去书写博士论文。
Wallace教授的初意是希望我去普林斯顿大学数学系任讲师,使能从
N. Steenrod教授做
代数拓朴的研究,但是没有成功。
1952年秋天我去了University of
Illinois数学系当
博士后研究,每周教授三小时,同时参加系里研究活动。那时候系里有一位代数拓朴的
教授 D.G.
Bourgin,带五、六位博士研究生,研究的主要对象是 (F.J.) Dyson 的猜
测。我不但去听 Bourgin
教授的课,也去参加他率领的讨论班。经过一年的努力,我得
到了 一个Dyson猜测的证明,Bourgin
教授知道后十分惊讶,当时只说他自己也做得差
不多了。这件事使我很尴尬,于是去向陈省身先生请教。他给我一个建议,说最好的解
决方法,是两人合写一篇文章去发表,不过必须由他提出来才是。如果他不提,我应该
自己发表,不过文章中应提及听说
Bourgin 教授有一独立的证明。结果我的文章于
1954
年发表在《Annals of
Math》上,Bourgin的文章于
1955年发表在瑞士一数学杂志上。在
University of Illinois
我停留了两年。我在那里的时候,施拱星先生正在那里读博士
学位。周元燊院士去读博士学位恰在我离开之后,我曾帮忙向系方推荐他。
我在
University of Illinois 所写的两篇文章颇引人注意,同时Wallace
教授继续努
力推荐我去普林斯顿做研究。
1954年秋天,我获得美国国科会一年的资助,去普林斯顿
高等研究院做研究,主要的对象是将Dyson猜测再扩充,使亦包括
Borsuk-Ulam 定理。
一切安排是Wallace教授透过 D. Montgomery
教授才办成功的。
Montgomery
教授出身于小型的大学,所以他十分同情非名校出身但工作能力强的年轻数
学工作者,也很同情来自他国学者,他的理由是由名校出身的美国人已经有很多的机
会,无须他人多帮忙。每年去普林斯顿高等研究院做研究的数学工作者在五十人之上,
年轻的较多,在大家的心目中,以
Montgomery
教授人缘最好。
我的研究计划,半年内就完成了。顺着同样路线做下去,前途并不乐观,所以我觉得有
必要另找途径。正在那时候,Montgomery教授和
L. Zippen 教授合写了一本书
《Topological Transxxxxation Group》。前半本解答
Hilbert's Fifth Problem,那
是四年前他们合作的 一篇文章和一篇A.M. Gleason
文章所得到的成果,后半本讨论拓
朴变换群。因为这些是当时大家公认最重要的贡献,当然非好好读不可,于是我自荐帮
忙那本书的校对工作。读完了全书,我觉得可以考虑某些问题,于是向Montgomery教授
请教。他听了以后,告诉我其中一个问题,正是他和H.
Samelson
教授研究的对象,立
即表示欢迎我加入他们的行列。因为这个偶然的机缘,使我在那两年中,和他们两人合
写了两篇文章。
1956年秋天我去
University of
Pennsylvania(简称宾大)工作,一个原因是宾大数学
系有一位教授在高等研究院进修,知道我的研究工作,也知道Montgomery
教授和我合
作,竭力向系里推荐我。另一个原因是宾大距离普林斯顿相当近,不论自己驾车或搭火
车,一个多小时可以到达,使我有较多机会向
Montgomery
教授请教。在宾大我一共工
作了三十五年,起先是助理教授,
1958年被提升为副教授,
1961年被提升为正教授。在
职期间,曾兼任数学系里研究生部主任四年,数学系系主任五年。在我指导下完成博士
论文的有L.Mann(
1959),后来任University
of Massachusetts
数学系系主任多年,
1961年有苏竞存,他于
1954年毕业于台大物理系,后来改念数学,现在是University
of
Massachusetts数学系教授。
来宾大教书最大的好处是可以常去看Montgomery教授,后来他干脆每星期留下一天,让
我去和他讨论数学。这样维持了二十多年,合写了二十多篇文章。
1968年我被选为中央研究院院士,
1972年列名于《美国名人录》(Who's
Who in
America)。
--
“我需要我的生活区域内有一家有文化的书店,里面放着一些我看不懂的书,
我知道是好书的书,我听人家谈起过的书。这样我才踏实地相信,我是一个
有理想的人,生活在一个理想有可能实现的城市里。”
------《南方周末》2003.01.23
※ 来源:·我爱南开站 nkbbs.org ·Web[FROM:
202.113.236.26]
[查看全文] [回复本文] [回复作者] [作者: littletiger ]
[讨论区:Mathematics]
发信人: littletiger (蟋蟀·从二维到四维), 信区: Mathematics
标
题: Re: 南开数学所原副所长杨忠道先生不幸去世(zz)
发信站: 我爱南开站 (2005年10月01日21:32:41 星期六),
站内信件
南开数学研究所副所长,是全职吗?
bless
【 在 dlmz (dlmz) 的大作中提到:
】
浙大杰出校友、宾夕法尼亚大学著名数学家杨忠道先生不幸去世
送交者: 陈玮 2005年9月29日20:10:
17 于
[教育与学术]http://www.bbsland.com
惊悉,浙江大学杰出校友、著名数学家杨忠道先生因病于近日不幸去世,享年82岁。杨
忠道先生早年就读浙江大学,曾长期担任美国宾夕法尼亚大学数学系主任,
1968年当选
为台湾“中央研究院”院士。杨忠道先生曾多次来浙江大学访问讲学,非常关心我校数
学学科的建设与发展。他生前曾多次表示,非常希望来浙江大学为大学生开基础课。他
的去世是国际数学界的重大损失,也是浙江大学数学学科的重大损失,在此表示沉痛哀
悼。
沉痛悼念杨忠道教授
惊悉杨忠道学长病逝,在温中和浙大时,他是我的高年级同学,更是我的辅导老师,他
对几何学的浓厚兴趣,我深受教益和感染,后来他还使我了解到拓扑学和代数学的重要
作用。他为人忠厚诚恳,主持正义,爱祖国,爱家乡,道德足为后人楷模。失此良师益
友,我不胜悲痛。学生时期的影响,
1949年的远别,
1972年的重逢,及此后在宾州家中
的多次接待,2002年在温州的最后面叙,六十多年的深情交往,我都历历在目,永记不
忘。他的数学贡献将永载史册,他将永远活在朋友们和学生们的心中。
谷超豪
2005年9月
著名数学家杨忠道先生简介
杨忠道(Chung-Tao
Yang),著名拓扑学家。
1923年5月生于浙江省平阳县;
1942年毕业于浙江省立温州中学高中部;
1946年毕业于国立浙江大学数学系;
1946-
1948年在浙江大学数学系任助教;
1948-
1950年在中央研究院数学研究所担任助理研究员;
1949-
1950年任台湾大学讲师;
1952年获美国Tulane大学数学博士学位;
1952-
1954年任Illinois大学研究助理;
1954-
1956年在普林斯顿高等研究所访问;
1956-
1991年在宾夕法尼亚大学数学系任教
1978-
1983年间曾担任美国宾夕法尼亚大学数学系主任;
1968年当选台湾中央研究院院士;
1972年入选美国Who
is
Who名人辞典。
杨忠道先生在射影几何学,一般拓扑学,代数拓扑学,李群等领域中做出了重要的贡
献,证明了著名的Dyon猜想,在一般拓扑学中有著名的杨忠道定理。他的儿子Deane
Yang是美国Polytechnic大学数学系教授。
杨忠道院士访谈
张海潮老师
访问,叶德财
纪录
(2000年1月17日)
「做数学要有一股傻劲和拼劲。」----杨院士给后学
我是在浙江省平阳县一个乡下地方长大的。现在属浙江省苍南县平等乡。那时候平阳县
很落后,全县没有一所初级中学,小学也不多。不过当地有一所私立初小,所以我自然
地在那里就读到四年级。上五年级时附近就没有学校了,最近的离家五里。天天走那么
远去上学非体弱的我所能做到,何况乡下多泥路,一下雨不好走,所以上高小时我就住
在学校的宿舍里,到周末才回家。
上四年级时,数学教师黄仲迪先生利用逻辑方法,讨论鸡兔同笼的问题,激发起我对数
学的兴趣,我喜爱数学,从此就开始了。仲迪先生是一位十分难得的小学教师。他家境
清寒,只读了半年初中就辍学了。不过他努力自修,以教小学谋生,调教出来不少好学
生。他给学生们的印象是口才好,而且智识丰富。
1983年我回故乡探亲,他得到消息
后,特地到我弟弟家找我,互谈半个世纪中的演变。
1991年我在回家乡探亲时,县教育
委员会安排我对数十位中学数学教师讲学一星期。我乘机提出邀请仲迪先生为贵宾,参
加讲学前的典礼。在典礼中我介绍仲迪先生是我读数学的启蒙老师,希望大家以后以他
为榜样。
因为当时平阳县没有初中,我上的初中在别的县里,离开家约一百四十里。乡下的交通
很不方便,从家里去学校须换舟车近十次,得花十五小时,所以一学期中难得回家一
次。父亲是地主的后代,到他当家时只有足以餬口的田地,对我上初中的费用负担的很
辛苦。所以我初中毕业后没有让我考高中,但是停学在家不是办法,于是安排我在当地
初小教二年级,继续让我用自己赚来的钱先去上高中,再看以后如何。因为失过学,我
成熟多了,也感到求学的可贵,所以在高中三年中,我的成绩总在班上前三名,因此得
到公费,使我完成高中学业。读高中时我的数理化都不错,以数学被老师及同学们认为
最出色。文科的成绩不坏,但是那都是靠死背强记得来的。
在艰苦的生活下,父亲知道祖产不能凭,也知道他年纪大了必须我去赡养他,因此他鼓
励我去念工科。当时我很喜欢数学,也是理化的好学生,于是去向数学教师陈仲武先生
请教。仲武先生早就了解我,而且有他个人的判断。他没有犹豫的说:「你当然去念数
学,如果连你也不去念,还有什么人该去念呢﹖!」凭仲武先生这一句话,我就义无反顾
去读数学了。
那时候平阳县的教育虽然很落后,但是出了两位数学家。第一位是姜立夫教授,他于
19
19年获得美国哈佛大学数学博士学位,是中央研究院数学研究所第一任所长。第二位
是苏步青教授,他于
1931
年获得日本东北帝大数学博士学位,是台湾大学理学院第一任
院长。两人都是中央研究院第
一届的院士。我从小就听过他们的大名,但到四十年代才
认识他们。
高中毕业会考,我的成绩不错,可以保送进国立大学就读。当时我决定进浙江大学,从
苏步青先生学习现代数学。抗战期间许多地方被日军占领,浙江大学已迁到贵州去了。
所以大学一年级我是在浙大龙泉分校念的,到第二年才到贵州去。
当时浙大数学系在贵州省湄潭县,步青先生是系主任。说起来很难使现在年轻人相信,
那时候系里没有职员,系主任必须总管系里大小事务。幸亏全系师生的总人数只有三四
十人,非有要事不会去麻烦系主任的。步青先生对学生亲如子女,照顾得很周到。我是
他的小同乡,觉得他对我更好些。
步青先生的努力,大概没有第二个人可以及得上,这是由下述的事实见到的。
1944年步
青先生家里有七个小孩,最大的上高一,最小的刚出生。那时候教授的薪水不高,他没
有办法顾人帮忙。一家九口的家事靠师母一个人做,事实上不可能,所以步青先生和大
的几个小孩都得帮忙。那时候数学系没有办公室,师生门有事情找他只好直接去他家。
因为没有电话,无法预先约定时间,所以白天和晚上,随时有人登门拜访。在那种情形
下,他不但处理系务、教课,而且继续作他自己的研究工作,也指导年轻教师做研究。
每年总有几篇论文发表在外国数学杂志上,真是谈何容易。步青先生很能利用他的时
间,好多次到他家时,见到他一只手抱小孩,同时阅读数学书籍,还用另一只手写笔
记。说他一个人做两三个人的工作,不算太过分吧!有这样一位老师摆在前面做榜样,想
偶而偷点小赖也找不到借口了。
四十年代浙大数学系的课程和现在台大数学系的课程大同小异。我读过的课程,在一年
级时有微积分和微分方程,在二年级时有高等微积分、级数概论、立体解析几何及选修
的数论和偏微分方程,在三年级时有综合几何、近世代数和复变量函数,在四年级时有
微分几何、实变量函数和数学研究。在浙大我没有念过泛函分析、拓朴学,原因是没有
教师能教授这两门课。据记忆,在大学四年中,我的数学课的成绩没有低于九十分者,
好像每学期的总平均都高过九十分。我让步青先生惊讶的不是这些高分数却是在二年级
读理论力学时得九十分。理论力学是数学系学生的必修课程,但可待至三四年级时去
读。这是一门出名难读的课程,数学系好学生去读时,有时也很困难,甚至不及格须补
考,使数学系很不满意。怪不得步青先生见到我的高分时,笑着对我说:「数学系多年
来的怨气,给你一下子出光了。」事实上物理系学生读这门课同样有困难,和我一起读
理论力学的同学有十多人,及格只有五人,而且都是数学系的。
上三年级的综合几何课是步青先生亲授。他鼓励学生阅读课外参考书籍,因此我读了一
本的德文版射影几何。也许他认为我还能担当一些工作,于是指派我义务替数学系管理
图书杂志,也能就近翻阅易懂的数据。因此我上四年级时,自己找题目完成一篇论文。
步青先生觉得还不错,结果那篇论文在美国发表(《Duke
J. of Math.》,
1947
)。大
学毕业后,我留在系里任助教,两年中又自己找题目作论文,除在国内发表的外,又有
一篇在美国数学杂志上发表,再有一篇在阿根廷数学杂志上发表。如何去找题目,求解
答,主要是受步青先生的训练,当时不够深入。文章虽然可以刊登出来,到后来再看,
太肤浅了。
1947年起政局相当混乱,想在学校里安心做研究工作事实上不可能,于是我征得步青先
生的同意,于
1948年夏天,去中央研究院数学研究所,从代所长陈省身教授学习代数拓
朴。目的是希望在两三年中,学到一些新的
知识,再回到浙大数学系。
没有料到去了中央研究院后,时局急转直下,数学研究所的研究活动完全停顿,同时陈
省身教授决定接受邀请,去美国普林斯顿高等研究院做研究。接着教育部发表历史语言
研究所博斯年所长将继任台湾大学校长,于是他提议将中央研究院迁往台湾。但是可以
想象,如物理研究所、化学研究所等有实验室设备的研究所根本不可能考虑搬迁,所以
最后决定搬迁的只有历史语言研究所和数学研究所,而且只准许部份人员去台湾。
根据我的了解,数学研究所的安排是所长姜立夫先生和代所长陈省身先生共同决定的,
一方面保全图书杂志,另方面保全部份研究实力,以备来日东山再起。随数学研究所到
台湾的研究工作人员,除立夫先生外,有副研究员王宪钟先生和胡世桢先生及助理员三
人,即廖山涛、陈杰和杨忠道。王、胡两位先生曾在英国得数学博士学位,打算到台湾
后在美国觅教职(后来都是中央研究院院士,已过世)。至于三位助理员,将协助他们
去美国留学。我知道有一位助理员要求去台湾被拒绝了,我是到所最晚的助理员,为什
么被挑中,则非我所知了。
到了台湾后,院方告诉数学所四位单身人员,没有办法安排我们在台北居住,暂居的地
方是杨梅镇。到了杨梅,才知道居住的地方是在一仓库里。历史语言研究所书籍很多,
堆积在杨梅的一所仓库里。临时把两个书箱排在一起,在上面摆一个塌塌米,就做为我
们每个人的床铺了。仓库的建设,并没有准备在里面住人的,窗户小,而且高逾一丈。
屋顶很高,只有近屋顶地方,才有几盏昏暗的电灯。大门一关,黑暗的很。加上杨梅镇
风大,非关大门不可,所以几天后大家都知道白天非出去不可。杨梅只是一个小镇,没
有图书馆,没有公园,一条小街上只有几间小铺子,进去后若不照顾生意,两三分钟就
得出来,所以我们四人决定必须自己设法回台北找居住地方。经过努力,也透过私人关
系,我们四人在台北厦门街台湾大学一个招待所里,找到了一间六塌塌米大的房间。因
为没有壁橱,四个人睡在四角落,让皮箱堆在中央。虽然如此,比在杨梅镇好多了,至
少在白天可以上公园、逛街、逛书店。那时候想找一个地方坐下来写一封信都不容易,
更谈不到做什么工作。
后来我知道师院附中(即后来的师大附中)急需一位数学教师,教高二三班的大代数,
于是去向立夫先生请示。
他说反正目前无法工作,先利用这机会解决眼前的困难再看
吧!所以我决定接那份教职,但是有条件的,就是说必须有单身宿舍可以住。因此我在师
院附中执教了一学期。
到
1949
年夏天,生活情况好多了,但人事上有变化。立夫先生去了广州,决定留在那里
帮岭南大学创办数学系。王、胡两位先生在美国找到教职,离开了台湾。陈杰因惦念未
婚妻,取道广州回四川。廖山涛和我两人正式在台大数学系兼任讲师,而且有宿舍可
住。由
1949至
1950,我教一班土木系的微积分和一班机械系的微分方程,其中许振荣先
生去美国进修,他的高等几何课也由我代授。记得那班上的同学有王典荣(已在香港中
文大学退休)和吴青木(已在淡江大学退休)。又在微分方程班上的吴达森同学,后来
转读数学系,留美而成为美国大学的教授
。
1950年王、胡两先生帮我获得Teaching Fellowship,去美国Tulane University
(Louisiana)读博士学位,旅费是中央研究院给的,到那时我才知道,这个安排在数学
研究所搬迁到台湾之前,已经取得院方同意。同时,廖山涛亦去美国留学,也受到同样
的待遇。
初到美国时,我的英语不好(后来也没有好过,只是能够应付而已。这一点我觉得去美
国留学的人必须注意!),一天到晚羞于开口。也许在十多位数学系的研究生中,我是唯
一的非美国人,所以大家对我都很照顾。第一学期我选了四门数学课及一门阅读报告。
其中一位授课老师是
A.D. Wallace 教授,也是我博士论文的指导教授,他教课的方法
是他的师祖 R.L. Moore
创造的,将课程内容分做许多小命题,预先发给学生。上课时
他要学生上台去证明,他自己坐在台下听。一个学生没完成时叫第二个上去,一个小时
没有完成就留到下一小时再继续,他自己绝不帮忙。我的英语虽然不好,在他的课中表
现得不错,所以一开始就给他一个好印象。他对学生们很友善,常常在课余时到研究生
的办公室,谈谈数学,也讲笑话。见到我的时候,总要提出或大或小的数学问题,嘱我
多想想。第二个学期一开始,他嘱我去读法国数学家H.
Cartan
在哈佛大学教授代数拓
朴的讲义。
第一学年结束后系里给我生活费,嘱我在暑期中好好用功。Cartan讲义中一个主要成果
是“For
compact Hausdorff spaces, certain two cohomology theories are
equivalent”在 Wallace 教授的课程中,我学到了fully normal
spaces的概念。经过
几个星期的思考,我觉得 Cartan讲义中那成果可以被扩充到 fully normal
spaces。当
我向Wallace教授提起这一发现时,他十分惊讶,于是抽空和我讨论我的构想。几星期后
他逐渐相信我的构想很可能是对的,可以作为我的博士论文,于是他开始筹划我的前
途。Tulane
University是美国南方一所好大学,在全美也称得上二三流学校,不过数学
系在我之前只出过不到十位的博士,于是Wallace教授通过系主任请研究院给我一个例外
待遇。得博士学位照惯例必须修满二十个学分,但Wallace教授觉得为我,为数学系,反
不如早点给我博士学位,而且推荐我去研究活动多的地方,求进一步的发展,所以系里
特许我于第二学期不选课,专心去书写博士论文。
Wallace教授的初意是希望我去普林斯顿大学数学系任讲师,使能从
N. Steenrod教授做
代数拓朴的研究,但是没有成功。
1952年秋天我去了University of
Illinois数学系当
博士后研究,每周教授三小时,同时参加系里研究活动。那时候系里有一位代数拓朴的
教授 D.G.
Bourgin,带五、六位博士研究生,研究的主要对象是 (F.J.) Dyson 的猜
测。我不但去听 Bourgin
教授的课,也去参加他率领的讨论班。经过一年的努力,我得
到了 一个Dyson猜测的证明,Bourgin
教授知道后十分惊讶,当时只说他自己也做得差
不多了。这件事使我很尴尬,于是去向陈省身先生请教。他给我一个建议,说最好的解
决方法,是两人合写一篇文章去发表,不过必须由他提出来才是。如果他不提,我应该
自己发表,不过文章中应提及听说
Bourgin 教授有一独立的证明。结果我的文章于
1954
年发表在《Annals of
Math》上,Bourgin的文章于
1955年发表在瑞士一数学杂志上。在
University of Illinois
我停留了两年。我在那里的时候,施拱星先生正在那里读博士
学位。周元燊院士去读博士学位恰在我离开之后,我曾帮忙向系方推荐他。
我在
University of Illinois 所写的两篇文章颇引人注意,同时Wallace
教授继续努
力推荐我去普林斯顿做研究。
1954年秋天,我获得美国国科会一年的资助,去普林斯顿
高等研究院做研究,主要的对象是将Dyson猜测再扩充,使亦包括
Borsuk-Ulam 定理。
一切安排是Wallace教授透过 D. Montgomery
教授才办成功的。
Montgomery
教授出身于小型的大学,所以他十分同情非名校出身但工作能力强的年轻数
学工作者,也很同情来自他国学者,他的理由是由名校出身的美国人已经有很多的机
会,无须他人多帮忙。每年去普林斯顿高等研究院做研究的数学工作者在五十人之上,
年轻的较多,在大家的心目中,以
Montgomery
教授人缘最好。
我的研究计划,半年内就完成了。顺着同样路线做下去,前途并不乐观,所以我觉得有
必要另找途径。正在那时候,Montgomery教授和
L. Zippen 教授合写了一本书
《Topological Transxxxxation Group》。前半本解答
Hilbert's Fifth Problem,那
是四年前他们合作的 一篇文章和一篇A.M. Gleason
文章所得到的成果,后半本讨论拓
朴变换群。因为这些是当时大家公认最重要的贡献,当然非好好读不可,于是我自荐帮
忙那本书的校对工作。读完了全书,我觉得可以考虑某些问题,于是向Montgomery教授
请教。他听了以后,告诉我其中一个问题,正是他和H.
Samelson
教授研究的对象,立
即表示欢迎我加入他们的行列。因为这个偶然的机缘,使我在那两年中,和他们两人合
写了两篇文章。
1956年秋天我去
University of
Pennsylvania(简称宾大)工作,一个原因是宾大数学
系有一位教授在高等研究院进修,知道我的研究工作,也知道Montgomery
教授和我合
作,竭力向系里推荐我。另一个原因是宾大距离普林斯顿相当近,不论自己驾车或搭火
车,一个多小时可以到达,使我有较多机会向
Montgomery
教授请教。在宾大我一共工
作了三十五年,起先是助理教授,
1958年被提升为副教授,
1961年被提升为正教授。在
职期间,曾兼任数学系里研究生部主任四年,数学系系主任五年。在我指导下完成博士
论文的有L.Mann(
1959),后来任University
of Massachusetts
数学系系主任多年,
1961年有苏竞存,他于
1954年毕业于台大物理系,后来改念数学,现在是University
of
Massachusetts数学系教授。
来宾大教书最大的好处是可以常去看Montgomery教授,后来他干脆每星期留下一天,让
我去和他讨论数学。这样维持了二十多年,合写了二十多篇文章。
1968年我被选为中央研究院院士,
1972年列名于《美国名人录》(Who's
Who in
America)。
18906(AX,X)>=0限制在实数域上考虑
(AX,Y)=(X,AY)为对称变换,可能很简单
18906结论是成立的,
关键在于理解正定变换和正定矩阵的关系
18906看不大懂,你们高代用的什么课本?
18906我好像在那一本矩阵论教材上看到过这个问题,当时没有关心,
现在也不太确定
难道是我理解错了,问题应该是另一个提法么,
但正定必然相似于对角形
对称变换也是所谓的单纯变换,即可对角化的变换
相似是等价的
18906我觉得我们考虑正定变换的时候都是假定它是对称变换的吧!
如果没有这样的限制,正定变换不一定对称变换。
如:
在2维欧氏空间,某一正定变换的矩阵如下:
1
1
3 5
但显然它不是对称变换!
18906ruti
18906能不能先问一下版主,什么是实欧氏正定变换?
18908小弟有个地方不明白!在附件中,In this case ,the numbers 1, 2,^^^,p-1 ,may be group
as xi ,p-xi and (1/2)(p-3) pairs of unequal associated numbers
.
为什么是(p-3)post-23-1128830930.ibf
18908因为1是单位元, -1的逆元是自己, 其他的元素可以与逆元两两配对!
18909博士一走廊,硕士一礼堂,本科一马路
18909培养方式本科化:当前研究生的课程采取大班形式,仍然沿用本科的那一套“教师上面讲,学生下面记”的填鸭式教育模式,创新、思考的能力未见进步,做笔记的功力倒有所增长。而且更为奇怪的是,授课内容竟然有些还停留在本科阶段,真不知道是老师的悲哀,还是学生的悲哀?
导师制虚名化:现在大学里研究生导师每一届要指导三四个学生,甚至更多,以现阶段的两年半学制为例,则每个导师需要指导十几个学生。导师有时间和精力指导如此多的学生吗?所以就出现另一个“怪现象”,学生和导师经常数月甚至半年不见面,交流就更不用提了,只有到节日的时候,学生才有机会识得导师的“庐山真面目”,而且还是“犹抱琵琶半遮面”,三言两语各自散去,导师的作用已然失去。
科研成果指标化:目前各个高校基本上都明文规定,研究生期间必须发表一定数量的科研成果,且这种科研成果还与学生能否毕业挂钩。于是,学生为了能够顺利毕业,想方设法、东拼西凑搞出一定数量的“科研成果”,而且还要自己花钱发表。最终结果可想而知,各种“垃圾”文章充斥着我们的眼睛,理论的发展没有看到,看到的只是各种濒临倒闭的杂志焕发出“勃勃生机”。
毕业设计(论文)形式化:目前研究生毕业设计(论文)形式化,内容不再重要,无实质内容可以,无创新点也可以,只要有“成果”的形式存在就可以。毕业设计(论文)答辩更是形式主义的集中体现,老师和学生共同努力完成了这场作秀,演出如此精彩,以至于事后仍回味无穷。
毕业学生标准化:毕业研究生作为学校向社会提供的“产品”,呈现的是标准化的现象——接受相同的填鸭式教育,具有同样的科研能力(成果),拥有同等的毕业设计(论文),握有一样的研究生学历,何其标准化的产品呀(也许所不同的只是与生俱来的个体差异)!
18909同意!特别是二三流的大学,和在职研究生教育!
18909建议楼主将此帖整理一下 写成一封信投给教育部,确实到了该管一下的时候了 ,要不然后果 不堪设想
18909一个真实的笑话:
某校一博士导师,带了数十硕士,带了若干博士。
某年新生报到后,导师同学生见面。该导师亲切地对一同学说:“你是今年的博士吧。你硕士是哪里毕业的呀?”学生回答:“X老师,我是您带的硕士。”
18909这样下去,我们的研究生岂不都成了垃圾?
18909研究生教育的现状确实让人担心,导师制徒有其名,导师与学生三月或半年见不着面,。。。。。。教育如此,怎堪其忧?
18909研究生......垃圾!!!
遍地都是!!!
可还有很多人往里挤,当教育的陪葬品!!!
18909我不同意楼上的说法。。多了有什么不好的。眼红吗???
18909的确现下中国的研究生教育在制造垃圾,形式主义,功利主义。
18909楼上说的都不错.不过说到中国研究生教育质量下降.原因很多.
以我熟悉的计算机学科为例,硕士生的培养和以前差别很大,以向西方国家学习为口号,研究型硕士已经不再提了,大家纷纷认为"本科打基础,博士搞研究",硕士做为一个学位,快要被取消了---在这种思想指导下,硕士三年变两年,研究生不再创新,拉及论文满天飞,等等等等,就一点都不奇怪了.----这和博士生教育不一样,博士生是想培养你的创新能力,但有些学校没这个能力,而硕士生是压根就不想也被认为不需要培养你的创新能力.
说到硕士生质量下降,有人提出新的质量观:既然硕士不再是研究型,那你看我质量是不是下降就不能根据我是不是能科技创新,而应该看我是不是能适应市场需求,打个比方,现在硕士扩招后,虽然导师少,实验条件不够,虽然论文没有创新,但只要我能让你就业,那你的质量就没有下降.硕士扩招后,有不少硕士生毕业后不再到高校,科研院所和企业研发部门从事研究与研发工作,而是到其它部门做技术含量不高的工作---在这种情况下,既使你没有技术创新能力,既使你读研时没有导师,没有实验条件,论文没有提出创新点---我也认为你受到的研究生教育不但质量没有下降,反而还提高了---因为你的教育更适应你未来的工作了.
我说这样多,只是把一种在一些人脑子里存在的观点表述一遍,并非表示赞成或反对这种观点.如果这种观点被决策层认同,下一步的研究生教育动向我们就清楚了.
18909有人说
18909现在每年硕士生的数量与80年代初本科生的数量相当,权当本科生吧
18910
Suppose
D is a digraph with chromatic number
χ
. Then its line digraph
L (D) has chromatic number at least log 2
χ .
18911这些题目真是简单!哼哼..
18911第一个被积函数是可以出来的
问题就归结为极限函数的不一致收敛性F(R,t)->G(t)
R趋于无穷
18911都干嘛去了啊?怎么现在回答问题的人那么少呢?
18911先谢谢了!post-38-1128782007.ibf
18911再加一题!post-38-1128782031.ibf
18911请教:第一题是不是考虑在无穷大处是不一致收敛的。我这样想不知道行不行:把t提出来,后面的那个广义积分是在区域内是收敛的。而当t趋于无穷大时就是发散的。不知道这样可不可以?请高手指教!!!
18911两个分析题目都作了一下,期盼网友多多交流!post-38-1128924627.ibf
18912不错,我回去在纸上一些也发现第二有误!思路不变!只不过A的特征值是0和正负根(q)i,另外正交阵在复数范围内特征值不一定是正负1,应该是模为正负1!答案不变,还是q=0同时求得的1和-2要舍去!
18912第二题的解答有误。
错误的原因在于A的特征值不正确。
正确结论是:
A的特征值应为:0,±
-
q
;
当且仅当q=0或1时,B是正交矩阵。
18912第二题,可以求出-q是A的特征植,假设Aa=-qa!
B正交则B的转置正交!易知A反对称,故 B的转置=A方-A+E
所以,
(B的转置)a=(A方-A+E)a=(2q方+1)a
故 2q方+1 是B的特征值,而正交阵特征值只能是1或-1,由此易得q=0
18912不好意思,更正一下:第一题,令J=E+L,原式可化为X(E-L)=LX递推得X[(E-L)的n次方]=[L的n次方]X=0而易知E-L可逆,故X=0
注:L的n次方等于零易证!其实L的特征多项式就是x的n次方!
18912第一题,令J=E+L,原式可化为X(E-L)=LX递推得X[(E-L)的n次方]=[LX的n次方]=0而易知E-L可逆,故X=0
注:L的n次方等于零易证!其实L的特征多项式就是x的n次方!
18912因对分块矩阵情有独钟,所以还是用分块法给出解答,简洁明快。见附件。post-38-1128946223.ibf
18912直接代入!
18912还是不会,到了这样的情况X=HX+XH之后怎么做呢?
给个更加具体的过程吧!
18912假设post-38-1128782314.ibf
18912求解方程组!post-38-1128782340.ibf
18912再加一道题目!post-38-1128782614.ibf
18912J=I+H!
最后可以得到:X=HX+XH!很好算了啊!
18912q=1不能舍去哦。
18912你验证了吗?我没算,但估计了一下,应该是不成立吧!
18912努力奋斗
18912同意springboshi的看法,我验证过
当q=0,B=E.显然是正交矩阵.
另外的一个值用它乘它的共轭=1
18914先做角平分线.
18914用位似。很容易的。如图:
先作圆O1;
连接OA与圆O1交于B;
连接O1B;
过A作AO2平行于BO1,与OO1的延长线交于O2,则O2就是所求圆的圆心,AO2就是半径;
附件加不上去!
18914
已知任意一角a和角内任意一点P,试作出满足以下两个条件的圆:
① 圆与角的两条边相切 ②
圆弧过点P
要求:尺规作图
初来,希望大家给予支持!
18914见附件
不能发附件,再想办法。。。。。。
18914I got it.post-7-1128878334.ibf
18914第一步,作出角 A 的平分线
L;
第二步,过点P作L的平行线,交A的一条边于Q;
第三步,做出线段PQ的垂直平分线,交L于O,以O为圆心,OP(=OQ)为半径作圆,即为所求。
18914楼上的做法不对,用几何画板一试可知
18914
引用 (llm3-1415926 @ 2005年01月
18日
19时50分) |
| 楼上的做法不对,用几何画板一试可知
|
你会证明吗?
18914作图题不是用画板来比划的!
18914好好学习!
18914
引用 (bravooo @ 2005年01月
17日
22时07分) |
第一步,作出角 A 的平分线
L;
第二步,过点P作L的平行线,交A的一条边于Q;
第三步,做出线段PQ的垂直平分线,交L于O,以O为圆心,OP(=OQ)为半径作圆,即为所求。
|
因为Q不在圆上,所以这种作法不对。
18914给你们来个正确的方法。
一,作出角a的角平分线L;
二,做出点P关于L的对称点P',连接PP'交角a一条边S于点R;
三,用尺规作图作出一条长度为b的线段,b满足
b*b=RP*RP',在S上R的两侧取两点Q和Q',
使得RQ=RQ'=b,分别过Q和Q'做垂线交L于O和O',分别以O和O'为圆心OQ和O'Q'
为半径作圆即可。
18914加上一个草图。[SIZE=1]post-7-1106210563.jpg
18914图画得不是很美观。
18914谢谢!终于等到了!
好象还少了特殊情况,当点P在角平线上时
18914我记得好像我初中时也作过,但全忘干净了。

18914这就是几何的美。
18914
| 引用 (ice7733 @ 2005年01月21日
10时46分) |
谢谢!终于等到了!
好象还少了特殊情况,当点P在角平线上时
|
P在角平分线上就很好画了

18914用尺规作图法,首先任意画一个角出来,然后在该角内任意找一点,经过该点做圆,但是要求该圆与角的两条边相切!
注意,必须尺规作图,不能用解析法!
18915原来这样的呀,谢谢楼上啦.^_^
18915设f(z)=u(z)+iv(z)在区域D内解析,并且满足:u(z)=kv(z),其中k为实数。证明f(z)在D中为常数
18915题目中的u(z)和v(z)应该理解为复变数吧,都没有说明是实变数呀,我找到一条相似的题也是把它理解为实变数做的.就是这儿不明白哦.
18915
| 引用 (yabcdy @ 2005年10月09日
14时44分) |
|
题目中的u(z)和v(z)应该理解为复变数吧,都没有说明是实变数呀,我找到一条相似的题也是把它理解为实变数做的.就是这儿不明白哦.
|
既然都写了是u(z)+i v(z)了,那么就默认u, v是实值函数
189
17考虑矩阵[0,1;E 0]的各个特征向量,其中E是n-1阶单位阵
189
17to baixueli88:
哦,是的,我也是算得这个答案,你算第二问了吗,求正交变换的时候,需要把其中n-1个向量正交化,不是太麻烦了吗,有没有简便的方法阿?
189
17在附件里,谢谢post-38-1128786165.ibf
189
17这个题目转换到对称矩阵之后应该很好做吧!
还要利用矩阵的正定和顺序子式的行列式恒大于0的性质
189
17我也不清楚我的思路是否正确我作出的第一问的答案很奇怪,只是确定a,b之间的关系,并未设计
a,b的范围.
在做第2问时,似乎道理很简单,但真的去求那个矩阵实在太麻烦了
189
17第一问是有范围的,比方我给你个,a>b>0的情况就是个范围啊,而且符合的!
好范围具体就是a>0,a-|b|>0吧!我没有算!
189
17利用特征值全大于零!a>b,a+(n-1)b>0
189
18谢谢
189
18在附件里,谢谢post-38-1128788
188.ibf
189
19强!!
189
19强!!
189
19
自己看吧
http://www.xiaohui.com/weekly/20050915.htm
189
19强!!
189
19强!!
189
19牛
189
19!!!!1!!!!!!!!!!!!!!!!!!
189
19强...
189
19niuren
18920怎么没有人解答呢?
18920请问楼上的,该怎么做啊,有什么启发??我很想知道!!
18920个人感觉这个题目还是挺有启发的!所以贴出来!post-38-1128794082.gif
18925我没有确切的邮政地址,可否用同学的邮政地址,他现在在读研
在他的地址后写 ***(转收)
这样不知可否?
若有人经历这样的情况,可否指教一下?
哎,都要报名了,麻烦的事多啊~~~~~~~
18925哎……没人应答!
问问各位兄弟了, :)
18925哦,什么意思呀,呵呵。没看明白呢,能说清楚一点吗
18925是的!
18925报考时不是要填一个邮政地址以供寄准考证、复试通知书、入学通知书
但是,我是往届的,住在租的房,没有确切的通信地址
想通过同学转,你们看行不行?
我现在为此事犯愁呢?
18926卜算子.思湘君(作者:
雾夜清风)
寂寞无涯处,绿柳烟如愁。疑是秦淮漾波里,荡舟已迷途。
梦到湘江浦,红伊风楚楚。无泪魂消化泥丘,为把湘君守。
好词大家共享
18926这位老师能把邮箱留下吗?
谢谢
18926zlf3412_75@msn.com
18927利用Taylor展式,见附件post-38-1129
176042.ibf
18927好像有点小问题!!!f[(a+b)/2]=<[f(a)+f(a)]/2好像不成立???
请高手指点!!!谢谢!!!
18927谢谢
18927另一种证法:post-38-1129082314.gif
18927“不妨设f"(w1)-f"(w2)>=0"
好像没起到作用
”构造函数g(x)=f'(x)-[f"(w1)-f"(w2)]/2*x
利用Rolle中值定理不难证明,存在w
[w1,w2]满足条件
得证“但g(a)不等于g(b)
18927首先利用Taylor 展开
(1)
f(x)=f(a)+(x-a)f'(a)+f"(w1)(x-a)^2/2
x=(a+b)/2带入
f((a+b)/2)-f(a)=f"(w1)(b-a)^2/8
同理
(2)
f(x)=f(b)+(x-b)f'(a)+f"(w2)(x-b)^2/2
x=(a+b)/2带入
f((a+b)/2)-f(b)=f"(w2)(b-a)^2/8
两式相减
f(b)-f(a)=[f"(w1)-f"(w2)]/2*(b-a)^2/4
不妨设f"(w1)-f"(w2)>=0
下证明存在某个w,f"(w)=[f"(w1)-f"(w2)]/2
构造函数g(x)=f'(x)-[f"(w1)-f"(w2)]/2*x
利用Rolle中值定理不难证明,存在w

[w1,w2]满足条件
得证
应该也可以用反证法来做的
18927怎么做呀?
18927利用泰勒展式!
18927设f(x)在[a,b]上有二阶导数,
且f'(a)=f'(b)=0,证明:存在一点w属于(a,b),s.t.
f''(w)>=(4/(b-a)^2)|f(b)-f(a)|.
18928
http://zgbdsyjxz.nease.net/fcd.htm可以连接到以下网站:
祁锋老师网站
杨必成老师网站
陈计老师网站
张志华的网站
景中网站
姜卫东老师网站
数学档案”网页
不等式世界
18928都是几位研究不等式的大师。我也是经常到那里看的
18928hao zhan
18929我的想法是讨论任意取三个正整数a,b,c,(a,b,c)=1的概率问题。当然,如果三个整数两两互素,则必然互素,但反之不成立,所以其概率不能简单地用两个情形的概率作乘积,需要作更复杂的估计和计算。
18929
引用 (疯猪 @ 2005年11月
18日
07时57分) |
本题的答案思想:
首先,要明确3个数互素的定义。定义为“两两互素”与定义为“3个数的大公因是1”是不相同的。从而有不相同的答案
青竹的答案是错误的,即使“两两互素”也不保证三项的独立的
我认为要解决这个问题要从6除以pai方是怎样得到的入手
|
该同学指出了三个整数互素与三个整数两两互素两个概念之间的差别,事实上针对这两个概念得到的答案是不相同的,他们都是两个整数互素情形的推广,至于两个整数互素的概率等于
6 π
2
,它的推导在前面的帖子中已经有介绍。
18929本题的答案思想:
首先,要明确3个数互素的定义。定义为“两两互素”与定义为“3个数的大公因是1”是不相同的。从而有不相同的答案
青竹的答案是错误的,即使“两两互素”也不保证三项的独立的
我认为要解决这个问题要从6除以pai方是怎样得到的入手
18929一元一次多项式的系数互素,换种说法就是“任取两个正整数,其互素的概率为
6 pai 2
”
那么一元二次多项式的系数互素,换种说法就是“任取三个正整数,两两互素”
那么我觉得概率应该是
(
6 pai 2
) 3
不过我觉得这个答案可能有点问题
18929问题:设集合A表示所有正整系数的一元一次多项式的集合,则任意取一个A中元素,其系数互素的概率是6/(pai*pai),
设集合B表示所有正整系数的一元二次多项式的集合,则任意取一个B中元素,其系数互素的概率是多少?
http://www.math.org.cn/forums/index.php?showtopic=5064
18929三个数互素,只要三个数中有两个数互素即可,对于一元二次方程和一元一次方程整系数构成的集合B.A其中的元素个数都是无限,对于所求概率是没有影响的,所以我认为一元二次方程中系数互素的概率=一元一次方程中系数互素的概率
18929任意三个整数互素,只要其中两个整数互素即可,所以概率应该是3*6/(pai*pai)
18929
| 引用 (alpsycl @ 2005年10月16日
22时28分) |
任意三个整数互素,只要其中两个整数互素即可,所以概率应该是3*6/(pai*pai)
三个数互素,只要三个数中有两个数互素即可,对于一元二次方程和一元一次方程整系数构成的集合B.A其中的元素个数都是无限,对于所求概率是没有影响的,所以我认为一元二次方程中系数互素的概率=一元一次方程中系数互素的概率
|
我认为这两位的答案都有问题,事实上,(a,b,c)=1可以推出(a,b)=(b,c)=(c,a)=1,但反之不真。故July的等于6/(pai*pai)的答案不对,而
18〉pai*pai,故alpsycl的答案也不成立。
18929是的,已经发现问题了,事实上三个数互素并不能推出其中存在两个数互素,比如(15,20,12)=1,但是任意两个都不互素。
18929
引用 (July @ 2005年10月
19日
00时29分) |
我觉得答案可能是"(1/2)*6/ pai*pai"
分析如下:任意的三个数(整数),设a,b
,C是B中的任意三元素,要使
a,b,c三数互素,只需c与a,b的最小公倍数互素即可,即:d=[a,b],有(c,d)=1成立时,则有(a,b,c)=1成立. d
显然属于正整数集,按是Z集的一半处理,则P[(c,d)=1]=(1/2)*6/pai*pai
希望同样的能的到大家的指教
|
要注意(a,b,c)=1当且仅当((a,b),c)=1,令d=(a,b)而不是d=[a,b]则(c,d)=1
18929我觉得答案可能是"(1/2)*6/ pai*pai"
分析如下:任意的三个数(整数),设a,b
,C是B中的任意三元素,要使
a,b,c三数互素,只需c与a,b的最大公约数互素即可,即:d=(a,b),有(c,d)=1成立时,则有(a,b,c)=1成立. d
显然属于正整数集,按是Z集的一半处理,则P[(c,d)=1]=(1/2)*6/pai*pai
希望同样的能的到大家的指教
谢谢帖主的纠正
18929我觉得这个概率要利用6/pi^2的由来计算,舍任意两个正整数互素的概率为p,则任意两个偶数的最大共因数为2的概率为p/2^2,依次类推可得:
1=p+ p/2^2+ p/3^3 +……
从而 p=1/(1+1/4+1/9……)=6/pi^2
对三个正整数可类推进行,当然要看三个正整数互素的定义,需要计算的实际上是利用傅立叶展开计算级数,不知楼主以为如何
18929
| 引用 (yzlv @ 2005年10月22日
14时15分) |
我觉得这个概率要利用6/pi^2的由来计算,舍任意两个正整数互素的概率为p,则任意两个偶数的最大共因数为2的概率为p/2^2,依次类推可得:
1=p+ p/2^2+ p/3^3 +……
从而 p=1/(1+1/4+1/9……)=6/pi^2
对三个正整数可类推进行,当然要看三个正整数互素的定义,需要计算的实际上是利用傅立叶展开计算级数,不知楼主以为如何
|
我正在研究这个问题。
两个整数互素的证明我是这样考虑的:
设N是任意一个正整数,则在前N个正整数中,任取两个互异的正整数m,n的取法种数是
组合数N(N-1)/2;而正整数m,n互素的可能情况时

k从1到N
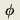
(k),
两者相比再让N趋于正无穷大取极限,即得所要的概率结果6/pi^2
三个整数互素的证明我换没有找到解决的思路,估计用富里叶级数难于突破。
18929我想所谓任意取两个正整数,并没有要求说是两个不同的,应该说是独立的取两个正整数,有可能相等的,当然也可以认为是有放回的取两个。
不过在下对搂住的想法很感兴趣,原闻其祥,在下的邮箱是yzlv@163.com,望不吝赐教。
18929
引用 (yzlv @ 2005年10月27日
18时59分) |
我想所谓任意取两个正整数,并没有要求说是两个不同的,应该说是独立的取两个正整数,有可能相等的,当然也可以认为是有放回的取两个。
不过在下对搂住的想法很感兴趣,原闻其祥,在下的邮箱是yzlv@163.com,望不吝赐教。
|
我们在这里考虑的是不放回的随机取两个正整数。
当然也可以考虑其他情形。
18929
| 引用 (magic9901 @ 2005年10月24日
11时46分) |
| 引用 (yzlv @ 2005年10月22日
14时15分) |
我觉得这个概率要利用6/pi^2的由来计算,舍任意两个正整数互素的概率为p,则任意两个偶数的最大共因数为2的概率为p/2^2,依次类推可得:
1=p+ p/2^2+ p/3^3 +……
从而 p=1/(1+1/4+1/9……)=6/pi^2
对三个正整数可类推进行,当然要看三个正整数互素的定义,需要计算的实际上是利用傅立叶展开计算级数,不知楼主以为如何
|
我正在研究这个问题。 两个整数互素的证明我是这样考虑的: 设N是任意一个正整数,则在前N个正整数中,任取两个互异的正整数m,n的取法种数是 组合数N(N-1)/2;而正整数m,n互素的可能情况时
 k从1到N
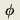
(k), 两者相比再让N趋于正无穷大取极限,即得所要的概率结果6/pi^2 三个整数互素的证明我换没有找到解决的思路,估计用富里叶级数难于突破。
|
不好意思我想请问一下 N取极限的时候
即使有收敛的话
那么这个极限就是任取两个自然数的概率么
要考虑即使是可数的无穷 也不见得就等于有穷的逼近呢
所以我的理解是
不能思考那个概率是怎么来的
只能理解所取的自然数是某个集合中的
使得2元互素的概率为6/pi*pi
然后后面的3元组合也是这个集合里面的
18929关于这一点可以从概率的大数定律得到恰当的合理的解释,也就是考虑概率的极限理论。
18929
| 引用 (yzlv @ 2005年10月22日
14时15分) |
我觉得这个概率要利用6/pi^2的由来计算,舍任意两个正整数互素的概率为p,则任意两个偶数的最大共因数为2的概率为p/2^2,依次类推可得:
1=p+ p/2^2+ p/3^3 +……
从而 p=1/(1+1/4+1/9……)=6/pi^2
对三个正整数可类推进行,当然要看三个正整数互素的定义,需要计算的实际上是利用傅立叶展开计算级数,不知楼主以为如何
|
感谢楼上的赐教
18929
引用 (疯猪 @ 2005年11月
18日
11时51分) |
| 引用 (yzlv @ 2005年10月22日
14时15分) |
我觉得这个概率要利用6/pi^2的由来计算,舍任意两个正整数互素的概率为p,则任意两个偶数的最大共因数为2的概率为p/2^2,依次类推可得:
1=p+ p/2^2+ p/3^3 +……
从而 p=1/(1+1/4+1/9……)=6/pi^2
对三个正整数可类推进行,当然要看三个正整数互素的定义,需要计算的实际上是利用傅立叶展开计算级数,不知楼主以为如何
|
感谢楼上的赐教
|
我们先假定三个数互素的表示(a,b,c)=1,概率是P
则任意3个整数的最大共因数为2的概率为p/2^3,依次类推可得:
1=p+
p/2^3+ p/3^3 +……
从而
p=1/(1+1/8+1/27……)=
(公式记不清楚了)
18931你写了不少,意思只有一个吧:完成作业~
可这是不可能的!除非你是天才。因为学习这些需要一些时间。
还是回答一下好了~
建议先看中文的,(干吗先看英文的?本来就难学!)
先学数学分析,才能学实变函数,
还有所谓测度论和实变的关系:国内各大学的教材都不错,就是侧重不同,
有的着重分析,讲L积分;有的着重公理化测度,学概率。看你的需要了。
数学思维好的话,直接读测度论吧,它是实变的抽象化。
网上资料不多,还是到大书店买吧。
(就是作业做不完了~)
18931好书太多了。
想学好的话,直接看研究生教材,简单明了,
本科教材太罗索,本质又不突出
18931徐森林的《实变函数论》基本就是北大周民强的 《实变函数》与
复旦夏道行的《实变函数与泛函分析教程》第一卷的混合。北大的分析成分重些,很有技巧性。而复旦的重测度论一块。徐森林的书就是综合版本,但是相对那两本没有什么特点。测度方面的书本来就很少。而且基本都是国外的。象哈尔莫斯的《测度论》,虽然经典但是太老了。这里我也说不上太多的好书。以个人经验是建议你看看
(美)Edwin Hewitt,(美)Karl R.Stromberg著; 孙广润译 的《实分析与抽象分析》好象这书副标题是:现代实变函数论
。很经典的,不知道能不能弄到。我反正是没有,就在图书馆借。但是这书是英文的教材。你可以在国外买到英文版本的。我感觉这书写的很清楚,相当经典。
18931教材有了几本。还是请推荐参考书吧。尤其是测度论的。就没有找到。
18931中国科技大学出版社。徐森林,《实变函数论》不错,条理清晰,还算好学。
18931
引用 (樱析光 @ 2005年10月09日
19时32分) |
你写了不少,意思只有一个吧:完成作业~
可这是不可能的!除非你是天才。因为学习这些需要一些时间。
还是回答一下好了~
建议先看中文的,(干吗先看英文的?本来就难学!)
先学数学分析,才能学实变函数,
还有所谓测度论和实变的关系:国内各大学的教材都不错,就是侧重不同,
有的着重分析,讲L积分;有的着重公理化测度,学概率。看你的需要了。
数学思维好的话,直接读测度论吧,它是实变的抽象化。
网上资料不多,还是到大书店买吧。
(就是作业做不完了~)
|
学习英文的原因是我现在国外上学。
但是数学基础不够,因此学习数学本科都有点吃力。
数学分析是否就是我学过的工科数学分析?
如果是的话,我就已经学过了。
现在我正是要看中文的参考书。
是否应该是找实变函数的参考书。
还请网上的高人指点一些。。
18931我是工科学生。正在学习本科生的实分析和测度论。
看那些英文的教材实在是看的云里雾里。
关键是概念和定义太多,记都记不过来。
看后面的忘了前面的。
而且很多概念都比较tricky...
一不小心就理解错误(还以为自己的理解是对的)。
看这些数学教材的问题就是几个小时看不了几页。头晕。想睡觉。
况且还是英文的教材。有些语言觉得很绕。。。
定义和概念更是绕的糊涂。
作业来不及做。
有什么中文的实分析和测度论的参考书和辅导书能够看一看呢?
请大家推荐学习辅助资料。
我真的很想把这两门课程学好。。。
实分析和测度论,我在网上搜了半天也没有找到一本习题解答,学习指南,复习参考等的学习指导书。
还请大家指点。非常感谢!
18931我看了些置顶的文章,其中提到了数学分析方面不少的好书。
比如:
数学分析中的典型问题与方法
等等。
不知道这个数学分析和我要找的实分析是否是一个内容?
------------------------------------
另外,我也听说了rudin等的英文教材,不过看起来还是太吃力。语言就够绕的。
还是想看中文的。
尤其是习题解答和学习辅导之类的。
因为必须以最快的速度理解概念然后做作业交作业。
明天就要交了,我到现在看书还是看不下去。
------------------------------------
请大侠一定要指点实分析和测度论方面的好参考书。救命!!!
18931还想请教大家:实变函数论和实分析和测度论是否是一个内容?
看到置顶文章有讨论实变函数论的。。。
-----------------------------------
不知道哪里有这些课程的视频资料。。。???
非常感谢!
18931测度论的可以看Donald Cohn的〈measure theory>
stanford数学系的math
205A的教材。
或者看Royden的〈real
analysis〉,harvard也用这本,测度讲的也比较多!
我在未名空间上也看到一个人提同样的问题,不知是不是你?
18933谢谢.
18933经过慎重选择,我有意进一步学习非线性分析与数学物理方向的知识,数学物理找到了几本很好的参考书.希望得到关于非线性分析的基础类经典书籍的指导.先谢谢了.
18933清华大学数学系的唐云教授有一本书,可以读一下的.
18933什么名字
18933非线性动力学的现代分析方法
18933用伯杰的书吧.
18934"谷山志村猜想"不是解决了“费马”大定理吗?应该还好找的吧!
18934Google搜了一下
http://modular.fas.harvard.edu/edu/Spring2003/21n/上面的
Other
Resources
1 Andrew Wiles's proof of Fermat's Last Theorem:
PDF (860kB pdf file instead of huge JSTOR scan, thanks to Derek Buchanan),
TeX file 就是
好像是证明了谷山志村猜想,也就是证明了Fermat's Last Theorem
18934原文发表在:
Annals of Mathematics 141(
1995),443-551
Title: Modular
elliptic curves and Fermal's Last Theorem
Author: Andrew Wiles
文章包括怀尔斯对谷山-志村猜想和费马大定理的证明的主要部分
Annals of Mathematics
142(
1995),553-572
Ring-theoretic properties of certain Hecke algebras
Richard Taylor , Andrew Wiles
介绍了用于克服怀尔斯
1993年证明中出现的缺陷的数学
18934代数几何中著名的"谷山志村猜想"于本世纪初被包(括怀尔斯的合作者?)泰勒在内的四人完整解决,这篇论文发表在什么刊物上?谢谢了!
18934不敢说看到,只是好奇:)
18934最近才看到这本书
18934如果对Fermat大定理的证明历史过程看一下,我也不知道会有这个猜想
18934
| 引用 (jixuan @ 2005年10月09日
13时32分) |
|
代数几何中著名的"谷山志村猜想"于本世纪初被包(括怀尔斯的合作者?)泰勒在内的四人完整解决,这篇论文发表在什么刊物上?谢谢了!
|
Wiles本人并未完全证明谷山-志村猜想,他只证明了其中的半稳定情形,从而导出Fermat's
last theorem!不过Wiles却作出了决定性的贡献!
关于完整的谷山-志村猜想的证明情况的介绍,请见
Eric W.
Weisstein. "Taniyama-Shimura Conjecture." From MathWorld--A
Wolfram Web Resource.
http://mathworld.wolfram.com/Taniyama-Shim...Conjecture.html
现将最后一段摘录如下:
The existence of a proof of the full Taniyama-Shimura
conjecture was announced at a conference by Kenneth Ribet on June, 21
1999
(Knapp
1999), and reported on National Public Radio's Weekend Edition
on July 31,
1999. The proof was completed by Christophe Breuil, Brian
Conrad, Fred Diamond, and Richard Taylor, building on the earlier work of
Wiles and Taylor (Mackenzie
1999, Morgan
1999). The best previous
published result held for all conductors except those divisible by 27
(Conrad et al.
1999; Knapp
1999). The general Breuil et al. proof for all
elliptic curves removed this restriction, in the process relying on
Wiles' proof for rational elliptic curves.
18935
求助 :江泽坚 吴智泉
编《实变函数论》习题答案 如果谁有的话,麻烦发到luowanchao@163.com
谢谢!
18935我也需要
18935rowang@163.com
我也想要,那位有的话发到这个邮箱里,谢谢了
18935我有,QQ21
195807
18935我在电子资源屋,发了一个贴,可以去看看,我自己做的
http://www.math.org.cn/forums/index.php?show...topic=29901&hl=
18935
我 也
需要这本答案,有的话也
和我说一声,邮箱huangrhx@163.com[COLOR=red]
18935不行啊,同志!
18940就是啊
数学网站吗
不聊聊什么啊
18940啊,是数学网站啊?数学博士网站。
18940博士家园是一个数学网站,所以只有数学板块
18940刚来的,请问博士家园怎么好像只有数学的板块,没有其他的呢?
18941见图:post-38-1128845081.ibf
18942有很多文件,对他们用textread执行相同的操作。我的方法如下:
files = cell(1,
10)
files = {'file1', 'file2', ...,
'file3'};
for i = 1 : 10,
textread(files(i),
....);
end
结果出错。请达人指点。谢谢!
18944谁有A.Connes的《Noncommutative geometry》一书,谢谢提供消息。在网上找了好久也没有哪里有下载的,希望能告知。
18944我有,给我邮箱地址,我发给你
18944我也想要,多谢了
zjdiamond@gmail.com
18947行列式的计算方法post-38-1128850786.ibf
18948谢谢了!
18948分块矩阵行列式计算方法探析post-38-1128851086.ibf
18949象这样的帖子楼主能不能多发一些啊!
18949求极限的方法与技巧post-38-1128851529.ibf
18951
控制论和信息论
一、
控制论的产生
二十世纪40年代末,维纳创立了控制论,申农创立了信息论。随着自动化系统和自动控制理论的出现,对信息的研究开始突破原来仅限于传输方面的概念。控制论作为一个相对独立的科学学科的形成却起始于本世纪20~30年代,而
1948年美国数学家维纳出版了《控制论》一书,标志着控制论的正式诞生。从控制的观点揭示了动物与机器的共同的信息与控制规律,研究了用滤波和预测等方法,从被噪声湮没了的信号中提取有用信息的信号处理问题,建立了维纳滤波理论。美国数学家申农是维纳的学生,这年发表了《通信的数学理论》和《在噪声中的通信》两篇著名论文,提出信息熵的数学公式,从量的方面描述了信息的传输和提取问题,创立了信息论。
维纳
1894年11月26日生于密苏里州的哥伦比亚,
1964年3月
18日卒于斯德哥尔摩。维纳少年时是一位天才的神童,他11岁上大学,学数学,但喜爱物理、无线电、生物和哲学,14岁考进哈佛大学研究生院学动物学,后又去学哲学,
18岁时获得了哈佛大学的数理逻辑博士学位。
1913年刚刚毕业的维纳又去欧洲向罗素、哈代、和希尔伯特这些数学大师们学习数学,正是多钟学科在他头脑里的汇合,才结出了控制论这颗综合之果。
19
19年维纳在麻省理工学院任教。在研究勒贝格积分时,就从统计物理方面萌发了控制论思想。第二次世界大战期间,为了对付德国的空中优势,英美两国极待提高他们的防空体系的性能。维纳两次参加了美国研制防空火力自动控制系统的工作,当时高射炮发射出的炮弹的速度比德国的飞机快不了多少,而飞机驾驶时有一定随机性,这就要求高射炮在描准时不能再直接对准目标或只是有个大约的提前量,而是要预测飞机将要飞到的精确位置,以使击中目标。这就产生了自动控制问题。维纳概率论和数理统计等数学工具用于火炮控制系统提出了一套最优预测方法。但这只能给出一种可能性最大预测,并不能给出百分之百的击中率。为此他开始把早年学的动物学知识用了起来。
1943年维纳与别格罗和罗森勃吕特合写了《行为、目的和目的论》的论文,从反馈角度研究了目的性行为,找出了神经系统和自动机之间的一致性。这是第一篇关于控制论的论文。这时,神经生理学家匹茨和数理逻辑学家合作应用反馈机制制造了一种神经网络模型。第一代电子计算机的设计者艾肯和冯.诺依曼认为这些思想对电子计算机设计十分重要,就建议维纳召开一次关于信息、反馈问题的讨论会。
1943年底在纽约召开了这样的会议,参加者中有生物学家、数学家、社会学家、经济学家,他们从各自角度对信息反馈问题发表意见。以后又连接举行这样的讨论会,对控制论的产生起了推动作用。《控制论》一书的副标题是“关于在动物和机器中控制和通信的科学”。
二、
控制、控制论和控制论的发展
1、控制——为了‘改善’某个或某些对象的功能员发展需要获得并使用信息,以这种信息为基础而选出的加于该对象的作用。其含义有:
a)
施加这种作用的目的为了改善对象,以达到预期目标;
b) 控制就是加在某个对象上一种作用;
c)
这种作用是通过信息的选择、使用而实现的。
2、控制论——即一般控制论,是一门研究各类系统的调节和控制规律的科学。
控制论一词Cybernetics,来自希腊语,愿意为掌舵术,包含了调节、操纵、管理、指挥、监督等多方面的涵义,维纳以它作为自己创立的一门新学科的名称,正是取它能够避免过分偏于哪一方面,“不能符合这个领域的未来发展”和“纪念关于反馈机构的第一篇重要论文”的意思。维纳给控制论下的定义是“设有两个变量,其中一个是能由我们进行调节的,而另一个则不能控制。这时我们面临的问题如何根据那个不可控制变量从过去到现在的信息来适当地确定可以调节的那个变量的最优值。以实现对于我们最为合适、最有利的状态。”
控制论是自动控制、通讯技术、计算机科学、数理逻辑、神经生理学、统计力学、行为科学等多种科学技术相互渗透形成的一门横断性学科。它研究生物体和机器以及各种不同基质系统的通讯和控制的过程,探讨它们共同具有的信息交换、反馈调节、自组织、自适应的原理和改善系统行为、使系统稳定运行的机制,从而形成了一大套适用于各门科学的概念、模型、原理和方法。
3、控制论的发展
控制论是多门科学综合的产物也是许多科学家共同合作的结晶。控制论诞生后,得到了广泛地应用与迅猛地发展,大致经历了三个发展时期。
第一个时期为本世纪50年代,是经典控制论时期。这个时期的代表除了生物控制论外,有我国著名科学家钱学森
1945年在美国发表的《工程控制论》。
第二个时期是60年代的现代控制论时期。导弹系统、人造恒星,生物系统研究的发展,使控制论的重点从单变量控制到多变量控制,从自动调节向最优控制,由线性系统向非线性系统转变。美国卡尔曼提出的状态空间方法以及其它学者提出的极大值原理和动态规划等方法,形成了系统测辨、最优控制、自组织、自适应系统等现代控制理论。
第三时期是70年代后的大系统理论时期。控制论由工程控制论、生物控制论向经济控制论、社会控制论和人口控制论等发展。
1975年国际控制论和系统论第三届会议,讨论的主题就是经济控制论的问题。
1978年的第四届会议,主题又转向了社会控制论。电子计算机的广泛应用和人工智能研究的开展,使控制系统显现出规模庞大,结构复杂,因素众多,功能综合的特点,从而控制论也向大系统理论发展。在
1976年国际自动控制联合会的学术会上,专题讨论了“大系统理论及应用”问题。控制论也形成了工程控制论、生物控制论、社会控制论。其中生物控制论又分化出神经控制论、医学控制论、人工智能研究和仿生学研究。社会控制论则把控制论应用于社会的生产管理、效能运输、电力网络、能源工程、环境保护、城市建议,以至社会决策等方面。维纳在
1950年出版的《人有人有的用处——控制论和社会》一书中着重论述了通信、法律、社会政策等等与控制论的联系。阿希贝
1958年发表的《控制论在生物学和社会中的应用》一文,认为运用非线性系统的控制理论,可以研究社会系统。
为了解决控制和决策中的非数值问题,和适应80年代以后智能机研究的需要,以及要解决知识信息处理的问题,遂产生了知识工程,并已研制成专家系统、自然语言理解系统和智能机器人等。
三、
控制论的基本概念和基本思想
控制论强调系统的行为能力和系统的目的性。维纳提出了负反馈概念和功能模拟法。
行为——系统在外界环境作用(输入)下所作的反应(输出)。人和生命有机体的行为是有目的、有意识的。生物系统的目的性行为又总是同外界环境发生联系,这种联系是通过信息的交换实现的。外界环境的改变对生物体的刺激对生物系统来说就是一种信息输入,生物体对这种刺激的反应对生物系统来说就是信息的输出。控制论认为任何系统要保持或达到一定目标,就必须采取一定的行为。输入和输出就是系统的行为。
反馈——系统输出信息返回输入端,经处理,再对系统输出施加影响的过程。
反馈分正反馈和负反馈。负反馈是控制论的核心问题。
正反馈——反馈信息与原信息起相同的作用,使总输入增大。系统目标偏离。加剧系统不稳定。
负反馈——反馈信息与原信息起相反的作用,使总输入减小。系统目标偏离减小。系统稳定。
控制论的研究表明,无论自动机器,还是神经系统、生命系统,以至经济系统、社会系统,撇开各自的质态特点,都可以看作是一个自动控制系统。在这类系统中有专门的调节装置来控制系统的运转,维持自身的稳定和系统的目的功能。控制机构发出指令,作为控制信息传递到系统的各个部分(即控制对象)中去,由它们按指令执行之后再把执行的情况作为反馈信息输送回来,并作为决定下一步调整控制的依据。这样我们就看到,整个控制过程就是一个信息流通的过程,控制就是通过信息的传输、变换、加工、处理来实现的。反馈对系统的控制和稳定起着决定性的作用,无论是生物体保持自身的动态平稳(如温度、血压的稳定),或是机器自动保持自身功能的稳定,都是通过反馈机制实现的。控制论就是研究如何利用控制器,通过信息的变换和反馈作用,使系统能自动按照人们预定的程序运行,最终达到最优目标的学问。它是自动控制、通讯技术、计算机科学、数理逻辑、神经生理学、统计力学、行为科学等多种科学技术相互渗透形成的一门横断性学科。它研究生物体和机器以及各种不同基质系统的通讯和控制的过程,探讨它们共同具有的信息交换、反馈调节、自组织、自适应的原理和改善系统行为、使系统稳定运行的机制,从而形成了一大套适用于各门科学的概念、模型、原理和方法。
四、控制论的基本方法
控制论是具有方法论意义的科学理论。控制论的理论、观点,可以成为研究各门科学问题的科学方法,这就是撇开各门科学的质的物点,把它们看作是一个控制系统,分析它的信息流程、反机制和控制原理,往往能够寻找到使系统达到最佳状态的方法。这种方法称为控制方法。
控制论的主要方法有控制方法、信息方法、反馈方法、功能模拟方法和黑箱方法等。
信息方法——是把研究对象看作是一个信息系统,通过分析系统的信息流程来把握事物规律的方法。
反馈方法——则是动用反馈控制原理去分析和处理问题的研究方法。所衷肠反馈控制就是由控制器发出的控制信息的再输出发生影响,以实现系统预定目标的过程,正反馈能放大控制作用,实现自组织控制。但也使偏差愈益加大,导致振荡。负反馈能纠正偏差,实现稳定控制,但它减弱控制作用、损耗能量。
功能模拟法——用功能模型来模仿客体原型的功能和行为的方法。所谓功能模型就是只以功能行为是相似为基础而建立的模型。如猎手瞄准猎物的过程与自动火炮系统的功能行为是相似的,但二者的内部结构和物理过程是截然不同的,这就是一种功能模拟。功能模拟法为仿生学、人工智能、价值工程提供了科学方法。
黑箱方法(又称系统辨识)——通过考察系统的输入与输出关系认识系统功能的研究方法。它是探索复杂大系统的重要工具。系统辨识是在输入、输出的基础上,从一类系统中确定一个与所测系统等价的系统。黑箱就是指那些不能打开箱盖,又不能从外部观察内部状态的系统。
黑箱方法也是控制论的主要方法。具体是:首先给黑箱一系列的刺激(系统输入),再通过观察黑箱的反应(系统输出),从而建立起输入和输出之间的规律性联系,最后把这种联系用数学的语言描述出来形成黑箱的数学模型。
黑箱方法不涉及复杂系统的内部结构和相互作用的大量细节,而只是从总体行为上去描述和把握系统、预测系统的行为,这在研究复杂系统时特别有用。
白箱方法——研究系统的可观性和可控性,通过定量分析找出两者之间的关系。
黑箱方法的目的在于通过为黑箱建立模型,是黑箱变成白箱。有时黑箱模型不止一个,这种情况下,系统辨识其中最合理的一个。
系统辨识主要步骤是:试验设计、选择模型、参数估计和检验模型。
五、信息科学
信息科学是以信息为主要研究对象,以信息的运动规律和应用方法为主要研究内容,以计算机等技术为主要研究工具,以扩展人类的信息功能为主要目标的一门新兴的综合性学科。信息科学由信息论、控制论、计算机科学、仿生学、系统工程与人工智能等学科互相渗透、互相结合而形成的。60年代中,由于出现复杂的工程大系统需要用计算机来控制生产过程,系统辨识成为重要研究课题。从信息科学的观点来看,系统辨识就是通过输入输出信息来研究控制系统的行为和内部结构,并用简明的数学模型来加以表示。控制就是根据系统结构和要求对信息加工、变换和利用。
“信息”使用的广泛性使得我们难以给“信息”下一个确切的定义,但是,一般说来,信息可以界定为由信息源(如自然界、人类社会等)发出的被使用者接受和理解的各种信号。作为一个社会概念,信息可以理解为人类共享的一切知识,或社会发展趋势以及从客观现象中提炼出来的各种消息之和。信息并非事物本身,而是表征事物之间联系的消息、情报、指令、数据或信号。一切事物,包括自然界和人类社会,都在发出信息。我们每个人每时每刻都在接收信息。在人类社会中,信息往往以文字、图象、图形、语言、声音等形式出现。
信息论是研究信息的产生、获取、变换、传输、存贮、处理识别及利用的学科。一般认为,
1948年申农发表的《通讯的数学理论》一文标志着信息论的诞生。信息论有狭义和广义之分。狭义信息论即申农早期的研究成果,它以编码理论为中心,主要研究信息系统模型、信息的度量、信息容量、编码理论及噪声理论等。广义信息论又称信息科学,主要研究以计算机处理为中心的信息处理的基本理论,包括评议、文字的处理、图像识别、学习理论及其各种应用。
信息量是信息论中量度信息多少的一个物理量。它从量上反映具有确定概率的事件发生时所传递的信息。信息的量度与它所代表的事件的随机性或各外事件发生的概率有关,当事件发生的概率大,事先容易判断,有关此事件的消息排队事件发生的不确定程度小,则包含的信息量就小;反之则大。从这一点出发,信息论利用统计热力学中熵的概念,建立了对信息的量度方法。在统计热力学中,熵是系统的无序状态的量度,即系统的不确定性的量度。
申农的信息量公式:H(x)
=ΣP(xi)h(xi)= —ΣP(xi)·log2P(xi)
其中:h(xi) =
—log2P(xi),表示某状态xi的不定性数量或所含的信息量。若P(xi)=1,则h(xi) =0;若P(xi)=0,则h(xi)
=∞;当n=2,且P1=P2=1/2时,H(x)=1比特。因此可见一个等几率的二中择一的事件具有1比特的不定性或信息量。
信息和控制是信息科学的基础和核心。70年代以来,电视、数据通信、遥感和生物医学工程的发展,向信息科学提出大量的研究课题,如信息的压缩、增强、恢复等图像处理和传输技术,信息特征的抽取、分类和识别的模式、识别理论和方法,出现了实用的图像处理和模式识别系统。
申农最初的信息论只对信息作了定量的描述,而没有考虑信息的其他方面,如信息的语义和信息的效用等问题。而这时的信息论已从原来的通信领域广泛地渗入到自动控制、信息处理、系统工程、人工智能等领域,这就要求对信息的本质、信息的语义和效用等问题进行更深入的研究,建立更一般的理论,从而产生了信息科学。
迄今为止,人类社会已经发生过四次信息技术革命。
第一次革命是人类创造了语言和文字,接着现出了文献。语言、文献是当时信息存在的形式,也是信息交流的工具。
第二次革命是造纸和印刷技术的出现。这次革命结束了人们单纯依靠手抄、撰刻文献的时代,使得知识可以大量生产、存贮和流通,进一步扩大了信息交流的范围。
第三次革命是电报、电话、电视及其它通讯技术的发明和应用。这次革命是信息传递手段的历史性变革,它结束了人们单纯依靠烽火和驿站传递信息的历史,大大加快了信息传递速度。
第四次革命是电子计算机和现代通讯技术在信息工作中的应用。电子计算机和现代通讯技术的有效结合,使信息的处理速度、传递速度得到了惊人的提高;人类处理信息利用信息的能力达到了空前的高度。今天,人类社会已经进入了所谓的信息社会。
18952有没有好心人整理武汉大学的高代数学分析答案阿
18955
共建“计算机数学”讨论班,我支持!只是我不懂,想在此能向各位多多学习!
18955计算机数学的基础是构造性数学,可行性保证是存在性数学,终极目标是计算机实现。
客观地讲,很多数学问题都可化为多项式计算,而目前最能完成计算机实现的恐怕就是多项式了。而复杂问题化为多项式后动不动就几万项(每一项可能又是成千上万项积),试想手工又如何能够完成??而目前的计算机代数系统也就是数学软件也无法实现,因此,计算机数学研究的重点依然是算法,而成果则是计算机实现。
吴方法原本就是目前国际流行的三大消元法之一,另外两种是子结式消元法和格罗博纳基消元法。因此,多项式计算的重点又是消元。
我个人的观点!!
18955冒昧的说,二楼的例子也许不能算"计算机数学",而应该叫"使用计算机来研究数学";
比如说,我建个生物网站不是"生物信息学",结合生物需要提出生命单元与系统及相互作用的逻辑模型与算法,这才是交叉学科"生物信息学".
同样,吴张几位院士的工作意义不是用计算机代替纸笔来研究数学,而是他们的数学机械化自动化算法化等等对数学和CS的发展都有意义和推动.
我胡扯几句......
18955你的帖子很不错,不过,我觉得在目前讨论班人气不够旺的情况下,把学科分的太细不是好事.而且,我个人看法,计算机数学做为一种构造性数学,也是计算机科学最关注的,比如数学机械化,在人工智能领域很有应用前景,因此你在CS版讨论这些数学问题是再恰当不过了.
18955最近,有朋友介绍来这个网站,发现真的很好的,能学习好些东西。
这几天,我自己在查文献,结果发现google可能是最好的搜索工具了,一般来说,年代较久远的(95前),大师的文献都可以在google中找到,具体方法是:
keywords
PDF
不信?不信你试试。
18955计算机科学与技术的飞速发展对数学学习、研究的观念和方法产生了巨大的影响,可以说单纯靠一支笔一张纸做数学的时代已经成为永久的历史,面对新的形势,我们这些以数学为生的人怎么办???
一个核心的问题是:我们应该如何借助计算机学习和研究数学。
诚恳希望大家共建“计算机数学”讨论班。
QQ:573490279
斑主:我的提议可否???
斑竹回复:支持你的想法,请到"计算机科学技术版"讨论.
18955非常的支持,或者“计算机代数“也行啊,作这方面的人和电脑接触的时间很多,肯定人气很旺
18955因为已经有计算机科学的版块,而这里本来又以理论讨论为主,大多数感觉在那边讨论就好了吧,感觉还不如直接把计算机科学版改成计算机科学与计算机数学,当然这只是个人看法,还是大家多讨论。
现在也准备重新认真学习理论了。
18955
计算数学作为数学的一个最大分支之一,在博士家园应该有一个讨论班的。
18955
今天刚来,就看见了关于"计算机代数"的帖子,强烈希望成立讨论班!
18955支持~
18956求武汉大学的2005数学分析答案
18957哈哈
恭喜啊
18957id: Euler
学历或职称: 本科
所在单位 (院校): 西北大学
电子邮件:
qccccccc@163.com
————————————————————————————————
专业专长或管理该版的优势:
控制论和信息论本来就是数学与电子科学的交叉学科,我是学电子的,而
且想朝这方面发展,对于控制论和信息论,我们更侧重于应用,对有关概
念的理解上,或许与你们搞数学的不完全一样,我真诚的希望能与大家交
流,我相信我一定能管理好该版!
————————————————————————————————
您认为该版目前现状是否需改进及您的管理方针:(顾问可不填)
我认为还行,因为上博士论坛的大多是学数学的,控制论和信息论虽然也
是数学的一个方向,但毕竟不是主流方向,所以帖子不是很多也是可以理
解的,如果我能当斑竹,我会尽量发一些有关控制论和信息论应用方面的
帖子,让更多非数学专业的网友对这个论坛感兴趣
————————————————————————————————
18959常微分方程教学大纲post-73-1128857715.ibf
18959Good
18959谢谢啊
18959谢谢了,
18959能不能详细点!
18959Thanks!
18959参考一下!
18961好东东呀!
18962[URL=C:\Documents and Settings\longly_bits\桌面]My
Webpage[/URL]
18962题目呢?
18965当我有问题需要请教,我该如何将其上传?好像这上面没有办法,我也有公式编辑器,但无论如何都不行
18967我查了很多排队论的书,里面只有讲M/G/1 FCFS的,没有M/G/1/B FCFS的。
请问,M/G/1/B
FCFS模型有解吗?
平均队长,平均等待时间的公式是什么?
急呀!
谢谢!
提示:提问请勿设定积分,请勿重复发贴.
18967不太清楚你的问题中的“B”什么意思,但是M/G/1模型是研究的很深刻的一个模型了,它的各种变体一般都已经研究过了,应该能找到,你可以看一下王梓坤的“随机服务系统”,估计会有
18967B表示队长有限,正在服务的和排队的最多不超过B。
谢谢!
18967希望能一快讨论
zhangpeng8323@sohu.com
18967是不是就是具有门限的排队系统
18970附件里面什么都没有啊!?
18970问题:post-38-1128859815.ibf
18971超星的那个烂东西!
又不清楚,又乱!
18971谢谢学长!
18971请问pdg是什么文件格式,需要用什么浏览器查看?
回复:超星
18973因为平衡便于求解。而且不平衡问题可以转化为平衡问题。。。谢谢
18973好用表上作业法进行手算。
18973请问:标准的运输模型为什么定义为供求平衡呢?
18974感激泣泠
18974ln[x+cos(x)]+C
tan(x)-x+ln|cos(x)|+C
-sin(1/x)+C
1/3*x^3*ln(x)-1/9*x^3+C
-1/(2a)cos(a(x^2+1))+C
18974∫(1-sinx)/(x+cosx)dx=

1/(x+cosx)
d(x+cosx)=ln(x+cosx)
∫tanx(tanx-1)dx(未能找到简捷方法,见谅)
∫(1/x平方)cos(1/x)dx=-
杠intcos(1/x) d (1/x)=-sin(1/x)
∫x平方lnxdx=(x^3)/3 lnx-

(x^3)/3 *(1/x)
dx
∫xsina((x平方)+1)dx=1/(2a) 杠intxsina(x^2+1) d(a(x^2+1))
数学与我们同在!
18974马上就要自考了我有几个典型的例题不知道步邹 哪位大姐大哥
帮俺写个过程谢谢
∫(1-sinx)/(x+cosx)dx
∫tanx(tanx-1)dx
∫(1/x平方)cos(1/x)dx
∫x平方lnxdx
∫xsina((x平方)+1)dx
18974马上就要自考了我有几个典型的例题不知道步邹 哪位大姐大哥
帮俺写个过程谢谢
∫(1-sinx)/(x+cosx)dx
∫tanx(tanx-1)dx
∫(1/x平方)cos(1/x)dx
∫x平方lnxdx
∫xsina((x平方)+1)dx
18975求M.P.Do Carmo著《Riemannian
geometry》,复印本也可以。
本人将赠送张奠宙著的《陈省身传》(六十多元人民币)作为交换。
有意者请发消息给我。
18976我自己的认识是:数学不好会很严重的限制自己在力学学科内的发展,但是因为不是数学专业,所以主要是掌握应用数学就好了。不要陷进数学的湖水中,向钱伟长所讲
18976建议:
汗,不知道你的力学需要那方面的知识。你的固体力学需要那方面的知识就去学那方面的知识嘛,没必要列表说明吧?不过感觉上高等数学与泛函分析肯定是不够用的,
你泛函分析学到线性的还是非线性的?微分方程,积分方程,非线形泛函分析深读一些,
物理里面分析力学用的多。
18976谢谢你了
我目前最需要学习的力学方面的课程是连续介质力学,里面用到最多的是张量分析的内容;然后在进行能量分析时,需要用到泛函的知识。
我也不怕别人笑话了,因为自己是工作了几年后又刚开始读博士,所以很多知识自己得复习补起来。
本来没有想很多,读博士也是一个自己谋生的饭碗,总的对得起自己吧,所以就打算从三个大方面补充[当然还有上课,和老师项目得需求,可是为了以后的发展,不能仅限与此吧,要发展,要多看,既然读了,就读好一点]:一是物理方面的知识,我计划看FEYNMAN的《Lecture
notes on
physics》;一是力学方面的知识,除了连续介质力学就是损伤力学和经典塑性理论;一就是高等应用数学。
目前国内的力学的博士在物理基础和数学上与国外的博士相差很远,这也是我自己的问题,所以提出来,希望能够得到高人的指点。老师怕自己走偏了,总是希望我们收着,但我希望自己能够更清楚的知道自己要学什麽和怎麽学,我想这也是读博士的一个目标之一吧
再次感谢“楼上”!
18976我刚开始读固体力学的博士,但发现自己的数学基础不够好,想补充这方面的知识,其实在硕士期间读的数学方面的书,感觉不好,反而没有本科时学的好,目前的学过的数学课程就是:高等数学,数理方程,偏微分方程及其数值解法(没学好),线性代数,概率论与数理统计方法,解析几何,变分法(没学好),张量分析(自学的),想请教一下我改学习那些,泛函分析一定要学,其他的呢?能给一个书单和看书顺序吗?任何建议我都不胜感激
18976泛函肯定是要的.还有就是常微分方程要深入不少.可以看看阿诺尔德的那本,挺不错的.还有就是偏微分方程和变分法都要学深刻一些.我还在这里推荐一本<经典力学的数学方法>,也是阿诺尔德的.对力学专业的很有帮助.研究透了会有很大收获.象开
18976力学需要很多的数学知识么?
18977不好意思,我还是不太懂,能说具体点吗?谢谢
18977谢谢post-38-1128869326.ibf
18977考虑A是对角阵
18977在附件里,谢谢
18977考虑A是对角阵,则可证Xn均为对角阵,那么就相当于Xn上每个元素均符合题目那种统一形式的递推式,因此可知极限存在
18977明白了,多谢
18978好的,谢谢咯!
18978积分用积分中值定理就可以看出不等式来,关键是单减。
18978请教一个题:设f(x)是在区间[0,+

)上单调减少切非负的连续函数,
An=

k=1的n项和
f(k) -

1到n
f(x)dx,证明数列{An}的极限存在.
答案解析中的这一步我不理解:
由提设 f(k+1)


k到k+1 f(x)dx

f(k)
,k=1,2...
这个不等式我理解f(k+1)

f(k)
不理解这个积分代表了什么?
如果它不是非负是否还能成立?
本人刚开始学高数....请各位高手教教我..
函数积分在判断函数单调性中有什么作用?...
还有一个问题:求当x

-

x倍根号x平方加100,再加x平方,的极限
18980呵呵有点意思
18980
| 引用 (dengdeng @ 2005年10月09日
22时55分) |
X --> ∞; Y
-->∞;a为常数,则X=Y+a?
为什么?
如果相等,那么“左”减去“右”=0;可是“左”比上“右”不一定等于1 ?
|
等号的用法有很多种。
并不是唯一的,只是语言和符号的一种约定的功能。
关键是符号语言的意义。
诸如如无穷大量,无穷小量,等价量,有界量等的记法
只是一种记法而已。
不要把语言和符号看作一种实在。这是中世纪时代和以前的哲学家常犯的错误。只是到了维氏的语言哲学之后,哲学经过了继本体论转向,认识论转向之后的语言学转向之后,语言学和哲学才又有了长足的发展。开创了语言学研究的新的局面。
完全可以把数学中的符号语言看作一种映射。到意义空间的映射。
18980你写的等式是推广意义下的
你的疑问是通常意义下的
18980
X --> ∞; Y
-->∞;a为常数,则X=Y+a?
为什么?
如果相等,那么“左”减去“右”=0;可是“左”比上“右”不一定等于1 ?
18980首先X=Y+a这个式子不是在什么情况下都相等的
只是说在都趋于无穷大的时候才会相等
你理解无穷大是一个过程,不会停止的趋向过程
这样的话你做减法就是不可能的
因为减法不是在这样的基础上定义的
18980呵呵~我也看过那本书哦,完全被他玄倒了~
书中的例子简直堪称经典。而现在的高等数学书都没解释清楚无穷。
什么时候,变数不再静止?期待~
18980X --> ∞; Y
-->∞;a为常数,则X=Y+a?
为什么?
如果相等,那么“左”减去“右”=0;可是“左”比上“右”不一定等于1
?
我最近看了一本微积分之谜(师教民
著)。他提出了一种辩证分析法:研究对象是变数(具有变化和数字双重性质正如波粒二象性)。我们通常认识的数只是静止的数,承认

是现实存在的数。所以你的问题应该以变数的观点解释:X,Y是两个不同步但同规律的变数,它们的数值是一样的,都是实无穷,只是变化状态不一样。我比较赞同作者的这种观点,尽管作者并不是什么名人。
18980无穷和无穷的相减是没有意义的
18980无穷大并不是隔数,只是个不断增大的数,对给定的任何数N>0,多大于N.OK
18980$ \infty $
只是为了方便而引进的一个符号,本生不具有实际意义.只是为了方便,有时人为的规定了一些运算,但这是以不牺牲合理的逻辑性为前提.总而言之,它不是一般的数,不能作一般的运算.
18980无穷大是一个变化过程!!简单说就是变量
18980你怎么回有这样的疑问啊!1你对无穷大理解有问题啊!
18980无穷大是一个趋近过程,并不是一个像1、2一样的数字,规定的运算只是人为的,目的是为了计算上提供方便,但不能影响到运算的逻辑性。
18980
| 引用 (dengdeng @ 2005年10月09日
22时55分) |
X --> ∞; Y
-->∞;a为常数,则X=Y+a.
|
我也不懂是什么意思,莫名其妙!也许只有作者自己清楚。
18980“无穷大=无穷大” 的确是成立的,而 “无穷大-无穷大”则被视为不允许的运算.
可以参看 江泽坚 吴智泉 编写的 《实变函数论》.
18981其实那就是对于实数的一种同余分类
不仅可以用有理数作同余分类,还可以用任意的有理数扩域作同余分类
总之实数的同于分类有很多种就是
其他的同余分类也可以用来构造不可测集合,并且不可测集合必然要用到实数的同余分类和选择公理,因为勒贝格测度具有平移不变性,不可测集合为不可数集
18981
| 引用 (magic9901 @ 2005年10月12日
13时49分) |
Rx=Ry当且仅当x
 y,如果x不等价于y,则Rx与Ry相交为空集。
y,如果x不等价于y,则Rx与Ry相交为空集。 |
这个说法有道理,就像可以用同余关系给整数分类一样。
18981Rx=Ry当且仅当x

y,如果x不等价于y,则Rx与Ry相交为空集。
18981
| 引用 (yeslijing @ 2005年10月10日
20时35分) |
|
你不是说X和Y都在(0,1)上取吗,那你怎能去成1,2呢 |
是我大意了,我的意思就是(0,1)中任意选两个数,好象很难作到R1不等于R2
谢谢
18981书上在证明并不是任意集合的外测度都具有完全可加性时,想象出一类集合:
对于(0,1)开区间上任意的点X,做点集:Rx =
{ξ;0<ξ<1,ξ-
X为有理数},然后说对于(0,1)上的两点X、Y,当Rx≠Ry,则必有Rx∩Ry=空集。
可如果X=1、Y=2,那么R1与R2是什么关系?还是说,X、Y并不是任意选取的?
18981你不是说X和Y都在(0,1)上取吗,那你怎能去成1,2呢
18982{f(x)}N是啥意思(其中N是下标,这里打不出来)?书上很突然的出现(江泽坚的《实变分析》),也没解释。
接下来书上说:则有,{f(x)}N
在集合E上的积分 小于等于 N*mE
谢谢
18982
| 引用 (dengdeng @ 2005年10月09日
23时00分) |
{f(x)}N是啥意思(其中N是下标,这里打不出来)?书上很突然的出现(江泽坚的《实变分析》),也没解释。
接下来书上说:则有,{f(x)}N
在集合E上的积分 小于等于 N*mE
谢谢 |
有的书上,用那表示的是截断函数,即在函数值绝对值大于N
的点上重新定义函数值为N之后得到的新函数,在积分理论中常用此函数
18982其实积分就是面积阿
书上的意思是不是每个函数的积分就是mE这么多
n个就是那样多
那本实变我没有看过,但就往体积上去想就是了
18983请各位知道的帮忙啦,大家也都知道实变函数比较难学的!
18983还是好好看看课本吧
指望视频是不行的
18983
http://www.bmrtvu.com/server/vodb.php
18983楼上的兄弟,谢谢了,可惜这个视频只是大头象,哪个老师在念讲稿.
18983老兄,这是许凤老师(东北师范大学)讲的中央电大课程。
18983不错 不错 真不错
18983谢谢啊!真是好人!顶啊!顶啊!
18983楼上的兄弟,谢谢了
18983Prove that every uniformly convergent sequence of bounded functions
is
uniformly bounded.
Pf: Let f_n -> f unformly on S in a
metric space, then given ε=1, there is
a positive integer N such that
as n, m ≧N, we have |f_n(x) - f_m(x)|<1
for all x in S. Let m = N,
we have: as n≧N, |f_n(x)|≦|f_N(x)| + 1 for
all x in S. Letting M = max
( M_1,.., M_N), where M_i = sup |f_i(x)| + 1
x in S
(It is
possible since each f_i is bounded. Therefore, |f_n(x)|≦M for all
x in
S and for all n. So, {f_n} is uniformly bounded on
S.
>----------------------------------------------------------------------------<
Another proof: 我們也可以繞一圈去證明上面的事情.(如果不想用 Cauchy uniform
的定理). 考慮 f_n
-> f uniformly on S in a metric space. Given ε=1, there
is a
positive integer N such that as n ≧ N, we have |f_n(x) - f(x)|<1
for
all x in S. Let n = N, we have |f(x)|≦|f_N(x)| + 1 for all x in S.
That is,
f is bounded on S. Let M = max (M_1,..,M_(N-1), M'),
where M_i = sup |f_i(x)|
x in S
and M' = 1+ sup |f(x)|.
x
in S
We have |f_n(x)| < M for all x in S and all n.
Note:
如果仔細點, 你會發現一個很奇特的現象, 那就是對於極限函數 f, 我們給予高
度差 ε, 我們就會有一塊小區域. 在 uniform
的世界中, 我們可以視此小區域為一個
函數.(這是想法, 不是真的). 如果你真能依此去
18983太谢谢了,我找了一星期才找见.好人有好报.
18983先谢了
18983555,现在不能下了啊!!!
楼上的兄弟,能不能给我发一下啊!!!
邮箱:babuzhu.happy@163.com
谢了啊!!!
18983mark
18983ce能看吗
18988证明当0<x<Pi时
∑ n
=0 ∞
(Sin(2n+1)x)/(2n+1)=Pi/4
18988没有人知道怎么做吗?
是不是用到F变换阿?
18989如何使用matlab中的一些概率统计命令啊?
18994很搞笑,很讽刺!:0顶
18994有意思啊
就是有点过分啊
18994我们国家的教育真的该思考一下了
18994转贴此文不代表同意其说法或描述,仅为提供更多信息,其文共欣赏,但愿LZ手下留情,别删!!!
18994
北京大学创建于
1898年,是我国近代第一所综合性大学。多年以来,我校一直致力于高级人才的培养并赢得广泛赞誉。最近我们欣喜的发现我校学生陆某某以自己的实际行动(卖猪肉)支持国家的西部大开发战略(为西安市的肉盆子工程尽了一份力),取得了良好的社会效益(经济效益稍差)。目前正值我校进行教育改革,得知这一情况后,我们决定自2003年起增设杀猪专业,为国家培养高级杀猪卖肉人材。
一、报名条件
凡热爱祖国、拥护党的基本路线、品德优良、遵纪守法、身体健康、膂力过人、热爱杀猪卖肉事业且具备相应文化程度者均可报名。
二、课程设置
必修科目有:杀猪学导论、杀猪成本核算、卖肉心理学、见风使舵学、买刀学、磨刀学、降猪十八掌、杀猪学历史、杀猪与国民经济之关系学、杀猪不算杀生学、白刀红刀学、杀猪英语、WTO与杀猪学导论、杀猪外贸等;
选修科目有:对付城管学、对付工商学、对付税务学、流动卖肉学、逃跑学、红包学、猪肉广告营销学、开水烫死猪学、杀猪用牛刀学、杀其它禽畜学等;
三、教学要求
培养学生对杀猪事业的热爱;了解我国杀猪业的悠久历史;让学生通过学习掌握杀猪专业理论以及操作技能,克服自卑等不利情绪的干扰。
四、毕业
本专业目前设有专科、本科、硕士、博士(目前尚无博士后)学位,国家承认学历。学生毕业后,我校负责向各省市杀猪场及菜市场推荐,享受高级杀猪、卖肉人材待遇。留京者解决户口问题,按引进高级专业人材的标准执行。
五、咨询方法
欲报名者可向西安市民打听一下北大陆某某的口碑,也可直接来我校咨询,简章备索。
六、附注
本专业授课人员一览表:
北大名誉教授、全国劳模,杀牛学博导、全国屠宰协会主席、世界屠联中国分会秘书长:疱丁;
杀狗学博导、全国屠协名誉理事:樊哙;
杀猪成本核算学专家、杀猪学教授(举人范进的岳丈):胡屠夫;
营销学专家:关羽;
营销学专家:卖炭翁;
卖肉学专家:张飞、国产凌凌漆;
逃跑学专家,神行百变学巨擎:韦小宝;
磨刀学、屠宰学专家:花木兰的弟弟(磨刀霍霍向猪羊那位)。
18994有意思,搞笑!!
18994那位陆**还在卖猪肉?也许是缺少野心吧...
18994呵呵
挺有意思
18996数学工作者的增多
也会导致
一些糟粕的产生,一些人浑水摸鱼,作一下没有任何价值意义的重复,甚至抄袭
但是这毕竟还是少数人的做法,这就是所谓的学术腐败的一种
我想这并不能影响数学应用化的进程
毕竟任何一种新的尝试,新的革命都会有一下不好的副产品的产生的
但是这只是一个小小的副产品而已
18996其实现在除了基础数学的发展需要加强外
我认为
以应用数学,计算数学,概率统计,计算机数学为基础的大范围的数学应该
向社会的各个行业进军,加强与现实社会的联系,将数学建模的作用发到最大
当然这个过程本身就是很漫长的,但是我相信,这个过程会逐步加强的,毕竟我们数学的
起源就是来自于社会,来自于生活的,所谓“合久必分,分久必合”,最终的数学肯定会
实现与应用的结合的。
所以我倒认为数学工作者的增多,倒是会促进这个进程的
现在各行各业工作者都在增加,数学工作者的增加也是情理之中的。
每个人都可以去选择适合自己的课题,这样百花齐放,倒是在无形之中促进了数学的
发展。
另外,数学应用化的进程,是整个社会的责任,只靠数学工作者的努力是远远不够的,
必须有全民素质的提高。例如,只有用人单位意识到数学的重要性,才可以实现数学的应用化。
所以我们应该加强数学的普及教育。
这是本人的粗浅看法
18996我到觉得搞数学研究是自己的事情,管他其他人有没有成果呢!
虽然我并不主张只注重现实应用的功力数学主义,但是,搞两年工程问题后,你确实会觉得你是科学之父。
可能你的数学在大手笔面前是垃圾,但在工程人员面前是却是神仙。他们就死在数学上,所以对于很多考研的工科学生来说,专业课不是问题,而考研数学成了畅销书。
所以我说让你搞工程并不是埋没数学,牛顿还是个物理家,但能藐视他在数学上的贡献吗?
没有现实问题作引子,当然没有研究方向;
不开辟新的研究流域,当然只能做重复的工作,何谈创新!
跟着教育走只能被教育,能不枯燥吗?
科学之父要有个科学之父的样子,中国的科技上不去,第一是数学不强,第二是数学与生产联系不上。这两个问题都不能等这工科学生去解决啊,这么大的发展空间和市场还不够你创新的吗?
18996楼主说的也不无道理,确实中国纯粹数学研究有点 简单的重复,新成果或创新成果基本不存在!无可奈何啊!
18996我建议你学习一下工科的课程 什么专业都行 有关工业的更好。
时代的发展离不开生产力
而工程问题更始生产力的核心问题。
也许你并不知道你千方百计的出的结果有什么用,但对于工程人员,你的结果可能是个宝贝。
重工业的效率哪怕提高百分之一,将带来巨大的经济收入。
但是,在大学数学专业联系点实际的也就是建模,而建模的经典例子无非是人口问题等等,空洞,所以从这就开始感觉到了它的无用,也就只能感觉到数学只能作些小小的预算,优化等问题了。
那为什么不拿工业例子呢?它涉及太多的物理及工艺问题,而且很多问题工程人员本身都无法解决,靠的是经验公式,怎么能用于教学。
如果你觉得你在这枯燥的学科中看不到什么希望的话,假设你还年轻,我建议你想方设法从事工业,你会有还大优势。
18996现在大部分学校都在扩招,有些学校的老师根本都不具备硕导资格,自己都没有文章,
更谈不上对前沿的把握和独特的见解,还招这么多学数学研究生博士生,基本上都在
自娱自乐,我就是我学数学这么多年的感悟.
成天的推一些不知道是什么东西的东西,
毫无实际用处的东西,
毫无价值的高级娱乐品!
数学到底拿来干什么,我说个现实的问题,中国搞数学的人太多了,都是低水平的重复!
18996搞基础的很多都不知道前沿在哪里,更不用说方向了.
18996我考研为了找工作!我喜欢学数学,但是现在是为了考试,每意思!
18996同意楼上的意见。教育的目的之一就是整体上提高国民的素质,因而提倡教育的普及。
所以学数学并不一定研究之。
然而一个爱数学的人,是这样的一种:
当他知道ZFC公里系统的相容性没有被证明时,他会有一种使命感。
数学与我们同在!
18996本人虽然是学数学的,计算机水平也不差,计算机专业硕士程度,我讲这话的目的是出于对中国数学现状的担心,看看吧,这些所谓的论文:
关于....的推广
关于....的一个注记
关于......的一个新的证法
....的推广与应用(看不出有什么应用的内容!)
....的性质及其应用(根本不着边际的推广)
..................................
注意:搞数学的人不是神仙,也要生存,那么如何才能生存,挣钱,那么凭什么挣钱,工作,
如何才能找到工作,必须有工作技能,目前各大学校的数学教师基本饱和,
则大部分学生都到哪里工作?如何生存?
空洞的东西是否可以创造价值?
我们国家应该真正把基础数学的东西让真正的精英去搞,保证他们的生活!
而不是普及,大部分人应该做的事情是把数学应用到实际中而不是重复低水平劳动,社会很现实,但是某些人的想法很幼稚!再这样下去出第二个陈景润概率几乎为0.我特别贴出一篇清华博士退学的文章,大家可以看看值得深思!
18996数学得人都去搞计算机了,编程啦.可悲....
18996不一定要搞计算机数学不拿去,应用跟神学是一样的,没有工程和实践的数学将被证明是短命的.
18996对于中国的教育特别是数学和英语教育,不要再给更多的表扬和赞许,相反我们缺的是更多的质疑和批评。
中国的数学发展了,中国人的数学精神没有发展。
中国的科学发展了,中国人的科学精神没有发展。
18996关键看自己的爱好,兴趣了
你如果希望从事基础学科,比如数学,那就切实从自我做起,莫管别人在干什么。
只要每个人都不成为社会的蛀虫,基础学科才有发展!
如果基础学科不发展,大家都学眼前看到易找工作的专业,相信你毕业了也找不到什么工作,因为,这方面的人才太多了。
做科研全凭个人兴趣,楼主不能一偏概全,当今中国还是有许多从事数学的学者
在辛勤的工作,他们并没有你想象的那样招很多研究生。
18996
引用 (fleshwound @ 2005年10月
18日
11时20分) |
本人虽然是学数学的,计算机水平也不差,计算机专业硕士程度,我讲这话的目的是出于对中国数学现状的担心,看看吧,这些所谓的论文:
关于....的推广
关于....的一个注记
关于......的一个新的证法
....的推广与应用(看不出有什么应用的内容!)
....的性质及其应用(根本不着边际的推广)
..................................
注意:搞数学的人不是神仙,也要生存,那么如何才能生存,挣钱,那么凭什么挣钱,工作,
如何才能找到工作,必须有工作技能,目前各大学校的数学教师基本饱和,
则大部分学生都到哪里工作?如何生存?
空洞的东西是否可以创造价值?
我们国家应该真正把基础数学的东西让真正的精英去搞,保证他们的生活!
而不是普及,大部分人应该做的事情是把数学应用到实际中而不是重复低水平劳动,社会很现实,但是某些人的想法很幼稚!再这样下去出第二个陈景润概率几乎为0.我特别贴出一篇清华博士退学的文章,大家可以看看值得深思!
|
十分同意,我大学写了篇质量很高的文章,关于正项级数的几乎是终极的判别法,就是因为这个社会腐败,让我的论文靠我原来的题目没有发表,因为学校的人瞧不起我,认为我一个学生根本没有这个资格写出这样的文章,而本来我的论文在外校专门的教授已经第一便审查通过了,而到学校编辑部,却被退了,说的理由就是什么不存在终极判别法!我晕地死
但是我的方法确实是判别了所有比较规范,但是现在一般的方法无法解决的题目,而且我钻研相关的很久,看了很多文章,越看我越不爽,那些文章简直是垃圾,小学生都可以看懂的也发表了,一个考试题目的解答方法就当作论文发表了!把我气着了
后来我们教授就劝我,不要生气,刚起步,别要求太多,以后有的是机会,之后我就听老师的发到高等代数研究这个杂志上去了,可是后来我看了下那个杂志,真他妈的不是论文杂志,而是习题解答杂志,研究生考试题目解答题,所以我又郁闷死了,觉得自己的论文投到那里去实在是浪费了!后来我的论文又被香港一个大学的杂志看上了,要我交600块钱的版面费转载,我心想,哎,这个中国是垃圾,在教育和研究上,所以我就没有指望再发表了,我发誓我再也不会发在垃圾杂志上,只要不发表,要发表就发表到像数学年刊这样的国际杂志上去!
现在我看着什么大学数学,高等代数研究,还有什么许多大学的校刊的自然科学版的文章都是超级简单,即便是教授写的也够垃圾,我记得我们学校一个教授发表的一个论文我他妈的在大一自学积分的时候就碰到过,而且我已经解决的比较完美了,后来没有想到学校的老师竟然把我搞出来的那样的东西当作论文竟然发表了,而且发表的杂志还比较不错,被认为是核心专业期刊,所以我现在特别不相信那些杂志的作者,我的眼中的教授是必须让我佩服的,无法让我这个后生佩服的和欣赏的老师我一律当作同志来看待的,所以至今很多老师
18996楼上的我也遇到同样情况啊
只有<<数学学报>>,<<中国科学>>这些杂志还行,其他的
18996感觉搞基础数学太烦,还是搞应用数学比较好,至少出来好找工作一点
18996
引用 (baixueli88 @ 2005年10月
17日
17时09分) |
|
我考研为了找工作!我喜欢学数学,但是现在是为了考试,每意思! |
我也是
18996为什么不投国际期刊啊?
18996本人现在正在数学系学习 十分支持
18996想学,但不知道学什么!
缺少指导!
18996说实在话,学数学理论上应该是很有用处的。
但依我看在中国大部分学数学的还是教书的多。
而在大学里没有好好钻研计算机和其他特长的人,
到了社会几乎是除了能教书,几乎和民工无异,甚至。。。。。。
民工能吃苦的多,更容易满足。。。。。。。。。。。。。。。。
18996当然,行行出状元。
学的精了,学得深了,就不怕杀不出一条路来!
总之,各位要努力,学总比不学来的好!
18996
| 引用 (fleshwound @ 2005年10月10日
11时01分) |
现在大部分学校都在扩招,有些学校的老师根本都不具备硕导资格,自己都没有文章,
更谈不上对前沿的把握和独特的见解,还招这么多学数学研究生博士生,基本上都在
自娱自乐,我就是我学数学这么多年的感悟.
成天的推一些不知道是什么东西的东西,
毫无实际用处的东西,
毫无价值的高级娱乐品!
数学到底拿来干什么,我说个现实的问题,中国搞数学的人太多了,都是低水平的重复!
|
要想知道数学有什么用?
可先放放数学,去学其他东西,特别是去参加一些实际工作.
你就能感觉到数学的用处了.
不识庐山真面目,只缘身在此山中!!!!!!!!!!!!
18996可以这么说,大多数人在学数学都是在浪费时间,因为只有创造性的成果才能为数学大厦添砖加瓦,但这只是极少数的天才所为,我们许多人正在学的东西也许早已经为其它人所证明,但由于信息的原因,很多人都不是对所学的专业前沿有十分清晰的了解,所以,大半生都在做重复前人的路子。
有志于数学研究的人,首先要把一切功名利禄抛到九霄云外,等于贫穷,你首先就要有这个准备。其次要在尽快短的时间内达到你所感兴趣的领域的前沿阵地,直接从事创造性的研究,这样成功的几率就大得多。否则,充其量只能做修修补补的工作。
当然了,向我等之流,纯粹是为了喜欢而娱乐,不在其列。兄弟们年青,要努力,如果不为数学,就不要搞数学了,浪费时间和精力。
18996数学:一者成家,二者成匠!
18996楼上的言论极其精辟
基础数学
是娱乐
更是学问
希望各位
不要重蹈一些所谓大家的覆辙
走出富强中国数学的希望之路
希望
80年代的人们能从堕落走向栋梁
18996大都是在教数学吧
18996
| 引用 (arthurlee @ 2005年10月11日
00时14分) |
我到觉得搞数学研究是自己的事情,管他其他人有没有成果呢!
虽然我并不主张只注重现实应用的功力数学主义,但是,搞两年工程问题后,你确实会觉得你是科学之父。
可能你的数学在大手笔面前是垃圾,但在工程人员面前是却是神仙。他们就死在数学上,所以对于很多考研的工科学生来说,专业课不是问题,而考研数学成了畅销书。
所以我说让你搞工程并不是埋没数学,牛顿还是个物理家,但能藐视他在数学上的贡献吗?
没有现实问题作引子,当然没有研究方向;
不开辟新的研究流域,当然只能做重复的工作,何谈创新!
跟着教育走只能被教育,能不枯燥吗?
科学之父要有个科学之父的样子,中国的科技上不去,第一是数学不强,第二是数学与生产联系不上。这两个问题都不能等这工科学生去解决啊,这么大的发展空间和市场还不够你创新的吗?
|
很对
18996喜欢就学咯!随心所欲,不管这么多!
18996确实中国纯粹数学研究有点 简单的重复,
18996同感阿
18996要是为了钱的建议不要学数学了!
18996关键看自己的爱好兴趣
18996中国的数学强国之路还很漫长,
数学工作者一定要放眼世界,向西方学习,
不能故步自封、闭门造车!
18996哈哈哈哈哈哈哈哈哈这是中国的现实。
18996确实有点迷茫啊,不知道自己能不能坚守清贫,也不清楚未来的方向
18996我是一名学信息与计算科学的大学生,说实话我的这个专业离真正的数学专业还有很大一段距离,我本人参加过数学建模比赛,所以对数学的实际应用有一点的了解,我们同专业的学生有去考程序员的,当他在开发程序时他来问我目前的一些较领先的算法,在此之前我一直很郁闷不知道自己学的东西有什么用,当和他讨论的时候我仿佛看到了我的未来去处.
我本人也很喜欢计算机,以后想致力于开发计算机的人工智能领域,我选择了考研,考的是计算数学专业,我觉得学计算数学的人去搞软件开发是一定会有一定优势的,大家好多人都谈到振兴中国数学,我虽然没有这个实力不过我个人的看法是学数学的大学生,硕士生,博士生不要再想自己未来会怎么样了,要是真的能吃苦那就去搞基础研究,要是不想搞基础研究,那么就向实际应用的领域迈出一步,当你真正迈进实践的领域中时,我相信你会觉的数学是多么重要的!
18997好啊
这是数学的普及进程的一个很好的开端
18997高等数学变大众宠儿
非理工类大学生也参加数学建模大赛
9月中旬,来自788所高校8443支队伍的2.5万多名大学生同时从互联网上下载题目,拉开了一年一度的全国大学生数学建模竞赛的大幕。
几位武汉大学图书情报专业的学生也参加了这场比赛。他们参赛的理由很简单:虽然
我们对高等数学学得不是很精,但是查资料的能力很强。
据介绍,非理工学科背景的选手不在少数。在8443支参赛队中,有
1920支参赛队,也就是将近四分之一的参赛队来自大学非理工科专业或者是大专学生。
全国大学生数学建模竞赛自从
1999年允许非理工类专业学生及大专生参赛以来,参加人数逐年递增。
很多人对此不理解:非理工类专业的大学生学数学吗?他们参加数学建模竞赛干什么?
“文科生与数学无关”的观念早已落伍
“你们说,上个世纪50年代的大学生用什么计算工具?”全国大学生数学建模竞赛组委会秘书长、清华大学教授姜启源在课堂上问学生。“算盘。”学生们说。“那也太落后了!”姜老师回答。“计算器?”“那是在‘文革’后进入中国的。”他说。
最后,姜老师自己揭开了谜底:学生用计算尺,老师用手摇的计算机。正是因为计算工具的落后,导致数学在其他学科的用处不大。
因此,相当一段时间内,数学被认为是理工科专业的工具课。很多人认为大学数学很难学,有的同学门门功课都通过,就数学课亮起了红灯。在高校内,不少人认为大学毕业后数学在工作中根本用不上。
时代变了。
计算机的出现和发展是一个重要原因。“如今,全国高校的大部分专业的大学生们都在接受或深或浅的数学教育。那种认为文科生与数学无关的观念早就落伍了。”姜启源说。
随着计算机的普及,很多数学公式有了用武之地,各种各样的数学模型在计算机上建立起来。
数学也进入了许多以往不曾涉及的领域。原来大学教学中只作定性分析的学科也开始了定量分析,比如说经济学、社会学、生态学、医学等等。这些学科与数学相互交*,大量的新学科纷纷出现。
如今,在大学,数学不再被理工科学生独享,更多的文科生加入到这个学科中来。
数学不再是一再重复的计算,它也可以用来解决实际问题。
这吸引了各个学科、专业同学的目光。
数学建模可判定《红楼梦》后四十回作者是不是曹雪芹
数学建模竞赛就是一个很好的切入点。它的宗旨就是要解决实际问题。长江水质的评价和预测、DVD的在线租赁等等就是今年的参赛题目。自从
1992年设立全国大学生数学建模竞赛以来,每年一届的竞赛已经成为全国高校规模最大的选拔活动。
北京理工大学叶其孝教授是全国大学生数学建模竞赛组委会副主任。他上课时常常举的一个例子是,《红楼梦》后四十回真假难辨,数学建模可以判定其真假。就是用统计的办法看这个作者的用词、短语和成语的几率,得出作者的写作风格,并与前八十回进行比较并得出结论。
姜启源老师从上个世纪80年代开始开设建模课程。那时这门课程属于理工科学生的专业课。从上个世纪90年代开始,这门课程也增设了选修课。英语专业、新闻专业……很多看起来与数学关系不大的专业学生都申请上这门选修课。几个月前,姜启源老师到北京第二外国语学院作演讲,今年这所以文科知名的学校就有学生报名参加建模竞赛。
天津有所武警医学院,是一所大专院校。学校规定学生必修50个学时的高等数学课程。学校领导认为医学院的学生必须懂数学,这样对专业的发展有好处。有的学生从大一开始就吃数学小灶。据了解,东北师范大学的音乐、体育、美术专业的学生都要学习高等数学。
学数学不只是为了计算和应用
能提升学生的基本素养
不止是学生对数学感兴趣,一些老师们也对数学发生了兴趣。据北京师范大学数学系刘来福教授介绍,该校对外汉语学院有位研究汉语言文学的教授。他的专业本来与数学毫不搭边儿,可是汉语言文学中有许多指标他不知道如何计算。一位英语教授点拨了这位汉语教授:英语中就有数学问题,我们一般都到数学系去了解,你不妨也去试试,他们应该能作这方面的研究。结果这位汉语言文学的教授找到数学系,向刘来福教授提出借研究生的要求。
这几年,北京师范大学给本科生设立科研基金,学生自己可以申报课题。刘来福教授介绍,原来数学专业的学生报课题主要与理论有关。2004年,学校通过了28个与数学有关的课题,24个与应用有关。
刘来福教授说,去年北京有600多支队伍参加建模比赛,今年又增加了150多支,增加比例为25%。“如果说,过去学数学是为了做题,现在是为了完成一件事情,有成就感。”他说。北京市在2005年专门立项,课题是在大学高等数学竞赛中如何体现建模思想。北京交通大学、北京化工大学、北京工业大学等几所大学参与了这个课题。
而教育部也有一个相关的项目进行了两年,题目是把数学建模的思想和方法融入大学教学之中。如今已经结题。“大学数学改革不是我们能完成的。我们只是希望通过建模比赛来改变数学教学。建模竞赛只是一个火种,让学生知道数学可以解决问题,引发对数学的兴趣。更重要的是,数学不只是计算,不只是应用,数学能提升学生的基本素养,完善思维能力。”叶其孝教授说。
189981:设工厂与客户签订一项合同,规定在时间T内提交Q件产品,由于产品易于腐败,必须考虑储存费,单位时间的储存费与储存量成正比,单位时间每增产一件产品所需成本与这时的生产率成正比,试制定一个生产计划,使生产与储存的总费用最小。
2:驶于河中的渡船,它的行驶方向要受到水流的影响。船在河中的位置不同,所受到的水流的影响也不同。试设计一条使渡船到达对岸时间最短的航线。
其中,我没理解第二题意思,它是说船没有动力系统,只能通过水流的作用到对岸还是怎样?谢谢大家,请大家帮忙解决
18998怎么下啊?我怎么点击了以后论坛提示出现错误呢?
18999初学gams,其中的coditional
equation该如何表达?$的意思,看不懂。请高手指教。
qq:369945546
18999想和你交流一下GAMS,你的QQ不让加好友
QQ:249912548
19000我是非数学专业的,现在想看一本《数值流形方法》(NMM),却怎么也看不懂,有哪位仁兄能够指点一下,告诉我怎么入门,感激涕零!
19001这个应该是拐点吧。表达式的二阶导数为0对应的点。
19001我有一段曲线如下,请问如何用数学方法求出曲线中箭头所指的外凸点?
post-27-1128927914.gif
19001不是拐点,拐点是凹面和凸面相交的点,而图中所示的点是凸面的顶点。
19001呵呵,我不知道R表示什么。
想了3个钟头,讲讲我菜鸟的看法:既然楼主要求这条曲线后半段那个外凸点,那么就先把这条曲线的拐点求出来。很明显,这个拐点可以把曲线分为两段,将前半段丢弃,留下有外凸点的后半段。
这样,后半段的起始点的二阶导数为0,如果后半段的末段也有拐点,那么也求出来,将两个拐点用直线连接,末段丢弃;如果后半段的末段没有拐点,那么直接将起始点与末点用直线相连。
这样此图形变得像一把弓的形状,由于知道这个图形起始点和末点的坐标,那么很容易求出这条直线,即弦的方程。
如左图,我菜鸟推想由于此弦经过两个拐点,那么这段曲线上的凸点与这条弦距离最远,且经过凸点的切线必与此弦平行。这条切线与弦不同的是,前者与这条曲线只有一个交点。我们只要算出这个交点的坐标,即是凸点的坐标。(这个有点像Lagrange中值定理,但在我的书上,没见他提到凸点。)
哈哈,由于楼主的那个曲线方程太繁了,所以我找了一个比较简单的曲线方程来作一个示范,这样可能讲得清楚点。
如右图,作一条曲线 y
=x 2
,我将曲线的左半段省略了,并作直线
l 1
:y=2x
,则此直线与曲线的两个交点之间的部分构成弦,作与弦平行,与曲线只有一个交点的切线,则这个交点与弦线距离最大。注意:这里虽然是距离最大,但这个交点不是 y
=x 2
的凸点,因为,这条弦不经过此曲线的两个拐点,当然此曲线也没有拐点。只有与经过拐点的弦距离最大才是凸点。
设此切线的方程为
l 2
:y=2x+b
,b为Y轴的截距。我们求出切线交点,
{ y
=2x+b
y =x
2
则
x 2
=2x+b
x 2
-2x-b=0
由于判别式=0,所以4+4b=0,即b=-1
则,
{ y
=2x-1
y =x
2
因此,切线交点坐标为(1,1)
验证:这个切线交点坐标应该与
l 1
:y=2x
的弦线距离最大,如右图中,绿色点到弦的距离最大。如果证明属实,就可以用此方法去算楼主的那条曲线,求出那个切线交点坐标,即为楼主要的凸点坐标。
我菜鸟是这么证明的:由于
{ y
2 =2x
2 y
1 =x
1 2
,代入到两点的距离公式中,
d
=(
x
2-x
1) 2
+( y
2-y
1)
2
d
=(
x
2-x
1) 2
+(
2x
2-x
1
2)
2
d
=5 x
2
2-2x
2x
1-4x
2x 1
2+x
1
2+x
1 4
对 x 1
求偏导数 α
d α
x 1
=1
2 (-2x
2-8x
2x
1+2x
1+4x
1 3)
-
1 2
对
x 2 求偏导数 α
d α
x 2
=1
2
(10x
2-2x
1-4x
1 2)
-
1 2
由于右图中,绿点到
l 1 的距离直线与
l 1 垂直,所以该直线方程是 y =-1
2
x+b
0 ,将切线交点坐标为(1,1)代入该方程,求出 b 0
=3
2 ,则该距离直线与
l 1 和曲线的交点分别是:
x 1
=1 ,
y 1
=1 ,
x 2
=3
5 ,
y 2
=6
5 ,
将它们代入两个偏导数的方程,算得
α d
α
x 1
=0 ,
α d
α
x 2
=0 。
根据极值存在的必要条件,证明这个切线交点坐标与 l 1
:y=2x
的弦线距离最大。
因此我菜鸟认为,这个方法对求凸点普遍适用,而且用判别式做比较容易,强烈希望有人找出反例,否则...哈哈
另,
1,请各位高手告诉我怎么直接用偏导数求出这个切线交点坐标,而不是通过判别式?
2,能否通过将曲线整体旋转一定的度数,使得凸点成为此曲线的一个极值,然后通过求一阶导数算出凸点吗?如果可以,那么旋转之后,曲线的表达式怎样表示?
跪谢之....post-27-1129437786.jpg
19001非常感谢Satanophany对本贴的关注!也对您的精彩发言表示钦佩!
下面就您的回复我有几个问题:
1、“只有与经过拐点的弦距离最大才是凸点”这个命题有推导吗?
2、在您所举的例子中,最后算出的x
_{2} 、y _{2}
到底指的是哪个点?
3、我觉得不一定要求切线点坐标吧,设(x1、y1)是凸曲线上的任意点,而其下弦的方程是知道的,那么就可以得出(x1、y1)到弦的距离,其最大值应该就是所要求的凸点。
19001
引用 (wsmnj @ 2005年10月
18日
21时05分) |
1、“只有与经过拐点的弦距离最大才是凸点”这个命题有推导吗?
|
呵呵,要推倒导这个,您必须得给出凸点的定义。
| 引用 |
| 2、在您所举的例子中,最后算出的x _{2} 、y _{2}
到底指的是哪个点? |
x 2 =3/5 , y 2
=6/5就是那个绿点对面的点,即过凸点(用绿点表示)作弦的垂线,垂线与弦的交点。
| 引用 |
| 3、我觉得不一定要求切线点坐标吧,设(x1、y1)是凸曲线上的任意点,而其下弦的方程是知道的,那么就可以得出(x1、y1)到弦的距离,其最大值应该就是所要求的凸点。 |
正如我的帖所说的,
由于
{ y
2 =2x
2 y
1 =x
1 2
,上面那个方程即是楼主要求的凸曲线上的任意点表达式,下面那个方程即是楼主要求的弦的方程。两个方程代入到两点的距离公式中,
d
=(
x
2-x
1) 2
+( y
2-y
1)
2
d
=(
x
2-x
1) 2
+(
2x
2-x
1
2)
2
d
=5 x
2
2-2x
2x
1-4x
2x 1
2+x
1
2+x
1 4
要求上面的等式的最大值,必须对求偏导数 α
d α
x 1
=1
2 (-2x
2-8x
2x
1+2x
1+4x
1 3)
-
1 2
对
x 2 求偏导数 α
d α
x 2
=1
2
(10x
2-2x
1-4x
1 2)
-
1 2
对于这两个十分复杂的偏导数的结果,以我有限的数学知识,无法求出最大值。所以只能求助求切线点坐标,用判别式求出凸点。
其实经过比较,通过求切线点坐标比求偏导数(即您所建议的方法)要简单的多。哈哈!
19001Satanophany,“只有与经过拐点的弦距离最大才是凸点”这个命题是您回复帖子中的结论阿,凸点我想应该就是指凸面的顶点吧。
另外,您使用的是两点间的距离公式,如果使用点(x,y)到直线l的公式,就不用求偏导数了,因为y是可以用x表达的,您觉得呢?
19001
| 引用 (wsmnj @ 2005年10月22日
20时55分) |
Satanophany,“只有与经过拐点的弦距离最大才是凸点”这个命题是您回复帖子中的结论阿,凸点我想应该就是指凸面的顶点吧。
|
我回复帖子中的结论是建立在您说的凸面的顶点模糊概念之上,所以我的结论也是想当然的结论。您得首先建立一个凸面顶点的严格定义。
比如,您的凸面的范围怎么定义?您的凸面的顶点怎么定义?到底指的哪个点?可否用简单的数学关系表示出来?
| 引用 |
| 另外,您使用的是两点间的距离公式,如果使用点(x,y)到直线l的公式,就不用求偏导数了,因为y是可以用x表达的,您觉得呢? |
恩,是个好方法!我再试试,看看求导数是不是比求切线点坐标简单些。但不管怎样,显而易见,这个方法比求偏导数简单。
19002谢谢子青老师,是这样的,做出来了,多谢多谢!
19002
| 引用 (澹台错 @ 2005年10月11日
07时42分) |
子青老师,谢谢您,但我可能把题目意思理解错了,应该还有一个条件:
f也是随机函数,也就是X哪怕取一个确定值x,f(x)也是一个随机变量
所以这样我猜想E[f(X)]=aE[X]并不能直接推出E[f(X的平方)]=aE[X的平方],因为求E[f(X)]的时候隐含的用到了两次积分。
|
那这样就更方便了,你就先计算E(Xf(X)|X)的条件期望,再对X取期望,就可以了.
19002子青老师,谢谢您,但我可能把题目意思理解错了,应该还有一个条件:
f也是随机函数,也就是X哪怕取一个确定值x,f(x)也是一个随机变量
所以这样我猜想E[f(X)]=aE[X]并不能直接推出E[f(X的平方)]=aE[X的平方],因为求E[f(X)]的时候隐含的用到了两次积分。
19002再补一句,其实那个a就是f这个函数作为二阶矩空间上一个算子的谱半径.具体算子谱的内容可以参考泛函分析
19002也就是说f其实就是一个Borel可测函数咯,不是一般意义下的线性算子咯??我原来认为既然是个算子就应该是二阶矩空间到二阶矩空间上的一般算子(换句话说就是函数空间到函数空间的算子,因为随机变量的本质是样本空间到R上的一个集合泛函).
而且你说的那个"概率意义下的"指的是依概率1(几乎处处)还是依概率(依测度)?这两个概念是不一样的.但是看你后面那个E(f(x))是线性泛函,应该表示的是依概率1相等(因为依概率1相等就是只有0测集不相等,算期望的积分的时候可以挖掉),同时,如果f是定义在二阶矩空间到二阶矩空间上的一般算子,二阶矩空间里的等于本来就是概率1下的等于.
这道题其实思路是很简单的,就是要证明的东西反着推(另,我做证明题一般都反着推)
既然要证:
E(Xf(X))=aE(X^2)
因为
aE(X^2)<=>E(f(X^2))所以就是要证明:E(Xf(X))=E(f(X^2))
按照你现在的解释,其实f(x)只是一个普通的Borel可测函数
那么显然按线性定义,对任意实数x,f(x^2)=xf(x).所以E(Xf(X))=E(f(X^2)),就证明出来了.
我之所以问你f是怎么定义的,是因为,l^2到l^2上的一般线性算子是不满足xf(x)=f(x^2)的.打个比方:
求导也是线性算子,但是d(x^2)/dt=2xdx/dt<>xdx/dt,不符合xf(x)=f(x^2)
19002f是定义在实数->实数上的
补充一下,f(X+Y)=f(X)+f(y)只是概率意义上的相等,这道题目有具体的物理含义,具体的线性意思是E[f(X+Y)]=E[f(X)]+E[f(y)],但是f写不出具体表达式和分布
麻烦子青老师了:)
19002严格证不好证,f是定义在什么空间到什么空间上的?
19002X是一个随机变量,f是一个线性算子,且有E[f (X)]=aE[X],a是一常数。求证:
E[X f
(X)]=aE[X的平方]。
19004
引用 (lhansheng @ 2005年10月11日
17时31分) |
|
你可以用块的初等变换来做。(A,E,E,E-A)可以变到(A^2-A,0,0,E)然后再由两端的秩相等都等于n,可以推出秩(A^2-A)=0从而推出(A^2-A)=0。
|
A^2-A的秩只要小于等于n就可以了吧
19004你可以用块的初等变换来做。(A,E,E,E-A)可以变到(A^2-A,0,0,E)然后再由两端的秩相等都等于n,可以推出秩(A^2-A)=0从而推出(A^2-A)=0。
19004是充要条件
19004R(A)+R(E-A)=n时,能证明A的平方等于A吗?
另外,能否帮看一下附件中题做的是否正确?post-38-1128928943.ibf
19004可以证明是充要条件!
19004我自己研究明白了:是用线性变换来做的,dim

(

)=r
dim(单位变换l-

)=n-r
只需证明(l-

)V=kerV即可
19004你可以用块的初等变换来做。(A,0,0,E-A)可以变到(A^2-A,0,0,E)然后再由两端的秩相等都等于n,可以推出秩(A^2-A)=0从而推出(A^2-A)=0。
不好意思,写错了。改正一下。不过你那样也是一种办法。呵呵!
19005其实,顾虑多了反而不好.信息很重要,信心和努力最重要!
19006题目:院子里有4个鼠洞,其中有一个通房基地。今有5只老鼠独立进入鼠洞。设任何一只老鼠进入每一个鼠洞都是等可能的,求正好有3只老鼠进入房基地的概率。
19006一个二项分布
19007
引用 (arthurlee @ 2005年10月10日
18时35分) |
不能
反例:
每2n个项为一组,组里以1/n为公差,得到的数列,如:
1,2,1,1.5, 2, 1.5,
1, 1.25, 1.5, 1.75, 2, 1.75, 1.5
......
振幅为1 不收敛 |
因为1.5与1相邻,
这个子序列极限不为1,按你思路稍作修改,请见附件.post-38-1129074263.ibf
19007不能 反例:
每2n个项为一组,组里以1/n为公差,得到的数列,如:
1,2,1,1.5, 2, 1.5, 1, 1.25,
1.5, 1.75, 2, 1.75, 1.5 ......
振幅为1 不收敛
19007有界正数列,
x 1
,x 2
,⋅ ⋅
⋅,x n
⋅ ⋅ ⋅ 满足
lim
n
→∞
x n
+1
x n
=1
能否得出
x n
收敛?如可以请证明, 不对,请举反例.post-38-1128939268.ibf
19008编写软件时如何调用lindo内核来解决问题,比如说有大量的数据要输入的时候如何用lindo来处理
19009dui
0
19009第一题很简单啊,结果是0
19009谢谢,可我没有此书,请告诉我答案是多少?
19009第一题见复旦欧阳光中教材,用分部积分作
19009请为愚人一言,谢谢。
post-21-1128940784.ibf
19010什么叫持续多久?
19010持续多久就是能排列出多少种可能性?
19010n个人分成k组,分在同一组的称为“相遇”,要求任意两人只能相遇一次,问这种分组序列能持续多久?参数应该满足什么条件? 跪求高手帮忙解决。
19011参见时间序列分析里的"控制模型"
19011我想用统计过程控制技术对电源参数进行监控,因为我们所监测到的电源参数是一个缓变的量。如果电源退化,则一定表现在其监测的电压参数上,请你赐教!!多谢
19012当前,我国考研人数急剧增加,想了解历届考研试题的学子们,非常希望能通过这些题目,来检验自己的水平,希望各位大侠慷慨相助
19014请教概率联合分布函数的问题
已知二元离散型随机向量的联合分布函数F(x,y)为分段函数,如何求:
1)边缘分布函数F(x)
2)(X,Y)的联合分布律
最好能给出例题!
谢谢!
19014第一个问题比较好回答,你只要把你不想要的那个变量加总掉就可以了;
第二个问题比较麻烦,从理论上讲,你是怎么样由概率分布求出CDF的,只要反向操作就可以
了,只不过这个操作很麻烦,我试过,可是太麻烦.
19014978301 ,你好!
看了还是不太明白,能否解释一下?如果将F(x,y)简单相加得到F(x),这个F(x)有一段就大于1了!
我的想法:如果由F(x,y)求得(X,Y)的联合分布律,再求得X的边缘分布律,最后求边缘分布函数F(x),但这样做太麻烦了!
谢谢你的热心帮助!
19014
| 引用 (mathewzhao @ 2005年10月20日
21时27分) |
978301 ,你好!
看了还是不太明白,能否解释一下?如果将F(x,y)简单相加得到F(x),这个F(x)有一段就大于1了!
我的想法:如果由F(x,y)求得(X,Y)的联合分布律,再求得X的边缘分布律,最后求边缘分布函数F(x),但这样做太麻烦了!
谢谢你的热心帮助!
|
以连续二唯随机变量的联合分布为例,你在求其边缘分布密度的时候只要把你不想要的那个变量积分掉就可以了
相对的,如果是离散二唯随机变量的联合概率,你只要把你不想要的那个变量加总掉就可以了
如果我说的你还不是很明白的话,可以去参考参考复旦大学
李贤平 的<概率论基础>.里面对这个问题有非常直观和简洁的介绍.
19014978301 ,你好!
李贤平<概率论基础>我查了一下:在(P134)由(X,Y)的联合分布律求边缘分布函数F(x)
,而不是由联合分布函数F(x,y)求边缘分布函数F(x).
希望你看看是不是我找的地方不对,谢谢!
19014由F(x,y)求得(X,Y)的联合分布律,再求得X的边缘分布律,最后求边缘分布函数F(x),是比较麻烦,但思路很清晰,小弟觉得还是可行的
19014
| 引用 (mathewzhao @ 2005年10月23日
20时15分) |
978301 ,你好!
李贤平<概率论基础>我查了一下:在(P134)由(X,Y)的联合分布律求边缘分布函数F(x)
,而不是由联合分布函数F(x,y)求边缘分布函数F(x).
希望你看看是不是我找的地方不对,谢谢! |
你好,今天才看到你发给我的信.
那天看到你帖的问题,我以为你只是要问如何从一个联合概率分布求其边缘分布率.你是要从一个联合分布函数求一个边缘分布函数,是吗?
对这个问题,我是这样理解的,第一,我还没有看到专门的关于这方面的讲座;第二,你可以试试先从一个联合分布函数求出他们的联合分布密度函数或者联合概率分布,再有这个求出边缘密度或者边缘概率分布,再由你得到的去求分布函数.从而去寻找一般的规律.
不知道我的回答你是否满意.不过我知道,这个过程肯定非常复杂,因为很多时候求边缘密度函数就已经够麻烦的了,还要求其他的,当然更麻烦.你可以试试看.
19014
引用 (mathewzhao @ 2005年10月10日
19时55分) |
请教概率联合分布函数的问题
已知二元离散型随机向量的联合分布函数F(x,y)为分段函数,如何求:
1)边缘分布函数F(x)
2)(X,Y)的联合分布律
最好能给出例题!
谢谢!
|
具体做法可以考虑如下:
由F(X,Y)求出f(x,y)
由f(x,y)求出p(x)
再由p(x)求出P(X)
过程会很复杂,不过思路应该是这样的。
19016谢谢两位的建议.这样我心里就有底了.
19016说实话,个人认为8本的<<教程>>根本不适合初学者.难倒不说,进度太慢!个人强烈推荐:1.郭大钧等<<数学分析>>,这书不难,更难得的是,进度快!最适合初学者2.张筑生<<数学分析新讲>>这书很难,结构上虽然严谨,但进度慢了些,不过这书还是很好,只是不太适于初学.3.柯朗&约翰<<微积分和数学分析引论>>,这书的经典不用多说了,作为初学的__参考书__很好.4.斯皮瓦克<<微积分>>,这书相当生动,别看书名不是数学分析,其内容值得数学专业的学生参考.5.李成章&黄玉民<<数学分析>>,这是南开的书,也好.6.常更哲&史济怀<<数学分析教程>>这是科大的书,难度比较大.7.克莱鲍尔<<数学分析>>这书有两个翻译本,一是庄亚栋译的,一是孙本旺译的,都可以.这书可以当作习题书.8.他还有一本<<Aspects
of
Calculus>>,没见到过翻译本,这书比上一本简单些,不过绝对值得一读.9.哈代<<纯数学教程>>这书只有单变量部分,机械工业出了英文本,有没有翻译本不知道,即使有也是很老的了.10.卓里奇<<数学分析>>这个是苏联人写的,觉得比8本的<<教程>>要好多了11刘玉链&傅??的那本<<数学分析讲义>>现在出了第4版了,虽然简单,但是很适合初学.其他的国内的书大都差不多.再说些别的少见的几本.12.高木贞治<<解析概论>>这书相当的古老,高木是日本现代数学第一人,他写的这本书质量无可怀疑,不过没见到翻译本,懂一点点日文就可以读这书,比如<<中日交流日本语>>的上册就可以了.适合硕士生读的13.迪厄多内<<现代分析基础>>把这书读完了,分析就到家了吧.
19016正在学微积分,在图书馆翻了一阵子,觉得柯朗的<微积分与数学分析引论>挺好的.不知道诸位有什么建议?
19016柯朗的<微积分与数学分析引论>是本很好的书,既直观又比较严谨,尤其是对很多其他的数学分支(与分析有关的,比如复变,变分法,常微分方程初步等)做了初步的介绍.相当精炼.而且我对此书感觉最好的地方就是它对于线性代数与几何,多元函数分析之间的关系讲得相当有特点.比如它对于行列式的定义与性质讨论是通过"行列式是最简单的多线性交替型"引入的,再将其与多元分析相结合.而且本书的习题不是很难,至少比我最早看的复旦陈纪修的<数学分析>与中科大常庚哲&史济怀<<数学分析教程>>的习题要简单不少,但很启发人,相当适于初学者.我看这书是在看上述两书之后拿来复习时用的.感觉很好.推荐楼主仔细阅读!!!
19016我想学微积分最好是把这一学科的基本思想,发展的过程搞清楚,这个方面龚升的新书不错。以上所说的书大部分都浏览过,我想同样是8册书,《微积分学教程》也不错。
19016柯朗的<微积分与数学分析引论>的书我读过,是我见过最好的书!
19016绝对是最好的书!!相信我!
19024南开近三年复试线及其它post-60-1128946800.ibf
19024什么格式?
19024thankS!
19024谢谢
19024

190243Q
19029是已知条件,可用构造法证明。
至于你说的第2个问题,是“没有有理数”吗?我记的是分了四类,分类标准是“有没有最大数或最小数”!
19029在用 戴德金分割 证明无理数存在时, 任意两个有理数之间必有有理数是不是已有条件?
若是为什么可以假设在第二类中没有有理数,既然其端点是两个有理数?
19029我怎么记得分了两类!
190292*2=4...
19035谢谢,我知道了
但有没有什么通用的公式可以求任意曲线的对称中心呢?
19035容易证明原曲线的拐点就是所求对称中心!
19035怎么求y=ax^3+bx^2+cx+d的对称中心?
19039计算数学前沿问题及其在物理科学中的应用高级研讨班将在香港举办
计算数学前沿问题及其在物理科学中的应用高级研讨班将在香港举办
Date: Tue, 4 Oct 2005
11:52:56 +0800 (HKT)
From: "Prof. T. Tang"
The
Croucher Foundation - Advanced Study Institute on
Frontiers in
Computational Methods and Their Applications in Physical Sciences
December 6 - 13, 2005
The Chinese University of Hong Kong
organized by
Department of Physics and Institute of
Theoretical Physics,
The Chinese University of Hong Kong
sponsored by
The Croucher Foundation
Organizing
Committee (tentative)
Director: Hai-Qing Lin (CUHK)
Sec'y:
Pui-Yee Ho (CUHK)
Che-Ting Chan (HKUST)
Zhi-Feng Liu (CUHK)
Chi-Fai Lo (CUHK)
Lei-Han Tang (HKBU)
Fu-Chun Zhang (HKU)
Rui-Qin Zhang (CityU)
Invited Lecturers (tentative)
Roberto Car, Princeton Univ.
David M. Ceperley, Univ. of Illinois
James E. Gubernatis, LANL
David P. Landau, Univ. of Georgia
Steven G. Louie, UC Berkeley
Andrew Chi-Chih Yao, Tsinghua Univ.
Associate Lecturers (tentative)
C. T. Chan, Hong Kong Univ. of
Sci. & Tech.
G. H. Chen, Univ. of Hong Kong
J. M. Dong,
Nanjing Univ.
Yong Duan, UC Davis
X. G. Gong, Fudan Univ.
Luhua Lai, Peking Univ.
T. K. Lee,, Institute of Physics, Academia
Sinica
P. W. Leung, Hong Kong Univ. of Sci. & Tech. H. Q. Lin,
Chinese Univ. of Hong
Kong
Z. F. Liu, Chinese Univ. of Hong Kong
Gerardo Ortiz, Los Alamos National Lab.
A. W. Sandvik, Boston
Univ.
L. H. Tang, Hong Kong Baptist Univ.
John Tse, National
Research Council, Canada
D. S. Wang, Institute of Physics, CAS
Enge Wang, Institute of Physics, CAS
J. Wang, Univ. of Hong Kong
J. S. Wang, National Singapore Univ.
X. C. Zeng, Univ. of
Nebraska-Lincoln
B. Zheng, Zhejiang Univ.
Tutorial Courses
In connection with the ASI, the Physics Department of CUHK will also
sponsor
one regular course and two tutorial courses, to provide some
background for ASI
students.
Advanced Computational Physics:
Lecturer: H. Q. Lin
Date: Sept. 5 - Dec. 3, 2005. Regular lecture
course. Introduction to ab
initio Methods:
Lecturers (Tentative):
X. G. Gong, John Tse, Z. F. Liu, J. Wang
Date: Nov. 14 - 25, 2005. 12
hours. Introduction to Computational
Bioscience:
Lecturers
(Tentative): Y. Duan, E. G. Wang, Luhua Lai, G. H. Chen
Date: Nov. 26
- Dec. 6, 2005. 10-12 hours.
Mission: To review recent advances in
computational physics by emphasizing the
impact that new developments
in large scale numerical computation have
significantly enhanced our
comprehension of the physical nature of materials as
well as our
capability in designing new materials.
To conduct in-depth
discussions on selected state-of-the-art methods for
solving important
numerical problems in statistical and materials physics.
To
facilitate a brain-storming forum for the generation of ideas on novel
methods and new applications.
Structure: Six morning 3-hour
lectures and presentations/discussions in five
afternoons. The working
language is English.
19039哪个网站有介绍近来计算数学的热点问题啊!
请高手指点一下啊!
19040科圣--墨子
(一)墨子及其主要成就
墨子是墨家学派的创始人,战国初期伟大的思想家
、政治家、军事家、教育家、社会活动家,也是一位有卓越贡献的自然科学家。在春秋战国时期,百家争鸣,诸子创说,学术空气十分活跃,涌现出了许多思想家和科学流派。其中孔子开创的儒家与墨子开创的墨家影响最大。
墨子名翟,生卒年不详。近代学者一般认为,墨子生于公元前476年左右,卒于公元前390年左右,也有人考证说墨子大约出生在周敬王四十年(公元前480年)左右,卒于周威烈王六年(公元前420年)左右。墨子出生何地,仍有争议。《史记·孟荀列传》说他是宋国的大夫。《吕氏春秋·当染》则认为他是鲁国人。也有文章相传他原为宋国人,但后来长期居住在鲁国。现代学者通过对“墨”姓的起源、墨子的学术渊源、科技发展的渊源以及当时人们的生活习俗等方面的论证,普遍认为:墨子可能出生于春秋战国时代的小邾国(今山东省滕州市)。
相传墨子初学于儒术,但由于不满儒术所提倡的繁琐的“礼”,学习大禹刻苦简朴的精神,因而自立新说,创建了墨家学派。墨子的学说对当时的思想界影响很大,与儒家并称“显学”,墨家学派是儒家学派的主要反对派。墨子的门徒很多,大多来自社会的下层。他们组成了一个组织严密的政治性团体,纪律要求非常严格。这些人能够吃苦耐劳,勤于进行实验,作战十分勇敢,平时从事生产劳动。墨子及其门人为人们做好事,即使是牺牲了个人性命也在所不惜。因此《淮南子》中说:“墨子服役者百八十人,皆可使赴火蹈刃,死不还踵。”而且他们功成不受赏,施恩不图报,过着极其简朴和艰苦的生活。
“尚贤、尚同、兼爱、非攻、节用、节葬、天志、明鬼、非乐、非命”是墨子的十大主张。
“尚贤”一般是指统制者任用贤人、能士为官当政;墨子认为尚贤是政治之本,是施政的首要原则。“尚同”即上同,指人们的是非观念必须统一于上级,并最终统一于天下。“兼爱”是墨子思想体系的核心和根本特征,墨子提出兼爱是指:第一、“视人之国,若视其国;视人之家,若视其家;视人之身,若视其身”。第二、“兼相爱,交相利”。第三、“爱人者,人必从而爱之;利人者,人必从而利之;爱人者,必见爱也”。第四、兼爱的主题是人,但人的兼爱源于天。第五、兼爱的反面是“别相恶,交相贼”。第六、兼爱易行,做到君惠臣忠、父慈子孝、兄友弟悌,就是奉行兼爱。第七、兼爱不仅是普遍的道德原则,而且是治理天下的根本法则。“非攻”是墨子最重要的军事思想,墨子从兼爱交利的伦理观出发,认为“亏人自利”不符合“义”,而且“亏人愈多,其不仁兹甚,罪益厚”,离义愈远,攻打、侵略无罪之国则是最大的不义;他从“对被侵略国家的危害、对本国的危害、对本国统制者的危害、违背天鬼之利”等方面历数了攻伐的危害。攻伐有害,但墨子以为正义的战争—“诛”却有益。“诛”是顺应天意、替天行道的争议之举,符合天、鬼、人之利。“节用”是针对统治者奢侈浪费而提出的生活方案和标准。墨子把“节用”看作是圣王的为政之道和天下大利之法。墨子在引用古圣人埋葬之法,提出“节葬”法则。“天志”即天的意志,墨子以为天有意志、欲恶,人们顺天意得赏、逆天意得罚。“明鬼”把鬼神分为天鬼、山水之鬼、人死而为鬼者三类,用“三表”法等证明鬼神存在,能赏善罚恶。“非乐”兼及雕刻、纹饰、美食、华宅等日用生活。墨子认为圣王治理天下重在事功,反对追求音乐享受。“非命”强调人力的作用,并以此批判命定论。
墨家学派著作的总汇是《墨子》,成书时间大约在公元前三世纪的战国后期。共七十一篇(留传至今的只有五十三篇),大体可分为四个部分:一、“经说”,包括《经上》、《经下》、《经说上》、《经说下》、《大取》和《小取》,即后人所称的“墨辩”或“墨经”;再加上《亲士》、《修身》、《所染》、《法仪》、《七患》、《辞过》、《三辩》,集中反映了墨子的学术思想;他所建立的逻辑体系,在人类逻辑思维发展史上,可与亚里斯多德逻辑和印度因明论互相媲美。二、“论说”,包括《尚贤》、《尚同》、《兼爱》、《非攻》、《节用》、《节葬》、《天志》、《明鬼》、《非乐》、《非命》十论和《非儒》,系统表现了墨子的政治观点,闪耀着一种平民思想的光辉。三、“墨语”,包括《耕柱》、《贵义》、《公孟》、《鲁问》、《公输》,记录了墨子与外界辩说时的一言一行。四、“战备”,包括《备城门》、《号令》、《备穴》、《杂守》等十一篇,集中反映了墨子怎样把科学知识应用到军事防御方面,在古代军事史上是极为罕见的材料。
《墨子》是一部内容丰富、结构严谨的科学著作。书中不仅涉及到认识论、逻辑学、经济学等社会科学范畴的广阔内容,还包含有时间、空间、物质结构、力学、光学和数学等自然科学方面的多种知识,其中有些问题阐述严密,说理透彻,立论准确,具有十分重要的科学价值。《墨子》在古典哲学和自然科学著作中是一部不可多得的珍品,是我国科学发展史上的一座里程碑。
总之,墨子在科学技术、自然哲学、逻辑学等领域中都有着极其辉煌的成果,如果把他放到古代世界科技史和哲学史中进行研究,显然杰出于同时代的希腊学者,称之为世界级的科学巨人也毫不夸张。当代著名墨学专家杨向奎先生认为:“一部《墨经》无论在自然科学的哪一方面,都超过了整个希腊,至少等于整个希腊”。国务委员、国家科委主任宋健高度评价为:“唯物始祖,科圣墨翟”。《墨子》作为一部百科全书式的杰作,给后人留下了一笔宝贵的精神财富,是中华民族的骄傲,也是世界人民的骄傲。
(二)墨子与墨家学派的数学思想
1.无穷的思想
墨家关于变数的思想,体现在《经上》中的:“穷,或(域)有前不容尺也”;《经说上》中的:“穷:或(域)不容尺,有穷:莫不容尺,无穷也”。“有穷”、“无穷”是墨家的常用术语,指数学上的“有限”、“无限”。墨家认为,区域有所限定,不能向外拓展一线之微,是为“有穷”;空间漫无边际,可以向外任意拓展,是为“无穷”。墨家以“或(域)不容尺”定义“有穷”;以“莫不容尺”定义“无穷”。这同现代数学中的“有限”、“无限”的概念十分相近。
变量数学涉及辩证法问题,墨家引入变数是数学上的一个很大的进步,这比笛卡儿把变量引入数学要早一千八百多年。
2.极限的思想
在《墨子》中,随时可以看到极限概念,如《经说上》中的:“时或有久,或无久,始当无久”。这里的“有久”、“无久”是指不等速运动,高速是“无久”,而低速是“有久”。“无久”的单位越小,它就越近于刹那速度,在刹那间而收敛于一个极限。又如在《经下》中墨家把极限思想表述为:“非半,弗著斤则不动,说在端”。《经说下》进一步解释为:“非,著斤半,进前取也。前则中无为半,犹端也。前后取,则端中也。著斤必半,无与非半,不可著斤也”。其意思是说:“物体分到不能再分成两半的时候,就不能再被分割而不动了,因为它已成为不能再分的质点”。“一条线段从中点处分成两半,取前一半,再将前一半破成两半,仍取其前半,一直取到不能从其中再分为部分的时候,自然就是一个点了。从前后两头分半去取,取到中也无半,只剩一点,就是不可再分的端中。破物一定是一半一半的,无和非半,是不可分割的”。这里墨家是用“著斤半”的方法来解释极限的道理。
数学发展史告诉我们,直到公元1655年,英国的约翰.沃利斯才创造出无穷算法,并用来解释极限的概念,这已经是《墨子》之后一千九百年的事了。
3.分类的思想
墨家对“类”这一逻辑范畴十分重视。《大取》中的“夫辞以类行者也、立辞而不明于其类则必困矣”,就阐述了“分类”的重要性。《小取》中的“以类取、以类予”,既是推理的逻辑方法,又是思维活动中必须遵守的分类标准。又如《经说下》中的“方尽类,俱有法而异;或木或石,不害其方之相合也,尽类。犹方也、物俱然”,则说明了分类的方法可以不唯一,但分类后的类应有相同的本质。《经下》中的“异类不比,说在量”,是说不同类的事物不能相比,因为它们的量不同。
4.转化的思想
《墨子》强调特殊与一般的相互转化、同和异的相互依存。如《经下》中的:“推类之难,说在之大小”,《经说下》进一步举例解释为:“谓四足兽,与牛马异,物尽异,大小也,此然是必然,则俱”。就是说,某事物或概念究竟属特殊还是一般,要看同它相比较的事物或概念的外延大小。特殊与一般不是固定不变的,随着参照对象的不同而发生变化。比如,四足兽与牛马相比是一般;与“物”相比是特殊。
5.化简的思想
墨家很注重语言叙述的简洁性和结构形式的简明性。如关于分数的记载就反映了这一点,《墨子》中分别用简单的术语“少半”、“大半”称呼1/3和2/3。
6.建立概念的思想
墨家非常重视定义,《经上》篇由92条定义组成,《经说上》则进一步解说了这些定义,其中有关数学的有9条。这些定义,在自然科学史上产生了巨大的影响。
如:“平,同高也。”说的是平的定义,指出高低相同就是平。“直,相参也”。这里参就是三,三点共一线就是直,这是直线的定义。“同长,以正相尽也。”是说两个形体相比较,恰好相尽就是长度相同。“中,同长也。”说的是形体的对承重心的定义。“端,体之无序而最前者也”,“端,是无同也”,墨家认为端点是线上排列在最前面而且没有其他任何一点可以取而代之的极端之点。“厚,有所大也”,“厚,惟无所大”,用来说明形体在空间上有大小。“圆,一中同长也”,“圆,规写交也”,是关于“圆”的定义以及作圆的方法,说明“圆”是到平面上一点距离相等的点的几何,画“圆”的工具是规。“方,柱隅四权也”、“方,矩见交也”,说明“方”是由四边、四角组成的平正图形,画方的工具是矩。
欧几里德几何大约产生于公元前三世纪,而《墨子》成书时间大约是公元前四世纪,从《墨子》中论列的几何知识的全面性和系统性来看,《墨子》与欧氏几何同为早期几何学的璀璨明珠,相映生辉!
7.推理论证的思想
《墨子》中关于数学概念的定义和解说,包含了严密的逻辑推理和朴素的数理思维。
如:《经上》:“倍,为二也”,《经说上》:“倍,二尺与尺,但去一”。说明“倍”是原来的数乘以二,或者说是自身相加;二尺是一尺的“倍”,从二尺中减去一尺,所剩余的就是原来的一尺。
《经下》:“一少于二而多于五,说在建位”,《经说下》:“一,五有一焉,一有五焉,十二焉”。说明“数位”,个位上的一比二少,十位上的一代表十,比五多;个位上的五有五个一,十位上的一有两个五。
《经上》:“端,体之无序而最前者也”, 《经说上》 :“端,是无同也”。
说明“点”,端是物体做前的一点,不可能在另一点之后,“端”不可能与另一点处于同一物体的同意位置。
《经上》:“中,同长也”, 《经说上》
:“心中,自是往相若也”。 说明“对称中心”,从对称性形体的对称中心到各对称点的长度都相等;为了区别线段中心和对称中心,《经说上》
用“心中”限定《经上》的“中”。
《经上》:“体,分于兼也”, 《经说上》 :“体,若二之一,尺之端也”。
说明“整体与部分的关系”,体(部分)是从整体(兼)中分出来的部分,例如:二中的一、尺(线)中的端(点)即是。
又如:《小取》说:“以说出故”,表明推理论证的目的在于揭示立论的根据,即确定结论与前提或论题与论据之间的必然联系,这种必然联系属于因果关系。
《经说上》说:“故也,必待所为之成也”,即是说,故是必然引起另一现象的现象,“故”又分为“大故”(充分条件)和“小故”(必要条件)。
《大取》说:“夫辞以故生……当辞而不明于其所生,妄也”,即是说,如果一个论断的理由、根据不充足、不明确,那么它就是虚妄的。《大取》中又说:“三物必具,然后(辞)足以生,夫辞以故生,以理长,以类行也者;立辞而不明于其所生,妄也;今人非道无所行,…立辞而不明于其类,则必困也”。
这说明了墨家关于推理的基本原则:“故”指推理的理由、根据,“理”指推理的思路、条理,“类”指推理论证所涉及的事物的界限和范围。“故”、“理”、“类”是推理得以有效进行的保证。只有具备了“大故”,方可“有之必然”,即推理才具备了充分条件和可靠前提;“理”与“类”保证推理的思路前后一致,不互相矛盾,并且合于事物的类别。
《墨子》中的数学知识涉及倍数、数位、点、线、面、体,推理的基本原则与方法,与《几何原本》极为相似,《墨子》也因此成为中国数学史上最早的、最珍贵的财富,在世界数学史上占有重要地位。
8.特殊与一般的转化思想
《墨子》强调特殊与一般的相互转化、同和异的相互依存。如《经下》中的:“推类之难,说在之大小”,《经说下》进一步举例解释为:“谓四足兽,与牛马异,物尽异,大小也,此然是必然,则俱”。就是说,某事物或概念究竟属特殊还是一般,要看同它相比较的事物或概念的外延大小。特殊与一般不是固定不变的,随着参照对象的不同而发生变化。比如,四足兽与牛马相比是一般;与“物”相比是特殊。
19041怎么求微分方程组的解析解啊?谢谢各位老师&大侠们!
19041In Maple: dsolve
19042招聘信息:挪威BERGEN大学招聘应用数学博士后
Date: Sun, 11 Sep 2005 07:44:00 +0200
From: Xue-Cheng Tai
POSTDOCTORAL POSITION IN APPLIED
MATHEMATICS AT THE UNIVERSITY OF
BERGEN, NORWAY.
A
postdoctoral position with a duration of two years is open at the
Department of Mathematics, starting from October 01, 2005 in the
project: ”Graphics cards as a high end computational resource”
(http://www.sintef.no/gpgpu). The project is a Strategic Research
Program funded by the Research Council of Norway, it is coordinated by
Department of Applied Mathematics in SINTEF ICT, and the University of
Bergen is one of the University partners.
The focus of the
project is to develop and analyze mathematical and
numerical methods
for image processing using partial differential
techniques. The work
will be done in cooperation with scientists from
SINTEF Oslo.
Applicants must have achieved a Norwegian doctorate or an
equivalent
degree from abroad, or have presented the dissertation for
assessment by
the closing date for applications. It is a prerequisite
that the
dissertation has been approved before appointment is granted.
Applicants must have demonstrated abilities in conducting
independent
research and publishing research results in journals of
international
level. Successful candidate will work in an
international environment.
Thus, ability to communicate and
collaborate is important.
Further details about the position can
be obtained from professor
Xue-Cheng Tai (http://www.mi.uib.no/~tai),
by phone (+47)
55584868 or e-mail: Xue-Cheng.Tai@mi.uib.no.
Applications must be submitted in 3 copies, sorted into 3
identical
bundles, each with a complete overview over education and
previous
practice (CV), certified copies of certificates and diplomas,
project
plan outline, and scientific publications with a list of these
(list of
publications), and should be forwarded to the University of
Bergen,
Department of Mathematics, Johannes Brunsgate 12, N5008
Bergen, Norway.
The deadline for the application has been extended to
Nov 15 2005.
19043数学发展史的三个时期:
古代数学时期(公元前—16世纪):主要研究对象是算术与几何(数与形);数学研究的中心和代表人物有古希腊(阿基米德、欧几里德等),中国(刘徽、祖冲之等)
近代数学时期(16世纪末—
18世纪末):主要研究对象是变量数学(解析几何、微积分、微分方程、线性代数、变分法);数学研究的中心和代表人物有法国(笛卡尔、费尔马)、英国(牛顿)、德国(莱布尼兹、高斯)、俄国(瑞士的欧拉)
现代数学时期(
19世纪—):主要研究领域有几何学(射影、非欧、线、圆、球几何,代数几何、微分几何、拓扑学),数论(代数数论、解析数论),代数学(群论),函数论(复分析、椭圆函数),几何学基础与公理理论(《几何基础》),数理逻辑与数学基础(布尔代数、集合论),计算机,控制论。
这一时期突出贡献的数学家有俄国的罗巴切夫斯基、德国的黎曼创立了非欧几何,黎曼创立了复分析,德国的克莱因发表了“爱尔兰根纲领”用变换群做工具将各种几何学化为统一的形式,法国的伽罗华关于置换群论的研究,德国的康托尔集合论,德国希尔伯特的集合基础。
19043原来如此
19044杨乐
post-13-1128954579.jpg
19044中国古代杰出的布衣数学大师--刘徽
(一)刘徽及其主要数学成就
刘徽(生于公元250年左右),是魏晋时代山东临淄或淄川一带人,是中国数学史上一个非常伟大的数学家,在世界数学史上,也占有杰出的地位.他的杰作《九章算术注》和《海岛算经》,是我国最宝贵的数学遗产.
《九章算术》约成书于东汉之初,共有246个问题的解法.在许多方面:如解联立方程,分数四则运算,正负数运算,几何图形的体积面积计算等,都属于世界先进之列,但解法比较原始,缺乏必要的证明,刘徽对此均作了补充证明.在这些证明中,显示了他在多方面的创造性。在算术方面,他是世界上最早提出十进小数概念的人,并用十进小数来表示无理数的立方根;他完成了齐同术理论,而且还推广到用齐同术去求几个分数的平均值,解释衰分术,解“均输”、“盈不足”和“方程”等问题;在代数方面,他正确地提出了正负数的概念及其加减运算的法则;改进了线性方程组的解法;在几何方面,提出了“割圆术”,即将圆周用内接或外切正多边形穷竭的一种求圆面积和圆周长的方法.他利用割圆术科学地求出了圆周率π=3.14的结果,刘徽在割圆术中提出的“割之弥细,所失弥少,割之又割以至于不可割,则与圆合体而无所失矣”,这可视为中国古代极限观念的佳作。《海岛算经》一书中,
对“重差术”进行了研究,刘徽精心选编了九个测量问题,编写成“重差”章,这些题目的创造性、复杂性和富有代表性,在当时都为西方所瞩目。
刘徽思想敏捷,方法灵活,既提倡推理又主张直观.他是我国最早明确主张用逻辑推理的方式来论证数学命题的人.
刘徽的治学思想,也是倍受世人推崇的。首先,他有孜孜不倦的学习态度,从《九章算术注》序中所言:“徽幼习九章,长再祥览”可见一斑。其次,他钻研学术严谨、求实,讲究“析理以辞,解体用图”,“约而能周,通而不黩”。对别人的错误绝不姑息,自己不懂也实言相告。
另外,在数学教学方面,他善于启发,主张“告往而知来,举一隅而三隅反”;还告诫后学者要抓住关键、提纲挈领。
刘徽的一生是为数学刻苦探求的一生.他终身未曾做官,故称为“布衣”;他虽然地位低下,但人格高尚.他不是沽名钓誉的庸人,而是学而不厌的伟人,他给我们中华民族留下了宝贵的财富.
(二)刘徽及其《九章算术注》的数学思想与方法
1.极限的思想
刘徽是世界上第一个在数学中运用极限思想的人。他在“割圆术”、“弧田术”、“开方术”、“阳马术”等中都用到了极限思想。“割圆术”是刘徽为“方田章”第23题的“圆田术”作注时引入的,用来求圆面积及推算圆周率。他用倍增圆内接正六边形的边数,以正3╳
边形当 时面积的极限来定义圆的面积;他说:“以六觚之一面乘半径,因而三之,得十二觚之幂;若又割之,次以十二觚之一面乘半径,因而六之,则得二十四觚之幂
。割之弥细,所失弥少。割之又割,以致于不可割,则与圆合体,而无所失矣”。刘徽根据上述思想求出圆内接正
192边形的面积,求得
,他继续求到圆内接正3072边形的面积,求得圆周率 。另外,刘徽还把
“割圆术”用到求弓形的面积、棱锥的体积上。
刘徽在数学上多次用极限思想处理问题,而且运用比较熟练,说明他已经对极限有了相当的认识,这是刘徽在数学上极其重要的成就,充分反映了他数学思想的先进。
2.数形结合的思想
“出入相补原理”,又称“以盈补虚法”,是刘徽发展并系统化了的一种独特的数学方法,发展了古代的数形结合思想。用现代语言来说,就是指这样的一个明显事实:“一个平面图形从一处移置他处,面积不变;又若把图形分割成若干块,那么各部分面积的和等于原来图形的面积,因而图形移置前后诸面积间的和、差有简单的相等关系;立体的情形也是这样”。刘徽在“方田”章第26题注中,把等腰三角形田变换成等积的矩形田(直田),再利用“方田术”求面积。在“勾股术”注中,论述到:“勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不移动也;合成弓玄方之幂,开方除之,即弓玄也”。在“少广”章的开平方术中,把数的开平方归结为求一个已知面积的正方形的一边长。
“出入相补原理”可以说贯穿在刘徽的整个《九章算术注》中,它反映了当时人们已具有较高的抽象概括能力,抽象概括出解决实际问题的一般原理,而这种一般原理又具有简明性和较强的直观性,用它能帮助人们把许多算法联系起来并得出更多的有效算法。“出入相补原理”的提出,反映了刘徽对中国古代传统的数学思想做了大的发展。
3.辩证的思想
刘徽主张对于具体问题具体分析,解决数学问题不应拘于一法。例如《九章算术注》
“均输”章第26题,他认为有两种解法,到底用哪种方法,刘徽认为“可随率宜也”。
4.转化的思想
刘徽用转化的思想指导运算中的化简工作,例如对于约分就明确地讲述了这一点。他注意到“分之为数,繁则难用”,因此要约分,而约分的结果数值不变;他说:“设有四分之二者,繁而言之,亦可为八分之四,约而言之,则二分之一也;虽则异词,至于为数,亦同归尔”。在“衰分”章中,刘徽还讲了分数的同值变换问题,“一乘一除适足相消,故所分犹存”。
5.逻辑推理的思想
刘徽很注意数学推理的逻辑性,他对《九章算术》中的所有数学概念都作了解释或逻辑定义,他还考虑了各问题间的逻辑关系。在“勾股”章中明确指出:这一章只所以一开始就提出了勾股定理,是因为“将以施于诸率,故先具此术,以见其源也”。他从逻辑严谨性出发,对于那些能从逻辑上证明的法则都进行了论证,他认为有些问题不能只限于感性认识,必须从理性上加以认识。
6.同一性的思想
刘徽在《九章算术注》的序文中说:“事类相推,各有攸归,故条枝虽分而本同干者,知发其一端而已”。意思是有许多问题,表面上看不相同,但在理论上都是一致的,它们有共同的根源;在整个注解中,都贯穿了这种思想,如在“勾股”章16题注中说:“言虽异矣,及其所以成法,实则同归矣”。
7.直观性的思想
刘徽也非常注意数学的直观性,他主张“析理以辞,解题用图”。理论与直观并用,只有这样,才能更好地使人理解数学内容,达到“庶亦约而能周,通而不黩,览之者思过半矣”的目的。因此他在数学研究中很注意使用图形、立体模型、剪纸和涂抹颜色。
8.无限的思想
刘徽超越前人、天才地将无限过程成功地运用于数学证明,特别是他的阳马术注展示了他所具有的非凡的高难技巧。刘徽在“阳马术”注中说“半之弥少,其余弥细,至细曰微,微则无形,由是言之,安取余哉?”,无限进行分割的结果最后得到一个“至细”“无形”的东西;在“割圆术”中利用边数增加的圆内接正多边形逼近圆,当边数增加到无穷多时,这个正无穷多边形就和圆重合。在刘徽那里,不可分量构成几何图形和“无厚”可积的观念取得了合法地位,并成为他成功地用于处理面积、体积问题的某些方法的基础。
(三)《九章算术》简介
《九章算术》的出现,标志着我国古代数学体系的正式确立,当中有以下特点:
1.
一个应用数学体系,全书表述为应用问题集的形式
2. 以算法为主要内容,全书以问、答、术构成,“术”是主要阐述的内容
3.
以算筹为工具。
《九章算术》取得了多方面的数学成就,包括:分数运算、比例问题、双设法、面积、体积计算、一次方程组解法、负数概念的引入及负数加减法则、开平方、开立方、一般二次方程解法等。《九章算术》的思想方法对我国古代数学产生了巨大的影响。自隋唐之际,《九章算术》已传入朝鲜、日本,现在更被译成多种文字。
《九章算术》成书于约公元50年左右,作者不详。很可能是在成书前一段历史时期内通过多人之手逐次整理、修改、补充而成的集体创作结晶。《九章算术》的内容十分丰富,全书采用问题集的形式,收有246个与生产、生活实践有联系的应用问题,其中每道题有问(题目)、答(答案)、术(解题的步骤)。这些问题依照性质和解法分别隶属于方田、粟米、衰分、少广、商功、均输、盈不足、方程、勾股九章。
第一章「方田」:平面图形面积的量法及算法,如矩形、三角形、圆、弧形、环形等田地的求积公式及分数算法,包括加减乘除法、约分﹝将分母,分子用辗转相除法求出它的最大公约数再作约分﹞、分数大小的比较及求几个分数的算术平均数等。
第二章「粟米」: 各种粮食交换之间的计算,讨论比例算法。
第三章「衰分」: 比例分配问题。
第四章「少广」:多位数开平方,开立方的法则。
第五章「商功」:立体形体积的计算。
第六章「均输」:处理行程和合理解决征税的问题,尤其是与人们从本地运送谷物到京城交税所需的时间有关的问题,还有一些与按人口征税有关的问题,其中还夹杂着衰分、比例及各种杂题。
第七章「盈不足」:算术中的盈亏问题的算法,实际上就是现在的线性插值法,它还有许多名称,如试位法、夹叉求零点、双假设法等。
第八章「方程」:有关一次方程组的内容,最后还有不定方程。将方程组的系数和常数项用算筹摆成「方程」,这是《九章算术》中解多一次方程组的方法,而整个消元过程则相当于代数中的线性变换。在方程章里提出了正负数的不同表示法和正负数的加减法则。
第九章「勾股」:专门讨论用勾股定理解决应用问题的方法。
(四)专题研究:刘徽的无限思想及其解释
1
刘徽注中的无限过程
刘徽直接用到无限过程的只有阳马术注和割圆术。
1.1
阳马术注中的无限过程:刘徽在证明从一般情形下的一个堑堵(斜割长方体后所得的直三棱柱)中分割出来的阳马(一棱垂直于底的四棱锥)和鳖臑(各面为直角三角形的四面体),其体积之比为2比1的定理(吴文俊称之为刘徽原理)时,采取这样的步骤:首先,把堑堵的三度分割成两半,成为一些小的阳马、堑堵和鳖臑,然后重新组合,便得到在原堑堵的四分之三中阳马和鳖臑所占体积之比为2比1,那就只要考虑余下的四分之一部分中情况了,由于这四分之一部分又是二个与原堑堵结构完全一样的堑堵,于是刘徽又可以进行同样的分割,然后重新组合这些更小的形体,这样他又证明了在这四分之一部分的四分之三中,阳马和鳖臑的体积之比为2比1,这个过程可以不断地进行下去,他说“半之弥少,其余弥细,至细曰微,微则无形,由是言之,安取余哉?”,无限进行分割的结果最后得到一个“至细”“无形”的东西,它刘徽认为可以舍弃不要了!
瓦格纳认为刘徽实际上使用了极限方法,但在观念上还遇到很大困难[4]。不知是不是瓦氏误解了反问句的意思,其实这反问是正面的肯定。我们认为在刘徽的观念里把分割到最后得到的“至细”“无形”的东西弃而不取不存在什么困难。这不仅因为刘徽在任何地方都没有表现出他对自己的处理有什么疑虑,而且这还可以从他的思想渊源上得到解释。
首先,刘徽受墨家的思想影响很深。墨家“非半弗著斤”的命题,认为分割的不断进行最后得到一个“端”,而“端”是没有大小、量度为零、但又不是什么都没有的东西。由于刘徽要考虑的是分割到最后所得到的东西的体积,所以,从他受墨家思想的影响看,刘徽把那个最后得到的东西的弃而不取(实际只是不取其体积),不存在什么观念上的困难。
其次,从道家思想传统看,也不存在刘徽对自己的处理产生怀疑的思想背景。刘徽这里用的“微”和“无形”两个概念,在刘徽之前已有密切的关系。《荀子·赋》说“知”“精微而无形”,瓦氏本人也注意到今传本河上公《老子注》有“无形曰微”之语。郭书春指出刘徽此语脱胎于《庄子·秋水》“河伯曰:世之议者皆曰,‘至精无形……。’……北海若曰,‘……夫精,小之微也;……夫精粗,期于有形者也;无形者,数之所不能分也;不可围者,数所不能穷也’”一段。这里,不仅“微”和“无形”通过概念“精”联系起来,而且充分体现了道家强调精微细小到极点就“无形”,“无形”就没有具体事物的规定性的思想。《庄子》说“无形者,数所不能分也”,认为“无形”便不能用数量来表示它的大小,从小这一方面来说,就是小到没有大小、没有体积可言。既然如此,刘徽把分割至最后得到的“至细”“无形”的东西的体积视为零,也就顺理成章了。处在王弼等玄学家提倡“贵无”的时代,万物始于“无”而复归于“无”的思想在当时影响甚剧,刘徽对自己这种处理问题的方式,是不存在怀疑其是否合理的思想背景的。
1.2
割圆术中的无限过程:刘徽用割圆术证明“半周半径相乘得积步”的圆面积公式时,从内接正六边形(“六觚”)开始割圆,依次得到内接正十二边形(“十二觚”)、正二十四边形(“二十四觚”)、……,“割之弥细,所失弥少。割之又割,以至于不可割,则与圆周合体而无所失矣”,认为割圆到最后得到一个和圆重合的正无穷多边形。他把这个和圆重合的多边形(“觚之细者”)分割成无限多个小三角形(有人认为刘徽是把多边形分割成筝形,这似是而非。诚然,在求正6边形面积时,刘徽分割成3个筝形来处理,求正12边形面积时他也是分割成6个筝形来处理,等等;但是刘徽说“以一面乘半径,觚而裁之”,这个“觚”是不可再割的极限状态下与圆重合的觚,“一面”乃是此觚之一边,它乘半径,当然不会是另一个由两个更小的三角形组成的筝形的面积,否则此觚就还可再割了。而从行文来看,也是按此觚之一边来“裁”的,此一边已是分割到最后所得的一边。至于6边形分成3个筝形来处理之类,实为具体计算之方便),由于每个三角形的面积的是其底边与圆半径乘积的一半,于是,刘徽就可以合并求和而得到这个正无穷多边形的面积公式,从而也就得到了圆的面积公式。
利用边数增加的圆内接正多边形逼近圆,当边数增加到无穷多时,这个正无穷多边形就和圆重合,这种处理并非始于刘徽。公元前5世纪的安提丰(Antiphon)探讨化圆为方问题时,先作一个内接多边形,例如一个正方形,然后作每一边的中垂线各交圆于一点,把每一点和与之相邻的正方形的顶点联结起来,于是得到一个正八边形,按照这样的方式不断进行下去,最后他得到一个多边形,其边和圆弧重合,圆便为它所穷尽了[11]。梁宗巨、王青建认为刘徽把边数不断增加的正多边形看成和圆越来越接近,以至最后与圆重合的思想,和安提丰的思想相一致。
值得注意的是安提丰的方法在古希腊被认为逻辑不缜密而遭到了抨击,亚里士多德甚至认为安提丰的作法不值一驳[14],攸多克索(Eudoxus,公元前4世纪)改造安氏的方法,避免了无限概念的直接使用,符合希腊人对逻辑严密性的要求,其方法一直为古代西方数学所采用,并对近代数学产生了深远的影响;但是刘徽对他的方法则没有表现出什么不满意,从现有材料看,甚至整个中国古代都没有人怀疑过刘徽割圆术的合理性。刘徽的态度可以从以下方面得到解释。
首先,刘徽的这种处理是比较符合直观的。从6边形到12边形、到24边形、……,在这样越来越接近圆面积的趋势中,圆以多边形代替,所失的面积会越来越少,这样他就很自然的会觉得多边形和圆会越来越接近重合。我们知道,讲求直观是中国古代数学的传统。郭书春认为刘徽割圆术受司马迁“汉兴,破觚而为圆”之说的影响,而其实物原型乃是工匠把带有棱角的原材料加工成圆形。刘徽从工匠的实际工作的中受到启发,获得其方法,是与中国古代数学讲求实际的特点相吻合的,而在这样的传统下,由于它来源于实际,所以更不容易被怀疑。刘徽对符合直观的方法比较信赖,还从他的其它注中能得到映证。
《九章》“勾股”章葛缠木问:“今有木长二丈,围之三尺。葛生其下,缠木七周,上与木齐。问葛长几何?”刘徽用笔管缠青线模拟葛缠木,然后解开来看,发觉每周之间都相间成勾股弦(笔管的周长和线两圈之间的距离分别为股和勾,线一周的长为弦),由此他解释了《九章》以木长为股,木围的七倍为勾(刘徽说在这里《九章》的术把勾和股颠倒了),然后求弦便得到葛的长度的术的合理性。
如果说葛缠木问还真可以把曲的拉直的话,那么要把曲池拉直就只能凭想象了。刘徽注曲池(上下底面都是环田的立体)体积公式时说要把它“引而伸之”,实际会得到一个楔形体,曲池的底面的内外周长(所谓“中外周”)便变为楔形体的底面的长,而广、高或深不变,于是他把曲面体化成了(平面)多面体了。但是,在他的思想中如何“引而伸之”,则语焉不详。
这样化曲为直,应该说其理论的根据是不足的。刘徽没有对这样的作法表示怀疑,也说明他对那种从直观中获得的知识的信任,进而也更说明他对自己大胆利用无限思想来处理问题是放心的(当然,要用无限分割的方法,解决这两个问题是很困难的)。
其次,从墨家传统看,刘徽的处理也比较好理解。《墨经》中“无穷不害兼,说在盈否”的命题,按郭书春的解释,具有这样的意思:一个含有无穷多个部分的整体,只要一个部分都不缺,就不会影响这个整体,虽然我们不能肯定这个解释是否一定符合《墨经》作者的原意,但后世学者从这样一个表述笼统的命题中获得某种思想是可能的,何况这个解释与《墨经》其它地方所表现的无限思想也不相矛盾。按照这个解释,在圆不可割状态下与之重合的无穷多边形,被分解为无穷多个三角形求和,是完全没有问题的;这无穷多个三角形只要一个不落就对无穷多边形、因而也就对圆的面积不会有影响。
此外,割圆术割圆到最后达到不可再割的极限状态,从道论传统看,达到无限的状态是不可言论、没法追究的,因而刘徽对割圆术满足于直观也就足够了。
刘徽大胆地直接用无限过程来处理数学问题,而没有什么顾虑,这与古希腊学者大不一样。这一方面是由于刘徽时期及其以前不存在怀疑无限观念的传统,另一方面这也与中国古代数学注重实际,讲求直观的传统相一致。刘徽在无限过程的运用上,其思想和墨、道两家是一脉相承的。
2
刘徽的不可分量的思想
除无限分割外,刘徽还利用不可分量可积的思想处理问题。在他的观念里,线可以看成是由一系列点组成的,面可以看成是由一系列线组成的,体可以看成是由一系列面组成的[
18]。他在注圭田(等腰三角形)术时说的“中平之数”,就是组成圭田的平行于底(广)的一系列线段的平均值;在注环田(圆环或夹在二半径间的圆环部分)术时说的“中平之周”也是组成环田的一系列同心圆(弧)的平均值;而在注城、垣、沟、堑、渠(都是底为等腰梯形的直棱柱)的体积公式时所说的“中平之广”则是组成底面梯形的一系列平行于梯形底边的线段的平均值。
刘徽把立体看成是由一系列面积组成的,这实际是他根据比较两个立体任意等高处的截面积来确立它们的体积是否相等的思想基础。祖暅之在刘徽工作的基础上研究球体积问题,他说“夫叠棊成立积,缘幂势既同,则积不容异”。他一方面说“叠棊成立积”,另一方面又说“幂(面积)势”怎么怎么,认为要根据截面积“幂”来确定立体体积的情况。虽然“棊”和“幂”具体是怎样的关系,尚难说定;不过,由于“棊”也正如郭世荣认为的存在于观念之中,所以并不妨碍我们认为祖暅之把立体看成是由面积叠合而成的。祖氏的话透露出面积为体的思想来源于对实际中把有一定厚度的薄的东西一层层地叠合成厚的东西的工作的抽象,同时也反映了刘徽叠面成体的思想来源。
这样一来就出现了这样的问题:组成面积的线段是不是有一定数量的宽度,组成体积的面是不是有一定数量的厚度呢?刘徽对此没有明说,考虑到他的割圆术和阳马术注中表现出的无限分割思想,我们认为这些线段或截面是被当做没有具体数量的宽度或厚度的来对待的。否则由这些具有一定数量的宽度或厚度的线段或面积,是不能构成真正理想的三角形或圆锥这一类图形的。这样一来则又出现了这样的问题:我们现在
19045兰大,试题简单
19045我想考兰州大学的应用数学,不知此校好不好考?
还有,录取比例大概是多少呀?
19045我是兰大毕业的哦,应该比较容易,出题很基本。恩,我们去年除去保送的,本系考上的没多少个,好多外边的。不知道今年怎么样,看每一届学生的情况了
19045这个总的来说是比较简单的!!不信你可以试试!!
19047顶一下。
19047
介绍数学分析内容体系中体现的函数\极限\连续\可导\积分\级数思想的产生,发展,内涵,本质及应用
微积分的诞生,是全部数学史上的一个伟大创举.它曾经历了两千多年的孕育和准备阶段;随着十六、十七世纪欧洲的文艺复兴、产业革命等一系列社会改革,社会生产得到了具大的发展,从而对数学的需求更加迫切,微积分也应运而生;经过十八、十九世纪数学家们的努力,使微积分逐步趋于完善,并发展成为今天具有广泛应用的庞大的基础数学分支学科——数学分析。
我们在本书中介绍的主要内容是:数学分析内容中体现的数学思想、蕴涵的哲学思想,数学分析内容中常用的数学思想、数学分析中的美学思想以及在创立微积分的过程中作出了卓越贡献的数学家所采用的思想和方法,
第一部分
数学分析内容中体现的数学思想
一、函数的思想
“用函数来思考”是大数学家克莱因领导的数学教育改革运动的口号。函数是数学中最重要的基本概念,也是数学分析的研究对象。函数的思想,就是运用函数的方法,必要时引入辅助函数,将常量视为变量、化静为动、化离散为连续,将所讨论的问题转化为函数问题加以解决的一种思想方法。
1.函数概念的产生与发展
(1)函数概念的起源
函数概念的萌芽,可以追溯到古代对图形轨迹的研究,随着社会的发展,人们开始逐渐发现,在所有已经建立起来的数的运算中,某些量之间存在着一种规律:一个或几个量的变化,会引起另一个量的变化,这种从数学本身的运算中反映出来的量与量之间的相互依赖关系,就是函数概念的萌芽。在代数学的方程理论中,对不定方程的求解,使得人们对函数概念逐步由模糊趋向清晰。
(2)函数概念的产生
恩格斯指出:“数学中的转折点是笛卡儿的变数,有了变数,运动进入了数学;有了变数,辩证法进入了数学”
。笛卡儿在1637年出版的《几何学》中,第一次涉及到变量,他称为“未知和未定的量”,同时也引入了函数的思想。英国数学家格雷果里在1667年给出的函数的定义,被认为是函数解析定义的开始。他在“论圆和双曲线的求积”中指出:从一些其他量经过一系列代数运算或任何其他可以想象的运算而得到的一个量。这里的运算指的是五种代数运算以及求极限运算,但这一定义未能引起人们的重视。
一般公认最早给出函数定义的是德国数学家莱布尼兹,他在1673年的一篇手稿中,把任何一个随着曲线上的点变动而变动的几何量,如切线、法线、点的纵坐标都称为函数;并且强调这条曲线是由一个方程式给出的。莱布尼兹又在1692年的论文中,称
幂的 、 、 等为
的幂数,把幂与函数看作同义语,以后又用“函数”表示依赖于一个变量的量。
(3)函数概念的扩张
函数概念被提出后,由于微积分学的发展,函数概念也不断进行扩张,日趋深化。致使函数概念日趋精确化、科学化。函数概念在发展过程中,大致经过了以下几个阶段的扩张。
第一次扩张主要是解析扩张,提出了“解析的函数概念”。瑞士数学家约翰.伯努利于1698年给出了函数新的定义:由变量
和常量用任何方式构成的量都可以叫做
的函数。这里的“任何方式”包括了代数式子和超越式子。
1748年欧拉在《无穷小分析引论》中给出的函数定义是:“变量的函数是一个解析表达式,它是由这个变量和一些常量以任何方式组成的”。
1734年欧拉还曾引入了函数符号
,并区分了显函数和隐函数、单值函数和多值函数、一元函数和多元函数等。在十八世纪占主要地位的观点是,把函数理解为一个解析表达式(有限或无限的)。
函数概念的第二次扩张是从几何方而的扩张,提出了“几何的函数概念”。十八世纪中期的一些数学家发展了莱布尼兹将函数看作几何量的观点,而把曲线称为函数(因为解析表达式在几何上表示为曲线)。达朗贝尔在
1746年研究弦振动问题时,提出了用单独的解析表达式给出的曲线是函数,后来欧拉发现有些曲线不一定是由单个解析式给出的,因此提出了一个新的定义,函数是:“
平面上随手画出来的曲线所表示的 与
的关系”。即把函数定义为由单个解析式表达出的连续函数,也包括由若干个解析式表达出的不连续函数(不连续函数的名称是由欧拉提出的)。
函数概念的第三次扩张,朴素地反映了函数中的辩证因素,体现了“自变”到“因变”的生动过程。形成了“科学函数定义的雏型”。
1775年,欧拉在《微分学》一书中,给出了函数的另一定义:“如果某些变量,以这样一种方式依赖于另一些变量,即当后者变化时,前者也随之变化,则称前面的变量为后面变量的函数”。值得指出的是,这里的“依赖”、“随之变化”等等的含义仍不十分确切。这个定义限制了概念的外延,它只能算函数概念的科学雏型。在这次函数概念的扩张中,十九世纪最杰出的法国数学家柯西在
1821年所著的《解析教程》中,给出了如下函数定义:“在某些变量间存在着一定的关系,当一经给定其中某一变量的值,其他变量的值也随之确定,则将最初的变量称为自变量,其他各个变量称为函数”。这个定义把函数概念与曲线、连续、解析式等纠缠不清的关系给予了澄清,也避免了数学意义欠严格的“变化”一词。函数是用一个式子或多个式子表示,甚至是否通过式子表示都无关要紧。
函数概念的第四次扩张,可称为“科学函数定义”进入精确化阶段。德国数学家狄利克雷于
1837年给出了函数定义:“若对x(a≤x≤b)的每一个值,y总有完全确定的值与之对应,不管建立起这种对应的法则的方式如何,都称y是x的函数”。这一定义彻底地抛弃了前面一些定义中解析式的束缚,强调和突出函数概念的本质,即对应思想,使之具有更加丰富的内涵。因而,此定义才真正可以称得上是函数的科学定义,为理论研究和实际应用提供了方便。狄利克雷还给出了著名的函数(人们称为狄利克雷函数),这个函数是难以用简单的包含自变量x的解析式表达的,但按照上述定义的确是一个函数。为使函数概念适用范围更加广泛,人们对函数定义作了如下补充:“函数y=f(x)的自变量,可以不必取[a,b]中的一切值,而可以仅取其任一部分”,换句话说就是x的取值可以是任意数集,这个集合中可以有有限个数、也可以有无限多个数,可以是连续的、也可以是离散的。这样就使函数成了一个非常广泛的概念。但是,自变量及函数仍然仅限于数的范围,而且也没有意识到“函数”应当指对应法则本身。
函数概念的第五次扩张,提出了“近代函数定义”。出现了美国数学家维布伦的函数定义,这个定义是建立在重新定义变量、变域和常量的基础上的。所谓变量,是代表某集合中任意一个“元素”的记号,由变量所表示的任一元素,称为该变量的值。变量x代表的“元素”的集合,为该变量的变域,而常量是上述集合中只包含一个“元素”情况下的特殊变量。这样的变量与常量的定义,比原来的定义更趋一般化了,而且克服了以往变量定义的缺陷,变量“变动”改进为变量在变域(集合)中代表一个个元素。利用这一变量的定义,维布伦给出了近代函数定义:“设集合X、Y,如果X中每一个元素x都有Y中唯一确定的元素y与之对应,那么我们就把此对应叫做从集合X到集合Y的映射,记作f:X
Y,y=f(x)”。映射的特殊情况,从数集到数集的映射就是前面狄利克雷的函数定义;从“数集”到“集”仅一字之差,但含意却大不相同。从而使函数概念摆脱了数的束缚,使得函数概念能广泛地应用于数学的各个分支及其它学科中。
函数概念的第六次扩张,提出了“现代函数定义”。
19世纪康托尔创建了集合论,函数概念进入了集合论的范畴,使函数概念纯粹地使用集合论语言进行定义。在这种情形下,函数、映射又归结为一种更为广泛的概念——关系。“设集合X、Y,定义X与Y的积集X
Y如下:X Y={(x,y)|x X,y Y}。积集X Y中的一个子集R称为X与Y的一个关系,若(x,y)
R,则称x与y有关系R,记为xR(y);若(x,y) R,则称x与y无关系R。设 是x与y的关系,即 X Y,如果(x,y)、(x,z)
,必有y=z,那么称
为X到Y的映射或函数”。这就是现代的函数定义,它在形式上回避了“对应”术语,使用的全部是集合论的语言,一扫原来定义中关于“对应”的含义存在着的模糊性,而使函数念更为清晰、正确,应用范围更加广泛了。
2.函数概念的本质
我们以
为例分析函数概念的本质。
①在抽象出的具体函数关系中, 、 的地位与作用是不相同的。因为客观事物的联系在分割开来考察时,总有确定的因果关系。在
中, 处于主动地位,我们称自变量, 处于被动地位,我们称因变量,y与
的关系是自变量与因变量的关系,其中自变量处于主动地位,因变量处于依从地位,所以自变量的变化处于主导地位。
②y与
之间用等号连结,但不是简单的数量上相等的关系,而是变量y与 之间的等价关系。等式左右两边y与 都是依赖于
的,这是同一性;但又包含着不容忽视的差异性:左边的 我们只知道它依赖于 ,但按怎样确定的方式依赖于 ,并没有表达出来。马克思称它为“依赖于
的函数”。而右边的 是直接用 的组合表示出来的,马克思称之为“用 表示的函数”和 (用
表示的函数)之间的等价关系。只有这时左边才是右边数量的表现。因此函数 左右两边是抽象与具体的统一。左边的 是抽象的,右边的
是具体的,因此活动的主动性在右边。也就是说,对于研究函数,我们关心的是用 表示出来的具体的依赖关系。
③
反映的是变量与变量之间的关系。但从式子本身看,我们直接得到的是状态间的关系,其中 与y之间可变性的关系虽然是变量本身所固有的,但是在关系式
中却是隐藏着的。所以函数关系是
与y之间明显的状态关系与隐藏的可变性关系的统一体,而函数关系式揭示明显状态关系是主要的方面。
根据以上分析,由第①点,自变量与因变量的主从地位中,自变量处于主导的地位,那么自变量的变化范围一一定义域与因变量的变化范围——值域中,值域是由定义域经过函数关系所决定的。因此自变量的变化范围起着主要的决定作用。这表现在数学上,将自变量的变化范围一—定义域,作为函数的基本要素之一。
由第②点分析的抽象与具体的对立统一,也就是“依赖于
的函数”与“用 表示的函数”二者的对立统一。其中“用 表示的函数”起主导作用。因为对一个函数,我们不但要了解y依赖于
,而且更重要的是了解y按照怎样的条件所规定的关系依赖于 。要确定一个函数,只抽象地知道y依赖于 是不够的,我们的目的在于要知道y怎样具体地依赖于
。在数学上就是要确定具体的对应法则。所以对应法则是构成函数的另一个基本要素。
由此可见,函数的基本要素有两条:(1)定义域,(2)对应法则。只要这两条确定了,函数就完全确定了,抓住了这两条,就在数学上抓住了函数慨念的本质。如,
与 在数学上代表完全相同的函数,因为它们的定义域相同,对应法则也相同。至于用什么字母表示自变量、因变量并非本质问题。而 与
是不同的函数,因为对应法则虽然相同,但定义域不同。又如, 与 代表同一个函数。因为对应关系是否相同的实质不在于表达式的形式是否一样,而在于对同一个
,是否对应着相同的y值。 同理 与
,也代表同一个函数。
由第③点,明显的状态关系与隐藏的可变性关系中,明显的状态关系是主要方面,函数刻划运动主要是从状态方面来表现运动,是从运动的反面“静止”来度量运动,而要揭示
与
之间的可变性关系,函数工具是有局限性的,这是数学分析发展中要进一步解决的课题。
3.函数思想在数学分析中的应用
(1)以函数为桥梁,实现函数与方程、不等式间的转化
①方程与函数相比,前者是静止,后者是运动。方程的根可视为对应函数在某种特定状态下的值。当研究方程问题时,特别是证明方程根的存在性与个数时,我们可以从函数的观点出发,化静为动,这样往往可以化难为易、化繁为简。
②我们在证明不等式时,可以将不等式问题化为函数问题,为解决问题带来方便。
(2)以函数为背景,实现函数思想在数列中的应用
数列和函数相比,前者离散,后者连续。从函数的观点出发,将数列问题转化为相应的函数问题,是求数列问题的一种有效方法。
(3)化离散为连续,解决级数问题
(4)引入辅助函数,证明有关问题
二、极限的思想
极限的思想是近代数学的一种重要思想,数学分析就是以极限概念为基础、极限理论(包括级数)为主要工具来研究函数的一门学科。
所谓极限的思想,是指用极限概念分析问题和解决问题的一种数学思想。用极限思想解决问题的一般步骤可概括为:对于被考察的未知量,先设法构思一个与它有关的变量,确认这变量通过无限过程的结果就是所求的未知量;最后用极限计算来得到这结果。
极限思想是微积分的基本思想,数学分析中的一系列重要概念,如函数的连续性、导数以及定积分等等都是借助于极限来定义的。如果要问:“数学分析是一门什么学科?”那么可以概括地说:“数学分析就是用极限思想来研究函数的一门学科”。
1.极限思想的产生与发展
(1)极限思想的由来.
与一切科学的思想方法一样,极限思想也是社会实践的产物。极限的思想可以追溯到古代,刘徽的割圆术就是建立在直观基础上的一种原始的极限思想的应用;古希腊人的穷竭法也蕴含了极限思想,但由于希腊人“对无限的恐惧”,他们避免明显地“取极限”,而是借助于间接证法——归谬法来完成了有关的证明。
到了16世纪,荷兰数学家斯泰文在考察三角形重心的过程中改进了古希腊人的穷竭法,他借助几何直观,大胆地运用极限思想思考问题,放弃了归缪法的证明。如此,他就在无意中“指出了把极限方法发展成为一个实用概念的方向”。
?(2)极限思想的发展
极限思想的进一步发展是与微积分的建立紧密相联系的。16世纪的欧洲处于资本主义萌芽时期,生产力得到极大的发展,生产和技术中大量的问题,只用初等数学的方法已无法解决,要求数学突破只研究常量的传统范围,而提供能够用以描述和研究运动、变化过程的新工具,这是促进极限发展、建立微积分的社会背景。
?起初牛顿和莱布尼茨以无穷小概念为基础建立微积分,后来因遇到了逻辑困难,所以在他们的晚期都不同程度地接受了极限思想。牛顿用路程的改变量ΔS与时间的改变量Δt之比ΔS/Δt表示运动物体的平均速度,让Δt无限趋近于零,得到物体的瞬时速度,并由此引出导数概念和微分学理论。他意识到极限概念的重要性,试图以极限概念作为微积分的基础,他说:“两个量和量之比,如果在有限时间内不断趋于相等,且在这一时间终止前互相靠近,使得其差小于任意给定的差,则最终就成为相等”。但牛顿的极限观念也是建立在几何直观上的,因而他无法得出极限的严格表述。牛顿所运用的极限概念,只是接近于下列直观性的语言描述:“如果当n无限增大时,an无限地接近于常数A,那么就说an以A为极限”。
?这种描述性语言,人们容易接受,现代一些初等的微积分读物中还经常采用这种定义。但是,这种定义没有定量地给出两个“无限过程”之间的联系,不能作为科学论证的逻辑基础。
?正因为当时缺乏严格的极限定义,微积分理论才受到人们的怀疑与攻击,例如,在瞬时速度概念中,究竟Δt是否等于零?如果说是零,怎么能用它去作除法呢?如果它不是零,又怎么能把包含着它的那些项去掉呢?这就是数学史上所说的无穷小悖论。英国哲学家、大主教贝克莱对微积分的攻击最为激烈,他说微积分的推导是“分明的诡辩”。
?贝克莱之所以激烈地攻击微积分,一方面是为宗教服务,另一方面也由于当时的微积分缺乏牢固的理论基础,连牛顿自己也无法摆脱极限概念中的混乱。这个事实表明,弄清极限概念,建立严格的微积分理论基础,不但是数学本身所需要的,而且有着认识论上的重大意义。
?(3)极限思想的完善
?极限思想的完善与微积分的严格化密切联系。在很长一段时间里,微积分理论基础的问题,许多人都曾尝试解决,但都未能如愿以偿。这是因为数学的研究对象已从常量扩展到变量,而人们对变量数学特有的规律还不十分清楚;对变量数学和常量数学的区别和联系还缺乏了解;对有限和无限的对立统一关系还不明确。这样,人们使用习惯了的处理常量数学的传统思想方法,就不能适应变量数学的新需要,仅用旧的概念说明不了这种“零”与“非零”相互转化的辩证关系。
?到了
18世纪,罗宾斯、达朗贝尔与罗依里埃等人先后明确地表示必须将极限作为微积分的基础概念,并且都对极限作出过各自的定义。其中达朗贝尔的定义是:“一个量是另一个量的极限,假如第二个量比任意给定的值更为接近第一个量”,它接近于极限的正确定义;然而,这些人的定义都无法摆脱对几何直观的依赖。事情也只能如此,因为
19世纪以前的算术和几何概念大部分都是建立在几何量的概念上面的。
?首先用极限概念给出导数正确定义的是捷克数学家波尔查诺,他把函数f(x)的导数定义为差商Δy/Δx的极限f′(x),他强调指出f′(x)不是两个零的商。波尔查诺的思想是有价值的,但关于极限的本质他仍未说清楚。
?到了
19世纪,法国数学家柯西在前人工作的基础上,比较完整地阐述了极限概念及其理论,他在《分析教程》中指出:“当一个变量逐次所取的值无限趋于一个定值,最终使变量的值和该定值之差要多小就多小,这个定值就叫做所有其他值的极限值,特别地,当一个变量的数值(绝对值)无限地减小使之收敛到极限0,就说这个变量成为无穷小”。
?柯西把无穷小视为以0为极限的变量,这就澄清了无穷小“似零非零”的模糊认识,这就是说,在变化过程中,它的值可以是非零,但它变化的趋向是“零”,可以无限地接近于零。
?柯西试图消除极限概念中的几何直观,作出极限的明确定义,然后去完成牛顿的愿望。但柯西的叙述中还存在描述性的词语,如“无限趋近”、“要多小就多小”等,因此还保留着几何和物理的直观痕迹,没有达到彻底严密化的程度。
?为了排除极限概念中的直观痕迹,维尔斯特拉斯提出了极限的静态的定义,给微积分提供了严格的理论基础。所谓
an=A,就是指:“如果对任何ε>0,总存在自然数N,使得当n>N时,不等式|an-A|<ε恒成立”。
?这个定义,借助不等式,通过ε和N之间的关系,定量地、具体地刻划了两个“无限过程”之间的联系。因此,这样的定义是严格的,可以作为科学论证的基础,至今仍在数学分析书籍中使用。在该定义中,涉及到的仅仅是数及其大小关系,此外只是给定、存在、任取等词语,已经摆脱了“趋近”一词,不再求助于运动的直观。
?众所周知,常量数学静态地研究数学对象,自从解析几何和微积分问世以后,运动进入了数学,人们有可能对物理过程进行动态研究。之后,维尔斯特拉斯建立的ε-N语言,则用静态的定义刻划变量的变化趋势。这种“静态——动态——静态”的螺旋式的演变,反映了数学发展的辩证规律。
?2.极限思想的思维功能
?极限思想在现代数学乃至物理学等学科中有着广泛的应用,这是由它本身固有的思维功能所决定的。极限思想揭示了变量与常量、无限与有限的对立统一关系,是唯物辩证法的对立统一规律在数学领域中的应用。借助极限思想,人们可以从有限认识无限,从“不变”认识“变”,从直线形认识曲线形,从量变认识质变,从近似认识精确。
?无限与有限有本质的不同,但二者又有联系,无限是有限的发展。无限个数的和不是一般的代数和,把它定义为“部分和”的极限,就是借助于极限的思想方法,从有限来认识无限的。
?“变”与“不变”反映了事物运动变化与相对静止两种不同状态,但它们在一定条件下又可相互转化,这种转化是“数学科学的有力杠杆之一”。例如,要求变速直线运动的瞬时速度,用初等方法是无法解决的,困难在于速度是变量。为此,人们先在小范围内用匀速代替变速,并求其平均速度,把瞬时速度定义为平均速度的极限,就是借助于极限的思想方法,从“不变”来认识“变”的。
?曲线形与直线形有着本质的差异,但在一定条件下也可相互转化,正如恩格斯所说:“直线和曲线在微分中终于等同起来了”。善于利用这种对立统一关系是处理数学问题的重要手段之一。直线形的面积容易求得,求曲线形的面积问题用初等的方法是不能解决的。刘徽用圆内接多边形逼近圆,一般地,人们用小矩形的面积来逼近曲边梯形的面积,都是借助于极限的思想方法,从直线形来认识曲线形的。
?量变和质变既有区别又有联系,两者之间有着辩证的关系。量变能引起质变,质和量的互变规律是辩证法的基本规律之一,在数学研究工作中起着重要作用。对任何一个圆内接正多边形来说,当它边数加倍后,得到的还是内接正多边形,是量变而不是质变;但是,不断地让边数加倍,经过无限过程之后,多边形就“变”成圆,多边形面积便转化为圆面积。这就是借助于极限的思想方法,从量变来认识质变的。
?近似与精确是对立统一关系,两者在一定条件下也可相互转化,这种转化是数学应用于实际计算的重要诀窍。前面所讲到的“部分和”、“平均速度”、“圆内接正多边形面积”,分别是相应的“无穷级数和”、“瞬时速度”、“圆面积”的近似值,取极限后就可得到相应的精确值。这都是借助于极限的思想方法,从近似来认识精确的。
3.建立概念的极限思想
极限的思想方法贯穿于数学分析课程的始终。可以说数学分析中的几乎所有的概念都离不开极限。在几乎所有的数学分析著作中,都是先介绍函数理论和极限的思想方法,然后利用极限的思想方法给出连续函数、导数、定积分、级数的敛散性、多元函数的偏导数,广义积分的敛散性、重积分和曲线积分与曲面积分的概念。如:
(1)函数
在 点连续的定义,是当自变量的增量 时,函数值的增量 趋于零的极限。
(2)函数 在 点导数的定义,是函数值的增量 与自变量的增量 之比 ,当
时的极限。
(3)函数 在 上的定积分的定义,是当分割的细度趋于零时,积分和式 的极限。
(4)数项级数 的敛散性是用部分和数列
的极限来定义的。
(5)广义积分 是定积分 其中 为任意大于 的实数)当
时的极限,等等。
4.解决问题的极限思想
极限思想方法是数学分析乃至全部高等数学必不可少的一种重要方法,也是数学分析与初等数学的本质区别之处。数学分析之所以能解决许多初等数学无法解决的问题(例如求瞬时速度、曲线弧长、曲边形面积、曲面体体积等问题),正是由于它采用了极限的思想方法。
有时我们要确定某一个量,首先确定的不是这个量的本身而是它的近似值,而且所确定的近似值也不仅仅是一个而是一连串越来越准确的近似值;然后通过考察这一连串近似值的趋向,把那个量的准确值确定下来。这就是运用了极限的思想方法。
三、连续的思想
数学分析的研究对象是函数,主要是连续函数。因此对函数连续性的讨论是数学分析的一个重要内容。我们有必要对数学分析中连续的思想做深入地探讨。
1.连续思想的产生和发展
客观世界的许多现象和事物不仅是运动变化的,而且其运动变化的过程往往是连绵不断的,这些连绵不断发展变化的事物在量的方面的反映就是连续函数,连续函数就是刻画变量连续变化的数学模型。
16、
17世纪微积分的酝酿和产生,直接开始于对物体的连续运动的研究。象伽利略所研究的落体运动、开普勒所研究的绕日运转的行星所扫描的扇形面积、牛顿所研究的“流”等都是连续变化的量。这个时期以及
18世纪的数学家,虽然已经大张旗鼓地研究了连续变化的量,即连续函数,但仍停留在几何直观上,把能一笔画成的曲线所对应的函数叫做连续函数。
直到
19世纪,当柯西以及维尔斯特拉斯等数学家建立起来严格的极限理论之后,才对连续函数作出了纯数学的精确表述。
2.连续思想的解释
(1)连续的直观含义
连续的直观含义就是连绵不断的,所以一个函数
在 上是一个“连续函数”的直观意义就是它的图象是一条连绵不断的曲线。若用函数值 随 的值的改变而变动的观点来说,就是当 逐渐改变时,函数
的相应变动也是逐渐的,不会有任何突增或突减的跳跃式振荡。从数量上来说,逐渐的改变也就是逐步作微小的改变,所以当我们把函数的连续性局部化到
的邻域来看时, 在 点连续的直观意义就是当 在 点的邻域内作微小变动时, 的相应函数值也在
的邻域内作微小变动。
(2)连续的精确表述
为研究函数的连续,先介绍增量的概念。
设函数 的定义域为 ,如
19047没人顶我顶一下!
19047
写得很有水平!强烈支持!
19047顶一下!!!
19047好比生物学上的进化论,数学思想的产生、数学理论体系的形成的确不是一件容易的事。
文章写得很好!只是有些冗长,若能精简之,更妙。
数学与我们同在!
19047有点长,先顶再看了
19047有的水平
19047非常希望看到更多谈论思想的帖子~~
19047顶一下!!!!!!
19047顶一下好文章!!
19047谢谢了
好东西,顶!!!
19047好 好 好
19047什么书?
19047顶
19047顶一个
19047好,只是还不详细
19047最精华的帖子![SIZE=14][COLOR=purple]
19047
太棒了!不过对级数的背景论述不够。
19047不错,应当顶上去啊
19047挺不错的
19048www.ttdown.com上有
19048有哪位有maple10 给兄弟传一下
QQ:20554
18
19048
http://elmo.jlu.edu.cn/Link/MathTools/show.asp?id=66
19050丘成桐--院士
国际数学会议决定将
1983年的数学界的诺贝尔奖——菲尔兹奖颁发给证明微分几何中卡拉比猜想和证明了广义相对论中正质量猜想的一位年仅34的华人数学家,这位才能非凡的年轻人就是丘成桐。
丘成桐原籍中国广东,后来迁居香港,
1966年进入香港中文大学数学系。
1971年获美国伯克莱加州大学博士学位。
1987年获美国哈佛大学名誉博士学位。曾任美国斯坦福大学、普林斯顿高等研究院、圣地亚哥加州大学数学教授;
1987年至今,任哈佛大学数学教授。他自幼迷恋数学,经过不懈的努力,在大学三年级时就由于出众的才华被一代几何学宗师陈省身发现,破格成为美国加州大学伯克利分校的研究生。在陈省身教授的亲自指导下,年仅22岁的丘成桐获得了博士学位。28岁时,丘成桐成为世界著名学府斯坦福大学的教授,并且是普林斯顿高级研究所的终身教授。
丘成桐的第一项重要研究成果是解决了微分几何的著名难题—卡拉比猜想,从此名声鹊起。他把微分方程应用于复变函数、代数几何等领域取得了非凡成果,比如解决了高维闵考夫斯基问题,证明了塞凡利猜想等。这一系列的出色工作终于使他成为菲尔兹奖得主。
丘成桐博士的主要科学技术成就与贡献有:
1.
解决Calabi猜想,
即一紧Kahler流形的第一陈类≤0时,任一陈类的代表必有一Kahler度量使得其Ricci式等于此陈类代表。这在代数几何中有重要的应用。
2.
与R.Schoen合作解决正质量猜想(或称Einstein猜想), 即广义相对论一个非平凡孤立系统中,
包括由物质与引力的贡献的整个能量为正。
3.
与郑绍远合作解决实Monge-Ampere方程的Dirichlet(边值)问题并对minkowski问题(即有关凸超曲面问题)给以完整的证明。
4. 与肖荫堂合作证明单连通Kahler流形若有非正截面曲率时必双全纯等价于复欧氏空间, 并给Frankel猜想一个解析的证明。
5.
与P.Li合作在各种Ricci曲率条件下估计紧黎曼流形上Laplace算子的第一与第二特征值。
6.
与Meeks合作用三维流形的拓扑方法解决极小曲面的一系列问题,反过来他们用极小曲面理论推导三维拓扑方面的结果,
并导致Smith猜想的解决。
7.
1984年与Uhlenbeck合作解决在紧Kahler流形上稳定的全纯向量丛与Yang-Mills-Hermite度量是一一对应的猜想,并得出陈氏的一
个不等式。
8. 最近丘成桐正研究的镜流形, 是Calabi-丘流形的一特殊情形, 与理论物理的弦理论有密切关系,
引起数学界的广泛注意。
丘成桐教授是第一位荣获菲尔兹奖的华裔人士。他热心于帮助发展我国的数学事业。自
1979年以来多次到中国科学院进行高质量的讲学。由科学出版社出版了专著《微分几何》,内容主要是他的研究结果。他还直接指导培养我国的数学博士生,至今已有10余人,成绩显著。
1994年6月8日当选为首批中国科学院外籍院士。
post-13-1128955239.jpg
19050支持!
19050我非常欣赏他.
19050我非常欣赏他.很羡慕他
19051陈省身
华裔美国籍数学家,
1911年生于浙江嘉兴市。芝加哥大学与加洲大学伯克利分校任终身教授。美国国家科学院院士,
1975年荣获由美国总统颁发的美国国家科学奖章,
1983年荣获美国数学会颁发的终身成就奖。担任北京大学.南开大学.暨南大学以及其他许多大学的名誉教授。
1994年当选为中国科学院的首批外籍院士。20世纪世界级的几何学家。少年时代即显露数学才华,在其数学生涯中,五经抉择,努力攀登,终成辉煌。他在整体微分几何上的卓越贡献,影响了整个数学的发展,被杨振宁誉为继欧几里德、高斯、黎曼、嘉当之后又一里程碑式的人物。曾先后主持、创办了三大数学研究所,造就了一批世界知名的数学家。晚年情系故园,每年回天津南开大学数学研究所主持工作,培育新人,只为实现心中的一个梦想:使中国成为21世纪的数学大国。主要著作有:微分几何讲义。
post-13-1128955377.jpg
19051厉害的人物,不过可惜实在可惜........
19051偶像
19051主题写错了吧?准确一些应该是“华人数学家”,恐怕还要加上一个“已故”!
人生本来万事空,在世岂知身后事?
数学本为宇宙根,入门哪想从业艰?
19051呵呵,他永远活在我心中
19051华罗庚和陈景润
19051关于科学家的国籍问题,可参看张奠宙的文章
19052宋代著名的数学教育家--杨辉
(一)杨辉及其主要数学成就
杨辉,南宋时期杰出的数学家和数学教育家。13世纪中叶活动于苏杭一带,其著作甚多。他的著名数学书籍共五种二十一卷。著有《详解九章算法》十二卷(1261年)、《日用算法》二卷(1262年)、《乘除通变本末》三卷(1274年)、《田亩比类乘除算法》二卷(1275年)、《续古摘奇算法》二卷(1275年)。
杨辉的数学研究与教育工作的重点是在计算技术方面,他对筹算乘除捷算法进行总结和发展,有的还编成了歌决,如九归口决。他在《续古摘奇算法》中介绍了各种形式的"纵横图"及有关的构造方法,同时"垛积术"是杨辉继沈括"隙积术"后,关于高阶等差级数的研究。杨辉在"纂类"中,将《九章算术》246个题目按解题方法由浅入深的顺序,重新分为乘除、分率、合率、互换、二衰分、叠积、盈不足、方程、勾股等九类。
他非常重视数学教育的普及和发展,在《算法通变本末》中,杨辉为初学者制订的"习算纲目"是中国数学教育史上的重要文献。
(二)杨辉的数学思想和方法
1.分类的思想方法
杨辉继承了刘徽等人的分类思想,把分类方法提高到了一个新的阶段。杨辉在研究《九章算术》时认为,九章中章次之间,无谓重叠,且有些问题不归章次,他对《九章算术》中的方法和例题重新进行了分类,将解题方法提高到了一个非常突出的位置;他提出的“相乘六法”、“乘算加法五术”、“除算加法四术”等,都是通过对乘数或除数进行分类而获得的。
2.部分确定组合法的思想
杨辉介绍了两种推求四阶纵横图的方法。在介绍纵横图的构造规律时,就用的是:部分确定组合法。所谓部分确定组合法,实际上就是:为了构造出纵横图来,分几步来完成这一工作,第一步,先构造出一个大致的图来(粗图)、“粗图”在大的方面符合我们的要求,第二步,对“粗图”中那些“细致”的不符合要求的地方,进行调整,直至满足条件。部分确定组合法处理问题的方式,在现代代数中随处可见。
3.数学教育的思想
杨辉是我国古代杰出的数学教育家,他的教学思想和教学主张现在仍然闪耀着智慧的光芒。他的数学教育思想主要表现在以下几个方面:
(1)
杨辉在“习算纲目”里,强调基础的重要,主张循序渐进。
(2)
杨辉在“日用算法”里,主张数学教育应当贯彻“须责实有”的思想,即数
学要密切联系实际。
(3)
在教学中,杨辉主张应针对学习者不同时期的不同特点,实施教学,他认为
应先掌握其用法,然后再钻研算理。杨辉著作中有很多通俗易记的诗歌,就是这种思想的体现。
(4)
杨辉注重启发式教学,引导学生探求数学知识。他说:“好学君子自动触类
而考,何必尽传”。
(5)
在学习方法上,杨辉反对死记硬背,强调理解记忆。
贯穿古今的杰出数学家--朱世杰
(一)朱世杰及其主要数学成就
朱世杰字汉卿,号松庭,元朝人,籍贯燕山(今北京附近)。他长期从事数学研究和教育事业,以数学名家周游湖海二十多年,四方登门来学习的人很多。
朱世杰全面继承了秦九韶(约公元1202--1261年),主要著作《数书九章》)、李冶(公元1
192--1279年),主要著作《测圆海镜》和《益古演段》,杨辉,主要著作《详解九章算法》、《日用算法》、《乘除通变算宝》、《田亩比类乘除捷法》、《续古摘奇算法》三人的数学成就和各种实用算法,并且创造性地予以发展,写出《算学启蒙》、《四元玉鉴》等著名著作,把我国古代数学推向更高的境界,形成宋、元时期中国数学的最高峰。
《算学启蒙》是朱世杰在元成宗大德三年(公元1299年)刊印的,全书分三卷,二十门,总计二百五十九个问题和相应的解答。自乘除运算起,一直讲到当时数学发展的最高成就“天元术”,全面介绍了当时数学所包含的各方面内容。它的体系完整,内容深入浅出,通俗易懂,是一部很著名的启蒙读物。这部著作后来流传到了朝鲜、日本等国,出版过翻刻本和注释本,产生过一定的影响。
《四元玉鉴》更是一部成就辉煌的数学名著。它受到近代数学史研究者的高度评价,认为是中国数学著作中最重要的一部,同时也是中世纪最杰出的数学著作之一。《四元玉鉴》成书于大德七年(公元13033年),共三卷,二十四门,二百八十八问,介绍了朱世杰在多元高次方程组的解法——“四元术”、高阶等差级数的计算——“垛积术”以及“招差术”(有限差分)等方面的研究成果。
秦、李、杨、朱的数学著作内容广泛而艰深,象高次方程的数值解法、天元术、四元术、大衍求一术、垛积术和招差术等,都是具有世界意义的学术成就,分别比欧洲要早出现四百年到八百年,在当时世界上居于遥遥领先的地位。这一丰富多彩的辉煌时期在我国数学史上也是罕见的。
朱世杰的“四元术”是在高次方程的数值解法以及“天元术”的基础上发展起来的。当未知数不止一个的时候,除设未知数天元(χ)外,还需要增设地元(y)、人元(z)乃至物元(u),再列写出二元、三元甚至四元的高次联立方程组,然后求解。这就是朱世杰在他的著作中所介绍的“四元术”。
朱世杰不仅提出了多元(最多到四元)高次联立方程组的算筹摆置记述方法,而且把《九章算术》等书中四元一次联立方程解法推广到四元高次联立方程,在欧洲,解联立一次方程开始于十六世纪,关于多元高次联立方程的研究还是十八、十九世纪的事。
朱世杰还把三角垛公式引用到“招差术”上,指出招差公式中的各项系数恰好依次是各三角垛的积,这样就得到了包含有四次差的招差公式,并且可以推广为包含任意高次差的招差公式,这在世界数学史上是第一次,比欧洲牛顿的同样成就要早近四个世纪。
除了“四元消法”和“垛积招差”以外,朱世杰在他的著作中还提出了许多值得注意的内容:在中国数学史上,朱世杰第一次正式提出了正负数乘法的正确法则。他对球体表面积的计算问题作了探讨,这是我国古代数学典籍中唯一的一次讨论。虽然结论不很正确,但是他的创新精神是可贵的。在《算学启蒙》中,朱世杰记载了完整的“九归除法”口诀,和现在流传的珠算归除口诀几乎完全一致。
总之,朱世杰继承和发展了前人的数学成就,为推进我国古代数学的发展做出了不可磨灭的重要贡献。由于朱世杰和其他同时代数学家的共同努力,使宋、元时期的数学水平达到光辉的高度,在很多方面居于世界前列。朱世杰不愧是我国乃至世界数学史上负有盛名的数学家。
美国科学史家萨顿称朱世杰是“贯穿古今的一位最杰出的数学家”。
(二)朱世杰的数学思想和方法
纵观上下四百年的宋元数学时,我们不仅会发现朱世杰的数学成果代表这一时期的最高水平,而且还会发现他具有超凡的数学思想。具体表现在:
1.重视算理的思想
在《四元玉鉴》中,朱世杰简要给出了天元术、二元术、三元术、四元术的解题模式,在《算学启蒙》中,给出了一整套数学概念及运算法则,明确给出了筹算识位制度、乘除歌诀、开方法则、正负数加减法则等,提出的正负数乘法法则,在中国数学史上还是第一次。
2.纯粹性与应用性相结合的思想
从《四元玉鉴》中可以看出,朱世杰突破了实际应用的局限,他的方程理论具有更加纯粹的数学性质;从另一个角度看,朱世杰也十分重视方程理论的应用,他用天元术解决了平面几何与立体几何中的大量问题,并在解决几何问题时导出了许多高次方程。值得注意的是,朱世杰在用天元术解决几何问题时,不再局限于图形的边长、周长、面积、体积等几何量,而是深入到图形内部,这是朱世杰数学思想的独到之处。他研究直角三角形和圆内各元素间的关系,发现了两个重要定理---射影定理和弓玄幂定理。
3.转化的思想
朱世杰在数学上取得的丰硕成果,重要原因之一是他自觉地运用了转化的思想。
(1)在解分数系数方程时,传统的方法是用各项乘以分母的最小公倍数,达到去分母的目的,朱世杰在《算学启蒙》中,采用设辅助未知数的方法,把分数系数转化为整数系数,用于解线性方程组;在《四元玉鉴》中,把设辅助未知数的方法用于解高次方程。这种方法在数学史上是很有意义的,系数越复杂,设辅助未知数的方法越有用。
(2)朱世杰在天元术、二元术、三元术、四元术中通过转化的思想,把无理方程转化为有理方程来解。
(3)朱世杰为了求解多元高次方程组,创造了一套完整的消未知数方法,称为四元消法。这种消法充分体现了朱世杰的转化思想,他通过方程组中不同方程的配合,依次消去未知数,化四元为三元、二元,最后化为一元高次方程,从而把新问题转化为旧问题,求得正确解答。
(4)在《四元玉鉴》中,朱世杰不仅用天元术解决了大量的平面几何问题,而且开始用
天元术解决立体几何问题,解题的关键就是把立体几何问题转化为平面几何问题,在一个截面上进行讨论。
4.抽象化的思想
抽象程度的提高,在朱世杰的数学研究中表现的非常突出。从天元术与四元术的比较中可以清楚地看到这一点,在天元术中由于未知数只有一个,未知数与常数的区别是十分明显的,而在四元术中有多个未知数,在特定的推演过程中,他往往把其中的一个当未知数,其他变量则看作常数,这说明各变量具有更加抽象的代数意义;推导方程离不开等值代数式,在天元术中等值代数式一般是指等于同一个几何量的两个代数式,标志着方程抽象程度的进一步提高。
5.一般化的思想
朱世杰的垛积术和招差术突出地表现了数学一般化程度的提高。朱世杰对垛积术进行了一般性研究,得出统一的三角垛公式,还发现招差公式和垛积公式的内在联系,从而掌握了任意次的招差法。在算法研究上,朱世杰不是把着眼点放在运算技巧上,而是放在运算公式和法则的概括上,从而提高了数学的一般化程度。
19053[SIZE=7][COLOR=red]数学界的无冕之王--希尔伯特[SIZE=7][COLOR=red]
(一)希尔伯特及其主要数学成就
希尔伯特(D.Hilbert,David,
1862~
1943)德国数学家,生于东普鲁士哥尼斯堡(前苏联加里宁格勒)附近的韦劳。中学时代,希尔伯特就是一名勤奋好学的学生,对于科学特别是数学表现出浓厚的兴趣,善于灵活深刻地掌握和应用老师讲课的内容。
1880年,他不顾父亲让他学法律的意愿,进入哥尼斯堡大学攻读数学。
1884年获得博士学位,留校任教,
1895年,转入哥廷根大学任教授,此后一直在哥廷根生活和工作。在此期间,他成为柏林科学院通讯院士,并曾获得施泰讷奖、罗巴切夫斯基奖和波约伊奖。
1930年获得瑞典科学院的米塔格-莱福勒奖,
1942年成为柏林科学院荣誉院士。希尔伯特是一位正直的科学家,第一次世界大战前夕,他拒绝在德国政府为进行欺骗宣传而发表的《告文明世界书》上签字。战争期间,他敢于公开发表文章悼念“敌人的数学家”达布。希特勒上台后,他抵制并上书反对纳粹政府排斥和迫害犹太科学家的政策。由于纳粹政府的反动政策日益加剧,许多科学家被迫移居外国,曾经盛极一时的哥廷根学派衰落了,希尔伯特也于
1943年在孤独中逝世。
希尔伯特是对二十世纪数学有深刻影响的数学家之一。他领导了著名的哥廷根学派,使格廷根大学成为当时世界数学研究的中心,并培养了一批对现代数学发展做出重大贡献的杰出数学家。希尔伯特的数学工作可以划分为几个不同的时期,每个时期他几乎都集中精力研究一类问题。按时间顺序,他的主要研究内容有:不变式理论、代数数域理论、几何基础、积分方程、物理学、一般数学基础,其间穿插的研究课题有:狄利克雷原理和变分法、华林问题、特征值问题、“希尔伯特空间”等。在这些领域中,他都做出了重大的或开创性的贡献。希尔伯特认为,科学在每个时代都有它自己的问题,而这些问题的解决对于科学发展具有深远意义。他指出:“只要一门科学分支能提出大量的问题,它就充满着生命力,而问题缺乏则预示着独立发展的衰亡和终止”。在
1900年巴黎国际数学家代表大会上,希尔伯特发表了题为《数学问题》的著名讲演。他根据过去特别是十九世纪数学研究的成果和发展趋势,提出了23个最重要的数学问题。这23个问题通称希尔伯特问题,后来成为许多数学家力图攻克的难关,对现代数学的研究和发展产生了深刻的影响,并起了积极的推动作用,希尔伯特问题中有些现已得到圆满解决,有些至今仍未解决。他在讲演中所阐发的想信每个数学问题都可以解决的信念,对于数学工作者是一种巨大的鼓舞。他说:“在我们中间,常常听到这样的呼声:这里有一个数学问题,去找出它的答案!你能通过纯思维找到它,因为在数学中没有不可知”。三十年后,
1930年,在接受哥尼斯堡荣誉市民称号的讲演中,针对一些人信奉的不可知论观点,他再次满怀信心地宣称:“我们必须知道,我们必将知道”。希尔伯特的《几何基础》(
1899年)是公理化思想的代表作,书中把欧几里得几何学加以整理,成为建立在一组简单公理基础上的纯粹演绎系统,并开始探讨公理之间的相互关系与研究整个演绎系统的逻辑结构。
1904年,又着手研究数学基础问题,经过多年酝酿,于二十年代初,提出了如何论证数论、集合论或数学分析一致性的方案。他建议从若干形式公理出发将数学形式化为符号语言系统,并从不假定实无穷的有穷观点出发,建立相应的逻辑系统。然后再研究这个形式语言系统的逻辑性质,从而创立了元数学和证明论。希尔伯特的目的是试图对某一形式语言系统的无矛盾性给出绝对的证明,以便克服悖论所引起的危机,一劳永逸地消除对数学基础以及数学推理方法可靠性的怀疑。然而,
1930年,年青的奥地利数理逻辑学家哥德尔(K.Godel,
1906~
1978)获得了否定的结果,证明了希尔伯特方案是不可能实现的。但正如哥德尔所说,希尔伯特有关数学基础的方案“仍不失其重要性,并继续引起人们的高度兴趣”。希尔伯特的著作有《希尔伯特全集》(三卷),其中包括他的著名的《数论报告》)、《几何基础》、《线性积分方程一般理论基础》等,与其他合著有《数学物理方法》、《理论逻辑基础》、《直观几何学》、《数学基础》。
(二)希尔伯特的数学思想与方法
(三)阅读材料:希尔伯特的二十三个数学问题及其解决情况
(1)
康托的连续统基数问题。
1874年,康托猜测在可数集基数和实数集基数之间没有别的基数,即著名的连续统假设。
1938年,侨居美国的奥地利数理逻辑学家哥德尔证明连续统假设与ZF集合论公理系统的无矛盾性。
1963年,美国数学家科思(P.Choen)证明连续统假设与ZF公理彼此独立。因而,连续统假设不能用ZF公理加以证明。在这个意义下,问题已获解决。
(2)
算术公理系统的无矛盾性。
欧氏几何的无矛盾性可以归结为算术公理的无矛盾性。希尔伯特曾提出用形式主义的证明论方法加以证明,哥德尔
1931年发表不完备性定理作出否定。根茨(G.Gentaen,
1909-
1945)
1936年使用超限归纳法证明了算术公理系统的无矛盾性。
(3)
只根据合同公理证明等底等高的两个四面体有相等之体积是不可能的。
问题的意思是:存在两个登高等底的四面体,它们不可能分解为有限个小四面体,使这两组四面体彼此全等德思(M.Dehn),
1900年已解决。
(4)
两点间以直线为距离最短线问题。
此问题提的一般。满足此性质的几何很多,因而需要加以某些限制条件。
1973年,苏联数学家波格列洛夫(Pogleov)宣布,在对称距离情况下,问题获解决。
(5)
拓扑学成为李群的条件(拓扑群)。
这一个问题简称连续群的解析性,即是否每一个局部欧氏群都一定是李群。
1952年,由格里森(Gleason)、蒙哥马利(Montgomery)、齐宾(Zippin)共同解决。
1953年,日本的山迈英彦已得到完全肯定的结果。
(6)
对数学起重要作用的物理学的公理化。
1933年,苏联数学家柯尔莫哥洛夫将概率论公理化。后来,在量子力学、量子场论方面取得成功。但对物理学各个分支能否全盘公理化,很多人有怀疑。
(7)
某些数的超越性的证明。
需证:如果α是代数数,β是无理数的代数数,那么αβ一定是超越数或至少是无理数(例如,
、e、π)。苏联的盖尔封特(Gelfond)于
1929年、德国的施奈德(Schneider)及西格尔(Siegel)于
1935年分别独立地证明了其正确性。但超越数理论还远未完成。目前,确定所给的数是否超越数,尚无统一的方法。
(8)
素数分布问题,尤其对黎曼猜想、哥德巴赫猜想和孪生素数问题。
素数是一个很古老的研究领域。希尔伯特在此提到黎曼(Riemann)猜想、哥德巴赫(Goldbach)猜想以及孪生素数问题。黎曼猜想至今未解决。哥德巴赫猜想和孪生素数问题目前也未最终解决,其最佳结果均属中国数学家陈景润。
(9)
一般互反律在任意数域中的证明。
1921年由日本的高木贞治,
1927年由德国的阿廷(E.Artin)各自给以基本解决。而类域理论至今还在发展之中。
(10)
能否通过有限步骤来判定不定方程是否存在有理整数解?
求出一个整数系数方程的整数根,称为丢番图(约210-290,古希腊数学家)方程可解。
1950年前后,美国数学家戴维斯(Davis)、普特南(Putnan)、罗宾逊(Robinson)等取得关键性突破。
1970年,巴克尔(Baker)、费罗斯(Philos)对含两个未知数的方程取得肯定结论。
1970年。苏联数学家马蒂塞维奇最终证明:在一般情况答案是否定的。尽管得出了否定的结果,却产生了一系列很有价值的副产品,其中不少和计算机科学有密切联系。
(11)
一般代数数域内的二次型论。
德国数学家哈塞(Hasse)和西格尔(Siegel)在20年代获重要结果。60年代,法国数学家外尔(A.Weil)取得了新进展。
(12)
类域的构成问题。
即将阿贝尔域上的克罗内克定理推广到任意的代数有理域上去。此问题仅有一些零星结果,离彻底解决还很远。
(13)
一般七次代数方程以二变量连续函数之组合求解的不可能性。
七次方程
的根依赖于3个参数a、b、c;x=x(a,b,c)。这一函数能否用两变量函数表示出来?此问题已接近解决。
1957年,苏联数学家阿诺尔德(Arnold)证明了任一在[0,1]上连续的实函数
可写成形式∑hi(ξi(x1,x2),x3)(i=1--9),这里hi和ξi为连续实函数。柯尔莫哥洛夫证明f(x1,x2,x3)可写成形式∑hi(ξi1(x1)+ξi2(x2)+ξi3(x3))(i=1--7)这里hi和ξi为连续实函数,ξij的选取可与f完全无关。
1964年,维土斯金(Vituskin)推广到连续可微情形,对解析函数情形则未解决。
(14)
某些完备函数系的有限的证明。
即域K上的以x1,x2,…,xn为自变量的多项式fi(i=1,…,m),R为K[X1,…,Xm]上的有理函数F(X1,…,Xm)构成的环,并且F(f1,…,fm)∈K[x1,…,xm]试问R是否可由有限个元素F1,…,FN的多项式生成?这个与代数不变量问题有关的问题,日本数学家永田雅宜于
1959年用漂亮的反例给出了否定的解决。
(15)
建立代数几何学的基础。
荷兰数学家范德瓦尔登
1938年至
1940年,外尔
1950年已解决。
(15)注一舒伯特(Schubert)计数演算的严格基础。
一个典型的问题是:在三维空间中有四条直线,问有几条直线能和这四条直线都相交?舒伯特给出了一个直观的解法。希尔伯特要求将问题一般化,并给以严格基础。现在已有了一些可计算的方法,它和代数几何学有密切的关系。但严格的基础至今仍未建立。
(16)
代数曲线和曲面的拓扑研究。
此问题前半部涉及代数曲线含有闭的分枝曲线的最大数目。后半部要求讨论备dx/dy=Y/X的极限环的最多个数N(n)和相对位置,其中X、Y是x、y的n次多项式。对n=2(即二次系统)的情况,
1934年福罗献尔得到N(2)≥1;
1952年鲍廷得到N(2)≥3;
1955年苏联的波德洛夫斯基宣布N(2)≤3,这个曾震动一时的结果,由于其中的若干引理被否定而成疑问。关于相对位置,中国数学家董金柱、叶彦谦
1957年证明了(E2)不超过两串。
1957年,中国数学家秦元勋和蒲富金具体给出了n=2的方程具有至少3个成串极限环的实例。
1978年,中国的史松龄在秦元勋、华罗庚的指导下,与王明淑分别举出至少有4个极限环的具体例子。
1983年,秦元勋进一步证明了二次系统最多有4个极限环,并且是(1,3)结构,从而最终地解决了二次微分方程的解的结构问题,并为研究希尔伯特第(16)问题提供了新的途径。
(
17)
半正定形式的平方和表示。
实系数有理函数f(x1,…,xn)对任意数组(x1,…,xn)都恒大于或等于0,确定f是否都能写成有理函数的平方和?
1927年阿廷已肯定地解决。
(
18)
用全等多面体构造空间。
德国数学家比贝尔巴赫(Bieberbach)
1910年,莱因哈特(Reinhart)
1928年作出部分解决。
(
19)
正则变分问题的解是否总是解析函数?
德国数学家伯恩斯坦(Bernrtein,
1929年)和苏联数学家彼德罗夫斯基(
1939年)已解决。
(20)
研究一般边值问题。
此问题进展迅速,己成为一个很大的数学分支。日前还在继续发展。
(21)
具有给定奇点和单值群的Fuchs类的线性微分方程解的存在性证明。
此问题属线性常微分方程的大范围理论。希尔伯特本人于
1905年、勒尔(H.Rohrl)于
1957年分别得出重要结果。
1970年法国数学家德利涅(Deligne)作出了出色贡献。
(22)
用自守函数将解析函数单值化。
此问题涉及艰深的黎曼曲面理论,
1907年克伯(P.Koebe)对一个变量情形已解决而使问题的研究获重要突破。其它方面尚未解决。
(23)
发展变分学方法的研究。
这不是一个明确的数学问题。20世纪变分法有了很大发展。可见,希尔伯特提出的问题是相当艰深的。正因为艰深,才吸引有志之士去作巨大的努力
19053支持,我也喜欢希尔伯特
19053太伟大了
19053希尔伯特的工作很深刻,范围也很广,是一代数学大家。就深刻性而言,历史上可以排进前5。但他的工作在创造性上略显逊色,比不上其同时代人彭加莱。
19053百年难得一见的神人,但愿下一个这样的伟人回出现在华夏大地上!
19054二十世纪最伟大的数理逻辑学家--哥德尔
(一)哥德尔及其主要数学成就
哥德尔(Godel,
1906~
1978)生于现捷克,卒于普林斯顿。廿世纪最伟大之数理逻辑学家,其不完备定理是廿世纪最具启发性的思想发现之一。
Godel自小便很好奇,青少年时即对数学、哲学、语言与历史产生极大的研究热诚。他在维也纳大学原主修理论物理,后转回数学,并参与
Schlick(石里克)领导的「维也纳学圈」,对数学与科学作本质的哲学探索,
1928年因听了 Brouwer 的演讲,乃致力于数理逻辑的研究。
自
19世纪中,由于非欧几何的确立、分析严格化的要求与罗素悖论的出现,数学基础的问题吸引许多一流数学家的眼光,当时数学∕哲学家热切地想将数学确定性的大厦奠基于某种不可怀疑的基础上,虽然多数人都很乐观,但是从
Hilbert 与 Ackermann
在
1928年提出下列的未解问题:「一阶逻辑是否完备(complete)或可决定(decidable)?」,显示整个基础化计画的进度十分缓慢。
1929年
Godel 初试啼声,漂亮地在他的博士论文中证明一阶逻辑的完备性,给 Hilbert 的计画打下一剂强心针,但是不久后(
1931),Godel
却证明了他最知名的「不完备定理」:
设S为一包含算术系统的公理系统,若 S 兼容(consistent,即不自我矛盾),则 S 不完备(即在
S 中有些叙述为真,却无法由 S 的公理推导出来)。
使数学界(尤其是 Hilbert 学派)戏剧性地经历烈火寒冰般的巨变。Godel
也因此声名如日中天。
1933年他应邀访美讲学演说,此行他结识日后的挚友爱因斯坦。30年代的欧洲弥漫着法西斯的气氛,Godel 亦师亦友的
Schlick
也因此被刺杀,这个噩耗使他陷入精神沮丧,终其一生困扰着他的研究生活。大战前夕,他完成另一个重要的工作─证明选择公理与连续统假设皆与ZF集合论兼容。
1940年他经由俄罗斯、日本到达美国,从此定居于普林斯顿。
Godel 在美国的研究重心,逐渐转移到其它方面。由于与爱因斯坦时相往来,40年代末,Godel
致力于探讨广义相对论与时间的意义,证明循环时间与爱因斯坦方程并无矛盾(他还因此在
1950年的国际数学家会议提出报告)。另外,Godel
一直从事于哲学的深度思考,专心研读 Leibniz、康德、Husserl(胡赛尔)等的著作,留下的哲学思考笔记无数,还没有充分地编注印行。Godel
晚年(
1971年起)时常与华裔逻辑∕哲学家王浩讨论,并因而促成王浩撰写《Reflection on Kurt Godel》的佳话。Godel
个人包办了数理逻辑几个经典定理,并为整个领域带来革命性的风貌,堪称是廿世纪最伟大的数理逻辑学家。尤其是他的「不完备定理」,由于暗示了一个理性系统不可能是全知的想法,经常被引申(或过度引申)到其它领域。例如:自然是无法被人类了解;语言是没有界限的;心灵无法认识自己等。非科学家最常引用的数学定理,竟然如此晦涩,也该算是廿世纪的数学奇谈了。
(二)阅读材料:感悟《哥德尔》
有一个人曾在不到两年的时间内让数学界感受了大喜与大悲的经历,他就是哥德尔(Kurt
Gödel,
1906.4.28-
1978.1.14)。
1929年秋,哥德尔在他的博士论文中证明了一阶逻辑的完全性,这对于当时试图以“公理化”方法构建数学基础的形式主义学派是一个莫大的鼓舞。希尔伯特,形式主义学派的领军人物,确信他的元数学和证明论将会成功地确立全部数学的相容性和完全性。哥德尔的逻辑完全性定理似乎表明曙光就在前头。
1930年夏天,柯尼斯堡,康德的诞生地,也是希尔伯特的故乡,在接受“荣誉市民”受礼仪式的演说中,希尔伯特坚定地说出最后一句话:“我们必须知道,我们必将知道(Wir
müssen wissen. Wir werden
wissen)”。
但就在第二年,哥德尔发表的另一篇论文却打开了“潘多拉的盒子”。这篇题为《论〈数学原理〉及有关系统的形式不可判定命题》(
1931年)的论文包含了两个惊世骇俗的结论,其中对数学界尤具毁灭性的断言是:任何数学系统,只要其能包含整数的算术,其相容性就不可能通过几个基础学派(逻辑主义学派、形式主义学派、集合论公理化学派)采用的逻辑原理建立。希尔伯特的幻想破灭了,数学的“灾难”降临了!有人悲叹地说:“上帝是存在的,因为数学无疑是相容的;魔鬼也是存在的,因为我们不能证明这种相容性。”(外尔)
哥德尔的影响是深远的,最新的一个例子足以说明。2002年夏天北京国际数学家大会,霍金的报告就是《哥德尔与M理论》。在当今国际物理研究领域,很多科学家提出有可能存在一个能描述一切物理现象的理论,并把这一理论称为超弦理论。霍金认为,建立一个单一的描述宇宙的大统一理论是不太可能的。霍金说他的这一推测正是基于数学领域的哥德尔不完全性定理。
可是,哥德尔却一直是一位被神秘所笼罩的传奇人物。他的生活特异独行,超然遁世,他的思想沉奥深邃,意蕴广远。我们中的很多人也许是读了侯世达(Hofstadter,D.R.)的《哥德尔、艾舍尔、巴赫—集异璧之大成》(《GEB—一条永恒的金带》是该书节译本)了解哥德尔的。其实,这部奇书在哥德尔的头上增添了更神秘的光环。感谢王浩先生,他的《哥德尔》(Reflections
on Kurt Gödel
,
1987,
1991,康宏魁译,上海世纪集团出版社,上海译文出版社,2002年9月第1版)一书使我们终于可以走近哥德尔,去感受那平凡躯体下伟大而真诚的心灵。
哥德尔的与众不同表现在他的思想、他的关注、他的生活格调、他内心深处的精神世界。王浩先生正是从献身基本理论的角度展开哥德尔的生平的。值得注意的是王浩先生首先将焦点聚集在与哥德尔生平和事业密切相关的三样重要的史料(哥德尔哥哥答复王浩的回信、格兰琼专为哥德尔设计的生平调查表、哥德尔获得洛克菲勒大学荣誉学位时王浩的引荐辞)。正是在许多珍贵史料基础上,王浩为我们仔细勾画了哥德尔毕生事业的全貌。似乎是历史的巧合,当哥德尔几经周折从维也纳抵达普林斯顿后,与爱因斯坦成了结交10年以上的好友。王浩先生巧妙地“假道爱因斯坦”,以对比的手法,描述了两位智者的友谊以及他们在物理、逻辑、哲学、政治、艺术甚至宗教上思想与见解。这样就为读者通达哥德尔的精神思想打开了一条便道。
哥德尔的科学工作令人赞叹,这也是王浩先生着力描写的重点。可是,照哥德尔自己说,他一生用于哲学的时间和精力比用于科学的还要多。在哲学中,哥德尔所推崇的5种好品格“善取舍、求准确、弃偏见、慎试验、有胆魄”
确实令人动心。哥德尔的博大视野与敏锐眼光还在他对科学、技术与社会的评述中显示出来。书中披露哥德尔在
1962年就指出“人类并不会因为登上月球就有所改进。这必定跟‘自然’科学与‘精神’科学之间的老冲突有关。如果史学、法权与国家学说、哲学、心理学、文学、艺术等等的进展像物理学那么大,原子战争的危险就不会有了。”读书至此怎能不掩卷感慨!诚可谓“哥德尔的事迹发人深省,其意境超乎学院天地,实在得有一种能顾盼几个世纪的历史眼光才行”。
作者王浩先生是著名的数理逻辑学家,早年在西南联大时就自学过哥德尔的初等逻辑完全性证明。后来与晚年的哥德尔频繁往来,广泛交谈,亲笔录下为数可观的口头资料。在他的笔下一个栩栩欲活、个性丰满的哥德尔跃然于纸上。在书中我们看到哥德尔生活的简朴、对荣华富贵的淡漠、做学问的坚韧刻苦、寻求根本原理的矢志不移和锲而不舍。
哥德尔处在另一时代,另一环境,他的专深研究也难免让常人觉得高不可攀。那么《哥德尔》对当代青年的意义何在呢?王浩先生“中译本序”的一段话是很有意义的:我想,译者的苦心是盼望一些有识有志的青年人拿他当一面镜子,学会净化自我,学会在荆棘丛中踏出自己该走的路,不论其所爱好的是艺术还是科学、是文科还是理科。哥德尔成功的事实还提醒我们,一个人天赋再高,想获得一点真重要真耐久的成绩,必须对外界诱惑保持清醒的头脑,永不懈怠地埋头苦干,靠众人的喝彩、神秘的灵感或不诚实的手段根本做不到。王浩先生
1995年5月病逝于纽约。当我们阅读《哥德尔》的事迹,回味王浩先生的忠告,必然会有一种超然的感悟。
19056大家能否告知[运筹学与控制论]是学什么的?
以后毕业之后有什么用?工作好找吗?
19056今天开始就报考了,希望大家能尽快回复。
不知的帮忙顶一下。
谢谢各位学长们!!!!!!!!!!!
19057最近买了本smooth的书在看,Jeffrey S. Simonoff的smoothing methods in
statistics
里面讲Histogram的性质的时候有一段:
suppose
f ^
(x) is the
histogram estimate of the density with in a given bin, that
is:
f ^
(x)=n
j/nh,x∈(b
j,b
j
+1]
然后后面跟着计算这个估计的MSE,先算Bias
E f
[f
^(x)]-f(x)=1
2 f
`
(x)(h-2(x-b
j))+O(h
2),x∈(b
j,b
j
+1]
它这一步怎么推出来的? 看起来有点像Taylor展开,但是好象也不对
19058赞!
19058控制论的创始人--维纳
(一)
维纳及其主要数学成就
维纳,美国数学家。
1894年11月26日生于密苏里州的哥伦比亚,
1964年3月
18日卒于斯德哥尔摩。维纳的父亲列奥•维纳是语言学家,又有很高的数学天赋。他出生于俄国,智力早熟,13岁就会好几种语言;他朝气蓬勃,富于冒险精神,
18岁那年单独一个漂洋过海,移居美国;他刻苦自学,凭掌握40多种语言的才能,成为哈佛大学斯拉夫语教授。这位才气横溢、不畏艰难而又性情急躁的人决心要使儿子在学术上超人一等。维纳认为他父亲是天生的学者,集德国人的思想、犹太人的智慧和美国人的精神于一身。从童年到青年,维纳一直在他的熏陶下生活,并逐步成长为一个学者。
1.昔日神童:维纳是一个名符其实的神童。维纳的父亲列奥很早就发现了儿子的天赋,并坚信借助于环境进行教育的重要性,他从一开始学习就实施的教育计划,用一种多少无情的方式驱使他不寻常的儿子。维纳三岁半开始读书,生物学和天文学的初级科学读物就成了他在科学方面的启蒙书籍。从此,他兴致勃勃,爱不释卷的埋首于五花八门的科学读本。七岁时,开始深入物理学和生物学的领域,甚至超出了他父亲的知识范围。从达尔文的进化论、金斯利的《自然史》到夏尔科、雅内的精神病学著作,从儒勒·凡尔纳的科学幻想小说到
18、
19世纪的文学名著等等,几乎无所不读。维纳怀有强烈的好奇心,而他父亲却以系统教育为座右铭,两者正好相得益彰。维纳自己学习科学,而他父亲则用严厉的态度坚持以数学和语言学为核心的教学计划。维纳极好地经受了这种严格的训练,他的数学长进显著。六岁那年,维纳有一次被A乘B等于B乘A之类的运算法则迷住了。为了设法弄清楚,他画了一个矩形,然后移转90°,长变宽、宽变长,面积并没变。维纳的拉丁语、希腊语、德语和英语也变成一种印在记忆中的书库,不论何时何处,都可以拿出来就用。在其他小男孩想当警察和火车司机的时候,维纳就渴望当一名博物学家,立志献身于科学了。父母几次设法送他到学校去受教育,但不寻常的智力和训练使维纳在学校里很难被安排。他的阅读远远地走在书写的前面,他刻苦地学习并掌握了初等数学,但仍需要扳着手指做算术。直到9岁时,才作为一名特殊的学生,进了艾尔中学,不满12岁就毕业了。
列奥很明智,决定送维纳进塔夫茨学院数学系就读,而不让他冒参加哈佛大学紧张的入学考试的风险,并避免由于把一个神童送进哈佛,而过分惹起人们的注意。在数学方面,维纳已超过大学一年级学生的水平,没有什么课程能确切地适合他的要求。于是他一开始就直接攻读伽罗瓦的方程论。列奥仍常和儿子讨论高等数学问题。就数学和语言学来说,维纳跨学科学习的惯例没有变。在这两方面,列奥依然是他的严师。维纳兴趣广泛,大学第一年,物理和化学给他的印象远比数学深。他对实验尤其兴致勃勃,与邻友—道做过许多电机工程的实验。他曾试图动手证实两个物理学方面的想法。一是供无线电通讯用的电磁粉末检波器,另一个设想是试制一种静电变压器。维纳的这两个想法都很出色。第二年,维纳又为哲学和心理学所吸引。他读过的哲学著作大大超出了该课程的要求。斯宾诺莎和菜布尼茨是对他影响最大的两位哲学家,前者崇高的伦理道德和后者的多才多艺,都使维纳倾倒。他还贪婪地阅读了詹姆士的哲学巨著,并通过父亲的关系,认识了这位实用主义大师。在同一年,维纳又把兴趣集中到生物学方面。生物学博物馆和实验室成了最吸引他的地方,动物饲养室的管理员成了他特别亲密的朋友。维纳不仅乐于采集生物标本,而且经常把大部分时间用在实验室的图书馆,在那里阅读著名的生物学家贝特森等人的著作。维纳用三年时间读完了大学课程,于
1909年春毕业。之后便开始攻读哈佛大学研究院生物学博士学位。维纳改学生物,并不是因为他知道自己能够干这一行,而是因为他想干这一行。从童年开始,他就渴望成为一名生物学家。但是,维纳的实验工作不幸失败了。他动手能力差,缺乏从事细致工作所必需的技巧和耐心,深度近视更增添了麻烦。在父亲的安排下,他转到康奈尔大学去学哲学,第二年又回到哈佛,研读数理逻辑,于
18岁获哈佛大学哲学博士学位。维纳在大学接受的跨学科教育,促使他的才能横向发展,为将来在众多领域之间,在各种交界面上进行大量的开发和移植,奠定了基础。从数学到生物学再到哲学,实际上就是维纳整个科学生涯所经历的道路。在哈佛的最后一年,维纳向学校申请了旅行奖学金并获得了批准。他先后留学于英国剑桥大学和德国哥丁根大学,在罗素、哈代、希尔伯特等著名数学家指导下研究逻辑和数学。罗素是维纳的主要良师益友,维纳跟他学习数理逻辑和科学与数学哲学,从这位大师身上得到许多深挚的教益。他的哲学课程和数学原理课,维纳感到很新鲜,富有启发性。罗素的讲授清晰晓畅,犹如无与伦比的杰作,给了他深刻的印象。罗素建议维纳阅读爱因斯坦
1905年发表的三篇论文,学习卢瑟福的电子理论和波尔的学说。罗素对物理学中的重要发现有着敏锐的嗅觉,他的教导使维纳牢牢记住,不仅数学是重要的。而且还需要有物理概念。尽管维纳当时的物理学基础对于学习最新的电子理论有困难,但罗素还是鼓励他去钻研。维纳以后选择了把数学和物理、工程学结合起来的研究方向,与罗素的启迪是分不开的。爱因斯坦的论文中有一篇是论述布朗运动的,正是在这个课题上,维纳在随后的10年内做出了重要的数学成果。
对于维纳未来的数学家生涯,罗素的另一个重要影响是,他向维纳提出,一个专攻数理逻辑和数学哲学的人最好能懂一些数学。因此,维纳选读了许多数学课程,接受了哈代等人的指导。哈代清晰、有趣和发人深思的讲演,涉及了包括勒贝格积分在内的实变函数基础和复变函数引论,给了维纳深刻的启示,并直接导致他早期生涯中的主要成就。维纳称哈代是他理想的导师和榜样。维纳原计划在剑桥读完这一年,但第二学期罗素要去哈佛讲学,他劝告维纳去哥丁根大学,攻读希尔伯特和兰道等人的课程。维纳上了兰道教授的一门群论课,并在希尔伯特的指导下研究了微分方程。希尔伯特代表着本世纪初期数学的伟大传统,是维纳所遇到的唯一真正样样精通的天才数学家。他视野广阔,善于把非凡的抽象能力和对物理现实的实事求是的认识很好地结合起来。他成了维纳所向往的数学家。在哥丁根所受的教育使维纳终生受益。从数学名师身上,他认识到科学力量和知识深度,第一次取得了集中和热情地干工作的经验,剑桥和哥丁根标志着维纳开始由一个神童而成长为青年数学家。
2.现代大师:
1913年,
19岁的维纳在《剑桥哲学学会会刊》上发表了一篇关于集合论的论文。这是一篇将关系的理论简化为类的理论的论文,在数理逻辑的发展中占据有一席之地。维纳从此步入学术生涯。同年,他以一篇有些怀疑论味道的哲学论文《至善》,获得哈佛大学授予的鲍多因奖。在转向函数分析领域之前,维纳在逻辑和哲学方面共发表了15篇论文。
19
18年,通过研读一位病逝的数学博士格林遗留的数学著作,维纳对现代数学有了进一步理解。他开始在数学领域寻找值得专心致力的问题。维纳虽是神童,但是作为一个数学家,他却姗姗来迟。维纳开始为函数分析所吸引,决心把自己的一生贡献给它。
19
19年,辛辛那提大学的年轻数学家巴纳特对他作了一次拜访。维纳请他推荐一个合适的研究课题。他叫维纳注意函数空间中的积分问题。这一建议对维纳以后的数学研究产生了重大影响。同年夏天,由于哈佛大学数学系主任奥斯古德的推荐,维纳到麻省理工学院数学系任教,并一直在该学院工作到退休。
1920年,维纳首次参加国际数学家会议。大会前,应弗雷歇邀请,他俩共同工作了一段时间。维纳试图推广弗雷歇的工作,提出了巴拿赫一维纳空间理论。他意识到自己关于布朗运动所做的工作是一个很有希望的开端,因而精神更加振奋,胸襟更加开阔了。
1924年维纳升任助理教授,
1929年为副教授。由于在广义调和分析和关于陶伯定理方面的杰出成就,
1932年晋升为正教授。
1933年,维纳由于有关陶伯定理的工作与莫尔斯分享了美国数学会五年一次的博赫尔奖。差不多同时,他当选为美国科学院院士。在他了解了这个高级科学官员组织的性质之后,感到十分厌烦,不久便辞去了自己的位置。通常给予取得成功的美国数学家的荣誉之一,就是要求他为美国数学会《讨论会丛书》写一本书。
1934年夏,维纳应邀撰写了《复域上的傅立叶变换》。不久,他当选为美国数学会副会长。只是因为他不喜欢担任行政职务,才免于被选作会长。30年代开始,维纳关注布什研究的模拟计算机。
1935~
1936年,他应邀到中国作访问教授。在清华大学与李郁荣合作,研究并设计出很好的电子滤波器,获得了该项发明的专利权。维纳把他在中国的这一年作为自己学术生涯中的一个特定的里程碑,即作为科学的一个刚满师的工匠和在某种程度上成为这一行的一个独当一面的师傅的分界点。在第二次世界大战期间,维纳接受了一项与火力控制有关的研究工作。这问题促使他深入探索了用机器来模拟人脑的计算功能,建立预测理论并应用于防空火力控制系统的预测装置。
1948年,维纳发表《控制论》,宣告了这门新兴学科的诞生。这是他长期艰苦努力并与生理学家罗森勃吕特等人多方面合作的伟大科学成果。维纳立即从声誉有限的数学家一跃成为一个国际知名人士,此时他早已年过半百。此后,维纳继续为控制论的发展和运用作出了杰出的贡献。
1959年,维纳从麻省理工学院退休。
1964年1月,他由于“在纯粹数学和应用数学方面并且勇于深入到工程和生物科学中去的多种令人惊异的贡献及在这些领域中具有深远意义的开创性工作”荣获美国总统授予的国家科学勋章。维纳是伽金汉基金会旅欧研究员,富布赖特研究员,英、德、法等国的数学会会员,但任过中国、印度、荷兰等国的访问教授。维纳在其50年的科学生涯中,先后涉足哲学、数学、物理学和工程学,最后转向生物学,在各个领域中都取得了丰硕成果,称得上是恩格斯颂扬过的、本世纪多才多艺和学识渊博的科学巨人。他一生发表论文240多篇,著作14本。他的主要著作有《控制论》(
1948)、《维纳选集》(
1964)和《维纳数学论文集》(
1980)。维纳还有两本自传《昔日神童》和《我是一个数学家》。他的主要成果有如下八个方面:
(1)建立维纳测度:维纳是第一个从数学上深刻地研究布朗运动的数学家。
1921年,他用函数空间的点来表示作布朗运动的粒子的路径,并证明,所有这些路径除了概率为O的集合外,都是连续但又不光滑即几乎处处不可微的。他运用勒贝格积分计算了这些路径上函数的平均值。
1923年,维纳第一次给出随机函数的严格定义,证明可以是布朗运动的理论模型。维纳从样本路程的观念出发,研究“路径”的集合,引进维纳测度,揭示了连续而不可微函数的物理特征,故布朗运动又称维纳过程。维纳的工作对于概率是极富成效的。它不仅给老问题注入了新生命,更重要的是开辟了崭新的研究领域,揭示了概率论和其他数学分支之间引人注目的联系。维纳的这项研究可以说是现代概率论的开创性工作。现在把定义在连续函数空间的一种描述布朗运动的测度称为维纳测度,关于这个测度的积分称为维纳积分。后来,日本数学家伊藤清在此基础上发展了随机积分论。
(2)引进巴拿赫—维纳空间:
1920年,维纳将法国数学家弗雷歇关于极限和微分的广义理论推广到矢量空间,并给出了一个完整的公理集合。维纳的结果与几个星期以后发表在波兰数学期刊上的巴拿赫的论文不谋而合,广义的程度也分毫不差。巴拿赫构想和发表他的理论比维纳早几个月,但两者的独立程度是一样的。故这两项工作一度被称为巴拿赫一维纳空间理论。维纳在短时间里继续发表了有关这方面的成果,为冯诺依曼
1927年提出希尔伯特空间以及希尔伯特空间中的算子的公理方法提供了基础。后来维纳逐渐离开了这个领域,但他对泛函分析这一20世纪产生和蓬勃发展的新兴数学分支所作出开拓性工作己载入数学史册。
(3)阐述位势理论:
1923~
1925年,维纳对位势理论作出基本的贡献。对于给定连续边值函数的狄利克雷问题,得出了确切的广义群。对于一般的紧集定义容度概念,并给出著名的正则性判据。早先关于一个区域内部的电磁势的概念认为,它应当同边界上给出的那些值完全一致。维纳遵照他业已研究过的类似于广义积分的概念,注意到一个区域内部的势可以被看作是由边界周围的势的线性组合决定,即使按照这个定义在接近边界点时不能给出一个连续函数边界。这是一个崭新的概念,维纳由此大大地扩展了位势理论的许多概念,包括电荷和电容的概念。
这一成果的意义在于,新理论认为,一个内点的势与边界值的关系是一种广义积分,而不是由一种将这些内部势与边界上的势结合起来的极限过程。这就把原有关于边界问题的观点颠倒了过来。就象数学上曾经有过的多次观点颠倒一样,重新阐述位势理论给多年来被一种过于因循守旧的论点弄得死气沉沉的局面吹进了一股清新的空气。
(4)发展调和分析:为了给亥维赛计算法建立一个扎实的逻辑基础,维纳走上了调和分析的新道路。
1926年初他发表了这方面的第一篇论文,此后五年的工作以一篇广义调和分析的长文而达到顶峰。维纳从物理学借来函数作为调和分析的钥匙,而后又把它同通讯理论联系起来,把写成傅立叶变换。他获得了现在所说的光谱分布状态。为了证明其中一个关键性的公式,维纳在哈代和李特尔伍德的陶伯定理中提出了一种强有力的高度独创的方法,即非零绝对收敛傅立叶级数的著名的反转定理。这是一个具有统一数学抽象意义的惊人例子。维纳在这方面的成果后来成为巴拿赫代数理论的基础,并由此导出诸如素数定理等结果。
(5)发现维纳—霍普夫方法:
1930年前后。维纳与天文学家霍普夫合作,共同研究一类给定在半无穷区间上的带差核的奇异积分方程。此类方程现在被称为维纳—维普夫方程。维纳推广了霍普夫关于辐射平衡态的研究,于
1931年得出其求解方法。其基本思想是通过积分变换,将原方程化为一个泛函方程,然后再用函数因子分解的方法来求解,因此维纳—霍普夫方法又称因子分解法。它已成为研究各种数学物理问题的一种常用方法。维纳创造性地说明,维纳—霍普夫方程最引人注目的应用表现在两种进程间的分界是时间上的而非空间的,这正是在预测理论的某些方面可应用的非常适当的工具。他进一步指出,还有许多关于仪器研究的更一般的问题可以用这种作用于时间的技术来解决。40年代以后,这一方程的理论在解析函数边值问题、调和分析和算子理论的基础上得到了系统的发展,其应用也从辐射问题扩展到许多其他领域,如中子迁移、电磁波衍射、控制论、多体问题及入口理论等。
(6)提出维纳滤波理论:在第二次世界大战期间,为了解决防空火力控制和雷达噪声滤波问题,维纳综合运用了他以前几方面的工作,于
1942年2月首先给出了从时间序列的过去数据推知未来的维纳滤波公式,建立了在最少均方误差准则下将时间序列外推进预测的维纳滤波理论。维纳的这项工作为设计自动防空控制炮火等方面的预测问题提供了理论依据,并为评价一个通讯和控制系统加工信息的效率和质量从理论上开辟了一条途径。它对自动化技术科学有重要的影响。维纳在问题中引进统计因素并使用了自相关和互相关函数,事实证明这是极其重要的。维纳滤波模型在50年代被推广到仅在有限时间区间内进行观测的平稳过程以及某些特殊的外平稳过程,其应用范围也扩充到更多的领域,至今它仍是处理各种动态数据(如气象、水文、地震勘探等)及预测未来的有力工具之一。
(7)开创维纳信息论:维纳是信息论的创始人之一。他从带直流电流或者至少可看作直流电流的电路出发来研究信息论,独立于申农,将统计方法引入通讯工程,奠定了信息论的理论基础。维纳把消息看作可测事件的时间序列,把通信看作统计问题,在数学上作为平稳随机过程及其变换来研究。他阐明了信息定量化的原则和方法,类似地用“熵”定义了连续信号的信息量,提出了度量信息量的申农—维纳公式:单位信息量就是对具有相等概念的二中择一的事物作单一选择时所传递出去的信息。维纳的这些开创性工作有力地推动了信息论的创立,并为信息论的应用开辟了广阔的前景。信息论创立者申农说:“光荣应归于维纳教授”。
(8)创立控制论:维纳对科学发展所作出的最大贡献,是创立控制论。这是一门以数学为纽带,把研究自动调节、通信工程、计算机和计算技术以及生物科学中的神经生理学和病理学等学科共同关心的共性问题联系起来而形成的边缘学科。
1947年10月,维纳写出划时代的著作《控制论》,
1948年出版后,立即风行世界。维纳的深刻思想引起了人们的极大重视。它揭示了机器中的通信和控制机能与人的神经、感觉机能的共同规律;为现代科学技术研究提供了崭新的科学方法;它从多方面突破了传统思想的束缚,有力地促进了现代科学思维方式和当代哲学观念的一系列变革。现在,控制论已有了许多重大发展,但维纳用吉
19058研究维纳现在是一个很热门的课题,希望有志趣的同志一起来研究
19058什么时候我国也有这样的人
19058仅仅良好的社会家庭教育能
创造一个像维纳那样的天才吗
19065感谢你帮翻译:
infeasible path gradient based
method
augmented-penalty/outer-approximation
19066郑大数学系不怎么样啊
19066郑大的数学系怎么样?
有没有同盟军,请留言
19066
| 引用 (qcc2005 @ 2005年10月11日
21时48分) |
?郑大数学系不怎么样啊“
|
你哪个学校的阿!不懂就不要乱讲
郑大数学系咋了?郑大基础数学全国排第
19名。你本事就考基础数学的公费 不懂还乱讲 鄙视
19067<<数学,新的黄金时代>>
19067用Fn,k 表示n阶Farey数列的第k项,并令 Dn=

|Fn,k-
k/an|
估计 Dn的极限阶.好象还与Riemann猜想有点联系
哪位高手指点一下
19068想考代数方面的
想找研一或二学长,学姐交个朋友
19068干什么,想考北大么!你考什么方向。
19068请问这里有没有北大研究生,能交个朋友吗?QQ196224353
19069好象是没把此文件加入VC工程中
19069给你说个论坛,是专门讨论 VC++ 的,你可以到那里问一问:
http://www.vckbase.net/
19069function
mydata(t)
x=0:0.1:t;
y=sin(x);
plot(x,y,'r');
B=char('x','y');
A=[x;y];
fp=fopen('use1.dat','w');
fprintf(fp,'
%c %c\n',B);
fprintf(fp,' %4.3f
%4.3f\n',A);
sta=fclose(fp);
这是在matcom中编的m文件,可以运行通过。想在vc中通过对话框调用,结果在调试的时候出现以下错误:
shujuDlg.obj : error LNK2001: unresolved external symbol "class Mm
__cdecl mydata(class Mm)"
(?mydata@@YA?AVMm@@V1@@Z)
Debug/shuju.exe : fatal error LNK1120: 1
unresolved externals
Error executing link.exe.
如何解决???
19070刚体的运动只要三维就够了。不过其状态空间则需要六维的描述。
这样可以考虑一个三维流形为底的纤维丛。一个刚体的运动其相空间就是纤维从的子流形。如果把状态空间的元素表示成那些几何参数和时间的函数(假定连续),这样的不同子流形就具有同伦关系
19070本人不是搞数学的,但用到微分几何的知识,想请高手给指点一些参考书目。具体问题是这样的。一个刚体有的运动形成六维的流形,这个流形和该刚体的几何参数(比如,长度,旋转角度等)有映射关系。当这个刚体受到约束(比如,只能转动)时,运动流形就是三维的子流形。我想知道的是,这个子流形和它被约束的子流形有何关系,它们和刚体的几何参数之间的映射关系如何确定,也就是说,当这些几何参数的微小变化和这两个子流形变化之间的映射关系如何确定,这需要用到那些数学知识?望告知
19070建议看看流形和流形上的纤维丛这方面的知识
19072
| 引用 (pccq_2002 @ 2005年10月11日
11时54分) |
令Q=P的逆
tr(B)=tr(QAP)=tr(QA*P)=tr(PQA)=tr(A)
这样做对吗?
|
上面的每一步都是怎么则得到的?
19072
| 引用 (deducemath @ 2005年10月11日
12时59分) |
上面证明正确,但我认为楼主需要的是这个定理:
若两矩阵在某数域上相似,则他们在任意数域上相似。(证明在杨子胥那本书上)
|
谢谢
我知道这个定理
应该叙述为数域F上的矩阵相似<===〉在其某一扩域上相似
19072同意楼上观点!
19072上面证明正确,但我认为楼主需要的是这个定理:
若两矩阵在某数域上相似,则他们在任意数域上相似。(证明在杨子胥那本书上)
19072令Q=P的逆
tr(B)=tr(QAP)=tr(QA*P)=tr(PQA)=tr(A)
这样做对吗?
19072如体
19073若不存在特征根呢或只存在一个特征根呢
最小多项式无重根
19073幂幺矩阵的特征根互不相同,当然可对角化.
19073如体
幂幺指A^m=E
19074顶一下
19074书上有向量的极小多项式吗?不懂!:(
19074任意两个向量的极小多项式之间要么有整除关系要么互质
19075我说的是带变换的线性空间的不可约分解
其不可约分解的不变子空间的
个数是否唯一?
19075不一定.看看近世代数的书就知道了.
19075不可约分解的标准形是否唯一?
19075线性算子为不可约的充要条件为线性算子为循环算子并且其最小多项式为不可约多项式的幂
不可约分解不必是若当分解
但若当分解必是不可约分解
不可约不变子空间不必是极小不变子空间,任意变换存在不可约分解,但不一定存在极小分解
19075唯一。
易证若A线性空间V上的一个线性变换,且V关于A不可约,则A必相似于一若当块(引理),再根据若当标准形的唯一性即得。
其实,更好的提法是对线空V上的线变A,求所有的A-不变。
19075请具体说一下不可约分解、极小分解、线性算子、循环线性算子的定义
19077请问从哪里可以找到Z.I.Borevich和I.R.SHAFAREVICH写的Number Theory
19078
| 引用 (hongming6662 @ 2005年10月11日
13时24分) |
|
A为n阶方阵,R(A)+R(E-A)=n,证明A可对角化 |
题设条件等价与幂等性,自然可对角化
19078没错,证明A(E-A)可以用块的初等变换来做。而且这个是充分必要条件。
19078可以证明A(E-A)=0,A的特征值为0和1.
19078A为n阶方阵,R(A)+R(E-A)=n,证明A可对角化
19078利用这样一个结论:rank(E _{n}-AB )+s=rank(E _{s} -BA)+n,其中,A _{n

s} ,B _{s

n}
知,设rankA=r,由于A=BC,代入,知rank(E _{r}-CB )=0,所以,BC=E _{r} ,所以,A ^{2}
=BCBC=B(CB)C=A
19078ding
19078顶!!
19078能不能写清楚一点啊
19078R(A)+R(E-A)=n
等价于 A^2=A
因为 n=r(diag(A,E-A))
经过初等变换以后可以变成 diag(E,A^2-A)
所以r(A^2-A)=0
19078还有一种方法是,给出AX=0的一组基础解系,和(A-E)X=0的一组基础解系,通过简单证明,可知,它们合起来刚好是空间的一组基,得A^2-A在此组基下的矩阵刚好为0,得证!!!
19078
| 引用 (hongming6662 @ 2005年10月11日
13时24分) |
|
A为n阶方阵,R(A)+R(E-A)=n等价于A^2=A |
证明:若A为n阶方阵,则A^3=E等价于rank(A-E)+rank(A^2+A+E)=n
19078应该差不多吧
可以多看看樊恽 钱吉林等主编代数学辞典
19078可以用线性变换的多项式的关系来做
19078用到一个结果
如果(f,g)=1
则
r(f(A))+r(g(A))=n+r(fg(A))
这里取 f=x g=x-1
就可以推出 A^2=A
19078
| 引用 (Godyalin @ 2005年11月28日
12时27分) |
| 引用 (hongming6662 @ 2005年10月11日
13时24分) | |
A为n阶方阵,R(A)+R(E-A)=n等价于A^2=A |
证明:若A为n阶方阵,则A^3=E等价于rank(A-E)+rank(A^2+A+E)=n
|
顺便也解决了这个问题
19078利用秩的第2降阶定理,易地:R(En-A)=R(En-BC)=R(E-B(En-)C=R(En)-R(Er)+R(Er-cEn-B)=n-r+R(Er-CB);再由题意得:R(Er-CB)=R(En-A)+R(A)-n=0;所以,CB=Er.所以,A*A=BC*BC=BErC=BC=A!
因为:A的平方等于A所以,A的最小多项式没有重根,A就可对角化
19078对不起刚才忘记写:B,C由来了
A的秩设为R,把A进行满秩分解A=BC
19078好没面子.....
19078觉得Godyalin的证明A^2=A的方法不错,呵呵。
19078fyg
1981,R(E-B(En-)C这个地方没弄好,再改改。
19078很经典的一个题
我才复习了一个星期,我也会:)
19078其实也可以用降阶定理来证明!
19078A的特征值只能是1和0
当特征值为0时,因为A(A-E)=0,A-E的线性无关列坐标为0的特向量,同理A线性无关列坐标为1的特向量,rA+r(A-E)=n所以有n个线无关的特向量即A能对角化......
19078怎么做,请写出来
19078可以知道

只能为=0;1。
可得0,1的dim和为n
19078请问:pccq_2002,你所用的结论"(f,g)=1,则rankf(A)+rankg(A)=n+rankfg(A),其中A是n阶方阵."如何证明?请给出谢谢!
19079继续post-48-1129009894.ibf
19079最近,blackwell在作活动,免费给出2004年10篇top 文章,我在这里提供两篇。post-48-1129009440.ibf
19079科学的困惑
The Wonder of Sciencepost-48-11302
17733.ibf
19079
Matrix
Models as a Tool for Understanding Invasive
Plant and Native Plant
Interactionspost-48-11302
18232.ibf
19079非常感谢.
19080没错,就是这样,也可以说它的零化多项式没有重根,所以它可以对角化。那对角矩阵就是以(a1^2+a2^2+^+an^2),0,0,^,0为特征值的对角阵。(后面有n-1个0)yi
19080B=a'a
B^2=(a1^2+...+an^2)B
f(x)=x^2-(a1^2+...+an^2)x
是 B的零化多项式
所以B的最小多项式整除f(x),所以B可以对角化
这样做对吗?
19080设a=(a1,a2,...,an)是n(n>=2)维非0向量,证明a的转置乘a可相似一对角矩阵,并求此对角矩阵。
19080是什么意思啊??AA'不是对称矩阵,当然就可以对角化了啊
19080是什么意思啊??AA'不是对称矩阵么,当然就可以对角化了啊
19080iii说的也行,
若是在复数域上显然成立
如果在实数域上,因为a'a是个实对称矩阵,所以可对角化
19080a'a秩是1.观察就得到0是其n-1重特征根.
最后一个特征根通过迹可求得.
19080谢谢,非常感谢!!!!!!!!!
19080请写具体一点
19081征求用Minitab软件进行multiple regression
分析的题例(30个数据点左右)--最好是英文版。兄弟现需交上述作业,请各位高手伸出援助之手。必有回报!!!!
19082看样子有点像代数结构之类的东西
19082谢谢子青兄,我开始也以为是关于信号处理、滤波什么,但是文章是关于可靠性和维修方面的,而且作者提到了这是概率论和随机过程里的,可是我实在找不出,呵呵,只好来求助了。我倒是还在中科院数学与系统科学研究院的韩继业一个报告《非线性优化的若干新研究》中见到过Filter方法,他称之为“过滤子”,报告地址如下:http://www.orsc.org.cn/conferences/orsc
2004/han-qd.pdf,另外我也把我那篇文章传上来,请你指教。谢谢了。post-
17-1129039352.ibf
19082应该是信号处理那部分的吧?翻译成滤子
19082最近看文章,文中经常出现filtering和filtration两个字,概率论中有名词吗?怎么翻译成中文?如何理解?请熟悉的人提供些资料。谢谢了。
19082Filtering: 常译为滤波。
Filtration:
严加安的“鞅与随机积分引论”中译为$\sigma$
域增族。
附件是汪嘉冈“现代概率论基础”(第二版)中的解说。post-
17-1129258363.jpg
19082我也找到了英文的定义,现在有中文的参考更是方便了,谢谢你们。
19083我们学校还不错
19083山大 彭实戈
中科院 严加安
都不错.
19083什么应用数学,中国的应用数学根本就没有自己的背景!
目前中国的基础数学是唯一值得学习的!
其他什么计算,应用都是dog-shit!
19083我想考应用数学专业的金融数学方向,不知哪所学校的实力比较强,也比较好考?
另外,我的英语水平比较差,很是担心.望大家给我支招,不胜感激.
19083我也想学,呵呵!
19083beijingdaxue bijiaohao
19083据了解,山大的彭实戈是这个方向最牛的
不过这个方向目前还是理论阶段
19083我业想考此方向,但不知其究竟怎样。哪个学校的好考一点
19083真的吗
应用没前景吗
19083想学金融数学的同学很多,而且是越来越多.很多保送生也都抢这个方向的名额.
19083好,不错
19083南开和复旦比较强
19084我这里只有几份试题,没答案的
你们要吗?
19084
给我也发一份啊,,
我也急要啊谢谢!!!
我的邮箱guozhiheng590@126.com
19084两位老兄能否给我发个邮件,我也需要。谢谢abcd302@163.com
19084我也想知道
19084可否给俺发个邮件啊?
谢谢啊!
mydata_janssen@163.com
19084有哪位有南京大学高代和数分考题和解答,本人找了很久,也不知道什么渠道可以得到
谁有可以联系我,QQ39954380
E-mail:lihuiqun33@sina.com
谢了!
19084要的话就发邮件给我E-mail:lihuiqun33@sina.com
你们谁有试题和解答的话也可以发给我
19084要呀,给我一份呀,大哥
yuxianzh@swu.edu.cn
19084我发现了一本《分析中的基本定理和典型方法》,是南大的宋国柱编的
有数分的92--03年试题和解答,你们谁要的可以去新华书店买。
我就只能提供这么多了。
19084我也想要
chunqueyiyi@126.com
19084我也想要一个
19084好像可以自己去南大复印历年的试题,不过好像没有答案的。
190870根个数不一定相等,其它根及其个数相同
19087设W1,W2为A的不变子空间且AW1=AW2
则A限制在W1,W2上的最小多项式有何关系?
19087为什么呀?
19087
设f(x)是A|W1的最小多项式,g(x)是A|W2的最小多项式
则f(A|W1)=0
对任意的y(-W2,因为AW2=AW1,存在x(-W1,使得(A|W2)y=Ay=Ax=(A|W1)x
由于W1,W2是A的不变子空间,故(A|W2)y(-W2,
(A|W1)x(-W1
则(A|W2)(A|W2)y=A(A|W2)y=A(A|W1)x=(A|W1)(A|W1)x
再由类似过程,可得(A|W2)^ny=(A|W1)^nx
从而f(A|W2)y=f(A|W1)x=0,由y的任意性知道f(A|W2)=0
f是A|W2的一个零化多项式,从而g|f
同理可证f|g,
得f=g(若f=0则g=0,否则二者首项系数都是1)
19088如题
19090啊,G(2)不能算出来吗,我算到这里,我还想把G(2)算出来的,所以求助。
19090不知对否?post-38-1129078720.gif
19090谢谢解答post-38-1129027963.ibf
19091对于一个连通网络,断开任意一对节点之间所有通路所需去掉的最少链路数以及断开一对节点之间所有通路所需去掉的最少节点数用什么算法?
19093看看有没有用post-60-1129032299.ibf
19093谢谢了,
19093thanks
19093thankS!
19093好东西总是这么多啊!
19093谢谢!
19093thank you
19093
| 引用 (liudianli @ 2005年10月11日
20时04分) |
| 看看有没有用
|
谢谢
19093用啥工具能打开?
word打开是乱码!
19093
| 引用 (zhuiyi288 @ 2006年03月07日
20时38分) |
用啥工具能打开?
word打开是乱码! |
PDF文件,用Adobe Reader打开
19093
| 引用 (zhuiyi288 @ 2006年03月07日
20时38分) |
用啥工具能打开?
word打开是乱码! |
Adobe Reader7.0,可以去下一个
19093谢谢
19093不知道还有最近一两年的不?
19099谢谢了!
19099一个推导,请指教.post-8-1129047433.ibf
19099其中C为常数
19099谢谢大哥大姐了,请看附件post-8-1129034660.ibf
19100那位朋友有<<实变函数论>>的参考答案
是北大版周民强编
在下不胜感激!
19100华中科技大学出版社 实变函数学习内容和方法一书
19100谢了
19101设f(x)=y'+y
那么(exp{x}y)'=exp{x}f(x)
上式积分就可以啊
19101各位大虾~~请教小弟啊~~~
怎么没人回答呢??
这题能不能用函数的连续性来做的啊??
19101把原式按微风方程解得 y=ce(-x) 为一指数函数,即可得结果
19101本人还未学会公式编辑,请大虾们见谅~
设y(x)在0<=x<+∞上连续可微且lim(x→+∞)((y'(x)+y(x))=0
证明:lim(x→+∞)y(x)=0
19103x^k+y^k=z^k Fermat equation
19103你指的是哪一类方程啊
19103请高手介绍一下一些经典有名的方程?
要是非微分方程的.
谢谢了.
19105请问怎么附图啊
回复:直接将<256k的图片用附件形式发上来.
19107单调性是显然的,不过此时严格单调性无法保证,
证明可用反证法,取适当三个点即可.
关于周期性,讨论下面的例子,
post-21-1129044545.jpg
19107如题
19107
| 引用 (mazl @ 2005年10月11日
23时29分) |
单调性是显然的,不过此时严格单调性无法保证,
证明可用反证法,取适当三个点即可.
关于周期性,讨论下面的例子,
|
首先单调性并不显然,因为函数列中可能既有单调增又有单调减的函数
第二个,还没搞懂
19107我都明白了,谢谢
若限定函数周期都相同会有什么结果?
19107
引用 (流形 @ 2005年10月13日
19时11分) |
我都明白了,谢谢
若限定函数周期都相同会有什么结果? |
回答是肯定的,考虑x和x+T即可,所以收敛就够了。
19107
1.
若不单调,则有点a,b,c,a<b<c,使得中间点的函数值比两端的点的函数值都真的大(或都真的小,此处只讨论大的情形),由于只有3个点,所以,根据收敛性(其实这里只需要收敛即可,并不需要一致性)得到矛盾。如此讨论,与函数列中的函数的增减无关,可以同时既有单调递增的,也有单调递减的。
2.
0点是函数的唯一的最大值点
19108浙大与复旦哪个比较难考?
19108有! 手机:13657164079
19108交流一下
QQ:34689628
Email:zhao_yunsong@163.com
19110请问
现在小波在图象压缩编码方面有没有新的进展,在这个领域最近比较热的技术是哪些方面的.?
本人是研究图象压缩编码的,现在不知道是该用矢量量化小波还是采用嵌入式小波来做.....????
有没有做这方面的师兄师姐,帮帮学弟吧:0
qq 32876407
email bhxiaobai@tom.com
谢谢噢~~~
19136两道分析post-38-11290764
19.ibf
19137具体过程哩?麻烦麻烦
19137怎么做?post-38-1129082538.gif
19137
4
πa 2
c
19137主教练,麻烦告诉我怎么做哩!
19137楼上给的是体积.。上次的答案化简不对,这是新的答案不知道对不对,大家帮忙看看吧post-38-1130425613.gif
19137=2


杠sqrt{1+Zx2+Zy2} dxdy
楼上答案有误,令a趋近c=1
19137汗,^^,zhe
19138这个我知道为什么我会算出来0啦,谢啦
19138我怎么会算出来0post-38-1129082853.gif
19138不知对否?post-38-1129088779.gif
19139这题麻烦谁写一下啦
19139麻烦写一写啦!
19139单凭题目的条件好象得不出z,结果只能得到一个表达式.
19139不是很明白,最后z要不要算出来的啊?post-38-1129083083.gif
19140再给一种证明post-38-1129086308.gif
19140如下:post-38-1129085623.gif
19140第1题也不难:
令

f(x)=F(x),则F'(x)F(x)=0
(F(x)^2)'=0
F(x)^2=C
故f(x)=0
19140对的,我怎么就没有想到呢,我还以为连续不能推出可积呢
那第2道呢?
19140第2题好象很多书上有啊,找一找应该可以找到.
19140两道历史遗留问题post-38-1129083520.gif
19141那还有一道题目怎么做哩?
19141是我搞错了,呵呵,谢谢啊!
19141请看一下教材!
19141ln(1-x)展错了吧?post-38-1129113270.gif
19141第2题:
-
π 2
6
post-38-1129086910.gif
19141怎么算不出倪!post-38-1129083741.gif
19141太贵了,帖子杂都要积分,太贵了,很快就没有,有没有卖积分的,这样回帖太慢了,买两百个积分慢慢用,要好多钱嘛
19143兄弟: 课上得再好也没用呀.
不能评职称, 不能加工资, 也没有奖金.
学生也不见得喜欢听.
课上得好的话会想:
总算没有误人子弟, 对得起自己的良心.
其他人会想: 看那小样, 只会上课, 顶个屁用!
19143昨天晚上看刘仪伟讲笑话:一学生入教室后拍了拍监考老师的肩说:“兄弟!今天就全靠你啦!”
想到本学期初的一个让我哭笑不得的事情:我进办公楼前,看见两个学生看本院所有老师的照片(名字和职称)。我进入办公楼后,她们问:“请问您知道杨XX老师吗?”我说:“我们院没这个人。”她们又说:“我们想查上学期考试试卷,杨XX老师教我们《高等数学》。”我再问:“你们是哪个班的?”答:“化学。”我心里打鼓,上学期不正是我上的那几个班吗?我再问:“你们是不是从来不去上课?”她们说:“我们每次都坐在后面。”(我在第一次课的时候已经做了自我介绍,但签名的时候比较潦草,学生从我的签名形状猜我的名字来问我。)
我的妈呀,我这老师当得,太不称职啦!!!
时时想另外去找一个工作,可上了这么多年的课,除了会上课,我还能干什么呢?
我该怎么办?
19143呵呵,有意思。还能怎么办呢?上好课呗
19143楼上说得好!!!!!!!!!!!!
19143多谢楼上兄弟支持!
学生不认识老师,除了老师应该承担一定的责任之外,是否应该挖掘出深层次的原因呢?
19143个人觉得这正反映了中国高等教育的落后,大班制教学,效果可想而知。假如50人左右班,老师上课怎么着在一年之内也会给自己留点印象,哪怕是课堂上突然出现的小插曲,大班制教学老师对学生的了解也是让人担忧,课间就那么几分钟,老师和同学谈心也没时间,更何况好多老师根本不关心学生,上完课就走人,学生有疑问自己解决。学生也敷衍老师,老师也搪塞学生。这样的情况在大学中可以说屡见不鲜!
19143楼上的说得很对,让我惊醒,我也该多和学生多聊聊了,多了解一下学生们到底在想什么。不应该只注重上课,课备的再好没有学生听也是很失败的!!!
19143个人经验:30人上课可以全部认识,70人上课可认识一半,100人上课可认识5-10人,200人上课最多认识5人。
奇怪不?
19143楼上地说得不错,但造成这种现象的原因是什么呢
?无非有两个,学生方面,老师方面.。学生方面已成定局(当然会有学生努力的),那作为老师就要尽量弥补这一方面!!
19143我班上有200多个学生,还真是认识的没超过10个
19144首届全国部分高校研究生数学建模竞赛总结post-37-1129085040.ibf
19145同感,请同志者多交流!!
19145有没有博士群的qq号。想了解些考博的信息!多谢!
回复:直接在硕博之路上发贴讨论即可.
19145也想知道
19145也想知道呀!
19145顶DDDDDDD
19146排列矩阵是一类基础矩阵,将这个矩阵左乘一个矩阵就相当于将这个矩阵进行行的重排(交换)
19146网上搜了一下,台湾都叫做交换矩阵.或者排序矩阵,也有叫分类矩阵的.忘记了我们上大学的时候是叫什么矩阵的。有谁知道并能解释一下什么是permutation
matrix吗?
谢谢先。
19146楼主说的单词是 置换矩阵!!
19147谢谢,我明白了
19147请看附件,推广的积分中值定理post-8-1129097237.ibf
19147M是
f(x)在[a,b]的最大值,能不能得出f(x)g(x)在[a,b]的定积分小于等于M乘以g(x)在[a,b]的定积分,谢谢了,根据什么,各位高手!!
19147如果
g
(x)
是负值,显然不能。
19148这个题目不怎么懂,其实我也想过把AA'当作对角阵来考虑,而之后该用什么知识点就无法知道了!reijin还是把具体的解答过程给一下吧!
19148谢谢,能详细说说吗?
19148顶一下
19148证明:设N阶方阵A,与其转置A'满足AA'=A'A,则存在一个多项式f(x),使A'=f(A)
19148牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛牛
19148reijin 是个小强,服了U
19148大概说一下
考虑AA'=A'A=C,C是对角阵且C=diag(入i*Ei),入i!=入j,入i>=0,则AA'A=CA=AC,于是可得A=diag(Ai),并且Ai*Ai'=入i*Ei,对于不等于0的入j,存在fi和gi,使得
fi(Ai)=0,fi(0)=0,gi(Ai)=Ai^(-1)=(1/入i)*Ai',且fj(Ai)可逆(i!=j)
对于不等于0的入i,作函数
Pi=入i*gi*f1*f2*..*f(i-1)*f(i+1)*..*fn*hi
F=sum(Pi)
其中有hi(Ai)=(f1..f(i-1)f(i+1)..fn)(Ai)^(-1)
则有F(Ai)=Ai'
于是F(A)=diag(F(Ai))=diag(Ai')=A'
19148请考虑AA'是对角阵的情况
19149
| 引用 (lchw @ 2005年10月14日
11时38分) |
能否给我也发一份.我的邮箱:
ezlchw@mailme.cn
谢谢!
|
lchw兄。已经发了一份《实分析与复分析》的课后解答英文版到你的邮箱,请注意查收!




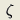
19149我要 Rudin 的答案 请楼上的那位兄台 发到我信箱里好吗 谢谢
binfengcq@yahoo.com.cn
19149ahu002_505,我怎么又被退信了?你这个域名的邮箱我一发就退信。你还有没有什么其他的联系方式或者邮箱之类的?
19149
| 引用 (ahu002_505 @ 2005年10月15日
11时29分) |
老兄可不可以也给我一份!
ahu002@gmail.com
多谢!
问。数学分析原理哪里可以买到或找到答案?
|
ahu002_505,偶已经发到年邮箱了。至于数学分析原理我只有英文版本的答案。
19149老兄可不可以也给我一份!
ahu002@gmail.com
多谢!
问。数学分析原理哪里可以买到或找到答案?
19149我也要一份,numbertheorylover@126.com 谢了
19149
19149请问Rudin的《实与复分析》课后习题解答哪有下载,学习此课程还要参阅那些相关的书
19149收到,谢谢
19149
| 引用 (renzhazero @ 2005年10月13日
20时34分) |
|
Rudin的《实分析与复分析》的课后解答我应该有前5章的。不过是英文版本的。不知道你是否有兴趣。不过他的〈数学分析原理〉我倒是有全部章节中主要习题的解答。不过还是英文版本的。我自己复印了。电子版本的弄丢了。
|
Rudin的《实分析与复分析》前5章的课后解答能传上来和发到我邮箱吗?
我现在很需要,
先再次感谢.
19149能否给我也发一份.我的邮箱:
ezlchw@mailme.cn
谢谢!
19149
| 引用 (renzhazero @ 2005年10月14日
10时55分) |
|
楼上的longgq兄,答案已经发到你邮箱了.注意查收啦! |
很可惜, 我一直都没有收到,
你能不能再次给我发一次呢?
发到我的邮箱: longgq@yahoo.com.cn
谢谢
19149楼上的longgq兄,答案已经发到你邮箱了.注意查收啦!
19149Rudin的《实分析与复分析》的课后解答我应该有前5章的。不过是英文版本的。不知道你是否有兴趣。不过他的〈数学分析原理〉我倒是有全部章节中主要习题的解答。不过还是英文版本的。我自己复印了。电子版本的弄丢了。
19149太需要了,能给我吗. longgq@21cn.com 谢谢.
19149谢谢上面的朋友,前五章的解答我也从网上搜到了,但是解答不全,不知哪里可以找到后面几章的解答
19149要不你试试这个ahu_002@yahoo.com或者ahu_002@163.com
w_xinghu@sina.com
英文版也行,我多少懂点数学英语!!
19149ahu002_505兄,<数学分析原理>与<实分析与复分析>习题解答英文版两份已经发到你的邮箱
ahu_002@163.com和你另外一个邮箱ahu_002@yahoo.com了。目前还没有收到系统退信。你注意查收一下吧。要是没有的话,我们再用其他方式联系也行。
19149多谢了。老兄!!
19149呵呵,8客气8客气。收到了就好。以后多多交流资料!
19149各位大师,我也非常想要一份答案,电子版本的发一份给我行吗,非常感谢,我正在学这个东西
yuxianzh@swu.edu.cn
另外全部答案再哪里能买到,或有的同志能否借我复印,请给我发邮件,我好联系你
我电话1310128
1982
19149楼上的yuxianzhi兄。答案发你yuxianzh@swu.edu.cn邮箱啦!是《实分析与复分析》前5章英文的。
19149我很需要,能否麻烦楼主也给我发一份?
我有邮箱:henmingz@163.com
先谢谢了!!
19149楼上的,《实分析与复分析》前5章英文答案已经发到你邮箱:henmingz@163.com。注意查收!
19149renzhazero,
我想问一下你的答案是否全的(chapter1-5),我找到的只是部分题目有解答.如果是全的话,请你发至我的邮箱qinjingonly@163.com.非常感谢!
19149偶的答案不全的。要是全就好啦。
19149想传上来给大家,但不知道怎么弄,要得给我发邮件
yuxianzh@swu.edu.cn
19149
| 引用 (renzhazero @ 2005年10月13日
20时34分) |
|
Rudin的《实分析与复分析》的课后解答我应该有前5章的。不过是英文版本的。不知道你是否有兴趣。不过他的〈数学分析原理〉我倒是有全部章节中主要习题的解答。不过还是英文版本的。我自己复印了。电子版本的弄丢了。
|
renzhazero兄, 能否把实复分析的答案和数学分析原理的答案发到我的邮箱.
我的邮箱是:
bmyuu@stu.snnu.edu.cn 或 bmyuu@hotmail.com
谢谢
19149楼上的operator。答案已经发到你两个邮箱了/
19149renzhazero 老兄,
可以把<数学分析原理>与<实分析与复分析>习题解答也给我发两份
gpscheng@126.com
正在学习,急需此资料。谢谢!!!
19149楼上的gpscheng.<数学分析原理>与<实分析与复分析>E文部分习题解答已经发你邮箱了.注意查收吧.
19149邮件已经收到,
感谢renzhazero 老兄,
19149再来要我<实分析与复分析>E文习题解答的朋友们.请去函数&分析版.我把解答放在那上面了.方便大家直接下载.
19149给我发一份吧!谢谢了!canjing_2001@sina.com
实分析和数学分析原理都要可以吗?谢谢
19149谢谢了!!我已经下过了。能不能给我发一份数学分析原理的答案?谢谢。canjing_2001@sina.com
19149能否也发一份Rudin《实分析与复分析》的习题解答(英文版)给我,不甚感激!我的邮箱unique_lee@sohu.com
最好还能有《数学分析原理》
19149我也想要一份《实分析与复分析》和《数学分析原理》的答案。有点贪心,不过真的很需要,谢了,我的邮箱:
tonykhm@hotmail.com
19149你好,实分析与复分析(Rudin)的练习题答案我也要,能麻烦发我一份吗,谢谢
我的邮件地址
www.kang_wei5@hotmail.com
19149Rudin--《数学分析原理》E文答案.大家都很推崇这书.在网上搜集了该书E文的主要参考答案.因为偶上邮箱实在很少.就放在解答库了.要下的朋友们也顺便顶吧,方便别人下载.
PS:另外Rudin--《实分析与复分析》E文1-6章部分答案我放在函数&分析版了.需要的朋友去那里下载吧.
19149引用 (renzhazero @ 2005年10月13日 20时34分)
Rudin的《实分析与复分析》的课后解答我应该有前5章的。不过是英文版本的。不知道你是否有兴趣。不过他的〈数学分析原理〉我倒是有全部章节中主要习题的解答。不过还是英文版本的。我自己复印了。电子版本的弄丢了。
Rudin的《实分析与复分析》前5章的课后解答能传上来和发到我邮箱吗?
我现在很需要,
先感谢!!!wychun112@126.com
19149把数学分析原理的也发一下吧!谢谢
19149renzhazero 好,
我也需要<数学分析原理>与<实分析与复分析>的习题解答
mathsle@gmail.com
麻烦了
19149maximumprinciple@sohu.com. Thank you!
19149Rudin的《实分析与复分析》前5章的课后解答能发到我邮箱吗?
我现在很需要,
先感谢!!!13665264320@e
172.com
19149发送一份到我的邮箱里吧,万分感谢yuling
1998@sina.com
19149《实分析与复分析》1-6章E文习题解答偶放在函数&分析版了。至于《数学分析原理》E文答案我放在解答库了。请诸位需要的朋友到那里下载。偶上邮箱发太麻烦了。
19149Wanted: solutions to "Real and Complex Analysis" by W.
Rudin.
johnzhang1234@yahoo.ca
Thanks a lot.
19149能否也发一份Rudin《实分析与复分析》的习题解答(英文版)给我,不甚感激!我的邮箱mark.lee@tom.com
最好还能有《数学分析原理》
19149可不可以给我也发一份Rudin《实分析与复分析》的习题解答给我啊?非常感谢!!!
我的邮箱:qhbing_2001@sohu.com
19149老兄可不可以也给我一份<实分析与复分析>的答案!我的邮箱是
smf2828@126.com
多谢!
数学分析原理的英文答案我也要
多谢!
19149楼主,给我发一份,急啊! 谢谢! 油箱:21caojian@163.com
19149各位仁兄.如果有Rudin的实与复分析的习题答案.请发一份给我好吗?我的邮箱:yuwenshenju@126.com.本人在此先谢过了.
19149renzhazero 老兄,
可以把<数学分析原理>与<实分析与复分析>习题解答也给我发两份
golee@126.com
正在学习,急需此资料。谢谢!!!
有空来武汉请你喝茶阿:)
19149我也想要<数学分析原理>与<实分析与复分析>习题解答
shangyilun2002@yahoo.com.cn
谢谢!!
19149Rudin--《数学分析原理》E文答案.大家都很推崇这书.在网上搜集了该书E文的主要参考答案.因为偶上邮箱实在很少.就放在解答库了.要下的朋友们也顺便顶吧,方便别人下载.
PS:另外Rudin--《实分析与复分析》E文1-6章部分答案我放在函数&分析版了.需要的朋友去那里下载吧.由于这个学期太忙。上网很少,那些帖子是否还在顶上不确定,大家可以注意查找一下。
19149刚刚找了一下。一份答案在http://www.math.org.cn/forums/index.php?showtopic=20303
属于解答库的精华区。另外一份《实分析与复分析》E文1-6章部分答案在
函数&分析版。可能已经沉了,等有时间或哪位有下到的朋友再发一份吧。我自己的因为早打印出来就没有保存在的电脑上了。不好意思!
19149朋友:
能给我一份答案吗?谢谢
我的邮箱是jgy_1121@163.com
19149我也想要一份duka712@yahoo.com.cn谢谢
19149谢谢《实分析与复分析》和《数学分析原理》答案
gandolphchou@yahoo.com.cn
19149老兄可不可以也给我一份!
zhanggang8531560@126.com多谢!
问。
19149我正在学《实分析与复分析》 (Rudin )急希望楼主能发我一分实分析与复分析 (Rudin
)习题解答。谢谢!!!
邮箱:tangguobiao2006@126.com
19149请问有没有后面的答案?急需啊
19149楼主有没有第五章之后的答案啊, 急要lengseshuijing@mail.nankai.edu.cn谢谢哈
19149在看Rudin的书,哪位好心人发一份“实分析与复分析”的答案给我,谢谢了。邮箱:jarint@163.com
19149可否也给我一份,我的邮箱是wangsongwang@tom.com,谢谢!
19149楼主您好:
我正在复习中,急须Rudin的书“实分析与复分析”的前五章的答案,谢谢了。邮箱:wangaf
1980@163.com
19149能不能也给我发一份数学分析原理的英文版答案,先在这谢谢啦!!!
19149有劳给我一份,十分感谢!jgy_1121@163.com
19149请给我一份!谢谢!E-mail:mygame2005@yahoo.com.cn
19149renzhazero:
能不能也给我一份,很巧,我就需要英文版的。我的邮箱是:twinnie2253@126.com
十分感谢!!!
19149能给我发一份吗
谢谢
tanwei59@163.com
19149
| 引用 (renzhazero @ 2005年10月13日
20时34分) |
|
Rudin的《实分析与复分析》的课后解答我应该有前5章的。不过是英文版本的。不知道你是否有兴趣。不过他的〈数学分析原理〉我倒是有全部章节中主要习题的解答。不过还是英文版本的。我自己复印了。电子版本的弄丢了。
|
给我也发一封吧,yanghuisanjiao@126.com
谢谢!
19149
| 引用 (renzhazero @ 2005年10月13日
20时34分) |
|
Rudin的《实分析与复分析》的课后解答我应该有前5章的。不过是英文版本的。不知道你是否有兴趣。不过他的〈数学分析原理〉我倒是有全部章节中主要习题的解答。不过还是英文版本的。我自己复印了。电子版本的弄丢了。
|
你好,能给我发份Rudin的《实分析与复分析》的课后解答吗?还有他的〈数学分析原理〉
习题的解答(英文版本OK),非常感谢!!!
我的邮箱:
dj_6
19_jun@hotmail.com
19149
| 引用 (renzhazero @ 2005年10月13日
20时34分) |
|
Rudin的《实分析与复分析》的课后解答我应该有前5章的。不过是英文版本的。不知道你是否有兴趣。不过他的〈数学分析原理〉我倒是有全部章节中主要习题的解答。不过还是英文版本的。我自己复印了。电子版本的弄丢了。
|
Rudin的《实分析与复分析》的课后解答能给我传一个吗?yanghuisanjiao@126.com!麻烦了!
19149
| 引用 (qinjingonly @ 2005年10月12日
13时28分) |
|
请问Rudin的《实与复分析》课后习题解答哪有下载,学习此课程还要参阅那些相关的书
|
Rudin自己的<<数学分析原理>>也是要看的!西西
19149可否也给我一份,我的邮箱是wangsongwang@tom.com,谢谢
19149可否也给我一份,我的邮箱是n91126@126.com,谢谢
19149弟兄们谁还有这个答案,拉我一把啊
xuhuicai2005@163.com
我在考博,这本是指定的参考书,题目大多都不会,快被逼疯啦
谢谢!!!1
19149能给一个我吗?谢谢!hyyboya@yahoo.com.cn
19149能否也给我一份:
chernfeifei@163.com
谢谢!!!!!
19149renzhazero 老兄,
可以把<数学分析原理>与<实分析与复分析>习题解答也给我发两份吗?
soldier_zhl@163.com
正在学习,急需此资料。谢谢!!!
19149
| 引用 (renzhazero @ 2005年10月13日
20时34分) |
Rudin的《实分析与复分析》的课后解答我应该有前5章的。不过是英文版本的。不知道你是否有兴趣。不过他的〈数学分析原理〉我倒是有全部章节中主要习题的解答。不过还是英文版本的。我自己复印了。电子版本的弄丢了。
|
我也需要Rudin的《实分析与复分析》的课后解答,你能给我吗?
我的邮箱是zangab05@yahoo.com.cn非常感谢!
19149我见过这个答案书!!可以到书店找找!!
19149哪位能发一份给我吗?万分感谢!!y.e.wang.04@cantab.net
19149能不能也发一份给我啊,谢谢!
limierr@126.com
19149楼上的大侠,麻烦你也发一份到我邮箱 limierr@126.com,
非常感谢!
19149如果可以的话也发给我一份吧,谢谢了,我的邮箱是:hypfljt@163.com
19149楼主,可以给我传一份吗?鲁丁的三本书我都买了,如果你都有的话传给我哈,非常感谢!
我的邮箱是sunjijiang2005@163.com
19152谢谢了!
19152一个证法。post-8-1129107599.gif
19152设f(x)在[0,1]上连续,f(0)=f(1).证明:对自然数n >= 2,必有 0<
ξ
<1, 使得f(
ξ )=f(
ξ +(1/n))
19153大家好,有没有合肥工业大学的数学人---
本科或研究生或有志于上数学研究生的同志?
19154谢谢啦!!以后继续努力!!!
19154
http://210.45.208.115/2004jpkc/maths/可惜上面没有后面几章的教案,俺这学期正在上数分,那位如果用的这本书有教案的话,发出来共享一下吧
谢谢
19154谢谢了!!!
19154哈,thanks!正好用的这本
19154去看看怎么样。
19154怎么页是打不开啊
19155谢谢了!
19155我觉得利用连续函数在闭区间有最大、最小值和介值定理就可以。
19155设f(x)在[a,b]上连续,a<c<b,c<d<b,m>0,n>0,证明:在[a,b]内必有点
ξ
,使得mf(c)+nf(d)=(m+n)f(
ξ )
谢谢!
19156两个无穷极限的该怎么交换次序???
请您将详细解答贴上!
19156我觉得跟两个极限的收敛性有关,如果都收敛那么就跟顺序无关,否则要具体讨论
19158在多元广义积分里的,你自己找找吧,好象书上有道题目就是证明积分可交换条件的,具体我实在记不清了
19158请明示相关定理!
还有高手呢????
19158这个正好我们老师讲过post-38-1129114295.gif
19158题目有没有问题我不知道!
这个。。。一致收敛交换次序的 对于
两个无穷区间也适用吗??可以对外边的取极限是吧,但交换后,怎么把极限移进去呢??
可不可以把交换的过程写具体一点,,请帮帮忙,虽然不难。:)
帮帮忙。。。。。
19158把原式代入所求积分右端,可得一2重积分,容易证明证明积分的一致收敛性,于是积分顺序可交换,即可得结果
19158怎么做啊???post-38-1129099383.ibf
19158题目有问题,把题目写清楚撒,条件就是个问题条件,怎么做啊!
19158to luting5:
你好,我们大学阶段很少学多元广义积分,但我在陈传璋的书中的含参变量的广义积分中找到的定理是“需要一致收敛的”,而不仅仅是“一致有界"
19158原来大家都不会做啊!!
19158见《吉米多维奇数学分析题解五》 P625 3830题
19160
γ
=0.577216...⋃abc
xyz 回复:主页暂时不支持公式编辑.请在论坛交流.
19161抽象代数奠基人--诺特
诺特(Emmy
Noether),近代杰出的德国女数学家。
1882年3月23日生于埃尔朗根。
1935年4月14日卒于布尔莫尔。是M.诺特的长女。
1900年入埃朗根大学,
1907年在数学家哥尔丹指导下获博士学位。
1915年4月去格丁根,因为她是妇女,一直没有得到正式教职。
19
19年,在著名数学家希尔伯特和克莱因的支持下,她才获准取得格丁根大学讲师资格。
1933年,因是犹太人而被纳粹政府解职,同年赴美国;先后在普林斯顿高等研究所及布尔莫尔女子学院工作。主要贡献在代数学方面,她是抽象代数的奠基人之一。
诺特的工作在代数拓扑学、代数数论、代数几何的发展中有重要影。
1907-
19
19年,她主要研究代数不变式及微分不变式。她在博士论文中给出三元四次型的不变式的完全组。还解决了有理函数域的有限有理基的存在问题。对有限群的不变式具有有限基给出一个构造性证明。她不用消去法而用直接微分法生成微分不变式,在格丁根大学的就职论文中,讨论连续群(李群)下不变式问题,给出诺特定理,把对称性、不变性和物理的守恒定律联系在一起。
1920~
1927年间她主要研究交换代数与「交换算术」。
1916年后,她开始由古典代数学向抽象代数学过渡。
1920年,她已引入「左模」、「右模」的概念。
1921年写出的<<整环的理想理论>>是交换代数发展的里程碑。建立了交换诺特环理论,证明瞭
19161可以堪称数学史上最伟大的女数学家了
19161我们系走廊里还有她的肖像呢。
19161近世代数的祖师爷,向她致敬!
19161向著名的女数学家诺特致敬,佩服佩服.代数很难学呀.
19162谢谢!
19162余维数为一的线性流形
19162什么叫N-1维超平面?
谢谢!!
19163数学史上的不朽之名--欧几里德
(一)欧几里德及其主要数学成就
埃及的亚历山大城,是地中海南岸的重要海港,经过托勒密王苦心经营,逐渐成为新的希腊文化的中心,希腊本土这时已经退居次要地位。欧几里德(Euclid,约公元前330-275)就生活在这个时代。欧几里德早期在雅典接受教育。他博览群书,汲取了前人积累的大量的几何知识,成为一位几何大家。成名之后,受托勒密王邀请,来到亚历山大教学。他是一位温良敦厚的教育家,对于有志数学之士,总是循循善诱地教导,而反对学习上不肯刻苦钻研,投机取巧的作风。据说有一位学生,才开始学习第一个命题,就问欧几里德,学习几何学之后有什么报偿。欧几里德说:“给他几个金币,让他离开吧,因为他想在学习中获利”。
公元前7世纪之后,希腊几何学迅猛地发展,积累了丰富的材料。希腊学者们开始对当时的数学知识作有计划的整理,并试图将其组成一个严密的知识系统。首先做出这方面尝试的是公元前5世纪的希波克拉底(Hippocrates),其后经过了众多数学家的修改和补充。到了公元前4世纪时,希腊学者们已经为建构数学的理论大厦打下了坚实的基础。
欧几里德在前人工作的基础之上,对希腊丰富的数学成果进行了收集、整理,用命题的形式重新表述,对一些结论作了严格的证明。他最大的贡献就是选择了一系列具有重大意义的、最原始的定义和公理,并将它们严格地按逻辑的顺序进行排列,然后在此基础上进行演绎和证明,形成了具有公理化结构的具有严密逻辑体系的《几何原本》。
《几何原本》的希腊原始抄本已经流失了,它的所有现代版本都是以希腊评注家泰奥恩(Theon,约比欧几里得晚七百年)编写的修订本为依据的。《几何原本》的泰奥恩修订本分13卷,总共有465个命题,其内容是阐述平面几何、立体几何及算术理论的系统化知识。
自它问世之日起,在长达二千多年的时间里一直盛行不衰。它历经多次翻译和修订,自1482年第一个印刷本出版后,至今已有一千多种不同的版本。除了《圣经》之外,没有任何其他著作,其研究、使用和传播之广泛,能够与《几何原本》相比。但《几何原本》超越民族、种族、宗教信仰、文化意识方面的影响,却是《圣经》所无法比拟的。
欧几里德的重大功绩是编写了《几何原本》。《几何原本》按照公理化结构,运用了亚里士多德的逻辑方法,建立了第一个完整的关于几何学的演绎知识体系。所谓公理化结构就是:选取少量的原始概念和不需证明的命题,作为定义、公设和公理,使它们成为整个体系的出发点和逻辑依据,然后运用逻辑推理证明其他命题。《几何原本》成为了两千多年来运用公理化方法的一个绝好典范。从来没有一本教科书,象《几何原本》这样长期占据着几何学教科书的头把交椅。从1482年出现活字印刷以来,《几何原本》竟然印刷了一千版以上。而在此之前,它的手抄本统御几何学达一千八百年之久。欧几里德的影响是如此深远,以至于欧几里德和几何学变成了同义语。
诚然,正如一些现代数学家所指出的那样,《几何原本》存在着一些结构上的缺陷,但这丝毫无损于这部著作的崇高价值。它的影响之深远.使得“欧几里德”与“几何学”几乎成了同义语。它集中体现了希腊数学所奠定的数学思想、数学精神,是人类文化遗产中的一块瑰宝。
《几何原本》的伟大历史意义在于它是用公理方法建立起演绎的数学体系的最早典范。这部著作给后人以极大的启发,不仅由此引出了公理化演绎的结构方法,给数学以及其他自然科学以典范的作用,而且由于其中第五公设的不可证明性质,引发了非欧几何的出现。
无疑,欧几里德是希腊几何的集大成者,在整个数学史上树立了丰碑。
(二)欧几里德及其《几何原本》的数学思想与方法
1.封闭的演绎体系的思想
《几何原本》是最早形成的演绎体系,是一个由一般到个别的表述体系。它是由少数不加定义的概念(原始概念)和少量不加证明的命题(公理和公设)出发,按一定的逻辑规则,定义出该体系中所有的其他概念,推演出所有其他的命题(定理)。《几何原本》中的定义、公理、定理等构成的数学理论体系,原则上不必依赖于其他东西;从《几何原本》的逻辑结构来看,它是一个演绎体系;从《几何原本》与社会生产、生活的关系来看,它的理论体系是独立于社会生活而展开的,在其发展中也回避任何与现实生活有关的应用问题,因而对于社会生活的各个领域来说,它是封闭的;同时,《几何原本》除所用的逻辑规则外,具备了其理论推导的所有前提,就是从理论发展形式来看也是封闭的。
2.内容抽象化的思想
《几何原本》中涉及的都是一般的、抽象的概念和命题,它所探讨的是这些概念和命题之间的逻辑关系,它不考虑这些概念和命题与社会具体生活的关系,也不研究这些数学“模型”所由之产生的那些现实原型。从它的命题自身来看是抽象的,而这正是它的主要内容。从另一方面来看,具体是多样性的统一,现实世界的客观存在是具体的,《几何原本》却极力排斥其理论命题的实际应用,因而从抽象与具体的关系来看,其内容也是抽象化的。
3.公理化的思想方法
公理法是从欧几里德的《几何原本》开始的,它采用比较严格的演绎体系—公理体系,而构造这种公理体系的方法就是公理化方法。《几何原本》的公理化方法的影响是十分深远的,现代数学和各门科学中的公理化方法正是由《几何原本》的公理化方法发展出来的。
《几何原本》思想方法上的这三个特点是相辅相成的。抽象化的内容适合于演绎体系,抽象化得到的命题具有普遍性,同时它也就是演绎推理中的一个环节,又适合于利用公理法确定它在公理体系中的位置。同时抽象命题自身又是演绎证明的产物。
(三)《几何原本》简介
《几何原本》是古希腊数学家欧几里德的一部不朽之作,是当时整个希腊数学成果、方法、思想和精神的结晶,其内容和形式对几何学本身和数学逻辑的发展有着巨大的影响。
《几何原本》的原著有13卷,共包含有23个定义、5个公设、5个公理、286个命题。
第一卷首先给出了一些必要的基本定义、解释、公设和公理,共列有23个定义,5条公理,5条公设。其中最后一条公设就是著名的平行公设,或者叫做第五公设。它引发了几何史上最著名的长达两千多年的关于“平行线理论”的讨论,并最终诞生了非欧几何。还包括一些关于全等形、平行线和直线形的熟知的定理。该卷的最后两个命题是毕达哥拉斯定理及其逆定理。
第二卷篇幅不大,主要讨论毕达哥拉斯学派的几何代数学。
第三卷包括圆、弦、割线、切线以及圆心角和圆周角的一些熟知的定理。这些定理大多都能在现在的中学数学课本中找到。
第四卷则讨论了给定圆的某些内接和外切正多边形的尺规作图问题。
第五卷对欧多克斯的比例理论作了精彩的解释,被认为是最重要的数学杰作之一。据说,捷克斯洛伐克的一位并不出名的数学家和牧师波尔查诺(Bolzano,
1781-
1848),在布拉格度假时,恰好生病,为了分散注意力,他拿起《几何原本》阅读了第五卷的内容。他说,这种高明的方法使他兴奋无比,以致于从病痛中完全解脱出来。此后,每当他朋友生病时,他总是把这作为一剂灵丹妙药向病人推荐。
第六卷讲相似多边形理论。
第七、八、九卷讨论的是初等数论,给出了求两个或多个整数的最大公因子的“欧几里德算法”,讨论了比例、几何级数,还给出了许多关于数论的重要定理。
第十卷讨论无理量,即不可公度的线段,是很难读懂的一卷。
最后三卷,即第十一、十二和十三卷,论述立体几何。目前中学几何课本中的内容,绝大多数都可以在《几何原本》中找到。
《几何原本》的公理系统如下:
公设(只用于几何)五个(欧氏将只在数学中有用的称为公设,对一切科学都适合的才叫公理,现代则统称为公理)
(1)
从任一点到任一别的点可作直线。
(2) 每条直线都可以向两端任意延长。
(3) 以任一点为中心和任意距离为半径可以作一圆。
(4)
所有的直角都相等。
(5)
(平行公设)若一直线和两直线相交,且若同侧所交两内角之和小于两直角,则两直线无限延长后必相交于该侧的一点。
公理五个:
(1)
跟同一件东西相等的一些东西,它们彼此也相等。
(2) 等量加等量,总量仍相等。
(3) 等量减等量,余量仍相等。
(4)
彼此重合的东西是相等的。
(5) 整体大于部分。
19164是不是看书要细腻,多做题
19164中在实践
19164多多作题,其实对于离散这种课程.多做题才能对其本质有更好的理解.当然同时也加强了运用的能力.
19164我到不这样认为,多做题是高中的思维.做为一个大学生我们要注重知识的积累.不要为了考试而去学习.那就失去上大学的意义了.
19164学数学,做题是必不可少的!!关键在与做题的动机和过程!!
19167如题
19168ruti
19169如题
19
170如题
19
171ruti
19
172如题
19
173若A,B相似,是否必有A*,B*(古典伴随)相似?
19
174美国数学会和台湾数学会联合召开的第一届国际会议将在台湾举行
美国数学会和台湾数学会联合召开的第一届国际会议将在台湾举行
Date: Tue, 4 Oct 2005
11:52:56 +0800 (HKT)
First Joint International Meeting Between AMS
and the Taiwanese Mathematical
Society
December 14-
18, 2005
Taichung, Taiwan
http://www.ams.org/amsmtgs/2123_other.html http://www.math.thu.edu.tw/2005ims/en/index.htm
Invited Addresses
Lawrence Ein, University of Illinois at
Chicago
Chang-Shou Lin, National Chung Cheng University
Richard M.
Schoen, Stanford University
Jing Yu, National Tsing Hua University
Jiu-Kang Yu, Purdue University
Organized by
Department
of Mathematics, TungHai University
The Mathematical Society of Taiwan
American Mathematical Society
National Center for Theoretical
Sciences
Institute of Mathematics, Academia Sinica
The meeting
will take place at Tunghai University,
181 Taichung
Harbor Road,
Section 3 Tiachung 40704, Taiwan. For more information
about the
campus see www.thu.edu.tw/english/enindex.htm.
19
175在核壳微结构中通过应力驱动可自组织形成三角和斐波纳契数花样
摘自《基础科学研究快报》2005年8月25日 第8期
<科研基地>栏目
在核壳微结构中通过应力驱动可自组织
形成三角和斐波纳契数花样
斐波纳契数(Fibonacci
number)和具有内禀缺陷的三角形花样结构常出现在自然界中的一些表面结构中,特别是植物如向日葵、雏菊以及菠萝等其种子、叶片或花序排列常表现出两组相临的斐波纳契数。中科院物理所北京凝聚态物理国家实验室(筹)李超荣、张晓娜和曹则贤设计了一种应力自组织实验,将氧化银和氧化硅混合物蒸发到保持在1000℃的基片上,形成一些10μm大小、核为银而壳为氧化硅的液滴,然后冷却。结果他们发现在近似球形的壳层表面上形成了三角形格子结构,而在非球形表面上形成了(5,8)和(8,13)等斐波纳契数花样结构。研究人员分析认为,由于银和氧化硅在冷却中收缩程度不同,导致该核壳结构中产生应力,并导致物质及结构的重新分布以降低表面的应力能,形成三角格子或斐波纳契数花样。该研究将有助于理解自然界存在的一些有趣结构,并为英国科学家Thompson在
1941年就提出的关于生物体的生长形状本质上是数学问题和物理问题的假说提供了一个证据。相关研究论文发表在2005年8月5日Science,
309 (5736): 909-911上。
19
176量子计算机遇到的根本性限制
摘自《基础科学动态监测快报》2005年8月1日
第15期
(Fundamental Limitation to Quantum Computers,
http://www.sciencedaily.com/releases/2005/...0708060942.htm)
量子计算机遇到的根本性限制
荷兰莱顿大学的理论物理学家在近期Phys Rev Lett
上发表的文章中指出,量子计算机面临一个根本性限制。
量子计算机只能在信息存储到足够长的时间才能运行。量子比特的所谓一致性确保了量子信息的完整保留。研究人员发现超过时间进程并且还要利用这个存储信息时,这种一致性会自然消失。这对量子计算机的发展是个重要问题。量子计算机利用的是量子力学系统——
一个电子、原子或更大的系统,比如可以模拟两个存在状态的超导量子比特。通常两个状态中的一个状态一消失,系统就会与外部产生接触,而导致一致性消失、量子比特中的信息丢失。
典型的量子比特由大量粒子组成,无奈受到环境影响的可能性很大,因此会受制于不一致性。莱顿大学罗伦兹研究所的Jasper van
Wezel等人己经开始研究是否可能在孤立的量子比特中保持一致性。他们的研究发现令人惊讶,一致性甚至在没有外界影响的情况下也会本能地趋向于消失。这个过程与量子力学的自然对称破缺有关。经典物理中,有一个与该过程等价的例子——溶液中的自然结晶化,在一个确定的位置,晶体自然形成,从而打破了流体的结构。
按照研究人员的预测,量子比特的一致性将会在一些很有希望的概念中消失。而且,量子比特越小发生消失就越快。所有这些对量子比特的发展似乎已经形成了一个基本限制。实验研究将会证明这种现象是否真会发生。
19
176好帖,为什么量子信息会丢失?有空再学学物理.
19
176什么是一致性啊?
19
176还需要进一步研究!
19
176
引用 (qinghuas @ 2005年10月12日
17时47分) |
量子计算机遇到的根本性限制
摘自《基础科学动态监测快报》2005年8月1日 第15期
(Fundamental Limitation to Quantum Computers,
http://www.sciencedaily.com/releases/2005/...0708060942.htm)
量子计算机遇到的根本性限制
荷兰莱顿大学的理论物理学家在近期Phys Rev Lett
上发表的文章中指出,量子计算机面临一个根本性限制。
量子计算机只能在信息存储到足够长的时间才能运行。量子比特的所谓一致性确保了量子信息的完整保留。研究人员发现超过时间进程并且还要利用这个存储信息时,这种一致性会自然消失。这对量子计算机的发展是个重要问题。量子计算机利用的是量子力学系统——
一个电子、原子或更大的系统,比如可以模拟两个存在状态的超导量子比特。通常两个状态中的一个状态一消失,系统就会与外部产生接触,而导致一致性消失、量子比特中的信息丢失。
典型的量子比特由大量粒子组成,无奈受到环境影响的可能性很大,因此会受制于不一致性。莱顿大学罗伦兹研究所的Jasper van
Wezel等人己经开始研究是否可能在孤立的量子比特中保持一致性。他们的研究发现令人惊讶,一致性甚至在没有外界影响的情况下也会本能地趋向于消失。这个过程与量子力学的自然对称破缺有关。经典物理中,有一个与该过程等价的例子——溶液中的自然结晶化,在一个确定的位置,晶体自然形成,从而打破了流体的结构。
按照研究人员的预测,量子比特的一致性将会在一些很有希望的概念中消失。而且,量子比特越小发生消失就越快。所有这些对量子比特的发展似乎已经形成了一个基本限制。实验研究将会证明这种现象是否真会发生。
|
看了半天,没真看明白。
这文章说的是碰到了个什么限制?
19
176这是去年的消息了……
19
177计算数学前沿问题及其在物理科学中的应用高级研讨班将在香港举办
计算数学前沿问题及其在物理科学中的应用高级研讨班将在香港举办
Date: Tue, 4 Oct 2005
11:52:56 +0800 (HKT)
From: "Prof. T. Tang"
The
Croucher Foundation - Advanced Study Institute on
Frontiers in
Computational Methods and Their Applications in Physical Sciences
December 6 - 13, 2005
The Chinese University of Hong Kong
organized by
Department of Physics and Institute of
Theoretical Physics,
The Chinese University of Hong Kong
sponsored by
The Croucher Foundation
Organizing
Committee (tentative)
Director: Hai-Qing Lin (CUHK)
Sec'y:
Pui-Yee Ho (CUHK)
Che-Ting Chan (HKUST)
Zhi-Feng Liu (CUHK)
Chi-Fai Lo (CUHK)
Lei-Han Tang (HKBU)
Fu-Chun Zhang (HKU)
Rui-Qin Zhang (CityU)
Invited Lecturers (tentative)
Roberto Car, Princeton Univ.
David M. Ceperley, Univ. of Illinois
James E. Gubernatis, LANL
David P. Landau, Univ. of Georgia
Steven G. Louie, UC Berkeley
Andrew Chi-Chih Yao, Tsinghua Univ.
Associate Lecturers (tentative)
C. T. Chan, Hong Kong Univ. of
Sci. & Tech.
G. H. Chen, Univ. of Hong Kong
J. M. Dong,
Nanjing Univ.
Yong Duan, UC Davis
X. G. Gong, Fudan Univ.
Luhua Lai, Peking Univ.
T. K. Lee,, Institute of Physics, Academia
Sinica
P. W. Leung, Hong Kong Univ. of Sci. & Tech. H. Q. Lin,
Chinese Univ. of Hong
Kong
Z. F. Liu, Chinese Univ. of Hong Kong
Gerardo Ortiz, Los Alamos National Lab.
A. W. Sandvik, Boston
Univ.
L. H. Tang, Hong Kong Baptist Univ.
John Tse, National
Research Council, Canada
D. S. Wang, Institute of Physics, CAS
Enge Wang, Institute of Physics, CAS
J. Wang, Univ. of Hong Kong
J. S. Wang, National Singapore Univ.
X. C. Zeng, Univ. of
Nebraska-Lincoln
B. Zheng, Zhejiang Univ.
Tutorial Courses
In connection with the ASI, the Physics Department of CUHK will also
sponsor
one regular course and two tutorial courses, to provide some
background for ASI
students.
Advanced Computational Physics:
Lecturer: H. Q. Lin
Date: Sept. 5 - Dec. 3, 2005. Regular lecture
course. Introduction to ab
initio Methods:
Lecturers (Tentative):
X. G. Gong, John Tse, Z. F. Liu, J. Wang
Date: Nov. 14 - 25, 2005. 12
hours. Introduction to Computational
Bioscience:
Lecturers
(Tentative): Y. Duan, E. G. Wang, Luhua Lai, G. H. Chen
Date: Nov. 26
- Dec. 6, 2005. 10-12 hours.
Mission: To review recent advances in
computational physics by emphasizing the
impact that new developments
in large scale numerical computation have
significantly enhanced our
comprehension of the physical nature of materials as
well as our
capability in designing new materials.
To conduct in-depth
discussions on selected state-of-the-art methods for
solving important
numerical problems in statistical and materials physics.
To
facilitate a brain-storming forum for the generation of ideas on novel
methods and new applications.
Structure: Six morning 3-hour
lectures and presentations/discussions in five
afternoons. The working
language is English.
19
178相识数学
张顺燕(北大数学系教授)
同学们好,老师们好,今天我讲的题目叫做相识数学,我打算展现给诸位一门特殊的学问和一门特殊的艺术,这就是数学。我希望通过这次讲座,能够改变你对数学的看法,能够丰富你对数学的理解,能够消除你可能对数学存在的误会,使你认识到数学的重要性,使得数学成为你的朋友,在你的学习和工作中,成为你的得力工具。那么我讲的主要内容包含着一,数学与艺术。二,什么是数学。也就是我准备给数学下一个定义,第三我讲数学的真理性,换句话说数学的定理,并不是客观真理。我想回答这个问题,四,我想讲数学的特点,那么,最后我可能提一下,数学的重要性,但是不会充分展开,因为时间不够,下面,我先讲第一,数学与艺术。
数学之美,是看不见的,它隐藏在大众的视线之后,因而,数学的美常常是被忽视的。而,只注意数学的使用方面,这样,使数学就变成一门枯燥的学问。或者只是为了应考,使得一些同学,或者一些人,对数学产生了一种厌烦,那么这是不符合数学本身的思想,也不符合现代素质教育的思想。因而,我要把数学之美,展现给诸位。那么,第一天,我要谈的就是说,数学是美学的四大支柱之一。美学哪四大支柱呢?就是我们屏幕上显示的,第一是诗歌,它展现了心灵的艺术。表达心灵之美,第二大支柱是音乐,第三个是造型艺术,造型艺术,包含绘画,雕塑,建筑,这三种艺术用来表达人的感情,表达人的情趣,那么,第四种支柱就是数学。数学展现的是心灵之美,展现的是思维的逻辑,是理性之光,只有把理性和感性的认识结合起来,那才是完美的美,这里面我要提提,为什么把美看得这么重要,我把美放在第一位来谈这个,那么我想有这么三条理由,第一条理由就是科学价值的评价有两个标准,一个标准是美学标准,一个标准是实用标准,任何一门科学,物理学,化学,生物学全是这两个标准。
过去我们讲数学忽略美学标准,重点地讲实用标准,甚至重点地只讲考试,所以这是不全面的我们把它纠正过来,第二个
讲科学研究的任务有两条,一条叫判美,一条叫做析理,什么叫判美呢?这是我从中国古代大哲学家庄子的话里面摘取的,就是你看银幕上写的叫判天地之美,析万物之理。什么叫判天地之美呢?就是要把宇宙间的和谐和韵律找出来,而且鉴赏它,这就是判天地之美。那么,简而言之叫判美。那么第二个就是析万物之理,我们光判美还不很,我们得把控制事物的自然规律找出来,所以,科学的任务就是两条一个是判美一个是析理,我们想通过这个讲座,把数学的魅力展现给大家,把数学推理的奥妙展现给大家,这是第二个理由。第三个理由,我们说美和真连接在一起的,美国著名博物学家赫胥黎此人名气很大,就是说,达尔文的进化论是靠着这位赫胥黎才奠定了他的基础的,所以这是一位大博物学家又是一位大演说家。他说了这样一段很深刻的话,就是我屏幕上写的,叫做科学和艺术是自然奖章的两面,一面是用感情来表达事物的秩序,一面用思想的形式,来表达事物的永恒秩序。所以,美和真本来应该是连在一起的,希腊箴言有这么一句话,叫做美是真理的光辉,因而我们一定把美和真联系在一起。
英国诗人济慈写了一段诗,这段诗写得很好,就四句话,叫做美就是真,真就是美,这就是你所知道的和你应该知道的。因而,我讲了三条理由,讲美是研究数学必不可少的有了美你就有兴趣,有了美你就可以深入,美既是激发你的感情,又是推动你前进的动力,所以我想应该让我们怀着美来探索数学的奥秘,这是我讲的第一段。
那么,我讲第二段,什么是数学,因而我今天要给数学下个定义,但是我们看到给数学下定义是一件困难的事情,为什么?你拿任何一个东西下定义都不容易。比如举个例子,咱们给狗下定义,什么叫狗?你说它有四条腿一个脑袋,两个耳朵一个尾巴这是狗的必要条件,每个狗都有这个,四条腿,两个耳朵一条尾巴,但是,猫也有,老鼠也有,你这个定义不能够把狗从老鼠和猫里面区别开来,因而,真下个定义并不容易。不信你回去试试看,那么这就是说,给数学下定义也不容易,因而数学定义不是唯一的。今天我讲一个最基本的最追求最精湛的定义是恩格斯给的定义,叫做数学是数和形的学问。
我首先讲,数学是数和形的学问,它包含着两大分支,数学这棵大树它的根深深扎在现实世界之中。它有两大主干,一个是几何一个是代数。代数又分成很多分支,比如说,线性代数,高等代数,群论等,几何又分成很多分支,欧式几何,非欧几何,包括双曲几何,椭圆几何微分几何很多支,同时,这两大支干还互相交叉,形成很多其他新的分支,我们讲,数学是一棵大树,这棵大树如此之古老它已经有上万年的历史,这棵大树如此之常青,它每年都在发新枝。这个大树是如此之繁茂,它从自然科学深入到社会科学的各个领域。现在已经深入到深入的各个领域。这个树又是此奇特,奇特在什么地方呢?这个树是同根异干,同干异枝。同枝异叶,同叶异花,同花异果。它没有两个枝是一样的。没有两个叶是一样的。是非常奇特的一个树。等一下我们摘那么一两枝来看看到底它怎么奇特,到底它多么地不同。那么,现在我们先来讲,它的两大主干,一大主干是几何,一大主干是代数,那么,什么叫几何?几何是研究空间形势的,那么,几何是是是视觉思维占主导地位,要用眼睛看,培养知觉能力,培养洞察力。
我们看代数,代数是数量关系的科学,它有序思维占主导地位,它培养逻辑能力,培养符号运算能力,我们通常学代数,学几何,如果你没有从整体上把握这两个特征,那么我说你的几何和代数没有学透。事实上,由知觉和洞察力发明的那些东西,要靠逻辑来证明。所以这两者是相辅相成的。不能互相分开。
华罗庚他关于形和数之间的关系,描写得非常好。他说,数缺形时少直觉,形少数时难入微。数形结合百般好,隔离分开万事非。那么现在我们回到数学定义,什么叫数学呢?在
19世纪末,恩格斯根据当时数学发展情况,做了一个精密的总结。他说,数学就是研究空间形式和数量关系的科学。恩格斯这个定义,直到现在,仍然概括了数学的大部分。但是
19世纪末,20世纪初又诞生了一个新的数学分支。比如数理逻辑,它里边没有形,也没有数,所以,很难数理逻辑又归到数和形的学问里边。这个定义也有它的局限性,因而,人们又企图寻找新的定义,那么今天新的定义我们就没有时间介绍,告诉大家的的确确还有,那么你自己也可以去寻找,我讲第三条。
第三条我讲花瓶上的几何学。大家看花瓶,这个花瓶上展现了三种几何。大家平时都听说过的,非欧几何三角形内角和不等于
180度,双曲几何三角形内角和小于
180度,这是双曲几何在底下呢。椭圆几何三角形内角和大于
180度,它在上面呢。欧氏集合2,三角形内角和等于
180度,在中间呢。所以,我们一下子就在这里看到了三种几何,那么,这三种几何是怎么诞生的呢?现在我来讲一讲。
首先我讲,一维几何就有三种不同的几何。那怎么说呢?咱们看看一维几何?一维空间就是一根线,或者一个曲线,用一个参数可以描述的。直线曲线都是一维的平面是二维的空间是三维现在我们来看看一维的几何。先看直线,直线画了三个点,我把直线左右分一下,我假定人站在B点,面向上,他的左手指左边,右手指右边,我这个图上写出来了,所以,A在B的左边。B在C的左边。那么,结论是A在B左,B在C左,结果A也在C左。对吧,但是,咱们再看看圆上的几何。我假定人站在B上,面朝外,他左手指的地方是左右手指的地方是右,所以,上面画出来左右了。那么,显然A在B左,B在C左,是不是A在C左呢?不是,现在,A在C右,这个位置关系不一样了,我们知道几何学是研究空间的几何形体在空间中的位置,及其相互关系的,现在它们的相互关系变了,在直线上B在C左,A在C左,那么,A比在B左,但是,到了圆上A在B左,B在C左,A在C右。展现的是不同的几何位置上表现了不同的含义
那么再看还也不同,看直线上三个点,ABC,B在中点,只有一个中点,AC都不是中点,但是看圆,A是中点,B是中点,C也是中点。每个点都是中点,因而,在一维空间,至少就有两种几何了,我们现在只考虑位置还没有考虑到长度。现在,回过头来,我们来看,二维几何。
讲二维几何,我们刚才讲了三种,叫欧氏几何,双曲几何,椭圆几何,我来讲讲这三种几何是怎么诞生的,首先我们看,欧几里得公设,我们必须回到出发点,欧几里得几何是公元前2000年前就已经诞生了这个几何一直是中学教育的重要内容,而且我们的几何,和欧几里得几何,本质上没有大的差别,只是后来做了些技术上的改进。那么,欧几里得集合是从5条公理出发,推演出几百条定理。非常复杂,非常深刻定理,那么,欧氏几何就成了一种样板,使得所有的人类文明的各个领域都以它为样板,把知识总结到,就是简化到最简,然后,再把复杂的理论推出来,这是非常好的一个模型。
那么,欧几里得几何5条公理我们把这5条公理重复一下。第一个就是接连任何两点可以做一个直线段,这没有任何怀疑,第二个一个直线段可以沿着两端任意延长,第三个,以任意点为中心,过另外任意一个点,只能做一个圆,第四个,凡直角都相等,第五条,如果在一个平面内,任意一条直线与两条直线相交,我们把图摆出来,任意一条直线与两条直线相交,如果,相交的一层的内错角之和小于π,那么它一定在这侧,如果α+β小于π,那么,这两个直线一定在这一层相交,这是欧几里得的第五公设,后来,人们觉得第五公设比较复杂,改成一种等价的形式,就是过直线的一点有一条平行线,且有一条平行线,有这个,直线L上面有一点P,过点P只能做一条平行线。这就是欧几里得几何,欧几里得几何诞生之后,人们就开始研究第五公设,为什么前四条公设都是有限平面内,看得见,摸得着,第五条谁也没有到过无穷远,它的要延长到无穷远不相交,谁也没到过无穷远。对于欧几里得本人也有怀疑,还有的人觉得这个东西,不像公理,像定理,我能不能把它证明。所以,从欧几里得开始,就有各种各样的数学家来研究第五公设,或者想代替它或者想证明它,研究的总人数超过一个军团,但是,始终没有任何结果。到了
17世纪
18世纪
19世纪,最著名的我们提出三个人来。
一个是
1829年,俄国数学家罗巴切夫斯基,他写了书,他的书名叫论几何基础,在这个书里面,他假定过线外一点,有两条线与所给直线平行,得到了个几何,其中得到很多奇妙的定理,但是没有矛盾,一个是
1832年,匈牙利的数学家叫鲍耶,他写一本绝对几何学,他也假定过线外一定,可以做两条线和已知直线平行,他也得到很多结论,他把他的几何学叫做星空几何学,他自己说,我通过自己的双手,建立了一个奇妙的新世界,也没有矛盾,他把这个东西寄给了高斯,大数学家高斯,高斯怎么看呢?高斯比他们早2、30年已经知道了这种几何形式存在,但是,高斯比较谨慎,他不敢说,他怕引起争论,他别人说他,他只是给鲍耶的爸爸回了封信,他说,你的这个想法我早就有了,所以使得鲍耶的爸爸感到很丧气,那么高斯的事情是从他死了之后,从他的手稿里面拿出来的,但是,当时这个思想是及其先进,大部分数学家没有接受它。一般人更不接受。
那么同时我们讲一讲欧氏几何有什么意义。我们得到了三几何,这三种几何都是相容的,彼此之间没有矛盾,那么,马上人们就怀疑,欧几里得几何是真理,这个事对不对,所以,这一点我们就提到数学的真理性。欧氏几何几何的诞生,动摇了人们的真理观使人们认识到数学是一种思维的产物,不是客观世界的产物,同时,又让人看到,三种几何不是两种几何,也就是说,数学是逻辑的产物,数学的结果比自然的结果要丰富,自然界只是其中之一。在这里边,我们顺便提及,三种几何在我们通常的尺度下,无法辨别,现在还没有测量仪器可以在正常尺度下辨别它的大小,在正常尺度下,三种几何的角度都接近于
180度,高斯曾经找了三个山头,他以为很远了,测的结果呢?当然不是
180度,为什么呢测量有误差,但误差非常小。到底是三角形不是
180度,还是仪器不精确造成的,这个没法分辨,我们说了三种几何,我们拿出来几何来看看,的的确确,数学是这样,同枝异干,同干异枝,同枝异叶是不同的。每两个东西都是完全不一样的。
那么,几何学是不是只有这三种,有没有别的种呢,我们说,还有很多种几何,还有摄影几何有限几何,拓扑学,种类很多。那么,今天,还想再介绍一个,跟几何学有关的课题,那是想先介绍一下绘画和几何的关系。
达芬奇是文艺复兴时期最杰出的画家,他画了很多非常出色的画,他一生画得不多,但,每一幅画都是镜片。比如说,蒙娜丽莎,这大家知道的,比如说,最后的晚餐,达芬奇自己这么说过,任何人类探求活动,也不能成为科学,除非这种活动通过数学来表达,或者,经过数学证明,为自己开辟道路。他的绘画的就是以数学开辟道路的。那么,这里面我们就讲,他要画东西,怎么画呢?这很简单的事就是近东西要画大,远东西要画下,那么,近处大,远处小小多少?你不能笼统讲,远人无目,我不画眼睛就完了。那不成,因为那精确,你要精确地再现,你就要有数学定理,还有,眼睛看到的几何学不是欧氏几何。
为什么?我们站在铁轨的两边,看铁轨,那么近处宽越靠远处越窄。站在马路的两旁,站在这边看着这边宽,站在那边看着那边宽。所以,眼睛看到的几何学和欧氏几何学是不一致的,另外,还应该研究一个,眼睛看到的几何学,视觉几何学,而且应该把这种几何学画到绘画里面去,那么,我现在展现给大家一个图。而且,绘画还要以数学定理作引导,我们看这个画。
这是个走廊,这个走廊,是平行的,但是,你画出来不能画平行,你怎么画呢?你看,这是两根平行线,而且,这两根线是要相交的,相交到这一点,这个交点叫做没影点,这个交点叫主没影点,这个线叫水平线,所以如果我们作一个真实地表达客观现实的画的话,我们首先要有几何定理来保证,那么,我现在给两条定理。一定定理就是说,凡是和画面垂直的,那些平行线要相交,看到没有?还有,凡是和画面平行的这些线要画成平行。这就两个定理,当然我是我是粗浅地讲绘画,你深入地讲绘画,还要有别的定理。很得更深入。所以,你看到,绘画是要用到精确的数学,现在我们来看达芬其的最后晚餐。
这是耶稣,这是他的六大门徒,靠上看这是天花板,那么,耶稣张开着手,扶在这儿,诸位看看这个里边到底有什么几何构图呢?我们来看看的达芬其最后晚餐的几何构图,他分成这么几块,一二三四五六七八,中间这个正方形画出的对角线,耶稣的脑袋就在这个中点,这个中点是没影点,那么看,详细地看,这是两个对顶角,这个对顶角这边画着门徒,这边画着门徒,耶稣就在这里,上边都画出了大的天花板的位置,那么这个图就更加详细了,这边是六大门徒,这边六大门徒,这是耶稣的脑袋,然后这里是天花板看得很清楚,那么,最后完成的结果呢?就是,这是天花板,这是耶稣的头,在这两个对角线里面,这是六大门徒,这是六大门徒,而耶稣的两个胳膊,正好构成三角形,趴在桌子上,所以,他做了精确的数学构思。那么,现在,我讲一讲数学的特点。
第一个特点是抽象性,数学非常抽象,点,就是很抽象的概念,为什么?没有大小,只有位置。直线,有长度,许多宽度,平面,没有厚度,这要靠抽象。数本就是抽象,三,三是什么东西呢?只有和狗马结合起来才有意义,光一个三是很抽象的是从各种不同的具有三性的东西里面抽象出来的。所以,数本来就抽象,然后我们又把数抽象到ABC,ABC还不够,我们抽象成函数,泛函,一级高一级,所以,数学的概念非常抽象,而且,数学的论证也非常抽象。数学不靠实验,你说,歌德巴赫定理,我验证到100万那不成,得不到承认,必须证明,所以,数学一是概念抽象,二是推理抽象,就是它非常抽象。
第二个数学非常精确,是任何一个其他自然科学达不到的,它精确的定义还有准确的结论。是它的特色。在数学中没有含糊,一等于一,二等于二,没有可以通融的,讲个故事。有一次,三位著名人物访问云南,一个是文学家,一个是物理学家,一个是数学家。走到云南,靠窗外一了望,文学家感叹,云南的羊都是黑的。这个物理学家一看,说,云南有一块地上有一只羊是黑的。数学家也看了看,数学家说,在云南,至至少有一块地上,至少有一只羊至少有半边是黑的。因为,那半边他没有看到,他说的是极其准确的。那半边是花布的不是花的呢?那可能还是花的呢,所以数学的一大特点是它的精确性。
数学最后一个特点,第三个特点,就是应用的广泛性,这里面我们引用一下,华罗庚教授的一段话,他是这样讲的,宇宙之大,粒子之微,火箭之速,化工之巧地球之变,生物之谜,日用之繁,数学处不在。凡是出现的量的地方,就少不了数学,研究量的关系,量的变化,量的变化关系,量的关系的变化,等现象,都少不了数学,数用之用,贯穿到一切科学的深处。而成为它们得力的助手和工具,缺少了它就不能准确地刻画客观事物的变化,更不能由已知数据推出其他数据,因而,就减少了科学的预见的可能性,或减弱了科学预见的精确性。
华罗庚先生,非常精确地讲了数学的应用,事实上,我们讲,二次世界大战之后,数学,和过去的面貌,发生了质的变化,来原因有两条,一条是数学已经直接深入到社会科学各个领域之中,直接应用。一条,计算机诞生,使得人们可以通过计算机做数学实验,所以,数学现在的用处,非常之大,非常之广,超出了我们的想象。那么,这里面,我顺便提一下,就是说,数学将成为以后,人们选择职业,或考核人的水平的一大重要标准。换句话说,数学,越来越将和就业紧密地天下在一起,现在我们就业要文凭,要学历,把这个文凭学历背后要求的东西,分析一下,只有两条,一条是你的语文水平,你表达能力如何,一条是你的数学水平,现在在西方先进国家,已经把学历的考察作为第二位,首先考察的是这两个能力。他们把这两个能力,分成六个阶梯,不同的人,你进不了这个阶梯,你就休想做这个阶梯的工作,所以,数学的应用,已经渗入到各个领域,今天,我就讲这么多,谢谢诸位。
问:您在这里能不能给我们大家介绍一下,您是怎么样做您的工作,您的治学经验,以及学数学的一些方法,可不可以?
答:那么,刚才我给大家念了华罗庚先生的四句诗,他就讲,数缺形时少直观,形少数时难入微,这个话讲得非常深刻。在我做学生的时候,我曾经亲自听过华先生几次讲座,他讲的时候,就教导我们一定要把它联系其他,同时要把这个东西搞得非常透,搞得非常直观。那么,你才能学好,而我们现在,常常是从逻辑出发,实际上前面并没有消化就讲后面的了,所以,无论从学习来讲,从教书来讲,都应该把知识弄得更彻底,更简单。更明确,更直观,和生活的联系更密切。
问:我们现在教的数学就是叫做一条鱼,给它烧中段,头是什么样的没有看到,尾巴是怎么样的也看不到,只给学生介绍鱼的中段,所以,我在讲课当中,学生就问我,老师这个东西有什么用,以及这个东西,你怎么想出来的?
答:我们讲逻辑讲得多,讲直观讲得少,我们只讲定理的证明,不讲定理证明是怎么发现的,也不讲定理当初是怎么发现的。那么,历史上,我刚才提了很多,数学大定理的发现,它都不是逻辑的结果,都是猜测的结果都是实验的结果,你解个例子,比如哥德巴赫猜想,任何大于6的偶数,都是两个奇素数的和,任何大于9的奇数,都是三个奇素数的和,这是很著名的,大家都知道,那么这个就是猜测的结果。作为一个定理成立不成立,现在还没有证明。比如说,还有在自然数当中,我们知道有些数很特殊,比如素数,三五七都是素数,换句话,它只能被自己和一除尽,被的数除不尽,那么,素数在自然数当中,到底占多少?这个问题是很深刻的。我们看看大数学家高斯他怎么处这个问题的高斯他就算,十之内有几个,100之内有几个,1000之内有几个,他真算,算了之后,他从这个数据当中,来找关系,到了契比舍夫,他证明了。,那他是在前提算的基础上,并不是什么人一下就想出一个奇妙的公式来。
但是我们现在上课追究完美,不愿意讲这些东西,也不讲数学家在获得这些真理的艰苦奋斗的过程,我觉得应该讲,为什么?这样讲的话,就使得同学可以增加勇气,知道就是那些大人物,大数学家,他们证明一个定理也要不花不少辛苦,不是他的天才,坐下在那儿一想就出来。不是这样的,也花功夫的,那么对于培养同学们自己去克服困难,发明新定理,这是非常有利的。
问:张老师,我想问一下,您讲的几何数学和我们现在中学学的那个数学有什么联系?
答:我们现在中学讲的几何就是欧氏几何,就是过一点,只能做一条平行线和底下平行,在这个基础上,得到几何学,我们在中学里没有讲非欧几何,我觉得,这应该是一个缺陷,当然是在初中讲高中讲这个我们不好说,据我所知,国外是要讲非欧几何的。因为,认识一个事物,是要靠比较,只有一种,你就不知道它好在哪?而且,欧氏几何,的的确确还有很多值得研究的地方,还有值得改进的地方。如果我们把欧氏几何讲成一个完美无缺的东西,这个东西,一是不符合事实,二是对学生的成长,是不利的。反而觉得会变成一种崇拜了,而不是钻研有什么不足,我们怎么改进,事实上欧氏几何有什么东西是值得改进的。它不研究乱七八糟的东西,云彩什么样的树什么样的,这种乱七八糟的它不研究,但是这是真实的现实世界,那么到了上世纪70年代,又诞生了个新的几何这个几何叫分形几何。
它就专门研究云彩,树枝,闪电,就是各种各样奇奇怪怪的形状,从这些形状中,包括我们的视网膜,我们的血管,这种复杂的形状,而这种几何又非常有用,我以为我们中学里应该适当地介绍分形几何。
19
178好!!
19
178写得很很好啊
顶
19
178又视频妈?
19
178晕 这是自己认为的把
19
178有点那个为纯科学呼吁里的感觉啊 这样的话就是50子7
19
179顶!
19
179数学与我们的生活
中科院系统科学研究所研究员:胡作玄
数学是一个我们费力很多,但是,好像所得甚少的这么一门科学,因为,大多数人,比如说要义务教育就是读9年的数学,要高中毕业就要读12年的数学,你要上大学里面,无论你学理公还是经济管理,又要学数学,所以,每一个人他的数学教育,花在数学上的时间是非常之长的,可是,现在,反过来,就是你在平常日常生活中,有没有用到数学。这些数学是不是有用,对你有什么帮助?好像就是不像其他的基础课程,那么明显。因为,从近代欧洲教育来说,就叫3R,有的人翻错了就是读写算对吧?这个从小学起就要读写算,读写算,就是这三个是基础课。现在,我们这个大学入学考试,也是要重点是三,这个三其实也是读写算,只不过读写这两个是学语文,或者外语,而数学又放在一个非常重要的地位。可是,你学完了数学以后,对数学究竟有多少了解,这个是不太可靠的,就是说,你平常用不到数学。我觉得,好像比如说,有的学会计的,他也要学三角,我就不知道,会计的时候,什么时候算过三角,就是这样。所以,你学了三角以后,在什么地方用不大清楚。
所以,总有这样的情况,第二个方面就是说,你学了数学以后,你学的数学,说了半天还是300年前,或者更早的一些知识,你对于近代的数学,是否有了解?那么,一般,很难了解。因为,比如媒体上讲,哥德巴赫猜想,好像哥德巴赫猜想就是数学。可是,你究竟对于现在的数学有多少了解呢?不仅仅一般人不了解,就是数学的专家,也对于隔行的数学也并不是很了解。
这种情况,正好跟其他的科学,恰巧成为一个鲜明的对照,这种对照就是非常明显,因为,即使就是一般老百姓,只要稍微注意一点科学或者技术的发展,都知道,你现在,比如这个微机,网络,网络比较普及的时候,只有几年的时间,那么你再说,比较近节是最近,也是比较普及的东西,激光,激光,什么时候有的呢?
1960年开始第一架激光器。还有基因组计划,也是80年代开始的这个一般了解科学的,克隆当然更普通了,97年开始的。这个大家知道,干细胞,98年才有,纳米技术也是90年代才有,可是,你要问别人,数学有哪些成就,你知道90年代有哪些成就吗?大多数不仅普通人不知道,数学家也不知道,换句话说20世纪数学有哪些成就?一般人也不知道,20世纪有哪些重要的数学家?你要知道物理学家你当然至少可以举爱因斯坦,或者是波尔,海森堡,薛丁谔,你还知道几个,但是,你数学家你知道谁呢?不知道。
所以,数学经过了这么费劲的教育,可是,你自己的知识和在日常生活的应用是非常之少,这个是一个矛盾,这个我们应该怎么理解这个问题?我们讲数学与日常生活之前,我们首先要谈谈,这个到底,这数学,现在有用没用?还是说,就是300年前那些学的算术代数了,最多到微积分就完了,我们说,我们首先要有这么一个概念,现代数学是非常重要的,而且,对于你现代的科学技术起了决定性的作用,不过,数学是一个幕后英雄,用一个平常常说的话,成功男人的背后,总有一个做奉献的女人,这个当然我可以反过来说,成功女人的背后,那么,数学起什么作用呢?你现在有很多的成功的科学技术,但是,数学呢是一个幕后的英雄,我现在想把这点,这就是20世纪的一些重要的成就,我们稍微提几句。
数学最重要的成就,当然,首先是数学家的成就,那么就是20世纪最重大的数学家之一就是叫做冯诺伊曼,冯诺伊曼也有译成纽曼的。当然,我们现在这个计算机已经是换了好几代了,但是它程序设计的思想,确实是冯诺伊曼给出来的,所以,人们常常称冯诺伊曼是电子计算机之父,而且,现在,常常说,你现在,还是冯诺伊曼型的计算机,冯诺伊曼因为翻译不好,有人翻译纽曼,这个我想大家还知道他的名字。那么冯诺伊曼实际上,是一个很伟大的数学家,他的计算机的成就只是他的1/10,可以说,冯诺伊曼是十大武功俱全,就好像乾隆似的,还有一个很重要的成就就叫做,大家都知道的就是叫做博弈论,应该翻成对策论,比较正确。因为对策论现在已经是一个,而且好多经济学家,就因为在对策论上面的成就,拿诺贝尔奖金了,所以,像冯诺伊曼这样的数学家,他就给出来一个计算机的设计思想的最基本的东西,而且,到现在没有太多的改进。唯一一点改进的就叫做并,并行计算,直接翻译就是平行计算,并行计算,并行计算的意思,也是冯诺伊曼的。
所以就是说,数学家,他所做出来的贡献,好多人当然就是说,当然也有很多工程技术人员,物理学家这些人,在计算机方面发展了做出不可低估的贡献,但是,整个的思想,冯诺伊曼是可以说是第一人。第二个例子就是说,影响20世纪,当然现在大家好像感觉到了,战后最重要的一件事情就是核战争了,害怕打核战争。
当然,最初,美国做核战争,做一个核武器,做原子弹和氢弹,当然,在做氢弹的物理学家化学家,还有好多重要的其他的科学家是主角。但是,做一个像原子弹这样的一个技术,没有数学行不行?就光靠你实验,错误实验行不行?这个你要翻开历史,你就发现,数学家在这里面起了很多作用,因为,比如做氢弹的时候,当时的物理学家就有这么一个估计,就是说,氢弹不能做出来,因为,氢弹要爆炸的话,就要把整个地球的大气要燃烧。整个地球都毁了,如果真正这样的话,那么你氢弹做不成。这样,你验证这个观点和否则这个观点,你都不能靠实验,我做一个氢弹试试看行不行,也可能就是说,你完全不知道,在完全不知道的情况下,数学就要起作用。
就是说,经过一些数学家的计算,他说没问题,不至于引起整个大气的燃烧,这样,在做原子弹的时候,你要做多大体积,它怎么样一个爆炸的方式,你也不能实验,而是完全靠数学的计算,当然,中国的情况我不太知道。这就是美国当时做这个原子弹的时候,在开始的时候,都要经历过,你不能做实验的时候,你就要靠数学了,这就是说,靠理论了,这是第二个例子。
第三个例子就是说,现在经济学是一门险学,因为,大家经济上是非常重要的一个科学了,经济上,当然,现在90年代最热门的经济的理论就是叫做金融数学。金融数学,就是说,你怎么投资了,你要把这个股票这些东西。在股票的研究方面,正好100年前,就是
1900年,有一位大数学家,叫做庞加莱,他是20世纪最了不起的一个数学家,他,是最早所谓混沌,好多人都知道了,名词混沌,他最早,100多年前,他就知道混沌这种情况了。只不过现在开始炒作,把这个东西炒热乎了。那么,他有一个学生,就叫做布特朗他就研究股票市场。他研究股票市场的时候,已经知道,这个股票市场,就跟布朗运动完全一样,而现在的布朗远东是最典型的随机过程,这个随机过程理论,当然是现在概率论里面一个最最重要的一个方面,现在的金融,更加用一些随机的问题,随机过程的理论,来研究,因此,设计出来许多所谓叫做衍生的金融产品,衍生的金融产品,现在在国内没有,只是在70年代开始,在美国就开始交易了,就是说,它不是说,具体的交易股票,而是股票的指数,或者是期货,期权,甚至于说你的合同,你应该怎么样交易,你想一个合同就是一张白纸,你到时候可以买这个股票,那么这个,合同,值多少钱?这个就是数学金融里面最重要的问题。
就是说一个合同一个和约,你购买权利,你怎么能够定价,因为你现在,比方说我买一个桌子椅子可以定价,可是,你买一个合同,你怎么定价,这就是比较要用到很多很多,概率论,现在的概率论最新的东西就叫做随机数学了这些东西。
说到经济学,当然就有整个一套经济学理论,20世纪最了不起的经济学家就是凯恩斯,凯恩斯首先最重要的贡献,就是引进了所谓宏观经济学,那么,他的老师,就叫马歇尔,马歇尔他们都是剑桥大学,英国剑桥大学,数学系毕业的都是的数学系毕业的,就是说,像真正的好的经济学家都是做了很多在数学上有很多基础的。
再说一个例子,就是我们常常说的CT,CT就是一个透视的方法,现在已经很普及了,CT是你怎么样通过每一段切片,合成出来一个整体的图象,这个是一个很难的数学问题,可是,这个数学问题,早在
19
17年就被拉东解决了。通过上面的例子来说明什么呢?就是说,数学是一个很的开放的领域,它还是不断地进步了,而且,这种不断进步,形成了一个非常丰富的资源,这个丰富的资源就摆在哪儿,你在某一个适当的时候,你就可能从这里面,发掘出来很重要的东西。这些就是说,数学走在你科学技术发展的前沿。这种现象,就说明了,数学在20世纪,已经跟以前不太一样了,数学已经成为了一个实现的诸葛亮,而不是一个事后的诸葛亮。
现在,对于一般老百姓,或者一般企业的决策人,总的来说,你就不是真正研究数学的人,这些人,数学对他有什么用?我想就两点,一点就是说,你设法有办法,能够利用数学这个整个的资源,就是你要有一定的向导,能够带你到数学的领域里转一转,你不必知道细节,你知道大致的数学里面,搞的是什么东西。这是一方面。第二个方面就是说,通过数学,使得你的思想方法有一个进步,我想,就是我下面随便举两个例子,来说明你的日常生活里面,你如何用数学的思想方法,其实这个就是说,你往前迈一个台阶,你往前迈一步,那么,你就会有许多收获。有的时候,你也可以不必上当受骗了。前不久我们开会,有人就知道,我是学数学的,他说,现在这个彩票,投奖你能不能想办法,你是不是能够知道,下次这个彩票的号码是多少?我就可以,,至少你可以证明,数学是不是有道理?
无独有偶,我还在参考消息上看到了,就是墨西哥有一个老太太,他很信任墨西哥总统,她说,我欠了300万,墨西哥大概是比索吧,我欠了那么多的债,总统先生你能不能告诉我下一次彩票号码是多少?这个是代表了,其实说了半天,当然,第一个是开玩笑的,我就回答说,假如我要知道这个号码,我自己就买了。我就不告诉你了,所以,我说,比如买彩票这种事情,我想,数学家,是不是能够通过这里面发财是不可能的,那么,数学家知道的是一个总体的现象,而一般人只关心他自己个别的现象,这两个是非常之不同的。我这个先说,彩票太复杂,我先说掷骰子,数学家研究概率论,并不能够,他就想赌博,他就能够,因为,概率论来源于赌博,这个也不必在乎它出身不好,但是,它形成了一个很大的科学,但是,概率论所考虑的是所有可能的情形都考虑在内,而不是考虑怎么样赢这个是两码事情,所以,概率论能告诉你的就是说,你掷一个骰子,掷一点,掷二点,掷三点,掷四点掷五点,掷六点那么,你不是掷成这个点就是掷成那个点,假如,这个骰子是均匀的,那么,你掷出来每一个点的概率是1/6,这是一个很简单的办法。
但是我们有一个假定,假定这个骰子是不作弊的话,那么这就是说,叫等可能性原理,就是概率论里面一个等可能性原理,实际上我们默认的假定,那么现在就说到彩票了,我不知道彩票的大致规矩,反正就是说,它是36个球摆在哪儿,然后,出来7个,但是还有一个是第8个,反正你要得到这7个号码,跟这7个球的数码一样,那么你就得了一个最好的奖吧。是特等奖还是一等奖我不知道,有的彩民就说,我买了好多次,为什么老不中?那我就知道,我就跟你说,这个,你的这个彩票,实际上是就是说,你在安排的过程中,有一个假定,假定你每一个球都是处于一个等可能性的状态,但实际上,所有的球不能完全可能,它的因素太多了,凡是因素多了,我们就不能够完全推断,当然,这些彩球是符合牛顿定律的,完全是决定性的,这个没有什么,不像量子力学,是非决定性的它是决定性的但是,这个决定性,由于它的差别,你无法确切地知道,所以,我们中间有一个假定,我们假定它是基本均匀的,它可能有误差,我上回有一次,听见广播里面说,差0.04克,反正就是说,差一点。但是,你这样,有一点差别,我们也是说,你是等可能性的,如果是等可能性的条件下,你就很容易算出来它的概率,大约是800多万分之一,这个概率你要下一注你可以赢,这个800多万分之一什么概念,就是说,你就是非常之少的这么样可能性。
那是我并不是说反对这种,因为这是一个好事,如果是比较保险的话,那么就是说,如果你确实也有人中了大奖了,你拿几百万,你中了大奖,可是你要不去赌这个你就什么也得不到,这个是可以告诉你的,但是,数学家能告诉你什么呢?就是说,如果,你要想一定中,有的人说,我花了8万,我怎么也没中,你用了8万才是0.5%的概率,概率只是0.5%,我们假定是800万分之一多,你在什么情况下能够中呢?必中,那么,你就要花1600百万买所有的号码,那么你必然就中,数学家只能告诉你这个。
还有一个问题也是挺有意思的问题,就是说,我现在,我这一个号码,比如说,1、2、3、4、5、6、7,因为这1、2、3、4、5、6、7,好像你看这些号码不大容易出来,但是,如果你按着假定的等可能性原理,那么,1、2、3、4、5、6、7跟你说,2、4、15、16或者怎么样32,这样,7个球的概率完全一样,就是说,你要有这个概念,所以,你就可以设一个号,我还有一个办法,我设一个号,我老是这个号,那我就每一次我都用这个号,那么你是不是到了一定的时候,你就碰见这个号,按说如此,但是不是说,第一个回合,就要说,你经过了800万次以后,你就能够等到这个也是概率论,这个就是一个随机过程了,所以说,数学家只能考虑这种可能性多大,那种可能性多大,而不能够说,你这一个号,因为你在汪洋大海里面你只是一种,所以,数学家的思想方法是这样的。
还有一个就是说,数学家对量有一个概念,过去,阿拉伯有一个君主,他有一个宰相,这个宰相,他立了很多功劳,他有很大的功劳,那么,国王就说,你要什么赏赐,那么这个宰相就说,你给我一个棋盘,当是的棋盘是这种8×8的这种国际象棋的棋盘,差不多是这么一个情况,你8×8就64个窟窿,这第一个格子里面,你给我放一粒大米,咱们就说大米,一粒米,第二个盒子你放两粒米,第三个盒子你给我放四粒米,就是每一个格都乘2,那么,第四个就是8粒米。于是这么放下去,到了最后一个格子当然就是2的63次方那么多。这2的63次方,就是把所有国家的粮食都搁到里面,也不行了。这就是一个指数增长,这也是一个等比级数,是指数增长的一个情况,这样我们就是说,假如你听到传销的这个问题,为什么它是骗局?到底完全跟象棋的道理一样,你现在为了方便起见,一个人发展10个人,你第一个人就是说,始做传销的人,你总觉得你这一个人发展10个人,他有多少利润,当然就是说,各种不同的人,我一个人发展10个人,第一个人就是10得零次方,你发展10个人,十的一次方,可是你要10个人再发展10个人那么就是10个二次方,你发展到10个三层四层五层,你就是十的5次方了。10的5次方是多少?10万人,10的6次方,100万人。这样呢,你要在一个局限的范围内,不管你是一个小县,还是一个很大的地方,没有几个,所以到四五层的人,他就根本传不下去了。就不可能传了,当然这个利润都给了上头的这个人了。但是,它到四五层,按照指数增长了,它到一定程度,就根本不可能再往下走了。就没有多的人,让你去发展。假如8层那就是1亿人了,那就是中国的差不多1/10的人,可能吗?根本不可能,所以,他的想法,当然你好像再往下传,但是,这个指数的增长,就跟你这个一个一个的增长不一样,一个米,两个米,三个米,四个米,这个等差级数,指数增长是如此之快,以至于你不可想像。这就是为什么好多人的传销上当受骗,到了一定的级它就不传不上去了,你只能往上传了。往上传当然人家不干,你只能往下传,往下传你就没有办法。所以,你倾家荡产,就只能这样。
这个就是你日常生活里碰到的,所以,并不是说,要求你学了什么数学的理论,而是说你要有一个数学的思维方式,往前走一步。
数学的最重要一点就是数学是一个精密的科学,这个大家都知道,精密的科学,就要求,你这个概念是什么意思,你要清楚,否则的话,你就是一个名词在那儿炒作,名词炒作,实际上你讲了半天,云山雾罩,那么,你是什么也没有。你可以糊弄老百姓,但是,实际上,就没有任何一个意义。就是你的语义不含有任何的意义,这个我们常常在广告词儿里听到,就是非常之多。广告里头,最多就是说,我这个产品呢,高科技含量50%,或者55%,给你还有一个小数点,55.98%,可是你这个首先什么叫高科技含量,不知道。你不是这55.98%,另外那部分叫什么呢?叫低科技还是什么呢?所以这个话,就迎合一般人,首先是一听是高科技,就眼睛一亮,还有一个就是说,对数字特别迷信,如果我14.56好像精确得不得了,一定靠得住,这完全是谎话。有许多时候,尽信数还不如无数,就是说,有许多这样什么,你说有这个数跟没这个数效果完全一样的时候,有的时候根本没有用是吓唬人的。
还有一个常常说,我以前是讲,因为药物的广告特别多,我以前是讲祖传秘方,我这个药,药到病除,一针就灵,反正,诸如此类的这些话,现在呢,当然比较高级了,就用到所谓数字了,实际上是用到数学的概念了,就是说我这个治愈率多少,有效率多少,45.8%,98.57%,那个是83点多少,这个83点多少,怎么来的?你可能不知道。如果我俩人,我一个治好了,一个治坏了我就说,我有效率,50%,而且这个治好的人是不是靠这个药治好的还是自然的就好了,你都不知道,你就听着50%,或者说,俩人都有效,你说百分之百,你这个所谓百分数,你取样是在一个什么集合之内,还有,统计上面有很多规则,不是说,你随便说的,所以,这些地方,不要不精确的语言,你这个数学家就要抠一抠,你这个意思到底怎么样,你这个数字怎么来的。那么,这个,是数学家的思维方式。就是说,你平常的训练有这个思想方法。
当然有一些我们就是说,平常,要抠一下,我们常常现在气象,报下雨的概率20%,40%,60%,80%,下雨的概率,是有20%的可能性下雨还是说,我在这个地区,一个不定的地区,有40%的地方下雨,当然不是这个了,我就是说。还有说,你有40%的时间下雨呢?所以,这个,就光说,下雨的概率有40%,这句话,实际上,我当然不是说,否则气象台的这种说法,但是,要抠一抠这什么意思。也就是说,它的意思无非是这样,你要是说50%以下下雨你可以不带伞,可是你要说80%、90%要下雨,那我出门就要带把伞。其实,目的就是说,或者你要有什么东西需要盖住,或者你不要洗衣服等等,实际上就是给老百姓一个参照的数字,可是这个数字只能说大概不太精确。所以,你就是说,只能作为一个参考,当然,幸好就是说,这个气象预报,也不是绝对的准确,就是说,因为有好多其他的原因了,它不像行星的运动,现在,即使行星的运动,也不像以前的牛顿力学是决定性的,那么因为有混沌这种概念,连天体的运动,原来说,天体的运动是决定性的是就是说,我完全可以精确地确定,比如行星的运动在哪儿,那么你现在,也有混沌,说不定,比如说,小行星降到地球上面来,究竟有多大的概率,那么,这个东西,不能只算概率,但是我们如果只能得到概率,那么就是概率。也只能够供大家参考。
如果说,小行星或者很小很小的小行星,靠近地球了,将来,真正跟地球相撞,这个是大事了,这个全世界都要出问题的,所以这些问题就是说,你要在每一种情况,你应该都能够对于数学要有一个概念上,要有一个抠一点,这个是学数学的一个思想,不要看见数,有了数就信,有以它为指导你的生活工具。那么这样就作出决策了,你就是比较成问题了。
最后,我就想谈谈,你怎么样通过数学上第一个台阶,我想就是说,现在再说,最后的总结,就是数学帮助你,先在你的思维方式上,上一个台阶,上一个台阶就是说,我觉得,主要先有四个方面,第一个方面就有数量的观念,但是有误区,第一,你这个数,确实是不是反映它的本质特征,就是有好多数,你比如说,现在,好多人说,人心不古,这个道德方面不太好,那么就有人说,道德值多少钱一斤,道德这个东西,就很难用数来衡量了,有好多东西是不能用数来衡量的,第二,用数来衡量,你要适可而止,不能说,你小数点后面,有多少位数,没用,对于指导你比如说概率,你刚才说,下雨的概率,是39.53%,这后头数目毫无意思,所以,你看,现在大家比较喜欢预测经济增长率,美国经济增长率,预测今年增长2.5%,现在2.1%,也可能到1.5%就是两位数,还差不多,两位数来不准的,那后头那位有什么用呢?这就是说,你对于数量的观念,要有一个正确的数量的观念。
第二就是说,刚才说的确切的含义,数学上每一个东西,它怎么来的,应该是有一个确切的含义,有好多东西是一个含糊不清的,特别是吴文俊先生得了奖以后,有好多人说,我这个东西是拓扑的,用拓扑方法怎么样怎么样做,我这个产品,你看看能不能支持什么的,这个就是说,他懂什么叫拓扑吗?恰巧我还懂,我说你用拓扑进行计算那么,你应该得到用什么拓扑方法,有多故意唬你,就是要把确切的含义讲清楚。
第三个就是叫做合理的思维,特别是合乎逻辑的思维,第四种就是要有一个简化的方法,就是说,数学家总是要考虑你的把复杂的东西,如何变成一个简单和的东西,并不是说,为简单而简单,而是你的脑筋里面盛不了太多的东西,你的脑筋里面能记住东西,实际上是人脑记住东西有限的,并不能够你把什么都记住,所以,把比较复杂的东西变成一个简单的东西。我看大宝有一个广告,这个广告说词说得挺有意思,他说,把复杂的东西变成简单的东西,贡献,把简单的东西变成复杂的东西,是累得慌,大概是这么说的我不记得了。确实是如此,因为,人现在生活在一个很复杂的世界,你要想什么都知道不可能,但是,你应该有一个把东西简化的方法,这个在数学里面,有很多。
比如说,平常我们常常说的优化,你要怎么样,投资,投资就是说,你不要把所有的鸡蛋放在一个篮子里面,这就是优化,优化的方法,这个在数学上都能够证明的,你差不多把这层概率,信息论里面都有这个东西,都是这种方法。这种简化的方法,其实,从小学一年级人家就学,一加二加三,加到100你要是傻加,你就是一个复杂的方法。复杂的方法,你就要用一个比较简单的办法,你要处理不是这么简单的问题,当然你要用一个简单的办法,高斯就用很简单的做出这个东西。但是,你要是注意到,这个简单的东西,数学家还有一个问题,什么叫做数学的简单,数学的简单就是说,跟常人说的简单不一样。
数学家把这个事情分成两个部分,一个部分是繁的部分就是这个做事做起来非常繁但是很常规,那么就是说,你可以机械和,这个就是吴文俊先生讲的把数学有好多东西可以机械化的东西,你机械化,凡是可机械化的东西,数学就认为你已经知道了,而把你的头脑主要放在那个难的问题上面来。难的问题上面,就是说,最重点的最核心的,最困难的东西,你要把它重点放在这个上头。凡是已知的,我们数学家就不再重复了。
所以我觉得,你在日常生活里面,确实有很多地方大家也这么做了,而且,尤其你要做公司了,或者你做各种东西,做决策的时候,你只要在你的思想方法上,往前推动一步,这样,你就可以有很多的收获,觉得数学还是挺有意思的。不要去念大书,念大书,我倒觉得不见得对你有效,所以呢,我就是说,你这个数学,要首先学会它的思想方法,第二你要能够怎么样能够通过你交谈了,或者通过你各种情况,你能够利用这个资源,因为,现在有好多资源确实在那儿,但是你不知道你还是不会用,今天就讲到这儿。
19
179恩,正是数学与我们的生活密切相关,我才选择了这条路...
19
179我觉得这个很好 支持
19
179嗯,说得有道理
慢慢体会!
19
179刚刚看了视频,蛮受启发的
19
180matlab中可以利用函数contour绘制等高线,不过我现在是要绘制与之相类似的等值面。不过它扩展到了三维空间。
我是基于如下的应用:
在电学中,电量为q的电荷o(x0,y0,z0)在点p(x,y,z)出产生的场强为:
E(x,y,z)=k*q/((x-x0)2
+(y-y0)2+(z-z0)2);
当然,方向是由o指向p或者相反.....
现在要在三维空间中将电场大小相等的点连接使之成为等值曲面(有一点类似将高度相等的点连接最后获得等高线),
当然,我们知道对于点电荷,这会获得一簇簇的球面。
关键在于,matlab中似乎还没有绘制等值曲面的函数,得想其他的办法。
哪位高手帮帮忙!!!
19
181喜欢就学,不管有多难!!
人生难得做几件自已想做的事。
19
181我是学信息与计算科学的,今年大三了,我比较喜欢信息方面,但物理又不是很好,应该考什么方面的研究生呀?
19
181也叫计算数学吗!!!
我就是这个专业的
找工作有些。。。
19
182偶看书很少去做题,觉得没啥意思,还不如坐在那里瞎想,可能因为偶觉得题是永远都做不完的,呵呵大家什么看法哈随便说说讨论下!
19
182偶尔还是要做做的
19
183请看附件谢谢啊!post-8-11291
17302.ibf
19
183先把它分[0,pi/2],[pi/2,pi],对后一个区间用t=pi-x变换
可以得到等于[0,pi/2];
再用
万能公式
设
t=tanx;
然后
化简
19
183附件里面post-8-1129694532.ibf
19
183看不懂啊可不可以清楚些
19
183\begin{equation}
\int_{0}^{\pi}
\frac{1}{1+\sin ^2 x} \, \mathrm{d} x
\Rightarrow \int_{0}^{\pi}
\frac{\mathrm{d}{\tan x}}{\sec ^2x+\tan ^2 x}
=\int_{0}^{\pi} \frac {\mathrm{d}{\tan
x}}{1+2\tan^2x}=\frac{\sqrt{2}}{2}\pi
\end{equation}
19
183给出原题的附件post-8-1129687011.ibf
19
183可不可以用word文件,pdf 文件看不了啊!谢了
19
185答案是否定的,我们可以构造反例如下:
x=0时f(0)=0,f(x)=x*x*sin(1/x),这个函数点点可导,但他的导函数在零点不连续!
19
185百思不得其解!!
19
185连续可导函数的定义就是导函数连续!
19
185
| 引用 (dhp @ 2005年10月13日
21时48分) |
|
连续可导函数的定义就是导函数连续! |
说的没错,建议楼主去看看课本
19
185就是,这是定义,基础只是要掌握好呀
19
185
| 引用 (lhansheng @ 2005年10月22日
15时55分) |
|
我看过的是连续可微表示导函数连续。可能参考书不一样吧! |
一元函数里面可导和可微是等价的
19
185
| 引用 (shehei @ 2005年10月13日
21时51分) |
| 引用 (dhp @ 2005年10月13日
21时48分) | |
连续可导函数的定义就是导函数连续! |
说的没错,建议楼主去看看课本
|
我这里有市面几乎所有主流的分析课本,请告诉我在哪里呀?
19
185<<数学分析>>上册 科学出版社 李成章,黄玉民著 133页
19
185连续可导就是所有的导函数连续
19
185我看过的是连续可微表示导函数连续。可能参考书不一样吧!
19
185
| 引用 (magic9901 @ 2005年10月13日
12时12分) |
答案是否定的,我们可以构造反例如下:
x=0时f(0)=0,f(x)=x*x*sin(1/x),这个函数点点可导,但他的导函数在零点不连续!
|
”连续可导函数”就是说f(x)的导数连续
不用看书了
问一下老师就可以了,这个地方没有不同的表述
19
185我已经查过书了,也和别人讨论过,连续可导就是指导函数连续
19
185楼主是大一?
19
185
| 引用 (daodan1234 @ 2005年10月29日
20时21分) |
| 楼主是大一?
|
真是没有脸面呀。。。是我基础不好呀
19
186构造函数F(x)=f(x)-f(a)-f'(x)(b-a),仔细分析一下F(a)和F©的关系即可
19
186证明题post-38-1129120326.gif
19
186虽然也构造出了该函数,但没有仔细考虑F(a) & F©的关系
这下知道了
19
188请高手介绍一下,这方面的结果.
19
189请高手介绍一下
19
189小弟学识浅薄,未曾学过拓扑学与微分几何.恳请兄弟解释一下代数流形.
19
189据我所知,代数流形属于抽象代数,是研究多项式理想与其公共解的,
基本没有联系。简言之:一个代数流形就是仿射空间的点族,它们是一组多项式的公共解。严格定义请参看抽象代数与计算代数的书。
斑竹的问题怎么没人答啊,哎~我也不会。
19
190一个n元m次多项式,所刻画得代数流形的维数有什么限制?
19
191哪么学友有最优化的课件或资料,请上传一下,小弟在此多谢了!!
19
192如果你能够帮我复印一本著M.P.Do Carmo《riemannian geometry》,则我可以给你一套该书英文版本的复印本。
19
192
这套书一共分四册!!上卷分两册,下卷也分两册!
题名/作者: 基础代数
/(美)雅各布森(Jacobson,N.)著
出版发行项: 北京-高等教育出版社
1987.9
上海师范大学数学系代数教研室
论题主题: 代数
附注项: 这是中译本,英文原书名为:Basic algebra 分上下两卷。
本书介绍了抽象代数的基础课题,包括幺半群和群,环,主理想整环上的模,方程的Galois理论等等。
寻找那里有这套书,预购之!!!不知有此书的电子版没有!!??若有那个大侠知道
那个出版社有卖,望告知在下!!不胜感谢!!
19
192我想要中文版的!
有的话顺便说一声!
19
192去各高校图书馆复印啊!
19
192我可以提供书籍的复印
如需求请联系
zlj
183@yahoo.com.cn
19
192
| 引用 (邓书生 @ 2005年10月13日
15时50分) |
如果你能够帮我复印一本著M.P.Do
Carmo《riemannian geometry》,则我可以给你一套该书英文版本的复印本。
|
作者
条件还有效吗?
19
198请问各位 2维2阶 波动方程 有关于x,y的系数 该用何种差分格式,谢谢
19
199在附件里,谢谢post-38-1129134483.ibf
19
199解答:post-38-1129259373.ibf
19
199谢谢,请指教
19200利用柯西-许瓦兹不等式
19200在附件里,谢谢post-38-1129136064.ibf
19200谢谢
19200我感觉首先判断f0(x)是有界的
然后递推得出f(n-1)(x)是有界的
再由

(x) 的定义试放大
19200光有以上的连续和收敛条件应该不能判断它有界啊
19200偶就是觉得这道题目的有界性部分比较难证明.偶用了一个方法证明.不过不是reijin所说的不等式.偶用的就是普通的反证法.但是感觉有点不太严密,不过自己又说不出问题在哪里?只要证明了f0(x)在[0,

)上有界.有归纳法就很容易证明最后的级数是一致收敛的.
19200请reijin 将具体过程写一下!!!
19200支持lchw,麻烦reijin了
19200^_^post-38-1129553395.gif
19200谢谢了
19200斑竹老大,你在证明中使用了柯西-许瓦兹不等式,十分精彩。但是我觉得你的证明中可能存在一个小小的问题:在你的附图的第一行。你认为,存在一个A,A>M,使得f0(x)^2的变上限积分(从0到x)是小于Ax的。然后在第八行的不等式放大中用到此结论,使得

1(x)<Acx/(2e^2).变成了一个很强的不等式。而且在接下来的证明中用到了它,(第10行和第14行)。但是这个不等式并不一定在x>=0都成立。可以说,“存在一个A,A>M,使得f0(x)^2的变上限积分(从0到x)是小于Ax的。”只能在x>=1的时候恒成立。所以应该是不能推导出不等式“

1(x)<Acx/(2e^2).”的。所以以后的证明也应该不能那样证。
我是有点太扣字眼了,可能是受到了苏联人的古怪影响吧。望斑竹老大再给出一个漂亮且没有瑕疵的证明。我自己的证明很朴实,甚至是很丑陋,(且没有用到柯西-许瓦兹不等式)又不怎么会用数学符号编辑,就没有发上来。有兴趣的可以跟我也交流一下。我QQ:248550244。
19200^_^,那我把楼上的问题细说一下吧,由于f0连续,则f0^2在[0,1]上存在一个最大值k,那么首先

0在[0,1]的变限积分就可以小于kx,然后由于f0^2无穷积分的有界性,我们取A=max(k,M),即可保证我的这个不等式
19200对了,刚刚受到斑竹用柯西-许瓦兹不等式 的启发,想到一个很简单的证明。有兴趣的跟我交流一下。我QQ:248550244。
19200恩。这样就肯定没有问题了。我没有注意到连续函数闭区间的性质。斑竹还是很强啦!
19200不如加入这个群吧11088655^_^
19200我已经加了这个群了。那斑竹是什么网名?^_^
19200欢迎加入^_^
19200zhichi
!!!!!!!!!!!!!!!!!!!
19201
"然后由f(x)的连续性得出 "这一步能否说细一点,我想用变量带换.可搞不通啊
19201将积分区间拆成0到t^(1/2)和t^(1/2)到1,然后注意到f(x)在[0,1]上连续,g(x)=t/(t^2+x^2)(t>0)在[0,1]上不变号,分别对两部分用推广的积分第一中值定理,再让t从0右侧趋于0即得结论。
19201怎么是t趋向于0的啊,t变量是哪里来的
19201在附件,谢谢post-38-1129136680.ibf
19201!!!!post-38-1129260733.gif
19201对不起,昨天太晚了,写错了.这是我改的post-38-1129213159.ibf
19201

t/(t^2+x^2)dx=pi/2
然后由f(x)的连续性得出
19202请问各位高手:
对一个幂级数求和后积分,是变上限积分,书上说可以先逐项积分然后再求和,但如果是定积分呢?还能
这样吗?因为李正元的四百题中就不这样做,却用了另外一个费劲的解法。所以我怀疑在定积分时不能改
变积分和求和的顺序,不知各位怎么认为。
19202定积分可以交换顺序的
19205
请研究如下定义的两个函数
在坐标原点处的偏导数和连续性:
当
0<y<x^2时,f(x,y)=1,否则 f(x,y)=0。
当 xy=0 时,g(x,y)=0,否则
g(x,y)=1。
19205先说说你的“可微”、“可导”的定义是什么。
漂亮的图片大家都爱看,但是用附件方式就会占用网站空间,http://www.math.org.cn/forums/index.php?showtopic=6365
不妨考虑把图片放到别的地方,然后用超级链接引用,有很多地方提供这种服务的。
19205李正元的考研数学复习全书中列了一张表,说二元函数的两个偏导数在M点连续,那么可以推出函数在该点可微,
可微又可推出函数在该点沿任意方向的方向导数存在。
方向导数存在又可推出函数在该点可偏导(有两个偏导)。
这里函数在该点可偏导(有两个偏导)与两个偏导数在M点连续似乎不是一回事。真是奇怪,搞不懂
以上的推导都是不可逆的,也很奇怪,比如为什么可导却不可微
想了许久(一年前就不懂)怎么也想不懂
19205一般来说的偏导数(对x,y)都是沿着彼此正交的x,y轴的导数
方向导数是沿着任意直线的导数
导数定义里面是有一个微小改变量delta
x,delta y的
如果是delta x,就是对x的偏导,,
现在我们把delta x改成delta l,,
这里delta
l是沿l方向的微小改变量
这样就得到了方向导数
19205可微只能推出两个偏导数存在,但不能得出两个偏导数连续.你觉得呢?
19205我认为假如函数在一点任意方向导数存在的话,那么该函数在该点可微也是成立的.而可微又可以推出在任意方向导数存在,故可导也就是可微的.请看附件post-8-11291625
19.ibf
19205
| 引用 |
| 定理
如果函数f(x,y)在点p.(x.,y.)可微,那么函数在该点沿任一方向l的方向导数存在 |
| 引用 |
| 对于多元函数来说,即使各偏导数在某点都存在,也不能保证函数在该点连续 |
(以上都摘自同一本书)
是不是矛盾了呢?比如f(x,y)在点p.(x.,y.)可微,即各偏导数在这点都存在,但如果函数在该点不连续,怎么理解函数在这点沿各个方向都可求导呢?
19205定理说得很清楚啊!!在多元函数中可导必连续是不成立的啊!因为有有限个间断点的函数也是可导的!!
19205多元函数可导是指偏导存在,即函数对单个变量x或y是连续的,但对二元变量(x,y)不一定是连续的
19205在不连续点当然不可导了。
19205
引用 (ytht @ 2005年01月25日
08时
18分) |
|
多元函数可导是指偏导存在,即函数对单个变量x或y是连续的,但对二元变量(x,y)不一定是连续的
|
既然多元函数在
某点可微的情况下也有可能不连续(照楼上说的“在不连续点当然不可导了
“
),那么怎么理解在这点沿任一方向导数都存在呢?

19205方向导数存在只要偏导存在就行啊
19205在学习“多元函数微分法及其应用”这章时,发现“连续”这个概念多次被提到,尤其是存在于一些定理或性质的条件中。
而课本上给的多元函数连续的定义
“limf(x,y)当(x,y)趋于(x.,y.)时等于f(x.,y.)即为f在(x.,y.)连续”,
我觉得对于理解一些条件中‘二阶偏导数连续‘比较抽象
怎样较好地理解多元函数连续的概念以帮助记忆呢?
附上整理的一些用到多元函数连续的定理/性质
| 引用 |
1、如果函数z=f(x,y)的两个二阶混合偏导数在区域D内连续,那么在该区域内这两个二阶混合偏导数必相等
2、如果函数z=f(x,y)的偏导数在点(x,y)连续,则函数在该点可微
3、(函数在某点可导的前提)
4、(隐函数存在的条件之一;另:隐函数确定若干连续且具有连续偏导数的函数)
5、(使用二元函数极值判定定理的条件之一“函数在某点的某邻域连续且有一阶和二阶连续偏导数”)
|
各位帮帮忙!
19205还有,那个“多元函数在某点各偏导数都存在但在这点有可能不连续”是什么情形呢?
..........xy/(x^2+y^2)
(x^2+y^2!=0)
f(x,y)=
..........0
(x^2+y^2=0)
据说就是这样的一个例子,那么在(0,0)这个“各偏导数都存在但在这点连续”的点究竟发生了什么事情呢?怎么想象呢?
19205
| 引用 (yyshuxue @ 2005年01月25日
16时36分) |
| 方向导数存在只要偏导存在就行啊
|
这个明白,证明的过程也明白!
只是搞不懂在一个不连续的点怎么求导(各方向的导数)……
首先,如果二元函数在一个点存在各偏导数但不连续,是怎样的情形呢?一个洞?
可能是因为我对连续的概念没有彻底搞清……
专门发了一个帖子“关于多元函数的连续性及求导条件“
有空的话多多指教

19205
| 引用 (边缘 @ 2005年01月25日
22时52分) |
| 引用 (yyshuxue @ 2005年01月25日
16时36分) | | 方向导数存在只要偏导存在就行啊
|
这个明白,证明的过程也明白! 只是搞不懂在一个不连续的点怎么求导(各方向的导数)…… 首先,如果二元函数在一个点存在各偏导数但不连续,是怎样的情形呢?一个洞? 可能是因为我对连续的概念没有彻底搞清…… 专门发了一个帖子“关于多元函数的连续性及求导条件“ 有空的话多多指教

|
可微的话一定是连续的,这可以直接用定义证明.可微的条件比偏倒数存在要强.
19205哦!
明白了!
但是对于多元函数连续的相关性质还是不大明,在本版“关于多元函数的连续性及求导条件(http://www.math.org.cn/forums/index.php?showtopic=7946)“帖子里,哪位帮忙看看~~~~
19205例子有误吧,你举的例子在原点处偏倒数也不存在.
事实上偏倒数只反映了沿某一方向的变化,不能反映在某一邻域内的所有性质.而连续至少要求极限存在,这个极限是重极限,要求按任意方式趋近极限都存在(并且相等).有些函数当(x,y)沿不同的直线趋近与同一点时得到不同的极限,那么在该点的极限就不存在,从而在该点不连续,很多时候情况如此.当然还有其他情况.
19205
| 引用 (oddspeed @ 2005年01月26日
22时04分) |
例子有误吧,你举的例子在原点处偏倒数也不存在.
|
不好意思那个函数表达式条件输错了(已经改过来了)
我觉得是这样的:
在点(0,0)的偏导数为
fx(0,0)=[limf(0+△x,0)-f(0,0)]/△x=lim0=0(当△x趋于0)
同样有fy(0,0)=0
所以在原点处偏导数存在
19205麻烦oddspeed帮忙看看一楼的问题吧

19205多元函数可导,仅仅指的是其偏导数存在而已,如果这个函数是二元函数,则该函数可导只指其两个偏导数存在。
关于偏导数连续,那是因为偏导数在更多的意义上仍然是函数,既然是函数,那就有连续不连续之说。
希望对作者理解这个概念有所帮助。
看到该帖子比较晚,因而回复晚一些,敬请谅解。
19205一元函数在某点不连续时图像中是个断点,那么对于“某点偏导数存在但不连续”的多元函数呢?曲面是个怎样的情形?
(肯定和“偏导数不存在也不连续”不同吧?)
这个版的人气确实不够旺一些所以等回复等得

,可能大家准备过年了吧

19205因为二元偏导数只是反映了曲面上两条曲线的切线斜率,故而偏导数不连续只是说明这两条曲线上有间断点而已。反映在整个曲面上,相当于这个曲面上有个小黑洞,小漏洞,瑕点而已。
19205谢谢小红帽版主

还有n个问题:
1、那么以下这三种情况反映在整个曲面上都是一个洞吗?还是有什么不同?
多元函数在(x,y)点:
a、不连续
b、存在偏导数,但多元函数在这点不连续
c、存在偏导数,但偏导数在这点不连续
2、多元函数有没可能像一元函数那样“在某点连续但没有偏导数”呢?
问题比较多,麻烦版主最好分别作答

先谢谢了!
19205第二个问题应该是肯定的吧,只要设g(x)是这样的一元函数,再令f(x,y)=g(x)(即f(x,y)的取值只与x有关而与y无关),那么f(x,y)在该点关于x的偏导数就不存在,但f(x,y)在该点连续.
19205
引用 (小红帽 @ 2005年01月27日
19时51分) |
因为二元偏导数只是反映了曲面上两条曲线的切线斜率,故而偏导数不连续只是说明这两条曲线上有间断点而已。反映在整个曲面上,相当于这个曲面上有个小黑洞,小漏洞,瑕点而已。
|
叙述有误,需要纠正一下。
二元函数的偏导数不连续,只是说明偏导数构成的曲面在该点上有漏洞,有瑕点,而不是原函数表示的曲面上的两条曲线间断。
一个函数可导但不一定连续,那是因为函数可导只说明函数在其中的有限条曲线上连续,而函数所表示的曲面上有无数条曲线,这无数条曲线当然不一定连续了。
19205
| 引用 (小红帽 @ 2005年01月28日
10时21分) |
……
一个函数可导但不一定连续,那是因为函数可导只说明函数在其中的有限条曲线上连续,而函数所表示的曲面上有无数条曲线,这无数条曲线当然不一定连续了。
|
如果曲面上的无数条曲线在某点都连续,但是这点的偏导数还是不一定存在,是吗?
比如苹果表面的一点(红色箭头所指处)?post-8-1106997841.jpg
19205
引用 (边缘 @ 2005年01月29日
19时24分) |
| 引用 (小红帽 @ 2005年01月28日
10时21分) |
……
一个函数可导但不一定连续,那是因为函数可导只说明函数在其中的有限条曲线上连续,而函数所表示的曲面上有无数条曲线,这无数条曲线当然不一定连续了。
|
如果曲面上的无数条曲线在某点都连续,但是这点的偏导数还是不一定存在,是吗?
比如苹果表面的一点(红色箭头所指处)?
|
那当然了,连续仍然不一定可导!
你这个例子确实不错,好!
19205

斑竹过奖了
对多元函数连续有了进一步的了解之后,我还是感到要记那些定理/性质的条件有些困难(汗……)
比如:
隐函数存在定理确定若干连续且具有
连续偏导数的函数;
使用二元函数极值判定定理的条件之一“函数在某点的某邻域连续且有一阶和
二阶连续偏导数”
该怎么办哪?
据说做题的时候基本是不用考虑连续阿什么的,给的都是能求的,真的吗?
19205呵呵
其实这个问题
只要理解了 没必要记那些规则
对于一元函数 可导即连续 但连续不见得可导
这个好理解吧?
对于多元函数 你要明白偏导数始终是个“偏的”,他一般不包含函数在这一点的全部信息,但是如果对于这个函数的这一点
在所有方向上的偏导数都存在的话,拿这一点自然连续了
一元函数只有一个方向,多元函数有无数个方向,都要考虑才行。
19205书上讲了; 若函数在一点可以微分的话,则这个函数在该点的任意直线方向上皆具有方向导数。那么,问题是:可导能否推出方向导数存在呢?
不能的话,能否找个反例呢?post-8-1111161435.jpg
19205你的标题和内容不符,到底前提是“偏导数存在”还是“可微”?
你可是带头破坏规矩,经常在帖子里加一些不必要的图片。
19205可微一定有方向导数存在。但可导则方向导数存在么?
这是我的问题。
再者,加图片是为了丰富论坛的界面,并没有别的意思。如果大家觉着不好的话,我以后绝对让她纯净!
19205偏微分 为什么叫方向导数 ---什么意思???
19205
| 引用 (1234567890 @ 2005年06月22日
20时25分) |
| 偏微分 为什么叫方向导数
---什么意思??? |
谁说偏微分叫方向导数的?!
19205
| 引用 (1234567890 @ 2005年06月22日
20时25分) |
| 偏微分 为什么叫方向导数
---什么意思??? |
微分和导数是不一样,但是在这里这么理解也可以.
19205c项和d项意思有什么区别呢?
我的问题在下方的文档中,希望大家使用word2003看,否则可能出错误post-8-1122
197963.ibf
19205
c
⇒d 但反过来不一定成立
19205还有,可微

偏导数一定存在
但是,反过来不一定成立!!
19205李正元的考研数学复习全书中列了一张表,说二元函数的两个偏导数在M点连续,那么可以推出函数在该点可微,
可微又可推出函数在该点沿任意方向的方向导数存在。
方向导数存在又可推出函数在该点可偏导(有两个偏导)。
这里函数在该点可偏导(有两个偏导)与两个偏导数在M点连续似乎不是一回事。真是奇怪,搞不懂!!
以上的推
19205“方向导数存在又可推出函数在该点可偏导(有两个偏导)”
这个结论,似乎有待商榷!!我个人认为是不对的啊!你前面的两个结论都对啊!
事实上,方向导数存在,但函数在该点偏导不存在的函数的却存在啊!!
19205最后一个结论我认为也是错误的.
19205方向导数在各个方向都存在,当然能够推出其关于x,y的两个偏导数存在的。因为沿x,y轴两个方向的方向导数就是关于x,y的偏导数!
19205
| 引用 (Goss_006 @ 2005年08月22日
12时21分) |
|
方向导数在各个方向都存在,当然能够推出其关于x,y的两个偏导数存在的。因为沿x,y轴两个方向的方向导数就是关于x,y的偏导数!
|
说的没错,其实上面的如果不懂的话可以拿数学分析的书去看一看就会明白一点,推荐华东师大编的《数学分析》下册里面讲二元函数的那部分内容,里面都有清楚的说明。
在这里要搞清这里讲的是二元函数,不要把一元的结论搬进来。
19205请教老师:函数z=f(x,y)在点(x0,y0)处可微一定可导吗?还是可导一定可微? 谢谢
19205可不可以说的详细一些
19205多元函数下,可微不一定可导,因为前者是整体的性质,后者是局部的性质
19205谢谢,那么多元函数下可导一定可微吗?
19205高等数学(下)p22页,可微必要条件:必须是偏导数存在,p23
页,第一段,偏导数存在不一定可微的,还必须偏导数连续才行
19205
引用 (小红帽 @ 2005年10月
19日
09时48分) |
|
多元函数下,可微不一定可导,因为前者是整体的性质,后者是局部的性质 |
值得探讨,据我所知,二元函数可微一定可导,否则你怎么表示微分呢?而可导则不一定可微,可导只是偏导数存在而已。
19205谢谢,那就是多元函数可微的充分必要条件是 函数连续并且可导了吧
19205
| 引用 (FARSEER @ 2005年10月23日
11时25分) |
|
谢谢,那就是多元函数可微的充分必要条件是 函数连续并且可导了吧 |
是偏导数存在且连续才可微,可微偏导数就一定存在的(好像不一定连续),所以二元函数可微没有充分必要条件
19205学习中
19205其实方向导数应该是以一个点为圆心向四周扩散,其实偏导数只是一个方向,对于方向导数来说,X正轴和X负轴的是不一样的,但对于偏导数来说并不存在X正轴和X负轴。你认为呢?对了你是大几的啊!谢谢你告诉我怎么贴图。
19205请看附件,请问哪个正确并说明理由。谢谢!post-8-1130391565.ibf
19205选B,我的思路是这样的,不对之处请指正!post-8-1130402778.gif
19205请看附件,请问怎么贴图啊 !谢谢!post-8-1130457866.ibf
19205请问如何上传啊,答案是C
19205抱歉,考虑漏了,谢谢指正!
这么说来,应该选哪个选项才对呢?
关于贴图,相信你也是用mathtype写的公式吧,只要写完之后另存为图片如GIF就行,上传这方面就不用说了,当然你也可以用截图工具~不过这样麻烦一点
19205上传的方法是一样的啊~上传附件一样的。可是图像画起来不光滑。所以我就凭感觉做而已,居然错了,看来要严格证明一下才行
19205用排除法,如果可微,则偏导数存在,则D成立,B同时成立,则D不成立,如果任意方向导数存在,则偏导数存在,(偏导数是方向导数沿X,Y轴的方向导数),所以C成立,B也同时成立,由图形知道,这是一个椎面,所以在(0,0)出偏导数也不存在,无正确答案
19205定理:若函数f(x,y)及其偏导数f ^{y} 在平面
区域D内连续,则初值问题dy/dx=f(x,y),y(x0)=y0的解存在且唯一,而且此解所表示的积分曲线可以向作或向右延伸,直到与区域D的边界无限接近.
这里的一个关键问题是, 偏导数f ^{y}(即f 对y求偏导)在平面 区域D内连续,这个条件能保证或推出什么?
另外,能否举出一个在区域D内连续的二元函数F(X,Y)中,F对Y的偏导数不连续的例子?
19205二元函数在(x。,y。)可微,但在此点偏导数不连续。
想不到具体例子!谁能举个例子?谢谢!!!
19205搞错了,导数求错了,懒得改了,将就看吧post-8-1133226553.jpg
19205到北大《数学分析解题指南》一书中找找找看!也许该书的多元函数部分的一些函数例子可以作为这个问题的反例。
19206谢谢post-38-1129143
192.ibf
19206题都是错题
19207谢谢了
19207请问版主,怎么将附图直接贴到上面啊!谢谢了!
19207键盘右上方有个键,名称为:PrtScSysRq.在浏览有图形的网页时,顺便按一下这个键,然后打开程序中的画图软件,点其中的编辑菜单,选粘贴,然后保存即可。回帖时,在附件栏中点击浏览二字(就在正下方),把图片所保存的地址附上即可。
19207
| 引用 (小红帽 @ 2005年10月13日
22时34分) |
|
键盘右上方有个键,名称为:PrtScSysRq.在浏览有图形的网页时,顺便按一下这个键,然后打开程序中的画图软件,点其中的编辑菜单,选粘贴,然后保存即可。回帖时,在附件栏中点击浏览二字(就在正下方),把图片所保存的地址附上即可。
|
以前好象可直接将粘帖板中的图片直接插入到输入框中与文本混排,现在没这个功能了,觉得不方便
19208拓扑学中的开集是利用对偶形式定义的。
19208导集公理不对,应改成边缘公理
192081 X={a,b,c}拓扑1为{空际,{a},X}
拓扑2为{空际,{b,c},X}
考虑集合{a}
2
X={a,b,c}拓扑为其幂集可考虑任意子集
我对1的理解是,{a}在拓扑1里面,所以在拓扑1里
它是开集,{b,c}在拓扑2里面,{b,c}是开集,而
{a}是它的补集,所以这里{a}是闭集.
在2里面,因为任一子集和它的补集都在拓扑里面,
所以都是开集,所以是既开又闭的.
不知道对不对,谢谢斑竹
另外在度量空间里面,开集的定义是该集合等同于
其内点的集合,在拓扑空间中是不是不能应用了?
19208最近自学微分几何,讲到拓扑空间的连通性
的时候,提到了既开又闭的子集这个概念,
想不清楚.我知道这对于各位数学专业的
来说肯定是小菜一碟啦,能不能帮我举个例子?
万分感谢
19208你的解释对了
一个是逻辑的对偶,一个是集合代数的对偶
不要把二者混了
19208我看的书是一个苏联人的<<微分几何与拓扑学>>,里面讲到连通性的时候又这么一段:
1.连通性:
若空间X含有不同于X合空集
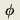
的既开又闭的子集 Y

X,则称X是不连通的拓扑空间.
例如,多于一点的任何离散拓扑空间是不连通的,因为它的任何子集是既开又闭的.
我的理解是,对于任何拓扑空间X,空集和X本身既是开集又是闭集,因为拓扑空间的定义里面要求它们是开集,但是又说开集的补集是闭集,我认为空集和X互为补集,所以只能是既开又闭了.但是我不清楚单个点的集合算开集还是闭集,好像是满足闭集的定义.
19208呵呵 任何非空集合上都可定义拓扑
至于
单个点的集合算开集还是闭集,好像是满足闭集的定义.
要看单点集上拓扑的定义了
事实上,单点集上拓扑只有一种,
19208谢谢解释,不知道能不能再举个例子说明
"相对不同的拓扑而言:一个集合可能是开集,也可能是闭集。"
以及
"即是说一个集合是开集,它的补集同时又是一个开集(属于同一个拓扑的)."
19208相对不同的拓扑而言:一个集合可能是开集,也可能是闭集。
对于同一个拓扑而言:开集的定义是已知的,而闭集的定义是它的补集是开集,
即是说一个集合是开集,它的补集同时又是一个开集(属于同一个拓扑的),
即同时是开集与闭集。
不知我的解释是否明白?
微分几何啊?你学的是大范围的喽?我也正在自学呢,不过卡在联络那动不了了~
19208理解的对
另外在度量空间里面,开集的定义是该集合等同于
其内点的集合,在拓扑空间中是不是不能应用了?
同样能用
定义或导出拓扑的公理或方法有很多
比如:闭包公理 闭集公理 导集公理 开集公理 内部公理 收敛公理
等它们可互相 导出
另外还有弱拓扑(乘积拓扑,商拓扑等的推广) 强拓扑 和拓扑
序拓扑(序结构和拓扑结构可以相互诱导)等等
度量,半度量结构也可以诱导拓扑 代数结构诱导的 代数拓扑
代数簇诱导的查
里斯基拓扑等等
呵呵,自学拓扑很不容易,我知道那过程的艰辛,不过概念熟了就好了
自己提概念很容易,这就是抽象的好处,就像玩积木
不过就是单纯的点集拓扑没有什么意思了除非结合集合论
现在做广义度量空间的还算热门
19208大家不懂拓扑吧?但也要先考虑好再说吗!
——————生气
19208是挺抽象的,完全要靠想象.这样才有意思.
不过就像樱析光说的,有个地方不能理解,
就卡在那儿动不了了.
192081 X={a,b,c}拓扑1为{空际,{a},X}
拓扑2为{空际,{b,c},X}
考虑集合{a}
2
X={a,b,c}拓扑为其幂集可考虑任意子集
相对不同的拓扑而言:一个集合可能是开集,也可能是闭集,更可能既不是开集也不是闭集
即使对同一拓扑而言也是这样的,
拓扑学很简单,没有多少意思,就是抽象的太厉害了点,呵呵
19208这个学期刚开始学点集拓扑,才学到度量空间.但在 超度量空间中(X,d)中, N(P;a)是X的开集,也是X的闭集.
19208"拓扑学很简单,没有多少意思"
为什么对点集拓扑那么不屑一顾呢?
19208我认为点集拓扑是拓扑中最为抽象的一种,其他则是在其基础上发展起来的,所以点集拓扑是最为基础的,只不过,它离我们现实生活远了点,大多数人多学微分拓扑等。
19208
引用 (Godyalin @ 2006年08月
18日
22时25分) |
|
我认为点集拓扑是拓扑中最为抽象的一种,其他则是在其基础上发展起来的,所以点集拓扑是最为基础的,只不过,它离我们现实生活远了点,大多数人多学微分拓扑等。
|
有谁知道一个实际的问题:比如在教室中间的一个座位有前后左右四面八方共8个相邻的座位,那么平面上一个点的直接相邻的点是什么样子呢?
曾经看到过之诺悖论,好像就是说运动无法发生,一个点要运动,在一个连通空间里面,因为找不到最初的那个新的位置,即不同于起点的下一个点位?
因为运动在发生,所以空间不连通?即使不连通的有理数空间也找不到?
19208引用流形 发帖时间 2005年10月13日 21时42分:
拓扑学很简单,没有多少意思,就是抽象的太厉害了点,呵呵
那你说什么有意思?
人们能认识到形象思维以外的东西,本身就是一种进步。
引用流形 发帖时间
2005年10月13日
21时42分:
代数簇诱导Zariski拓扑
Zariski拓扑是怎么定义出来的?Zariski拓扑是代数簇上的哪个拓扑诱导出来的?而且代数簇怎么诱导这个拓扑?
19208一个集合X,它的一些子集构成的满足"开集三条基本性质"的集族,便是X的一个拓扑,记为T,这个时候便可称(X,T)为拓扑空间了,并称拓扑T中的元素,便是拓扑空间(X,T)的开集.
并不是每个拓扑空间都有既开且闭的非空真子集的.比如说,在一维欧氏空间R中,便没有.
在X的离散拓扑中P(X)={
A|A包含于X},即X的所有子集构成的集族.所以,在拓扑空间(X,T)中,每个X的非空真子集都是P(X)中的元素,即为开集.该子集的补集也是P(X)中的元素,也是开集.从而,得到每个X的非空真子集既开且闭.
19208"开集三条基本性质"本质上有什么意义?开集定义形式和闭集上差不多:都是说全集和空集是开/闭集的元素,开/闭集的元素都是全集的子集,开/闭集的元素的交,并也是开/闭集的元素。直觉上一集合的闭集似乎是同一集合另一个开集。(空集,空集)是个什么拓扑?
19208finiteness
19209请问中科大和中科院的数学卷子相同吗?
有考过中科大的同学问一下啊,
还有,
有没考解析几何??
谢谢啊
!!!!!!
很急啊!!!!!
19209哥哥(姐姐?),中科院早改革了,今年自己命题。
http://www.amss.ac.cn/amss/training.html自己看吧!
祝好运
我看了蒋尔雄的线性代数,头都大了。
我忍了,不考那鬼地方了。
你试试吧!
我们班一妹妹被俺忽悠的也不考了!
192
17谢谢哈。。
192
17请大家证明::一个n阶可逆A可以 分解为一个正交阵Q和一个正定阵S之积即,A=QS
华中科技05
192
17A可逆 那么A'A正定 设其特征根为 a1 a2 ... an 他门都大于零 则存在正交矩阵P 使得
A'A=P'diag(a1,...,an)p 即 A=A'~P'diag(a1,...,an)P
A=P'~diag[squ(a1),...,squ(an)]PP'diag[squ(a1),...,squ(an)]P
记Q=P'~diag[squ(a1),...,squ(an)]P
S=P'diag[squ(a1),...,squ(an)]P
注:A'~代表A'的逆 Q, S即为所求
192
17这个题是矩阵的极分解,很有名的!:)
192
17楼主,好人,谢谢
192
19请看附件post-8-1129
178428.ibf
192
19直接用分步积分法就可以啊!
192
19求教微积分post-8-1129
174354.ibf
19223a的(2n+1)次方应为a的(2n-1)次方
19223我的解答,估计在某些小的方面有问题!post-38-1129
187729.gif
19223建立递推公式即可得到。
19223以前会的,怎么现在不会了!晕!post-38-1129
178622.gif
19224这个显然是成立的,好象要证明太简单了,第一,函数在每点处连续的,这个显然,用定义
第二,函数在有限区间的左右极限都也存在,从条件就知道了,所以就可以知道了函数是在有限区间上是一致连续的了!
19224大家帮忙看看post-38-1129
181540.ibf
19225真的很抱歉,漏掉ln

ln(e^x+1)
dx
也许昨晚太累了---
数学与我们同在!
19225请看附件post-21-1129
184857.ibf
19225

(e^x+1)
dx
它难了我好几个月的时间。
数学与我们同在!
19225
| 引用 (qcc2005 @ 2005年10月13日
14时27分) |
| 请看附件
|
兄弟的有点小毛病:是e^x+x+c
19225我也看了一下。这个题目可能很难正常的积分出来。我觉得你就干脆先把ln(1+x)泰勒展开。在用e^x代x。然后在逐项积分。这样得出的式子就成了{x-

(n从1到无穷大)(-1)^ne^(nx)/n^2} 这么一个级数的和了。这个级数很容易证明是在x<0为绝对收敛的。
19225不可积
19225积分还是可以积分的。就是至少我觉得他就和

sinx/x
dx一样原函数很难用初等函数表示出来。所以我才决定用级数展开的方法对其逐项积分。积分后其也是有收敛域的。
19225要是定积分的情况就好办了。象我印象里理论物理中很多这种类型的定积分,比如Stefan-Boltzmann规律的推导积分就是这一类的。它也不能用初等函数表示。但是由于在物理中它是定积分,于是就可以得到所需要的结论。
19225同意楼上几位的意见。我也觉得

ln(e^x+1)
dx的原函数不是初等函数,只是不能证明之。
19225

ln(e^x+1)dx=xln(e^x+1)-1/2x^2+

x/(e^x+1)dx

x/(e^x+1)dx通过换元u=e^x+1,化成

ln(u-1)/udu
而最后一个不定积分杠int ln(u-1)/udu的原函数不能用初等函数表达式
19228A为n级反对称矩阵,D为n级实对角矩阵并且对角线上的元素均大于0,证明:|A+D|>0.
我用的数学归纳法,不知道还有没有更好的方法?
谢谢!
19228我来试试看:post-38-1129204395.ibf
19228妙,正在发愁
终于找到你了
19228是否应补充“A是实矩阵”?
19229
| 引用 (子青 @ 2005年10月14日
15时16分) |
| 引用 (978301 @ 2005年10月14日
14时39分) |
引用 (子青 @ 2005年10月14日
14时
19分) | |
其实上,E(XY)是一个内积定义,E(X-EX)(Y-EY)是一个中心化过以后二阶矩空间,因为协方差说到底讨论的是线性关系,所以先要中心化
|
你这个解释还是没有解释清楚啊老大.每个人都知道"协方差说到底讨论的是线性关系",可
是我们现在要问的是这个"协方差"是怎么样表达这种线性关系的.上面我说过,期望和方差
都很好地利用自己的特点表达了各自要表达的东西,可是这个混合矩并不是很直观.
本人请教过其他人,不知道这种解释正确与否:以E(XY)为例,若E(XY)>0,则可以说平面(X,Y)
上第一三象限内的点的(权重)概率相对其他象限要大,而且E(XY)的取值越大,说明这两个象
限的点的权重也越大,这样E(XY)的正负表达了变量X与Y在哪个方向上具有更大的权重,而它
的大小则表示一三象限方向与二四象限方向权重的差异的大小.
本人觉得这种接受还能说的过去,不知道子青兄能不能象这样说说你的解释.大家一起交流
交流!
|
我不喜欢用直观的东西来解释,直观的东西只能帮助记忆,用来解释是不牢靠的,而且不是所有的东西都有直观的解释.你这种解释基本合理吧,不过可攻击的地方也很多,比如说凭什么说两个随机变量大部分时候都是同号的就线性关系大,完全有可能是两个独立的只取正值的随机变量.
|
也许你是数学天才,所以你不需要从直观到抽象这个过程.但是可惜并不是每个人都能有你
这种天赋,我们大多数的人都只能从直观中慢慢体会,然后过度到抽象的概念.谢谢你的指点
^_^.
E(XY)中的X,Y当然可以只取正值,但是你考虑到没有,(X-EX)(Y-EY)中以(EX,EY)为中心设置
一个直角坐标,这样一定可以得到一个在四个象限都取值的情况.所以,我们在讨论E(XY)的
的时候,往往考虑的就是这种一般的情况.
不知道我的解释是否正确.以后多联系联系?
19229
| 引用 (978301 @ 2005年10月14日
10时14分) |
引用 (子青 @ 2005年10月13日
18时09分) | |
E((X-EX)(Y-EY))是二阶矩空间上一个内积的定义 |
俺知道那是二阶矩空间上的内积的定义,但是用这个来表示两个随机变量之间的线性关系不太直观.相对来说,期望和方差就要直观的多,期望就是用平均水平来表示变量的整体水平,方差就是用一个平均距离来表达一个变量的整体离散程度.这些都很直观,但是如果用这种思路去考量那个协方差和其他的混合矩,我发现他们没有上述两者这样直观,所以我在这里发帖请教各位高手.
|
内积里隐含了夹角的cos关系啊
19229最近重新温习概率论,突然发现有个问题:为什么协方差可以描叙两个随机变量之间的关系?
偶想了很久,还是不懂.有没有哪位帮帮我?最好是能说的明白点.
19229傻傻的问:子青兄能为小弟解释一下为什么说协方差是二阶矩空间上的一个内积的定义吗?而那个夹角是X与Y的夹角,还是X-EX与Y-EY的夹角?
一直不明白协方差的几何意义,借机请教一下
19229
| 引用 (978301 @ 2005年10月14日
14时39分) |
引用 (子青 @ 2005年10月14日
14时
19分) | |
其实上,E(XY)是一个内积定义,E(X-EX)(Y-EY)是一个中心化过以后二阶矩空间,因为协方差说到底讨论的是线性关系,所以先要中心化
|
你这个解释还是没有解释清楚啊老大.每个人都知道"协方差说到底讨论的是线性关系",可
是我们现在要问的是这个"协方差"是怎么样表达这种线性关系的.上面我说过,期望和方差
都很好地利用自己的特点表达了各自要表达的东西,可是这个混合矩并不是很直观.
本人请教过其他人,不知道这种解释正确与否:以E(XY)为例,若E(XY)>0,则可以说平面(X,Y)
上第一三象限内的点的(权重)概率相对其他象限要大,而且E(XY)的取值越大,说明这两个象
限的点的权重也越大,这样E(XY)的正负表达了变量X与Y在哪个方向上具有更大的权重,而它
的大小则表示一三象限方向与二四象限方向权重的差异的大小.
本人觉得这种接受还能说的过去,不知道子青兄能不能象这样说说你的解释.大家一起交流
交流!
|
我不喜欢用直观的东西来解释,直观的东西只能帮助记忆,用来解释是不牢靠的,而且不是所有的东西都有直观的解释.你这种解释基本合理吧,不过可攻击的地方也很多,比如说凭什么说两个随机变量大部分时候都是同号的就线性关系大,完全有可能是两个独立的只取正值的随机变量.
19229
引用 (子青 @ 2005年10月14日
14时
19分) |
|
其实上,E(XY)是一个内积定义,E(X-EX)(Y-EY)是一个中心化过以后二阶矩空间,因为协方差说到底讨论的是线性关系,所以先要中心化
|
你这个解释还是没有解释清楚啊老大.每个人都知道"协方差说到底讨论的是线性关系",可
是我们现在要问的是这个"协方差"是怎么样表达这种线性关系的.上面我说过,期望和方差
都很好地利用自己的特点表达了各自要表达的东西,可是这个混合矩并不是很直观.
本人请教过其他人,不知道这种解释正确与否:以E(XY)为例,若E(XY)>0,则可以说平面(X,Y)
上第一三象限内的点的(权重)概率相对其他象限要大,而且E(XY)的取值越大,说明这两个象
限的点的权重也越大,这样E(XY)的正负表达了变量X与Y在哪个方向上具有更大的权重,而它
的大小则表示一三象限方向与二四象限方向权重的差异的大小.
本人觉得这种接受还能说的过去,不知道子青兄能不能象这样说说你的解释.大家一起交流
交流!
19229其实上,E(XY)是一个内积定义,E(X-EX)(Y-EY)是一个中心化过以后二阶矩空间,因为协方差说到底讨论的是线性关系,所以先要中心化
19229
引用 (子青 @ 2005年10月13日
18时09分) |
|
E((X-EX)(Y-EY))是二阶矩空间上一个内积的定义 |
俺知道那是二阶矩空间上的内积的定义,但是用这个来表示两个随机变量之间的线性关系不太直观.相对来说,期望和方差就要直观的多,期望就是用平均水平来表示变量的整体水平,方差就是用一个平均距离来表达一个变量的整体离散程度.这些都很直观,但是如果用这种思路去考量那个协方差和其他的混合矩,我发现他们没有上述两者这样直观,所以我在这里发帖请教各位高手.
19229E((X-EX)(Y-EY))是二阶矩空间上一个内积的定义
192301、微分流形。
个人推荐华盛顿大学(西雅图)John M.Lee所著的《Introduction to Smooth
Manifolds》,该书内容全面而丰富(甚至包含定理这样的高级问题),由于可以有选择的阅读,因而篇幅不是很大。在上该书被七个人一致评为最高级别的书。
该书可在的主页上下到。(用搜他的名字即可)
至于现在国内流行的陈维桓的那本书,则感觉有点过于烦琐和细致。
2、黎曼几何。
据说多卡莫的书很经典,但我一直没见过,从感情上说,我仍然倾向于推荐的John
M.Lee《Riemannian Manifolds:an introduction to
curvature》(GTM的一本,世图已出,应该还能买到),该书能够着眼于基础,篇幅较小而且叙述相当清楚简明,非常值得初学者阅读。在读完该书之后,建议再读一下的J.Cheeger&D.Ebin《Comparison
Theorems in Riemannian
Geometry》,从方法论的角度,该书自然已经有些古典,但其中许多几何概念确实应该掌握的。
至于陈为环或白正国等人的书,个人认为,前者对几何结果不够重视,反倒有点陷入了基本方法的汪洋大海,而且编排体例不太好,后者我只是翻过,无法评论。
19231有哪位有南京大学高代考题和解答,本人找了很久,也不知道什么渠道可以得到
谁有可以联系我,QQ47092601
E-mail:abcd302@163.com
谢了!
1923103南京大学答案post-38-1132455733.ibf
19232能够获得诺贝尔奖当然是件大事,但是我们不能以此为目的和最终的目标。我想,我们更不能教育我们的学生把诺贝尔奖当成学习和研究的目的,那样的功利性会使他们耐不住寂寞,坐不住冷板凳,不能使他们踏踏实实的搞研究了!
19232说实话这是我今年读到的最令我感慨的消息.
虽然数学界没有诺贝尔奖,但是就象一位围棋圣手说过的那样,聂卫平在"抗日颠峰时期"是世界第一.
既然选择数学,就没有什么可遗憾的.
19232诺贝尔化学奖得主 尴尬兴奋害羞同在http://news.qq.com 2005年10月08日11:
17 人民网
兴奋的获奖者罗伯特·格拉布
美国科学家罗伯特·格拉布
1942年生于美国肯塔基州凯尔弗特市,
1968年从哥伦比亚大学取得化学博士学位,现为加利福尼亚州加州理工学院化学教授。罗伯特直言获奖是个奇迹,而感觉奇妙极了。
本报综合报道瑞典皇家科学院昨日宣布,将2005年诺贝尔化学奖授予在发现有机物合成转换方面做出贡献的法国科学家伊夫·肖万和美国科学家罗伯特·格拉布及理查德·施罗克。今年的诺贝尔化学奖奖金为1000万瑞典克朗,约合130万美元,三位科学家将分享这一奖金。
让原子学会“跳舞”
诺贝尔委员解释了换位合成的概念:所有有机物质都含有碳这种化学元素。碳原子可形成长的链条和链环,将氢和氧等原子固定在一起,形成双原子化学分子。
地球上的所有生命都以这些碳混合物为基础,不过所有生命体都可以通过人工有机合成而成。在换位反应中,双原子分子可以在碳原子的作用下断裂,从而使原来的原子组改变位置。当然,换位过程要靠某些特殊化学催化剂的帮助才能完成。打个简单的比方,换位合成法就类似于跳舞时两对舞者相互交换舞伴。
早在
1971年,伊夫·肖万就详细解释了换位反应的化学机理,说明是何种金属化合物能够充当有机化学反应中的催化剂。现在,换位合成法的“处方”已经为世人所知。理查德·施罗克是世界上第一个生产出可有效用于换位合成法中的金属化合物催化剂的科学家,这已经是
1990年的事情了。在
1992年,罗伯特·格拉布研制出一种更好的催化剂,这种催化剂在空气中很稳定,因此在实际生活中有多种用途。
使化学走向“绿色”
诺贝尔委员会在授奖文告中称,三位科学家是因在有机化学的烯烃复分解合成转换研究方面作出贡献而获奖的,该方法已被广泛地用于生物制药和生化领域,对最终攻克艾滋病等疾病也有很大帮助。文告称:“他们所发现的复分解方法被广泛应用于化工业,主要用于研发药品和先进塑料材料……只要能够想到,任何新的化学分子都可被制造出来。”
换位合成法在化学工业中每天都在应用,主要用于研制新型药物和合成先进的塑胶材料。在上述三名科学家的努力下,换位合成法现在变得更加有效,反应步骤比以前简化了,所需要的资源也大大减少,材料浪费也少多了;使用起来也更加简单,只需要在正常温度和压力下就可以完成,对环境的污染也大大降低。换位合成法使“人们向着绿色化学迈出了重要一步”,大大减少了有害废物对人们的危害。(参孙)
获奖感言:
平静生活一去不返
得知今年的诺贝尔化学奖名花有主之后,媒体对获奖的三位科学家进行了采访,谈到获奖,三人各有各的感受。
追忆亡妻
法国科学家伊夫·肖万坦言获奖让他感到的并不是喜悦,而是尴尬。他说:“我一直以来过着平静的生活,但现在这种平静一去不返了。”
伊夫对同时获奖的两位美国科学家给予了高度评价。他说:“我知道我所从事的研究工作是非常重要的,是的,是我最先走在了这条路上。然而我的美国同行研究了我的足迹,而且走得更远,是他们使我今天能够分享诺贝尔化学奖这一荣誉。”
“在实验室中,我付出了整整三十年的时间。而这三十年中,我工作的目的就是使世人对我从事的研究感兴趣而已,”伊夫说,“如今,我独自一人生活。至于获奖感受,我首先想到的是我的妻子,一年前她去世了。”
如饮醇浆
美国科学家罗伯特·格拉布得知获奖消息时正在新西兰。他通过电话接受美国媒体采访时表示自己正在庆祝,手中就拎着一瓶上好的波特酒。“味道真是好极了,”
他说,“获得诺贝尔奖对我来说是可望而不可及的事情,我一直醉心于自己的研究,想不到一抬头,它就出现在我面前。”罗伯特坦言搞科学尤其是化学,需要一个人长时间地付出努力,“在这条路上,我们已经走了30多年。”
咖啡时光
美国科学家理查德·施罗克得知获奖消息后接受了瑞典媒体的采访,他说:“我觉得很含羞,这就意味着现在我可能说话都不利索。得到(获奖)消息的时候我刚刚起床,正在享受一杯美味咖啡。坦白地讲,我很难相信这一切,然而这一切却真实地发生了。”(参孙)
成果解读:
“交换舞伴”的舞蹈
在今年获奖的三位科学家中,伊夫和理查德的贡献主要体现在烯烃复分解反应的基本原理方面,罗伯特继承和发展了他们的成果。
据新华社电(记者王艳红)碳是地球生命的核心元素。碳原子能以不同方式与多种原子连接,形成小到几个原子、大到上百万个原子的分子。这种独特的多样性奠定了生命的基础,它也是与人类生活密切相关的学科———有机化学的核心。
问题的提出
原子之间的联系称为键,一个碳原子可以通过单键、双键或三键方式与其他原子连接。有着碳-
19232寄语小学生 诺贝尔奖得主:人人都能成为科学家(图)http://news.qq.com 2005年09月22日05:39 东北新闻网
举起小手争先提问的是八九岁的孩子,始终站着谦逊回答的是诺贝尔奖获得者。面对孩子们形形色色的问题,他说:“只要你们问,我回答到明天早晨也行。”
特殊的大课堂是诺贝尔化学奖获得者恩斯特于昨天下午在铁西工人会堂举行的《我的成功之路》报告会。恩斯特此次来沈的第一场报告会,留给了铁西区1000名中小学生。演讲后,他特别给孩子们安排了自由提问。 长达2个小时的演讲和半个小时的自由提问,72岁的恩斯特一直站着讲,面带笑容。
作为一名物理化学家,恩斯特昨天面对孩子们的演讲,并没出现人们难以理解的数据和词汇。相反,他用几十幅照片、十几幅漫画深入浅出的讲解,针对他发明的核磁共振技术,也仅仅用按下几个钢琴键做以形象地说明。
以至于台下有孩子说:“原来,核磁共振就是这样一个道理呀!”
教育观:“其实得诺贝尔很简单!”
在演讲之初,恩斯特就说,他要以个人经历阐述在科学领域的追求。“以我为例,你们每个人都能成为一个科学家。”恩斯特在演讲即将结束时鼓励在座的孩子们:“其实,得诺贝尔很简单。”这句话激起孩子们的热情:“看着吧,我也能得像恩斯特爷爷那样,得诺贝尔!”
学术观:“克服,克服,再克服”
在30多年的学术研究里,恩斯特遇到很多困难。他谈道:“我从美国回到瑞士时,我发现我研究的课题,没人感兴趣。当时,我感觉天都要塌下来了。”“不过,这一切都慢慢地变了。我研究的课题现在已经被广泛应用到医学等领域。”
(
辽沈晚报 陈志馨 高望) [编辑:
钱文胜]1
回首学术路,恩斯特总结:“每次我遇到困难,我就会克服,克服,再克服!”
家庭观:“妻子是我的最大后盾!”
在回答一名老师关于“成功背后是什么”时,恩斯特说:“我的妻子对于我是最重要的。并不是说,她给我学术上什么帮助,而是她给了我一个温馨的家。”演讲期间,恩斯特的妻子一直坐在会场前排,始终注视着恩斯特。
幽默观:“我比爱因斯坦强”
一本杂志上,上面是正在拉小提琴的爱因斯坦,下面是正在演奏大提琴的恩斯特。恩斯特笑着说:“我比爱因斯坦强,因为我拉的是大提琴。”
恩斯特关键词
提前到场15分:昨天下午1点45分,恩斯特提前15分钟到达会场。
停电连声道歉:演讲期间,笔记本电脑突然断电,恩斯特赶紧修理,并连声向孩子们说对不起。
音乐催化事业:恩斯特总结:“人必须这样才够精彩,有事业追求,也有兴趣。化学是我的事业,音乐是我的兴趣。”
恩斯特小档案
1933年,恩斯特出生在瑞士温德萨。13岁那年对化学产生兴趣。
1991年,他以傅立叶变换核磁共振分光法和二维核磁共振技术获得诺贝尔化学奖。(辽沈晚报陈志馨
高望) [编辑: 钱文胜]
2(来源:东北新闻网)
http://news.qq.com/a/20050922/000505.htmpost-51-1129
196553.jpg
19232
理论走向应用这一理论提出后,越来越多的化学家意识到,烯烃复分解在有机合成方面有着巨大的应用前景,但这对催化剂的要求也很高。到底含有什么金属元素的卡宾化合物最理想呢?在开发实用的催化剂方面,作出最大贡献的是美国科学家罗伯特·格拉布和理查德·施罗克。
1990年,施罗克和他的合作者报告说,金属钼的卡宾化合物可以作为非常有效的烯烃复分解催化剂。这是第一种实用的此类催化剂,该成果显示烯烃复分解可以取代许多传统的有机合成方法,并用于合成新型有机分子。
1992年,格拉布等人发现了金属钌的卡宾化合物也能作为催化剂。此后,格拉布又对钌催化剂作了改进,这种“格拉布催化剂”成为第一种被普遍使用的烯烃复分解催化剂,并成为检验新型催化剂性能的标准。
以这些发现为基础,学术界和工业界掀起了研究烯烃复分解反应、设计合成新型有机物质的热潮。
专家点评
“他们的成果每天惠及人类”据新华社电(记者潘治颜亮)“他们的成果得奖,是化学界认为理所当然的事情。这不仅是因为他们的科研成果本身非常重要,更重要的是这一成果在生产生活领域有着极其广泛的实际应用,他们的成果推动了有机化学和高分子化学的发展,每天都惠及人类。”中国科学院戴立信院士在其上海的家中接受电话采访时,对今年诺贝尔化学奖得主的获奖成果作出了这样的评价。
81岁高龄的戴立信院士介绍说,烯烃复分解反应非常重要。这是因为,化学键的断裂与形成是化学研究领域中最基本的问题,研究碳-碳键的断裂与形成规律是有机化学中需要解决的核心问题之一,而格拉布等人正是在此方面作出了贡献。
“我的印象中,格拉布是一个非常努力的人,他早年只是个有机化学家,对高分子化学所知不多,但他利用业余时间给自己开课,最终获得了优秀的成果,成为目前世界化学界这一领域最为活跃的科学家”,戴立信说。
戴立信认为,将诺贝尔化学奖同时授予三人,“体现了诺贝尔奖评选的原则,那就是记住那些在基础研究方面作出巨大贡献的科学家。”害羞的获奖者理查德·施罗克:美国科学家理查德·施罗克
1945年生于美国印第安纳州伯尔尼市,
1971年在哈佛大学取得化学博士学位,现在麻省理工学院担任化学教授。他在得知获奖消息后觉得有些不好意思。尴尬的获奖者: 伊夫·肖万法国科学家伊夫·肖万生于
1930年,现在法国石油学院任职。伊夫坦言获奖的感觉是尴尬,而不是喜悦。来源:《新京报》
19234A^2=A,考虑化成若当距阵已经可以证得它是对称的了,为什么还要有这个条件x'A'Ax<=x'x
19234A为n阶方阵,A^2=A,对任意n维列向量a,有x'A'Ax<=x'x,证明:A=A'
19234A^2=A推不出A对称的!
19234由A'A的特征值全小于1能不能得A'=A?
19238如题
19239如题
19240是啊,怎么办呢?
19240大家看看,到底是怎么回事呢?post-28-1129205003.ibf
19240什么意思?是用公式显示的不好??
19240用LaTeX
19240是不是行间距没有设置好?
19240好像不是行间距的事情,是否在其他计算机上就应该显示正常
19241
非常感谢 急人之需 雪中送碳
19241楼主,好人,谢谢
19241第四题能直接证,还反证??
第9题是有问题的
19241仅供参考post-38-1129205703.ibf
19241非常感谢楼主!!!!
19241非常感谢!
19241该解答的第九题必要性证明有问题
19241好啊 !!谢谢!!
19241感谢 楼主~~~
19241请将不足之处改正.
19241非常之感谢!!
19241无私搂主
好人呀
19241好哟!!
顶一下!
19241谢谢楼主
19241谢谢楼主 你太伟大了
19241不知道说什么好,楼主的恩情我永记于心!
19241请问楼主是哪个学校得老师,我最崇拜数学老师了!
19241非常感谢楼主!!!!
19241xiexieni ,dage!
19241楼主,好人,谢谢
19241thanks
19241请问第四题怎么正面来证?谢谢
19241谢谢
19242不会错的吧,是资料书上的,被一个学生问我,却解决不出!
原题目是这样的:(1/2+1)+(1/3+2)+(1/4+3)+

(1/100+99)=?
难到真的没有方法解的?
19242或者吧,我也解不出,可能是书有问题的了,多谢各位了!
19242原书有误吧,分母的加号应为乘号。
19242这个具体的结果应该得不出来,楼主是不是把题目理解错了?
192421/3+1/5+1/7+

1/
199=?
不知这个点样算?
19242想问一下怎么你的标题是极根求和的题目呢
我们可以用微积分求的啊
19242f(x)=x+1/2 x^2+1/3 x^3 +...+1/
199
x^
199
求f'(x)=1+x+x^2+...+x^
198=(1-x^
199)/(1-x),在定积分求出f(x)
在求[f(1)-f(-1)]/2既可了
19242to
liukewencn:
你的方法:求f'(x)=1+x+x^2+...+x^
198=(1-x^
199)/(1-x),在定积分求出f(x)
好像是求不出确切的解析解的,(1-x^
199)/(1-x)的原函数f(x)本身,你绕了一圈又回来了。否则用数值解法。我觉得这道题目只能求出近似解。是不是我理解的有错误,请您指教!
不妨设1+1/2+1/3+...+1/
199+1/200=A~=ln200-gamma
1+1/2+1/3+...1/100=B~ln100-gamma
原式=A-B/2~=ln200-ln10-0.5gamma=ln20-0.5gamma
19242
| 引用 (Buzzard @ 2005年10月13日
20时27分) |
1/3+1/5+1/7+…+1/
199=? |
解答1:
sum(1/(2*k+1),k=1..99)
=60
19484
1808750942937757710259539
18105702575294840
19104565796832460214046785
1923044049097/2635106162757236442495826303084698495565581115509040892412867358728390766099042109898375
=23371*758581050533*1092640788667*3107438795275335986
1805705013
1960763869616940512307367022637/3^4/5^3/7^2/11^2/13^2/
17/
19/23/29/31/37/41/43/47/53/59/61/67/71/73/79/83/89/97/101/103/107/109/113/127/131/137/139/149/151/157/163/167/
173/
179/
181/
191/
193/
197/
199
=2.284342
1893016343456548…
解答2:
sum(1/ithprime(n),n=2..46)
=5651
176410092883481211240411
186976500395614667593880762599927616086725682375647981/389996102084
173077662459955316490693834399839495
1775472546516237434255768082350405
=1447*910471*4289475742660948811213266216096855561523106460646894
188260321272133994013/3/5/7/11/13/
17/
19/23/29/31/37/41/43/47/53/59/61/67/71/73/79/83/89/97/101/103/107/109/113/127/131/137/139/149/151/157/163/167/
173/
179/
181/
191/
193/
197/
199
=1.449034074928571
1845309…
19242用电脑相加的是小数,什么用?
19243我就是不怎么擅长编辑数学符号才没有发答案的。要是熟练一点的话。估计早就放到论坛上和大家交流了。对不起啊。你还有没有其他的联系方式。比如QQ的?
19243本人在 考研也在做北大数分卷子 能否帮助一下 看看解答 多谢 xuhua_max@126.com[COLOR=red]
19243偶刚刚做完了北大2005的数分卷子,就是不太清楚答案有没有问题。看看哪位朋友愿意交流一下答案和感受。我QQ:248550244
19244我知道实数矩阵的特征值和特征向量的意义和算法,现在迫切想知道对于复数矩阵是否也有类似的推广,如果有如何计算?是否也有相应的几何意义?希望高手指教
先谢谢了
19244可做完全一致的推广,甚至还有更多的结果
19244非常感谢!麻烦你给我推荐一本有关这方面的参考书行吗?
19244是呀,这个我也不是很懂呀,呵呵,希望哪位高手指点一下
19247哥们,咋使用编辑公式,我有几道题目想请教诸位老师
回复:看看置顶主题.
19248如图(附件),已知圆1与圆2相交于A、B两点,过A的直线交两圆于C、D,过B的直线交两圆于E、F,试判断CE与FD的位置关系,并加以说明。post-7-1129209
178.jpg
19248如图(附件),已知圆1与圆2相交于A、B两点,过A的直线交两圆于C、D,过B的直线交两圆于E、F,试判断CE与FD的位置关系,并加以说明post-8-1129209642.jpg
19248证明:连接AB,因为同弧所对圆周角相等,所以角ECD等于EBA.而且角FBA等于FDA,所以有角ECD等于FDA.由内错角相等可得CE,FD平行.请指教.
19248平行。连接AB,ABCE,ABDF均公园。
19249诸位师哥师姐,我想考公费的研究生,不知形势砟样,请告知
19252请知道的介绍一下
19253微软2003server的集群计算服务器介绍网址:
http://www.microsoft.com/china/windowsserv...pc/default.mspx另附高性能计算从UNIX到WINDOWS迁移的资料:
http://download.microsoft.com/download/0/b...e_Computing.zip若大家无法下载资料请PM我。我将做为附件上传。
19253好啊
楼主真是好人!
19254abel不等式处理
19254谢谢post-38-1129213437.ibf
19254cauchy收敛准则!
要用abel不等式放缩
19254我想应该用迪里克来判定把,但我不知道怎么处理sin(nx)
19254ok,我明白了,另外,你说的abel不等式是abel引哩吗?
19255怎么没有人解答啊 ???
19255最后一题
怎么能得出3啊??post-38-1129214306.gif
19255为什么没有人解答啊??
谢谢啊!
19255题目显然是错误的,每个
a
n
同时乘上一个参数t,则f的积分应该是t的线性函数,但现在要证明它是一个常数3,这是绝对不可能的事情。
19255
不可能啊??
19255题目有问题!!
19255
| 引用 (janssen @ 2005年10月16日
15时40分) |
|
不可能啊??
|
为什么不可能?
19255这是原题,应该没写错吧,最后是3吗??看不清啊post-38-1129557241.gif
19255仍然是错题。
19255最后不是3是S吧,post-38-1129602
197.ibf
19255
引用 (Sainter @ 2005年10月
18日
10时23分) |
| 最后不是3是S吧,
|
最后是S似乎也有问题,这只要取a0=1,其余的an=0即可以看出。
19256matlab中符号表达式什么命令用求值呢?
19257你真强啊!
19257明白了,用taylor展开!
19257由f是正函数即f>0,f'

0知f递减,故f有极限,
下面就和裴礼文书的一题一样,自己查找,我就不写了
19257无从下手啊???post-38-1129216943.gif
19258呵呵张老师 是我导师:)
19258我一直都找不到这本书的习题解答.好像这里也有很多人在找.不知道找到没有.如果找到就通知我下.如果没找到,那我想我们之间的交流应该还是很有用的.
我想我们以电子邮件的形式交流比较好,编一个邮件发群体.然后大家看了,自己发表下自己的见解.
希望愿意加入的同学留下自己的id和e-mail
我的id:
w_oneyear
e-mail: w_oneyear@126.com[SIZE=7][COLOR=red]
19258我一直都找不到这本书的习题解答.好像这里也有很多人在找.不知道找到没有.如果找到就通知我下.如果没找到,那我想我们之间的交流应该还是很有用的.
我想我们以电子邮件的形式交流比较好,编一个邮件发群体.然后大家看了,自己发表下自己的见解.
希望愿意加入的同学留下自己的id和e-mail
我的id: w_oneyear
e-mail:
w_oneyear@126.com[SIZE=7][COLOR=red]
19258这也要钱,气愤
19258估计除了狂热分子没人会买你的门票钱
19258信箱里的邮件是不是被人给删了啊?已经没有了啊
19258z楼上的真幸运,有这么厉害的导师,我做梦都想呀,可惜没得这个本事,我导师一点名气没有,太差了,只知道找钱,科研什么都不搞了,郁闷的很呀,
对了,楼主,ID是什么,我也想要那个答案,有的发份给我哈
yuxianzh@swu.edu.cn
19258张老师的书很好,可惜一时半会无法领会其精髓,拜托拜托,我也需要答案.wuguocheng2002@163.com
19258有答案吗。
我也非常需要阿!!!
我的邮箱:
1982-wzb@163.com
谢谢各位楼主
19258我也需要阿
正在学习中
rarelb@126.com
19258张恭庆编的<<泛函分析>>的习题解答部分
雅虎邮箱:www_bossh@yahoo.com.cn
密码:bosshnet 里有。
19258谢了,下了三个附件,不知全不全?
19258
| 引用 (maths @ 2006年01月08日
23时47分) |
张恭庆编的<<泛函分析>>的习题解答部分
雅虎邮箱:www_bossh@yahoo.com.cn
密码:bosshnet 里有。 |
我下了三个附件,谢谢
19258我也急需
ID Jennykong
E-MAIL kongzhaoli@163.com
谢谢
19258这本书读起来很好,尤其是应用方面,和别的书不一样。
习题部分很有难度啊!
19258我也要
monier2005@126.com
19258我也十分需要
如果有顺便给我一份
先谢了
邮箱lhwjt@sina.com
19258我也要
xiangsun@mail.ustc.edu.cn
19258我的ID:xiaoyan2006
moxiaoyan
1983@126.com
19258有些习题搞不定,急需,发我alex79123@163.com,谢谢
19258
xd4907 你好!你说你从雅虎邮箱:www_bossh@yahoo.com.cn 密码:bosshnet 里
下了三个附件,能发给我么?因为我都打不开啊,我的邮箱:xxc570@163.com,能加我的QQ嘛:89246682,非常感谢!
19259不错,应该是本很好的数学思想书!我有时间买本看看,谢谢楼主了!!!
19259推荐书籍如下:
《数学分析的思想与方法》明清河著 山东大学出版社出版 2004年4月第一次印刷
目 录
第一部分 数学分析内容中体现的数学思想
一、函数的思想
1. 函数概念的产生与发展
2.
函数概念的本质
3.
函数思想在数学分析中的应用
二、极限的思想
1.极限思想的产生与发展
2.极限思想的思维功能
3.建立概念的极限思想
4.解决问题的极限思想
三、连续的思想
1.
连续思想的产生与发展
2. 连续思想的解释
3. 连续思想的应用
四、导数的思想
1. 导数概念的引入
2.
导数的定义
3. 导数定义的理解
4. 导数思想的应用
五、微分的思想
1. 微分思想的产生和发展
2.
微分思想的解释
3. 导数与微分的联系与区别
4. 微分思想的应用
六、积分的思想
1. 积分思想的产生与发展
2.
积分思想的理解
3. 积分思想中的辩证法
4. 不定积分与定积分的比较
5. 定积分的应用
七、级数的思想
1.
级数理论的意义
2. 数列与数项级数的关系
3. 函数项级数的一致收敛的作用
4. 付立叶级数研究的基本问题
5.
级数理论的应用
第二部分 数学分析内容中蕴涵的哲学思想
一、 直与曲的思想
1. 近似计算中的直与曲
2.
利用积分解决实际问题中的直与曲
二、 常量与变量的思想
1. 常量与变量的相对性
2. 通过常量来刻划变量
3.
通过变量来研究常量
三、 有限与无限的思想
1. 有限与无限的质的差异
2. 有限与无限的联系与转化
3.
阿基里斯悖论中的有限与无限
4. 《庄子》中的有限与无限
5. 数列极限 定义中的有限与无限
6.
几个等式中的有限与无限
四、 局部与整体的思想
1. 微元法中的局部与整体
2. 闭区间套定理应用中的局部与整体
3.
有限覆盖定理应用中的局部与整体
4. 闭区间上连续函数性质中的局部与整体
5. 证明函数项级数和函数分析性质中的局部与整体
五、
近似与精确的思想
1. 概念建立中的近似与精确
2. 微元法中的近似与精确
六、 特殊与一般的思想
1.
一般与特殊举例
2. 解题中的特殊与一般
3. 概念建立中的特殊与一般
4. 概念和定理获得中的特殊与一般
七、
连续与不连续的思想
1. 解题中连续与离散的转化
2. 理论中连续与离散的对应
3.
内容中连续与间断的转化
八、对立与统一的思想
1.概念定义中的对立与统一
2.解题过程中的对立与统一
九、量变与质变的思想
1.解题中的量变与质变
2.推广中的量变与质变
十、否定与肯定的思想
1.
概念形成中的否定与肯定
2. 解题过程中的否定与肯定
第三部分
数学分析内容中常用的数学思想
一、类比的思想
1.运用类比揭示概念
2.运用类比引出命题
3.运用类比解决问题
二、变换的思想
1.恒等变换
2.映射变换
3.参数变换
4.
离散—连续变换
三、构造的思想
1.构造函数
2.构造数列(级数)
3.构造结论
4.构造不等式
5.构造图形
6.构造反例
四、递推的思想
1. 极限运算中的递推
2. 求导运算中的递推
3. 求积运算中的递推
4.
级数理论中的递推
五、猜想的思想
1. 由归纳产生猜想
2. 由直观产生猜想
3.
有类比产生猜想
六、反例的思想
1. 数学分析中反例的作用
2. 数学分析中反例的构造
七、不动点的思想
1.
连续函数的不动点问题
2. 单调函数的不动点问题
3.
递推数列的不动点问题
八、化归转化的思想
1.概念建立中的化归转化
2.内容处理上的化归转换
3.解题策略上的化归转化
九、以退求进的思想
1.概念建立中的以退求进
2.解题过程中的以退求进
十、分段处理的思想
1.
分段函数性质讨论的分段处理
2. 复杂和式、乘积式的分段处理
3. 函数分析性质讨论中的分段处理
4.
积分等式证明中的分段处理
5.
中值定理应用中的分段处理
十一、数形结合的思想
1.通过数形结合掌握概念
2.通过数形结合理解与证明性质
3.通过数形结合解决问题
十二、分类讨论的思想
1.
极限问题中的分类讨论
2. 连续问题中的分类讨论
3. 可积问题中的分类讨论
4.
级数敛散性问题中的分类讨论
十三、特殊化与一般化的思想
1.由特殊到一般建立概念
2.由特殊到一般发展理论
3.由特殊到一般推广结论
5.
先特殊后一般,由特殊推一般
6. 先一般后特殊,由一般求特殊
第四部分
数学美与数学分析中的美学思想
一、数学美
1. 有关数学美的一些论述
2. 数学美的本质与特征
3.
数学美与数学创造
4. 数学美的基本内容
二、数学分析中的美学思想
1. 统一美
2. 对称美
3.
奇异美
4. 简洁美
5. 符号美
6. 形式美
7. 抽象美
8. 实用美
第五部分
微积分创立过程中数学家的思想和方法
一、微积分孕育时期数学家的思想方法
1.德莫克利特的数学原子论思想
2.欧多克斯的穷竭法
3.刘徽的割圆术
4.祖暅原理
5.阿基米德的求积方法
二、微积分创立时期数学家的思想方法
1.开普勒的同维无穷小方法
2.伽利略的运动观点
3.卡瓦列利的不可分量法
4.瓦里斯和巴斯卡的分析方法
5.费马的“分割求和”方法
6.费马的求切线方法
7.费马的求极值方法
8.巴罗的求切线方法
9.牛顿建立微积分的思想方法
10.莱布尼兹建立微积分的思想方法
三、微积分的发展与完善时期数学家的思想方法
1.欧拉对微积分内容的扩展方法
2.波尔查诺的严格论证方法
3.柯西的极限理论与方法
4.魏尔斯持拉斯的分析算术化方法
5.戴德金的实数理论方法
附
录 古代数学家解题思想举例
19259在北京图书大厦能买到吗
19259可是不知道怎么样才能看到这本书
刚查了学校的图书馆,里面没有收藏这本书啊
19259那么请问在那里可以买的到了?
或者在那里可以下载的到啊。。。。。。以此那里有好的下载数学书籍的网站?
如有给个否?不甚感激!
19259统一美
2. 对称美
3. 奇异美
4. 简洁美
5. 符号美
6. 形式美
7. 抽象美
8.
实用美
请问楼主有没有电子版啊
19259能传电子版的吗?谢了!
19259关于数学思想的书不多啊~~
我想这是一本好书~~
大家还能推荐一些比较好的关于数学分析和微积分之类的外文书吗?
19259请问楼主,在哪里能买到阿
19259
谢谢各位对该书的关注!
该书是本人的愚作,是对数学分析思想方法研究所做的一点尝试.主要是用数学方法论的思想来指导而进行的学科思想方法探讨.该书写成后得到了山东大学出版社的大力支持并出版印刷.如果想索要该书,请与山东大学出版社联系.
19259[SIZE=7][COLOR=green]真诚希望浏览过该书的朋友,能不吝赐教,提出宝贵意见[SIZE=7]
19259[FONT=Times][SIZE=1][COLOR=red]
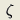

post-68-1166502474.ibf
19259这是明清河写的<数学分析的思想与方法>一书的介绍,山东大学出版社出版,这本书我买了,很不错,对学生和授课教师都是大有帮助的,并且很便宜,
18.80元.
19259请问再哪里能够买到这本书
19259很好的书啊,对提高数学思想有很大的好处
19260谢谢你的回复
能否给我一个完整的解题答案?非常感谢
19260这个是一个Poisson过程的问题.
平均三个星期出一次故障就是说
E(P(3
λ
))=3*
λ =1,于是有
λ
=1/3
1.参数为
λ 的Poisson过程的第n个事件发生的事件服从一个参数为
λ ,n的Gamma分布.然后把n=4,
λ
=1/3带入Gamma分布带进去算一下第4次事件到达时间小于21的概率.
2.Poisson过程无记忆性,也就是说接下来的三个星期发生事件的次数服从一个P(3
λ
)的Poisson分布,算一下概率最大的
3.同1,带入n=5的Gamma分布,算密度最大点.
19260第一次发贴,本身并不是学数学的,帮我在国外读书的朋友问,翻译的不好请原谅,谢谢大家帮助
网络每三个星期就会出一次状况,平均来讲,请计算以下三题
1)
在21个星期中,出现超过4次状况的概率
2) 计算接下来三个星期最有可能会出现状况的次数
3)
请问第五次状况最有可能在哪个时间段出现?
我朋友刚到这里,因为语言问题老师上课听不太懂,希望大家能帮帮他,再次感谢
19262请大家帮忙解决几道数份题(4)谢谢!post-21-1129250965.ibf
19266G.Birkhoff,Lattice Theory, American Mathematical Society,Colloquium
Publications,Vol.25,
1967
各位前辈,如果您有电子版本,烦请发到Yumingfeng25928@163.com
如果你有Hard paper也请您给我个提示,我只需要复印下。谢谢。
19267怎么没有大侠帮我解决一下呢??
谢谢各位了!
19267最近遇到个问题,搞了好久都没有结果,现在只好求助数理学院的各位朋友了,呵呵,谢谢了先!是关于坐标变换方面的:如题:有(o1,x1,y1,z1)和(o,x,y,z)两个坐标系,知道z1轴和z轴夹角,z1投影到xoy平面后与x轴的夹角,要求将坐标系(o1,x1,y1,z1)变换到(o,x,y,z)的变换矩阵。谢谢了,我的qq:43287220,电话:60607862
19268是否为正态变换呢?
19268可以帮忙讲解一下高斯变换吗?十分感谢
19268应该是Gauss标准变换吧 !
19269谢谢斑竹精辟的论述,因为本人刚开始
接触微分几何,又是自学,所以总会有一
些低级的问题.
另外樱析光说的为什么要加时间轴,是因为
我认为这样想象起来方便.比如说:四维时
空里的一个非线性方程确定的一个三维流形:
x
^{2} + y ^{2} + z ^{2} + t ^{2} =1,
你让时间从[0,1]之间变,
那么在一个确定
的时刻,这个流形实际上是一个三维空间里
的球面(半径随时间改变),然后随着时间推移,
它扫过了四维空间里的一个区域,这个区域我
就认为是四维空间的一个流形了.
19269高维流形谁都想象不出来
注意流形作为一个数学概念(当然是几何所研究的对象,是几何中的基本概念)不要必然的有“直观形象”的。
不过我们还是可以用某种方式(比如投影的方式或截面的方式)来“近似“的描述和刻画高维几何空间的一些位形关系。比方说我们可以在黑板上“画一个立方体”。自然的我们也可以选择某种方式在平面上“画一个超立方体”,这是可能的,不过随着维数的升高困难也就越大。这都依赖于我们所采用的方式。好象现在可以计算机在平面上“表现“一个5维的几何运动。
不过就数学而言,几何研究完全没有必要把几何对象画出来。
另外,流形不必要有一个整体的仿射坐标系(只有一些特殊的流形具有),流形是一个具有局部坐标系的几何空间,这对流形的研究和应用已经足够了。坐标完全是次要的,只是工具而已。
19269人的大脑是三维的,怎么能够想出四维的东西?
19269我不太懂流形,有些疑问,望顺便解答:(谢谢!)
你干嘛加一个“时间轴”,怎么加的?怎么不加一个空间轴?
你这的“嵌入”是什么意思?难道是“镶嵌”?有定义吗?
流形的例子很多,又不一定全是几何图形。想一个代数的例子理解可以吗?
19269我在想,三维空间里的一个曲面
是一个二维流形,它是不能嵌入到一
个二维平面的.只能在三维空间来
想象它.但是对一个三维流形,它也
应该是不能嵌入到三维空间的,只能
到四维空间去想象它,我尝试加上一个
时间轴,但还是想不出来三维流形是
什么样的.
流形斑竹,能不能教我一个法子
把它想象出来,万分感谢!
19269
四维立方体的一种画法,同理也可画出四维锥体。在二维介质中画的图形的维数越高,图中损失的信息就越多。比如,在纸上画一个三维正方体,实际上这个正方体图形已经失去了确定性,它可以用来表示两个从不同角度看上去的正方体。post-22-1129640757.jpg
19269如:post-22-1129641565.jpg
19269第一个图是什么东西?最右边的为什么是虚线?
19270非常感谢,问题已解决
19270n阶贝赛耳函数
post-8-1129301246.jpg
19270问题在下面的图中post-8-1129259679.gif
19272如主题所说,希望哪位知道的同仁帮助.
谢谢.
192732005年的经济学奖被一个美国人和一个以色列人得到了,可是为什么到目前为止,没有一个本土的学者或科学家获得这项荣誉呢??????郁闷!是我们的智商有问题吗?抑或是我们的教育有问题?无非就是这两个原因.中国人还是很聪明的,所以,肯定不是人的问题,而是教育的问题.从报纸上看到一则消息,说是海南的高考状元被香港中文大学录取了,还有奖学金,可是清华北大却不要,说人家是移民,真是脸脏的都忘檫了,看看他一年从北京本地录多少人,净是些二路货色,还不要人家,还有脸不要.真是服了他了.
19273综合国力的事情
19273那就加油啊
19273这和体制的有关吧
19277这是我自己收集得,有需要得就下!!!!post-38-1129265335.ibf
19278请各位高手帮个忙!谢谢!post-38-1129265535.ibf
19278!!!!post-38-1129277025.gif
19278
等价吗?我就是觉得不等价才问大家的。希望明确写一下好吗?
谁会第一题?帮帮忙!
19278原积分等于

x*cos(x)/sin(x)dx(0~

/2),再把(

/4~

/2)上的积分用t=

/2-x代换后整理可得一关于原积分的等式,据此可求解
19278
| 引用 |
| 等价吗?我就是觉得不等价才问大家的。希望明确写一下好吗? |
post-38-1129800088.gif
19278
| 引用 |
| 原积分等于 x/sin(x)dx(0~
/2), |
to reijin:
积分怎么变为:
∫ 0
π 2
x
sinx dx
19278不好意思,打错了,原贴以更改
19279中科院考题post-38-1129265670.ibf
19280我觉得可以用taylor展开证明出f''(x)=0
19280是啊,我也觉得可以用展开式来做,看上去应该不难,不知道做起来怎么样!
19280详细见附件。post-38-1129266025.ibf
19280什么叫广义二阶导数啊?
19280这个问题里面的f(x)并没可导的条件,这样的话,可以先证明下命题,然后再推出结论:
f的广义二阶导数存在且连续,则对于x<y,存在z,使得f在z上的广义二阶导数等于[f(x)+f(y)-2f((x+y)/2)]/h^2,h=(y-x)/2
此命题可用类似证明罗尔、中值定理等方法证明
根据上述命题,在本问题中可得出f(x)+f(y)=2f((x+y)/2),这是一个柯西函数方程,可直接得到结论
19281这个容易!根据下面的附件,可以将Entry-wise翻译成“对应元素相加”。
有很多数学专业词不用翻译,知道原理即可。实在不行,可以查网上。post-33-1129284984.jpg
19281谁知道 Matrix addition is defined entry-wise for arrays of the same
dimensions and is denoted by +("A+B")
中的entry-wise是什么意思?
另外,大家怎么查到一些不会的数学专业单词?
19281装一个金山快译吧,挺方便的!
19281金山快译上没有
19281很多单词都是金山词霸,快译里面查不到的..............
19289数学文化及其应用
数学既不严峻,也不遥远,它既和所有的人类活动有关,又对每一个真正感兴趣的人有益。
R.C.Buck
数学的传奇就是攀登智慧之山的传奇。
J.N.Kapur
诗人对宇宙人生,须入乎其内,又须出乎其外.入乎其内,故能写之.出乎其外,故能观之. .入乎其内,故有生气,
出乎其外,故有高致.
王国维
数学是研究现实世界中的数量关系与空间形式的一门学科。由于实际的需要,数学在古代就产生了,现在已发展成一个分支众多的庞大系统。数学与其他科学一样,反映了客观世界的规律,并成为理解自然,改造自然的有力武器。
对任何一门科学的理解,单有这门科学的具体知识是不够的,那怕你对这门知识掌握得足够丰富,还需要对这门学科的整体有正确的观点,需要了解这门学科的本质。我们的目的就是从历史的、哲学的和文化的高度给出关于数学本质的一般概念。今从以下几个方面来谈这个问题。
1 数学与美。庄子说:”判天地之美,析万物之理”。日本物理学家,诺贝尔奖得主汤川秀树把这两句话印在他的书的扉页上,作为现代物理的指
19289呵呵,这个学期我们刚好学业习了,数学史。呵呵,刚好适应了,中学的发展呵呵。
19290顶!!
19290算法
张奠宙
算法,一个既陌生又熟悉的名词。说陌生,因为算法概念从未进入我国中学数学教学大纲。新的高中数学课程标准破天荒地把算法作为重要内容列入必修课,自然出乎人们的意料。说到熟悉,那是因为从小学就开始接触算法。例如做四则运算要先乘除后加减,从里往外脱括弧,竖式笔算等等都是算法,只要按照一定的程序一步一步做,一定不会错。至于乘法口诀、珠算口诀更是算法的具体体现。因此,算法其实是耳熟能详的数学对象。一般地,算法是指在解决问题时按照某种机械程序步骤一定可以得到结果的处理过程。这种程序必须是确定的、有效的、有限的。
中国古代数学以算法为主要特征。吴文俊指出:“我国传统数学在从问题出发以解决问题为主旨的发展过程中,建立了以构造性与机械化为其特色的算法体系,这与西方数学以欧几里得《几何原本》为代表的所谓公理化演绎体系正好遥遥相对。……肇始于我国的这种机械化体系,在经过明代以来几百年的相对消沉后,由于计算机的出现,已越来越为数学家所认识与重视,势将重新登上历史舞台[1]。”吴文俊创立的几何定理的机器证明方法(世称吴方法),用现代的算法理论,焕发了中国古代数学的算法传统,享有很高的国际声誉。他因此于2001年获得了第一届国家最高科学技术奖。
20世纪上半叶,科学研究方式归结为两种方式:理论+实验。后来由于计算机技术能力的开发,计算成为第三种重要手段。未来的趋势是,“理论+实验+计算”将成为标准的科学研究方法。那么,计算机如何按照人的意愿进行计算呢?这就要靠算法。因此,毫不夸张地说,算法既是数学科学的重要基础,也是计算机科学的核心。
虽然算法的历史悠久,而且几乎和计算机技术共生共长,但是力图使之成为现代公民的基本数学素质,列入中小学教育的基础课程,则只是近十余年的事。在我国,
1980年的《辞海》还没有收入“算法”,只有“算法论”的条目(
那是“数理逻辑”学科的一个分支,相当专门)。
1988年出版的《中国大百科全书(数学卷)》,才有了莫绍揆先生撰稿的“算法”辞条。其中详细地分析了算法的主要特征:能行性。其意思是:
1.输入输出的数据必须是由字母组成的有限符号串(例如不能输入一条曲线);
2.算法的处理过程必须可以明确地分解成有限多个不能再分解的步骤(例如不能把画无限多个点的曲线作为算法过程);
3.算法的继续进行和结束要有明确的条件加以规定;
4.算法的变换规则必须是非常简单而机械,不依赖于使用者的聪明才智。
用以上的四条来分析,小学里做四则运算,输入输出都是字母(阿拉伯数字),计算规则都是按一定次序执行有限步,而且按这一步骤去做一定成功,无须技巧,到了最后一步,结果自然就出来了。因此,“四则运算”的过程符合上述四条。
算法的思想,
不一定仅仅用于数字计算,它可以广泛地描述许多操作过程。例如,有一队士兵要过河,但当时只有一条小船,上面有两个小孩。小船至多可以载一个士兵或者两个小孩,请问这队士兵依照何种程序才能渡过此河?可以用流程图加以表示:
同样可以画出求解一元一次方程的流程图(算法流程图的详细程度依赖于读者的需要)。
那么如何在计算机上实施这一算法呢?那就要设计程序语言。例如要求非负整数 a, b
的最大公因子,熟知的方法是欧几里得算法。与该算法相应的计算机程序可以是:
input(a,b)
(x,y) ← (a,b)
more:if x=0 then goto enough
if y≧x then y ← y-x else
(x,y) ← (y,x)
goto more
enough: output(y)
算法程序是由语句组成的。符号(x,y) ← (a,b) 的意思是同时把 a 和 b的值赋给 x和y,称为赋值语句。 If …
then… else表示条件语句。
计算机执行上述的指令,按部就班地操作即可得到结果。例如,将 a= 4,b=10
作为初始值赋予(x,y)。那么按照指令就有 (4,10)→(4,6)→(4,2)→(2,4)→(2,2)→(0,2),得到结论:最大公因子为2。
在处理迭代过程等程序时,还要使用循环语句。上面的士兵过河问题,就需要机械地循环操作。新课程标准要求学生了解赋值、条件、循环等三种语句,并尽可能在计算机上进行实际操作,亲身体验由人指挥机器的效果。在信息时代,这是一种人人都需要具备的科学素养。数学和信息技术课的教师可以密切合作,完成算法的教学。
最后,谈谈算法复杂性问题。
假定一个班上有50名学生,现在要按照姓名的拼音顺序排成一张表。
一个最笨的算法是将50个学生所有可能排列的表都打出来,然后从中挑选一张符合拼音顺序的表。要知道,50个人的不同排列有50!种,即这样的表有50!张,它大约是3×1064。这个数目之大,用每秒100万次的计算机不停地运算需要9.6
×1048世纪,显然是不能实施的。
但是可以不用这样的笨办法,采用以下大家常用的算法来排。随便拿一位同学的名字排在第一位。任取第二位同学的名字先放在第一位,然后依拼音顺序和第一位的名字比较一次,放在适当位置。第三位则需要和前两位的名字比较至多两次。依次类推,第k位至多要比较k-1次,第50
位至多需要比较49次。这样,只要比较1+2+…+49=49×50/2=1225次,就完成了排序。如果班上有n 个学生,第一种算法需要运算
n!(当n>25, n!>10n )次,第二种算法至多需要 (n –1)n/2 次。前者的次数随n的增加,按超10n
的指数方式增加,后者则只按n
的二次多项式的方式增加。一般地,假如在一个问题中有n个数据需要处理,而处理的算法的计算次数依指数n方式增加,称之为指数算法;若按n
的多项式方式增加,则称为多项式算法。当今的计算机无法承受指数算法的运算。因此寻找各种问题的多项式算法,乃是数学发展的一个重大的关节点。
算法, 披着时代的盛装,沿着信息传递的脚步,正在悄悄地走进人们的生活,跨入中学的课堂。让我们举起双手,欢迎算法的到来!
19291
引用 (mathguy @ 2005年10月14日
18时33分) |
| 南开的组合数学强啊!
|
没脑子的
19291为了加强组合数学与图论研究的学术交流,受全国组合数学与图论学会理事会的委托,全国第二届组合数学与图论学术会议将于
2006年8月8日-8月14日 在天津南开大学举行,由南开大学组合数学中心承办。
19291南开的组合数学强啊!
19292为了加强组合数学与图论研究的学术交流,受全国组合数学与图论学会理事会的委托,全国第二届组合数学与图论学术会议将于
2006年8月8日-8月14日 在天津南开大学举行,由南开大学组合数学中心承办。
19292能否就投稿事宜说的具体些,谢谢.
19293请问,中科大和中科院卷子相同吗??
有考过中科大的说一下,有没考几何?
谢谢啊,
19296基础数学:
数论:古典数论 解析数论,代数数论,超越数论, 模型式与模函数论
代数学:线性代数 群论, 群表示论,
李群, 李代数, 代数群, 典型群, 同调代数, 代数K理论, Kac-Moody代数, 环论, 代数, 体, 格, 序结构. 域论和多项式 拓扑群
矩阵论 向量代数 张量代数
几何学:(整体,局部)微分几何, 代数几何, 流形上的分析, 黎曼流形与洛仑兹流形, 齐性空间与对称空间,
调和映照, 子流形理论, 杨--米尔斯场与纤维丛理论, 辛流形. 凸几何与离散几何 欧氏几何 非欧几何 解析几何
拓扑学:微分拓扑,
代数拓扑, 低维流形, 同伦论, 奇点与突变理论, 点集拓扑. 流形和胞腔复形 大范围分析,微分拓扑 同调论 复流形
函数论:
函数逼近论.
泛函分析:(非)线性泛函分析, 算子理论, 算子代数, 差分与泛函方程, 广义函数. 变分法,积分变换
积分方程
微分方程:泛函微分方程, 特征与谱理论及其反问题, 定性理论, 稳定性理论、分支理论,混沌理论, 奇摄动理论,动力系统, 常微分方程
非线性椭圆(和抛物)方程,偏微分方程, 微局部分析与一般偏微分算子理论, 调混合型及其它带奇性的方程,
非线性发展方程和无穷维动力系统.
数学物理:规范场论, 引力场论的经典理论与量子理论, 孤立子理论.
概率论:马氏过程, 随机过程,
随机分析, 随机场, 鞅论, 极限理论, 平稳过程, 概率论 统计学;
数理逻辑与数学基础:递归论, 模型论, 证明论, 公理集合证,
数理逻辑 范畴论
组合数学:组合计数, 图论.
分析学:序列、级数、可求和性 微积分 实变函数 抽象测度论 逼近与展开
特殊函数(单,多)复变函数论,调和分析, Fourier分析
应用数学:
边缘学科:系统论;控制论 运筹学,
位势论
计算数学与科学工程计算:偏微分方程数值计算,初边值问题数值解法,非线性微分方程及其数值解法,边值问题数值解法,有限元、边界元数值方法,变分不等式的数值方法,辛几何差分方法,数理方程反问题的数值解法,常微分方程数值解法及其应用,二点边值问题,
STIFF问题研究, 奇异性问题, 代数微分方程, 不确定性的数学理论, 分形论.大型稀疏矩阵求解, 代数特征值问题及其反问题, 非线性代数方程,
一般线性代数方程组求解, 快速算法.
函数逼近:多元样条, 多元逼近, 曲面拟合, 有理逼近,
散乱数据插值.
二十世纪的数学
谢谢邀请我来这里参加这个活动.当然,如果有人想谈论一个世纪的终结以及下一个
世纪的开始,那么他有两个具有相当难度的选择:一个是回顾过去百年的数学;另一个是
对未来百年数学发展的预测,我选择了前面这个比较困难的任务,任何人都可以预测未来
而且我们并不能判定是对还是错.然而对过去的任何评述,每个人都可以提出异议.我在这里所讲的是我个人的观点.这个报告不可能包含所有内容,特别是,有一些重
要的内容我不准备涉及,一部分是因为我不是那些方面的专家,一部分也是出于它们已经
在其他地方被评述过了.例如,我不会去谈论那些发生在逻辑与计算领域内的著名事件,
这些事件往往是与像Hilbert,Godel,Turing这些伟大的名字相关的,除了数学在基础物
理中的应用之外,我也不会谈论太多数学的其他应用,这是因为数学的应用太广泛了,而
且这需要专门的论述.每一个方面都需要一个专门的报告.也许大家在这次会议的其他报
告中会听到很多关于这些内容的演讲.另外,试着罗列一些定理,甚至是列出在过去一百
年的著名数学家的名字也是毫无意义的,那简直是在做枯燥的练习.所以,代替它们的是
,我试着选择一些我认为在很多方面都是很重要的主题来讨论并且强调围绕这些主题所发生的事情.
首先我有一个一般性的说明.世纪是一个大约的数字概念.我们不会真地认为在过整
整一百年的时候,有些事情会突然停下来,再重新开始,所以当我描述二十世纪的数学时
,有些内容实际上可能是跨世纪的,如果某件事件发生在十九世纪九十年代,并持续到二
十世纪初,我将不去计较这种时间方面的细节.我所做的就象一个天文学家,工作在一个
近似的数字环境中.实际上,许多东西始于十九世纪,只不过在二十世纪才硕果累累.这个报告的难点之一是很难把我们自己放回到
1900年时作为一位数学家的位置上,这
是因为上个世纪的数学有非常多的内容已经被我们的文化和我们自己吸收掉了.难以想象
人们不用我们的术语来思考的那个时代是什么样子的.实际上,如果现在有人在数学上有
一个真正重要的发现,其后他也一定会与之一起被忽略掉了!他会完全地被融入到背景之
中,于是为了能够回顾过去,我们必须努力去想象在不同时代,人们用不同方式思考问题
时的情景.
从局部到整体
作为开始,我准备列一些主题并且围绕它们来讨论.我谈论的第一个主题概括地讲,
就是被大家称为从局部到整体的转变.在古典时期,人们大体上已经研究了在小范围内,
使用局部坐标等等来研究事物.在这个世纪,重点已经转移到试图了解事物整体和大范围
的性质.由于整体性质更加难以研究,所以大多只能有定性的结果,这时拓扑的思想就变
得非常重要了.正是Poincaré,他不仅为拓扑学发展作出先驱性的贡献,而且也预言拓
扑学将成为二十世纪数学的一个重要的组成部分,顺便让我提一下,给出一系列著名问题
的Hilbert并没有意识到这一点.拓扑学很难在他的那些问题中找到具体体现.但是对Poincaré而言,他相当清楚地看出拓扑学将成为一个重要的内容.
让我试着列一些领域,然后大家就能知道我在想什么了.例如,考虑一下复分析(也被称为“函数论”),这在十九世纪是数学的中心,也是象Weierstrass这样伟大人物工
作的中心.对于他们而言,一个函数就是一个复变量的函数;对于Weierstrass而言,一个
函数就是一个幂级数.它们是一些可以用于写下来,并且可以明确描绘的东西或者是一些
公式.函数是一些公式:它们是明确可以用显式写下来的.然而接下来Abe1,Riemann和其
后许多人的工作使我们远离了这些,以至于函数变得可以不用明确的公式来定义,而更多
地是通过它们的整体性质来定义:通过它们的奇异点的分布,通过它们的定义域位置,通
过它们取值范围.这些整体性质正是一个特定函数与众不同的特性.局部展开只是看待它 们的一种方式.
一个类似的事情发生在微分方程中,最初,解一个微分方程,人们需要寻找一个明确
的局部解!是一些可以写下来的东西.随着事物的发展,解不必是一个显函数,人们不一
定必须用好的公式来描述它们.解的奇异性是真正决定其整体性质的东西.与发生在复分 析中的一切相比,这种精神是多么的类似,只不过在细节上有些不同罢了.
在微分几何中,Gauss和其他人的经典工作描述了小片的空间,小块的曲率以及用来
描述局部几何的局部方程.只要人们想要了解曲面的整体图象以及伴随它们的拓扑时,从
这些经典结果到大范围的转变就是很自然的了.当人们从小范围到大范围时,最有意义的 性质就是拓扑的性质.
数论也有一个类似的发展,尽管它并不是很明显地适用于这一框架.数论学家们是这
样来区分他们称之为“局部理论”和“整体理论”的:前者是当他们讨论一个单个的素数
,一次一个素数,以及有限个素数时;后者是当他们同时讨论全部素数时.这种素数和点
之间,局部和整体之间的类似性在数论发展过程中起了很重要的作用,并且那些在拓扑学 发展中产生的思想深深地影响了数论.
当然这种情况也发生在物理学中,经典物理涉及局部理论,这时我们写下可以完全描
述小范围性质的微分方程,接下来我们就必须研究一个物理系统的大范围性质.物理学涉
及的全部内容就是当我们从小范围出发时,我们可以知道在大范围内正在发生什么,可以
预计将要发生什么,并且沿着这些结论前进.
维数的增加
我的第二个主题有些不同,我称之为维数的增加.
我们再次从经典的复变函数理论开
始:经典复变函数论主要是详细讨论一个复变量理论并加以精炼.推广到两个或者更多个
变量基本上发生在本世纪,并且是发生在有新现象出现的领域内.不是所有的现象都与一
个变量的情形相同,这里有完全新的特性出现,并且n个变量的理论的研究越来越占有统
治地位,这也是本世纪主要成就之一.
另一方面,过去的微分几何学家主要研究曲线和曲面,我们现在研究n维流形的几何
,大家仔细想一想,就能意识到这是一个重要的转变.在早期,曲线和曲面是那些人们能
真正在空间里看到的东西.而高维则有一点点虚构的成分,在其中人们可以通过数学思维
来想象,但当时人们也许没有认真对待它们.认真对待它们并且用同样重视程度来研究它
们的这种思想实际上是二十世纪的产物.同样地,也没有明显的证据表明我们十九世纪的
先驱者们思考过函数个数的增加,研究不单单一个而是几个函数,或者是向量值函数(ve
ctor-valued
function).所以我们看到这里有一个独立和非独立变量个数增加的问题.
线性代数总是涉及多个变量,但它的维数的增加更具有戏剧性,它的增加是从有限维
到无穷维,从线性空间到有无穷个变量的Hilbert空间.当然这就涉及到了分析,在多个变
量的函数之后,我们就有函数的函数,即泛函.它们是函数空间上的函数.它们本质上有
无穷多个变量,这就是我们称为变分学的理论.一个类似的事情发生在一般(非线性)函
数理论的发展中.这是一个古老的课题,但真正取得卓越的成果是在二十世纪.这就是我
谈的第二个主题.
从交换到非交换
第三个主题是从交换到非交换的转变.这可能是二十世纪数学,特别是代数学的最主
要的特征之一.代数的非交换方面已经极其重要,当然,它源自于十九世纪.它有几个不
同的起源.Hamilton在四元数方面的工作可能是最令人惊叹的,并且有巨大的影响,实际
上这是受处理物理问题时所采用的思想所启发.还有Grassmann在外代数方面的工作,这
是另一个代数体系,现在已经被融入我们的微分形式理论中.当然,还有Cayley以线性代
数为基础的矩阵方面的工作和Galois在群论方面的工作等.
所有这些都是以不同的方式形成了把非交换乘法引入代数理论的基石,我形象地把它
们说成是二十世纪代数机器赖以生存的“面包和黄油”.我们现在可以不去思考这些,但
在十九世纪,以上所有例子都以各自不同的方式取得了重大的突破,当然,这些思想在不
同的领域内得到了惊人的发展.矩阵和非交换乘法在物理中的应用产生了量子理论.Hei
senberg对易关系是非交换代数在物理中的一个最重要的应用例子,以至后来被von Neum
ann推广到他的算子代数理论中.
群论也是在二十世纪占重要位量的理论,我稍后再回来谈它.
从线性到非线性
我的下一个主题是从线性到非线性的转变.古典数学的大部分或者基本上是线性的,
或者即使不是很精确的线性,也是那种可以通过某些扰动展开来研究的近似线性,真正的
非线性现象的处理是非常困难的,并且只是在本世纪,才在很大的范围内对其进行了真正
的研究.
我们从几何开始谈起:Euclid几何,平面的几何,空间的几何,直线的几何,所有这
一切都是线性的.而从非欧几何的各个不同阶段到Riemann的更一般的几何,所讨论的基
本上是非线性的.在微分方程中,真正关于非线性现象的研究已经处理了众多我们通过经
典方法所看不到的新现象.在这里我只举两个例子,孤立子和混沌,这是微分方程理论两
个非常不同的方面,在本世纪已经成为极度重要和非常著名的研究课题了.它们代表不同
的极端.孤立子代表非线性微分方程的无法预料的有组织的行为,而混沌代表的是无法预
料的无组织的行为(disorganized
behavior).这两者出现在不同领域,都是非常有趣和
重要的,但它们基本土都是非线性现象.我们同样可以将关于孤立子的某些工作的早期历
史追溯到十九世纪下叶,但那只是很少的一部分.
当然,在物理学,Maxwell方程(电磁学的基本方程)是线性偏微分方程.与之对应
的是著名的Yang-Mills方程,它们是非线性方程并被假定用来调控与物质结构有关的力.
这些方程之所以是非线性的,是因为Yang-Mills方程本质上是Maxwell方程的矩阵体现,
并且由矩阵不可交换这一事实导致方程中出现非线性项.于是在这里我们看到了一个非线
性性与非交换性之间的有趣的联系.非交换性产生一类特殊的非线性性,这的确是很有意
思和很重要的.
几何与代数
至此我谈的是一些一般性的主题,现在我想谈论一下数学中的一个二分叉现象,它来
回摇摆却始终伴随着我们,这就给了我一个机会来做一些哲学上的
19296顶!
在下个世纪,有大
量的工作在等着你们去完成.
19296好贴
19296好!!
19296以前看过
写得很好
再读一遍 受益匪浅
19296是一篇好文章!还应该写的再细一点!
19296非常好!非常感谢!
不知道是哪位数学家的演讲?
谢谢。
19296好文章呀!真该好好看看!
19297感谢!
19297刚才发错啦,这是答案post-68-1129277673.ibf
19297谢谢!
19297不错啊!
好人啊!
继续啊!
加油啊!
啊:::::::
thank you
so much!
19297好啊
19297谢谢
19298如果D为整环但不是域,求证D[x]不是主理想整环
19298构造一个同构,利用不是域就可以证明了
19299某木材公司经营的木材储存在仓库中,最大储存量为20万立方米.由于木材价格随季节变化,
该公司于每季初购进木材,一部分当季出售,一部分储存以后出售.储存费为a+bu,其中a=7元/立方米,b=10元/立方米/季,u为储存的季度数.由于木材久存易损,因此当年所有库存木材应与秋末售完.各季木材单价及销量如下表所示.为获全年最大利润,该公司各季应分别购销多少木材?试建立数学模型.
季
购进价(元/立方米) 售出价(元/立方米) 最大销售量(万立方米)
冬 310 321 10
春 325 333 14
夏 348 352 20
秋 340 344
16
想了很久都不会做....求救...............
19299各位帮帮手拉............帮手建立一下数学模型拉......
19299顶到有人帮我为止
19299楼主好,我随便做了一下,不知道对不对。
假设冬天购买x1大于10,则剩余的木材可以在以后三个季节出售,换算价格依次为:327,337,347,因此可以多买存储在夏天卖(337小于348)。
假设春天购买x2大于14,则则剩余的木材可以在以后二个季节出售,换算价格依次为:342,352,因此可以多买存储在夏天卖(342小于348)。但是,342大于337,所以应该冬天一个季节多购买,x1=30,正好满足存储量要求。
冬季:x1=30,卖出10
春季:x2=14,卖出14
夏季:x3=0,卖出20(冬天的)
秋季:x4=16,卖出16。
总利润:10×(321-310)+14×(333-325)+(352-310-7-10-10)×20+16×(344-340)=110+112+300+64=586。
时间仓促,瞎做的,还请各位多赐教。
19304[COLOR=red]小弟 需要 本人正考研 水生火热之中[COLOR=red]
19304有人需要的话,我可以贴出来。是我用手抄的,保证真实,
与大家共享一下,希望对大家有一些用处。
回复:直接发到试题集,用附件的形式,斑竹会及时整理加分的.注意查询是否已经存在.
19304我现在正需要这个,麻烦你发到我的邮箱好么?liwangno_1@yahoo.com.cn
19304我的信箱是yezhuangliang@yahoo.com.cn
谢谢你我真的很需要
19304谢谢了
19305有叫<数学学报>的,也有叫<数学物理学报>的,反正中科院的事我不关心.
19305好多杂志有acta ,包括中科院的acta mathematic,不晓得意思?
19305常见的翻译是"学报"!
19306自学很好阿 听老师将有些浪费时间
19306出于对数学的爱好和其他一些原因,我在自考数学本科,
要考 常微分方程 和
复变函数论。
发现自考是挺难的。问大家,如果常微分方程要考证明题,
比如里面的恰当方程或其他存在唯一性定理什么的,
我可真的是考不出.做些计算题还可以啊...
请您说说啊.
自考又没人交流.....
19306的确,学好常微分必须具备扎实的基础!(数学分析与高等代数)
19306我倒是比较喜欢证明题,常微分的证明题一般都是使用数学分析的方法分析。象存在和唯一性定理的证明就是这样。仔细学好数学分析会对做这些题目很有帮助。而且有的时候是出些要你求解的存在区间和延展特性的题目,也用到数学分析的技巧很多。不过我倒是对自考没有什么了解。可能你要问问其他对自考熟悉的友人了。
19306
我几乎没有看过数分,却想考数学本科(自考),
我想我应该去把那两本数分和高代都看了,
以提高我的基础(我仅有高等数学的基础,学的是工科),那些对于实数理论和
微积分的许多证明,我都感到烦琐和冗长,难以理解.自学数学太难了!
怎么办???难道又让我放弃这陌生而又熟悉的数学吗???????
纳闷中,请求高手指点一二.
万分感谢!
19306也是.数分和高代不学是不可能有扎实的基础进行接下来的学习的.证明是必须仔细钻研的.难道你没有注意到普通工科的高等数学和数学系专业数学课程就是差在这个方面吗?证明是培养严格的逻辑思维能力的.尤其是数学分析这门再基础不过的经典课程.说句不好听的话,如果不能从这些经典的证明中看到数学的魅力,那以后的课程就更不会感到熟悉和有趣.象后续的常微分方程,复变函数,偏微分方程,实变函数,泛函分析等等.基本都是证明与逻辑推理型的课程.计算的成分只是很小的一部分.当然自学是辛苦一点.不过我建议楼主可以想办法找数学系的课程旁听一下.这样效果会好不少.
19306
哪有机会去旁听啊,
我看了数分,证明起来真的是难.
常微分方程,高数里面有点学过啊,不知道考试能不能过?
如果是基础的证明题,就真的难死我了...
工科出来的学生都差不多,基础差,
缺乏对证明的系统逻辑性
19306工科的学生想学数分确实有困难,尤其是自学。我想你要是真想学,就必需下苦功夫,先学会分析和逻辑推理的能力,多做数分习题。碰到难题,要找人交流。
19306现在数学系也有自考,透露一下,哪个大学有?在下QQ383256136
1930611111
19307可以用Matlab试一下看看。
19307我有个问题不知道怎么方程不知道怎么求解请大家帮忙!
问题如下:
min R
x+y=3
y+z=1
x<=2R
y<=2R
z<=2R
x,y,z均大于0
0=<R=<1
19307给出具体解题步骤好吗?
19307min R
x+y=3
y+z=1
x<=2R
y<=2R
z<=2R
x,y,z均大于0
0=<R=<1
x,y,z均非负,
y+z=1
则y<=1
则x>=2
而x<=2R<=2
感觉这个数字简单,不用线性规则也能想出来
19307最优解为R=1 X=2 Y=1 Z=0 最优目标函数值=1
19307用gams 把模型输入就可以了
19308有没有深入研究n维球的拓扑性质的朋友?我遇到一个与之相关的组合设计问题要用到n维球拓扑性质的知识,希望帮一下
19308n维球性质都是比较平凡的
19308我认为n维球面和n+1阶正交矩阵有很大的关系,可以研究
19313ruti
19314如题
19314我想这个应该对的.
可把空间分成线性算子的不变子空间(最好是 lambda
不变子空间)的直和.
证明在每个分解子空间上的限制是可换的.
19315我用ode45求解振动的瞬态响应,但是自动的变步长使步长太小,我不需要那么大的精度,试着用odeset设置精度也不行,请问怎么才能是精度降低而使步长小一些。
谢谢!
19316是否有:线性空间的线性变换A,对A的任意不变子空间W,都存在多项式F(x),
使得W=kerF(A)?
19316这个不对.考虑A为单位矩阵I
193
17我是应用数学专业的,现在已经大二了,数学分析和高等代数等几门基础课已经上完了,最让我痛心的是英语什么都不知道了,哎,还是自己有时候看点电影学点英语单词,哎,现在正处于思想的斗争阶段,感觉自己好像是计算机专业的,配电脑,修电脑,哎
193
17呵呵,lz真逗,修电脑,配电脑用的着计算机专业的人啊?随便找个中专生就行啦。
193
17加油!!
193
17什么都没学到
193
17本身数学基础课的学习与其说是技能不如说是方法,显然数分几乎不能解决生活中任何问题,不如修电脑来的实用,有这种感觉很正常的,继续努力吧
193
17
要好好发掘数学的优点,那就会看见乐趣了
193
19现在一般想看他的书也只有在图书馆里了——反正我是没见到新印刷的!
193
19最近看到关于汪林的大作“反例“系列和评注系列,我对汪林的敬仰如滔滔江水!有谁有汪林老师的资料请和我联系 m0o0n@126.com
(注意是“零欧零”),另外重金求购汪林老师的书,这么优秀的书竟然绝版了!!!什么世道呀!
193
19汪林的书确实很有特色。绝版倒没有。还是有新出版的。好象是实分析中的反例吧。
193
19可以到FTP里去下啊。
193
19在书店里见过拓扑空间中的反例
汪林好像是程民德的学生
193
19我也想见到
19320请问密码攻击side channel attack中文如何翻译?谢谢!
19320侧渠道攻击啊
19324帮帮忙发一下答案,谢谢!!!
19325有一段时间没上论坛了,刚刚看到有几个帖子是问是否为无理数的证明的(比如Pi和根号3的),使我回忆起自己当初才接触这些时的经历。
当然这是最基础的东西,但其实也有许多东西是比较难搞清楚的,比如我自己,起先看了卢丁的《数学分析原理》的第一章,知道了些关于实数的理论,就以为自己知道了,掌握了原理,拿起华罗庚的《数论导引》就没看上面关于实数的几节,一做习题,居然发现有要证明log2为无理数的——傻了(那时候才进大学,几本书是一起看的)!
——关于这方面的证明方法很多,但好象还没有一个统一的工具来解决——欧拉常数的无法解决就是一个最明显的例子!
——实际上,就算欧拉常数的问题解决了,几乎也可以肯定我们不会找到这样的工具!
什么时候?怎样才可能找到这样的统一的工具??——我们对于数的体系的认识是不是还可以延拓!?个人认为这是个很值得研究的问题!
19325以前上高中时物理老师说现在你们学的东西日后就会发现是有问题的,我们现在是在骗你们。
其实在求知的过程中一直有这种感觉。
19325都是反证法!先x=a/b,且(a,b)=1,然后推矛盾。废话!哈哈,我的数学也一般啊。有高人知道哪个无理数不能用这个方法做出来啊(或者特别麻烦)??哈哈。
19325数论中的无穷递降法
19327不好意思,小弟是菜鸟。
就是Institute of Mathematical
Statistics
是不是只有牛的人才能进这个组织?
19327应该不错,有些牛人,今年暑假IMS和中国概率统计协会搞了个联合会议,来了些牛人
19328哪位朋友有关于图论的英文文章啊,告诉网址就OK了,最好是关于图论的英文论文
19328到 南开大学组合数学中心网站上
19328
| 引用 (yuxi @ 2005年10月22日
21时16分) |
| 到 南开大学组合数学中心网站上
|
这里有很多
各个方向的都有
19328到 google 搜索'graph theory pdf', 有五百多万条。
19329概率论与数理统计词汇英汉对照表
A
absolute value 绝对值
accept
接受
acceptable region 接受域
additivity 可加性
adjusted
调整的
alternative hypothesis 对立假设
analysis 分析
analysis
of covariance 协方差分析
analysis of variance 方差分析
arithmetic
mean 算术平均值
association 相关性
assumption 假设
assumption
checking 假设检验
availability 有效度
average
均值
B
balanced 平衡的
band 带宽
bar chart
条形图
beta-distribution 贝塔分布
between groups 组间的
bias
偏倚
binomial distribution 二项分布
binomial test
二项检验
C
calculate 计算
case 个案
category
类别
center of gravity 重心
central tendency
中心趋势
chi-square distribution 卡方分布
chi-square test
卡方检验
classify 分类
cluster analysis 聚类分析
coefficient
系数
coefficient of correlation 相关系数
collinearity
共线性
column 列
compare 比较
comparison
对照
components 构成,分量
compound 复合的
confidence interval
置信区间
consistency 一致性
constant 常数
continuous variable
连续变量
control charts 控制图
correlation 相关
covariance
协方差
covariance matrix 协方差矩阵
critical point
临界点
critical value 临界值
crosstab 列联表
cubic
三次的,立方的
cubic term 三次项
cumulative distribution function
累加分布函数
curve estimation 曲线估计
D
data 数据
default
默认的
definition 定义
deleted residual 剔除残差
density
function 密度函数
dependent variable 因变量
description
描述
design of experiment 试验设计
deviations 差异
df.(degree
of freedom) 自由度
diagnostic 诊断
dimension 维
discrete
variable 离散变量
discriminant function 判别函数
discriminatory
analysis 判别分析
distance 距离
distribution 分布
D-optimal
design D-优化设计
E
eaqual 相等
effects of interaction
交互效应
efficiency 有效性
eigenvalue 特征值
equal size
等含量
equation 方程
error 误差
estimate
估计
estimation of parameters 参数估计
estimations
估计量
evaluate 衡量
exact value 精确值
expectation
期望
expected value 期望值
exponential 指数的
exponential
distributon 指数分布
extreme value 极值
F
factor
因素,因子
factor analysis 因子分析
factor score
因子得分
factorial designs 析因设计
factorial experiment
析因试验
fit 拟合
fitted line 拟合线
fitted value
拟合值
fixed model 固定模型
fixed variable 固定变量
fractional
factorial design 部分析因设计
frequency 频数
F-test F检验
full
factorial design 完全析因设计
function 函数
G
gamma distribution
伽玛分布
geometric mean 几何均值
group 组
H
harmomic mean
调和均值
heterogeneity 不齐性
histogram 直方图
homogeneity
齐性
homogeneity of variance 方差齐性
hypothesis
假设
hypothesis test 假设检验
I
independence
独立
independent variable 自变量
independent-samples
独立样本
index 指数
index of correlation 相关指数
interaction
交互作用
interclass correlation 组内相关
interval estimate
区间估计
intraclass correlation 组间相关
inverse 倒数的
iterate
迭代
K
kernal 核
Kolmogorov-Smirnov test
柯尔莫哥洛夫-斯米诺夫检验
kurtosis 峰度
L
large sample problem
大样本问题
layer 层
least-significant difference
最小显著差数
least-square estimation 最小二乘估计
least-square method
最小二乘法
level 水平
level of significance 显著性水平
leverage
value 中心化杠杆值
life 寿命
life test 寿命试验
likelihood
function 似然函数
likelihood ratio test 似然比检验
linear
线性的
linear estimator 线性估计
linear model 线性模型
linear
regression 线性回归
linear relation 线性关系
linear term
线性项
logarithmic 对数的
logarithms 对数
logistic
逻辑的
lost function 损失函数
M
main effect 主效应
matrix
矩阵
maximum 最大值
maximum likelihood estimation
极大似然估计
mean squared deviation(MSD) 均方差
mean sum of square
均方和
measure 衡量
media 中位数
M-estimator M估计
minimum
最小值
missing values 缺失值
mixed model 混合模型
mode
众数
model 模型
Monte Carle method 蒙特卡罗法
moving average
移动平均值
multicollinearity 多元共线性
multiple comparison
多重比较
multiple correlation 多重相关
multiple correlation
coefficient 复相关系数
multiple correlation coefficient
多元相关系数
multiple regression analysis 多元回归分析
multiple
regression equation 多元回归方程
multiple response
多响应
multivariate analysis 多元分析
N
negative relationship
负相关
nonadditively 不可加性
nonlinear 非线性
nonlinear
regression 非线性回归
noparametric tests 非参数检验
normal
distribution 正态分布
null hypothesis 零假设
number of cases
个案数
O
one-sample 单样本
one-tailed test 单侧检验
one-way
ANOVA 单向方差分析
one-way classification 单向分类
optimal
优化的
optimum allocation 最优配制
order 排序
order statistics
次序统计量
origin 原点
orthogonal 正交的
outliers
异常值
P
paired observations 成对观测数据
paired-sample
成对样本
parameter 参数
parameter estimation 参数估计
partial
correlation 偏相关
partial correlation coefficient
偏相关系数
partial regression coefficient 偏回归系数
percent
百分数
percentiles 百分位数
pie chart 饼图
point estimate
点估计
poisson distribution 泊松分布
polynomial curve
多项式曲线
polynomial regression 多项式回归
polynomials
多项式
positive relationship 正相关
power 幂
P-P plot
P-P概率图
predict 预测
predicted value 预测值
prediction
intervals 预测区间
principal component analysis 主成分分析
proability
概率
probability density function 概率密度函数
probit analysis
概率分析
proportion 比例
Q
qadratic 二次的
Q-Q plot
Q-Q概率图
quadratic term 二次项
quality control
质量控制
quantitative 数量的,度量的
quartiles 四分位数
R
random
随机的
random number 随机数
random number 随机数
random
sampling 随机取样
random seed 随机数种子
random variable
随机变量
randomization 随机化
range 极差
rank 秩
rank
correlation 秩相关
rank statistic 秩统计量
regression analysis
回归分析
regression coefficient 回归系数
regression line
回归线
reject 拒绝
rejection region 拒绝域
relationship
关系
reliability 可靠性
repeated 重复的
report
报告,报表
residual 残差
residual sum of squares
剩余平方和
response 响应
risk function 风险函数
robustness
稳健性
root mean square 标准差
row 行
run 游程
run test
游程检验
S
sample 样本
sample size 样本容量
sample space
样本空间
sampling 取样
sampling inspection 抽样检验
scatter
chart 散点图
S-curve S形曲线
separately 单独地
sets
集合
sign test 符号检验
significance 显著性
significance level
显著性水平
significance testing 显著性检验
significant
显著的,有效的
significant digits 有效数字
skewed distribution
偏态分布
skewness 偏度
small sample problem 小样本问题
smooth
平滑
sort 排序
soruces of variation 方差来源
space
空间
spread 扩展
square 平方
standard deviation
标准离差
standard error of mean 均值的标准误差
standardization
标准化
standardize 标准化
statistic 统计量
statistical quality
control 统计质量控制
std. residual 标准残差
stepwise regression
analysis 逐步回归
stimulus 刺激
strong assumption 强假设
stud.
deleted residual 学生化剔除残差
stud. residual 学生化残差
subsamples
次级样本
sufficient statistic 充分统计量
sum 和
sum of squares
平方和
summary 概括,综述
T
table 表
t-distribution
t分布
test 检验
test criterion 检验判据
test for linearity
线性检验
test of goodness of fit 拟合优度检验
test of homogeneity
齐性检验
test of independence 独立性检验
test rules 检验法则
test
statistics 检验统计量
testing function 检验函数
time series
时间序列
tolerance limits 容许限
total 总共,和
transformation
转换
treatment 处理
trimmed mean 截尾均值
true value
真值
t-test t检验
two-tailed test 双侧检验
U
unbalanced
不平衡的
unbiased estimation 无偏估计
unbiasedness
无偏性
uniform distribution 均匀分布
V
value of estimator
估计值
variable 变量
variance 方差
variance components
方差分量
variance ratio 方差比
various 不同的
vector
向量
W
weight 加权,权重
weighted average 加权平均值
within
groups 组内的
Z
Z score Z分数
Ⅱ.2
最优化方法词汇英汉对照表
A
active constraint 活动约束
active set
method 活动集法
analytic gradient 解析梯度
approximate
近似
arbitrary 强制性的
argument 变量
attainment factor
达到因子
B
bandwidth 带宽
be equivalent to 等价于
best-fit
最佳拟合
bound 边界
C
coefficient
系数
complex-value 复数值
component 分量
constant
常数
constrained 有约束的
constraint 约束
constraint function
约束函数
continuous 连续的
converge 收敛
cubic polynomial
interpolation method
三次多项式插值法
curve-fitting
曲线拟合
D
data-fitting 数据拟合
default 默认的,默认的
define
定义
diagonal 对角的
direct search method 直接搜索法
direction
of search 搜索方向
discontinuous 不连续
E
eigenvalue
特征值
empty matrix 空矩阵
equality 等式
exceeded
溢出的
F
feasible 可行的
feasible solution
可行解
finite-difference 有限差分
first-order
一阶
G
Gauss-Newton method 高斯-牛顿法
goal attainment problem
目标达到问题
gradient 梯度
gradient method 梯度法
handle
句柄
Hessian matrix 海色矩阵
I
independent variables
独立变量
inequality 不等式
infeasibility 不可行性
infeasible
不可行的
initial feasible solution 初始可行解
initialize
初始化
inverse 逆
invoke 激活
iteration 迭代
iteration
迭代
J
Jacobian 雅可比矩阵
L
Lagrange multiplier
拉格朗日乘子
large-scale 大型的
least square 最小二乘
least
squares sense 最小二乘意义上的
Levenberg-Marquardt method
列文伯格-马夸尔特法
line search 一维搜索
linear 线性的
linear
equality constraints 线性等式约束
linear programming problem
线性规划问题
local solution 局部解
M
medium-scale
中型的
minimize 最小化
mixed quadratic and cubic polynomial
interpolation and extrapolation method
混合二次、三次多项式内插、外插法
multiobjective 多目标的
N
nonlinear
非线性的
norm 范数
O
objective function 目标函数
observed
data 测量数据
optimization routine 优化过程
optimize
优化
optimizer 求解器
over-determined system
超定系统
P
parameter 参数
partial derivatives
偏导数
polynomial interpolation method
多项式插值法
Q
quadratic 二次的
quadratic interpolation
method 二次内插法
quadratic programming 二次规划
R
real-value
实数值
residuals 残差
robust 稳健的
robustness
稳健性,鲁棒性
S
scalar 标量
semi-infinitely problem
半无限问题
Sequential Quadratic Programming method
序列二次规划法
simplex search method 单纯形法
solution
解
sparse matrix 稀疏矩阵
sparsity pattern 稀疏模式
sparsity
structure 稀疏结构
starting point 初始点
step length
步长
subspace trust region method 子空间置信域法
sum-of-squares
平方和
symmetric matrix 对称矩阵
T
termination message
终止信息
termination tolerance 终止容限
the exit condition
退出条件
the method of steepest descent 最速下降法
transpose
转置
U
unconstrained 无约束的
under-determined system
负定系统
V
variable 变量
vector 矢量
W
weighting matrix
加权矩阵
Ⅱ.3 样条词汇英汉对照表
A
approximation
逼近
array 数组
a spline in b-form/b-spline b样条
a spline
of polynomial piece /ppform spline
分段多项式样条
B
bivariate
spline function 二元样条函数
break/breaks
断点
C
coefficient/coefficients 系数
cubic interpolation
三次插值/三次内插
cubic polynomial 三次多项式
cubic smoothing spline
三次平滑样条
cubic spline 三次样条
cubic spline interpolation
三次样条插值/三次样条内插
curve 曲线
D
degree of freedom
自由度
dimension 维数
E
end conditions 约束条件
I
input
argument 输入参数
interpolation 插值/内插
interval
取值区间
K
knot/knots 节点
L
least-squares approximation
最小二乘拟合
M
multiplicity 重次
multivariate function
多元函数
O
optional argument 可选参数
order 阶次
output
argument 输出参数
P
point/points 数据点
R
rational spline
有理样条
rounding error 舍入误差(相对误差)
S
scalar
标量
sequence 数列(数组)
spline 样条
spline approximation
样条逼近/样条拟合
spline function 样条函数
spline curve
样条曲线
spline interpolation 样条插值/样条内插
spline surface
样条曲面
smoothing spline 平滑样条
T
tolerance
允许精度
U
univariate function 一元函数
V
vector
向量
W
weight/weights 权重
Ⅱ.4
偏微分方程数值解词汇英汉对照表
A
absolute error 绝对误差
absolute
tolerance 绝对容限
adaptive mesh 适应性网格
B
boundary condition
边界条件
C
contour plot 等值线图
converge 收敛
coordinate
坐标系
D
decomposed 分解的
decomposed geometry matrix
分解几何矩阵
diagonal matrix 对角矩阵
Dirichlet boundary conditions
Dirichlet边界条件
E
eigenvalue 特征值
elliptic
椭圆形的
error estimate 误差估计
exact solution
精确解
G
generalized Neumann boundary condition
推广的Neumann边界条件
geometry 几何形状
geometry description
matrix 几何描述矩阵
geometry matrix 几何矩阵
graphical user
interface(GUI)
图形用户界面
H
hyperbolic
双曲线的
I
initial mesh 初始网格
J
jiggle
微调
L
Lagrange multipliers 拉格朗日乘子
Laplace equation
拉普拉斯方程
linear interpolation 线性插值
loop 循环
M
machine
precision 机器精度
mixed boundary condition 混合边界条件
N
Neuman
boundary condition Neuman边界条件
node point 节点
nonlinear solver
非线性求解器
normal vector 法向量
P
Parabolic 抛物线型的
partial
differential equation 偏微分方程
plane strain 平面应变
plane stress
平面应力
Poisson's equation 泊松方程
polygon 多边形
positive
definite 正定
Q
quality 质量
R
refined triangular mesh
加密的三角形网格
relative tolerance 相对容限
relative tolerance
相对容限
residual 残差
residual norm 残差范数
19329Thank you !
19329谢谢了
请问在哪里找的,还有其他学科的吗?
19329支持!!!!!!!!!!1
19329
| 引用 (海纳百川 @ 2005年10月15日
09时37分) |
谢谢了
请问在哪里找的,还有其他学科的吗? |
我不知道网上有没有哦.这些都是偶平时看那些洋屁书的时候收集起来的.
你要是要其他学科的,到网上去收应该可以找到吧.
19329搜索专业词汇请到
http://cb.kingsoft.com/有n本专业词典.很准
19329很不错
谢谢版主
19329学习中,谢谢
19329
| 引用 (夏寒 @ 2005年11月02日
08时06分) |
| 学习中,谢谢
|
又发了一部分,大家可以去看看
19329thanks
19329谢谢!
19329谢谢了!
19329挺不错的
19329very good!
19329好东西啊
19329非常好
19329好东西
19329谢谢,最近看概率和数理统计一些英文单词搞的晕头转向的
19329谢谢,楼主辛苦了:)
19329晕倒,买本数学字典来什么都有了。
19329太感谢了!!!
19329不错!谢谢
19329很好啊
喜欢啊
以后都来点好东西
19329比较难记阿 俄不是数学专业的
19329非常有用的东西,谢谢!
19329thanks
19329非常好,支持牙
19329这个楼主一定花了不少力气的,谢谢分享!
19329多谢!!!
19329不错!虽然暂时用不上!谢谢!
19329thanks!
19329好东西!
19329xiexie 谢谢楼主
19329想把这个补习全面,可惜太麻烦。
19329
http://bbs.6sq.net/thread-27962-1-2.html在这个网址里面
19329好帖!
19329多谢了
19329看看这个东西,对大家有用没有。post-
17-1215562930.ibf
19329很好,谢谢!
19329谢了~bow~~
19329很好啊!
19329很好啊!
19330大致有以下几种:
(1)抵抗性 群落抵抗外界干扰而保持原状的能力
(2)恢复性
群落在受到外界干扰后回到原来状态的能力
(3)持久性 生态系统在一定边界范围内保持恒定或维持某一特定状态的持续时间
(4)变异性和一致性
变异性指系统在受到干扰后,种群密度随时间变化的大小。一致性指生态系统中物种数、结构、群落配置、生活型或环境的物理特征等参数保持原状不发生变化
(5)轨迹稳定性
一个系统无论其初始状态如何,总是向着某一终点(或区域)移动的特性。如,在一定条件下,生物群落演替的结果最终是一个稳定的顶级群落
(6)兼容性和集合稳定性
兼容性指低层次非平衡过程被整合到高层次稳定过程的现象;而系统在这种高层次上表现出的“准”平衡特性称为集合稳定性其它如局域稳定性、全局拒稳定性、稳定极限环、物种去除稳定性(可行稳定性或扇性稳定性)、弹性、变幅、滞变性、替代性、循环稳定性皆可归结为恢复性。post-48-1129338375.jpg
19330这个附图是干什么用的?
这么奇怪的图,居然画有9个以上的人脸....有意思
haha
19330俺很土, 但是俺看了半天也只找出了 5个人的脸.
上面的同学能不能指点一下,9个人都在哪里?
19330我看到了九个,不知道还有的是在哪里呢?九个分别在:半圆门左上边就可以看到四张脸,有侧脸有正面象,半圆门右边有一个,然后下面的很明显的有个大脑袋,然后是这个大脑袋的胡须那里有张脸,然后就是一个女的抱着一个娃娃,这样就一共有九张脸!哈哈,只是我个人看到的,不知道还有的怎么看呢?可要请教大家了!这些还真有趣!
19330晕,主题都变了
19330嘻嘻, 小红帽,不好意思,捣乱有俺的一份。
19330什么是Lagrange稳定性?
“另一方面,任何一个种群的大小不会少到不能繁衍后代,乃至绝灭;另一方面,没有一个种群的大小会无限增大。换言之,从相空间正象限的某一有界闭区域出发的数学模型的轨线在很长的一段时间内上、下以某些正数为界,即轨线不离开某一有界闭区域。所以这一数学模型是Lagrange稳定的。”那么,什么是Lagrange稳定性呢?
19330我看到了十一个脸,呵呵
19332我们在求级数[SIZE=7][COLOR=red]

1/n**2的和
我已经收集了三种做法
第一种是有欧拉解的主要思想是多项式分解理论和将有限维空间类比到无限维空间
第二种是构造函数的方法函数是

x**n/n**2当x=1时既为所求
第三种是富氏展开法
我想问的是还有其他解答吗?
在第二种解法里有困难
就是幂函数的和函数不好求解 在于有一个积分不能用初等解法求解
19333
在一次集会中有n个人参加(n>=6),证明其中的任意6个人中必有3个人互相认识或有3个
人互相不认识.举例说明如果将6人改为5人,结论不一定成立.
19333可以用完全图试一下看看。
在《离散数学》上应该有解答的啊
19333这个属于图论(离散数学也可以)里面的的Ramsey问题。
证明不是很多。
先用到“鸽笼原理”:若将n+1个物体放入n个盒子中,则必存在一个盒子最多装两个物体。
问题被转化成一个图论的问题:在任意的6阶(6个顶点)图G中,或存在3个点的团(三角形)或存在三个点的独立集(互不邻接的点构成的集合)。
19333A,B,C,D,E五个人,A与B,E认识;B与A,C认识;C与B,D认识;D与C,E认识;E与D,A认识
19333可以参考一些基本的图论书,都有相应的内容。Ramsey数问题。
19333一般组合数学的书上都有这个结论及其证明
19333这是组合数学一个结论 证明只要构造六个点用红蓝线相连 必存在兰色完全K3图或红色完全K3图
19333好高深呀!
19336h中国科学院数学与系统科学研究院-中国科学技术大学2004年硕士研究生入学试题--数学分析 高等代数试题
http://www.math.org.cn/forums/index.php?showtopic=12320http://www.math.org.cn/forums/index.php?act=...e=post&id=77401
19339请大家集思广益,帮忙解答一下。
不胜感谢!!!
19339试题呢??
19339你可以找人帮你在浙大买,或者自己邮购
19339诶,被误导了
19340原华中科大2004年数学分析解答有误,第二题理解有误,第九题的证明不完整,我做了补充.
请看附件.为什么我不能上载我的文件?
19340你可以说说你的意思吗?难道证明有误吗?
我的理解是可以改进如下:
post-38-1129367244.ibf
19340取函数[Math] $f(x)=x(1-x)$ [math], 则f满足条件,但[Math]
$\sup_{0<x<1}f'(x)=1$
[Math].这里的改进要这样理解.
第九题的后半证明,要利用条件中给定的点是所有的零点.这是此题的关键.
19340第九题第二问好做,但感觉步骤难写!!!谁写下看看??
19340我写出来,我已编了几次,它总是掉了一些.我已尽力了..
设
∑ n
=0 ∞
∫ x
n x
n +1
f(x)dx
收敛.记其极限为s, 则有
lim
N
→∞
∑ n
=0
N∫
x n
x n
+1
f(x)dx=s
, 且有与之间不变号,这是此题的关键
19340若谁想要,请发email给我.jingshixu@126.com
19340我已写在上面,编辑太麻烦了,不完全,但意思已出来.
19340看不懂!!:(
19341P(x)=ax*x-bx+c为整系数多项式,求出使P(x)在(0,1)具有两个不同零点的a的最小正整数值
还请大家多帮帮忙
19341这么考虑对不对?
a决定的是抛物线的开口程度,a越大,抛物线开口越大。所以要使a最小,那么,抛物线的开口程度越小。而-b最要是决定抛物线左右偏移的程度,对开口大小的程度不造成影响。
在a和b确定的情况下,c决定抛物线的上下移动情况,因为(4ac-(-b)*(-b))/4a。
因此,要使得a最小,那么抛物线必须经过(几乎刚好经过)点(0,0)、(1,0),并且最好顶点在0.5处。解得抛物线中,c=0,a=b。此时让a为1,b为1,c只要比0的整数就可以。
19342在吉米多维奇的习题集中,利用斯托克斯公式计算时,经常用到曲面的法线方向余弦,但是我的教材中并为讲解曲面的法线方向余弦的计算方式,请问如何计算?
谢谢!
19343在高等教育出版社,北京大学数学系几何与代数教研室代数小组编的那本《高等代数〉重13页定理6:一矩阵的秩是r的充分必要条件是存在一个r级子式不为零,任意r+1级子式全为零。证明中,他不放设前r航线性无关,接着又不防设前r列线性无关,为什么
这个r级子式a11....a1r 满秩呢?
........
ar1 arr
19343满秩必须是一个极大的线性无关组,所以一定是矩阵中的各行各列不能为零,这样就是一个满秩的矩阵了,因为是设的所以不需要任何的条件承认其,存在即可
19344
| 引用 (子青 @ 2005年10月16日
16时35分) |
| 引用 (978301 @ 2005年10月16日
16时05分) |
引用 (子青 @ 2005年10月15日
18时09分) | |
你确定这本书叫这个名字?书都定了什么叫不能太难?所有敢叫这个名字的书都很难
|
呵呵,随机分析是一门课吧严格说来,我知道有很多版本,有的是专门针对纯数学专业学生的
有的是针对非数学专业学生的,俺看过针对纯数学专业学生的教材,巨难!看了一年还没有看
完一半,而且理解的也不是很好,自己感觉.所以想找一本针对非数学专业的随机分析教材.
哪位大哥大姐要是有的话,请发发慈悲,给俺一份好不好!!俺先谢谢了.
|
清华有一本给电子的本科生用的随机分析的教材,你可以去看一下
|
谢谢了,老大.不知道能不能提供更具体一点的信息!万分感谢!!
19344哪位大哥大姐有<随机分析>这本书,能不能发一个给小弟!!
不能太高深哦.如果是纯数学的,俺水平有限看不懂哦.
xiaoyaobujing@126.com
先谢谢!!!
19344你确定这本书叫这个名字?书都定了什么叫不能太难?所有敢叫这个名字的书都很难
19344
引用 (子青 @ 2005年10月15日
18时09分) |
|
你确定这本书叫这个名字?书都定了什么叫不能太难?所有敢叫这个名字的书都很难
|
呵呵,随机分析是一门课吧严格说来,我知道有很多版本,有的是专门针对纯数学专业学生的
有的是针对非数学专业学生的,俺看过针对纯数学专业学生的教材,巨难!看了一年还没有看
完一半,而且理解的也不是很好,自己感觉.所以想找一本针对非数学专业的随机分析教材.
哪位大哥大姐要是有的话,请发发慈悲,给俺一份好不好!!俺先谢谢了.
19344
| 引用 (978301 @ 2005年10月16日
16时05分) |
引用 (子青 @ 2005年10月15日
18时09分) | |
你确定这本书叫这个名字?书都定了什么叫不能太难?所有敢叫这个名字的书都很难
|
呵呵,随机分析是一门课吧严格说来,我知道有很多版本,有的是专门针对纯数学专业学生的
有的是针对非数学专业学生的,俺看过针对纯数学专业学生的教材,巨难!看了一年还没有看
完一半,而且理解的也不是很好,自己感觉.所以想找一本针对非数学专业的随机分析教材.
哪位大哥大姐要是有的话,请发发慈悲,给俺一份好不好!!俺先谢谢了.
|
清华有一本给电子的本科生用的随机分析的教材,你可以去看一下
19344
引用 (978301 @ 2005年10月
17日
08时23分) |
| 引用 (子青 @ 2005年10月16日
16时35分) |
| 引用 (978301 @ 2005年10月16日
16时05分) |
引用 (子青 @ 2005年10月15日
18时09分) | |
你确定这本书叫这个名字?书都定了什么叫不能太难?所有敢叫这个名字的书都很难
|
呵呵,随机分析是一门课吧严格说来,我知道有很多版本,有的是专门针对纯数学专业学生的
有的是针对非数学专业学生的,俺看过针对纯数学专业学生的教材,巨难!看了一年还没有看
完一半,而且理解的也不是很好,自己感觉.所以想找一本针对非数学专业的随机分析教材.
哪位大哥大姐要是有的话,请发发慈悲,给俺一份好不好!!俺先谢谢了.
|
清华有一本给电子的本科生用的随机分析的教材,你可以去看一下
|
谢谢了,老大.不知道能不能提供更具体一点的信息!万分感谢!!
|
清华出的随机分析好象就那一本,一本大本的,有点薄的一本
19345题如图,谢谢post-38-1129364468.gif
19345不好意思,我提供的一个解答自己都不太满意,仅供参考,起抛砖之意.是否有更好的方法?请高手指教.post-38-1129370937.ibf
19345符号可能看不清楚,再把辅助多项式重新放大post-38-1129371605.ibf
19345利用范德蒙行列式,解答在附件里面。post-38-1129394539.ibf
19345谢谢两位
19356判断函数列f_n(x)=sin(n*x)/[n* 杠sqrt{x}]的一致收敛性并证明之;
19356我觉得应该是在[

,+

]上一致收敛于0
19357一个有有限个元素的可交换环R ,无零因子 证明它是一个域
19357无零因子导致消去律成立,从而R-{0}为群.得证
19357今天我也是这么想了
还有个问题:是不是环对其内的元素的乘法是封闭的呢 数环有这样的性质 是不是环也有呢
我看了两本高代数
都没有明确给出
19357这是当然
19357环的定义中就有对乘法封闭之要求,很多教材只说环R中定义了乘法运算,虽无封闭字样,一般说运算即指封闭.另外要注意:R-{0}对乘法未必封闭,但对无零因子环却是封闭的,需说明一下,从而R-{0}对乘法作成群.
19357也许你是对的~~~~
19358
我是一个应届本科毕业生,想要考川大的研究生,川大考唱微分方程,我问我们学校的老师哪一部分最重要,问了两个老师,得到两个不同的答案,一个说解方程和解的存在唯一性定理是重点,而另一个说解的稳定性重要。有谁能帮我这个忙啊,谢谢了。
19358我也是考川大的啊!解方程自然是重点了啊!你说的好象都是重点啊!微分方程也就那么多内容了啊!咱们一起努力说不一定哪天在川大还会遇到你啊!祝你顺利!
19358卖笔记,今年川大10.1到10.7的数学专业补习班笔记
简略版
19358我也是呀
我的QQ276912963,和我联系
19358还有补习班啊
19359
我们考研用的教材是丁同仁老师和李承治老师的《常微分方程教程》,这本书的习题较难,很多题目我都不会做,想找一本答案,有人能帮我这个忙吗?谢谢!
19359这本书是不是没有答案啊!我现在也需要!
19361
1. 代数
有限群及其表示的理论与方法,在代数编码和组合学中有重要应用。
导师:徐明曜、张继平、丘维声、赵春来、蓝以中、方新贵、田青春、刘连生、蔡金星
2
几何
以微分几何的基本理论与基本方法为近代大范围分析的发展起重要作用。
导师: 陈维桓、王长平、莫小欢
3
调和分析、复分析、几何分析
以调和分析、函数逼近论、复分析、应用分析与非线性函数分析为主要内容,是当代国际上比较受重视的研究方向。联系实际问题遍及工程及物理等许多方面。
导师:张恭庆、李 忠、刘嘉荃、彭立中、谭小江、刘和平、蒋美跃、伍胜建、朱学贤、肖 杰、刘建明、朱小华
4 常微分方程
以常微分方程与大范围分析为主要内容,是近代分析的一个重要分支,一些自然现象可作为它的实际背景,有重要应用价值。
导师:李承治、郑志明、柳彬、李伟固
5
数论
以代数数论的理论与方法为基本内容,在代数编码中有重要应用。
导师:潘承彪
6
拓扑
以当代拓扑学的基本理论与基本方法为重要内容对于近代大范围分析的发展起重要作用。
导师:姜伯驹、王诗宬、段海豹、尤承业、丁 帆
7
动力系统
以常微分分析方程与偏微分方程及大范围分析为主要内容,是近代分析的一个重要分支,一些自然现象可作为它的实际背景,有重要应用价值。
导师:文
兰、王 铎、张筑生、董镇喜、林源渠、孙文祥、刘培东、朱 澍、王冠香
8.信息安全与密码学 (可划为应用数学)
导师:王 杰、丘维声、冯荣权
9.数学物理
数学物理在近十多年来的发展表明基础数学开始融合,主要研究量子力学系统和量子场的几何和拓扑性质。有关的数学领域为李代数,李群及表示论(有限及无穷维)这是一个十分活跃并有生命力的研究方向。
导师: 郭懋正、刘张炬、王正栋、李正元、庄大蔚、刘旭峰、赵 强
10.偏微分方程及其应用
以具有实际背景的非线性偏微分方程为学习和研究的主要对象,重点掌握解的估计和泛函框架的运用等一些近代方法,无论在数学理论及实际应用上当前在国内外都受到广泛重视。
导师:陈亚浙、黄少云、刘西垣、王耀东、周蜀林
19361很难过的说,有的老师退休了,有的甚至已经驾鹤西去了.
大家可以自己去网上报名的网站查06年的最新信息.
19361请问以下,北大的代数几何学研究如何?有哪几位老师?数论怎么样
19362不知哪位有这本书!! 书的简介如下:
基础代数 /(美)雅各布森(Jacobson,N.)著
出版发行项:
北京-高等教育出版社
1987.9
翻译者: 上海师范大学数学系代数教研室
论题主题: 代数
书名原文:Basic algebra
本书介绍了抽象代数的基础课题,包括幺半群和群,环,主理想整环上的模,方程的Galois理论等等。
不知哪位大侠有其电子版!!???
19362我也想要
19364我想问一下
数学课程教学论里哪个学校或者研究机构比较好
谢谢
19364我是西师的,我们老师说我们学校的较好
19364北师大或华东师大是最好的
19365一般说来,对好些极限计算题可利用罗必达法则来做,对其中较繁的可考虑结合泰勒公式来做,且上述两方法常常机械地使用即可。
可对于以下二个极限计算题,解起来似乎颇需要技巧,现向高手求这二个题目的机械或接近机械的计算法!(a是常数)
post-8-1129382208.gif
19365可考虑提公因子,两题的解法类似
19365谢谢楼上,对第二题楼上能否给出较机械的方法呢?!
19366一个n阶对称行列式,如下图,主对角线上全是1,其余是n(n-1)/2个角的余弦值,证明这个行列式的值
大于等于0,小于等于1。post-38-1129385329.gif
19366直接化简
数值代数有类似的
19366怎么化简?
19366ding
19366我也帮助顶起哈!这个题目也不会!或许是昨天约会让我的心乱了,没有一点思考的创意,哎,晕,谁来帮助解答一下吧!
19366如果是正定的就好了
detA<=a11*a22*...*ann
19366呵呵,这个题目我算是看转了,第一次看,还以为是求行列式呢!
如果判断它的范围,那就容易了,
利用矩阵和线性映射的关系,假设该行列式对应的矩阵为某个对称线性映射在自然基下的表示矩阵,然后该线性变换会在某个特殊的标准正交基下对应的矩阵是又特征值排成的对角阵!然后再想办法证明特征值绝对值都是小于1的就可以了,至于证明特征值小于1
可以假设对应的特征值的特征向量为e,则容易知道|e'Ae|=
|

e'e|<=e'e
从而就知道了|

|<=1
(e'Ae就直接利用A去展开,不用参与特征值,

e'e就是因为e是特征向量,自然就有了Ae=

e)
从而问题就获得了解决了!
19366特征值不一定都小于等于1的,比如
[ 1
1 /2
1 /2
1 ]
有一个特征值是3/2
19366
| 引用 (pccq_2002 @ 2005年10月26日
16时44分) |
如果是正定的就好了
detA<=a11*a22*...*ann
|
只要半正定就行了.
如果A是半正定的,则A的n个特征值全>=0
于是det(A)=特征值之积<=(特征值之和/n)^n=1
而半正定根据它的一个兖要条件所有主子式的行列式都大于0
用归纳法立得
19366
| 引用 |
| 特征值不一定都小于等于1的,比如 [ 1 1 /2 1 /2 1 ] 有一个特征值是3/2
|
[ 1 1 /2 1 /2 1 ] 不是对称的矩阵
19366轮换行列式有套路的
把2,3,^n加到第1列.若干还不会,
19366谢谢大家
19367CNKI 数据预处理工具,类似林营志先生提供的工具,不过处理数据更加完善,可调整数据为标准 RIS 格式,用 EN 或 NE 的
“RefMan - (RIS)” 的过滤器均能正确导入。另,该工具还可以生成适用于 NE 提供的 CNKI 过滤器的结果。 。可用于对 CNKI
4.0 及 CNKI 4.0 Free 的数据进行添加页码项的处理。
http://www.scinote.com/supportcn/cgi-bin/t...gi?id=
172&age=0帖子中的
EN = EndNote
NE =
NoteExpress
关于NoteExpress的一些资料:
免费下载地址:
http://www.scinote.com/support/cgi-bin/dow...ownload_chs.cgi最新的教程地址:
http://www.scinote.com/support/noncgi/down...ss_Tutorial.pdfword插件演示视频:
http://www.scinote.com/supportcn/noncgi/at...-NEVedio_WordAddin.rar
技术支持地址:
http://www.scinote.com/supportcn/cgi-bin/f.../forum_show.cgi
19369
各位好呀,今友学习计算机的形式语言,急需元数学的基础知识,请那位朋友有这方面的资料传递一下!
万分感谢!
联系方式:msn:wang.y.j@163.com(由于我一般不加陌生人,所以加的时候请说明一下)
email:wang.y.j@163.com
19369你去图书馆借那本经典的[美]S.C.克林著--《元数学导论》吧。那可是好书啊!偶一直想找到。可惜都失败了。
19369太高深了,不懂
19369我有此书!
谁要就留下邮件地址
19369agnostic_why@163.com
thank you!!!!!!!
19369
| 引用 (zheng8145 @ 2005年10月28日
22时06分) |
我有此书!
谁要就留下邮件地址
|
能给我一本吗?另外,你能提供下列书吗?
递归论
1 Anil Nerode,
Richard A. Shore合著的《Logic for applications》,Springer出版社
1997出版
2 Nigel
Cutland在
1980年写的《Computability: an introduction to recursive function
theory》,Cambridge University Press
3 Robert I. Soare
1987年写的《Recursively enumerable sets and degrees :a study of computable
functions and computably generated sets》,Springer出版社
1987出版
4
Piergiorgio Ddifreddi写的《Classical recursion theory :the theory of
functions and sets of natural numbers》(North-Holland
1989年)
5 Rogers,
H.写的《Theory of recursive functions and effective
computability》
模型论
6 C.C.Chang和H.J.Keisler合著的《Model
theory》,North-Holland
1973年出版
7 David Marker在2002年刚出版的《Model theory :an
introduction》
该书是Springer出版社的GTM丛书中的一本
集合论
8 Kenneth
Kunen的《Set theory :an introduction to independence
proofs》,这本书是North-Holland出版社在
1980年出版的书
9 Thomas Jech的《Set
theory》(Springer,
1997出版)
10 On Formally Undecidable
Propositions of Principia Mathematica and Related Systems (Basic Books,
1962)
我的Email:chenshi23@tom.com
手机:013509932656
《Introduction
to Axiomatic Set Theory》
《A Course of Mathematical Logic》 GTM系列
世界图书出版社的引进版
19370各位好呀,今友学习计算机的形式语言,急需元数学的基础知识,请那位朋友有这方面的中文电子资料传递一下!
万分感谢!
联系方式:msn:wang.y.j@163.com(由于我一般不加陌生人,所以加的时候请说明一下)
email:wang.y.j@163.com
19371豆豆老师:
您好。
皮格尔和蒂勒合著的<<the nurbs
book>>这本书,国内是否有出售书店,我急需这本书,如果有这本书的电子版本更好,我曾在大连理工大学的图书馆查过有此书,但可惜我不能去借,希老师能帮忙。
还有一事,您在学习nurbs的基础理论时,书中所描述的关于曲线、曲面的基础理论如何通过计算机实现,您是否有这方面的开放软件,谢。
19375小弟初来乍到觉得各位都很高!
19377 我现在是一个大3的学生,已经下决心考研,但是对考研很多东西都不是了解,
有些问题很疑惑,希望朋友们能帮助解决一下,感激不尽
问题一:比如说,我是个偏僻学校的学校的学生,但是想考北京的某个大学,那么初试的时候是不是得到北京的那个学校去考试?
问题二:有些好的学校保送名额非常多,所以报考的时候得避开这种情况,可是我怎么能知道想考的学校究竟除去保送名额之后还剩几许?(通过上该学校的研究生论坛或者找该学校的研究生,这听上去的确很简单实效,可是办起来不是很难吗,上哪去找这些研究生呢,他们平常也不定上论坛)
问题三:假设清华有个专业比福州大学差很多(似乎这种情况不存在,所以仅是假设),但是福州大学整体实力比不上清华的缘故,这时候究竟考这个专业难度福州大学要比清华难还是简单些?
^^^^^^^^^^^
19377考试在本地考!报送生数量一般查不到的!学校比专业重要些!
19379大家好啊~我是数学专业的学生!希望能和大家成为好朋友啊~
QQ是 :494882227
19379很希望能和你成为朋友,不过我不用QQ,能经常上这个论坛就好
19379你好啊,很高兴能在这认识你,我也是数学系的学生,我今年大三了,希望年能和你成为朋友,交流数学上的问题。
qq:
190344312
tel:0451——82133380
19379我不是数学系的学生,但很喜爱数学。
非常乐意在本论坛和大家交流
19379还有我啊.
hytcmath031g@163.com
数学与我们同在!
19379交流一下好的。。我加你,,顶!!!!!!!!
19379加我一个,364779593
19379也加我一个吧。但我没qq
19379QQ282878784
19379我也算一个28357
1966
相约数学家园!
19379加我一个,湘潭大学应用数学专业,QQ:
179049974
19379我也算一个164590375
相约博士家园!
19379我也愿意交朋友
19379我是数学大一,很高兴认识大家。
qq:59558511, msn:
sjx1008@hotmail.com
ps,大家怎么都不用msn啊,555~~~
19379我也算一份
277363443
19379好好交流呀
19379我不是数学专业的,但是一直在自学,大3的。也加我一个。229292351 相约数学的明天。谢谢。
19379也算我一个 40310539 喜欢数学的请加
19380
引用 (Baoqi @ 2005年10月16日
12时
19分) |
|
有谁学完了测度论的,能说说怎么样才能学好这门课程的?有没有其它的参考资料推荐一下!
|
测度论比较难一点,主要讲的是如何在群,环,域等上面建立测度函数以及研究这些测度函数
有什么特点.一般的测度论教材开始讲述的都是基本的代数结构,譬如什么叫做群,环,域,它
们之间有什么关系,其中最重要的就是

-域了.因为我们所要着重了解的就是这个
集类上的集函数----测度.
除了这些东西以外,接下来的就是讨论测度的特点.
说到测度其实也不难理解,测量大家都知道吧,测量物体的质量或者其他什么性质的,测度就
是对这个的一种抽象,概括来说所有这些测量实际上就是对某个集合类中的每个集合的一种
赋值,这个就是测度的最最本质的含义.
讲述了测度的特点之后,一般还要讲述他的积分啊极限啊什么的,实际上就是对我们的高等
数学以及实变函数等的进一步抽象.所以在这些课程中讲到的问题基本上在测度论中都有对
应的内容.
我所能说的也就这些了,我也不是学数学的,测度论俺自己花过几年的时间硬啃过好几遍,理
解的也不是很深刻,那是两年前的事了,当时我用的教材是南开大学朱成熹的,这个很基础,
内容比较全,很适合初学者学习,然后就是严加安写的测度论讲义了,中科院的教材,学了这
些,如果你还有精力和兴趣,你还可以认真的读一读严加安和刘士秀合写的概率与测度,北京
师范大学出版的,新版本已经有发行了.
本人觉得学习这个东西最重要的是要求你能静得下心来,只要你能做到这点,并能长期坚持,
那你就不会有任何困难了。
祝你好运兄弟!!
19380唠叨两句~
“本人觉得学习这个东西最重要的是要求你能静得下心来,要你能做到这点,并能长期坚持,那你就不会有任何困难了。”
楼上的话简直经典啊,学数学就是要静心啊,不过外面这浮躁的社会,应该不是我们想要的。
测度论啊,大体上一开始讲各种集合或集族,基础知识,容易掌握。
然后是测度,主要是测度在西格马环上的延拓(封闭),再就是可烈可加(面积),最后得到一个西格马环上的完备测度,发挥骨头啃蚂蚁的精神啃下来!
然后是可测函数与测度上的积分,类似分析的有各种收敛及交换条件。
最后是重积分的抽象,采用类似于公里化的方法定义一个可测函数的积分为乘积测度(证明),然后推广到N维。
······
基本就这些,还是楼上说的,学数学要静心啊。学的好坏看你自己了~
教材嘛~看一些老版本的研究生教材比较好,线路清楚。
19380有谁学完了测度论的,能说说怎么样才能学好这门课程的?有没有其它的参考资料推荐一下!
19380……
严加安和刘士秀合写的概率与测度
……
两位作者没一个写对的 :(
19380[COLOR=purple][SIZE=7]晕
是严士健与刘的概率与测度
19380……两年了
正在学……
19380如果学过实变函数后再学测度论会轻松许多,虽然学测度论会有难度,而且难度根据个人发展要求不同会不同,但一般来讲也不要觉得它很难,快乐学习,不要当成任务。
如果只是一般要求的话--程式宏的《测度论与概率论基础》就可以满足
深一点是严加安《测度论讲义》
再全面一点的是
P.R.Halmos 的《measure theory》
19380感觉学习测度论需要熟悉一些例子,

代数那关过去了,应该很愉快的.
19386请问有理数与无理数是连续间隔分布的吗?
19386当然不是,有理数是可数的,无理数是不可数的,二者都是稠密的,即有理数集的闭包等于无理数集的闭包等于实数集。
任何两个有理数之间都有无穷多个有理数,也有无穷多个无理数;任何两个无理数之间也有无穷多个无理数,也有无穷多个有理数。
建议找本数学分析(不是微积分)的书好好读一读最开始的那一章讲实数理论的。
19386楼上的说的对,任意两个有理数之间至少存在一个无理数,任意两个无理数之间至少存在一个有理数,但无理数比有理数多的多。离散数学中关于集合的势也有讲这方面内容,实变函数中讲的很数学。
19386记得王树禾写的《数学聊斋》讲,有理数如同粥里面的米,而无理数就是粥,有理数浸泡在无理数的海洋中。可见,无理数比有理数多得多,无理数的基数比有理数大。
不太可能是连续间隔分布。因为要连续间隔分布,就起码要规定一个尺度。比如,自然数中的奇数和偶数,虽然奇数和偶数都是无穷多个,但它们是间隔分布,“自然数中”就是这个尺度。再比如,规定取数轴上所有只包含小数点后5位的数,如,0.22815、101.63850,小数点后第5位的数为奇数分为一组,为偶数分为另一组,虽然它们都是无穷多个,它们仍可以间隔分布了,而“规定取数轴上所有只包含小数点后5位的数”就是这个尺度。
这个尺度的实质目的就是要使任意两个元素之间只有有限个元素相隔。比如,“自然数中”,元素2和6之间只有3、4、5三个元素相隔;“规定取数轴上所有只包含小数点后5位的数”中,0.22815和101.63850也只有10141034有限个元素相隔。只有有了这个尺度,间隔分布才有可能。间隔和尺度是密不可分的。
而无理数都有无限位小数,那么尺度必须拉到无穷位才可以比较。有理数也不能放在有限位的尺度上比较,因为它是由无限循环小数组成的,所以尺度同样要拉到无穷位。那么这个尺度就没有存在的意义了,连续间隔分布就更不可能。
不过,楼主不要灰心!你的问题很深奥!任何两个有理数之间都有无穷多个有理数,也有无穷多个无理数;任何两个无理数之间也有无穷多个无理数,也有无穷多个有理数。这句话讲得好,也是正确的!
但同时也意味着有理数与无理数是连续间隔分布的,只是它们的间隔的“长度”是无穷少个元素。哈哈!而上面的奇数与偶数的间隔的“长度”,以及“小数点后第5位的数为奇数”与“小数点后第5位的数为偶数”的间隔的“长度”都是1个元素。
这里暂且说是间隔的“长度”,显得比较直观。间隔的“长度”为1个元素好理解,就是隔了一个元素,这是我们通常说是间隔的起码要求;但间隔的“长度”为无穷少个元素就不好理解了!这好比数学上说的维度空间,1维空间、3维空间好理解,那么0.41维空间怎么理解?1条人命、2条人命好理解,那么7.975条人命怎么理解?
确切地说,有理数与无理数的间隔“长度”应小于1个元素,这就包含了无穷少个元素和零点几个元素。至于到底比1个元素少多少,呵呵,问Cantor、问Dedekind吧...
19386感谢楼上的,真有意思,受益了.
很受鼓励.
193863.0000000000000...........1是无理数吗?
他等于3+1-0.9999999999999999999
19386不用谢,因为这都是没有经过证明的,说不定是根本经不起证明的想象。我只有一个爱思考的脑袋,但许多数学基本知识仍处于极度匮乏中。I'm
hungry!
19386如果楼主的命题是真
则可有实数abc,ac是有理数b是无理数,且2b=a+c。
有理数乘无理数是无理数
有理数加有理数是有理数
显然上等式右边不等于左边
故命题假
19386任意两个不相等的有理数之间至少存在一个无理数,任意两个不相等的五理数之间至少存在一个有理数。Satanophany分析的非常正确,佩服佩服!
19386为了表达我对有理数和无理数的某些看法,我建立了一个很菜的数学模型。
0 1 2 3 4 5 6 7 8 9
10 11 12 13
14 15 16
17
18
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
34可以把以个位数为0的整数(即红字表示的数)看作有理数,把个位数为非0的整数(即蓝字表示的数)看作无理数。
红色的数均匀地浸泡在蓝色数的海洋中!啊!多美!可以说,红色数在蓝色数中是连续间隔分布,每隔9个数,就会有一个红色数出现。
按照朋友wdcyc的提议,如果连续间隔分布地话,则有命题:则可有实数a、b、c,a、c是有理数b是无理数,且2b=a+c。
于是,我们取蓝色数中的11为b,看有没有红色数a、c对应。
2*11=22=a+c
由于a、c必须是以0为个位数的整数,所以无论如何,也找不到a、c,使等式2b=a+c成立。故朋友wdcyc的提议仍需改进。
由此看来,这个很菜的数学模型有一定的说服力,也比较形象但又十分简单地描述了有理数与无理数之间的某些肤浅的关系。
19386
引用 (wdcyc @ 2005年10月
18日
19时36分) |
如果楼主的命题是真
则可有实数abc,ac是有理数b是无理数,且2b=a+c。
有理数乘无理数是无理数
有理数加有理数是有理数
显然上等式右边不等于左边
故命题假
|
有这么简单的证法我确实想不到。不过经过我的思考,我想提出质疑。
命题:则可有实数a、b、c,a、c是有理数b是无理数,且2b=a+c。
当提出这个命题时,就似乎已经加入“尺度”这个概念。2b=a+c似乎只适合于特殊的有理数。比如,奇整数3,与奇数3相邻的元素是偶整数2、4。
2*3=2+4。
命题成立。那么这个“尺度”就规定“必须在自然数中”。离开这个“尺度”,这个命题无法生存。
现在屏弃“尺度”,或将“尺度”拉到无穷位,看这个命题是否正确。依然取那个奇数3。与奇数3相邻元素是,哈哈,是2.99999999999999......和数3.00000000000000.....1。
前者2.999...好商量,因为它是无限循环小数。但可恶的后者,3.00000....1却是个无理数。所以命题就成了:
2*3=2.99999999999999......+3.00000000000000.....1
2*有理数=相邻的有理数+相邻的无理数。哈哈!
2*3=2.99999999999999......+3.00000000000000.....1这样表示是为了直观。事实上,要找出某个有理数的相邻数也是不可能找到的。比如,上面的例子中的3,它的相邻数不是2.99999999999999......和3.00000000000000.....1,因为,2.999...=3.000....1=3,那个3.000...后面的1是没有意义的,因为1的前面有无穷多个0,同样,无穷多个9与无穷多个0也是没有区别的。根据这个道理可推知,2.9999....998812也等于3,也不是3的邻近元素,因为8812前面有无穷多个9,所以8812没有意义。有理数的相邻数不可能找到,它的相邻数是有理数,还是无理数,我们都不知道。
所以这个命题不适合有理数。
那么无理数呢?比如无理数根号2,我们得先找到与根号2相邻的无理数,智商有点不够的人类可以找到吗?
2
*2 =相邻的无理数x+相邻的无理数y
因此这个命题也不适合无理数。
既然这个命题对有理数和无理数都不适合,那么就不能拿来证明楼主的命题。因为那个该死的“尺度”是关键,如果“尺度”不同,就无从谈起。
谢wdcyc,您让我想得更深刻了!
193863.000000000000000000000000000001就是3
19386能不能完善一下尺度这个概念呢,我觉得这个概念在本质上有点误区,
不能很好地描述实数集.我觉得数是人创造的抽象概念,楼上的让我觉得尺度本身就基于实数是连续间隔分布这个存在条件.一点小小的想法.
19386
| 引用 |
wdcyc说:3.0000000000000...........1是无理数吗?
他等于3+1-0.9999999999999999999
lz2000说:3.000000000000000000000000000001就是3 |
你们两个看帖不认真!我不是已经写了吗?
| 引用 |
| 事实上,要找出某个有理数的相邻数也是不可能找到的。比如,上面的例子中的3,它的相邻数不是2.99999999999999......和3.00000000000000.....1,因为,2.999...=3.000....1=3,那个3.000...后面的1是没有意义的,因为1的前面有无穷多个0,同样,无穷多个9与无穷多个0也是没有区别的。根据这个道理可推知,2.9999....998812也等于3,也不是3的邻近元素,因为8812前面有无穷多个9,所以8812没有意义。有理数的相邻数不可能找到,它的相邻数是有理数,还是无理数,我们都不知道。 |
19386
| 引用 |
| 能不能完善一下尺度这个概念呢,我觉得这个概念在本质上有点误区,
不能很好地描述实数集.我觉得数是人创造的抽象概念, |
哈哈,其实"尺度"是一个非常不严谨的概念,我的词库里面又没有太好的词汇来形容这一概念,故拿"尺度"来代替.
要判定间隔,首先要规定一个法则可以将被判定的元素分为两组或两组以上,通过分析两组或两组以上的元素,判断他们是否间隔.其中的法则就是我所谓的"尺度".
比如"在自然数中,按奇偶分为两组";"取数轴上所有只包含小数点后5位的数,第5位的数按奇偶分为两组".就是这个法则.
要判定"有理数与无理数是连续间隔分布的",那么此法则就是"在实数中,按有理数和无理数把实数分为两组."
我所谓的"尺度"同时也意味着精确位数.比如"在自然数中,按奇偶分为两组",那么这个法则只能精确到正整数."取数轴上所有只包含小数点后5位的数,第5位的数按奇偶分为两组"这个法则可以精确到小数点后5位.
而"在实数中,按有理数和无理数把实数分为两组."这个法则可以精确到无限位小数,也可以说只能精确到实数范围内.
我所谓的"尺度"也是命题的要求,比如,必须分为三组,或分为四组,看这四组元素是否互相间隔.
把上面的内容加起来,就是我所谓的"尺度".晕!总之要搞间隔,就必须有前提条件,那些前提条件都是限定"尺度"的,都属于"尺度"的范畴.
| 引用 |
| 楼上的让我觉得尺度本身就基于实数是连续间隔分布这个存在条件.一点小小的想法. |
对于您的看法,我不是太理解,您能举一个例子说明,尺度本身就基于实数是连续间隔分布这个存在条件吗?
要解释这个尺度,对于我这个学外语专业的人好象吃力的点.
19386觉得不是分析的观点
19386Satanophany真能写。
赞一下。
大家讨论的又涉及到极限(无穷)了,又牵涉到实无限与潜无限的认同问题了。讨论到这个问题就有很多东西会讲不清楚。
我非常佩服Satanophany的猜疑精神。
我也提点我的非常大逆不道的想法(跟这个问题多少有点涉及)
康托的集合论用到了对等(1-1对应)的关系来比较集合间的势的大小,于是有了任意n维空间的势都与一维相等。
个人认为非常不符合常理。能不能在在1-1对应上加上连续的条件呢(同构),当然要先规定度量(拓扑也可)。
19386有理数是可数的,无理数是不可数的,二者都是稠密的。
任何两个有理数之间都有无穷多个有理数,也有无穷多个无理数;任何两个无理数之间也有无穷多个无理数,也有无穷多个有理数。
建议大家看一些相关的数学分析书,会有解释的
19387任意矩阵都与自己相似E^-1AE=A
有意思的问题应该是
仅与自己相似的矩阵
当且仅当他与任意可逆矩阵可换必为数量矩阵
19387帮忙看看这个该怎么算啊
19387题呢
19387求所有与自己相似的n阶矩阵
19387我知道了
不好意思
呵呵
19387就是
但是为什么仅与自己相似就可以跟任意的可逆矩阵交换啊。
19389
对数学的再认识 邱崇光
不少同学对数学总这有一点畏惧感,对数学好的人有一种敬佩感。自己对数学总有一点信心不足,拿到一个新课本,一翻,十分庆幸,好在数学公式不多,如果拿到一本书,中间数学推导公式多,就十分沮丧,甚至想回避。
大家都不是搞数学专业的,为什么非要讲一讲对数学的再认识、反复强调要学好数学?如何提高数学素养呢?我想,作为一个现代大学生,数学是回避不了的。华罗庚在五十年代就说过:“宇宙之大、粒子之微、光箭之速、生物之迷、日用之繁,无处不用数学”。到了今天这个信息时代,可以说每一项高新技术的背后都有着极其抽象的数学,高新技术本质上就是数学技术。我们想有所作为,要想取得突出的成就,必要的数学知识,较好的数学素养,较高的数学思维是必须的,请注意我这里用了三个不同的定语,要求是逐步升高的。而且你们已不再是中学生,不是爸爸妈妈要送你读书了,你们已进入人生悟性期,自觉的理解意识正在升起,有的同学甚至对科研、创造、创新已跃跃欲试了,这很好。从课堂和书本里学来的只能是知识,是外来信息,人们最终需要开发和建立的是自己的意识和悟性,当然知识也可以促进意识和悟性的迅速提高。在这个人生的春天季节里,我来和你们一起对数学整体性地温习一次,鸟瞰一次,相信对你们是大有好处的。
一、 从数学与其它学科的关系来看数学
就从数学的外部来论说这个问题。
1、
数学是一种语言,是一种科学的共同语言,若没有数学语言,宇宙就是不可描述的,因而也就是永远是无法理解的。任何一门科学只有使用了数学,才成其为一门科学,否则就是不完善与不成熟的。社会在进步,它的数学化程度也正在不断提高,数学语言已成为人类社会中交流和贮存信息的重要手段,宇宙和人类社会就是用数学语言写成的一本大书。
2、
培根(Bacon)说:“数学是打开科学大门的钥匙”。忽视数学必将伤害所有的知识,因为忽视数学的人是无法了解任何其他科学乃至世界上任何其他事物的。几千年来,凡是有意义的科学理论与实践成就,无一例外地借助于数学的力量。例如,没有微积分就谈不上力学和现代科学技术,没有麦克斯威尔方程就没有电波理论,伦琴因发现X射线于
1901成为诺贝尔的第一位获奖人,记者问他需要什么时,他回答:“第一是数学,第二是数学,第三还是数学。”
3、
数学是一种工具,一种思维的工具。自然哲学认为:任何事物都是量和质的统一体,数学就是研究量的科学,它不断地发现、总结和积累了很多人类对量的方面的规律,这些都是人们认识世界的有力工具。这里举两个例子:一个是自然科学的,一个是社会科学的。我们企图找到一个不经手术就可以准确确定人体内的器官位置、密度和三维形状的方法,可惜借助X射线只能绘出二维信息图。这个问题难倒了工程师很多年,后来遇到数学家的工作,即Radon变换,考尔麦克(Cormack)把X射线从许多不同角度照射人体,再运用计算机进行数学变换,导致CT数据透视仪的诞生,获得了
1979年的诺贝尔医学奖。现在这一方法进一步推广到核磁共振领域,使图像分辨率更高。从本质上说,这两项技术只不过是,先大量测量一维的物理量,再用数学技巧来重构三维图像而已。
另一个例子:现代经济学家使数学进入了经济学领域,构建了平衡模型,可以预言自由市场的经济行为,这方面的工作使阿洛(Arrow)获得了诺贝尔经济学奖,他的哈佛大学的同事看了这篇得奖论文说,这些应用在数学中是很基本的,很多哈佛大学一年级学生就可以完成。可见掌握数学工具后,在其它领域中进行应用,并不是一件困难的事,而且有时甚至是一个很大的成就。
4、
数学是一门艺术,一门创造性艺术。美是艺术的一种追求,美也是数学中一种公认的评价标准。数学的美体现在和谐性、对称性、简洁性,这三性上。数学家不断地追求美好的新概念、新方法、新结论,因此数学是创造性艺术。人们掌握了数学,可以陶冶人的美感,培养理性的审美能力,一个人数学造诣越深,越是拥有一种直觉力,这种直觉力实际就是理性的洞察力、由美感驱动的选择力,最终成为创造美好新世界的驱动力。
这里突出地谈一谈简洁性。A、数学问题提得简洁。这是因为数学突出了本质的因素,必然是简洁的。例如尺规作图三分角问题。
B、数学语言是精炼的。例如欧拉公式:eix
=cosx+isinx.把实数域中看不出有任何联系的指数函数和三角函数在复数域中巧妙地联系在一起。其特例:eiπ+1=0 把0、1、i、e、π五个重要常数简单而巧妙的结合在一起,太神奇了。又如,爱因斯坦把茫茫宇宙中的质能关系,用E=MC2
简单地表达出来,简单得令人拍案叫绝。
C、数学概念是简洁的。数学概念的内涵历经沧桑,千锤百炼,每一次变化都使概念更加清晰和更具一般性。例如函数概念:1673年,莱布尼兹定义:函数就象曲线上的点的坐标那样随点的变化而变动。
1821年,柯西定义:对于X的每个值,如果Y有完全确定的值与之对应,则Y叫做X的函数。近代定义:设有A、B是非空的集合,F是A到B的一个对应法则,则A到B的F映射:A→B称为A到B上的函数。一步一步更简洁、更具一般性。
D、数学证明是简洁的。数学的目的就是尽可能用简单而基本的词汇尽可能地解释世界。因此,如果我们积累的经验要一代一代传下去的话,就必须不断地努力把它们加以简化和统一。
二、
从数学自身的研究对象来看数学
就是从数学内部来看数学。
恩格斯说:数学是现实世界中的空间形式与数量关系。数学就是研究数量、形状和他们之间关系的科学,这是数学的三大领域。当前数学还在发展,目前已经发展成为包括一百多个分枝的庞大系统。数学已经不是原来人们头脑中仅仅是数和形,仅仅是陈景润的概念了。随着计算机的发明和技术迅速提高,数学学科也进入了新的黄金时代。数学包括三个方面,模式、结构和模拟现实世界。它不光是理论,也是能力,是文化,是素质。
1、
数学发生图
数学可分为五大学科:纯粹(基础)数学、应用数学、计算数学、运筹与控制、概率论与数理统计。
应用数学则以以上数学为综合理论基础,可分为:价值数学、运筹学、数理统计学、系统科学、决策论等。目前又发展出混沌、小波变换、分形几何等。
2、
算术
人类逐步有了数的概念,由自然数开始。由于人有十个手指,所以多数民族建立了十进位制的自然数表示方法。二十个一组的太多太大,不能一目了然,还要用上脚趾,五个一组又太少,使组数太多,十个一组是比较会让人喜爱的折衷方法。有古巴比仑记数法、希腊记数法、罗马记数法、中国记数法,发展进步了5000年后,印度人第一次发明了零,零加自然数称为为整数,传入伊斯兰世界形成目前通用的阿拉伯数字。计算机的出现又需要二进位制,就是近几十年的事了。
算术运算起步只需要有加法的概念,乘是多次加的简化运算,减是加的逆运算,除是乘的逆运算,这就是四则运算。除法很快导致了分数的出现,以十、百等为分母的除法,简化表达就是小数和循环小数。不是拥有钱而是欠人的钱如何表示,这就出现了负数,以上这些数放在一起,就是有理数,可以表示在一个数轴上。
人们曾经很长时间以为数轴上的数都是有理数,后来有人发现,正方形的边是1,它的对角线长度就无法用有理数表示,用园规在数轴上找到那个对应点就是无理数的点,这是第一次数学危机。
1761年德国物理学家和数学家兰伯卢格严格证明了π也是一个无理数,这样把无理数包入之后,有理数与无理数统称为实数,数轴也称之为实数轴。后来人们发现,如果在实数轴上随机的抽取,得到有理数的概率几乎是零,得到无理数的概率几乎是1,无理数比有理数多得多。为什么会如此,因为我们生活的这个客观世界,本来就是无理的多过有理的。
为了解决负数的开平方是什么,16世纪出了虚数i,虚轴与实轴垂直交叉形成一个复平面,数也发展成为由虚部和实部组成的复数。数的概念会不会继续发展,我们试目以待。
3、代数
对实数的运算进入代数学阶段,有“加、减、乘、除、乘方、开方、指数、对数”八则,用符号代表数,列出方程,求解方程成了比算术更有力的武器。这个时期称为初等数学,从5世纪一直到
17世纪,大约持续了一千多年。初等数学是常数的数学。对一组数群体性质的研究就导致线性代数。
4、几何
以上是研究数的,在研究形方面也平行的发展着,古希腊的欧几里得用公理化的方法,构建了几何学是最辉煌的成就。二千多年前的平面几何成就已经与目前中学几何教科书几乎一样了。他们还了解了众多曲线的性质,在计算复杂图形的面积时,接近了高等数学。还初步了解到三角函数的值。在几何学方面,后来进一步发展出非欧几何,包括罗巴切夫几何、黎曼几何、图论和拓扑学等分支。
直到
17世纪,笛卡尔的工作终于把平行发展的代数与几何联系起来,除建立了平面坐标系之外,还完善了目前通行的符号运算系统。
5、变量数学
变化着的量以及它们间的依赖关系,产生了变量与函数的概念,研究函数的领域叫数学分析,其主要内容是微积分,牛顿由物理力学推动了微积分的产生,莱布尼兹从数学中求曲线多边形的面积出发推动了微积分的发现,两人的工作殊途同归,目前的微积分符号的记法,都是莱布尼兹最先采用的。他们都运用了极限的概念和无穷小的分析方法。
有了微积分,一系列分支出现了,如级数理论、微分方程、偏微分方程、微分几何等等。级数是无穷项数列的求和问题,微分方程是另一类方程,它们的解不是数而是函数,多元的情况下就出现了偏微分概念和偏微分方程。微分几何是关于曲线和曲面的一般理论,将实数分析的方法推广到复数域中就产生了复变函数论。
6、概率论和数理统计
前面涉及的数量,无论是常量还是变量都是确定的量,但自然界中存在大量的随机现象,其中存在很多不确定的、不可预测的量、是具有偶然性的量,这就由赌博中产生了概率论及其统计学等相关分枝。
7、模糊数学
前面涉及的数量,无论是常量还是变量都是“准确”的量,但自然界中存在大量的不准确现象,人为地准确化只能使我们对客观世界的描述变得不准确。“乏晰数学”Fuzzy就是以这种思想观点和方法研究问题的数学。
三、什么是数学素养
数学素养属于认识论和方法论的综合性思维形式,它具有概念化、抽象化、模式化的认识特征。具有数学素养的人善于把数学中的概念结论和处理方法推广应用于认识一切客观事物,具有这样的哲学高度和认识特征。具体说,一个具有“数学素养”的人在他的认识世界和改造世界的活动中,常常表现出以下特点:
1、 在讨论问题时,习惯于强调定义(界定概念),强调问题存在的条件;
2、
在观察问题时,习惯于抓住其中的(函数)关系,在微观(局部)认识基础上进一步做出多因素的全局性(全空间)考虑;
3、
在认识问题时,习惯于将已有的严格的数学概念如对偶、相关、随机、泛涵、非线性、周期性、混沌等等概念广义化,用于认识现实中的问题。比如可以看出价格是商品的对偶,效益是公司的泛涵等等。
更通俗地说,数学素养就是数学家的一种职业习惯,“三句话不离本行”,我们希望把我们的专业搞得更好,更精密更严格,有些这种优秀的职业习惯当然是好事。人的所有修养,有意识的修养比无意识地、仅凭自然增长地修养来得快得多。只要有这样强烈的要求、愿望和意识,坚持下去人人都可以形成较高的数学素养。
一位名家说:真正的数学家应能把他的东西讲给任何人听得懂。因为任何数学形式再复杂,总有它简单的思想实质,因而掌握这种数学思想总是容易的,这一点在大家学习数学时一定要明确。在现代科学中数学能力、数学思维十分重要,这种能力不是表现在死记硬背,不光表现在计算能力,在计算机时代特别表现在建模能力,建模能力的基础就是数学素养。思想比公式更重要,建模比计算更重要。学数学,用数学,对它始终有兴趣,是培养数学素养的好条件、好方法、好场所。希望同学们消除对数学的畏惧感,培养对数学的兴趣,增进学好数学的信心,了解更多的现代数学的概念和思想、提高数学悟性和数学意识、培养数学思维的习惯。
请注意,我们往往只注意到数学的思想方法中严格推理的一面,它属于“演绎”的范畴,其实,数学修养中也有对偶的一面――“归纳”,称之为“合情推理”或“常识推理”,它要求我们培养和运用灵活、猜想和活跃的思维习惯。
下面举一个例子,看看数学素养在其中如何发挥作用。18世纪德国哥德堡有一条河,河中有两个岛,两岸于两岛间架有七座桥。问题是:一个人怎样走才可以不重复的走遍七座桥而回到原地。
这个问题好像与数学关系不大,它是几何问题,但不是关于长度、角度的欧氏几何。很多人都失败了,欧拉以敏锐的数学家眼光,猜想这个问题可能无解(这是合情推理)。然后他以高度的抽象能力,把问题变成了一个“一笔画”问题,建模如下:见图右,能否从一个点出发不离开纸面地画出所有的连线,使笔仍回到原来出发的地方。
以下开始演绎分析,一笔画的要求使得图形有这样的特征:除起点与终点外,一笔画问题中线路的交岔点处,有一条线进就一定有一条线出,故在交岔点处汇合的曲线必为偶数条。七桥问题中,有四个交叉点处都交汇了奇数条曲线,故此问题不可解。欧拉还进一步证明了:一个连通的无向图,具有通过这个图中的每一条边一次且仅一次的路,当且仅当它的奇数次顶点的个数为0或为2。这是他为数学的一个新分枝――图论所作的奠基性工作,后人称此为欧拉定理。
这个例子是使用数学思维解决了现实问题,另一个例子“正电子”的发现正好相反,是先有数学解,预言了现实问题。1928年英国物理学家狄拉克Dirac在研究量子力学时得到了一个描述电子运动的Dirac方程,由于开平方,得到了正负两个完全相反的解,也就是说,这个方程除了可以描述已知的带负电的电子的运动,还描述了除了电荷是正的以外,其他结构、性质与电子一样的反粒子的运动。1932年物理学家安德森(Anderson)在宇宙射线中得到了正电子,并于1936年获得诺贝尔物理学奖。我国物理学家赵忠尧1930年正在加州理工学院读研究生,他的试验结果一出来,安德森在他的办公室隔壁办公,他受启发,立刻意识到试验结果表明:一种尚未认知的物质出现了,进一步做工作获得成功,赵忠尧与诺贝尔奖擦肩而过。
四、如何提高数学修养
要讲这个题目确实很困难,要提高数学素养只有自己去探索、去总结,世界上没有一种万能的学习方法对所有人都适用,可是回避这个问题,又十分遗憾。我们还是用一个折衷的办法:介绍数学中一个人和一件事,相信青年朋友们能从其中得到许多力量和启迪。
1、读读欧拉
1707年4月15日,欧拉Euler
(
1707-
1783)
出生于瑞士,在大学时受到著名教授伯努利及其家族的影响,阅读了不少数学家的原著,
17岁获得硕士学位,
18岁开始发表数学论文,26岁成为数学教授、科学院院士。
他一生论著数量巨大,涉猎面广,开创性成果多,发表论文和著作500多篇(部),
加上生前未及出版和发表的手稿共886篇(部)之多。在数学的各领域,及物理学、天文学工程学中留下了举不胜数的数学公式、数学定理。如欧拉常数、欧拉恒等式、欧拉级数、欧拉积分、欧拉微分方程、欧拉准则、欧拉变换、欧拉坐标、欧拉求积公式、欧拉方程、欧拉刚体运动方程,欧拉流体力学方程等。
欧拉有坚忍的毅力和勤奋刻苦的拼搏精神。他28岁时,为计算彗星的轨迹,奋战三天三夜,因过度劳累,患了眼疾,使右眼失明,又不顾眼病回到严冷的俄国彼得堡工作,左眼也很快视力减退,他深知自己将会完全失明,没有消沉和倒下,他抓紧时间在黑板上疾书他发现的公式,或口述其内容,让人笔录。双目失明后,他的寝室失火,烧毁了所有的专著和手搞,后来妻子又病故了,他在所有这些不幸面前不仅没有退缩,而是以非凡的毅力继续拼搏,他以罕见的记忆力和心算能力,继续研究,让人笔录,直到生命的最后一刻。在双目失明的
17年中,他口授论文达400篇和几本书,包括经典名著《积分学原理》,《代数基础》。
欧拉学识渊博品德高尚,非常注重培养与选拔人才,当时
19岁的拉格朗日把自己对“等周问题”的研究成果寄给他,他发现其解决问题的方法解题与自己的不同,立即热情的给予赞扬,并决定暂不发表自己的成果,使年轻的拉格朗日先后两次荣获巴黎科学院的科学奖,后来他又推荐30岁的拉格朗日代替自己任科学院物理数学所所长,他的品德赢得了全世界的尊敬。他晚年的时候,全世界的大数学家都尊称他为“我的老师”。法国著名的数学家、天文学家拉普拉斯曾多次深情地说:“
读读欧拉,他是大家的老师”,他不愧为“数学家之英雄”,他这种精神境界至今仍是年轻人学习的榜样。
2、关于费马(Fermat,1601-1665)大定理的证明
法国业余数学家费马猜想:Xn
+ Yn =Zn
,对于大于2的整数,不存在x,y,z的非零整数解。他在一本算术书的页边空白处写着“我对此有一种奇妙的证明,只是此处空白太小写不下”。后人称此为费马大定理,人们曾查遍他的手稿和用过的书籍,始终未能得到这个证明。后来的事实证明,这是难于上青天的事。莱布尼兹、高斯、欧拉、柯西
等大数学家都失败了,仅在
1909年到
1911年这三年间就有一千多篇论文,提出各种证明都因为不严格而否定,几百年来有人废寝忘食,有人神魂颠倒,甚至于有人失败后自杀了。
韦尔斯(
Wiles)
1953年生于英国剑桥,
1977年在剑桥大学获博士学位,
1982年成为普林斯顿大学数学教授,他在10岁时就被费马大定理迷住了,立志要证明它。
1986年他开始下决心要征服这个难题。当教授必须每年发表论文,否则影响职务和前途,这个难题不知道何时才能征服,是否能成为论文都很难说,他想了个两全之策,他将其它项目中的成果写成几篇论文,留着以后慢慢发表。他深知必须运用最近的数学成果和创造出新的方法才能解决这个问题。为了避免干扰,他闭门谢客,只有妻子知道此事,七年后,他完成了证明的论文。
1993年6月21日他应邀在剑桥大学的国际数学会议上宣读论文。当时座无虚席,他的论文朗读了3天,黑板上写了擦,擦了又写,几万名听众急于想听到结果。到6月23日快结束时,他最终在黑板上写出了费马大定理,然后转身过来,谦逊地说,我想就到此为止了,大厅响起热烈的掌声,消息立刻传遍了世界。韦尔斯被“人物”(people)杂志列为与克林顿、黛安娜王妃齐名的本年最有魅力人物。
可惜高兴得太早,不久后他自己给数学界同行发了一个电子邮件,信中说到他发现证明中有漏洞,这可不是小事,如果仍旧解决不了,一环扣一环的证明将全部瓦解,七载心血将付诸东流,将不成熟的论文公开发表也是十分难堪的事情。但是他不灰心,在最艰难的日子里,他的好友萨尔纳克(Sarnak)不仅鼓励他,并提议他找一位值得依靠的年轻帮手,经过考虑,他邀请他在英国的学生――剑桥大学讲师泰勒(Taylor)一起工作,又经过一年的功夫终于把漏洞部分补上了。
1994年8月国际数学大会在苏黎世又召开大会,他做了最后的报告,人们热烈地鼓掌,肯定了他们部分证明了预备定理的成绩和数论方面的其它成果。又过了2个月,在
1994年9月
19日的早晨,他与泰勒讨论问题时,突然有了新的想法,又经过一个月的努力终于取得了完全的证明。
1994年10月25日,他们向数学界的朋友发了另一个电子邮件,
由两篇论文组成,第一篇是“模椭圆曲线与费马最后定理”,作者韦尔斯 ,第二篇是“某些Hooke代数环论的性质” 作者是泰勒和韦尔斯
。第一篇长文证明了费马定理,其中关键一步依赖于第二篇短文。
这一次人们十分谨慎,直到
1998年(四年以后)在柏林举行的国际数学大会上,第一次向45岁上的数学家颁发了一个费尔兹(Fields)特别奖,正式承认他们卓越贡献。证明过程中开辟了好多数学的新领域与使用了很多新的方法,证明了很多新的猜想与得到许多新的定理,为数学的发展,特别是在数论的重要分支——代数数论和环论方面做出了重要贡献,上述前仆后继、艰苦卓绝的证明的现实意义也在于此。
讲到这里我觉得自己的任务差不多完成了,让我们再一次回到这次讲话的初衷:习惯优秀才是真正的优秀,数学素养才是高层次的素养。希望大家能够在今后的学习中,重视数学课的学习,更要重视数学思维的培养,努力提高自己的数学素养。
19389写得不错
19389“习惯优秀才是真正的优秀,数学素养才是高层次的素养。希望大家能够在今后的学习中,重视数学课的学习,更要重视数学思维的培养,努力提高自己的数学素养。”
受教了!
19389深感传承的重要,需要大家。
1939026岁华裔博士两上《自然》封面轰动学界
中新网10月11日电 一位年仅26岁、在美国出生的华裔博士胡立德
(David
Hu),在2003年
和2005年分别以《昆虫在水上行走》及《昆虫如何爬上岸》题获刊《自然》(Nature)杂志
封面,在学术界造成轰动。
据
“中央社”报道,26岁的胡立德9月底才取得麻省理工学院数学所博士。2003年8月7日
《自然》以“The hydrodynamics of
water strider locomotion”
(水黾移动的动力学)
为题,刊出以胡立德为封面的报导;今年9月29日,《自然》e杂志封面再度以“A
Slippery
Slope”(非常滑的斜坡)为题,刊登他和指导教授John W.M. Bush合力研究的
“Meniscus-climbing
in-sects”
(爬弯月的昆虫)研究报告,引起全球媒体关注。
胡立德三年多在麻省数学所博士班,无法完全解释昆虫在水上行走的物理原理。他捞了几
只小水黾(Water
Strider)和昆虫回实验室观察,真相终于大白。他表示,昆虫在水面行
走,主要是依靠在水表面产生波纹的表面张力,利用三对多毛的长足,在水中制造出螺旋
状的漩涡,借助漩涡推力,以每秒一百个身长以上的长度前进,而人类跑得最快的运动
员,也不过每秒前进五个身长的距离。
经过一年精确计算,他把研究结果投稿《自然》,2003年8月7日他的研究就上了杂志封
面。这个大发现,燃起人类在水上快速前进又能大幅节省能源的希望,也引起美国海军和
国防部的关切。
胡立德再接再厉,继续观察这些小水昆虫如何从水面爬上岸。
他把研究结果再次投稿,果然,今年9月29日的《自然》封面再刊登他和指导教授John
W.M. Bush合力研究的“Meniscus-climbing insects”
(爬弯月的昆虫)研究报告。
胡立德
1979年生于美国芝加哥,他从小上中文学校也练空手道,中文程度不错,也能写毛
笔字,早年心目中偶像之一是李小龙。
19390自古英雄出少年!
在那儿能找到这两篇文章瞧瞧?
19390那种小虫子,好像不光在水上跑得快,而且还会飞!
小时候就抓过
19391大家好:
我现在急需一本《高等代书新方法》(上册)(王品超,中国矿业大学出版社),请问在哪能买到?谢谢!!
19391大家好:
我发错了是这一本 高等代数新方法 王品超编著 山东教育出版社
1989.12 在那能买到或谁有电子版?谢谢!!
19391我有下!
19391你的是书还是电子版的?怎么与你联系?谢谢!
19392吴大任:数学家、教育家纪事
(2005-10-15)
吴大任的一生与数学和教育结下了不解之缘。他是那种经历过万水千山、惊
涛骇浪却使人无从觉察的人。一双睿智的眼睛炯炯有神,脸上总是带着善意的微
笑。给人印象最深的,是他那像爱因斯坦一样高高的、充满智慧的额头。数学家
的严明精确和教育家的远见卓识在他身上得到了和谐的、充分的体现。这里所记
叙的,只是反映他执著、坚韧、冷峻如水又热情似火的性格的几个小小片段。
藏在“囊中”的博士
1921年的一天,享誉全国的天津南开中学来了四位风度翩翩的少年,他
们年龄、个头相仿,神态、气质亦相似。4人同住一间宿舍,同姓吴,又同出同
入,颇引人注目。他们就是日后考入南开大学、皆成大器的吴大业、吴大猷、吴
大任、吴大立兄弟(吴大立因母病中途返乡,后到香港学造船业),人称“南开
四吴”。
吴氏兄弟的祖籍在广东的肇庆。吴大任于1908年出生于天津。他自幼生
长在一个知识分子大家庭里,母亲早逝,兄弟姐妹共12人,他排行第二。曾在
天津担任过广东旅津学校校长的父亲一度担负着四兄弟的学习费用(大业是大任
的胞兄;大猷为二叔之子,幼年丧父;大立为四叔之子),虽竭尽全力工作,仍
不堪重负。家境的贫寒使大任的求学之路充满艰辛。他靠父亲一位朋友的资助,
才读完了高中,但又常常因资助不能及时送达,自己又不敢向父亲说明真相,只
好向同学借债维持最低水平的生活,却又因此被父亲斥责为不知节俭,个中委屈
他都默默承受了。然而大任的学业却异常优秀,父亲在期末收到学校盖有“该生
品学均有可称,请贵家长鉴察”戳子的成绩单时,才备感欣慰。由于大任学习勤
奋,成绩优秀,于1926年作为三个免试生之一,免交大学四年的学宿费进入
南开大学学习(大猷、大业已于1925年考入南开,被人称为“吴氏三雄”)
。陈省身先生与大任同年入南开。陈省身回忆起60年前的情景时,怀着由衷的
敬意说,那时“大任已是名人”。吴大任靠两次奖学金完成了大学学业。当时南
开大学理学院每年仅设一个奖学金名额,而他却获得两次(大猷亦获得两次)。
1930年他与陈省身同时考取清华大学数学系研究生后,由于父亲失业,不得
不请假一年,到中山大学任教挣钱养家,又借钱为家里准备了足够三年的生活费
,才得以奔赴他渴望继续深造的清华念研究生。
在一般人看来颇具吸引力的东西,吴大任却视之淡如水。按说,像他这样一
个视学业如生命的学子,对象征着学业金字塔顶尖的博士学位的渴求是可想而知
的。但吴大任却两次放弃了唾手可得的博士学位。他认为,获得真才实学最重要
,其他的都没有关系。
由于品学兼优,吴大任于1933年考取首届中英庚款公费留学生,入英国
伦敦大学学习,注册为博士研究生。当时的中英庚款董事会规定,公费三年中的
第三年可以转到别的国家,“而19世纪德国数学执世界牛耳,20世纪初年此
势未衰”(陈省身语),所以吴大任渴望到那里去。在伦敦大学,他计划用两年
时间拿到博士学位。然而,一年快过去了,导师们却还没有给他提出研究课题。
他想,德国一定要去,宁可放弃博士学位。那时,陈省身已经到了德国的汉堡,
吴大任就写信和他商量。陈省身告诉他,汉堡大学有三位高水平的教授,可以指
导当时的任何数学研究课题。于是,吴大任就毫不犹豫地在伦敦大学申请改为硕
士研究生。按照规定,取得硕士学位一篇论文就可以了,他却用半年时间完成了
两篇,并在数学系的科学报告会上作了报告。其中有一篇他没用讲稿和提纲,两
手空空地走上讲台,其挥洒自如、充满自信的演讲征服了全场听众。报告后,系
主任说:“在科学报告会上可以不用讲稿,真是惊人的成就。”
来到德国汉堡大学,吴大任与陈省身第三次同学,两人都非常高兴。然而大
任只剩下一年的留学时间了,而取得该大学的博士学位,至少需要一年半,他决
定作为访问学者学习。后来,了解到可以向中华教育文化基金会申请研究补助,
他申请后得到批准,可以继续留德一年。开始,导师勃拉舒克给了他一个有分量
的课题,他做出后导师很满意,对他说:“你进行得这么好,我很高兴。”他建
议大任拿博士学位。大任的新婚妻子陈?也劝他,但他不同意,因为那样的话,需
要念一年半副课课程,就会缩短做研究的时间。他对妻子说:“我只要学会做研
究,有没有学位没关系。”接着,勃拉舒克又给了他一项意义重大的课题,别人
曾经做过,但没能做出来。他愉快地接受了,只用了两个多月,就得出了圆满的
结果。导师听了他的汇报,看了他的草稿,惊喜地说:“你几乎把一切都做完了
!”接着,他又一次问:“你论文都有了,为什么不申请个学位?中国人不是很
重视学位的吗?”大任告诉他:“我在德国只有两三个月了,没有时间了。”6
0年后,当陈?回忆起这段经历时,仍然满怀深情地说:“那时我就已经看出,他
对名利十分淡泊。”
对此,陈省身在吴大任逝世后撰写的纪念文章中写道:“汉堡是大任数学研
究最出色的两年,他发表了关于椭圆积分几何的两篇文章,文中有好几个漂亮的
公式。这两文足够他在汉堡获得博士学位,可惜他入学时未正式注册。事实上有
勃拉舒克帮忙,可以补救,但他急于回国,所以博士藏在‘囊中’了。”
点石成金
在“吴氏三雄”中,吴大任的教育生涯最长,达60年。
60年的教育生涯,是一个什么样的概念?经年累月地默默地劳作,像蜡烛
一样,不断地燃烧自己,照耀他人。在吴大任那谦和平静的外表下面,滚动着一
位爱国知识分子对祖国教育事业永恒的激情,流溢着对青年学生强烈的关切和热
忱。无怪乎人们说,吴大任的一生只有两件事:教育和数学。
如今国内外许多的知名教授学者是吴大任当年的学生,他们谈起老师,仍然
满怀崇敬和怀念。他们说,听老师讲课,就是一种享受,其艺术性、逻辑性之强
,非一般人所能企及;那洪亮的声音,简洁的语言,至今仍声声在耳。老师以教
育家和数学家特有的广博和深邃,对中国高等教育所做出的贡献,所倾注的心血
,更是令人永远铭记。
在南开园,几十年来流传着吴大任关于对学生加强基础课教学和基本技能训
练,“点石成金”的佳话。吴大任认为,学校教育的任务不仅是传授知识,更重
要的是通过基本训练,培养学生的自学能力、获取新知识和创造性地发展知识的
能力。他指出:“学校不可能把学生毕业后所需要的知识全教给学生,但只要帮
助学生打好坚实的基础,端正学习态度,掌握学习方法和研究方法,他们就一生
受用不尽。”他形象地比喻说,培养学生要“点石成金”,而不是赠他们一枚“
金戒指”。因此,他主张高校教育要加深加厚基础,使学生有扎实的基本功,能
够独立分析与解决问题。南开培养的学生,多年来以基础扎实、适应能力强和素
质高而深受社会的欢迎,与他的这一主张有着密切的关系。
就是在“文革”那样的非常时期,在“牛棚”里,吴大任也没有放弃他所钟
爱的教育事业。那是1970年的冬天,凛冽的寒风狂吼着卷过大地,有人求见
被囚禁在“牛棚”里的吴大任。来人恭敬地表达了前来求教的意图,吴大任从容
地同他们走到一张落满灰尘的书桌前坐了下来。原来,他们是搞机械齿轮啮合研
究的科研人员。针对他们所提出的微分几何问题,吴大任略加
19392另一介绍:
http://www.gmw.cn/content/2006-03/14/conte...tent_387759.htmpost-50-11651
19293.jpg
19393设A,B是N维欧几里得空间的线性变换,A与AB都是自伴的,且ker(A)属于ker(B),证明存在V的自伴变换C,使CA=B
19394我想解一个微分方程f(x)*f''(x)+cf(x)^2*f'(x)-2f(x)-1=0
(知道边界条件:f(x=无穷大)=0,f'(x=无穷大)=0,用数值方法把他的图形画出来,该怎末办?请求高人指点
我找到一个求竿的温度分布的例子(在附件中),试了一下却无法运行:
M=input('give
the number of subintervals
(M):');
deltax=1/M;
xx=0:deltax:1;
funcstr=input('Give
f(x),the extra heat source
(e.g.,x.^3);','s');
T0=input('Give y(0)
(left):');
T1=input('Give y(1)
(right):');
vectorOnes=ones(M-1,1);
A=spdiags([-vectorOnes,2*-vectorOnes,-vectorOnes],[-1
0
1],M-1,M-1);
x=xx(2:end-1);
f=eval(funcstr);
b=detax^2*f;
b(1)=b(1)+T0;
b(end)=b(end)+T1;
b=b';
Y=A/b';
Y=[T0;Y;T1];
cal;
subplot(2,1,1);
plot(x,f);
grid
on;
title('externalheat
f(x).',');
subplot(2,1,2);
plot(xx,y,'r');
grid
on;
title('tem distribution f(x).',');
give the number
of subintervals (M):
??? Error using ==> /
Matrix dimensions must
agree.
19397那位大哥能说说北大应用数学的情况?
19398请问BL van der Waerden的A history of algebra: from al-Khwarizmi to Emmy
Noether. Springer-Verlag, Berlin-New York,
1985
这一本书在网上有吗?到哪里能找到?
19398哪位大哥找到了网络版的?把下载地址贴出来吧.感谢!!!
19398这个确是没有,不过我倒是有他的两本代数学,很难的
19398是电子版的吗?能不能发上来?
19398那位大虾知道在哪里能找到这本书呀?
19400各位大侠,我想考经济类的数理统计专业,初试时只需要考数分高代概率的,不知道哪些学校有这样的专业阿?可否相告。
19400你可以看下人大的统计学院,不过那里的竞争爆激烈哦!
19401想问一下,什么地方可以买或邮购?
19401九章数学书店
jiuzhang.chiuchang.com.tw/books.php
19401我有,怎么联系你?
19401如果方便的话,请发给我一份,先谢谢了!我的电子邮箱如下:
pgser@126.com。
19401我也希望能够有一份,希望有的朋友发给我一份,十分感谢!
joantom@163.com
19401方便的话请给我发一分。谢谢!
19401如果方便的话,请发给我一份,先谢谢了!我的电子邮箱如下:
litingtime@yahoo.com.cn
19401多谢诸位了,我已经在芜湖的步行街的新华书店买了一本.大致的翻了一下,发现好象参考书目和书中给出的对不上号啊,郁闷!---------敲掉我68个大元的说!
19401我也希望能够有一份,希望有的朋友发给我一份,十分感谢!
jgy_1121@163.com
19401我也想要一份 不知道是否可以給我
我是supermathkimo@yahoo.com.tw
1940105年在广州开会,见过匡继昌本人,问其书后参考文献不对的问题,他说原来是对的,可被排版的人弄错了,不知真假.不过除去这个毛病外,这到是一本很好的参考用书.
19401这本书太厚了,不方便带,认为这本书用来查合适
不知哪里有电子版的?
19401我提供下载地址,诸位自己下吧!
http://tycx.gbaopan.com/Default.aspx?sort=...e5%ad%a6&page=4
19401杭州下沙区,boku书店有售!好象没人去买
19404如果是3位数
A=a*100+b*10+c 和
B=c*100+b*10+c
A-B=99(a-c)
如果是4位数
A=a*1000+b*100+c*10+d 和
B=d*1000+c*100+b*10+c
A-B=999(a-c)+90(b-c)
所以,不论有多少位,总是由系数位(9*10^m-1*10^n)的多个数相加
9*10^m-1*10^n
能被9整除,与它们相乘的数又是个自然数,因此得证
19404任意一个两位或两位以上的数减去这个数的反数,都能被9整除
例如:123的反数是321,依此类推
(321—123)/9=22
(90-09)/9=9
求证此命题为真命题。
19404数论题
19407谢谢了,以后要继续努力啊!
19407数学分析专题研究试题模拟试题及参考答案
post-8-1129467360.ibf
19407还可以,顶一下。
19407比较简单!
19407没有别的什么了吗
19407简单了点吧!!!
19407简单了点
19407很不错的试卷啊
19407顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶██████████顶顶顶顶
顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶████████████████顶顶顶顶
顶顶顶顶顶顶顶顶顶顶████顶顶██████████顶顶顶顶顶顶顶顶顶
顶顶顶顶顶顶████████顶顶██顶顶顶████顶顶顶顶顶顶顶顶顶顶
顶█████████████顶顶顶顶顶顶顶███顶顶顶顶顶顶顶顶顶顶顶
顶███████████顶顶顶顶顶顶顶顶█████████顶顶顶顶顶顶
顶顶█████████顶顶顶顶顶顶顶顶████████████顶顶顶顶
顶顶顶█顶顶顶████顶顶顶顶顶顶████顶顶顶顶顶█████顶顶顶顶
顶顶顶顶顶顶顶顶███顶顶顶顶顶顶██顶顶顶█顶顶顶顶███顶顶顶顶顶
顶顶顶顶顶顶顶顶███顶顶顶顶顶███顶顶顶██顶顶顶███顶顶顶顶顶
顶顶顶顶顶顶顶顶███顶顶顶顶顶███顶顶顶██顶顶顶███顶顶顶顶顶
顶顶顶顶顶顶顶顶███顶顶顶顶顶███顶顶███顶顶顶███顶顶顶顶顶
顶顶顶顶顶顶顶顶███顶顶顶顶顶███顶顶███顶顶顶███顶顶顶顶顶
顶顶顶顶顶顶顶顶███顶顶顶顶顶███顶顶███顶顶顶███顶顶顶顶顶
顶顶顶顶顶顶顶顶███顶顶顶顶顶███顶顶███顶顶顶███顶顶顶顶顶
顶顶顶顶顶顶顶顶███顶顶顶顶顶██顶顶顶██顶顶顶顶███顶顶顶顶顶
顶顶顶顶顶顶顶顶███顶顶顶顶顶██顶顶顶██顶顶顶顶███顶顶顶顶顶
顶顶顶████████顶顶顶顶顶顶█顶顶██顶顶顶顶████顶顶顶顶顶
顶顶顶顶███████顶顶顶顶顶顶顶顶顶██顶顶█顶顶顶██顶顶顶顶顶
顶顶顶顶顶顶█████顶顶顶顶顶顶顶顶███顶顶████顶顶顶顶顶顶顶
顶顶顶顶顶顶顶顶███顶顶顶顶顶顶顶████顶顶顶██████顶顶顶顶
顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶█████顶顶顶顶顶██████顶顶顶
顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶████顶顶顶顶顶顶顶顶█████顶顶顶
顶顶顶顶顶顶顶顶顶顶顶顶顶█████顶顶顶顶顶顶顶顶顶顶████顶顶顶
顶顶顶顶顶顶顶顶顶顶顶顶██顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶██顶顶顶顶
顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶
19407有点简单
19407太简单了点吧,那个学校的考研题目有这么简单呀?我一定考。呵呵。不过还是要谢谢你了,有几个题目还是不错的
19407有点简单,不过还是要谢谢你了
19407既然大家
19407比较一般阿
19407向所有为数学繁荣作出贡献的人致敬!
19407符号看不懂
19407支持!!强烈支持!!谁还有的?我虽主张少弄资料,要少而精.可是有些小题目连练练也是可以的
19407一般
19407谢谢楼主!
19407下载了,谢谢楼主啊。
19407研究个球阿,都是些无聊的问题
19409如题
19410求两算子可换的充要条件
特别的可以限制线性算子均为规范算子,即任意不变子空间都存在不变补空间
19411解出一个参数,代入另一个方程。
19411<!--Math $ $ MathEndBegin--><!--End
Math--> {y(t) = -1/2*g*t^2+v0*sin(

)*t, x(t) =
v0*cos(

)*t}
怎么用maple消去参数t ??
有谁知道请告之,感激不尽!!
19411如果方程很复杂怎么办?
有没有具体的函数可调用的
19412F(x)在(a,b)可导,x

a+0和x

b-0时,F(x)都等于负无穷,则存在c属于(a,b),使得f'©=0,这是根据啥定理,谢谢··
19412应该是罗尔定理吧
19412拉格朗日中值定理
19412以上的说法都正确,罗尔中值是拉氏中值的特例
19414我不知道上面我提出的那个问题是不是有什么不妥的地方,如果有的话,请大家指出来,
我自己现在也被自己搞糊涂了.谢谢大家.
19414我们假设X与Y都是同一概率空间(Ω,F,P)上的两个随机变量,那么X-Y与X(ω)-Y(ω)的
含义是不是相同的?
为什么这么问呢?因为我在温习随机变量序列的收敛的时候发现随机变量序列的收敛性一般
都是这样定义的,例如如果LimP{|Xn(ω)-X(ω)|<ε}=1,那么说变量序列Xn依概率收敛于变量X
再看如果Fn(x)→F(x),则说变量序列Xn依分布收敛于X.
我们仔细看看上面的定义,他们都是以Xn(ω),X(ω)来表达的.但是平时我们也经常遇到做两
个随机变量的差和积商等运算的情况,那么这两种情况表达的是不是同一个意思呢?
我们知道随机变量序列的收敛性描叙的是一个变量序列变化的最终趋势,但是随机变量实际
也是一个函数,它是以样本点为定义域的可测函数,所以说到底,随机变量序列也是一个函数
序列,那么随机变量序列的收敛性也就是一个函数序列的收敛性了.这样说没有问题吧!
我们再接着看.一般的函数序列的收敛性定义都是这样的,对于函数序列Fn(x)与F(x),如果
对于任意的x,都有Fn(x)→F(x),那么我们说函数序列Fn(x)收敛于F(x).注意,我
们是以固定点x对应的一个点列的收敛性来定义函数序列的收敛性的.
那么,对于随机变量序列的收敛性,例如LimP{|Xn(ω)-X(ω)|<ε}=1中,Xn(ω)-X(ω)就应该
是对同一个样本点ω而言的,是不是?也就是说,所有满足{|Xn(ω)-X(ω)|<ε}的ω构成的
一个集合首先是属于代数域中的一个元素,同时它的概率是→1的.这样说应该没有问题
吧.
那对于平时我们所说的两个随机变量的加减乘除等运算(X+Y,XY,X/Y...)是
不是也是这样的呢?
19414to
楼主:
先提两点建议:
1.建议复习实变
2.建议复习泛函分析
首先,依概率收敛就是依测度收敛是正确的,但是你没有理解正确,假设u是一个普通测度函数,那么依测度收敛的完整写法是:
lim
n
u(E{x||f(x)-f
n(x)|≥eps})=0
对概率论来说,P{X<x}=F(x)只是一种简写,完整的写法应该是:
P
(E{ω|X(ω)<x})=F(x)
也就是说P是一个测度函数,它的定义域是你那个样本空间上的sigma-域,是一个集合函数
F(x)是分布函数,它的定义域是R,是一个普通函数,这两个是不一样的
其次,依分布收敛,其实是泛函中的弱*收敛,其实如果仔细一点,你会发现依分布收敛用的符号就是弱收敛的符号.至于弱*收敛的定义比较复杂,你可以去看下泛函的书.但是绝对不是固定一个x点来收敛,应该是对任意x
所以,回到你的问题:
X-Y与X(ω)-Y(ω)的含义
这两个的含义是一样的,就好象我们写f(x)-g(x)和f-g是一样的
19414
引用 (子青 @ 2005年10月
17日
12时07分) |
to
楼主:
先提两点建议:
1.建议复习实变
2.建议复习泛函分析
首先,依概率收敛就是依测度收敛是正确的,但是你没有理解正确,假设u是一个普通测度函数,那么依测度收敛的完整写法是:
lim
n
u(E{x||f(x)-f
n(x)|≥eps})=0
对概率论来说,P{X<x}=F(x)只是一种简写,完整的写法应该是:
P
(E{ω|X(ω)<x})=F(x)
也就是说P是一个测度函数,它的定义域是你那个样本空间上的sigma-域,是一个集合函数
F(x)是分布函数,它的定义域是R,是一个普通函数,这两个是不一样的
其次,依分布收敛,其实是泛函中的弱*收敛,其实如果仔细一点,你会发现依分布收敛用的符号就是弱收敛的符号.至于弱*收敛的定义比较复杂,你可以去看下泛函的书.但是绝对不是固定一个x点来收敛,应该是对任意x
所以,回到你的问题:
X-Y与X(ω)-Y(ω)的含义
这两个的含义是一样的,就好象我们写f(x)-g(x)和f-g是一样的
|
谢谢!
俺上午仔细看了相关资料,对X-Y与X(w)-Y(w)的含义基本上明白了.
子青兄知识渊博,佩服!
19415郑大真的很差吗?应用数学怎么样?
考郑大的数学系研究生是不是比较容易?
北科大的数学系难考吗?
请高人指点
19415我只知道郑大的基础数学不错
计算数学现在还可以
19415我准备郑大的计算数学
19415我是郑大的学生!郑大的应用数学是很不错的专业!
19415不怎么样
郑大方程是特色
19424本人学MATHEMATICA,最头痛的事情是在其中录入数据,要是数据少还要说一点,数据一多,
麻烦就大了.哪位大哥大姐有什么方法能解决这个问题,请指点指点小弟!!跪谢!!!!!!!!!!!!!!!1
19424录入数据不都是靠键盘往里敲吗,还能有什么快捷的方法。如果是已有的数据文件,当然直接读入就可以了。
19424
引用 (yuezheng @ 2005年10月
18日
16时44分) |
|
录入数据不都是靠键盘往里敲吗,还能有什么快捷的方法。如果是已有的数据文件,当然直接读入就可以了。
|
大哥,你耍我呢!
MATLAB中有一个连接程序,可以和EXCEL连接后直接从EXCEL中读取数据,MATHEMATICA有没有
类似的功能啊?要是有的话,就免得偶一个一个的从键盘敲了.MATHEMATICA什么都好,就是这
个不好!!如果哪位大哥知道怎么处理这个问题,请告诉小弟一个千万千万!!!!!!!!!!!11
19425Fn(x)→F(x)指的是函数序列的收敛,我想了半天还是不明白它是怎样表达出Xn的收敛性的.
其他几个收敛定义到很好理解.哪位大哥帮忙解释一下!!!!
19425这个是泛函上的弱收敛,去看下泛函
19425
引用 (子青 @ 2005年10月
17日
12时14分) |
| 这个是泛函上的弱收敛,去看下泛函
|
对这个问题,俺也查看过相关的资料,但是基本上所有的资料的对这个问题的解释都不能让
俺满意,所以俺还想对这个问题本身做个更细致的描述.
收敛是什么?直观一点说,收敛就是考察一个序列的趋势:
在LimP{|Xn-X|<ε}=1中,对序列Xn趋势的考察是通过{|Xn-X|<ε}的概率来实现的,|Xn-X|的
距离可以任意变小,但是无论怎么小,只要n足够大,他的概率总可以为一,这样,"|Xn-X|的
距离可以任意变小"就表明了序列Xn的收敛性;
在P{LimXn=X}=1中,这个更容易理解,LimXn=X直接表示了序列Xn的收敛;
在LimE{|Xn-X|
^{r} }=0中,我们用|Xn-X| ^{r} 的平均距离

0来表示序列
收敛;
但是在Fn(x)→F(x)中呢?在这里这种对趋势的表达好象不是很明显,Fn(x)→F(x)只是表示
Xn与X两者的CDF之间有这种极限关系,但是CDF之间存在极限关系好象并不能说明Xn与X之间
就一定也有某种收敛关系啊!
各位大哥能不能替小弟解释这个问题.俺想了好久!
19425哈哈,这个问题俺自己想明白了.
这个弱收敛的含义应该是这样的:自己本身可能没有那么明显的收敛性,可是经过一个函数
加工后却表现出来很明显的收敛性,所以称原来的为弱收敛,弱字就是这个意思,应该是这样
的吧.
19427各位朋友,你们有没有网络安全与模糊数学结合方面的资料或者网站,教材呀?麻烦推荐!
19430对,我打错了
19430分析post-38-1129520681.ibf
19430利用不等式
|lnX1-lnX2|=|ln[1+(X1+X2)/X2]|<=|X1-X2|
其中
X1=X1^sqrt(X1)
X2=X2^sqrt(X2)
19430那如何证明一致收敛性
19430是证明(0,infty)一致连续吧?
19430分成二个区间考虑(0,1]和
[
1,+∞)
,在x=0,
f
(x)=x
lnx
存在极限.在
[
1,+∞)
上
导数有界.
19430
引用 (lchw @ 2005年10月
17日
20时23分) |
分成两个区间考虑 (
0,1] 和 [
1,+∞)
:
f
(x)=x
lnx
在 x
=0 存在极限;
在
[
1,+∞)
上导数有界. |
不用Cantor定理与Lagrange中值定理,
直接用一致连续定义的证明:
对于任意给定的
ε >0
, 存在
δ
(ε)=(ε
1
+1
+2ε)
3 , 使得:
当
| x
1-x
2|<δ(ε)
时, 有
| x
1
lnx
1-x
2
lnx
2|≤2|x
1-x
2|
2 3
+2|x
1-x
2|
1 3
<ε
,
其中, 第一个不等式见:
http://www.mathlinks.ro/viewtopic.php?t=245730所以
f
(x)=x
lnx 在
(
0,,+∞)
上一致连续.
注记
本题被用于三峡大学2006年研究生入学《数学分析》考试第二1题,
它是北京大学2001年研究生入学《数学分析》考试第3题的延拓.
19430
引用 (ji23 @ 2008年12月
19日
01时03分) |
引用 (lchw @ 2005年10月
17日
20时23分) | 分成两个区间考虑 (
0,1] 和 [
1,+∞)
:
f
(x)=x
lnx
在 x
=0 存在极限;
在
[
1,+∞)
上导数有界. |
不用Cantor定理与Lagrange中值定理,
直接用一致连续定义的证明: 对于任意给定的 ε >0
, 存在 δ
(ε)=(ε
1
+1
+2ε)
3 , 使得: 当 | x
1-x
2|<δ(ε)
时, 有 | x
1
lnx
1-x
2
lnx
2|≤2|x
1-x
2|
2 3
+2|x
1-x
2|
1 3
<ε
, 其中, 第一个不等式见: http://www.mathlinks.ro/viewtopic.php?t=245730所以 f
(x)=x
lnx 在 (
0,,+∞)
上一致连续. 注记
本题被用于三峡大学2006年研究生入学《数学分析》考试第二1题, 它是北京大学2001年研究生入学《数学分析》考试第3题的延拓.
|
怎么可能一致连续?导数在正无穷远处的极限为正无穷!
19430取x_n=n, y_n=n+1/(ln n),则y_n-x_n\to 0, f(y_n)-f(x_n)\to
1(n\to \infty). 从而不一致连续.
19430 f
(x)=x
lnx 及其导函数 f `
(x)=2
+lnx2
x
的图像:post-38-1229649227.jpg
19430导数算错了吧?
19430
引用 (Hansschwarzkopf @ 2008年12月
19日
09时16分) |
| 导数算错了吧? |
要知道算错总是难免的
在每一个梦醒时分

19431论坛设置了灌水限制,请等待 60 秒后再发帖子, 郁闷
part 6post-61-1129523453.ibf
19431最后一部分post-61-1129523563.ibf
19431djvu格式, 本论坛上有阅读器.
另外求助以下文献:
O. Christensen 的 An introduction
to frames and Riesz Bases 这本书.
和
http://www.jstor.org/journals/00029939.html
的用户或代理服务器.
可发送到bmyuu@hotmail.compost-61-1129522753.ibf
19431附件只能上传512K, 太小了 :(post-61-1129522932.ibf
19431part 3post-61-1129523027.ibf
19431part 4post-61-1129523109.ibf
19431part 5post-61-1129523255.ibf
19432an

0 lim
inf(1/an)/lnn>1

an 的敛散性
19433我要报的学校,比较好的导师研究方向是微分方程应用,细胞神经网络及应用,线形和非线性系统,计算机图形学,混沌和适应控制,我不知该选哪一个,每个方向都具体做什么?前景怎样?恳请帮助!
19433金融
19433还是要看你喜欢什么了啊!喜欢什么就选 什么啊!考上了以后是进去深造啊!
19434
何梁何利基金2005年度颁奖大会前天在上海国际会议中心隆重举行。中共中央政治局委员、上海市委书记陈良宇为荣获“科学与技术成就奖”的杰出科学家徐光宪、谷超豪颁奖。
何梁何利基金是由香港爱国金融实业家何善衡、梁?琚、何添、利国伟先生共同捐资创建的公益性科技奖励基金。这次获奖的47位科学家中,除徐光宪、谷超豪外,其余45位获得“科学与技术进步奖”。
谷超豪,著名数学家,
1926年5月生于浙江温州。浙江大学本科毕业、莫斯科大学博士、中国科学院院士、复旦大学教授。谷超豪院士在50多年科研生涯中,在纯粹数学和应用数学领域做出多项开拓性工作。
post-52-1129523698.jpg
19435附件post-38-1129523847.gif
19435是不是论坛出问题了,老是提示我没有发出去,回头一看发了这么多
回复:发贴后耐心等待,刷新后再看看.
19435帮忙做一下啊
19435(1)->(2)利用对称矩阵的半正定性
(2)->(1)利用r(A)+r(B)>=r(A+B)的相关定理
19435能不能详细点啊
19435
1
)⇒2)∵A
i 幂等,
令
R (A i
)=r
i
,则存在可逆矩阵
T
i
,使
T
i - 1
A i
T i
=[E
r i
0
0 0
]
∴ trA i
=r
i
=R(A
i ) ,于是
R
(A 1
)+⋅ ⋅
⋅+R(A
k
)=tr(A
1
)+⋅ ⋅
⋅+tr(A
k
)=tr(A
1 +⋅ ⋅
⋅+A k
)=tr(E)=n
2
)⇒1)
也可用线性空间理论证明。
19435帮忙看看
2-->1怎么做啊
19435怎么做啊?????????????????????????????
19435A为幂等阵的充要条件是秩(A)+秩(E-A)=n
n=秩(Ai+E-Ai)<=秩(Ai)+秩(E-Ai)<=秩(Ai)+秩(A1+A2+……+Ai-1+Ai+1+……+As)<=秩(Ai)+秩(A1)+秩(A2)+……+秩(Ai-1)+秩(Ai+1)+……+秩(As)=n
所以秩(Ai)+秩(E-Ai)=n,i=1,2,……,s.
则Ai为幂等阵,i=1,2,……,s.
19435不好意思,那是k不是s.
19435好像钱吉林的高代书上有
19439请解答这道题:
设f(x),g(x)和h(x)是实多项式。证明:若有f^2(x)=xg^2(x)+xh^2(x).则f(x)=g(x)=h(x)=0
19439看首项次数 左边为偶数,右边为奇数
19440看看这个post-38-1129524384.gif
19440因为A可逆,所以与A等价当且仅当可逆!在与A等价的矩阵中,正惯性指数为2的与A合同!因为A的特征值互异,所以与A相似当且仅当与A特征值相同!
19441由于论坛一些id长期不用占用资源,我们近期将开展清理工作.
请大家注意,我们将于2005年10月25日清理掉那些长期不登陆论坛的会员ID,一般清理以下两种ID:
1、连续超过一年未登陆论坛.
2、连续超过一年在论坛未发言的ID.
清除ID是手动进行的,请会员们务必注意,如果您有上述二种情况的话,你的ID很可能就会被清理掉!请相互转告,并请尽快登陆论坛去成员交流室发帖确认您还将使用这个帐号.
如果会员有什么特殊原因请事先说明情况并申请保留您的注册ID,谢谢!
19441不好意思,我现在上网不方便,一般在网吧上,所以常用游客身份浏览家园。不要删我的ID哦 $_*
19441前一段时间(国庆期间),这个网站老是登陆不了,显示“找不到服务器”。是不是这里国庆也要放假?
19441
引用 (呼呼 @ 2005年10月
17日
12时58分) |
由于论坛一些id长期不用占用资源,我们近期将开展清理工作.
请大家注意,我们将于2005年10月25日清理掉那些长期不登陆论坛的会员ID,一般清理以下两种ID:
1、连续超过一年未登陆论坛.
2、连续超过一年在论坛未发言的ID.
清除ID是手动进行的,请会员们务必注意,如果您有上述二种情况的话,你的ID很可能就会被清理掉!请相互转告,并请尽快登陆论坛去成员交流室发帖确认您还将使用这个帐号.
如果会员有什么特殊原因请事先说明情况并申请保留您的注册ID,谢谢!
|
晕,幸好我今天来了一下
我现在一般只是潜水的啦
希望不要删除哟~~~
19441Support the action!
I think it is essential for a good
forum to encourage menbers to interact actively.
19441fayan to avoid be cleared. hehe
19441别删我啊!不过我好像不在你说的两种情况之一
19441刚上油香看到了,我最近很多课,有点忙.
不要删我哦.
19441这样做不好,大家都不是来玩的,有人没发贴是因为多种情况,但若要封ID就太小肚鸡肠了,大家都想到这来学东西嘛,一年没登录的人也许可能是不想来了,但一年没发贴的能说不用了吗?
19441鼎立支持!!!
19441对呀,没什么东西可写,就是来感受一下数学氛围,不行吗?
19441我支持,我们需要一些真正爱数学的同志在论坛里交流。
而不是来这里逛逛的。所以我顶。
19441但是怎么知道哪些号码长时间不用呢?其标志是什么?怎样鉴定?
19441像我这样学其它专业的的数学爱好者的确有长时间未登陆家园的情况,当然也有经常登陆而很少发言的情况。希望论坛管理人员能够进一步斟酌,尽可能让大家都满意。谢谢!
19441明白
19441不要删除啊!!!
19441保留帐户啊!虽然俺基本潜水!
19441哦了!这个算是发言了!
19441知道了,以后会常来并发言的!^.^
19441收到!~~~
19441非常明白和支持!!!!!!!!
19441明白,支持
19441不要删除我的ID啊
我现在有点忙 学习任务有点重
19443代数和几何重数一致。
19443附件:post-38-1129525297.ibf
19443我说说我的想法
存在正交矩阵O,使得
O'AO=diag(入,...,入,入1,入2,...,入n-r)
r(入E-A)=r(O'(入E-A)O)=r(入E-diag(入,...,入,入1,入2,...,入n-r))
=diag(0,...,0,入1-入,入2-入,...,入n-r-入)
似乎条件不太够,还是我做的不对
19446sin(n)的极限不存在,怎样证明?希望大虾给于说明,先谢了!
19446反证法,利用三角公式sin(n+1)=sinncos1+cosnsin1即可!
19446不明白,能否再解释得清楚一点?
19446反证法:设limsinn存在且等于

,则可证

不等于0(否则limcosn=
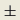
1,由sin(n+1)=sinncos1+cosnsin1,取极限得到
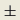
sin1=0,矛盾!)
则由sin(n+1)=sinncos1+cosnsin1,

=sqrt(0.5ctg0.5),
由sin(n+0.5)=sinncos0.5+cosnsin0.5,将

=sqrt(0.5ctg0.5)代入上式即导出矛盾!
19446wonderful
19446我认为sinn中n应该为整数,sin(n+0.5)极限应该怎么说呢?
19446可以证明集合{sin(n)}的闭包为[-1,1], 见周民强的《实变函数论》(北京大学出版社,2001版)第37页的例5中
19446
引用 (magic9901 @ 2005年10月
18日
09时49分) |
反证法:设limsinn存在且等于
 ,则可证 ,则可证
 不等于0(否则limcosn=
不等于0(否则limcosn= 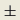 1,由sin(n+1)=sinncos1+cosnsin1,取极限得到
1,由sin(n+1)=sinncos1+cosnsin1,取极限得到 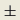 sin1=0,矛盾!)
sin1=0,矛盾!)
则由sin(n+1)=sinncos1+cosnsin1,  =sqrt(0.5ctg0.5),
=sqrt(0.5ctg0.5),
由sin(n+2)=sinncos2+cosnsin2,将  =sqrt(0.5ctg0.5)代入上式即导出矛盾! =sqrt(0.5ctg0.5)代入上式即导出矛盾!
|
sin(n+0.5)改成sin(n+2)
19446[/QUOTE]magic9901 发帖时间 2005年10月
18日 09时49分
反证法:设limsinn存在且等于 ,则可证
不等于0(否则limcosn= 1,由sin(n+1)=sinncos1+cosnsin1,取极限得到
sin1=0,矛盾!)[QUOTE]
再用sin2n=2sinn*cosn sin4n=2sin2n*cos2n 可得sinn收敛于0矛盾!
19446lim (sinn/n) = 1 (n->inf) ( * )
if lim(sin n ) = alpha and
alpha is some constant
lim (sinn/n) = 0 which contradicts with ( * )
.
according to the l'hopital law , lim(sinn) = inf
.
这样行吗
19446可以参见有关书籍,可以证明sin(n)在[-1,1]上稠密..当然无极限
19446还有一种方法是用cauchy 法则,即存在两个子列收敛于不同的极限.
19446你可以采用反证法啊!可以令n1=k*PI,再让n1趋于无穷大,也即k趋于无穷大!的到结果为0,另外,你再让n2=2*k*PI+PI/2,同样采用上面的方法,得到极限为1。由于0不等于1,从而得到极限不相等啊!也就得到极限不存在啊!
19448心灵的拓扑
毛光寿
(注:蓝色的字系拓扑学术语)
因为平庸
才想到自我提升
终于有一天
发现新的轨道空间
找到了理想的邻域
放松的神经
开始出现自由的生成元
那天傍晚
头戴交叉帽
漫步初阳湖的边缘
思绪就像无理流
眼神犹如泛宇宙天线
一位女孩
身穿纽结群
腰系Mobius带
胸前有个三瓣扭结
一副精致的夏威夷耳环
迎面而来
又投影而去
她
立刻成了心的向量场
我的目光回转
心脏急剧收缩
脸皮快速加厚
转步向她单纯逼近
突然
一个滑动反射
手中的Klein瓶
掉
落
同胚
不再是粘合空间
同构
成了单纯剖分
我俩同调
合作剜补
根据同伦
送去焊接
尽管粗野纽结
增厚
但是组合曲面
依然连通
小心翼翼地给复迭空间
完全闭包
用懒散结
装饰覆盖
外系同心结
迟了
她请我吃火腿三明治
眼神有了示性数
不管离散子群
忘却亏格
相悦的网距在拉近
脑中嵌入
Poincare猜想
19449分析post-38-1129530053.ibf
19450请教老师: 已知通解的情况下如何求“原微分方程”?详细步骤是什么,我查了很多书没查到。 能不能用这道题演示一下?
y=Cx/2
+1 (分母是2,Cx/2是个整体再加1)
非常感谢。
19450顺道的疑问:知道方程的解,求出的原方程唯一吗?积分行吗?
19450我找到了一个微分方程.大家指教.post-8-1129561061.gif
19450题的答案是y'-y/x=-1/x
也不知道是怎么得出来的,大家都不会做这种题吗?反正一般的高等数学教材上都没有。
哪位会的给指导一下,谢谢
19450这不就是上面的那个吗?!
19450哦,移项后是的,请问你是怎么做出来的?能说一下具体步骤和思路吗?谢谢
19450原则上是从f(x,y,c)=0解出c=g(x,y),dg/dx=0就是所需的方程,如果解里有n个常数,表示这是n阶方程的解,可以引进y的n-1阶以下导数作为“已知量”来解出那些常数。
举个例子:
y=Asinx+Bcosx,有两个任意常数,可以对原方程求导一次得y'=Acosx-Bsinx,联立解得
A=ysinx+y'cosx,B=ycosx-y'sinx,求导得(y+y'')cosx=0,(y+y'')sinx=0,等价于y+y''=0。
具体操作时可以各显神通,不必拘泥。但是切记常数的个数决定最后结果的阶数。
19450谢谢大家,终于会做了,高兴ing ....
19450看来,新手都往这里逛呀
19451应该是-99的阶乘
19451请教老师:
f(x)=(x-1)(x-2)(x-3)...(x-100)
求f(x)的导数
这个怎么做呀?请老师给个思路。谢谢。
19451对数求导法:对f(x)取对数得,lnf(x)=
ln(x-1)+ln(x-2)+...+ln(x-100),
再求导就有:f'(x)/f(x)=1/(x-1)+1/(x-2)+...+1/(x-100)
然后整理就得到导数f'(x)
19451谢谢magic9901朋友,对数求导法理解了,这道题最后是让求f'(1),那答案是多少呀?谢谢,第一项中就有1/(x-1)当x=1时这项无意义了,怎么办呀?
19451-99!
19451f'(x)=[1/(x-1)+1/(x-2)+...+1/(x-100)]f(x)其中除了第一项外均含有X-1则都为0:)则可知结果为-99!
19451谢谢大家,明白了,要把f(x)代进去了。谢谢
19452K是n维欧式空间的一点集,若任意两点X1

K,x2

K
请问为什么

x1+

x2是x1,x2两点连线上的点呢 (注


[0,1])

不是0到1行吗?请说明白。谢谢。
脑子一下想不出来了
19452你是不是打错了?系数怎么都是u?有一个是(1-u)吧?如果是的话就好办了,
那个式子代表连接两点的凸包,就是两点间的线段,解析几何里应该有解释,
我忘了为什么了~你翻翻书。
如果不是0到1,就表示线段以外的点了。
19453形如:
min=

(xi-ci),
(i=1,2,......n)
st.
xi+ai

di;
xi

ci;
(i=1,2,......n)
(xj-xi+aj)*(xi-xj+ai)

0;
(i=1,2.....n-1;j=i+1,i+2,......n)
( n*(n+1)/2个非线性约束
)
的规划问题,可以用很多算法求解,比如内点法,外点法,变尺度法等,哪一种算法求解效率最高,速度最快?
或者有什么算法可以专门求解类似于上述形式的规划问题?要求其求解速度和Lingo相当或更快?本人寻求这样的源代码,请高手帮助!!!!!!!!!!!!!
实在不行,罚函数的C程序也可以,希望程序是完全正确的,不需要再改来改去,呵呵
QQ:229623684
19453偶也在做一个关于罚函数的问题!不过我不是学数学的,是学机械的,请大家帮一下忙,推荐一下解罚函数类问题有什么好的办法?谢谢!
我得QQ:37470575。欢迎大家指导!
19454哪位知道下载张量分析电子教程的网址啊,http的行,ftp的也可以.谢谢了
19455婚前
女:你原先有过女朋友?
男:十年生死两茫茫,不思量,自难忘。
女:死了?怎么死的?
男:山天陵,江水为竭,冬雷阵阵夏雨雪。
女:喔,是天灾。那这些年你怎么过来的?
男:满面尘灰烟火色,两手苍苍十指黑。
女;唉,不容易。那么你看见我的第一感觉是什么?
男:忽如-夜春风来,千树万树梨花开。
女:(红着脸)有那么好?
男:糟粕所传非粹美,丹青难写是精神。
女:马屁精--你有理想吗?
男:他年若遂凌云志,敢笑黄巢不丈夫。
女:你……对爱情的看法呢?
男:只在此山中,云深不知处。
女:那你喜欢读书吗?
男:军书十二卷,卷卷有爷名!
女:这十吹大了吧?你那么大才华,怎么还独身?
男:小姑未嫁身如寄,莲子心多苦自知。
女:(笑)假如,我是说假如,我答应嫁给你,你打算怎样待我?
男:一片冰心在玉壶!
女:你保证不会对别的女人动心?
男:波澜誓不起,妾心古井水。
女:暂且信你一回,不过,我正打算去美国念书,你能等我吗?
男:宁饮建业水,不食武昌鱼,宁还建业死,不止武昌居。
女:不过……
男:独自凭栏,无限江山,别时容易见时难!
女:但是…….
男:望夫处,江悠悠,化为石,不回头!
女;好了好了,怕了你………
婚后
女:结婚那么久,你还在想你原先妁女朋友?
男:曾经沧海难为水,除却巫山不是云。
女:那为什么当年还和我结婚?
男:梦里不知身是客,一晌贪欢。
女:太过分了吧。我们好歹是夫妻。
男:夫妻本是同林鸟,大难临头各自飞。
女:那我们这段婚姻,你怎么看?
男:醒来几向楚巾看,梦觉尚心寒!
女:有那么惨吗?你不是说对我的第一印象……
男:美女如花满春殿,身边惟有鹧鸪飞。
女:不是这么说的吧,难道,你竟然……
男:昔日龌龊不足夸,今朝放荡思无涯。
女:一直以来朋友写信告诉我我都不相信,没想到竟是真的!
男:纸上得来终觉浅,绝知此事要躬行。
女:你原先的理想都到哪儿去了?
男:且把浮名,换了斟低唱。
女:(泪眼朦胧)你,你不是答应一片冰心的吗?
男:不忍见此物,焚之已成灰。
女:你就不怕亲朋耻笑,后世唾骂?
男:宁可抱香枝头死,何曾吹落北风中。
女:我要不同意分手呢?
男:分手尚且为兄弟,何必非做骨肉亲。
女:好,够绝
19455好像有点无聊呀,真是的,呵呵,随便看看,发点水,换点考卷
19455好像有点无聊
不过支持下
19455像有点无聊呀,真是的,呵呵,随便看看,发点水,换点考卷
19455像有点无聊呀,真是的,呵呵,随便看看,发点水,换点考卷
19455呵呵,可能婚前婚后有些不同,但应该不会是这样吧!
19455广大单身们还是应该持乐观态度的!当然也包括我自己!
19455呵呵 挺强
19455不是吧?
19455有点看头!原来古诗这么有味道!
19455有点诗意!
19455呵呵,
19455
顶一下
19455
顶
19455
顶
19455上帝!
19455楼主知道的诗词可不少啊!
19455厉害
19455不错
19455能把古典诗词用得如此精妙,不容易啊
19455够无聊!
19455有文才啊,,小弟我灌水来了
19455有点晕,看不太懂
19455还不错呀,好搞../
19456入题
19457
+ plus 加号;正号
- minus 减号;负号
± plus or minus 正负号
× is
multiplied by 乘号
÷ is divided by 除号
= is equal to 等于号
≠ is not
equal to 不等于号
≡ is equivalent to 全等于号
≌ is equal to or approximately
equal to 等于或约等于号
≈ is approximately equal to 约等于号
< is less
than 小于号
> is more than 大于号
≮ is not less than 不小于号
≯ is not more
than 不大于号
≤ is less than or equal to 小于或等于号
≥ is more than or equal
to 大于或等于号
% per cent 百分之…
‰ per
mill 千分之…
∞ infinity 无限大号
∝ varies as 与…成比例
√ (square)
root 平方根
∵ since; because 因为
∴ hence 所以
∷ equals, as
(proportion) 等于,成比例
∠ angle 角
⌒ semicircle 半圆
⊙ circle 圆
○ circumference 圆周
π pi
圆周率
△ triangle 三角形
⊥ perpendicular to 垂直于
∪ union
of 并,合集
∩ intersection of 交,通集
∫ the integral of …的积分
∑ (sigma)
summation of 总和
° degree 度
′ minute 分
″ second 秒
℃ Celsius
system 摄氏度
{ open brace, open curly 左花括号
} close brace, close
curly 右花括号
( open parenthesis, open paren 左圆括号
) close parenthesis,
close paren 右圆括号
() brakets/ parentheses 括号
[ open bracket
左方括号
] close bracket 右方括号
[] square brackets 方括号
. period,
dot 句号,点
| vertical bar, vertical virgule 竖线
& ampersand, and,
reference, ref 和,引用
* asterisk, multiply, star,
pointer 星号,乘号,星,指针
/ slash, divide, oblique 斜线,斜杠,除号
// slash-slash,
comment 双斜线,注释符
# pound 井号
\ backslash, sometimes
escape 反斜线转义符,有时表示转义符或续行符
~ tilde 波浪符
. full
stop 句号
, comma 逗号
: colon 冒号
; semicolon 分号
? question
mark 问号
! exclamation mark (英式英语) exclamation point
(美式英语)
' apostrophe 撇号
- hyphen 连字号
-- dash 破折号
... dots/
ellipsis 省略号
" single quotation marks 单引号
"" double
quotation marks 双引号
‖ parallel 双线号
& ampersand = and
~ swung
dash 代字号
§ section; division 分节号
→ arrow 箭号
19457数学 mathematics, maths(BrE), math(AmE)
公理 axiom
定理 theorem
计算 calculation
运算 operation
证明 prove
假设 hypothesis,
hypotheses(pl.)
命题 proposition
算术 arithmetic
加 plus(prep.),
add(v.), addition(n.)
被加数 augend, summand
加数 addend
和 sum
减 minus(prep.), subtract(v.), subtraction(n.)
被减数 minuend
减数
subtrahend
差 remainder
乘 times(prep.), multiply(v.),
multiplication(n.)
被乘数 multiplicand, faciend
乘数 multiplicator
积 product
除 divided by(prep.), divide(v.), division(n.)
被除数
dividend
除数 divisor
商 quotient
等于 equals, is equal to, is
equivalent to
大于 is greater than
小于 is lesser than
大于等于 is
equal or greater than
小于等于 is equal or lesser than
运算符 operator
平均数mean
算术平均数arithmatic mean
几何平均数geometric mean n个数之积的n次方根
倒数(reciprocal) x的倒数为1/x
有理数 rational number
无理数 irrational
number
实数 real number
虚数 imaginary number
数字 digit
数
number
自然数 natural number
整数 integer
小数 decimal
小数点
decimal point
分数 fraction
分子 numerator
分母 denominator
比
ratio
正 positive
负 negative
零 null, zero, nought, nil
十进制
decimal system
二进制 binary system
十六进制 hexadecimal system
权
weight, significance
进位 carry
截尾 truncation
四舍五入 round
下舍入
round down
上舍入 round up
有效数字 significant digit
无效数字
insignificant digit
代数 algebra
公式 formula, formulae(pl.)
单项式
monomial
多项式 polynomial, multinomial
系数 coefficient
未知数
unknown, x-factor, y-factor, z-factor
等式,方程式 equation
一次方程 simple
equation
二次方程 quadratic equation
三次方程 cubic equation
四次方程
quartic equation
不等式 inequation
阶乘 factorial
对数 logarithm
指数,幂 exponent
乘方 power
二次方,平方 square
三次方,立方 cube
四次方
the power of four, the fourth power
n次方 the power of n, the nth power
开方 evolution, extraction
二次方根,平方根 square root
三次方根,立方根 cube
root
四次方根 the root of four, the fourth root
n次方根 the root of n,
the nth root
sqrt(2)=1.414
sqrt(3)=1.732
sqrt(5)=2.236
常量
constant
变量 variable
坐标系 coordinates
坐标轴 x-axis, y-axis,
z-axis
横坐标 x-coordinate
纵坐标 y-coordinate
原点 origin
象限quadrant
截距(有正负之分)intercede
(方程的)解solution
几何geometry
点
point
线 line
面 plane
体 solid
线段 segment
射线 radial
平行 parallel
相交 intersect
角 angle
角度 degree
弧度 radian
锐角 acute angle
直角 right angle
钝角 obtuse angle
平角 straight
angle
周角 perigon
底 base
边 side
高 height
三角形 triangle
锐角三角形 acute triangle
直角三角形 right triangle
直角边 leg
斜边
hypotenuse
勾股定理 Pythagorean theorem
钝角三角形 obtuse triangle
不等边三角形 scalene triangle
等腰三角形 isosceles triangle
等边三角形
equilateral triangle
四边形 quadrilateral
平行四边形 parallelogram
矩形
rectangle
长 length
宽 width
周长 perimeter
面积 area
相似
similar
全等 congruent
三角 trigonometry
正弦 sine
余弦 cosine
正切 tangent
余切 cotangent
正割 secant
余割 cosecant
反正弦 arc
sine
反余弦 arc cosine
反正切 arc tangent
反余切 arc cotangent
反正割
arc secant
反余割 arc cosecant
补充:
集合aggregate
元素 element
空集 void
子集 subset
交集 intersection
并集 union
补集
complement
映射 mapping
函数 function
定义域 domain, field of
definition
值域 range
单调性 monotonicity
奇偶性 parity
周期性
periodicity
图象 image
数列,级数 series
微积分 calculus
微分
differential
导数 derivative
极限 limit
无穷大 infinite(a.)
infinity(n.)
无穷小 infinitesimal
积分 integral
定积分 definite
integral
不定积分 indefinite integral
复数 complex number
矩阵 matrix
行列式 determinant
圆 circle
圆心 centre(BrE), center(AmE)
半径 radius
直径 diameter
圆周率 pi
弧 arc
半圆 semicircle
扇形 sector
环 ring
椭圆 ellipse
圆周 circumference
轨迹 locus,
loca(pl.)
平行六面体 parallelepiped
立方体 cube
七面体 heptahedron
八面体 octahedron
九面体 enneahedron
十面体 decahedron
十一面体
hendecahedron
十二面体 dodecahedron
二十面体 icosahedron
多面体
polyhedron
旋转 rotation
轴 axis
球 sphere
半球 hemisphere
底面 undersurface
表面积 surface area
体积 volume
空间 space
双曲线 hyperbola
抛物线 parabola
四面体 tetrahedron
五面体 pentahedron
六面体 hexahedron菱形 rhomb, rhombus, rhombi(pl.), diamond
正方形 square
梯形 trapezoid
直角梯形 right trapezoid
等腰梯形 isosceles trapezoid
五边形 pentagon
六边形 hexagon
七边形 heptagon
八边形 octagon
九边形
enneagon
十边形 decagon
十一边形 hendecagon
十二边形 dodecagon
多边形
polygon
正多边形 equilateral polygon
相位 phase
周期 period
振幅
amplitude
内心 incentre(BrE), incenter(AmE)
外心 excentre(BrE),
excenter(AmE)
旁心 escentre(BrE), escenter(AmE)
垂心 orthocentre(BrE),
orthocenter(AmE)
重心 barycentre(BrE), barycenter(AmE)
内切圆 inscribed
circle
外切圆 circumcircle
统计 statistics
平均数 average
加权平均数
weighted average
方差 variance
标准差 root-mean-square deviation,
standard deviation
比例 propotion
百分比 percent
百分点 percentage
百分位数 percentile
排列 permutation
组合 combination
概率,或然率
probability
分布 distribution
正态分布 normal distribution
非正态分布
abnormal distribution
图表 graph
条形统计图 bar graph
柱形统计图 histogram
折线统计图 broken line graph
曲线统计图 curve diagram
扇形统计图 pie
diagram
19457很有耐心
19457鼎力支持
19457强烈支持啊!
19457辛苦了,呵呵!
19457非常好!
19459当x趋向于0时求{[(cosx)^2][(sinx)^2]-(x^2)[(1-x^2)^(4/3)]}/(x^6)的极限。我除了洛比塔法则外,一点别的想法也没有。可用洛比塔法则可能是一个浩大工程。泰勒公式?
19459用阶的估计的方法可以简化运算
19459泰勒公式可以,这是一个万能的公式
19459首先谢谢你们的回复:)
但请问阶的估计的方法具体怎么用啊。谢谢
19460请教:对于给定的一个一般分布函数F(X),要在MATLAB中产生他的随机数,
除了通常根据定义:1。先产生均匀分布的随机数,
2。在F的定义域内取适当的格子点(通常较大,至少是几百)
3。根据格子点和均匀数筛选出随机数。
可是这样做,如果程序要模拟几百/千次,实在太慢了,
请问大家有没有比较优化的算法,提高速度,谢谢了!
如果F稍微特殊一点呢,是混合分布,或更特别一点,是混合正态分布。
19460不太明白你的意思,F是一维连续的吧?这样产生了一个均匀分布的样本
经过变换就得到了一个来自F的样本。你需要多少个样本就抽取多少个,需要
得多当然抽的多
如果是混合正态分布,抽样分两步,首先按混合比例确定(随机的)下一步
应该从哪个正态分布里抽
第二步就是从相应的正态分布里抽取
19460比方说是混合正态分布,其分布函数为F:
F(X)=P*F1(X,A1,B1)+F2(X,A2,B2)
其中P为(0,1)之间的常数,F1,F2分别是均值为A1,A2
协方差阵为B1,B2的
正态分布函数。
请问该怎样抽?
我觉得,若按你说的方法,所抽取的仍是正态分布。
但混合正态分布一般不是正态分布(只在很特殊的情况才会是正态的)
不知该怎样处理交好?
19460对混合正态分布的分布函数为F,不容易求其反函数,没显式表达式。
19460如果分布函数为F(X)=p*F1(X,A1,B1)+(1-p)*F2(X,A2,B2)
先抽取[0.1]上的均匀随机数u,如果u\in
[0,p],则抽取z服从F1
如果u\in
[1-p,1],则抽取z服从F2,
这样分两步抽取的z就服从你那个混合分布F
你可以证明
其实很容易
P(z<x)=P(z<x.u\in[0,p])+P(z<x,u\in[1-p,1])
=P(u\in[0,p])*P(z<x|u\in[0,p])+P(u\in[1-p,1])*P(z<x|u\in[1-p,1])
=pF1(x)+(1-p)F2(x)
19460是的,果然如你所说。
当初是我理解错了。非常感谢!
1946110件产品中有4件次品,现在逐个进行检查,则不连续出现2个次品的概率是多少?
我在解时想:
1、10个产品的全排列是10!
2、只有3个次品在一起的全排列是:6!*(4*3*2/3*2*1)*3!*7*6
3、4个次品在一起的全排列是:6!*4!*7
4、2个次品在一起,另2个次品也在一起的全排列:6!*(4*3/2*1)*2!*7*2!*6
5、2个次品在一起,另2个次品不在一起的全排列:6!*(4*3/2*1)*2!*7*2*6*5
但这样明显是不对的,单第5个就大于第一个了,请大家指教,我的概率比较差,敬请各位大侠详述,谢谢!
19461请大家不吝赐教,谢谢!
19461我的想法是这样的,可以把剩下的六个正品排成一排,中间还有两头共有7个位置可以随机的放次品,这就相当于把4个小球放进7个盒子里,但盒子中的小球个数不多1
的概率,此概率很容易计算,等于7*9*5*4/7^4,不知你是否满意这样解释
19461不管什么情况都必须检查完10件产品么?
如果是的,则用上面同学的方法
P=(
6!*(7!/3!))/(10!)
19461谢谢你们,你们的解法讲得很清楚,我明白了:)
19462请问谁有华中科技05 年高代,分析的答案 ??
非常感谢
19462华工的考题大部分在钱吉林的《数学分析精粹》都能找到。
19462
你可以在下列链接中找到华中科大2005年高代、数分试题答案:
http://www.math.org.cn/forums/index.php?show...ndpost&p=112072http://www.math.org.cn/forums/index.php?show...ndpost&p=1
17106
19465已知X

N(u,a^2), Y

N(2u,b^2),X与Y相互独立,而且P(X

-1)=1/4,则P{max(x,y)

2,min(x,y)

-1}=?
我解时认为P{max(x,y)

2,min(x,y)

-1}=P{max(x,y)

2}P{min(x,y)

-1}
=p(x

2)P(y

-1)=1/2*1/2=1/4
因为max(x,y)和min(x,y)在x,y相等或不等的情况下都可一个取X另一个取Y、
请问这样解错在哪里了?怎么解才正确呢?
19465请大家不吝赐教,谢谢!
19465max(x,y)与 min(x,y)是不独立的,你将他们当作独立的来求
19465首先谢谢您的回复:)
我是想在max(x,y)与 min(x,y)中肯定是一个取X一个取Y,而XY是相互独立的,我才这么做的?
19465
| 引用 (xzdrainbow @ 2005年10月28日
08时13分) |
首先谢谢您的回复:)
我是想在max(x,y)与 min(x,y)中肯定是一个取X一个取Y,而XY是相互独立的,我才这么做的?
|
但可能有时取x,有时取y啊, 你这个是一个顺序统计量, 两个不是独立的.
19465其实你就可以直接分情况讨论的
p(max<2min<-1)=p(x<y,y<2x,2x<-1)+p(y<x,x<2y,2y<-1)
(由于不太会用这里的符号所以改用<号
其实结论是一样的 因为独立的
而且正态分布是连续分布)
之后就属于纯粹计算了
比如p(x<y,y<2x,2x<-1)=E[p(t<y<2t)|x=t,2x<-1]
就可以了
19465我的做法如下:
P{max(X,Y)<=2,min(X,Y)<=-1}
=P{max(X,Y)<=2}-P{max(X,Y)<=2,min(X,Y)>-1}
=P{X<=2,Y<=2}-P{X<=2,Y<=2,X>-1,Y>-1}
=P{X<=2}P{Y<=2}-P{<-1X<=2}P{-1<Y<=2}
接下来的就好做了.
不知道有没有问题
19465啊 不好意思 我看错题目了
看成了 max(x,y)<2min(x,y)<-1 了
楼上的解法是对的
19465
| 引用 (子青 @ 2005年10月28日
15时14分) |
| 引用 (xzdrainbow @ 2005年10月28日
08时13分) |
首先谢谢您的回复:)
我是想在max(x,y)与 min(x,y)中肯定是一个取X一个取Y,而XY是相互独立的,我才这么做的?
|
但可能有时取x,有时取y啊, 你这个是一个顺序统计量, 两个不是独立的.
|
所谓独立,可以理解彼此互不影响,其一是否发生,对其二并不影响。对于最大与最小这二个事件,如果前面发生结果,在势必影响后面事件的结果,因而不独立。可以分为几种条件来处理
19467新华社快讯:中国一代文学巨匠巴金10月
17日
19时零6分在上海逝世。巴金
1904年11月25日出生在四川成都正通顺街。

巴金简历
全国政协副主席,中国作家协会主席。
男,汉族,1904年11月生,四川成都人,无党派,1921年于成都外语专门学校肄业。
1927年至1929年赴法国留学。1929年回国后,从事文学创作。1935年至1950年上海文化生活出版社、平明出版社总编辑。1950年后任平明出版社总编辑,上海市文学艺术界联合会副主席,中国作家协会上海分会主席。1953年9月后先后任中国作家协会副主席,《文艺月报》、《收获》、《上海文学》主编。1962年后任上海市文学艺术界联合会主席,“文化大革命”中受冲击。1977年至1983年中国作家协会主席、中国文学艺术界联合会副主席,上海市政协副主席。1983年任全国政协副主席,中国作家协会主席。2003年3月在全国政协十届一次会议上当选为第十届全国政协副主席。
2003年11月,国务院授予巴金先生“人民作家”荣誉称号。
第一届政协全体会议代表,第六届、七届、八届、九届全国政协副主席。第一届、二届、三届、四届、五届全国人大代表,第五届全国人大常委会委员。
19467好像这家伙死的和我们数学没什么关系吧,本人语文不好,他死不死
19467也不能这么说啦。一代文学巨匠还是值得我们尊敬的。默哀。。。。。。。。
另外偶觉得语文很重要,我语文还不错。至少在看逻辑学和集合论这些分支的时候很需要语言功底的。
19467路过!!
19467默哀
19468如题,求各种可能性的概率
19468n*n
19469模糊数学中那个方向比较好?请赐教
19469其实我也十分想知道啊
19470我是没听说过冥集,也许是很尖端的数学知识吧
19470我找了很多地方,才找到这里,希望这里的大侠们多给我帮助,谢谢!
我在作业上有很多地方都不懂,希望各位指导一下!
请问:
何为冥集?写出P={A,B,C}的冥集?
19470幂集吧?楼主不要误导我,我眼花...
幂集是以给定集合的全部子集为元素的集合。见集合论。
P={A,B,C}的幂集P(p)={空集,{A},{B},{C},{A,B},{A,C},{B,C},{A,B,C}}。
19471大学数学参考书目:
1.菲赫今哥尔茨
"微积分学教程","数学分析原理".
前一本书,俄文版共三卷,中译本共8本;
后一本书,俄文版共二卷,中译本共4本.
此书堪称经典.
"微积分学教程"其实连作者(莫斯科或者
列宁格勒大学的教授,门下弟子无数,包括
后来得诺贝尔经济学奖的著名数学家Kantorovitch)
都承认不太合适作为教材,为此他才给出了
能够做教材的后一套书,可以说是一个
精简的版本(有所补充的是在最后给出了
一个后续课程的简介).
相信直到今天,很多老师在开课的时候
还是会去找"微积分学教程",因为里面
的各种各样的例题实在太多了.如果想
比较扎实的打基础的话,可以考虑把里面的
例题当做有答案的习题来做,当然不是每道
题都可以这么办的.如果你全部做完了
那里的题目然后考试的时候碰到你做过的
可别怪我.
毫无疑问,这套书代表了以古典的方式
处理数学分析内容(指不引入实变,泛函的观念)
的最高水平,考虑到在中国的印数就以十万
计,可能在世界范围内也只有Goursat的书可以与之相比了.
这两套书在理图里面都有.
194712.Apostol
"Mathematical
Analysis"
在西方(西欧和美国),这应该算得上是
一本相当完整的课本了,在总书库里面
有.
3.W.Rudin
"Principles
of Mathematical
Analysis"
(有中译本:卢丁"数学分析原理",理图里有)
这也是一本相当不错的书,后面我们可以看到,
这位先生写了一个系列的教材.该书的讲法,
(指一些符号,术语的运用)也是很好的.
这里附带说一句,因为在理基里面当年念的是
后来复旦出版社出的秦老师和余跃年编的"高等数学",
虽然我一向认为该书编的很是不好,但是在这里
想引秦老师的一句话,希望能对非数学专业的
ddmm有所帮助:就是学完"高等数学"以后,可以
找一本西方advanced
calculus水平的书来看,
基本上就能够达到一般数学系的要求了.当时秦老师
曾特别指出Rudin的书.
说到Advaced
Calculus,在这个标题下面有一本书也是
可以一看的,就是
L.Loomis和S.Sternberg的Advanced
Calculus,
其第一版在总书库里面有不少,第二版在理图
外国教材中心有一本,系资料室是不是有不清楚.
这本书的观点还是很高的,毕竟是人家Harvard的
课本.
4."数学分析"(北大版)方企勤,沈燮昌等
"数学分析习题集","数学分析习题课教材".
北大的这套课本写得还是可以的,不过最好的东西
还是两本关于习题的东西.大家知道,吉米多维奇
并不是很适合数学系的学生的,毕竟大多是计算题
(一个比较有意思的地方是那套被广大教师痛骂的
习题解答其实有一个题的第二小题是没答案的,
原因好象是编书的人也没做出来,好象是关于级数
收敛的一个题目).相比之下北大的这本习题集就
要好许多,的的确确值得一做.那本习题课教材也
是很有意思的书,包括一些相当困难的习题的解答,
96年那会理图里面有一本,现在不知道怎么样了.
5.克莱鲍尔"数学分析"
记得那是一本以习题的形式讲分析的书,题目也很不错.
理图里有.
6.张筑生"数学分析新讲"(共三册)
我个人认为这是中国人写的观点最新的数学分析课本,
张老师写这书也实在是呕心沥血,手稿前后写了差不多
五遍.象他这样身有残疾的人做这样一件事情所付出的
是比常人要多得多的.以致他自己在后记中也引了"都
云作者痴,谁解其中味".在这套书里,对于许多材料的
处理都和传统的方法不太一样.非常值得一读.唯一的
遗憾是,按照张老师本人的说法,北大出版社找了家根
本不懂怎么印数学书的印刷厂,所以版面不是很好看.
理图里有.
下面的一些书可能是比较"新颖"的.
7a.尼柯尔斯基"数学分析(教程?)"
理图里有,是清华的人翻译的,好象没翻全.那属于
80年代以后苏联的新潮流的代表,不管怎么说,
人家是苏联科学院院士.
7b."数学分析"
忘了是谁写的了,
也是苏联的,莫斯科大学的教材.
理图里面有第一卷的中译本,分两册.那里面从极限
的讲法(对于拓扑基的)开始就能够明显得让人感觉
到观点非常的"高".
8.狄多涅"现代分析基础(第一卷)"
那是一套二十世纪的大家写的一整套教材的第一卷,
用的术语相当"高深",可能等以后学了实变,泛函再
回过头来看感觉会更好一些.
9.说两句关于非数学专业的高等数学.
这里强烈推荐理图里面几本法国人写的数学书.
因为在法国高等教育系统里面,对于最好的学生,
中学毕业以后念的是两年大学预科,这样就是不
分系的,所以他们的高等数学(比如理图里面有
J.Dixmier院士的"高等数学"第一卷)或者叫
"普通数学"(理图里面有一套书就是这个标题),
其水平基本上介于国内数学系和物理系的数学课
之间.
19471
10.再补充一个技术性的小问题.对于函数项级数收敛,
一致收敛是充分而非必要的,有一个充要条件叫
"亚一致收敛性",在"微积分学教程"里面提了一句,
其详细讨论,似乎仅见于
鲁金(Lusin)的"实变函数论"
里面,总书库里面有.
11.华罗庚先生的"高等数学引论"第一卷
这套书(其实没有完成最初的计划)是六十年代初
华先生在王元先生的辅助下对科大学生开课时
的讲义.那时候他们做过一个实验,就是一个教授
负责一届学生的教学,所以华先生这书里面其实
是涉及很多方面的(附带提一句,另外两位负责过一
届学生的是关肇直先生和吴文俊先生).也是出于
一种尝试吧,华先生这书里面有一些不属于传统
教学内容的东西,还包括一些应用.可以一读.
理图里有.
12.何琛,史济怀,徐森林
"数学分析"
这应该是科大的教材,虽然好象影响不是很大,
我本人还是很喜欢的,高一的时候第一次学数分
就是用的这套书,感觉是条理清晰,配的习题也很好.
印刷质量也相当不错.可惜的是学校里面没有,所以
放在最后.
19471空间解析几何实在是一门太经典,
或者说古典的课.从教学内容上说,
可以认为它描述的主要是三维欧氏
空间里面的一些基本常识,包括最
基本的线性变换(那是线性代数的特例),
和二阶曲面的不变量理论.在现行
的复旦的教材,苏先生,胡先生他们编的
"空间解析几何"里面,最后还有一章讲
射影几何.
这本书非常之薄.但是内容还是比较丰富的.
特别是有些习题并不是非常容易.最后一章射影
的内容还不是很好念的.
当然,这里还要提到十来年前大概
做过教材的一本书:
项武义,潘养廉等
"古典几何学".
这书的内容与课本不是很一样,不过处理方法还是
很不错的.项先生应当算做很能侃的那种类型的.
可以考虑的参考书包括:
1.陈(受鸟)
"空间解析几何学"
内容基本上和课本差不多,不过要厚许多,自然要好念点.
陈先生是吴大任先生(大猷先生的堂弟,南开多年的教务长)
的夫人,也是中国早期留学海外的女学者.
2.朱鼎勋
"解析几何学"
这本书基本上只在欧氏空间里面讨论问题.优点是非常易懂,
连二维的不变量理论也在附录里面交代得异常清楚.那里面
的习题也比较合理,不是非常的难(如果我没有记错的话).
朱先生相当有才华,可惜英年早逝.
关于数学分析的习题,还有一本书,就是
G.Polya(波利亚),G.Szego(舍贵)的
"数学分析中的问题和定理"
在学习数学分析的阶段,可以考虑其第一卷的
前面一半,后面就全是复变的东西了.
该书的内容还是非常丰富的.
在历史上,这是一套曾经使好几代数学家
都受益匪浅的经典著作.这套书的一个好处就是
题目难归难,后面还是有答案或提示的.
"微积分学教程"的第一卷有一册在理图里面似乎很少,
到总书库里面去看看吧!
如果想了解比较"新"的动态,可以考虑
3.Postnikov
"解析几何学与线性代数(?)"(第一学期)
这是莫斯科大学新的课本,从课程形式就可以看
出,解析几何这样一门课如果不是作为对刚进大学的
学生的一个引导,给出一些具体的对象的话,迟早
是要给吃到线性代数里面去的.
海外教材中心有一本英文本.
我个人以为,现在教委的减轻学生负担的做法迟早
是要遭报应的.中国的中学教育水平也就比美国最
糟糕的中学好点,从整体上说,比整个欧洲都要差.
我相信所谓三维的"解析"几何的内容总有一天要
下放到高中里面去.
上面的书如果撑不饱你,你又不想学其它的课程的话.
可以考虑下面两本经典.其好处是看过以后可以对很多
几何对象(当然具体说是指三维空间里面的二次曲面)有
相当深刻的了解.
4.狄隆涅
"(解析)几何学"
这套三卷本的大书包括了许多非常有意思的讨论,记得五年
前看的时候感觉非常有意思.这位苏联科学院院士真是够能
写的.总书库里面有.
5.穆斯海里什维利
"解析几何学教程"
这套书在上面提到的陈先生的书里面就多次引用了.
具体的说特别值得参考的是它里面关于射影的一些观点
和讲法(比如认为椭圆也是有渐近线的,只不过是"虚"的
而已).
19471高等代数可以认为处理的是有限维
线性空间的理论.如果严格一点,
关于线性空间的理论应该叫线性代数,
再加上一点多项式理论(就是可以完完
全全算做代数的内容的)就叫高等代数了.
这门课在西方的对应一般叫Linear
Algebra,
就是苏联人喜欢用高等这个词,你可以在外国
教材中心里面找到一本Kurosh(库落什)的
Higher
Algebra.
现在用的课本好象是北大的"高等代数"(第二版?).
用外校的课本在基础课里面是不常见的.
这本书可以说是四平八稳,基本上该讲
的都讲了.但是你要说它有什么地方讲
的特别好,恐怕说不出来.
值得注意的是95-96学年度,北大现在的
校党委组织部长王杰老师(段学复先生
的弟子)给北大数学科学学院95级1班
开课时曾经写过一本补充材料,把空
间理论的讲得非常清楚.如果谁能搞到
的话翻印出来是件很好的事情(我的那
本舒五昌老师给96开课的时候送给他
了,估计是找不到了).
好象上面有一点说得不对,就是北大的书用的
还是第一版.第二版在书店里似乎看见过.
从这门课的内容上说,是可以有很多种讲法的.
线性空间的重点自然是线性变换,那么如果在
定义空间和像空间里面取定一组基的话,就有一
个矩阵的表示.因此这门课的确是可以
建立在矩阵论上的.
而且如果要和数值搭界的话还必须这么做.
复旦以前有两本课本就是这么做的.
1.蒋尔雄,吴景琨等
"线性代数"
这是那时候计算数学专业的课本,其教学要求据说是比
数学专业相应的课程要高的.
因为是偏向计算的缘故,你可以找到一些比较常用的算法.
我个人以为还是比较有意思的.理图里有.
2.屠伯埙等
"高等代数"
这就是在上海科技出版的一整套复旦数学系教材里
讲高等代数的那本.不记得图书馆里面有,不过系里
可能可以买到翻印的.
这本书将80%的篇幅贡献给矩阵的有关理论.有大量
习题,特别是每章最后的"选做题".能独立把这里面
的习题做完对于理解矩阵的
各种各样的性质是非常有益的.
当然这不是很容易的:
据说屠先生退休的时候留下这么句话:"今后如果有谁
开高等代数用这本书做教材,在习题上碰到麻烦的话
可以来找我."有此可见一斑.
如果从习题方面考虑,觉得上面的书太难吃下去的话,
那么下面这本应该说是比较适当的.
3.屠伯埙等
"线性代数-方法导引"
这本书比上面那本可能更容易找到,里面的题目也
更"实际"一些.值得一做.
另外,讲到矩阵论.就必须提到
4.甘特玛赫尔"矩阵论"
我觉得这恐怕是这方面最权威的一本著作了.其中译者
是柯召先生.
在这套分两册的书里面,讲到了很多不纳
入通常课本的内容.举个例子,大家知道矩阵有Jordan
标准型,但是化一个矩阵到它的Jordan标准型的变换矩
阵该怎么求?请看"矩阵论".
这书里面还有一些关于矩阵方程的讨论,非常有趣.
总书库里有.
图书馆里面还有一本书的名字和矩阵论沾边.
5.许以超
"线性代数和矩阵论"
虽然许先生对复旦不甚友好(高三那会他对我说要在中国
念大学数学系要么去北大,要么去科大--他是北大毕业的,
现在数学所工作--我可没听他的),但是必须承认这本书还
是写得很不错的,习题也不错.必须指出,这里面其实对于
空间的观念很重视.不管怎么样,他还是算华先生的弟子的.
194716.华罗庚
"高等数学引论"
华先生做数学研究的特点是其初等直观的方法别具一格,在
矩阵理论方面他也有很好的工作.甘特玛赫尔的书里面你
只能找到两个中国人的名字,一个是樊畿先生,另一个就是华先生.
可能是他第一次把下述观点引进中国的数学教材的
(不记得是不是在这本书里面了):
n阶行列式是n个n维线性空间的笛卡尔积上唯一一个
把一组标准基映到1的反对称线性函数.
这就是和多线性代数或者说张量分析的观点很接近了.
高等代数的另外一种考虑可能是更加代数化的.比如
7.贾柯勃逊(N.Jacobson)
Lectures
on Abstract Algebra ,II:Linear Algebra
GTM(Graduate Texts in
Mathematics)No.31
("抽象代数学"第二卷:线性代数)
这里想说的是,这套书的中译者黄缘芳先生,大概数学系里面
已经没多少人还记得文革前复旦有这么一位代数学教授了.
此书英文版总书库里有,中文版(字体未完全简化)理图里有.
8.Greub
Linear
Algebra(GTM23)
这里面其实更多讲的是多线性代数.里面的有些章节还是
值得一读的.
9.丘维声
"高等代数"(上,下)
北大94级的课本,相当不错.特点是很全,虽然在矩阵那个方向
没有上面提到的几本书将得深,但是在空间理论,具体的说一些
几何化的思想上讲得还是非常清楚的.多项式理论那块也讲了不少.
10.李炯生,查建国
"线性代数"
这是中科大的课本,可能是承袭华先生的一些传统把,里面有一些
内容的处理在国内可能书属于相当先进的了.
19471常微分方程(一)
从常微分方程开始,数学课就变成
没底的东西,每一个标题做下去都
是数学研究里面庞大的一块.
对于一门基本课程应该讲些
什么也始终讨论不断.
这里我打算还是从现行课本讲起.
常微分方程这门课,金福临先生
和李迅经先生在六十年代写过
一本课本,后来在八十年代由
控制那一块的老师们修订了
一下,变成第二版,就是现在常用的课本.
上海科技出版社出版.
应该说,金先生他们的第一版在今天
看来还是很好的一本课本(这本书估计
受了下面的一本参考书
的不小的影响),
该书在理图老分类的
那一块里有.
但是第二版有那么点不敢恭维.
不知为什么,似乎这本书对具体
方程的求解特别感兴趣,对于一
些比较"现代"的观点,比如定性的
讨论等等相当地不重视.最有那么
点好笑的是在某个例子中(好象是
介绍Green函数方法的),在解完了之
后话锋一转,说"这个题其实按下面
的办法解更简单..."
而这个所谓更简单的办法是根本不具一般性的.
下面开
19471好!
19472看附件post-33-1129558544.jpg
19472Ck其实都可以算出来的,由于n-1次多项式n-1个根,又在一点处为1所以可以把用带顶系数法算出来。之后再讨论以下吧
19473求证:n维空间中的n+2个向量,每两个向量之间的夹角不可能都是钝角
19473归纳法
19473
引用 (reijin @ 2005年10月
17日
22时37分) |
| 归纳法
|
请问,n维和n+1维怎么联系?
19473李师正那本书上有啊 自己找以下
顺便问以下 兄弟考山大什么专业?
19473n+1个向量必线性相关,第n+2个向量与前n+1个的内积不能全小于0
19475谢谢!
19475谢了
19475ok
19475刚下,有时间好好看一下
19475之11post-11-1129559898.ibf
19475共14篇优秀学士论文,如果需要湖北省其它高校的优秀学士论文(04年数学类),本人可以提供.
之一post-11-1129559325.ibf
19475之12post-11-1129559939.ibf
19475之2post-11-1129559373.ibf
19475之3post-11-1129559438.ibf
19475之4post-11-1129559472.ibf
19475之5post-11-1129559507.ibf
19475之6post-11-1129559560.ibf
19475之7post-11-1129559586.ibf
19475之8post-11-11295596
17.ibf
19475之9post-11-1129559651.ibf
19475之10post-11-1129559677.ibf
19475之13post-11-1129560
193.ibf
19475唉!都不顶了?我自己顶一下
19475感谢
在看《交通信号灯的机理研究》
19475太感谢了
19475很好。不过怎么全是规划问题呢。有没有函数论一类的啊
19475谢谢,学习一下
19475不错,我下载了亮篇。学习学习
19475想打开看看。
19475谢了在看
19475先下载看看
19475谢谢分享!
19475我来顶一下!!
19475怎么都是规划类的???
没有分析类的么?
19475好
麻烦贴一下
华中师大的把?
谢谢!
19475顶一个
要写论文了,参考下
19475顶你一下哟
19475顶!
19475顶一下可以可以,我悄悄的学习以下
19475感谢共享!!
19475都是很优秀的论文阿,借此参考参考
19475谢谢
不知有没有
关于用积分求面积方面的资料
我想谢谢这方面的论文
19475斑竹,麻烦登一些函数论的优秀论文行吗?? 拜谢.
19475
谢谢楼主的学生管理系统,现求关于江苏经济方面的数学论文!!Thank
you
19475谢谢了啊,呵呵,找到了我想要的.
19475谢谢各位啊!
本来我还一直担心论文不知道怎么办好呢,现在好了,真的要谢谢谢谢!!
19475不错,就是水平有限,看不懂啊
19475有和我们今年相似的题目的,可惜和我选的不同哦,真失望!
19475谢谢了
有一篇可能还有用
19475感谢了
19475太牛太牛太牛了,太好太好太好了!
19475太感谢了
19475ding
19475好东西,谢谢了
19475高手高手高高手
19475支持
19475还想看看
19475顶!
19475很不错
不过,有没有关于分块矩阵广义初等变换方面的
请教
谢谢
19475好东西
多谢
19475拿回一分来。。。。。
19475顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶
19475
这些都这么好的。
可是我的毕业论文的选题知道老师都给了。
我是咋也咋找就是没个头绪的,请各位大虾帮帮忙,小女子先在
这里道谢了啊~~~~~~~~~
题目是:浅谈构造法在存在性命题中应用
19475我来帮你顶的来啦,咯咯
19475顶一下
19475多多交流!多多分享!
19475有数值积分方面的文章吗?
19475ding
19475用什么打开啊?
密码是多少
19475顶一下啊,呵呵
19475谢谢哦
19475顶··· 好可怜 想看没有分下···
19475楼主,有没基础数学方向的??
19475狂顶
19475很好呀!!!!!!!!!!!!!!!!!!!!!!!!
谢谢
19475谢谢您!
19475顶,能下不!
19475ding
19475非常感谢啊!我正好可以看一下毕业论文是咋写的啊,要不是还有几年 的时间准备,我都快急死了!!感谢啦!!!
19475请问有关rough方面的论文吗?偶想看一看啊。多谢阿
19475请问这个怎么看?怎么打开后是下载的?安装后都是英文,看不懂,不知道怎么用~~~~~帮忙说下
19475太棒了,顶一个
19475下了,多谢楼主
19475有拓扑方面的吗?感谢提供。
19475非常感谢,我们很需要!
19475非常感谢啊。我正在寻找……
19475为什么有的要积分,有的不要积分呢?我的分值不够……
19475谢谢!
19475best to you!thanks !
19475疑问:pdf的文件我怎么打不开啊?
19475yeah!!!thanks
19475顶一下,不错。谢谢国!
19475下了看看啊
19475帮你顶一下!
19475顶一下,谢谢版主
19475谢谢你啦..能不能再上传点有关数学的论文..最好属于大学毕业论文性质
19475能不能再多传一些本科毕业论文,多谢
19475非常好的文章。再接再励!
19475非常感谢!
19475很好。。
谢谢楼主
19475毕业论文要求字数1.5万,同志们,数学论文哪里吹得出这般。
制定这种规定的人真没大脑。。。
19475同意楼上的!!
19475谢谢分享
19475则么还要密码?
19475谢谢!写论文了参考一下。
19475有没有题目是求极限的若干方法的论文~很急~~谢谢~~
19475bangdingle
!!!!!!!!!hehe
19475怎么没认顶?
19475真强
19475楼主辛苦了,谢谢
19475好,多谢
19475罪过,罪过.....
我有想法了....
19475刚下载。有时间看一下。谢谢!
19475
我来顶一下!!
19475看一看,和自己的学生有个比较
19477知识,技巧与想象力
刘克峰
原文Knowledge,Technique and
Imagination,是我在2004年首届西湖青年数学家论坛上的演讲,现在的中文版由徐浩增加整理。
在国内工作一年多,接触了许多中学生,大学生和研究生。为了吸引优秀的学生到数学中来,我与他们进行了许多的对话与交流,这引发了我对数学教育从各方面的思考。迄今已有许多文章对我们的教育体制提出批评,认为它扼杀了学生们的想象力。但我觉得我们的教育从中学起就过分强调技巧,根本没有开拓学生的知识面才是根本的弊病。见多才能识广,而没有宽广的知识面,想象力就是无源之水。在中学里,以奥数为甚的题海战术使学生忘记了做题的目的是为了理解知识,只是机械地为做题而做题,不是为个人的喜欢与好奇心。在大学里,有些老师的知识就过于陈旧和狭窄,更不可能拓宽学生的知识面了。许多学生也以能做上万道习题为荣,或者早早就把自己限制在某个狭隘的研究方向。这样的教育只能培养给别人打工的工匠,不可能培养出真正的科学家。我觉得对数学专业的学生而言,要首先拓宽眼界,不仅在数学里的各个学科之间,更包括物理等相关学科,然后在尽可能的融会贯通,激发出想象力。种种感想促成了这篇文章,希望我自身的经历与体会能起到抛砖引玉的作用。
我将结合自己的治学经验讨论一下知识的重要性以及知识,技巧与想象力的关系。从我读研究生开始,我的工作就一直围绕着物理学中出现的几何与拓扑问题。物理学家需要数学作为工具,反过来他们又借助物理理论提出数学上的猜想,虽然物理学家的推导很多时候是不严格的,但是这些猜想往往最后都被证明是正确的。这是非常令人感到惊奇的!
为了解决物理学家提出的数学猜想,我们发展了全新的数学理论,发现了不同数学分支之间意想不到的联系。这些数学上的革命又为物理学的继续发展提供了严格的理论基石。数学和物理学的相互交织造就了科学史上的多次革命,大家熟知的有“微积分与牛顿力学定律”,“广义相对论与黎曼几何”,近年来的大小例子更是层出不穷,“量子场论与指标理论结合得到椭圆亏格刚性定理”,“共形场论给出的模空间Verlinde公式”,“Yang-Mills场与4维拓扑”,“陈-Simons理论与3维拓扑,纽结理论”,“关于弦理论中镜像对称与Calabi-丘空间的镜公式”,“关于陈-Simons理论,Calabi-丘空间与Gromov-Witten不变量的Marino-Vafa猜想”,“弦理论与Ricci流,3维拓扑的关系”,“镜像对称与数论的关系”等等。近20年数学菲尔兹奖得主的获奖工作,有一半与量子场论,弦理论有关。无论你研究哪一个方向,总会在弦理论中找到用武之地。而弦论学家们也贪婪和迫不及待地注视着数学中每一点一滴的新进展,迅速地理解并应用到他们的理论中去。这种交流激发了数学与物理学无尽的活力。这也使得我们有理由猜测:上帝根据数学公式创造了世界?但毫无疑问,数学是开启大自然的钥匙。
要指出的是物理学家对数学的贡献不仅仅限于预测数学结论,很多时候,他们也用严格的数学语言为我们指出数学上重要的研究对象。Witten和Vafa是两位杰出的代表,他们的数学甚至要好过绝大部分数学家。有人形容他们就像从未来时空穿梭回来的一样,只记住了未来数学支离破碎的景象,凭着记忆叙述出来,成了挑战当代数学家的猜测。物理学家学习数学的方式也许值得我们借鉴,Witten他们大概从来不做数学习题,但却用最快的速度学到他们所需要的数学。哈佛大学数学教授Taubes
曾说,“物理学家先学指标理论,然后才是黎曼几何”。我觉得我们数学家不仅要时刻留意物理学的发展,更要注意物理学家掌握知识的技巧,那就是在研究中学习,在学习中研究。
物理学家特别青睐“无穷”,甚至有时候不惜以牺牲“严格性”作为代价,比如SL(2,Z)对称,大N极限的陈-Simons理论,路径积分。虽然Feynman的路径积分还缺少严格的数学基础,该理论因其物理上的直观性和便于形式演算在现代量子物理中产生了深远的影响。正所谓“妙在无穷,美即有用”。这种不严格也给了他们无穷的想象空间。
那么我们应该如何学习数学呢?
我去美国留学时,随身只带了两本书,一本是丘成桐与Schoen著的“微分几何”,一本是Gilbarg与Trudinger的“二阶椭圆偏微分方程”。我想在分析与几何里大展身手,就不需要学习别的了。
1988年9月底,我走进丘成桐先生的办公室,开始了我在哈佛的学习生活。他问我,想开始做研究还是继续学更多的数学。我回答想开始做研究。可是丘先生对我说,“你要尽可能多的学习数学,因为毕业以后要想学什么新东西都不容易了。”他让我学习代数几何,代数数论,几何分析…有许多内容直到今天我仍然无法完全理解。但这却深刻影响了我的学术生涯和人生轨迹。在当上教授以后,繁重的教学和科研压力让我体会到丘先生的话是多么的语重心长。
知识与技巧,到底哪一个更加重要呢?我的观点是,对年轻人而言,知识更重要!知识让我们站得更高,看到正确的方向,因为方向错了,一切努力都不会有结果。但是也要承认,研究中关键的突破往往来自于技巧上的创新。做个比喻,一个武林高手,学了很多门派的武功,但是内功不行,就容易走火入魔。大家知道丘先生在众多数学领域都有开创性工作,得益于他极强的分析功底及广博的知识面。现在国内热衷的中学生数学竞赛,就太过于强调技巧。其实我们的学生从中学开始就应该接受多方面知识的熏陶,让孩子多看名人传记,培养对科学的好奇心。我最近读的牛顿传记就写的非常精彩。正是由于好奇心,牛顿大学二年级给自己提出了几十个有关大自然的问题,为了解决它们,他发展了微积分作为基础,进而发展了四大物理定律。
下面我将联系自己的经历讨论拥有宽广知识面的重要性,数学与物理、及其它学科交叉的必要性,以及与朋友学术上交流的好处。
我在中国科学院研究生院读书时,同学中有张伟平,周向宇,现在都成了国内最杰出的青年数学家。那时很少有机会能听到前沿的课程。我们自己组织讨论班,报告陈类,指标理论,Mordell猜想…开始还无法完全弄明白,但是却开阔了眼界,至少知道了什么是“好的”、值得学习的数学。这对每个人来说都是非常重要的,我们需要培养自己对于数学的鉴赏力。如果你还是无法确信什么是好的数学,那么就去读大数学家的著作和文章,跟着大师走总是没错的。后来在我研究中成为重要工具的局部化思想也是在国内学习与做硕士论文期间掌握的。后来我用局部化思想来理解我所学到的一切数学知识,就像用一根线串起了许多珠子。从我来到哈佛大学开始,让我感触最深的就是那里教授和学生勤奋工作的作风。现在国内最缺少的正是这样一种风气。一流的大学其实就是这样一流的氛围。而推动他们如此投入的是对数学的好奇与热爱和对知识的渴求。哈佛举办各种讨论班,参加的学生非常积极,座位不够了,甚至会坐在地上。我感觉好像一头扎进了知识的海洋,每个早晨都感受到不同的阳光,那是非常令人兴奋的日子。
Witten的文章“超对称与Morse理论”,对我的工作影响是最大的,还有哈佛大学教授Bott“厚积薄发,举重若轻”的研究风格也令我颇多受益。Bott说过,“要顺流而下,不要逆流而上”。就是说做数学永远要顺流而下,不要太费劲,太勉强,要追求“轻舟已过万重山”般的流畅,但也不要随波逐流,两方面要协调好,否则就谈不上创新。
数学上的每一次变革都离不开新的思想与方法,以及不同分支学科的融会贯通。这就要求我们在掌握丰富知识的基础上更具创造性的思考问题,才能在数学发展的前沿占有一席之地。数学与物理的交互作用无疑将是今后相当长时间里数学研究的主流分支。举几个学科间交叉的例子,微积分与线性代数结合创造了微分几何;Faltings用综合代数数论与代数几何的Arakelov理论证明Mordell猜测;从对称函数或更一般的,从紧群表示论出发,可以得到陈类,K-理论,Riemann-Roch公式和指标理论;集模形式,表示论和拓扑于一体的椭圆亏格;物理学家揭示的弦论中的各种对偶性在数学上的许多应用等等。
数学家对整个社会和人们的日常生活都有很大的贡献。从计算机,互联网,到生命科学,金融业,处处可见数学的踪影。尽管现在美国找工作不容易,华尔街还招大量的数学系毕业生,培训三个月就能胜任。诺贝尔经济学奖获得者中也有好几位是数学家,包括“美丽心灵”的主人公Nash,Debreu等。在生物学里也数学出身的有诺贝尔奖获得者Gilbert。可以说,数学是最无私、最有潜力的专业。进可努力成为大科学家,退可过有质量的生活。数学要转到别的专业很容易,但反过来,别的专业要转到数学可就不容易了,数学可以给你很好的逻辑思维训练,即使以后不做数学了,也可以在别的领域做得很好。但这却是单程车票。我在北大数学系的150个同学,虽然现在做纯数学的就我一个,但他们现在生活得也都很好。
爱因斯坦说过,“想象力比知识更重要”。可是没有深厚的知识底蕴,想象力也只能是空中楼阁。想象力就是将各种知识融会贯通而激发出的火花。所谓“天才”,就是脑袋里时刻放着七八个问题,在阅读文献的同时,不断用新学到的技巧和方法来分析这些问题,看能否找到突破,只要用心坚持,总能解决掉其中两三个问题,那么别人就会觉得你是天才了。
我的博士论文主要研究椭圆亏格,它是指标理论和模形式的结合体,可以看作环路空间上的指标理论。在Witten受到量子场论启发提出椭圆亏格的刚性猜想以后,Bott和Taubes花了很大精力研究这个问题,可是他们给出的证明技巧性太强,很复杂。我参加了哈佛和MIT关于椭圆亏格的讨论班。我注意到环路空间上椭圆算子在模群SL(2,Z)作用下的对称性,接下来用了几个月时间给出了刚性猜想的一个极其简洁的证明,其中用到数论中的Jacobi-theta
函数和模形式。SL(2,Z)对称性也是弦论中的基本原理。这个证明的思想最初萌发于去普林斯顿参加乒乓球比赛的路上,最后一步证明的豁然开朗则是产生在看一部电影的时候。记得开始的几次证明总是有漏洞,我苦恼至极。但我坚定地相信这么美妙的思想一定是对的,不然数学就一点都不有趣了,也许我也早就放弃做数学了。这就是我多方面学习培养的数学感觉在起关键作用了。后来我继续推广了刚性定理,使之与无穷维李代数结合到一起。我不仅通过这新的方法发现了新的消灭和刚性定理,还凭借数论和代数几何的知识,通过模曲面的几何来理解刚性现象。这些方法现在仍然非常有用,完全超出了我的预期。这全新的方法也引发了我与麻晓南,张伟平及董崇英等朋友的合作,将顶点算子等理论与椭圆算子的刚性结合到一起。
我研究生涯的第一步正是得益于广泛的知识积累。数论的知识却用到了拓扑之中。在研究的过程中,我也更加深了对所学知识的理解。哈佛几年的学习,我觉得最重要的收获是对“好的数学“的感觉和把握能力。
80年代末,物理学家Verlinde在研究2维共形场论时提出了著名的计算黎曼面上稳定丛模空间的典则线丛的全纯截面维数的猜测,即Verlinde公式,这是一个90年代初非常热门的研究专题。黎曼面上稳定丛的模空间在数学的许多分支中都有研究,特别是代数几何与拓扑学。数学家尝试了很多办法计算其上典则线丛的全纯截面维数,但都失败了。可是弦论学家却出人意料的给出了一个非常简洁的闭公式。不久Witten在研究二维规范理论时提出了一个关于黎曼面上主丛的模空间上相交数闭公式的猜测,原则上Witten公式结合
Riemann-Roch公式或者指标公式就可以得到Verlinde公式。当时我在MIT任教,参加了许多关于这方面问题的讨论班,尝试了许多不同的方法来理解Witten公式,这是一个对紧李群所有不可约表示求和的无穷和式。那段时间我对辛几何也有了较深刻的理解。
直到有一天在MIT的图书馆里,我和往常一样翻阅感兴趣的文献,不经意间看到了李群上热核的表达式,是由一个与Witten公式相同类型的无穷和式给出的。我立刻确信自己找到了证明Witten公式的工具,就是李群的热核。有了思想只是第一步,还有许多技巧上的困难需要克服,我用了几个月时间才写下了全部的证明细节,而所学的辛几何知识也起到了极其关键的作用。
受到我的工作激励,Bismut得以用我的方法给出了一般Verlinde公式的证明。
“研究”的英文单词“research”,就是反复寻找,很好的体现了研究的本质。丘成桐与杨振宁先生都有常在图书馆翻阅杂志的好习惯,不求懂,只为见多识广。丘先生更以“好读书,而不求甚解“作为广泛猎取知识的好方法。与其他学科一样,数学的每一点进步都是建立在前人工作基础之上的。可谓“开卷有益”!
1996年我接到斯坦福大学聘书,就在我将要驱车离开波士顿前的一小时,丘成桐先生打电话来要和我谈论有关镜像对称的问题。
1990年英国物理学家Candelas等人在镜像对称的基础上,提出了五次Calabi-丘空间上有理曲线计数公式的猜测。近百年来代数几何学家都在试图计算这些有理曲线的数目,却只能得到不超过3次的有理曲线数目。而Candelas的公式通过计算一个很简单的常微分方程,即Picard-Fuchs方程,便给出了任意次数有理曲线的数目,引起很大的轰动,镜像对称也由此而发展成为近年来数学中的主流。许多数学家尝试证明这个公式,包括Witten,
Kontsevich,Givental等著名数学家都作出了贡献。我先前并未特别关注镜像对称这个研究领域,于是开始加倍努力的阅读文献。有时候冥思苦想多日却不得其解,甚至会在经历繁复的计算后换取一个“此路不通”的经验。后来在不经意间,当我注意到稳定映射模空间上的递归结构的重要性时,问题好像一下子豁然开朗了,这种美妙的感觉是旁人很难体会的。很快,丘成桐,连文豪和我就给出了Candelas镜像猜想的第一个完整证明。证明的关键是“函子局部化”技巧,这在我今后的研究工作中也是一个非常重要的工具。此后我们又一起将镜像定理推到极其广泛的情形。这是一次非常愉快的合作,我们彼此的特长相互结合在一起,使困难的问题很快地得到解决。
我在UCLA的这些年中在研究上有很多收获,我们还证明了Grassmann流形的Hori-Vafa镜像猜测。其中除了函子局部化公式外,还要用到很复杂的组合技巧与代数几何,这些困难是在与刘剑豪讨论后才得以克服的。剑豪的刻苦和不惧一切困难的勇气都给了我深刻的印象。所以与好朋友,特别是彼此了解对方工作与能力的朋友交往是很重要的。
90年代初,Kontsevich证明了Witten的一个著名猜测并由此获得Fields奖,即代数曲线模空间上某些陈类积分(称为Hodge积分)的生成级数满足无穷多个KdV型的微分方程。我很早就开始关注Kontsevich的这项工作以及相关的发展,而且镜像对称在高亏格的推广也需要计算更广泛的Hodge积分。2001年Marino和Vafa从Chern-Simons理论和Calabi-Yau空间的对偶关系出发,猜测曲线模空间上一类更广泛Hodge积分的生成级数可以表达为关于对称群表示的组合闭公式,也就是Chern-Simons纽结不变量。
我在浏览众多物理文献时看到这个猜测,立刻就被它的漂亮吸引住了,并且意识到需要先在组合方法上找到突破口。2002年暑假,正值国际数学家大会在国内召开,我与周坚在北京到杭州,上海到北京的飞机上讨论了许多例如镜像对称方面的问题,当然也提到了Marino-Vafa猜想。此后又继续通过email进行了许多富有成果的讨论。不久,周坚就理清了Marino-Vafa公式中的组合部分,即对称群表示的组合公式。他注意到这个组合公式满足一个所谓的“切割-连接”方程。因为这个“切割-连接”方程等价于一组常微分方程,由解的唯一性定理,剩下的问题只要证明Marino-Vafa公式中的几何部分,即Hodge积分的生成级数也满足这个“切割-连接”方程,同时与组合部分具有相同的初值。这却要困难得多,因为几何表达式的结构极其复杂,不象组合表达式那样直截了当,可以直接验算。
Marino-Vafa公式几何部分的证明进行得相当的曲折和困难,我们用函子局部化技巧作了许多尝试。2003年4月,刘秋菊来到加州大学洛杉矶分校,参加了我主持的讨论班,我把与周坚的研究进展告诉刘秋菊,在我们三人的合作努力下,很快就完成了几何部分的证明。记得我们三个人当时曾被极其复杂的表达式困惑住,百思不得其解,曾经想到放弃而只写下部分结果。最后刘秋菊从Lake
Arrowhead赶回来与我讨论,做无奈的最后一试,用了类似我们证明镜公式的办法,居然成功!那一刹那的感觉是非常令人难忘的。当这个猜想被证明时,真有一种天地人合一的感觉,那是一种灵魂激荡的美妙感觉。证明的预印本于2003年6月发表,在国际上引起了很大的反响。这是一次极其愉快地合作经验,三个朋友的长处得到了最完美的结合与发挥,也是可遇不可求的美好经历。
Marino-Vafa公式与Witten-Kontsevich的公式相比,不但前者的Hodge积分更加广泛,而且Marino-Vafa公式是一个非递归的闭公式。更重要的是,我们的证明是几何方法与组合技巧的美妙融合,对今后类似公式的证明都具有方法论上的很好借鉴。我们继续用我们的方法建立了数学拓扑顶点理论。许多更有意思的结论可由此推出,包括我们建立的与指标理论的联系及我的学生彭攀用这新的理论证明了圈形Calabi-丘流形上著名的Gopakumar-Vafa猜想。就像Atiyah讲的,中国数学家在数学物理这个最有影响的主流领域可说是一直引领风骚。周坚与刘秋菊也成为此领域中公认的一代青年领袖。
近朱者赤,和一群聪明的人在一起,你会变得更聪明。
黎曼面的模空间和Teichmuller空间的几何是一个古老的问题。丘成桐在80年代初期与郑绍远,莫毅明合作证明Teichmuller空间上Kahler-Einstein度量的存在性。之后他猜测黎曼面的Teichmuller空间上的Kahler-Einstein度量与经典的Teichmuller度量,Bergman度量等价。最近,通过引进并详细研究两类全新的完备度量,Ricci度量与摄动Ricci度量,丘成桐,孙晓峰和我证明了丘成桐的猜测。而且还证明了所有经典的完全度量都与我们新引进的度量是等价的,这澄清了这个领域里许多的老问题。更重要的是我们进一步得到了模空间的logarithmic余切丛是稳定的代数几何结果。这个结果至今代数几何学家仍不知如何下手。
在我还是学生时,我就对模空间和Teichmuller空间的几何问题有浓厚的兴趣。我参加各种讨论班,还写了两篇论文,用模空间上的Weil-Petersson度量的曲率性质证明了代数几何中的几个重要结果。我认为这是学习一门新课程最行之有效的方法,比做习题有益的多,理解问题和概念也深刻的多。
孙晓峰是我在斯坦福任教时结识的,当时他是Schoen的博士生,跟我上一些读书课。他人很聪明而且坚持不懈,这是难得的数学家素质。我们与丘先生一起在黎曼面模空间问题上进行了许多卓有成效的讨论,使得这项工作得以顺利完成。我们的工作对于黎曼面模空间几何学是很重要的贡献。我们还在继续研究许多很有意思的问题,许多结果很快会写出来。
通过上面的讨论,希望大家已经能够感受到知识的重要,而要获取知识,惟有勤奋,而且与朋友多交流,共同创造一个好的探讨和吸收知识的氛围。宽广的知识面使我们能够正确地选择和提出有意义的问题,把握正确的研究方向,培养出对“好的数学“的敏感和洞察力。这种能力远比掌握几个解题技巧来的重要,是真正的科研能力。学生们也不应过分限制自己的领域,要解决的问题需要什么知识就要去努力获取。另一方面,读懂一篇文章,我们会有成就感,但那只是看别人唱戏,我们需要发展自己的技巧来解决问题。当知识和技巧插上想象力的翅膀,你会发现数学的一切都变得那么美妙。
我一直相信大自然都是可以用数学公式来描述的,所以说数学的力量是无穷的。长期以来,数学已经成了我生活的一部分,是数学的魅力在牵着我走。从某种意义上讲数学就是人生的一种感觉,这说不出的感觉真是好极了。这种感觉只有在宽广的知识海洋里徜徉才能欣赏得到。
19478很高兴能找到这个网站,有没有象这样的关于物理的网站呢?
回复:http://www.physicsforums.com/
19478不知道啊!!帮不了你了
19479谢谢.post-38-1129563379.ibf
19479(b-a)*|f(x)/[(x-a)(x-b)]|=|f(x)/(x-b)-f(x)/(x-a)|=|f'(e)-f'©|<=

|f''(x)|dx
19479麻烦了
19480我隶属于北京化工大学软件测试和知识管理实验室,正在做非数值型软件自动化测试,现在写论文需要证明一个函数是双射函数,我数学系本科毕业,但数学水平确实不怎么样,望大家给点帮助,不胜感激。
我把问题的大意描述一下:
由于我试验了半天此论坛的公式编辑也没有成功,所以只有用附件了,请原谅。
谢谢大家的帮助。
post-23-1129565104.ibf
19481请问一般一个函数单射和双射是怎么证明的啊?如果函数是双射,他一定就可逆吗?谢谢
194811.没有关于证明单射,双射的一般方法;
2.双射一定有逆映射.
19481根据定义好像就可以说明问题,出此之外没有什么办法。
双射是可逆的。因为双射既是单射又是满射。
19481if for any x_{1} \neq x_{2}, it follows that $f(x_1)
\neq f(x_2)$, then $f$ is one-to-one. If you are to
prove it is onto, you can use the orthoganal method.
19482谢谢post-38-1129566374.ibf
19482先证f(0)的n阶导数有极限,再套用(e^(-x)*f(x))'=e^(-x)*(f'(x)-f(x))即可
19486我是刚学关于矩阵特征值的问题,我想请教大家,使用那个软件最好,而且容易学希望大家帮忙,谢谢大家!!!
另外我有一个矩阵如下:
请问大家其特征值是多少?post-28-1129598835.ibf
19487附件中post-38-1129600045.gif
19487(1)利用定理,假设f可分解,我们能找到f的一个次数不超过m的整系数多项式因式h,则h在ai上取值1,-1,那么必有取值1的ai个数或取值-1的ai个数至少是m+1,则可得h是一个常数,与假设矛盾
(2)对于正交的两个向量x,y,由于T是保距变换,那么必有<T(x+y),T(x+y)>=<Tx,Tx>+<Ty,Ty>,从而得<Tx,Ty>=0,据此易知其结论
19487但是题目中并没有说T是线性映射啊,不要证明T是线性变换吗
19487 你有05高代的全部试题吗?如果有的话,麻烦你上传一下.我现在就差这套题了.谢谢!
19487(1)题利用定理:如果整系数多项式能在有理域上分解,那么也能在整数域上分解
(2)题利用空间内积证明
19487有时间我打一下传上来,解答能不能详细点啊
19487哦,没注意到,不过保距且T(0)=0的变换必是线性变换,这个这在欧氏距离空间中利用三角不等式和内积不难证明的
另一种结论和提法如下:
http://www.math.org.cn/forums/index.php?showtopic=12752
19487也给我发一份试题吧 king_0577@hotmail.com
19488《微积分学教程》菲赫金哥尔茨著。现有六本:(缺第二卷第三分册,三卷第三分册)
第一卷第一分册(
1954年1月初版,商务印书馆)
第一卷第二分册(
1959年2月印刷,高等教育出版社,书脊用牛皮纸粘贴)
第三卷第一分册(
1953年10月初版,商务印书馆)
第三卷第二分册(
1953年12月初版,商务印书馆,书脊用牛皮纸粘贴)
以上四本书比较旧,因年代已久,一卷二分册,三卷二分册书页有些发黄,平均6成以上近7品。
第二卷第一分册(
1954年2月初版,商务印书馆)
第二卷第二分册(
1954年5月初版,高等教育出版社)
以上两本,品相较好,近9品。
现有意低价转让(35元包括挂号费),注意以上书全是“繁体的馆藏书”,六本一起转让,不单卖。
还有一套数学分析原理,共四本,人民教育出版社出版,近8品,35元。
有意者,请发邮件联系
goodbyefaith@sina.com
19488我八本全有了,不需要了,全部买的书原价,只要几块钱,好便宜,你喊60,抢人亚
19488其实楼主这个价格也不错了。我经常买旧书。很多店家都会把这种品相很好又很常用的经典书籍狮子开大口的要钱。这里楼主60一套可以啦。楼上的你运气好啊。能用原价弄到。羡慕。。。。我的是家里继承的。
19488tttttttt
19488哈哈哈,我是运气好了,我们学校图书馆处理旧书,全部原价卖,我去淘的,哈哈哈
而且很好了,^^_^哈哈哈,刚才又下到电子版本的,哈哈哈,朋友们,不用买它的书的了,要的留下邮箱,我把电子版本传给你们拉,哈哈哈哈
19488大家都是同路中人,没必要!
194885楼的仁兄,能给俺传一套电子的吗?谢谢了先。.
我的E-MAIL是 executivezhao@163.com
19488好书啊,已经联系楼住收购事宜了
19488我有电子版本,而且有三个版本,两个中文版本,一个俄文版本,需要的加我
QQ
21
1858079]]]]]]211
21
195807zheg
21
195807这个,上面的错了
19488楼主,已经打款了,请寄书吧。
19488书已收到,谢谢楼主。
19488好心人,能不能给我也发一份!
gaochao121212@163.com
19489开门见山吧:
1,
一个白噪声的无穷滑动和在其系数绝对收敛的情况下,期望等于0
2,从条件协方差的角度推导偏相关系数的表达式(可以以三维为例,在Z的条件下X与Y的相关系数)
子青和其他各位高手请赐教
194891.绝对收敛,所以极限和期望(积分)可互换(见实变函数),所以得证
2.E[(X|Z-E(X|Z))(Y|Z-E(Y|Z))]=E(XY|Z)-E(X|Z)E(Y|Z)
F
(z)=∫
x∫
ydF(x,y,z)
E
(XY|Z)=∫xydF(x,y,z)/F(z)
19489没有推导完啊!最后结果是什么能帮忙推导一下吗?
19489另外,那个系数绝对收敛的条件是充要条件嘛?
可否举出一个例子,在系数的平方和收敛的条件下,均值为0,但是在系数绝对收敛的条件下均值不存在??????????
19489第2个问题你看张尧庭、方开泰先生的《多元统计分析引论》第二章第二节、第三节即可!
19490设A是 n阶方阵,记C(A)={X|AX=XA}为A的中心化子,证明dimC(A)大于等于n.且等号成立当且仅当A有n个不同的特征值。
19490记得以前出现过此题的解答,你查查看。
19490我也要!!!急需
19490那我也顶一下吧,以前确实有人做过发了,不过现在很难找,呼吁大家发题时一定要像幻星提的那样标注清楚这样以后好查
19490下午我已经全查了,没有查到
19490用到了对角化的一点知识post-38-1130809774.ibf
19490看了楼上的解答,应该是错误的,对称是从哪里来的。
19490好题阿
19490我的钱没了,不过这个对我很重要
19492分形数学的最新研究方向是什么?
19492分形虽然只有20几年的历史,但是发展迅速,在各个领域里均有突破
19492感觉现在研究分形的人和文章太少了,过不了多久就要消失了!现代数学的东西用不上啊!!
19492现在做的是分形,发现分形太不景气了.我想换个热门方向,给个意见!
19492我觉得这不是一个方向,没有什么进展,你还是转行吧.
19493王垠出名了,这是迟早的事。
但这一次,他的出名更多是以争议的方式出现:还有不到一年时间就可以拿到清华计算机专业的博士学位,但他放弃了。他为此写了1万字的博客文章:《清华梦的粉碎》。他说:“现在我已经厌烦了国内所谓的‘学术’。我准备放弃清华的博士学位,出国找个好老师,进行真正的研究。博士第4年了,做出这样的决定真是不容易。有人告诉我不要放弃,你知道有多少人正在羡慕你?你知道一个清华的博士学位有多么值钱吗?但是我不能这么沉默下去了!
”
这篇文章更像一篇“战斗的缴文”(尽管王垠不这么认为),它痛数一个不断“进阶”的学子在中国学历教育道路上感受到的种种弊端、愚蠢、麻木和弱智,它像一个文本病毒入侵中国教育系统,并在更大范围内引起波澜。
王垠从四川大学97级本科毕业后,保送到清华大学计算机系硕博连读。现就读于清华大学计算机系软件所,主要进行集成电路布线算法的研究。2004年左右发表题为《完全用linux工作》和《写给支持和反对<完全用linux工作>的人们》的文章,在中国的计算机和linux阵营引起极大轰动,成为水木清华linuxapp版和中国多个linux社区的偶像级人物。
王垠可能不是个天才,但他一定是个重视创造性、有意识培养自己创造力的自我教育者。
与其说是学院教育让他受益,倒不如说他是在自我成长中找到心性、学识与把握力的。
退学并不意味着自毁前途,并不意味着死机,并不意味着神经错乱,恰恰相反,退学是对苍白学术的抗议、是逃避窒息的唯一手法、是胸有成竹者的最优选择而非次优选择、是人生的一次重启。王垠目前尚在清华,他被告知,学校每年的退学在12月份办理。
此前,王垠以优异出名,他的论文两度获得国际性刊物的认可,这在清华历史上尚属首次;王垠也以帅气出名,看过王垠博客上的照片的人,都会有这种感觉。2005年,王垠为第一作者的论文参加IEEE/ACM
Asia andSouth acific Design Automation Conference (ASP-DAC
2005)国际学术会议获得Best Paper
Award。这是自ASP-DAC会议举办以来中国大陆论文首次获奖。
王垠的这次出名非他所愿,却连累了他:有记者在他宿舍外守候到凌晨一点,这让他看不过去,出门劝走对方。
王垠的困惑在于:他随手而为之的论文“垃圾”能够引起那么大的重视和认可,这让他不屑却又可怜那些埋头论文的人。王垠的内心一定苍凉地狂笑过。
到底是什么让王垠选择退出万人向往的清华学府呢?王垠说他的清华梦被粉碎了,又是什么粉碎了他的清华梦?越来越多地听到硕、博在退学,我们的大学究竟出了什么问题?
国庆节的早晨,人们高兴地看到王垠的博客已经恢复了往日的样子,他很大方地把为避免媒体刊登才删掉的自己的照片又挂了上去,把反驳他抨击他的博客网址也公布了,一句“过十一去啦,懒得理你们”,让人们不难感到,年轻的王垠在这场漩涡中经历了一场迅速的蜕变。
《新周刊》:你说你已经厌烦了国内所谓的“学术”,那么你所了解的所谓学术的现状是什么?引发你厌烦的原因又是什么?
王垠:我认为现状就是一切都是为了paper的数量。这就导致了大家都忙着写没有价值的论文。没有实际的问题,就只有把国外的论文拿来看看有什么可以改进一点点的,继续写论文,没有创新。甚至很多人写论文时还把跟自己有关系的人的名字都挂到作者里面。不管参考了与否,引用自己人的论文,增加他的引用数。开会审论文时放水,看到某篇paper的话题似乎是熟人的就录取。这一切已经使学术空洞无物。
同样的问题发生在教育上,做表面文章,没有实际的东西,课程设置不合理,教条主义,学很多没用的东西。国外也有同样的问题,但是至少还有很多实干家。对比一下学术上的成果就可以看出来。
“理论的东西将来才会有用”是一句很有用的借口,几乎可以掩盖所有的失败和没用的论文。这句话已经被滥用了,只有具备天才的直觉和预见力的人,才有资格说一个理论在遥远的将来会有用。
《新周刊》:在你的退学申请中,对研究生教育的不满大概包括论文、讨论环境等等,能不能针对这些问题,谈谈你觉得应该是什么样子的,以及你的同学中有没有类似的呼声?
王垠:我觉得理想的样子可能有些过于理想化。不过研究至少应该有一个实际又可行的目标来驱动,而不是为了写论文而写论文。出发点不同,结果就大不相同。很多同学都感觉到这个问题,但是都没有公开说出来。慢慢的不满意的同学就熬毕业了,或者退学了,或者就被同化了。
我刚刚写了那篇文章(指《清华梦的粉碎》,在王垠博客上),就有一个师弟打来电话,说其实我们都知道是这么回事,但是谁也不敢说,都想毕业啊。一个师兄也在我的blog回帖说这个问题他也明白的。其他很多同学都有类似情况,甚至更糟的就是像我隔壁同学那样做体力“民工”。本科的教育也缺乏创造性。总是知识灌输式的,老师在上面讲,学生就只有听的份。考试太紧张,很多学生变得只会应付考试。一个清华本科生给我写信说他早就觉得有这个问题,他想在紫荆的小石头桌子那里建立一个露天的common
room,可是始终无法成功。
《新周刊》:在“中国教育操作系统下”作为一个并不优良的程序,你有怎样的感受?种种不适应有没有可能是由于你自身的特性造成的,因为如你一般经历的人并不在多数。
王垠:我所说的“不优良”是因为我这个程序直到现在才“喧闹”地退出。如果是按照UNIX的哲学,优良的程序应该早就退出了,不会等到这个时候。就像Oracle总裁说的那样,研究生时辍学,虽然开化得稍晚了些,总比永远不开化的好。
每个人生下来都无所谓优良不优良,每个人的智力都足以学会东西。而教育系统经常把责任推卸到学生身上。你听不懂课,那么就是因为你理解能力差。你考试分数低,是因为你比别人笨。但却没有人发现,其实很多时候,原因正是上课的老师没有吸引力,他自己都对学科没有深入的理解,他不知道那些理论是怎么得出来的,当然无法给学生直觉。学生就一味地接受知识,而不能知道这些知识是怎么来的。看不懂国内的计算机教材,很多人就觉得自己笨。但是我就知道一般的计算机教材是怎么粗制滥造的,看不懂的原因应该归咎到作者或者译者,而不是读者。好的计算机教材都会看起来很清晰,只会要求很少的基础知识,而且通常都放在附录里面供参考。
有人说我不适应这个科研环境,他们说的适应就等于被同化,我当然不可能“适应”。其实,我曾试图适应过一段时间,但是我醒悟了。我知道有人又想乱用达尔文的理论,说我不能生存。我想告诉他们,我虽然不“适应”,但是我照样可以生存。
《新周刊》:虽然你认为中国的教育操作系统有很多令人失望之处,但无法否认你依然是由此系统下制造出的程序,你认为自己有没有什么获益之处?你会坚持把退学进行到底吗?
王垠:获益之处肯定是有的。所以我才指出它的问题,希望能改善,而没有把教育系统当作敌人。
我会把退学坚持到底的。虽然得到很多好处,但是我觉得我不配得到一个博士学位。
《新周刊》:无力改变的人全都选择了离开,有没有设想今后的自己会朝着哪个方向去努力,会不会回来为令人担忧的中国教育操作系统书写一个崭新的程序呢?
王垠:离开当然是为了获得力量后再回来。我相信一切会好起来的。
我记得我在退学申请的最后曾经说过:“其实我不后悔进入川大,不后悔来到清华,珍惜一切的历史,因为没有它们,我也许就不是现在的我,有着自己想法的我。我也许就在安逸的生活中变得堕落。它们不完美甚至给我痛苦,但是我还是珍惜,珍惜这里的朋友,这里的一草一木。也许这就是爱。我会变得更好,我会挂念我的满目疮痍的祖国母亲。我会回来告诉你我学到的一切,我会给你和其他儿女真正的幸福,一定的!”这就是我最想说的。
19495设 -
∞
<X1< X2<……<Xn< +
∞
(n>=2),并设次数不超过n-1的代数多项式Ck(X)(k=1,2,……,n)满足条件:
Ck(Xi)=1,i=k ;
Ck(Xi)=0,i
≠
k.
试证:Ck(X)+Ck+1(X)>=
1,Xk<=X<=Xk+1,1<=k<=n-1.(k+1为下标)。
另:线空V上的线变A具有什么特征时只有有限个不变子空间,若有限,如何求出所有A-不变?
19495我只知道:
若A _{n}在F中有n个不同的特征值,则对应的线性变换恰有2 ^{n}个不变子空间;
若A
^{n} =0,而A ^{n-1}

0,则对应的线性变换恰有n+1个不变子空间;
19495顶一下
19495顶顶顶
19495………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………
19495re
19495!!!!?????
19495^^^^^^^^^^^^^^^^^
19495好
19495ding ding
19495yTGJHL
19495
http://www.math.org.cn/forums/index.php?show...topic=
18078&hl=
19495为何没人?!
19497据我所知,中科院许多专业硕博连读;我现在读中科院的在职研究生,计算机应用技术专业,太差劲了!老师不认真教,我们不认真听!
19497教学方式也是填鸭式。从小到大习惯了,可能别的学习方式我们还不适应!
19497还是北大清华好!
19498谁能告诉我现在能分解的大整数是多少?感谢!!
19498150位左右的十进制数
19498
引用 (chinhuazhao @ 2005年10月
18日
14时27分) |
|
谁能告诉我现在能分解的大整数是多少?感谢!! |
2
2 n
-1=(2
n
-1)(2
n
+1)
这里的n要多大就可以有多大!
19498
| 引用 (magic9901 @ 2005年11月14日
11时43分) |
2
2 n
-1=(2
n
-1)(2
n
+1)
这里的n要多大就可以有多大!
|
很感谢各位的回复,不过我还是有问题:
如果n很大时只是存储量就有一个问题,
并且这是一个特别的情况,于一般的情况呢?
对于任意给定的一个数现在能分解到多大呢?
有这方面的文章吗?
多谢!
19501Thx!
19501谢谢了,我也早知道了,那是个好地方
19501虽然早知道这个地方,并收藏之,还是谢谢你了
19501我要一个!
19501尽管我已经知道了
还是要谢谢楼主
资源共乡
19501
 http://elmo.jlu.edu.cn/index.asp
http://elmo.jlu.edu.cn/index.asp 
本站是吉林大学普通一员Elmo所建, 本站资源主要为数学类资源, 包括2000年以来Elmo所收集到的数学书籍和数学软件, 同时,
本站还提供大家日常所需软件资源. 同时, 根据实际情况本站将随时提供大家日常关心的信息.
本站的下载多数提供ftp链接,
您也可以直接登陆Elmo's ftp直接下载资源, 地址: elmo.jlu.edu.cn, 提供匿名下载,
为了得到更多资源请使用帐号/密码: math/math2004
登陆.
本站资源仅为教育网内学习、科研使用。任何个人或团体不得将本站资源用于商业用途,对于由此引发的任何纠纷,本人概不负责。[URL=http://elmo.jlu.edu.cn/Kaoyan/index.asp]考研特区
19501以前已有人((免費))貼過 , 吉林大學elmo站
19501这个网站我早就知道了!!
19501那里是个好地方
19501好象速度太慢了
19501非常非常感谢!!!
19501绝对好东西,感谢楼主分享了
19501尽管早就知道了,还是要感谢楼主和我们一起分享
19501呵呵 确实以前就有帖子 不过还是谢谢了
19501早就知道了
19501我不知道以前有没有,也不管以前有没有,这是我的发现.我那麽多积分,只是不希望不劳而获而已,象征性卖一分!
19501谢谢
19501我换钱
19501谢谢楼主
我晕
那些早知道的不早说
19501不错
19501真是个好网站
19501非常非常感谢!!!
19501up
19501怎么看不到啊?
19501怎么连不上去?
19501要了
19501真好,谢谢~

19501很喜欢这个网站,顶一个!
19501呵呵
19501^_^



19501怎么搞钱
19501挺好!吉大elmo真好!
19501谢谢 来到这个论坛 佩服大家
19501几米多维奇中文的么
19501不过有的时候进不去啊?
19501好网 已经收藏了
19501thank you
19501绝对好东西,感谢楼主分享了
19501谢谢,顶了
19501我早就知道了,怎么这样赚取积分呢?
19501好站,顶!!!
19501多谢了, 可惜新手没钱
19501是个好地方 hehe
19501不知怎么,最近上不去了
19502帮忙一下post-38-11296
174
18.ibf
19502这个题目主要是利用一个经典的不等式子(1+1/x)^x<e<(1+1/x)^(x+1),可以把这个不等式取对数,然后在结合这经典不等式的取对数之后的情况来结合处理!
第二种方法就是结合连续函数的求极值的方法来处理,在处理的过程中要适当的注意进行防缩,这个有可能需要!
19503请教:如何在Delphi中调用lingo?
最近想作一个程序,在Delphi做的前台输入参数,在lingo计算,然后将计算结果返回到Delphi的前台。
有人告诉我可以用lindoapi,但是我是个新手,以前没弄过lingo和lindoapi,
不知道如果实现,请各位帮忙说详细些,先谢了^_^
19504数学和中国文学的比较
丘成桐
二零零五年六月二十四日
很多人会觉得我今日的讲题有些奇怪,中国文学与数学好象是风马牛不相及,
但我却讨论它。其实这关乎个人的感受和爱好,不见得其它数学家有同样的感觉,
“如人饮水,冷暖自知”。每个人的成长和风格跟他的文化背景、家庭教育有莫
大的关系。我幼受庭训,影响我至深的是中国文学,而我最大的兴趣是数学,所
以将他们做一个比较,对我来说是相当有意义的事。
中国古代文学记载最早的是诗三百篇,有风雅颂,既有民间抒情之歌,朝廷
礼仪之作,也有歌颂或讽刺当政者之曲。至孔子时,文学为君子立德和陶冶民风
而服务。战国时,诸子百家都有著述,在文学上有重要的贡献,但是诸子如韩非
却轻视文学之士。屈原开千古辞赋之先河,毕生之志却在楚国的复兴。文学本身
在古代社会没有占据到重要的地位。司马迁甚至说:“文史、星历,近乎卜祝之
间,固主上所戏弄,倡优畜之,流俗之所轻也。”一直到曹丕才全面肯定文学本
身的重要性:“盖文章,经国之大业,不朽之盛事。”即使如此,曹丕的弟弟曹
植却不以为文学能与治国的重要性相比。他写信给他的朋友杨修说:
“吾虽德薄,位为蕃侯,犹几戮力上国,流惠下民,建永世之业,留金石之
功。岂徒以翰墨为勋绩,辞赋为君子哉。”
至于数学,中国儒家将它放在六艺之末,是一个辅助性的学问。当政者更视
之为雕虫小技,与文学比较,连歌颂朝廷的能力都没有,政府对数学的尊重要到
近年来才有极大的改进。西方则不然,希腊哲人以数学为万学之基。帕拉图以通
几何为入其门槛之先决条件,所以数学家得到崇高地位,在西方蓬勃发展了两千
多年。
一、数学之基本意义
数学之为学,有其独特之处,它本身是寻求自然界真相的一门科学,但数学
家也如文学家般天马行空,凭爱好而创作,故此数学可说是人文科学和自然科学
的桥梁。
数学家研究大自然所提供的一切素材,寻找它们共同的规律,用数学的方法
表达出来。这里所说的大自然比一般人所了解的来得广泛,我们认为数字、几何
图形和各种有意义的规律都是自然界的一部份,我们希望用简洁的数学语言将这
些自然现象的本质表现出来。
数学是一门公理化的科学,所有命题必需由三段论证的逻辑方法推导出来,
但这只是数学的形式,而不是数学的精髓。大部份数学著作枯燥乏味,而有些却
令人叹为观止,其中的分别在那里?
大略言之,数学家以其对大自然感受的深刻肤浅,来决定研究的方向,这种
感受既有其客观性,也有其主观性,后者则取决于个人的气质,气质与文化修养
有关,无论是选择悬而未决的难题,或者创造新的方向,文化修养皆起着关键性
的作用。文化修养是以数学的功夫为基础,自然科学为副,但是深厚的人文知识
也极为要紧,因为人文知识也致力于描述心灵对大自然的感受,所以司马迁写史
记除了“通古今之变”外,也要“究天人之际”。
刘勰在文心雕龙.原道篇说文章之道在于:
“写天地之辉光,晓生民之耳目。”
刘勰以为文章之可贵,在尚自然,在贵文采。他又说:
“人与天地相参,乃性灵所集聚,是以谓之三才,为五行之秀气,实天地之
灵气。灵心既生,于是语言以立。语言既立,于是文章着明,此亦原于自然之道
也。”
文心雕龙.风骨:
“诗总六义,风冠其首,斯乃化感之本源,志气之符契也。”
历代的大数学家如阿基米德如牛顿莫不以自然为宗,见物象而思数学之所出,
即有微积分的创作。费尔玛和尤拉对变分法的开创性发明也是由于探索自然界的
现象而引起的。
近代几何学的创始人高斯认为几何和物理不可分,他说:“我越来越确信几
何的必然性无法被验证,至少现在无法被人类或为了人类而验证,我们或许能在
未来领悟到那无法知晓的空间的本质。我们无法把几何和纯粹是先验的算术归为
一类,几何和力学却不可分割。”
二十世纪几何学的发展,则因物理学上重要的突破而屡次改变其航道。当狄
拉克把狭义相对论用到量子化的电子运动理论时,发现了狄拉克方程,以后的发
展连狄拉克本人也叹为观止,认为他的方程比他的想象来得美妙,这个方程在近
代几何的发展起着关键性的贡献,我们对旋子的描述缺乏直观的几何感觉,但它
出于自然,自然界赋予几何的威力可说是无微不至。
广义相对论提出了场方程,它的几何结构成为几何学家梦寐以求的对象,因
为它能赋予空间一个调和而完美的结构。我研究这种几何结构垂三十年,时而迷
惘,时而兴奋,自觉同诗经、楚辞的作者,或晋朝的陶渊明一样,与大自然浑为
一体,自得其趣。
捕捉大自然的真和美,实远胜于一切人为的造作,正如文心雕龙说的:
“云霞雕色,有逾画工之妙。草木菁华,无待锦匠之奇,夫岂外饰,盖自然
耳。”
在空间上是否存在满足引力场方程的几何结构是一个极为重要的物理问题,
它也逐渐地变成几何中伟大的问题。尽管其它几何学家都不相信它存在,我却锲
而不舍,不分昼夜地去研究它,就如屈原所说:
“亦余心之所善兮,虽九死其犹未悔。”
我花了五年工夫,终于找到了具有超对称的引力场结构,并将它创造成数学
上的重要工具。当时的心境,可以用以下两句来描述:
“落花人独立,微雨燕双飞。”
以后大批的弦理论学家参与研究这个结构,得出很多深入的结果。刚开始时,
我的朋友们都对这类问题敬而远之,不愿意与物理学家打交道。但我深信造化不
致弄人,回顾十多年来在这方面的研究尚算满意,现在卡拉比-丘空间的理论已
经成为数学的一支主流。
二、数学的文采
数学的文采,表现于简洁,寥寥数语,便能道出不同现象的法则,甚至在自
然界中发挥作用,这是数学优雅美丽的地方。我的老师陈省身先生创作的陈氏类,
就文采斐然,令人赞叹。它在扭曲的空间中找到简洁的不变量,在现象界中成为
物理学界求量子化的主要工具,可说是描述大自然美丽的诗篇,直如陶渊明“采
菊东蓠下,悠然见南山”的意境。
从欧氏几何的公理化、到笛卡儿创立的解析几何,到牛顿、莱布尼兹的微积
分,到高斯、黎曼创立的内蕴几何,一直到与物理学水乳相融的近代几何,都以
简洁而富于变化为宗,其文采绝不逊色于任何一件文学创作,它们轫生的时代与
文艺兴起的时代相同,绝对不是巧合。
数学家在开创新的数学想法的时候,可以看到高雅的文采和崭新的风格,例
如欧几里得证明存在无穷多个素数,开创反证法的先河。高斯研究十七边形的对
称群,使伽罗华群成为数论的骨干。这些研究异军突起,论断华茂,使人想起五
言诗的始祖苏(武)李(陵)唱和诗和词的始祖李太白的忆秦娥。
三、数学中的赋比兴
中国诗词都讲究比兴,钟爃在“诗品”中说:
“文已尽而意有余,兴也。因物喻志,比也。”
刘勰在文心雕龙中说:
“故比者,附也。兴者,起也。附理者切类以指事,起情者依微以拟议。起
情故兴体以立,附理故比例以生。”
白居易:
“噫,风雪花草之物《三百篇》中岂含之乎?顾所用何如耳,设如北风其凉,
假风以刺威虐也,雨雪霏霏,因雪以愍征役也……比兴发于此而义归于彼。”
他批评谢朓诗“‘余霞散成绮,澄江净如练。’丽则丽矣,吾不知其所讽焉,
故仆所谓嘲风雪,弄花草而已,文意尽去矣。”
有深度的文学作品必需要有“义”、有“讽”、有“比兴”。数学亦如是。
我们在寻求真知时,往往只能凭已有的经验,因循研究的大方向,凭我们对大自
然的感觉而向前迈进,这种感觉是相当主观的,因个人的文化修养而定。
文学家为了达到最佳意境的描述,不见得忠实地描写现象界,例如贾岛只追
究“僧推月下门”或是“僧敲月下门”的意境,而不在乎所说的是不同的事实。
数学家为了创造美好的理论,也不必依随大自然的规律,只要逻辑推导没有问题,
就可以尽情的发挥想象力,然而文章终究有高下之分。大致来说,好的文章“比
兴”的手法总会比较丰富。
中国古诗十九首,作者年代不详,但大家都认为是汉代的作品。刘勰说:
“比采而推,两汉之作乎。”这是从诗的结构和风格进行推敲而得出的结论。在
数学的研究过程中,我们亦利用比的方法去寻找真理。我们创造新的方向时,不
必凭实验,而是凭数学的文化涵养去猜测去求证。
举例而言,三十年前我提出一个猜测,断言三维球面里的光滑极小曲面,其
第一特征值等于二。当时这些曲面例子不多,只是凭直觉,利用相关情况模拟而
得出的猜测,最近有数学家写了一篇文章证明这个猜想。其实我的看法与文学上
的比兴很相似。
我们看洛神赋:
“翩若惊鸿,婉若游龙。荣曜秋菊,华茂春松。仿彿兮若轻云之蔽月,飘飘
兮若流风之回雪。”
由比喻来刻划女神的体态,又看诗经:
“高山仰止,景行行止。四牡騑騑,六辔如琴,靓尔新婚,以慰我心。”
也是用比的方法来描写新婚的心情。
我一方面想象三维球的极小子曲面应当是如何的匀称,一方面想象第一谱函
数能够同空间的线性函数比较该有多妙,通过原点的平面将曲面最多切成两块,
于是猜想这两个函数应当相等,同时第一特征值等于二。
当时我与卡拉比教授讨论这个问题,他也相信这个猜测是对的。旁边我的一
位研究生问为甚么会做这样的猜测,不待我回答,卡教授便微笑说这就是洞察力
了。
数学上常见的对比方法乃是低维空间和高维空间现象的对比。我们虽然看不
到高维空间的事物,但可以看到一维或二维的现象,并由此来推测高维的变化。
我在做研究生时企图将二维空间的单值化原理推广到高维空间,得到一些漂亮的
猜测,我认为曲率的正或负可以作为复结构的指向,这个看法影响至今,可以溯
源到十九世纪和二十世纪初期曲率和保角映像关系的研究。
另外一个对比的方法乃是数学不同分枝的比较,记得我从前用爱氏结构证明
代数几何中一个重要不等式时,日本数学家Miyaoka利用俄国数学家
Bogomolov
的代数稳定性理论也给出这个不等式的不同证明,因此我深信爱氏结构和流形的
代数稳定有密切的关系,这三十年来的发展也确是朝这个方向蓬勃地进行。
事实上,爱因斯坦的广义相对论也是对比各种不同的学问而创造成功的,它
是科学史上最伟大的构思,可以说是惊天地而泣鬼神的工作。它统一了古典的引
力理论和狭义相对论。爱氏花了十年功夫,基于等价原理,比较了各种描述引力
场的方法,巧妙地用几何张量来表达了引力场,将时空观念全盘翻新。
爱氏所用的工具是黎曼几何,乃是黎曼比他早五十年前发展出来的,当时的
几何学家唯一的工具是对比,在古典微积分、双曲几何和流形理论的模拟后得出
来的漂亮理论。反过来说,广义相对论给黎曼几何注入了新的生命。
二十世纪数论的一个大突破乃是算术几何的产生,利用群表示理论为桥梁,
将古典的代数几何、拓朴学和代数数论比较,有如瑰丽的歌曲,它的发展,势不
可挡,气势如虹,“天之所开,不可当也”。
Weil研究代数曲线在有限域上解的问题后,得出高维代数流形有限域解的猜
测,推广了代数流形的基本意义,直接影响了近代数学的发展。筹学所问,无过
于此矣。
伟大的数学家远瞩高瞻,看出整个学问的大流,有很多合作者和跟随者将支
架建立起来,解决很多重要的问题。正如曹雪芹创造红楼梦时,也是一样,全书
既有真实,亦有虚构。既有前人小说如西厢记、金瓶梅、牡丹亭等的踪迹,亦有
作者家族雕零、爱情悲剧的经验,通过各种不同人物的话语和生命历程,道出了
封建社会大家族的腐败和破落。红楼梦的写作影响了清代小说垂二百年。
西厢记和牡丹亭的每一段写作和描述男女主角的手法都极为上乘,但是全书
的结构则是一般的佳人才子写法,由金瓶梅进步到红楼梦则小处和大局俱佳。
这点与数学的发展极为相似,从局部的结构发展到大范围的结构是近代数学
发展的一个过程。往往通过比兴的手法来处理。几何学和数论都有这一段历史,
代数几何学家在研究奇异点时通过爆炸的手段,有如将整个世界浓缩在一点。微
分几何和广义相对论所见到的奇异点比代数流形复杂,但是也希望从局部开始,
逐渐了解整体结构。数论专家研究局部结构时则通过素数的模方法,将算术流形
变成有限域上的几何,然后和大范围的算术几何对比,得出丰富的结果。数论学
家在研究
Langlands理论时也多从局部理论开始。
好的作品需要赋比兴并用。钟爃诗品:
“直书其事,寓言写物,赋也。宏斯三义,酌而用之,干之以风力,润之以
丹采,使味之者无极,闻之者动心,是诗之至也。若专用比兴,则患在意深,意
深则词踬。若但用赋体,则患在意浮,意浮则文散。”
在数学上,对非线性微分方程和流体方程的深入了解,很多时需要靠计算器
来验算。很多数学家有能力做大量的计算,却不从大处着想,没有将计算的内容
与数学其它分枝比较,没有办法得到深入的看法,反过来说只讲观念比较,不作
大量计算,最终也无法深入创新。
有些工作却包含赋比兴三种不同的精义。近五十年来数论上一个伟大的突破
是由英国人Birch和Swinneton-Dyer提出的一个猜测,开始时用计算器大量计算,
找出L函数和椭圆曲线的整数解的连系,与数论上各个不同的分枝比较接合,妙
不可言,这是赋比兴都有的传世之作。
四、数学家对事物的看法的多面性
由于文学家对事物有不同的感受,同一事或同一物可以产生不同的吟咏。例
如对杨柳的描述:
温庭筠:
“柳丝长,春雨细……”
吴文英:
“一丝柳,一寸柔情,料峭春寒中酒……”
李白:
“年年柳色,灞陵伤别。”
“风吹柳花满座香,吴姬压酒劝客尝。”
周邦彦:
“柳阴直,烟里丝丝弄碧,隋堤上,曾见几番,拂水飘绵送行色……长亭路,
年去岁来,应折柔条过千尺。”
晏几道:
“舞低杨柳楼心月,歌尽桃花扇底风。”
柳枝既然是柔条,又有春天时的嫩绿,因此可以代表柔情,女性体态的柔软
(柳腰、柳眉都是用柳条来描写女性),又可以描写离别感情和青春的感觉。
对事物有不同的感受后,往往通过比兴的方法另有所指,例如“美人”有多
重意思,除了指美丽的女子外,也可以指君主:屈原九章“结微情以陈词兮,矫
以遗夫美人。”也可以指品德美好的人:诗经邶风:“云谁之思,西方美人。”
苏轼赤壁赋“望美人兮天一方”。
数学家对某些重要的定理,也会提出很多不同的证明。例如勾股定理的不同
证明有十个以上,等周不等式亦有五、六个证明,高斯则给出数论对偶定律六个
不同的看法。不同的证明让我们以不同的角度去理解同一个事实,往往引导出数
学上不同的发展。
记得三十年前我利用分析的方法来证明完备而非紧致的正曲率空间有无穷大
体积后,几何学家Gromov开始时不相信这个证明,以后他找出我证明方法的几何
直观意义后,发展出他的几何理论,这两个不同观念都有它们的重要性。
小平邦彦有一个极为重要的贡献叫做消灭定理,是用曲率的方法来得到的,
它在代数几何学上有奠基性的贡献,代数几何学家却不断的企图找寻一个纯代数
的证明,希望对算术几何有比较深入的了解。
对空间中的曲面,微分几何学家会问它的曲率如何,有些分析学家希望沿着
曲率方向来推动它一下看看有甚么变化,代数几何学家可以考虑它可否用多项式
来表示,数论学家会问上面有没有整数格点。这种种主观的感受由我们的修养来
主导。
反过来说,文学家对同一事物亦有不同的歌咏,但在创作的工具上,却有比
较统一的对仗韵律的讲究,可以应用到各种不同的文体。从数学的观点来说,对
仗韵律是一种对称,而对称的观念在数学发展至为紧要,是所有数学分枝的共同
工具。另外,数学家又喜欢用代数的方法来表达空间的结构,同调群乃是重要的
例子,由拓朴学出发而应用到群论、代数、数论和微分方程学上去。
五、数学的意境
王国维在人间词话说:
“词以境界为最上。有境界则自成高格……有造境,有写境,此理想与写实
二派之所由分。然二者颇难分别,因大诗人所造之境必合乎自然,所写之境亦必
邻于理想故也。有有我之境,有无我之境。‘泪眼问花花不语,乱红飞过秋千
去。’……有我之境也。‘采菊东蓠下,悠然见南山。’……无我之境也。有我
之境,以我观物,故物皆着我之色彩。无我之境,以物观物,故不知何者为我,
何者为物……无我之境,人唯乎静中得之。有我之境,于由动入静时得之,故一
优美,一宏壮也。自然之物互相关系,互相限制。然其写之于文学及美术中也,
必有其关系限制之处。故虽写实家亦理想家也。又虽如何虚构之境,其材料必求
之于自然,而其构造亦必从自然之法律。故虽理想家亦写实家也。”
数学研究当然也有境界的概念,在某种程度上也可谈有我之境、无我之境,
当年尤拉开创变分法和推导流体方程,由自然现象引导,可谓无我之境,他又凭
自己的想象力研究发散级数,而得到zeta函数的种种重要结果,开三百年数论之
先河,可谓有我之境矣。另外一个例子是法国数学家
Grothendick,他著述极丰,
以个人的哲学观点和美感出发,竟然不用实例,建立了近代代数几何的基础,真
可谓有我之境矣。
在几何的研究中,我们发现狄拉克在物理上发现的旋子在几何结构中有魔术
性的能力,我们不知道它的内在的几何意义,它却替我们找到几何结构中的精髓,
在应用旋子理论时,我们常用的手段是通过所谓消灭定理而完成的,这是一个很
微妙的事情,我们制造了曲率而让曲率自动发酵去证明一些几何量的不存在,可
谓无我之境矣。以前我提出用Einstein结构来证明代数几何的问题和用调和映像
来看研究几何结构的刚性问题也可作如是观。
不少伟大的数学家,以文学、音乐来培养自己的气质,与古人神交,直追数
学的本源,来达到高超的意境。
文心雕龙.神思:
“文之思也,其神远矣。故寂然凝虑,思接千载;悄然动容,视通万里。吟
咏之间,吐纳珠玉之声,眉睫之前,卷舒风云之色,其思理之致乎。”
六、数学的品评
好的工作应当是文已尽而意有余,大部份数学文章质木无文,流俗所好,不
过两三年耳。但是有创意的文章,未必为时所好,往往十数年后始见其功。
我曾经用一个崭新的方法去研究调和函数,以后和几个朋友一同改进了这个
方法,成为热方程的一个重要工具。开始时没有得到别人的赞赏,直到最近五年
大家才领会到它的潜力。然而我们还是锲而不舍地去研究,觉得意犹未荆
我的老师陈省身先生在他的文集中引杜甫诗“文章千古事,得失寸心知。”
而杜甫就曾批评初唐四杰的作品“王杨卢骆当时体,轻薄为文哂未休,尔曹身与
命俱灭,不废江河万古流。”
时俗所好的作品,不必为作者本人所认同。举个例子,白居易留传至今的诗
甚多,最出名之一是《长恨歌》,但他给元微之的信中却说:
“及再来长安,又闻有军使欲聘倡伎,伎大夸曰:‘我诵得白学士《长恨
歌》,岂同他伎哉。’……偖伎见仆来,指而相顾曰:‘此是《秦中吟》、《长
恨歌》主耳。’自长安抵江西,三四千里……每每有咏仆诗者,此诚雕虫之技,
不足为多,然今时俗所重,正在此耳。”
白居易说谢朓的诗丽而无讽。其实建安以后,绮丽为文的作者甚众。亦自有
其佳处,毕竟钟爃评谢朓诗为中品,以后六朝骈文、五代花间集以至近代的鸳鸯
蝴蝶派都是绮丽为文。虽未殝上乘,却有赏心悦目之句。
数学华丽的作品可从泛函分析这种比较广泛的学问中找到,虽然有其美丽和
重要性,但与自然之道总是隔了一层。举例来说,从函数空间抽象出来的一个重
要概念叫做巴拿赫空间,在微分方程学有很重要的功用,但是以后很多数学家为
了研究这种空间而不断的推广,例如有界算子是否存在不变空间的问题,确是漂
亮,但在数学大流上却未有激起任何波澜。
在七十年代,高维拓朴的研究已成强弩之末,作品虽然不少,但真正有价值
的不多,有如“野云孤飞,去留无迹。”文气已尽,再无新的比兴了。当时有拓
朴学者做群作用于流形的研究,确也得到某些人的重视。但是到了八零年代,值
得怀念的工作只有Bott的局部化定理。
能经得起时间考验的工作寥寥无几,政府评审人材应当以此为首眩历年来
以文章篇数和被引用多寡来做指针,使得国内的数学工作者水平大不如人,不单
与自然隔绝,连华丽的文章都难以看到。
七、数学的演化
王国维说:
“四言敝而有楚辞,楚辞敝而有五言,五言敝而有七言,古诗敝而有律绝,
律绝敝而有词。盖文体通行既久,染指遂多,自成习套。豪杰之士亦难于其中自
出新意,故遁而作他体以自解脱。一切文体所以始盛中衰者,皆由于此,故谓文
体后不如前,余未敢言。但就一体论,则此说固无以易也。”
数学的演化和文学有极为类似的变迁。从平面几何至立体几何,至微分几何
等等,一方面是工具得到改进,另一方面是对自然界有进一步的了解,将原来所
认识的数学结构的美发挥尽至后,需要进入新的境界。江山代有人才,能够带领
我们进入新的境界的都是好的数学。上面谈到的高维拓朴文气已尽,假使它能与
微分几何、数学物理和算术几何组合变化,亦可振翼高翔。
我在香港念数学时,读到苏联数学家Gelfand的看法,用函数来描述空间的
几何性质,使我感触良深,以后在研究院时才知道。代数几何学家也用有理函数
来定义代数空间,于是我猜想一般的黎曼流形应当也可以用函数来描述空间的结
构。但是为了深入了解流形的几何性质,我们需要的函数必需由几何引出的微分
方程来定义。可是一般几何学家厌恶微分方程,我对它却情有独钟,与几个朋友
合作将非线性方程带入几何学,开创了几何分析这门学问,解决了拓朴学和广义
相对论一些重要问题。在一九八一年时我建议我的朋友Hamilton用他创造的方程
去解决三维拓朴的基本结构问题,二十多年来他引进了不少重要的工具,运用上
述我和李伟光在热方程的工作,深入地了解奇异点的产生。两年前俄国数学家
Perelman更进一步地推广了这个理论,很可能完成了我的愿望,将几何和三维拓
朴带进了新纪元。
八年前我访问北京,提出全国向Hamilton先生学习的口号,本来讨论班已经
进行,却给一些急功近利的北京学者阻止,在国外也遇到同样的阻力,中国几何
分析不能进步都是由于年青学者不能够自由发展思想的缘故。广州的朱熹平却锲
而不舍,他的工作已经远超国内外成名的中国学者。
当一个大问题悬而未决的时候,我们往往以为数学之难莫过于此。待问题解
决后,前途豁然开朗,看到比原来更为灿烂的火花,就会有不同的感受。
这点可以跟庄子秋水篇比较:
“秋水时至,百川灌河,泾流之大,两涘渚崖之间,不辩牛马。于是焉河伯
欣然自喜,以天下之美为尽在已,顺流而东行,至于北海,东面而视,不见水端,
于是焉河伯始旋其面目,望洋向若而叹曰:‘野语有之曰:‘闻道百,以为莫已
若者,我之谓也。且夫我尝闻少仲尼之闻,而轻伯夷之义者,始吾弗信,今我睹
子之难穷也。吾非至于子之门,则殆矣。吾长见笑于大方之家。’’”
科学家对自然界的了解,都是循序渐进,在不同的时空自然会有不同的感受。
有学生略识之无后,不知创作之难,就连陈省身先生的大作都看不上眼,自以为
见识更为丰富,不自见之患也。人贵自知,始能进步。
庄子:
“今尔出于崖涘,观于大海,乃知尔丑,尔将可与语大理矣。”
我曾经参观德国的葛庭根大学,看到十九世纪和廿世纪伟大科学家的手稿,
他们传世的作品只是他们工作的一部份,很多杰作都还未发表,使我深为惭愧而
钦佩他们的胸襟。今人则不然,大量模仿,甚至将名作稍为改动,据为己有,尽
快发表。或申请院士,或自炫为学术宗匠,于古人何如哉。
八、数学的感情
为了达到深远的效果,数学家需要找寻问题的精华所在,需要不断的培养我
们对问题的感情和技巧,这一点与孟子所说的养气相似。气有清浊,如何寻找数
学的魂魄,视乎我们的文化修养。
白居易说:
“圣人感人心而天下和平,感人心者,莫先乎情,莫始乎言,莫切乎声,莫
深乎义……未有声入而不应,情交而不感者。”
严羽沧浪诗话:
“盛唐诸公唯在兴趣,羚羊挂角,无迹可求。故其妙处透澈玲珑,不可凑拍,
如空中之音,相中之色,水中之影,镜中之象,言有尽而意无穷。”
我的朋友Hamilton先生,他一见到问题可以用曲率来推动,他就眉飞色舞。
另外一个澳洲来的学生,见到与爱因斯坦方程有关的几何现象就赶快找寻它的物
理意义,兴奋异常,因此他们的文章都是清纯可喜。反过来说,有些成名的学者,
文章甚多,但陈陈相因,了无新意。这是对自然界、对数学问题没有感情的现象,
反而对名位权力特别重视。为了院士或政协委员的名衔而甘愿千里仆仆风尘地奔
波,在这种情形下,难以想象他们对数学、对自然界有深厚的感情。
数学的感情是需要培养的,慎于交友才能够培养气质。博学多闻,感慨始深,
堂庑始大。欧阳永叔:
“人间自是有情痴,此恨不关风与月。”
“直须看尽洛城花,始与东风容易别。”
能够有这样的感情,才能够达到晏殊所说:
“昨夜西风雕碧树,独上高楼,望尽天涯路。”
浓厚的感情使我们对研究的对象产生直觉,这种直觉看对象而定,例如在几
何上叫做几何直觉。好的数学家会将这种直觉写出来,有时可以用来证明定理,
有时可以用来猜测新的命题或提出新的学说。
但数学毕竟是说理的学问,不可能极度主观。诗经蓼莪、黍离,屈原离骚、
九江,汉都尉河梁送别,陈思王归藩伤逝,李后主忆江南,宋徽宗念故宫,俱是
以血书成、直抒胸臆,非论证之学所能及也。
九、数学的应用
王国维说:
“诗人对宇宙人生须入乎其内,又须出乎其外。入乎其内,故能写之,出乎
其外,故能观之,入乎其内,故有生气,出乎其外,故有高致。美成能入而不能
出,白石以降,二事皆未梦见。”
“词之雅郑,在神不在貌。永叔少游虽作艳语,终有品格,方之美成,便有
淑女与倡伎之别。”
数学除与自然相交外,也与人为的事物相接触,很多数学问题都是纯工程上
的问题。有些数学家毕生接触的都是现象界的问题,可谓入乎其内。大数学家如
尤拉、如富里哀、如高斯、如维纳、如冯纽曼等都能入乎其内,出乎其外,既能
将抽象的数学在工程学上应用,又能在实用的科学中找出共同的理念而发展出有
意义的数学。反过来说,有些应用数学家只用计算器作出一些计算,不求甚解,
可谓二者皆未见矣。
富里哀在研究波的分解时,得出富里哀级数的展开方法,不但成为应用科学
最重要的工具,在基本数学上的贡献也是不可磨灭的。近代孤立子的发展和几何
光学的研究,都在基本数学上占了一个重要的位置。
应用数学对基本数学的贡献可与元剧比较。王国维评元剧:
“其作剧也,非有藏之名山,传之其人之意也,彼以意兴之所至为之,以自
娱娱人,关目之拙劣,所不问也;思想之卑陋,所不讳也;人物之矛盾,所不顾
也。彼但摹写其胸中之感想与时代之情状,而真挚之理与秀杰之气时流露于其
间。”
例如金融数学旨在谋利,应用随机过程理论,间有可观的数学内容。正如王
国维评古诗“何不策高足,先据要路津,无为久贫贱,轗轲长苦辛。”认为“无
视其鄙者,以其真也。”伟大的数学家高斯就是金融数学的创始人,他本人投资
股票而获利,Klein则研究保险业所需要的概率论。
然而近代有些应用数学家以争取政府经费为唯一目标,本身无一技之长,却
巧立名目,反诬告基本数学家对社会没有贡献,尽失其真矣。有如近代小说以情
欲、仇杀、奸诈为主题,取宠于时俗,不如太史公刺客列传中所说:
“自曹沫至荆轲五人,此其义或成或不成,然其立意较然,不欺其志,名垂
后世,岂妄也哉。”
应用数学家不能立意皎然,而妄谈对社会有贡献,恐怕是缘木求鱼了。
十、数学的训练
好的数学家需要领会自然界所赋予的情趣,因此也须向同道学习他们的经验。
然而学习太过,则有依傍之玻顾亭林云:
“君诗之病在于有杜,君文之病在于有韩,欧。有此蹊径于胸中,便终身不
脱依傍二字,断不能登峰造极。”
今人习数学,往往依傍名士,凡海外毕业的留学生,都为佳士,孰不知这些
名士泰半文章与自然相隔千万里,画虎不成反类犬矣。李义山:
“刘郎已恨蓬山远,更隔蓬山一万重。”
很多研究生在跟随名师时,做出第一流的工作,毕业后却每况愈下,就是依
傍之过。更有甚者,依傍而不自知,由导师提携指导,竟自炫“无心插柳柳成
荫”,难有创意之作矣。
有些学者则倚洋自重,国外大师的工作已经完成,除非另有新意,不大可能
再进一步发展。国内学者继之,不假
19505科学史的现实性还表现在为我们今日的科学研究提供经验教训和历史借鉴,以使我们明确科学研究的方向以少走弯路或错路,为当今科技发展决策的制定提供依据,也是我们预见科学未来的依据。多了解一些数学史知识,也不会致使我们出现诸如解决三等分角作图、证明四色定理等荒唐事,也避免我们在费尔马大定理等问题上白废时间和精力。同时,总结我国数学发展史上的经验教训,对我国当今数学发展不无益处。
(2)数学史的文化意义
美国数学史家m.克莱因曾经说过:“一个时代的总的特征在很大程度上与这个时代的数学活动密切相关。这种关系在我们这个时代尤为明显”。“数学不仅是一种方法、一门艺术或一种语言,数学更主要是一门有着丰富内容的知识体系,其内容对自然科学家、社会科学家、哲学家、逻辑学家和艺术家十分有用,同时影响着政治家和神学家的学说”。数学已经广泛地影响着人类的生活和思想,是形成现代文化的主要力量。因而数学史是从一个侧面反映的人类文化史,又是人类文明史的最重要的组成部分。许多历史学家通过数学这面镜子,了解古代其他主要文化的特征与价值取向。古希腊(公元前600年-公元前300年)数学家强调严密的推理和由此得出的结论,因此他们不关心这些成果的实用性,而是教育人们去进行抽象的推理,和激发人们对理想与美的追求。通过希腊数学史的考察,就十分容易理解,为什么古希腊具有很难为后世超越的优美文学、极端理性化的哲学,以及理想化的建筑与雕塑。而罗马数学史则告诉我们,罗马文化是外来的,罗马人缺乏独创精神而注重实用。
(3)数学史的教育意义
当我们学习过数学史后,自然会有这样的感觉:数学的发展并不合逻辑,或者说,数学发展的实际情况与我们今日所学的数学教科书很不一致。我们今日中学所学的数学内容基本上属于
17世纪微积分学以前的初等数学知识,而大学数学系学习的大部分内容则是
17、
18世纪的高等数学。这些数学教材业已经过千锤百炼,是在科学性与教育要求相结合的原则指导下经过反复编写的,是将历史上的数学材料按照一定的逻辑结构和学习要求加以取舍编纂的知识体系,这样就必然舍弃了许多数学概念和方法形成的实际背景、知识背景、演化历程以及导致其演化的各种因素,因此仅凭数学教材的学习,难以获得数学的原貌和全景,同时忽视了那些被历史淘汰掉的但对现实科学或许有用的数学材料与方法,而弥补这方面不足的最好途径就是通过数学史的学习。
在一般人看来,数学是一门枯燥无味的学科,因而很多人视其为畏途,从某种程度上说,这是由于我们的数学教科书教授的往往是一些僵化的、一成不变的数学内容,如果在数学教学中渗透数学史内容而让数学活起来,这样便可以激发学生的学习兴趣,也有助于学生对数学概念、方法和原理的理解与认识的深化。
科学史是一门文理交*学科,从今天的教育现状来看,文科与理科的鸿沟导致我们的教育所培养的人才已经越来越不能适应当今自然科学与社会科学高度渗透的现代化社会,正是由于科学史的学科交*性才可显示其在沟通文理科方面的作用。通过数学史学习,可以使数学系的学生在接受数学专业训练的同时,获得人文科学方面的修养,文科或其它专业的学生通过数学史的学习可以了解数学概貌,获得数理方面的修养。而历史上数学家的业绩与品德也会在青少年的人格培养上发挥十分重要的作用。
中国数学有着悠久的历史,14世纪以前一直是世界上数学最为发达的国家,出现过许多杰出数学家,取得了很多辉煌成就,其渊源流长的以计算为中心、具有程序性和机械性的算法化数学模式与古希腊的以几何定理的演绎推理为特征的公理化数学模式相辉映,交替影响世界数学的发展。由于各种复杂的原因,16世纪以后中国变为数学入超国,经历了漫长而艰难的发展历程才渐渐汇入现代数学的潮流。由于教育上的失误,致使接受现代数学文明熏陶的我们,往往数典忘祖,对祖国的传统科学一无所知。数学史可以使学生了解中国古代数学的辉煌成就,了解中国近代数学落后的原因,中国现代数学研究的现状以及与发达国家数学的差距,以激发学生的爱国热情,振兴民族科学。
19505我想数学史有必要放到中学数学教学上去,至少我们可以在中学开设一些相关的课程,这样一方面可以提高学生对数学的兴趣,另一方面还可以让那些对数学原本感兴趣的同学沿正确的路子走,正如陈省身所说的,“做好的数学”。再就是学习数学史,对数学科学的学习也是很有帮助的,如一些定理什么的它们很多都有一些很有趣的故事,或者有一定的社会背景。让学生们了解这些对学习是很有帮助的!
19505同意,数学史确实很有用
19506为什么没有数学诺贝儿奖呢
19506据说诺贝尔怕他的情敌得奖呢?呵呵
19506
引用 (yzp471 @ 2005年10月
18日
15时09分) |
| 为什么没有数学诺贝儿奖呢
|
我比较认同史树中在《诺贝尔经济学奖与数学》中的说话
呵呵
他说一是诺贝尔偏于应用学科
二是当时有“奥斯卡奖”
史树中,诺贝尔经济学奖与数学,2002,清华大学出版社
19506好像是这样
19506听说是这样的
19506诺贝尔本人所接触的数学仅限于三角学和初等代数(数系和代数式),
他没有意识到高等的数学对于自然科学的重要意义,所以诺贝尔没设奖.
19506同意
19509转自 中国运筹学会
由香港运筹学会和中国运筹学会共同协助承办的2006年INFORMS (Institute for
Operations Research and Management
Science)国际学术大会将于2006年6月25-28日在中国香港举行(详情请见会议网站http://www.informs.org/Conf/Hongkong06/)。为了配合2006年INFORMS学术大会,《中国运筹学会2006年学术年会》将于2006年6月30日-7月2日在深圳召开,会议主题为:中国运筹学面向世界。
大会主席
袁亚湘(中国运筹学会理事长)
组织委员会
主 任:张汉勤(中国运筹学会秘书长)
副主任:刘德刚(中国运筹学会常务副秘书长)
委 员:胡洁、吴凌云、
程序委员会
主
任:胡晓东(中国运筹学会学术交流工作委员会主任)
副主任:修乃华、杨晓光(中国运筹学会学术交流工作委员会副主任)
委
员:曹炳元、曹晋华、程 兵、郭田德、龚循华、韩继业、胡毓达、胡智全、简金宝、刘宝碇、刘 斌、刘光中、刘
克、刘彦奎、李建平、李少远、唐国春、邢文训、闫桂英、张 峰、张汉勤、赵云彬
大会特邀报告
Mark S.
Daskin讲座教授
(INFORMS当选主席;美国西北大学,工业工程与管理科学系)
David D.
Yao讲座教授
(美国哥伦比亚大学,工业工程与运筹系)
陈光亚研究员
(中国科学院数学与系统科学研究院)
专题特邀报告
本届年会还将邀请参加2006年INFORMS大会的一些国际知名学者和专家分别针对五个领域做专题报告:金融工程、物流管理、随机规划、数学规划、离散优化,介绍国际上相关研究方向的发展状况和最新成果,以提高国内运筹学研究和应用的水平。
希望国内从事运筹学领域研究和应用的科技工作者和研究生,踊跃投稿和积极参加本次学术交流活动,抓住这次与国内外同行进行学术交流的难得的机会。
投稿注意事项
1. 提交的论文应未在其它学术会议论文集或者期刊上公开发表过。
2.
来稿请在注明通信作者的详细工作单位、通信地址(邮编)和电子邮件地址,及联系电话和传真。
3.
论文以中英文撰写均可(中文文章须附英文摘要,英文文章须附中文摘要)。
4.
论文限用CCT-LaTex或MS-Word两种软件排版,格式可在中国运筹学会网站(http://www.orsc.org.cn/)上下载。
5. 提交的论文由标题、作者、摘要、关键词、正文和参考文献构成。论文全文应不超过6页。
6.
投稿时必须提交论文的电子版和两份打印稿。论文电子版请通过电子邮件发到orsc2006@amt.ac.cn,打印稿请通过邮局寄到:
胡洁,中国运筹学会,北京2734信箱,北京100080。
7.
提交的论文将由相关专业方向的专家评审。所有被会议接受的论文将收录到由正式出版社出版的论文集中(论文集在会议期间发给作者)。被接受的论文的作者必须到会上报告自己的论文。
会议收费说明
1. 会议注册费:注册费须通过邮局用电子汇款汇寄给胡洁。
代表类别 提前注册
(2006年5月26日前汇款) 正常注册
(2006年5月26日以后)
会员 450元 550元
非会员 550元
650元
研究生 220元 320元
2.
版面费标准:每篇论文360元(最多6页;每增加一页加收60元);另外,采用MS-Word排版格式的,每页加收10元。版面费于2006年5月26日前汇寄给胡洁(请注明文章编号及作者;逾期未收到版面费,论文将不能收录到会议论文集中)。
3. 收费收据:会议注册费和版面费都将开正式发票,并在会议期间发给缴费人。
重要日期
1.
提交论文截至日期:2006年4月14日。
2. 发布论文录用或拒绝通知截至日期:2006年5月5日。
3.
提交论文修改稿和版面费截至日期:2006年5月
19日。
4. 提前交纳注册费截至日期:2006年5月26日。
5.
会议报到日:2006年6月29日。
6. 会议时间:2006年6月30日-7月2日。(30日晚召开理事会全体会议。)
其它事项
本通知未说明的事项(如会议的举办地点,住宿安排等),待第二轮通知说明,并刊登在国运筹学会网站2006年学术年会专栏上。
中国运筹学会
二零零五年九月十
19511拓扑空间有这样几个性质:连通性、可数性、分离性和紧致性。请问实数空间、度量空间、拓扑空间就这四种性质而言有什么内在的逻辑联系?
19511you can read about measure .
19511
引用 (lhky
1984 @ 2005年10月
18日
16时12分) |
|
拓扑空间有这样几个性质:连通性、可数性、分离性和紧致性。请问实数空间、度量空间、拓扑空间就这四种性质而言有什么内在的逻辑联系?
|
读一读日本人编的《数额百科辞典》上有一附图,给出了拓扑空间主要性质之间的逻辑关系。该书有中文版,请自己查一下。
19514求高等代数课件(北大)
19520matlab里面的那个改变部分元素的乔斯基分解R1 =
cholupdate(R,x)
只有N^2量级,我想问问大家他是如何实现的
我感觉他是指平均意义上的计算量.因为我觉得计算量和要该变的元素的位置有关
Rank
1 update to Cholesky factorization
Syntax
R1 =
cholupdate(R,x,'+')
R1 = cholupdate(R,x,'-')
[R1,p]
= cholupdate(R,x,'-')
_________
help cholupdate
19520斑竹我们要更多的插件,看问题太费事了。
发个牢骚楼主海涵啊
19522请教老师:求函数在f(x)=x^2+1在[1,3]上的平均值,这道题的意思是求在1,3区间上积分的平均值吗?我按这个求出得10/3,但答案不对,请问老师应当如何求,我用公式求的。
19522利用积分中值定理
19522老师:我是求平均值,用中值定理能求出来吗?你能不能给做一下给个答案?我用平均值定理求出10/3答案接近,但不对,麻烦你能给求一下结果吗?谢谢了。
19522第二个式子就是几分中值定理。post-8-1129822154.gif
19522谢谢了,这次我做对了。
19522
引用 (FARSEER @ 2005年10月
18日
17时14分) |
|
请教老师:求函数在f(x)=x^2+1在[1,3]上的平均值,这道题的意思是求在1,3区间上积分的平均值吗?我按这个求出得10/3,但答案不对,请问老师应当如何求,我用公式求的。
|
(int((x^2+1)^(-4),x=1..3)/(3-1))^(-1/4)
=2^(1/4)/(-5/64*Pi-
193/1500+5/16*arctan(3))^(1/4)
=3.33…
19522嗯,不错
1953320世纪的第二次世界大战引发的一系列科学和技术的竞争推动了应用数学的极大进展,人们在战后的年代里前所未有地感受到了数学的概念和数学方法的力量。但是,林家翘教授说在中国,应用数学领域的研究还相当欠缺。
数学的重要性不言而喻。纵观近代科学技术的发展,可以看到数学是使科学和技术取得重大进展的一个重要因素,它奠定了现代科学和高技术时代发展的基矗数学的研究分为两个方面,一是充实和扩展这个学科的核心领域,这是纯粹数学的工作;二是解决科学问题,或创造各种提出和解决问题的技巧与方法,这是应用数学以及统计学等的工作。20世纪的第二次世界大战引发的一系列科学和技术的竞争推动了应用数学的极大进展,人们在战后的年代里前所未有地感受到了数学的概念和数学方法的力量。但是,林家翘教授说在中国,应用数学领域的研究还相当欠缺。
林家翘先生认为这一现象存在的原因是,在中国应用数学往往被误认为是实用数学。应用数学是用数学的方式提出科学或工程学中的问题,并将这些问题归结或表示为能够运用计算手段处理的数学问题,这是学术的问题,因而也是科学的问题;而实用数学是用数学的方法帮助解决科学或工程学中的计算问题,这是服务性的,因而是实用的。在中国实用数学之所以被误认为是应用数学,这与新中国建国之初高等学校院系调整有关。当时中国向苏联学习,将所有的人才集中在一起,解决实际的问题,但不一定是学术的问题,因此逐渐远离了大学的主要职责。大学的主要职责应该是教育新的人才,促进学术发展。大学也有义务帮助国家、社会完成急需的工作,可是这不应是大学的主要任务,不应喧宾夺主。比如,美国麻省理工学院的林肯实验室是学院与政府订合同替政府工作的,完全为政府服务,因此它是政府机构,不属于学校本部,学院的教授也有些人在里面做顾问工作,但每周的工作时间大抵不超过一个工作日。
林家翘说,学术性的研究工作与由任务推动的研究工作走的是两条路。学术的研究是为了长期前途的发展,是为未来,而任务推动型研究是为了解决当前的实际问题,满足现在的需要;学术型研究应当向国家自然科学基金委员会申请经费,而实用型研究应当由国家科学和技术部拨款。但是,因为实用型研究项目的经费多,容易产生误导。清华大学当年最大的损失是从全面型大学变为有任务的大学,替政府做具体工作,因此有些该做的研究就被耽误了。做政府的项目,规模大、钱多,但与教学的距离就远了。从历史的观点来看,当初国家正在建设,大家都在做与任务有关的事,与苏联是一样的,大学也得做建国方面的事。但是,现在已经走过了科学建国的阶段,是科学兴国的时候了,清华也要改回去,以学术研究和教学为主。
一个学科要健康地发展,还必须能吸引最聪明的学生到这一领域里来,从事这一学科的研究。林先生说,将实用数学误认为是应用数学,聪明的学生就认为做应用数学研究只是为了帮助其它学科的计算,因此,他就不会选择从事应用数学的研究,对应用数学事业来说这是很大的损失。林先生指出,中国的教育当年学苏联学错了一大步。苏联的模式是专业化太早,苏联的教育可以将工程学分为404门,这种做法是行不通的。专业化太早,学生的适应力就会太差,会做普通发动机的人不会做喷气式发动机。学生们学会了做什么,而不是学懂了做什么。专业分得太细,教师和学生的眼光都会变得太窄,将来只能做旧的东西,不敢做创新的东西,这是很不幸的事。
林先生认为,中国的教育经过了科学救国、科学建国的时期,现在才是科学兴国的时期,这是一个历史性的发展。过去的做法对将来不一定合适,20世纪的科学也与21世纪不一样,因此,必须有所改变。他说他回到清华是为了帮助清华大学走向世界一流大学,发展应用数学也是使中国科技有可能跻身世界一流水平的一条重要通道。
科研中国SciEi.com。
数学被誉为是科学的皇冠,这是人们对它的赞美,也是对它的敬畏。纯数学更是皇冠上的明珠,在普通人的眼中是高处不胜寒。但应用数学家们却走下了圣坛,将数学思想和方法渗透到自然科学、实用科学、工程科学、经济学和社会学等人类生活的各个领域,促进这些学科的进步和发展。林家翘教授一生致力于应用数学的研究和发展,并身体力行积极倡导应用数学学科的发展,被誉为当代应用数学学派的领路人。
2002年,86岁的林家翘教授携夫人回北京清华大学居祝为纪念周培源先生百岁诞辰,在他的建议下清华大学今年8月成立了周培源应用数学研究中心,王大中校长聘请他为中心名誉主任。当记者问及他为什么要在清华建立这个中心时,林家翘教授说:“因为我是清华大学的校友,也是科学家,我要做科学工作。”
谈到他最大的心愿时,他说:“清华当年的理科是有名的,我要帮助清华理学院恢复当年的光辉。”
采访就从应用数学和它的发展开始。
数学思维比数学运算更重要
数学的证明依靠严密的逻辑推理,一经证明就永远正确,所以,数学证明是绝对的。相对而言,科学的证明则依赖于观察、实验数据和理解力,科学理论的证明难以达到数学定理证明所具有的绝对程度,只能提出近似于真理的概念。因此,在思维严密的数学家眼里,物理学、化学、生物学、天文学等自然科学都是经验科学。林家翘先生说,应用数学家要将数学的严密和精确引入经验学科,将这些学科中的实验问题归结或表示为能够用运算手段处理的数学问题,从而促进经验科学的发展。
林家翘向记者介绍:
过去的经验告诉我们,所有的科学问题在本质上都是简单而有序的。物理学所有的定理都可以用数学公式在一张纸上表示出来,而与此同时,人类的智慧又坚持用简单的概念阐明科学的基本问题,这样做,数学就是一个基本的方法。
应用数学是利用数学的方法来发展经验科学的学科。应用数学始于经验性事实,止于对经验性事实进行规律性预测,这些规律还必须被其它的实验数据所证实。同时,用数学理论来发展经验科学往往又会向数学提出深刻的挑战,并对纯数学的研究启示新的方向。科研中国SciEi.com。
近代应用数学发端于英国,牛顿是应用数学的鼻祖。为了解释观察到的大量天体运行的资料,解释天体运行的基本规律(开普勒三大定律),牛顿建立起天体运行的数学模型,提出了划时代的三大力学定律和万有引力定律。但是,力学定律的内涵超越了那个时代传统数学的范围,牛顿不得不开拓新的领域,发明了微积分,然后再用微积分、力学定律和万有引力,求得了行星运行的规律。在19世纪末的英国,所有的理论物理被称为应用数学。我在加州理工学院的博士导师冯·卡门也是一位应用数学的实践者和倡导者,他坚信自然界具有数学的本质,并用他毕生的经历从那些光凭经验无法澄清的混沌领域中寻求数学解答。冯·卡门的导师是德国哥丁根大学应用物理系主任、有“空气动力学之父”称号的普朗特尔教授,他最大的贡献是阐明了飞机为什么会飞。他的一个科学准则是“概括法”,即从一个复杂的物理过程中(无论是机器运行还是河水流动)概括出关键的物理因素,然后再用数学进行分析。
冯·诺伊曼是20世纪最伟大的纯粹数学家和应用数学家,在他发表的150篇论文中,60篇研究的是纯粹数学,60篇研究的是应用数学,包括统计学和博弈论,那篇著名的会客室博弈论文就是他在20岁那年完成的。他和莫根施特恩合作的《博弈论与经济行为》在1944年出版,在这部著作中他们将数学科学的逻辑语言,尤其是集合论与组合数学方法,应用到社会理论的改革过程中,将经济学置于严谨的数学基础上。评论员赫维茨认为:“只要再有10部这样的著作,经济学的未来就有保障了。”学生们将这本书称为“那部《圣经》”。冯·诺伊曼勇敢无畏地走出数学领域,他应用相似的方法解决不同的问题的成功经历,激励着年轻的天才竞相仿效,约翰·福
19538表上作业计算运输问题时,考虑转运费,为什么在表上标记为负?(运筹学教程 第二版 胡运权 p101)
19539是不难,考虑含参变量积分.记原积分为I(a),对a求导,推粗关系式
19539不是很难 啊
19539谢谢post-38-1129646660.ibf
19539请高手提示一下哈
19539是不是要化为二重积分啊
19539然后用先求导再求积分
19539好解法
19539不知道,我原来想交换积分次序,但还是做不出来
19539楼上,你说的求导是对谁求导?
19539请高手把这个问题再讲细点哈
19539怎么没人讲一下啊
19539不好意思,小弟愚苯,这道题按照各位大侠提点还是作不出,我也感觉应该
用求导,但真的去化关系式的时候实在化不出,
肯定高手把此题的解答过程写一下,谢谢
19539记所求积分为I(a),则所求积分可以化成一个微分方程:
I''(a)=a*a*I(a),I(0)=pai/2,I'(0)=0
19539楼上的,I(a)的交换次序二阶导并不收敛,必须乘以收敛因子之后才可求导。
这题我也想了很久了,还是没算出来。
19539magic9901,你还没作完啊,那个常微方程怎么解
19539楼上兄弟够清楚了
195401,找出两个n*n矩阵A,B,使得A和B的特征值全为零,但AB的特征值不全为零。
2,设A是n维线性空间V的线性变换,A的核为A^-1(0),A的值域为AV,举例说明V不一定等于A^-1(0)+AV
19540谢谢
195400 0 0
0 0 1
0 0 0
和
0 0 0
0 0 0
0 1 0
应该可以把
19540第二个可以随便举一个让 AV包含于A^-1(0)就可以了把
19540第二个问题在附件中解答post-38-1130228585.ibf
19541去查查计算机算法方面的书
这是有关算法的问题
19541背包问题,找找讲算法的
19541装箱问题。
有N个不同规格的小箱子,装入一个或多个大箱中,要以怎样的算法才能最优地利用大箱子空间?
查了很多资,只看到模糊概念,但还是不明白。
请说说你的看法。谢谢
19541比较难啊。
19541用状态转移方程 或者用lindo解
19541找任何一本图论的书都应该有吧
19541呵呵,是呀,既然是老难题了应该很多书都有的
19543请问华东理工大学数学系怎么样!!!
19544证明:f(0)=0,f(1)=1,故任给

在0和1之间,存在

在0和1之间,
使得f(

)=

,由Lagrange定理,
f(

)-f(0)=f'(

)

=

f(1)-f(

)=f'(

)(1-

)=1-

取

=a/(a+b)计算得到:
a/f'(

)+b/f'(

)=a+b
19544看看这样做可以吗?
嗯
先设
y=a*x
则
(a-0)/(f(1)-f(0))=a/f'(q1);~~~~~~(1)
再设
y=b*x;
则由
拉格朗日得
(b-0)/(f(1)-f(0))=b/f'(q2);~~~~~~~~~(2)
由
(1)+(2)得
a+b=a/f'(q1)+f'(q2);
19544中值定理的题目post-38-1129660725.ibf
19544这里(0,1)内的两个数是否要求一定不相等?
19544此题还可推广!
见斐礼文的<<数学分析中典型问题与方法>>p149.3.2.12
19544
引用 (magic9901 @ 2005年10月
19日
13时05分) |
证明:f(0)=0,f(1)=1,故任给  在0和1之间,存在 在0和1之间,存在
 在0和1之间,
在0和1之间,
使得f(  )= )=
 ,由Lagrange定理,
,由Lagrange定理,
f(  )-f(0)=f'( )-f(0)=f'(
 ) )
 = =

f(1)-f(
 )=f'(
)=f'(  )(1- )(1-
 )=1- )=1-

取
 =a/(a+b)计算得到:
=a/(a+b)计算得到:
a/f'(  )+b/f'( )+b/f'(
 )=a+b )=a+b
|
但怎么证明那两个分母不为0呢?
19544
由

,

均在0和1之间,即知两个分母都不为0
19545一张试卷6道题,批改全班15个学生的卷子,每道题平均要用30分钟.批改时间呈指数分布,且相互独立.
问1)小等于150分钟改完卷子的概率是多少?2)最可能的值是多少?3)期望值是多少?
(要求用中心极限定理
解)
不好意思,实在没钱,请大侠帮忙!
19545长这么大第一次见到有人问问题还要收钱的?
19545不好意思,是我把功能搞错了,我还以为,是可以给回答问题的分数呢.因为最多只能输入1,闹笑话了.谢谢,提醒我和帮我修改的呼呼,否则我还不知到呢.
19545希望你没抄错题吧。
既然是用中心极限定理,那只要有每道题批改时间这个随机变量的期望值和标准差就行了。对指数分布,两者相等。
故90道题批改时间X可视为N(90*30,90*30^2)分布。
P(X<=150)=P(Z<=(150-2700)/30/sqrt(90))=P(Z<=-8.96)=0
对于正态分布,期望值与最可能值相等,均为90*30=2700。
150与2700相差太大了(9个标准差之多),估计不会这样出题吧。
真不知是否该答这道题。
19545楼主的意思有歧异吧,我的理解是把每道题的改卷时间设为变量X,则
X
i
∼Exp(1
30
),i=1,⋅
⋅ ⋅,90 ,则改完试卷花费的时间是
T n
=∑ i
=1 90
,利用中心极限定理我们知道
T
n
-E(T
n)Var
(T
n)
=T
n
-90×3090
×30
2→N(0,1)
,下面就很简单了,不过这个数据好像是有点问题
19546拜托上传吧 m(_ _)m m(_ _)mm m(_ _)m m(_ _)mm m(_ _)m m(_ _)mm
or
提供连结下载
19546你给我邮件发个你的邮箱,我有,我发给你
yuxianzh@swu.edu.cn
19546coldtown2000@yahoo.com.tw 真的急的用到~~ 大大拜托你了~~ 感恩~~~~ m(_ _)m m(_ _)mm
m(_ _)m m(_ _)mm m(_ _)m m(_ _)mm
19546我也需要,pyghcb@yahoo.com
先谢谢了
19546我邮箱有问题,要的加我QQ21
195807,我传给大家
19546我也需要,grignard@gmail.com
谢谢!
19547不胜感谢!
1: Let G be a multiplicative group, let S be
a subset of G and let H be the subgroup of G generated by S.
gSg-1:={gsg-1| s∈S } and gHg-1:={ghg-1| h∈H }
(a) Prove: H
is normal in G if and only if gsg-1∈H for all s∈S and all
g∈G
(bProve: if S is the union of the finite subgroups of G, then H
is normal in G.
C) Prove: If S is the union of the finite subgroups
of G(other than G itself) of finite index, then H is normal in
G.
(d) Suppose S is the union of the subgroups of G(other than G
itself) of finite index, prove that there exist no subgroups H’ of G such
that H is a proper subset of H’ and H’ is a proper subset of G.
(e)
Prove that |G:H| =|G: gHg-1|, for all g G. (Do not assume that G is
finite).
2.Let G be a multiplicative group, and let X be the set of
nontrivial finite subgroups of G
(a) Prove that G acts on X via
g·H= gHg-1 for all g∈G and all H∈X
(b) Set N= ∩H.( H∈X)
Prove that N is normal in G.
19547use the definitions of nomal subgroup and others
19548请教高手。
19548上传完毕post-61-1129732370.ibf
19548用这个试试,绿色软件,
用它阅读超星读不了的,用超星阅读它读不了的,我还没遇见他们都阅读不了的。post-61-1129732025.ibf
19548好人哪,谢了。
19548太感谢了!!!
19548在下感激不尽
19548只能看。但是打印是一张一张打印的。太麻烦了。怎么办呢?
19548只能看。但是打印是一张一张打印的。太麻烦了。怎么办呢?
19548怪了,我怎么就看不了呢
19548好象用不成吧
19548告我怎么用,不会用啊
19549论数学奥林匹克的教育价值
(转自《光明日报》)
所谓数学奥林匹克的教育价值,即数学奥林匹克教育对人的发展价值。如何认识数学奥林匹克的教育价值,是数学奥林匹克的一个基本理论问题。目前,国内外举办了一系列的数学奥林匹克活动,那么,为什么要举办这些活动?要回答这个问题,有赖于对数学奥林匹克教育价值的认识和理解。
有利于培养青少年数学人才
数学奥林匹克的初始目的就是及时发现和选拔具有优秀数学才能的青少年,并通过适当的方式加以特殊培养,因材施教,促进人才健康的成长。和奥运会不同的是:数学奥林匹克竞赛决不是找出“世界上最优秀的数学家”,而是强调参与精神,希望借以鼓励更多的有数学才能的青少年成长,这是一项十分广泛的群众性活动。有利于培养学生钻研精神由于计算机的出现,数学已不仅是一门科学,还是一种普适性的技术。数学奥林匹克将公平竞争、重在参与的精神引进到青少年的数学学习之中,激发他们的竞争意识,激发他们的上进心荣誉感,特别是近年来我国中学生在数学奥林匹克竞赛中连续获得团体冠军,个人金牌数也名列前茅,消息传来,全国振奋。这对青少年学好数学无疑是极大的鼓舞和鞭策,将激发青少年学习数学的极大兴趣。
数学奥林匹克问题具有挑战性,有利于增强学生的好奇心、好胜心,有利于激发学生学习数学的兴趣,有利于调动学生学习的积极性和主动性。新颖而有创意的数学奥林匹克问题使学生有机会享受沉思的乐趣,经历“山重水复疑无路,柳暗花明又一村”的欢乐,在学生遇到问题困难时,它还帮助他们树立战胜困难的决心,不轻易放弃对问题的解决,鼓励他们坚持下去,这样做可以使学生逐步养成独立钻研的习惯,克服困难的意志和毅力,进而形成锲而不舍的钻研精神和科学态度。
有利于促进学生人性的完善
数学奥林匹克是奥林匹克精神在数学领域的体现,虽然从形式上看是一种智力的竞技活动,但其实质是体现奥林匹克的基本精神,发展人的创造性,最终实现人性的彰显和完善。使人成其为人,这是教育的基本任务,也是数学奥林匹克教学的基本责任。不能否认,数学奥林匹克教育是一种专业的智力教育,然而,数学奥林匹克教育作为一种教育活动不仅仅是要培养某一领域的“专家”,而是首先要促进学生人性的完善。数学奥林匹克教育中促进学生的人性完善的具体体现就是在智力的竞技活动中发展丰富的情感,发展合作、互助、团结意识,锻炼坚忍不拔、敢于挑战、敢于创新的意志和品质。
有利于促进学生创造性的发展
学生的创造性是其完善人性的集中体现,而完善的人性也是学生创造性发展的基础和保障。因而,培养学生以完善人性为基础的创造性,是数学奥林匹克教育的根本任务,通过数学奥林匹克教育促进学生创造性的发展,应该是其全面发展的重要内涵和数学奥林匹克教育价值的集中体现。
在数学奥林匹克教育中促进学生创造性的发展是其教育功能的集中体现。从本质上看,教育是培养人的社会现象。从培养人的角度分析,教育既要满足人的素质性和发展性要求,又要满足人的功能性和社会性要求。这就要求教育将人的全面发展和社会发展有机统一起来。促进人的全面发展从而促进社会的进步也正是教育功能的根本体现,而发展人的创造性不仅能满足人性发展和完善的需要,同时也是社会进步的必然要求。因此,数学奥林匹克教育对学生的创造性的发展,集中体现了教育的个体发展功能和社会性功能。
有利于学生数学能力提高
学生在学习和掌握数学奥林匹克知识方法及其过程中,对发展其数学能力具有的重要的教育作用和意义。数学奥林匹克是智力的竞赛,它的一个重要目的是为了尽早地发现并培养有数学才能的青少年,它考查的学生的研究能力、综合素质和创新精神,每年的题目都是新的,没有考纲,没有界定范围,学生必须具备过硬的基本功和很强的思维能力。因此数学奥林匹克的命题和培训选手的宗旨以数学能力为重点。
有利于中学数学教育的发展
数学奥林匹克有利于中学数学课程内容的改革,数学奥林匹克教育作为较高层次的基础教育,从一定意义上说是某种数学教育试验,是中学数学课程改革的“试验区”。一些现代化的数学知识、思想、方法、技巧,通过奥林匹克数学教育进行“试验”,得以筛选、过滤和简化,逐步普及和传播,再逐渐为中学数学课程调整架设了桥梁。
数学奥林匹克有利于中学数学教师的专业发展,是提高数学教师业务素质的重要途径,是数学教师继续教育的课堂。
数学奥林匹克内容广泛,不仅包含中学数学,还涉及到趣味数学、数学分析、高等代数、初等数论、组合数学、传统的初等数学内容和现代数学的思想方法,这就要求任课教师自身应该达到更高的水平。由于数学奥林匹克中的涉及的题目更新速度快、难度较高,这就要求教师不断搜集国内外最新资料、了解最新动态、研究命题趋势,通过不断自学探索和总结,“教学相长”,教师的自学能力和数学教研能力也就随之提高。
(转自《光明日报》)
19549现在竞赛不被看好了
19549外行人说外行话(虽然八股文写得不错)
19549被一种功利的心玷污!
19550《系统工程理论与实践》期刊被EI收录率连年提高,连续四期达百分之百
转自
中国系统工程学会
中国系统工程学会主办的学术期刊《系统工程理论与实践》2003年被Ei Page
one数据库收录文章
174篇,占全年发表文章总数 299 篇的58%;2004年被收录文章204篇,占全年发表文章总数 285
篇的72%。其中,2004年第11、12期和2005年第1、2期连续四期收录率均为100%。
19551中国数学奇葩“香飘”法兰西――二十载年华付与一本书
中国数学奇葩“香飘”法兰西――二十载年华付与一本书
(转自《光明网》)
在今年上半年出版的新书《红楼梦在法兰西的命运》中,旅法华人女作家郑碧贤讲述了李治华等3人花费27年时间翻译《红楼梦》的故事,译事艰难,令人感叹。
而去年由巴黎DUNOD出版社出版的中法对照本《九章算术》(Les Neuf Chapitres Le classique
mathématiquede la Chine
Ancienne)的翻译,从很多方面来说堪比《红楼梦》的翻译。如果说《红楼梦》是中国古典文学的巅峰之作,那么《九章算术》则是中国古代数学的奠基性著作;《红楼梦》的翻译“吞噬”了3位译者27年生命,《九章算术》的翻译则“耗费”了中、法两位译者20年以上的时光。
“上世纪80年代初我们刚开始准备翻译《九章算术》的时候,K.Chemla(林力娜)还是一个刚从大学毕业的小姑娘,我也年富力强。而书出来的时候,她已步入中年,而我则年逾花甲。”谈起这段经历,郭书春感慨丛生。
1981年4月,法国女子高师数学系毕业生林力娜来中国科学院自然科学史研究所留学,学习中国数学史,郭书春是主要教师。
当时郭书春主攻《九章算术》及刘徽注已经三四年,基本上弄通了其数学内容,解决了前人未解决或未正确解决的许多重大问题,并对它的版本和校勘做了深入研究。《九章算术》及刘徽注是中国古代最重要的数学成就之一,刘徽是中国古代最伟大的数学家,可是,国内外学术界对刘徽知之甚少,李约瑟的《中国科学技术史·数学》谈到刘徽的地方还不如杨辉多,美国权威的《科学家传记大辞典》“刘徽”的释文是一位国际上颇负盛名的中国科学史家写的,实际上是讲的《九章算术》的成就,刘徽本人的成就基本上没有讲。郭书春深感有让国内外认识《九章算术》和刘徽的必要。
郭书春发现林力娜非常聪明,而且通过8个月的学习,她对中国数学史,对《九章算术》及刘徽注有了相当程度的了解。在她结束学习前夕,郭书春建议,在她回国获得博士学位,找到工作后,能够合作翻译《九章算术》及刘徽注。林力娜欣然同意。
林力娜回国后获博士学位并进入法国CNRS(国家科学研究中心)工作。大约同时,他们获悉,中国科学院和法国CNRS有科学交流合作协议,遂分别向中国科学院和法国CNRS提出合作研究翻译《九章算术》的申请,希望纳入两家的科学合作协议。中国科学院国际合作局与法国CNRS协商,于
1983年批准在中国科学院和法国国家科学研究中心科学合作协议中立项。从
1984年6月至
1993年12月,K.Chemla三次来华,郭书春二次去法,共同翻译,互相磋切,几易其稿,不断修改。
“都云译者痴,谁解其中味?”翻译本来就是一件难事,何况翻译的是2000年前的一部科学经典。“早知道这么难,当初也许就不敢着手这件事了。”郭书春说。
自
1774年戴震在《四库全书》馆从《永乐大典》中辑录出《九章算术》并加校勘200余年以来,许多学者都曾投身《九章算术》的研究,戴震、李潢、钱宝琮等大学者做出极大的贡献,但是,由于种种原因,他们都有不同程度的失误,而且错校,特别是对不误的原文因为没有看懂而改错的情况极为严重。经过艰苦的工作,郭书春较好地完成了《九章算术》的版本和校勘工作,于
1990年出版了《汇校〈九章算术〉》。读懂原文的工作也有极大难度,特别是刘徽注非常难懂。上世纪60年代以前的俄、德、日译本《九章算术》都未译刘徽注,就是因为读不太懂。而翻译与写论文不同。写论文,遇到不懂的地方可以略而不论,但翻译则必须对每个字、每句话都得弄懂。经过几年努力,郭书春基本上弄通了刘徽注。准确地译成法文,也是此项工作成败的关键。因为古文与现代汉语差别相当大,与法语差别更大。为了找到准确的表达方式,林力娜付出了十分艰辛的劳动。两位译者边讨论边翻译,修改,再修改,直至找到双方满意的文句。
译事催人老。2004年10月,在自己63岁的时候,郭书春终于等来了洋洋1150页、印制精美的中法对照本《九章算术》的出版。
从法国传来消息说,该书首印约850本,3个月后即告脱销,另外,法国学术界对此书的反响极为热烈。国际学界认为,在《九章算术》英、德、日、俄等多个译本中,法文本的水准堪称一枝独秀。2004年12月31日,法国科学史科学哲学学会会长Jean
Pierre
Kahane院士给我国吴文俊院士来信,建议与吴先生联合发起一个关于中法对照本《九章算术》的研讨会,作为法国文化年的一项活动,吴先生欣然同意。
在7月30日下午由中科院、法国CNRS、法国驻华大使馆主办的,在北京举行的关于此书的一个高规格研讨会上,法国学者不吝溢美之词地赞美了中国2000年前的这部数学著作,并向译者表达了敬意。“两位译者的杰出工作使得西方读者能以可能做到的最好方式接近这部世界数学的杰作”,法国伦理与政治科学院院长Emmanuel
Poulle教授说。他说,以往历史学家认为,十进制、分数等数学思想起源于印度。但《九章算术》表明了,很可能许多思想是来自中国,中国的数学成就也许曾通过丝绸之路影响了阿拉伯地区乃至欧洲的数学。Poulle教授就刘徽注有关算理的证明提出一个课题:证明算理的正确性在世界证明史上起到了什么作用?Poulle教授说,事实上,《九章算术》法文译本的出版向法国乃至整个西方学界提出了许多新的研究课题。“这是送给我们的珍贵礼物”,法国国家科学研究中心特级研究员Sinaceur说。在研讨会上,她向人们介绍了《九章算术》引发的关于数学哲学问题的若干新思考。
1981年11月,《红楼梦》由伽里玛出版社列入法国最负盛名的“七星丛书”中出版后,社会上掀起一股“红楼热”,把对自身文化非常自负的法兰西,着实搅了一下。也许,中法对照本《九章算术》的影响将仅限于学术界,但想想2000多年前的一本数学著作能够激起法国人这么大的热情,仍令人惊异。“中法对照本《九章算术》是中法文化交流和科学合作一个重大成果。”法国驻华公使Nicolas
Chapuis说。
(转自《光明网》)
相关链接
郭书春,男,现为中国科学院自然科学史研究所研究员、党委委员、学术委员会副主任、工会主席,全国数学史学会理事长、博士导师。长期从事中国数学史研究,在《九章算术》的编纂,刘徽《九章算术注》的结构、成就,刘徽的数学体系、逻辑思想渊源、时代背景,以及贾宪、秦九韶、杨辉等的研究方面有突出贡献,发表学术论著300余万字,主编学术著作1000余万字。
19552书上对紧致空间的定义是:如果拓扑空间的的每一个开覆盖
都有一个有限的子覆盖,它就是紧致空间.现在我知道在实数
数集上,有界的闭区间是紧致空间,比如说[a
b],无界的闭区
间 [a

)不是紧致空间,开集(a
b)不是紧致空间,谁能
给我从覆盖的角度讲讲为什么是或不是,尤其是最后一个不能
只说它和实数集同胚,所以不紧,它在哪种情况下找不到有限
子覆盖?谢谢
19552(a-1/n,b)
19552应该是(a+1/n,b)吧? 当n是正整数是,它是(a b)的
一个开覆盖,但是任何一个有限的子覆盖都不能覆盖
(a
b).
但是对于[a b]怎么解释它可以被有限个子集覆盖呢?
19552for [a,b] it can be 'proved'
19552不证自明?
看来我还要修炼100年.
19552你可以看看《数学分析》里的极限论部分的
“有限覆盖定理”(E.Borel预备定理 或
波莱尔预备定理),
那里会告诉你,必须被覆盖的是闭区间(开区间或半开半闭区间都不行)
且用于覆盖的必须是“开区间族”(闭区间族或半开半闭区间族都不行)。
不过那是一维的,但也更形象。
19552这个问题搞清楚了,
谢谢
19553《小波分析及其应用》孙延奎 机械工业出版社出版
2005.3月
个人认为讲的比较浅显,适合初学者。其它的一些教材,我是看得有些模糊的。
19554先发个帖子,以后交流。QQ:41539868。
19555
第三届工程计算流体力学学术研讨会一号通报
1.会议召开时间
经会议组委会反复商议,本次会议最后定于2006年1月5-6日在哈尔滨工业大学召开,请计划与会的各位会员和代表提前安排好各自的日程安排。
2.会议宣传及筹备
在会议筹备工作的第一阶段,会议宣传是我们工作的重点之一。会议组委会已经通过电子邮件、传统信件的形式给国内我们目前能联系到的,计算流体力学界的科研工作者发送征文通知,同时我们还在各大相关的论坛广发征文通知。此外,有关本次会议的各项筹备工作正在紧锣密鼓地进行着,我们将及时通报相关情况,请大家随时关注。清洁能源网/清洁能源网学术会议专版
3.
会议征文情况的通报
截止到10月15日,会议组委会已经收到来自清华大学、中国科学技术大学、浙江大学、西安交通大学、上海交通大学、同济大学、天津大学、东南大学、北京航空航天大学、国防科学技术大学、湖南大学、大连理工大学、中国矿业大学、哈尔滨工程大学、华南理工大学、北京工业大学、华北电力大学、中航第一飞机研究院气动研究室、香港理工大学、北京化工大学、中原工学院、山东科技大学、东北大学、西北工业大学、解放军理工大学、北京建筑工程学院、山东科技大学、西南石油学院、山东建筑工程学院、天津城市建设学院、中南大学、深圳大学、兰州理工大学、长庆油田油气院、中国科学院力学研究所、中国航天空气动力技术研究院、哈尔滨工业大学等近四十家国内各大高校、科研院所和企业的近70篇稿件。
应一些会员及版主的要求,我们将本次会议论文截止日期延至2005年11月15日,请大家抓紧时间,及时投稿。
4.会议特邀嘉宾的通报
(1)陶文铨老师等著名专家将与会指导
考虑到目前从事工程数值计算的同行普遍存在着理论基础薄弱、对计算过程中的基本原理不甚了解等共性问题。应广大会员的要求,我们邀请了一些从事数值计算研究工作的知名学者专家与会,并和各位代表和会员给予指导和交流。尤其令人欣喜的是,陶文铨老师在百忙之中,欣然接受了我们的邀请,并特意调整日程安排来参加本次会议,与代表进行面对面的交流。其它相关专家的邀请工作正在进行中,各位会员也可以积极邀请您熟悉的本领域专家学者与会交流。
(2)各大商用软件公司将派专业工程师与会交流
此外,我们已经与FLUENT,PHOENICS等商用软件公司的高级工程师和技术人员联系,届时各大软件公司也将派出高级工程师参与会议讨论并做专题报告。这也为院校师生、软件公司与企业之间进一步有效的沟通提供了一个宝贵的机会,同时会议还打算邀请一些相关企业单位的技术人员与会,为产学研一体化创造有利的条件。
5.本次研讨会将是一次全新体验的,有焦点、有讨论、有收获的会议
为了使我们的会议更加有效率,我们将充分利用网络的优势,在会议召开前,将有关会议筹备情况、会议交流论文的摘要等信息发布在:清洁能源网/清洁能源网学术会议专版,请与会代表进行初步交流,找出大家共同关心的问题,形成会议的焦点。随后我们将根据代表的意见,有选择地安排专题报告,使大家能够进行更加充分有效的交流,使我们收获能够最大化。我们将集思广益、全力以赴,力争使本次研讨会真正成为一次让全体与会代表满意的会议。
第三届工程计算流体力学研讨会筹委会
主办:清洁能源网、《热能动力工程》杂志社
承办:哈尔滨工业大学燃烧工程研究所
2005年10月
17日
19556当然,也可以是你所了解的。
我先来一个:
西北师范大学,常微分方程——马如云
代数——刘仲奎
兰州大学,
非线形方程——李万同
19556武汉大学的分析:刘培德,胡适耕;函数论:余家荣。
湖北大学代数:刘合国;微分几何:吴传喜。
华中师范大学代数:钱吉林,樊恽。
武汉的我就知道这么多了。
19556上海交大: 周青
19556胡适耕 是 华中科技大学的哦
19557大家好!
请问怎么样用MATLAB求解超越方程的虚根?谢谢!!
19558高级群号码:9401106
群名:数学与物理
共享空间256M,人数上限200
功能:讨论数学或者物理方面内容(限大学以上水平,欢迎相关专业师生及专业人士加入)
目前人数:120
∫ j 0
dV=∫j
i dS
i
19558偶有兴趣。偶本身是物理类的,对数学也比较有兴趣。能保证每周上线两次以上。现在毛遂自荐!大学到现在为止已经自修了数学分析,高等代数,拓扑基础,解析几何,常微分方程,偏微分方程,复分析,特殊函数,概率。
但是做管理员有些什么任务?(以前没有经验)是解题还是怎么的?楼主能否给我一个说明?我QQ:248550244。
19560我有一个函数,形式是 sqrt( C( a+x ) + S( a-x ) )*exp( i*b*x
),要求它在某一区间的里的积分。我觉得不太可能得到解析解(如果哪位高手指点能得到解析解更好!),想用数值解来计算。但是得到的结果却不稳定。请高手指点一下思路!
谢谢!
19562谢谢了,不麻烦了,我算出来了:)
19562m个点均匀分布在一个区域中,区域由n个完全一样
一样的格子组成,问每个格子都不为空的概率。 m>=n
19564求:柯召《数论讲义》的习题解答
哪位有的话,请贴出来共享吧
谢谢!
19564我也需要!
19564我也要,哪位有,麻烦给我也发一份,谢谢
gjy112@yahoo.com.cn
19565Thanks
19565一个不错的英文资料下载地址.网页打开后上边有资料的介绍.你们自己看吧
http://www.math.gatech.edu/~cain/textbooks...nlinebooks.html
19565老兄,值啊!多谢 !!!
19565
19565准备购买,好东西就应该买!!!
195653 x
19565看看
19565是应用数学方面的
19565今天的收获可不少,谢谢了
19565好东西
19565谢谢!我们不是资料少,而是资料太多了
19565
引用 (flyplay1127 @ 2005年10月
19日
12时14分) |
| 出售内容 |
谢谢!!
19565let me check. maybe i 'm interesting
19565谢谢了,已经收藏
19565谢谢
19565看看。什么东西。
19565在哪里,我急需电子数学教材,我 这个鬼佬的地方买不到中文数学书,我 需要实变function
19565怎么我看不见啊?
19565thanx for u share
19565有没有有关脉冲微分方程的书阿?
19565可以,顶!!!!!!
19565不值阿!
19565顶一下先
19565好值啊,谢谢了
195653ks a lot
19565谢谢
19565值啊!多谢
19565强啊
19565哈哈不会把
195653ks
19565我想买,回帖赚点银子
19565THX
楼主辛苦了
19565同感, thanks.
19565
引用 (flyplay1127 @ 2005年10月
19日
12时14分) |
|
楼主地址如下:
http://www.math.gatech.edu/~cain/textbooks...nlinebooks.html
19565
http://www.math.gatech.edu/~cain/textbooks...nlinebooks.html还行,可惜没找到我需要的那本书。
19565不会要分吧!
19565

thx
19565去看看,多谢提供
19565再次感谢楼主,请问楼主是怎么得到这个地方的?
19565thank you
19565thank you!!!!!
19565没有我需要的啊 555555555555555
19565非常感谢!这对我的帮助很大呀!
19565看看
19565很好很好!谢谢!可惜太少了
19565thanks a million.好像不是很多啊
19565多谢了 回用的上的!!
19565thanks
19565好东西
19565感谢分享
19565have a look
19565东西太少呀
19565It is a web page open to public. Just google "math books
online".
19565谢谢
19565看看
19565确实是个不错的资源网站,下面一个网站也有很多不错的数学书籍,希望有用.
http://www.justpasha.org/math/links/books/online.html
19565let me see
19565打不开,郁闷
19565最好把英文网站上的一些关键词汉化,那就效果更佳了.
19565谢谢先
19565有没有运筹方面的,凸分析的啊?
19565sadfaadsfffffffffff
19565感谢啊,很爽
19565看看先
19565谢了
19565太好了,可惜我暂时没有积分。
19565謝謝....已經收了....
雖然暫時對我没什么用.....
但以后一定會有用的
19565也不知道我有没有分,我来买下。
19565


19565thank you very much.
19565看看是否上当
19565xiexie
19565thanks
195653q
19565我要买
19565看看啊!
19565
19565非常丰富的书..太谢谢了..
19565kankan
19565好用,多谢
19565好的.不过也不是很多书.
1956565本,还可以了
19565看看有没有我想要得书
19565GOOD
19565谢谢,朋友
19565希望是还能用
19565kankan
19565资料太多了
---------------------------------------------------
我只等候着爱
要最终把
腰倍好交在他手里。这是我迟误的原因 我对这延误负咎。他们要用法律和规章 来紧紧地约束我;但是
和慈颈椎治疗仪总是躲着他们 因为我只等候着爱 要最终把我交在他手里。
19565真是一个不错的网站,买的值了!
19565Ths。
19565谢谢分享!
19565谢谢
19565非常感谢!
19565看起来还可以
19565好啊
19565kan budong
19565good!thank you
19565想看看
19565速度挺快的,不错,谢谢
19565挺好的,
19565
真的不错!
19565真的很好!
19565ding
19565老兄,为什么我的是找不到服务器?
郁闷咧。。。
19565
引用 (此刻的奇点 @ 2005年11月14日
18时01分) |
| 谢谢了,已经收藏
|
想看看,谢谢喽
19565还可以
19565hao dongdong
19565总算找到了感兴趣的!
19565我是复分析方向的,好象没合适的
19565谢谢了
19565还可以,谢谢喽
19565可以,可以作为参考书。
19565Online Mathematics Textbooks
呵呵。很不错。收藏。
19565准备购买,好东西就应该买
19565
引用 (tybcm @ 2005年11月11日
17时41分) |
| let me check. maybe
i 'm interesting |
语法错误。。
19565好东西,谢谢楼主,非常感谢:)
19565怎么看不见啊哈哈,楼主加油!
19565谢谢
19565a good place to study maths
19565好东西,谢谢楼主,非常感谢:)
19565thank you very much
19565try it
19565确实是好东西
19565谢谢,确实不错
19565打开看看
19565看
19565thank you very much!great!
19565原来是我母校的link啊
19565谢谢了!
19565看看
19565非常非常不错~~
19565想看看
195653xs
19565我也想看看,
19565谢谢
19565xiexiela.....
19565呵呵
19565真想看看
19565Thanks for your sharing.
195679月2日至3日,中央电视台,中央人民广播电台都在用各自的方式纪念抗战胜利60周年。不可不指出:牢记历史,是为了今日的和平。那么,在那段时间中,现代数学在中国的发展是什么样子呢?欢迎大家参与讨论。
在中国进入半殖民地和半封建社会时,谭嗣同说:“变法的急务在‘教育贤才’,求才的第一步在‘兴算学’

$
MathEndBegin-->
Unknown character Unknown
charactercdots
人们了解了算学就能了解其他自然科学”。中国的数学就是本着这个目的去的。
中国第一个高校数学系即北大数学系创办于
1913年,而第二个是南开大学数学系,创立于
1920年。
1931年-
1937年,清华大学数学研究所正式开班招收研究生,陈省身成为在我国本土取得硕士学位的第一个研究生。
1938-
1945年,日本大举侵略中国,中华民族面临生死存亡的抗战时期,中国数学在国外发表的研究论文和博士论文共314篇,是
1931-
1937年总篇数
179篇的1.75倍,在全国自然科学各学科中起了率先作用,创造了历史辉煌。
19568求北大的《数学分析解题指南》林源渠、方企勤,谁有的话上传一下,在此谢过了!!!
19568只见过书,我就有,没见过电子版!!
19568内容也不错 !好象没电子版!
19568我以前见过。在考研论坛里面应该有
19568[EMAIL]
4 方企勤等 北大教材.rar[/EMAIL]
19568你要哪个版本的?
PDG格式的比较小, 推荐用UnicornViewer阅读;
下载:
http://ifile.it/tzkrgv6另外附上PDF格式的...
下载:
http://ifile.it/4dx8c12
19569我准备考要,要报考计算数学,但是不知道谁比较有名。
计算数学的排名大家到能在网上查到,但是大学的导师情况大家就不知道了,
也不知道这所大学到底都有哪些牛人?
最牛的是中科院的那帮人,但是好像都比较老了,在年轻一代有谁牛?
19569年轻的多了,袁雅湘,周爱辉,陈志明,等等
19569考计算就考大连理工么
19569楼主搞错了,中科院计算数学所牛人几乎都是年龄在30多,40多的,没什么老的呀,而且西安交大也有一帮年轻的牛人,基本上都在30多!
19569袁雅湘,周爱辉是我的
学校毕业的~~呵呵
还有许进超也是~~~
还有曹道泯,和周向宇~~~~~~~~~~~都是我学校毕业的~~~~湘潭大学~!!嘿嘿~~!
19569来湘大吧,
19569我想考名校 中山是首选
19569suolou楼二的说得正确
19569电子科技大学黄廷祝教授在矩阵理论特别是H-矩阵方面比较有造诣,而且现在计算数学方面的专业面也较广
19569有博士点的学校里重点专业是计算的有吗
19569考上海大学
19569中南大学向淑晃教授
!
19569
大连理工大学有好多很牛的教授,而且都很负责任,像吴微,于波,王仁宏,罗中玄,苏志勋......欢迎报考大连理工!!!
19569我今年就去大工
19569中山大学这边也不错。。主要是积分方程数值解,小波应用,正反问题。
19569我是大工的,今年开始要读计算数学研究生,大工数学很不错了,欢迎各位到来了。
19569Esmong Ng,Raymong Chan,Shuhuang Xiang are outstanding!!!
19569湖南师范大学 陈传淼教授、谢资清教授 牛
19569中南大学很不错
19569都不错啊
19569院士级别的不是每个人都能考的哦
19569中南大学数学
19569同济的计算数学怎么样啊
19569国内计算数学的科学院院士(数学的不算物理的)也就2个 石钟慈, 林群 都在科学院
19569今年刚考的西工大的。。。
19569中南大学向淑晃教授
19569上海师范大学的郭本瑜,田红炯,丛玉豪教授教授都不错。
19569若选择报考上海师范大学的计算数学可联系我哦。邮箱:yxh27
18@163.com.QQ:63687577
我是上海师大计算数学专业的。
19569读研究生后,我想大家都会发现读研究生并不象想象中的好,牛导师都不理我们这些硕士生,只有那些年轻的没多大资力的老师当我们的导师.所以选学校时要慎重,要看一下在一个学术梯队里的第二第三层次的导师多不多,质量如何,因为只有那些人才有可能当你的导师.
牛的只会带博士,有可能连博士都不带,去带博士后流动站的学生了.
19569jinling_long说的没错,大工的计算数学在国内比较牛,主要是样条函数方向,王仁宏教授应该是国内搞样条的泰斗级人物了,他的学生中很多都是博导啦!
19569计算数学大连理工应该比较牛
19571题:设E是直线上一有界集合,m*E>0,则对任意小于m*E的正数C,恒有E的子集E1,使m*E1=C.
19571duide
可构造一个区间函数利用连续性作
19571
引用 (1305251 @ 2005年10月
19日
14时
19分) |
|
题:设E是直线上一有界集合,m*E>0,则对任意小于m*E的正数C,恒有E的子集E1,使m*E1=C.
|
如果是学数学的,最好还是自己多想想.
这样的题在实变函数当中恐怕算是容易的.
19571
引用 (1305251 @ 2005年10月
19日
14时
19分) |
|
题:设E是直线上一有界集合,m*E>0,则对任意小于m*E的正数C,恒有E的子集E1,使m*E1=C.
|
证明:E有界,故存在区间[-a,a]包含E,令f(x)=m*(E交[-a,x]),检验知道
f(x)是区间[-a,a]上的连续函数,有介值定理即得命题结论。
19571
引用 (1305251 @ 2005年10月
19日
14时
19分) |
|
题:设E是直线上一有界集合,m*E>0,则对任意小于m*E的正数C,恒有E的子集E1,使m*E1=C.
|
你的老师是怎样证明的?你的怀疑在哪儿呢?
19571就是连续函数介值定理的应用嘛.
19571
引用 (mazl @ 2005年10月
19日
22时58分) |
引用 (1305251 @ 2005年10月
19日
14时
19分) | |
题:设E是直线上一有界集合,m*E>0,则对任意小于m*E的正数C,恒有E的子集E1,使m*E1=C.
|
如果是学数学的,最好还是自己多想想.
这样的题在实变函数当中恐怕算是容易的.
|
不怕您笑话,我现在正在学《实变函数与泛函分析基础》。我基础差,老师的水平也不高,所以课本后的一些简单的习题也搞不懂。还希望您以后多多帮助啊!
19572证明:f(x)在E上为可测函数的充要条件是对任意有理数r,集E[f>r]可测。如果E[f=r]可测,问f(x)是否可测?
19572
引用 (1305251 @ 2005年10月
19日
14时33分) |
|
证明:f(x)在E上为可测函数的充要条件是对任意有理数r,集E[f>r]可测。如果E[f=r]可测,问f(x)是否可测?
|
前一问用可测函数的定义即可证明
如果E{f(x)=r}是可测集合,则f(x)不一定可测,反例如下:
设W是[0,1]中的不可测集合,构造函数f(x)为:
x在W中时,f(x)=x;x在[0,1]-W中时,f(x)=-x。
则对任意有理数r,E{f(x)=r}是空集合或者单点集合,是可测集合,
但是f(x)是不可测函数。
19572甚为感谢!!!!!!!!!
19573

如题
19573忘说谢谢拉,哈哈
19573说说有没有就好拉】
给个文献就更好了。
19573肯定是有的啊,如果这个度两是按椭圆上两点的最最短线来定义的话,这满足d(x,x)>=0;
d(x,y)=d(y,x).....的嘛
不过公式可以微分几何的两点的法曲率为0这样来算吧,楼主算好给我说一下吧~
OK,THX~
19573好像不是那么简单吧。我做出来个积分公式,但很不好积,改天发上来,看大家会积吗??
19573我看可以用测地线来算
19574呵呵,最近弄到不少好数学书。但是有几本和以前看的书重复了。现在拿来卖啦!书目如下(都是绝版的老书):复旦
1960年版本的<数学物理方程>,(美)F.W.拜仑
R.W.富勒的《物理学中的数学方法(第一卷)》,E.C.温特切勒的《概率论》,56年交流讲义的北大的《复变函数论》。M.R.SPIEGEL
的《高等数学的理论与习题》,艾利斯哥尔兹的《微分方程》,方企勤的《多元函数微积分 》,苏步青的《微分几何 》,R.柯朗 F.约翰
的《微积分和数学分析引论(第二卷.第一分册)》,H.H.勃立瓦洛夫
1956年版本的《解析几何学》,王联
王慕秋的《常微分方程定性理论及稳定性理论基础(上.下)》。C.GOFFMAN 史济怀等译 的《多元微积分》。刘绍学
的《环与代数》。B.N.斯米尔诺夫著,叶彦谦译的《高等数学教程》第三卷的前两册,IN.史奈登的《富利叶变换》
有需要的朋友跟我联系一下吧。我用E-MALE很少,直接在BOSSH上发我消息或者跟贴就是。以上书籍正文大多很好,不影响学习。要想找参照的,去图书馆看看就行。价格都在20以下。最好能一次性多买几本。我在武汉上学,最好同城交易,一本一本卖太麻烦啦。交换也行。其他的好商量。我QQ:248550244,欢迎有兴趣的朋友问询和交流!
19574唯一例外的是 IN.史奈登的《富利叶变换》的这本可能比较贵,不只20,要30。有兴趣的朋友联系我吧
19574要是不是一个地方的话。那最好你能多挑几本书。我再先邮寄给你,你看到了书再付款不就可以啦。反正大家都是学生,没有必要象商场那样斤斤计较的。信誉可以保证的。我还是有些没有列在帖子的书可以转让或者交换,有兴趣的朋友QQ联系我就是。
19574你一般再哪里买到这些旧书哟,如果不是一个地方的,怎么买,汇款邮寄行吗,信誉怎么保证
19574呵呵。谢啦!
19574我是西南师大的余显志,老朋友了,再顶你的贴
19574好样的!
19574不在同城交易比较麻烦
19574仁兄够黑. 这些书只要多留意旧书摊就可买到嘛.我前几天还得了好几套不同的书呢.还是全套的.
19574这些书我又没有说都高价?有兴趣的再联系不就是了.挑旧书是要运气的.有的你可能10快钱弄到了.我就要30才弄得到.地域,时间都成了价格起伏不定的因素.很多经典的好书,就算再贵也不可能弄到,象哈尔莫斯的<测度论>之类就是这样.
19574就是,老兄,在顶你,我给你QQ留言了
19574搂主的信誉绝对信得过!请大家放心!他在购书方面还是很有一套的!
19574
| 引用 (renzhazero @ 2005年11月01日
21时24分) |
|
这些书我又没有说都高价?有兴趣的再联系不就是了.挑旧书是要运气的.有的你可能10快钱弄到了.我就要30才弄得到.地域,时间都成了价格起伏不定的因素.很多经典的好书,就算再贵也不可能弄到,象哈尔莫斯的<测度论>之类就是这样.
|
今天鼓捣了半天,终于把哈尔莫斯的《测度论》(中文版)给打印出来了。
先重新安排页的顺序,然后用Acrobat
将两页打印到一页。A4纸对开,效果很不错。
19574<多元微积分> C.GOFFMAN 著 史济怀 彭家贵 何琛 李世雄 徐森林 龚升等译 人民教育出版社
1978年9月第一版
定价0.55元 10元出售 32开本
190页
书号 13012.0235
第一章 欧氏空间
第二章
映射及其微分
第三章 实映射
第四章 映射的主要定理
第五章 流形 微分形式
第六章 向量分析
<微分方程>艾利斯哥尔兹著 南开大学数学系编译中队译 崔士英校 人民教育出版社出版
1959年5月第一版 32开本
292页 书号13012.0116 定价0.90元
10元出售
北京五环地区免费送货
内容
一阶微分方程,高阶微分方程,微分方程组,稳定性理论,带偏差变元的微分方程,一阶偏微分方程
联系电话:13146421515
QQ:85024026
19574多谢大哥!
19575请教各位大虾:怎样将cetx 文档转化成word?菜鸟谢谢各位了.
19576概率论中有些地方是比较难以理解,譬如说对小弟来说,就概率这个概念小弟就花了三年时
间才算弄了个明白,开始接触这个东西的时候的那个难啊,哎,还是不说了,免得各位笑话^_^
大家都是学习概率的,相信在学习理解的过程中多少会有些难以理解的地方,但是最终你还
是理解了,这个过程对于你宝贵,对于其他人同样宝贵,大家不妨来说说吧,也算是一种交流
吧!
可以先说哪个地方对你来说难以理解,后来是怎么理解的,然后再给点启示,以供网友
学习之用.
19577大家有考北师大的硕士吗?今年考试改革了。大家都是怎么复习的呢?考的多了是不是难度降低了呢?
对于复变,概率,方程这三门合卷,大家是怎么看的???
多多交流啊!
19577我也考北师,基数,复习中……
改革又是机会又是挑战!
复变,常微,概率统计当作期末考试那般复习罢。(我还没开统计,要自学,小郁闷。)
19577我也是考基础数学
19577我也考呀
19577我看还是不要太大意了!去年北大的综合就不简单。
19577我把握不好复习的度。
考的多是不是就简单点呢?
怎么把握那三门的度?搞的太难了时间来不及了。大家有谁来谈谈概率,复变,方程的复习方法。谢谢了。
19577不好说啊!我看以前的北师的复试卷子常微,复变概率统计都小有难度啊!
好好复习,我觉得复习多了可能会分英语政治的时间啊。如果英语政治卡线了那就不好了。
19577您有北师复试概率和复变及常微的题吗?有的话能给我分享下吗?谢谢您
19577是些90年代的题,考到北师的学长给寄回来的。
净是些手抄版,不好上传啊。
19577时间紧的话就把基础复习好吧,这是最岂码的了。
19578本人在自考数学教育本科,
有人说这个专业太难了,,,我没什么其他的爱好,
还是报了这个.
看了数分,发现真的是太难了,书后面的题目几乎都不会做!
我以前是工科的大专生,只学过高数...
问怎么才能学好数分,做为数学专业最基础的科目,我想是必须学好的.
实数的连续性定理需要会证明和应用吗?
关于做题你有什么好的办法吗,,,尤其是证明题..
先谢了....
19578我说点建议,仅供参考:
理科的特点就是没人愿意读,所以难嘛,只要你有兴趣,加努力,学好不成问题。
高数跟数分差不多,就是多了一章分析基础,讲实数系定理,建议这一章无论如何要
啃下来,最少把所有证明全看懂。这样就有一个基础,加上你学过高数,剩下的拿下来不成问题。做题没什么好方法,多做一点,并思考。
19578
.
19578你这个人有点浮躁,说句实话数学还是很有意思的,不然的话不会有哪多人学习数学
并且很多人还称了家,数分根高数的为区别是数分的很多问题是要用力论证名的,
话说到这,数分如何学就很明了了
要加强理论的完善,即,要有自己的一个体系,你要明白的体系是有很多种的,
要做的只是由小到大不断的完善
耐下心来,坚持一段时间,你会有收获的。
19578学过高数就已经很有底了啊!实数理论那一张最好看懂它吧!!真的是有帮助的,关于证明,你先要吃透书里证明的方法,一些技巧还是要学的,多做点题,,应该可以学好的
19578考数学自考,说明你很有勇气,剩下的就是要沉下心去读、去做、去理解!
19578学好极限理论,理解透彻,就没有什么难度了
这是我从高二开始自学大学数学形成的经验!
19578个人认为,
定义理解透彻最重要。这可能需要一定的时间,不理解可以先放一放,过一周再看你会有惊奇的发现;-)
当然还有所有的定理都应该会证明!
19578对于大学数学系的学生来说,数学分析的重要性是不言而喻的,数学分析的理论基础是实数的极限理论,它的研究对象是函数(特别是连续函数),研究的基本问题是函数的连续性、可微性,可积性。
195781.如果基础不扎实,有必要做机密多维奇习题集
2.对于实数基础定理的证明,我在初学时掌握得不熟练,但后来学了实变函数,复变函 数.
泛函分析后,这些问题就很清楚了
3.对考试来说,作基本的题就行了
4.强烈推荐《微积分学教程》本人是在大四时读的,受益匪浅,里面讲得很细,内容丰富,论坛有下载
19578我也在自学数分,不知哪儿有菲哥的微积分教程下载
19578多思考,刚开始不会做不要急,看看别人做的,或参考书作的难题,经过一定的积累,某一天你会突然间分析的精华,切记,最主要的是要多思考!!!还要做题
19578菲哥的《微积分教程》或者《数学分析教程》的确是好书,但是,比较冗长。如果不是专业学的话,我建议还是看看教科书,我看过复旦大学陈传璋的书和陈纪修的书。前者简洁,后者通俗。我觉得都适合自学和初学者的。另外听说华师大的书也很好,不过一直没有机会看看。
19578自学的话强烈建议用师范类的教材,不要注重数学技巧,理解好基本概念。另外刚开始不能求全,把每一科的主线抓住了再考虑细节。
19578
| 引用 (princens @ 2005年10月20日
16时35分) |
巧的很,我也在自考数学!我是退学来自考的,以前的学校我学工科.学的很郁闷,于是退学了哦.现在想结识学数学的朋友,你是自考吗,我很想结识你啊!我的email是world
1948@sohu.com,qq
358644427. |
也是自学基础数学的,希望认识一些精研基础数学的朋友.网上见吧!
post-21-1134
196260.ibf
19578
| 引用 (magic9901 @ 2005年11月24日
10时46分) |
|
对于大学数学系的学生来说,数学分析的重要性是不言而喻的,数学分析的理论基础是实数的极限理论,它的研究对象是函数(特别是连续函数),研究的基本问题是函数的连续性、可微性,可积性。
|
十分敬佩magic9910的见解,愿请教以下问题:
用柯西收敛原理直接推出康托一致连续定理.
这是本人近期来一直未解决的问题.
19578其实,单单是极限,其问题就已经有非常的多了!数学的确是很难的,她的思维比起哲学来并不逊色.
19579谁能推荐一些关于最优化的国外的比较好的教材?
19579难道国外不学最优化吗..............
19582南大数学系有专业课辅导班吗,最近听说南大对本校生开了一门叫数分高代后续课程的课,是不是真的啊,请知情的告诉我一下,谢谢
19582辅导班应该没有,教育部禁止了。
19582有数分高代的选讲课么?
19582应该有的
19582南大好像是由一个
19582大家确定有吗,知情的战友给个确定的答案吧
19582禁止不了的
上有政策下有对策啊
是吧
19583我想问问关于我们在大学中所学习的《高等数学》和应用数学专业的学生所学习的数学,在内容上是否相差极大?
我想研究计算机编程的算法,在数学方面应该学到什么哪种程度才好呢?
还有就是在论坛上看到大哥哥们所说的“神经网络”是研究什么的?计算机上应用得到吗?
学生在这里谢过了。
19583数学分析和高数还是有一些差别,高数不讲一致收敛的相关的问题.
19583学一些数值计算方面的课程,离散数学等很重要
19583神经网罗是优化算法的一种,和遗传算法一样,是一种仿生学算法.
如果你要具体到编程,我觉得你学数学分析和离散数学比较好.
19583是有些差别的。。
19584我们知道,极限是在考察一个序列的变化趋势,那么对于一个抽象的集合序列来说,它的极限也应该是表示这个集列的变化趋势吧!我想问的是,集列极限考察的是这个集合序列的哪种变化趋势!!
从上极限与下极限的定义来看,上极限与下极限似乎在考察一个集合序列中各集合的公共元素构成的集合的变化趋势;另外,从上确界和下确界的定义来看,好象也是这么回事.但是我还是不能确定.
哪位大哥对这个问题了解的透彻些的,请千万帮忙指点指点小弟!!1
19584上极限是所有出现过无穷多次元素的集合
排除所有只出现过有穷多次的元素的集合
上下极限集里的元素虽然都是出现无穷多次的,但是上极限里的元素不用从某个集合开始连续出现,而下极限的元素必然从某个集合开始连续出现
19584
| 引用 (zhglwl @ 2005年10月20日
12时00分) |
抽象集合序列的极限定义是从数列极限中转移过来的。数列的极限我们都很清楚:
若数列单调,那么极限存在。但一般的数列只能定义上下极限,即:a
_{n} 可以不单调,
但sup _{n  k}单调递减,存在下确界,有数列上极限的定义,知 杠overline{lim}a _{n} =inf _{k
k}单调递减,存在下确界,有数列上极限的定义,知 杠overline{lim}a _{n} =inf _{k  1}sup _{n 1}sup _{n
 k}a
_{n}.对集合来讲,同样可以如此定义。把上面的a _{n}换为A _{n} ,先构造单调的集列。 k}a
_{n}.对集合来讲,同样可以如此定义。把上面的a _{n}换为A _{n} ,先构造单调的集列。
|
我明白抽象集列的极限是从我们常见的数列的极限中抽象出来的.正是因为这点,我在比较
两者的时候才发现抽象集列的极限不太好理解,对于单调集列来说,极限还是非常好理解的
但是对于任意给定的集列的上下极限,理解起来就不那么容易了,兄弟你要是真想帮我,能不
能把你的理解用WORD写出来,做成附件贴在这里,让小弟我好好体会体会.我看你发的帖子
正是我想知道的,而且你理解的思路也正是我在理解之中的,但是用这个论坛里的工具非常
不方便.拜托了!!
19584
引用 (子青 @ 2005年10月
19日
18时56分) |
上极限是所有出现过无穷多次元素的集合
排除所有只出现过有穷多次的元素的集合
上下极限集里的元素虽然都是出现无穷多次的,但是上极限里的元素不用从某个集合开始连续出现,而下极限的元素必然从某个集合开始连续出现
|
谢谢子青兄先!
也就是说对于集列{A1,A2,A3,A4,...An....}来说,该集列的上极限指的是这样一个集合,它
的元素是{A1,A2,A3,A4,...An....}中无穷个但是不知道具体是哪些的Ai的公共元素?
而集列的下极限指的是这样一个集合,它的元素是除去{A1,A2,A3,A4,...An....}中的有穷
个但是不知道具体是哪几个的其他的Ai的公共元素?
另外,对于"上下极限集里的元素虽然都是出现无穷多次的,但是上极限里的元素不用从某
个集合开始连续出现,而下极限的元素必然从某个集合开始连续出现"中的"从某个集合开
始连续出现"是什么意思?能不能帮我说的更具体点?
19584抽象集合序列的极限定义是从数列极限中转移过来的。数列的极限我们都很清楚:
若数列单调,那么极限存在。但一般的数列只能定义上下极限,即:a
_{n} 可以不单调,
但sup _{n

k}单调递减,存在下确界,有数列上极限的定义,知 杠overline{lim}a _{n} =inf _{k

1}sup _{n

k}a
_{n}.对集合来讲,同样可以如此定义。把上面的a _{n}换为A _{n} ,先构造单调的集列。
19584抽象集合序列的极限定义是从数列极限中转移过来的。数列的极限我们都很清楚:
若数列单调,那么极限存在。但一般的数列只能定义上下极限,即:$a
_{n}$ 可以不单调,
但$sup _{n

k}$单调递减,存在下确界,有数列上极限的定义,知 $杠overline{lim}a _{n}$ =$inf
_{k

1}sup _{n

k}a
_{n}$.对集合来讲,同样可以如此定义。把上面的$a _{n}$换为$A _{n}$
,先构造单调的集列。
19584抽象集合序列的极限定义是从数列极限中转移过来的。数列的极限我们都很清楚:
若数列单调,那么极限存在。但一般的数列只能定义上下极限,即:
a _{n} 可以不单调,
但
sup _{n

k}单调递减,存在下确界,有数列上极限的定义,知 杠 overline{lim}a _{n} =inf _{k

1}sup _{n

k}a
_{n}.对集合来讲,同样可以如此定义。把上面的 a _{n}换为 A
_{n} ,先构造单调的集列。
不好意思第一次发不会用公式。
19584
| 引用 (978301 @ 2005年10月20日
16时46分) |
| 引用 (zhglwl @ 2005年10月20日
12时00分) |
抽象集合序列的极限定义是从数列极限中转移过来的。数列的极限我们都很清楚:
若数列单调,那么极限存在。但一般的数列只能定义上下极限,即:a
_{n} 可以不单调,
但sup _{n  k}单调递减,存在下确界,有数列上极限的定义,知 杠overline{lim}a _{n} =inf _{k
k}单调递减,存在下确界,有数列上极限的定义,知 杠overline{lim}a _{n} =inf _{k  1}sup _{n 1}sup _{n
 k}a
_{n}.对集合来讲,同样可以如此定义。把上面的a _{n}换为A _{n} ,先构造单调的集列。 k}a
_{n}.对集合来讲,同样可以如此定义。把上面的a _{n}换为A _{n} ,先构造单调的集列。
|
我明白抽象集列的极限是从我们常见的数列的极限中抽象出来的.正是因为这点,我在比较
两者的时候才发现抽象集列的极限不太好理解,对于单调集列来说,极限还是非常好理解的
但是对于任意给定的集列的上下极限,理解起来就不那么容易了,兄弟你要是真想帮我,能不
能把你的理解用WORD写出来,做成附件贴在这里,让小弟我好好体会体会.我看你发的帖子
正是我想知道的,而且你理解的思路也正是我在理解之中的,但是用这个论坛里的工具非常
不方便.拜托了!!
|
论坛支持latex,请看论坛帮助
19584
引用 (子青 @ 2005年10月
19日
18时56分) |
上极限是所有出现过无穷多次元素的集合
排除所有只出现过有穷多次的元素的集合
上下极限集里的元素虽然都是出现无穷多次的,但是上极限里的元素不用从某个集合开始连续出现,而下极限的元素必然从某个集合开始连续出现
|
对这个问题,我终于理解明白了.非常感谢子青兄!
19586急急急,有GAMS的使用高手请与我联系,有问题请教,可以是有偿的。
19587设某批量很大的产品的次品率为p=0.01,今从中任取100件,求取得的次品数至少为
3的概率.
19587令
ξ
i =1 当一次取得产品为次品;
ξ i
=0 当一次取得产品为正品。如果记
n =∑ i
=1 100
ξ i
, 则n为100次试验后次品的总数,即我们要求
P
(n≥3)=1-P(n=0)-P(n=1)-P(n=2)=1-0.99
100-0.99
99×0.01-0.99
98×0.01
2
19588非常好贴!
19588怎么下不了了啊?!
19588???????????打不开!!!!!!!!!
19588202。113。29。16
可以下载(速度很快),也可以在线观看
另外,美河学习在线(www.emihe.com)上也有一些数学视频
19588怎么进不去?
19588什么地址啊
19588
http://www.eimhe.com/index.php现在是进不去!!!
19588废的,打不开
19588是这个地址
http://202.113.29.16/
19588楼上的同志:你给的那个我能打开页面,能看到下载页面,可就是下载不了……速度趋向于零的……
19588进去也打不开。
19589
各位师兄师姐们;
你们好!
我是数学专业的本科生,现在大三了,准备考研,但现在还不知该考数学专业哪方面的,我个人比较心细,喜欢搞统计和金融方面的,但计算数学这方面优势挺大的(小时候专门从事过奥林匹克培训)
又挺羡慕中科院的老院士们,想步他们的后尘,所以现在最想考中科院数学与系统科学研究所,但数学这几个方向还没确定到底该选哪个好?
敢问各位师兄师姐,在研究生期间数学这些方向主要是上课还是只搞研究,主要都干些什么?我想到研究生时多学一些能跟实际联系较多的,而不是纯研究的。希望各位师兄师姐能给我这小弟出出主意,指点指点,小弟在这谢谢了!
一个真挚想得到师兄师姐指点的人
19590我是初学者,请教大家一下,请问在Matlab软件中如何做morlet小波变换
19590我也想要,楼上的,到时一起交流呀
19591谢谢!
19591看看吧!post-73-1129724500.jpg
19591学习指导书!post-73-1129724702.ibf
19591来源于华东师范大学精品课程网!post-73-1129724622.ibf
19591ding
19591又要分的,就不能免费吗?
19591谢谢!
19591重复下载了,不好意思啊。
19591直接进入华东师范大学数学系就能下载啊
19591能打印下来吗?或者有书卖吗
19591哎!!!直接进入华东师范大学数学系就能下载啊 !!
19591华师大的我已下载装订好了。谢谢
19591
引用 (cjchxshh @ 2005年11月
18日
19时11分) |
|
哎!!!直接进入华东师范大学数学系就能下载啊 !! |
哎!!!直接进入华东师范大学数学系就能下载啊 !!
19591可怜呀,这个我早下过了,又下了一次!有没有第二版的呀?
19591这个世道,什么都要钱!!!!
19591good
19591太好了.我正找这本书.
谢谢斑竹.
19591这种书有什么意义?
19591多谢
19591good
19591俺刚来,没钱买,遗憾。
19591春节期间,访问http://2
18.249.29.200/bookhtm/index.asp成功,偶狂下了4。31G数学书籍,运气还真不错哦。
19591答案?
19591谢谢
19591[COLOR=blue]好遗憾!新来的我没有钱……
好东东,没钱买呀…………
19591好东东,原来我也可以购买……
正好,这学期我要教这门课程,太谢谢了……
期待更好的…………
19591太贵了,没钱买!
19591 楼主,你的高尚情操太让人感动了.在现在这样一个物欲横流的金钱社会里,竟然还能见到楼主这样的性情中人,无疑是我这辈子最大的幸运.让我深深感受到了人性的伟大.楼主的帖子,就好比黑暗中刺裂夜空的闪电,又好比撕开乌云的阳光,一瞬间就让我如饮甘露,让我明白了永恒的真理在这个世界上是真实存在着的.只有楼主这样具备广阔胸怀和完整知识体系的人,才能作为这真理的惟一引言者.看了楼主的帖子,我陷入了严肃的思考中.我认为,如果不把楼主的帖子顶上去,就是对真理的一种背叛,就是对谬论的极大妥协.因此,我决定义无返顾地顶了
19591很好.顶.
19591有没有高教的第二版的啊?
就是 王高雄,周之铭,朱思铭,王寿松 编的
19591我正在学习!感谢了!
19591感谢了!我正在学习!
19591谢谢斑竹
19591我想要
19591不是王高雄的答案
19591谢谢分享!
19591好书啊
19591真实好东西呀!
19591不必要答案,有时候答案把人的头脑变懒!
19591直接进入华东师范大学数学系就能下载啊
19591这不是王高雄的
19591不错,好书
19591可是我没有分啊,好可怜
19591这可是货真价实的东东哦,每天一个哦post-73-1144391
181.ibf
19591打不开啊,能不能打包上传呢,这样就可以多传些。
19591真是的,我又不能下载了,5555555555555555555555
19591好东东,谢谢
19591谢谢了!好东西大家要一起分享哦!呵呵
19591谢谢
19591非常感谢阿!
19591haodongdong,希望多发点!
19591谢谢
19591谢谢啊,好东东
19591good
19591好东西 谢谢
19591谢谢,我正需要。
19591是高教出的吗
19591thank you!
19591还是看看再说吧
19591谢谢
19591这个世道,什么都要钱!!!!
19591好好啊
19591新来的 没钱啊 怎么办啊??
19591怎么打不开啊?
19591这种东西要免费啊
19591支持!!!
19591我们学的是中山大学版的微分方程,这个没有用呀
19591我也正想找王高雄的常微分方程答案呢!
不知道哪里买!
附图的那本书是答案书么?
可不可以把作者的名字告诉我呢?
我还想找丁同仁和李承治编写的常微分方程答案书!
可不可以帮个忙阿?
谢谢啦!
19591shenshidao
19591看一看,好不好
19591不是第二版的
19591谢谢大家!
19591顶!!!!
19591有不要钱的
19591为什么我有的帖子不能回复呀 是我的积分太低了吗??
19591下了。多年前学德,在此谢过
19591不错
谢谢了
19591王高雄的《常微分方程》不必看了,水平一般。各位应当看丁同仁的《常微分方程教程》,虽然难一点,但是胜其十倍。
19591谢谢楼主,终于找到了
19591谢谢
19591xiexie
19591good
19591谢谢!!!!!!!!!!!!!!!!!!!!!!
19591国内的基础教材大部分是低水平重复出版,内容千篇一律,稍微深一点的可谓是凤毛麟角,没有几本可以称颂的。国内自诩为牛人的不少,可就是写不出一本牛书。
19591有没有 王高雄编写的《常微分方程》电子版啊?
19591一本很浅的书,有什么好看的,都是废品
19591thanks
19591
引用 (pbka @ 2006年12月03日
18时21分) |
|
王高雄的《常微分方程》不必看了,水平一般。各位应当看丁同仁的《常微分方程教程》,虽然难一点,但是胜其十倍。
|
yes
19591好东西 谢谢楼主!
19591真的不错,谢谢!
19591谢谢提供 只是不方便看 呵呵
19591Thank you very much!!!
19591好东西,谢谢楼主。。。
19591王高雄版早期版本字迹模糊,非常难看。不知新版如何?
19591我下了,谢谢楼主,顶一下。
19591好像不是王高雄《常微分方程》,这是华东师范大学林武忠编写《常微分方程》的精品课程!不过也不错!我曾经在华师大下过!还是收藏了一次!
19594各位高手:
大家好
本人大学学的是计算机,对数学研究不深,但是工作5年后,在实际工作中想做相关数学模型方面的研究,这里哪位高手愿意帮忙,我不胜感激。我对数学建模知之甚少。
我的邮箱地址:sierra_2000@sina.com
我的QQ:14243462
不胜感激
19595
The QR algorithm for unitary Hessenberg matrices
WB Gragg
- J. Comput. Appl. Math,
1986 - portal.acm.org
... Pages: 1 - 8. Year
of Publication:
1986. ISSN:0377-0427. Author, WB Gragg,
Publisher,
我的e-mail:gsfjs6567@sohu.com
19595?不明白
19596若以变换的最小多项式不能完全化为一次因式的积,它是否一定不相似于上三角形???
另外,是否有变换可化为若当形当且仅当相似于上三角形/???
19596一定不相似于若当型矩阵。
19598一子空间V1含V2正交补非零元素的充要条件????
感觉很平凡,不知怎么答合适
19598不知道这个命题的目的是什么,冲要条件应该就是那个什么向量正交的定义来确定吧!
如果V1中存在某个向量与V2的某个基正交,那么就可以了!
1960011月5-7日,北京师范大学-图书馆。
信息科学交叉研究学术研讨会邀请函
**同志:由北京师范大学主办,上海系统科学研究院和西安交通大学协办的“信息科学交叉研究学术研讨会”,将于2005年11月5-7日在北京师范大学召开。经评议,您撰写的“***”等论文已被大会录用。现特发此函,邀请您参加大会并做大会发言。现将有关事宜通知如下:
1.大会报告。凡向大会投稿并且稿件被录用的撰稿者,每位请准备20分钟的大会报告,各人报告之后将会有不超过10分钟的代表提问。会议提供计算机和投影仪,但不提供胶片幻灯机。报告中需要计算机和投影仪的与会者只需携带U盘,或者软盘。
2.报到注册。外地代表请于11月4日之前到京。从首都机场进京的代表,请乘坐机场大巴至北太平庄,向南400米进入北师大;从北京站进京的代表,请乘坐公交车到“前门站”换乘22路、或726路、或826路到“铁狮子坟站”下车;从北京西站进京的代表,请乘坐47路到“铁狮子坟站”下车;北京本地的与会代表,乘相关线路的公交车至北太平庄站、或铁狮子坟站下车,或乘出租车从师大东门直接入校。外地代表请于11月4日全天或5日上午8:30之前在北京师范大学图书馆报到与注册,本地代表请于11月5日上午8:30在北京师范大学图书馆报到与注册。
3.需要住宿的代表,请提前与会务组联系。
4.返程票务。需要返程票的代表,请回函至大会秘书处,并在回函中注明您欲乘坐的从北京起始的回程飞机班次或火车车次,以及需要到达的终点站。
需要住宿和返程票的与会者,请在10月15日前函告大会会务组。
联
系 人:糜 凯
通讯地址:北京师范大学管理学院“信息科学交叉研究学术研讨会”会务组(100875)
电
话:010-58809911
传
真:010-58800733
电子信箱:huiwu@lib.bnu.edu.cn
信息科学交叉研究学术研讨会筹备组
19601我是排队论方向的硕士,想问一下考博可以选择什么方向?
19601我有二个师弟考的是交通
你老板是谁啊
19601我是江苏大学的,你是哪个学校的?
19601
| 引用 (crazy_pc02 @ 2006年06月04日
21时35分) |
| 我是江苏大学的,你是哪个学校的? |
你是朱老师的学生吧?考中科院的张的博士呀。

19601呵呵,我是朱老师的学生。
我想换个专业,想请教换什么专业比较好?
19602哈发post-38-1129735947.ibf
19602关于第一问,可以用反证法来处理,如果结论不成立,则容易推出条件的不可以分解是不成立的,于是就得到了解决!
关于第二问可以结合第一问,容易知道,对于任何基e1,e2,...en;如果设V1=L(e1,e2,....,e(n-1)),则容易知道A(V1)和V1不存在包含关系,然而对应的像空间也可以由这个基来表示,所以对应的像空间的维数不可能是n维的,而如果是小于n-1维的呢?容易知道,当小于n-1维的时候会出现对应的最小多项式是可以分解的,所以就只有是n-1维了,而A(V1)与V1是等维数的,所以再利用这个特点转化到矩阵的东西,利用相似变换,实际上在几何空间里,可以适当的选择非奇异变换来变换选择的基,让新的基下对应的矩阵是对角阵,然后去完善,就应该可以解决了!
不好意思,没有办法把具体的过程写出来!毕竟是网吧里的电脑,不是我自己的电脑!
19602呵呵,多谢了
19602to 蓝戈:
你好,按照你的思路,我证明出了第一个问,但感觉自己证的不是太令人信服.
另外,第二问,我怎么思路觉得与解决第二问的关系不大.
方便的话,能不能把具体过程贴出来呀
19602有点复杂
19603努力啊post-38-1129736308.ibf
19603n为奇数不可约
19603请问要用到什么什么定理
19603能把过程写一下吗?
19603不要沉了,顶一下
19603用反证法,结合多项式在ai的值可证。
19604努力吧post-38-1129737
173.ibf
19604用迹做
19604用迹做,反证假设存在,这时左边的迹等于零而右边的迹等于n,矛盾。
19605努力啊post-38-1129737612.ibf
19605用许耳瓦茨不等式.
19605太难拉 啊
19605看看这样可以吗?post-38-1129904373.gif
19606
19题,设f(x)为连续函数,且
∫ 0
π
f(xsinx)sinxdx=1
, 则
∫ 0
π
f(xsinx)cosxdx=
, A,0,B,1,C,-1,D,
π .
此题的条件不够.
19607这是导数与极限相结合的题目,见附件,请各位高手帮帮忙,谢谢!post-8-11297684
17.ibf
19607先取对数,再用罗毕达法则,两题答案如下:
1.exp(f'(a)/f(a))
2.exp(2)
19607已明白,谢谢magic9901.
19608Z/p2Z=<1>
|
<p>
|
<p2
>={0}
那么它的子群是<1>, <p> ,<p2
>吗?
还有一个问题,对称群S6中的元素最大的阶是多少?我觉得应该是6,不知道对不对。
请各位大侠赐教!
19609请问各位大侠,谁有Morlet小波变换的源程序,提供一下,谢谢了
19610问题在附件中,各位大哥帮忙指点指点小弟!!post-
17-1129770493.ibf
19610
| 引用 (978301 @ 2005年10月20日
09时08分) |
|
问题在附件中,各位大哥帮忙指点指点小弟!! |
各位大哥,小弟对这个问题很糊涂,希望各位能帮帮小弟!!
19610 ε
ij 是测量误差
τ
i 是每个产品生产出来以后与理论设计量的误差
所以我们关系的是每个产品的真值,所以关心的是 u
+τ i
而不关心测量误差
ε ij
这个问题只属于ANOVA ,还没有进入实验设计的范畴
19610
引用 (子青 @ 2005年10月20日
18时54分) |
ε
ij 是测量误差
τ
i 是每个产品生产出来以后与理论设计量的误差
所以我们关系的是每个产品的真值,所以关心的是 u
+τ i
而不关心测量误差
ε ij
这个问题只属于ANOVA ,还没有进入实验设计的范畴
|
子青兄的意思是说,因为最后那个

因为是随机误差,所以就不与考虑?这个原因
似乎没有太大的说服力!能不能解释清楚一点?谢谢先!!
19610
引用 (子青 @ 2005年10月20日
18时54分) |
ε
ij 是测量误差
τ
i 是每个产品生产出来以后与理论设计量的误差
所以我们关系的是每个产品的真值,所以关心的是 u
+τ i
而不关心测量误差
ε ij
这个问题只属于ANOVA ,还没有进入实验设计的范畴
|
也就是说,每次实验的真实值是有三个部分组成的,可是为什么在做参数估计的时候只估计
两个部分?
19610因为设计产品的时候有一个理论值u, 理论上每个生产出来的产品都应该是这个理论值u,但是实际生产中由于生产误差,
生产出来的产品是这个理论值加上一个误差tao,所以每个产品的真值是u+tao,
现在我们测量每个产品,在每个产品的真值上再加一个测量误差eps,才是测量值,我们关心的是产品的真值,所以是u+tao.tao就是非抽样误差,
eps是抽样误差
19610
| 引用 (子青 @ 2005年10月21日
11时58分) |
| 因为设计产品的时候有一个理论值u,
理论上每个生产出来的产品都应该是这个理论值u,但是实际生产中由于生产误差,
生产出来的产品是这个理论值加上一个误差tao,所以每个产品的真值是u+tao,
现在我们测量每个产品,在每个产品的真值上再加一个测量误差eps,才是测量值,我们关心的是产品的真值,所以是u+tao.tao就是非抽样误差,
eps是抽样误差 |
子青兄,对这个问题,我今天复习体会的时候发现了一点,不知道答案对还是不对:
事实上,对这种统计模型做参数估计,的确是要考虑那个误差项,因为每次的数据都是由三
部分构成的,所以一定要考虑三项作为它的估计才可以,只不过由于最后的那个误差项很特
殊,它是一个以0为均值的正态分布,对这个项做估计的时候只要估计出它的方差就可以了,
所以在做最小二乘估计的时候只需要考虑两个就可以了.
你说呢??
19610不是这么理解的,是我的那个解释
19610
引用 (子青 @ 2005年10月21日
19时
19分) |
| 不是这么理解的,是我的那个解释
|
谢谢,也许你的是对的,但是我还需要仔细考虑.
19615我在作硬件滤波器设计研究中,需要分解一种特定的高次方程。算法已经作出,但无法保证收敛性,具体情况和要求见附件。post-23-112977
1968.ibf
196
17希望高手给小弟一点建议
有程序最好了
感激不尽
196
18大学学的心理学,学过一些数学和统计
但现在想去搞金融,
不知道数学要学些什么东西,基本上没什么数学基础
如果自学的话应该学些什么东西(高等数学?线性代数?概率论?)
如何自学?
例如:高数能不能用蔡高厅的视频来学习
各位先谢了
196
18我是金融专业的,是新生,概率论和线性代数肯定要学的
我想要专门搞金融,概率论和线性代数必须学的很好很精
要是加上一定的计算机操作能力(对数学模型程序应用)就好了
196
18谢谢了
推荐一两本教材啊
196
18既然学心理学的,建议你去搞behavioral finance去吧,别费劲追人家asset pricing了,对你来说弯路太多
196
18楼上的朋友,behavioral finance
应该译为“行为金融学”吧。上网查了查,有些不太清楚,能不能简单介绍一下啊?
例如:数学要学些什么?就业方向?
196
18楼主还是改个适当的专业,这个对你来说已经很难了,金融对数学要求是很高的,不是如上面几为仁兄说学好概率就可以的,学的数学知识多了去了而且会很深,建议选修数学系的相关课程
196
18我爱金融数学!!!
196
18楼主还是改个适当的专业,这个对你来说已经很难了,金融对数学要求是很高的,不是如上面几为仁兄说学好概率就可以的,学的数学知识多了去了而且会很深,建议选修数学系的相关课程
196
18同意楼上的观点。
196
18没有必要,我是数学系的所以我才学的,你没的数学基础,很难学好的,除非你是华罗庚
196
18随机过程对金融数学很重要.
196
18我刚开始学金融数学,主要是期权定价和Black-Schole方程的,
我们现在开课程是偏微分方程,偏微分方程数值解,本科阶段学的期权定价;
但其实对基础课程,如泛函分析,实变函数,随机过程等的要求都挺高的。
196
19问题如下:见附件00005post-21-1129777944.ibf
196
19用Abel判别法证明该瑕积分收敛即可。并且sin1+cos1-1>0.
18
196
19
| 引用 (superyyzg @ 2005年10月20日
16时56分) |
用Abel判别法证明该瑕积分收敛即可。并且sin1+cos1-1>0.
18
|
能写写更详细一点的解体过程吗?
19620我03年毕业于一所师范学院,个人的智商好象也不怎么高,大学时候也没好好学。毕业了以来,一直在做初中教师。专业上就只记得数分和高代的一些基本概念了。还好英语不怎么烂。我27了,以前觉得读书没什么用,看惯了世态炎凉之后,还是觉得读书好。每天可以看书的时候也就晚上6点到11点,加上周末;
我在杭州地区的一个中学教书,我父母就我一个孩子,他们特保守的,而且家境也很一般,我不敢辞职了去考研;书买了不少,但是有点无从下手的感觉,而且年纪也不小了,还是孤身一人,压力不小。
请教各位,如何才能知道自己是不是有继续读下去的潜力?因为我大学时候没用心读过,不知道自己行不行
19620如果你准备今年考研,我想准备的时候可能不够.
如果你真的想考研,准备一年,从现在开始,考明年的研究生.
如果下定决心了,放下工作,拉开与恋人的距离(如果你没有结婚的话),并希望她体谅.
全身心的头入进去,从数分,高代开始看,了解相关信息,一定会成功的.
同时也要考虑机会成本,根据你自己的情况看看这样是不是值得.
19620的确要想好,现在研究生去高中的很多,考上研究生不读博的话处境很尴尬的。
以后情况可能还要不好。
如果你现在生活不如意的话考考也没什么,想学,年龄绝对不是问题。
19620事在人为嘛
我们支持你。
19620现在在职考研的很多,考研不就是为了找个好工作嘛!
保住这个工作,然后再考研。
以后会很有前途的。
19620以前读书的时候以为教书是很有创新的工作,以为自己会喜欢这个工作。而且我读的学校学风也不好,我自制力不够,也就跟着混了4年。现在才觉得生活的无奈。要说工作,其实也许在各位看来已经不错了,年收入也不算太少。只是实在从心里不喜欢了。放下工作不管似乎不大可能,不管怎么样,我还是会有时间就看数学。结婚这个词对我来说比较奢侈了。在杭州这个地方,读过大学的女孩子一般比较重视钱,象我们学数学的不会有多少钱。
谢谢各位指点
19621路过
19621著名数学家谷超豪先生
来源:国际在线 时间:2005-10-08 09:23:34
--------------------------------------------------------------------------------
在线收听
听众朋友,欢迎收听《龙的传人》节目。听众朋友,前不久,著名数学家谷超豪先生刚刚度过80华诞,今天的节目中,我们将带您一起走进数学家谷超豪先生的生活。
听众朋友,谷超豪先生是中国著名数学家,复旦大学教授,中国科学院院士。在2002年的世界数学家大会上,世界数学联盟主席帕利斯在开幕词中谈到,中国数学之树是由若干位中国数学家培育起来的。在他提到的数学家中,长期在国内工作,尚健在的数学家有两位,一位是吴文俊,一位是谷超豪。
谷超豪先生
1926年出生,浙江温州人。他从小对数学感兴趣,小学三年级学除法,谷超豪被除法中的现象迷住了:1被3除,那就是0.3333……一直循环下去,除不尽,但是可以用循环小数表示。这让他觉得,数学里面有非常神奇的东西,你抓不住它但可以想象。到了六年级的时候,算术上的应用问题是很难的,例如鸡兔同笼,童子分桃等等。这些问题列一个式子解决是不太容易的,当时有些升学指导一类的书就针对各类问题写出了解题公式,好多同学就背公式,应付考试。但是谷超豪感觉到,数学不应该是背公式,应该动脑子找到更好的方法。当时谷超豪的哥哥在读初中,他抽屉里面有中学的代数教科书,谷超豪就把代数教科书拿出来看,觉得书上的知识并不难懂,设一个未知数X,用这个X把那些算术问题列作方程式,很方便就解出来了。这件事让他非常高兴,在课堂上还跟老师讲了,老师很是赞赏。
又有一次,数学老师出了一道题,说一个四边形,每边边长都是1,问面积是不是1?许多同学都肯定地回答是1,谷超豪说不是。因为,四边形每边都是1,你可以把它压扁,变成一条线,这样面积就差不多没有了,所以面积不一定是1,可以是1,也可以比1小很多。
老师对谷超豪的想法特别欣赏。当时,谷超豪还不知道菱形面积的公式,而是从形状的变化来说明这个问题的。但这种求新求变的思维方式却在他浙江大学毕业后多年的研究中真正显现出来。上世纪末,法国科学院的一位院士,把谷超豪数学成果的风格概括为“优雅、独特、深入、多变”。谷超豪最初跟随苏步青先生从事微分几何的研究,
1957年9月,31岁的谷超豪来到了莫斯科大学,开始了变换拟群的研究。
1959年7月,谷超豪综合了多项成果,完成了题为《李-嘉当变换拟群的通性及其对微分几何的应用》的学位论文,被认为是继大数学家艾里·嘉当之后,第一个在无限变换拟群理论方面取得重要进展的人。通过了答辩,跨越“副博士”这一等级,直接被授予物理-数学科学博士学位。第二年,苏联人造卫星上天,正在莫斯科留学的谷超豪同时进入了偏微分方程这块国内数学的薄弱领域。他参加了莫斯科大学校长彼得洛夫斯基院士的偏微分方程讨论班,并听了流体力学的相关课程。在莫斯科的两年是谷超豪辉煌学术之路的重要开始。
听众朋友,您正在收听的是龙的传人节目今天的节目中,我们为您介绍的是数学家谷超豪先生。
谷超豪在浙江大学求学时,有幸师从中国微分几何的领衔人物苏步青。同时他还向著名的前辈数学家陈建功学复变函数,又选修了物理系的量子力学、相对论和理论物理等课程。这样的经历,为他以后在数学研究中的传承与超越奠定了基础。
苏步青先生不止一次地讲:“我的学生超过我了。”又说:“谷超豪只有一点没有超过老师,就是没有培养出像谷超豪似的学生来。”谷超豪却认为:“我觉得我在好多地方不如苏先生,苏先生的这句话--我培养出超出我的学生了,你要培养出超出你的学生--他这是在将我的军,要我好好培养学生。”
1957年至今,谷超豪培养了近40名研究生,其中2人已成为中科院院士;在他教过的本科生中,还有3名中科院院士,3名工程院院士。谷超豪总是把自己已取得突破的重要成果立即告诉学生,指
19621充满快乐的数学人生,令人敬佩!
19621谷先生倡导返璞归真的数学思想,我辈应坚持下去。
19623我本科是读信息与计算科学专业的,学过的数学课程有:数学分析,线形代数,概率论与数理统计,离散数学,计算方法,常微风方程及数值解(含有限元)。
感觉和数学系的相比,有些数学课程没学,学得也比较浅,读计算数学研究生之前想补修一下数学课程,为今后研究生阶段的学习做好充分的准备,但不知道还要修哪些,请指点,不胜感激。
另外,计算数学研究生阶段,要修哪些课程,请高手帮忙指点,3q!
19623先学一门编程语言. FORTRAN 或者C,
19623这要看你选的什么方向,如果选图形学方面的话,要学的数学太多了
19623C语言学过的,我选的导师是搞有限元和微分方程数值解的。
19623
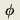
19623泛函分析最重要~
19623
引用 (jihas @ 2005年12月11日
19时53分) |
| 泛函分析最重要~
|
多谢指点,能推荐一些泛涵方面好的教材或资料吗?
19623Yosida 泛函分析,几十年经典
19623吉田的书是不是深了点。
19623数值逼近、数值分析
19623多了,数值分析是分为三本书的:《数值逼近》,《数值线性代数》,《微分方程数值解法》。学一种语言:FORTRAN
会好点儿——我学的是VC,结果最近发现程序的精度总是达不到理论的效果,还得知道一些存储方面的知识,就得看看《数据结构》了!!当然,微分方程的知识不能少了,也有的叫《数学物理方程》,在循环迭代是常会用到矩阵,也得了解矩阵论的知识了。为了理论分析,实函泛函是少不了的!!总之这个专业想学好会很累,不过没事慢慢来,还有博士,读本科时老师就说,学这个的不读博就浪费了!
19623数值分析那本教材较好?
19623易大义的 数值分析 不错
19623数学分析,空间解析几何,高等代数,矩阵论
复变分析,常微分方程,运筹学,离散数学,
组合数学,抽象代数,一般拓扑,概率论,物理,随机过程
数理统计,实变函数,微分几何,金融数学,西方经济学,证券投资,
时间序列分析入门,广义函数论,模论,实分析
傅立叶分析,泛函分析,计算机辅助几何造型,分形
数值代数,数值逼近,偏微分方程,偏微分方程数值解
c,c++,matlab,数据结构,opengl,java,mathmatical科学计算软件,Scheme,
以上是我本科阶段学的,有些学的不精,9月份研一,计算数学。
19624我做的过程中有些问题,希望能给个 详细的解答
谢谢!post-38-1129790422.gif
19624容易证明rank(Ak)=k
19624能不能详细些!
19624拜托了,帮解答一下
谢谢
19624期待解答中
19624等了好几天了....不知道自己的盲点在哪里?
有谁可以帮解答?谢谢!
19624其实不存在你说的那样的情况,主要是因为最大线性无关向量组存在有限的最大的值
对于你的这个题目可以常识分析一下,A1,A2,A3,。。。的秩会越来越大,而它的最大就是n,你问的如果存在无限的话,就会使得某个之后出现A(n)=A(n+1),假设存在这样的情况,你可以去利用这个去推理,看有什么性质,往往会出现矛盾!
这个题目我没有去认真的做,你就按照反证法来处理这个题目吧,然后当问题获得了解决之后,也许你就会问为什么你想的那个情况不存在,而至于这个就可以结合AX=0的解空间和A的秩的关系来思考和理解,应该就可以了吧!
我现在是没有自己的电脑,我就无法给你个具体的思考和具体的解答了,不好意思!
关于你发给我的短信息,我感到困惑,如果你有什么问题就直接发到我的信箱里去吧!我会至少给你个思路,在我的能力范围内!
我的信箱有两个zhiping_zhao@tom.com,或者iloveyanyi@163.com
我的上网时间又到了,我该下了!
希望我说的对你有点帮助!
19624这是汕头大学2004年的考题,以前曾经讨论过,请到前面去找。
19624这是汕头大学2004年的高等代数考题之一,关于它的解答可看我给出的答案post-38-1130242156.ibf
19625各位大虾,请问哪里有STATISTICA 6.0下载,很需要!
19625兄弟,不知道你找到STATICSTIC没有.
我也需要这个哦.
如果你找到了的话,
可不可以给我一个?
QQ31648058
19625我也要
QQ:30674
1815
注明博士论坛就行了
19627好书!post-24-1129794121.ibf
19627书全吗,谢谢搂住了
19627全,但是是DOC格式的
19627老兄,你的书不全ok?
doc版的我至今还没发现一本是全的!
19627谢谢
19627xiexieluuzhu
19627xiexieluuzhu
19628能给我一份吗?十分感谢啊。我在自学微积分。谢谢
我的邮件:sunlei3448@yahoo.com.cn
19628
| 引用 (zsy7758 @ 2005年11月26日
15时30分) |
|
有他的<<数学分析原理>>电子版的,要吗?? |
哪位朋友有《数学分析原理》电子版的?发一份给我可以吗?在此先感谢!!!我的邮箱是:hong2990@163.com
19628谁有简体的〈微积分学教程〉电子版啊,菲赫金戈尔茨写的那套
我下载的都是繁体的,看的痛苦死了
19628能把你下载的电子版本发份给我吗,太感谢了
yuxianzh@swu.edu.cn
或者QQ21
195807传给我
交个朋友
19628这是一套老书,那个年代哪来的简体字版哦,后来又没有再版过,你也太不了解历史了。
19628这点功底应该有才对哦.
19628阿,给我发本吧,我正在自学微积分。谢谢你
sxczdfz@163.com
19628我也要 给我发本
willinechen@yahoo.com
谢谢
19628有他的<<数学分析原理>>电子版的,要吗??
返回顶部
博士数学论坛版权所有,转载请注明出处 MATH.ORG.CN 2004-2009













